1. Introduction
Geo-hazards and structural damage caused by coal mining have attracted much attention in research over the past few years. Surface subsidence prediction methods are essential for accurate assessment and mitigation by decision-makers. Traditionally, modeling mining-induced subsidence behavior requires repeated monitoring of subsidence data [
1,
2]. The monitoring methods may include measurements obtained by using total station instruments, automatic levels, Global Navigation Satellite Systems (GNSS), and/or terrestrial laser scanners (TLS). These methods establish monitoring stations along the main plane of a deformation basin and then measure the observed subsidence rate over various periods. These approaches exhibit shortcomings such as low spatial resolution, high cost, low efficiency, and high labor intensity, besides also being a life-threatening activity [
3,
4]. In the specific case of China’s Loess Plateau, the practical applications of the traditional approaches for modeling mining subsidence are dramatically limited due to the difficulty in establishing these observation lines. The ravines and gullies of the Loess Plateau make establishing monitoring stations highly inconvenient.
Over the past 20 years, interferometric synthetic aperture radar (InSAR) technology has emerged as a viable subject for research on this topic. A wealth of commercial InSAR data is now widely available to the research community. Instead of relying on limited discrete observational data, continuous surface deformation information can be collected using radar interferograms. Specifically, InSAR has a unique advantage in its ability to offer researchers wide coverage, high spatial resolutions, and almost all-weather-independent reliability at low cost. Differential InSAR (DInSAR) technology was developed in 1989 [
5] for monitoring slight ground deformation along the line-of-sight (LOS) of the satellite. Since then, other applications have used this approach, including the monitoring of landslides [
6,
7], mining subsidence [
8], urban water-loss settlement [
9,
10,
11], volcanic activities [
12,
13], glacial shift [
14,
15], earthquake deformation [
16,
17,
18], and dam stability [
19,
20,
21,
22]. Due to the benefits mentioned, DInSAR has emerged as a particularly efficient medium for surveying the subsidence that occurs in coal mines [
23]. However, DInSAR technology’s monitoring gradients may present crucial limitation in mining subsidence analysis. This limitation occurs more specifically when a massive deformation occurs in a short time. As a consequence, a decorrelation may appear in the interferogram generated.
Moreover, it is difficult to remove phase errors, including atmospheric delay and topography-residual error, when using the traditional DInSAR. A least-squares (LS) database approach was presented in [
24] for SAR interferometric data, in which the subsidence velocity of persistent scatter is computed via LS estimation. As a result, the shortcomings of DInSAR were successfully overcome, and accurate subsidence data were achieved. After that, small baseline subset differential interferometric synthetic aperture radar (SBAS-InSAR) technology was developed from the traditional DInSAR technology. Berardino et al. [
25] proposed the small baseline subset algorithm, which is based on the least-squares model. The SBAS-InSAR method was successfully used in [
26] in the South Wales coalfield. Crosetto et al. provided a review about DInSAR-PS in 2016, demonstrated that it has ability of measuring mill-metric displacements [
27]. Wasowski and Bovenga assessed the quality of the DInSAR products in 2014; they found that a precision of a few millimeters and 1 mm/year can be achieved by SBAS-InSAR method under the best conditions [
28].
From the above, the advantage of DInSAR is very high accuracy measured from space. This is a highly advanced geodetic tool to observe ground surface changes; it can tell us what happened accurately. But further, we want to know what will happen in future. So, a prediction algorithm combined with DInSAR data needs to be found; and geological and geo-engineering interpretation of these research data is conducive to evaluating geo-hazards and preventing structural damage caused by future underground activities. A few scholars have proposed several methods to predict mining-induced subsidence based on InSAR technology in recent years [
29,
30,
31]. For instance, the InSAR subsidence value was obtained in [
8] and used as the input variable to invert the main parameters of the probability integral method (PIM) in order to predict subsidence in deep coal mines. A model was built using the InSAR technique and elastic–plastic algorithm in [
32] to monitor the Crandall Canyon Mine (Utah) collapse. The PIM model was directly coupled in [
33] with InSAR-derived LOS deformation, inverting most parameters. However, in these studies, some of the parameters of the prediction algorithm were back-calculated from DInSAR, and the remaining parameters were empirical parameters for the given coal mine. Hou et al. [
34] proposed superposition models with rheology and the PIM model to analyze subsidence in the mining area of a thick loose layer. Other scholars have applied other modeling techniques of mining subsidence, such as the time function of Knothe, and the influence function. However, these models have no extensive universality or suitability in general coal mining environments.
In practice, accurate geology data associated with mines are helpful in studying deformation mechanisms. Nevertheless, due to the fragile geological conditions and perilous operation environment, it is difficult for engineers to monitor conditions under the ground in mines. The deformation data obtained on the ground seem to be the only available data. Through analyzing existing data, deducing new unknown data by traditional physical statistical models is meaningful work [
35]. Deng et al. [
36] demonstrated a wonderful piece of work combining a statistical model and DInSAR data, which predicted the future land subsidence by analyzing existing data. However, they presented a Grey–Markov model as the prediction model, which needs long time-series data sequences following a smooth curve, or otherwise it tends to produce errors. Unlike statistical models, support vector machine (SVM) regression models have the ability to describe the pattern of a system’s evolution with only a limited amount of data. The model has fewer constraints on the data; it can solve small sample learning problems better, and the SVM parameters can be determined by a gird search algorithm more efficiently. Thus, an SVM regression model is suitable for predicting mining-related subsidence.
In this paper, we propose a novel approach that combines InSAR-derived deformation with an SVM regression algorithm optimized by grid search (abbreviated as GS-SVR) for predicting mining-related subsidence. We considered the consecutive DInSAR subsidence values from the Dafosi coal mine area (NO.40301 working panel) as an input variable to invert the GS-SVR parameters and predict mining-induced surface subsidence. The rest of this paper is organized as follows:
Section 2 describes the area of interest.
Section 3 presents the materials and methods adopted in this study.
Section 4 and
Section 5 present and discuss the results obtained in the experiments. Finally,
Section 6 presents the main conclusions and points out future directions.
2. Study Site
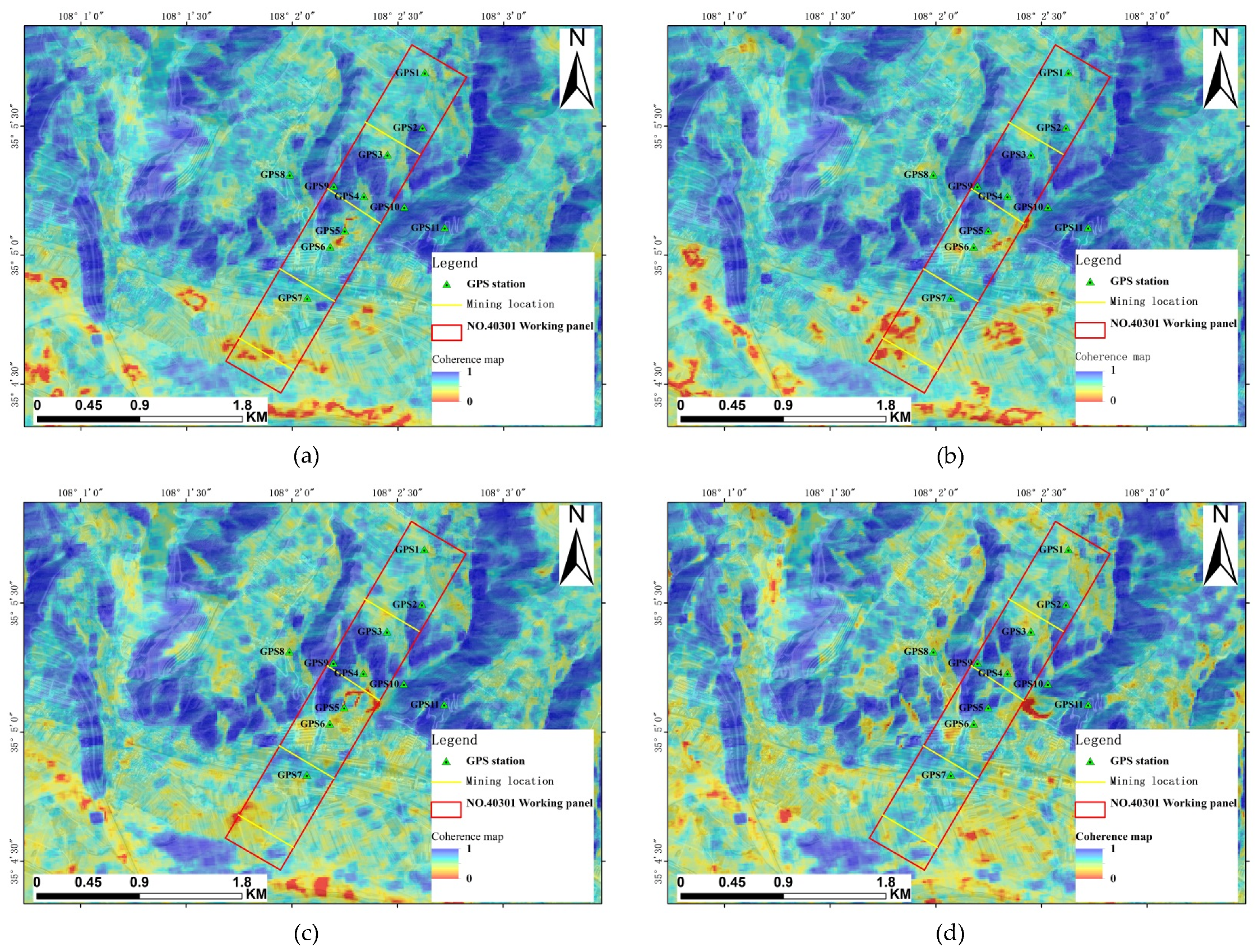
The NO.40301 working panel of Dafosi coal mine is located between the Binxian and Changwu counties in Shaanxi province, China. It is one coal mine of the Binchang coalfield, which is the national plan coal mining base. Mine geological structure is simple, consists of a series of folds (NE-NEE), rare faults; coal seam is thick and gentle. It is located in the Weibei fold area which belongs to the Ordos basin in Northwestern China. The geomorphological features are broken gullies and loose soil in the Loess Plateau; the terrain is high in the northwest and low in the southeast at an altitude of 900–1200. The Jinghe river, which is located in the south of the working panel, runs from the northwest to the southeast. The types of land cover over the coal mine include agricultural lands 72%, construction lands 8%, and other lands 20%. Among agricultural lands, 55% are arable lands, 38% are grasslands, 5% are forest lands, and 2% are others. Among construction lands, 93% are urban and rural construction lands, 6% are transportation and water conservancy, and 1% are others. Among other lands, 17% are water, and 93% are bare land and wasteland. There is a national highway, a national road and a railway running through the coal mine. Binxian city is located in the southeast of the coal. Consequently, the subsidence induced by mining would threaten the safety of this infrastructure. The area in which this coal mine is located has a typical continental monsoon climate; the mean annual precipitation is 561.3 mm, and the mean annual temperature is 11.1 degrees centigrade. The soil is classified as loessial, including the gully and plateau landforms. The vegetation coverage is low and the vegetation type is monotonous; the dominant species are warm sparse shrub grasses.
Dafosi coal mine is located in the Loess Plateau tableland of the Wei-He river beam and gully region, and the topography slopes down toward the middle valley from the Loess Tableland. There are 6.729 billion tons of coal reserves in Dafosi coal mine, and it has a total mine production capacity of 5 million tons per year. The direction of the NO.40301 working panel is from north to south, and it was begun in July 2007. The red rectangle shown in
Figure 1 presents the mining location of this working panel. The mining activity adopted was long wall mining on the strike and comprehensively mechanized coal mining. The average mining depth was 680 m and the coal seam thickness was 2.1–2.5 m. The mining location from July 2007 to January 2008 is shown in
Figure 1. The mining direction, known as the strike-line, was from northeast to southwest. The dip-line is the direction perpendicular to the strike-line. Dafosi coal mine suffered from a large area of mining subsidence and ground damage. Some houses were destroyed; some walls suffered cracks over 10 cm. Caved steps collapsed over 30 cm in the farmland. Cracks larger than 10 cm appeared on the highway pavement.
3. Materials and Methods
3.1. SAR Data Description
In this paper, we took the NO.40301 working panel of the Dafosi mine area as an example, choosing five Advanced Land Observing Satellite (ALOS)/Phased Array type L-band Synthetic Aperture Radar (PALSAR) images with high resolution mode. The Japanese Earth-observation satellite ALOS, developed by Japan Aerospace Exploration Agency (JAXA), was launched on 24 January 2006 and lost on 22 April 2011. PALSAR is an SAR system that was on board the ALOS satellite and has advanced functions and performance. It has the advantage of imaging the Earth day and night and ignoring atmospheric weather conditions. PALSAR has a high-resolution mode in which it can scan wide swaths of 35–70 km.
In order to reduce the influence of time, the time interval of interference was selected so as to be as small as possible. Therefore, five L-band (23.6 cm) ALOS/PALSAR scenes acquired from 4 July 2007 to 4 January 2008 were used in the experiment. These signals were assembled using a radar look angle of 34.3° along the ascending orbits; the ground resolution of the original Single-Look-Complex (SLC) images is 13.36 m in the range and 3.17 m in azimuth. Radar sensors can transmit horizontal (H) or vertical (V) electric field vectors and receive horizontal (H) or vertical (V), or both, as return signals. HH (transmit-horizontal and receive-horizontal) polarization means that signals are transmitted and received in horizontal; and it is good for receiving the maximum signal intensity. The basic parameters of the ALOS/PALSAR images are shown in
Table 1.
3.2. GPS Data Description and Signal Processing
There were 11 GPS stations above the working panel (see in
Figure 1)—6 stations in the strike-line, 4 stations in the dip-line, and 1 station in the cross—providing measurements between 4 July 2007 and 4 January 2008. The GPS results were used to test the accuracy of the predicted results.
The GPS data were collected using Chinese Southsurvey GPS receivers in real-time kinematic (RTK) mode. One receiver was installed at the base station, located on a stable surface; others monitored displacements at the GPS stations. The horizontal and vertical accuracy of the GPS receiver are mm and mm (where D is the distance), respectively.
GPS-RTK was measured three times from 4 July 2007 to 4 January 2008. The first time, a GPS receiver with a tripod was installed on the reference station which was located at the stable surface. The antenna height was measured, the receiver was opened, and then the reference station height, antenna height, and WGS84 coordinate were recorded. We then turned on the radio and checked then channel. We then opened the roving station GPS receiver with centering rod, input the exact parameters, and checked the radio channel and the number of satellites. The reference station and roving station GPS receiver make simultaneous observations. A roving station GPS receiver was used to measure the 11 GPS stations’ coordinates and heights. Data were obtained at the sampling rate of 20 Hz; the observation time was more than 180 s. The second time, the 11 GPS stations were measured again in the same way after 115 days. The third time, the 11 GPS stations were measured in the same way after 230 days. The deformation value was calculated by the difference value of these three times.
It should be emphasized that quality control measurements were performed every time. The method of comparison with quickly static measurement was used to verify the reliability of the RTK results. At least 3 points were selected as the check points every time; the observation time of quickly static measurement is more than 600 s. After data processing, the maximum error between quickly static measurement and RTK was less than 2 cm in height. The RTK measurements of 11 GPS stations are listed in
Table 2.
3.3. Consecutive DInSAR
DInSAR technology is based on wave interference. It uses two microwave images obtained from satellites flying over the same area twice (repeat track mode). The technology then processes these two images, produces interference fringes, and produces an image reflecting the change in phase. This image is called an interferogram. Ideally, the real phase value of each point can be calculated from the unwrapped interferogram; and then the height can be calculated. According to the theory of DInSAR technology, the composition of the interferogram phase can be expressed as follows:
where
expresses the unwrapping phase of the interferogram,
expresses the phase of topographic data,
expresses the phase of deformation,
expresses the phase of earth-flat, and
expresses the phase of noise, including the system thermal noise, as well as the noise due to the loss of time and space correlation. In order to obtain an accurate deformation phase
, the other terms should be eliminated by the item on the right side of Equation (1). This study used the ENVI5.5 SARscape software procedure, including co-registration, creating an interferogram, filtering, unwrapping, calculating the differential interferometric phase, and geocoding. Ultimately, this method generates a deformation image. We were able to create four figures based on the interference data displayed in
Table 1.
3.3.1. Co-Registration
The purpose of co-registration is registering the slave SAR image to the reference geometry of the master image. It consists of spatially registering two or more images with subpixel accuracy. First, a shift estimate is performed based on the initial orbit data. Second, the shift estimate is improved to subpixel accuracy by using a grid of small windows. Third, the final shift is further refined to the accuracy of 1/10 of a pixel by using oversampled data.
3.3.2. Creating an Interferogram
Assume that there is a pixel footprint in both master and slave images mapping on the ground P. The master and slave images measure phase
and
from the sensor to P respectively.
where MP is the distance from first sensor to ground P; SP is the distance from second sensor to ground P;
is the wavelength of the radar sensor.
The subtraction of these two phases
forms the interferogram:
The interferometric phase
is related to the distance subtraction of SP and MP, which is fundamental to generate the Digital Elevation Model (DEM) [
27]. In practice, the ground point P moves to P’ during the satellite repeatedly flying. The slave images measurement of phase
is different from above:
where PP’ is the deformation distance of ground point P.
The interferogram phase is informed in following:
If the external DEM is obtained, the phase can be calcuted which related to the deformation of point P. In practice, the noise may also be mixed up in the interferogram during measurement.
3.3.3. Filtering
An iterative, adaptive filtering procedure is performed to remove the noise in the interferogram, thus preserving information about local deformation. The coherence values are used to set the filter window size; the mean intensity difference among adjacent pixels is used to identify a stationary area, which defines the maximum dimension (in any case not bigger than the input parameter setting) and the shape of the filtering windows. The process is aimed at preserving even the smallest interferometric fringe patterns.
3.3.4. Unwrapping
The differential interferogram is unwrapped using the minimum cost flow (MCF) method. In order to limit the possibility of introducing erroneous phase jumps in the output unwrapped phase image, it is suggested to avoid setting a high coherence threshold; good values are typically between 0.15 and 0.2 [
37]. We set a coherence threshold of 0.2.
3.3.5. Calculating the Differential Interferometric Phase
This step is crucial for correct transformation of the unwrapped phase information into displacement values. It removes the topographic phase, earth-flat phase from the unwrapped phase values, leaving only the displacement phases. The Shuttle Radar Topography Mission (SRTM) DEM was used to remove these phases. It was interpolated and re-sampled, then simulated as an interferogram phase. The topography-related errors were negatively correlated with perpendicular baselines. All perpendicular baselines were less than 345 m (
Table 1), and the altitude of ambiguity [
38] was larger than 190 m. Hence, topography-residual phase in the interferograms can be neglected [
13].
3.3.6. Geocoding
The SAR images are projected into the slant range geometry. This step is performed to geocode the displacement phases from the SAR projection into a map projection. During this procedure, SAR projection and geodetic transforms are considered in order to convert the displacement values from the SAR system into the Global Cartesian coordinate system (WGS-84).
Nevertheless, in this study we focused on consecutive DInSAR technology; to obtain consecutive DInSAR interferograms, the four advanced SAR images were each used as the master image in turn, and the subsequent one was used as the slave. Consecutive DInSAR means that for two scenes of SAR images for which the time interval is the shortest, we produce interferograms one by one and ultimately obtain complete time series interferometric results. Subsidence within a single period can be acquired; meanwhile, interferometric phase changes can be analyzed easily in a quantitative way. As an advantage, this helps to evaluate the various characteristics of mining subsidence from different spatio-temporal perspectives.
3.4. Support Vector Machine Regression
The principle of the prediction algorithm based on a support vector machine (SVM) regression algorithm optimized by grid search (GS-SVR) supposes that there is a set of training sample data D = {(X
1,Y
1),(X
2,Y
2),…,(X
i,Y
i),…,(X
n,Y
n)} (where Y
i∈
,
i = 1,2,3,…,
n), and we hope to find a function
f(X) = Y. If so, we can easily obtain Y
n + 1, which is the prediction value.
Here, is a feature space vector, , and b is a threshold.
We introduced the loss function parameter
and make the function
f(
x) subject to the following expression:
If the function cannot estimate all the data with the loss function parameter
, error
must be added. The expression mentioned above should be expressed as follows [
39]:
where
c is the penalty factor,
is the error, and
is the loss function parameter.
By introducing Lagrange functions and dual variables, the function
f(
x) in Equation (7) was found. However, it could only solve a linear regression problem; mining subsidence prediction is a nonlinear regression problem. The kernel SVM function
needs to be introduced to solve a nonlinear regression problem. The kernel SVM can handle the complexity of ascending dimension and avoid a high-dimension kernel function expression by using the expansion theorem. There are three kernel SVM forms: radial basis function (RBF), polynomial, and sigmoid kernel. Our purpose was to acquire an optimal regression model to predict mine subsidence using the least amount of data. The RBF function is suitable for this, as shown in Equation (11). Compared with other functions, it has the advantages of fewer parameters and faster calculation speed [
40]. It is also robust against the interference of noise in the data.
Here, the penalty factor c in Equation (11) and the kernel parameter gamma (henceforth denoted g) are vital parameters of the SVM regression model. To improve the accuracy of the SVM regression algorithm, a grid search (GS) algorithm was applied. This GS algorithm was used for model parameter optimization. We determined the initial values of g and c, searched for g and c globally using the grid method, in order to obtain the optimal values for g and c, and, finally, establish the prediction equation.
3.5. Summary of InSAR and GS-SVR
Based on the concept described previously, the time series subsidence data in the coal mine obtained via InSAR technology are used as training sample data. These data are characterized by a nonlinear relationship: {xi} = {x1, x2, …xn}. We considered the values of these data as the GS-SVR algorithm training samples, to establish a prediction function such as Equation (7), and solve Equation (10) to establish the prediction model. We compared the predicted values with the surveyed values to determine the accuracy of the prediction model. The mine prediction model was computed using MATLAB software, and constructed as follows:
Step 1: The dataset of InSAR subsidence values was acquired as the training dataset, and the GPS measurement data were selected as the validation dataset.
Step 2: The fixed range for parameter c was split up into a set of values with the same interval between. Further, the fixed range for g was segmented evenly to form a set with the same cardinality as that for c. Each c and g were grouped together, and each (c, g) pair was established as a grid cell.
Step 3: For each (c, g) pair in the grid, the prediction accuracy of the model was obtained by cross-validation. The InSAR subsidence values were divided into a training dataset and a testing dataset using leave-one-out cross-validation.
Step 4: The (c, g) pair with the highest accuracy was used as the SVM regression parameters. The InSAR subsidence values were used as the model input in the training dataset, and the prediction values were then calculated.
Step 5: The accuracy of the prediction values was evaluated by determining the absolute error [
13] and relative error (RE), which are defined as follows:
where
represents the GPS measurement values and
represents the prediction values obtained by the GS-SVR algorithm.
The mean absolute percentage error (MAPE) was used as an index for assessing prediction results. Willmott’s Index of Agreement (WIA) was used for evaluating the generalization performance of the prediction method. MAPE is an indicator of relative error, and WIA varies between 0 and 1. The WIA value is a standardized measurement of the degree of SVM regression model error. They are defined as follows:
where
is the GPS measurement values,
is the prediction values acquired by the GS-SVR,
n is the number of test samples, and
is the mean value of all
.
5. Discussion
The nonlinearity and large gradient of mining deformation limit the coherence and phase unwrapping in the InSAR procedure. Nevertheless,
Figure 2 demonstrates that the coherence is higher than 0.2, and it was set as a coherence threshold.
Figure 3 shows that there was no empty data; all the wrapped phase were unwrapped and the two-pass DInSAR results were robust. First, this was due to the low vegetation coverage in the study area. Second, the PALSAR L-band sensor is applicable to monitoring deformations in mining areas. Third, consecutive DInSAR interferometry divided a temporally long cumulative deformation process into several small-temporal-interval InSAR procedures. The small-temporal-interval unwrapping phases were then accumulated, and the true consecutive DInSAR results were obtained.
The consecutive subsidence maps provide some interesting data regarding mining subsidence trends. A tendency towards deformation area expansion was seen in
Figure 3a–d. These four graphs suggest that in the 184 days from 4 July 2007 to 4 January 2008, as the accumulation of mining subsidence became larger, the surface above the working panel became a subsidence basin. The subsidence formation developed from north to southeast, which is in the same direction as the underground mining. In addition, another subsidence area located in the southeast of the NO.40301 working panel was detected. After exploration at this spot, an illegal mine was discovered, which was closed in 2010. Fortunately, it was far away from the NO.40301 working panel, and the subsidence was mainly influenced only by the NO.40301 working panel, which gives good conditions for inversion of the prediction parameters of the SVM regression.
According to the theory of DInSAR technology’s monitoring gradient [
41,
42], the monitoring gradient is correlated with wavelength, coherence, and spatial resolution. ALOS/PALSAR has a long wavelength and high spatial resolution; its gradient is 11.8 cm at 46 days in one pixel. That means DInSAR can’t detect deformation when the ground sinks more than 11.8 cm over 46 days. Fortunately, the maximum subsidence value in this mine area was 11 cm at 46 days. This indicates that using consecutive DInSAR is appropriate. Moreover, long wavelength can reduce atmospheric delay, and short perpendicular baseline can reduce topography-residual error. The altitude of ambiguity is larger than 190 m when the perpendicular baseline is less than 345 m. That means an external DEM’s 190 m relative elevation error will cause 2π phase error in the interferogram. The relative elevation error of SRTM DEM is less than 10 m [
43]. Topography-residual error is so small as to be negligible. Above all, consecutive DInSAR combined with L-band and short perpendicular baseline is a feasible method to detect mining deformation.
The prediction error distribution for each GPS station is shown in
Figure 7. The maximum AE (abbreviate to MAX. AE) of the prediction results, at GPS5, was less than 3.1 cm, and the maximum RE (abbreviate to MAX. RE) occurred at GPS4, with less than 14%. The MAX. AE and MAX. RE of the prediction results are recorded in
Table 3 and can help us to quantitatively analyze the prediction result errors. Here, as we know, the underground mining activity was intense over the 230 days, and GPS4 and GPS5 were in the center of the subsidence basin. The deformation values at these two stations were influenced by many factors, such as geological structure, mining speed, coal pillar, and others. Here, in order to improve the prediction accuracy, a long time-series SAR system and a prediction model with multiple parameters should be taken consideration. The WIA value was 0.994 and the MAPE was 5.6%, as shown in
Table 3. These values indicate that the prediction function established in Equations (1), (4) and (6) is valid, suggesting that the combined approach using consecutive DInSAR and the GS-SVR method is effective for coal mining subsidence prediction in the Loess Plateau of China.
6. Conclusions
In this paper, we presented a theoretical and experimental study of DInSAR technology and a GS-SVR prediction algorithm. Considerable attention has been paid to InSAR technology in recent years. The contribution of this paper was to introduce a new mining subsidence prediction algorithm for the Loess Plateau of China, where coal mining is widespread. Based on the above experiment and discussion, DInSAR technology is highly efficient in mining surface monitoring, and the GS-SVR prediction algorithm is valid for mining subsidence prediction.
The results demonstrate that InSAR technology is an effective method of monitoring mining surface subsidence in all weathers on the Loess Plateau of China. DInSAR can be used to obtain the entire dataset for a mining subsidence area. Consecutive DInSAR technology can reveal developing mining settlement trends, and these data are good samples for a prediction model of mining subsidence.
The abovementioned GS-SVR prediction algorithm is a new method for predicting mine subsidence with fewer learning samples. The experimental results indicate that the GS-SVR method calculates accurate prediction values, with a maximum relative error and an absolute error of 13.3% and 3.08 cm, respectively. These results prove that the GS-SVR algorithm is reliable and practical.
In the future, we plan to use long time-series SAR images, such as PALSAR-2 images, to predict mine subsidence. The prediction model should also take geological structure, mining speed, coal pillar, and other factors into consideration. For example, SVR and rheology could be combined as a prediction model, or we could combine the influence function and Knothe function.