Next Article in Journal
Quantifying the Climate Co-Benefits of Hybrid Renewable Power Generation in Indonesia: A Multi-Regional and Technological Assessment
Previous Article in Journal
Reassessing and Extending the Composite Rainfall Record of Manchester, Northwest England: 1786–Present
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Climate
Volume 12
Issue 2
10.3390/cli12020022
climate-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Precipitation Anomalies and Trends Estimated via Satellite Rainfall Products in the Cananeia–Iguape Coastal System, Southeast Region of Brazil

by
Jakeline Baratto
1,*,
Paulo Miguel de Bodas Terassi
1,
Nádia Gilma de Beserra de Lima
2 and
Emerson Galvani
1
1
Department of Geography, University of São Paulo, São Paulo 05508-000, Brazil
2
The School of Arts, Sciences and Humanities, University of São Paulo, São Paulo 03828-000, Brazil
*
Author to whom correspondence should be addressed.
Climate 2024, 12(2), 22; https://doi.org/10.3390/cli12020022
Submission received: 12 December 2023 / Revised: 29 January 2024 / Accepted: 31 January 2024 / Published: 5 February 2024
(This article belongs to the Section Weather, Events and Impacts)
Browse Figures
Versions Notes

Abstract

:
The objective of this research is to select the best orbital sensor for rainfall estimates (monthly and annual scales) and to analyze the frequency and magnitude of extreme rainfall events and their trends and disruptions based on the use of satellite rainfall product data for the Cananeia–Iguape Coastal System (CICS). Data from four satellite rainfall products were used to identify the correspondence with seven points on the surface of the study area. Statistical metrics were used to identify the best satellite rainfall product. After identifying the sensor with the best performance in estimating orbital precipitation, extreme events were identified by the Standardized Precipitation Index (SPI) on a one-month (SPI-1), three-month (SPI-3), and twelve-month (SPI-12) scale. Trend and rupture detection in the time series were performed using different statistical techniques (Mann–Kendall, Pettitt, Standard Normal Homogeneity Test, or Buishand test). Among the satellite rainfall products, CHIRPS had the best measurements for the analyzed points on the surface. The year 1983 was characterized as very rainy, also marked by the occurrence of El Niño, and was marked by the rupture of the rains at all points (IDs 1, 2, 3, 4, 5, 6, and 7) analyzed in the month of June. The decrease in monthly rainfall was more significant in the months of February (at points IDs 1, 2, 3, 5, and 7) and April (IDs 1, 3, 5, and 7). Decreased rainfall may cause CICS mangrove shrinkage. These results showed the importance of studying rainfall in an area with mangroves in order to understand the dynamics of vegetation in the face of climate change.

1. Introduction

Rainfall is the main source of water in different ecosystems. Thus, the dynamics of vegetation and its ecological importance may be affected by changes in rainfall patterns, such as the frequency of extreme events and the decrease or increase in annual volumes [1].
In mangrove environments, the climate change scenario can modify mangrove dynamics and cause changes in the global distribution, diversity, and abundance of species [2,3,4]. Thus, climate change can modify the dynamics of mangroves and cause changes in the global distribution, diversity, and abundance of species [5]. Climate plays a key role for mangroves and can limit the colonization growth and development of their flora. In addition to air temperature, rainfall plays an important role in mangrove maintenance and development. On a global scale, the increase or decrease in the volume of rainfall, for example, can lead to the distribution of mangroves around the world [3,5]. Therefore, understanding the dynamics, extreme events, and trends of rainfall in places with mangroves can be a strategy to minimize the adverse effects of climate change in this environment.
Associated with climate change, the occurrence of extreme rainfall events can negatively affect mangroves. Decreased rainfall can increase salinity in mangrove areas and affect species that are less tolerant of high salinity. On the other hand, increased rainfall influences the expansion of this ecosystem. Oscillations in rainfall can cause changes in its limits, even the abundance or loss of species [6]. In addition, extreme events cause stress in the mangrove environment [3], whether in the increase or reduction in rainfall [7], and affect the extension or retraction of the mangrove. Therefore, identifying the anomalies of rainfall can help preserve the mangrove. One of the methods used to identify extreme events is the Standardized Precipitation Index (SPI), which detects extreme events regardless of local climate characteristics [7,8,9]. Furthermore, to understand future rainfall scenarios, rainfall trend analysis [10,11,12] becomes a valuable resource to mitigate the effects of possible changes resulting from changes in rainfall.
However, rainfall data on the south coast of São Paulo (Brazil), where the Cananeia–Iguape Coastal System (CICS) is located, do not have a large scope, being limited to a few rainfall stations. In this region, the absence of surface rainfall data makes these analyses difficult locally. To meet this demand, these rainfall values from reanalysis are being widely used in climatological research in the search for more complete analyzes in certain regions [13,14,15,16,17]. Rainfall products from satellite rainfall are tools with great potential for analyzing rainfall time series for locations where there is a shortage of historical data from surface rainfall stations [16].
Different satellite rainfall products have been validated and widely used in different studies in the Southeast region of South America [18], on the coast of Ecuador [14], in Morocco [19], in Vietnam [20], and, finally, in Northern Argentina [21]. In Brazil, research using data from satellite rainfall products is expanding. These studies sought to analyze and evaluate satellite data both for Brazil as a whole [13,17] and for certain regions or watersheds [13,18,22,23,24,25].
In view of this, understanding the variation in rainfall for areas with mangroves is important to understand how mangrove vegetation can change in the face of climate change, mainly referring to extreme events and rainfall trends. Orbital rainfall products are allies in this analysis in places where rainfall stations on surfaces are scarce, incomplete, or non-existent.
Therefore, the objective of this research is to select the satellite rainfall that presents the best performance on the monthly and annual scales and analyze the frequency and magnitude of extreme events and the trends and disruptions in rainfall for the best estimate found for the Cananeia–Iguape Coastal System, São Paulo, Brazil.

2. Materials and Methods

2.1. Study Area

The Cananeia–Iguape Coastal System (CICS) is located on the southeastern coast of Brazil (Figure 1a). In addition, it is formed by a complex of lagoon channels [26], composed of four islands, namely Cardoso, Comprida, Cananeia, and Iguape. They are separated from each other by systems of channels and rivers that communicate with the ocean through mouths (Figure 1b) [27].
Conservation units are situated in the study area. The Environmental Protection Area of Cananéia–Iguape–Peruíbe was created by Decree N° 90347 of 1985 [28], and the Ilha do Cardoso State Park was created by State Decree N° 40319 of 1962 [29].
The main economic activities in the region are banana and tea culture [30] Furthermore, the creation of fish, crustaceans, and mollusks and tourist activities such as ecotourism are also sources of economic income for the population [31].
The southern coast of the state of São Paulo is classified as climate type “Cfa”, which defines a humid subtropical climate with hot summers and no well-defined dry season, with an average temperature in the coldest month below 18 °C and a temperature in the hottest month above 22 °C, according to the previous classification [32,33].
The Köppen climate classification was adapted for Brazil [32] and took specific geographic characteristics into account. The Köppen climate classification [33] was reworked to a resolution of 1 km for the period 1980–2016, seeking greater accuracy of the climate classification.
Annual precipitation varies between 2000 mm and 3000 mm [34,35] throughout the CICS. The rainfall totals are highest in the summer (December, January, and February), a period in which the rains are the result of the incidence of sunshine, which is greater at this time of the year, and, consequently, greater heating favors the convection of the air, resulting in cloud formation and precipitation [36]. One of the main atmospheric mechanisms operating in this sector of South America, the South Atlantic Convergence Zone (SACZ), can develop and cause high total rainfall throughout the summer in this sector of the Brazilian territory [37]. In addition, the passages and interactions between the atmospheric mechanisms highlighted below correspond to factors that also cause rainfall in the CICS: the Atlantic Polar Front, extratropical cyclones, tropical and prefrontal squall lines, and the sea breeze circulation [38,39,40,41]. During the less-rainy period, corresponding to winter (July, June, and August), the rainfall totals are lower due to the restricted activity of the Atlantic Polar Front.

2.2. Acquisition of Observed Data and Satellite Rainfall Product Data

The surface rainfall data were extracted from seven weather stations belonging to the Integrated Center for Agrometeorological Information (CIIAGRO) (ID1 and ID2), the National Institute of Meteorology (INMET) (ID3), and the Department of Water and Electric Energy (DAEE) (ID4, ID5, ID6, and ID7) (Figure 1). Monthly and annual data were acquired from the respective platforms for the 2009–2019 period (validation period) and show record failures of less than 10% (Table 1).
The data of the satellite rainfall products used are from the Tropical Rainfall Measuring Mission (TRMM) [42], Climate Hazards Group InfraRed Precipitation with Stations (CHIRPS) [17,23], Remotely Sensed Information using Artificial Neural Networks–Climate Data Record (PERSIANN) [43], and Modern-Era Retrospective Analysis for Research and Applications (MERRA-2) [44] (Table 2).
TRMM (TRMM 3B42) data provided by the Goddard Earth Sciences Data and Information Services Center have a temporal resolution of 3 h and are available in a spatial resolution of 0.25° (about 25 km) as of 1 January 1998 to 31 December 2019 [45,46]. TRMM data are combined from different platforms onboard some satellites. Furthermore, these data come from a combination of precipitation data estimated by remote sensing, rain gauges, and radar observations [25,47].
CHIRPS data are developed by the United States Geological Survey (USGS) and the Climate Hazards Group at the University of California, Santa Barbara (UCSB) and it can be freely accessed https://www.chc.ucsb.edu/data (accessed on 3 February 2022). This type of dataset is available daily with a spatial resolution of 0.05° (5 km) from 1981 to the present [48]. CHIRPS rainfall data come from some other data sources such as monthly climatological precipitation data CHPClim (1); observations from geostationary satellites with practically global coverage with thermal infrared (IR) sensor from the National Oceanic and Atmospheric Administration (NOAA), products from the Climate Prediction Center and B1 IR from the National Climatic Data Center (2); precipitation estimates from the Tropical Rainfall Measuring Mission Multi-satellite Precipitation Analysis version 7 (TMPA 3B42 v7) (3); atmospheric precipitation field models from NOAA Climate Forecast System version 2 (4); in situ precipitation observations from diverse sources, including the Global Historical Climate Network, Global Summary of the Day dataset, and the World Meteorological Organization’s (WMO) Global Telecommunications System (5) [18,49,50].
In turn, MERRA-2 can be considered a good alternative to monitor precipitation and hydrological applications in certain regions where the station is very sparse [44,51]. This study used MERRA-2 data on total monthly average precipitation (M2TMNXFLX) with a spatial resolution of 0.50° × 0.625°, obtained from the NASA website https://power.larc.nasa.gov/data-access-viewer/ (accessed on 20 February 2022) [42]. MERRA-NC is the model generated by precipitation data, while MERRA-C is corrected with the NOAA Climate Prediction Center’s (CPC) unified gauge-based analysis of the global daily precipitation product and the rainfall analysis based on the CPC’s [44,52].
PERSIANN CDR data are available from NOAA/PERSIANN-CDR. Daily data are estimated on the 0.25° scale from 1 January 1983 to the present [53,54]. PERSIANN CDR (Climate Data Record) is an automated system for precipitation estimates based on remote sensing information using artificial neural networks. This product uses infrared brightness temperature information from Gridded Satellite (GridSat-B1I). Next, the National Center for Environmental Prediction (NCEP) Stage IV radar data are used to create the nonlinear regression parameters of the neural network model. To improve the reliability of PERSIANN-CDR, it is calibrated using the Global Precipitation Climatology Project’s (GPCP) and it can be freely accessed https://www.ncei.noaa.gov/products/global-precipitation-climatology-project (accessed on 22 February 2022) product version 2.3 monthly [55]. The GPCP product contains precipitation gauge data generated by the Global Precipitation Climatology Center (GPCC) mission [53,56].
TRMM, CHIRPS, and PERSIANN satellite rainfall product data were extracted using the Google Earth Engine (GEE) platform and it can be freely accessed https://earthengine.google.com (accessed on 20 February 2022), which provides computational services for advanced images [57,58] (see codes in supplementary material I). Data extraction codes from satellite images were used to compile hourly and daily data into monthly and annual totals. The period used for the analysis was from 2009 to 2019, a period that covers all products tested; months that had failures were discarded. The PERSIANN and MERRA products did not fail at the analyzed points. CHIRPS and TRMM data had monthly failures on ID2 (4.1%) and ID3 (1.3%) each.

2.3. Exploratory Statistics

The performance metrics used to validate the four satellite rainfall products in relation to the surface data were the correlation (r) and determination (R²) coefficients, root mean squared error (RMSE) [59,60], mean percentage error (Pbias), mean absolute error (MAE) [61,62], and Willmott’s concordance I (Index d) [13,15,17,18,23,24,62]. RMSE and MAE evaluate the average magnitude error between estimated and observed data, where the closer to zero, the better the adherence of the estimated data in relation to the observed data [61]; the closer to zero, the Pbias indicates the better accuracy between the observed data and the estimated data; Index d indicates the improvement in accuracy of estimated data in relation to observed data when closer to one [63,64]. Thus, the lower the PBias, RMSE, and MAE values, the closer the satellite estimates are to the surface measurements [61]. These metrics and graphics were performed in Rstudio (2022) and it can be freely accessed https://posit.co/download/rstudio-desktop/ (accessed on 20 February 2022).

2.4. Standardized Precipitation Index

After applying the metrics, the CHIRPS data were chosen to identify the extreme events and, subsequently, the trend analysis (item 2.5) at the locations of the surface rainfall stations. CHIRPS monthly and annual data were acquired by GEE for the seven points in the 1981–2022 period to identify extreme events.
Although it is widely used to identify drought events [65,66,67], the SPI is also used to characterize rainfall anomalies in Brazil [68] and to understand the variability of rainfall [8,69,70,71].
The SPI is an index that estimates the dry index for several reference periods, adapting to the different response times of typical hydrological characteristics to rainfall [72]. Thus, the history series is adjusted to a gamma probability distribution, in which it is transformed into a normal distribution, where the SPI index for each desired location and period has a value of zero for its mean and unit variance [73].
Therefore, SPI [73] was used to identify extreme events (dry and rainy). The SPI was calculated on the one-month (SPI-1), three-month (SPI-3), and twelve-month (SPI-12) scales. The standardized SPI was calculated using the Rstudio program [71,72].
The SPI is the number of standard deviations that can observe the deviation of rainfall from its mean and distribute it normally. SPI values range from −2 to 2. A value below zero indicates a dry condition, and a value above zero specifies a wet condition. The SPI is designed to estimate rainfall deficiencies on multiple time scales. It is the most efficient and reliable for various topographic areas [71,73].

2.5. Trend Analysis

The Mann–Kendall test (TMK) was applied to assess trends in rainfall change for monthly and annual data from rainfall stations [54,55,56]. These methods have been widely used in many studies to analyze rainfall trends in different regions, including both natural and human-induced factors [8].
The TMK evaluates the trend of alteration of the time series, and the hypothesis is that stability occurs in the time series, that the succession of values occurs independently, and that the probability distribution must remain the same (simple random series) [74]. The values calculated by the Sen curvature were compared to the values of the ZMK (parameterized statistical test), a statistical test that measures if a series of data fits a normal distribution. For the significance level of 10% probability, Z lies between the −1.645 and 1.645 intervals.
Furthermore, the Pettitt tests [75], the Standard Normal Homogeneity Test (SNHT) [76], and the Buishand test [77] were applied to identify whether rupture occurs in the time series. The Pettitt test seeks to identify periods of rupture in time series [78]. The SNHT consists of the null hypothesis that the values of the test variable are independent and identically distributed [24]. Finally, the Buishand test admits that the data are normally distributed independently and randomly according to the H0 hypothesis [79]. Calculations were performed using the r 3.3.2 software [80].

3. Results

3.1. Validation of Satellite Rainfall Products

3.1.1. Annual Scale

The results of the statistical metrics for the annual data showed that there is not a unique satellite rainfall product for all the analyzed stations. The correlation and determination coefficients varied for all stations and satellite rainfall products. Some stations did not have significant correlations for all satellites. The r ranged from 0.0 (ID1 and ID6 in CHIRPS and ID1 in PERSIANN) to 0.8 (ID2 for TRMM and ID3 for CHIRPS). ID4 (CHIRPS and PERSIANN) and ID5 (CHIRPS) had negative and little significant correlations (Figure 2A and Table S1—Supplementary Material II).
The relationship between CHIRPS rainfall data and surface observed in [23] for the Apeú River Sub-Basin, Castanhal (Pará, Brazil) was higher than this research, with the correlation varying between 0.95 for stations controlled by INMET and 0.99 for those of ANA. This difference in correlations in the annual data can be influenced by the dynamics of rainfall in each region.
The TRMM data had the largest discrepancies in relation to the surface observed data, ranging from 725.9 mm (ID2) to 1661.3 mm (ID6) for the MAE and from 776.9 mm to 1690.7 mm at the respective points for the RMSE. The other products had similar MAE (Figure 2B) and RMSE (Table S1—Supplementary Material II) variations for the same stations. MAE ranged from 235.3 mm for CHIRPS (ID7) to 675.7 mm for MERRA (ID6). RMSE recorded larger values ranging from 294.5 mm for CHIRPS on ID7 to 805.9 mm for CHIRPS on ID1 (Table S1—Supplementary Material II).
For the Apeú River Sub-Basin [23], the RMSE ranged from 43.9 mm (ANA) to 98.6 mm (INMET) for CHIRPS annual rainfall data, and in the rainiest periods, the values were higher for 136.2 mm (INMET) and 60.6 mm (ANA).
The d-index values show that there is agreement between the estimated data and those observed at the rainfall stations; the measure varies between 0 and 1. Being closer to 1 indicates the best model or the greatest agreement [23]. In general, the d ranged from 0.1 (ID4 for CHIRPS) to 0.8 (ID3 for CHIRPS). The agreement of 0.5 (25%) and 0.6 (20.4%) had the highest occurrence for the annual period for the IDs and satellite rainfall products analyzed (Figure 2D).
In general, data from the TRMM satellite product (all IDs) had the lowest agreement values (d-index), which corroborates the results of the other metrics (MAE and RMSE, mainly). Thus, as also pointed out in the literature [24,61].
The agreement with the MERRA data showed the greatest similarity between the points, ranging from 0.4 (ID1) to 0.7 (ID2). Thus, PERSIANN and CHIRPS rainfall data had more variations between stations (Figure 2C). PERSIANN recorded the Index-d varying from 0.3 (ID4 and 6) to 0.7 (ID7), and CHIRPS had the Index-d ranging from 0.2 (ID4 and 6) to 0.8 (ID 7).
The mean percentage error (Pbias) measures the tendency of the estimated data to be underestimated or overestimated [23,24,81]. The TRMM presented data underestimation at all points, with high values greater than −56.9% (ID2). ID4 showed the lowest percentage of Pbias for the products, being 1.3% (CHIRPS), −7.3% (PERSIANN), and 0.4% (MERRA). Only with PERSIANN was the Pbias negative, underestimating the satellite data for this ID.
The other points, for the most part, had positive PBias values for CHIRPS and negative PBias values for PERSIANN and MERRA (Table S1—Supplementary Material II). Therefore, it is concluded that the CHIRPS precipitation values are overestimated while the PERSIANN and MERRA rainfall values are underestimated. Furthermore, the CHIRPS rainfall values are closer to Pbias 0, which indicates that the CHIRPS rainfall data are closer to the rainfall data found on the surface, corroborating previous research [23,64].
For this research, the results found by CHIRPS corroborate the previous study [24], in which this satellite product showed a good correlation with surface data and overestimated rainfall in the Amazon region. The use of CHIRPS data underestimated the total rainfall in the rainiest months in the Brazilian Amazon [82,83] and, therefore, proved to be ineffective in representing trends and changes in extreme climate indicators related to rainfall. However, in this dataset research, CHIRPS presented the best metrics and proved to be a satellite rainfall product that can estimate extreme climatic indicators.
CHIRPS data also measured the best metrics in relation to PERSIAN-CDR data for the Mearim river basin in the transition area of the Amazon and Caatinga in the state of Maranhão [65]. The authors also highlighted that in the rainiest period, between December and May, CHIRPS data performed better.

3.1.2. Monthly Scale

The monthly data of the satellite rainfall products and the stations analyzed had the coefficients of correlation and determination varying over the months and between the stations. Negative correlations were more present in the winter months (June, July, and August) for ID4, ID5, and ID6 for all types of satellites. In September, correlation values were higher for all stations. In January, ID2 recorded the highest values of correlation (0.9) and determination (0.8 and 0.9) for all satellite rainfall products (Table S2—Supplementary Material II). Thus, the highest values of r and R² were obtained in a period in which we expect rainfall to be more irregularly distributed due to the complexity of atmospheric mechanisms that operate in this region.
Better correlations between CHIRPS rainfall and surface data were found for the Tekeze–Atbara Basin (Ethiopia) [61]. The authors identified correlations (r) ranging from 0.55 to 0.71. TRMM rainfall for different regions of Brazil was studied by [13]. The southeast region had high correlations (0.9) for the TRMM for all months. For the Amazon region [24], both TRMM and CHIRPS also showed high correlations (0.8 to 0.9) for all months of the year.
The period between January and May had the highest MAE and RMSE (Table S3—Supplementary Material II) values. The highest MAE and RMSE values were recorded on ID6 for the TRMM satellite for March and May, respectively. These differences were between months and between points. The spatial difference in rainfall between sensors has been previously observed in Ethiopia [61].
The months between June and December had the lowest values (MAE and RMSE); in addition, the discrepancies between the points were smaller. In August, all MAE and RMSE values were less than 100 mm. The months of July and August had the closest MAE values between satellites and stations. In July, ID6 for TRMM recorded the largest MAE (120.8 mm), and ID1 for CHIRPS had the lowest MAE (18.6 mm), which is the smallest value found among all satellite rainfall products. The lowest RMSE was at ID1 for CHIRPS (24.1 mm) in July (Table S3—Supplementary Material II).
For the study area, it was observed that in the months with less precipitation, the smallest MAE and RMSE values occurred between June and September [35]. These results are consistent with other studies [24], which indicated that the greatest MAE and RMSE values occurred in the rainy season. In CICS, the period of June is marked by rainfall from frontal passages [36,40], which corroborates the more homogeneous distribution of rainfall, corroborating the smaller differences between the MAE and RMSE values between stations. However, in summer, the biggest discrepancies between the MAE and RMSE values of the stations may be related to the rainfall in the ZCAS, which, in addition to not having a uniform distribution, causes high rainfall volumes [40].
The RMSE values found in CICS were higher than the values found in other studies (Table S3—Supplementary Material II). For example, for TRMM rainfall data in the Southeast region of RMSE Brazil, the monthly RMSE ranged from 3.78 mm (July) to 39.14 mm (December) for monthly data [13]. For the same satellite, in the state of Mato Grosso do Sul (Brazil), they found a monthly variation in RMSE between 7.1 and 29.1 mm [84].
According to MAE data, RMSE results were also lower from June to September and higher from October to May. However, January, February, and March had the highest values. The month of May registered the highest RMSE value, being 328.0 mm in ID6 for the TRMM (Table S3—Supplementary Material).
The Pbias results showed that 66% of the satellite rainfall data (monthly and product data) underestimated the values observed on the surface. From 66%, 40% (89 results) underestimated more than 50% of the values observed on the surface. That is, the underestimated rainfall data (monthly and by-product) acquired by satellite were values bigger than values measured on surfaces (Figure 3B and Table S4—Supplementary Material II).
Most of the underestimated rainfall data correspond to the TRMM data, which also had the smallest variation in Pbias between the quarters of January, February, and March (JFM), April, May, and June (AMJ), July, August, and September (JAS), and October, November, and December (OND). The CHIRPS rainfall data had 61% (51 data) of the data overestimated compared to surface measured data. These values corroborate the annual data, as the annual TRMM values are also underestimated and the CHIRPS values are overestimated (Figure 3A and Table S4—Supplementary Material II). However, some studies point out [24] that data estimated by TRMM and CHIRPS tend to overestimate rainfall on the surface in most months, differing from the values found in CICS. Other studies indicate that CHIRPS overestimated the data, such as in the southeast region, where CHIRPS rainfall values overestimated surface rainfall data between 6.6% (March) and 42.8% (August) [17].
The MERRA and PERSIANN products had 63% of the data underestimated and 37% overestimated (Figure 3B). Data from CHIRPS, MERRA, and PERSIANN had similar fluctuations between the positions analyzed in the periods for the Pbias metric (Figure 3B and Table S4—Supplementary Material II).
The d-index showed that the highest percentage of rainfall data had d-index values between 0.4 (22.6%) and 0.5 (22.0%). However, this distribution is not uniform for all months of the year and for each station analyzed. The TRMM had a more similar d index over the months, but it was lower in most of the points analyzed. MERRA was the one with the highest monthly variation in the d index. PERSIANN and CHIRPS had the closest monthly variation in the d index. The AMJ and OND quarters had the smallest variations in the d index for these two satellite precipitation data (Figure 3A and Table S4—Supplementary Material II).
PERSIANN and MERRA had the highest concentration in the rainfall data, with d-index values of 0.6, 17.8%, and 19.0%, respectively. CHIRPS had 23.8% of its rainfall data with a d-index of 0.5. By the way, the TRMM recorded 46.4% of the data with a d-index of 0.4. This variation in the d-index is also visible between the months (Figure 3A and Table S4—Supplementary Material II) and between stations. In general, the highest indexes are in the months of May and September for all stations. Thus, these months had the greatest agreement between rainfall data collected by satellites and surface data.
In the Amazon region [24], TRMM and CHIRPS data showed the highest indexes of agreement (d-index) and the highest correlation values. For this research, it was also observed that in some months (May to October), the largest d-index values correspond to the highest correlation values. For the Yarlung Zangbo river basin (China) [43], different rainfall data such as TRMM, CHIRPS, CMORPH (Climate Prediction Center Morphing Method), and PERSIANN were highlighted. The results showed that TRMM presents the best performance (d-index), differing from this research.
According to the results presented and in view of the best responses of the CHIRPS rainfall data for the MAE and RMSE for the indexes of agreement (d) and Pbias, the CHIRPS rainfall data were chosen to carry out the analysis of the extreme events (dry and rainy) and the trend of the data. The CHIRPS data allow a complete analysis of the historical series [11]. In addition, compared to surface data, they have higher compatibility, as other research has also demonstrated [16,17,23,24,61,83].

3.2. Application of the SPI to Identify Rainfall Extremes

Considering the annual analysis (SPI-12), of the 42 years analyzed (1981–2022), 1983 was considered an extremely rainy year in practically all rainfall stations, with the exception of ID1 (Figure 4), as also demonstrated by research carried out in the state of São Paulo [16,38,69,71].
The year 1983 was classified as a rainy pattern [38] due to the increase in tropical systems associated with frontal systems. In 1983, there were 60 frontal systems with an increase in rainy days, 222 in Iguape, and 235 in Cananeia. This year also recorded the occurrence of El Niño [85]. The correlation between SPI and ENSO events is not always found, as occurred in the northern region of Paraná [86]. However, during the occurrence of El Niño (ENSO), rainfall volumes are higher in the state of São Paulo [69].
For the classification of extremely dry years, the years 1985 (ID2, ID4, and ID6) and 1992 (ID6) stood out. In 1985, rainfall volumes were lower than usual due to the reduced participation of frontal systems [38]. In other parts of the world, in Cairo (Egypt), the year 1985 was also marked as an extremely humid period (>2.0) for SPI-12 [8].
Figure 4 presents the SPI-12, and it is observed that in the last years, 2020–2022, the rainfall volumes were below normal (with an SPI index < −0.9), being considered moderately and very dry. These values are in line with the occurrence of La Niña during the last years of the series [85]. In recent years, in the central region, the state of São Paulo [16] has also recorded that dry years are more recurrent.
The different analysis scales of the SPI consolidated the year 1983 as an extremely rainy year in the 3-month and 12-month analyses. However, for the year 1985, this agreement between the SPI-3 and SPI-12 was not verified since, in the spring of that year, the precipitations were close to average due to the increased participation of the frontal systems [38].
In the SPI-3 analysis, the rainiest quarters were April, May, and June for the years 1983 and 1987, which usually do not correspond to the rainiest period of the year. ID6 also recorded the 1998 and 2009 July–August–September quarters as extremely rainy. In research already carried out, the year 1983 recorded in all seasons of the year (quarters) the participation of frontal systems above the average on the south coast of São Paulo [38].
The SPI corresponds to an index that is related to the number of standard deviations that can observe the deviation of rainfall from its mean and distribute it normally over multiple time scales [68,73]. Thus, the SPI considers the precipitation for that period, whether it be one month, three months, or one year. When the analyzed location has well-defined rainfall variability and dry and rainy periods (on a 3-month scale), the SPI considers the average rainfall of the period for its classification. Therefore, lower volumes of rain can be considered a rainier period.
For CICS, some months highlighted as extremely rainy are considered more dry periods (winter) for the study area. In these cases, rainfall was above average, thus being considered by the SPI as rainy. The winter months record the lowest rainfall totals [36,87] as it increases the activity of the Atlantic Tropical Anticyclone, which has its scope more over the continent [31], reducing rainfall volumes. These results corroborate those described in the validation of satellite rainfall data, where in the winter period, data estimated by satellites are more similar to data collected on surfaces (Figure 3B—JAS), also reducing the difference between these data.
The ID3, ID5, and ID7 stations did not have extremely dry quarters. The driest quarter was July–August–September (2020) at the ID1, ID2, ID4, and ID6 stations. In 2012, the January–February–March quarter was extremely dry for the ID1 and ID2 stations. Normal quarters account for between 63% (ID2) and 70% (ID1) of the data per station (Figure 5).
On the monthly scale (SPI-1), the extremely humid months that stood out were June (ID1—4 months, ID2—2 months, ID3—3 months, ID5—3 months, ID6—2 months, and ID7—2 months), May (ID2—2 months), February (ID4—2 months), November (ID4—2 months), and December (ID7—2 months) in practically all rainfall stations analyzed.
The extremely dry months were predominantly April (ID1, ID2, and ID6) and November (ID3, ID5, and ID7), with 2 months at each station. The month of January was extremely dry at stations ID4 and ID6 (2 months). The ID6 station also recorded the extremely dry months in February and September (2 months each). The months considered normal totaled close to 65% for each rainfall station analyzed (Figure 6).
The month of October 2014 was considered [71] a month with rainfall levels below normal for SP, considered a situation of extreme drought, but for the south coast of São Paulo, the rain condition was considered normal by the authors and by this research.
In recent years, the months with negative SPI (drought) have intensified for most of the points analyzed, corroborating the results found by SPI-3 and SPI-12.
Thus, the SPI 1-month scale (SPI-1) and SPI 3-month scale (SPI-3) corroborated the results presented in SPI-12. Despite the region’s rainfall regime being well defined (dry season and rainy season), it was observed that extreme conditions do not follow this definition, as July 2009 was considered extremely humid. These findings were also observed for the state of São Paulo [71]. In addition, the state of São Paulo has shown an increase in the frequency of rainfall deficits, with maximum peaks in the transition months (March to April) of the rainy and dry seasons [82]. In this research, drought events have been intensifying in recent years for all quarters, which can interfere with mangrove health, potentially causing the shrinkage of the mangrove forest. Decreased rainfall increases water salinity, and less-tolerant mangrove species tend to decline, causing mangrove death [3,88].
The different SPI analysis scales consolidated the year 1983 as an extremely rainy year in the 3-month and 12-month analyses. However, for the year 1985, this agreement between SPI-3 and SPI-12 was not found, as in the spring of that year, rainfall was close to average due to the increased participation of frontal systems [34]. It was proven that recent years (2019–2022) had more drought events at the three scales analyzed. This may be a result of La Niña in the southeastern region of Brazil, but more in-depth studies are needed to verify this influence with greater precision.

3.3. Trends and Ruptures in Historical Series of Rainfall

3.3.1. Annual Trends and Ruptures

The application of the Mann–Kendall test for the total annual rainfall showed a statistically significant trend of decreasing rainfall at stations ID3, ID5, and ID7. ID3 and ID5 showed a decrease of 1.67 mm/year (90% significance) (Table 3). With 99% significance, ID7 recorded a trend towards a greater decrease in rainfall of 2.71 mm/year, which corresponds to a decrease of 113.82 mm at the end of the historical series (42 years). The trend of decreasing rainfall in the central region of the state of São Paulo for CHIRPS products is also observed in other studies [16].
However, on the north coast of Paraná, which borders the south of the area of this study [74], an increase in annual precipitation of more than 0.4 mm was identified. This result differs from that found in CICS, which shows a decrease in rainfall. The same pattern of increase in total annual rainfall was identified for 45% of weather stations in the state of São Paulo [89] and for this sector of South America [90].
There are locations in Brazil where the climate is getting wetter, and this was most evident in the southern region of Brazil [91], with a reduction in consecutive dry days, especially in spring. However, these authors highlighted that there is no strong sign of clear change, but positive and negative trends were obtained without statistical significance, mainly in the Southeast region. Therefore, previous results in the Southeast region [91] were partly in line with those obtained by the present research, with a negative trend or without statistical significance.
On the south coast of São Paulo [35], there is no trend of increase or decrease for the 1972–2003 historical series. Thus, the authors concluded that the historical series for points F4-028, F4-029, and F4-040 are stationary. To some extent, the data are similar to those observed in this study because, among the common points ID5 (F4-028) and ID6 (F4-029), only ID5 showed a negative trend of rainfall in this study. ID6 did not show any trend with significant values, although it showed a tendency towards an increase in annual precipitation [35].
For the annual data, the Pettitt, SNHT, and Buishand tests showed that the year 1998 presented a rupture in the historical series of precipitation for the ID7 station. In 2017, the SNHT and Buishand tests showed ruptures in the ID1 station. In addition, the SNHT test found a rupture in ID2 and ID6 in the years 2018 and 2017, respectively. At all these points, the ruptures represent a subsequent decrease in rainfall. This decrease validates the SPI-12 values found for all stations analyzed from 2018 onwards, which show a decrease in annual rainfall, as shown in Table 3.

3.3.2. Monthly Trends and Ruptures

The months of January, March, June, August, November, and December did not show a trend in the time series at the stations analyzed. The months of February, April, July, and September showed negative trends, that is, a trend towards a decrease in monthly precipitation, with significance above 90% (Tables S5 and S6—Supplementary Material II). In the research [92] on the trend of rainfall and air temperature data for all of Brazil, using data interpolated by the Climatic Research Unit-CRU (University of East Anglia—United Kingdom), the authors identified that positive trends occurred for the months of January and March in the study region; in the other months, there were no significant trends. In parts, these results corroborate those found by this research.
In February, ID2, ID3, ID5, and ID7 showed a tendency towards a decrease in monthly rainfall, being 1.9, 2.04, 2.04, and 3.46 mm, respectively (Figure 7). In April (Figure 7), the ID1 (2.14 mm), ID3 (1.39 mm), ID5 (1.39 mm), and ID7 (1.25 mm) stations had a tendency towards a decrease in precipitation. In the months of July and September, only ID7 showed a tendency towards a decrease in monthly precipitation (90% significance). In July, monthly precipitation decreased by 0.87 mm and in September by 1.44 mm/month (Tables S5 and S6—Supplementary Material II). Thus, it is observed that the monthly decrease in rainfall is not very expressive for CICS. However, it is observed that this decrease occurs in some of the stations analyzed. In addition, the decreasing trend in rainfall corroborates previous studies for the central region of the state of São Paulo [11].
October was the only month in which the trend showed an increase in rainfall in ID1 (1.42 mm), ID2 (1.25 mm), ID4 (1.42 mm), and ID6 (1.59 mm) (Figure 7), with significance above 90% (Tables S5 and S6—Supplementary Material II). The trend towards an increase in annual rainfall was found for Curitiba and Paranaguá (Paraná) [93] and in other surveys for this sector of the Brazilian territory [91,94,95,96] and the state of São Paulo [89].
In February, ID7 ruptured in 2011 (Pettitt test), 1999 (SNHT test), and 2000 (Buishand test). The Buishand test also showed a rupture in ID3 and ID5 for the year 2001. In March, the year 1996 presented a rupture in ID3, ID5, and ID7 for the three tests investigated (Figure 8). After this discontinuity, rainfall decreased. In April, ID1 had a rupture in 2012 in the Pettitt and Buishand tests and in 2015 in the SNHT test. The SNHT test still showed a rupture in ID6 (2017) and ID7 (2014) (Tables S5 and S6—Supplementary Material II).
In June, the year 1983 (Figure 9) presented rupture for all points in the SNHT test (Tables S5 and S6—Supplementary Material II). This rupture shows a decrease in rainfall afterward at all points. This year was marked by the occurrence of El Niño [85], and the data showed that it was an extremely rainy month for the analyzed period (SPI-3) and an extremely rainy year. June corresponds to an autumn month, and the frontal passages were above the usual for the south coast of São Paulo, causing high rainfall volumes in 1983 [38]. Thus, the action of the El Niño phenomenon led to an increase in frontal passages in the CICS.
Pettitt and Buishand tests revealed a rupture for ID7 in September 2000. In October, only the Buishand test showed a rupture in the year 1994 in ID1 and ID6. In November, the SNHT test showed a rupture in the year 1982 in IDs 2, 3, 4, and 5. In general, it is observed that the monthly ruptures do not constitute homogeneity between the stations, except for 1982, which marked a rupture in most stations for the SNHT test (Tables S5 and S6—Supplementary Material II).
Based on previous research [94,97,98] in nearby areas, it is assumed that the ruptures associated with increased precipitation are directly linked to the greater frequency and intensity of the warm phase of the Pacific Decadal Oscillation (PDO) and the El Niño-Southern Oscillation (ENSO), especially over the period between 1976 and 1997 [97]. This pattern is mainly concentrated in the month of October (spring), when El Niño acts with the greatest impact on the increase in precipitation in the southern region and parts of Southeastern Brazil [94,98]. In contrast, in the period from the late 1990s to the 2020s, the PDO was characterized by the predominance of a cold phase and a higher frequency of La Niña events, a condition that may be responsible for the occurrence of ruptures and trends of decrease in precipitation during this period, especially between February and April.
It is important to emphasize that the normality tests also showed a pattern predominantly consistent with that obtained in the literature since the Pettitt and Buishand tests were more sensitive to ruptures in the middle of the historical series, while SHNT detected ruptures at the beginning and at the end of the weather series [78,95,99,100]. In fact, the SHNT test was the one that most sensitively obtained ruptures in the historical series of data used and derived from CHIRPS.
Trend analysis and rainfall ruptures confirmed by SPI indicate that rainfall in the CICS is decreasing. This decrease in precipitation becomes a focus of concern in relation to the mangroves present in the region. Recent research proves that extreme events are causing harmful effects in the northern sector of the CICS [101]. The increase in extreme events, associated with the decrease in rainfall, could affect mangrove vegetation in an unpredictable way, even in more protected environments, such as the southern portion of CICIC [101].
The volume of rainfall within the pattern is essential for the better performance of the ecosystem functions that mangroves have in the conservation of the coastline, the habitat and nursery for marine life, and in the accumulation of sediments, carbon, and nutrients [3,102,103]. Therefore, the decrease in rainfall could considerably affect these functions and will be responsible for an imbalance in the environmental quality of the mangroves, and consequently, there is a projection of reducing the area of mangroves.

4. Conclusions

The identification of adequate satellite rainfall for the study region is a fundamental step toward validating scientific research. Satellite precipitation products have different responses for each location, which can be influenced by topography or atmospheric circulation, for example. Thus, the analyzed satellite rainfall products showed good estimates compared to surface data in the Cananeia–Iguape Coastal System. The correlation values (r and R²) showed that the TRMM data corresponded better to the surface station data. However, the MAE and RMSE metrics and agreement indicated that rainfall data estimated by CHIRPS had the best performance compared to rainfall data estimated by the other satellites. The CHIRPS product has the best estimate and the lowest rainfall errors due to the best spatial resolution (5 km).
The SPI showed that rainfall in the Cananeia–Iguape Coastal System is predominantly normal. However, extreme rainfall events were more frequent than extreme dry events for the three scales analyzed (SPI-1, SPI-3, and SPI-12). The year 1983 was characterized as very rainy on all scales analyzed. This year was marked by the rupture of the rains at all the points analyzed in June. In recent years, it has been observed that drier events predominated compared to rainier events. Although extreme rainfall events are more frequent between the analyzed years, all rainfall stations presented trends of decreased rainfall in the annual period and in most months. IDs 1, 2, 4, and 6 showed trends of increased rainfall only in October. Thus, these climatic techniques were key to understanding the dynamics of rainfall in the CICS. An analysis of trends and ruptures in daily rainfall values could also be a complement to a better understanding of how rainfall influences mangrove dynamics in the study area.
With this, it is pointed out that the rains present a trend of decrease, and this could affect the health of the SCCI mangrove. Decreased rainfall can cause mangroves to shrink. These results also show the importance of weather research in mangrove areas, as they shed light on how precipitation variability occurs in the region and how its changes can interfere with the mangrove ecosystem. Questions aimed at understanding whether this reduction in precipitation would already be worrying for the mangrove still need answers, but considering the scenarios of climate change, this reduction can still intensify and actually affect the health of the SCCI mangrove. Thus, there is a need to monitor this rainfall variability and how mangroves can respond to it. Thus, the increased frequency and intensity of drier years could interfere with the health and ecosystem functions of the CICS mangrove.

Supplementary Materials

The following is available online at https://zenodo.org/records/8399867 (accessed on 11 December 2023), Supplementary Material I: Data_CHIRPS; Data_PERSIANN; Data_TRM; https://zenodo.org/records/10606066 (accessed on 11 December 2023), Supplementary Material II: Table S1. Statistical metrics used to validate the annual data of satellite rainfall products with data from the surface weather station; Table S2. Statistical metrics (r and R²) used to validate the monthly data of satellite rainfall products with data from the surface weather station; Table S3. Statistical metrics (MAE and RMSE) used to validate the monthly data of satellite rainfall products with data from the surface weather station; Table S4. Statistical metrics used to validate the monthly data of satellite rainfall products with data from the surface weather station; Table S5. Results of non-parametric Mann-Kendall test (TMK) and normality tests (Pettitt, SNHT and Buishand) for CHIRPS monthly data from rainfall stations; Table S6. Results of non-parametric Mann-Kendall test and normality tests (Pettitt, SNHT and Buishand’s) for CHIRPS monthly data from rainfall stations.

Author Contributions

Conceptualization, J.B.; methodology, J.B.; formal analysis, J.B.; investigation, J.B.; resources, J.B.; data curation, J.B.; writing—original draft preparation, J.B.; writing—review and editing, P.M.d.B.T. and N.G.d.B.d.L.; visualization, E.G. and N.G.d.B.d.L.; translation, E.G.; supervision, E.G.; project administration, E.G.; funding acquisition, E.G. All authors have read and agreed to the published version of the manuscript.

Funding

The first author would like to thank FAPESP (Fundação de Amparo à Pesquisa do Estado de São Paulo) for granting the Postdoctoral Grant (process number n° 22/02383-3). The second author expresses gratitude to the Brazilian Coordination for the Improvement of Higher Education Personnel (CAPES) for granting the doctorate scholarship and to the Brazilian National Council for Scientific and Technological Development (CNPq) for the current postdoctoral grant (Process 165450/2020-7). The fourth author is grateful to the National Council for Scientific and Technological Development (CNPq) for the Research and Productivity Grant (Level 1D) process number 304973/2017-3.

Data Availability Statement

Data will be available upon request.

Acknowledgments

The first author thanks the following institutions: Fundação de Amparo à Pesquisa de São Paulo for funding this research. The fourth author thanks the National Council for Scientific and Technological Development (CNPq) for financial assistance through the Research and Productivity Research grant.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Gessner, U.; Naeimi, V.; Klein, I.; Kuenzer, C.; Klein, D.; Dech, S. The Relationship between Precipitation Anomalies and Satellite-Derived Vegetation Activity in Central Asia. Glob. Planet. Chang. 2013, 110, 74–87. [Google Scholar] [CrossRef]
  2. Duke, N.C.; Ball, M.C.; Ellison, J.C. Factors Influencing Biodiversity and Distributional Gradients in Mangroves. Biogeogr. Lett. 1998, 7, 27–47. [Google Scholar] [CrossRef]
  3. Alongi, D.M. The Impact of Climate Change on Mangrove Forests. Curr. Clim. Chang. Rep. 2015, 1, 30–39. [Google Scholar] [CrossRef]
  4. Osland, M.J.; Day, R.H.; From, A.S.; McCoy, M.L.; McLeod, J.L.; Kelleway, J.J. Life Stage Influences the Resistance and Resilience of Black Mangrove Forests to Winter Climate Extremes. Ecosphere 2015, 6, 1–15. [Google Scholar] [CrossRef]
  5. Osland, M.J.; Day, R.H.; Hall, C.T.; Brumfield, M.D.; Dugas, J.L.; Jones, W.R. Mangrove Expansion and Contraction at a Poleward Range Limit: Climate Extremes and Land-Ocean Temperature Gradients. Ecology 2017, 98, 125–137. [Google Scholar] [CrossRef] [PubMed]
  6. Asbridge, E.; Lucas, R.; Accad, A.; Dowling, R. Mangrove Response to Environmental Changes Predicted under Varying Climates: Case Studies from Australia. Curr. For. Rep. 2015, 1, 178–194. [Google Scholar] [CrossRef]
  7. Feher, L.C.; Osland, M.J.; Griffith, K.T.; Grace, J.B.; Howard, R.J.; Stagg, C.L.; Enwright, N.M.; Krauss, K.W.; Gabler, C.A.; Day, R.H.; et al. Linear and Nonlinear Effects of Temperature and Precipitation on Ecosystem Properties in Tidal Saline Wetlands. Ecosphere 2017, 8, e01956. [Google Scholar] [CrossRef]
  8. Tsesmelis, D.E.; Leveidioti, I.; Karavitis, C.A.; Kalogeropoulos, K.; Vasilakou, C.G.; Tsatsaris, A.; Zervas, E. Spatiotemporal Application of the Standardized Precipitation Index (SPI) in the Eastern Mediterranean. Climate 2023, 11, 95. [Google Scholar] [CrossRef]
  9. dos Santos, A.L.M.; Gonçalves, W.A.; Rodrigues, D.T.; Andrade, L.d.M.B.; e Silva, C.M.S. Evaluation of Extreme Precipitation Indices in Brazil’s Semiarid Region from Satellite Data. Atmosphere 2022, 13, 1598. [Google Scholar] [CrossRef]
  10. Mann, H.B. Non-Parametric Test against Trend. Econometrika 1945, 13, 245–259. [Google Scholar] [CrossRef]
  11. Kendall, M.G. Rank Correlation Methods, 5th ed.; Charles Griffin: London, UK, 1990. [Google Scholar]
  12. Sneyers, R. On the Statistical Analysis of Series of Observations; World Meteorological Organization: Geneva, Sweiterland, 1990; Volume 415. [Google Scholar]
  13. Pereira, G.; Silva, M.E.S.; Moraes, E.C.; Cardozo, F. da S. Evaluation of Precipitation Data Estimated by the TRMM Satellite for Brazil. Rev. Bras. De Recur. Hídricos 2013, 18, 139–148. [Google Scholar]
  14. Erazo, B.; Bourrel, L.; Frappart, F.; Chimborazo, O.; Labat, D.; Dominguez-Granda, L.; Matamoros, D.; Mejia, R. Validation of Satellite Estimates (Tropical Rainfall Measuring Mission, TRMM) for Rainfall Variability over the Pacific Slope and Coast of Ecuador. Water 2018, 10, 213. [Google Scholar] [CrossRef]
  15. Silva, G.K.d.; Marcos Júnior, A.D.; Lima, C.E.S.; Silva, M.V.M.d.; da Silveira, C.S.; da Silva, E.M.; de Lima, I.R. Analysis of the Spatio-Temporal Variability of the SPI: A Decaso Study for the Choró Sub-Basin, Ceará, Brazil. Rev. Bras. Meteorol. 2021, 36, 539–549. [Google Scholar] [CrossRef]
  16. Santos, B.C.d.; Sanches, R.G.; Moreira, R.M.; Bourscheidt, V.; de Souza, P.H. Análise Espaço-Temporal Da Precipitação Na Região Central Do Estado de São Paulo Utilizando Dados CHIRPS. Rev. Bras. Geogr. Física 2022, 15, 2582–2600. [Google Scholar] [CrossRef]
  17. Costa, J.; Pereira, G.; Siqueira, M.E.; Cardozo, F.; da Silva, V.V. Validation of Precipitation Data Chirps Estimated to Brazil. Rev. Bras. Climatol. 2019, 24, 243–288. [Google Scholar]
  18. Silva, C.B.; Silva, M.E.S.; Ambrizzi, T.; Tommaselli, J.T.G.; Patucci, N.N.; Mataveli, G.A.V.; Lima, B.S.; Correa, W.C. Precipitation in South America—Data Obtained from Automatic Stations and Orbita Systems. Rev. Bras. Climatol. 2019, 25, 54–79. [Google Scholar]
  19. Ouatiki, H.; Boudhar, A.; Tramblay, Y.; Jarlan, L.; Benabdelouhab, T.; Hanich, L.; El Meslouhi, M.R.; Chehbouni, A. Evaluation of TRMM 3B42 V7 Rainfall Product over the Oum Er Rbia Watershed in Morocco. Climate 2017, 5, 1. [Google Scholar] [CrossRef]
  20. Gummadi, S.; Dinku, T.; Shirsath, P.B.; Kadiyala, M.D.M. Evaluation of Multiple Satellite Precipitation Products for Rainfed Maize Production Systems over Vietnam. Sci. Rep. 2022, 12, 485. [Google Scholar] [CrossRef]
  21. Medina, F.D.; Zossi, B.S.; Bossolasco, A.; Elias, A.G. Performance of CHIRPS Dataset for Monthly and Annual Rainfall-Indices in Northern Argentina. Atmos. Res. 2023, 283, 106545. [Google Scholar] [CrossRef]
  22. Soares, A.S.D.; da Paz, A.R.; Piccilli, D.G.A. A Evaluation of TRMM Satellite Rainfall Estimates in the State of Paraíba. Rev. Bras. Recur. Hidr. 2016, 21, 288–299. [Google Scholar] [CrossRef]
  23. Silva, E.R.M.; Barbosa, I.C.C.; Silva, H.J.F.; Costa, L.G.S.; Rocha, E.J. Evaluating the Performance of Precipitation Estimate from CHIRPS Product for the Apeú River Basin, Castanhal-PA. Rev. Bras. Geogr. Física 2020, 13, 1094–1105. [Google Scholar] [CrossRef]
  24. de Moraes Cordeiro, A.L.; Blanco, C.J.C. Assessment of Satellite Products for Filling Rainfall Data Gaps in the Amazon Region. Nat. Resour. Model. 2021, 34, e12298. [Google Scholar] [CrossRef]
  25. Brasil Neto, R.M.; Santos, C.A.G.; Silva, J.F.C.B.d.C.; da Silva, R.M.; dos Santos, C.A.C.; Mishra, M. Evaluation of the TRMM Product for Monitoring Drought over Paraíba State, Northeastern Brazil: A Trend Analysis. Sci. Rep. 2021, 11, 1097. [Google Scholar] [CrossRef]
  26. Cunha-Lignon, M.; Kampel, M.; Menghini, R.; Schaeffer-Novelli, Y.; Cintrónβ, G.; Dahdouh-Guebas, F. Mangrove Forests Submitted to Depositional Processes and Salinity Variation Investigated Using Satellite Images and Vegetation Structure Surveys. Proc. Pol. J. Coast. Res. 2011, 64, 2011. [Google Scholar]
  27. Tessler, M.G.; Goya, S.C.; Yoshikawa, P.S.; Hurtado, S.N. In Erosion and Progradation of the Brazilian Costline; Muehe, D., Ed.; Ministério do Meio Ambiente: Brasilia, Brasil, 2006; p. 474. Available online: https://erosioncostera.furg.br/images/PDFs/livro_dieter_2006.pdf. (accessed on 12 August 2022).
  28. Brasil Decreto No 90.347, de 23 de Outubro de 1984. Available online: https://www.planalto.gov.br/ccivil_03/atos/decretos/1984/d90347.html (accessed on 29 August 2023).
  29. São Paulo Decreto N°. 40.319, de 03 DE Julho de 1962. Available online: https://www.al.sp.gov.br/repositorio/legislacao/decreto/1962/decreto-40319-03.07.1962.html (accessed on 29 August 2023).
  30. Ross, J.L.S. The Morphogenesis of the Ribeira Do Iguape Basin and Environmental Systems. GEOUSP—Espaço E Tempo 2002, 12, 21–46. [Google Scholar] [CrossRef]
  31. Dias, R.L.; Oliveira, R.C. de Socioeconomic Characterization and Mapping of Land Use and Occupation on the South Coast of the State of São Paulo. Soc. Nat. 2015, 27, 111–123. [Google Scholar] [CrossRef]
  32. Alvares, C.A.; Stape, J.L.; Sentelhas, P.C.; De Moraes Gonçalves, J.L.; Sparovek, G. Köppen’s Climate Classification Map for Brazil. Meteorol. Z. 2013, 22, 711–728. [Google Scholar] [CrossRef] [PubMed]
  33. Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and Future Köppen-Geiger Climate Classification Maps at 1-Km Resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef]
  34. Sant’Anna Neto, J.L. Climate Rhythm and the Genesis of Rain in the Coastal Zone of the State of São Paulo-Brazil. Master’s Thesis, Universidade de São Paulo, São Paulo, Brazil, 1990. [Google Scholar]
  35. Galvani, E.; Gilma, N.; De Lima, B.; Alves, R.R. Variability and Trend of Precipitation on the South Coast of São Paulo. Rev. Geonorte 2012, 1, 1163–1176. [Google Scholar]
  36. Reboita, M.S.; Alonso Gan, M.; Porfírio, R.; Rocha, D.A.; Ambrizzi, E.T. Precipitation Regimes in South America: A Bibliography Review. Rev. Bras. Meteorol. 2010, 25, 185–204. [Google Scholar] [CrossRef]
  37. Mello, Y.R.d.; Lopes, F.C.A.; Roseghini, W.F.F. Climatic characteristics na rhythic analysis applied to extreme events of precipitation and temperature in the city of Paranaguá, Paraná. Rev. Bras. Climatol. 2017, 13, 313–336. [Google Scholar]
  38. Sant’Anna Neto, J.L. Atmospheric Dynamics and the Transitional Character of the Climate in the Coastal Zone of São Paulo. Rev. Dep. Geogr. 1994, 8, 35–49. [Google Scholar]
  39. Seluchi, M.E.; Chou, S.C. Synoptic Patterns Associated with Landslide Events in the Serra Do Mar, Brazil. Theor. Appl. Clim. 2009, 98, 67–77. [Google Scholar] [CrossRef]
  40. Reboita, M.S.; Ambrizzi, T.; Porfírio Da Rocha, R. Underrstanding Weather and Climate in South America. Terra E Didat. 2012, 8, 34–50. [Google Scholar] [CrossRef]
  41. Verdan, I.; Silva, M.E.S. South Atlantic Convergence Zone variability in relation to ENSO events from 2000 to 2021. Geogr. Dep. Univ. Sao Paulo 2022, 42, e193110. [Google Scholar] [CrossRef]
  42. Dehaghani, A.M.; Gohari, A.; Zareian, M.J.; Torabi Haghighi, A. A Comprehensive Evaluation of the Satellite Precipitation Products across Iran. J. Hydrol. Reg. Stud. 2023, 46, 101360. [Google Scholar] [CrossRef]
  43. Ye, X.; Guo, Y.; Wang, Z.; Liang, L.; Tian, J. Extensive Evaluation of Four Satellite Precipitation Products and Their Hydrologic Applications over the Yarlung Zangbo River. Remote Sens. 2022, 14, 3350. [Google Scholar] [CrossRef]
  44. Reichle, R.H.; Liu, Q.; Koster, R.D.; Draper, C.S.; Mahanama, S.P.P.; Partyka, G.S. Land Surface Precipitation in MERRA-2. J. Clim. 2017, 30, 1643–1664. [Google Scholar] [CrossRef]
  45. Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Adler, R.F. TRMM (Tmpa) Precipitation L3 1 Day 0.25 Degree × 0.25 Degree V7; Savtchenko, A., Ed.; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2016. [Google Scholar] [CrossRef]
  46. NASA (National Aeronautics and Space Administration); Goddard Earth Sciences Data and Information Services Center. Tropical Rainfall Measurement Mission (TRMM). Available online: http://disc.sci.gsfc.nasa.gov/SSW/#keywords=TRMM_3B42_daily%207 (accessed on 29 August 2023).
  47. Wang, J.; Petersen, W.A.; Wolff, D.B. Validation of Satellite-Based Precipitation Products from TRMM to GPM. Remote Sens. 2021, 13, 1745. [Google Scholar] [CrossRef]
  48. Climate Hazards Center InfraRed Precipitation with Station Data (CHIRPS). Available online: https://www.chc.ucsb.edu/data (accessed on 29 August 2023).
  49. Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The Climate Hazards Infrared Precipitation with Stations—A New Environmental Record for Monitoring Extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
  50. de Oliveira-Júnior, J.F.; da Silva Junior, C.A.; Teodoro, P.E.; Rossi, F.S.; Blanco, C.J.C.; Lima, M.; de Gois, G.; Correia Filho, W.L.F.; de Barros Santiago, D.; dos Santos Vanderley, M.H.G. Confronting CHIRPS Dataset and in Situ Stations in the Detection of Wet and Drought Conditions in the Brazilian Midwest. Int. J. Climatol. 2021, 41, 4478–4493. [Google Scholar] [CrossRef]
  51. Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.K.; et al. MERRA: NASA’s Modern-Era Retrospective Analysis for Research and Applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
  52. Zandler, H.; Haag, I.; Samimi, C. Evaluation Needs and Temporal Performance Differences of Gridded Precipitation Products in Peripheral Mountain Regions. Sci. Rep. 2019, 9, 15118. [Google Scholar] [CrossRef]
  53. Ashouri, H.; Hsu, K.L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily Precipitation Climate Data Record from Multisatellite Observations for Hydrological and Climate Studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef]
  54. Sorooshian, A.; Alexandrov, M.D.; Bell, A.D.; Bennett, R.; Betito, G.; Burton, S.P.; Buzanowicz, M.E.; Cairns, B.; Chemyakin, E.V.; Chen, G.; et al. Spatially Coordinated Airborne Data and Complementary Products for Aerosol, Gas, Cloud, and Meteorological Studies: The NASA ACTIVATE Dataset. Earth Syst. Sci. Data 2023, 15, 3419–3472. [Google Scholar] [CrossRef]
  55. Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M.; Rudolf, B. GPCC’s New Land Surface Precipitation Climatology Based on Quality-Controlled in Situ Data and Its Role in Quantifying the Global Water Cycle. Theor. Appl. Clim. 2014, 115, 15–40. [Google Scholar] [CrossRef]
  56. Sadeghi, M.; Nguyen, P.; Naeini, M.R.; Hsu, K.; Braithwaite, D.; Sorooshian, S. PERSIANN-CCS-CDR, a 3-Hourly 0.04° Global Precipitation Climate Data Record for Heavy Precipitation Studies. Sci. Data 2021, 8, 157. [Google Scholar] [CrossRef] [PubMed]
  57. Kumar, L.; Mutanga, O. Google Earth Engine Applications since Inception: Usage, Trends, and Potential. Remote Sens. 2018, 10, 1509. [Google Scholar] [CrossRef]
  58. Shiff, S.; Helman, D.; Lensky, I.M. Worldwide Continuous Gap-Filled MODIS Land Surface Temperature Dataset. Sci. Data 2021, 8, 74. [Google Scholar] [CrossRef] [PubMed]
  59. Willmott, C.J.; Matsuura, K. Advantages of the Mean Absolute Error (MAE) over the Root Mean Square Error (RMSE) in Assessing Model Performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
  60. Chai, T.; Draxler, R.R. Root Mean Square Error (RMSE) or Mean Absolute Error (MAE)? -Arguments against Avoiding RMSE in the Literature. Geosci. Model. Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
  61. Gebremicael, T.G.; Mohamed, Y.A.; Zaag, P.v.d.; Gebremedhin, A.; Gebremeskel, G.; Yazew, E.; Kifle, M. Evaluation of Multiple Satellite Rainfall Products over the Rugged Topography of the Tekeze-Atbara Basin in Ethiopia. Int. J. Remote Sens. 2019, 40, 4326–4345. [Google Scholar] [CrossRef]
  62. Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; Legates, D.R.; O’Donnell, J.; Rowe, C.M. Statistics for the Evaluation and Comparison of Models. J. Geophys. Res. 1985, 90, 8995. [Google Scholar] [CrossRef]
  63. Aghakouchak, A.; Mehran, A. Extended Contingency Table: Performance Metrics for Satellite Observations and Climate Model Simulations. Water Resour. Res. 2013, 49, 7144–7149. [Google Scholar] [CrossRef]
  64. Xavier, A.C.F.; Rudke, A.P.; Serrão, E.A.d.O.; Terassi, P.M.d.B.; Pontes, P.R.M. Evaluation of Satellite-Derived Products for the Daily Average and Extreme Rainfall in the Mearim River Drainage Basin (Maranhão, Brazil). Remote Sens. 2021, 13, 4393. [Google Scholar] [CrossRef]
  65. Reyes, L.J.C.; Rangel, H.Á.; Herazo, L.C.S. Adjustment of the Standardized Precipitation Index (SPI) for the Evaluation of Drought in the Arroyo Pechelín Basin, Colombia, under Zero Monthly Precipitation Conditions. Atmosphere 2022, 13, 236. [Google Scholar] [CrossRef]
  66. Gozzo, L.F.; Palma, D.S.; Custódio, M.d.S.; Drumond, A. Climate Patterns Associated to Drought Events in Eastern São Paulo. Rev. Bras. Climatol. 2021, 28, 321–341. [Google Scholar]
  67. Ul Moazzam, M.F.; Rahman, G.; Munawar, S.; Tariq, A.; Safdar, Q.; Lee, B.G. Trends of Rainfall Variability and Drought Monitoring Using Standardized Precipitation Index in a Scarcely Gauged Basin of Northern Pakistan. Water 2022, 14, 1132. [Google Scholar] [CrossRef]
  68. Gois, G.d.; de José Francisco, O.-J.; Paiva, R.F.d.P.d.S.; Freitas, W.K.; Terassi, P.M.d.B.; Sobral, B.S. Pluviomect variability, drought indicators and the application of the Spi index to the middle Vale of Paraíba do Sul region-Rio de Janeiro. Rev. Bras. Climatol. 2020, 27, 122–157. [Google Scholar]
  69. Siqueira, B.; Nery, J.T. Analysis of the Standardized Precipitation Index for the State of São Paulo. Rev. Bras. Geogr. Física 2017, 10, 1775–1783. [Google Scholar] [CrossRef]
  70. Terassi, P.M.d.B.; Oliveira-Júnior, J.F.d.; de Góis, G.; Galvani, E. Standardized Precipitation Index Variability in the Northern Region of Paraná State Associated with the El Niño Southern Oscillation. Rev. Bras. Meteorol. 2018, 33, 11–25. [Google Scholar] [CrossRef]
  71. Almeida, L.P.d.; Pampuch, L.A.; Moraes Drumond, A.R.d.; Gozzo, L.F.; Negri, R.G. Multivariate Analysis of the SPI in the State of São Paulo. Rev. Bras. Climatol. 2023, 32, 337–362. [Google Scholar]
  72. Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
  73. Mckee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 17–22. [Google Scholar]
  74. Sneyers, R. Sur L’analyse Statistique Des Séries D’observations; Secrétariat de l’Organisation Météorologique Mondiale: Genève, Switerzerland, 1975. [Google Scholar]
  75. Pettitt, A.N. A Non-Parametric Approach to the Change-Point Problem. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
  76. Alexandersson, H.; Moberg, A. Homogenization of Swedish Temperature Data. Part i: Homogeneity Test for Linear Trends. Int. J. Climatol. 1997, 17, 25–34. [Google Scholar] [CrossRef]
  77. Buishand, T.A. Some Methods for Testing the Homogeneity of Rainfall. J. Hydrol. 1982, 58, 11–27. [Google Scholar] [CrossRef]
  78. Kocsis, T.; Kovács-Székely, I.; Anda, A. Homogeneity Tests and Non-Parametric Analyses of Tendencies in Precipitation Time Series in Keszthely, Western Hungary. Theor. Appl. Clim. 2020, 139, 849–859. [Google Scholar] [CrossRef]
  79. Akinsanola, A.A.; Ogunjobi, K.O. Recent Homogeneity Analysis and Long-Term Spatio-Temporal Rainfall Trends in Nigeria. Theor. Appl. Clim. 2017, 128, 275–289. [Google Scholar] [CrossRef]
  80. R Development Core Team A Language and Environment for Statistical Computing. Available online: http://www.r-project.org (accessed on 29 August 2023).
  81. Ma, Y.; Tang, G.; Long, D.; Yong, B.; Zhong, L.; Wan, W.; Hong, Y. Similarity and Error Intercomparison of the GPM and Its Predecessor-TRMM Multisatellite Precipitation Analysis Using the Best Available Hourly Gauge Network over the Tibetan Plateau. Remote Sens. 2016, 8, 569. [Google Scholar] [CrossRef]
  82. Martins, L.L.; Sobierajski, G.D.R.; Blain, G.C. Increases in the Frequency of Meteorological Droughts in the São Paulo State, Brazil, under Climate Change Conditions. Derbyana 2023, 44, 1–13. [Google Scholar] [CrossRef]
  83. Cavalcante, R.B.L.; Ferreira, D.B.d.S.; Pontes, P.R.M.; Tedeschi, R.G.; da Costa, C.P.W.; de Souza, E.B. Evaluation of Extreme Rainfall Indices from CHIRPS Precipitation Estimates over the Brazilian Amazonia. Atmos. Res. 2020, 238, 10489. [Google Scholar] [CrossRef]
  84. Abreu, M.; Souza, A.; Lins, T.M.P.; Oliveira-Junior, J.F.; Oliveira, S.S.; Fernandes, W.; Almeida, L.T.d.; Torsen, E. Comparison and Validation of Trmm Satellite Precipitation Estimates and Data Observed in Mato Grosso Sul State, Brazil. Rev. Bras. Climatol. 2020, 27, 566–589. [Google Scholar]
  85. NOAA (National Oceanic and Atmospheric Administration) El Niño-Southern Oscillation (ENOS). Available online: https://origin.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/ONI_v5.php (accessed on 29 August 2023).
  86. Terassi, P.M.d.B.; Galvani, E. Identification of Homogeneous Rainfall Regions in the Eastern Watersheds of the State of Paraná, Brazil. Climate 2017, 5, 53. [Google Scholar] [CrossRef]
  87. Monteiro, C.A.F. Climate Dynamics and Rain in the State of São Paulo: Geographic Study in the Form of an Atlas; Climatology Laboratory, Institute of Geography: São Paulo, Brazil, 1973. [Google Scholar]
  88. Alongi, D.M. Climate Change and Mangroves. In Mangroves: Biodiversity, Livelihoods and Conservation; Springer Nature: Singapore, 2022; pp. 175–198. ISBN 9789811905193. [Google Scholar]
  89. Dufek, A.S.; Ambrizzi, T. Precipitation Variability in São Paulo State, Brazil. Theor. Appl. Clim. 2008, 93, 167–178. [Google Scholar] [CrossRef]
  90. Haylock, M.R.; Peterson, T.C.; Alves, L.M.; Ambrizzi, T.; Anunciação, Y.M.T.; Baez, J.; Barros, V.R.; Berlato, M.A.; Bidegain, M.; Coronel, G.; et al. Trends in Total and Extreme South American Rainfall in 1960-2000 and Links with Sea Surface Temperature. J. Clim. 2006, 19, 1490–1512. [Google Scholar] [CrossRef]
  91. Regoto, P.; Dereczynski, C.; Chou, S.C.; Bazzanela, A.C. Observed Changes in Air Temperature and Precipitation Extremes over Brazil. Int. J. Climatol. 2021, 41, 5125–5142. [Google Scholar] [CrossRef]
  92. Salviano, M.F.; Groppo, J.D.; Pellegrino, G.Q. Trend Analysis in Precipitation and Temperature Data in Brazil. Rev. Bras. Meteorol. 2016, 31, 64–73. [Google Scholar] [CrossRef]
  93. Terassi, P.M.d.B.; da Silva Oscar-Júnior, A.C.; Galvani, E.; de Oliveira-Júnior, J.F.; Sobral, B.S.; Biffi, V.H.R.; de Gois, G. Daily Rainfall Intensity and Temporal Trends in Eastern Paraná State—Brazil. Urban. Clim. 2022, 42, 101090. [Google Scholar] [CrossRef]
  94. Correa, M.G.G.; Galvani, E. The Impact of El Niño-Southern Oscillation on the Rainfall Temporal Variability in the Piquiri Watershed, Paraná State, Brazil. Rev. Do Inst. Geol. 2020, 41, 21–33. [Google Scholar] [CrossRef]
  95. Arikan, B.B.; Kahya, E. Homogeneity Revisited: Analysis of Updated Precipitation Series in Turkey. Theor. Appl. Clim. 2019, 135, 211–220. [Google Scholar] [CrossRef]
  96. Penereiro, J.C.; Meschiatti, M.C. Trends in the Annual Rainfall and Temperatures Series in Brazil. Eng. Sanit. E Ambient. 2018, 23, 319–331. [Google Scholar] [CrossRef]
  97. Nascimento Júnior, L.; Lima Sant, J.; Neto, A. Contribution to Precipitation Studies in Paraná State: The Pacific Decadal Oscillation-PDO. Raega O. Espaço Em Análise 2015, 35, 314–343. [Google Scholar]
  98. Nery, J.T.; Carfan, A.C. Re-Analysis of Pluvial Precipitation in Southern Brazil. Atmósfera 2014, 27, 103–115. [Google Scholar] [CrossRef]
  99. Martínez, M.D.; Serra, C.; Burgueño, A.; Lana, X. Time Trends of Daily Maximum and Minimum Temperatures in Catalonia (Ne Spain) for the Period 1975-2004. Int. J. Climatol. 2010, 30, 267–290. [Google Scholar] [CrossRef]
  100. Göktürk, O.M.; Bozkurt, D.; Şen, Ö.L.; Karaca, M. Quality Control and Homogeneity of Turkish Precipitation Data. Hydrol. Process 2008, 22, 3210–3218. [Google Scholar] [CrossRef]
  101. Lima, N.; Cunha-Lignon, M.; Martins, A.; Armani, G.; Galvani, E. Impacts of Extreme Weather Event in Southeast Brazilian Mangrove Forest. Atmosphere 2023, 14, 1195. [Google Scholar] [CrossRef]
  102. Giri, C.; Ochieng, E.; Tieszen, L.L.; Zhu, Z.; Singh, A.; Loveland, T.; Masek, J.; Duke, N. Status and Distribution of Mangrove Forests of the World Using Earth Observation Satellite Data. Glob. Ecol. Biogeogr. 2011, 20, 154–159. [Google Scholar] [CrossRef]
  103. Alongi, D.M. Present State and Future of the World’s Mangrove Forests. Environ. Conserv. 2002, 29, 331–349. [Google Scholar] [CrossRef]
Climate 12 00022 g001
Figure 1. Location of the study area and rainfall stations.
Figure 1. Location of the study area and rainfall stations.
Climate 12 00022 g001
Climate 12 00022 g002
Figure 2. Statistical metrics are used to validate the monthly data of satellite rainfall products with data from the surface weather station.
Figure 2. Statistical metrics are used to validate the monthly data of satellite rainfall products with data from the surface weather station.
Climate 12 00022 g002
Climate 12 00022 g003
Figure 3. Result of the statistical metrics Pbias (A) and d-index (B) were used to validate the monthly data of satellite rainfall products with data from the surface weather station.
Figure 3. Result of the statistical metrics Pbias (A) and d-index (B) were used to validate the monthly data of satellite rainfall products with data from the surface weather station.
Climate 12 00022 g003
Climate 12 00022 g004
Figure 4. Standardized Precipitation Index (SPI-12) for CHIRPS monthly precipitation data at rainfall station locations.
Figure 4. Standardized Precipitation Index (SPI-12) for CHIRPS monthly precipitation data at rainfall station locations.
Climate 12 00022 g004
Climate 12 00022 g005
Figure 5. Standardized Precipitation Index (SPI-3) for CHIRPS monthly precipitation data at rainfall stations.
Figure 5. Standardized Precipitation Index (SPI-3) for CHIRPS monthly precipitation data at rainfall stations.
Climate 12 00022 g005
Climate 12 00022 g006
Figure 6. Standardized Precipitation Index (SPI-1) for CHIRPS monthly precipitation data at rainfall stations.
Figure 6. Standardized Precipitation Index (SPI-1) for CHIRPS monthly precipitation data at rainfall stations.
Climate 12 00022 g006
Climate 12 00022 g007
Figure 7. Spatial distribution of trends in the Mann–Kendall test of monthly rainfall for the most representative months.
Figure 7. Spatial distribution of trends in the Mann–Kendall test of monthly rainfall for the most representative months.
Climate 12 00022 g007
Climate 12 00022 g008
Figure 8. Change in monthly rainfall for the month of March in the normality tests (Pettitt, SNHT, and Buishand’s) to identify the breakpoint (year) for the study area in IDs 3, 5, and 7.
Figure 8. Change in monthly rainfall for the month of March in the normality tests (Pettitt, SNHT, and Buishand’s) to identify the breakpoint (year) for the study area in IDs 3, 5, and 7.
Climate 12 00022 g008
Climate 12 00022 g009
Figure 9. Change in monthly rainfall for the month of June in the SNHT normality test to identify the breakpoint (year) for the study area.
Figure 9. Change in monthly rainfall for the month of June in the SNHT normality test to identify the breakpoint (year) for the study area.
Climate 12 00022 g009
Table 1. Identification and characteristics of the analyzed pluviometric stations.
Table 1. Identification and characteristics of the analyzed pluviometric stations.
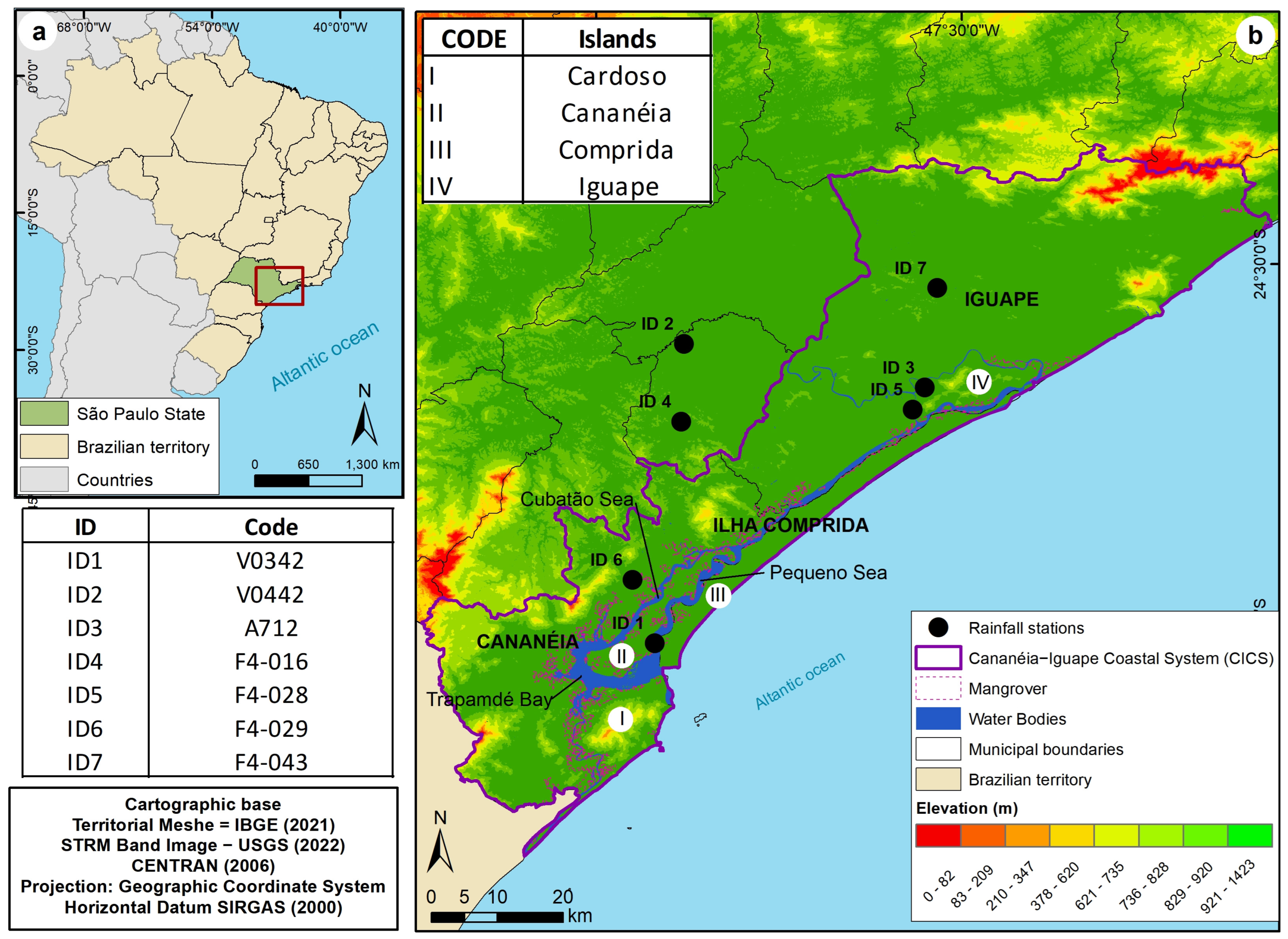
IDLatitudeLongitudeElevation (m)PeriodFailure (%)InstitutionCity
ID125°1′13″ S47°55′30″ W12009–20190CIIAGROCananéia
ID224°36′39″ S47°53′0″ W342009–20194.1CIIAGROPariquera-Açu
ID324°40′18″ S47°32′43″ W62009–20198.3INMETIguape
ID424°43′0″ S47°53′0″ W302009–20193.4DAEEPariquera-Açu
ID524°42′0″ S47°34′0″ W32009–20191.3DAEEIguape
ID624°56′0″ S47°57′0″ W72009–20196.2DAEECananéia
ID724°32′0″ S47°32′00″ W302009–20193.4DAEEIguape
Legend: INMET—National Institute of Meteorology; CIIAGRO—Integrated Center for Agrometeorological Information; DAEE—Department of Water and Electric Energy.
Table 2. Summary of selected satellite rainfall products for this study.
Table 2. Summary of selected satellite rainfall products for this study.
ProductTemporal ResolutionSpatial ResolutionCoverageStarting Data
TRMM3 h0.25°50° N–50° S, 0°–360° E1998–2018
CHIRPSdaily0.05°50° N–50° S, 0°–360° E1981
PERSIANN CDRdaily0.50° × 0.625°Global1983
MERRA-2daily0.25°Global1980
Table 3. Results of non-parametric Mann–Kendall test (TMK) and normality tests (Pettitt, SNHT, and Buishand’s) for CHIRPS data from rainfall stations.
Table 3. Results of non-parametric Mann–Kendall test (TMK) and normality tests (Pettitt, SNHT, and Buishand’s) for CHIRPS data from rainfall stations.
Mann–KendallPettittSNHTBuishand’s
IDTAUP.VAZMKSen’s SlopeKP.VAtT0P.VAtQP.VAt
1−0.1170.286−1.00−8.2271640.256201711.7710.005 *20177.2780.098+2017
2−0.0900.412−0.650−3.4281500.40720178.4450.091+20186.1410.2352017
3−0.2070.058+−1.67−7.0861580.31619987.3040.12220177.0480.1101998
4−0.0100.937−0.043−0.5181460.46120177.5980.10320185.7390.2972017
5−0.2070.058+−1.67−7.0861580.31319987.3040.12220177.0480.1101998
6−0.0100.937−0.09−1.1061520.38220178.9270.034 *20176.3380.2022017
7−0.3100.004 **−2.71−10.6832460.008 **199810.3060.061+199810.2530.004+1998
Legend: ** = 99% significance; * = 95% significance; = 90% significance; TAU = trend curvature magnitude; P.VA = significance level; K = value that indicates the possibility of locating the point where the ruptures occurred in the series; t = value that indicates the position of ruptures; T0 and Q = critical values of the SNHT and Buishand’s tests. Results with statistical significance are highlighted in bold.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Baratto, J.; de Bodas Terassi, P.M.; de Beserra de Lima, N.G.; Galvani, E. Precipitation Anomalies and Trends Estimated via Satellite Rainfall Products in the Cananeia–Iguape Coastal System, Southeast Region of Brazil. Climate 2024, 12, 22. https://doi.org/10.3390/cli12020022

AMA Style

Baratto J, de Bodas Terassi PM, de Beserra de Lima NG, Galvani E. Precipitation Anomalies and Trends Estimated via Satellite Rainfall Products in the Cananeia–Iguape Coastal System, Southeast Region of Brazil. Climate. 2024; 12(2):22. https://doi.org/10.3390/cli12020022

Chicago/Turabian Style

Baratto, Jakeline, Paulo Miguel de Bodas Terassi, Nádia Gilma de Beserra de Lima, and Emerson Galvani. 2024. "Precipitation Anomalies and Trends Estimated via Satellite Rainfall Products in the Cananeia–Iguape Coastal System, Southeast Region of Brazil" Climate 12, no. 2: 22. https://doi.org/10.3390/cli12020022

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop