On the Equality Assumption of Latent and Sensible Heat Energy Transfer Coefficients of the Bowen Ratio Theory for Evapotranspiration Estimations: Another Look at the Potential Causes of Inequalities
Abstract
:1. Introduction
2. Theoretical Synopses
2.1. Law of Turbulent Diffusion
2.2. Theory of Bowen Ratio
2.3. Theory of Eddy Covariance Method
3. Methodology
3.1. Site Description
3.2. Data Collection and Modifications
- (I)
- Coordinate rotation: as mentioned during the theoretical analyses, the eddy covariance method relies on the movement of a parcel of air through an isobaric surface and the conservation of mass principle inside that parcel of air. The procedure assumes homogeneity of the properties of air (i.e., air temperature, vapor pressure, etc.) inside a parcel of air. To accommodate the two aforementioned assumptions in the calculations, it is often necessary to measure or estimate the flow of material fluxes across each surface of the parcel, and the most convenient way to make such estimations are by assuming Cartesian coordinate system. The shape of the parcel of air depends on the coordinate systems used. For example, in Cartesian coordinate system the shape is rectangular. Therefore, if for a Cartesian coordinate system the X–axis is aligned along the mean wind vector, or in other words, the mean wind speeds along the Y and Z axes are equaled to zero, that essentially eliminates the effect of any long-term (longer than the averaging period) fluctuations of atmospheric variables [23]. The coordinate rotation corrections were applied to the eddy covariance data.
- (II)
- Moisture correction: the CSAT3 sonic anemometer functions based on the properties of sound propagation in the air. The sonic anemometer consists of two transducers separated by a specified distance, and each transducer consists of one sound emitter and one sound receiver. In general, the two transducers are installed along Z-direction. The time taken by the sound wave to travel from one emitter to a receiver is a function of vertical distance between the two transducers, the speed of sound wave in the zero wind speed, the vertical wind speed and the angular deviation of the sound wave, from a vertical direction, caused by the horizontal wind [24,25]. The speed of the sound wave in calm wind depends on the air temperature and atmospheric moisture content [24]. As a result, the humidity and the horizontal wind speed influence on the temperature measured by the sonic anemometer [24,25]. Data were subjected to the correction steps suggested by [24] to overcome this deficiency.
- (III)
- Frequency response correction: the frequency response correction is an “umbrella term” under which corrections related to several different reasons may appear. These are mostly related to the limitations of the instruments used in the EC systems, failing to completely satisfy the theoretical assumptions behind eddy covariance method. A few examples of such sources of errors are sensor response functions, sensor time averaging, sensor separation, frequency response of data acquisition, etc. [27]. The author in [27] also suggested alternative correction steps to overcome such limitations, which were implemented in the eddy covariance datasets.
- (IV)
- Oxygen correction: the KH20 functions based on the properties of ultra-violet (UV) light absorption by atmospheric moisture. The KH20 consists of an emitter and a receiver, separated by a very small distance (usually around 0.01 m). The emitter emits two monochromatic beams of wavelengths 1165 Å and 1236 Å, and the receiver receives the light beams after they have passed through the air gap between the emitter and the receiver. The amount of light absorbed in the gap is directly related to the amount of moisture content in air in the gap, and this is the relationship that is used to estimate the atmospheric moisture content. However, along with moisture, the UV light (especially the one with λ = 1236 Å) is also absorbed by atmospheric oxygen, giving rise to the necessity of oxygen correction to the eddy covariance data [26].
- (V)
- Webb-Pearman-Leuning (WPL) correction: this is an important correction for eddy covariance estimation of trace gases, such as CO2, water vapor, etc. An eddy is nothing but a circulating wind; so in an eddy there are both upward and downward motion of air. During the transfer of heat the warmer air is lighter than the colder air and, as a result, the warmer air tends to ascend upwards and the colder air tends to descend downwards. Therefore, when measured in the field, the total mass of the upward air tends to be lower than that of the downward air. This creates a net downward movement of air mass; violating the first principle of mass balance in eddies. To compensate this error, the correction applied for is called the WPL correction, named after the first initials of the authors who first observed this error and suggested this correction [28].
3.3. Stability Assessment
4. Results and Discussion
4.1. Interrelations between KV and KH
4.2. Seasonal Variations of KV and KH



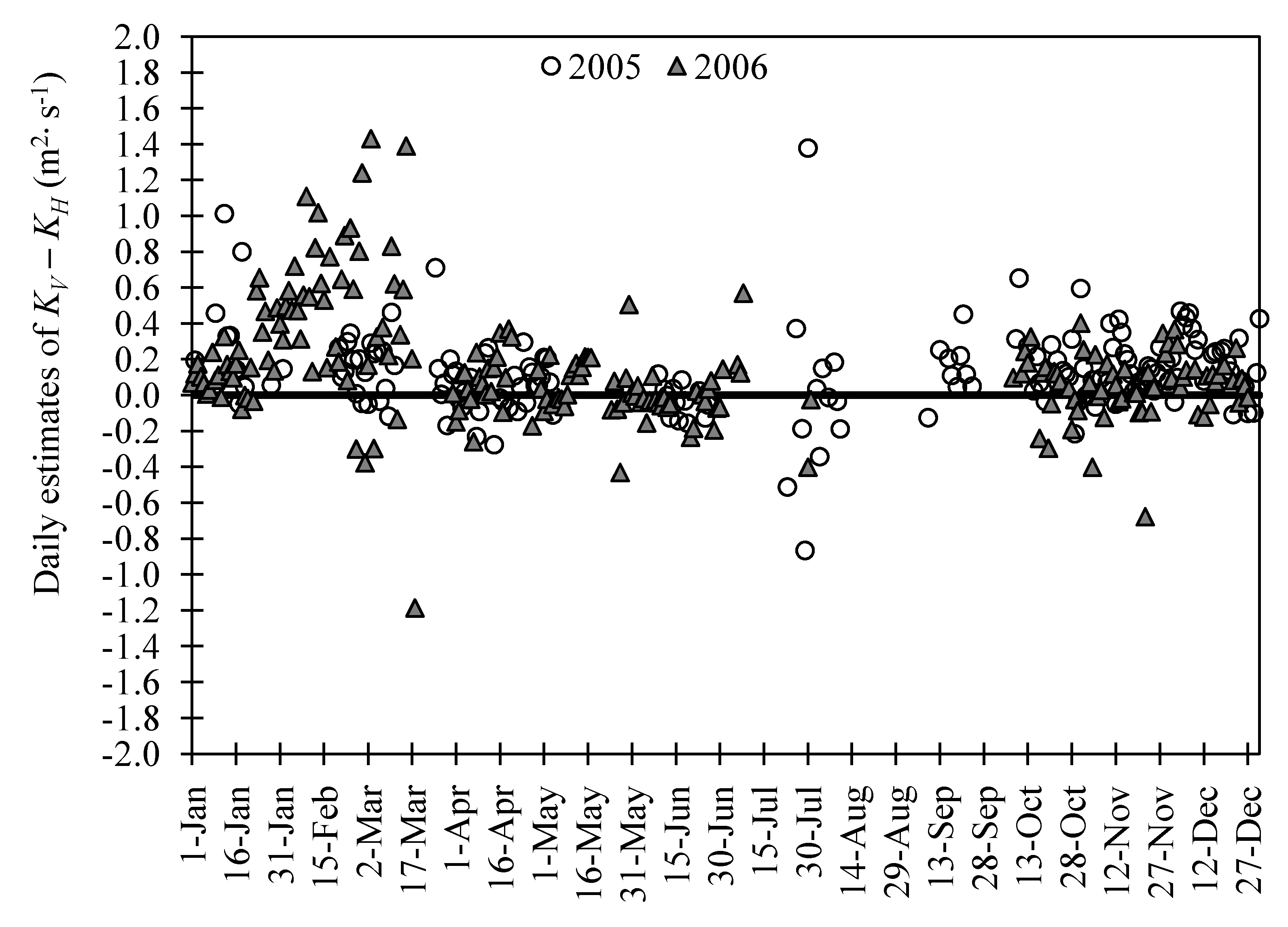
4.3. Diurnal Variations of KV and KH


4.4. Correction for Inequalities between KV and KH
4.4.1. Theoretical Analysis for Correction of KV and KH

4.4.2. Empirical Estimation of Bowen Ratio



5. Conclusions
Author Contributions
Conflicts of Interest
Disclaimer
References
- Alfieri, J.G.; Blanken, P.D.; Smith, D.; Morgan, J. Concerning the measurement and magnitude of heat, water vapor,and carbon dioxide exchange from a semiarid grassland. J. Appl. Meteorol. Clim. 2009, 48, 982–996. [Google Scholar] [CrossRef]
- Bowen, I.S. The ratio of heat losses by conduction and by evaporation from any water surface. Phys. Rev. 1926, 27, 779–787. [Google Scholar] [CrossRef]
- Monin, A.S.; Obukhov, A.M. The basic laws of turbulent mixing in the surface layer of the atmosphere. Akad. Nauk. SSSR Trud. Geofiz. Inst. 1954, 24, 163–187. [Google Scholar]
- Gavilan, P.; Berengena, J. Accuracy of the Bowen ratio-energy balance method for measuring latent heat flux in a semiarid advective environment. Irrig. Sci. 2007, 25, 127–140. [Google Scholar] [CrossRef]
- Brotzge, J.A.; Crawford, K.C. Examination of the surface energy budget: A comparison of Eddy correlation and Bowen ratio measurement systems. J. Hydrometeorol. 2003, 4, 160–178. [Google Scholar] [CrossRef]
- Lee, X.H.; Yu, Q.; Sun, X.M.; Liu, J.D.; Min, Q.W.; Liu, Y.F.; Zhang, X.Z. Micrometeorological fluxes under the influence of regional and local advection: A revisit. Agric. For. Meteorol. 2004, 122, 111–124. [Google Scholar] [CrossRef]
- Laubach, J.; McNaughton, K.G.; Wilson, J.D. Heat and water vapor diffusivities near the base of a disturbed internal boundary layer. Bound. Layer Meteorol. 2000, 94, 23–63. [Google Scholar] [CrossRef]
- De Bruin, H.A.R.; van den Hurk, B.J.J.M.; Kroon, L.J.M. On the temperature-humidity correlation and similarity. Bound. Layer Meteorol. 1999, 93, 453–468. [Google Scholar]
- Lang, A.R.G.; McNaugton, K.G.; Fazu, C.; Bradley, E.F.; Ohtaki, E. Inequality of eddy transfer coefficients for vertical transport of sensible and latent heats during advective inversions. Bound. Layer Meteorol. 1983, 25, 25–41. [Google Scholar] [CrossRef]
- Motha, R.P.; Verma, S.B.; Rosenberg, N.J. Exchange of coefficients under sensible heat advection determined by eddy correlation. Agric. For. Meteorol. 1979, 20, 273–280. [Google Scholar] [CrossRef]
- Verma, S.B.; Rosenberg, N.J.; Blad, B.L. Turbulent exchange coefficients for sensible heat and water vapor under advective conditions. J. Appl. Meteorol. 1978, 17, 330–338. [Google Scholar] [CrossRef]
- Warhaft, Z. Heat and moisture flux in the stratified boundary layer. Q. R. J. Meterol. Soc. 1976, 102, 703–720. [Google Scholar] [CrossRef]
- Blad, B.L.; Rosenberg, N.J. Lysimetric calibration of the Bopwen ratio-energy balance method for evapotranspiration estimation in the Central Great Plains. J. Appl. Meteoreol. 1974, 13, 227–236. [Google Scholar] [CrossRef]
- Laubach, J.; Raschendorfer, M.; Kreilein, H. Determination of heat and water vapour fluxes above a spurse forest by eddy correlation. Agric. For. Meteorol. 1994, 71, 373–401. [Google Scholar] [CrossRef]
- McNaughton, K.G.; Laubach, J. Unsteadiness as a cause of non-equality of eddy diffusivities for heat and vapour at the base of an advective inversion. Bound. Layer Meteorol. 1998, 88, 479–504. [Google Scholar] [CrossRef]
- Irmak, S.; Mutiibwa, D. On the dynamics of stomatal resistance: Relationships between stomatal behavior and micrometeorological variables and performance of Jarvis-type parameterization. Trans. ASABE 2009, 52, 1923–1939. [Google Scholar] [CrossRef]
- Priestley, H.B.; Swinbank, W.C. Vertical transport of heat by turbulence in the atmosphere. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1947, 189, 543–561. [Google Scholar] [CrossRef]
- Swinbank, W.C. The measurement of vertical transfer of heat and water vapor by eddies in the lower atmosphere. J. Meteorol. 1951, 8, 135–145. [Google Scholar] [CrossRef]
- Irmak, A.; Irmak, S. Reference and crop evapotranspiration in South Central Nebraska. II: Measurement and estimation of actual evapotranspiration for corn. J. Irrig. Drain. Eng. 2008, 134, 700–715. [Google Scholar]
- Irmak, S.; Mutiibwa, D. On the dynamics of evaporative losses from Penman-Monteith with fixed and variable canopy. Trans. ASABE 2009, 52, 1139–1153. [Google Scholar] [CrossRef]
- Irmak, S. Nebraska water and energy flux measurement, modeling, and research network (NEBFLUX). Trans. ASABE 2010, 53, 1097–1115. [Google Scholar] [CrossRef]
- Irmak, S.; Mutiibwa, D. On the dynamics of canopy resistance: Generalized-linear estimation and its relationships with primary micrometeorological variables. Water Resour. Res. 2010, 46, 1–20. [Google Scholar] [CrossRef]
- Finnigan, J.J.; Clement, R.; Malhi, Y.; Leuning, V.; Cleugh, H.A. A re-evaluaion of long-term flux measuremtn techniques Part I: Averaging and coordinate rotation. Bound. Layer Meteorol. 2003, 107, 1–48. [Google Scholar] [CrossRef]
- Schotanus, P.; Neuwstadt, F.T.M.; de Bruin, H.A.R. Temperature measurement with a sonic anemometer and its application to heat and moisture fluxes. Bound. Layer Meteorol. 1983, 26, 81–93. [Google Scholar] [CrossRef]
- Kaimal, J.C.; Businger, J.A. A continuous wave sonic anemometer-thermometer. J. Appl. Meteorol. 1963, 2, 156–164. [Google Scholar] [CrossRef]
- Van Dijk, A.; Kosher, W.; de Bruin, H.A.R. Oxygen sensitivity of Krypton and Lyman-α hygrometers. J. Atmos. Ocean. Technol. 2003, 20, 143–151. [Google Scholar]
- Moore, C.J. Frequency response corrections for eddy correlation systems. Bound. Layer Meteorol. 1986, 37, 17–35. [Google Scholar] [CrossRef]
- Webb, E.K.; Pearman, G.I.; Leuning, R. Correction of flux measurements for density effects due to heat and water vapour transfer. Q. R. J. Meteorol. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Ohmura, A. Objective criteria for rejecting data for Bowen-Ratio flux calculations. J. Appl. Meteorol. 1982, 21, 595–598. [Google Scholar] [CrossRef]
- Veihemeyer, F.J. Evapotranspiration. In Handbook of Applied Hydrology; Chow, V.T., Ed.; McGraw-Hill Company: New York, NY, USA, 1964; pp. 11:1–11:38. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Irmak, S.; Kilic, A.; Chatterjee, S. On the Equality Assumption of Latent and Sensible Heat Energy Transfer Coefficients of the Bowen Ratio Theory for Evapotranspiration Estimations: Another Look at the Potential Causes of Inequalities. Climate 2014, 2, 181-205. https://doi.org/10.3390/cli2030181
Irmak S, Kilic A, Chatterjee S. On the Equality Assumption of Latent and Sensible Heat Energy Transfer Coefficients of the Bowen Ratio Theory for Evapotranspiration Estimations: Another Look at the Potential Causes of Inequalities. Climate. 2014; 2(3):181-205. https://doi.org/10.3390/cli2030181
Chicago/Turabian StyleIrmak, Suat, Ayse Kilic, and Sumantra Chatterjee. 2014. "On the Equality Assumption of Latent and Sensible Heat Energy Transfer Coefficients of the Bowen Ratio Theory for Evapotranspiration Estimations: Another Look at the Potential Causes of Inequalities" Climate 2, no. 3: 181-205. https://doi.org/10.3390/cli2030181
APA StyleIrmak, S., Kilic, A., & Chatterjee, S. (2014). On the Equality Assumption of Latent and Sensible Heat Energy Transfer Coefficients of the Bowen Ratio Theory for Evapotranspiration Estimations: Another Look at the Potential Causes of Inequalities. Climate, 2(3), 181-205. https://doi.org/10.3390/cli2030181



