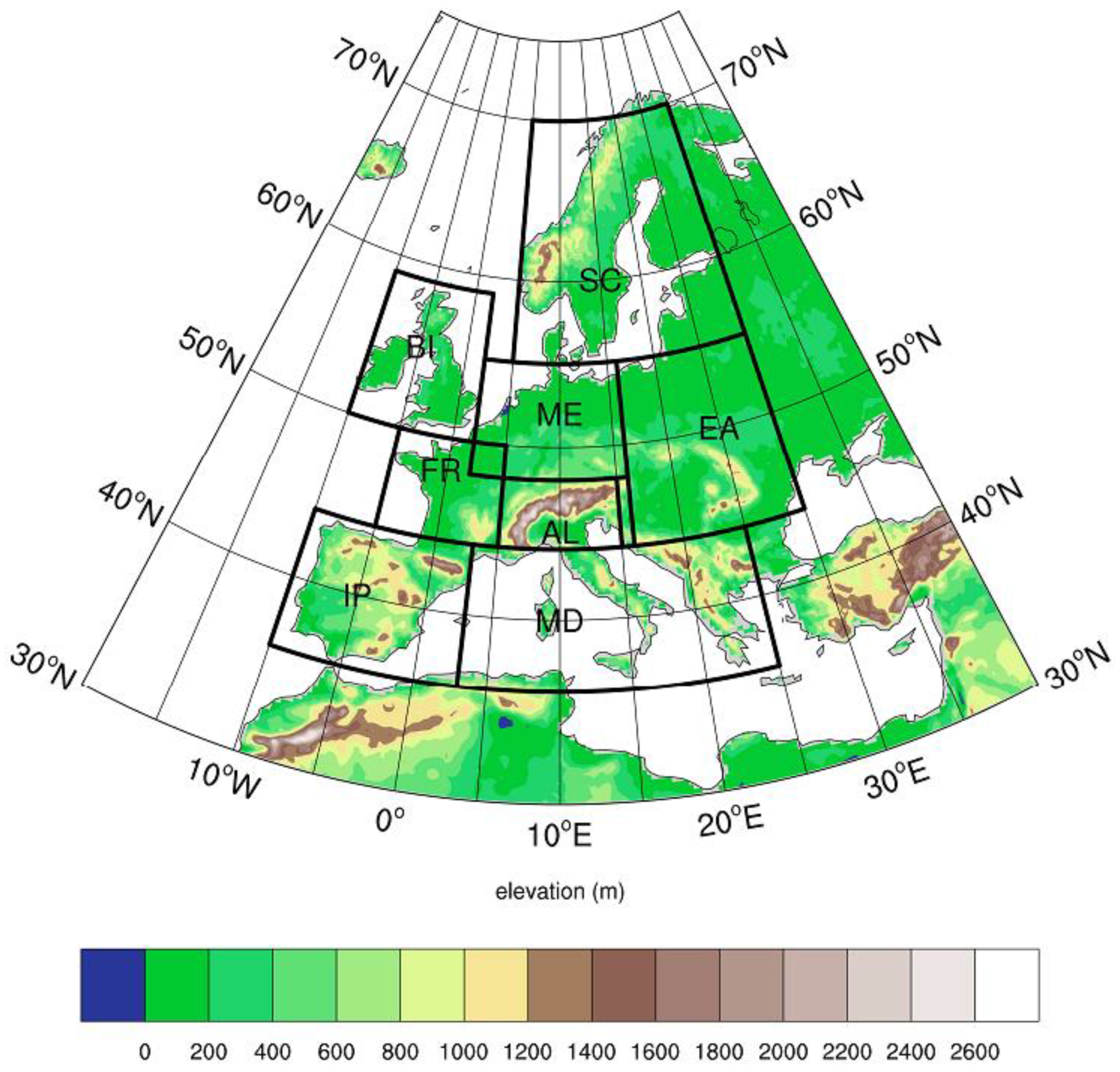
Figure 1.
Subdomains based on the Prudence project: the Alps (AL), the British Isles (BI), Eastern Europe (EA), France (FR), the Iberian Peninsula (IP), the Mediterranean (MD), Mid-Europe (ME) and Scandinavia (SC).
Figure 1.
Subdomains based on the Prudence project: the Alps (AL), the British Isles (BI), Eastern Europe (EA), France (FR), the Iberian Peninsula (IP), the Mediterranean (MD), Mid-Europe (ME) and Scandinavia (SC).
Figure 2.
Simulated K-G climate classification according to E-OBS (A) and in ALADIN (B), HIRHAM (C), RegCM (D), RAMCMO2 (E) and RCA (F) without bias correction.
Figure 2.
Simulated K-G climate classification according to E-OBS (A) and in ALADIN (B), HIRHAM (C), RegCM (D), RAMCMO2 (E) and RCA (F) without bias correction.
Figure 3.
Simulated K-G climate classification according to E-OBS (A) and empirical quantile mapping (eQM) corrected precipitation and temperature with 90-day moving window in ALADIN (B), HIRHAM (C), RegCM (D), RAMCMO2 (E) and RCA (F).
Figure 3.
Simulated K-G climate classification according to E-OBS (A) and empirical quantile mapping (eQM) corrected precipitation and temperature with 90-day moving window in ALADIN (B), HIRHAM (C), RegCM (D), RAMCMO2 (E) and RCA (F).
Figure 4.
Simulated K-G climate classification according to E-OBS (A) and quantile mapping of precipitation and temperature based on a gamma + Generalized Pareto Distribution (gpQM) correction of precipitation and eQM correction of temperature with 90-day moving window in ALADIN (B), HIRHAM (C), RegCM (D), RAMCMO2 (E) and RCA (F).
Figure 4.
Simulated K-G climate classification according to E-OBS (A) and quantile mapping of precipitation and temperature based on a gamma + Generalized Pareto Distribution (gpQM) correction of precipitation and eQM correction of temperature with 90-day moving window in ALADIN (B), HIRHAM (C), RegCM (D), RAMCMO2 (E) and RCA (F).
Figure 5.
Simulated K-G climate classification according to E-OBS (A) and power transformation of precipitation and variance scaling of temperature correction in ALADIN (B), HIRHAM (C), RegCM (D), RAMCMO2 (E) and RCA (F).
Figure 5.
Simulated K-G climate classification according to E-OBS (A) and power transformation of precipitation and variance scaling of temperature correction in ALADIN (B), HIRHAM (C), RegCM (D), RAMCMO2 (E) and RCA (F).
Figure 6.
Simulated K-G climate classification according to E-OBS (A) and local intensity scaling of precipitation and variance scaling of temperature correction in ALADIN (B), HIRHAM (C), RegCM (D), RAMCMO2 (E) and RCA (F).
Figure 6.
Simulated K-G climate classification according to E-OBS (A) and local intensity scaling of precipitation and variance scaling of temperature correction in ALADIN (B), HIRHAM (C), RegCM (D), RAMCMO2 (E) and RCA (F).
Figure 7.
Simulated K-G climate classification according to E-OBS (A) and eQM corrected precipitation and temperature with 90-day moving window in ALADIN (B), HIRHAM (C), RegCM (D), RAMCMO2 (E) and RCA (F) in the test period in 1981−2000.
Figure 7.
Simulated K-G climate classification according to E-OBS (A) and eQM corrected precipitation and temperature with 90-day moving window in ALADIN (B), HIRHAM (C), RegCM (D), RAMCMO2 (E) and RCA (F) in the test period in 1981−2000.
Figure 8.
Simulated K-G climate classification according to E-OBS (A) and gpQM corrected precipitation and eQM corrected temperature with a 90-day moving window in ALADIN (B), HIRHAM (C), RegCM (D), RAMCMO2 (E) and RCA (F) in the test period in 1981−2000.
Figure 8.
Simulated K-G climate classification according to E-OBS (A) and gpQM corrected precipitation and eQM corrected temperature with a 90-day moving window in ALADIN (B), HIRHAM (C), RegCM (D), RAMCMO2 (E) and RCA (F) in the test period in 1981−2000.
Figure 9.
Simulated K-G climate classification according to E-OBS (A) and power transformation of precipitation and variance scaling of temperature correction in ALADIN (B), HIRHAM (C), RegCM (D), RAMCMO2 (E) and RCA (F) in the test period in 1981−2000.
Figure 9.
Simulated K-G climate classification according to E-OBS (A) and power transformation of precipitation and variance scaling of temperature correction in ALADIN (B), HIRHAM (C), RegCM (D), RAMCMO2 (E) and RCA (F) in the test period in 1981−2000.
Figure 10.
Simulated K-G climate classification according to E-OBS (A) and local intensity scaling of precipitation and variance scaling of temperature correction in ALADIN (B), HIRHAM (C), RegCM (D), RAMCMO2 (E) and RCA (F) in the test period in 1981−2000.
Figure 10.
Simulated K-G climate classification according to E-OBS (A) and local intensity scaling of precipitation and variance scaling of temperature correction in ALADIN (B), HIRHAM (C), RegCM (D), RAMCMO2 (E) and RCA (F) in the test period in 1981−2000.
Table 1.
Key to calculate K-G zones in Europe and their third index. Pann is the accumulated annual precipitation. Pmin is the precipitation of the driest month. Psmin, Psmax, Pwmin and Pwmax are defined as the lowest and highest monthly precipitation values for the summer and winter half-years. Pth is the dryness threshold. Tann is the annual mean temperature, and the monthly mean temperatures of the warmest and coldest months are marked by Tmax and Tmin, respectively. The precipitation and temperature are given in mm and °C, respectively.
Table 1.
Key to calculate K-G zones in Europe and their third index. Pann is the accumulated annual precipitation. Pmin is the precipitation of the driest month. Psmin, Psmax, Pwmin and Pwmax are defined as the lowest and highest monthly precipitation values for the summer and winter half-years. Pth is the dryness threshold. Tann is the annual mean temperature, and the monthly mean temperatures of the warmest and coldest months are marked by Tmax and Tmin, respectively. The precipitation and temperature are given in mm and °C, respectively.
| Type | Description | Criterion |
|---|
| | | |
| B | Arid climates | Pann< 10 Pth |
| BS | Steppe climates | Pann> 5 Pth |
| BW | Desert climates | Pann ≤ 5 Pth |
| | | |
| C | Warm temperate climates | −3 °C < Tmin< + 18 °C |
| Cs | Warm temperate climates with dry summers | Psmin< Pwmin, Pwmax> 3 Psmin and Psmin< 40 mm |
| Cw | Warm temperate climates with dry winters | Pwmin< Psmin and Psmax> 10 Pwmin |
| Cf | Warm temperate climates, fully humid | neither Cs nor Cw |
| | | |
| D | Snow climates | Tmin ≤ −3 °C |
| Ds | Snow climates with dry summers | Psmin< Pwmin, Pwmax> 3 Psmin and Psmin< 40 mm |
| Dw | Snow climates with dry winters | Pwmin< Psmin and Psmax> 10 Pwmin |
| Df | Snow climates, fully humid | neither Ds nor Dw |
| | | |
| E | Polar climates | Tmax< + 10 °C |
| ET | Tundra climates | 0 °C ≤ Tmax< + 10 °C |
| EF | Frost climates | Tmax< 0 °C |
| third index for C and D climate zones |
| Type | Description | Criterion |
| | | |
| a | Hot summers | Tmean> 22°C |
| b | Warm summers | not (a) and at least 4 Tmon ≥ +10 °C |
| c | Cool summers and cold winters | not (b) and Tmin> −38°C |
| d | Extremely continental | like (c) and Tmin ≤ −38°C |
| third index for B climate zone |
| Type | Description | Criterion |
| | | |
| h | Hot steppe/desert | Tann ≥ +18 °C |
| k | Cold steppe/desert | Tann< +18 °C |
Table 2.
The institute, global climate models (GCMs), regional climate models (RCMs) and resolution of chosen models from the ENSEMBLES EU project.
Table 2.
The institute, global climate models (GCMs), regional climate models (RCMs) and resolution of chosen models from the ENSEMBLES EU project.
| | INSTITUTE/
REFERENCE | GCM | RCM | RESOLUTION |
|---|
| 1 | Centre National de Researches Météorologiques (CNRM)/
[33] | ARPÈGE | ALADIN | 25 km |
| 2 | Danish Meteorological Institute (DMI)/
[34] | ARPÈGE | HIRHAM | 25 km |
| 3 | Koninklijk Nederlands Meteorologisch Instituut
(KNMI)/
[35] | ECHAM5-r3 | RACMO2 | 25 km |
| 4 | Swedish Meteorological and Hydrological Institute (SMHI)/
[36] | ECHAM5-r3 | RCA | 25 km |
| 5 | International Centre for Theoretical Physics (ICTP)/
[37] | ECHAM5-r3 | RegCM | 25 km |
Table 3.
Residual bias of seasonal amount of simulated precipitation (a) and of seasonal mean of simulated temperature (b) in the case of eQM bias correction in eight different regions: the Alps (AL), the British Isles (BI), Eastern Europe (EA), France (FR), the Iberia Peninsula (IP), the Mediterranean (MD), Mid-Europe (ME) and Scandinavia (SC) in DJF and JJA The bias values are in % and in °C in the case of precipitation and temperature, respectively.
| a) | ALADIN | HIRHAM | RegCM | RACMO2 | RCA |
|---|
| Region | DJF | JJA | DJF | JJA | DJF | JJA | DJF | JJA | DJF | JJA |
|---|
| AL | −2 | −9 | 2 | −23 | −4 | −6 | −5 | −6 | −5 | −7 |
| BI | 1 | −2 | 2 | −7 | 1 | −3 | 0 | −3 | 1 | −2 |
| EA | −8 | −11 | −4 | −17 | −7 | −6 | −8 | −3 | −9 | −3 |
| FR | −1 | −5 | 0 | −20 | −6 | 0 | −6 | −5 | −7 | −4 |
| IP | −6 | −5 | −8 | −23 | −8 | −11 | −8 | −21 | −9 | −23 |
| MD | −6 | −8 | 0 | −34 | −4 | −9 | −4 | −9 | −5 | −14 |
| ME | −4 | −9 | −2 | −12 | −4 | −3 | −5 | −3 | −5 | −2 |
| SC | −6 | −1 | −3 | −8 | −3 | −2 | −2 | −2 | −4 | 1 |
| b) | ALADIN | HIRHAM | RegCM | RACMO2 | RCA |
|---|
| Region | DJF | JJA | DJF | JJA | DJF | JJA | DJF | JJA | DJF | JJA |
|---|
| AL | 0.2 | 0.1 | 0.3 | −0.4 | 0.3 | 0.1 | 0.1 | 0.1 | −0.1 | 0.0 |
| BI | 0.3 | 0.0 | 0.2 | −0.3 | 0.2 | 0.0 | 0.1 | 0.1 | 0.1 | 0.1 |
| EA | 0.5 | −0.2 | 0.4 | −0.8 | 0.4 | 0.0 | 0.2 | 0.0 | 0.0 | 0.0 |
| FR | 0.3 | 0.0 | 0.2 | −0.3 | 0.2 | 0.2 | 0.0 | 0.3 | 0.0 | 0.1 |
| IP | 0.1 | 0.5 | −0.1 | 0.3 | 0.1 | 0.6 | 0.0 | 0.3 | 0.0 | 0.1 |
| MD | 0.1 | 0.6 | 0.1 | −0.3 | 0.2 | 0.4 | 0.0 | 0.4 | −0.1 | 0.2 |
| ME | 0.5 | −0.2 | 0.5 | −0.7 | 0.3 | −0.1 | 0.2 | 0.0 | 0.0 | 0.0 |
| SC | 0.1 | −0.6 | 0.3 | −0.8 | 0.2 | 0.0 | 0.2 | 0.0 | −0.1 | 0.0 |
Table 4.
Residual bias in the seasonal amount of simulated precipitation (a) in the case of gpQM bias correction in eight different regions: the Alps (AL), the British Isles (BI), Eastern Europe (EA), France (FR), the Iberian Peninsula (IP), the Mediterranean (MD), Mid-Europe (ME) and Scandinavia (SC) in DJF and JJA. The bias values are in %.
Table 4.
Residual bias in the seasonal amount of simulated precipitation (a) in the case of gpQM bias correction in eight different regions: the Alps (AL), the British Isles (BI), Eastern Europe (EA), France (FR), the Iberian Peninsula (IP), the Mediterranean (MD), Mid-Europe (ME) and Scandinavia (SC) in DJF and JJA. The bias values are in %.
| | ALADIN | HIRHAM | RegCM | RACMO2 | RCA |
|---|
| Region | DJF | JJA | DJF | JJA | DJF | JJA | DJF | JJA | DJF | JJA |
|---|
| AL | 3 | −12 | 0 | −57 | 5 | −11 | 0 | −22 | 3 | −10 |
| BI | −2 | −5 | −3 | −39 | 3 | −2 | 3 | −4 | 5 | 1 |
| EA | 3 | −20 | 6 | −46 | 3 | −11 | −2 | −22 | −3 | −3 |
| FR | 5 | −11 | −6 | −57 | 0 | 4 | −1 | −9 | 1 | −3 |
| IP | −11 | −10 | −33 | −67 | −3 | −11 | −3 | −36 | −5 | −30 |
| MD | −7 | −15 | −14 | −68 | 0 | −15 | −4 | −49 | −3 | −25 |
| ME | 8 | −16 | 8 | −42 | 5 | −4 | 1 | −9 | 1 | 4 |
| SC | −7 | −1 | 3 | −19 | −1 | 1 | 2 | −2 | −3 | 8 |
Table 5.
Residual bias of seasonal amount of simulated precipitation in the case of power transformation of the precipitation bias correction method in eight different regions: the Alps (AL), the British Isles (BI), Eastern Europe (EA), France (FR), the Iberian Peninsula (IP), the Mediterranean (MD), Mid-Europe (ME) and Scandinavia (SC) in DJF and JJA. The bias values are in %.
Table 5.
Residual bias of seasonal amount of simulated precipitation in the case of power transformation of the precipitation bias correction method in eight different regions: the Alps (AL), the British Isles (BI), Eastern Europe (EA), France (FR), the Iberian Peninsula (IP), the Mediterranean (MD), Mid-Europe (ME) and Scandinavia (SC) in DJF and JJA. The bias values are in %.
| | ALADIN | HIRHAM | RegCM | RACMO2 | RCA |
|---|
| Region | DJF | JJA | DJF | JJA | DJF | JJA | DJF | JJA | DJF | JJA |
|---|
| AL | 0 | −6 | 0 | 0 | 0 | −6 | 0 | −6 | −1 | −6 |
| BI | −8 | 14 | 0 | 0 | −8 | 14 | −8 | 14 | −8 | 14 |
| EA | −9 | −14 | 0 | 0 | −9 | −14 | −9 | −14 | −9 | −14 |
| FR | −5 | 4 | 0 | 0 | −5 | 3 | −5 | 3 | −5 | 4 |
| IP | −12 | 8 | 0 | 0 | −12 | 7 | −12 | 7 | −12 | 7 |
| MD | −10 | 0 | 1 | 0 | −10 | 4 | −10 | 4 | −10 | 4 |
| ME | −9 | −11 | 0 | 0 | −9 | −10 | −9 | −10 | −9 | −10 |
| SC | −12 | 10 | 0 | 0 | −12 | 10 | −12 | 10 | −12 | 9 |
Table 6.
Residual bias of the seasonal amount of simulated precipitation in the case of local intensity scaling of the precipitation bias correction method in eight different regions: the Alps (AL), the British Isles (BI), Eastern Europe (EA), France (FR), the Iberia Peninsula (IP), the Mediterranean (MD), Mid-Europe (ME) and Scandinavia (SC) in DJF and JJA. The bias values are in %.
Table 6.
Residual bias of the seasonal amount of simulated precipitation in the case of local intensity scaling of the precipitation bias correction method in eight different regions: the Alps (AL), the British Isles (BI), Eastern Europe (EA), France (FR), the Iberia Peninsula (IP), the Mediterranean (MD), Mid-Europe (ME) and Scandinavia (SC) in DJF and JJA. The bias values are in %.
| | ALADIN | HIRHAM | RegCM | RACMO2 | RCA |
|---|
| Regio | DJF | JJA | DJF | JJA | DJF | JJA | DJF | JJA | DJF | JJA |
|---|
| AL | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 |
| BI | −2 | −2 | −2 | −2 | −2 | −2 | −2 | −2 | −2 | −2 |
| EA | −6 | −1 | −6 | −2 | −6 | −1 | −6 | −1 | −6 | −2 |
| FR | −2 | −2 | −2 | −2 | −2 | −2 | −2 | −2 | −2 | −2 |
| IP | −1 | −2 | −1 | −2 | −1 | −2 | −1 | −2 | −1 | −2 |
| MD | −2 | −1 | −2 | −1 | −2 | −1 | −2 | 1 | −2 | −1 |
| ME | −5 | −2 | −6 | −2 | −5 | −2 | −6 | −2 | −6 | −2 |
| SC | −5 | −2 | −5 | −2 | −5 | −2 | −5 | −2 | −5 | −2 |
Table 7.
Residual bias of the seasonal amount of simulated precipitation (a) and of the seasonal mean of the simulated temperature (b) in the case of eQM bias correction in the test period in eight different regions: the Alps (AL), the British Isles (BI), Eastern Europe (EA), France (FR), the Iberia Peninsula (IP), the Mediterranean (MD), Mid-Europe (ME) and Scandinavia (SC) in DJF and JJA. The bias values are in % and in °C for precipitation and temperature, respectively.
| a) | ALADIN | HIRHAM | RegCM | RACMO2 | RCA |
|---|
| Region | DJF | JJA | DJF | JJA | DJF | JJA | DJF | JJA | DJF | JJA |
|---|
| AL | −2 | 3 | 7 | −26 | 3 | −9 | 1 | −2 | 3 | −5 |
| BI | −9 | 7 | −10 | 0 | −12 | −7 | −15 | −9 | −15 | −11 |
| EA | −3 | 5 | 2 | −6 | 4 | 0 | 0 | 5 | 3 | 3 |
| FR | −8 | 4 | −6 | −24 | −17 | −13 | −17 | −19 | −18 | −17 |
| IP | 9 | 3 | 5 | −17 | 13 | −1 | 14 | −18 | 11 | −21 |
| MD | 0 | −5 | 7 | −23 | 14 | 0 | 18 | 12 | 12 | 3 |
| ME | −7 | 10 | −5 | −4 | −7 | −2 | −14 | −2 | −8 | −1 |
| SC | −18 | 0 | −15 | −8 | −14 | −9 | −11 | −11 | −13 | −9 |
| b) | ALADIN | HIRHAM | RegCM | RACMO2 | RCA |
|---|
| Region | DJF | JJA | DJF | JJA | DJF | JJA | DJF | JJA | DJF | JJA |
|---|
| AL | 0.3 | −0.4 | 0.3 | −0.4 | −0.2 | −0.4 | −0.5 | −0.5 | −0.6 | −0.5 |
| BI | 0.5 | −0.5 | 0.3 | −0.7 | −0.3 | −0.3 | −0.4 | −0.2 | −0.5 | −0.4 |
| EA | 0.1 | 0.1 | 0.1 | 0.0 | 0.0 | −0.5 | −0.1 | −0.6 | −0.2 | −0.6 |
| FR | 0.2 | −0.9 | 0.2 | −0.9 | −0.6 | −0.4 | −0.7 | −0.3 | −0.9 | −0.5 |
| IP | −0.3 | −0.2 | −0.3 | −0.4 | −0.5 | 0.1 | −0.5 | 0.1 | −0.6 | 0.1 |
| MD | 0.2 | 0.2 | 0.2 | −0.2 | 0.1 | −0.5 | −0.1 | −0.7 | −0.2 | −0.6 |
| ME | 0.2 | −0.3 | 0.3 | −0.5 | −0.2 | −0.5 | −0.3 | −0.6 | −0.4 | −0.7 |
| SC | 0.9 | 0.4 | 1.1 | −0.1 | −0.1 | −0.3 | 0.0 | −0.4 | −0.1 | −0.2 |
Table 8.
Residual bias of seasonal amount of simulated precipitation in the case of gpQM bias correction in the test period in eight different regions: the Alps (AL), the British Isles (BI), Eastern Europe (EA), France (FR), the Iberian Peninsula (IP), the Mediterranean (MD), Mid-Europe (ME) and Scandinavia (SC) in DJF and JJA. The bias values are in %.
Table 8.
Residual bias of seasonal amount of simulated precipitation in the case of gpQM bias correction in the test period in eight different regions: the Alps (AL), the British Isles (BI), Eastern Europe (EA), France (FR), the Iberian Peninsula (IP), the Mediterranean (MD), Mid-Europe (ME) and Scandinavia (SC) in DJF and JJA. The bias values are in %.
| | ALADIN | HIRHAM | RegCM | RACMO2 | RCA |
|---|
| Region | DJF | JJA | DJF | JJA | DJF | JJA | DJF | JJA | DJF | JJA |
|---|
| AL | 6 | 0 | 6 | −59 | 11 | −12 | 10 | −20 | 12 | −8 |
| BI | −10 | 3 | −13 | −36 | −9 | −5 | −11 | −9 | −10 | −6 |
| EA | 12 | −7 | 11 | −40 | 14 | −5 | 7 | −15 | 9 | 4 |
| FR | 0 | −7 | −10 | −62 | −10 | −10 | −11 | −23 | −10 | −17 |
| IP | 7 | −2 | −24 | −64 | 21 | 0 | 20 | −34 | 16 | −33 |
| MD | 1 | −14 | −8 | −62 | 17 | −8 | 16 | −42 | 15 | −16 |
| ME | 7 | 2 | 3 | −38 | 1 | −1 | −8 | −7 | −2 | 6 |
| SC | −19 | 0 | −11 | −19 | −10 | −5 | −7 | −9 | −11 | 0 |
Table 9.
Residual bias of seasonal amount of simulated precipitation (a) in the case of power transformation of precipitation and the seasonal mean of the simulated temperature, (b) in the case of variance scaling of the temperature bias correction methods in the test period in eight different regions: the Alps (AL), the British Isles (BI), Eastern Europe (EA), France (FR), the Iberia Peninsula (IP), the Mediterranean (MD), Mid-Europe (ME) and Scandinavia (SC) in DJF and JJA. The bias values are in % and in °C for precipitation and temperature, respectively.
| a) | ALADIN | HIRHAM | RegCM | RACMO2 | RCA |
|---|
| Region | DJF | JJA | DJF | JJA | DJF | JJA | DJF | JJA | DJF | JJA |
|---|
| AL | 1 | 16 | 4 | −7 | 7 | −2 | 8 | 7 | 6 | 5 |
| BI | −8 | 9 | −12 | 9 | −12 | −5 | −15 | −6 | −15 | −9 |
| EA | 5 | 20 | 4 | 11 | 11 | 8 | 11 | 8 | 14 | 9 |
| FR | −7 | 10 | −7 | −9 | −11 | −12 | −11 | −14 | −11 | −11 |
| IP | 15 | 12 | 14 | 123 | 25 | 11 | 26 | 5 | 25 | −4 |
| MD | 7 | 3 | 8 | 23 | 20 | 7 | 24 | 20 | 20 | 15 |
| ME | −3 | 23 | −4 | 8 | −3 | 4 | −8 | 3 | −2 | 3 |
| SC | −12 | 1 | −12 | 1 | −11 | −6 | −8 | −9 | −9 | −8 |
| b) | ALADIN | HIRHAM | RegCM | RACMO2 | RCA |
|---|
| Region | DJF | JJA | DJF | JJA | DJF | JJA | DJF | JJA | DJF | JJA |
|---|
| AL | 0.1 | −0.8 | 0.2 | −0.8 | −0.5 | −0.4 | −0.7 | −0.6 | −0.6 | −0.6 |
| BI | 0.4 | −0.6 | 0.2 | −0.7 | −0.6 | −0.3 | −0.6 | −0.2 | −0.6 | −0.4 |
| EA | −0.2 | −0.1 | −0.1 | −0.1 | −0.2 | −0.5 | −0.3 | −0.5 | −0.2 | −0.6 |
| FR | 0.1 | −1.1 | 0.1 | −1.1 | −0.7 | −0.4 | −0.9 | −0.4 | −0.9 | −0.5 |
| IP | −0.3 | −0.5 | −0.2 | −0.6 | −0.6 | 0.1 | −0.6 | 0.1 | −0.7 | 0.0 |
| MD | 0.1 | −0.1 | 0.2 | −0.4 | 0.0 | −0.5 | −0.1 | −0.8 | −0.2 | −0.7 |
| ME | −0.1 | −0.6 | 0.1 | −0.6 | −0.4 | −0.4 | −0.5 | −0.5 | −0.4 | −0.6 |
| SC | 0.8 | 0.4 | 0.9 | 0.0 | −0.2 | −0.2 | −0.2 | −0.3 | 0.0 | −0.2 |
Table 10.
Residual bias of the seasonal amount of simulated precipitation (a) in the case of local intensity scaling of the precipitation bias correction method in the test period in eight different regions: the Alps (AL), the British Isles (BI), Eastern Europe (EA), France (FR), the Iberia Peninsula (IP), the Mediterranean (MD), Mid-Europe (ME) and Scandinavia (SC) in DJF and JJA. The bias values are in %. The extremely large bias in the case of HIRHAM RCM in IP in the in JJA season is denoted by NA where the bias value is about 3 × 1012.
Table 10.
Residual bias of the seasonal amount of simulated precipitation (a) in the case of local intensity scaling of the precipitation bias correction method in the test period in eight different regions: the Alps (AL), the British Isles (BI), Eastern Europe (EA), France (FR), the Iberia Peninsula (IP), the Mediterranean (MD), Mid-Europe (ME) and Scandinavia (SC) in DJF and JJA. The bias values are in %. The extremely large bias in the case of HIRHAM RCM in IP in the in JJA season is denoted by NA where the bias value is about 3 × 1012.
| | ALADIN | HIRHAM | RegCM | RACMO2 | RCA |
|---|
| Regio | DJF | JJA | DJF | JJA | DJF | JJA | DJF | JJA | DJF | JJA |
|---|
| AL | 0 | 18 | 5 | −3 | 7 | −2 | 8 | 8 | 8 | 4 |
| BI | −10 | 8 | −14 | 9 | −14 | −7 | −17 | −9 | −17 | −12 |
| EA | −1 | 19 | −3 | 11 | 4 | 6 | 4 | 7 | 7 | 6 |
| FR | −11 | 8 | −11 | −6 | −15 | −16 | −16 | −18 | −16 | −16 |
| IP | 13 | 14 | 11 | NA | 24 | 12 | 24 | 4 | 22 | −4 |
| MD | 4 | 5 | 6 | 43 | 19 | 5 | 23 | 27 | 18 | 14 |
| ME | −9 | 22 | −9 | 6 | −9 | 2 | −14 | 0 | −8 | 0 |
| SC | −16 | 0 | −16 | −1 | −15 | −8 | −13 | −11 | −14 | −10 |
Table 11.
Disagreement between observed and simulated K-G zones in eight different regions: the Alps (AL), the British Isles (BI), Eastern Europe (EA), France (FR), the Iberia Peninsula (IP), the Mediterranean (MD), Mid-Europe (ME) and Scandinavia (SC) and in the whole study area in DJF and JJA in the case of eQM-eQM, gpQM-eQM, power transformation of precipitation and variance scaling of temperature and LOCI and variance scaling of temperature bias correction combination. The values are in %.
Table 11.
Disagreement between observed and simulated K-G zones in eight different regions: the Alps (AL), the British Isles (BI), Eastern Europe (EA), France (FR), the Iberia Peninsula (IP), the Mediterranean (MD), Mid-Europe (ME) and Scandinavia (SC) and in the whole study area in DJF and JJA in the case of eQM-eQM, gpQM-eQM, power transformation of precipitation and variance scaling of temperature and LOCI and variance scaling of temperature bias correction combination. The values are in %.
| DISAGREEMENT | AL | BI | EA | FR | IP | MD | ME | SC | Study Area |
|---|
| eQM-eQM | | | | | | | | | |
| ALADIN | 8.9 | 1.5 | 15.5 | 8.8 | 12 | 17.8 | 2.3 | 4.5 | 9 |
| HIRHAM | 38.6 | 1.5 | 29.5 | 44.2 | 31.6 | 35.4 | 2.4 | 7.8 | 20 |
| RegCM | 9.4 | 1.3 | 10.3 | 1.5 | 16.2 | 17.2 | 0.7 | 6 | 8.4 |
| RACMO2 | 8.9 | 2.2 | 12.9 | 1.5 | 12.9 | 19 | 0.7 | 6.4 | 9 |
| RCA | 10.3 | 2.5 | 8.6 | 1 | 14.2 | 11.7 | 0.9 | 10.5 | 9 |
| Ensemble mean | 15.2 | 1.8 | 15.4 | 11.4 | 17.4 | 20.2 | 1.4 | 7.0 | |
| gpQM-eQM | | | | | | | | | |
| ALADIN | 11.8 | 2.7 | 18.5 | 39.3 | 19.3 | 29.9 | 3.4 | 4.7 | 13.1 |
| HIRHAM | 73.9 | 46.9 | 47.4 | 99 | 51.2 | 55.8 | 46.9 | 8.9 | 38.2 |
| RegCM | 9.9 | 1.5 | 10.9 | 2.5 | 17.4 | 21.8 | 0.5 | 6.6 | 9.4 |
| RACMO2 | 24.7 | 2.4 | 17.5 | 6.4 | 19.5 | 36.8 | 1.5 | 7.2 | 13.7 |
| RCA | 18.1 | 2.5 | 10 | 4.7 | 19.5 | 20.1 | 0.9 | 11.2 | 11.4 |
| Ensemble mean | 27.7 | 11.2 | 20.9 | 30.4 | 25.4 | 32.9 | 10.6 | 7.7 | |
| power_variance | | | | | | | | | |
| ALADIN | 1.2 | 0 | 0 | 0 | 2.9 | 3.8 | 0 | 0.2 | 0.8 |
| HIRHAM | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.2 | 0.1 |
| RegCM | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.2 | 0.1 |
| RACMO2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.2 | 0.1 |
| RCA | 0 | 0 | 0 | 0 | 1.1 | 0 | 0 | 0.2 | 0.2 |
| Ensemble mean | 0.2 | 0.0 | 0.0 | 0.0 | 0.8 | 0.8 | 0.0 | 0.2 | |
| loci-variance | | | | | | | | | |
| ALADIN | 0 | 0 | 0.3 | 1.2 | 2.7 | 1.1 | 0.8 | 0.3 | 0.7 |
| HIRHAM | 0 | 0 | 0.4 | 2.5 | 3.2 | 1.4 | 0.8 | 0.3 | 0.8 |
| RegCM | 0 | 0 | 0.3 | 1.2 | 2.7 | 1.1 | 0.8 | 0.3 | 0.7 |
| RACMO2 | 0 | 0 | 0.3 | 1.2 | 2.9 | 3.4 | 0.8 | 0.3 | 0.9 |
| RCA | 0 | 0 | 0.3 | 1.2 | 2.6 | 1.2 | 0.8 | 0.3 | 0.7 |
| Ensemble mean | 0 | 0 | 0.3 | 1.4 | 2.8 | 1.6 | 0.8 | 0.3 | |