Next Article in Journal
Climatically Driven Holocene Glacier Advances in the Russian Altai Based on Radiocarbon and OSL Dating and Tree Ring Analysis
Next Article in Special Issue
Coastal Wave Extremes around the Pacific and Their Remote Seasonal Connection to Climate Modes
Previous Article in Journal
Interannual Variability and Trends of Extreme Rainfall Indices over Benin
Previous Article in Special Issue
Functional Data Visualization and Outlier Detection on the Anomaly of El Niño Southern Oscillation
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Climate
Volume 9
Issue 11
10.3390/cli9110161
climate-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Testing the CMIP6 GCM Simulations versus Surface Temperature Records from 1980–1990 to 2011–2021: High ECS Is Not Supported

by
Nicola Scafetta
Department of Earth Sciences, Environment and Georesources, University of Naples Federico II, Complesso Universitario di Monte S. Angelo, Via Cinthia, 21, 80126 Naples, Italy
Climate 2021, 9(11), 161; https://doi.org/10.3390/cli9110161
Submission received: 17 October 2021 / Revised: 26 October 2021 / Accepted: 27 October 2021 / Published: 29 October 2021
(This article belongs to the Special Issue Climate Change Dynamics and Modeling: Future Perspectives)
Browse Figures
Versions Notes

Abstract

:
The last-generation CMIP6 global circulation models (GCMs) are currently used to interpret past and future climatic changes and to guide policymakers, but they are very different from each other; for example, their equilibrium climate sensitivity (ECS) varies from 1.83 to 5.67 °C (IPCC AR6, 2021). Even assuming that some of them are sufficiently reliable for scenario forecasts, such a large ECS uncertainty requires a pre-selection of the most reliable models. Herein the performance of 38 CMIP6 models are tested in reproducing the surface temperature changes observed from 1980–1990 to 2011–2021 in three temperature records: ERA5-T2m, ERA5-850mb, and UAH MSU v6.0 Tlt. Alternative temperature records are briefly discussed but found to be not appropriate for the present analysis because they miss data over large regions. Significant issues emerge: (1) most GCMs overestimate the warming observed during the last 40 years; (2) there is great variability among the models in reconstructing the climatic changes observed in the Arctic; (3) the ocean temperature is usually overestimated more than the land one; (4) in the latitude bands 40° N–70° N and 50° S–70° S (which lay at the intersection between the Ferrel and the polar atmospheric cells) the CMIP6 GCMs overestimate the warming; (5) similar discrepancies are present in the east-equatorial pacific region (which regulates the ENSO) and in other regions where cooling trends are observed. Finally, the percentage of the world surface where the (positive or negative) model-data discrepancy exceeds 0.2, 0.5 and 1.0 °C is evaluated. The results indicate that the models with low ECS values (for example, 3 °C or less) perform significantly better than those with larger ECS. Therefore, the low ECS models should be preferred for climate change scenario forecasts while the other models should be dismissed and not used by policymakers. In any case, significant model-data discrepancies are still observed over extended world regions for all models: on average, the GCM predictions disagree from the data by more than 0.2 °C (on a total mean warming of about 0.5 °C from 1980–1990 to 2011–2021) over more than 50% of the global surface. This result suggests that climate change and its natural variability remain poorly modeled by the CMIP6 GCMs. Finally, the ECS uncertainty problem is discussed, and it is argued (also using semi-empirical climate models that implement natural oscillations not predicted by the GCMs) that the real ECS could be between 1 and 2 °C, which implies moderate warming for the next decades.

Graphical Abstract

1. Introduction

Global climate models (GCMs) are complex computer programs that are used to understand and forecast how the Earth’s climate has changed in the past and may change in the future according to specific emission scenarios: see the assessment reports produced by the Intergovernmental Panel on Climate Change [1,2,3]. To achieve this goal, the GCMs attempt to simulate all physical, chemical and biological known processes occurring in the atmosphere, land surface and oceans, their mutual interactions and global circulation. The models are also driven by a set of climatic radiative forcings deduced from several records describing the evolution of the solar irradiance and volcano eruptions plus the so-called human-induced climate drivers derived from changes in the atmospheric concentration of CO2, CH4, aerosols and others.
The available GCMs have evolved greatly during the last 20 years and their characteristics and results have been coordinated and collected by the World Climate Research Programme (WCRP) Coupled Model Intercomparison Projects (CMIP). Their third version (CMIP3) was used in the 2007 IPCC fourth assessment report (AR4) [1] and their fifth version (CMIP5) was used in the 2013 IPCC AR5 [2]. The sixth and latest version of these models (CMIP6) was adopted in the 2021 IPCC sixth assessment report (AR6) [3].
However, the proposed GCMs cannot be considered satisfactory for several reasons. For example, the CMIP3 and CMIP5 GCMs poorly reconstruct the natural oscillations of the climate system, which appear to be associated with several solar and lunisolar tidal cycles at periods of about 9.1, 10.4, 20, 60, 115, and nearly 1000 years [4,5]. Moreover, Scafetta [6] showed that the climate models fail to reconstruct the warm periods of the past—such as the Roman and the Medieval Warm Period—that correspond to the warm phase of a quasi-millennial oscillation that is prominent in several multi-millennial temperature reconstructions [7,8,9,10,11,12,13,14,15].
The available climatic models also appear to overestimate the warming observed during the last 40 years—since 1980—and in particular from 2000 to 2020 when the warming rate has decreased relative to the previous 20 years despite the fact that the years 2015–2016 and 2021 experienced two strong natural warming peaks [4,5,6,16]. A significant discrepancy between the model predictions and the temperature data is also observed above the tropics at the 200- to 300-hPa atmospheric layer, where the models predict a strong hot-spot not observed in the data [17]. A persistent warming bias confirming that the CMIP6 models overestimate atmospheric warming is also observed in the vertical profile of recent tropical temperature trends [18].
Indeed, climate models are affected by large physical uncertainties mostly because the water vapor feedback and the cloud system are poorly modeled and understood. Moreover, additional astronomical forcings (for example, due to long-range lunisolar tides, accurate solar irradiance records, cosmic ray and interplanetary dust incoming fluxes) and their related mechanisms are still missing and/or debated [5,19,20,21].
The physical uncertainty of the GCMs becomes evident when their equilibrium climate sensitivity (ECS) is compared. The ECS is defined as the global surface warming (at the thermal equilibrium) induced by doubling the atmospheric concentration of CO2 from the pre-industrial value of 280 to 560 ppm. The ECS of the CMIP5 models varied from 2.1 to 4.5 °C; and in 2013 the IPCC [2] estimated that it likely ranges from 1.5 to 4.5 °C, as already proposed by Jule Charney in 1979 [2,22]. Paradoxically, the ECS of the novel CMIP6 GCMs present even a larger range: from 1.83 to 5.67 °C (see Figure 1). The issue is of great concern because the ECS of many of these new models (at least 13 of them are shown in the figure) even exceeds 4.5 °C, which was the previously accepted upper-limit value [2,23].
The ECS problem is both challenging and crucial because several empirical studies concluded that its value should be usually lower than the GCM estimates: that is, between 0.5 and 2.5 °C.
For example, Lindzen and Choi [24] estimated an ECS of 0.7 °C (with the confidence interval 0.5—1.3 °C at 99% levels). Scafetta [5] deduced that the real ECS had to be at most half of that estimated by the CMIP5 climate models, which is roughly between 1 and 2.2 °C. Lewis and Curry [25] calculated an ECS median of 1.50 °C (with 5–95% range: 1.05–2.45 °C). Bates [26] and Monckton et al. [27] evaluated a climate sensitivity in the neighborhood of 1 °C. Kluft et al. [28] found an ECS range of 2.09–2.40 °C depending on the radiative feedback related to the chosen relative humidity profile. van Wijngaarden and Happer [29] found an ECS range of 1.4–2.3 °C for different model configurations but ignoring a possible negative feedback from the cloud system. The high ECS of some of the CMIP6 models is also not supported by paleoclimatic records [30], and some studies have already reported that high ECS models predict historical warming trends that are too large [31].
These results led Knutti et al. [22] to acknowledge both the great uncertainty regarding the ECS value and the existence of a scientific dichotomy between observations and models; these authors stated that “evidences from climate modelling favours values of ECS in the upper part of the likely range, whereas many recent studies based on instrumentally recorded warming—and some from paleoclimate—favour values in the lower part of the range”.
It is, therefore, crucial to solve this dichotomy by narrowing the uncertainty regarding the ECS. Such information is necessary also for better estimating the magnitude of future climatic changes. For example, Huntingford et al. [32] showed that by assuming an instantaneous climatic response to radiative forcing, the various ECS values of the CMIP6 GCMs predict a 1860–2020 global warming between 1 and 3.3 °C, while the observed warming has been about 1 °C. These authors concluded that the CMIP6 climate models, taken as a set, imply high committed warming levels for the 21st century even without additional CO2 emissions. This result would require very aggressive and expensive mitigation policies for keeping the temperature below 1.5–2.0 °C, above the pre-industrial (1850–1900) levels. In fact, Huntingford et al. [32] concluded that such a situation “may eventually require the massive implementation of technologies that can extract CO2 from the atmosphere”.
In any case, the current GCMs are quite different from each other and they poorly agree with the observations despite the tuning and parameterization (for example, for modeling the clouds, the convective processes, etc.) of their internal variables for obtaining the best matching with the data [33]. However, at the moment there are no definitive criteria to prefer one specific model over the others, and the IPCC [3] lists all of them equally, although the AR6 has narrowed the ECS likely range to 2.5–4.0 °C by considering multiple lines of evidence [34]. It may also happen that all CMIP6 GCMs are wrong because important solar-astronomical forcings, which could be responsible for an oscillating natural climatic variability, are not modeled in the GCMs [5,19,20].
In this paper, we test 38 CMIP6 models in simulating the surface temperature changes observed between the periods 1980–1990 and 2011–2021 using surface distributions to better identify the regions where the models mostly fail. The time range was chosen because it is covered by both land and satellite temperature records and is sufficiently long (over 30 years) for evaluating the models. Finally, the relevance of the results regarding the ECS uncertainty issue is discussed.

2. Data and Method

Herein, we analyze the temperature at the surface (tas) produced by 38 (over 40) CMIP6 model runs downloaded from Climate Explorer from 1980 to 2021. Two models (GFDL-CM4 and HadGEM3-GC31-MM f3) could not be analyzed because the data were missing. The analyzed models are listed in Table 1. We adopt GCM simulations for the shared socioeconomic pathway (SSP) 370 with the exception for 4 cases (CIESM, FIO-ESM-2-0, HadGEM3-GC31-LL f3, NESM3) where the SSP 585 simulations were used because the former were missing; in the chosen time range—from 1980 to 2021—the various SSPs produce nearly identical results. Moreover, we adopt the CMIP6 mean (one member per model).
From Climate Explorer, three temperature records were downloaded: the monthly reanalysis field ERA5 Near-Surface Air Temperature (T2m) record; the ERA5 air temperature record at 850 mb [35]; and the UAH MSU v6.0 lower troposphere temperature (Tlt) [36]. We also downloaded other three popular temperature records: HadCRUT [37], GISTEMP [38] and NOAA [39,40].
The ERA5 records are reanalysis temperature data modeled from observed data, that is, they are derived from a combination of in-situ and model simulations. The ERA5-T2m record is here preferred for our analysis because it covers the entire surface. An advantage of also adopting two temperature records referring to the low-elevation planetary boundary layer (ERA5 at 850mb and UAH MSU v6.0 Tlt) is that they are likely free of non-climatic surface temperature biases such as those due to urbanization development that, since 1850–1900, could have added about 20% of warming to the surface temperature records [16,21,41,42]. Instead, the HadCRUT, GISTEM and NOAA records have missing data over large world regions, in particular over the poles and other scarcely inhabited regions, and will be briefly discussed.
For each temperature record and for each location of the world map, we calculate the temperature average in the 11-year periods 1980–1990 and 2011–2021. However, at the time of the present study, the ERA5-T2m record was available on Climate Explorer up to June 2021. To minimize a possible 1–2% error (note that 6 months over 31 years cover 1.6% of the period), for the computer simulations we average the values for the periods 2011–2020 and 2011–2021 and use them as the GCMs’ best estimates from January 2011 to June 2021, and compare these estimates against the data. This approach is preferred over analyzing the period 2010–2020 because during 2020 a strong temperature peak (not reproduced by the models) occurred [6], which could bias the proposed analysis. The temperature changes between the two periods are evaluated by differentiating the two averages and then they are plotted on a map. Finally, the temperature latitude profiles are also analyzed for the land, the ocean and the land+ocean regions.
The model simulations are evaluated against the temperature records by measuring the percentage of the world surface (using a weighting with the cosine of the latitude) where the (positive or negative) discrepancy exceeds three chosen temperature thresholds at 0.2, 0.5 and 1.0 °C. Finally, we rank the models according to their accuracy and comment on the results.

3. Results

Figure 2 shows several CMIP6 GCM surface temperature simulations (red curves, models with ECS > 3; blue curves, models with ECS ≤ 3) against the temperature observations (green) (ERA5-T2m, ERA5-850mb, and UAH MSU v6.0 Tlt) using as a reference the 1980–1990 period. The 2021 point for ERA5-T2m and ERA5-850mb is calculated using the months from January to June; the 2021 point for UAH MSU v6.0 Tlt is calculated using the months from January to August. The models with high ECS (red curves) predict significantly faster warming than those with low ECS (blue curves).
The figure shows that the observations (green curves) agree better with the predictions of the low ECS models (blue curves). From 1980 to 2021, a better agreement is found against the ERA5-T2m record; the ERA5-850mb and UAH MSU v6.0 Tlt records show an even lower warming trend that hardly agrees only with the less warm simulations. Thus, the general impression is that most CMIP6 models, and in particular, those with high ECS values, overestimate the warming trend, as already found for the CMIP3 [4] and CMIP5 models [5].
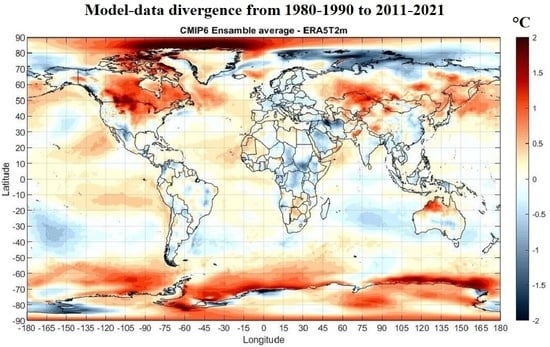
Figure 3 shows the climatic temperature changes that occurred from 1980–1990 to 2011–2021 together with the correspondent latitude temperature profiles for the CMIP6-tas ensemble average record (top) and the six temperature records (ERA5-T2m, ERA5-850mb, UAH MSU v6.0 Tlt, HadCRUT, GISTEM and NOAA temperatures).
On average, the CMIP6 models predict a diffused warming over the entire world. The Arctic is the fastest-warming region. In fact, the melting of the northern glaciers and of the Arctic sea-ice [43] activates a strong positive albedo feedback. However, the three panels on the left (referring to the ERA5-T2m, ERA5-850mb and UAH MSU v6.0 Tlt records) show lighter colors, which indicates lower warming trends. The three panels on the right (referring to the HadCRUT, GISTEM and NOAA records) present numerous similarities with the other three temperature records but are on average slightly warmer.
The right panels also show that the corresponding three temperature records do not cover vast regions of the Earth such as at the poles and several poorly inhabited regions such as in central Africa, South America and in other continents. This problem may bias a statistical comparison with the CMIP6 simulations. Therefore, in the following, we use the ERA5-T2m, ERA5-850mb and UAH MSU v6.0 Tlt records that cover the entire world’s surface. UAH MSU v6.0 Tlt misses small areas in the poles, from 81° to 90° latitude north and south that, however, does not matter much.
The six temperature panels present extended blue areas indicating that in those regions from 1980–1990 to 2011–2021 a cooling occurred. These cooling areas are missing in the CMIP6 ensemble mean record. They occur mostly over the ocean around Antarctica where the sea-ice extent has usually been increasing [43]. However, some places on the coast of Antarctica show red-spots indicating local warming due to the melting and fracturing of some ice sheets that induce a decrease in the local albedo yielding a local warming [44]. Other blue areas are observed over some regions of the Antarctic continent, in the Eastern Pacific ocean at the latitude band of 10° S–20° S (close to where the ENSO develops), and in the middle of the North Atlantic ocean at a latitude of about 50° N. Over the land, blue regions are observed in North America and Asia around latitude 50° N, in Northwest Australia, and over a few other regions.
The ERA5-T2m panel shows stronger colors than ERA5-850mb and UAH MSU v6.0 Tlt, which indicates that near the surface, larger temperature changes are observed. The land has usually warmed more than the ocean within the latitude range from 60°S and 60°N, likely because of the different heat capacity of the two systems.
Figure 4 depicts the land temperature profile minus the ocean one for each of the four records. The three panels show the CMIP6 ensemble prediction (black curves) against each of the temperature records in red (ERA5-T2m, ERA5-850mb, and the UAH MSU v6.0 Tlt). Within the latitude range from 60° S and 60° N—which excludes the polar regions—the difference between land and ocean temperatures for the CMIP6 ensemble prediction has an average of 0.25 °C; ERA5-T2m gives 0.32 °C, ERA5-850mb gives 0.10 °C, and UAH MSU v6.0 Tlt gives 0.12 °C.
Thus, relative to the ocean, the land temperature reported by ERA5-T2m warmed on average 0.07 °C (near 28%) more than the ensemble model simulation and nearly three times more than the two low troposphere temperature records. The overwarming of the land relative to the ocean in the latitude band from 60° S and 60° N shown by the ERA5-T2m record relative to the model simulation is consistent with the results of Scafetta [16], Scafetta and Ouyang [41] and Connolly et al. [21] where it was argued that the land record is partially affected by urban heat and other non-climatic biases, which are not simulated by the models and are not efficiently filtered off in the land surface temperature records. Moreover, the ERA5-T2m record shows that near the poles (above 75° N and below 75° S), the ocean cooled more than the land (negative values in the red curves) than the GCM simulations (black curves).
Figure 5 shows the difference between the areal distribution of the warming from 1980–1990 to 2011–2021 predicted by the CMIP6-tas ensemble average record and those produced by the three temperature records: ERA5-T2m, ERA5-850mb, and UAH MSU v6.0 Tlt, respectively. The left panel indicates the latitudinal profiles for the land, ocean and land+ocean temperatures. The three panels confirm that the CMIP6 mean simulation is closer to ERA5-T2m than to the other two records, which on average look more reddish than the top one. This result is confirmed by the statistical analysis of the graphs:
  • The percentage of the world surface area where the disagreement between the synthetic record and the ERA5-T2m record is | Δ T | ⩾ 0.2 °C is 53%, for | Δ T | ⩾ 0.5 °C is 17% and for | Δ T | ⩾ 1.0 °C is 3.6%;
  • By comparing the synthetic record and ERA5-850mb, we find | Δ T | ⩾ 0.2 °C for the 67% of the world surface, | Δ T | ⩾ 0.5 °C for the 23% of the world surface and | Δ T | ⩾ 1.0 °C for the 4.9% of the world surface;
  • Finally, by comparing the synthetic record and UAH MSU v6.0 Tlt, we find | Δ T | ⩾ 0.2 °C for the 65% of the world surface, | Δ T | ⩾ 0.5 °C for the 21% of the world surface and | Δ T | ⩾ 1.0 °C for the 5.9% of the world surface.
Figure 5 also shows that at the symmetric latitude ranges 40°–70° N and 50°–70° S, the CMIP6 models predict an exaggerated warming trend relative to the three temperature records. This anomaly is particularly evident in the top panel (where the model is compared against the ERA5-T2m record) over North America and Russia and the ocean around Antarctica. The result is important because such latitude bands approximately correspond to the intersection between the Ferrel and the polar cells where low-pressure patterns and clouds form. The result suggests that the CMIP6 models poorly simulate the circulation of the atmosphere and/or exaggerate the magnitude of some positive feedback mechanisms by poorly modeling the cloud system that could activate a negative feedback between the temperate and subpolar zones.
Figure 5 highlights other discrepancies that suggest poor modeling of the air–ocean circulation. The synthetic record predicts some too fast warming oceanic areas relative to the ERA5-T2m data; these areas correspond to the regions most affected by the Peru and South Equatorial Pacific currents, the California and the Canary currents, which drive upwelling of cold water from the deep ocean. The models also show too warm polar regions at 80°–90° N (in particular at the north of Greenland) and over Antarctica at 85°–90° S. In fact, both the ocean surrounding Antarctica and large regions of the continent experienced ice mass gains that have exceeded the losses [43,45].
Figure 6 shows the latitudinal warming profile from 1980–1990 to 2011–2021 produced by the analyzed 38 CMIP6 different models. The three panels refer to the land, the ocean and the land+ocean areas, respectively. A large variability among the models is observed in the polar regions and, in particular, over the Arctic ocean (the range is about 6 °C over the ocean and 4 °C over the land) and around Antarctica (the range is up to 2 °C over the land and the ocean). This result suggests that the physical processes characterizing these regions—such as the formation and melting of the glaciers and sea-ice—are poorly modeled. Only the band from 40°S to 30°N, which involves mostly the Hadley cells, appears to be more consistent among the models that show a variability range of just above 0.6 °C over the ocean and about 1 °C over the land. Note that one model—the Community Integrated Earth System Model (CIESM, ECS = 5.67 °C) [46]—significantly fails because it predicts a very large warming of the equatorial land between 30° S and 15° N.
Figure 7 compares the latitudinal warming profile from 1980–1990 to 2011–2021 produced by three adopted temperature records (ERA5-T2m, ERA5-850mb, and the UAH MSU v6.0 Tlt) (red curves) against the CMIP6 models: their average profile (black curves) plus/minus one standard deviation ( ± 1 σ ) (blue curves). The land, the ocean, and the land+ocean areas are shown in different panels. Each panel also reports the correspondent mean Student t-test value calculated by averaging the weighted values for each latitude: t = ( x ¯ − μ ) / ( σ / n ) , where x ¯ and σ are the sample mean and standard deviation among the n models and μ represents the data. There are n = 38 independent models and the degree of freedom is n − 1 = 37 . The hypothesis that the CMIP6 model ensemble reconstructs the temperature profile can be rejected at the significance level 0.05 when t ≥ 2.03 ; this happens in all cases but for the ERA5-T2m land record.
In fact, Figure 7 highlights that the ocean surface of the ERA5-T2m, the ERA5-850mb and of the UAH MSU v6.0 Tlt records are usually cooler than what the CMIP6 GCMs predict on average by an amount approximately equal to 1 σ of their ensemble variability. The land area of the ERA5-T2m appears more consistent with the simulations. The results suggest that the models usually overestimate the warming although in some land regions they may agree with the observations. A similar result was observed in Scafetta [16] where, however, it was argued that the land warming could be biased by uncorrected urban heats and other non-climatic surface phenomena and that the climate models had to be scaled down using as a comparison metric the less-warming ocean temperature record.
The Appendix A shows the performance of all 38 CMIP6 models herein studied in reconstructing the climatic changes observed from 1980–1990 to 2011–2021 against the ERA5-T2m record. A very large variability among the models is observed. The performance of each model can be evaluated by calculating the percentage of the world surface area where the disagreement between each of the synthetic records and the ERA5-T2m record is | Δ T | ⩾ 0.2 °C, | Δ T | ⩾ 0.5 °C and | Δ T | ⩾ 1.0 °C for each location. These values are reported in Table 1 and ranked in Figure 8.
We observe a large variability among the models. The CMIP6 GCMs disagree with the data by | Δ T | ⩾ 0.2 °C over an area that varies from 45–47% to 80–86% of the total world surface (we have considered five models for each of the given lower and higher range estimates). Regarding the | Δ T | ⩾ 0.5 °C condition, the CMIP6 GCMs disagree with the data over an area that varies from 14–16% to 39–50% of the world surface. Regarding the | Δ T | ⩾ 1.0 °C condition, the CMIP6 GCMs disagree with the data over an area that varies from 2.6–3.9% to 16–18% of the world surface. By considerring that on average the world surface has warmed by about 0.5 °C, these results demonstrate that, in general, the CMIP6 GCMs poorly reconstruct the observed warming patterns.
Figure 9 (top panels) compares the ECS of the same models against their predicted mean world surface warming from 1980–1990 to 2011–2021. A positive correlation is found ( R 2 ≈ 0.56 with a correlation coefficient of r ≈ 0.75 , p-value < 0.1 ) so that larger ECSs imply warmer models. The temperature records are compatible only with the low ECS models (for example, ECS ≤ 3 °C), as demonstrated by the green segments that represent the warming levels of the temperature data.
Figure 9 (bottom panels) depicts the scatterplots and the linear regression lines of the ECS of the same CMIP6 GCMs against their percentage of the world area where the disagreement with the ERA5-T2m record is | Δ T | ⩾ 0.2 °C, | Δ T | ⩾ 0.5 °C and | Δ T | ⩾ 1.0 °C. The linear regression analysis gives a positive correlation ( R 2 ≈ 0.45 with a correlation coefficient of r ≈ 0.67 , p-value < 0.1 ). Thus, the GCMs that perform better are usually those with a low ECS; for example, those with ECS ≤ 3 °C. The CMIP6 model that performs worst is the CanESM5 (used in Canada) [47], which also has the second-highest ECS (5.62 °C); according to the graphs depicted in the Appendix A, this model greatly overestimates, in particular, the warming of the Arctic and of the ocean surrounding Antarctica where, on the contrary, a cooling is observed.
See Table 1 for the statisticsl results regarding each model.

4. Discussion

The above results confirm that the CMIP6 models are quite different from each other and suggest those with high ECS are incompatible with the ERA5-T2m record; such a model-data discrepancy increases using low-troposphere temperature records. In any case, also the models with low ECS do not seem to perform well because even the best among them disagree by more than 0.2 °C with the temperature record over more than 45% of the world surface, while the mean world surface warming observed from 1980–1990 and 2011–2021 has been about 0.5 °C. Thus, none of the CMIP6 models are satisfactory yet in interpreting the climate system. It may be pointed out that if as a minimum quality control check we want to confine attention to models where excess warming of at least 0.2 °C is observed in no more than 50% of grid cells, according to the regression lines depicted in Figure 9, only models with ECS around 2 °C or less should be used. Let us discuss such a possibility.
There is a persistent disagreement in the scientific community regarding the real value of the ECS of the Earth climate system. The IPCC [1,2,3] and recent literature propose values ranging from about 0.5 to 6 °C [22]. Such an uncertainty also makes the climate model temperature projections for the 21st century highly dubious. However, our results suggest that the climate sensitivity can not be high because we found that the climate models with high ECS run too hot relative to the observations. Figure 2 and Figure 9 suggest that the real ECS should likely be 3 °C or less. The result is also relevant for policymakers because it indicates that alarming climate change scenario forecasts based on models that are too sensitive to anthropogenic greenhouse gas emissions should be already dismissed.
The Earth’s ECS value has been debated for more than 140 years because it strongly depends on the model assumptions regarding the response of the climatic system to radiative perturbations such as those induced by changes in greenhouse gas concentrations. Doubling the C O 2 concentration of the atmosphere produces a radiative forcing of about 3.7 W/m 2 that should induce a global warming of about 1 °C without any feedback [48]. In fact, the Stefan–Boltzmann law ( J = σ T 4 ) predicts a radiation rate of ∂ J / ∂ T = 4 σ T 3 = 3.8 W/m 2 K for a black-body at the temperature of T = 255 K, which would be the mean Earth’s temperature without the greenhouse effect. However, the Earth’s climate system is also made of numerous and poorly understood feedback mechanisms such as the response of the water vapor and cloud system to a radiative perturbation, which makes it difficult to correctly evaluate its ECS [22].
In 1896, Arrhenius [49] evaluated that doubling the C O 2 concentration could potentially induce a temperature increase of 5–6 °C; however, 10 years later, in 1906, he [50] concluded that his previous estimate was erroneous and proposed lower ECS values ranging from 1.6 to 3.9 °C according to the model adopted for the water vapor feedback response. In 1963, Möller [51] showed that the ECS could vary greatly, up to one order of magnitude, according to how water vapor and/or cloudiness responded to the C O 2 perturbation; the author concluded that such a large uncertainty implied that “the theory that climatic variations are affected by variations in the C O 2 content becomes very questionable”. Manabe and Wetherald [52] developed a one-dimensional model of radiative-convective equilibrium and concluded that the ECS had to be around 2 °C (which is compatible only with the very low ECS end predicted by the modern CMIP5 and CMIP6 GCMs, see Figure 1). In 1974, the same authors [53] used early computer facilities, upgraded their model into a theoretical circulation climate model, and estimated ECS = 2.93 °C. Determining the value of the real Earth’s ECS is still unsettled and debated today because of the uncertain nature of the climate feedback simulated in various models and because of the difficulty of measuring it empirically.
Low ECS values agree with some alternative studies that have found serious disagreements between observations and the CMIP6 model predictions [17,18,30]. In fact, several observational-based and Earth thermal radiation studies suggest low ECS values between 0.5 and 2.5 °C with a median around 1.5 °C [4,5,24,25,26,27,28,29]. These estimates are significantly lower than most of the GCM ECS values.
Some empirical determination yielding to high estimates of the Earth’s ECS seems based on erroneous physical assumptions. For example, Lacis et al. [54] roughly evaluated that the condensing GHG forcing (water vapor and clouds) and the non-condensing GHG forcing ( C O 2 , O 3 , N 2 O , C H 4 , and CFCs) account for about 75% and 25%, respectively, of the total Earth’s greenhouse effect of the atmosphere. The latter raises the global mean surface temperature from the global mean black-body temperature of the Earth, T S ≈ 255 K, to the observed T E ≈ 288 K: that is, by 33 °C. T S is derived from the Stefan–Boltzmann equation assuming S F ≈ 240 W/m 2 of global mean solar radiation absorbed by Earth after the removal of the albedo ( a ≈ 0.3 ) and by dividing by four the incoming total solar irradiance ( I S ≈ 1361 W/m 2 ) because of the spherical shape of the planet: T S = ( 1 − a ) I S / 4 σ 4 , where σ = 5.67· 10 − 8 W/m 2 K 4 . Thus, the additional radiative forcing induced by the atmosphere adds to the system G F = σ T E 4 − σ T S 4 ≈ 150 W/m 2 . However, Lacis et al. [54] assumed that the condensing GHG forcing was the climatic feedback to the non-condensing GHG forcing alone and concluded that the climatic warming effect of the latter had to be amplified by a factor of four by the climatic response of the water vapor and cloud systems. This reasoning yields to an ECS of about 4 °C because doubling C O 2 should induce a warming of about 1 °C without any feedback [48]. It happens that 4 °C is also the approximate ECS average of the CMIP6 GCMs, which suggests that such a reasoning roughly validate the latters.
Lacis et al. [54]’s argument, however, appears flawed because the condensing GHG feedback also responds to the total solar irradiance input responsible for T S , which dominates the thermodynamic process by contributing 240 W/m 2 on the required 390 W/m 2 : that is, about 62% of the total. Thus, by using a similar logic, if it is assumed that the non-condensing GHG total forcing is equal to 150 / 4 = 37.5 W/m 2 and is independent of the total solar forcing, the condensing GHG total forcing should induce an amplification of the total radiative input (240 + G F /4 = 277.5 W/m 2 ) equal to 390 / 277.5= 1.4 . Alternatively, differentiating the Stefan–Boltzmann equation yields to Δ T = T / 4 F · Δ F , where F is the radiative input; thus, assuming T = 288 K (which includes all feedbacks), F = 277.5 W/m 2 (which includes the solar and non-condensing GHG forcing) and Δ F = 3.7 W/m 2 for doubling C O 2 , the temperature increase should be Δ T ≈ 1 °C. Thus, it appears that the water vapor and cloud feedback can amplify the warming of the surface induced by the Sun plus the non-condensing GHGs by a factor ranging between 1 and 1.5, which corresponds to an ECS of about 1.0–1.5 °C.
The above reasoning is very approximate, but the result would agree well with several studies [4,5,24,25,26,27,28,29]. For example, Scafetta [5] proposed an interpretation of the dynamics observed in the global surface temperature records based on natural oscillations since 1850 and concluded that the ECS central estimate had to be around 1.5 °C; however, the proposed ECS value could also be lower (that is between 1.0 and 1.5 °C) because the observed 0.9–1.0 °C warming from 1850 to 2020 is likely partially exaggerated (by about 20%) by non-climatic warming biases such as those induced by the urbanization of extended land regions [16,41]. Similarly, van Wijngaarden and Happer [29] found that the ECS could range from 1.4 to 2.3 °C, but their models did not consider the response of the cloud system, which could also activate a negative feedback [24] and reduce further the provided estimates. Indeed, Lindzen and Choi [24] estimated an ECS of 0.7 °C (with the confidence interval 0.5—1.3 °C at 99% levels). Lewis and Curry [25] calculated an ECS median of 1.5 °C (with 5–95% range: 1.05–2.45 °C). Bates [26] and Monckton et al. [27] evaluated a climate sensitivity in the neighborhood of 1 °C. There are also some authors who, by comparing the various terrestrial planets of the solar system, have proposed that the atmospheric greenhouse effect should be reconsidered from a different physical point of view and would depend on the solar input and the atmospheric pressure of the planets more than on its chemical composition [55].
The IPCC acknowledges that the ECS uncertainty lays mainly in the difficulty of accurately modeling the water vapor and cloud system because even small changes in cloudiness could easily amplify or dampen any C O 2 effect, as already noted about 60 years ago by Möller [51]. However, part of the uncertainty also persists in how the internal variability and the Sun or other astronomical mechanisms control the climate, which is not fully understood yet. For example, total solar irradiance records are highly uncertain both in amplitude and in their temporal evolution, and climate records could also be affected by climatic warming biases induced by the urbanization development and its enlarging urban heat islands [21]. The climate could also be modulated by solar-lunar tides and additional astronomical corpuscular forgings (cosmic rays and interplanetary dust) that could directly influence the cloud system [20,56], which are not included in the CMIP6 GCMs nor in the original works by Manabe and Wetherald [52], Manabe and Wetherald [53] or in other studies attempting to evaluate the Earth’s ECS.
Unknown astronomical forcings or internal mechanisms could generate natural oscillations in the climate system that the models can not reproduce because of missing physical mechanisms; yet, since a number of their internal parameters are tuned against the observations [33], the GCMs could approximately reproduce the warming observed from 1850 to 2020 and, simultaneously, mistake its real physical attributions [5,6]. Indeed, alternative total solar irradiance and global climate estimates already proposed in the scientific litterature suggest everything from no role for the Sun since the pre-industrial period (1850–1900), which implies that recent global warming is mostly human-caused, to most of the recent global warming being due to changes in solar activity, which would mean that recent global warming is mostly natural [21].
The CMIP6 models, such as the previous generation models, predict that nearly 100% of the warming observed since the pre-industrial period (1850–1900) is anthropogenic. The proposed argument is that using only the natural (solar and volcanic) forcing, they produce nearly no warming from 1850 to 2020 [1,2,3]: see, for example, Figure SPM.1 (b) in the Summary for Policymakers of the IPCC AR6 WGI. However, a significant portion of the observed 20th century warming could also have been induced by natural oscillations. In particular, by a quasi millennial cycle (that is evident in several climatic records [7,8,9,10,11,12,13,14,15] and should reach its maximum during the 21st century [57,58]) plus shorter cycles such as a 60-year cycle that appears responsible for the rapid and comparable warming trends occurred in the periods 1850–1980, 1910–1940 and 1970–2000, the cooling trends observed in the periods 1880–1910 and 1940–1970 and the modest warming observed since 2000. This 60-year-like oscillation is also clearly visible in the sea level change and in the North Atlatic Oscillation since 1700 [59,60], in the tropical cyclone activity [61] and in several other climatic indices [62].
Yet, such a 60-year oscillation is not reproduced by the GCMs because the anthropogenic emissions continuously increased and accelerated during the 20th century [5,6,63] despite some cooling in the 1960s because of volcanic and anthropogenic aerosols. In particular, no computer model has predicted the pause (known also as the “hiatus”) observed between 1998 and 2014 in the global temperatures [64]. Moreover, a strong argument against the current climate models is that they also do not reproduce the millennial oscillation by failing to reconstruct warm periods of the Holocene such as the Medieval and the Roman ones [5,6], which are well reproduced by solar data and solar models [7,15,19,57,58]. The presence of unmodeled natural climatic oscillations implies low ECS values to radiative forcings because, according to their phases, part of the 20th century warming would have been produced by them.
For example, in 2013 Scafetta [5] showed that a semi-empirical climate model made of cycles with periods of about 9.1, 10.4, 20, 60, 115, and nearly 1000 years (which have astronomical meanings), plus a volcano and anthropogenic contribution calculated by halving the ECS of the CMIP5 models, performed significantly better than the original CMIP5 models in reconstruction the global surface climate changes. Scafetta [6] extended the same model using 13 harmonics. In general, several climatic and solar oscillations appear to be related to astronomical oscillations [19,57,58], which are found to be similar to the harmonics that need to be chosen for the proposed semi-empirical models. The halving of the GCMs’ ECS could also be justified by observing that the volcano cooling spikes produced by several models appear too deep relative to the observations: see, for example, the simulated climatic effect of the eruption of Mt. Pinatubo between 1991 and 1992 produced by the E3SMv1 GCM (ECS = 5.3 °C) shown in Figure 23 in Golaz et al. [33]: cf. also with Figure 2.
Figure 10 shows the semi-empirical models proposed by Scafetta [5,6] against the ERA5-T2m, ERA5-850mb, and UAH MSU v.6.0 Tlt records since 1950. A comparison is made against the CMIP5 and CMIP6 ensemble mean simulations. Each panel also reports the root-mean-square error (RMSE) between the proposed model and the average among the three temperature records (at the monthly resolution) for three periods 1950–2021, 1980–2021 and 2000–2021. Smaller RMSE values imply a better agreement between the two records.
The semi-empirical models (Figure 10A,C) agree with the data significantly better—in particular after 2000—than how the currently adopted GCMs do (Figure 10B,D), although in the period 2015–2020, two warming peaks due to oceanic oscillations were observed. These two peaks were not supposed to be captured in the model proposed in Reference [5] and were partially predicted by the model proposed in Reference [6], which was calibrated using the temperature data up to 2014. The result suggests that halving the ECS of the CMIP5 or CMIP6—that is, assuming it ranges between 0.9 and 2.8 °C—could be sufficient in modeling the observed climatic changes under the conditions that there are natural oscillations that are not modeled by the GCMs because of missing or erroneous astronomical forcings or other internal mechanisms.
Figure 10 also shows that the semi-empirical models predict for the future a significantly more moderate warming trend than those predicted by both the CMIP5 or CMIP6 models, that, on the contrary, appear to be increasingly diverging from the data.
Finally, we note that although the AR6 has narrowed the ECS likely range to 2.5–4.0 °C by adopting the suggestions of Sherwood et al. [34], the considered line of evidence did not include the possibility that a significant part of the warming occurred since 1850–1900 could have been induced by a natural quasi-millennial oscillation during its warming phase, which followed the Little Ice Age between 1300 and 1850 [5,6]. The millennial oscillation was predicted to peak in the 21st century [57,58] and is superimposed to other natural oscillations such as a quasi 60-year one that has further stressed the warming observed from 1910 to 1940 and from 1970 to 2000, which are likely induced by the Sun and other astronomical forcings. The inclusion of such natural climatic oscillations necessarily implies low ECS. See also the extended discussion in Connolly et al. [21].

5. Conclusions

Herein we tested the performance of 38 last-generation CMIP6 GCMs in simulating the temperature changes that occurred between the periods 1980–1990 and 2011–2021. The climatic changes were estimated using three temperature records: ERA5-T2m, ERA5-850mb, and UAH MSU v6.0 Tlt. We found a better model-data agreement using the ERA5-T2m probably because the analyzed model simulations referred to the temperature at the surface (tas), while ERA5-850mb and UAH MSU v6.0 Tlt are lower troposphere temperatures. But there may be another interpretation.
In fact, the CMIP6 GCMs tend to significantly overestimate the warming recorded in the two lower troposphere temperature records. However, they also overestimate the ocean temperature of the ERA5-T2m, while they generally agree better with its land temperatures. This result can also be interpreted by claiming that the models usually overestimate the warming trend during the observed period and that their better agreement with the surface temperature land record is accidental because the latter could be affected by UHI and other non-climatic warming biases, as extensively discussed by some authors [16,21,41].
We found that the CMIP6 GCMs poorly simulate the temperature changes that occurred in the Arctic, where a very large variability among the models is observed. At the symmetric latitudes ranges 40°–70°N and 50°–70°S, the CMIP6 models predict a warming that is not confirmed by the data. Over the ocean around Antarctica, where an increase in sea ice has been observed [43], there are also vast regions that have experienced a cooling from 1980–1990 to 2011–2021. These cooling regions are usually not predicted by the models. The models also predict on average oceanic currents that are warming too fast, such as the Peru and South Equatorial Pacific currents (where the ENSO phenomenon occurs), the Pacific California and the Atlantic Canary currents.
The above results suggest that the CMIP6 models present some serious problems in modeling the atmospheric and oceanic circulations, the albedo feedback related to glaciers and sea ice formation and melting, and the cloudiness between the temperate and sub-polar regions. Serious differences among the 38 CMIP6 GCMs herein analyzed are also highlighted by a simple visual comparison among the images depicted in the Appendix A.
Therefore, the CMIP6 models are very different from each other, as also demonstrated by their large ECS variability range spanning from 1.83 to 5.67 °C (Table 1, Figure 1), and a major scientific challenge is to narrow such a large uncertainty range.
To do this, we have evaluated the ability of each of the CMIP6 GCMs in properly reconstructing the climatic changes that occurred in each region of the Earth by evaluating the percentage of the world surface where the (positive or negative) discrepancy against the observations exceeds 0.2, 0.5 and 1.0 °C. As Figure 9 shows, the models with low ECS (e.g., 3 °C or less) tend to perform better than those generating high ECS values. The result is important because also several empirical studies have found low ECS values to be more realistic [5,22,24,25,30] while other studies also reported that high ECS models produce historical warming trends that are too large and that look incompatible with the observations [31,36].
The CMIP6 GCM that performs the worst is the CanESM5 (used in Canada) [47] (ECS = 5.62 °C). According to the graphs depicted in the Appendix A, this model greatly overestimates the warming of the Arctic and the ocean surrounding Antarctica. The CIESM GCM (ECS = 5.67 °C) [46] also performs very poorly in greatly exaggerating the warming of the inter-tropical land region.
The main conclusion of this study is that, in general, the CMIP6 GCMs with high ECS (e.g., larger than 3 °C) should not be used to guide policymakers because it is clear that these models run too hot (see Figure 2 and Figure 9) relative to the observations. Therefore, their scenario forecasts for the 21st century would be misleadingly alarming. Another conclusion is that the CMIP6 models are, in general, not satisfactory yet for interpreting climate changes because our detailed analysis highlighted the persistence of several physical issues related, for example, with the sea ice melting, the different response over land and ocean, cloudiness and, in general, with the atmosphere–ocean circulation of the climate system.
Alternative modeling of the climate system that makes use of natural oscillations [5,6] seems to perform better than the current GCMs in reconstructing the global surface temperature. These semi-empirical models predict very low ECS between 1 and 2 °C: a fact supported by alternative studies [8,9,10,11,12,13,14]. These alternative models predict moderate warming for the next decades. In general, also a very low ECS (e.g., between 1 and 1.5 °C) cannot be excluded because the water vapor and cloud feedback respond both to the other GHGs present in the atmosphere and to the full solar irradiance input—not just to its variation—which dominates and regulates the climate of the Earth. Other issues regarding the current uncertainty referring to the solar and climatic data that could also imply low ECS are extensively discussed by Connolly et al. [21].

Author Contributions

N.S. is the only author of this study. The author has read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data used in this study were downloaded from Climate Explorer: https://climexp.knmi.nl/start.cgi Retrieved on 7 July 2021 and 29 September 2021.

Conflicts of Interest

The author declares no conflict of interest.

Appendix A

Figure A1,Figure A2,Figure A3,Figure A4,Figure A5,Figure A6,Figure A7,Figure A8 depict the warming patterns observed from 1980–1990 to 2011–2021 for each of the 38 CMIP6-tas GCMs herein studied (left panels) and their comparison against the ERA5-T2m record (right panels). Each panel also contains the latitudinal temperature profile for the ocean, land, and ocean+land areas. The statistical analysis referring to each model is reported in Table 1 and summarized in Figure 8 and Figure 9.
Climate 09 00161 g0a1 550
Figure A1. Warming patterns from 1980–1990 to 2011–2021 for the indicated CMIP6-tas GCM (left) and its comparison against the ERA5-T2m record (right).
Figure A1. Warming patterns from 1980–1990 to 2011–2021 for the indicated CMIP6-tas GCM (left) and its comparison against the ERA5-T2m record (right).
Climate 09 00161 g0a1
Climate 09 00161 g0a2 550
Figure A2. Warming patterns from 1980–1990 to 2011–2021 for the indicated CMIP6-tas GCM (left) and its comparison against the ERA5-T2m record (right).
Figure A2. Warming patterns from 1980–1990 to 2011–2021 for the indicated CMIP6-tas GCM (left) and its comparison against the ERA5-T2m record (right).
Climate 09 00161 g0a2
Climate 09 00161 g0a3 550
Figure A3. Warming patterns from 1980–1990 to 2011–2021 for the indicated CMIP6-tas GCM (left) and its comparison against the ERA5-T2m record (right).
Figure A3. Warming patterns from 1980–1990 to 2011–2021 for the indicated CMIP6-tas GCM (left) and its comparison against the ERA5-T2m record (right).
Climate 09 00161 g0a3
Climate 09 00161 g0a4 550
Figure A4. Warming patterns from 1980–1990 to 2011–2021 for the indicated CMIP6-tas GCM (left) and its comparison against the ERA5-T2m record (right).
Figure A4. Warming patterns from 1980–1990 to 2011–2021 for the indicated CMIP6-tas GCM (left) and its comparison against the ERA5-T2m record (right).
Climate 09 00161 g0a4
Climate 09 00161 g0a5 550
Figure A5. Warming patterns from 1980–1990 to 2011–2021 for the indicated CMIP6-tas GCM (left) and its comparison against the ERA5-T2m record (right).
Figure A5. Warming patterns from 1980–1990 to 2011–2021 for the indicated CMIP6-tas GCM (left) and its comparison against the ERA5-T2m record (right).
Climate 09 00161 g0a5
Climate 09 00161 g0a6 550
Figure A6. Warmingpatterns from 1980–1990 to 2011–2021 for the indicated CMIP6-tas GCM (left) and its comparison against the ERA5-T2m record (right).
Figure A6. Warmingpatterns from 1980–1990 to 2011–2021 for the indicated CMIP6-tas GCM (left) and its comparison against the ERA5-T2m record (right).
Climate 09 00161 g0a6
Climate 09 00161 g0a7 550
Figure A7. Warmingpatterns from 1980–1990 to 2011–2021 for the indicated CMIP6-tas GCM (left) and its comparison against the ERA5-T2m record (right).
Figure A7. Warmingpatterns from 1980–1990 to 2011–2021 for the indicated CMIP6-tas GCM (left) and its comparison against the ERA5-T2m record (right).
Climate 09 00161 g0a7
Climate 09 00161 g0a8 550
Figure A8. Warming patterns from 1980–1990 to 2011–2021 for the indicated CMIP6-tas GCM (left) and its comparison against the ERA5-T2m record (right).
Figure A8. Warming patterns from 1980–1990 to 2011–2021 for the indicated CMIP6-tas GCM (left) and its comparison against the ERA5-T2m record (right).
Climate 09 00161 g0a8

References

  1. Intergovernmental Panel on Climate Change (IPCC): 2007. Working Group I Contribution to the Third Assessment Report (AR3), Climate Change 2007: The Physical Science Basis. 2007. Available online: https://www.ipcc.ch/assessment-report/ar3/ (accessed on 15 October 2021).
  2. Intergovernmental Panel on Climate Change (IPCC): 2013. Working Group I Contribution to the Fifth Assessment Report (AR5), Climate Change 2013: The Physical Science Basis. 2013. Available online: https://www.ipcc.ch/assessment-report/ar5/ (accessed on 15 October 2021).
  3. Intergovernmental Panel on Climate Change (IPCC): 2007. Working Group I Contribution to the Sixth Assessment Report (AR6), Climate Change 2021: The Physical Science Basis. 2021. Available online: https://www.ipcc.ch/assessment-report/ar6/ (accessed on 15 October 2021).
  4. Scafetta, N. Testing an astronomically based decadal-scale empirical harmonic climate model versus the IPCC (2007) general circulation climate models. J. Atmos. Sol.-Terr. Phys. 2012, 80, 124–137. [Google Scholar] [CrossRef] [Green Version]
  5. Scafetta, N. Discussion on climate oscillations: CMIP5 general circulation models versus a semiempirical harmonic model based on astronomical cycles. Earth-Sci. Rev. 2013, 126, 321–357. [Google Scholar] [CrossRef] [Green Version]
  6. Scafetta, N. Reconstruction of the Interannual to Millennial Scale Patterns of the Global Surface Temperature. Atmosphere 2021, 12, 147. [Google Scholar] [CrossRef]
  7. Kerr, R.A. A variable sun paces millennial climate. Science 2001, 294, 1431–1433. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  8. Alley, R.B. GISP2 Ice Core Temperature and Accumulation Data; IGBP PAGES/World Data Center for Paleoclimatology Data Contribution Series #2004-013; NOAA/NGDC Paleoclimatology Program: Boulder, CO, USA, 2004. [Google Scholar]
  9. Moberg, A.; Sonechkin, D.M.; Holmgren, K.; Datsenko, N.M.; Karlén, W. Highly variable Northern Hemisphere temperatures reconstructed from low- and highresolution proxy data. Nature 2005, 433, 613–617. [Google Scholar] [CrossRef] [PubMed]
  10. Ljungqvist, F.C. A new reconstruction of temperature variability in the extratropical northern hemisphere during the last two millennia. Geogra-Fiska Ann. Ser. A 2010, 92, 339–351. [Google Scholar] [CrossRef]
  11. Christiansen, B.; Ljungqvist, F.C. The extra-tropical Northern Hemisphere temperature in the last two millennia: Reconstructions of low-frequency variability. Clim. Past. 2012, 8, 765–786. [Google Scholar] [CrossRef] [Green Version]
  12. Esper, J.; Frank, D.C.; Timonen, M.; Zorita, E.; Wilson, R.J.S.; Luterbacher, J.; Holzkämper, S.; Fischer, N.; Wagner, S.; Nievergelt, D.; et al. Orbital forcing of tree-ring data. Nat. Clim. Chang. 2012, 2, 862–866. [Google Scholar] [CrossRef]
  13. Matskovsky, V.V.; Helama, S. Testing long-term summer temperature reconstruction based on maximum density chronologies obtained by reanalysis of tree-ring data sets from northernmost Sweden and Finland. Clim. Past 2014, 10, 1473–1487. [Google Scholar] [CrossRef] [Green Version]
  14. Kutschera, W.; Patzelt, G.; Steier, P.; Wild, E.M. The tyrolean iceman and his glacial environment during the holocene. Radiocarbon 2017, 59, 395–405. [Google Scholar] [CrossRef]
  15. Zhao, X.; Soon, W.; Velasco Herrera, V.M. Holocene Millennial-Scale Solar Variability and the Climatic Responses on Earth. Universe 2021, 7, 36. [Google Scholar] [CrossRef]
  16. Scafetta, N. Detection of non-climatic biases in land surface temperature records by comparing climatic data and their model simulations. Clim. Dyn. 2021, 56, 2959–2982. [Google Scholar] [CrossRef]
  17. McKitrick, R.; Christy, J. A test of the tropical 200 to 300 hPa warming rate in climate models. Earth Space Sci. 2018, 5, 529–536. [Google Scholar] [CrossRef] [Green Version]
  18. Mitchell, D.M.; Lo, Y.T.E.; Seviour, W.J.M.; Haimberger, L.; Polvani, L.M. The vertical profile of recent tropical temperature trends: Persistent model biases in the context of internal variability. Environ. Res. Lett. 2020, 15, 1040b4. [Google Scholar] [CrossRef]
  19. Scafetta, N. Solar Oscillations and the Orbital Invariant Inequalities of the Solar System. Solar Phys. 2020, 295, 33. [Google Scholar] [CrossRef]
  20. Scafetta, N.; Milani, F.; Bianchini, A. A 60-Year Cycle in the Meteorite Fall Frequency Suggests a Possible Interplanetary Dust Forcing of the Earth’s Climate Driven by Planetary Oscillations. Geophys. Res. Lett. 2020, 47, e2020GL089954. [Google Scholar] [CrossRef]
  21. Connolly, R.; Soon, W.; Connolly, M.; Baliunas, S.; Berglunded, J.; Butler, C.J.; Cionco, R.G.; Elias, A.G.; Fedorov, V.M.; Harde, H.; et al. How much has the Sun influenced Northern Hemisphere temperature trends? An ongoing debate. (Invited Review). Res. Astron. Astrophys. 2021, 21, 131. [Google Scholar] [CrossRef]
  22. Knutti, R.; Rugenstein, M.A.; Hegerl, G.C. Beyond equilibrium climate sensitivity. Nat. Geosci. 2017, 10, 727–736. [Google Scholar] [CrossRef]
  23. Zelinka, M.D.; Myers, T.A.; McCoy, D.T.; Po-Chedley, S.; Caldwell, P.M.; Ceppi, P.; Klein, S.A.; Taylor, K.E. Causes of higher climate sensitivity in CMIP6 models. Geophys. Lett. 2020, 47, e2019GL085782. [Google Scholar] [CrossRef] [Green Version]
  24. Lindzen, R.S.; Choi, Y.-S. On the observational determination of climate sensitivity and its implications. Asia Pac. J. Atmos. Sci. 2011, 47, 377–390. [Google Scholar] [CrossRef]
  25. Lewis, N.; Curry, J. The Impact of Recent Forcing and Ocean Heat Uptake Data on Estimates of Climate Sensitivity. J. Clim. 2018, 31, 6051–6071. [Google Scholar] [CrossRef]
  26. Bates, J.R. Estimating climate sensitivity using two-zone energy balance models. Earth Space Sci. 2016, 3, 207–225. [Google Scholar] [CrossRef] [Green Version]
  27. Monckton, C.; Soon, W.-H.; Legates, D.R.; Briggs, W.M. Why models run hot: Results from an irreducibly simplemodel. Sci. Bull. 2015, 60, 122–135. [Google Scholar] [CrossRef] [Green Version]
  28. Kluft, L.; Dacie, S.; Schmidt, H.; Stevens, B. Re-Examining the First Climate Models: Climate Sensitivity of a Modern Radiative-Conective Equilibrium Model. J. Clim. 2019, 32, 8111–8125. [Google Scholar] [CrossRef] [Green Version]
  29. Van Wijngaarden, W.A.; Happer, W. Dependence of Earth’s Thermal Radiation on Five Most Abundant Greenhouse Gases. arXiv 2020, arXiv:2006.03098. [Google Scholar]
  30. Zhu, J.; Poulsen, C.J.; Otto-Bliesner, B.L. High climate sensitivity in CMIP6 model not supported by paleoclimate. Nat. Clim. Chang. 2020, 10, 378–379. [Google Scholar] [CrossRef]
  31. Tokarska, K.B.; Hegerl, G.C.; Schurer, A.P.; Forster, P.M.; Marvel, K. Observational constraints on the effective climate sensitivity from the historical period. Environ.Res. Lett. 2020, 15, 034043. [Google Scholar] [CrossRef] [Green Version]
  32. Huntingford, C.; Williamson, M.S.; Nijsse, F.J.M.M. CMIP6 climate models imply high committed warming. Clim. Chang. 2020, 162, 1515–1520. [Google Scholar] [CrossRef]
  33. Golaz, J.-C.; Caldwell, P.M.; Van Roekel, L.P.; Petersen, M.R.; Tang, Q.; Wolfe, J.D.; Abeshu, G.; Anantharaj, V.; Asay-Davis, X.S.; Bader, D.C.; et al. The DOE E3SM coupled model version 1: Overview and evaluation at standard resolution. J. Adv. Model. Earth Syst. 2019, 11, 2089–2129. [Google Scholar] [CrossRef]
  34. Sherwood, S.C.; Webb, M.J.; Annan, J.D.; Armour, K.C.; Forster, P.M.; Hargreaves, J.C.; Hegerl, G.; Klein, S.A.; Marvel, K.D.; Rohling, E.J.; et al. An assessment of Earth’s climate sensitivity using multiple lines of evidence. Rev. Geophys. 2020, 58, e2019RG000678. [Google Scholar] [CrossRef] [PubMed]
  35. Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
  36. Spencer, R.W.; Christy, J.R.; Braswell, W.D. UAH Version 6 global satellite temperature products: Methodology and results. Asia-Pac. J. Atmos. Sci. 2017, 53, 121–130. [Google Scholar] [CrossRef]
  37. Morice, C.P.; Kennedy, J.J.; Rayner, N.A.; Jones, P.D. Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: The HadCRUT4 dataset. J. Geophys. Res. 2012, 117, D08101. [Google Scholar] [CrossRef]
  38. Lenssen, N.; Schmidt, G.; Hansen, J.; Menne, M.; Persin, A.; Ruedy, R.; Zyss, D. Improvements in the GISTEMP uncertainty model. J. Geophys. Res. Atmos. 2019, 124, 6307–6326. [Google Scholar] [CrossRef]
  39. Menne, M.J.; Williams, C.N.; Gleason, B.E.; Rennie, J.J.; Lawrimore, J.H. The Global Historical Climatology Network Monthly Temperature Dataset, Version 4. J. Clim. 2018, 31, 9835–9854. [Google Scholar] [CrossRef]
  40. Huang, B.; Thorne, P.W.; Banzon, V.F.; Boyer, T.; Chepurin, G.; Lawrimore, J.H.; Menne, M.J.; Smith, T.M.; Vose, R.S.; Zhang, H.-M. Extended reconstructed sea surface temperature version 5 (ERSSTv5), Upgrades, validations, and intercomparisons. J. Clim. 2017, 30, 8179–8205. [Google Scholar] [CrossRef]
  41. Scafetta, N.; Ouyang, S. Detection of UHI bias in China climate network using Tmin and Tmax surface temperature divergence. Glob. Planet Chang. 2019, 181, 102989. [Google Scholar] [CrossRef]
  42. McKitrick, R.R.; Tole, L. Evaluating Explanatory Models of the Spatial Pattern of Surface Climate Trends using Model Selection and Bayesian Averaging Methods. Clim. Dyn. 2012, 39, 2867–2882. [Google Scholar] [CrossRef]
  43. Scafetta, N.; Mazzarella, A. The Arctic and Antarctic Sea-Ice Area Index Records versus Measured and Modeled Temperature Data. Adv. Meteorol. 2015, 2015, 481834. [Google Scholar] [CrossRef] [Green Version]
  44. Emetc, V.; Tregoning, P.; Morlighem, M.; Borstad, C.; Sambridge, M. A statistical fracture model for Antarctic ice shelves and glaciers. Cryosphere 2018, 12, 3187–3213. [Google Scholar] [CrossRef] [Green Version]
  45. Zwally, H.; Li, J.; Robbins, J.; Saba, J.; Yi, D.; Brenner, A. Mass gains of the Antarctic ice sheet exceed losses. J. Glaciol. 2015, 61, 1019–1036. [Google Scholar] [CrossRef] [Green Version]
  46. Lin, Y.; Huang, X.; Liang, Y.; Qin, Y.; Xu, S.; Huang, W.; Xu, F.; Liu, L.; Wang, Y.; Peng, Y.; et al. Community Integrated Earth System Model (CIESM): Description and evaluation. J. Adv. Modeling Earth Syst. 2020, 12, e2019MS002036. [Google Scholar] [CrossRef]
  47. Swart, N.C.; Cole, J.N.S.; Kharin, V.V.; Lazare, M.; Scinocca, J.F.; Gillett, N.P.; Anstey, J.; Arora, V.; Christian, J.R.; Hanna, S.; et al. The Canadian Earth System Model version 5 (CanESM5.0.3). Geosci. Model Dev. 2019, 12, 4823–4873. [Google Scholar] [CrossRef] [Green Version]
  48. Rahmstorf, S. Anthropogenic Climate Change: Revisiting the Facts. In Global Warming: Looking Beyond Kyoto; Zedillo, E., Ed.; Brookings Institution Press: Washington, DC, USA, 2008; pp. 34–53. [Google Scholar]
  49. Arrhenius, S. On the Influence of Carbonic Acid in the Air upon the Temperature of the Ground. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1896, 41, 237–275. [Google Scholar] [CrossRef] [Green Version]
  50. Arrhenius, S. Die vermutliche Ursache der Klimaschwankungen (The Probable Cause of Climate Fluctuations). Medd. Från K. Vetenskapsakademiens Nobelinst. 1906, 1, 1–10. [Google Scholar]
  51. Möller, F. On the influence of changes in the CO2 concentration in air on the radiation balance of the Earth’s surface and on the climate. J. Geophys. Res. 1963, 68, 3877–3886. [Google Scholar] [CrossRef] [Green Version]
  52. Manabe, S.; Wetherald, R.T. Thermal Equilibrium of the Atmosphere with a Given Distribution of Relative Humidity. J. Atmos. Sci. 1967, 24, 241–259. [Google Scholar] [CrossRef] [Green Version]
  53. Manabe, S.; Wetherald, R.T. The Effects of Doubling the CO2 Concentration on the climate of a General Circulation Model. J. Atmos. Sci. 1975, 32, 3–15. [Google Scholar] [CrossRef] [Green Version]
  54. Lacis, A.A.; Schmidt, G.A.; Rind, D.; Ruedy, R.A. Atmospheric CO2: Principal control knob governing Earth’s temperature. Science 2010, 330, 356–359. [Google Scholar] [CrossRef] [Green Version]
  55. Nikolov, N.; Zeller, K. New Insights on the Physical Nature of the Atmospheric Greenhouse Effect Deduced from an Empirical Planetary Temperature Model. Environ. Clim. Chang. 2017, 1, 112. [Google Scholar] [CrossRef]
  56. Svensmark, H.; Enghoff, M.B.; Shaviv, N.J.; Svensmark, J. Increased ionization supports growth of aerosols into cloud condensation nuclei. Nat. Commun. 2017, 8, 2199. [Google Scholar] [CrossRef] [Green Version]
  57. Scafetta, N. Multi-scale harmonic model for solar and climate cyclical variation throughout the Holocene based on Jupiter-Saturn tidal frequencies plus the 11-year solar dynamo cycle. J. Atmos. Sol.-Terr. 2012, 80, 296–311. [Google Scholar] [CrossRef] [Green Version]
  58. Scafetta, N. Discussion on the spectral coherence between planetary, solar and climate oscillations: A reply to some critiques. Astrophys. Space Sci. 2014, 354, 275–299. [Google Scholar] [CrossRef] [Green Version]
  59. Jevrejeva, S.; Moore, J.C.; Grinsted, A.; Woodworth, P. Recent global sea level acceleration started over 200 years ago? Geophys. Res. Lett. 2008, 35, L08715. [Google Scholar] [CrossRef]
  60. Scafetta, N. Multi-scale dynamical analysis (MSDA) of sea level records versus PDO, AMO, and NAO indexes. Clim. Dyn. 2014, 43, 175–192. [Google Scholar] [CrossRef] [Green Version]
  61. Vecchi, G.A.; Knutson, T.R. 2011. Estimating annual numbers of Atlantic hurricanes missing from the HURDAT database (1878–1965) using ship track density. J. Clim. 2011, 24, 1736–1746. [Google Scholar] [CrossRef]
  62. Wyatt, M.; Curry, J. Role of Eurasian Arctic shelf sea ice in a secularly varying hemispheric climate signal during the 20th century. Clim. Dyn. 2014, 42, 2763–2782. [Google Scholar] [CrossRef]
  63. Gervais, F. Anthropogenic CO2 warming challenged by 60-year cycle. Earth-Sci. Rev. 2016, 155, 129–135. [Google Scholar] [CrossRef]
  64. Hedemann, C.; Mauritsen, T.; Jungclaus, J.; Marotzke, J. The subtle origins of surface-warming hiatuses. Nat. Clim. Chang. 2017, 7, 336–339. [Google Scholar] [CrossRef]
Climate 09 00161 g001 550
Figure 1. Equilibrium climate sensitivity of 42 CMIP6 GCMs. (From Table 7.SM.5 in Ref. [3]).
Figure 1. Equilibrium climate sensitivity of 42 CMIP6 GCMs. (From Table 7.SM.5 in Ref. [3]).
Climate 09 00161 g001
Climate 09 00161 g002 550
Figure 2. CMIP6 GCM surface temperature simulations (red, models with ECS > 3; blue, models with ECS ≤ 3) against the temperature observations (green): ERA5-T2m, ERA5-850mb, and UAH MSU v.6.0 Tlt.
Figure 2. CMIP6 GCM surface temperature simulations (red, models with ECS > 3; blue, models with ECS ≤ 3) against the temperature observations (green): ERA5-T2m, ERA5-850mb, and UAH MSU v.6.0 Tlt.
Climate 09 00161 g002
Climate 09 00161 g003 550
Figure 3. Regional distribution of warming patterns from 1980–1990 to 2011–2021 for the CMIP6-tas ensemble average record and the six temperature records: ERA5-T2m, ERA5-850mb, and UAH MSU v6.0 Tlt, HadCRUT4, GISTEMP 250km, NOAA v5. Gray areas indicate missing data.
Figure 3. Regional distribution of warming patterns from 1980–1990 to 2011–2021 for the CMIP6-tas ensemble average record and the six temperature records: ERA5-T2m, ERA5-850mb, and UAH MSU v6.0 Tlt, HadCRUT4, GISTEMP 250km, NOAA v5. Gray areas indicate missing data.
Climate 09 00161 g003
Climate 09 00161 g004 550
Figure 4. Comparison between the CMIP6 ensemble mean and the temperature records (ERA5-T2m, ERA5-850mb, and UAH MSU v6.0 Tlt) using the latitudinal profile of the difference between land and ocean temperatures.
Figure 4. Comparison between the CMIP6 ensemble mean and the temperature records (ERA5-T2m, ERA5-850mb, and UAH MSU v6.0 Tlt) using the latitudinal profile of the difference between land and ocean temperatures.
Climate 09 00161 g004
Climate 09 00161 g005 550
Figure 5. Difference between the warming from 1980–1990 to 2011–2021 predicted by the CMIP6-tas ensemble average record and those produced by the three temperature records ERA5-T2m, ERA5-850mb and UAH MSU v6.0 Tlt.
Figure 5. Difference between the warming from 1980–1990 to 2011–2021 predicted by the CMIP6-tas ensemble average record and those produced by the three temperature records ERA5-T2m, ERA5-850mb and UAH MSU v6.0 Tlt.
Climate 09 00161 g005
Climate 09 00161 g006 550
Figure 6. Latitudinal warming profile from 1980–1990 to 2011–2021 produced by 38 CMIP6 models.
Figure 6. Latitudinal warming profile from 1980–1990 to 2011–2021 produced by 38 CMIP6 models.
Climate 09 00161 g006
Climate 09 00161 g007 550
Figure 7. Latitudinal warming profile from 1980–1990 to 2011–2021 produced by three adopted temperature records (ERA5-T2m, ERA5-850mb, and the UAH MSU v6.0 Tlt) (red curves) against the CMIP6 models: their average profile (black curves) plus/minus one standard deviation of the model ensemble ( ± 1 σ ) (blue curves). Each panel also reports the mean Student t-test value for each case calculated by averaging the values for each latitude. A model-data agreement can be rejected at the significance level 0.05 when t ≥ 2.03 .
Figure 7. Latitudinal warming profile from 1980–1990 to 2011–2021 produced by three adopted temperature records (ERA5-T2m, ERA5-850mb, and the UAH MSU v6.0 Tlt) (red curves) against the CMIP6 models: their average profile (black curves) plus/minus one standard deviation of the model ensemble ( ± 1 σ ) (blue curves). Each panel also reports the mean Student t-test value for each case calculated by averaging the values for each latitude. A model-data agreement can be rejected at the significance level 0.05 when t ≥ 2.03 .
Climate 09 00161 g007
Climate 09 00161 g008 550
Figure 8. Model ranking relative to the percentage of the world area where the disagreement between each of the CMIP6 GCMs and the ERA5-T2m record is Δ T ⩾ 0.2 °C, Δ T ⩾ 0.5 °C and Δ T ⩾ 1.0 °C.
Figure 8. Model ranking relative to the percentage of the world area where the disagreement between each of the CMIP6 GCMs and the ERA5-T2m record is Δ T ⩾ 0.2 °C, Δ T ⩾ 0.5 °C and Δ T ⩾ 1.0 °C.
Climate 09 00161 g008
Climate 09 00161 g009 550
Figure 9. Top panels: scatterplots and linear regressions between the ECS of the mean warming predicted by the CMIP6 GCMs from 1980–1990 and 2011–2021. The green segments represent the warming levels of the temperature data: ERA5-T2m, ERA5-850mb, and UAH MSU v6.0 Tlt. Bottom panels: scatterplots and linear regressions between the ECS of the CMIP6 GCMs and their percentage of the world area where the disagreement with the ERA5-T2m record is | Δ T | ⩾ 0.2 °C, | Δ T | ⩾ 0.5 °C and | Δ T | ⩾ 1.0 °C, respectively. See Table 1.
Figure 9. Top panels: scatterplots and linear regressions between the ECS of the mean warming predicted by the CMIP6 GCMs from 1980–1990 and 2011–2021. The green segments represent the warming levels of the temperature data: ERA5-T2m, ERA5-850mb, and UAH MSU v6.0 Tlt. Bottom panels: scatterplots and linear regressions between the ECS of the CMIP6 GCMs and their percentage of the world area where the disagreement with the ERA5-T2m record is | Δ T | ⩾ 0.2 °C, | Δ T | ⩾ 0.5 °C and | Δ T | ⩾ 1.0 °C, respectively. See Table 1.
Climate 09 00161 g009
Climate 09 00161 g010 550
Figure 10. ERA5-T2m, ERA5-850mb, and UAH MSU v.6.0 Tlt against: (A) the semi-empirical model proposed in Scafetta [5], which uses 6 harmonics plus the volcano and anthropocentric component obtained from halving the CMIP5 ensemble mean simulation; (B) the CMIP5 ensemble mean simulation; (C) the semi-empirical model proposed in Scafetta [6] with 13 harmonics plus the volcano and anthropocentric component obtained from halving the CMIP6 ensemble mean simulation; (D) the CMIP6 ensemble mean simulation. The gray area is fixed at ± 0.15 °C, which approximately corresponds to the fluctuation range of the observations. Each panel also reports the RMSE values between the proposed model and the average among the three temperature records for the three indicated periods. Smaller RMSE values imply a better agreement between the two records.
Figure 10. ERA5-T2m, ERA5-850mb, and UAH MSU v.6.0 Tlt against: (A) the semi-empirical model proposed in Scafetta [5], which uses 6 harmonics plus the volcano and anthropocentric component obtained from halving the CMIP5 ensemble mean simulation; (B) the CMIP5 ensemble mean simulation; (C) the semi-empirical model proposed in Scafetta [6] with 13 harmonics plus the volcano and anthropocentric component obtained from halving the CMIP6 ensemble mean simulation; (D) the CMIP6 ensemble mean simulation. The gray area is fixed at ± 0.15 °C, which approximately corresponds to the fluctuation range of the observations. Each panel also reports the RMSE values between the proposed model and the average among the three temperature records for the three indicated periods. Smaller RMSE values imply a better agreement between the two records.
Climate 09 00161 g010
Table
Table 1. The CMIP6 GCMs herein studied using the listed SSP simulation, the mean warming from 1980–1990 and 2011–2021 (over the total surface, land and ocean), and their performance estimated by the percentage of the world area where they disagree with the ERA5-T2m record by | Δ T | ⩾ 0.2 °C, | Δ T | ⩾ 0.5 °C and | Δ T | ⩾ 1.0 °C regarding the warming from 1980–1990 and 2011–2021. The last six raws add information about the used temperature records.
Table 1. The CMIP6 GCMs herein studied using the listed SSP simulation, the mean warming from 1980–1990 and 2011–2021 (over the total surface, land and ocean), and their performance estimated by the percentage of the world area where they disagree with the ERA5-T2m record by | Δ T | ⩾ 0.2 °C, | Δ T | ⩾ 0.5 °C and | Δ T | ⩾ 1.0 °C regarding the warming from 1980–1990 and 2011–2021. The last six raws add information about the used temperature records.
CMIP6SSPECSMean | Δ T | Mean | Δ T | Mean | Δ T | | Δ T | ⩾ 0.2 °C⩾ 0.5 °C⩾ 1.0 °C
GCM (°C)Total (°C)Land (°C)Ocean (°C)(%)(%)(%)
ACCESS-CM23704.720.871.040.7871286.3
ACCESS-ESM1-53703.870.841.040.7466316.8
AWI-CM-1-1-MR3703.160.760.870.7158215.1
BCC-CSM2-MR3703.040.650.780.5950184.9
CAMS-CSM1-03702.290.380.410.3753215.3
CanESM5 p13705.621.191.421.07864616
CanESM5 p23705.621.231.461.11865018
CanESM5-CanOE p23705.621.171.381.07844316
CESM23705.160.760.950.6759227.8
CESM2-WACCM3704.750.891.070.7971278.4
CIESM5855.670.701.030.53703617
CMCC-CM2-SR53703.520.680.710.6750226.8
CNRM-CM6-1 f23704.830.650.760.6051186.0
CNRM-CM6-1-HR f23704.280.710.810.6656237.4
CNRM-ESM2-1 f23704.760.620.750.5547163.6
EC-Earth33704.300.891.050.8065288.7
EC-Earth3-Veg3704.310.841.000.7562247.8
FGOALS-f3-L3703.000.700.870.6257184.1
FGOALS-g33702.880.570.680.5148164.3
FIO-ESM-2-0585 0.780.900.7155207.2
GFDL-ESM43703.90.660.820.5958194.0
GISS-E2-1-G p13702.720.710.820.6656194.9
GISS-E2-1-G p33702.720.410.490.3753226.3
HadGEM3-GC31-LL f35855.551.081.251.00803915
INM-CM4-83701.830.540.630.5052217.0
INM-CM5-03701.920.650.770.5947174.6
IPSL-CM6A-LR3704.560.760.870.7056185.1
KACE-1-0-G3704.480.931.110.84702911
MCM-UA-1-03703.650.800.800.8071327.5
MIROC63702.610.470.610.4052163.5
MIROC-ES2L f23702.680.570.710.5055227.0
MPI-ESM1-2-HR3702.980.590.690.5446153.0
MPI-ESM1-2-LR3703.000.570.680.5245142.6
MRI-ESM2-03703.150.630.760.5647153.9
NESM35854.721.041.220.93723516
NorESM2-LM3702.540.771.060.62673311
NorESM2-MM3702.500.690.910.5768307.2
UKESM1-0-LL f23705.341.091.221.02813915
CMIP6 Ens. Mean3703.90.750.890.68
ERA5 T2m 0.560.730.4753173.6
ERA5 850mb 0.460.480.4567234.9
UAH MSU v6.0 Tlt 0.430.520.3965215.9
HadCRUT4 0.610.860.50
GISTEMP 0.680.950.59
NOAAv5 0.641.020.49
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Scafetta, N. Testing the CMIP6 GCM Simulations versus Surface Temperature Records from 1980–1990 to 2011–2021: High ECS Is Not Supported. Climate 2021, 9, 161. https://doi.org/10.3390/cli9110161

AMA Style

Scafetta N. Testing the CMIP6 GCM Simulations versus Surface Temperature Records from 1980–1990 to 2011–2021: High ECS Is Not Supported. Climate. 2021; 9(11):161. https://doi.org/10.3390/cli9110161

Chicago/Turabian Style

Scafetta, Nicola. 2021. "Testing the CMIP6 GCM Simulations versus Surface Temperature Records from 1980–1990 to 2011–2021: High ECS Is Not Supported" Climate 9, no. 11: 161. https://doi.org/10.3390/cli9110161

APA Style

Scafetta, N. (2021). Testing the CMIP6 GCM Simulations versus Surface Temperature Records from 1980–1990 to 2011–2021: High ECS Is Not Supported. Climate, 9(11), 161. https://doi.org/10.3390/cli9110161

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop