The Solar Radiation Climate of Greece
Abstract
:1. Introduction
2. Materials and Methods
3. Results
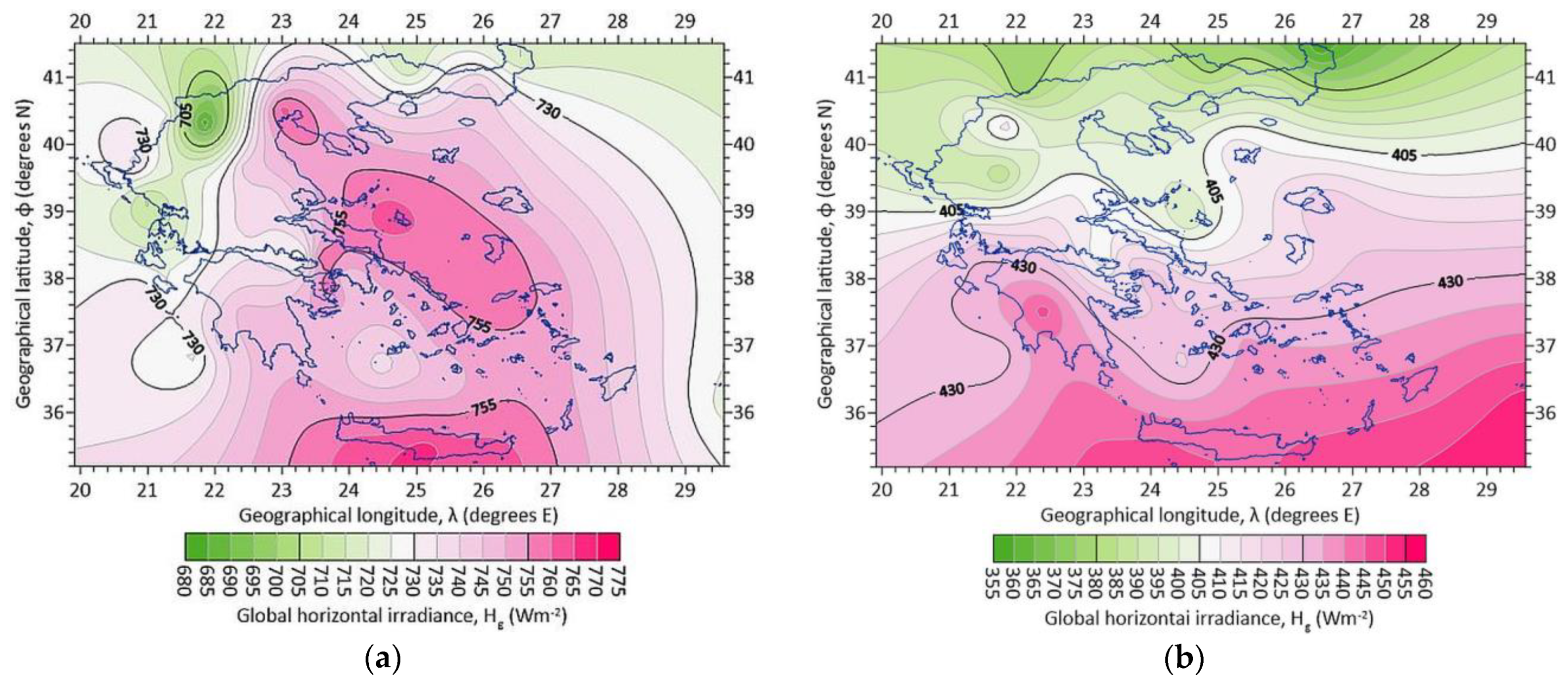
3.1. Annual Mean Values
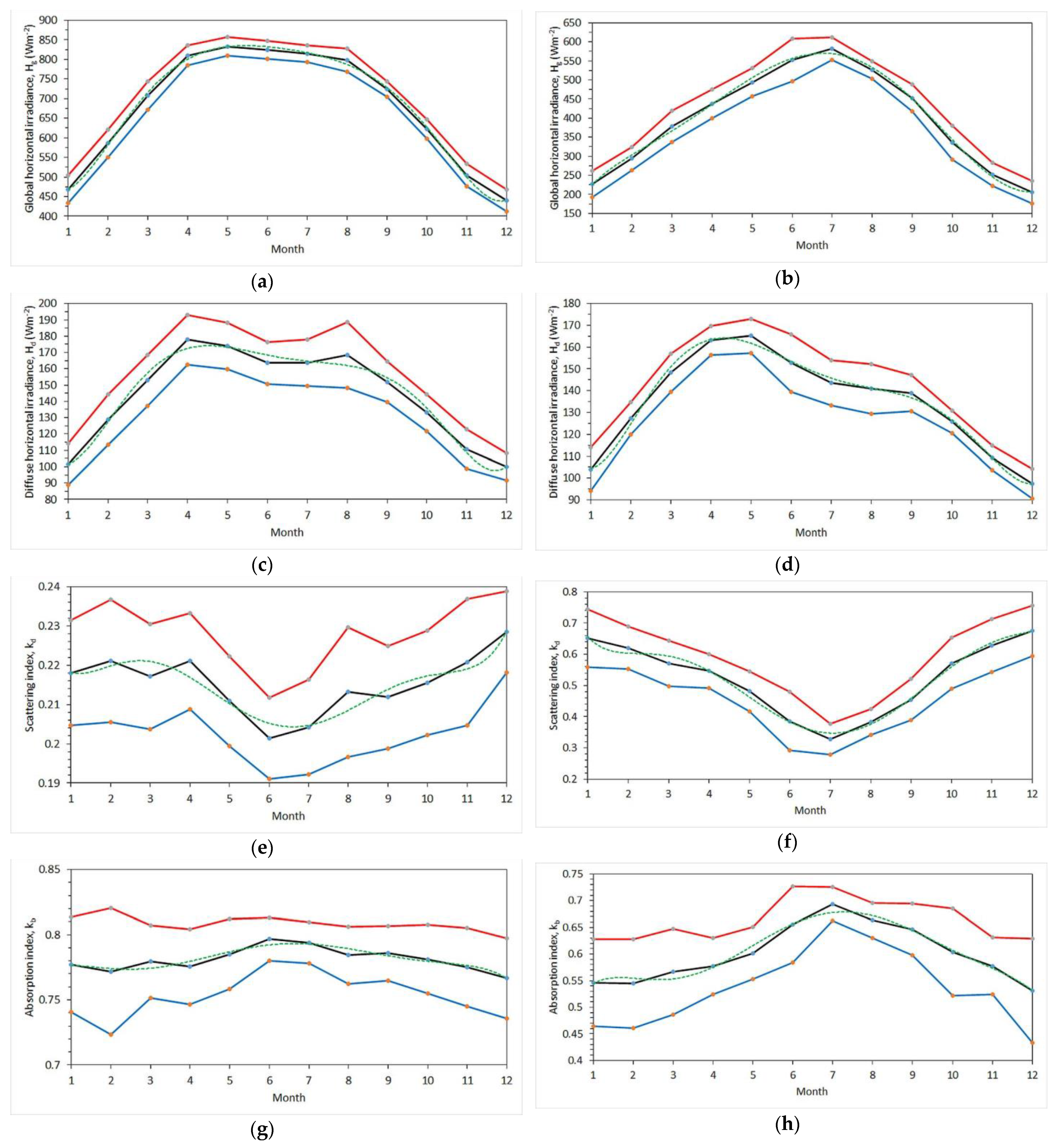
3.2. Monthly Mean Values
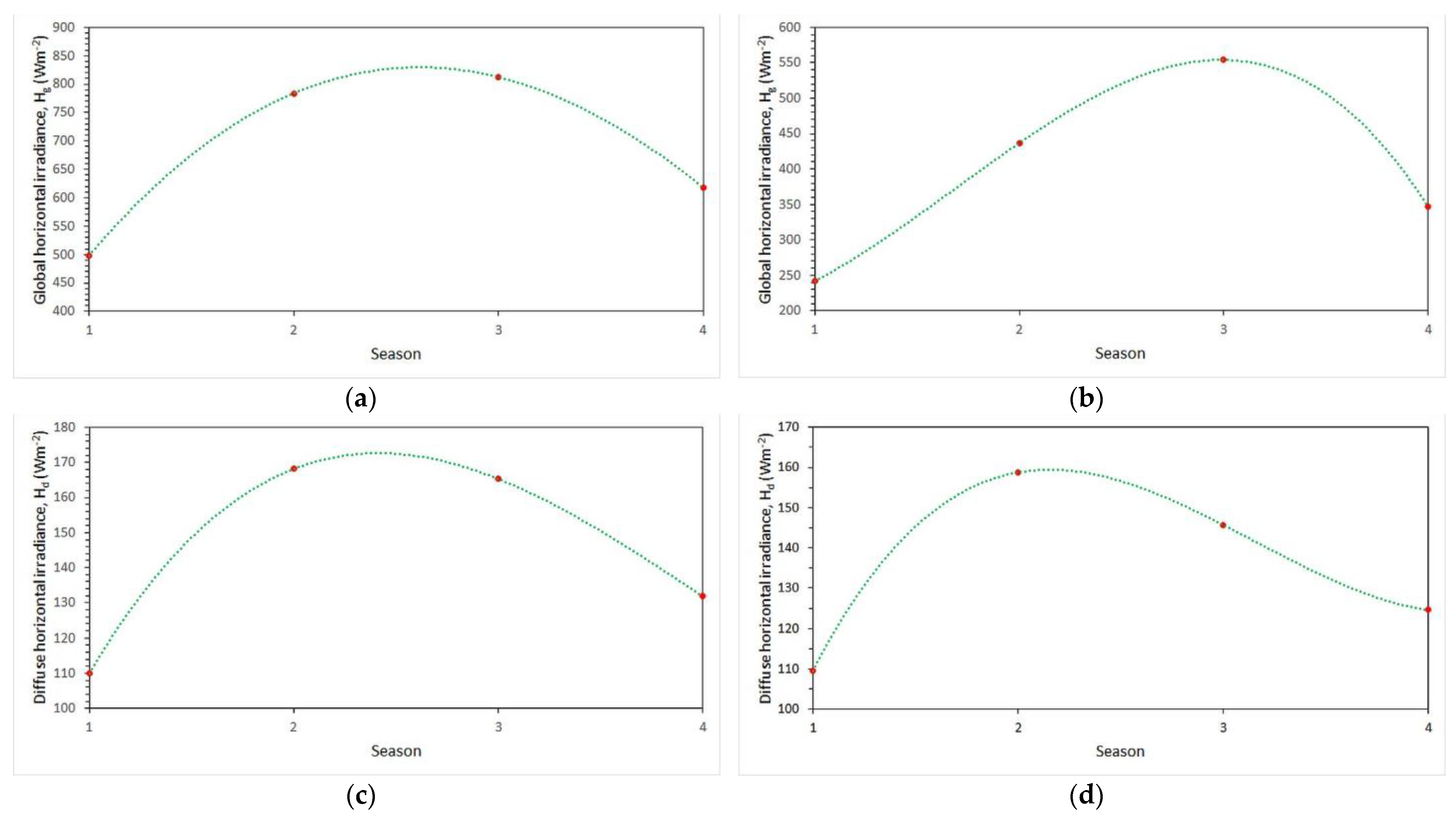
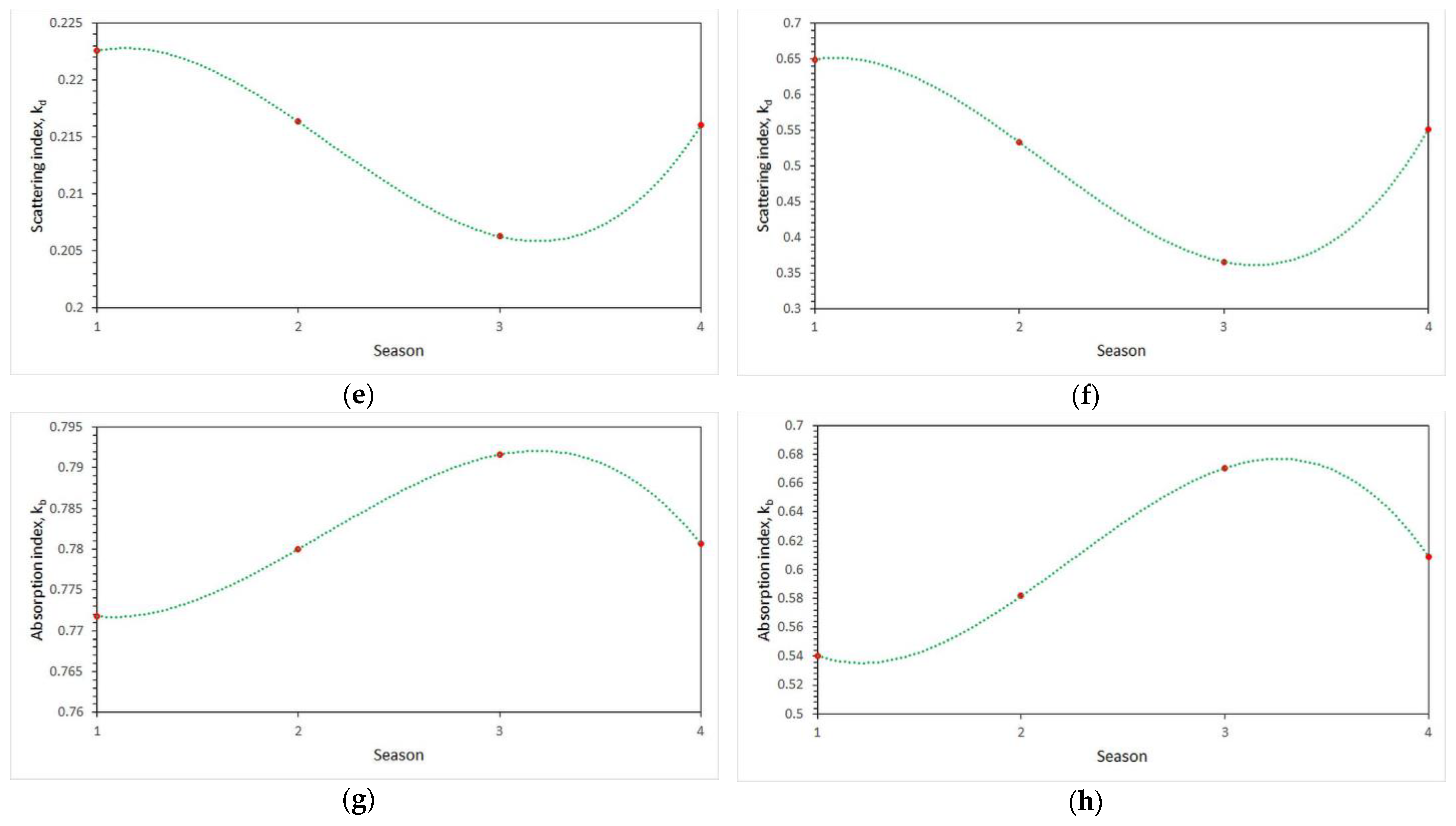
3.3. Seasonal Mean Values
3.4. Direct Solar Radiation
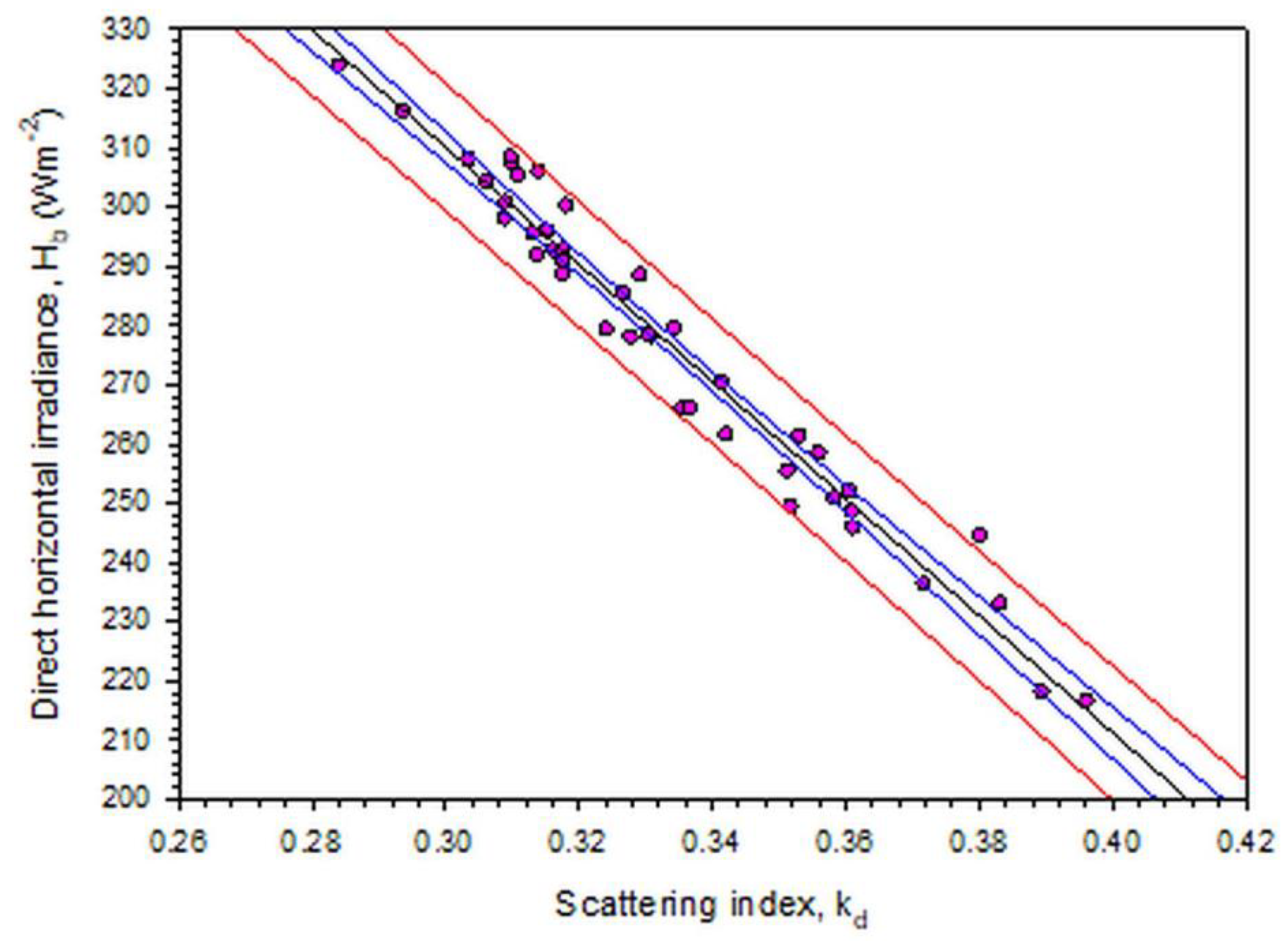
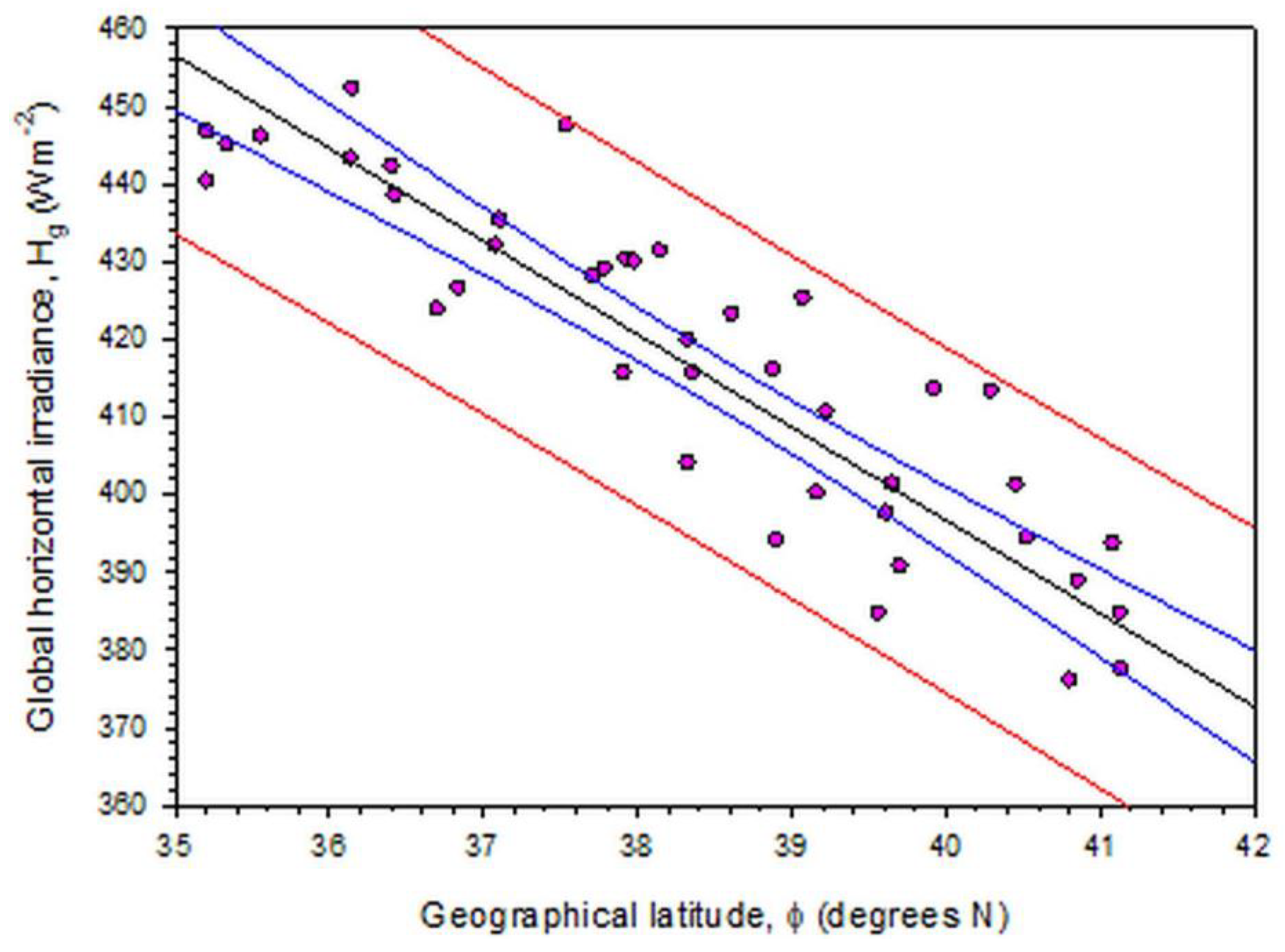
3.5. Dependence of Hg on kd or on φ
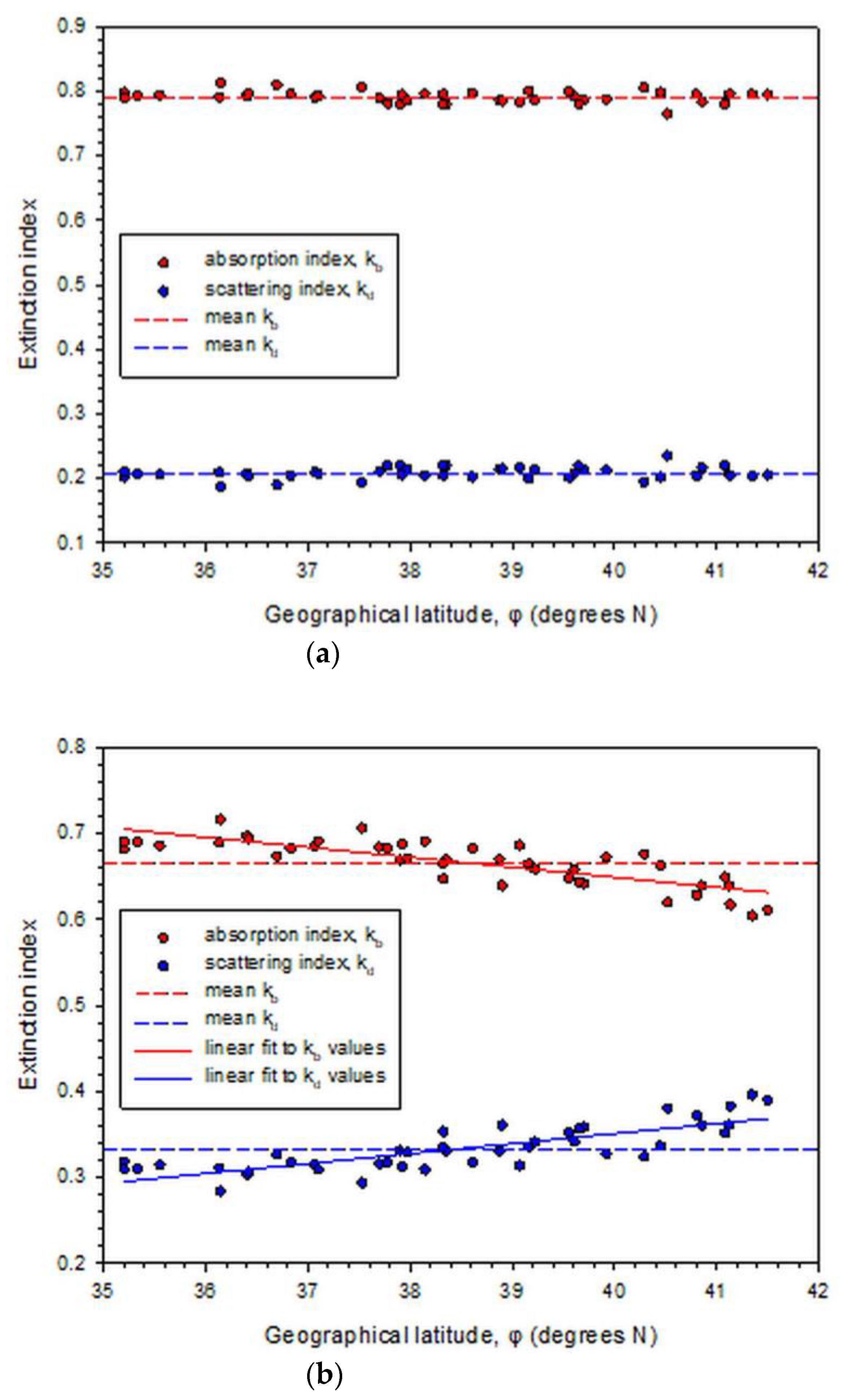
3.6. Extinction of Solar Radiation over Greece
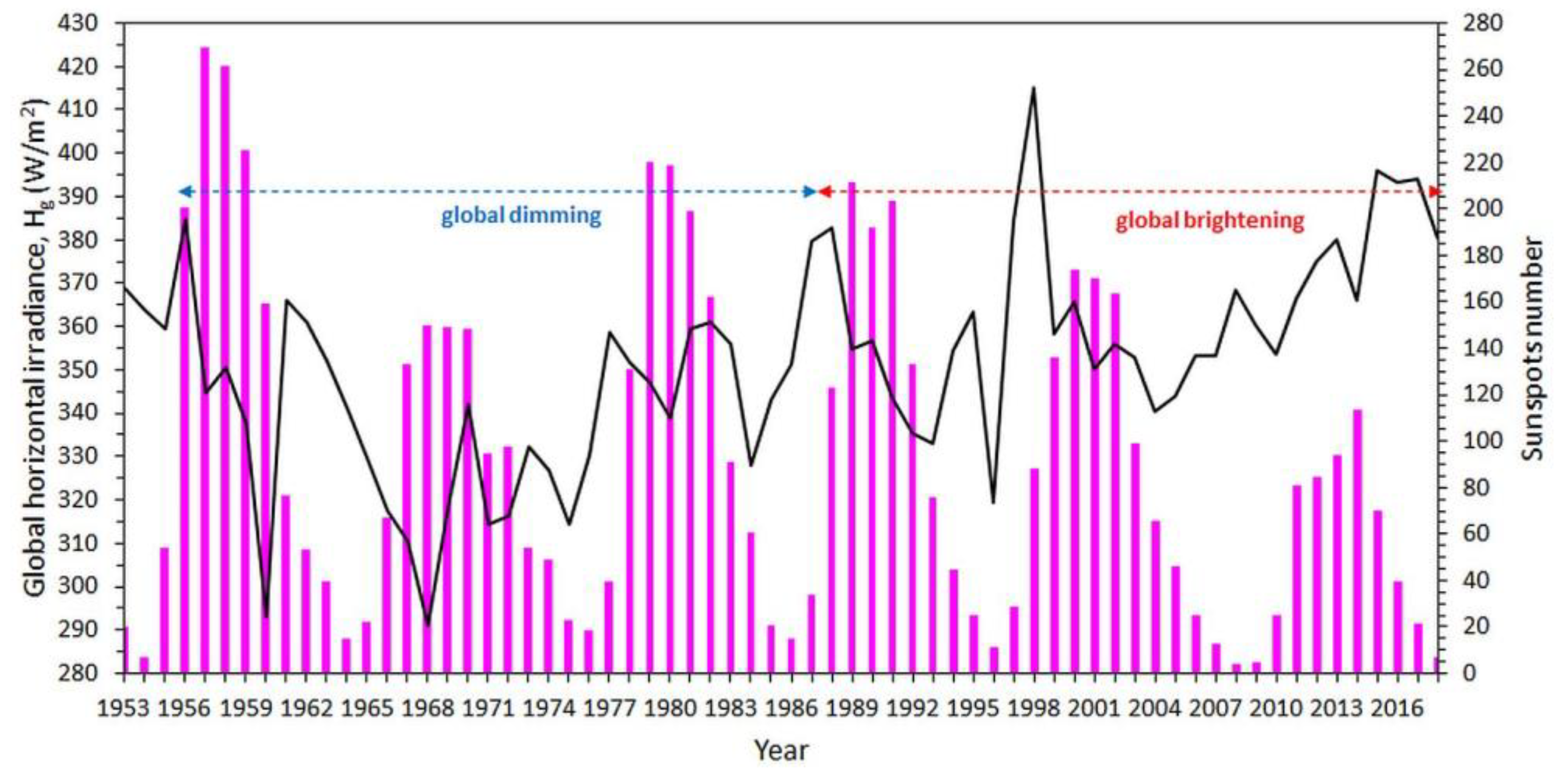
3.7. Solar Variability and Solar Radiation over Athens
4. Discussion
5. Conclusions
- Under clear skies, higher annual Hg values occur in northern Greece (Thessaloniki area), over most of the Aegean and all over Crete. On the contrary, lower annual Hg values exist over northwestern Greece (Epirus and most parts of western Macedonia). The annual kd pattern resembles that of Hd. High values of kb dominate almost all over Greece.
- Under all-sky conditions, the annual Hg pattern is split into two halves, one in the north and another in the south with a dividing line at the latitude of about 39° N. The distribution of the annual Hd levels is similar to that for clear skies. The annual kd pattern resembles much that of Hg, while that for kb is quite the opposite.
- Under clear skies, the intra-annual Hg levels present a rather broad maximum during the months of May–July. In the case of Hd, this parameter presents two main maxima, one in April and another in August. As far as kd is concerned, this parameter experiences lower values during the summer. The absorption index shows a rather flat behaviour throughout the year.
- Under all-sky conditions, the monthly mean Hg values are higher in the summer (here in July). The diffuse solar radiation, though, obtains higher values in springtime (April, May). The intra-annual variation of kd shows a clear minimum in the summer (June, July), whereas kb obtains maximum values in the summer.
- Under clear skies, the average summer value of Hg is slightly higher and the average summer value of Hd slightly lower than that of spring. The average summer value of kd is the lowest among all seasons, while that for kb is the highest. The same conclusions apply in the case of all skies.
- Under all skies, Hg decreases with increasing kd; the same behaviour exists for increasing φ.
- The kd and kb indices reflect the scattering and absorption mechanisms of solar radiation in the atmosphere. The expression kd + kb = 1 was validated.
- kd increases and kb decreases with increasing φ under all-sky conditions.
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Giesen, R.H.; van den Broeke, M.R.; Oerlemans, J.; Andreassen, L.M. Surface energy balance in the ablation zone of Midtdalsbreen, a glacier in Southern Norway: Interannual variability and the effect of clouds. J. Geophys. Res. 2008, 113, D21111. [Google Scholar] [CrossRef]
- Asaf, D.; Rotenberg, E.; Tatarinov, F.; Dicken, U.; Montzka, S.A.; Yakir, D. Ecosystem photosynthesis inferred from measurements of carbonyl sulphide flux. Nat. Geosci. 2013, 6, 186–190. [Google Scholar] [CrossRef]
- Bojinski, S.; Verstraete, M.; Peterson, T.C.; Richter, C.; Simmons, A.; Zemp, M. The concept of essential climate variables in support of climate research, applications, and policy. Bull. Am. Meteorol. Soc. 2014, 95, 1431–1443. [Google Scholar] [CrossRef]
- Kambezidis, H.D. The solar resource. In Comprehensive Renewable Energy; Elsevier: Amsterdam, The Netherlands, 2012; Volume 3. [Google Scholar] [CrossRef]
- Kambezidis, H.D. The solar radiation climate of athens: Variations and tendencies in the period 1992–2017, the Brightening Era. Sol. Energy 2018, 173, 328–347. [Google Scholar] [CrossRef]
- Forster, P.M. Inference of climate sensitivity from analysis of earth’s energy budget. Annu. Rev. Earth Planet. Sci. 2016, 44, 85–106. [Google Scholar] [CrossRef]
- Haywood, J.; Boucher, O. Estimates of the direct and indirect radiative forcing due to tropospheric aerosols: A review. Rev. Geophys. 2000, 38, 513–543. [Google Scholar] [CrossRef]
- Puetz, S.J.; Prokoph, A.; Borchardt, G. Evaluating alternatives to the milankovitch theory. J. Stat. Plan. Inference 2016, 170, 158–165. [Google Scholar] [CrossRef] [Green Version]
- Madhlopa, A. Solar radiation climate in malawi. Sol. Energy 2006, 80, 1055–1057. [Google Scholar] [CrossRef]
- Jiménez, J.I. Solar radiation statistic in Barcelona, Spain. Sol. Energy 1981, 27, 271–282. [Google Scholar] [CrossRef]
- Dissing, D.; Wendler, G. Solar radiation climatology of Alaska. Theor. Appl. Climatol. 1998, 61, 161–175. [Google Scholar] [CrossRef]
- Petrenz, N.; Sommer, M.; Berger, F.H. Long-time global radiation for Central Europe derived from ISCCP Dx data. Atmos. Chem. Phys. 2007, 7, 5021–5032. [Google Scholar] [CrossRef] [Green Version]
- Nottrott, A.; Kleissl, J. Validation of the NSRDB-SUNY global horizontal irradiance in California. Sol. Energy 2010, 84, 1816–1827. [Google Scholar] [CrossRef]
- Persson, T. Solar radiation climate in Sweden. Phys. Chem. Earth 1999, 24, 275–279. [Google Scholar] [CrossRef]
- Exell, R.H.B. The solar radiation climate of Thailand. Sol. Energy 1976, 18, 349–354. [Google Scholar] [CrossRef]
- Diabaté, L.; Blanc, P.; Wald, L. Solar radiation climate in Africa. Sol. Energy 2004, 76, 733–744. [Google Scholar] [CrossRef] [Green Version]
- Kambezidis, H.D.; Psiloglou, B.E. Climatology of the Linke and Unsworth-Monteith turbidity parameters for Greece: Introduction to the notion of a typical atmospheric turbidity year. Appl. Sci. 2020, 10, 4043. [Google Scholar] [CrossRef]
- Unsworth, M.H.; Monteith, J.L. Aerosol and solar radiation in Britain. Q. J. R. Meteorol. Soc. 1972, 98, 778–797. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Adamopoulos, A.D.; Zevgolis, D. Determination of Ångström and Schüepp’s parameters from ground-based spectral measurements of beam irradiance in the ultraviolet and visible spectrum in Athens, Greece. Pure Appl. Geophys. 2001, 158, 821–838. [Google Scholar] [CrossRef]
- Janjai, S.; Kumharn, W.; Laksanaboonsong, J. Determination of angstrom’s turbidity coefficient over Thailand. Renew. Energy 2003, 28, 1685–1700. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Psiloglou, B.E.; Kaskaoutis, D.G.; Karagiannis, D.; Petrinoli, K.; Gavriil, A.; Kavadias, K. Generation of typical meteorological years for 33 locations in Greece: Adaptation to the needs of various applications. Theor. Appl. Climatol. 2020, 141, 1313–1330. [Google Scholar] [CrossRef]
- Huld, T.; Müller, R.; Gambardella, A. A new solar radiation database for estimating PV performance in Europe and Africa. Sol. Energy 2012, 86, 1803–1815. [Google Scholar] [CrossRef]
- Urraca, R.; Gracia-Amillo, A.M.; Koubli, E.; Huld, T.; Trentmann, J.; Riihelä, A.; Lindfors, A.V.; Palmer, D.; Gottschalg, R.; Antonanzas-Torres, F. Extensive validation of CM SAF surface radiation products over Europe. Remote Sens. Environ. 2017, 199, 171–186. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Urraca, R.; Huld, T.; Gracia-Amillo, A.; Martinez-de-Pison, F.J.; Kaspar, F.; Sanz-Garcia, A. Evaluation of global horizontal irradiance estimates from ERA5 and COSMO-REA6 reanalyses using ground and satellite-based data. Sol. Energy 2018, 164, 339–354. [Google Scholar] [CrossRef]
- ELOT. Information and Documentation: Conversion of Greek Characters into Latin Characters. Standard 743; Multiple. Distributed through American National Standards Institute: Washington, DC, USA, 2001; ICS 01.140.10. [Google Scholar]
- ISO. Information and Documentation: Conversion of Greek Characters into Latin Characters. Standard 843; Multiple. Distributed through American National Standards Institute: Washington, DC, USA, 1997; ICS 01.140.10. [Google Scholar]
- Kambezidis, H.D.; Kampezidou, S.I.; Kampezidou, D. Mathematical determination of the upper and lower limits of the diffuse fraction at any site. Appl. Sci. 2021, 11, 8654. [Google Scholar] [CrossRef]
- Sahsamanoglou, H.S.; Bloutsos, A.A. Cleansing of the atmosphere in the Athens area by means of rainfall and wind. Energy Build. 1982, 4, 125–128. [Google Scholar] [CrossRef]
- Adamopoulos, A.D.; Kambezidis, H.D.; Zevgolis, D. Total atmospheric transmittance in the UV and VIS spectra in Athens, Greece. Pure Appl. Geophys. 2005, 162, 409–431. [Google Scholar] [CrossRef]
- Giavis, G.M.; Kambezidis, H.D.; Lykoudis, S.P. Frequency distribution of particulate MATTER (PM10) in urban environments. Int. J. Environ. Pollut. 2009, 36, 99–109. [Google Scholar] [CrossRef]
- Perez, R.; Ineichen, P.; Seals, R.; Zelenka, A. Making full use of the clearness index for parameterizing hourly insolation conditions. Sol. Energy 1990, 45, 111–114. [Google Scholar] [CrossRef] [Green Version]
- Katopodis, T.; Markantonis, I.; Politi, N.; Vlachogiannis, D.; Sfetsos, A. High-resolution solar climate atlas for Greece under climate change using the weather research and forecasting (WRF) model. Atmosphere 2020, 11, 761. [Google Scholar] [CrossRef]
- Ioannidis, E.; Lolis, C.J.; Papadimas, C.D.; Hatzianastassiou, N.; Bartzokas, A. On the intra-annual variation of cloudiness over the Mediterranean region. Atmos. Res. 2018, 208, 246–256. [Google Scholar] [CrossRef]
- Adamopoulos, A.D.; Kambezidis, H.D.; Kaskaoutis, D.G.; Giavis, G. A study of aerosol particle sizes in the atmosphere of Athens, Greece, retrieved from solar spectral measurements. Atmos. Res. 2007, 86, 194–206. [Google Scholar] [CrossRef]
- Dumka, U.C.; Kaskaoutis, D.G.; Sagar, R.; Chen, J.; Singh, N.; Tiwari, S. First results from light scattering enhancement factor over central Indian Himalayas during GVAX campaign. Sci. Total Environ. 2017, 605–606, 124–138. [Google Scholar] [CrossRef] [PubMed]
- Schmeisser, L.; Andrews, E.; Ogren, J.A.; Sheridan, P.; Jefferson, A.; Sharma, S.; Kim, J.E.; Sherman, J.P.; Sorribas, M.; Kalapov, I.; et al. Classifying aerosol type using in situ surface spectral aerosol optical properties. Atmos. Chem. Phys. 2017, 17, 12097–12120. [Google Scholar] [CrossRef] [Green Version]
- Gkikas, A.; Hatzianastassiou, N.; Mihalopoulos, N.; Katsoulis, V.; Kazadzis, S.; Pey, J.; Querol, X.; Torres, O. The regime of intense desert dust episodes in the Mediterranean based on contemporary satellite observations and ground measurements. Atmos. Chem. Phys. 2013, 13, 12135–12154. [Google Scholar] [CrossRef] [Green Version]
- Bai, J.; Zong, X. Global solar radiation transfer and its loss in the atmosphere. Appl. Sci. 2021, 11, 2651. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Kaskaoutis, D.G.; Kharol, S.K.; Moorthy, K.K.; Satheesh, S.K.; Kalapureddy, M.C.R.; Badarinath, K.V.S.; Sharma, A.R.; Wild, M. Multi-decadal variation of the net downward shortwave radiation over South Asia: The solar dimming effect. Atmos. Environ. 2012, 50, 360–372. [Google Scholar] [CrossRef]
- Nastos, P.T.; Kambezidis, H.D.; Demetriou, D. Solar dimming/brightening within the Mediterranean. In Proceedings of the 13th International Conference on Environmental Science and Technology, Athens, Greece, 5–7 September 2013; Global NEST: Athens, Greece, 2013. ISBN 978-960-7475-51-0. [Google Scholar]
- Kambezidis, H.D.; Kaskaoutis, D.G.; Kalliampakos, G.K.; Rashki, A.; Wild, M. The solar dimming/brightening effect over the Mediterranean basin in the period 1979–2012. J. Atmos. Sol.-Terr. Phys. 2016, 150–151, 31–46. [Google Scholar] [CrossRef]
- Gilgen, H.; Wild, M.; Ohmura, A. Means and trends of shortwave irradiance at the surface estimated from global energy balance archive data. J. Clim. 1998, 11, 2042–2061. [Google Scholar] [CrossRef]
- Gilgen, H.; Roesch, A.; Wild, M.; Ohmura, A. Decadal changes in shortwave irradiance at the surface in the period from 1960 to 2000 estimated from global energy balance archive data. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Wild, M. Global dimming and brightening: A review. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Chan, A.L.S. Generation of typical meteorological years using genetic algorithm for different energy systems. Renew. Energy 2016, 90, 1–13. [Google Scholar] [CrossRef]
- Farah, S.; Saman, W.; Boland, J. Development of robust meteorological year weather data. Renew. Energy 2018, 118, 343–350. [Google Scholar] [CrossRef]
- Janjai, S.; Deeyai, P. Comparison of methods for generating typical meteorological year using meteorological data from a tropical environment. Appl. Energy 2009, 86, 528–537. [Google Scholar] [CrossRef]
- Bre, F.; e Silva Machado, R.M.; Lawrie, L.K.; Crawley, D.B.; Lamberts, R. Assessment of solar radiation data quality in typical meteorological years and its influence on the building performance simulation. Energy Build. 2021, 250, 111251. [Google Scholar] [CrossRef]
- Mosalam Shaltout, M.A.; Tadros, M.T.Y. Typical solar radiation year for egypt. Renew. Energy 1994, 4, 387–393. [Google Scholar] [CrossRef]
- Chang, K.; Zhang, Q. Improvement of the hourly global solar model and solar radiation for air-conditioning design in China. Renew. Energy 2019, 138, 1232–1238. [Google Scholar] [CrossRef]
- Huang, K.T. Identifying a suitable hourly solar diffuse fraction model to generate the typical meteorological year for building energy simulation application. Renew. Energy 2020, 157, 1102–1115. [Google Scholar] [CrossRef]
- Soneye, O.O. Evaluation of clearness index and cloudiness index using measured global solar radiation data: A case study for a tropical climatic region of Nigeria. Atmosfera 2021, 34, 25–39. [Google Scholar] [CrossRef]
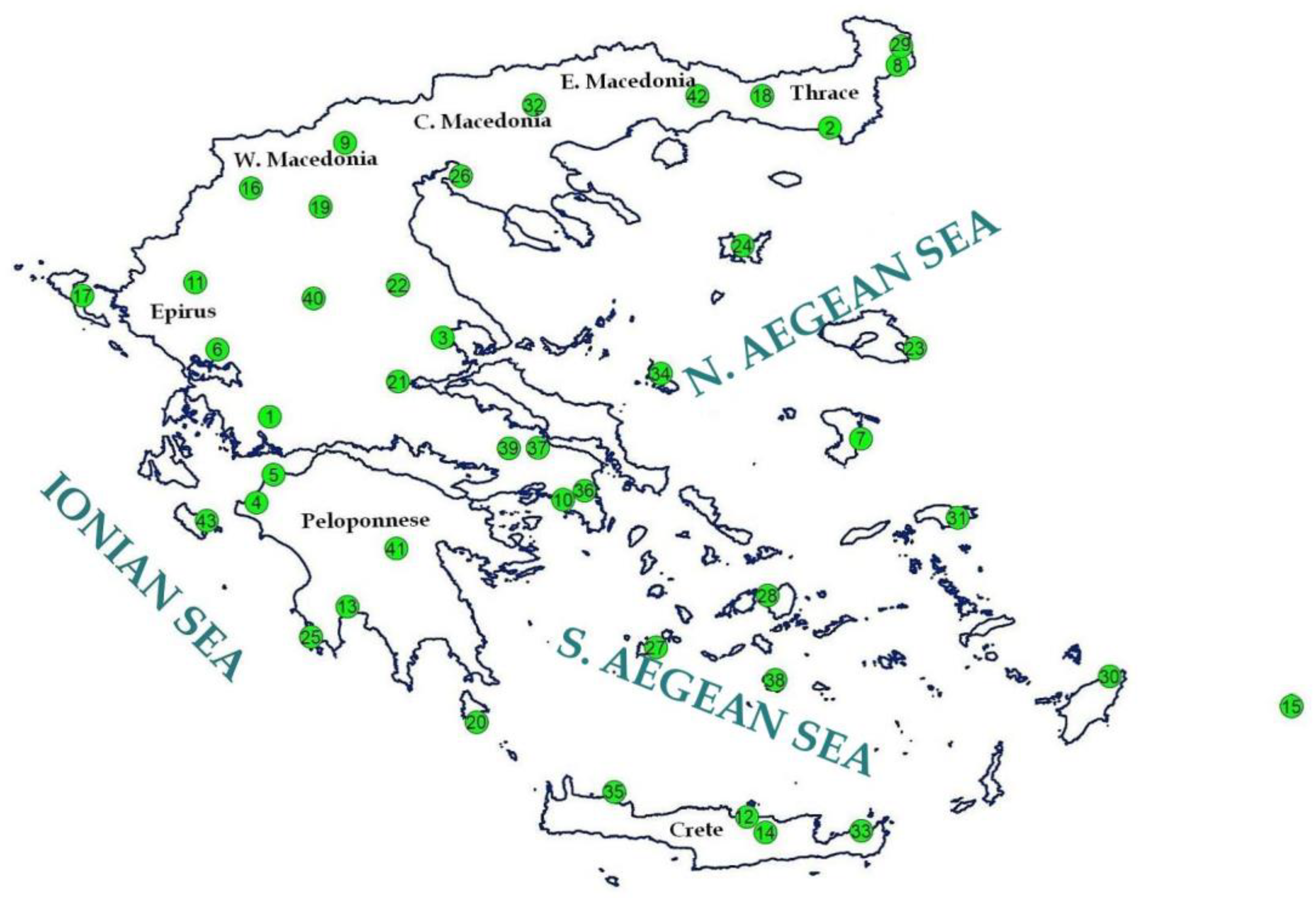




| Site # | Site Name/Region/Altitude above Sea Level (m) | λ (° E) | φ (° N) |
|---|---|---|---|
| 1 | Agrinio/Western Greece/25 | 21.383 | 38.617 |
| 2 | Alexandroupoli/Eastern Macedonia and Thrace/3.5 | 25.933 | 40.850 |
| 3 | Anchialos/Thessaly/15.3 | 22.800 | 39.067 |
| 4 | Andravida/Western Greece/15.1 | 21.283 | 37.917 |
| 5 | Araxos/Western Greece/11.7 | 21.417 | 38.133 |
| 6 | Arta/Epirus/96 | 20.988 | 39.158 |
| 7 | Chios/Northern Aegean/4 | 26.150 | 38.350 |
| 8 | Didymoteicho/Eastern Macedonia and Thrace/27 | 26.496 | 41.348 |
| 9 | Edessa/Western Macedonia/321 | 22.044 | 40.802 |
| 10 | Elliniko/Attica/15 | 23.750 | 37.900 |
| 11 | Ioannina/Epirus/484 | 20.817 | 39.700 |
| 12 | Irakleio/Crete/39.3 (also written as Heraklion) | 25.183 | 35.333 |
| 13 | Kalamata/Peloponnese/11.1 | 22.000 | 37.067 |
| 14 | Kastelli/Crete/335 | 25.333 | 35.120 |
| 15 | Kastelorizo/Southern Aegean/134 | 29.576 | 36.142 |
| 16 | Kastoria/Western Macedonia/660.9 | 21.283 | 40.450 |
| 17 | Kerkyra/Ionian Islands/4 (also known as Corfu) | 19.917 | 39.617 |
| 18 | Komotini/Eastern Macedonia and Thrace/44 | 25.407 | 41.122 |
| 19 | Kozani/Western Macedonia/625 | 21.783 | 40.283 |
| 20 | Kythira/Attica/166.8 | 23.017 | 36.133 |
| 21 | Lamia/Sterea Ellada/17.4 | 22.400 | 38.850 |
| 22 | Larisa/Thessaly/73.6 | 22.450 | 39.650 |
| 23 | Lesvos/Northern Aegean/4.8 | 26.600 | 39.067 |
| 24 | Limnos/Northern Aegean/4.6 | 25.233 | 39.917 |
| 25 | Methoni/Peloponnese/52.4 | 21.700 | 36.833 |
| 26 | Mikra/Central Macedonia/4.8 | 22.967 | 40.517 |
| 27 | Milos/Southern Aegean/5 | 24.475 | 36.697 |
| 28 | Naxos/Southern Aegean/9.8 | 25.533 | 37.100 |
| 29 | Orestiada/Eastern Macedonia and Thrace/41 | 26.531 | 41.501 |
| 30 | Rodos/Southern Aegean/11.5 (also written as Rhodes) | 28.117 | 36.400 |
| 31 | Samos/Northern Aegean/7.3 | 26.917 | 37.700 |
| 32 | Serres/Central Macedonia/34.5 | 23.567 | 41.083 |
| 33 | Siteia/Crete/115.6 | 26.100 | 35.120 |
| 34 | Skyros/Sterea Ellada/17.9 | 24.550 | 38.900 |
| 35 | Souda/Crete/140 | 21.117 | 35.550 |
| 36 | Spata/Attica/67 | 23.917 | 37.967 |
| 37 | Tanagra/Sterea Ellada/139 | 23.550 | 38.317 |
| 38 | Thira/Southern Aegean/36.5 | 25.433 | 36.417 |
| 39 | Thiva/Sterea Ellada/189 | 23.320 | 38.322 |
| 40 | Trikala/Thessaly/114 | 21.768 | 39.556 |
| 41 | Tripoli/Peloponnese/652 | 22.400 | 37.533 |
| 42 | Xanthi/Eastern Macedonia and Thrace/83 | 24.886 | 41.130 |
| 43 | Zakynthos/Ionian Islands/7.9 (also known as Zante) | 20.900 | 37.783 |
| Parameter | Regression Equation |
|---|---|
| Hg, clear skies | Hg = 0.020·t6 − 0.760·t5 + 11.342·t4 − 82.338·t3 + 282.550·t2 − 304.810·t + 562.620 R2 = 0.998 |
| Hg, all skies | Hg = −0.005·t6 + 0.226·t5 − 3.927·t4 + 29.859·t3 − 107.730·t2 + 244.860·t + 61.800 R2 = 0.996 |
| Hd, clear skies | Hd = 0.007·t6 − 0.262·t5 + 3.870·t4 − 27.435·t3 + 91.751·t2 − 107.980·t + 141.700 R2 = 0.984 |
| Hd, all skies | Hd = 0.005·t6 − 0.203·t5 + 3.148·t4 − 23.284·t3 + 80.597·t2 − 99.505·t + 143.740 R2 = 0.993 |
| kd, clear skies | kd = 0.000003·t6 − 0.0001·t5 + 0.0014·t4 − 0.0093·t3 + 0.0286·t2 − 0.0371·t + 0.2347 R2 = 0.874 |
| kd, all skies | kd = 0.00002·t6 − 0.0008·t5 + 0.0128·t4 − 0.0970·t3 + 0.3487·t2 − 0.5883·t + 0.9802 R2 = 0.987 |
| kb, clear skies | kb = −0.000002·t6 + 0.00008·t5 − 0.0011·t4 + 0.0070·t3 − 0.0195·t2 + 0.0213·t + 0.7688 R2 = 0.875 |
| kb, all skies | kb = −0.00001·t6 + 0.0004·t5 − 0.0062·t4 + 0.0453·t3 − 0.1559·t2 + 0.2419·t + 0.4185 R2 = 0.972 |
| Parameter | Regression Equation |
|---|---|
| Hg, clear skies | Hg = 5.556∙t3 − 161.920∙t2 + 732.780∙t − 78.504, R2 = 1 |
| Hg, all skies | Hg = −41.229∙t3 + 208.770∙t2 − 143.150∙t + 217.880, R2 = 1 |
| Hd, clear skies | Hd = 5.069∙t3 − 60.891∙t2 + 205.260∙t − 39.339, R2 = 1 |
| Hd, all skies | Hd = 9.010∙t3 − 85.160∙t2 + 241.590∙t − 55.834, R2 = 1 |
| kd, clear skies | kd = 0.004∙t3 − 0.026∙t2 + 0.043∙t + 0.201, R2 = 1 |
| kd, all skies | kd = 0.067∙t3 − 0.430∙t2 + 0.701∙t + 0.310, R2 = 1 |
| kb, clear skies | kb = −0.004∙t3 + 0.028∙t2 − 0.045∙t + 0.793, R2 = 1 |
| kb, all skies | kb = −0.033∙t3 + 0.222∙t2 − 0.393∙t + 0.745, R2 = 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kambezidis, H.D. The Solar Radiation Climate of Greece. Climate 2021, 9, 183. https://doi.org/10.3390/cli9120183
Kambezidis HD. The Solar Radiation Climate of Greece. Climate. 2021; 9(12):183. https://doi.org/10.3390/cli9120183
Chicago/Turabian StyleKambezidis, Harry D. 2021. "The Solar Radiation Climate of Greece" Climate 9, no. 12: 183. https://doi.org/10.3390/cli9120183
APA StyleKambezidis, H. D. (2021). The Solar Radiation Climate of Greece. Climate, 9(12), 183. https://doi.org/10.3390/cli9120183






