Prediction of the Propulsive Performance of an Atmosphere-Breathing Electric Propulsion System on Cathode-Less Plasma Thruster
Abstract
:1. Introduction
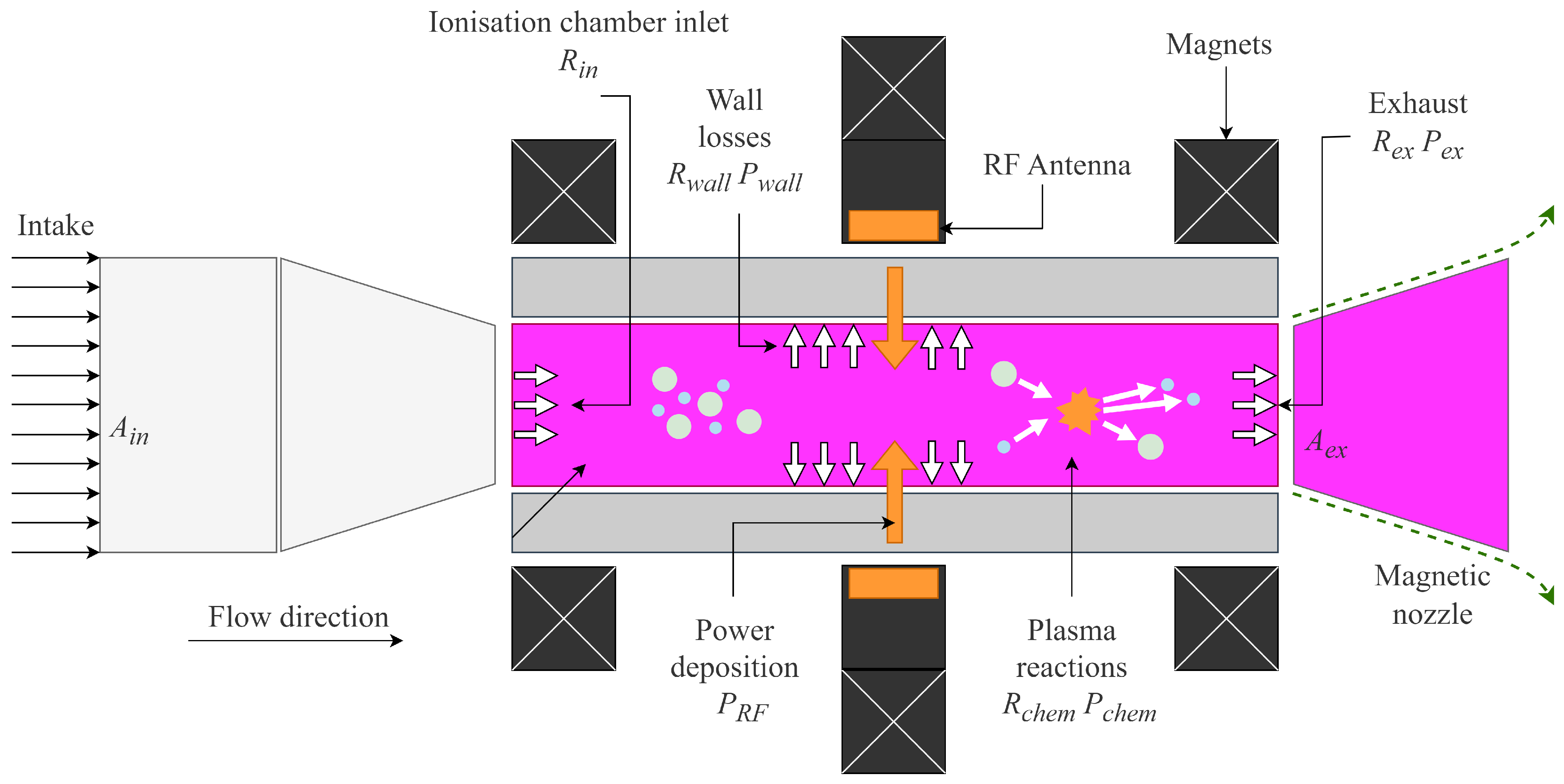
2. Methodology
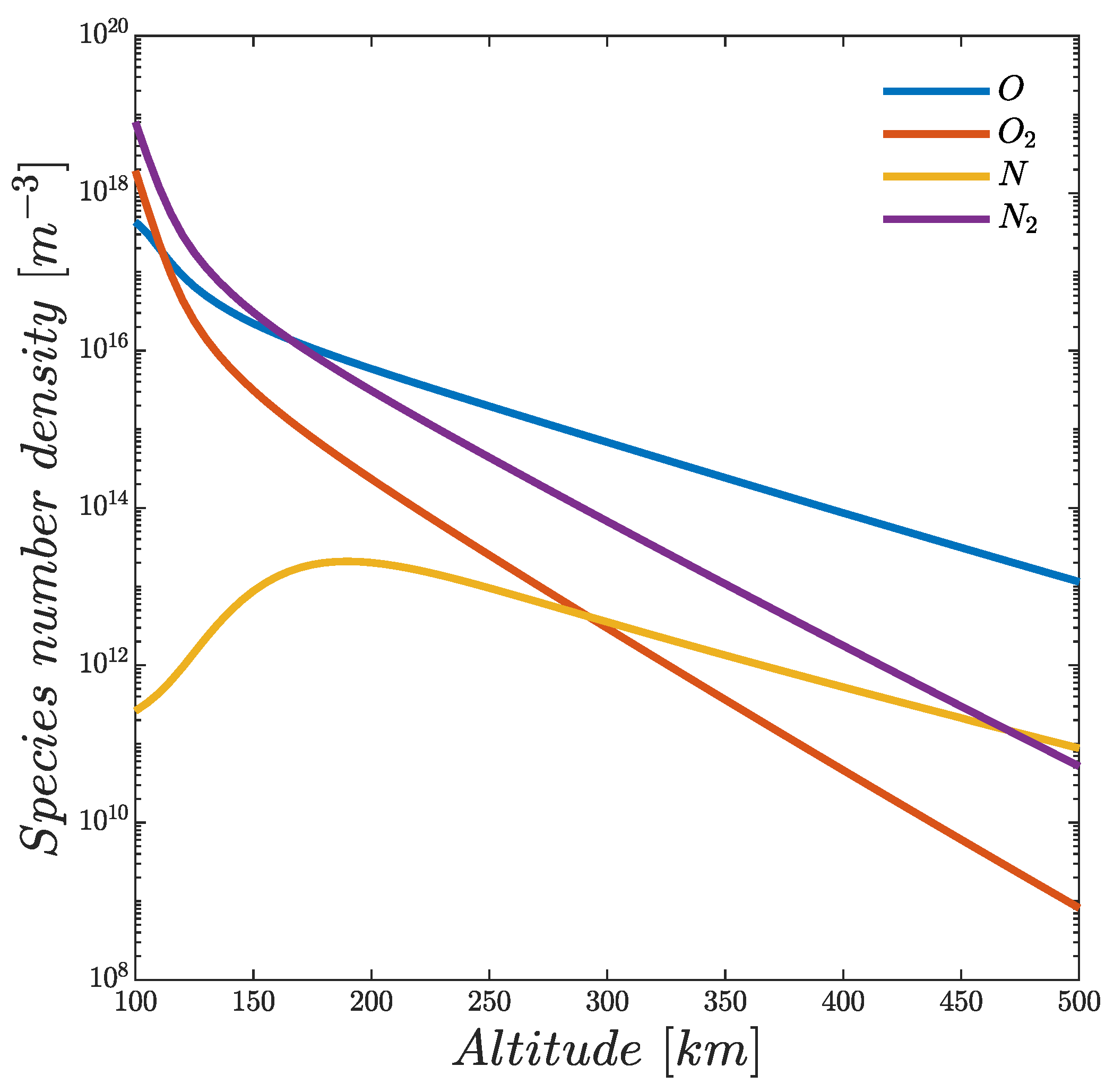
2.1. Plasma Chemistry
2.2. Thrust Model
3. Results
3.1. Comparison of the GM with Air and Iodine
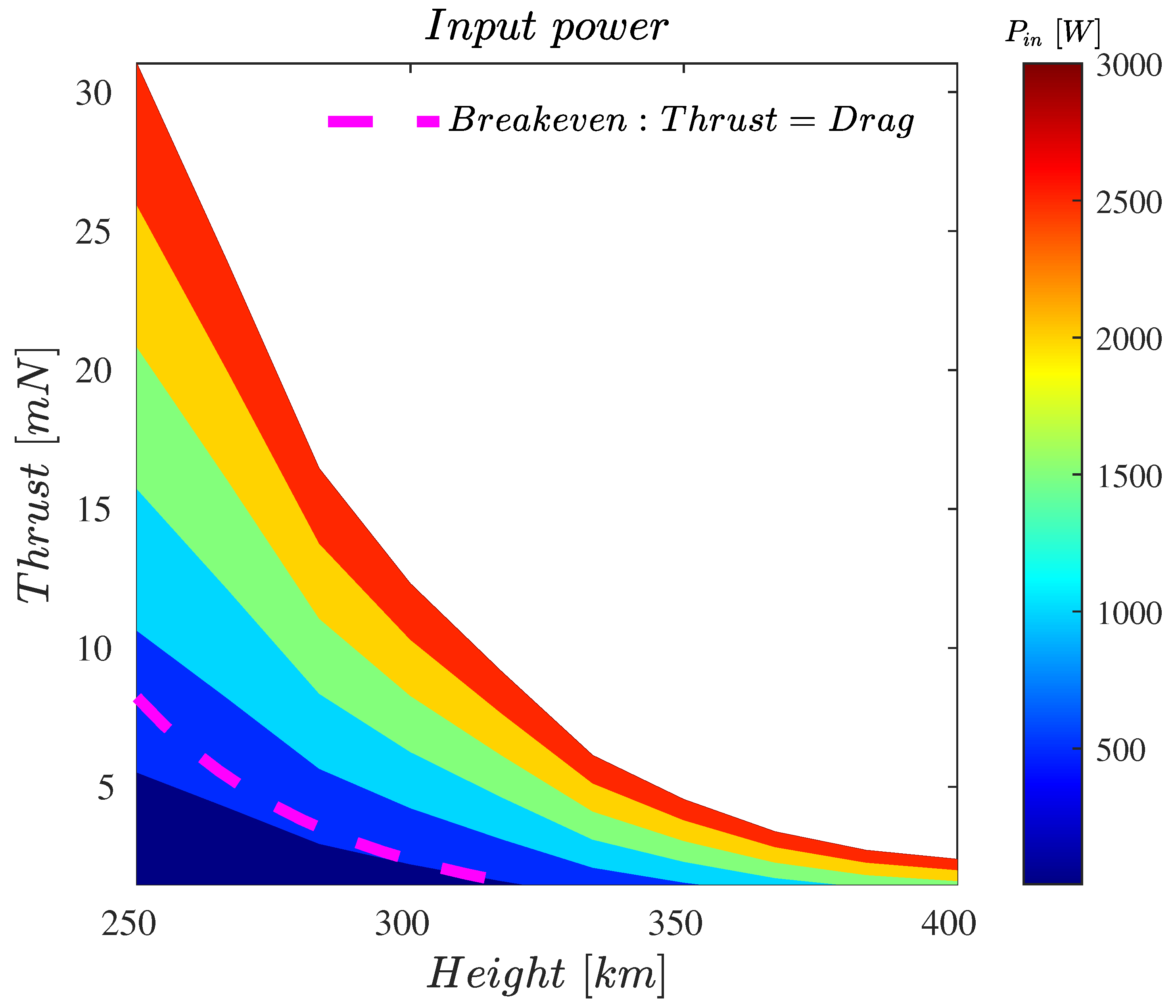
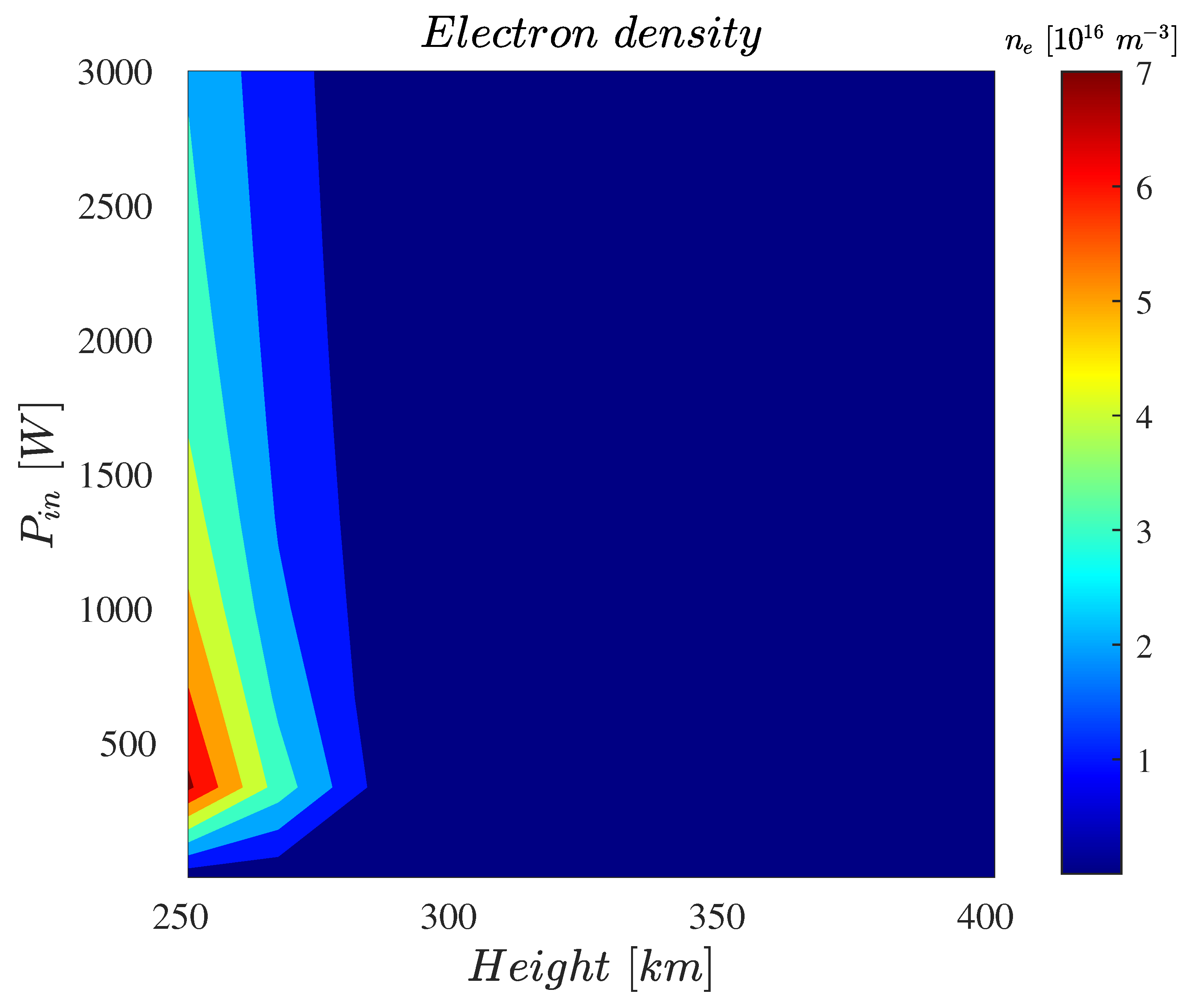
3.2. Feasibility Analysis of an ABEP Cathode-Less RF Plasma Thruster
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Andreussi, T.; Ferrato, E.; Giannetti, V.; Piragino, A.; Paissoni, C.A.; Cifali, G.; Andrenucci, M. Development Status and Way Forward of SITAEL’s Air-breathing Electric Propulsion Engine. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019. [Google Scholar]
- Crisp, N.; Roberts, P.; Livadiotti, S.; Oiko, V.; Edmondson, S.; Haigh, S.; Huyton, C.; Sinpetru, L.; Smith, K.; Worrall, S.; et al. The benefits of very low earth orbit for earth observation missions. Prog. Aerosp. Sci. 2020, 117, 100619. [Google Scholar] [CrossRef]
- Virgili-Llop, J.; Roberts, P.; Hao, Z.; Ramio, L.; Beauplet, V. Very Low Earth Orbit Mission Concepts for Earth Observation. Benefits and Challenges. 2014. Available online: https://research.manchester.ac.uk/en/publications/very-low-earth-orbit-mission-concepts-for-earth-observation-benef (accessed on 1 December 2022).
- Vaidya, S.; Traub, C.; Romano, F.; Herdrich, G.; Chan, Y.A.; Fasoulas, S.; Roberts, P.; Crisp, N.; Edmondson, S.; Haigh, S.; et al. Development and analysis of novel mission scenarios based on Atmosphere-Breathing Electric Propulsion (ABEP). CEAS Space J. 2022, 14, 689–706. [Google Scholar] [CrossRef]
- Schönherr, T.; Komurasaki, K.; Romano, F.; Massuti-Ballester, B.; Herdrich, G. Analysis of Atmosphere-Breathing Electric Propulsion. IEEE Trans. Plasma Sci. 2015, 43, 287–294. [Google Scholar] [CrossRef]
- Andreussi, T.; Ferrato, E.; Paissoni, C.A.; Kitaeva, A.; Giannetti, V.; Piragino, A.; Schäff, S.; Katsonis, K.; Berenguer, C.; Kovacova, Z.; et al. The AETHER project: Development of air-breathing electric propulsion for VLEO missions. CEAS Space J. 2022, 14, 717–740. [Google Scholar] [CrossRef]
- Xu, J.; Wu, Z.; Chen, P.; Xia, Q.; Xie, K.; Liu, X. Parametric Study of an Air-Breathing Electric Propulsion for Near-Space Vehicles. J. Propuls. Power 2018, 34, 1297–1304. [Google Scholar] [CrossRef]
- Fujita, K. Air-intake Performance Estimation of Air-breathing Ion Engines. Trans. Jpn. Soc. Mech. Eng. B 2004, 70, 3038–3044. [Google Scholar] [CrossRef] [Green Version]
- Fujita, K. Air Intake Performance of Air Breathing Ion Engines. Jpn. Soc. Aeronaut. Space Sci. 2005, 52, 514–521. [Google Scholar] [CrossRef] [Green Version]
- Tisaev, M.; Ferrato, E.; Giannetti, V.; Paissoni, C.; Baresi, N.; Lucca Fabris, A.; Andreussi, T. Air-breathing electric propulsion: Flight envelope identification and development of control for long-term orbital stability. Acta Astronaut. 2022, 191, 374–393. [Google Scholar] [CrossRef]
- Hohman, K. Atmospheric Breathing Electric Thruster for Planetary Exploration. In Proceedings of the NIAC Spring Symposium, Pasadena, CA, USA, 27–29 March 2012. [Google Scholar]
- Romano, F.; Binder, T.; Herdrich, G.H.; Fasoulas, S.; Schönherr, T. Air-Intake Design Investigation for an Air-Breathing Electric Propulsion System IEPC-2015-90524/ISTS-2015. 2015. Available online: https://electricrocket.org/ (accessed on 1 December 2022).
- Romano, F.; Massuti-Ballester, B.; Binder, T.; Herdrich, G.; Fasoulas, S.; Schönherr, T. System analysis and test-bed for an atmosphere-breathing electric propulsion system using an inductive plasma thruster. Acta Astronaut. 2018, 147, 114–126. [Google Scholar] [CrossRef]
- Haigh, S.; Lyons, R.; Oiko, V.; Rojas, A.; Smith, K.; Becedas, J.; González, G.; Vázquez, I.; Braña, A.; Antonini, K.; et al. Discoverer–Radical redesign of earth observation satellites for sustained operation at significantly lower altitudes. In Proceedings of the 68th International Astronautical Congress (IAC), Adelaide, Australia, 25–29 September 2017. [Google Scholar]
- Taploo, A.; Lin, L.; Keidarc, M. Analysis of ionization in air-breathing plasma thruster. Phys. Plasmas 2021, 28, 093505. [Google Scholar] [CrossRef]
- Mrózek, K.; Dytrych, T.; Moliš, P.; Dániel, V.; Obrusník, A. Global plasma modeling of a magnetized high-frequency plasma source in low-pressure nitrogen and oxygen for air-breathing electric propulsion applications. Plasma Sources Sci. Technol. 2021, 30, 125007. [Google Scholar] [CrossRef]
- Obrusník, A.; Mrózek, K.; Šťastný, M.; Kubečka, M.; Juřík, K.; Dytrych, T.; Daniel, V. Simulation-guided engineering of an air-breathing electric propulsion concept. CEAS Space J. 2022, 14, 741–747. [Google Scholar] [CrossRef]
- Bellomo, N.; Magarotto, M.; Manente, M.; Trezzolani, F.; Mantellato, R.; Cappellini, L.; Paulon, D.; Selmo, A.; Scalzi, D.; Minute, M.; et al. Design and In-orbit Demonstration of REGULUS, an Iodine electric propulsion system. CEAS Space J. 2022, 14, 79–90. [Google Scholar] [CrossRef]
- Manente, M.; Trezzolani, F.; Magarotto, M.; Fantino, E.; Selmo, A.; Bellomo, N.; Toson, E.; Pavarin, D. REGULUS: A propulsion platform to boost small satellite missions. Acta Astronaut. 2019, 157, 241–249. [Google Scholar] [CrossRef]
- Bellomo, N.; Manente, M.; Trezzolani, F.; Gloder, A.; Selmo, A.; Mantellato, R.; Toson, E.; Cappellini, L.; Duzzi, M.; Scalzi, D.; et al. Enhancement of microsatellites’ mission capabilities: Integration of Regulus electric propulsion module into UniSat-7. In Proceedings of the 70th International Astronautical Congress (IAC), Washington, DC, USA, 21–25 October 2019. [Google Scholar]
- Manente, M.; Trezzolani, F.; Mantellato, R.; Scalzi, D.; Schiavon, A.; Souhair, N.; Duzzi, M.; Cappellini, L.; Barbato, A.; Paulon, D.; et al. REGULUS: Iodine Fed Plasma Propulsion System for Small Satellites. In Proceedings of the 36th International Electric Propulsion Conference, Vienna, Austria, 15–20 September 2019. [Google Scholar]
- Souhair, N.; Magarotto, M.; Dalle Fabbriche, S.; Andriulli, R.; Andrews, S.; Ponti, F.; Pavarin, D. Simulation and modelling of an iodine fed Helicon Plasma Thruster. In Proceedings of the 37th International Electric Propulsion Conference, Cambridge, MA, USA, 19–23 June 2022. [Google Scholar]
- Souhair, N.; Magarotto, M.; Majorana, E.; Ponti, F.; Pavarin, D. Development of a lumping methodology for the analysis of the excited states in plasma discharges operated with argon, neon, krypton, and xenon. Phys. Plasmas 2021, 28, 093504. [Google Scholar] [CrossRef]
- Majorana, E.; Souhair, N.; Ponti, F.; Magarotto, M. Development of a Plasma Chemistry Model for Helicon Plasma Thruster analysis. Aerotec. Missili Spaz. 2021, 100, 225–238. [Google Scholar] [CrossRef]
- Guaita, M.; Magarotto, M.; Manente, M.; Pavarin, D.; Lavagna, M. Semi-Analytical Model of a Helicon Plasma Thruster. IEEE Trans. Plasma Sci. 2022, 50, 425–438. [Google Scholar] [CrossRef]
- Magarotto, M.; Di Fede, S.; Souhair, N.; Andrews, S.; Ponti, F. Numerical suite for cathodeless plasma thrusters. Acta Astronaut. 2022, 197, 126–138. [Google Scholar] [CrossRef]
- Goebel, D.M.; Katz, I. Fundamentals of Electric Propulsion: Ion and Hall Thrusters; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Chabert, P.; Arancibia Monreal, J.; Bredin, J.; Popelier, L.; Aanesland, A. Global model of a gridded-ion thruster powered by a radiofrequency inductive coil. Phys. Plasmas 2012, 19, 073512. [Google Scholar] [CrossRef]
- Lieberman, M.A.; Lichtenberg, A.J. Principles of Plasma Discharges and Materials Processing; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Zhou, J.; Taccogna, F.; Fajardo, P.; Ahedo, E. Performance analysis of alternative propellants for a helicon plasma thruster. In Proceedings of the 7th Space Propulsion Conference, Estoril, Portugal, 17–19 March 2021. [Google Scholar]
- Andrews, S.; Di Fede, S.; Magarotto, M. Fully kinetic model of plasma expansion in a magnetic nozzle. Plasma Sources Sci. Technol. 2022, 31, 035022. [Google Scholar] [CrossRef]
- Guaita, M. Semi-Analytical Mono-Dimensional Modelling of Cathodeless Plasma Thrusters. Master’s Thesis, Politecnico di Milano, Milano, Italy, 2021. [Google Scholar]
- Marmuse, F. Iodine Plasmas: Experimental and Numerical Studies. Application to Electric Propulsion. Ph.D. Thesis, University of Sorbonne, Paris, France, 2020. [Google Scholar]
- Lafleur, T.; Habl, L.; Rossi, E.Z.; Rafalskyi, D. Development and validation of an iodine plasma model for gridded ion thrusters. Plasma Sources Sci. Technol. 2022, 31, 114001. [Google Scholar] [CrossRef]
- Chabert, P. An Expression for the Hl Factor in Low-Pressure Electronegative Plasma Discharges. Plasma Sources Sci. Technol. 2016, 25, 025010. [Google Scholar] [CrossRef]
- Picone, J.M.; Hedin, A.E.; Drob, D.P.; Aikin, A.C. NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues. J. Geophys. Res. Space Phys. 2002, 107, SIA 15-1–SIA 15-16. [Google Scholar] [CrossRef]
- Hagelaar, G.J.; Pitchford, L.C. Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models. Plasma Sources Sci. Technol. 2005, 14, 722–733. [Google Scholar] [CrossRef]
- LXcat. The Plasma Data Exchange Project. Available online: https://nl.lxcat.net (accessed on 1 December 2022).
- Lafleur, T. Helicon plasma thruster discharge model. Phys. Plasmas 2014, 21, 043507. [Google Scholar] [CrossRef]
- Bittencourt, J.A. Fundamentals of Plasma Physics; Springer Science & Business Media: New York, NY, USA, 2004. [Google Scholar] [CrossRef] [Green Version]
- Fruchtman, A.; Takahashi, K.; Charles, C.; Boswell, R. A magnetic nozzle calculation of the force on a plasma. Phys. Plasmas 2012, 19, 033507. [Google Scholar] [CrossRef]
- Andrews, S.; Andriulli, R.; Souhair, N.; Di Fede, S.; Magarotto, M.; Pavarin, D.; Ponti, F. Multiscale Modelling of Alternative Propellants in Helicon Plasma Thrusters. In Proceedings of the 73rd International Astronautical Congress (IAC), Paris, France, 18–22 September 2022. [Google Scholar]
- Romano, F.; Chan, Y.A.; Herdrich, G.; Traub, C.; Fasoulas, S.; Roberts, P.; Smith, K.; Edmondson, S.; Haigh, S.; Crisp, N.; et al. RF helicon-based inductive plasma thruster (IPT) design for an atmosphere-breathing electric propulsion system (ABEP). Acta Astronaut. 2020, 176, 476–483. [Google Scholar] [CrossRef]
- Romanazzo, M.; Steiger, C.; Tran, V.; Niño, A.; Emanuelli, P.; Floberghagen, R.; Fehringer, M. Low Orbit Operations of ESA’s Gravity Mission GOCE. In Proceedings of the 5th European Conference for Aeronautics and Space Sciences (EUCASS), Munich, Germany, 1–5 July 2013. [Google Scholar]
- Romano, F.; Herdrich, G.; Chan, Y.A.; Crisp, N.; Roberts, P.C.; Holmes, B.E.; Edmondson, S.; Haigh, S.; Macario-Rojes, A.; Oiko, V.T.A.; et al. Design of an intake and a thruster for an atmosphere-breathing electric propulsion system. CEAS Space J. 2022, 14, 707–715. [Google Scholar] [CrossRef]
- Takahashi, K. Thirty percent conversion efficiency from radiofrequency power to thrust energy in a magnetic nozzle plasma thruster. Sci. Rep. 2022, 12, 18618. [Google Scholar] [CrossRef]
- Berenguer, C.; Katsonis, K.; Gonzalez, J. Using of an Iodine Detailed Global Model for Characterization and for Optical Diagnostics of Helicon Thrusters. In Proceedings of the 6th Space Propulsion Conference, Seville, Spain, 9–11 July 2018. [Google Scholar]

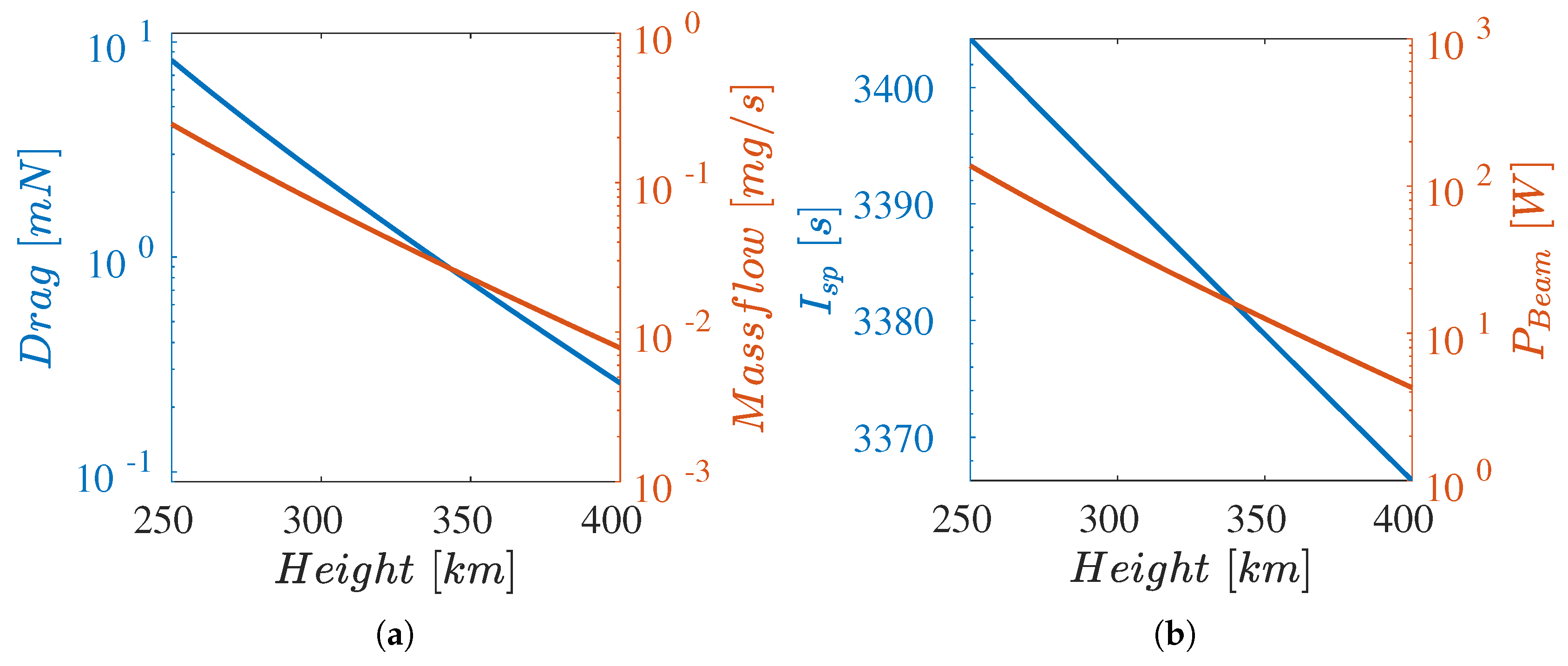
| ABEP System Parameters | Values | Unit |
|---|---|---|
| 1 | [m] | |
| 1 | [m2] | |
| 1 | [m2] | |
| 10 | [-] | |
| 0.43 | [-] | |
| 3.7 | [-] | |
| B | 0.15 | [T] |
| 5–3000 | [W] |
| [eV] | [m−3] | [m−3] | [m−3] | [m−3] | [m−3] | [m−3] | [m−3] | [m−3] |
|---|---|---|---|---|---|---|---|---|
| 18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Souhair, N.; Magarotto, M.; Andriulli, R.; Ponti, F. Prediction of the Propulsive Performance of an Atmosphere-Breathing Electric Propulsion System on Cathode-Less Plasma Thruster. Aerospace 2023, 10, 100. https://doi.org/10.3390/aerospace10020100
Souhair N, Magarotto M, Andriulli R, Ponti F. Prediction of the Propulsive Performance of an Atmosphere-Breathing Electric Propulsion System on Cathode-Less Plasma Thruster. Aerospace. 2023; 10(2):100. https://doi.org/10.3390/aerospace10020100
Chicago/Turabian StyleSouhair, Nabil, Mirko Magarotto, Raoul Andriulli, and Fabrizio Ponti. 2023. "Prediction of the Propulsive Performance of an Atmosphere-Breathing Electric Propulsion System on Cathode-Less Plasma Thruster" Aerospace 10, no. 2: 100. https://doi.org/10.3390/aerospace10020100
APA StyleSouhair, N., Magarotto, M., Andriulli, R., & Ponti, F. (2023). Prediction of the Propulsive Performance of an Atmosphere-Breathing Electric Propulsion System on Cathode-Less Plasma Thruster. Aerospace, 10(2), 100. https://doi.org/10.3390/aerospace10020100









