Prepositive Synergistic Bulge Design for Improving Aerodynamic Performance of Submerged Inlet
Abstract
:1. Introduction
2. Baseline Model and Numerical Method Validation
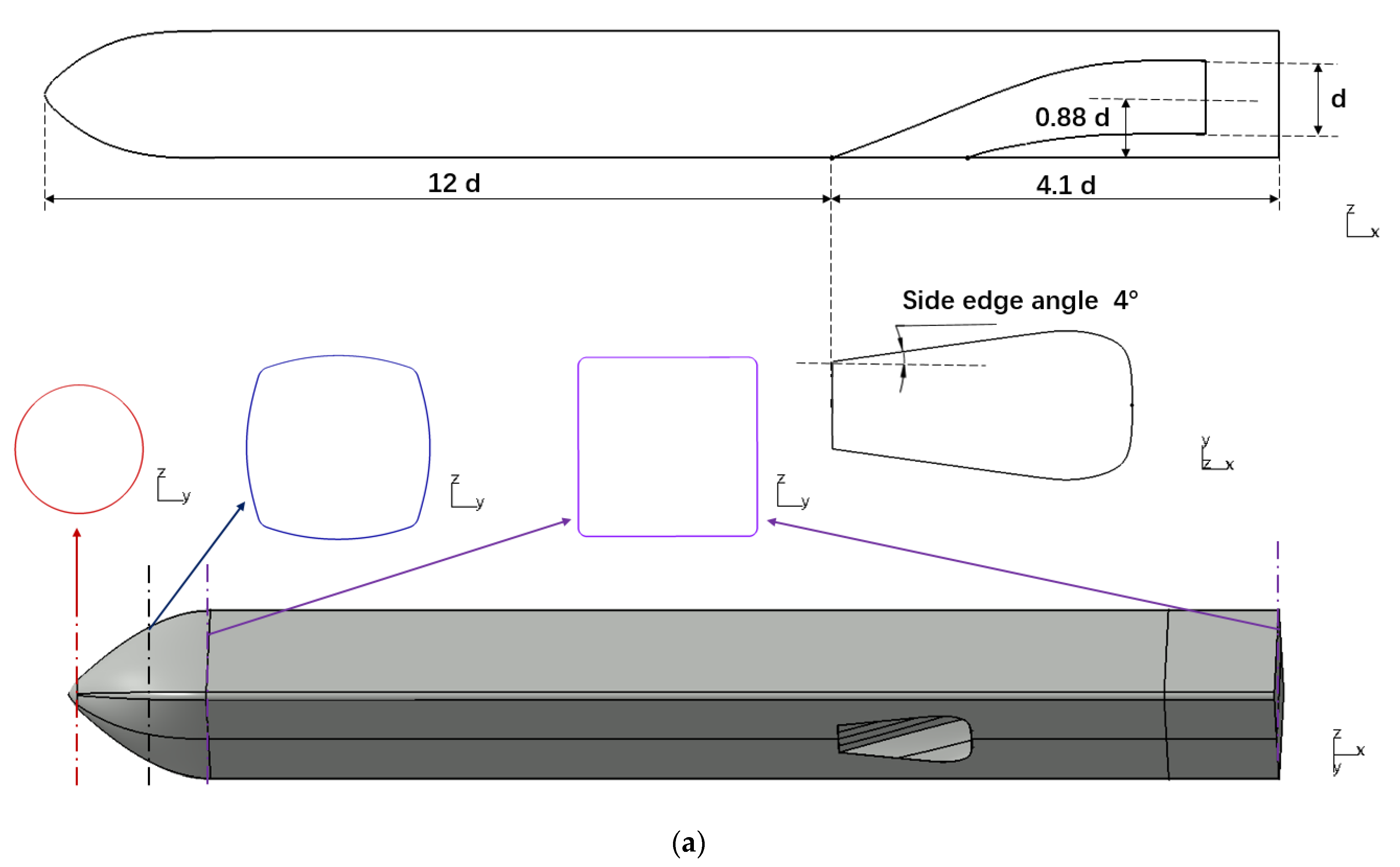
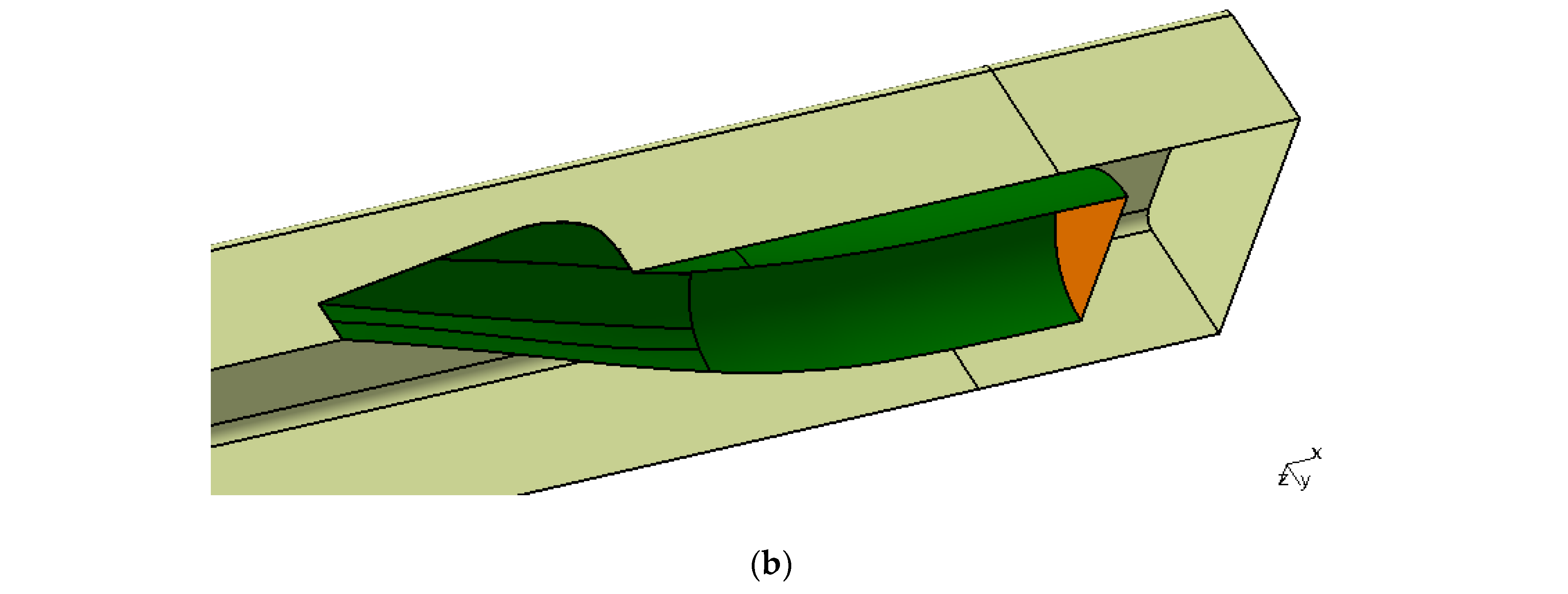
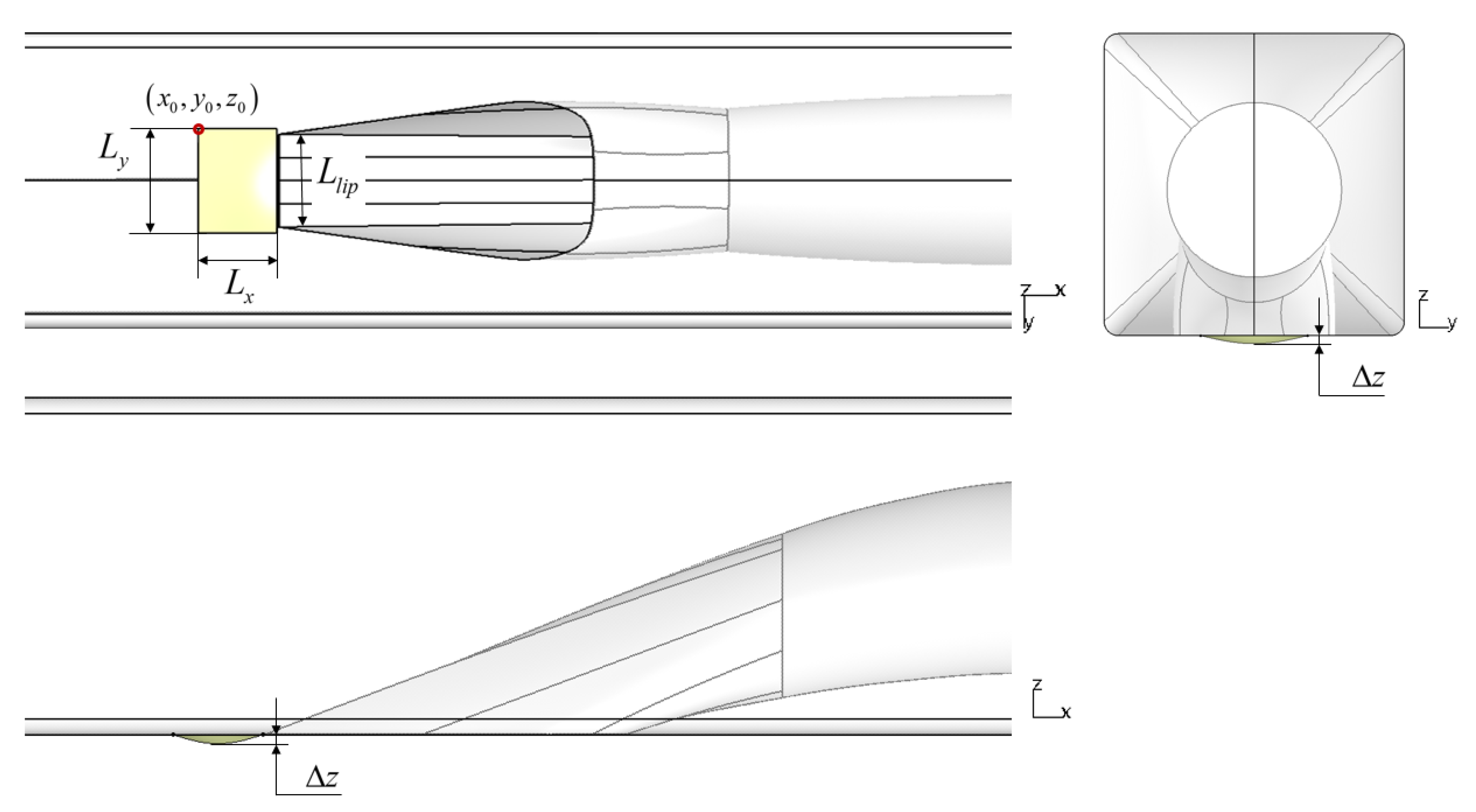
2.1. Baseline Model of Submerged Inlet
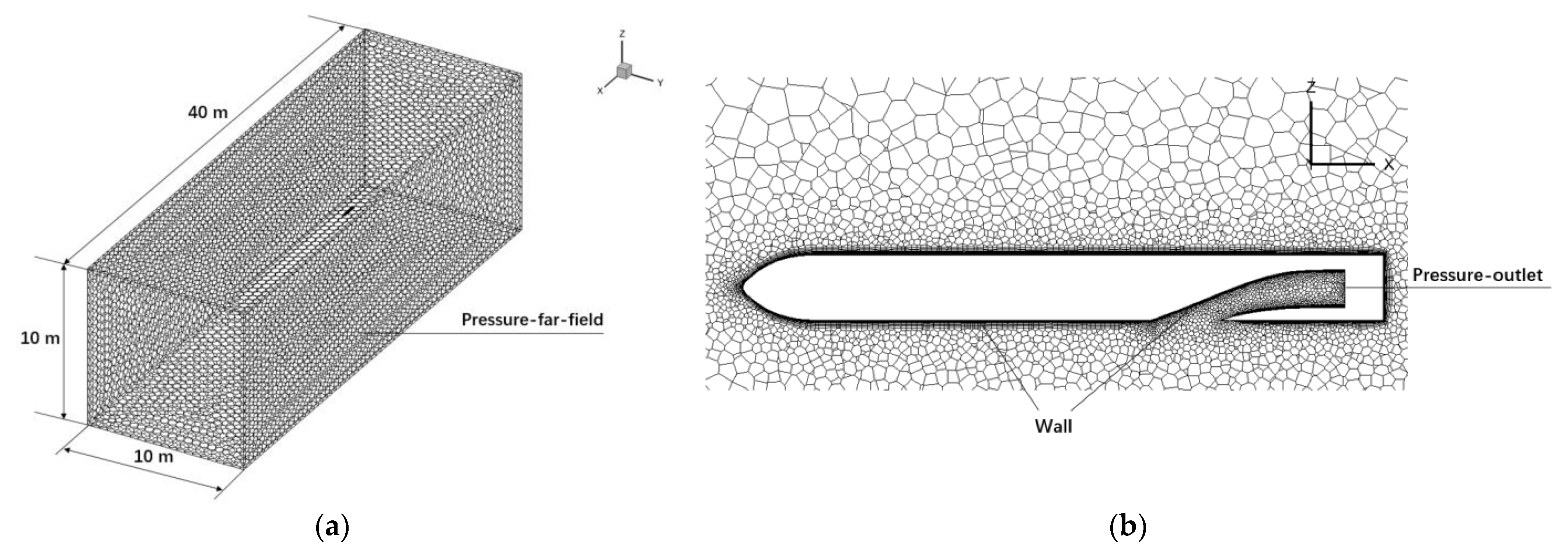
2.2. Numerical Calculation Method and Grid Division
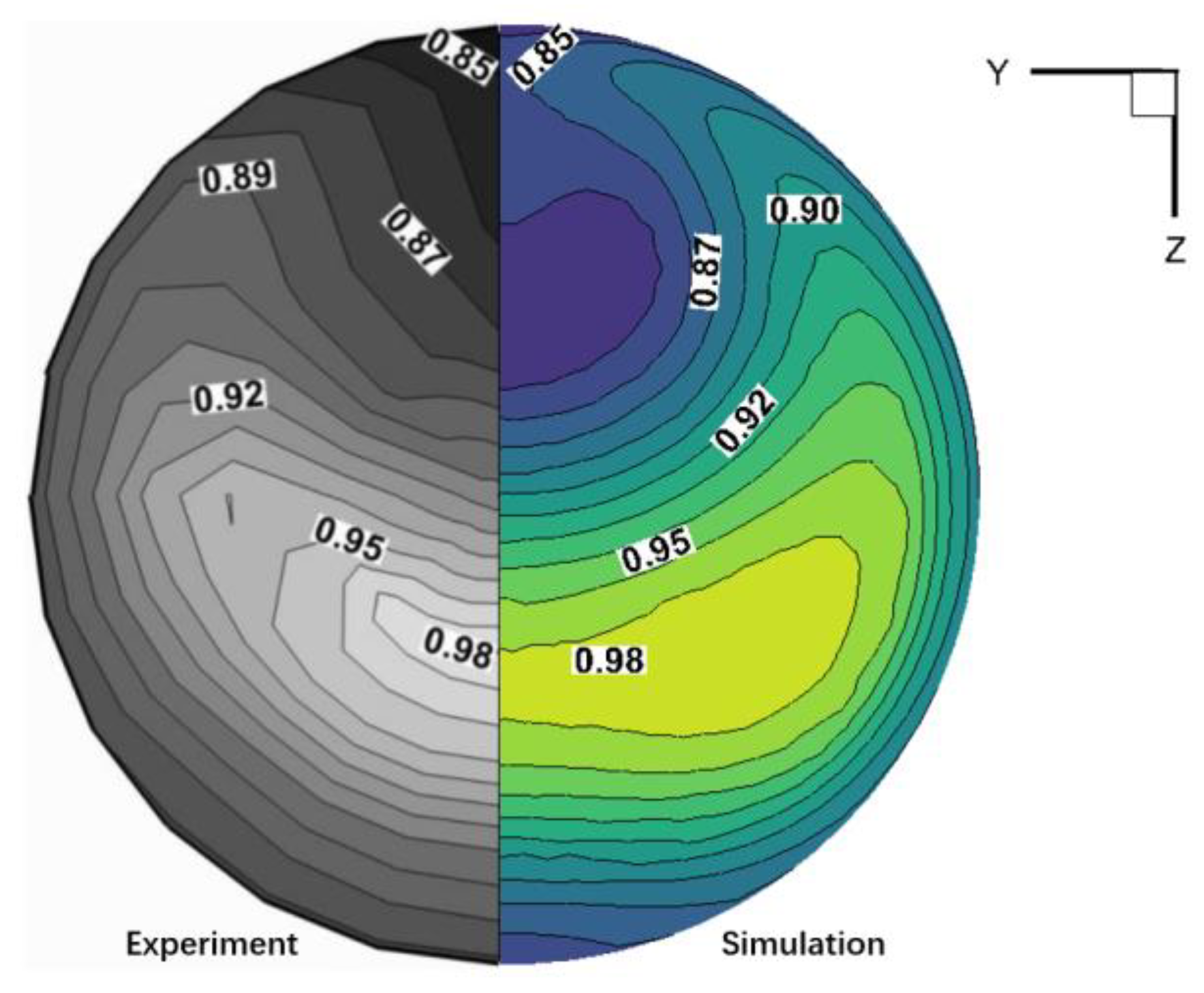
2.3. Case Validation
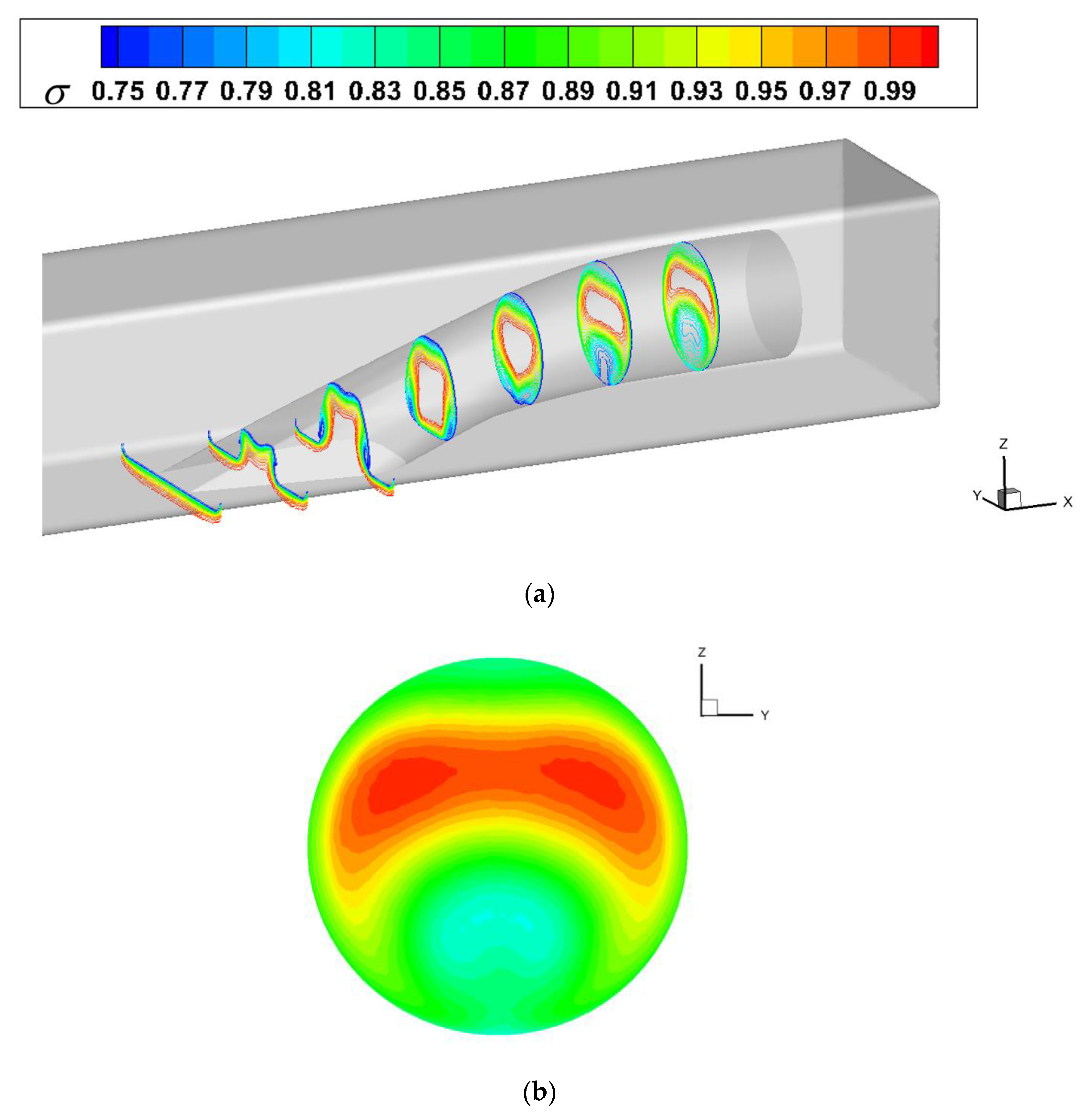
3. Analysis of Internal Flow Characteristics of Submerged Inlet
4. Design of Synergistic Bulge Submerged Inlet and Internal Flow Characteristics Analysis
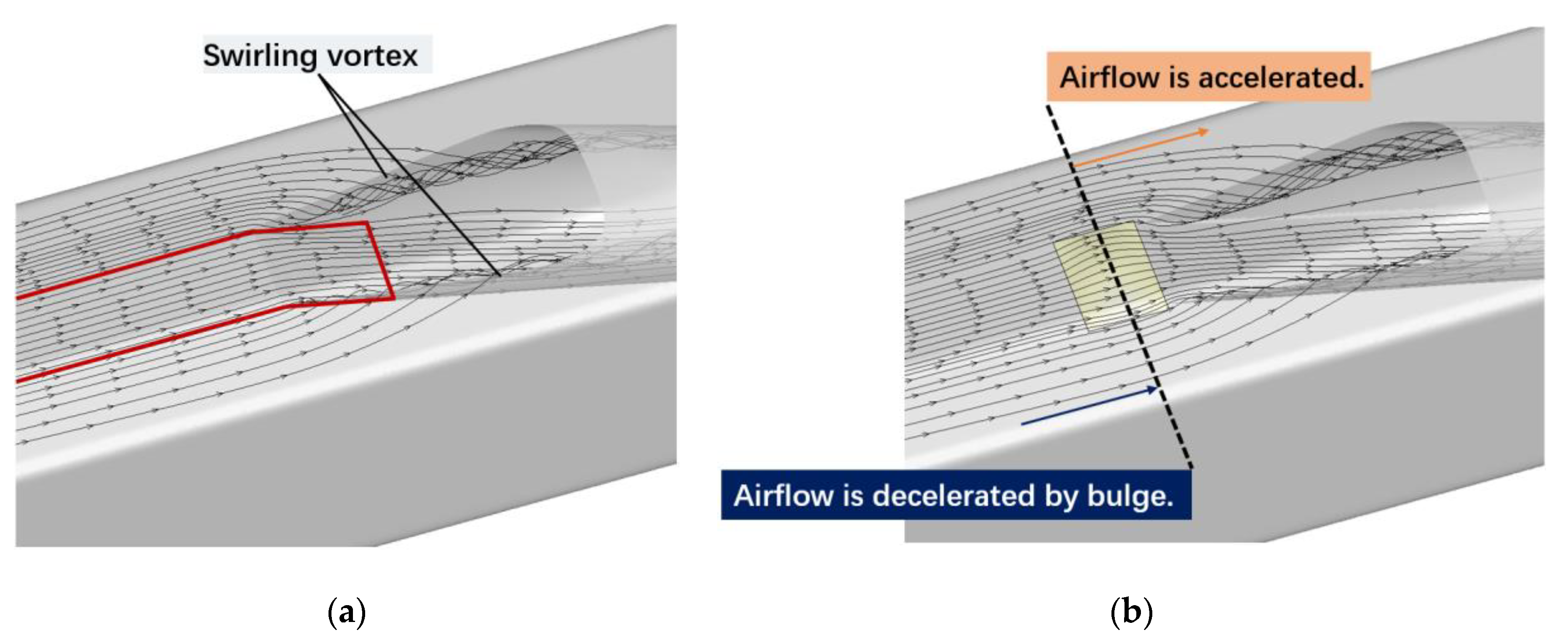
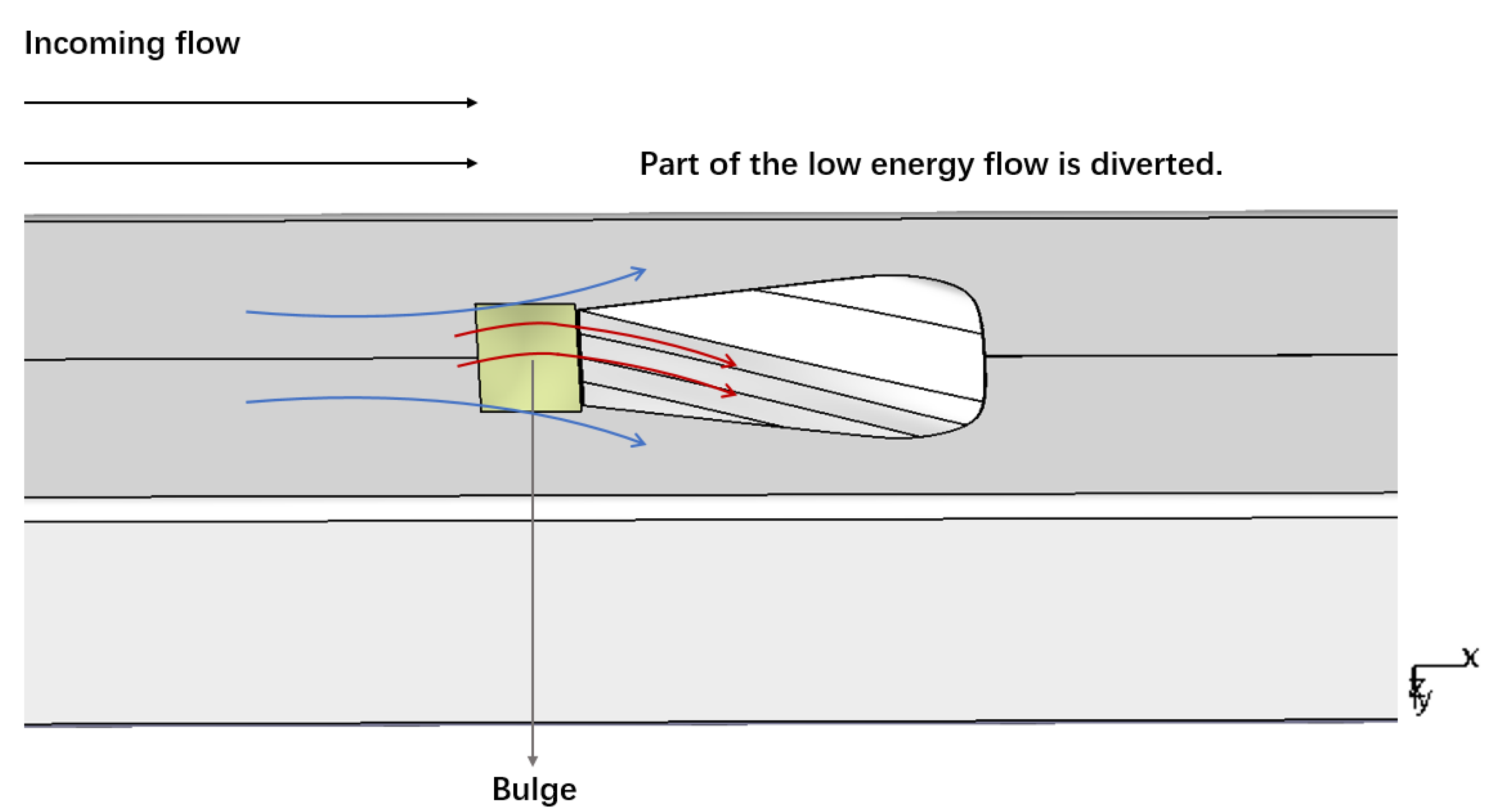
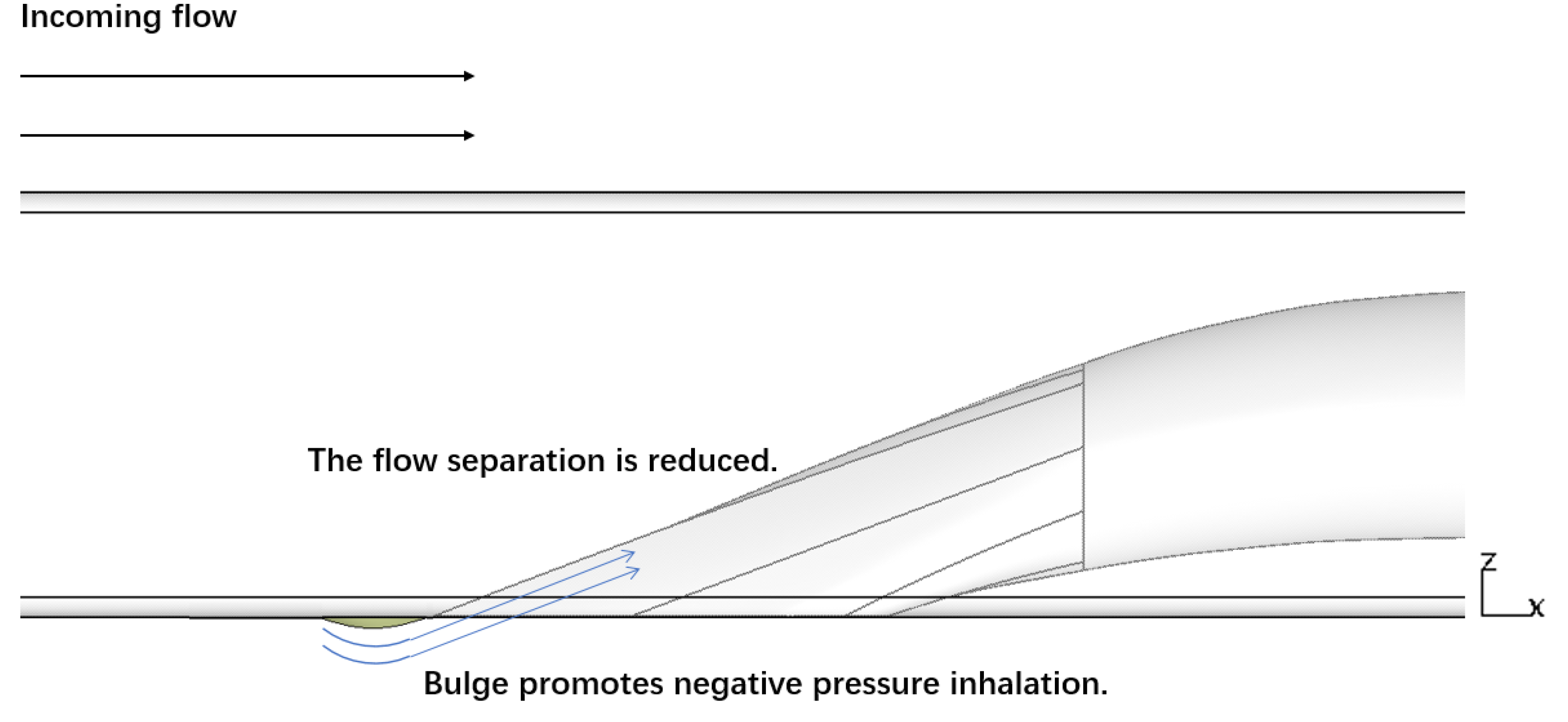
4.1. Design Principle of Prepositive Synergistic Bulge for Submerged Inlet
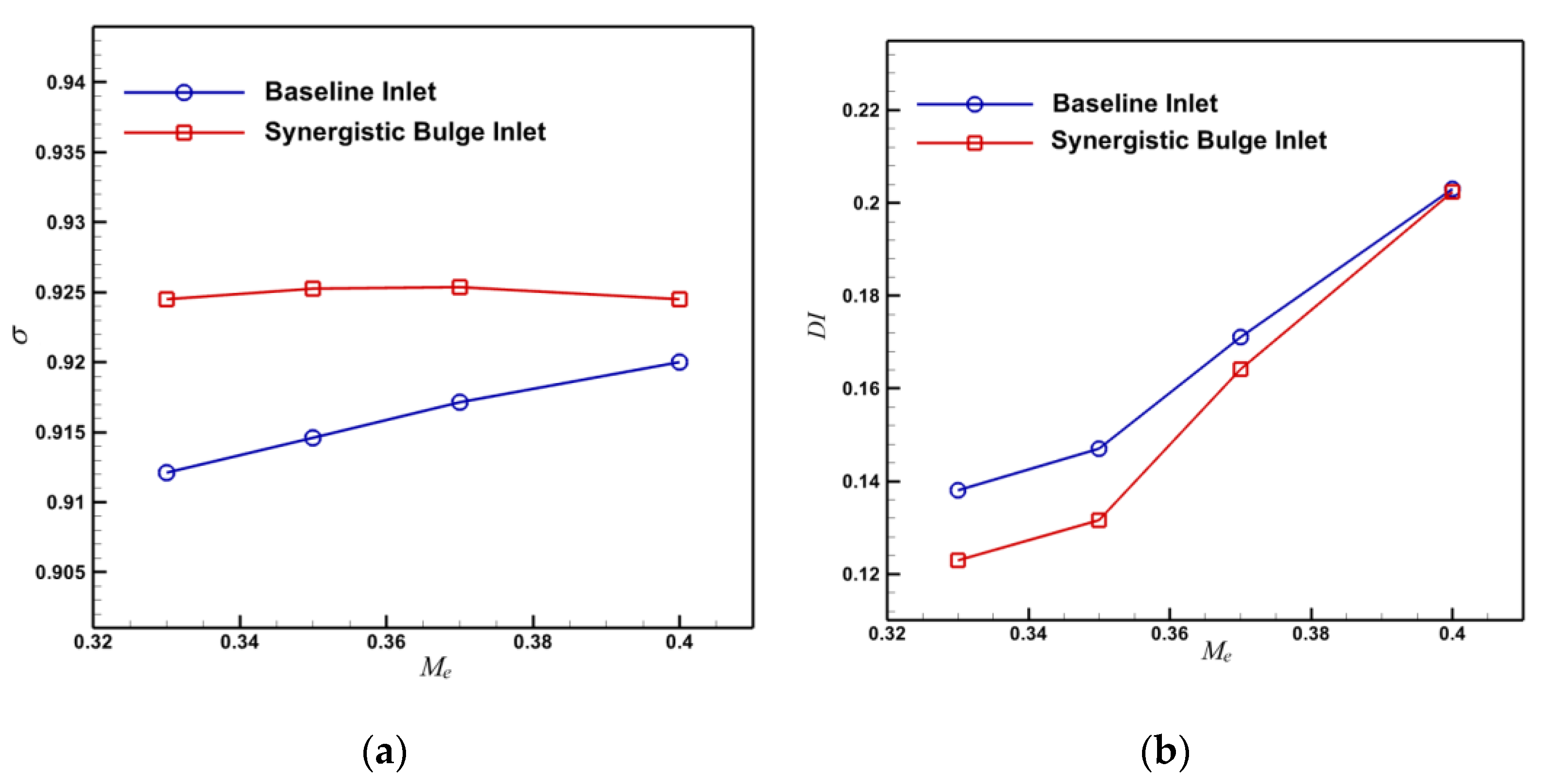
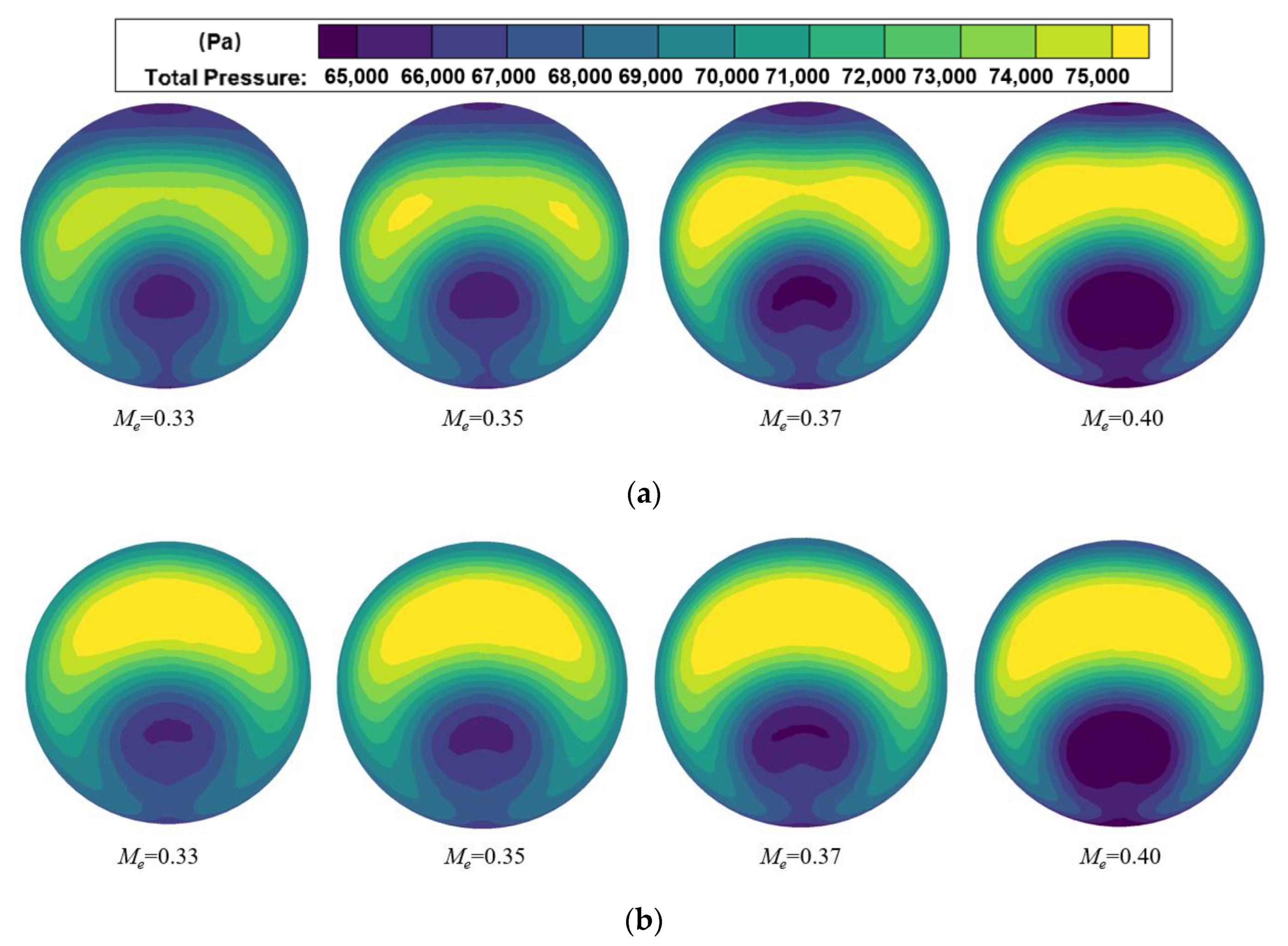
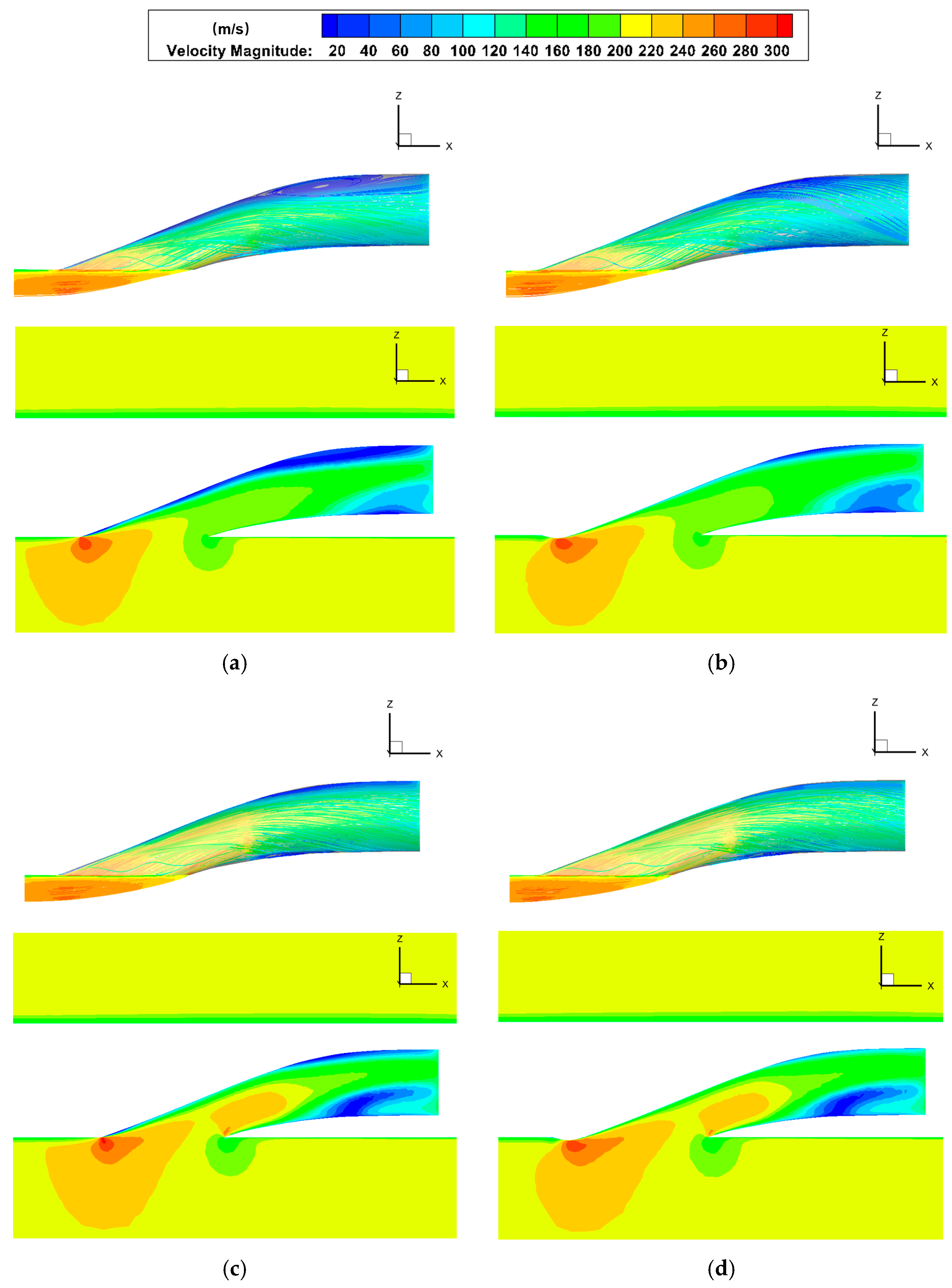
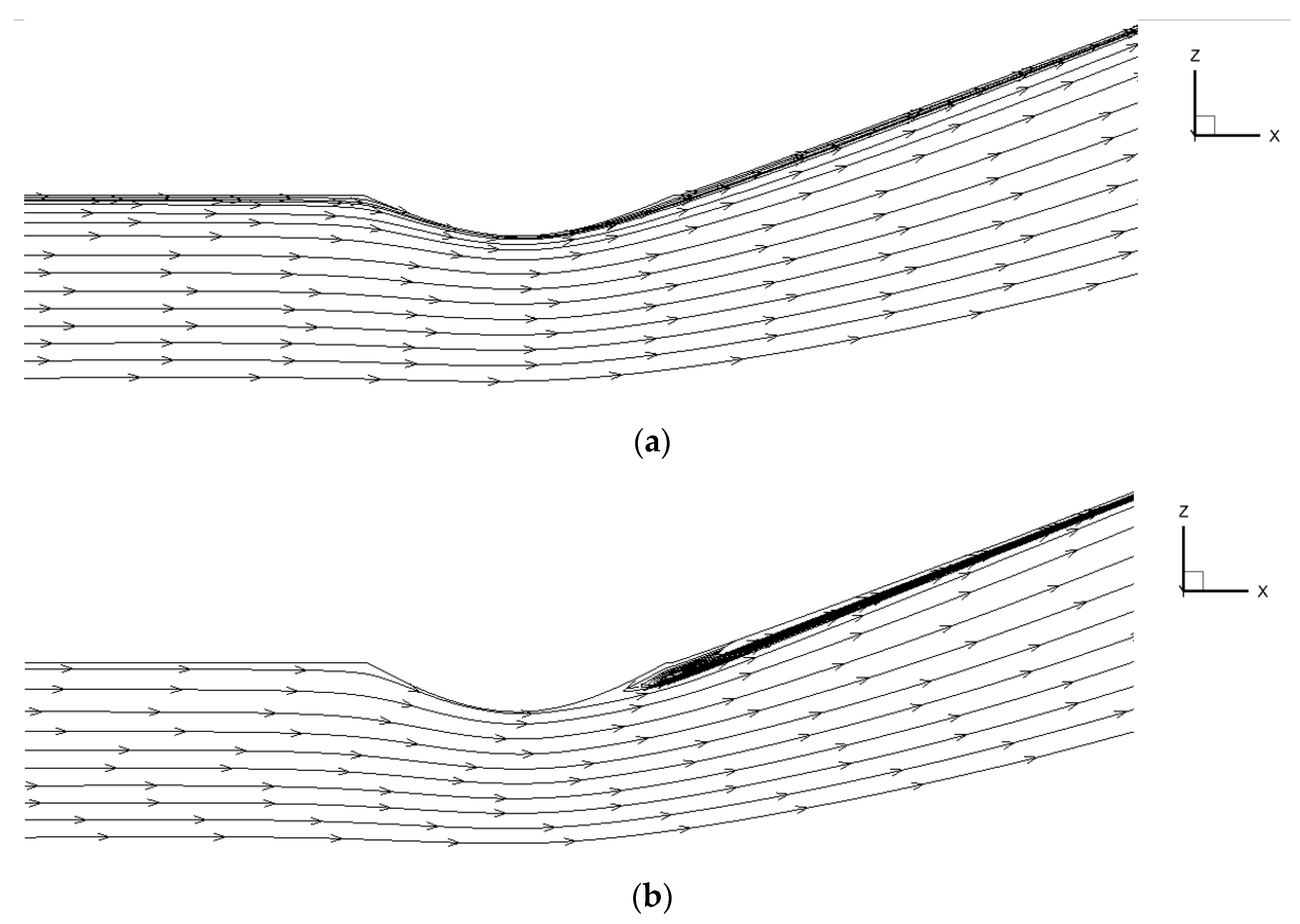
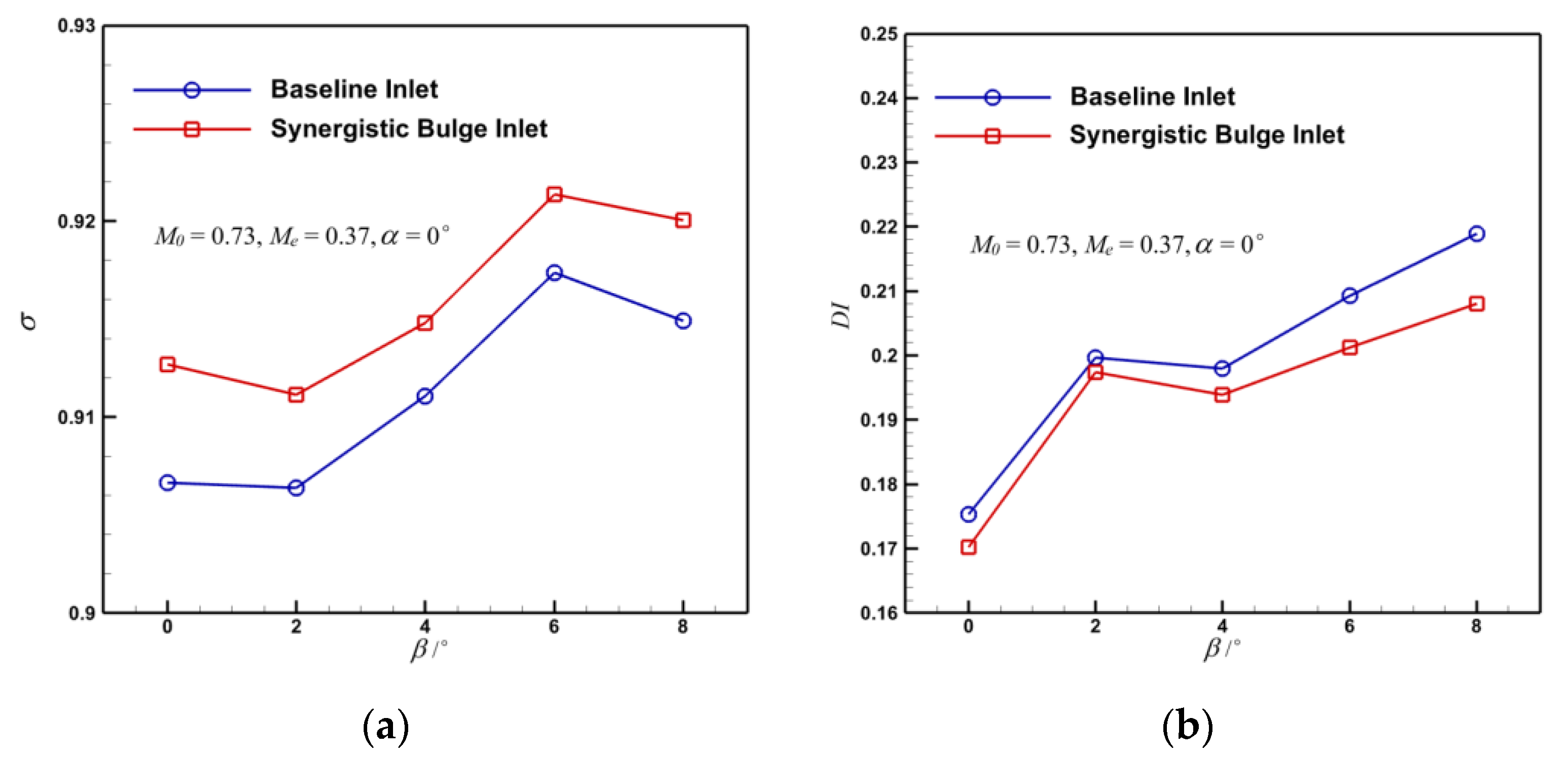
4.2. Comparison of Internal Flow Characteristics of Submerged Inlet with or without Synergistic Bulge
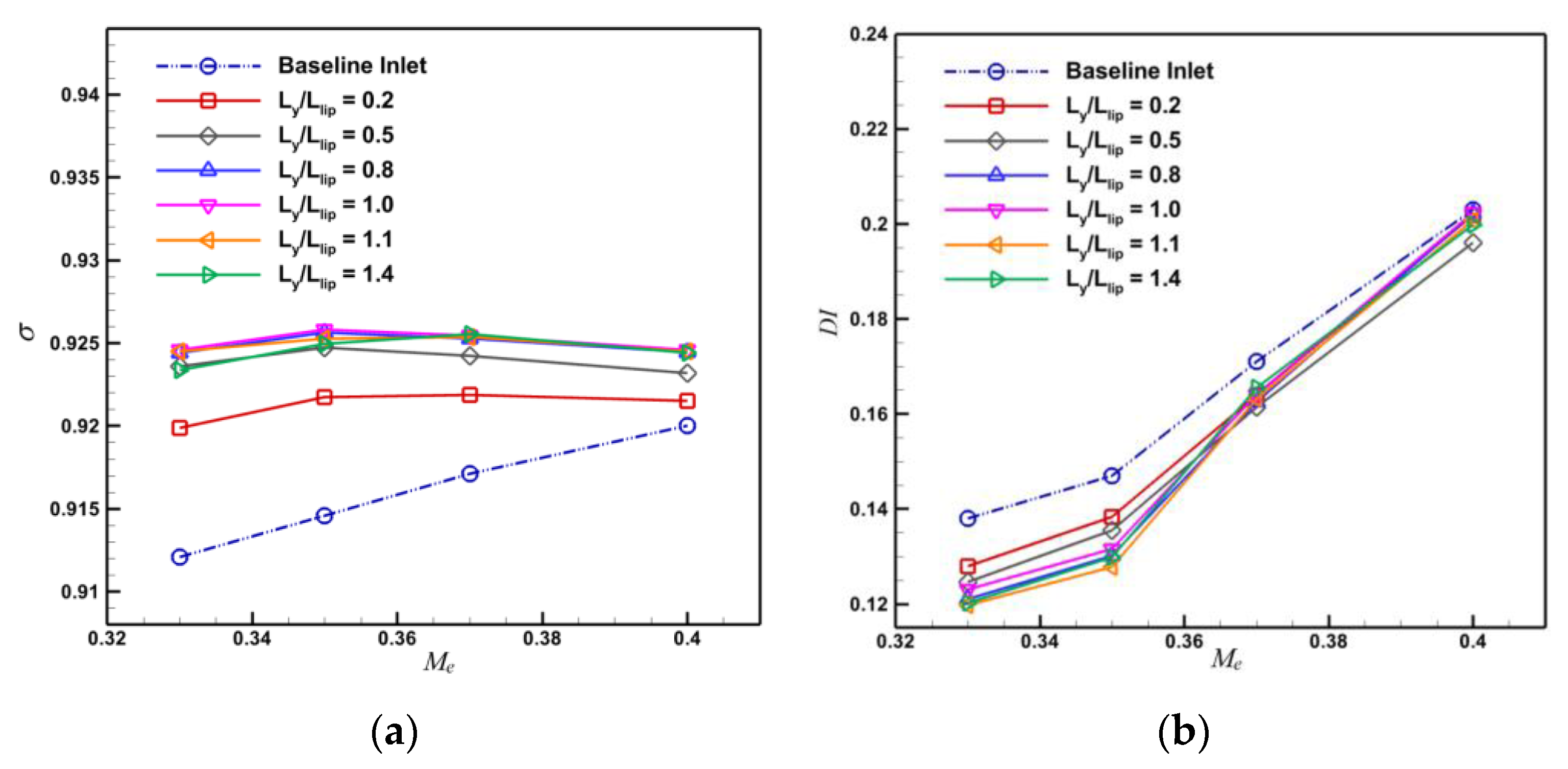
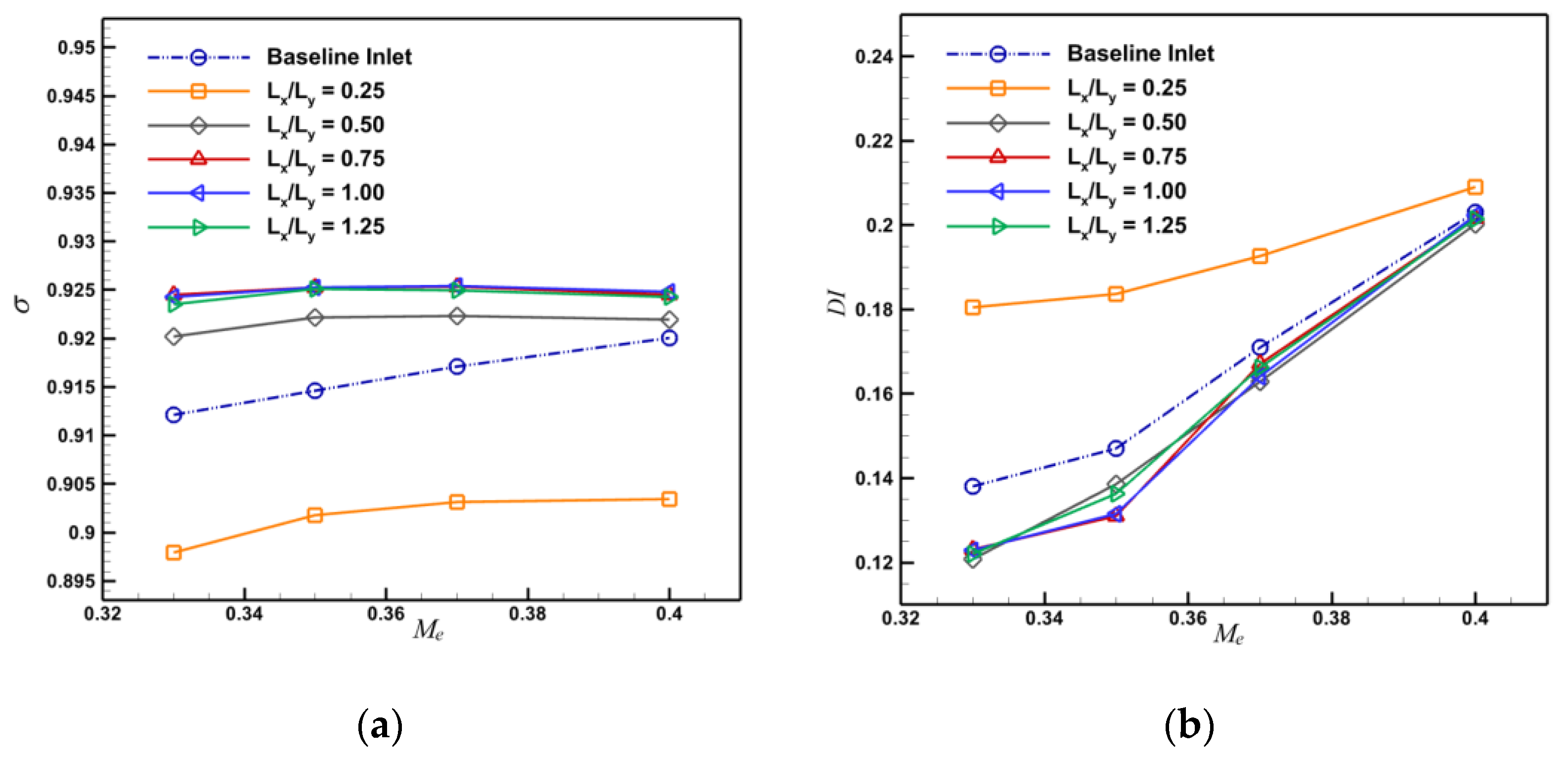
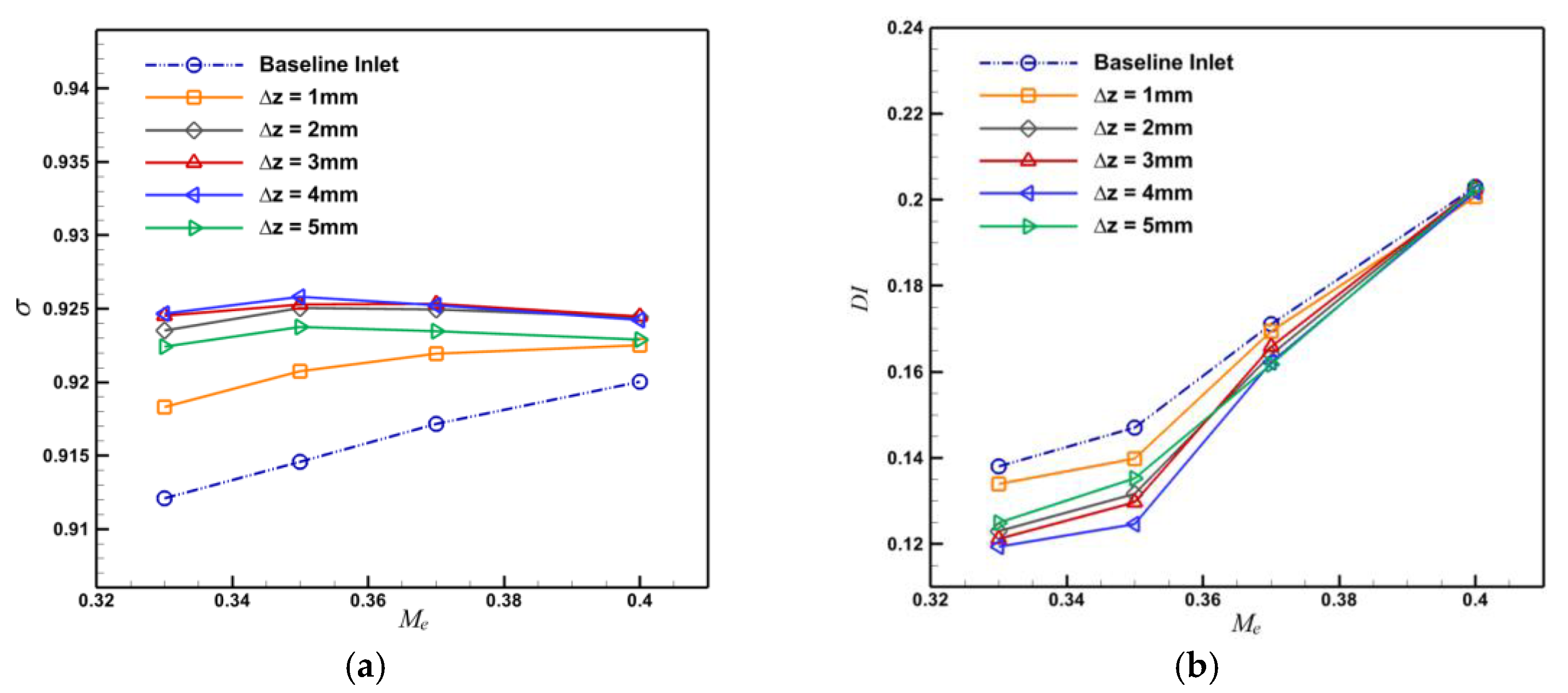
4.3. Analysis of the Influence of Synergistic Bulge Design Parameters
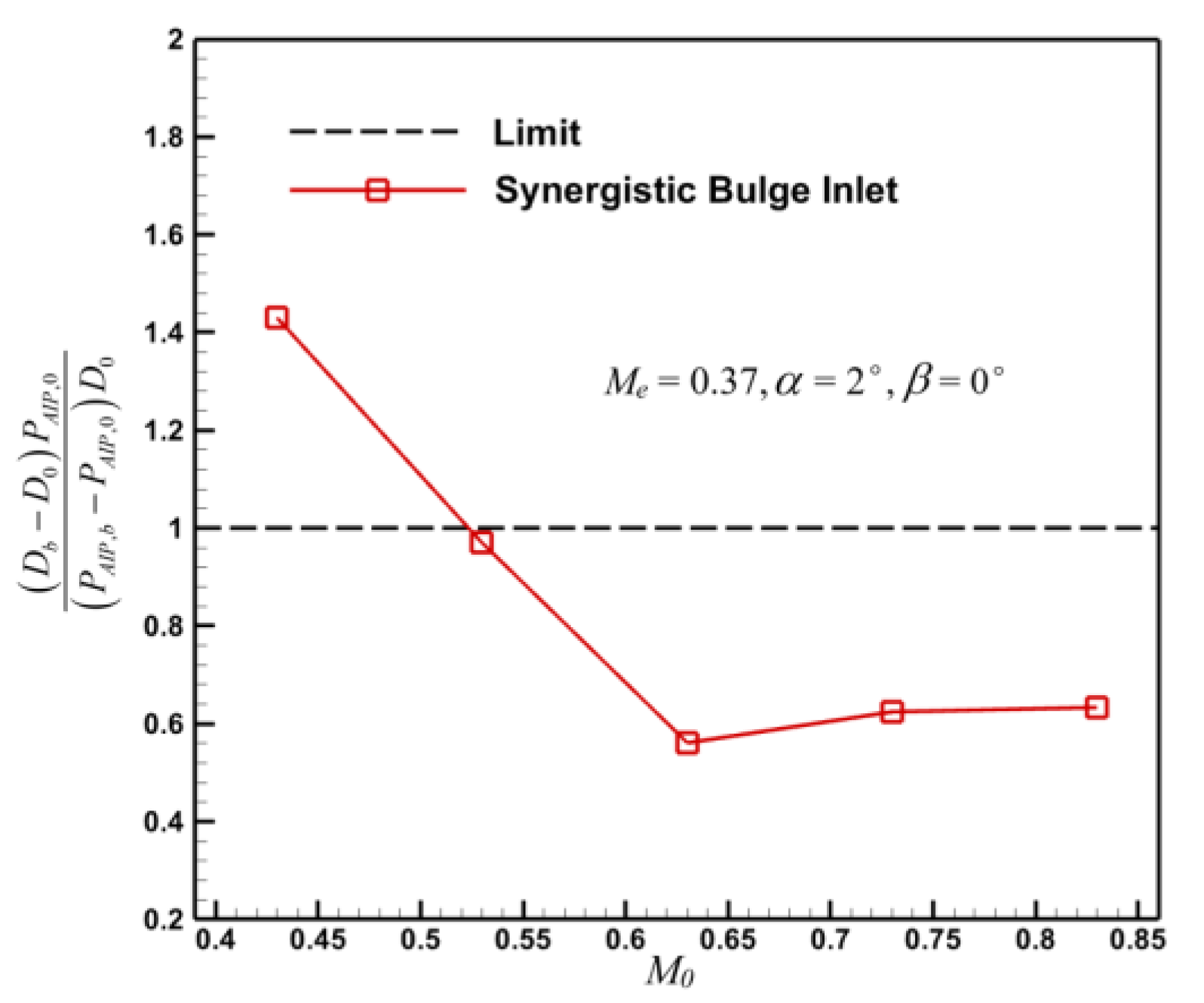
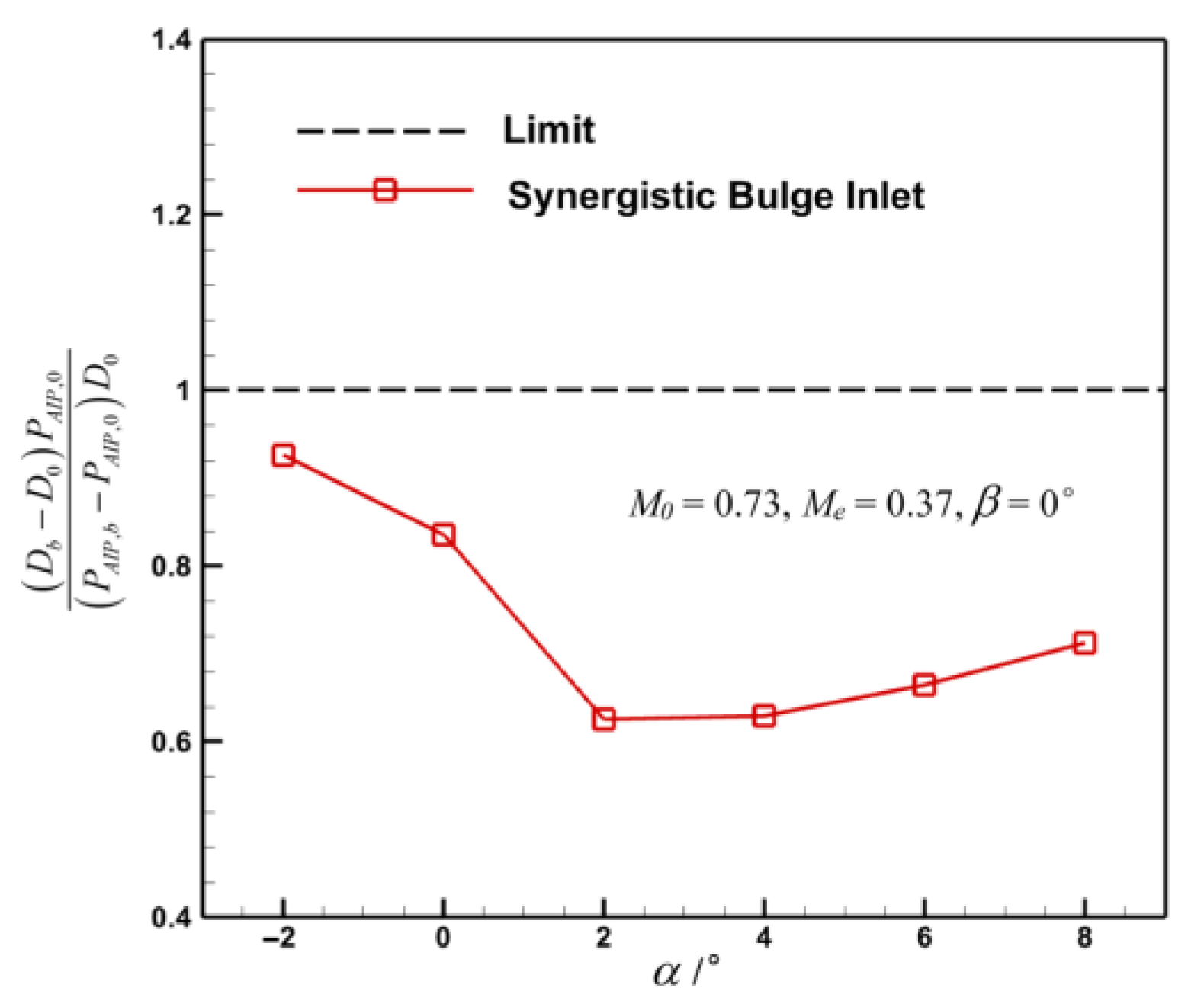
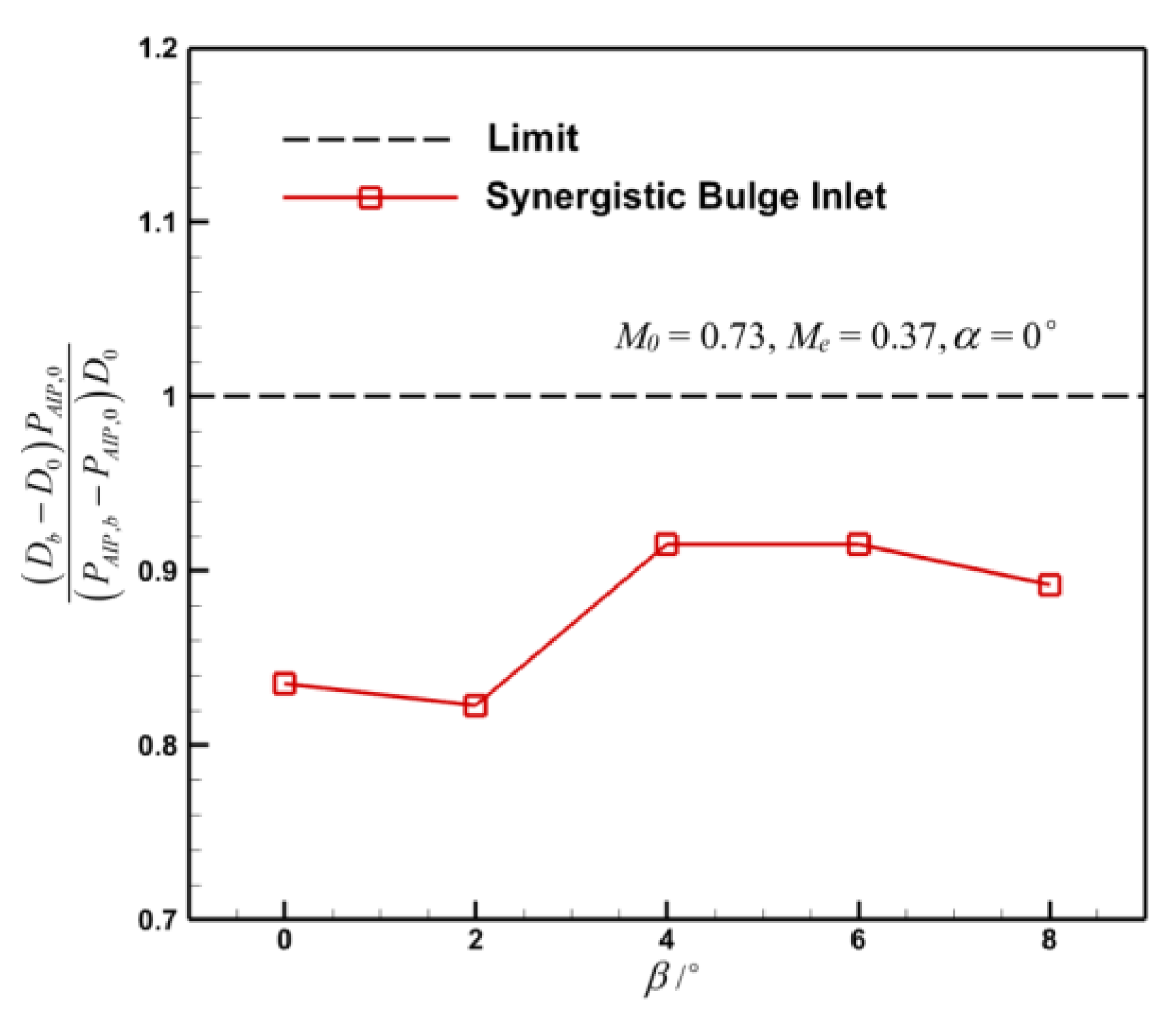
5. Applicability Evaluation of Internal and External Flow Interference Effect of Prepositive Synergistic Bulge Inlet
6. Conclusions
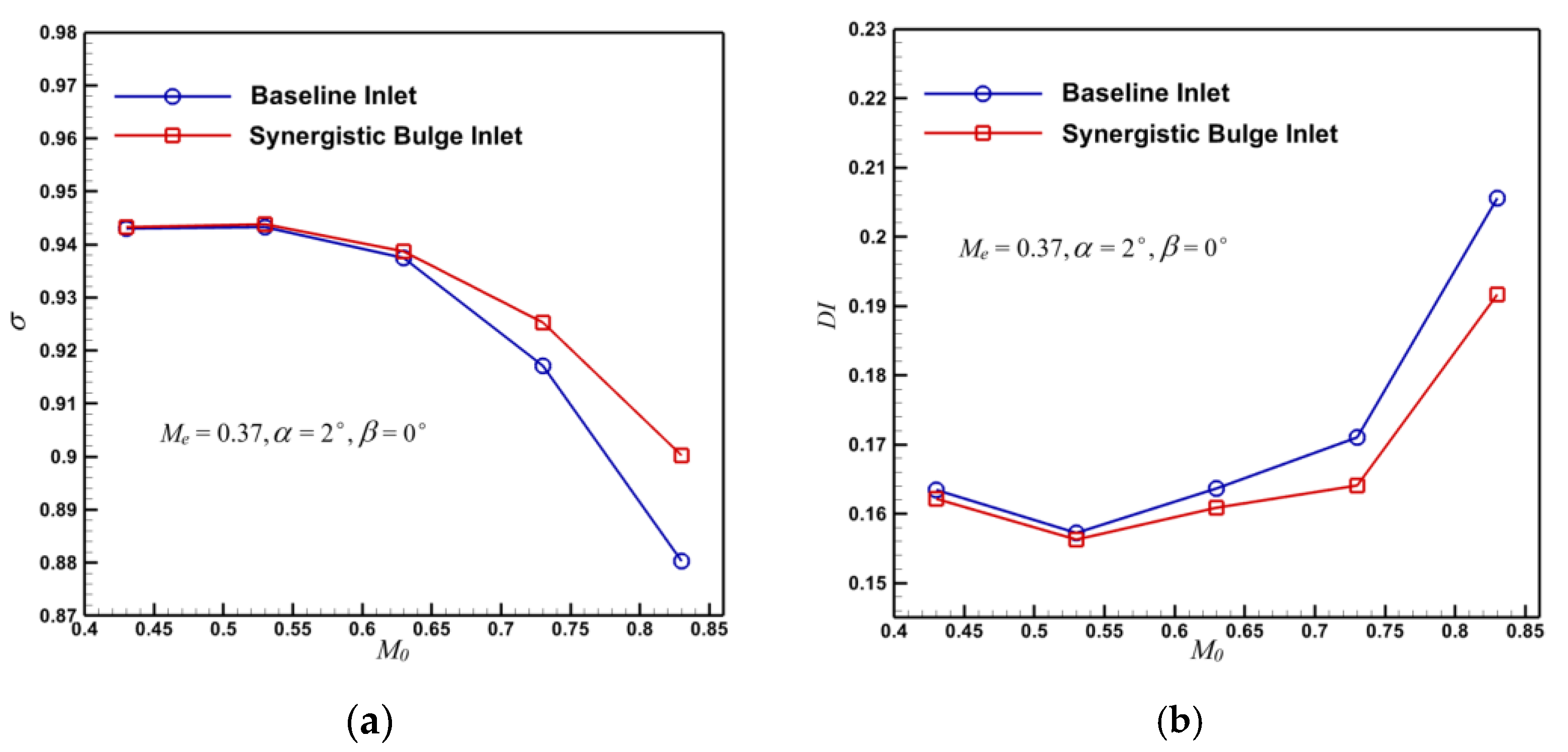
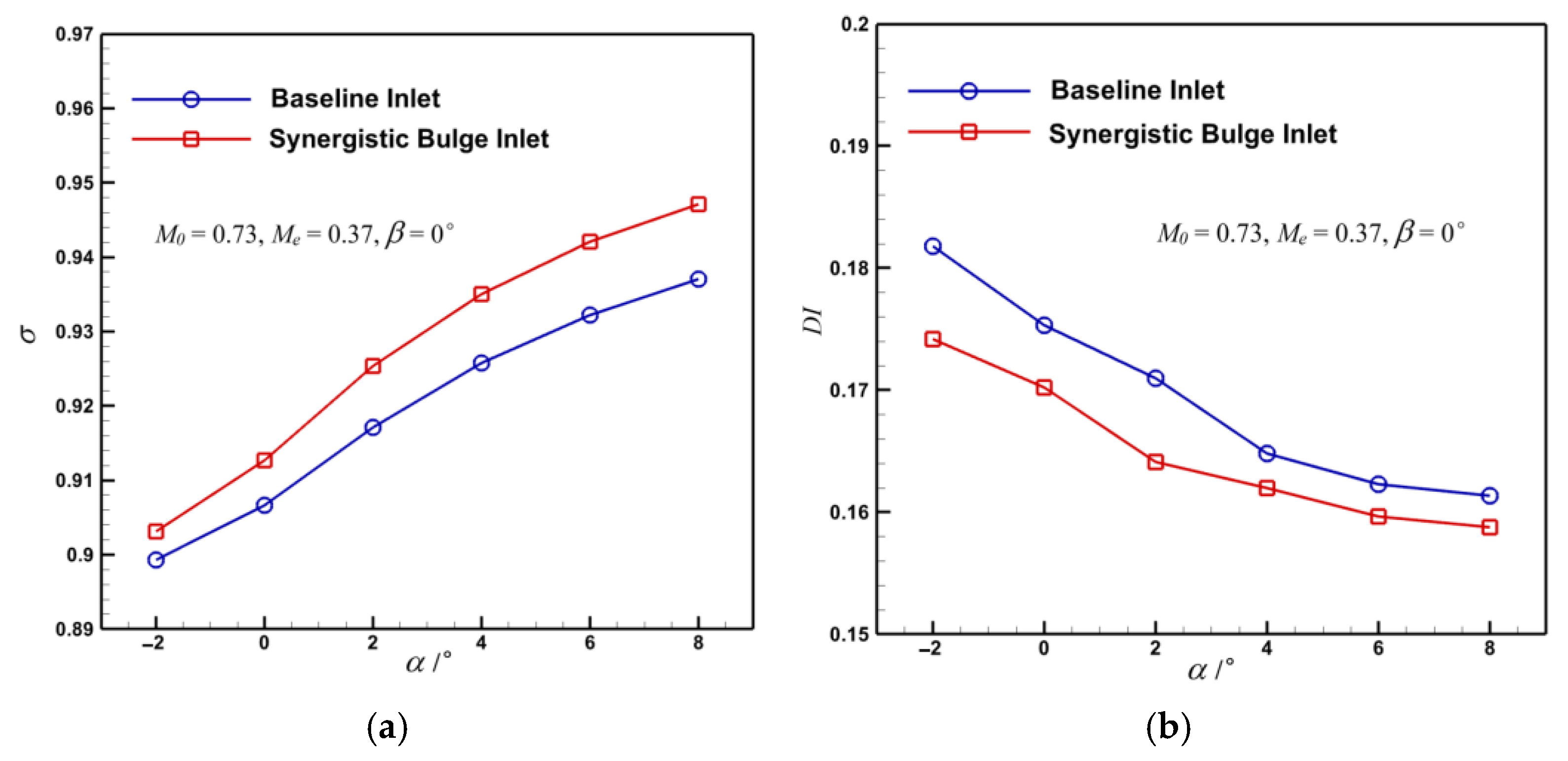
- The synergistic bulge diverts part of the low-energy boundary layer away from the inlet’s entrance, which improves the inlet flow quality of the submerged inlet. There is a large velocity increase at the wall near the anterior lip in the inlet channel, which eliminates the separation vortex formed by low-energy fluid in the baseline inlet, and improves the performance of the submerged inlet. After setting the bulge, the total pressure recovery coefficient of inlet increased by up to 1.36%, total pressure distortion index decreased by 10.86%, and the projectile drag increased by 0.37%, which means the bulge can meet the design requirements.
- The efficiency enhancement effect of the prepositive synergistic bulge inlet configuration is relatively stable. Among the three design parameters, the aspect ratio of bulge has the greatest influence on the aerodynamic performance of the inlet. When the aspect ratio is too small, not only the low-energy boundary layer at the inlet cannot be excluded, but also a low-pressure area will be formed after the synergistic bulge, which seriously reduces the inlet’s performance. Therefore, it should be ensured that the aspect ratio is no less than 0.75. The additional drag brought to the projectile by the bulge increases with its height, and the drag increases by 0.86% compared with the baseline model when the bulge height is 5 mm.
- Under different exit Mach numbers, incoming Mach numbers, attack angles, and sideslip angles, the method of adding the synergistic bulge before the submerged inlet can improve the performance of the baseline inlet, and the increment of the additional drag can basically meet the design requirements, meaning it has wide applicability. When the inlet exit’s Mach number in the calculation condition is smaller or the incoming flow’s Mach number is larger, the effect of this method on the improvement of the inlet’s performance is more obvious.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| d | Outlet diameter of the inlet |
| Total pressure recovery coefficient | |
| DI | Total pressure distortion index |
| Flow-weighted average total pressure on the exit of the inlet | |
| Total pressure of the incoming flow | |
| Maximum total pressure on the exit of the inlet | |
| Minimum total pressure on the exit of the inlet | |
| Average total pressure on the exit of the inlet | |
| Incoming flow Mach number | |
| Inlet exit Mach number | |
| Attack angle | |
| Sideslip angle | |
| Drag around the projectile with the baseline configuration | |
| Drag around the projectile and the bulge with the synergistic bulge inlet configuration | |
| Baseline inlet exit’s flow-weighted average total pressure | |
| Synergistic bulge inlet exit’s flow-weighted average total pressure | |
| Length of the bulge | |
| Width of the bulge | |
| Width of the inlet’s anterior lip | |
| Height of the bulge | |
| Coordinates of the initial point on the bulge | |
| Coordinates of any point on the bulge | |
| Swirl angle | |
| Circumferential velocity component at a certain point on the inlet’s exit | |
| Axial velocity component at a certain point on the inlet’s exit |
References
- Jia, G.W.; Yin, P.; Shao, S.; Wang, J. Review of RCS measurement and imaging methods of stealth aircraft. J. Natl. Univ. Def. Technol. 2022, 44, 93–103. [Google Scholar]
- Anderson, B.H.; Reddy, D.R.; Kapoor, K. Study on computing separating flows within a diffusion inlet S-duct. J. Propuls. Power 1994, 10, 661. [Google Scholar] [CrossRef]
- Harloff, G.J.; Smith, C.F.; Bruns, J.E.; DeBonis, J.R. Navier-Stokes analysis of three-dimensional S-ducts. J. Aircr. 1993, 30, 526–533. [Google Scholar] [CrossRef]
- Axelson, J.A.; Taylor, R.A. Preliminary Investigation of the Transonic Characteristics of an NACA Submerged Inlet; Technical Report Archive & Image Library: Washington, DC, USA, 1950. [Google Scholar]
- Sun, S.; Guo, R.W. Numerical Analysis and Experimental Validation of a Submerged Inlet on the Plane Surface. Chin. J. Aeronaut. 2005, 18, 199–205. [Google Scholar] [CrossRef] [Green Version]
- Sun, S.; Guo, R.W.; Wu, Y.Z. Characterization and Performance Enhancement of Submerged Inlet with Flush-Mounted Planar Side Entrance. J. Propuls. Power 2007, 23, 987–995. [Google Scholar] [CrossRef]
- Wang, Y.G.; Wang, C.H.; Xiao, Y.C.; Chen, B.; Zhou, S.; Guo, J.T.; Sun, M.W. Construction methodology for lip surface of a submerged inlet. Aerosp. Sci. Technol. 2016, 54, 340–352. [Google Scholar] [CrossRef]
- Mehdi, M.; Sajad, G.; Davood, T. Numerical Investigation of Geometrical Design Effect on the Submerged Inlet Aerodynamics Characteristics. Int. J. Aeronaut. Space Sci. 2020, 21, 25–38. [Google Scholar] [CrossRef]
- Pei, H.; Cui, Y.; Kong, B.; Jiang, Y.; Shi, H. Structural parameters optimization of submerged inlet using least squares support vector machines and improved genetic algorithm-particle swarm optimization approach. Eng. Appl. Comput. Fluid Mech. 2021, 1, 503–511. [Google Scholar] [CrossRef]
- Harper, D.K.; Leitch, T.A.; Ng, W.F.; Guillot, S.G. Boundary Layer Control and Wall-Pressure Fluctuation in a Serpentine Inlet. In Proceedings of the 36th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Las Vegas, NV, USA, 24–28 July 2000. [Google Scholar]
- Owens, L.R.; Allan, B.G.; Gorton, S.A. Boundary-Layer-Ingesting Inlet Flow Control. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 9–12 January 2006. [Google Scholar]
- Ng, Y.T.; Luo, S.C.; Lim, T.T.; Ho, Q.W. Three Techniques to Control Flow Separation in an S-Shaped Duct. AIAA J. 2011, 49, 1825–1832. [Google Scholar] [CrossRef]
- Harouni, A.G. Flow control of a boundary layer ingesting serpentine diffuser via blowing and suction. Aerosp. Sci. Technol. 2014, 39, 472–480. [Google Scholar] [CrossRef]
- Keerthi, M.C.; Kushari, A. Effectiveness of vortex generator jets and wall suction on separated flows in serpentine-duct diffuser. Aerosp. Sci. Technol. 2014, 34, 12–19. [Google Scholar] [CrossRef]
- Paul, A.R.; Joshi, S.; Jindal, A.; Maurya, S.P.; Jain, A. Experimental Studies of Active and Passive Flow Control Techniques Applied in a Twin Air-Intake. Sci. World J. 2013, 2013, 523759. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yadav, K.R.; Paul, A.R.; Hegde, N.; Jain, A. A Comparison of Circular and Slotted Synthetic Jets for Flow Control in a Twin Air-Intake. Def. Sci. J. 2020, 70, 113–121. [Google Scholar] [CrossRef]
- Taskinoglu, E.S.; Knight, D.D. Design Optimization for Submerged Inlets—Part I. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 6–9 January 2003. AIAA Paper 2003-1247. [Google Scholar]
- Taskinoglu, E.S.; Jovanovic, V.; Knight, D.D. Design Optimization for Submerged Inlets- Part II. In Proceedings of the 21st AIAA Applied Aerodynamics Conference, Orlando, FL, USA, 23–26 June 2003. AIAA Paper 2003-3926. [Google Scholar]
- Taskinoglu, E.S.; Jovanovic, V.; Knight, D.D. Multi-objective design optimization and experimental measurement for a submerged inlet. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 5–8 January 2004. AIAA Paper 4478-4491. [Google Scholar]
- Jovanovic, V.; Taskinoglu, E.S.; Knight, D.D. Experimental investigation of a submerged subsonic inlet. Appl. Aerodyn. Conf. Exhib. 2004, 22, 214–217. [Google Scholar] [CrossRef]
- Pérez, C.C.; Ferreira, S.B.; da Silva, L.F.F.; de Jesus, A.B.; Oliveira, G.L. Computational Study of Submerged Air Inlet Performance Improvement Using Vortex Generators. J. Aircr. 2007, 44, 1574–1587. [Google Scholar] [CrossRef]
- Cheng, D.S.; Tan, H.J.; Sun, S.; Tong, Y. Computational Study of a High-Performance Submerged Inlet with Bleeding Vortex. J. Aircr. 2012, 49, 852–860. [Google Scholar] [CrossRef]
- Sun, S.; Tan, H.J.; Wang, C.X. Submerged inlet performance enhancement using a unique bump-shaped vortex generator. J. Propuls. Power 2016, 32, 1275–1280. [Google Scholar] [CrossRef]
- Saheby, E.B.; Shen, X.; Huang, G.; Hays, A.P. Flow structure of the ridge integrated submerged inlet. Aerosp. Sci. Technol. 2021, 119, 107136. [Google Scholar] [CrossRef]
- Xie, W.; Yang, S.; Zeng, C.; Liao, K.; Ding, R.; Zhang, L.; Guo, S. Effects of forebody boundary layer on the performance of a submerged inlet. Aeronaut. J. 2021, 125, 1260–1281. [Google Scholar] [CrossRef]
- Xie, W.Z.; Zeng, C.; Wang, Z.Y.; Guo, S. Flow Control for a Submerged Inlet. J. Fluids Eng. 2022, 144, 121202. [Google Scholar] [CrossRef]
- Askari, R.; Soltani, M.R. Numerical Simulation of a Y-Shaped Diverterless Supersonic Inlet. J. Aircr. 2023. [Google Scholar] [CrossRef]
- Tanguy, G.; MacManus, D.G.; Garnier, E.; Martin, P.G. Characteristics of unsteady total pressure distortion for a complex aero-engine intake duct. Aerosp. Sci. Technol. 2018, 78, 297–311. [Google Scholar] [CrossRef] [Green Version]
- Gil-Prieto, D.; Zachos, P.K.; MacManus, D.G.; McLelland, G. Unsteady characteristics of S-duct intake flow distortion. Aerosp. Sci. Technol. 2019, 84, 938–952. [Google Scholar] [CrossRef] [Green Version]
- Tanguy, G.; MacManus, D.G.; Garnier, E. Numerical investigation of the unsteady distortion for an S-duct intake with mechanical vortex generators. Int. J. Heat Fluid Flow 2022, 95, 108975. [Google Scholar] [CrossRef]
- Patel, V.C.; Rodi, W.; Scheuerer, G. Turbulence models for near-wall and low Reynolds number flows: A Review. AIAA J. 1985, 23, 1308–1319. [Google Scholar] [CrossRef]
- SAE International. A Methodology for Assessing Inlet Swirl Distortion: AR 5686; SAE International: Warrendale, PA, USA, 2010. [Google Scholar]





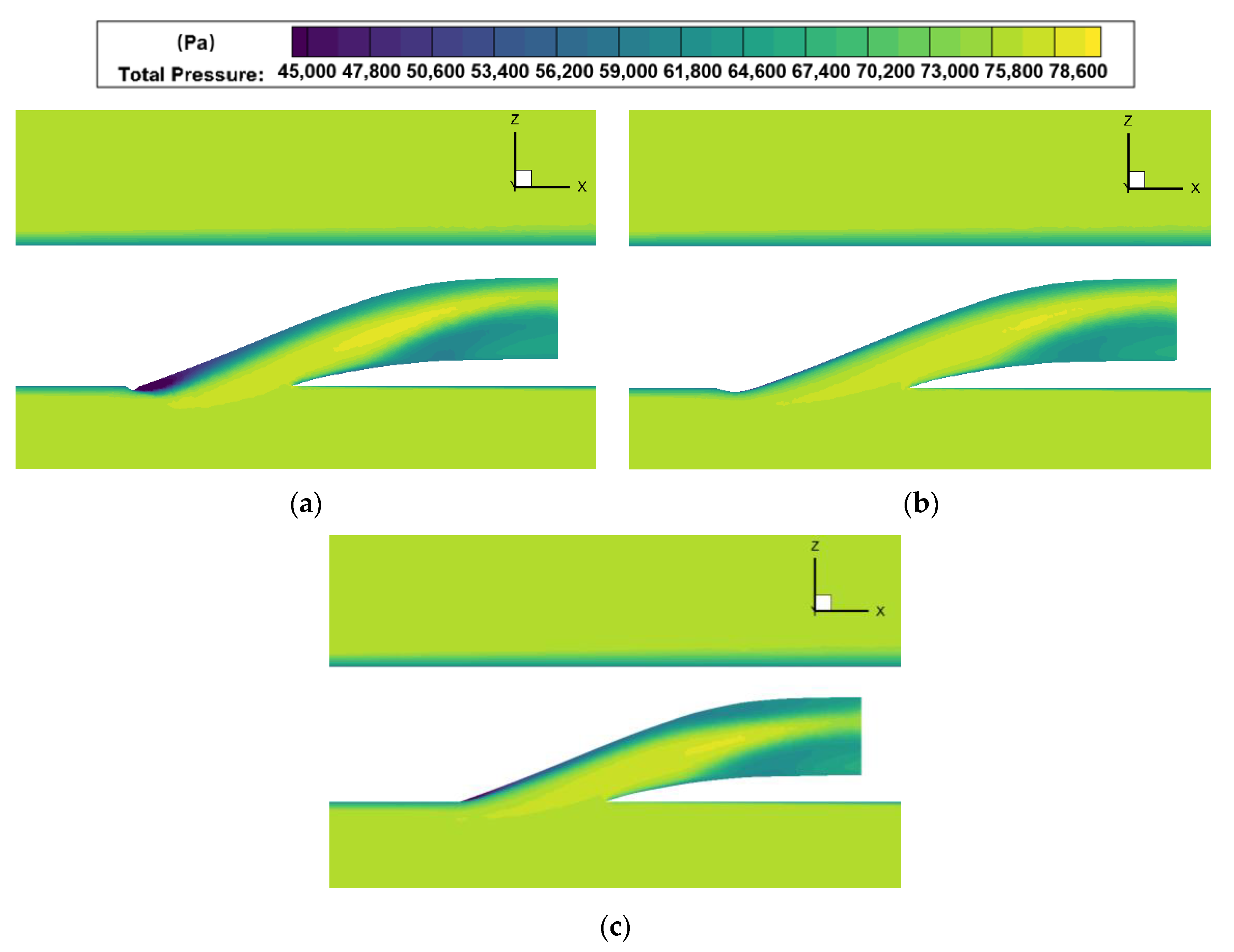
| Grid Scheme | Number of Grids (Millions) | Total Pressure Recovery Coefficient | Error (%) | Total Pressure Distortion Index DI | Error (%) |
|---|---|---|---|---|---|
| 1 | 0.86 | 0.9159 | 0.174 | 0.1735 | 1.225 |
| 2 | 1.24 | 0.9171 | 0.043 | 0.1712 | 0.116 |
| 3 | 3.32 | 0.9182 | 0.076 | 0.1715 | 0.058 |
| 4 | 5.71 | 0.9175 | / | 0.1714 | / |
| Exit Mach Number Me | Total Pressure Recovery Coefficient | Relative Error (%) | |
|---|---|---|---|
| Experimental Values [5] | Simulation Values | ||
| 0.33 | 0.903 | 0.912 | 0.996 |
| 0.35 | 0.910 | 0.914 | 0.444 |
| 0.37 | 0.916 | 0.917 | 0.109 |
| 0.40 | 0.922 | 0.920 | 0.217 |
| Ratio of the Width of the bulge to the width of the inlet’s anterior lip | 0.2 | 0.5 | 0.8 | 1 | 1.1 | 1.4 |
| The aspect ratio of the bulge | 0.25 | 0.5 | 0.75 | 1 | 1.25 | |
| The height of the bulge (mm) | 1 | 2 | 3 | 4 | 5 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, X.; Mi, B. Prepositive Synergistic Bulge Design for Improving Aerodynamic Performance of Submerged Inlet. Aerospace 2023, 10, 649. https://doi.org/10.3390/aerospace10070649
Bai X, Mi B. Prepositive Synergistic Bulge Design for Improving Aerodynamic Performance of Submerged Inlet. Aerospace. 2023; 10(7):649. https://doi.org/10.3390/aerospace10070649
Chicago/Turabian StyleBai, Xuan, and Baigang Mi. 2023. "Prepositive Synergistic Bulge Design for Improving Aerodynamic Performance of Submerged Inlet" Aerospace 10, no. 7: 649. https://doi.org/10.3390/aerospace10070649
APA StyleBai, X., & Mi, B. (2023). Prepositive Synergistic Bulge Design for Improving Aerodynamic Performance of Submerged Inlet. Aerospace, 10(7), 649. https://doi.org/10.3390/aerospace10070649





