Aerodynamic Instabilities in High-Speed Air Intakes and Their Role in Propulsion System Integration
Abstract
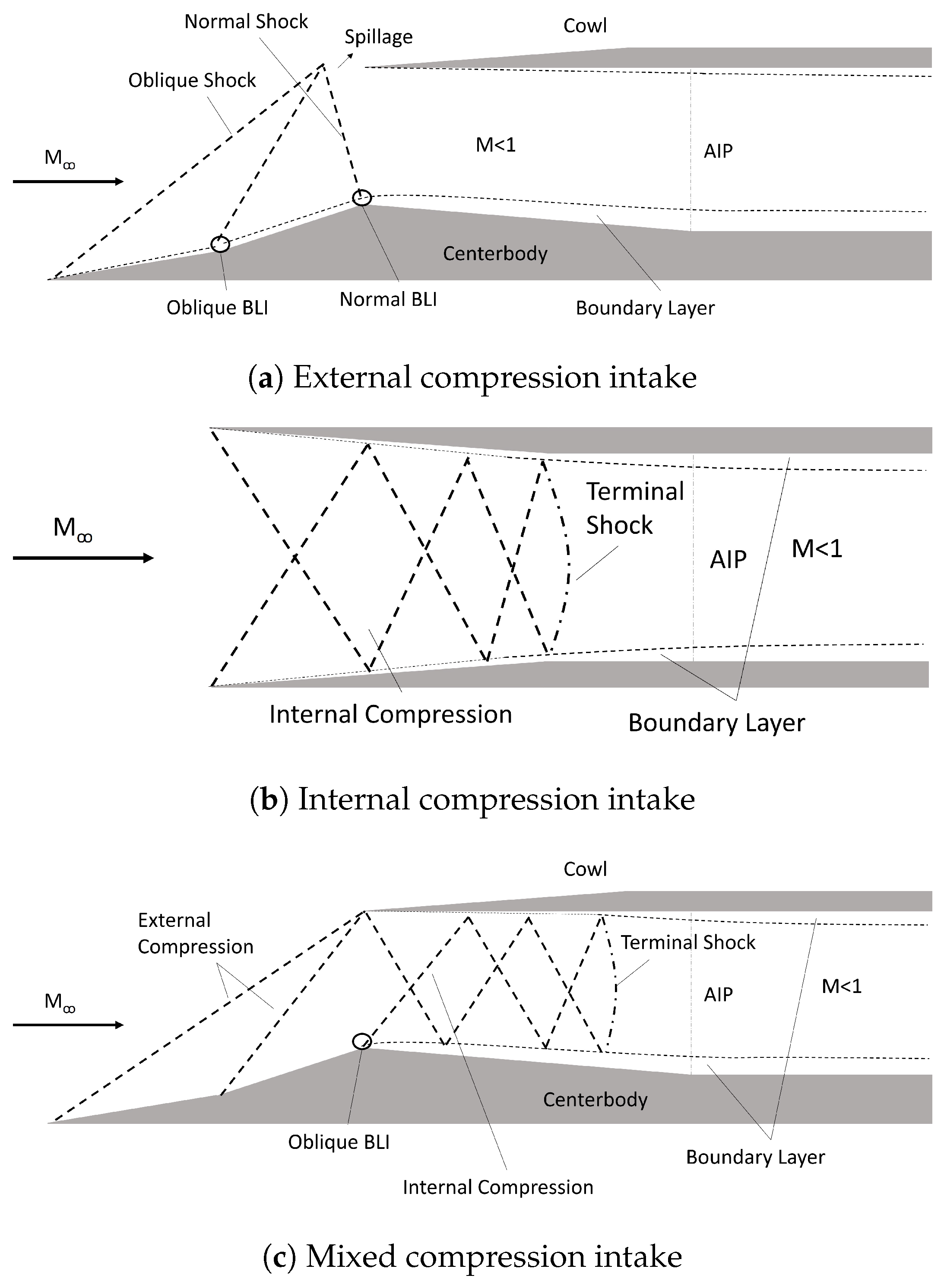
:1. Introduction
2. Flow Instabilities in Air Induction Systems
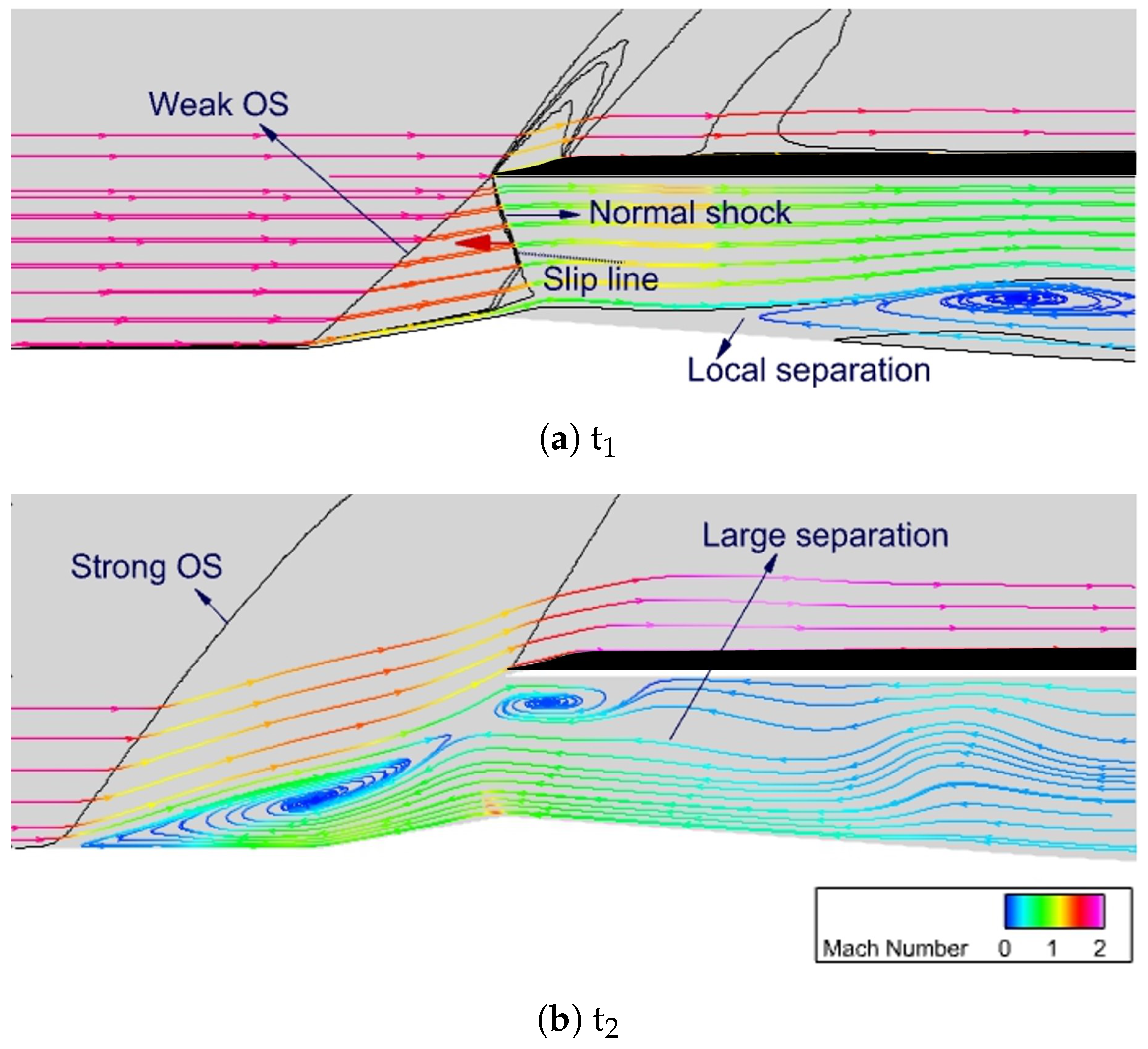
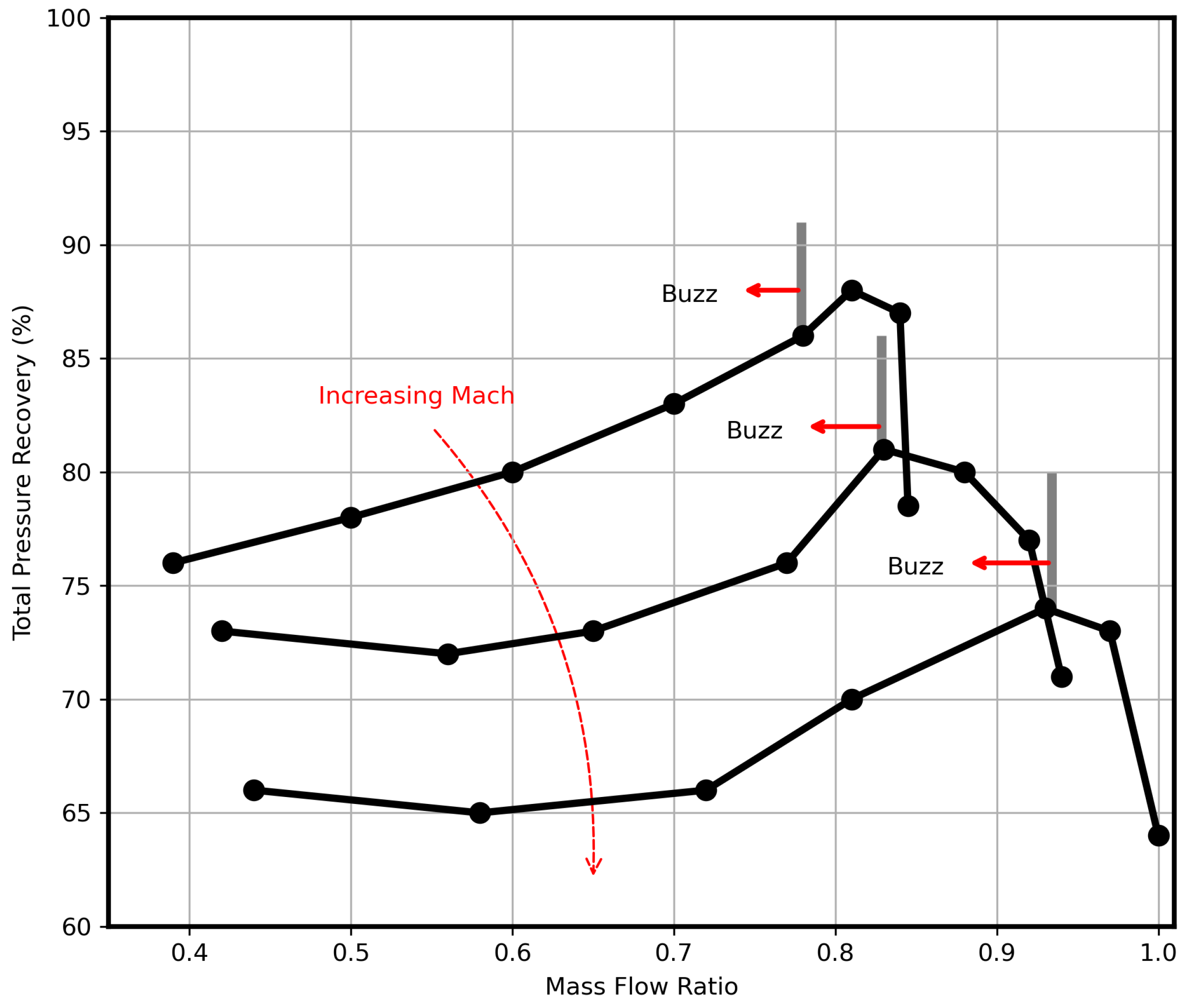
2.1. Physics and Characterization of Intake Buzz
| Reference | Method (E/N) | Intake Geometry | Compression System | Mach | Buzz Type Definition | Dominant Frequency (Hz) | Buzz Cycle (s) | Strouhal No. St = fL/U |
|---|---|---|---|---|---|---|---|---|
| Trapier et al. [48] | E | 2D | Mixed | 1.8, 2, 3 | Ferri (Low amplitude) | 120–140 | 0.007–0.008 | N/A |
| Dailey (High amplitude) | 12–20 | 0.08–1 | ||||||
| Nagashima et al. [50] | E | A/S | External | 2 | Frequency-Based | 100 | 0.01 | N/A |
| (Similar amplitude) | 360 | 0.0027 | ||||||
| Fisher [33] | E | Rectangular (Build A) | External | 1.9 | Ferri (Low amplitude) | 45 | N/A | N/A |
| Dailey (High amplitude) | 48 | |||||||
| Chima [79] | N | A/S | External | 1.66 | Dailey (High amplitude) | 16.9 | 0.059 | 0.089 |
| Herrmann et al. [58] | E | Rectangular | External | 2.5 | Dailey (High amplitude) | 43 | N/A | 0.085 |
| Trapier et al. [44] | N | Rectangular | Mixed | 1.8 | Dailey (High amplitude) | 17 | ≈0.057 | 0.064 |
| Soltani and Younsi [37] | E | A/S | Mixed | 2 | Dailey | 96 | 0.01 | N/A |
| Chang et al. [60] | E | 2D | Mixed | 5 | Dailey (Weak cycle = low Strong cycle = high) | 110 | Weak = 0.011 Strong = 0.017 | N/A |
| Nishizawa et al. [51] | N | 2D | External | 1.64 | Dailey | 640 | N/A | 0.078 |
| Hong and Kim [43] | N | A/S | External | 2 | Dailey | 367 | N/A | 0.35 |
| Soltani, Farahani [62] | E | A/S | External | 2.5 | Ferri (Low amplitude) | 125 | 0.0072 | N/A |
| Dailey (High amplitude) | 138 | 0.012 | ||||||
| Chen et al. [63] | E | Rectangular | External | 2 | Dailey | 179.7 | 0.0056 | 0.094 |
| Grenson and Benedine [80] | E and N | Rectangular | External | 1.8 | Amplitude Based (Low amplitude) | E = 107 N = 750 | 0.0016 | 0.09 |
| (High amplitude) | E = 83 N = 550 | 0.0018 | 0.069 | |||||
| Abedi et al. [38] | N | A/S | Mixed | 2 | Dailey (High amplitude) | 112.5 | 0.009 | N/A |
| Zhu et al. [81] | N | A/S | External | 2 | Frequency-based (High amplitude) | 120 | N/A | 0.116 |
| (Low amplitude) | 360 | 0.35 |
2.2. Effect of Operating Conditions on Intake Unsteadiness
2.2.1. Effect of Mach Number
2.2.2. Effect of Angle of Attack
2.3. Suppression of Intake Buzz and Unstart Mode
2.3.1. Boundary Layer Bleed
2.3.2. Passive Vortex Generators
2.3.3. Mass Injection and Energy Deposition
| Description | Boundary Layer Porous Bleed | Vortex Generators | Energy Deposition through Plasma Jet Injection |
|---|---|---|---|
| System Implementation | Consists of perforated bleed holes on the surface through which a fraction of the intake flow is extracted, mostly from the low−momentum portion of the boundary layer. This action results in the remaining boundary layer having an increased average momentum, thereby enhancing its capability to navigate adverse pressure gradients associated with SBLIs. | Strategically placed in areas prone to shock−induced separation to counteract its adverse effects. When the airflow encounters a VG, it induces a rotational motion, introducing high−energy vortices into the boundary layer, preventing or delaying separation. This energization helps maintain the attachment of the boundary layer to the aerodynamic surface, reducing the likelihood of flow separation. | Energy deposition in the form of plasma introduces a stream of ionized gas or plasma into the airflow over specific regions of the aerodynamic surface, which interacts with the boundary layer leading to an energetic mixing. This mixing disrupts the stagnant layer near the aerodynamic surface, preventing or delaying separation. |
| System Schematic |  | 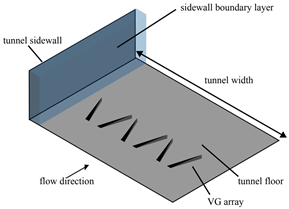 |  |
| System Illustration | 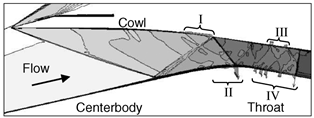 | 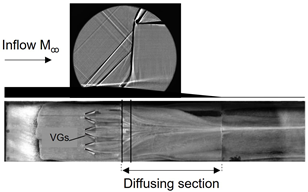 |  |
3. Unsteady Shock Trains in Isolators
3.1. Origin of Shock Train Oscillations
3.2. Effect of Back Pressure
3.3. Three-Dimensionality of Flow Field in Isolators
4. Current and Future Perspectives in Engine-Intake Aerodynamic Compatibility
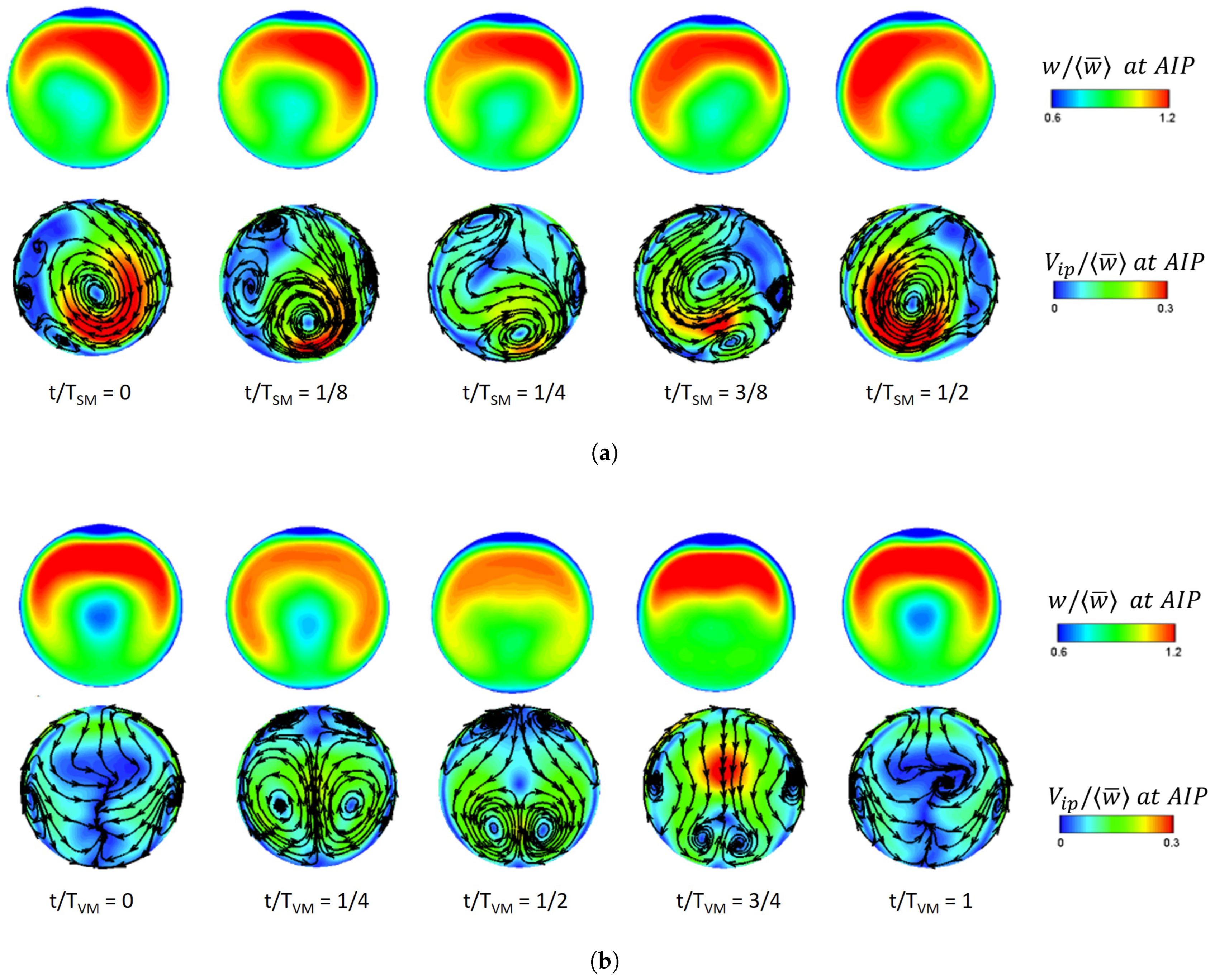
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| AIP | aerodynamic interface plane |
| AOA | angle of attack |
| BS | bow shockwave |
| DBD | dielectric barrier discharge |
| DDES | delayed detached eddy simulations |
| EBR | exit blockage ratio |
| LAFPA | localized arc filament plasma actuator |
| LDV | laser Doppler velocimetry |
| LES | large eddy simulations |
| NS | normal shockwave |
| OS | oblique shockwave |
| PSJ | plasma synthetic jet |
| SS | separation shockwave |
| SBLI | shockwave boundary layer interaction |
| S-PIV | stereo-particle image velocimetry |
| TP | triple point |
| operators | |
| time average | |
| area average | |
| Roman symbols | |
| A | area, m |
| D | diameter, m |
| F | frequency, Hz |
| H | height, m |
| L | length, m |
| M | Mach number |
| St | Strouhal number |
| U | velocity, m/s |
| V | in-plane velocity modulus, m/s |
| w | axial velocity, m/s |
| sub/super-scripts | |
| ∞ | quantity at freestream |
| ref | reference quantity |
| max | maximum quantity |
References
- Oates, G.C. Aircraft Propulsion Systems Technology and Design; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1989. [Google Scholar]
- Faro, I.D. Supersonic Inlets; North Atlantic Treaty Organization, Advisory Group for Aerospace Research and Development: Brussels, Belgium, 1965. [Google Scholar]
- Seddon, J.; Goldsmith, E. Intake Aerodynamics; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1999. [Google Scholar]
- Ebrahimi, A.; Zare Chavoshi, M. Numerical investigation of back pressure and free-stream effects on a mixed compression inlet performance. Sci. Iran. 2017, 25, 751–761. [Google Scholar] [CrossRef]
- ARP1420B; Gas Turbine Engine Inlet Flow Distortion Guidelines. SAE International: Warrendale, PA, USA, 2011; p. 24. [CrossRef]
- S-16 Turbine Engine Inlet Flow Distortion Committee. Assessment of the Inlet/Engine Total Temperature Distortion Problem; SAE International: Warrendale, PA, USA, 2017; p. 57. [Google Scholar] [CrossRef]
- Turbine Engine Inlet Flow Distortion Committee. AIR1419C; Inlet Total-Pressure-Distortion Considerations for Gas-Turbine Engines. Technical Report. SAE International: Warrendale, PA, USA, 2017. [Google Scholar] [CrossRef]
- S-16 Turbine Engine Inlet Flow Distortion Committee. A Methodology for Assessing Inlet Swirl Distortion; SAE International: Warrendale, PA, USA, 2017; p. 110. [Google Scholar] [CrossRef]
- Das, S.; Prasad, J.K. Starting characteristics of a rectangular supersonic air-intake with Cowl Deflection. Aeronaut. J. 2010, 114, 177–189. [Google Scholar] [CrossRef]
- Timofeev, E.; Tahir, R.; Molder, S. On recent developments related to flow starting in Hypersonic Air Intakes. In Proceedings of the 15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Dayton, OH, USA, 28 April–1 May 2008. [Google Scholar] [CrossRef]
- Wagner, J.L.; Yuceil, K.B.; Valdivia, A.; Clemens, N.T.; Dolling, D.S. Experimental investigation of unstart in an inlet/isolator model in mach 5 flow. AIAA J. 2009, 47, 1528–1542. [Google Scholar] [CrossRef]
- Van Wie, D.; Kwok, F.; Walsh, R. Starting characteristics of supersonic inlets. In Proceedings of the 32nd Joint Propulsion Conference and Exhibit, Lake Buena Vista, FL, USA, 1–3 July 1996. [Google Scholar] [CrossRef]
- Hawkins, W.; Marquart, E. Two-dimensional generic inlet unstart detection at Mach 2.5-5.0. In Proceedings of the International Aerospace Planes and Hypersonics Technologies, Chattanooga, TN, USA, 3–7 April 1995. [Google Scholar] [CrossRef]
- Chang, J.; Fan, Y.; Bao, W.; Yu, D.; Shen, Y. Unstart margin control of hypersonic inlets. Acta Astronaut. 2010, 66, 78–87. [Google Scholar] [CrossRef]
- Im, S.; Do, H. Unstart phenomena induced by flow choking in scramjet inlet-isolators. Prog. Aerosp. Sci. 2018, 97, 1–21. [Google Scholar] [CrossRef]
- Kantrowitz, A.; Donaldson, C.D. Preliminary Investigation of Supersonic Diffusers; NACA ACR-L5D20; NACA: Boston, MA, USA, 1945. [Google Scholar]
- Kantrowitz, A. The Formation and Stability of Normal Shock Waves in Channel Flows; NACA TN 1225; NACA: Boston, MA, USA, 1947. [Google Scholar]
- Oswatitsch, K. Pressure Recovery for Missiles with Reaction Propulsion at High Supersonic Speeds (the Efficiency of Shock Diffusers); NACA TM No. 1140; NACA: Boston, MA, USA, 1947. [Google Scholar]
- Williams, D.D.; Yost, J.O. Some aspects of inlet/engine flow compatibility. Aeronaut. J. 1973, 77, 483–492. [Google Scholar] [CrossRef]
- Wenzel, L.M.; Blaha, R.J. Analysis of Dynamic Inlet Distortion Applied to a Parallel Compressor Model; NASA TM-X-352; NASA: Washington, DC, USA, 1977. [Google Scholar]
- Cousins, W.T. History, Philosophy, Physics, and Future Directions of Aircraft Propulsion System/Inlet Integration. In Proceedings of the ASME Turbo Expo 2004 Power for Land, Sea, and Air, Vienna, Austria, 14–17 June 2004. [Google Scholar]
- Tanguy, G.; MacManus, D.G.; Garnier, E.; Martin, P.G. Characteristics of unsteady total pressure distortion for a complex aero-engine intake duct. Aerosp. Sci. Technol. 2018, 78, 297–311. [Google Scholar] [CrossRef]
- McLelland, G.; MacManus, D.G.; Zachos, P.K.; Gil-Prieto, D.; Migliorini, M. Influence of upstream total pressure profiles on S-duct intake flow distortion. J. Propuls. Power 2020, 36, 346–356. [Google Scholar] [CrossRef]
- Gil-Prieto, D.; Zachos, P.K.; MacManus, D.G.; McLelland, G. Unsteady characteristics of S-duct intake flow distortion. Aerosp. Sci. Technol. 2019, 84, 938–952. [Google Scholar] [CrossRef]
- Kächele, T.; Rademakers, R.P.; Schneider, T.; Niehuis, R. Numerical simulations of an intake-compressor system. J. Glob. Power Propuls. Soc. 2018, 2, 442–452. [Google Scholar] [CrossRef]
- Mehdi, A.; Pachidis, V.; MacManus, D. Effect of Swirl Distortion on Gas Turbine Operability. 2014. Available online: https://dspace.lib.cranfield.ac.uk/handle/1826/12129 (accessed on 1 September 2023).
- Zachos, P.K.; MacManus, D.G.; Prieto, D.G.; Chiereghin, N. Flow distortion measurements in convoluted aeroengine intakes. AIAA J. 2016, 54, 2819–2832. [Google Scholar] [CrossRef]
- Fisher, S.A.; Ford, D.J. An Investigation of Starting Problems in a Specialised Wind Tunnel for Testing a Rectangular Mixed Compression Intake at Mach 3; Publication 138; Aeronautical Research Laboratories Mechanical Engineering, Department of Supply, Australian Defence Scientific Service: Adelaide, Australia, 1972. [Google Scholar]
- Kimzey, W.F.; Ellis, S.H. Supersonic Inlet Simulator—A Tool for Simulation of Realistic Engine Entry Flow Conditions. SAE Int. 1974, 83, 2812–2824. [Google Scholar] [CrossRef]
- Syberg, J. Performance of Highly Integrated Inlets for Supersonic Aircraft; AGARD Conference Proceedings No.301; AGARD: Neuilly-sur-Seine, France, 1981. [Google Scholar]
- Ferri, A.; Nucci, L.M. The Origin of Aerodynamic Instability of Supersonic Inlets at Subcritical Conditions; NACA RM L50K30; NACA: Boston, MA, USA, 1951. [Google Scholar]
- Dailey, C.L. Supersonic diffuser instability. J. Aeronaut. Sci. 1955, 22, 733–749. [Google Scholar] [CrossRef]
- Fisher, S.A.; Neale, M.C.; Brooks, A.J. On the Sub-Critical Stability of Variable Ramp Intakes at Mach Numbers Around 2. UK Ministry of Defence Reports and Memoranda R. & M. 1972. Available online: https://reports.aerade.cranfield.ac.uk/handle/1826.2/2987 (accessed on 1 September 2023).
- Jungclaus, G. Neue experimentelle Ergebnisse zur Entstehung und Struktur von Ferri- und Dailey-Instabilitäten (“Brummen"). Z. Für Flugwiss. Und Weltraumforsch. (ZFW) 1990, 14, 256–262. [Google Scholar]
- Orlin, W.J.; Dunsworth, L.C. A Criterion for Flow Instability in Supersonic Diffuser Inlets; Report No. 5144; Marquardt Aircraft Co.: Los Angeles, CA, USA, 1951. [Google Scholar]
- Soltani, M.; Farahani, M.; Asgari Kaji, M. An experimental study of buzz instability in an axisymmetric supersonic inlet. Sci. Iran. 2011, 18, 241–249. [Google Scholar] [CrossRef]
- Soltani, M.R.; Sepahi-Younsi, J. Buzz cycle description in an axisymmetric mixed-compression air intake. AIAA J. 2016, 54, 1040–1053. [Google Scholar] [CrossRef]
- Abedi, M.; Askari, R.; Soltani, M. Numerical simulation of Inlet Buzz. Aerosp. Sci. Technol. 2020, 97, 105547. [Google Scholar] [CrossRef]
- Newsome, R.W. Numerical simulation of near-critical and unsteady, Subcritical Inlet Flow. AIAA J. 1984, 22, 1375–1379. [Google Scholar] [CrossRef]
- Lu, P.; Jain, L. Numerical Investigation of Inlet Buzz Flow. J. Propuls. Power 1998, 14, 90–100. [Google Scholar] [CrossRef]
- Fujimoto, A.N.N.; Sawada, K. Numerical investigation of Supersonic Inlet with realistic bleed andbypass systems. In Proceedings of the 29th Aerospace Sciences Meeting, Reno, NV, USA, 7–10 January 1991. [Google Scholar] [CrossRef]
- Fujiwara, H.M.A.; Murakami, A.; Watanabe, Y. Numerical analysis on shock oscillation of two-dimensional external compression intakes. In Proceedings of the 32nd AIAA Fluid Dynamics Conference and Exhibit, St. Louis, MO, USA, 24–26 June 2002. [Google Scholar] [CrossRef]
- Hong, W.; Kim, C. Computational study on Hysteretic Inlet Buzz characteristics under varying mass flow conditions. AIAA J. 2014, 52, 1357–1373. [Google Scholar] [CrossRef]
- Trapier, S.; Deck, S.; Duveau, P. Delayed detached-eddy simulation and analysis of Supersonic Inlet Buzz. AIAA J. 2008, 46, 118–131. [Google Scholar] [CrossRef]
- Watanabe, Y.; Ueno, A.; Murakami, A. Design Of Top Mounted Supersonic Inlet For Silent Supersonic Technology Demonstrator S3TD. In Proceedings of the 27th Congress of the International Council of the Aeronautical Sciences, Nice, France, 19–24 September 2010. [Google Scholar]
- John, B.; Senthilkumar, P. Alterations of cowl lip for the improvement of supersonic-intake performance. J. Appl. Fluid Mech. 2018, 11, 31–41. [Google Scholar] [CrossRef]
- Slater, J.W. Design factors for two-dimensional, external-compression supersonic inlets. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- Trapier, S.; Duveau, P.; Deck, S. Experimental Study of Supersonic Inlet Buzz. AIAA J. 2006, 44, 2354–2365. [Google Scholar] [CrossRef]
- Trapier, S.; Deck, S.; Duveau, P.; Sagaut, P. Time-frequency analysis and detection of Supersonic Inlet Buzz. AIAA J. 2007, 45, 2273–2284. [Google Scholar] [CrossRef]
- Nagashima, T.; Obokata, T.; Asanuma, T. Experiment of Supersonic Air Intake Buzz; Institute of Space and Aeronautical Science: Toyko, Japan, 1972; Volume 481, pp. 165–209. [Google Scholar]
- Nishizawa, U.; Kameda, M.; Watanabe, Y.; Yamamoto, S. Computational simulation of shock oscillation around a supersonic air-intake. In Proceedings of the 36th AIAA Fluid Dynamics Conference and Exhibit, San Francisco, LA, USA, 5–8 June 2006. [Google Scholar] [CrossRef]
- Masuya, G. Aerodynamic performances of a combined Cycle Inlet. J. Propuls. Power 2006, 22, 900–904. [Google Scholar] [CrossRef]
- Lu, H.; Yue, L.; Chang, X. Flow characteristics of hypersonic inlets with different cowl-lip blunting methods. Sci. China Phys. Mech. Astron. 2014, 57, 741–752. [Google Scholar] [CrossRef]
- Das, S.; Prasad, J.K. Effect of cowl deflection angle in a supersonic air-intake. Def. Sci. J. 2009, 59, 99–105. [Google Scholar] [CrossRef]
- Das, S.; Prasad, J.K. Flow field investigation of a rectangular supersonic air-intake with cowl bending. J. Aerosp. Sci. Technol. 2009, 61, 312–324. [Google Scholar] [CrossRef]
- Lanson, F.; Stollery, J.L. Some hypersonic intake studies. Aeronaut. J. 2006, 110, 145–156. [Google Scholar] [CrossRef]
- Shi, W.; Chang, J.; Wang, Y.; Bao, W.; Liu, X. Buzz Evolution Process Investigation of a two-ramp inlet with translating cowl. Aerosp. Sci. Technol. 2019, 84, 712–723. [Google Scholar] [CrossRef]
- Herrmann, D.; Siebe, F.; Gülhan, A. Pressure fluctuations (buzzing) and inlet performance of an airbreathing missile. J. Propuls. Power 2013, 29, 839–848. [Google Scholar] [CrossRef]
- Tan, H.; Sun, S.; Yin, Z. Oscillatory flows of rectangular hypersonic inlet unstart caused by downstream mass-flow choking. J. Propuls. Power 2009, 25, 138–147. [Google Scholar] [CrossRef]
- Chang, J.; Wang, L.; Bao, W.; Qin, J.; Niu, J.; Xue, W. Novel oscillatory patterns of Hypersonic Inlet Buzz. J. Propuls. Power 2012, 28, 1214–1221. [Google Scholar] [CrossRef]
- Soltani, M.; Daliri, A.; Younsi, J.; Farahani, M. Effects of bleed position on the stability of a supersonic inlet. J. Propuls. Power 2016, 32, 1153–1166. [Google Scholar] [CrossRef]
- Soltani, M.; Farahani, M. Experimental investigation of effects of Mach number on the flow instability in a supersonic inlet. Exp. Tech. 2011, 37, 46–54. [Google Scholar] [CrossRef]
- Chen, H.; Tan, H.J.; Zhang, Q.F.; Zhang, Y. Buzz flows in an external-compression inlet with partially isentropic compression. AIAA J. 2017, 55, 4286–4295. [Google Scholar] [CrossRef]
- Chen, H.; Tan, H.; Zhang, Q.; Zhang, Y. Throttling process and buzz mechanism of a supersonic inlet at Overspeed mode. AIAA J. 2018, 56, 1953–1964. [Google Scholar] [CrossRef]
- Chen, H.; Tan, H. Buzz flow diversity in a supersonic inlet ingesting strong shear layers. Aerosp. Sci. Technol. 2019, 95, 105471. [Google Scholar] [CrossRef]
- Nakayama, T.; Sato, T.; Akatsuka, M.; Hashimoto, A.; Kojima, T.; Taguchi, H. Investigation on shock oscillation phenomenon in a supersonic air inlet. In Proceedings of the 41st AIAA Fluid Dynamics Conference and Exhibit, Honolulu, HI, USA, 27–30 June 2011. [Google Scholar] [CrossRef]
- Lee, H.J.; Jeung, I.S. Experimental and numerical investigation on the Supersonic Inlet Buzz with angle of attack. In Proceedings of the 26th International Symposium on Shock Waves, Göttingen, Germany, 15–20 July 2009; Volume 2, pp. 1111–1116. [Google Scholar] [CrossRef]
- Chen, H.; Tan, H.; Liu, Y.; Zhang, Q. External-compression supersonic inlet free from violent buzz. AIAA J. 2019, 57, 2513–2523. [Google Scholar] [CrossRef]
- Grossman, I.J.; Bruce, P.J. Effect of confinement on shock wave-boundary layer interactions in rectangular intakes. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar] [CrossRef]
- Grossman, I.J.; Bruce, P.J. Confinement effects on regular–irregular transition in shock-wave–boundary-layer interactions. J. Fluid Mech. 2018, 853, 171–204. [Google Scholar] [CrossRef]
- Sridhar, T.; Chandrabose, G.; Thanigaiarasu, S. Numerical investigation of geometrical influence on isolator performance. Int. J. Theor. Appl. Mech. 2013, 2, 7–12. [Google Scholar]
- Chang, J.; Li, N.; Xu, K.; Bao, W.; Yu, D. Recent research progress on Unstart mechanism, detection and control of Hypersonic Inlet. Prog. Aerosp. Sci. 2017, 89, 1–22. [Google Scholar] [CrossRef]
- Tan, H.; Li, L.; Wen, Y.; Zhang, Q. Experimental investigation of the Unstart process of a generic hypersonic inlet. AIAA J. 2011, 49, 279–288. [Google Scholar] [CrossRef]
- Tan, H.; Guo, R. Experimental study of the unstable-unstarted condition of a hypersonic inlet at mach 6. J. Propuls. Power 2007, 23, 783–788. [Google Scholar] [CrossRef]
- Sekar, K.R.; Karthick, S.K.; Jegadheeswaran, S.; Kannan, R. On the unsteady throttling dynamics and scaling analysis in a typical hypersonic inlet–isolator flow. Phys. Fluids 2020, 32, 126104. [Google Scholar] [CrossRef]
- Liu, K.L.; Zhang, K.Y. Numerical investigation of 2-D hypersonic inlet starting characteristic caused by dynamic angle-of-attack. In Proceedings of the 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Nashville, TN, USA, 25–28 July 2010. [Google Scholar] [CrossRef]
- Zhang, Q.F.; Tan, H.J.; Sun, S.; Bu, H.X.; Rao, C.Y. Unstart of a hypersonic inlet with side compression caused by downstream choking. AIAA J. 2016, 54, 28–38. [Google Scholar] [CrossRef]
- Xu, S.; Wang, Y.; Wang, Z.; Fan, X.; Xiong, B. Experimental investigations of Hypersonic Inlet Unstart/restart process and hysteresis phenomenon caused by angle of attack. Aerosp. Sci. Technol. 2022, 126, 107621. [Google Scholar] [CrossRef]
- Chima, R. Analysis of Buzz in a Supersonic Inlet; NASA TM-2012-217612; NASA: Washington, DC, USA, 2012. [Google Scholar]
- Grenson, P.; Beneddine, S. Analysis of shock oscillations of an external compression supersonic inlet through unsteady numerical simulations. In Proceedings of the 2018 Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar] [CrossRef]
- Zhu, J.; Luo, W.; Wei, Y.; Yan, C.; You, Y. Acoustic modeling and vibration characteristics of Supersonic Inlet Buzz. Energies 2020, 13, 2048. [Google Scholar] [CrossRef]
- Wang, C.; Yang, X.; Xue, L.; Kontis, K.; Jiao, Y. Correlation Analysis of separation shock oscillation and wall pressure fluctuation in unstarted hypersonic inlet flow. Aerospace 2019, 6, 8. [Google Scholar] [CrossRef]
- Sterbentz, W.H.; Davids, J. Amplitude of Supersonic Diffuser Flow Pulsations; NACA TN 3572; NACA: Boston, MA, USA, 1955. [Google Scholar]
- Yeom, H.; Sung, H.; Yang, V. A numerical analysis of supersonic intake buzz in an axisymmetric ramjet engine. Int. J. Aeronaut. Space Sci. 2015, 16, 165–176. [Google Scholar] [CrossRef]
- Kwak, E.; Lee, S. Numerical Study of the effect of exit configurations on Supersonic Inlet Buzz. In Proceedings of the 31st AIAA Applied Aerodynamics Conference, San Diego, CA, USA, 24–27 June 2013. [Google Scholar] [CrossRef]
- Grenson, P.; Beneddine, S. Large-Eddy Simulation of a Supersonic Air Inlet in Subcritical Regime; AERO2020+1. 2021. Available online: https://hal.science/hal-03368456/ (accessed on 1 September 2023).
- Candon, S.; Loth, E.; Rybalko, M. Near-on-design unsteadiness in a supersonic low-boom inlet. J. Propuls. Power 2016, 32, 360–372. [Google Scholar] [CrossRef]
- Kurth, G.; Bauer, C. Air Intake Development for a mach 5+ throttleable ducted rocket propelled lower tier interceptor. In Proceedings of the 51st AIAA/SAE/ASEE Joint Propulsion Conference, Orlando, FL, USA, 27–29 July 2015. [Google Scholar] [CrossRef]
- Farahani, M.; Jaberi, A. Study of buzz phenomenon using visualization of external shock structure. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 233, 2690–2698. [Google Scholar] [CrossRef]
- Soltani, M.R.; Sepahi Younsi, J.; Daliri, A. Performance investigation of a supersonic air intake in the presence of the boundary layer suction. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 229, 1495–1509. [Google Scholar] [CrossRef]
- Sepahi-Younsi, J.; Soltani, M.; Abedi, M.; Masdari, M. Experimental investigation into the effects of Mach number and boundary-layer bleed on flow stability of a supersonic air intake. Sci. Iran. 2020, 27, 1197–1205. [Google Scholar] [CrossRef]
- K James, J.; Suryan, A.; Kim, H.D. Buzz characteristics and separation bubble dynamics in Supersonic Intake. Aerosp. Sci. Technol. 2021, 115, 106795. [Google Scholar] [CrossRef]
- Van, W.; David, M. Scramjet inlets. Scramjet Propuls. 2001, 189, 447–511. [Google Scholar] [CrossRef]
- Stephen, E.J.; Hoenisch, S.R.; Riggs, C.J.; Waddel, M.L.; Bolender, M.A.; McLaughlin, T.E. HIFiRE-6 unstart conditions at off-design mach numbers. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar] [CrossRef]
- Yuan, H.C.; Liang, D.W. Analysis of characteristics of restart performance for a hypersonic inlet. J. Propuls. Technol. 2016, 27, 390–398. [Google Scholar]
- Jiao, X.; Chang, J.; Wang, Z.; Yu, D. Mechanism study on local unstart of Hypersonic Inlet at high Mach number. AIAA J. 2015, 53, 3102–3112. [Google Scholar] [CrossRef]
- Jiao, X.; Chang, J.; Wang, Z.; Yu, D. Investigation of Hypersonic Inlet Pulse-starting characteristics at high Mach number. Aerosp. Sci. Technol. 2016, 58, 427–436. [Google Scholar] [CrossRef]
- Jiao, X.; Chang, J.; Wang, Z.; Yu, D. Hysteresis phenomenon of hypersonic inlet at high Mach number. Acta Astronaut. 2016, 128, 657–668. [Google Scholar] [CrossRef]
- Soltani, M.R.; Farahani, M. Effects of angle of attack on Inlet Buzz. J. Propuls. Power 2012, 28, 747–757. [Google Scholar] [CrossRef]
- NamKoung, H.; Hong, W.; Kim, J.; Yi, J.; Kim, C. Effects of angles of attack and throttling conditions on Supersonic Inlet Buzz. Int. J. Aeronaut. Space Sci. 2012, 13, 296–306. [Google Scholar] [CrossRef]
- Boychev, K.; Barakos, G.N.; Steijl, R. Numerical simulations of multiple shock wave boundary layer interactions. In Proceedings of the AIAA Scitech 2021 Forum, Virtual Event, 11–21 January 2021. [Google Scholar] [CrossRef]
- Herrmann, D.; Triesch, K. Experimental investigation of isolated inlets for high agile missiles. Aerosp. Sci. Technol. 2006, 10, 659–667. [Google Scholar] [CrossRef]
- Herrmann, D.; Triesch, K.; Gülhan, A. Experimental study of chin intakes for airbreathing missiles with high agility. J. Propuls. Power 2008, 24, 236–244. [Google Scholar] [CrossRef]
- Guo, S.; Gao, W.; Zhang, E.; Li, Z.; Yang, J. Effects of attack angle on starting performance of a hypersonic inlet. In Proceedings of the 30th International Symposium on Shock Waves 1, Nagoya, Japan, 9–14 July 2017; pp. 155–160. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, K. Experiment of dynamic angle-of-attack on a side wall compression scramjet inlet at mach 3.85. In Proceedings of the 17th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, San Francisco, CA, USA, 11–14 April 2011. [Google Scholar] [CrossRef]
- Zuo, F.; Molder, S.; Chen, G. Performance of wavecatcher intakes at angles of attack and sideslip. Chin. J. Aeronaut. 2021, 34, 244–256. [Google Scholar] [CrossRef]
- Sepahi-Younsi, J. Effects of boundary-layer bleed parameters on supersonic intake buzz. Aerosp. Sci. Technol. 2022, 120, 107246. [Google Scholar] [CrossRef]
- Sepahi-Younsi, J.; Esmaeili, S.; Forouzi Feshalami, B.; Pellerito, V.; Hassanalian, M. Performance enhancement of an external compression intake by the boundary layer suction. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019. [Google Scholar] [CrossRef]
- Petha Sethuraman, V.R.; Kim, T.H.; Kim, H.D. Effects of back pressure perturbation on shock train oscillations in a rectangular duct. Acta Astronaut. 2021, 179, 525–535. [Google Scholar] [CrossRef]
- Sethuraman, V.R.P.; Kim, T.H.; Kim, H.D. Control of the oscillations of shock train using boundary layer suction. Aerosp. Sci. Technol. 2021, 118, 107012. [Google Scholar] [CrossRef]
- Reza Maadi, S.; Sepahi-Younsi, J. Effects of bleed type on the performance of a supersonic intake. Exp. Therm. Fluid Sci. 2022, 132, 110568. [Google Scholar] [CrossRef]
- Slater, J.W.; Saunders, J.D. Modeling of fixed-exit porous bleed systems for supersonic inlets. J. Propuls. Power 2010, 26, 193–202. [Google Scholar] [CrossRef]
- Slater, J.W. Improvements in modeling 90-degree bleed holes for supersonic inlets. J. Propuls. Power 2012, 28, 773–781. [Google Scholar] [CrossRef]
- Choe, Y.; Kim, C.; Kim, K. Effects of optimized bleed system on Supersonic Inlet Performance and buzz. J. Propuls. Power 2020, 36, 211–222. [Google Scholar] [CrossRef]
- Giehler, J.; Grenson, P.; Bur, R. Porous Bleed Boundary Conditions for Shock-Induced Boundary Layer Separation Control. In Proceedings of the 56th 3AF International Conference AERO2022, Toulose, France, 28–30 March 2022. [Google Scholar]
- Wang, C.; Eri, Q.; Kong, B.; Wang, Y.; Ding, W. Novel simplified numerical simulation method for modeling bleed holes in supersonic inlets. AIAA J. 2022, 60, 6926–6939. [Google Scholar] [CrossRef]
- Soltani, M.R.; Sepahi-Younsi, J.; Farahani, M. Effects of boundary-layer bleed parameters on supersonic intake performance. J. Propuls. Power 2015, 31, 826–836. [Google Scholar] [CrossRef]
- Kang, K.; Kato, N.; Im, S.; Do, H. Fast-acting boundary-layer suction control of unstarting flows in an ethylene-fueled dual-mode scramjet. AIAA J. 2021, 59, 3106–3117. [Google Scholar] [CrossRef]
- Suryanarayana, G.K.; Dubey, R. Image analyses of supersonic air-intake buzz and control by natural ventilation. J. Vis. 2017, 20, 711–727. [Google Scholar] [CrossRef]
- Suryanarayana, G.K.; Dubey, R. Performance enhancement of a ramjet air intake by passive bleed of Boundary Layer. J. Spacecr. Rocket. 2019, 56, 875–886. [Google Scholar] [CrossRef]
- Ogura, S.; Fujii, M.; Hoshiya, Y.; Fujimori, Y.; Sato, T.; Taguchi, H.; Kojima, T.; Oki, J. Experimental study of high-speed air intake performance by side clearance. Aerosp. Sci. Technol. 2022, 123, 107439. [Google Scholar] [CrossRef]
- Griggs, C.F. An Investigation of Two Methods of Suppressing Shock Oscillation Ahead of Conical Centre-body Intakes; HER MAJESTY’S STATION OFFICE. 1962; C.P. No. 605. Available online: https://reports.aerade.cranfield.ac.uk/bitstream/handle/1826.2/618/arc-cp-0605.pdf?sequence=1 (accessed on 1 September 2023).
- Ferrero, A. Control of a supersonic inlet in off-design conditions with plasma actuators and bleed. Aerospace 2020, 7, 32. [Google Scholar] [CrossRef]
- Loth, E.; Roos, F.; Davis, D.; Mace, J.; Jaiman, R.; White, S.; Dutton, C.; Dutton, C. Mesoflap and Bleed Flow Control for a mach 2 inlet. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 5–8 January 2004. [Google Scholar] [CrossRef]
- Karbasizadeh, M.; Babaei, A.; Bazazzadeh, M.; Menshadi, M. Optimization of slot geometry in shock wave boundary layer interaction phenomenon by using CFD–ann–ga cycle. Aerosp. Sci. Technol. 2017, 71, 163–171. [Google Scholar] [CrossRef]
- Zhang, J.; Yuan, H.; Wang, Y.; Huang, G. Experiment and numerical investigation of flow control on a Supersonic Inlet Diffuser. Aerosp. Sci. Technol. 2020, 106, 106182. [Google Scholar] [CrossRef]
- Yuan, H.; Liu, F.; Wang, X.; Zhou, Z. Design and analysis of a supersonic axisymmetric inlet based on controllable bleed slots. Aerosp. Sci. Technol. 2021, 118, 107008. [Google Scholar] [CrossRef]
- Yuan, H.; Zhang, J.; Wang, Y.; Huang, G. Experimental and numerical investigation on a supersonic inlet with large bleed window. Aeronaut. J. 2021, 126, 425–449. [Google Scholar] [CrossRef]
- Cai, F.; Huang, X. Study on self-excited oscillation suppression of supersonic inlet based on parallel cavity. Front. Energy Res. 2022, 10, 884540. [Google Scholar] [CrossRef]
- Babinsky, H.; Ogawa, H. SBLI control for wings and inlets. Shock Waves 2008, 18, 89–96. [Google Scholar] [CrossRef]
- Babinsky, H. Understanding Micro-Ramp Control of Supersonic Shock Wave Boundary Layer Interactions; Technical Report 0074; Air Force Research Laboratory, United States Air Force: Wright-Patterson Air Force Base, OH, USA, 2007. [Google Scholar] [CrossRef]
- Titchener, N.; Babinsky, H. A review of the use of vortex generators for mitigating shock-induced separation. Shock Waves 2015, 25, 473–494. [Google Scholar] [CrossRef]
- Vyas, M.; Hirt, S.; Chima, R.; Davis, D.; Wayman, T. Experimental investigation of micro vortex generators on a low boom supersonic inlet (invited). In Proceedings of the 29th AIAA Applied Aerodynamics Conference, Honolulu, HI, USA, 27–30 June 2011. [Google Scholar] [CrossRef]
- Herges, T.; Dutton, J.; Elliott, G. High-speed schlieren analysis of Buzz in a relaxed-compression supersonic inlet. In Proceedings of the 48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Atlanta, GA, USA, 30 July–1 September 2012. [Google Scholar] [CrossRef]
- Baydar, E.; Lu, F.K.; Slater, J.W. Vortex Generators in a Two-Dimensional External-Compression Supersonic Inlet. J. Propuls. Power 2018, 34. [Google Scholar] [CrossRef]
- Castner, R.S.; Simerly, S.; Rankin, M. Supersonic Inlet test for a Quiet Supersonic Transport Technology Demonstrator in the NASA Glenn 8-foot by 6-foot supersonic wind tunnel. In Proceedings of the 2018 Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar] [CrossRef]
- Gao, W.; Li, Z.; Yang, J.; Zeng, Y. Effects of trips on the oscillatory flow of an axisymmetric hypersonic inlet with downstream throttle. Chin. J. Aeronaut. 2018, 31, 225–236. [Google Scholar] [CrossRef]
- Gao, W.; Chen, J.; Liu, C.; Li, Z.; Yang, J.; Zeng, Y. Effects of vortex generators on unsteady unstarted flows of an axisymmetric inlet with nose bluntness. Aerosp. Sci. Technol. 2020, 104, 106021. [Google Scholar] [CrossRef]
- Gahlot, N.K.; Singh, N.K. Control of shock-induced separation inside air intake by vortex generators. Heat Transf. 2021, 51, 766–788. [Google Scholar] [CrossRef]
- Valdivia, A.; Yuceil, K.B.; Wagner, J.L.; Clemens, N.T.; Dolling, D.S. Control of Supersonic Inlet-isolator unstart using active and passive vortex generators. AIAA J. 2014, 52, 1207–1218. [Google Scholar] [CrossRef]
- Teh, E.J.; Johansen, C. Effect of particle momentum transfer on an oblique-shock-wave/laminar-boundary-layer interaction. Acta Astronaut. 2016, 128, 431–439. [Google Scholar] [CrossRef]
- Jagannathan, R.; Hinman, W.S.; Johansen, C. Performance assessment of supersonic and hypersonic intake systems with nano-particle injection. Acta Astronaut. 2019, 159, 609–621. [Google Scholar] [CrossRef]
- Titchener, N. An Experimental Investigation of Flow Control for Supersonic Inlets. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2013. [Google Scholar]
- Narayanaswamy, V.; Raja, L.L.; Clemens, N.T. Control of unsteadiness of a shock wave/turbulent boundary layer interaction by using a pulsed-plasma-jet actuator. Phys. Fluids 2012, 24, 076101. [Google Scholar] [CrossRef]
- Jagannathan, R.; Johansen, C. Stability Analysis of high-speed intakes with nanoparticle injection. AIAA J. 2021, 59, 1786–1797. [Google Scholar] [CrossRef]
- Wang, J.; Feng, L. Plasma actuator. In Flow Control Techniques and Applications; Cambridge Aerospace Series; Cambridge University Press: Cambridge, UK, 2018; pp. 206–245. [Google Scholar] [CrossRef]
- Grossman, K.; Bohdan, C.; VanWie, D. Sparkjet actuators for Flow Control. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003. [Google Scholar] [CrossRef]
- Grossman, K.; Cybyk, B.; VanWie, D.; Rigling, M. Characterization of SparkJet actuators for Flow Control. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 5–8 January 2004. [Google Scholar] [CrossRef]
- Narayanaswamy, V.; Shin, J.; Clemens, N.; Raja, L. Investigation of plasma-generated jets for supersonic flow control. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008. [Google Scholar] [CrossRef]
- Greene, B.R.; Clemens, N.T.; Magari, P.; Micka, D. Control of mean separation in shock boundary layer interaction using pulsed plasma jets. Shock Waves 2014, 25, 495–505. [Google Scholar] [CrossRef]
- Webb, N.; Clifford, C.; Samimy, M. Control of oblique shock wave/boundary layer interactions using plasma actuators. Exp. Fluids 2013, 54, 1545. [Google Scholar] [CrossRef]
- Leonov, S.B.; Yarantsev, D.A. Near-surface electrical discharge in supersonic airflow: Properties and flow control. J. Propuls. Power 2008, 24, 1168–1181. [Google Scholar] [CrossRef]
- Leonov, S.; Falempin, F.; Yarantsev, D.; Firsov, A.; Miller, A. Active steering of shock waves in compression ramp by nonuniform plasma. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010. [Google Scholar] [CrossRef]
- Yan, H.; Liu, F.; Xu, J.; Xue, Y. Study of oblique shock wave control by surface arc discharge plasma. AIAA J. 2017, 56, 532–541. [Google Scholar] [CrossRef]
- Falempin, F.; Firsov, A.A.; Yarantsev, D.A.; Goldfeld, M.A.; Timofeev, K.; Leonov, S.B. Plasma control of shock wave configuration in off-design mode of M = 2 Inlet. Exp. Fluids 2015, 56, 54. [Google Scholar] [CrossRef]
- Liu, F.; Yan, H.; Zhan, W.; Xue, Y. Effects of steady and pulsed discharge arcs on shock wave control in mach 2.5 flow. Aerosp. Sci. Technol. 2019, 93, 105330. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, H.; Liang, H.; Guo, S. Plasma-based experimental investigation of double compression ramp shock wave/boundary layer interaction control. J. Phys. D Appl. Phys. 2022, 55, 325202. [Google Scholar] [CrossRef]
- Pham, H.S.; Shoda, T.; Tamba, T.; Iwakawa, A.; Sasoh, A. Impacts of laser energy deposition on flow instability over double-cone model. AIAA J. 2017, 55, 2992–3000. [Google Scholar] [CrossRef]
- Pham, H.S.; Myokan, M.; Tamba, T.; Iwakawa, A.; Sasoh, A. Effects of repetitive laser energy deposition on supersonic duct flows. AIAA J. 2018, 56, 542–553. [Google Scholar] [CrossRef]
- Russell, A.; Myokan, M.; Bottini, H.; Sasoh, A.; Zare-Behtash, H.; Kontis, K. Application of laser energy deposition to improve performance for high speed intakes. Propuls. Power Res. 2020, 9, 15–25. [Google Scholar] [CrossRef]
- Wang, H.; Hu, W.; Xie, F.; Li, J.; Jia, Y.; Yang, Y. Control effects of a high-frequency pulsed discharge on a hypersonic separated flow. Phys. Fluids 2022, 34, 066102. [Google Scholar] [CrossRef]
- Sasoh, A.; Myokan, M.; Kubota, A.; Maeda, K.; Wu, Y.L. Impacts of repetitive laser pulse energy deposition on supersonic intakes. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar] [CrossRef]
- Myokan, M.; Kubota, A.; Iwakawa, A.; Sasoh, A. Repetitive energy deposition at a supersonic intake in subcritical and Buzz Modes. AIAA J. 2020, 58, 107–117. [Google Scholar] [CrossRef]
- MacManus, D.G.; Chiereghin, N.; Prieto, D.G.; Zachos, P. Complex aeroengine intake ducts and dynamic distortion. AIAA J. 2017, 55, 2395–2409. [Google Scholar] [CrossRef]
- Gil-Prieto, D.; MacManus, D.G.; Zachos, P.K.; Tanguy, G.; Menzies, K.R. Convoluted intake distortion measurements using stereo particle image velocimetry. AIAA J. 2017, 55, 1878–1892. [Google Scholar] [CrossRef]
- Migliorini, M.; Zachos, P.K.; MacManus, D.G.; Haladuda, P. S-duct flow distortion with non-uniform inlet conditions. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2023, 237, 357–373. [Google Scholar] [CrossRef]
- Sullins, G.; McLafferty, G. Experimental results of shock trains in rectangular ducts. In Proceedings of the AlAA 4th International Aerospace Planes Conference, Orlando, FL, USA, 1–4 December 1992. [Google Scholar] [CrossRef]
- Billig, F.S.; Pandolfini, P.P.; Corda, S. Design Techniques for Dual Mode Ram Scramjet Combustors. In Proceedings of the AGARD 75th Symposium of Hypersonic Combined Cycle Propulsion, Madrid, Spain, 28 May–1 June 1990; pp. 1–20. [Google Scholar]
- Matsuo, K.; Miyazato, Y.; Kim, H. Shock train and pseudo-shock phenomena in internal gas flows. Prog. Aerosp. Sci. 1999, 35, 33–100. [Google Scholar] [CrossRef]
- Sullins, G.A. Demonstration of mode transition in a scramjet combustor. J. Propuls. Power 1993, 9, 515–520. [Google Scholar] [CrossRef]
- Hunt, R.L.; Gamba, M. On the origin and propagation of perturbations that cause shock train inherent unsteadiness. J. Fluid Mech. 2018, 861, 815–859. [Google Scholar] [CrossRef]
- Gaitonde, D.V. Progress in shock wave/boundary layer interactions. Prog. Aerosp. Sci. 2015, 72, 80–99. [Google Scholar] [CrossRef]
- Gnani, F.; Zare-Behtash, H.; Kontis, K. Pseudo-shock waves and their interactions in high-speed intakes. Prog. Aerosp. Sci. 2016, 82, 36–56. [Google Scholar] [CrossRef]
- Huang, H.; Tan, H.; Li, F.; Tang, X.; Qin, Y.; Xie, L.; Xu, Y.; Li, C.; Gao, S.; Zhang, Y.; et al. A review of the shock-dominated flow in a hypersonic inlet/isolator. Prog. Aerosp. Sci. 2023, 143, 100952. [Google Scholar] [CrossRef]
- Gnani, F. Investigation on Supersonic High-Speed Internal Flows and the Tools to Study Their Interactions. Ph.D. Thesis, University of Glasgow, Glasgow, UK, 2018. [Google Scholar]
- Sajben, M.; Kroutil, J.C. Effects of initial boundary-layer thickness on transonic diffuser flows. AIAA J. 1981, 19, 1386–1393. [Google Scholar] [CrossRef]
- Su, W.; Zhang, K. Back-pressure effects on the hypersonic inlet-isolator Pseudoshock motions. J. Propuls. Power 2013, 29, 1391–1399. [Google Scholar] [CrossRef]
- Hsieh, T.; Coakley, T. Downstream boundary effects on the frequency of self-excited oscillations in Transonic Diffuser flows. In Proceedings of the 25th AIAA Aerospace Sciences Meeting, Reno, NV, USA, 24–26 March 1987. [Google Scholar] [CrossRef]
- Gawehn, T.; Gülhan, A.; Al-Hasan, N.S.; Schnerr, G.H. Experimental and numerical analysis of the structure of pseudo-shock systems in Laval nozzles with parallel side walls. Shock Waves 2010, 20, 297–306. [Google Scholar] [CrossRef]
- Ligrani, P.; Cox, M.; Goethals, K. Spatial coherence of low-frequency unsteadiness associated with a normal shock wave. Aerosp. Sci. Technol. 2021, 112, 106637. [Google Scholar] [CrossRef]
- Pirozzoli, S.; Larsson, J.; Nichols, J.; Bernardini, M.; Morgan, B.; Lele, S. Analysis of unsteady effects in shock/boundary layer interactions. In Proceedings of the Summer Program, Stanford, CA, USA, 23–26 July 2010; pp. 153–164. [Google Scholar]
- Hou, W.; Chang, J.; Xie, Z.; Wang, Y.; Wu, L.; Bao, W. Behavior and flow mechanism of shock train self-excited oscillation influenced by background waves. Acta Astronaut. 2020, 166, 29–40. [Google Scholar] [CrossRef]
- Ikui, T.; Matsuo, K.; Nagai, M.; Honjo, M. Oscillation phenomena of pseudo-shock waves. Bull. JSME 1974, 17, 1278–1285. [Google Scholar] [CrossRef]
- Yamane, R.; Kondo, E.; Tomita, Y.; Sakae, N. Vibration of pseudo-shock in straight duct: 1st report, fluctuation of Static Pressure. Trans. Jpn. Soc. Mech. Eng. Ser. B 1983, 49, 2326–2335. [Google Scholar] [CrossRef]
- Sugiyama, H.; Takeda, H.; Zhang, J.; Okuda, K.; Yamagishi, H. Locations and oscillation phenomena of pseudo-shock waves in a straight rectangular duct. JSME Int. J. Ser. 2 Fluids Eng. Heat Transf. Power Combust. Thermophys. Prop. 1988, 31, 9–15. [Google Scholar] [CrossRef]
- Lustwerk, F. The Influence of Boundary Layer on the “Normal” Shock Configuration; Massachusetts Institute of Technology, Guided Missiles Program: Cambridge, MA, USA, 1950. [Google Scholar]
- Fiévet, R.; Koo, H.; Raman, V.; Auslender, A.H. Numerical investigation of shock-train response to inflow boundary-layer variations. AIAA J. 2017, 55, 2888–2901. [Google Scholar] [CrossRef]
- Bruce, P.J.; Babinsky, H. Unsteady Shock Wave Dynamics. J. Fluid Mech. 2008, 603, 463–473. [Google Scholar] [CrossRef]
- Wang, C.; Cheng, C.; Cheng, K.; Xue, L. Unsteady behavior of oblique shock train and boundary layer interactions. Aerosp. Sci. Technol. 2018, 79, 212–222. [Google Scholar] [CrossRef]
- Klomparens, R.; Driscoll, J.F.; Gamba, M. Response of a shock train to downstream back pressure forcing. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar] [CrossRef]
- Tan, H.J.; Sun, S.; Huang, H.X. Behavior of shock trains in a hypersonic inlet/isolator model with complex background waves. Exp. Fluids 2012, 53, 1647–1661. [Google Scholar] [CrossRef]
- Waltrup, P.J.; Billig, F.S. Prediction of precombustion wall pressure distributions in scramjet engines. J. Spacecr. Rocket. 1973, 10, 620–622. [Google Scholar] [CrossRef]
- Deng, R.; Kim, H.D.; Chen, Q. Effects of back pressure fluctuation on pseudo-shock waves in a rectangular duct. J. Mech. Sci. Technol. 2020, 34, 4649–4655. [Google Scholar] [CrossRef]
- Cheng, C.; Wang, C.; Cheng, K. Response of an oblique shock train to downstream periodic pressure perturbations. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 233, 57–70. [Google Scholar] [CrossRef]
- Wang, Z.; Chang, J.; Wu, G.; Yu, D. Experimental investigation of shock train behavior in a supersonic isolator. Phys. Fluids 2021, 33, 046103. [Google Scholar] [CrossRef]
- Leonard, M.D.; Narayanaswamy, V. Investigation of shock dynamics in an Axisymmetric Inlet/isolator with attached boundary layers. J. Fluid Mech. 2020, 908, A42. [Google Scholar] [CrossRef]
- Bur, R.; Benay, R.; Galli, A.; Berthouze, P. Experimental and numerical study of forced shock-wave oscillations in a transonic channel. Aerosp. Sci. Technol. 2006, 10, 265–278. [Google Scholar] [CrossRef]
- Xiong, B.; Wang, Z.; Fan, X.; Wang, Y. Experimental study on the flow separation and self-excited oscillation phenomenon in a rectangular duct. Acta Astronaut. 2017, 133, 158–165. [Google Scholar] [CrossRef]
- Xiong, B.; Fan, X.; Wang, Z.; Tao, Y. Analysis and modelling of Unsteady Shock Train motions. J. Fluid Mech. 2018, 846, 240–262. [Google Scholar] [CrossRef]
- Koo, H.; Raman, V. Large-eddy simulation of a Supersonic Inlet-Isolator. AIAA J. 2012, 50, 1596–1613. [Google Scholar] [CrossRef]
- Jiao, X.; Chang, J.; Wang, Z.; Yu, D. Periodic forcing of a shock train in a scramjet inlet-isolator at Overspeed Condition. Acta Astronaut. 2018, 143, 244–254. [Google Scholar] [CrossRef]
- Fan, X.; Bing, X.; Wang, Y.; Yuan, T. Experimental study on the self-excited oscillation and the forced oscillation of shock train in a rectangular isolator. In Proceedings of the 21st AIAA International Space Planes and Hypersonics Technologies Conference, Xiamen, China, 6–9 March 2017. [Google Scholar] [CrossRef]
- Hou, W.; Chang, J.; Wang, Y.; Kong, C.; Bao, W. Experimental study on the forced oscillation of shock train in an isolator with background waves. Aerosp. Sci. Technol. 2020, 106, 106129. [Google Scholar] [CrossRef]
- Wang, Z.; Chang, J.; Hou, W.; Yu, D. Propagation of shock-wave/boundary-layer interaction unsteadiness in attached and separated flows. AIP Adv. 2020, 10, 105011. [Google Scholar] [CrossRef]
- Wang, Z.; Chang, J.T.; Hou, W.X.; Yu, D.R. Low-frequency unsteadiness of shock-wave/boundary-layer interaction in an isolator with background waves. Phys. Fluids 2020, 32, 056105. [Google Scholar] [CrossRef]
- Babinsky, H.; Oorebeek, J.; Cottingham, T. Corner effects in reflecting oblique shock-wave/boundary-layer interactions. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar] [CrossRef]
- Wang, B.; Sandham, N.D.; Hu, Z.; Liu, W. Numerical study of oblique shock-wave/boundary-layer interaction considering sidewall effects. J. Fluid Mech. 2015, 767, 526–561. [Google Scholar] [CrossRef]
- Geerts, J.S.; Yu, K.H. Shock train/boundary-layer interaction in rectangular isolators. AIAA J. 2016, 54, 3450–3464. [Google Scholar] [CrossRef]
- Huang, H.; Tan, H.; Sun, S.; Ling, Y. Evolution of supersonic corner vortex in a hypersonic inlet/isolator model. Phys. Fluids 2016, 28, 126101. [Google Scholar] [CrossRef]
- Huang, H.; Sun, S.; Tan, H.; Ning, L.; Wang, J. Characterization of two typical unthrottled flows in hypersonic inlet/Isolator Models. J. Aircr. 2015, 52, 1715–1721. [Google Scholar] [CrossRef]
- Morajkar, R.R.; Klomparens, R.L.; Eagle, W.E.; Driscoll, J.F.; Gamba, M.; Benek, J.A. Relationship between intermittent separation and vortex structure in a three-dimensional shock/boundary-layer interaction. AIAA J. 2016, 54, 1862–1880. [Google Scholar] [CrossRef]
- Liu, X.; Liang, J.; Wang, Y. Flow mechanism in a hypersonic sidewall compression inlet with a rectangular-to-circular isolator. J. Spacecr. Rocket. 2016, 53, 549–557. [Google Scholar] [CrossRef]
- Huang, H.x.; Tan, H.j.; Sun, S.; Sheng, F.j. Unthrottled flows with complex background waves in curved isolators. AIAA J. 2017, 55, 2942–2955. [Google Scholar] [CrossRef]
- Huang, H.; Tan, H.; Sun, S.; Wang, Z. Behavior of Shock Train in Curved Isolators with Complex Background Waves. AIAA J. 2018, 56, 329–341. [Google Scholar] [CrossRef]
- Liang, G.; Huang, H.; Tan, H.; Luo, Z.; Tang, X.; Li, C.; Cai, J. Shock train/glancing shock/boundary layer interaction in a curved isolator with sidewall contraction. Phys. Fluids 2022, 34, 116106. [Google Scholar] [CrossRef]
- Bowditch, D.; Coltrin, R. A survey of Inlet/engine distortion compatibility. In Proceedings of the 19th Joint Propulsion Conference, Seattle, WA, USA, 27–29 June 1983. [Google Scholar] [CrossRef]
- Doll, U.; Migliorini, M.; Baikie, J.; Zachos, P.K.; Röhle, I.; Melnikov, S.; Steinbock, J.; Dues, M.; Kapulla, R.; MacManus, D.G.; et al. Non-intrusive flow diagnostics for Unsteady Inlet Flow Distortion Measurements in novel aircraft architectures. Prog. Aerosp. Sci. 2022, 130, 100810. [Google Scholar] [CrossRef]
- Davis, M.; Hale, A.; Beale, D. An argument for enhancement of the current inlet distortion ground test practice for aircraft gas turbine engines. J. Turbomach. 2002, 124, 235–241. [Google Scholar] [CrossRef]
- Young, P. Propulsion controls on the Concorde. J. R. Aeronaut. Soc. 1966, 70, 863–881. [Google Scholar] [CrossRef]
- Bissinger, N.C.; Breuer, T. Basic principles—Gas turbine compatibility—Intake aerodynamic aspects. In Encyclopedia of Aerospace Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010; pp. 1–10. [Google Scholar] [CrossRef]
- Rademakers, R.P.; Bindl, S.; Niehuis, R. Effects of flow distortions as they occur in S-duct inlets on the performance and stability of a jet engine. J. Eng. Gas Turbines Power 2015, 138, 022605. [Google Scholar] [CrossRef]
- Berens, T.M.; Delot, A.; Chevalier, M.; van Muijden, J. Numerical simulations for high offset intake diffuser flows. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar] [CrossRef]
- Fiola, C.; Agarwal, R.K. Simulation of secondary and separated flow in diffusing s ducts. J. Propuls. Power 2015, 31, 180–191. [Google Scholar] [CrossRef]
- Chiereghin, N.; MacManus, D.; Savill, M.; Dupuis, R. Dynamic distortion simulations for curved aeronautical intakes. In Proceedings of the Applied Aerodynamics Conference 2014 (RAeS): Advanced Aero Concepts, Design and Operations, Bristol, UK, 22–24 July 2014. [Google Scholar]
- Gil-Prieto, D.; MacManus, D.G.; Zachos, P.K.; Tanguy, G.; Wilson, F.; Chiereghin, N. Delayed detached-eddy simulation and particle image velocimetry investigation of S-Duct Flow Distortion. AIAA J. 2017, 55, 1893–1908. [Google Scholar] [CrossRef]
- Gil-Prieto, D. Unsteady Flow Distortion in Complex Aero-Engine Intakes. Ph.D. Thesis, Cranfield University, Cranfield, UK, 2018. [Google Scholar]
- Zachos, P.K.; Frascella, M.; MacManus, D.G.; Gil-Prieto, D. Pressure Flowfield and inlet flow distortion metrics reconstruction from velocity data. AIAA J. 2017, 55, 2929–2941. [Google Scholar] [CrossRef]
- Breuer, T.; Bissinger, N.C. Basic Principles—Gas Turbine Compatibility—Gas Turbine Aspects; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2010. [Google Scholar] [CrossRef]
- Giuliani, J.E.; Chen, J.P. Fan response to boundary-layer ingesting inlet distortions. AIAA J. 2016, 54, 3232–3243. [Google Scholar] [CrossRef]
- Migliorini, M.; Zachos, P.; MacManus, D. An assessment on the unsteady flow distortion generated by an S-duct intake. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019. [Google Scholar] [CrossRef]
- Migliorini, M.; Zachos, P.; MacManus, D. The impact of inlet boundary layer thickness on the unsteady aerodynamics of S-Duct intakes. In Proceedings of the AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 19–22 August 2019. [Google Scholar] [CrossRef]
- Soltani, M.R.; Daliri, A.; Sepahi Younsi, J. Effects of shock wave/boundary-layer interaction on performance and stability of a mixed-compression inlet. Sci. Iran. 2016, 23, 1811–1825. [Google Scholar] [CrossRef]
- Migliorini, M.; Szymanski, A.; Zachos, P.K.; MacManus, D.; Martin, P.G. Design of a high-speed intake distortion simulator for propulsion integration research. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA; Online, 23–27 January 2023. [Google Scholar] [CrossRef]



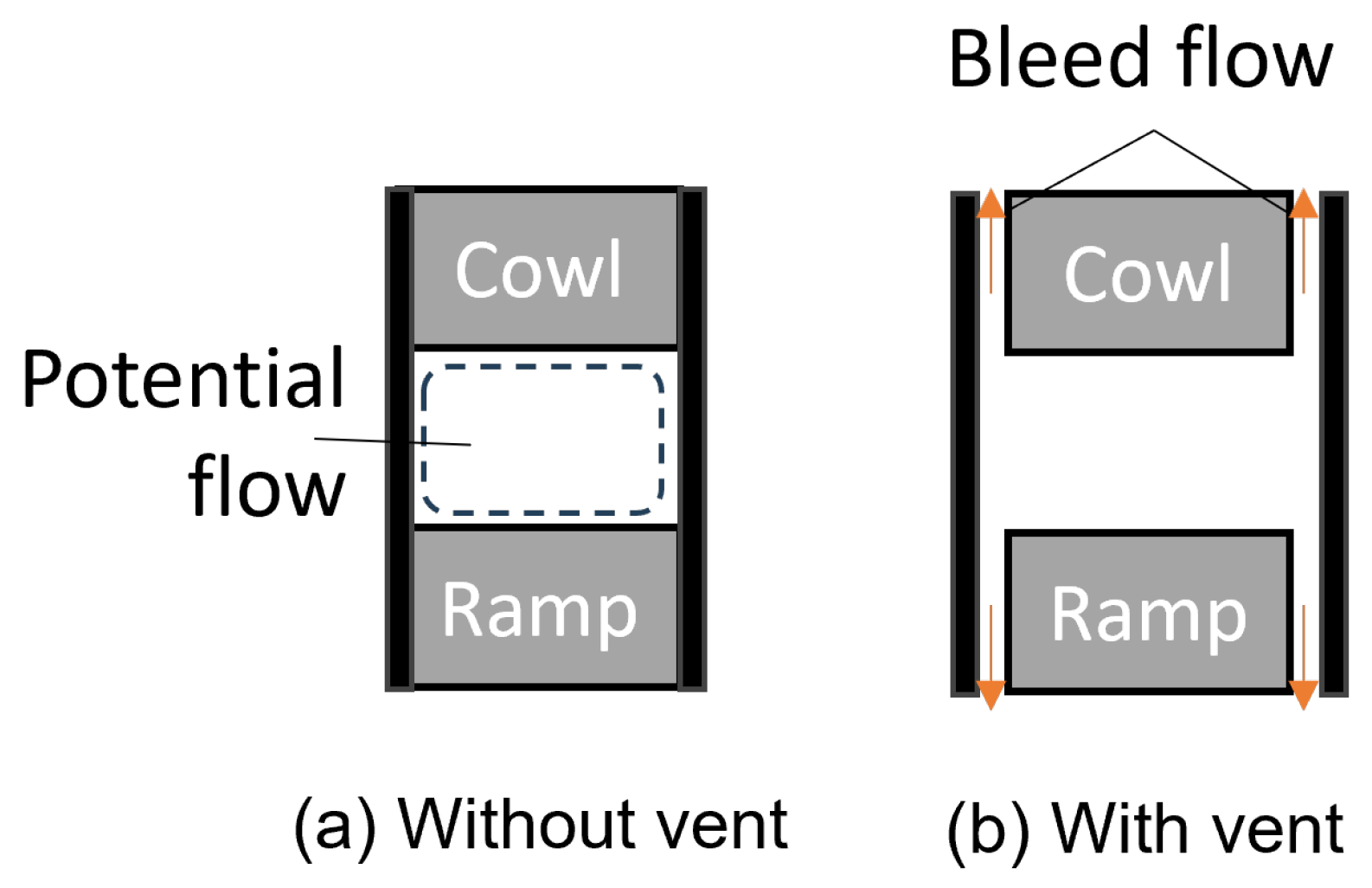



| Reference | Research Topic | Method (E/N) | Model | Onset Mach Number | Key findings |
|---|---|---|---|---|---|
| Jagannathan and Johansen [145] | Effect of particle injection on Ferri instability and unstart | N (2D) | External compression | 2.0 | Particles promoted the growth of separation and increased buzz frequency, demonstrating the importance of the location where the particle momentum and energy exchange occurs. |
| Webb et al. [151] | Effect of LAFPA on controlling SBLI | E | Compression Ramp | 2.33 | LAFPA did not control the SBLI through instability manipulation, but through the interaction between the LAFPA and the upstream boundary layer, which caused an increase to the thickness of the boundary layer displacement |
| Falempin et al. [155] | Effect of plasma discharge on shock configuration at off-design conditions | E and N | Two-dimensional mixed compression intake | 2.0 | At off-design conditions, the plasma discharge can increase the air mass flow rate with moderate deposition of power, illustrating the importance on the power deposition. With a further power increase, the MFR decreases due to the shock angle elevation increasing the boundary layer thickness on the compression ramp. |
| Pham et al. [159] | Effect of repetitive laser energy deposition on suppressing instabilities within intake at off-design conditions | E | Axisymmetric intake | 1.92 | Repetitive energy deposition can reduce the separation length and suppress the shock system oscillation at a deposition frequency of 60 kHz. |
| Russell et al. [160] | Effect of laser energy deposition on improving the intake performance at off-design conditions | E | Axisymmetric intake | 1.92 | Laser energy deposition with a deposition frequency of 10 kHz is able to reduce the flow separation and, in turn, improve the intake pressure recovery. The laser frequency is a determining factor in maximizing the length of the attached flow. At higher deposition frequencies, the pressure recovery shows a decline. |
| Reference | Research Topic | Method (E/N) | Model | Onset Mach Number | Key Findings |
|---|---|---|---|---|---|
| Hunt and Gamba [171] | Origin of shock train’s unsteadiness | E | Isolator | 2.0 | Background waves affect the leading shock. Vortices generated from the shear layer affect the downstream shocks. |
| Xiong et al. [198] | Characterization of self-excited shock train oscillations | E | Rectangular duct | 3.0 | The shock train adjusts its moving speed relative to the upstream Mach number to compensate for the fluctuating back pressure. |
| Wang et al. [204] | Characterization of low-frequency unsteadiness | E and N | Isolator | 2.94 | Three oscillation types were observed. Feedback mechanism of the shock train oscillation was related to the propagation of acoustic waves (associated with oscillation Type I), the duct volume effect, and Kantrowitz limits (Type II). Type III oscillation is an independent process dominated by the shock motion. |
| Jiao et al. [201] | Response of the shock train to forcing back pressure | N | 2D inlet- isolator | 7.0 | Phase difference between back pressure fluctuation and shock train oscillation, especially for high forcing frequencies, where the phase of the shock train is opposite to the fluctuating back pressure. |
| Reference | Method (E/N) | Geometry | MAIP | Key Findings |
|---|---|---|---|---|
| Chiereghin et al. [224] | N | H/L = 0.49 | 0.39 | Higher offset configuration gives rise to pressure fluctuations in the central part of the AIP |
| Gil-Prieto et al. [225] | N | H/L = 0.49; 0.27 | 0.27; 0.60 | Vertical swirl switching originates from the centerline shear layer. Lateral swirl switching promotes bulk swirl events |
| Gil-Prieto et al. [24] | E (SPIV) | H/L = 0.49; 0.27 | 0.6 | Vertical swirl switching promotes streamwise and in-plane velocity fluctuations |
| McLelland et al. [23] | E (TR-PIV) | H/L = 0.49 | 0.27 | Greatest contribution to flow unsteadiness in spectral band St = 0.4–0.6 |
| Migliorini et al. [231] | E (TR-PIV) | H/D = 2.44 | 0.27 | Boundary layer orientation of 90 increases the probability of distortion events giving rise to the probability of compatibility issues |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Philippou, A.L.; Zachos, P.K.; MacManus, D.G. Aerodynamic Instabilities in High-Speed Air Intakes and Their Role in Propulsion System Integration. Aerospace 2024, 11, 75. https://doi.org/10.3390/aerospace11010075
Philippou AL, Zachos PK, MacManus DG. Aerodynamic Instabilities in High-Speed Air Intakes and Their Role in Propulsion System Integration. Aerospace. 2024; 11(1):75. https://doi.org/10.3390/aerospace11010075
Chicago/Turabian StylePhilippou, Aristia L., Pavlos K. Zachos, and David G. MacManus. 2024. "Aerodynamic Instabilities in High-Speed Air Intakes and Their Role in Propulsion System Integration" Aerospace 11, no. 1: 75. https://doi.org/10.3390/aerospace11010075
APA StylePhilippou, A. L., Zachos, P. K., & MacManus, D. G. (2024). Aerodynamic Instabilities in High-Speed Air Intakes and Their Role in Propulsion System Integration. Aerospace, 11(1), 75. https://doi.org/10.3390/aerospace11010075






