Evaluation of the Multiaxial Fatigue Life of Electro-Mechanical Actuator for Aircraft Blade Pitch Control Based on Certification Standards
Abstract
:1. Introduction
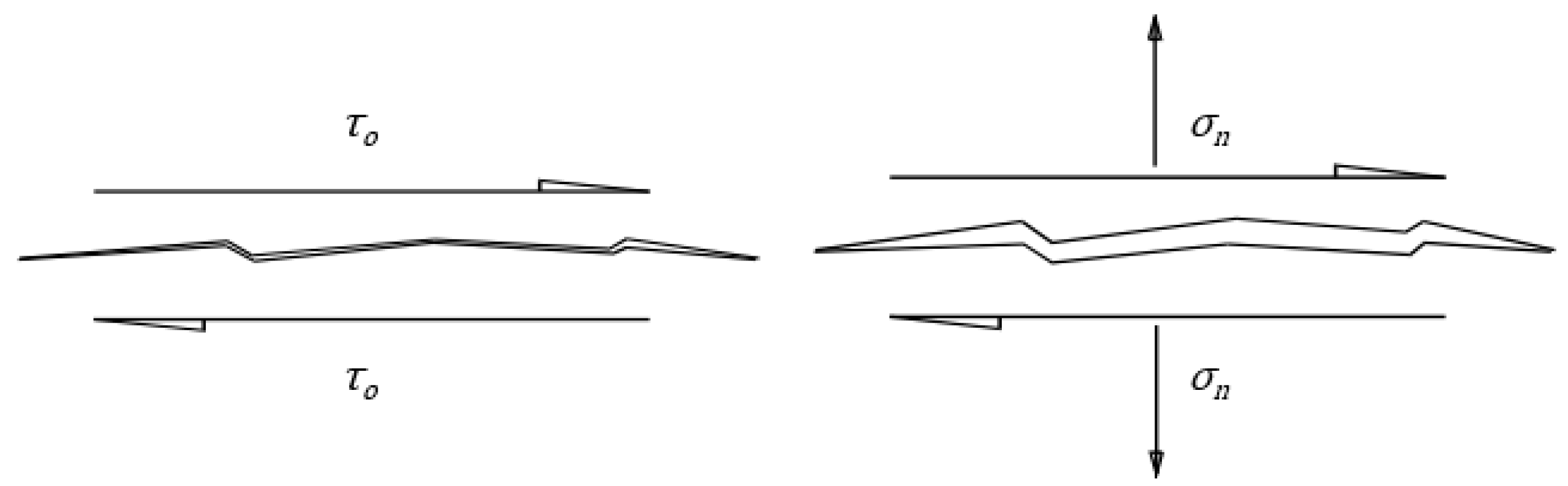
2. Fatigue Theory
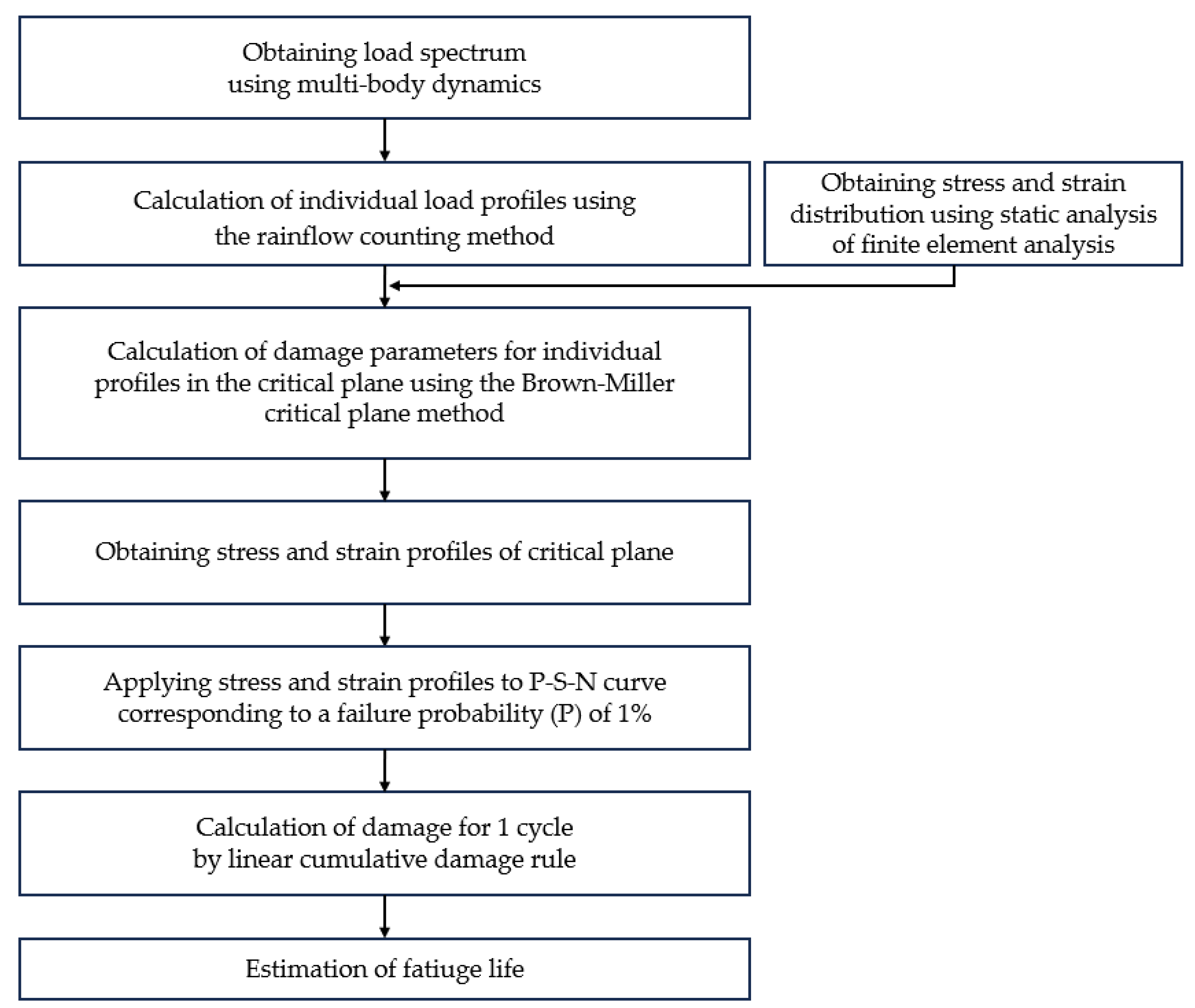
3. Methodology
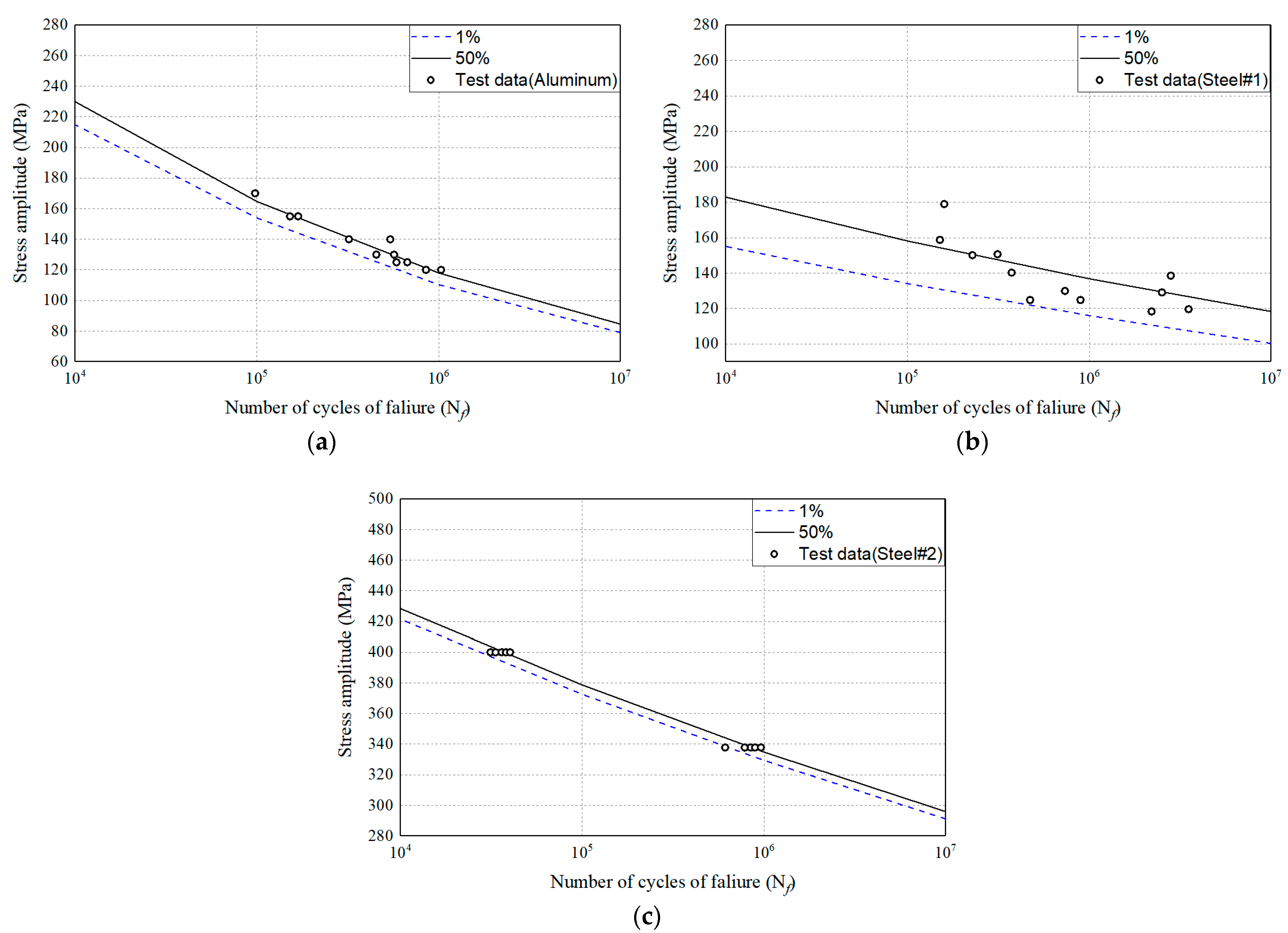
3.1. Mechanical Properties for Calculation
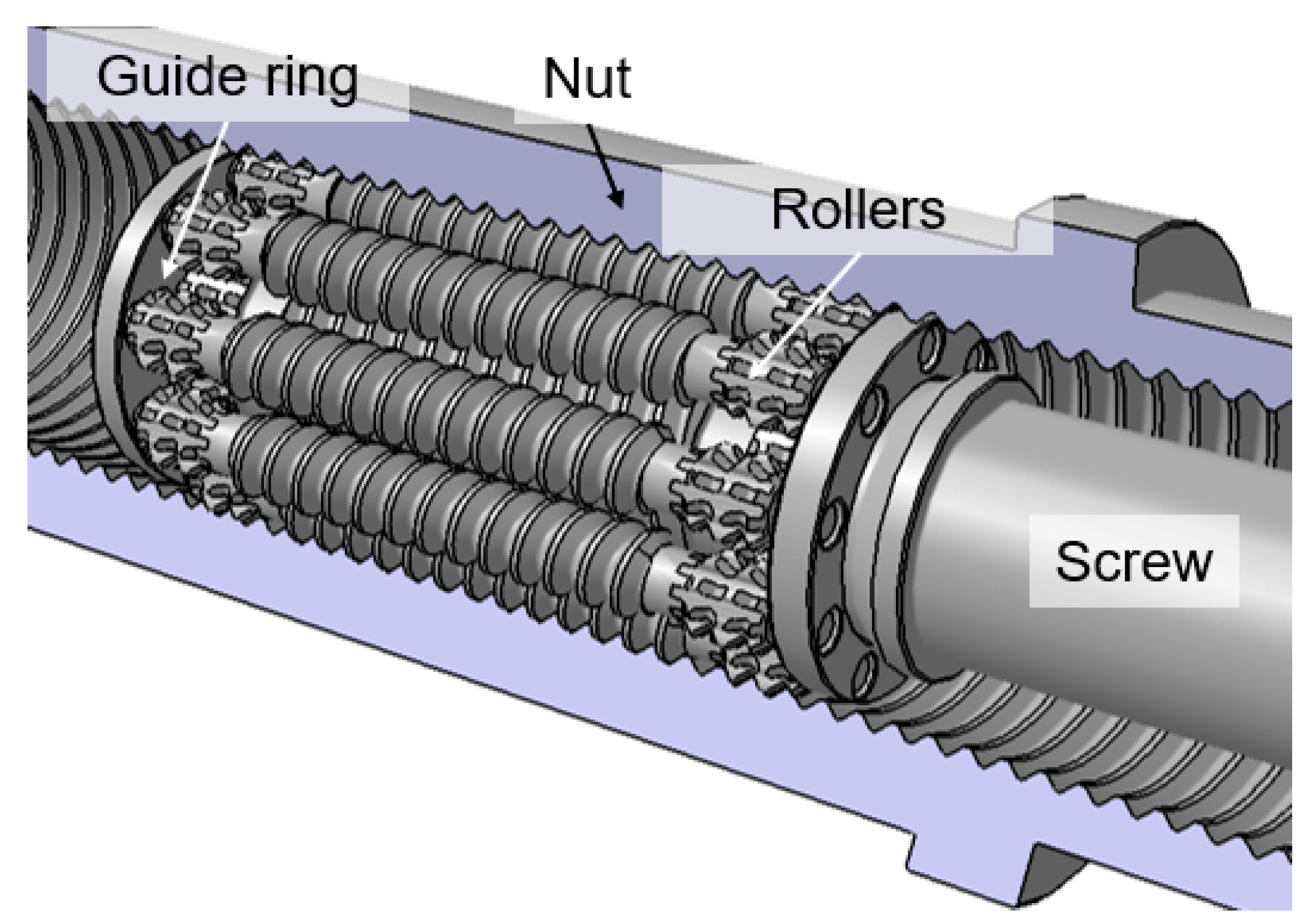
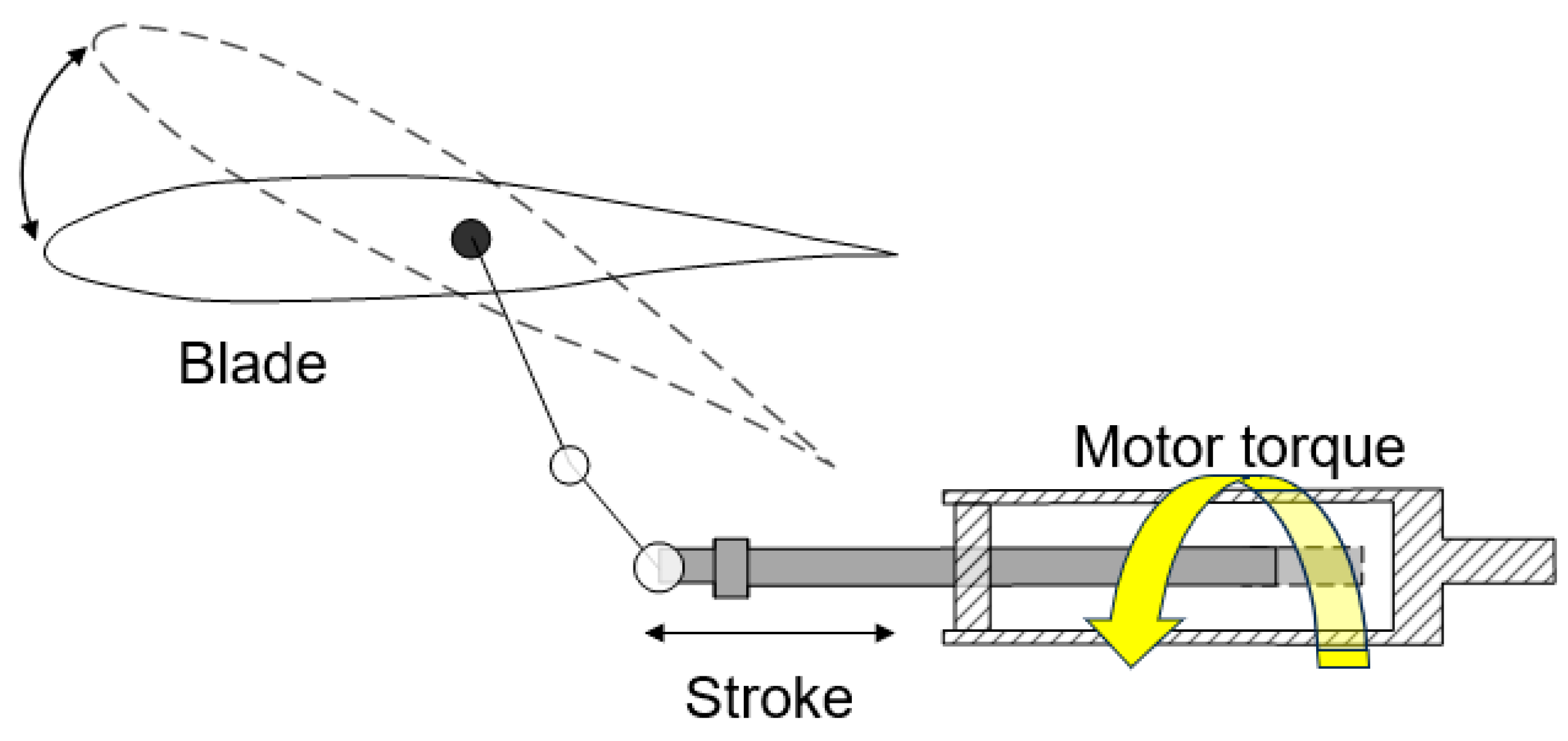
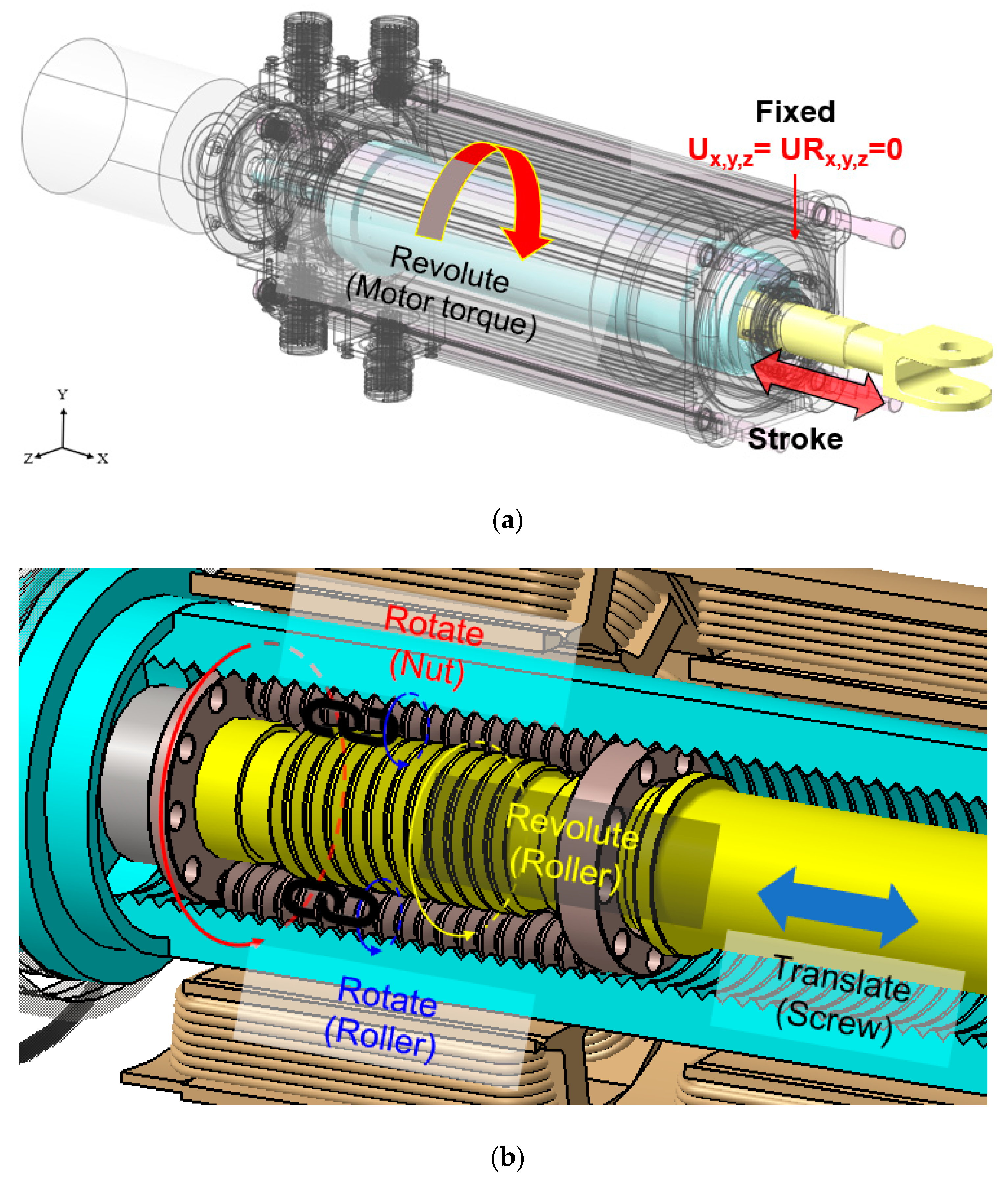
3.2. Multibody Dynamics
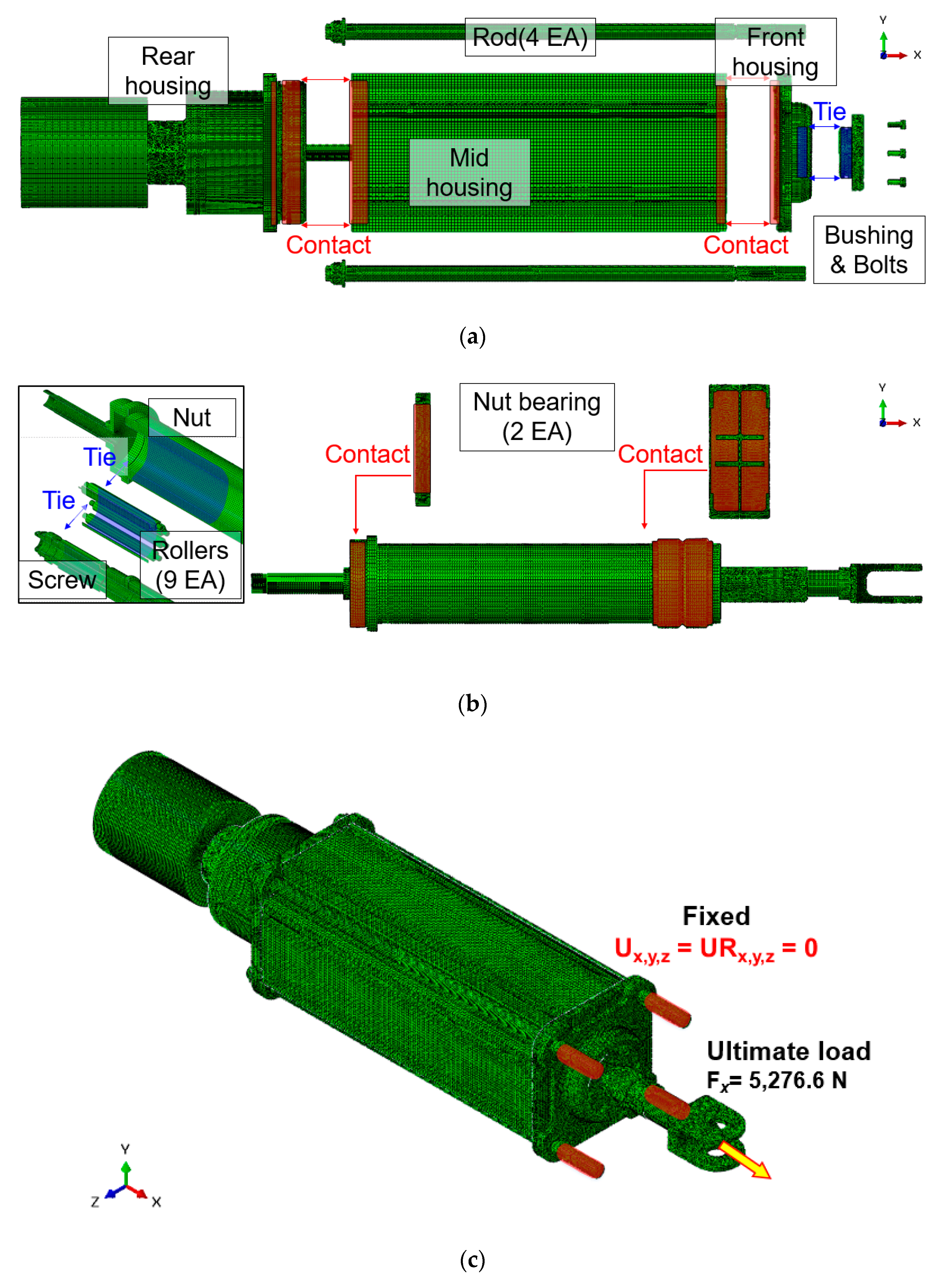
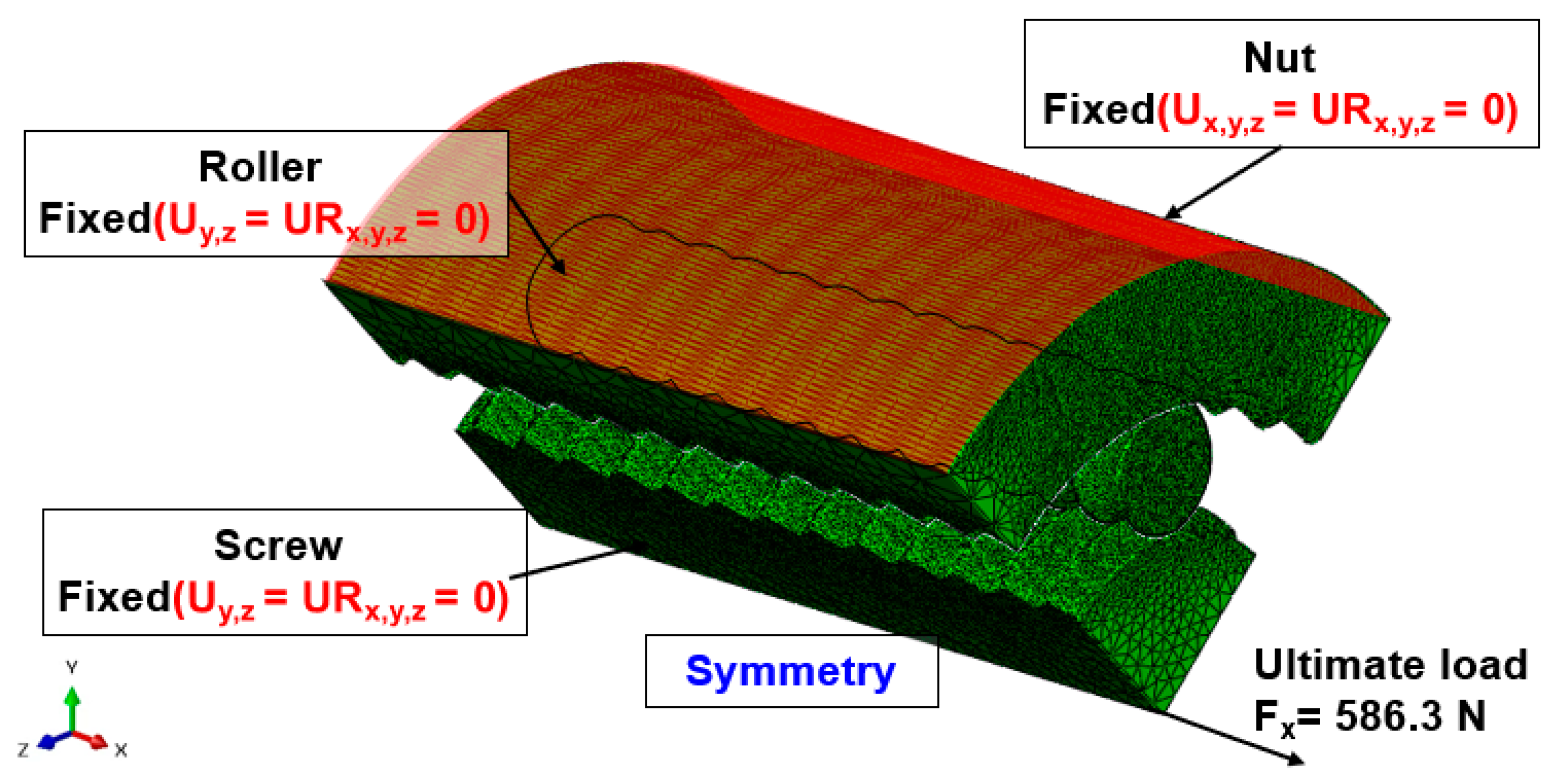
3.3. Static Analysis
3.4. Fatigue Analysis
4. Results
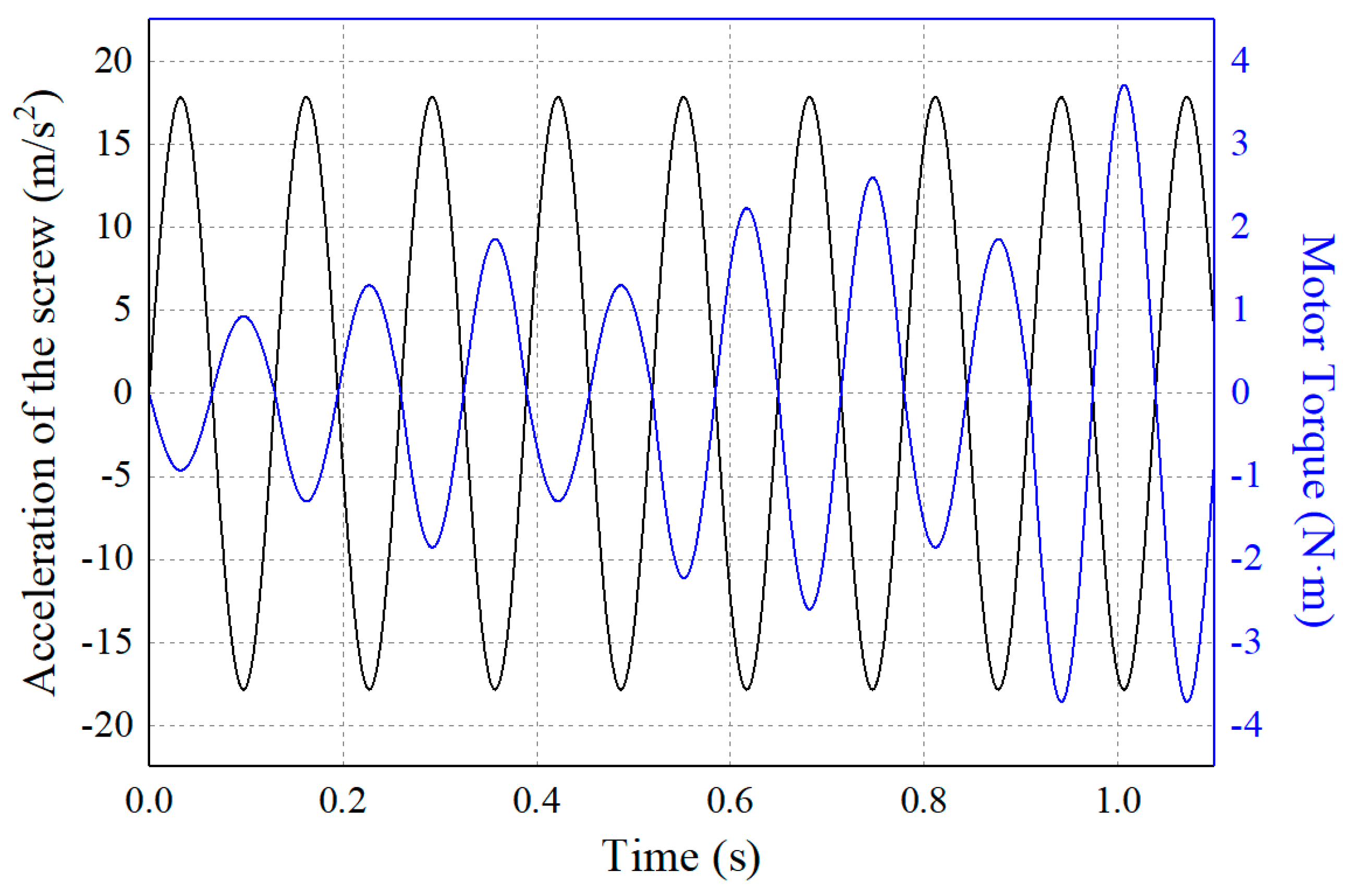
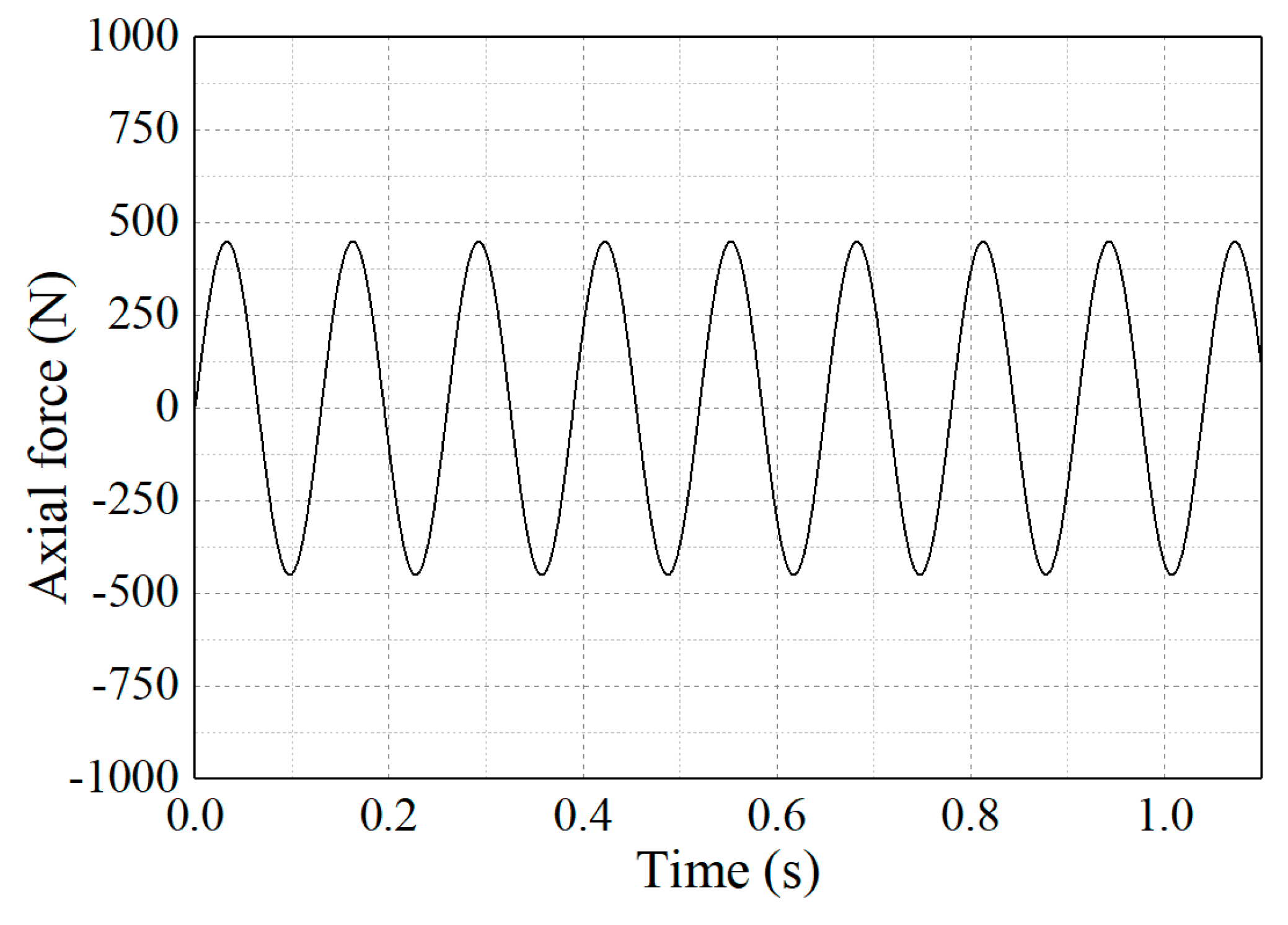
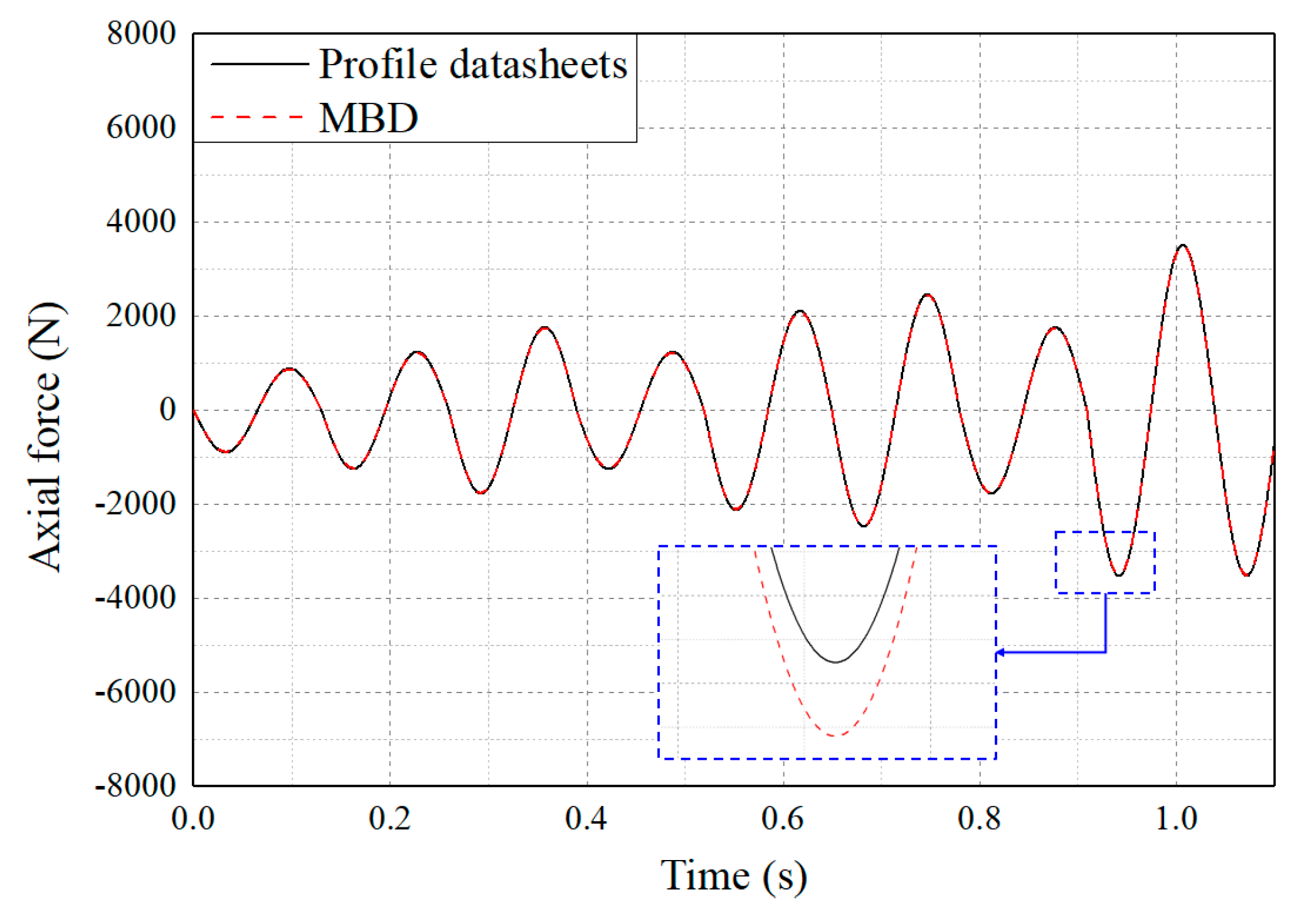
4.1. Multibody Dynamics
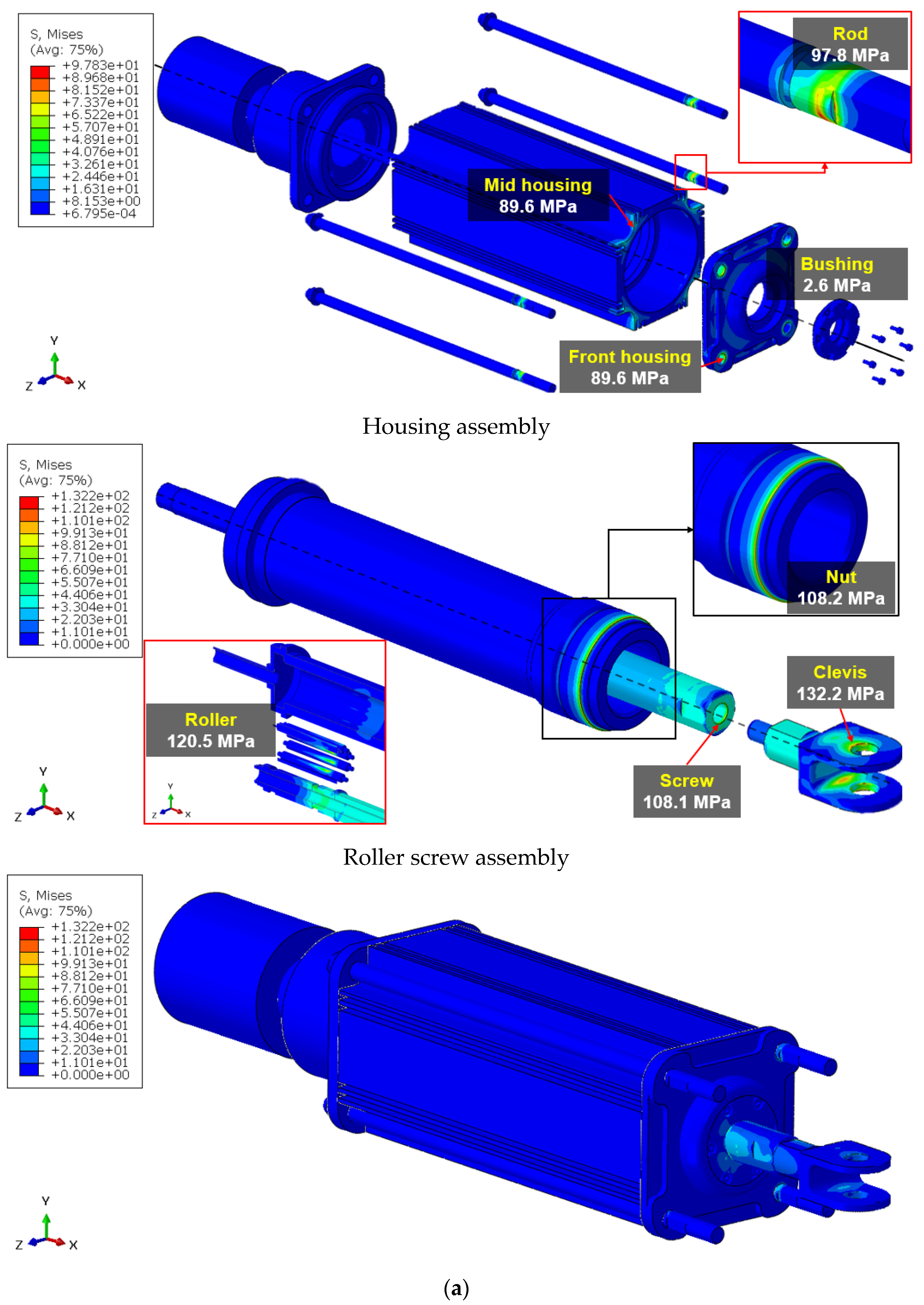
4.2. Static Analysis
4.3. Fatigue Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schlabe, D.; Lienig, J. Energy management of aircraft electrical systems—state of the art and further directions. In Proceedings of the 2012 Electrical Systems for Aircraft, Railway and Ship Propulsion, Bologna, Italy, 16–18 October 2012; pp. 1–6. [Google Scholar]
- Schefer, H.; Fauth, L.; Kopp, T.H.; Mallwitz, R.; Friebe, J.; Kurrat, M. Discussion on Electric Power Supply Systems for All Electric Aircraft. IEEE Access 2020, 8, 84188–84216. [Google Scholar] [CrossRef]
- Yokota, K.; Fujimoto, H.; Kobayashi, H. Observer-based Angle of Attack Estimation for Tilt-Wing eVTOL Aircraft. In Proceedings of the 2021 IEEE International Conference on Mechatronics (ICM), Chiba, Japan, 7–9 March 2021; pp. 1–6. [Google Scholar]
- Ngo, T.D.; Sultan, C.; VanZwieten, J.H.; Xiros, N.I. Constrained Control of Moored Ocean Current Turbines with Cyclic Blade Pitch Variations. IEEE J. Ocean. Eng. 2021, 46, 594–610. [Google Scholar] [CrossRef]
- Chou, T.; Ying, Q.; Qian, Y.; Zhuge, W.; Zhang, Y. Study on Overall Design of a Vertical Take-Off and Landing Unmanned Aerial Vehicle Powered by Electric Ducted Fans. In Proceedings of the ASME 2021 Fluids Engineering Division Summer Meeting. Volume 2: Fluid Applications and Systems; Fluid Measurement and Instrumentation, Online, 10–12 August 2021; Volume 2, pp. 10–12. [Google Scholar]
- Giangrande, P.; Madonna, V.; Sala, G.; Kladas, A.; Gerada, C.; Galea, M. Design and Testing of PMSM for Aerospace EMA Applications. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 2038–2043. [Google Scholar]
- Qiao, G.; Liu, G.; Shi, Z.; Wang, Y.; Ma, S.; Lim, T.C. A review of electromechanical actuators for More/All Electric aircraft systems. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 4128–4151. [Google Scholar] [CrossRef]
- Kim, D.H.; Kim, S.W. Evaluation of structural safety of linear actuator for flap control of aircraft. J. Aerosp. Syst. Eng. 2019, 13, 66–73. [Google Scholar]
- Kim, D.H.; Kim, S.W. Evaluation of Structural Safety of Critical Design Model of Linear Actuator for Flap Control of Aircraft and Test Rig. Int. J. Aeronaut. Space Sci. 2020, 44, 115–116. [Google Scholar]
- Kim, D.H.; Kim, M.G.; Kim, S.W. Structural Behavior of Linear Actuator for Control of Aircraft Flap in Critical Design Phase. Trans. Korean Soc. Mech. Eng. A 2020, 44, 733–744. [Google Scholar] [CrossRef]
- Li, X.; Liu, G.; Fu, X.; Ma, S. Review on motion and load-bearing characteristics of the planetary roller screw mechanism. Machines 2022, 10, 317. [Google Scholar]
- Lim, D.J.; Yee, K.J. A Study on the Certification System for eVTOL Aircraft. J. Aerosp. Syst. Eng. 2021, 15, 20–29. [Google Scholar]
- Choi, J.W.; Hwang, C.J. Status and Approach on Certification Basis of eVTOL for Urban Air Mobility. In Proceedings of the Korean Society for Aeronautical and Space Sciences Fall Conference, Jeju, Republic of Korea, 20–23 November 2019; pp. 621–622. [Google Scholar]
- Johnson, W.; Silva, C. NASA concept vehicles and the engineering of advanced air mobility aircraft. Aeronaut. J. 2022, 126, 59–91. [Google Scholar] [CrossRef]
- Fatemi, A.; Shamsaei, N. Multiaxial fatigue: An overview and some approximation models for life estimation. Int. J. Fatigue 2011, 33, 948–958. [Google Scholar] [CrossRef]
- Wang, C.H.; Brown, M.W. A path-independent parameter for fatigue under proportional and non-proportional loading. Fatigue Fract. Eng. Mater. Struct. 1993, 16, 1285–1297. [Google Scholar]
- Fatemi, A.; Socie, D.F. A critical plane approach to multiaxial fatigue damage including out-of-phase loading. Fatigue Fract. Eng. Mater. Struct. 1988, 11, 149–165. [Google Scholar]
- Smith, K.N.; Watson, P.; Topper, T.H. A stress-strain function for the fatigue of metals. J. Mater. 1970, 5, 767–778. [Google Scholar]
- Miller, K.J.; Brown, M.W. Multiaxial fatigue: A brief review. Fracture 1984, 84, 31–56. [Google Scholar]
- Xue, L.; Shang, D.G.; Li, D.H.; Li, L.J.; Liu, X.D.; Chen, H. Equivalent energy-based critical plane fatigue damage parameter for multiaxial LCF under variable amplitude loading. Int. J. Fatigue 2020, 131, 105350. [Google Scholar] [CrossRef]
- Huang, H.Z.; Liu, D.; Li, Y.F.; Bai, S. Multiaxial fatigue life prediction of an aero-engine turbine shaft with a modified critical plane-based model. In Proceedings of the 12th International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering, Sichuan, China, 27–30 July 2022; pp. 1807–1811. [Google Scholar]
- Kwofie, S. An exponential stress function for predicting fatigue strength and life due to mean stresses. Int. J. Fatigue 2001, 23, 829–836. [Google Scholar] [CrossRef]
- Choi, J.H.; Koo, J.M.; Seok, C.S.; Song, W.K. Evaluation of Fatigue Life Characteristic of a Real Waterwork Pipe Using the Probability Density Function. Trans. Korean Soc. Mech. Eng. A 2008, 32, 707–712. [Google Scholar] [CrossRef]
- Jones, M.H.; Velinsky, S.A.; Lasky, T.A. Dynamics of the planetary roller screw mechanism. J. Mech. Robot. 2016, 8, 014503. [Google Scholar] [CrossRef]
- Jin, J.H. Dynamic Models of Blade Pitch Control System Driven by Electro-Mechanical Actuator. J. Aerosp. Syst. Eng. 2022, 50, 111–118. [Google Scholar]
- FAA Federal Aviation Administration. Part 23—Airworthiness Standards: Normal Category Airplanes—Amendment 1-49; FAA Federal Aviation Administration: Washington, DC, USA, 1996.
- FAA Federal Aviation Administration. Part 27—Airworthiness Standards: Normal Category Rotorcraft—Amendment 1-37; FAA Federal Aviation Administration: Washington, DC, USA, 1999.
- ISO 898-1; Mechanical Properties of Fasteners Made of Carbon Steel and Alloy Steel-Part 1: Bolts, Screws and Studs with Specified Property Classes-Coarse Thread and Fine Pitch Thread. International Organization for Standardization: London, UK, 2013.
- Brown, M.W.; Miller, K.J. A theory for fatigue failure under multiaxial stress-strain conditions. Proc. Inst. Mech. Eng. 1973, 187, 745–755. [Google Scholar] [CrossRef]
- Fonseca Junior, T.M.I.; Magnabosco, R. Evaluation of methods for estimating fatigue properties applied to stainless steels and aluminum alloys. Tecnol. Em Metal. Mater. Mineração 2013, 9, 284–293. [Google Scholar] [CrossRef]
- Kim, D.H.; Kim, Y.C.; Kim, S.W. Numerical Evaluation of Structural Safety of Linear Actuator for Flap Control of Aircraft Based on Airworthiness Standard. Aerospace 2021, 8, 104. [Google Scholar] [CrossRef]
- Thawre, M.M.; Verma, K.K.; Jagannathan, N.; Peshwe, D.R.; Paretkar, R.K.; Manjunatha, C.M. Effect of ply-drop on fatigue life of a carbon fiber composite under a fighter aircraft spectrum load sequence. Compos. Part B Eng. 2016, 86, 120–125. [Google Scholar] [CrossRef]
- Abdelhafeez, A.M.; Soo, S.L.; Aspinwall, D.K.; Dowson, A.; Arnold, D. The influence of burr formation and feed rate on the fatigue life of drilled titanium and aluminium alloys used in aircraft manufacture. CIRP Ann. 2018, 67, 103–108. [Google Scholar] [CrossRef]
- Al-Bahkali, E.A.; Elkenani, H.; Souli, M. Failure and fatigue life due to random vibration in aircraft applications. In Multiphysics Simulations in Automotive and Aerospace Applications; Academic Press: Cambridge, MA, USA, 2021; pp. 131–154. [Google Scholar]
- Nicholas, T. Critical issues in high cycle fatigue. Int. J. Fatigue 1999, 21, 221–231. [Google Scholar] [CrossRef]





| Properties | Materials | ||
|---|---|---|---|
| Aluminum | Steel#1 | Steel#2 | |
| Elastic modulus (GPa) | 69.8 | 193 | 210 |
| Poisson’s ratio | 0.33 | 0.29 | 0.30 |
| Yield strength (MPa) | 275.8 | 215.0 | 1700 |
| Tensile strength (MPa) | 310.3 | 505.0 | 2300 |
| Fatigue strength coefficient, | 872.1 (P = 50%) 815.2 (P = 1%) | 326.7 (P = 50%) 277.0 (P = 1%) | 701.3 (P = 50%) 689.9 (P = 1%) |
| Fatigue strength exponent, | −0.145 | −0.063 | −0.054 |
| Fatigue strength (107 cycles, MPa) | 84.5 (P = 50%) 79.0 (P = 1%) | 118.3 (P = 50%) 100.3 (P = 1%) | 295.9 (P = 50%) 291.1 (P = 1%) |
| Parameter Name | Symbol | Value | Unit |
|---|---|---|---|
| Effective diameter of screw | 21 | mm | |
| Effective diameter of roller | 7 | mm | |
| Effective diameter of nut | 35 | mm | |
| Pitch | pz | 3.333 | mm |
| Number of rollers | - | 9 | - |
| Type | Base Elements | Action Elements | Boundary Conditions | Remark |
|---|---|---|---|---|
| Merge | Housing | Rod (4EA) | - | - |
| Merge | Housing | Connector (4EA) | - | - |
| Merge | Nut | Mount | - | - |
| Revolute | Housing | Nut | X-axis rotation | - |
| Revolute | Housing | Carrier | X-axis rotation | - |
| Revolute | Carrier | Rollers | X-axis rotation | - |
| Translate | Housing | Screw | X-axis translation | - |
| Coupler | Revolute (nut) | Revolute (carrier) | Scale c2 = 1.6 | : = 1.60:1 |
| Coupler | Revolute (carrier) | Revolute (roller) | Scale c2 = 0.25 | : = 0.25:1 |
| Coupler | Revolute (roller) | Translate (screw) | Scale c2 = 4.71 | : = 4.71:1 |
| Parameter Name | Components | Materials | The Number of Elements and Nodes |
|---|---|---|---|
| Model#1 | Housings | Aluminum | 975,204/1,336,435 |
| Clevis | 79,544/115,990 | ||
| Rod | 119,474/169,646 | ||
| Bushing | Steel#1 | 108,601/160,171 | |
| Screw | 130,280/180,784 | ||
| Rollers | 73,120/79,507 | ||
| Nut | 97,334/116,358 | ||
| Retainer | Steel#2 | 5686/13,372 | |
| Carrier | 3240/4761 | ||
| Model#2 | Screw | Steel#1 | 283,611/405,910 |
| Rollers | 432,119/604,546 | ||
| Nut | 606,813/858,098 |
| Components | Static Analysis | Fatigue Analysis | |
|---|---|---|---|
| MS (von Mises Stress) | Fatigue Life (Cycles) | ||
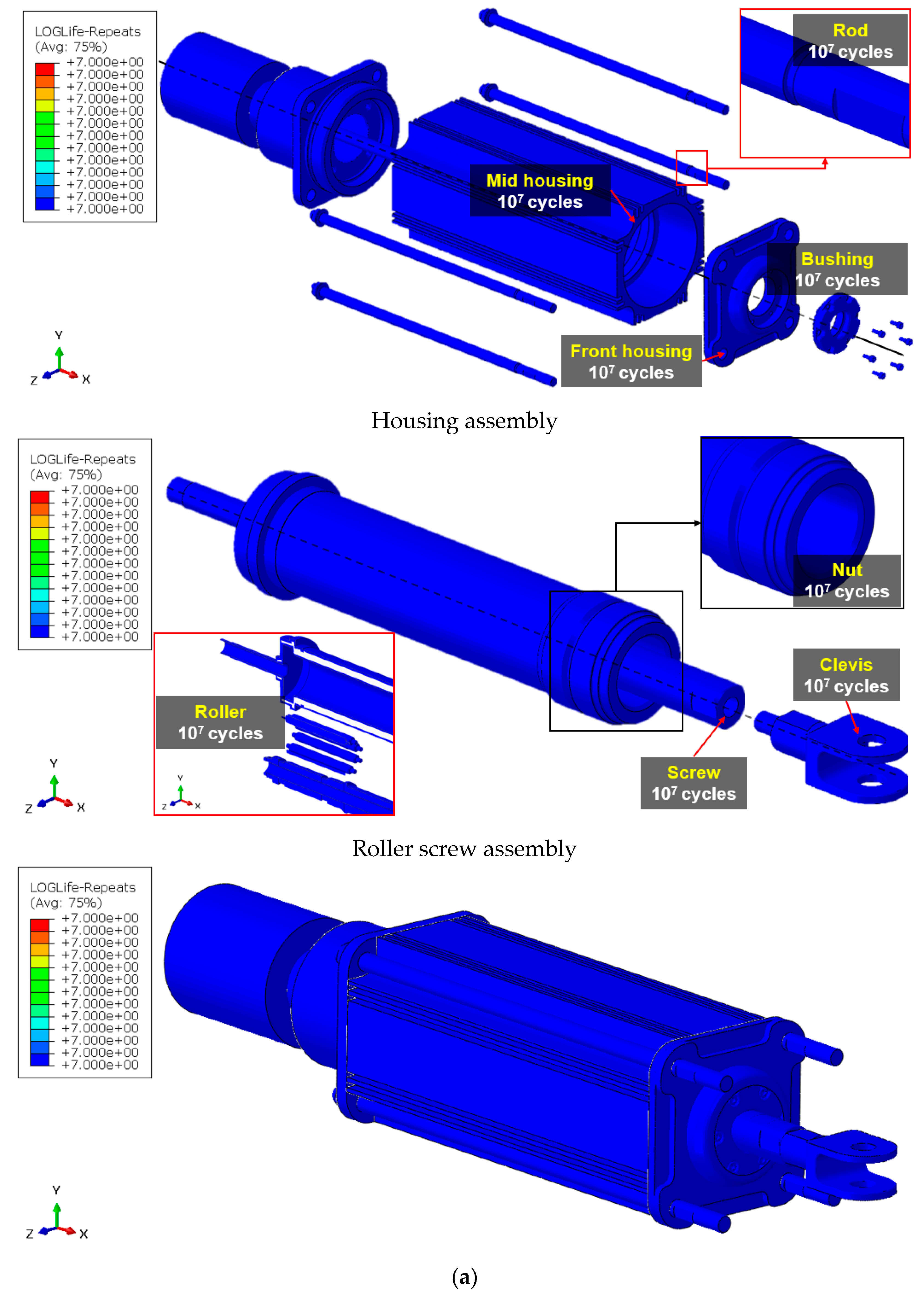
| Model#1 | Housings | 3.3 (89.6 MPa) | 107 |
| Clevis | 1.9 (132.2 MPa) | ||
| Rod | 2.9 (97.8 MPa) | ||
| Bushing | 645.3 (2.6 MPa) | ||
| Screw | 14.7 (108.1 MPa) | ||
| Rollers | 13.1 (120.5 MPa) | ||
| Nut | 14.7 (108.2 MPa) | ||
| Retainer | 338.3 (1.4 MPa) | ||
| Carrier | 1806.6 (0.3 MPa) | ||
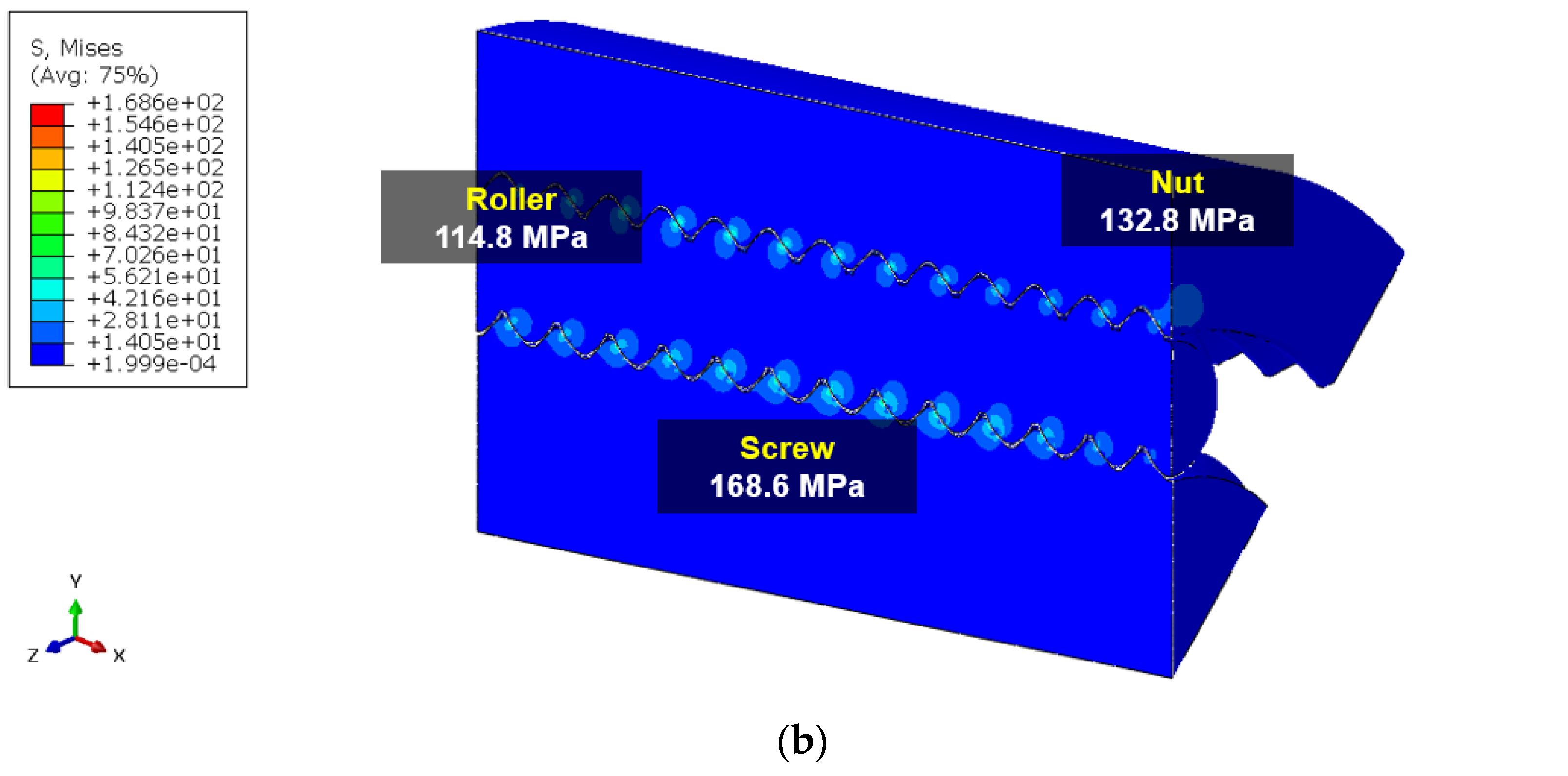
| Model#2 | Screw | 9.1 (168.6 MPa) | 107 |
| Rollers | 13.8 (114.8 MPa) | ||
| Nut | 11.8 (132.8 MPa) | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.-C.; Kim, D.-H.; Kim, S.-W. Evaluation of the Multiaxial Fatigue Life of Electro-Mechanical Actuator for Aircraft Blade Pitch Control Based on Certification Standards. Aerospace 2024, 11, 91. https://doi.org/10.3390/aerospace11010091
Kim Y-C, Kim D-H, Kim S-W. Evaluation of the Multiaxial Fatigue Life of Electro-Mechanical Actuator for Aircraft Blade Pitch Control Based on Certification Standards. Aerospace. 2024; 11(1):91. https://doi.org/10.3390/aerospace11010091
Chicago/Turabian StyleKim, Young-Cheol, Dong-Hyeop Kim, and Sang-Woo Kim. 2024. "Evaluation of the Multiaxial Fatigue Life of Electro-Mechanical Actuator for Aircraft Blade Pitch Control Based on Certification Standards" Aerospace 11, no. 1: 91. https://doi.org/10.3390/aerospace11010091






