A Discontinuous Galerkin–Finite Element Method for the Nonlinear Unsteady Burning Rate Responses of Solid Propellants
Abstract
:1. Introduction
2. The Formulation of the Algorithm
2.1. The Physical Problem
2.2. The DG-FEM Algorithm
3. Results and Discussion
3.1. An Exact Solution
3.1.1. The FDM
3.1.2. The SM
3.1.3. The DG-FEM
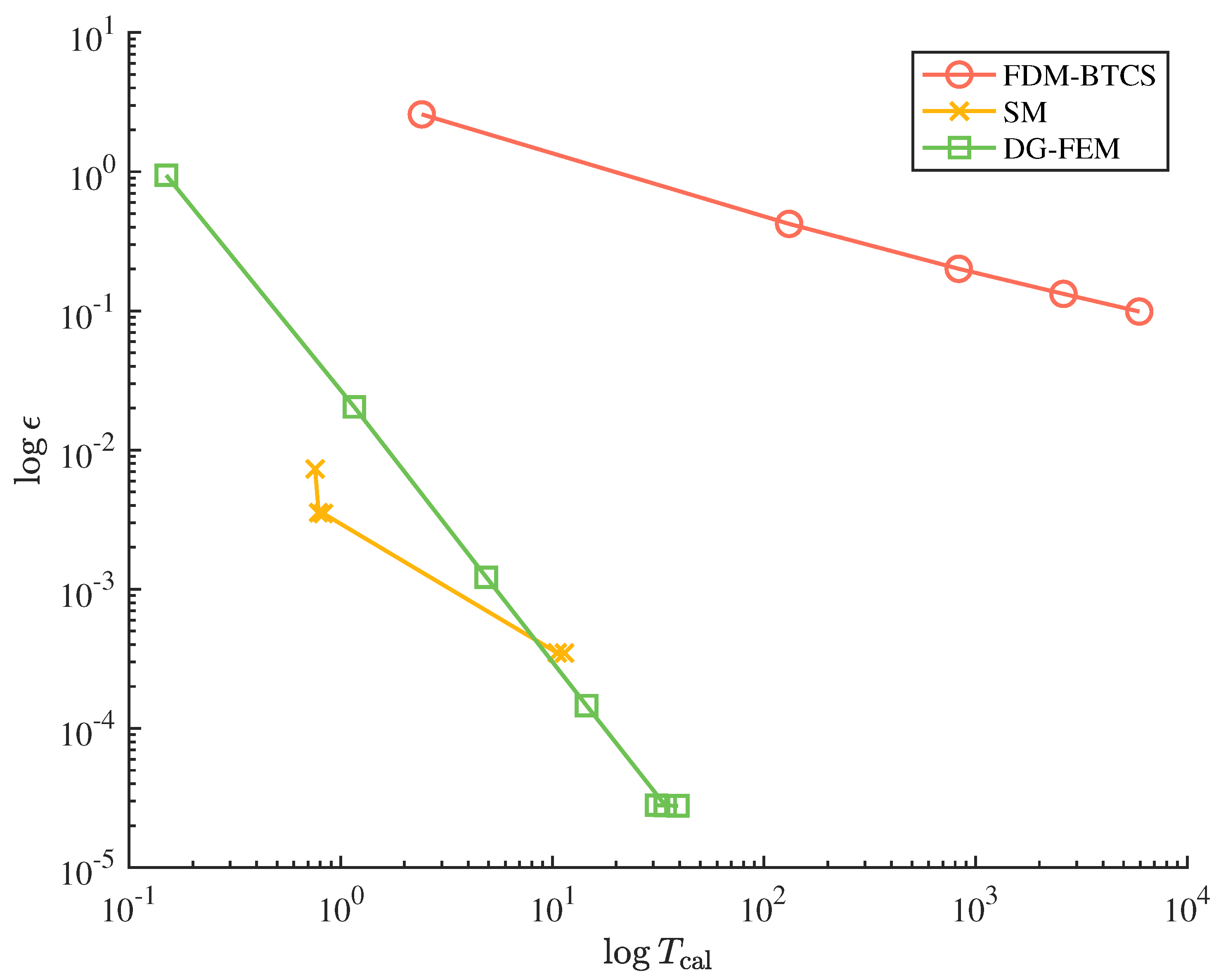
3.1.4. The Overall Comparison
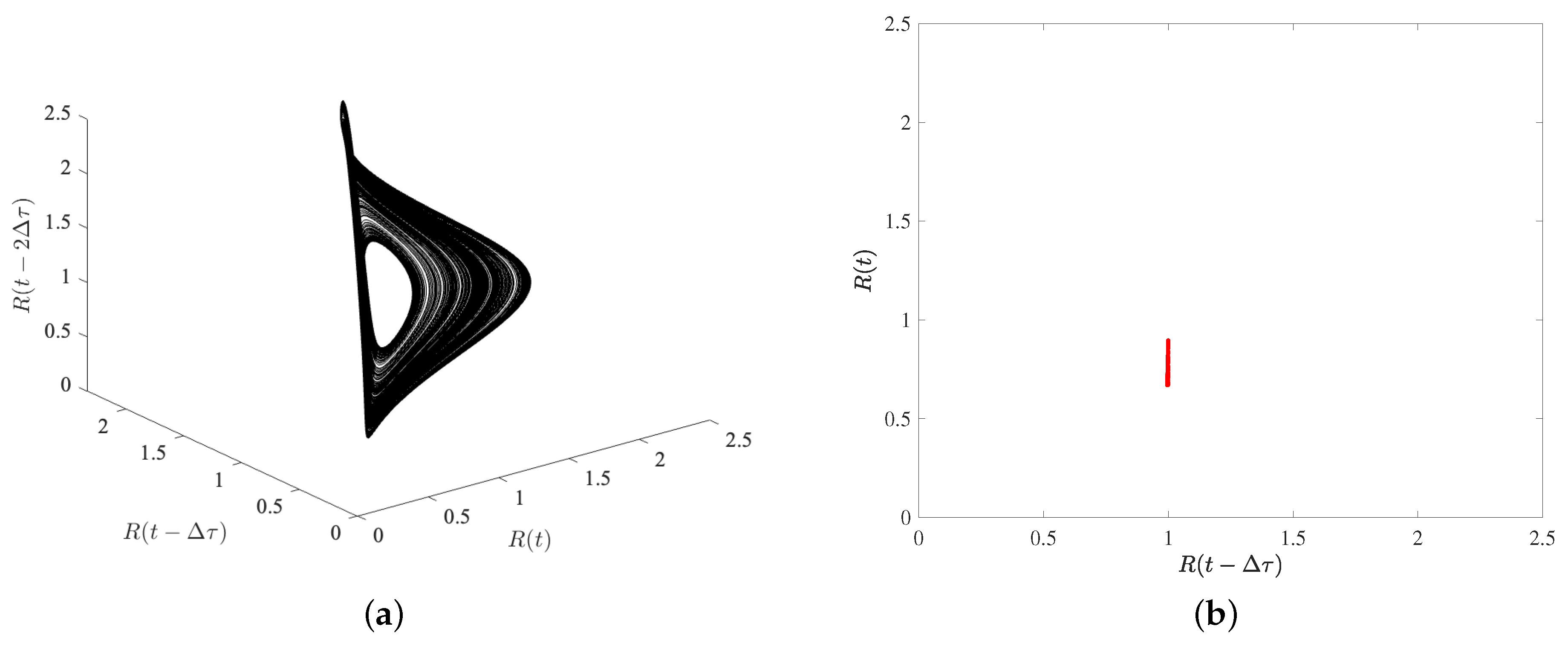
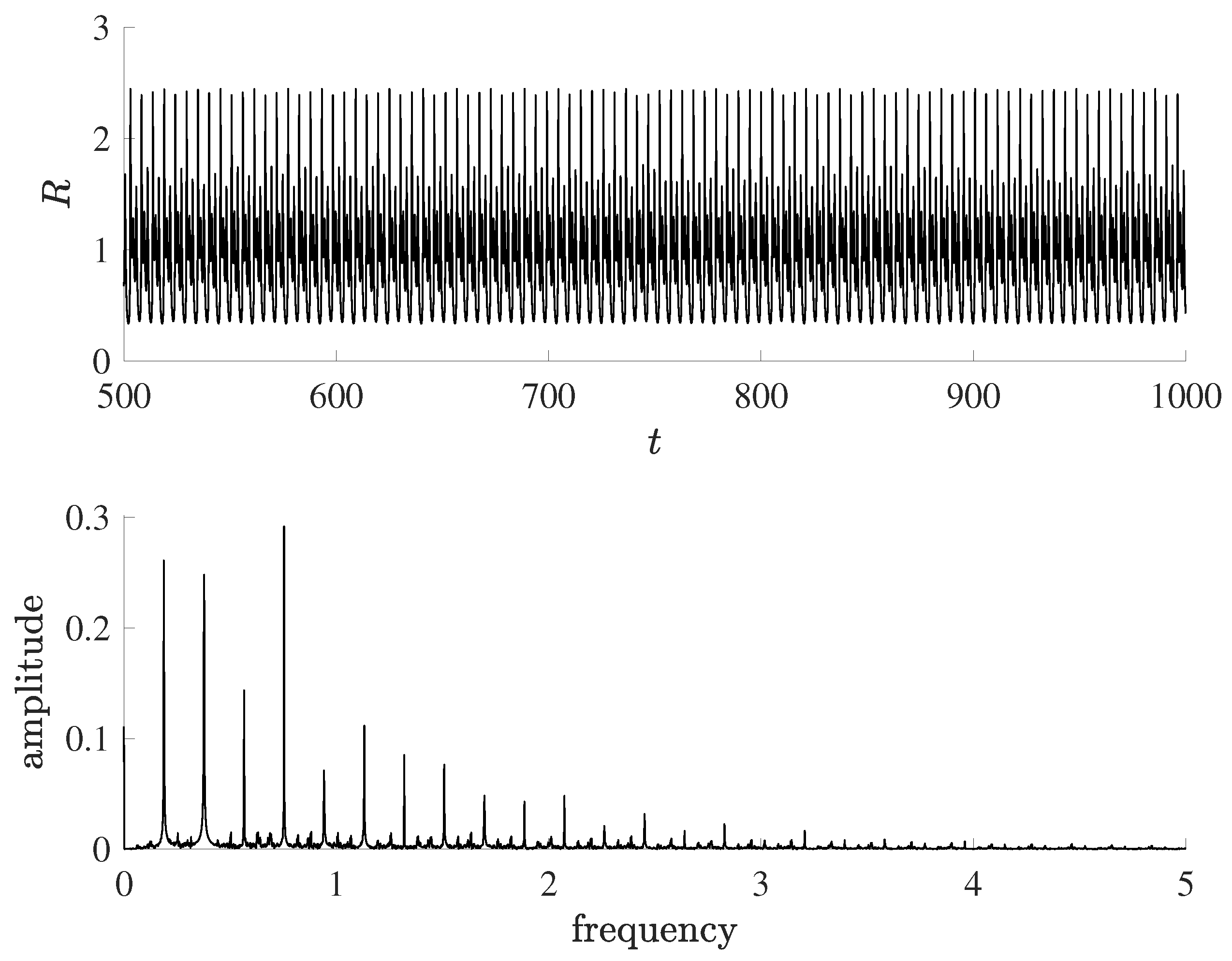
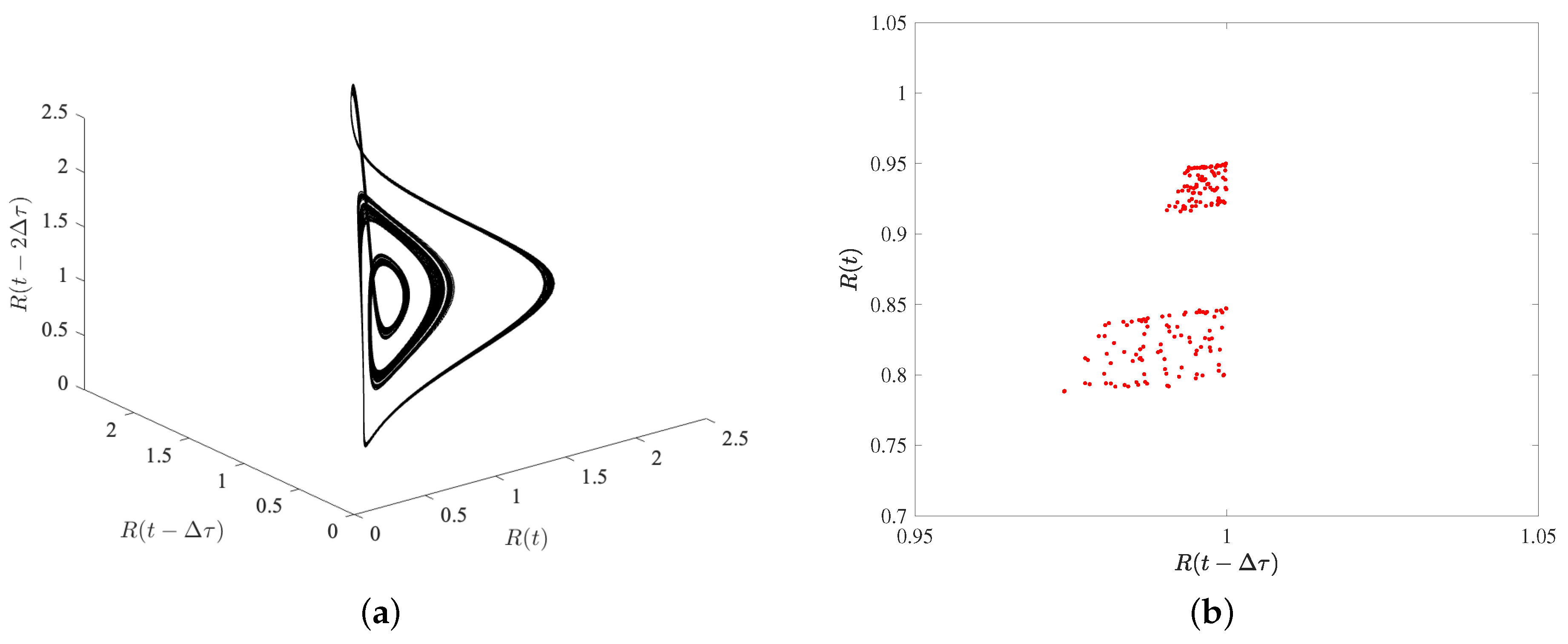
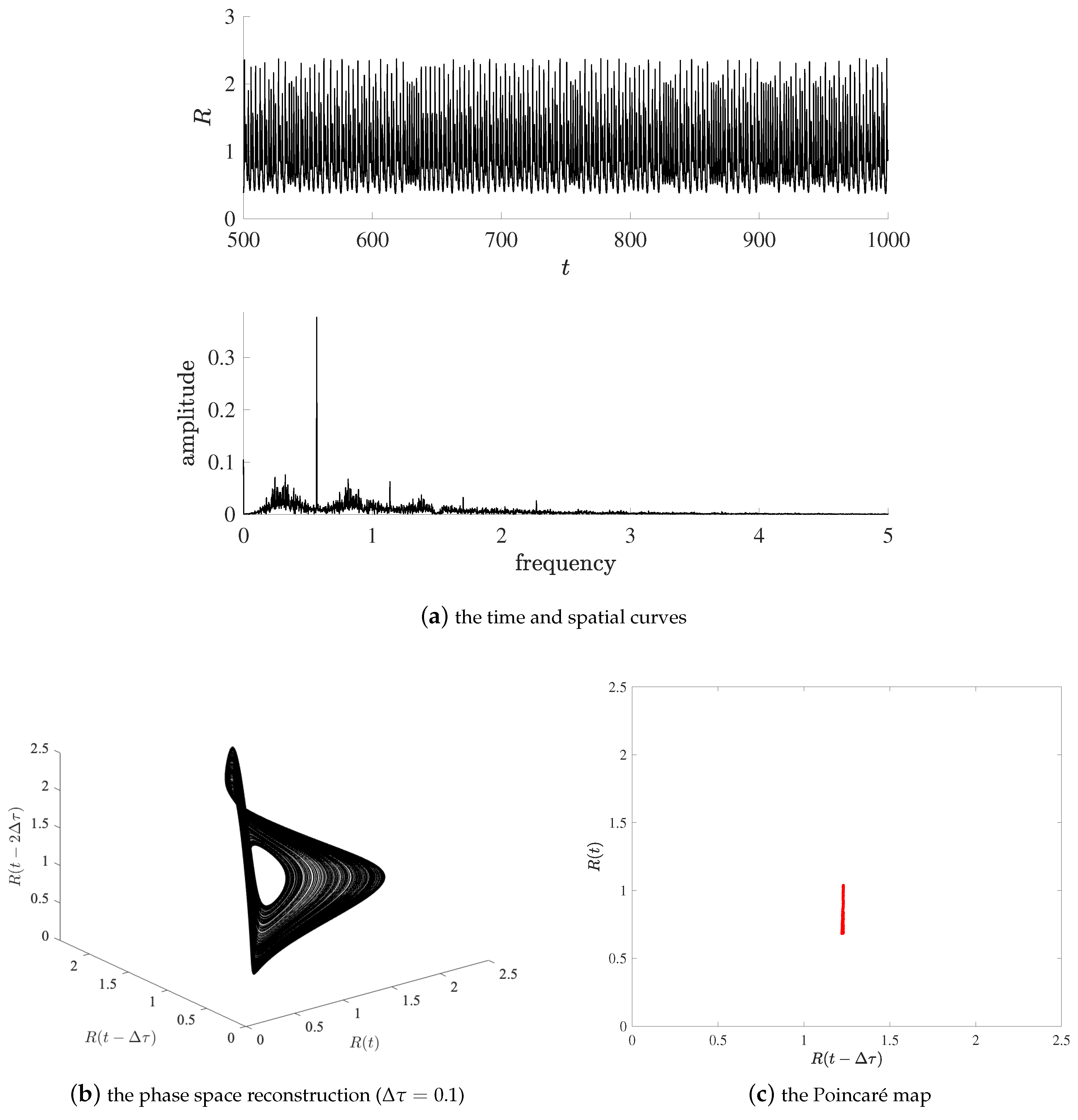
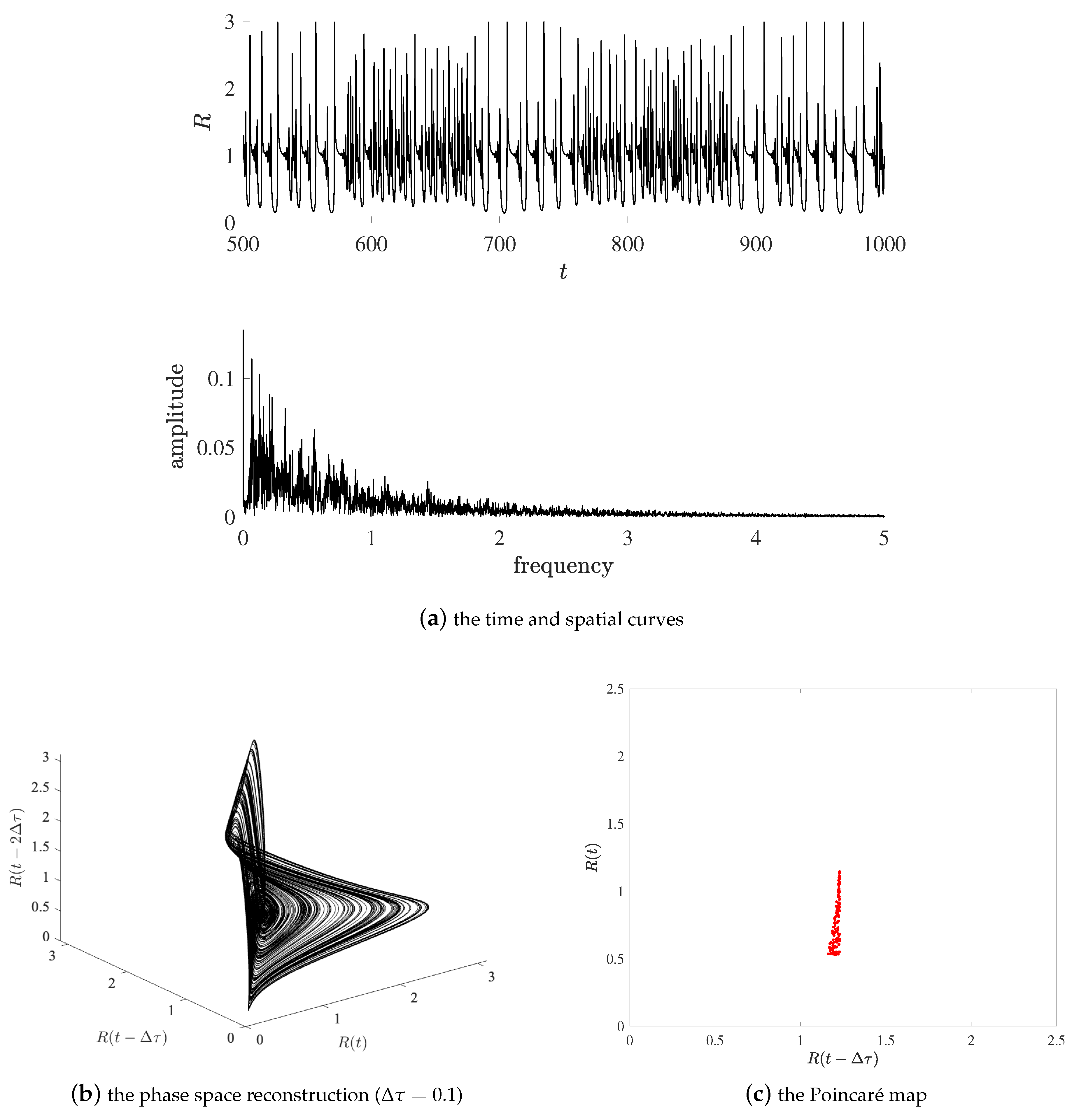
3.2. The Capture of Complex Dynamics
3.2.1. The SM
3.2.2. The DG-FEM
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FDM | finite difference method |
| FVM | finite volume method |
| FEM | finite element method |
| DG | discontinuous Galerkin |
| ZN | Zel’dovich–Novozhilov |
| PDE | partial differential equation |
| ODE | ordinary differential equation |
| BTCS | backward time central space |
References
- Culick, F. Combustion Instabilities in Solid Propellant Rocket Motors; Technical report; California Institute of Technology Pasadena: Pasadena, CA, USA, 2004. [Google Scholar]
- Novozhilov, V.B.; Novozhilov, B.V. Theory of Solid-Propellant Nonsteady Combustion; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Mariappan, S.; Sujith, R. Thermoacoustic instability in a solid rocket motor: Non-normality and nonlinear instabilities. J. Fluid Mech. 2010, 653, 1–33. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, P.; Ao, W. A reduced-order model of thermoacoustic instability in solid rocket motors. Aerosp. Sci. Technol. 2020, 97, 105615. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, P.; Jin, B.; Ao, W. Nonlinear characteristics of the triggering combustion instabilities in solid rocket motors. Acta Astronaut. 2020, 176, 371–382. [Google Scholar] [CrossRef]
- Summerfield, M.; Price, E.W.; Luca, L.D. Nonsteady Burning and Combustion Stability of Solid Propellants; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1992. [Google Scholar]
- Wang, Z.; Zhang, X.; Bai, Y.; Gan, X.; Wang, J.; Jin, B.; Liu, P. A Comparison of the Nonlinear Unsteady Responses of Two Classical Models for Solid Propellant. In Proceedings of the 2022 13th International Conference on Mechanical and Aerospace Engineering (ICMAE), IEEE, Bratislava, Slovakia, 20–22 July 2022; pp. 258–263. [Google Scholar]
- Wang, Z.; Zhang, W.; Liu, Y. A Phenomenological Model for the Unsteady Combustion of Solid Propellants from a Zel’dovich-Novzhilov Approach. Aerospace 2023, 10, 767. [Google Scholar] [CrossRef]
- Krier, H.; Sirignano, W.; Summerfield, M.; T’ien, J. Nonsteady burning phenomena of solid propellants-Theory and experiments. AIAA J. 1968, 6, 278–285. [Google Scholar] [CrossRef]
- Novozhilov, B. Combustion of energetic materials in an acoustic field. Combust. Explos. Shock Waves 2005, 41, 709–726. [Google Scholar] [CrossRef]
- Culick, F.E.C.; Burnley, V.; Swenson, G. Pulsed instabilities in solid-propellant rockets. J. Propuls. Power 1995, 11, 657–665. [Google Scholar] [CrossRef]
- Wang, J. Non-linear analysis of solid propellant burning rate behavior. Int. J. Numer. Methods Fluids 2000, 33, 627–640. [Google Scholar] [CrossRef]
- Novozhilov, B.V. Randomization of the unsteady burning rate of gunpowder. Russ. J. Phys. Chem. 2004, 23, 68–74. [Google Scholar]
- Hesthaven, J.S.; Warburton, T. Nodal Discontinuous Galerkin Methods: Algorithms, Analysis, and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Krais, N.; Beck, A.; Bolemann, T.; Frank, H.; Flad, D.; Gassner, G.; Hindenlang, F.; Hoffmann, M.; Kuhn, T.; Sonntag, M.; et al. FLEXI: A high order discontinuous Galerkin framework for hyperbolic–parabolic conservation laws. Comput. Math. Appl. 2021, 81, 186–219. [Google Scholar] [CrossRef]
- Yao, C.; Liu, J.; Yan, J. Numerical investigation of nonlinear effects in a standing wave thermoacoustic engine using the discontinuous Galerkin method. Int. J. Heat Mass Transf. 2023, 216, 124526. [Google Scholar] [CrossRef]
- Noventa, G.; Massa, F.; Rebay, S.; Bassi, F.; Ghidoni, A. Robustness and efficiency of an implicit time-adaptive discontinuous Galerkin solver for unsteady flows. Comput. Fluids 2020, 204, 104529. [Google Scholar] [CrossRef]
- Ghidoni, A.; Massa, F.C.; Noventa, G.; Rebay, S. Assessment of an adaptive time integration strategy for a high-order discretization of the unsteady RANS equations. Int. J. Numer. Methods Fluids 2022, 94, 1923–1963. [Google Scholar] [CrossRef]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]


| Number of Meshes | -Error | Normalized Calculation Time |
|---|---|---|
| 10 | 2.582 | 1 |
| 50 | 0.4218 | 54.42 |
| 100 | 0.2006 | 344.52 |
| 150 | 0.1325 | 1076.08 |
| 200 | 0.0989 | 2454.0 |
| Order of Polynomials | Time Step Size | -Error | Normalized Calculation Time |
|---|---|---|---|
| 5 | |||
| 10 | |||
| 15 | |||
| 15 | |||
| 20 |
| Order of Polynomials | Number of Elements K | -Error | Normalized Calculation Time |
|---|---|---|---|
| 2 | 10 | ||
| 4 | 10 | ||
| 6 | 10 | ||
| 8 | 10 | ||
| 10 | 10 | ||
| 10 | 5 | ||
| 10 | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Yu, K.; Liu, Y. A Discontinuous Galerkin–Finite Element Method for the Nonlinear Unsteady Burning Rate Responses of Solid Propellants. Aerospace 2024, 11, 97. https://doi.org/10.3390/aerospace11010097
Wang Z, Yu K, Liu Y. A Discontinuous Galerkin–Finite Element Method for the Nonlinear Unsteady Burning Rate Responses of Solid Propellants. Aerospace. 2024; 11(1):97. https://doi.org/10.3390/aerospace11010097
Chicago/Turabian StyleWang, Zhuopu, Kairui Yu, and Yuanzhe Liu. 2024. "A Discontinuous Galerkin–Finite Element Method for the Nonlinear Unsteady Burning Rate Responses of Solid Propellants" Aerospace 11, no. 1: 97. https://doi.org/10.3390/aerospace11010097
APA StyleWang, Z., Yu, K., & Liu, Y. (2024). A Discontinuous Galerkin–Finite Element Method for the Nonlinear Unsteady Burning Rate Responses of Solid Propellants. Aerospace, 11(1), 97. https://doi.org/10.3390/aerospace11010097







