Efficient Power Conditioning: Enhancing Electric Supply for Small Satellite Missions
Abstract
:1. Introduction
2. Converter Design
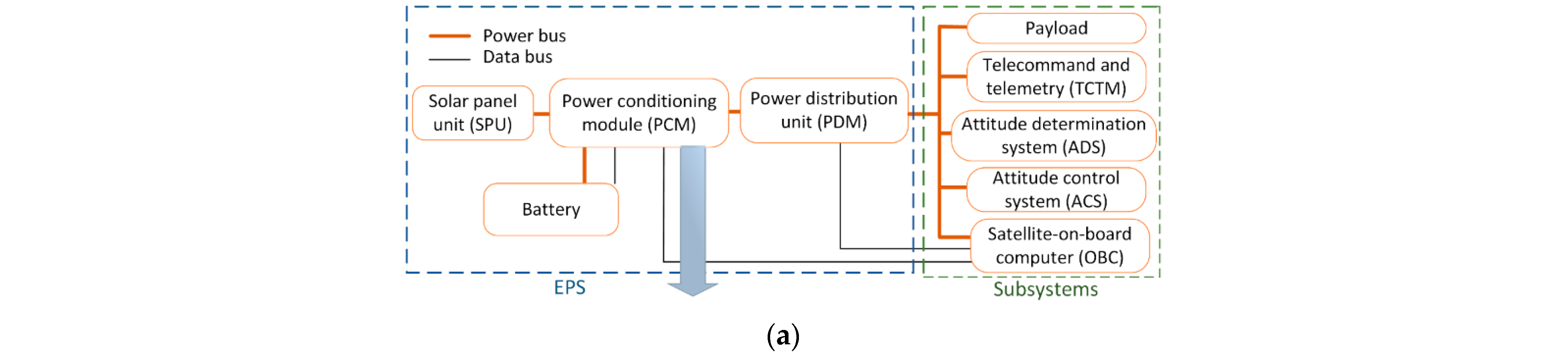
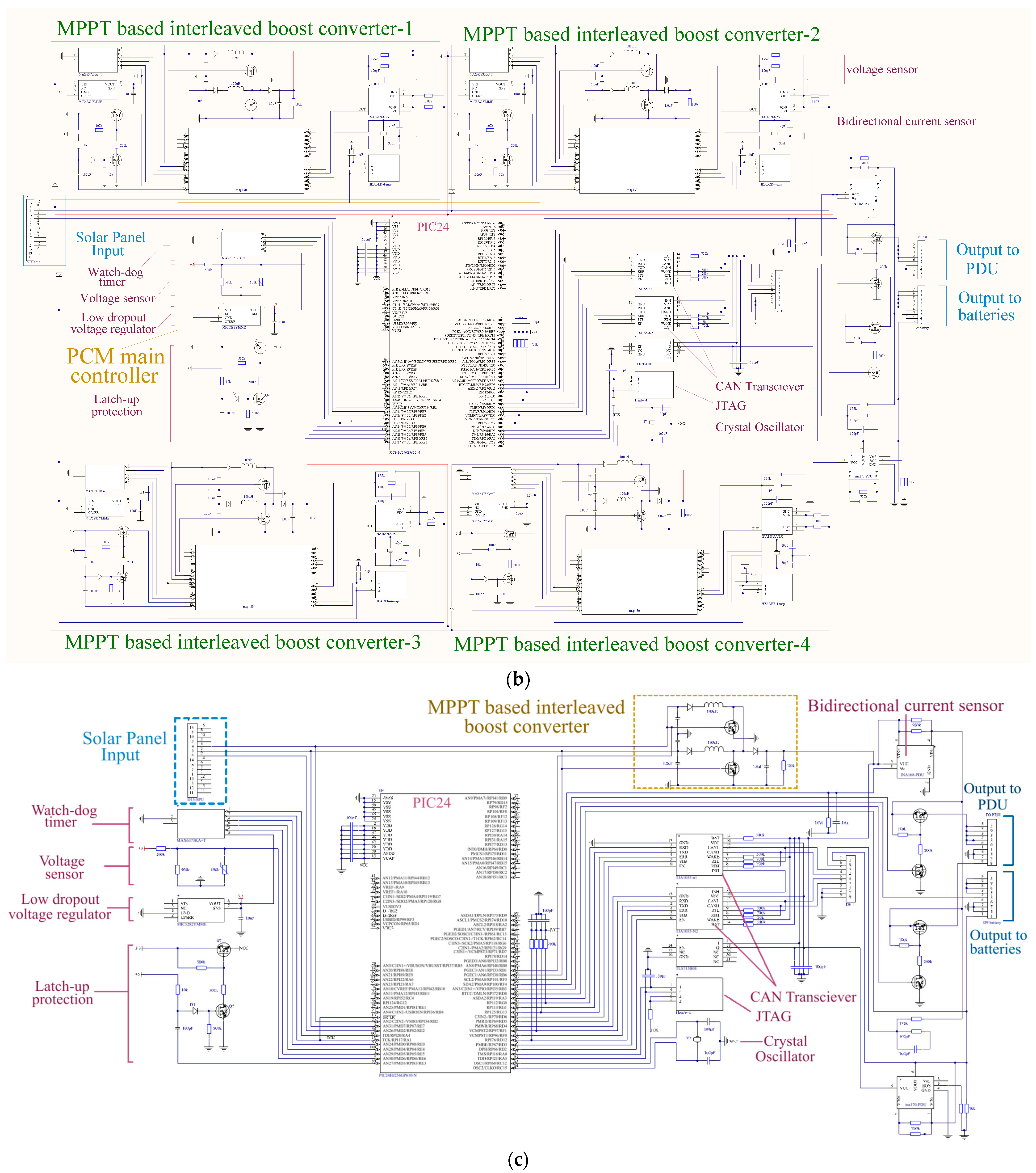
2.1. Schematic Design Description
2.2. MPPT Based on Constant Voltage Technique
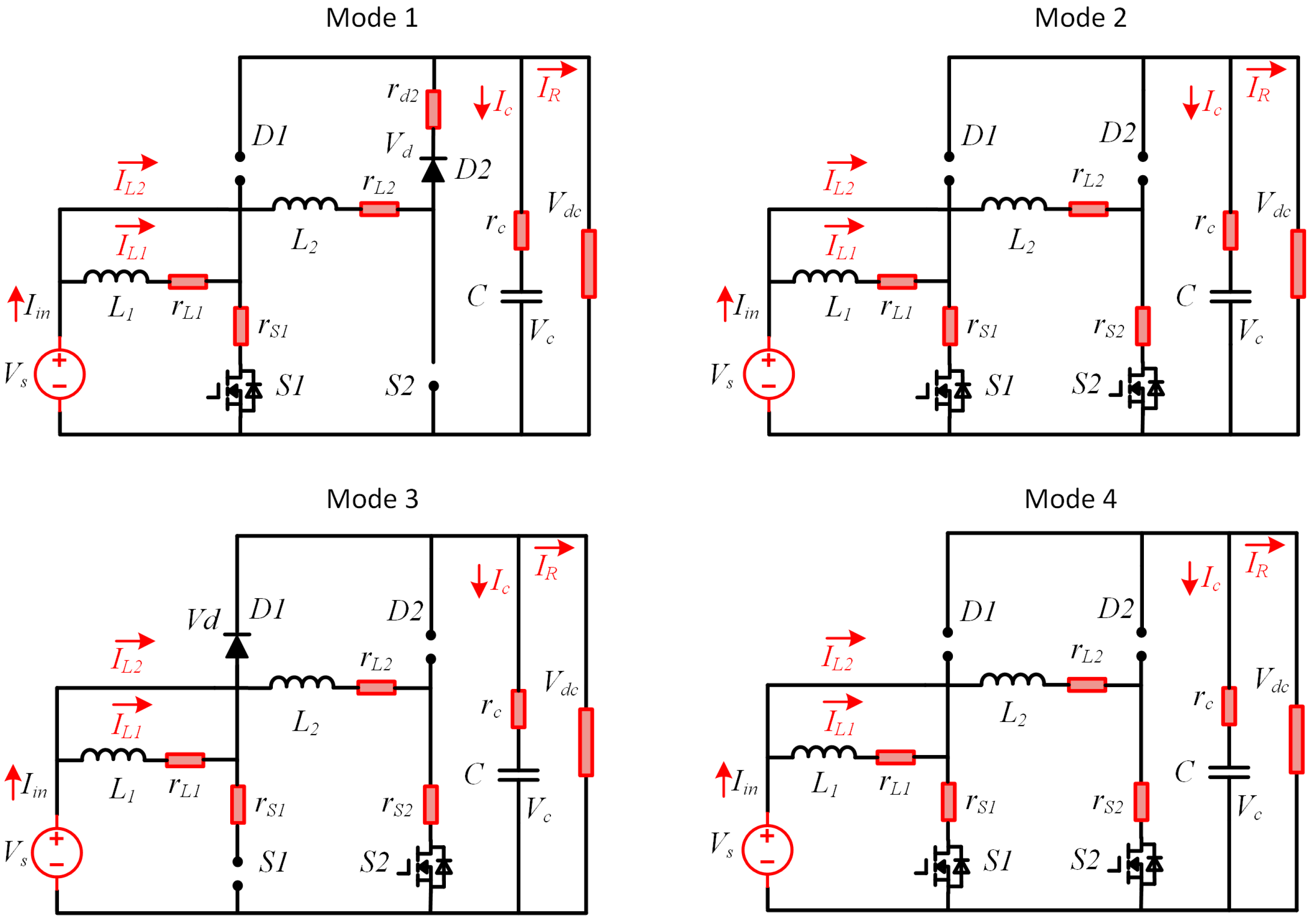
2.3. Mathematical Model
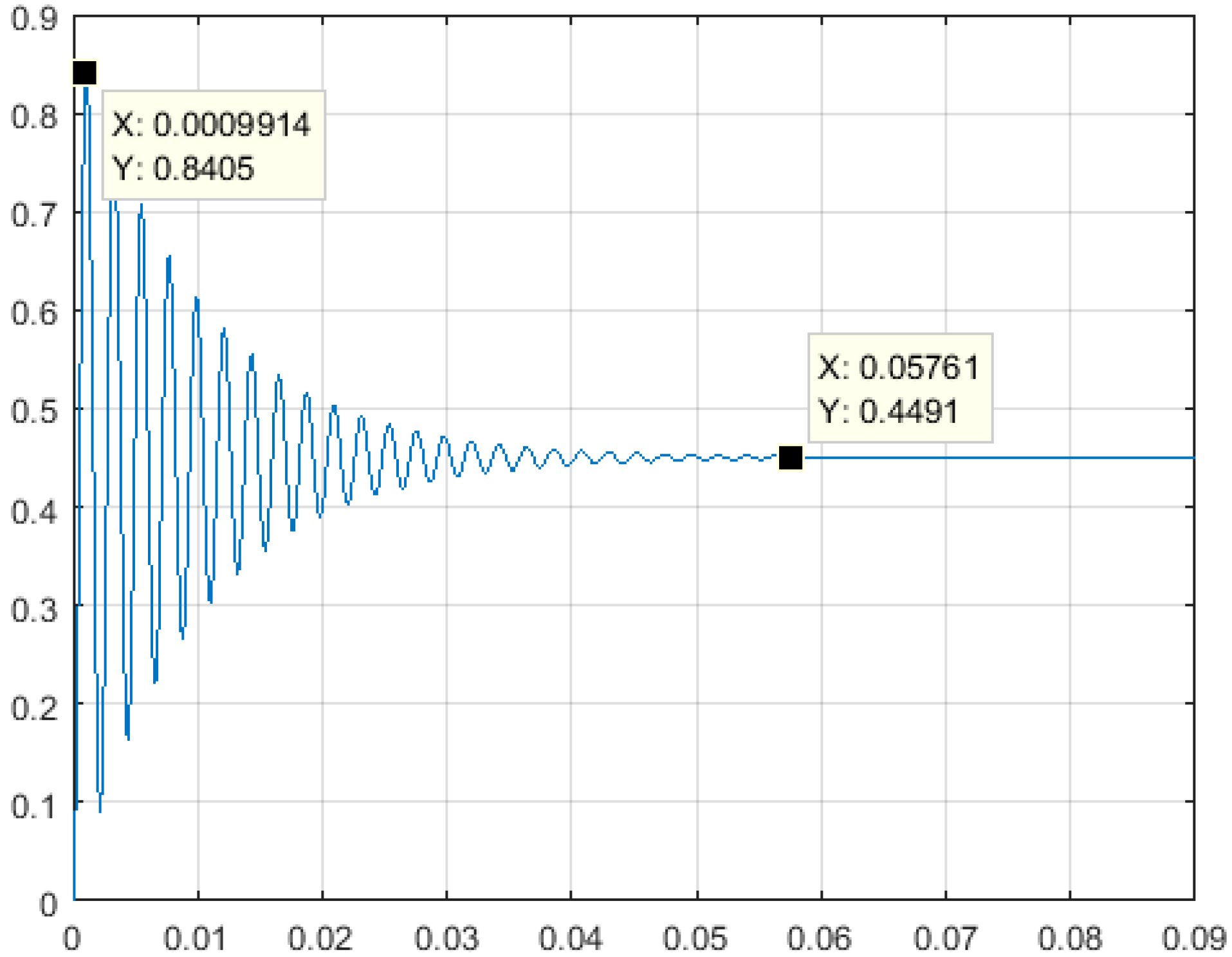
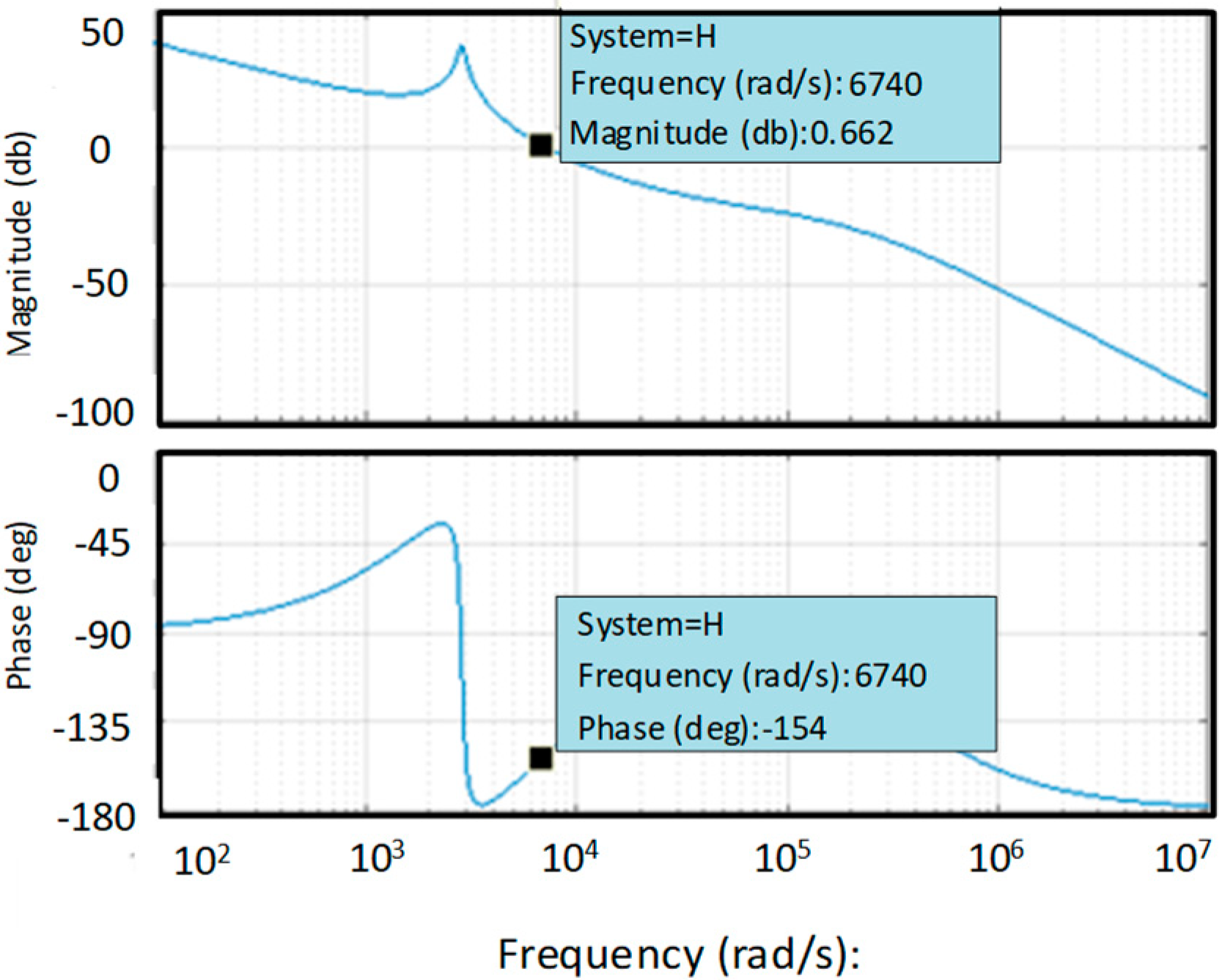
2.4. Stability Analysis of the Converter Without a Compensator
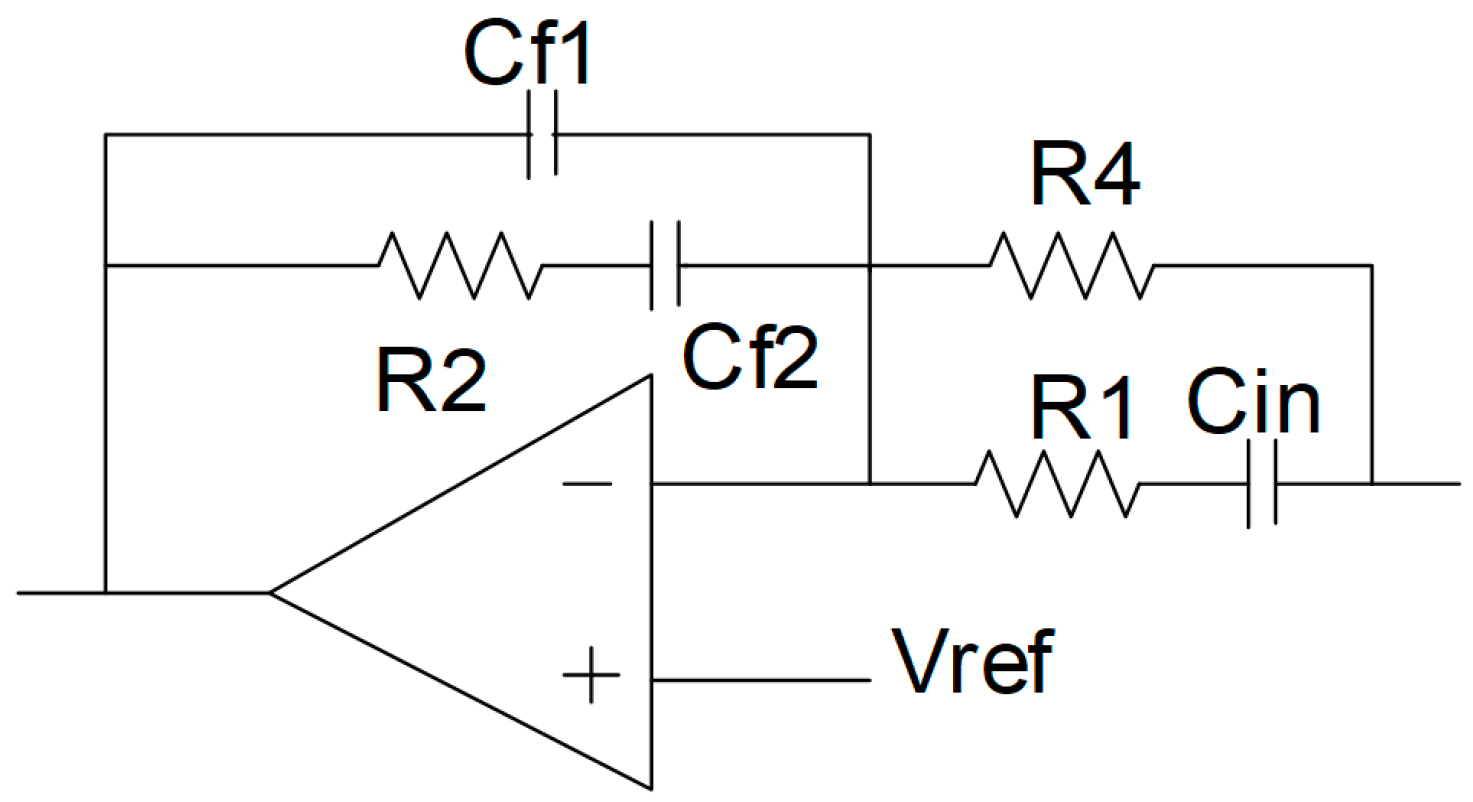
2.5. Compensator Design
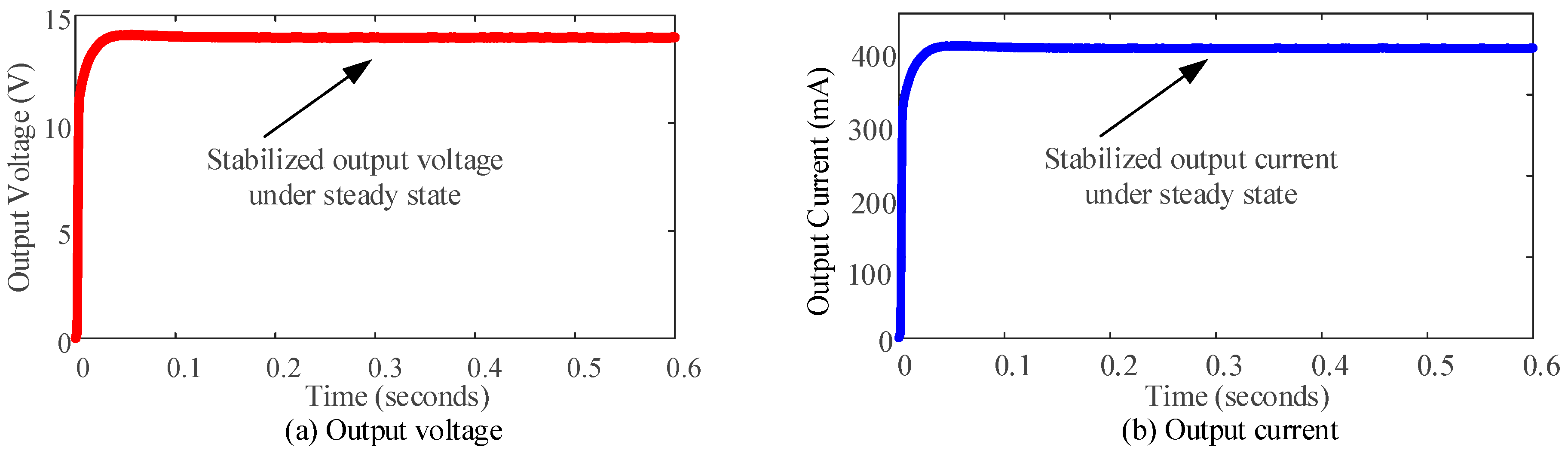
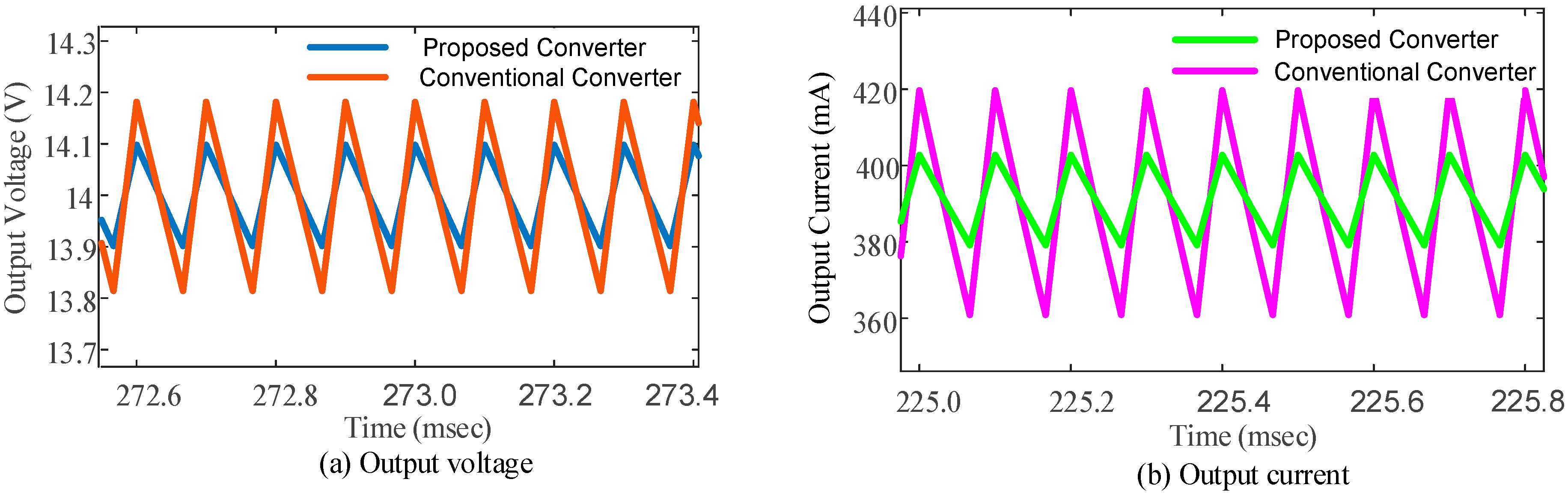
3. Simulation Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ahmed Khan, S.; Tao, Z.; Fahad, S.; Salman, M.; Tahir, M.; Ali, A. Reliable Attitude Control Integrating Reaction Wheels and Embedded Asymmetric Magnetorquers for Detumbling CubeSats. Adv. Sp. Res. 2024, in press. [CrossRef]
- Olsen, J. The Possibility of Powering a Light Aircraft by Releasing the Energy Stored in Hydrogen within a Fuel Cell Stack. Aerospace 2024, 11, 469. [Google Scholar] [CrossRef]
- Orts, C.; Garrigós, A.; Marroquí, D.; Arrizabalaga, A.; Franke, A. Enabling High-Power Conditioning and High-Voltage Bus Integration Using Series-Connected DC Transformers in Spacecrafts. Aerospace 2024, 11, 690. [Google Scholar] [CrossRef]
- Ahmed Khan, S.; Ali, A.; Shiyou, Y.; Fahad, S.; Tong, J. Optimized Design and Analysis of Printed Magnetorquer for a 3-U Nano-Satellite. J. Aerosp. Eng. 2022, 35, 04021103. [Google Scholar] [CrossRef]
- Ali, A.; Mughal, M.R.; Ali, H.; Reyneri, L.M.; Aman, M.N. Design, implementation, and thermal modeling of embedded reconfigurable magnetorquer system for nanosatellites. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2669–2679. [Google Scholar] [CrossRef]
- Ali, A.; Mughal, M.R.; Ali, H.; Reyneri, L. Innovative power management, attitude determination and control tile for CubeSat standard NanoSatellites. Acta Astronaut. 2014, 96, 116–127. [Google Scholar] [CrossRef]
- Ali, A.; Tong, J.; Ali, H.; Mughal, M.R.; Reyneri, L.M. A Detailed Thermal and Effective Induced Residual Spin Rate Analysis for LEO Small Satellites. IEEE Access 2020, 8, 146196–146207. [Google Scholar] [CrossRef]
- Khan, S.A.; Ali, A.; Shiyou, Y.; Tong, J. Reconfigurable Asymmetric Embedded Magnetorquers for Attitude Control of Nanosatellites. IEEE J. Miniaturization Air Sp. Syst. 2021, 2, 236–243. [Google Scholar] [CrossRef]
- Ali, A.; Khan, S.A.; Dildar, M.A.; Ali, H.; Ullah, N. Design & thermal modeling of solar panel module with embedded reconfigurable Air-Coil for micro-satellites. PLoS ONE 2018, 13, e0199145. [Google Scholar]
- Ahmed Khan, S.; Ali, A.; Shiyou, Y.; Tong, J.; Guerrero, J.M. Optimized Design of Embedded Air Coil for Small Satellites with Various Dimensions. J. Aerosp. Inf. Syst. 2021, 18, 269–279. [Google Scholar] [CrossRef]
- Llaveria, D.; Camps, A.; Park, H. Correcting the ADCS Jitter Induced Blurring in Small Satellite Imagery. IEEE J. Miniaturization Air Sp. Syst. 2020, 1, 130–137. [Google Scholar] [CrossRef]
- de Melo, A.C.C.P.; Cafe, D.C.; Alves Borges, R. Assessing Power Efficiency and Performance in Nanosatellite Onboard Computer for Control Applications. IEEE J. Miniaturization Air Sp. Syst. 2020, 1, 110–116. [Google Scholar] [CrossRef]
- Faria, R.P.; Gouvea, C.P.; De Castro, J.C.V.; Rocha, R. Design and implementation of a photovoltaic system for artificial satellites with regulated DC bus. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017. [Google Scholar]
- Lee, J.; Kim, E.; Shin, K.G. Design and management of satellite power systems. In Proceedings of the 2013 IEEE 34th Real-Time Systems Symposium, Vancouver, BC, Canada, 3–6 December 2013. [Google Scholar]
- Binxin, Z.H.; Jiaxin, L.I.; Yu, L.I.; Kaihong, W.A. Fault-tolerance wide voltage conversion gain DC/DC converter for more electric aircraft. Chinese J. Aeronaut. 2023, 36, 420–429. [Google Scholar]
- Bai, Y.; Hu, S.; Yang, Z.; Tahir, M.; Zhi, Y. A Selective Common Mode Noise Mitigation Method Using Phase-Shifted Modulation for Four-Switch Buck–Boost DC/DC Converter. IEEE Trans. Power Electron. 2023, 38, 7183–7196. [Google Scholar] [CrossRef]
- Hu, S.; Tahir, M. Editorial: Modular power converters for renewable energy integration. Front. Energy Res. 2023, 10, 1060071. [Google Scholar] [CrossRef]
- Tahir, M.; Hu, S.; Liang, Z.; Meng, Y. Unit Partition Resonance Analysis Strategy for Impedance Network in Modular Power Converters. Front. Energy Res. 2022, 10, 823938. [Google Scholar] [CrossRef]
- Tahir, M.; Hu, S.; Zhu, H. Advanced Levelized Cost Evaluation Method for Electric Vehicle Stations Concurrently Producing Electricity and Hydrogen. Energies 2024, 17, 2682. [Google Scholar] [CrossRef]
- Tahir, M.; Hu, S.; Khan, T.; Zhu, H. Multi-energy station design for future electric vehicles: A synergistic approach starting from scratch. Appl. Energy 2024, 372, 123765. [Google Scholar] [CrossRef]
- Tahir, M.; Hu, S.; Khan, T.; Zhu, H. Sustainable hybrid station design framework for electric vehicle charging and hydrogen vehicle refueling based on multiple attributes. Energy Convers. Manag. 2024, 300, 117922. [Google Scholar] [CrossRef]
- Khan, T.; Tahir, M.; Agyekum, E.B.; Yu, M. A multi-criteria design framework for sustainable electric vehicles stations. Sustain. Cities Soc. 2024, 101, 105076. [Google Scholar] [CrossRef]
- Tahir, M.; Hu, S.; Zhu, H. Strategic operation of electric vehicle in residential microgrid with vehicle-to-home features. Energy 2024, 308, 132772. [Google Scholar] [CrossRef]
- Khan, S.A.; Tao, Z.; Agyekum, E.B.; Fahad, S.; Tahir, M.; Salman, M. Sustainable rural electrification: Energy-economic feasibility analysis of autonomous hydrogen-based hybrid energy system. Int. J. Hydrogen Energy 2024, in press. [CrossRef]
- Zhang, Z.; Zhang, R.; Jihong, Z.H.; Tong, G.A.; Fei, C.H.; Zhang, W. Integrated batteries layout and structural topology optimization for a solar-powered drone. Chin. J. Aeronaut. 2021, 34, 114–123. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, S.; Diepolder, J.; Holzapfel, F. Battery package design optimization for small electric aircraft. Chin. J. Aeronaut. 2020, 33, 2864–2876. [Google Scholar] [CrossRef]
- Gorji, J.G.; Abbaszadeh, K.; Bagheroskouei, F. A New Two-input and Multi-output Interleaved DC_DC Boost. Converter for Satellites Power system. In Proceedings of the 2019 10th International Power Electronics, Drive Systems and Technologies Conference (PEDSTC), Shiraz, Iran, 12–14 February 2019. [Google Scholar]
- Uno, M.; Inoue, M.; Sato, Y.; Nagata, H. Bidirectional Interleaved PWM Converter with High Voltage-Conversion Ratio and Automatic Current Balancing Capability for Single-Cell Battery Power System in Small Scientific Satellites. Energies 2018, 11, 2702. [Google Scholar] [CrossRef]
- Li, X.; Mi, J.; Zhang, Y.; Fan, G.; Jie, D.U. Distributed power conditioning unit of large-scale space solar power station. Chin. J. Aeronaut. 2024, 37, 421–434. [Google Scholar] [CrossRef]
- Salas, V.; Olías, E.; Barrado, A.; Lázaro, A. Review of the maximum power point tracking algorithms for stand-alone photovoltaic systems. Sol. Energy Mater. Sol. Cells 2006, 90, 1555–1578. [Google Scholar] [CrossRef]
- Jeong, D.E.; Ko, J.S.; Lee, J.G.; Chung, D.H. MPPT control of photovoltaic system using optimization voltage with temperature. In Proceedings of the 2012 12th International Conference on Control, Automation and Systems, Jeju Island, Republic of Korea, 17–21 October 2012. [Google Scholar]
- Ahmed khan, S.; Shiyou, Y.; Ali, A.; Rao, S.; Fahad, S.; Jing, W.; Tong, J.; Tahir, M. Active attitude control for microspacecraft; A survey and new embedded designs. Adv. Space Res. 2022, 69, 3741–3769. [Google Scholar] [CrossRef]
- Ahmed khan, S.; Shiyou, Y.; Ali, A.; Tahir, M.; Fahad, S.; Rao, S. CubeSats detumbling using only embedded asymmetric magnetorquers. Adv. Space Res. 2023, 71, 2140–2154. [Google Scholar] [CrossRef]
- Ali, A.; Khan, S.A.; Usman Khan, M.; Ali, H.; Rizwan Mughal, M.; Praks, J. Design of modular power management and attitude control subsystems for a microsatellite. Int. J. Aerosp. Eng. 2018, 2018, 2515036. [Google Scholar] [CrossRef]
- Khan, S.A.; Shiyou, Y.; Ali, A.; Tahir, M.; Fahad, S.; Rao, S.; Waseem, M. PCB-integrated embedded planar magnetorquers for small satellites intelligent detumbling. Comput. Electr. Eng. 2023, 108, 108719. [Google Scholar] [CrossRef]
- Tahir, M.; Ahmed Khan, S.; Khan, T.; Waseem, M.; Khan, D.; Annuk, A. More electric aircraft challenges: A study on 270 V/90 V interleaved bidirectional DC–DC converter. Energy Rep. 2022, 8, 1133–1140. [Google Scholar] [CrossRef]
- Zhu, H.; Hu, S.; Tahir, M.; Bai, Y.; Wu, X. CLLC Modeling and Control in V2G Mode to Mitigate Double-Line Frequency Current for High-Power Density On-Board Charger. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 219–230. [Google Scholar] [CrossRef]
- Jeyaseelan, C.; Jain, A.; Khurana, P.; Kumar, D.; Thatai, S. Ni-Cd Batteries. Recharg. Batter. Hist. Prog. Appl. 2020, 2020, 177–194. [Google Scholar]





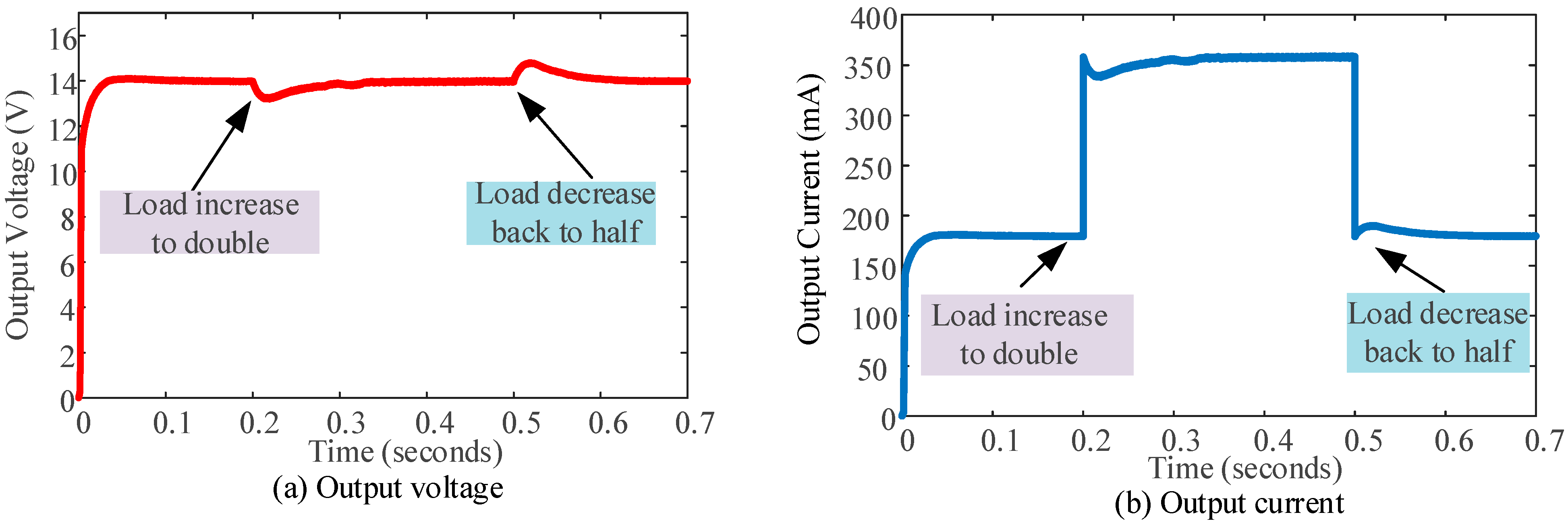
| Parameter | Requirement | Achieved Result |
|---|---|---|
| Voltage ripple | up to 5% of output voltage | 2% |
| Current ripple | 10% to 20% of load current | 7.5% |
| Voltage overshoot under load change | 10% to 20% of output voltage | 2.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, S.A.; Ali, A.; Tahir, M.; Tao, Z. Efficient Power Conditioning: Enhancing Electric Supply for Small Satellite Missions. Aerospace 2024, 11, 920. https://doi.org/10.3390/aerospace11110920
Khan SA, Ali A, Tahir M, Tao Z. Efficient Power Conditioning: Enhancing Electric Supply for Small Satellite Missions. Aerospace. 2024; 11(11):920. https://doi.org/10.3390/aerospace11110920
Chicago/Turabian StyleKhan, Shoaib Ahmed, Anwar Ali, Mustafa Tahir, and Zou Tao. 2024. "Efficient Power Conditioning: Enhancing Electric Supply for Small Satellite Missions" Aerospace 11, no. 11: 920. https://doi.org/10.3390/aerospace11110920
APA StyleKhan, S. A., Ali, A., Tahir, M., & Tao, Z. (2024). Efficient Power Conditioning: Enhancing Electric Supply for Small Satellite Missions. Aerospace, 11(11), 920. https://doi.org/10.3390/aerospace11110920






