Autonomous and Earth-Independent Orbit Determination for a Lunar Navigation Satellite System
Abstract
:1. Introduction
2. Lunar Scenario
2.1. Orbital Design
2.2. Satellite Design
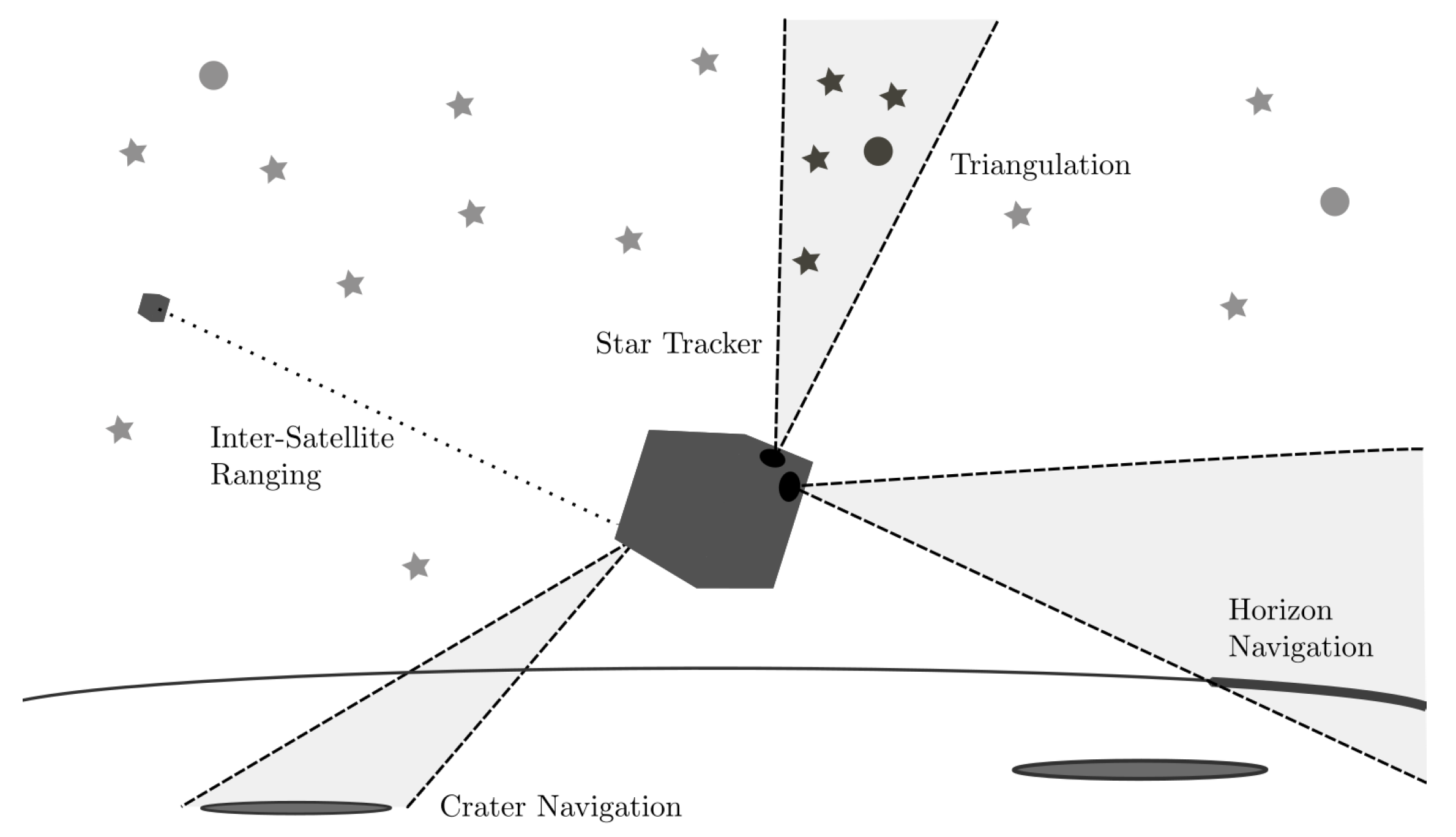
3. Proposed Sensors
3.1. Star Tracker
3.2. Horizon Navigation
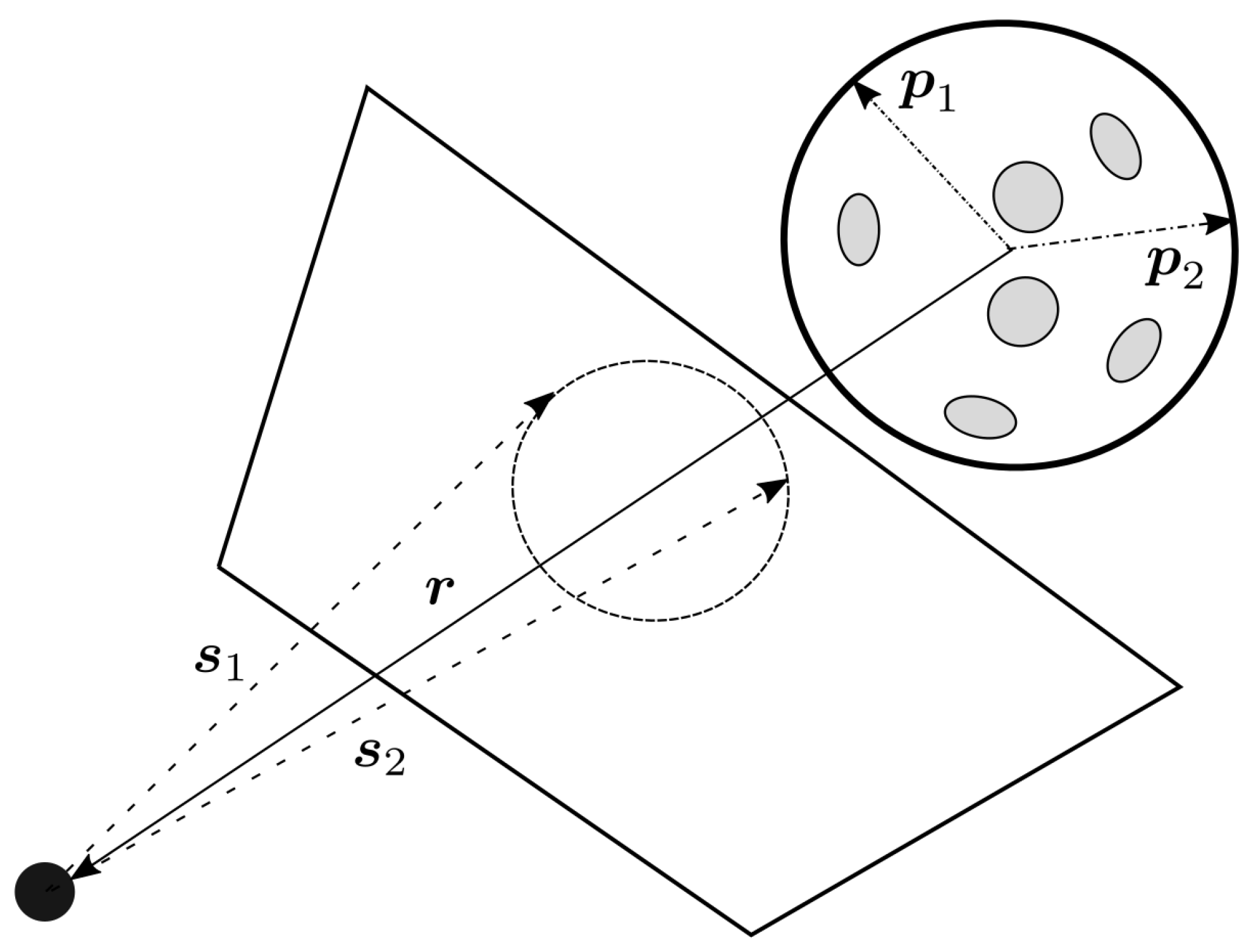
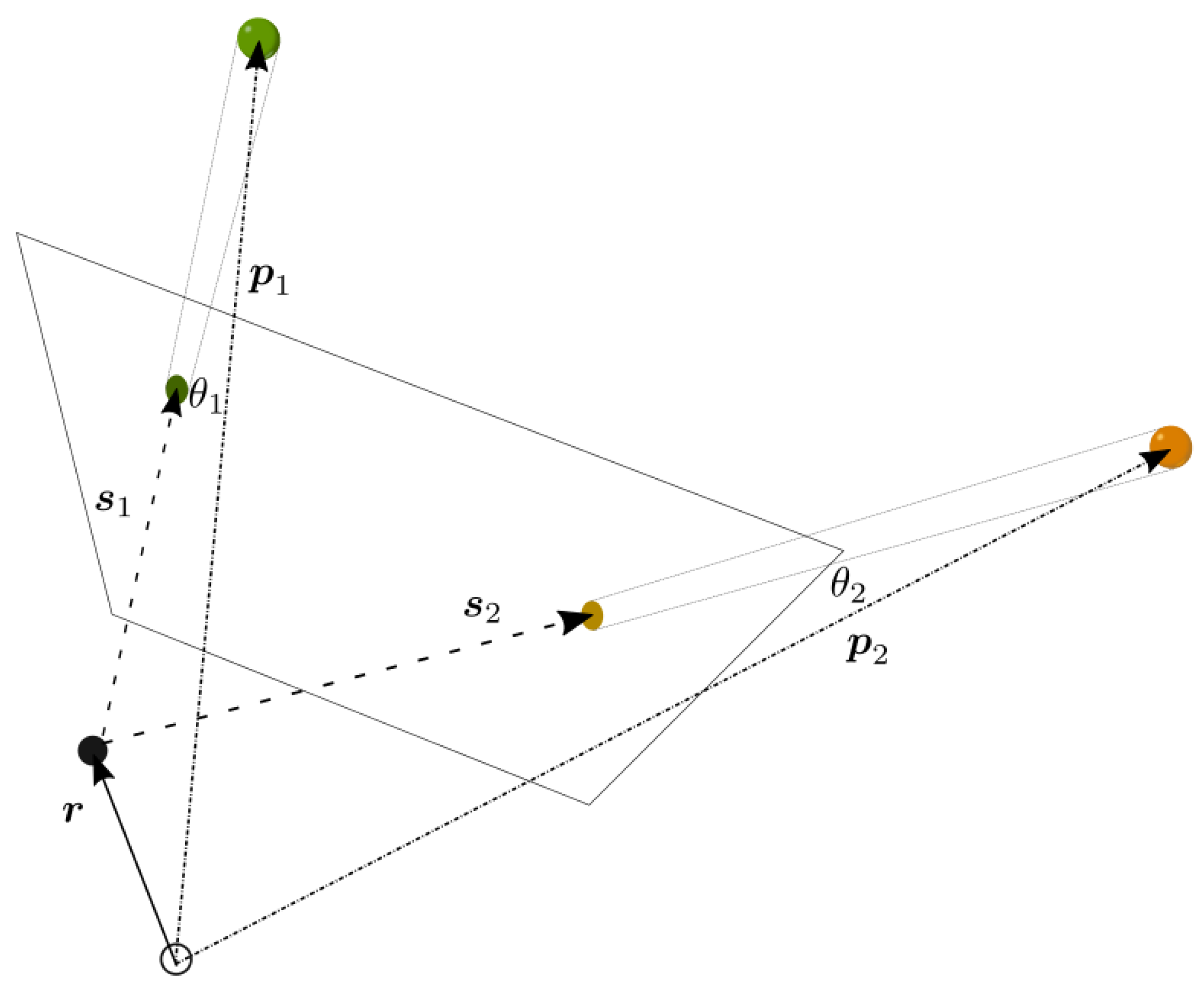
3.3. Triangulation
3.4. Crater Navigation
3.5. Inter-Satellite Ranging
4. Lunar Orbital Filter
4.1. Orbital Propagation
4.2. Kalman Filter Application
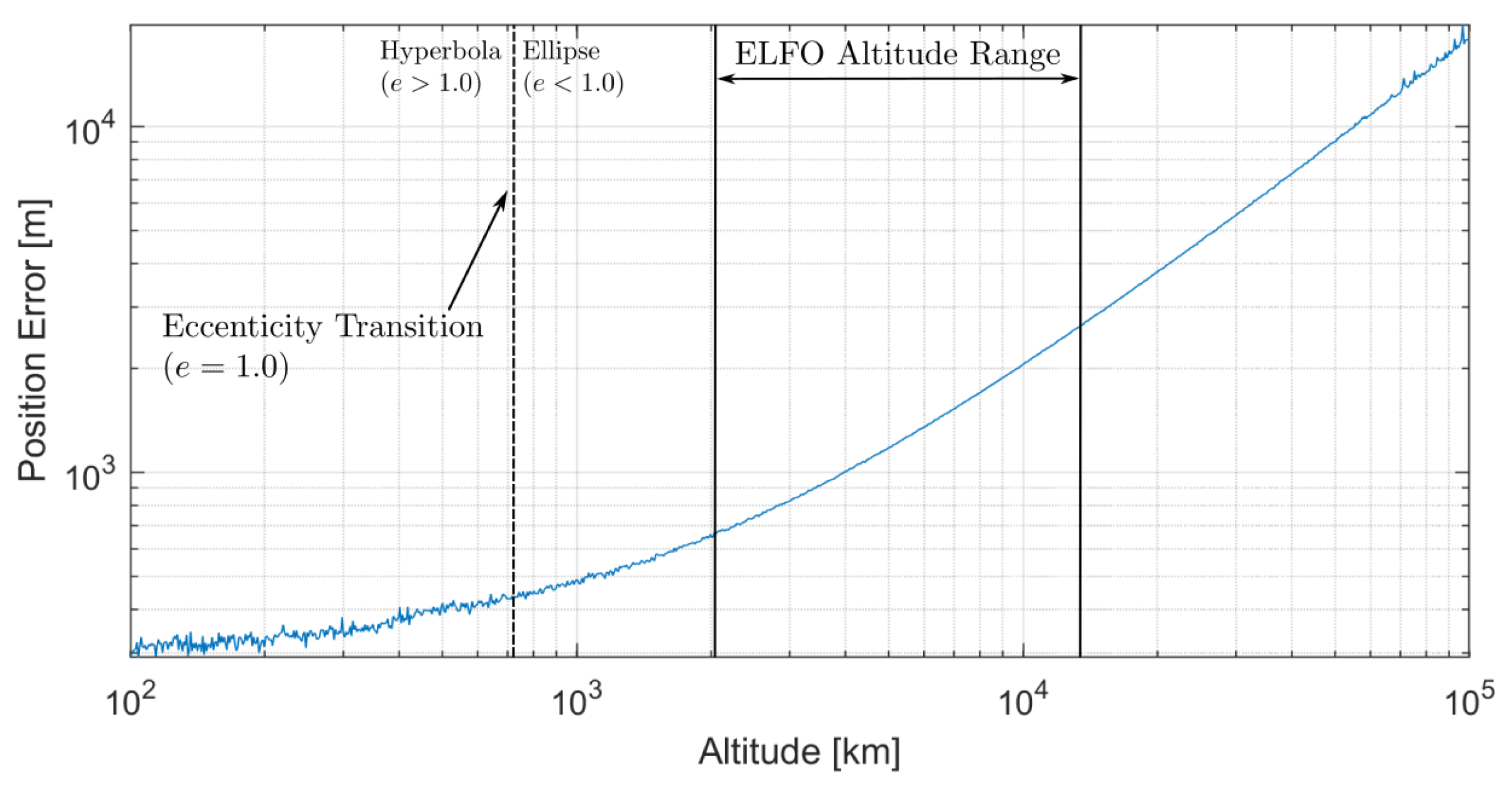
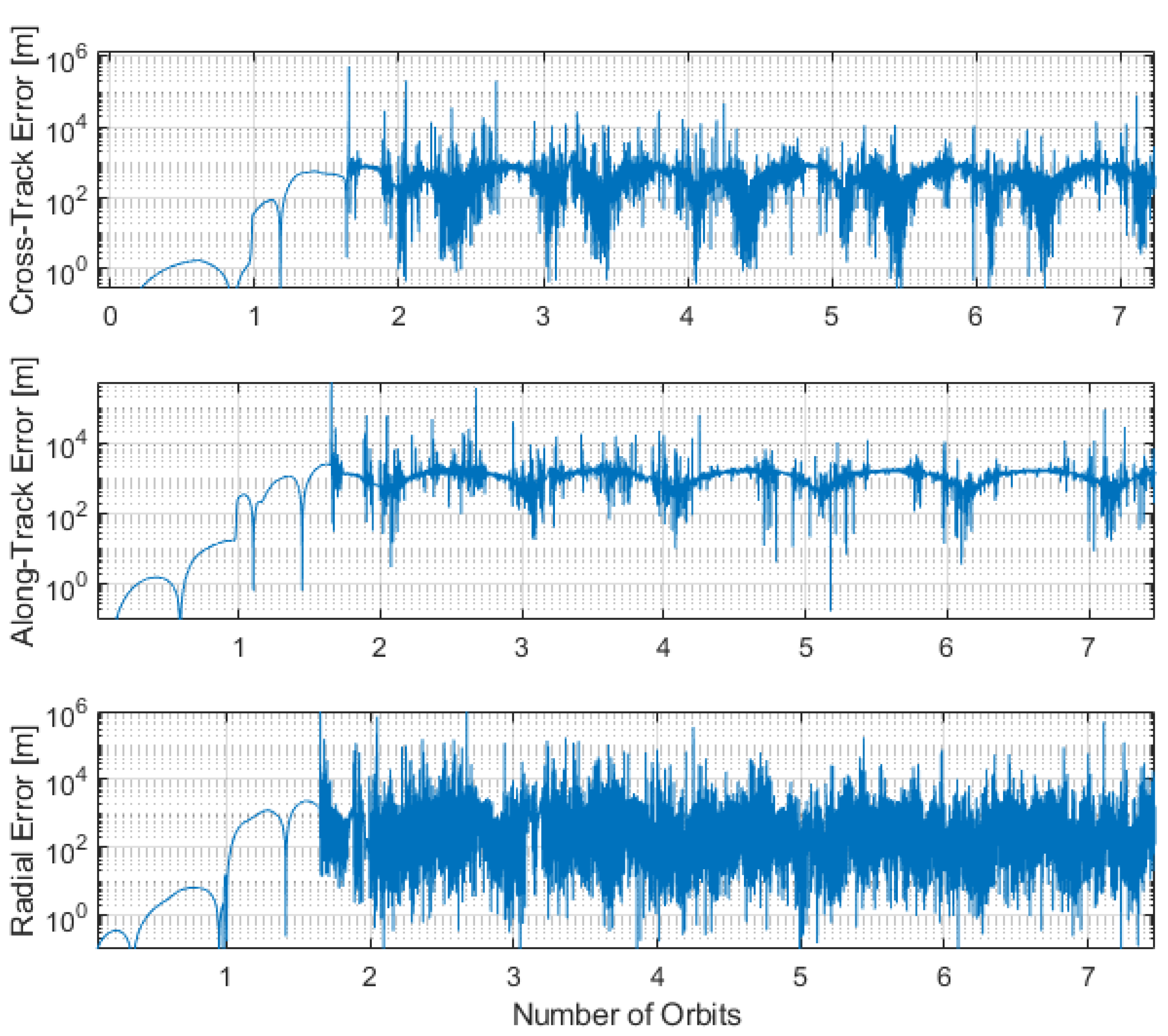
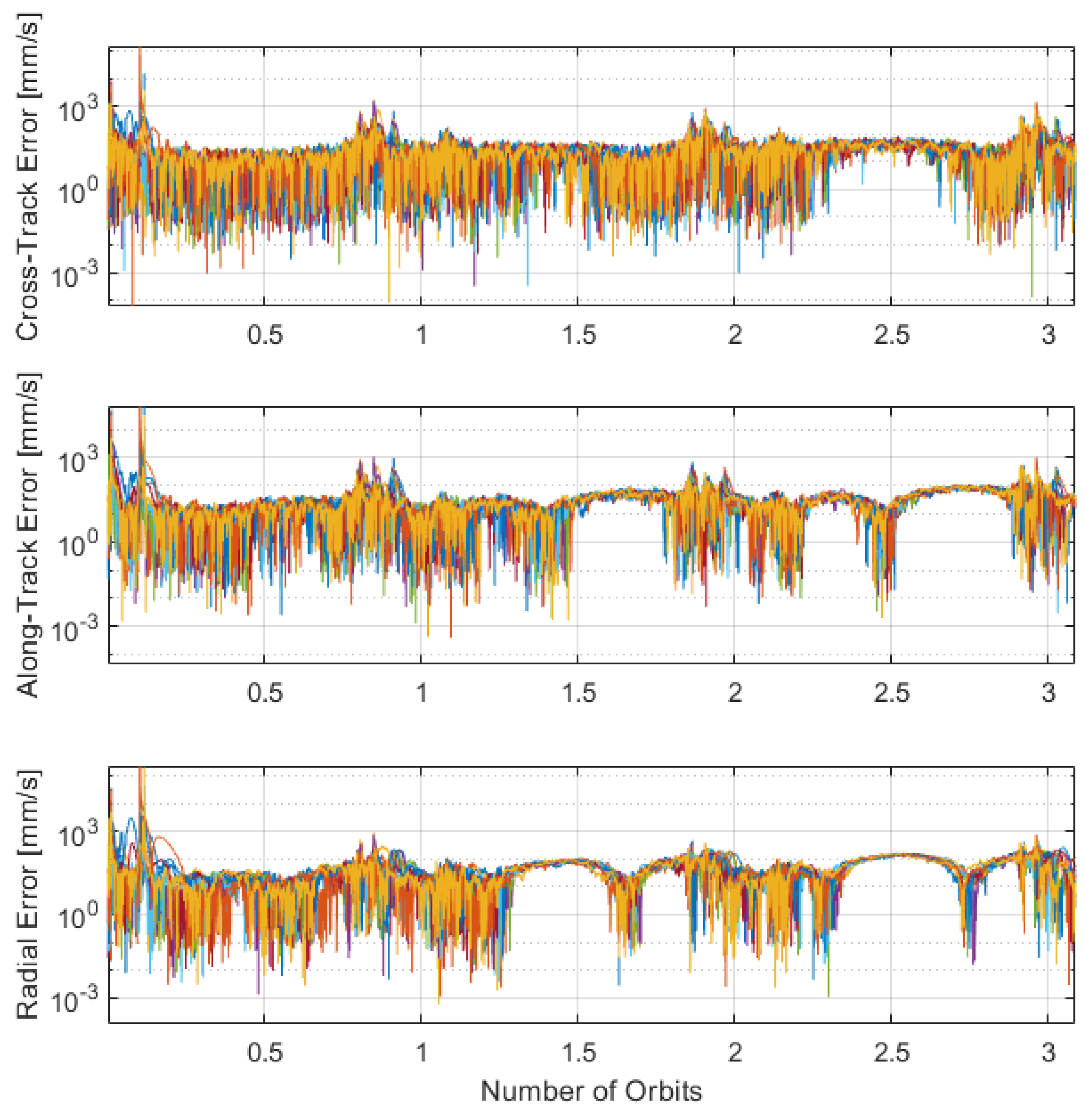
4.3. Kalman Filter Performances
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tripathi, S. It’s Going to Get Very Busy on the Moon; India Today: New Delhi, India, 2022. [Google Scholar]
- Skibba, R. Humans Are Revisiting the Moon—And the Rules of Spacefaring; Wired Magazine: New York, NY, USA, 2022. [Google Scholar]
- McKie, R. The Moon, Mars and Beyond… the Space Race in 2020. In The Observer; The Guardian: London, UK, 2020. [Google Scholar]
- Israel, D.J.; Mauldin, K.D.; Roberts, C.J.; Mitchell, J.W.; Pulkkinen, A.A.; Cooper, L.V.D.; Johnson, M.A.; Christe, S.D.; Gramling, C.J. LunaNet: A Flexible and Extensible Lunar Exploration Communications and Navigation Infrastructure. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–14. [Google Scholar] [CrossRef]
- Giordano, P.; Grenier, A.; Zoccarato, P.; Bucci, L.; Cropp, A.; Swinden, R.; Gomez Otero, D.; El-Dali, W.; Carey, W.; Duvet, L.; et al. Moonlight navigation service—How to land on peaks of eternal light. In Proceedings of the 72nd International Astronautical Congress, Dubai, United Arab Emirates, 25–29 October 2021; pp. 1–14. [Google Scholar]
- Kakihara, K.; Shibukawa, T.; Takahashi, R.; Tsuji, M.; Chikazawa, T.; Suzuki, N.; Ichimura, S.; Nakahashi, S.; Shinbo, H.; Takahashi, T.; et al. Study on Lunar Communications and Navigation Architecture Utilizing Micro-Satellites. In Proceedings of the 66th Joint Conference on Space Science and Technology, Kumamoto, Japan, 8–10 November 2022; pp. 1–6. [Google Scholar]
- Ogino, K.; Kawabata, Y. Research on orbit optimization of lunar South Pole positioning by small satellites focusing on elliptical orbit. In Proceedings of the 66th 34th International Symposium on Space Technology and Science, Kurume, Japan, 3–9 June 2023; pp. 1–8. [Google Scholar]
- Kim, Y.R.; Song, Y.J.; Park, J.I.; Lee, D.; Bae, J.; Hong, S.; Kim, D.K.; Lee, S.R. Ground Tracking Support Condition Effect on Orbit Determination for Korea Pathfinder Lunar Orbiter (KPLO) in Lunar Orbit. J. Astron. Space Sci. 2020, 37, 237–247. [Google Scholar] [CrossRef]
- Iiyama, K.; Bhamidipati, S.; Gao, G. Precise Positioning and Timekeeping in Lunar Orbit via Terrestrial GPS Time-Differenced Carrier-Phase Measurements. In Proceedings of the 2023 International Technical Meeting of The Institute of Navigation, Long Beach, CA, USA, 24–26 January 2023; pp. 213–232. [Google Scholar] [CrossRef]
- Parker, J.J.K.; Dovis, F.; Anderson, B.; Ansalone, L.; Ashman, B.; Bauer, F.H.; D’Amore, G.; Facchinetti, C.; Fantinato, S.; Impresario, G.; et al. The Lunar GNSS Receiver Experiment (LuGRE). In Proceedings of the 2022 International Technical Meeting of the Institute of Navigation, Long Beach, CA, USA, 25–27 January 2022; pp. 420–437. [Google Scholar] [CrossRef]
- Christian, J.A. A Tutorial on Horizon-Based Optical Navigation and Attitude Determination with Space Imaging Systems. IEEE Access 2021, 9, 19819–19853. [Google Scholar] [CrossRef]
- Franzese, V.; Di Lizia, P.; Topputo, F. Autonomous Optical Navigation for LUMIO Mission. In Proceedings of the 2018 Space Flight Mechanics Meeting. American Institute of Aeronautics and Astronautics, 2018, AIAA SciTech Forum, Kissimmee, FL, USA, 8–12 January 2018; pp. 1–11. [Google Scholar] [CrossRef]
- Zanetti, R.; Crouse, B.; D’souza, C. Autonomous Optical Lunar Navigation. In Proceedings of the AAS Spaceflight Mechanic Conference, Savannah, GA, USA, 8–12 February 2009; pp. 1–3. [Google Scholar]
- Mortari, D.; D’Souza, C.; Zanetti, R. Image Processing of Illuminated Ellipsoid. J. Spacecr. Robot. 2016, 53, 448–456. [Google Scholar] [CrossRef]
- Critchley-Marrows, J.; Wu, X.; Cairns, I. Stellar Navigation on the Moon—A Compliment, Support and Back-up to Lunar Navigation. In Proceedings of the ION ITM 2022, Long Beach, CA, USA, 25–27 January 2022; pp. 616–631. [Google Scholar]
- Maass, B.; Woicke, S.; Oliveira, W.M.; Razgus, B.; Krüger, H. Crater Navigation System for Autonomous Precision Landing on the Moon. J. Guid. Control. Dyn. 2020, 43, 1414–1431. [Google Scholar] [CrossRef]
- Qi, D.; Oguri, K. Investigation on Autonomous Orbit Determination in Cislunar Space via GNSS and Horizon-based Measurements. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, Orlando, FL, USA, 8–12 January 2023; pp. 1–20. [Google Scholar]
- Iiyama, K.; Kawabata, Y.; Funase, R. Autonomous and Decentralized Orbit Determination and Clock Offset Estimation of Lunar Navigation Satellites Using GPS Signals and Inter-satellite Ranging. In Proceedings of the ION GNSS+ 2021, St. Louis, MO, USA, 20–24 September2021; pp. 936–949. [Google Scholar]
- Hesar, S.G.; Parker, J.S.; Leonard, J.M.; McGranaghan, R.M.; Born, G.H. Lunar far side surface navigation using Linked Autonomous Interplanetary Satellite Orbit Navigation (LiAISON). Acta Astronaut. 2015, 117, 116–129. [Google Scholar] [CrossRef]
- Critchley-Marrows, J.; Kawabata, Y.; Ogino, K.; Nakasuka, S. Autonomous Orbit Determination for Lunar Satellite Infrastructure in View of Continuity and Assurance. In Proceedings of the International Symposium on Space Technology and Science, Kurume, Japan, 3–9 June 2023; pp. 1–8. [Google Scholar]
- Flahaut, J.; Carpenter, J.; Williams, J.P.; Anand, M.; Crawford, I.A.; van Westrenen, W.; Füri, E.; Xiao, L.; Zhao, S. Regions of interest (ROI) for future exploration missions to the lunar South Pole. Planet. Space Sci. 2020, 180, 104750. [Google Scholar] [CrossRef]
- Bender, T.E.; Gabhart, A.S.; Steffens, M.J.; Mavris, D.N. Defining and Parameterizing the Design Space for Cislunar PNT Architectures. In Proceedings of the AIAA SCITECH 2023 Forum. American Institute of Aeronautics and Astronautics, 2023, AIAA SciTech Forum, National Harbor, MA, USA, 23–27 January 2023; pp. 1504–1510. [Google Scholar] [CrossRef]
- Pasquale, A.; Zanotti, G.; Prinetto, J.; Ceresoli, M.; Lavagna, M. Cislunar distributed architectures for communication and navigation services of lunar assets. Acta Astronaut. 2022, 199, 345–354. [Google Scholar] [CrossRef]
- Pereira, F.; Reed, P.M.; Selva, D. Multi-Objective Design of a Lunar GNSS. NAVIGATION J. Inst. Navig. 2022, 69, navi.504. [Google Scholar] [CrossRef]
- Zanotti, G.; Ceresoli, M.; Pasquale, A.; Prinetto, J.; Lavagna, M. High performance lunar constellation for navigation services to Moon orbiting users. Adv. Space Res. 2023; in press. [Google Scholar] [CrossRef]
- Ely, T.A. Stable Constellations of Frozen Elliptical Inclined Lunar Orbits. JAnSc 2005, 53, 301–316. [Google Scholar] [CrossRef]
- A Standardized Lunar Coordinate System for the Lunar Reconnaissance Orbiter and Lunar Datasets; National Aeronautics and Space Administration (NASA): Moffett Field, CA, USA, 2008.
- Montenbruck, O.; Gill, E. Satellite Orbits–Models, Methods, Applications; Springer: Berlin, Germany, 2000. [Google Scholar]
- Markley, F.L.; Crassidis, J.L. Filtering for Attitude Estimation and Calibration. In Fundamentals of Spacecraft Attitude Determination and Control; Springer Science and Business Media: New York, NY, USA, 2014; pp. 235–343. [Google Scholar]
- Liebe, C.C. Accuracy performance of star trackers—A tutorial. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 587–599. [Google Scholar] [CrossRef]
- Critchley-Marrows, J.; Wu, X. Investigation into Star Tracker Algorithms using Smartphones with Application to High-Precision Pointing CubeSats. Trans. Jpn. Soc. Aeronaut. Space Sci. 2019, 17, 327–332. [Google Scholar] [CrossRef]
- Mortari, D.; Samaan, M.A.; Bruccoleri, C.; Junkins, J.L. The Pyramid star identification technique. Navig. J. Inst. Navig. 2004, 51, 171–183. [Google Scholar] [CrossRef]
- Brown, J.; Stubis, K.; Cahoy, K. TETRA: Star Identification with Hash Tables. In Proceedings of the 31st Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 5–10 August 2017; pp. 1–12. [Google Scholar]
- Suntup, M.; Cairns, I.; Critchley-Marrows, J.; Wu, X.; Albertson, D.; Guinane, J.; Jarvis, B. Implementation of a WFOV Star Tracker in CubeSat and Small Satellite Attitude Determination Systems. In Proceedings of the 43rd COSPAR Scientific Assembly, Sydney, Australia, 28 January–2 February 2021; Volume 43, p. 59. [Google Scholar]
- Christian, J.A.; Benhacine, L.; Hikes, J.; D’Souza, C. Geometric Calibration of the Orion Optical Navigation Camera using Star Field Images. J. Astronaut. Sci. 2016, 63, 335–353. [Google Scholar] [CrossRef]
- Critchley-Marrows, J.J.R.; Wu, X.; Cairns, I.H. An architecture for a visual-based PNT alternative. Acta Astronaut. 2023, 210, 601–609. [Google Scholar] [CrossRef]
- Mortari, D.; Romoli, A. StarNav III: A three fields of view star tracker. IEEE Aerosp. Conf. Proc. 2002, 1, 47–57. [Google Scholar] [CrossRef]
- Lampkin, B.A.; Smith, D.W. A Hand-Held Sextant Qualified for Space Flight; Technical Report; NASA: Washington, DC, USA, 1968. [Google Scholar]
- Critchley-Marrows, J.; Mortari, D. Vision-based navigation in low Earth orbit—Using the stars and horizon as an alternative PNT. Adv. Space Res. 2023, 71, 4802–4813. [Google Scholar] [CrossRef]
- Christian, J.A. Accurate Planetary Limb Localization for Image-Based Spacecraft Navigation. Am. Inst. Aeronaut. Astronaut. 2017, 54, 708–730. [Google Scholar] [CrossRef]
- Henry, S.; Christian, J.A. Absolute Triangulation Algorithms for Space Exploration. J. Guid. Control. Dyn. 2023, 46, 21–46. [Google Scholar] [CrossRef]
- Poirot, J.L.; McWilliams, G.V. Navigation by Back Triangulation. IEEE Trans. Aerosp. Electron. Syst. 1976, AES-12, 270–274. [Google Scholar] [CrossRef]
- Cleaver, R.F.; Sothcott, P.; Robinson, F.J. An automatic radio triangulation system. Proc. IEE—Part B Electron. Commun. Eng. 1960, 107, 22–32. [Google Scholar] [CrossRef]
- Dempster, A. Dilution of precision in angle-of-arrival positioning systems. Electron. Lett. 2006, 42, 291–292. [Google Scholar] [CrossRef]
- Cheng, Y.; Ansar, A. Landmark Based Position Estimation for Pinpoint Landing on Mars. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 1573–1578. [Google Scholar] [CrossRef]
- Leroy, B.; Medioni, G.; Johnson, E.; Matthies, L. Crater detection for autonomous landing on asteroids. Image Vis. Comput. 2001, 19, 787–792. [Google Scholar] [CrossRef]
- Christian, J.A.; Derksen, H.; Watkins, R. Lunar Crater Identification in Digital Images. J. Astronaut. Sci. 2021, 68, 1056–1144. [Google Scholar] [CrossRef]
- Hanak, C.; Crain, T. Crater Identification Algorithm for the Lost in Low Lunar Orbit Scenario. In Proceedings of the 33rd Annual AAS Guidance and Control, Breckenridge, CO, USA, 29 January–3 February 2010; pp. 1–27. [Google Scholar]
- Clerc, S.; Spigai, M.; Simard-Bilodeau, V. A crater detection and identification algorithm for autonomous lunar landing. IFAC Proc. Vol. 2010, 43, 527–532. [Google Scholar] [CrossRef]
- Park, W.; Jung, Y.; Bang, H.; Ahn, J. Robust Crater Triangle Matching Algorithm for Planetary Landing Navigation. J. Guid. Control. Dyn. 2019, 42, 402–410. [Google Scholar] [CrossRef]
- Silvestrini, S.; Piccinin, M.; Zanotti, G.; Brandonisio, A.; Bloise, I.; Feruglio, L.; Lunghi, P.; Lavagna, M.; Varile, M. Optical navigation for Lunar landing based on Convolutional Neural Network crater detector. Aerosp. Sci. Technol. 2022, 123, 107503. [Google Scholar] [CrossRef]
- Losiak, A.; Wilhelms, D.E.; Byrne, C.J.; Thaisen, K.; Weider, S.Z.; Kohout, T.; O’Sulllivan, K.; Kring, D.A. A New Lunar Impact Crater Database. In Proceedings of the 40th Lunar and Planetary Science Conference, The Woodlands, TX, USA, 23–27 March 2009; pp. 1–8. [Google Scholar]
- Fitzgibbon, A.; Pilu, M.; Fisher, R.B. Direct least square fitting of ellipses. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 476–480. [Google Scholar] [CrossRef]
- Abusali, P.A.M.; Tapley, B.D.; Schutz, B.E. Autonomous Navigation of Global Positioning System Satellites Using Cross-Link Measurements. J. Guid. Control. Dyn. 1998, 21, 321–327. [Google Scholar] [CrossRef]
- Chaudhry, A.U.; Lamontagne, G.; Yanikomeroglu, H. Laser Intersatellite Link Range in Free-Space Optical Satellite Networks: Impact on Latency. IEEE Aerosp. Electron. Syst. Mag. 2023, 38, 4–13. [Google Scholar] [CrossRef]
- Zech, H.; Biller, P.; Heine, F.; Motzigemba, M. Optical intersatellite links for navigation constellations. In Proceedings of the International Conference on Space Optics—ICSO 2018, Khania, Greece, 9–12 October 2018; SPIE: Stockholm, Sweden, 2019; Volume 11180, pp. 370–379. [Google Scholar] [CrossRef]
- Qin, T.; Macdonald, M.; Qiao, D. Fully Decentralized Cooperative Navigation for Spacecraft Constellations. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2383–2394. [Google Scholar] [CrossRef]
- Lidov, M.L. The evolution of orbits of artificial satellites of planets under the action of gravitational perturbations of external bodies. Planet. Space Sci. 1962, 9, 719–759. [Google Scholar] [CrossRef]
- Butcher, J.C. Numerical methods for ordinary differential equations in the 20th century. J. Comput. Appl. Math. 2000, 125, 1–29. [Google Scholar] [CrossRef]
- Kenneally, P.W.; Schaub, H. High Geometric Fidelity Solar Radiation Pressure Modeling usingGraphics Processing Unit. In Proceedings of the AAS/AIAA Spaceflight Mechanics Meeting, Napa Valley, CA, USA, 14–16 February 2016. [Google Scholar]
- di Stefano, I.; Cappuccio, P.; Iess, L. Precise Modeling of Non-Gravitational Accelerations of the Spacecraft BepiColombo During Cruise Phase. J. Spacecr. Rocket. 2023, 60, 1625–1638. [Google Scholar] [CrossRef]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. An Earth Gravitational Model to Degree 2160: EGM2008. In Proceedings of the General Assembly of the European Geosciences Union, Vienna, Austria, 13–18 April 2008. [Google Scholar]
- Lemoine, F.G.; Goossens, S.; Sabaka, T.J.; Nicholas, J.B.; Mazarico, E.; Rowlands, D.D.; Loomis, B.D.; Chinn, D.S.; Neumann, G.A.; Smith, D.E.; et al. GRGM900C: A degree 900 lunar gravity model from GRAIL primary and extended mission data. Geophys. Res. Lett. 2014, 41, 3382–3389. [Google Scholar] [CrossRef]
- Konopliv, A.S.; Asmar, S.W.; Carranza, E.; Sjogren, W.L.; Yuan, D.N. Recent Gravity Models as a Result of the Lunar Prospector Mission. Icarus 2001, 150, 1–18. [Google Scholar] [CrossRef]
- Montenbruck, O.; Ramos-Bosch, P. Precision real-time navigation of LEO satellites using global positioning system measurements. GPS Solut. 2008, 12, 187–198. [Google Scholar] [CrossRef]
- Lundberg, J.B.; Schutz, B.E. Recursion formulas of Legendre functions for use with nonsingular geopotential models. J. Guid. Control. Dyn. 1988, 11, 31–38. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Fluids Eng. Trans. ASME 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Carlson, N. Federated square root filter for decentralized parallel processors. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 517–525. [Google Scholar] [CrossRef]
- Crassidis, J.L.; Markley, F.L. Unscented filtering for spacecraft attitude estimation. J. Guid. Control. Dyn. 2003, 26, 536–542. [Google Scholar] [CrossRef]



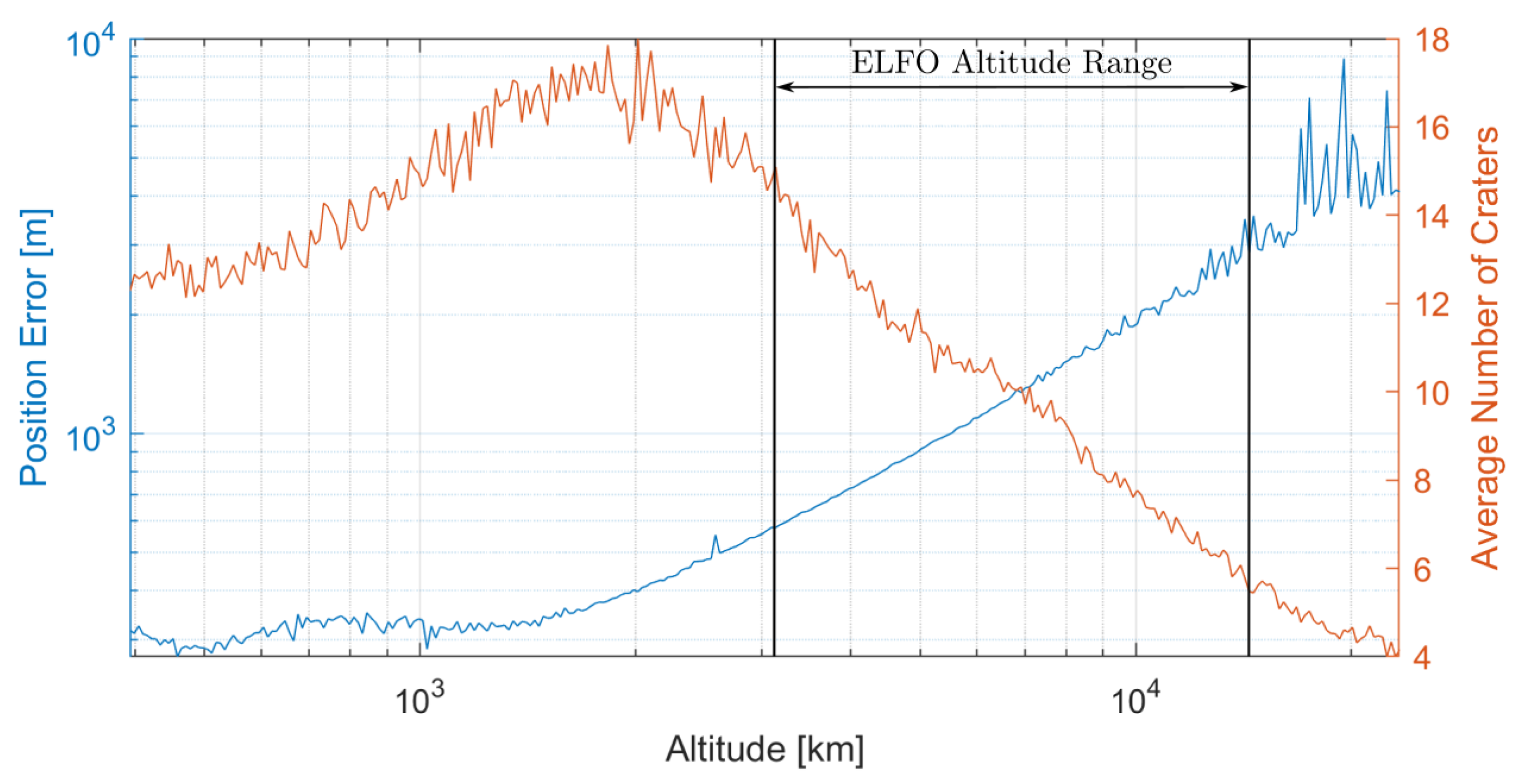
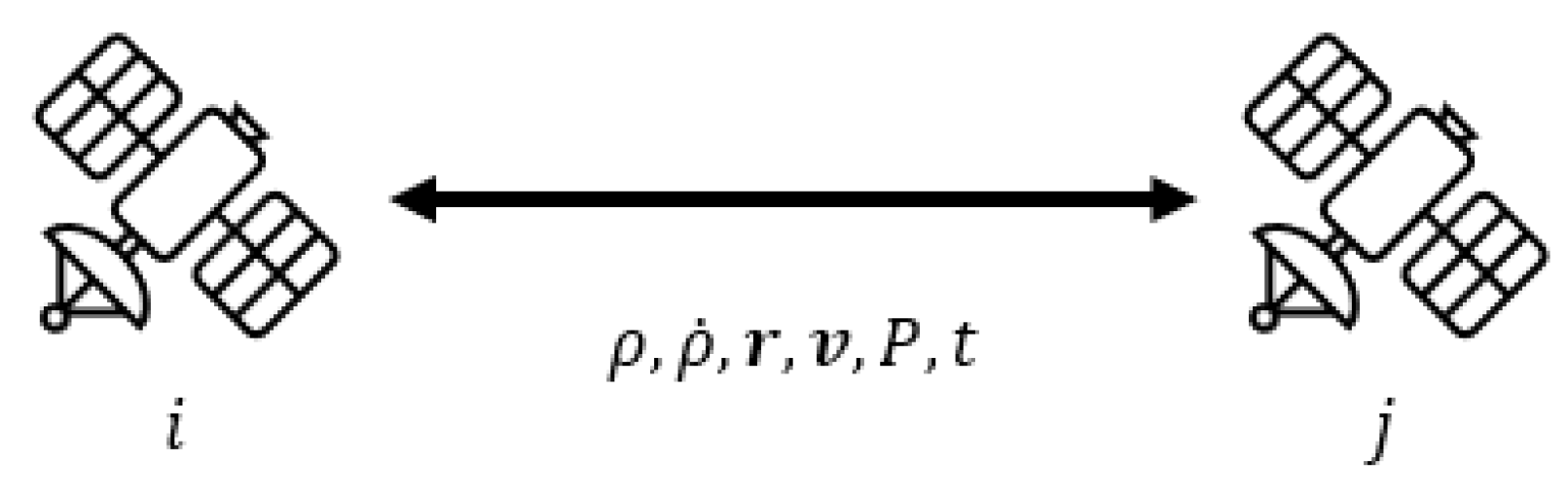
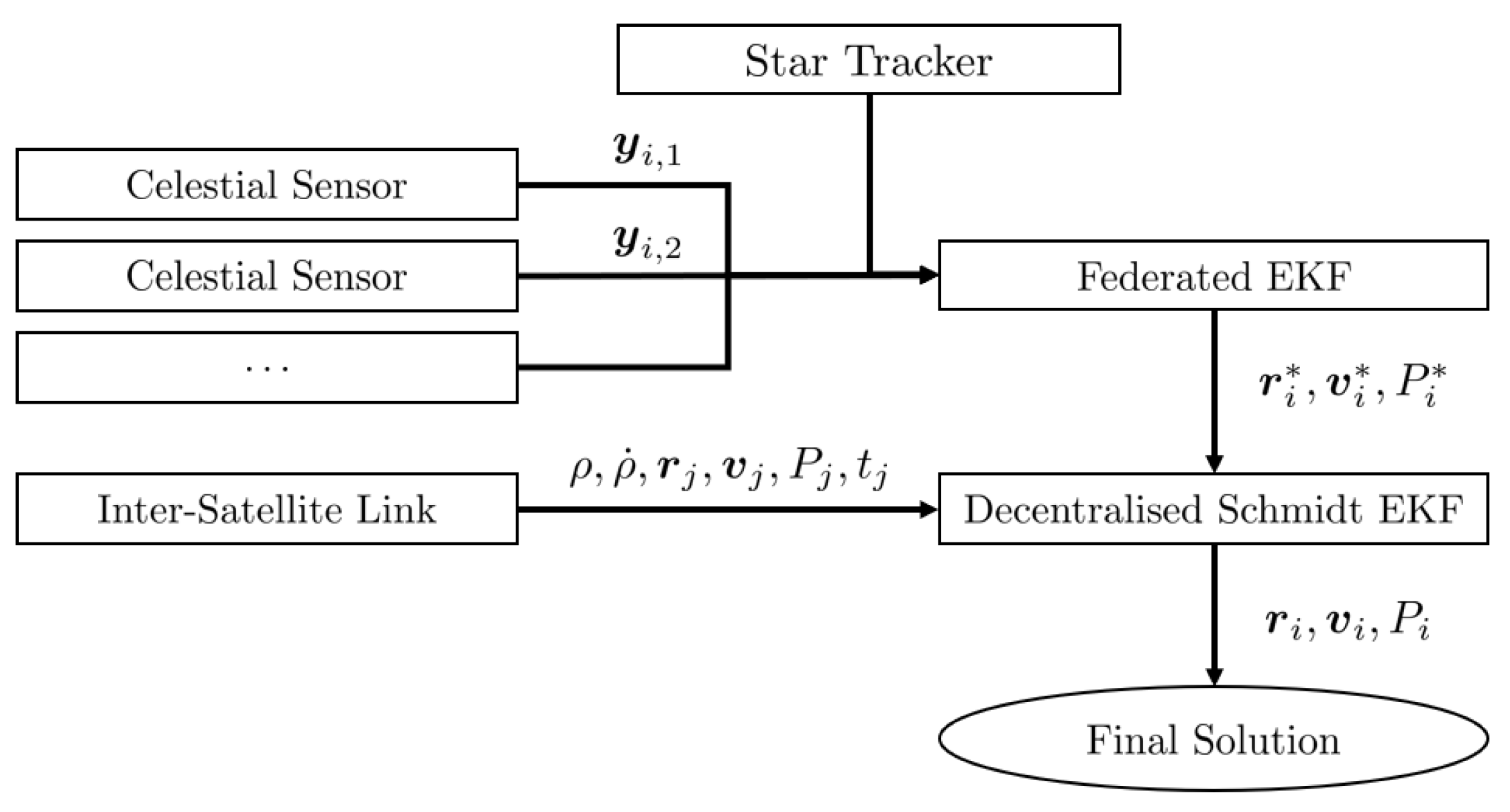
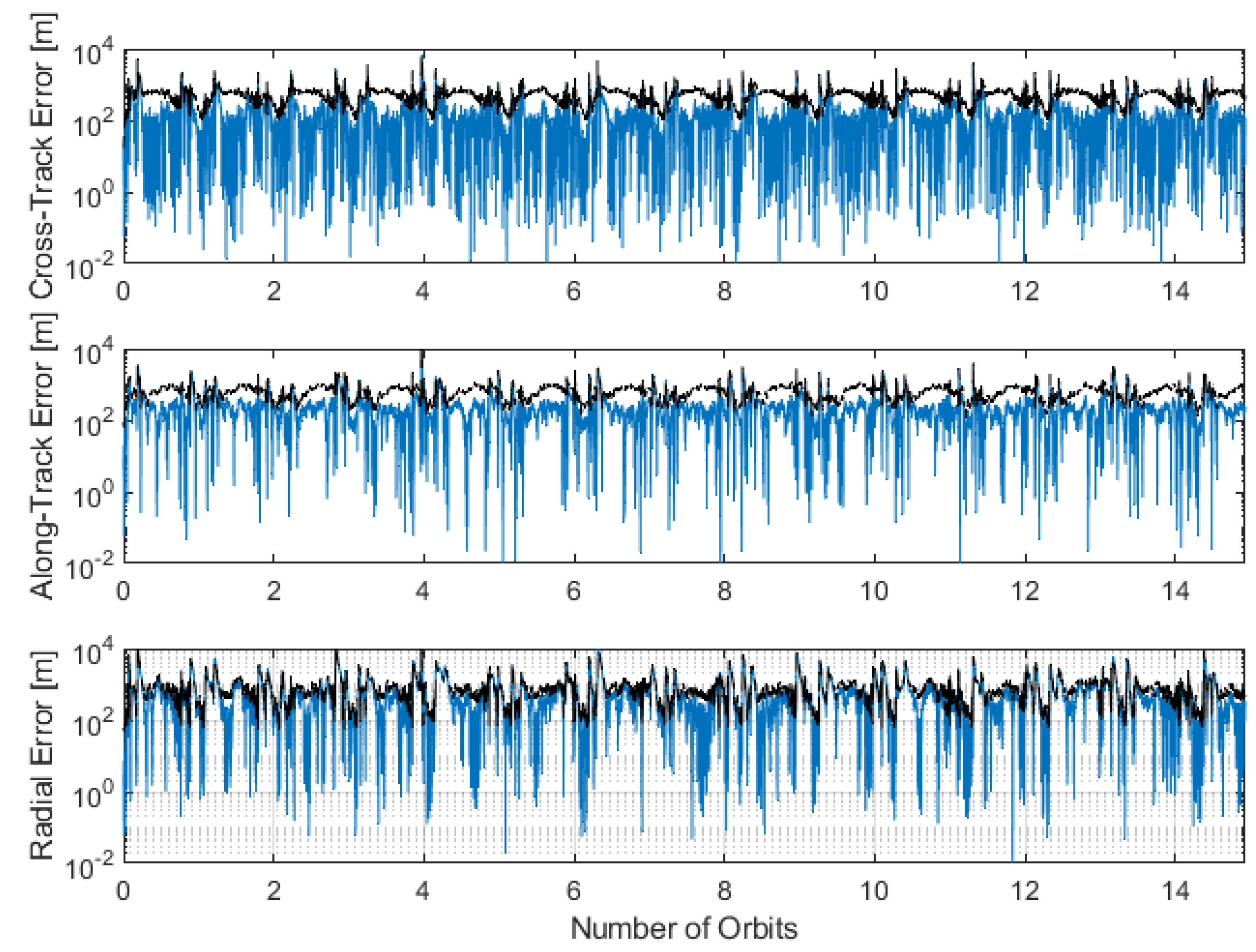

| Parameter | Value |
|---|---|
| Semi-Major Axis | 8049 km |
| Eccentricity | 0.4082 |
| Inclination | 56° |
| Orbital Period | 19 h |
| Number of Satellites | 9–10 |
| Sensor | Design Limitations | Challenges to Performance |
|---|---|---|
| Star Tracker |
|
|
| Horizon Navigation |
|
|
| Triangulation |
|
|
| Crater Navigation |
|
|
| Inter-Satellite Link |
|
|
| Sensor | Cross-Track [m] | Along-Track [m] | Radial [m] |
|---|---|---|---|
| Lunar Horizon | 234 ± 492 | 1352 ± 381 | 8 ± 93 |
| Lunar Craters | 170 ± 3531 | 1013 ± 6620 | 170 ± 20,754 |
| Lunar Horizon and Craters | 23 ± 442 | 162 ± 533 | 567 ± 1376 |
| State | Cross-Track | Along-Track | Radial |
|---|---|---|---|
| Position [m] | 1.3 ± 41.0 | 12.6 ± 28.5 | 19.9 ± 96.0 |
| Velocity [mm/s] | 4.4 ± 58.3 | 12.9 ± 50.4 | 4.3 ± 70.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Critchley-Marrows, J.J.R.; Wu, X.; Kawabata, Y.; Nakasuka, S. Autonomous and Earth-Independent Orbit Determination for a Lunar Navigation Satellite System. Aerospace 2024, 11, 153. https://doi.org/10.3390/aerospace11020153
Critchley-Marrows JJR, Wu X, Kawabata Y, Nakasuka S. Autonomous and Earth-Independent Orbit Determination for a Lunar Navigation Satellite System. Aerospace. 2024; 11(2):153. https://doi.org/10.3390/aerospace11020153
Chicago/Turabian StyleCritchley-Marrows, Joshua J. R., Xiaofeng Wu, Yosuke Kawabata, and Shinichi Nakasuka. 2024. "Autonomous and Earth-Independent Orbit Determination for a Lunar Navigation Satellite System" Aerospace 11, no. 2: 153. https://doi.org/10.3390/aerospace11020153
APA StyleCritchley-Marrows, J. J. R., Wu, X., Kawabata, Y., & Nakasuka, S. (2024). Autonomous and Earth-Independent Orbit Determination for a Lunar Navigation Satellite System. Aerospace, 11(2), 153. https://doi.org/10.3390/aerospace11020153





