A Fruit Harvesting Mechanism Capable of Multidimensional Movements: A Preliminary Study on the Integrated Mechanism with a Hexacopter

Abstract

This study introduces a fruit harvesting mechanism powered by a single motor, designed for integration with unmanned aerial vehicles (UAVs). The mechanism performs reciprocating motion by converting linear motion into rotational motion. Consequently, the end-effector can execute multi-dimensional kinematic trajectories, including biaxial and rotational movements, synchronized with the motor’s position. These axial and rotational motions facilitate the gripper’s ability to reach, retrieve, and detach fruit from branches during the harvesting process. Notably, a critical consideration in designing this fruit harvesting mechanism is to generate the necessary torque at the end-effector while minimizing reaction forces and torque that could destabilize the UAV during flight. With these considerations in mind, this preliminary study aimed to harvest a Fuji apple and conduct a dynamic analysis. We constructed a prototype of the single motor-driven fruit harvesting mechanism using a suitable servo motor. To assess its mechanical performance and evaluate its impact on the hexacopter, we developed both a specific test platform featuring a six-spherical-prismatic-spherical parallel structure and a virtual environmental flight simulator. Overall, the results demonstrate the successful harvesting of a Fuji apple weighing approximately 300 g by the single motor-driven fruit harvesting mechanism, with no adverse effects observed on the hexacopter’s operation.

1. Introduction

Despite the global population growth, the number of orchardists has steadily declined over the past decade or more relative to the labor required during the fruit harvesting season. For instance, Europe experienced a roughly 50% decline in its agricultural population from about 35 million to 18 million from 2000 to 2020 [1]. This lack of labor results in reduced productivity, which threatens the global food supply. To address these issues, attempts have been made to develop mobile robotic platforms adapted for use with Unmanned Aerial Vehicles (UAVs), which would potentially lead to improved agricultural productivity and work safety [2,3,4,5]. Indeed, over the past few years, UAVs have been an emerging technology that has been spotlighted due to their promising potential in a variety of applications, e.g., delivery, emergency medical support, agriculture, etc. [6,7,8,9,10,11]. These real-world applications have the potential to improve productivity, solve labor shortages, and improve safety in industrial workplaces [12,13].

Of particular interest within the array of approaches harnessed by UAVs is the field of aerial manipulation, which has achieved significant milestones. This advancement has broadened the horizons of robotics, enabling UAVs to excel in versatile and dexterous grasping and manipulation tasks. These accomplishments have been made possible through the implementation of specific design strategies, as referenced in [14,15,16].

An essential consideration in the design of aerial manipulators and end-effectors is the achievement of lightweight structures with compact dimensions. Simultaneously, there is a focus on developing a straightforward and dependable control system with the aim of minimizing computational demands and reducing overall operational loads, as discussed in [17,18,19]. Finally, because conventional UAVs have a limited battery capacity, which determines maximum flight times and payloads, minimizing power consumption needs to be considered during the design phase.

Taking these factors into account, TEVEL Aerobotics Technologies recently introduced a pioneering study in which they developed a Flying Autonomous Robot (FAR) for fruit harvesting using low-cost drones with enhanced mobility compared to ground-mobile robots [5,20]. While these innovative design strategies yield promising mechanical traits such as a lightweight, compact form, and a reliable, straightforward control system, the FAR does have a notable limitation due to its wired system. Specifically, it relies on a cable connected to the vehicle to provide power for movement, which restricts its workspace [21].

On the other hand, from a botanical perspective, accurately separating fruits from their branches is a challenging task, because the difference in stiffness between the fruit’s surface and its branch depends on its stage of ripening [22]. Therefore, from an engineering perspective, different grasping and manipulation strategies need to be explored to create a task-oriented gripper and manipulator that can employ proper force and torque to successfully harvest fruits without damaging them while optimizing and minimizing the power consumption of the actuators, sensors, and overall system.

In [23,24], the authors proposed an optimal fruit harvesting operation where the robots perform particular picking patterns to grasp an apple. These picking patterns were achieved through multidimensional kinematic motions, which mainly consisted of horizontal pulling, bending, and twisting movements. The successful manipulations showed a required torque of 55.35 ± 18.05 N·mm and a maximum detachment force of 29.65 N [25]. However, according to our knowledge, a comprehensive study on fruit harvesting mechanisms integrated with wireless UAVs has not been presented to date.

With these considerations in mind, this work focuses on a wireless fruit harvesting mechanism that operates remotely and uses a combination of linear and rotational motions based on a single actuator. For our initial test, we aimed to harvest a Fuji apple weighing approximately 260.9 g. Our primary goals were to enable multidimensional motions at the end-effector while minimizing power consumption. By doing so, we aimed to reduce the effort and payload required by the UAV for fruit harvesting, as multidimensional motions, including translation and rotation, are typically more efficient than end-effectors that rely solely on linear motion [22,23].

To achieve this, our harvesting mechanism transforms the rotational motion of the actuator into linear motion at the end-effector using a scotch yoke. Simultaneously, the barrel cam operates in conjunction with the linear motion of the end-effector. To assess the mechanical properties of the actuator, we analyzed the torque required for the harvesting mechanism using Lagrangian methods and conservation laws, and then validated the feasibility of our approach by conducting experiments with the harvesting mechanism, demonstrating its capabilities within a virtual environment flight simulator.

2. Materials and Methods

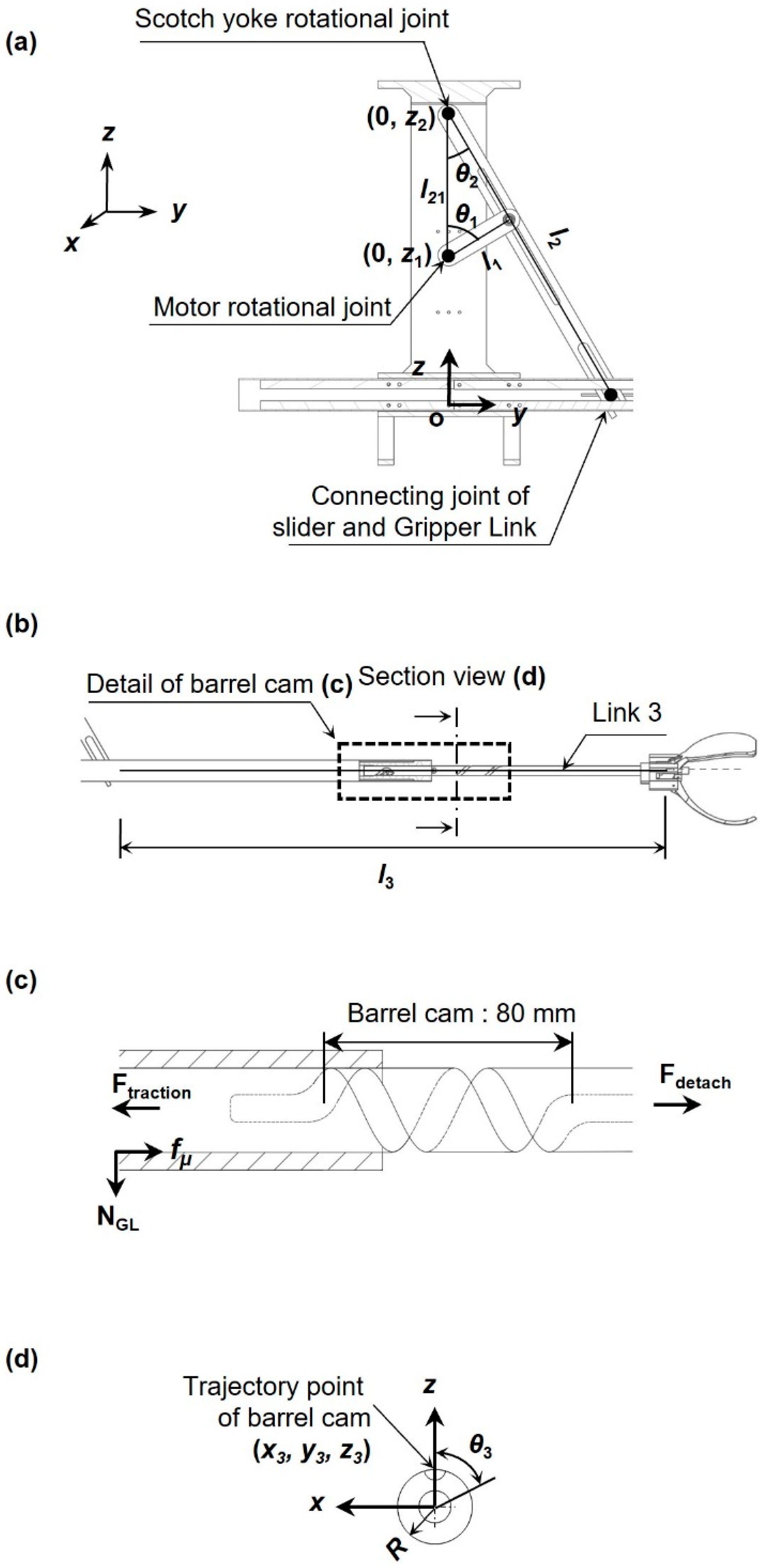
2.1. Design of an Apple Harvesting Mechanism

A proof-of-concept of the fruit harvesting mechanism integrated with the hexacopter is depicted in Figure 1a. The WMD-1200 hexacopter which utilizes Hobbywing’s XRotor Pro X6 motors was considered [26]. Given that each motor has a 3 kg payload lifting capacity, the overall payload of the hexacoptor (i.e., six motors) can approach 18 kg. Considering that the hexacopter frame and battery weigh 11 kg, and the fruit (up to 20 apples) weighs approximately 5.2 kg, the mechanism’s maximum weight is limited to 1.8 kg [24]. The hexacopter is equipped with a basket, allowing multiple fruits to be harvested during a single flight. Given the hexacopter’s axle span of 1200 mm, the entire length of the fruit harvesting mechanism was set at 1060 mm, which is 300 mm longer than the radius of the axle span (i.e., 600 mm) (See Figure 1b). Accordingly, interference with propeller operation due to collision with the branches or trees of the fruit can be prevented. To allow the device to operate with a single motor, a scotch yoke mechanism is employed, enabling the conversion of motor rotation into the linear motion required by the gripper link. The cam of the gripper link helps achieve the desired rotational motion of the gripper during fruit picking. To achieve a lightweight structure, the base link and fixed link were fabricated by 3D printing a composite of polylactic acid (PLA) material and carbon fiber. The total weight of the structure, including the motor and control system, was only 1.2 kg.

2.2. Working Principle

The working principle of the single motor-driven fruit harvesting mechanism consists of four stages: (1) approach to target, (2) grasping, (3) rotation and harvesting, and (4) retrieving and releasing fruit (see Figure S1). The first stage is the process of the gripper approaching the fruit. Once the motor rotates counterclockwise, the rotational motion of the crank generates linear motion of the gripper link through the slider, making the gripper open. The second stage is the process of picking the fruit. Once the motor rotates clockwise, the gripper closes, engaging and grasping the fruit. The third stage is the process of harvesting the fruit. In parallel with the second stage, the clockwise rotation of the motor moves the follower, which is fixed at the outer barrel, along the path engraved on the gripper link surface, retrieving the fruit through linear motion. Finally, the fourth stage is the process of dropping the harvested fruit into the net. Once the motor rotates counterclockwise, a steel ball, which acts as a cam follower, moves along a spiral-shaped barrel cam on the interior surface of the outer barrel. The fore-aft tracking of this steel ball cam follower through the barrel cam opens and releases the gripper link to perform either holding or releasing tasks as required. In other words, the movement of this linkage can control the opening distance or size of the gripper by tracking counterclockwise or closing and securing the target by operating the motor and tracking the linkage in a clockwise direction.

2.3. Numerical Analysis

The free body diagram for dynamic analysis is depicted in Figure 2. The rotation angle of the crank is represented by θ₁, which is equivalent to the rotation of the motor, and the rotation angle of the slider (determined by the rotation of the crank) is denoted by θ₂, which is derived as Equation (1).

$${tan\theta }_2=\frac{l_1·sin{\theta }_1}{l_{21}-l_1·cos{\theta }_1}$$

(1)

where l₁ and l₂₁ represent the length of the crank and the distance between the rotational joint of the crank and the rotational joint of the slider, respectively, as shown in Figure 2a. The crank rotates with the motor’s angular velocity ($\dot{{\theta }_1}$), which results in rotating the slider, accordingly. The angular velocity of the slider is derived as Equation (2).

$$\dot{{\theta }_2}=\frac{l_{21}{l}_1·cos{\theta }_1-{l_1}^2}{{(l_{21}-l_1·cos{\theta }_1)}^2}·{cos}^2{\theta }_2·\dot{{\theta }_1}$$

(2)

As the slider rotates, the effective length of the slider (l₂) of the scotch yoke mechanism is derived, as follows:

$$l_2=z_2·sec{\theta }_2$$

(3)

As shown in Figure 2b, the connecting joint of the slider and gripper link (which is placed at the end of the slider) exhibits linear movements along the guide. Once the linear motion occurs, the gripper link then rotates along the barrel cam, as shown in Figure 2c. Thus, as shown in Figure 2d, the displacement and rotation angle of the gripper link can be written by:

$$y_3=z_2\left(\tan \frac{\pi }{6}-tan{\theta }_2\right)$$

(4)

$$x_3=\left\{\begin{array}{cc}R·\sin \left(\frac{4\pi }{80}{y}_3\right)& rotates\\ 0& not rotates\end{array}\right.$$

(5)

$$z_3=\left\{\begin{array}{cc}R·\cos \left(\frac{4\pi }{80}{y}_3\right)& rotates\\ 0& not rotates\end{array}\right.$$

(6)

$${\theta }_3=\left\{\begin{array}{cc}0& (0\le ∆y_3<0.05 m)\\ \frac{4\pi }{0.08}{z}_2\left(tan\frac{\pi }{6}-tan{\theta }_2\right)& (0.05 m\le ∆y_3<0.13 m)\\ 0& (0.13 m\le ∆y_3<0.3 m)\end{array}\right.$$

(7)

Here, note that the barrel cam length is 80 mm, and the pitch of the barrel cam is set at 2 revolutions. The torque required to operate the actuator was identified by using the energy analysis through the Lagrangian method and conservation laws [27,28]. The driving energy of the mechanism comprises kinetic energy (K_i, i = 1, 2, 3), potential energy (P_i, i = 1, 2, 3), and frictional energy (W_μ) of each linkage generated by the rotation of motor (ranging from π/3 ≤ θ₁ ≤ 5π/6), which are denoted by:

$$\sum E=\sum K_i+\sum P_i+\sum {(W}_{\mu }+W_{required})=T_m·{\theta }_1$$

(8)

$$K_1=\frac{1}{2}{I}_1{\dot{{\theta }_1}}^2$$

(9)

$$K_2=\frac{1}{2}{I}_2{\dot{{\theta }_2}}^2=\frac{1}{2}{I}_2·{\left(\frac{l_{1}cos{\theta }_1-{l_1}^2}{{(l_{21}-l_{1}cos{\theta }_1)}^2}\right)}^2{cos}^2{\theta }_2$$

(10)

$$K_3=\frac{1}{2}{m}_3{v_3}^2+\frac{1}{2}{I}_3{\dot{{\theta }_3}}^2$$

(11)

$$P_1=m_{1}g·\left(z_1+\frac{1}{2}{l}_{1}cos{\theta }_1-\left(\frac{1}{2}{l}_{1}sin\frac{\pi }{6}+z_1\right)\right)$$

(12)

$$P_2=m_{2}g·\left(z_2-\frac{1}{2}{l}_{2}cos{\theta }_2-{\frac{1}{2}l}_{2\mathrm{at}{\theta }_2=60°}cos\frac{\pi }{6}\right)$$

(13)

$$P_3=0$$

(14)

Given that the crank and slide are rotating around only the fixed point, the linear kinetic energy can be neglected. Moreover, while the gripper link generates both linear and rotational kinetic energies (i.e., Equations (12) and (13)), the potential energy does not change because of zero displacements along the z-axis (i.e., Equation (14)).

In addition to kinetic and potential energies, friction among the components should be carefully studied because the inherent geometry of the sliding gripper and fixed linkages could generate excess friction (f_μ). This friction can be represented by:

$$f_{\mu }=\mu ·\left(m_3+m_f\right)g$$

(15)

where m₃, m_f, g, and μ are the mass of the gripper link, mass of the fruit, gravity, and friction coefficient, respectively. Then, the friction energy (W_μ) generated along the distance that the gripper link moved can be described by:

$$W_{\mu }=f_{\mu }·y_3$$

(16)

Overall, the energy required to harvest the fruit (W_required) can be appreciated by applying the detachment force (F_detach), as follows:

$$W_{required}=F_{detach}·\delta$$

(17)

where δ is the instantaneous displacement of the manipulator. The force is continuously applied until the fruit is detached. The torque (T_m) necessary to operate the motor can be determined by utilizing both the energies obtained from Equations (8)–(17), and the Lagrangian method along with the conservation laws.

2.4. Experimental Setup and Simulator Design

We developed a parallel structure test platform specifically designed for measuring the reaction forces and torques that could affect the intended flight paths of the hexacopter, as illustrated in Figure S2. This platform allowed us to establish six measurable physical parameters, including three axial forces and their corresponding moments. The test platform we employed is a 6-SPS (Spherical-Prismatic-Spherical) structure, which serves as a force and moment measurement device, as depicted in Figure S2a. This structure comprises two disks connected by six axes of load cells with ball joints at both ends. The smaller disk acts as the mobile platform where the fruit harvesting mechanism is attached, while the larger disk remains fixed to an aluminum profile structure. In essence, it is important to note that the upper and lower disks correspond to the fixed and free ends, respectively.

As shown in Figure S2b, coordinate systems were selected for both the fixed and moving disks. More specifically, the fixed and moving disks employ the $xyz$ coordinate system with the origin $O_B$, and the $uvw$ coordinate system with origin $Q_B$, respectively. We assumed that structural deformations that each beam and joint undergo are negligible. Accordingly, the test platform does not exhibit undesired moments (i.e., rotation) during the experiment. Accordingly, the positions of the spherical joints attached to the fixed and moving disks are written by:

$$a_i=r_a{\left[cos{\theta }_{ai},sin{\theta }_{ai},0\right]}^T=r_b{\left[cos{\theta }_{bi},sin{\theta }_{bi},0\right]}^{\mathrm{T}} for i=1,\dots ,6$$

(18)

where $r_a$ and $r_b$ represent the radii of the fixed and moving disks, respectively. Then, the vector $d_i$ is expressed by:

$$d_i=R{b}_i+p+b_i-a_i for i=1,\dots ,6$$

(19)

where R is the rotation matrix of the moving coordinate system with respect to the fixed coordinate system, and $p$ is $Q_B-O_B$. Given that $f_B$ and $n_B$ are the force and moment acting on the center $Q_B$ of the moving disk, the force and moment acting on the test platform can be expressed by a six-dimensional vector spatial force, wrench ${\omega }_B$, as:

$${\omega }_B={\left[f_B^T,n_b^T\right]}^T$$

(20)

The load cell is attached to both ends by a ball joint and undergoes only axial loads (i.e., tension or compression force). Therefore, the measured value ${\tau }_B$ can be represented by:

$${\tau }_B=\left[f_1, f_2, f_3, f_4, f_5, f_6\right]$$

(21)

The kinematic relationship of the platform (6-SPS structure) can be expressed by ${\omega }_B=J{\tau }_B$, and thus the Jacobian matrix of the 6-SPS structure with respect to $Q_B$ can be written by:

$$\begin{gathered} s_i=\frac{d_i}{‖d_i‖},r_i=b_i \\ J=\left[\begin{array}{ccc}{s}_1& \dots & s_6\\ b_1\times s_1& \dots & b_6\times s_6\end{array}\right] \end{gathered}$$

(22)

where $s_i$ is the unit directional vector of $d_i$, and $r_i\approx \overline{Q_B{B}_i}$ is the distance vector. Using the above relationship, the 3-axis force and moment upon the external force imposed at the moving disk are obtained.

2.5. Simulator Design

Given the hexacopter’s geometry, dynamic modeling was performed as referenced in [29], and the hexacopter’s equation of motions was derived, as summarized in Appendix A. Then, the rotational speed of each motor can be obtained by the following matrix:

$$U^T=\left[\begin{array}{c}\begin{array}{c}{u}_1\\ u_2\\ u_3\end{array}\\ u_4\end{array}\right]=\left[\begin{array}{cccccc}b& b& b& b& b& b\\ -\frac{bl}{2}& -bl& -\frac{bl}{2}& -bl& -\frac{bl}{2}& -bl\\ -\frac{bl\sqrt{3}}{2}& 0& \frac{bl\sqrt{3}}{2}& \frac{bl\sqrt{3}}{2}& 0& -\frac{bl\sqrt{3}}{2}\\ -d& d& -d& d& -d& d\end{array}\right]\left[\begin{array}{c}{\mathsf{\Omega }}_1^2\\ {\mathsf{\Omega }}_2^2\\ {\mathsf{\Omega }}_3^2\\ {\mathsf{\Omega }}_4^2\\ {\mathsf{\Omega }}_5^2\\ {\mathsf{\Omega }}_6^2\end{array}\right]$$

(23)

where $U^T=\left[\begin{array}{cccc}{u}_1& u_2& u_3& u_4\end{array}\right]$ represents the vector of the control input variables of the hexacopter, which consists of the net (thrust) force (i.e., $u_1$) and torque control inputs (i.e., $u_2$, $u_3$, and $u_4$). Here, given that the matrix is an asymmetric matrix, the inverse matrix can be obtained through the pseudo-inverse technique, as reported in [30,31]. Accordingly, the rotational speed of each motor is analyzed below.

The final motion equations for translational and rotational movements of the hexacopter system are deduced, as:

$$\ddot{\phi }=\frac{1}{J_{xx}}(\dot{\theta }\dot{\psi }\left(J_{yy}-J_{zz}\right)-K_{fax}{\dot{=\phi }}^2-J_r{\mathsf{\Omega }}_r\dot{\theta }+u_2)$$

(24)

With these in mind, we implemented a virtual environmental simulator with a closed-loop control through proportional, integral, and derivative (i.e., PID) gains [32]. More specifically, the position and the altitude of the hexacopter are controlled by PID and PD controllers, respectively (see Figure S3), and the control inputs are as follows:

$$\begin{gathered} u_{PID}\left(t\right)=K_{p}e\left(t\right)+K_i{\int }_0^{t}e\left(\tau \right)d\tau +K_d\frac{de\left(t\right)}{dt} \\ {u}_{PD}\left(t\right)=K_{p}e\left(t\right)+K_d\frac{de\left(t\right)}{dt} \end{gathered}$$

(25)

The simulator aimed to enable the hexacopter to follow the target position (i.e., $x_d$, $y_d$, and $z_d$) while obtaining the control inputs (i.e., $u_x$, $u_y$, $u_z$ for the three axes of translational motion). Establishing this objective then made it possible to obtain the thrust control input ($u_1$) and the target attitude angles (${\phi }_d$, ${\theta }_d$, and ${\psi }_d$ for the three axes of rotational motion), resulting in control commands $u_2$, $u_3$, $u_4$.

3. Results and Discussion

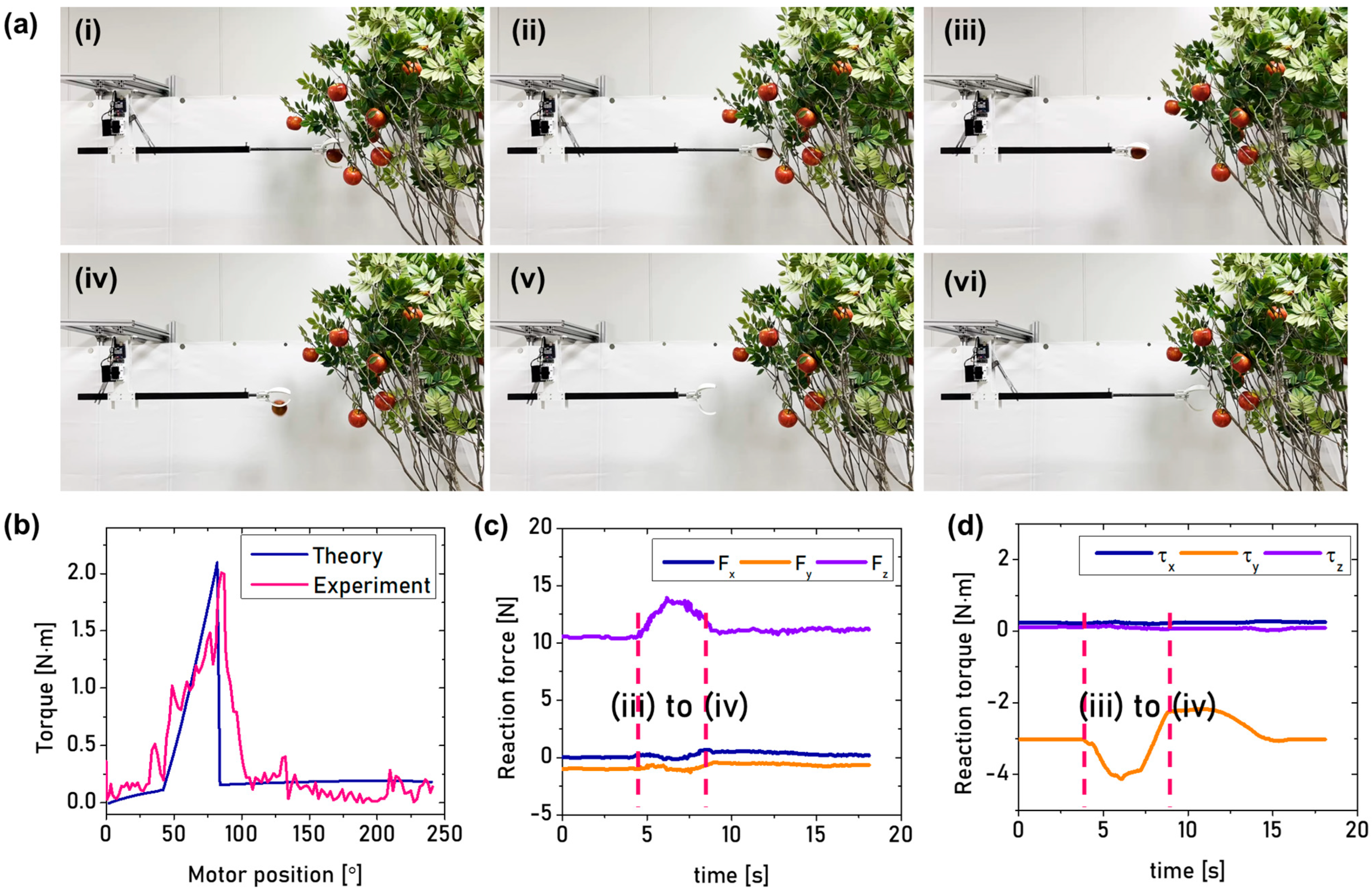
3.1. Numerical and Experimental Results

Figure 3a shows the fabricated fruit-harvesting mechanism with a particular scene mimicking an actual fruit harvesting environment. The experiments were conducted through remote control using a Bluetooth module (as depicted in Figure S4). The single motor-driven fruit harvesting mechanism was able to perform its desired tasks within the given environment setup, as shown in Figure 3a. To operate the harvesting mechanism, a motor torque of 0.2 N·m was identified by Equations (8)–(17) (See Video S1). It is noted that a peak torque of 2.33 N·m is necessary to separate the Fuji apple from its branch, as shown in Figure 3b and Video S2. Comparing the result of dynamic analysis with the measurements, the load generated by the servo motor was equivalent to the maximum torque of 2.2 ± 0.436 N·m, when picking a fruit weighing 220 ± 22.58 g. In summary, when picking the fruit, the error rate between theoretical and experimental maximum torques was 5.6%.

Meanwhile, the reaction force and torque generated by the fruit harvesting mechanism were measured through the 6-SPS parallel structure test platform. The reaction forces in the x and y axes (representing roll and pitch motions, respectively) remained almost constant, which resulted in the reaction force in z-axis (representing yaw motion) increasing from 10.5 N to 14 N as the gripper moved and retrieved the fruit (See Figure 3c). It is important to note that at the beginning phase, the reaction force of 10.5 N in z-axis corresponds to the weight of the fruit harvesting mechanism and that the 3.5 N variation is mainly due to the gripper movement and the weight of the Fuji apple. Given this, it is worth noting that the reaction torques in the x and z axes remained almost constant, yet the reaction torque in y-axis was significantly influenced by the variation of the reaction force in z-axis; increasing from 3.5 N∙m to 4 N∙m, as shown in Figure 3d. This is because of variations in both the weight (due to the fruit being engaged) and length (due to the gripper movement).

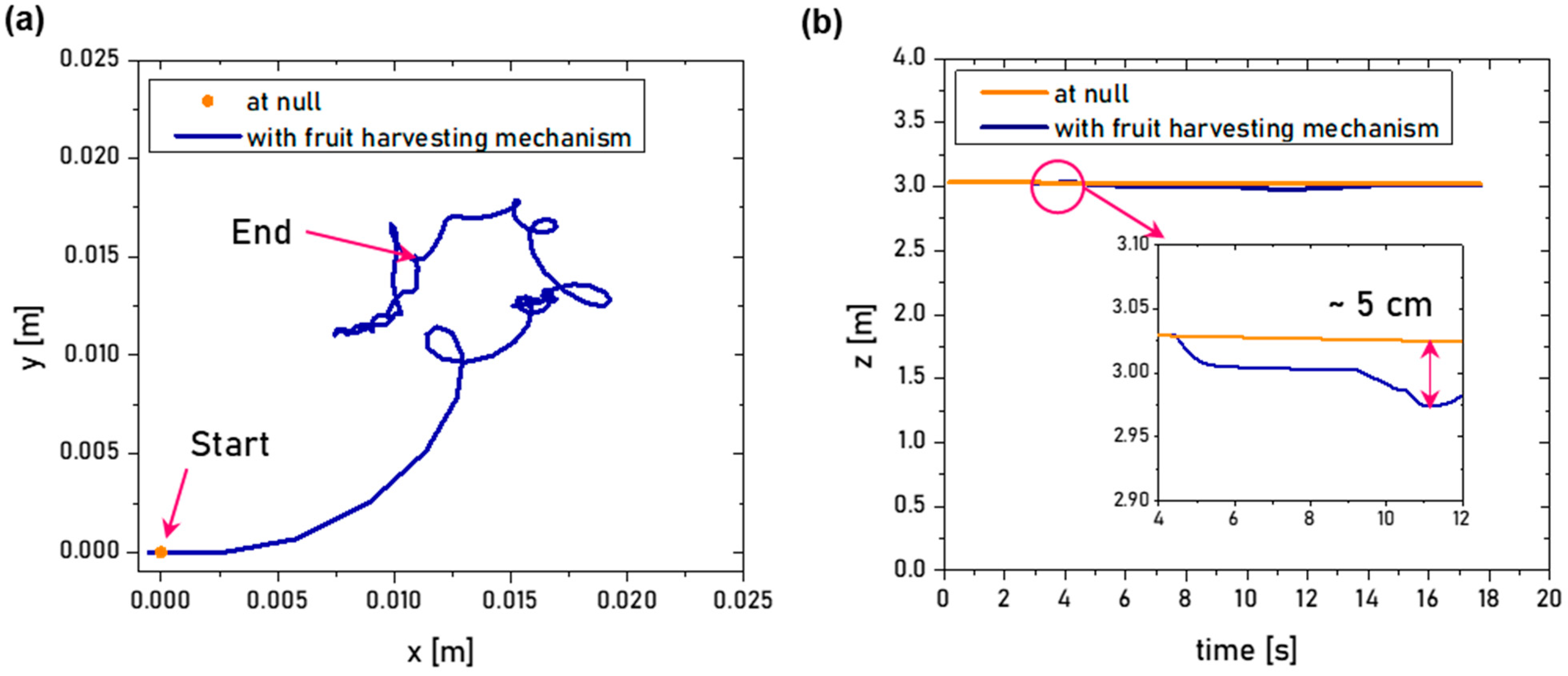
3.2. Demonstration through Simulator with Virtual Environment

The flight (hexacopter) simulator with a virtual environment was developed by using MATLAB. Assuming that the hexacopter is hovering at a 3-m altitude (0, 0, 3 m) without any possible disturbances (i.e., wind shear, ground effect, etc.) while operating the fruit harvesting mechanism, the simulation was performed. The simulation time was set to 17.7 sec, which is relevant to the time measured when the reaction force and torque were retrieved. We used the reaction force and torque obtained from the 6-SPS platform. We conducted an iterative simulation until the simulated results reached a stable state. We utilized suitable control parameters, specifically the gains for the PID controller, as summarized in Table S1.

As a result, the hexacopter successfully reached its designated position with these PID gains in place. To illustrate, in Figure 4a, the hexacopter exhibited minimal deviation (within a 20 mm range) when compared to the initial and final positions. It is worth emphasizing that these PID gains played a critical role in ensuring adaptive control in the xy plane. This promising observation is likely due to the symmetric geometry of the hexacopter. Meanwhile, the hexacopter with the fruit harvesting mechanism has an asymmetric geometry in the z-axis along the center of gravity. For this reason, once the harvesting mechanism operates, the altitude (along the z-axis) varies from 3 m to 2.95 m, as shown in Figure 4b. However, given that this variation occurs after the apple is engaged, it is worth mentioning that the hexacopter with its harvesting mechanism performed desired tasks without incurring any significant computational load to compensate for issues in the control algorithm.

4. Conclusions and Future Work

This work presents a single motor-driven harvesting mechanism that can be integrated with a hexacopter. The harvesting mechanism features multidimensional (i.e., axial and torsional) movements. These movements are determined according to the embedded motor position. Herein, the key to successfully harvesting the fruit is to identify proper motor torque and investigate mechanical influences that could possibly encumber the hexacopter’s flight. As a preliminary study, we selected the Fuji apple and performed explicit numerical analysis, experiments, and simulation. A peak torque of 2.3 N∙m occurred when the apple was being separated from the branch. The torque applied during the process of picking fruit represents the current that is necessary to operate the motor. Given that an average of 80 mA is used for each harvesting and that the harvesting process completes within 5 s, the entire system consumes 0.11 mAh. Thus, it is worth noting that a low power consumption can be accomplished, which is highly useful in repeating operations with UAVs.

Another key point is that the mechanism’s multidimensional movements were useful in harvesting the apple, yet this approach may not ensure higher success rates while harvesting other, different types of fruits. In other words, given that the torque required to separate the apple from the branch depends on apple types and their ripeness, future works would be necessary to investigate mechanical characteristics (i.e., separation force, stiffness, etc.) with respect to different ripeness and types of fruits.

Meanwhile, in our preliminary study on the flight simulation in a virtual environment, we observed that the closed-loop control via PID and PD gains enhance the adaptive feedback with respect to the position and altitude of the hexacopter while the harvesting mechanism is operating. More specifically, it is remarkable that variation in xy planar movements was within ±10 mm and that variation in the z-axis was up to 5 cm. Accordingly, it can be tentatively concluded that the hexacopter is not strongly influenced by either the presence of the harvesting mechanism with an apple or its operation (which leads to variations in inertia due to multidimensional movements). Nonetheless, given that our assumptions for implementing the virtual simulation were based on a linear system, the simulation results might not be a true representation of the values that could be seen in a real operating scenario. Indeed, the hexacopter has been generally conceived as a nonlinear system. Another consideration is that the control hardware setups were not investigated in this work. Therefore, control parameters like clock time, computational load for fruit recognition, and other control demands would need to be further investigated in future studies.