Investigation on Accelerated Initiation of Oblique Detonation Wave Induced by Laser-Heating Hot-Spot
Abstract
:1. Introduction
2. Physical and Mathematical Models
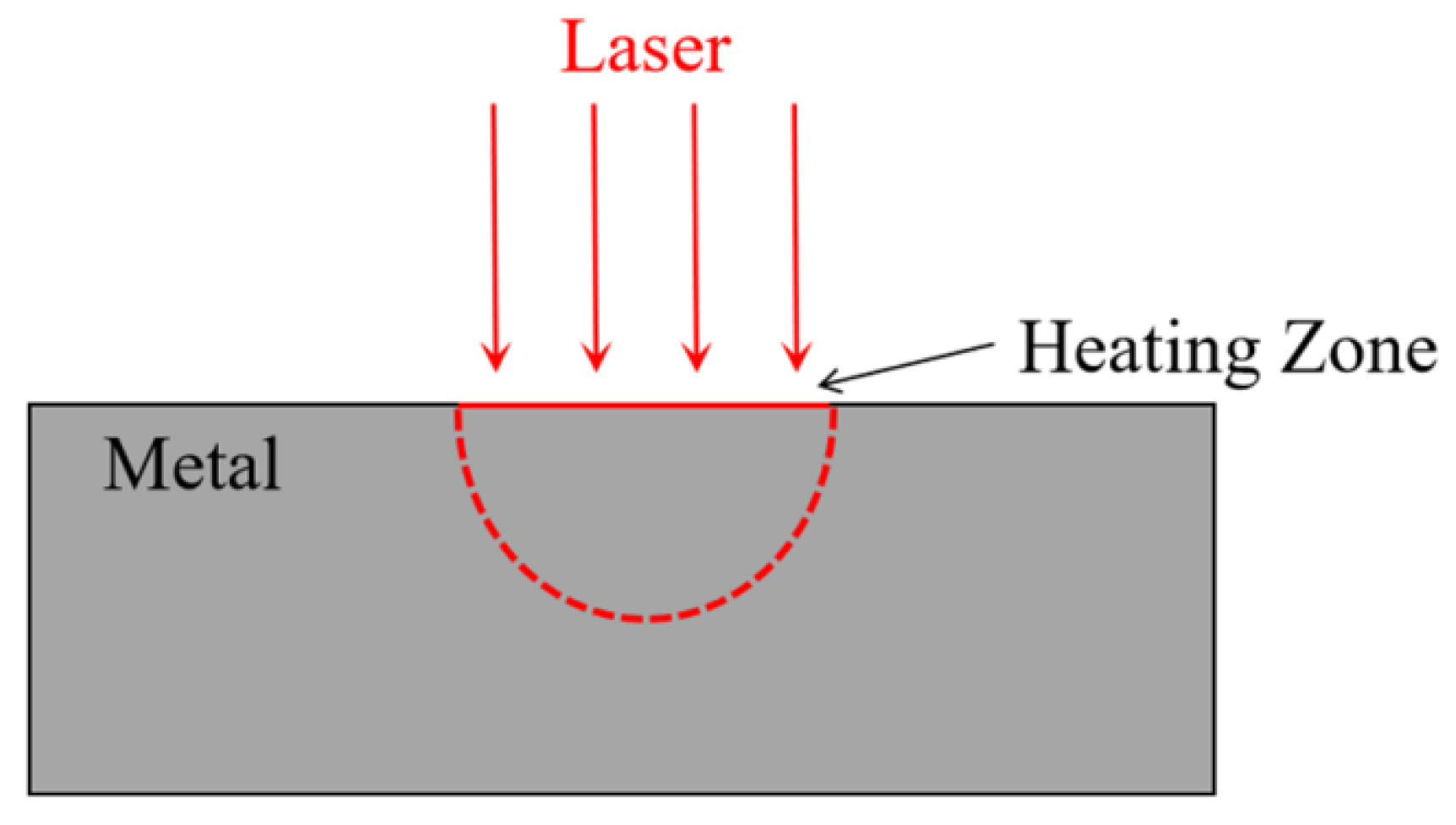
2.1. Physical Models
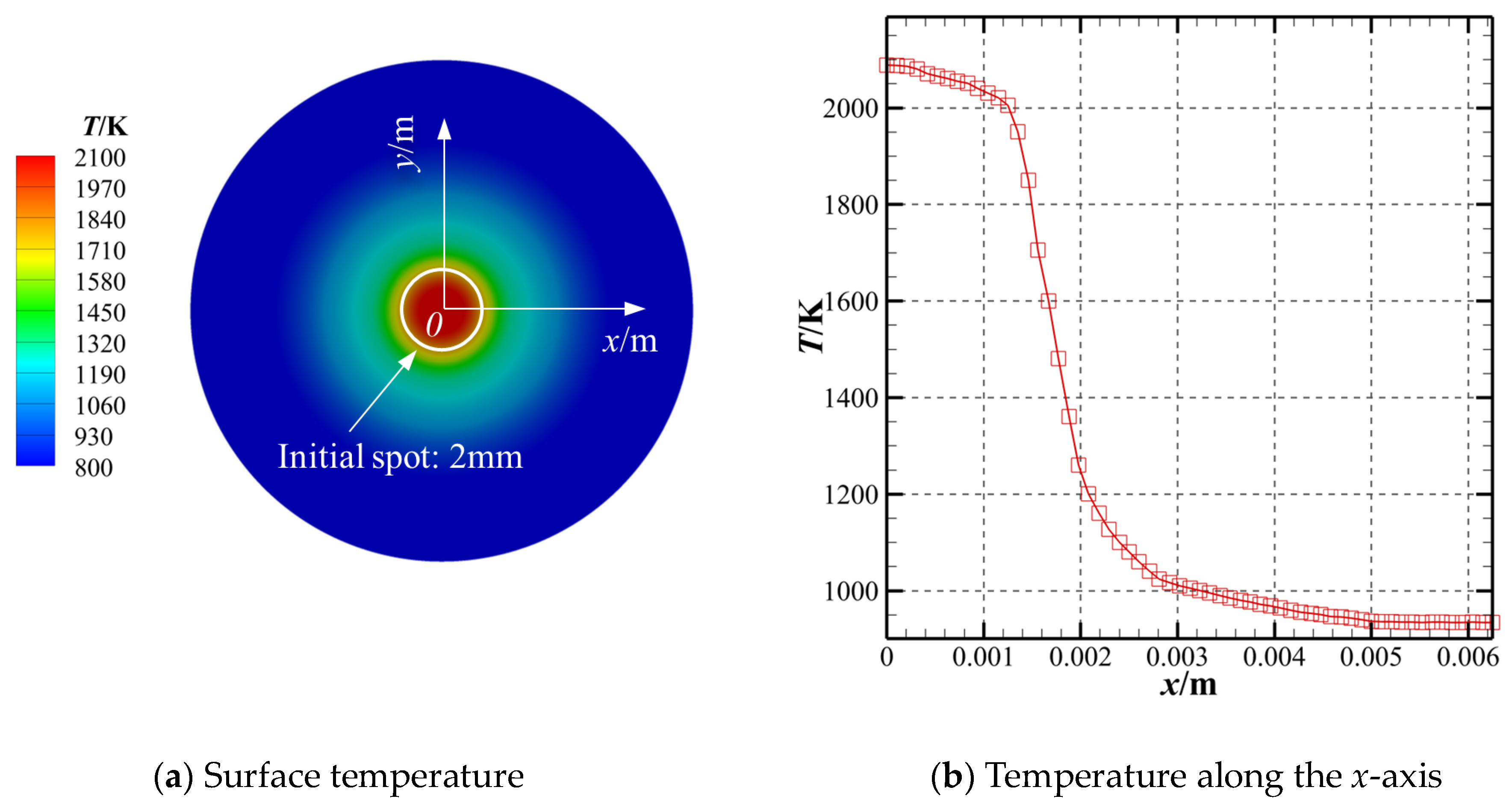
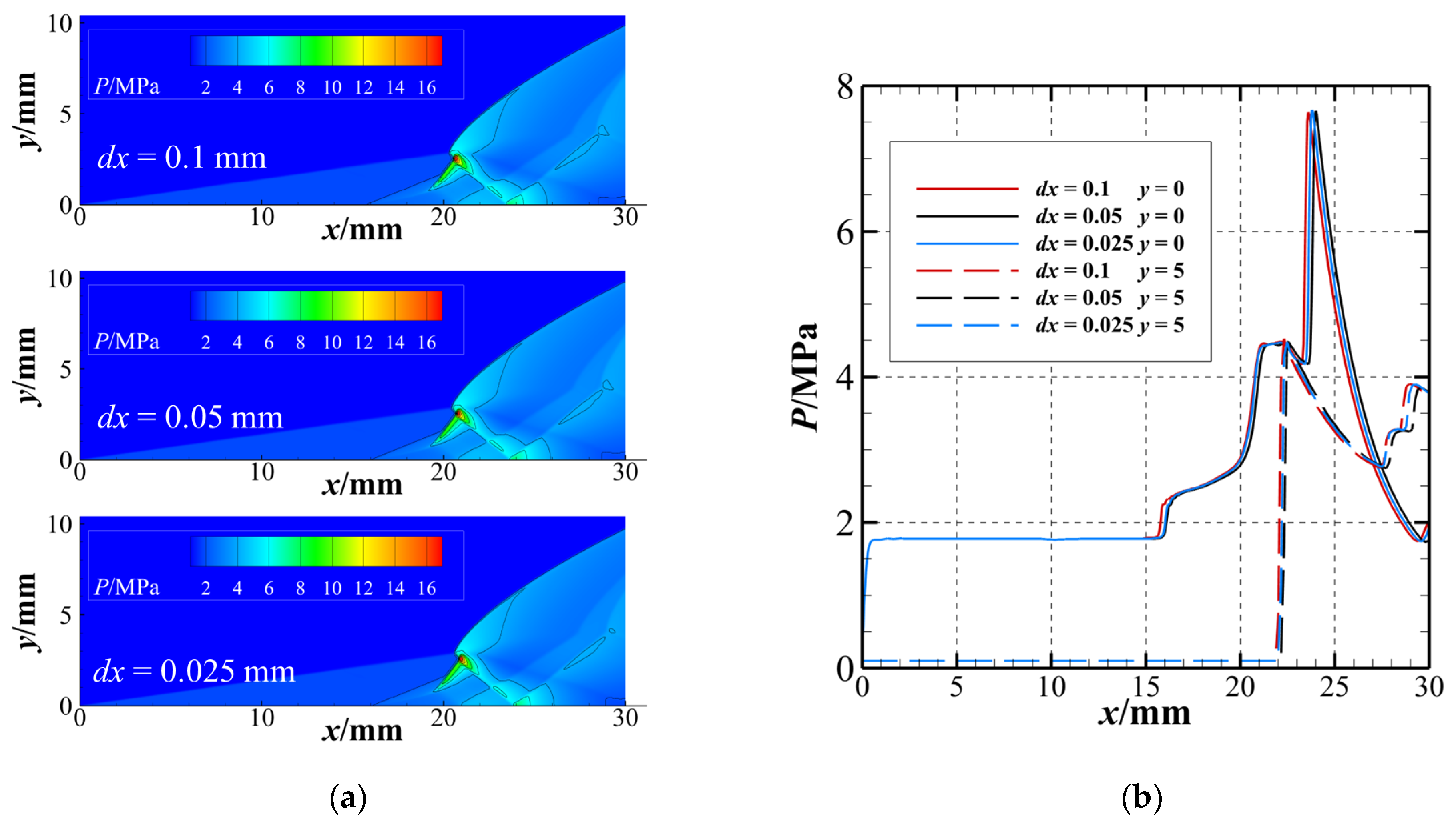
2.2. Numerical Methods
3. Results and Discussion
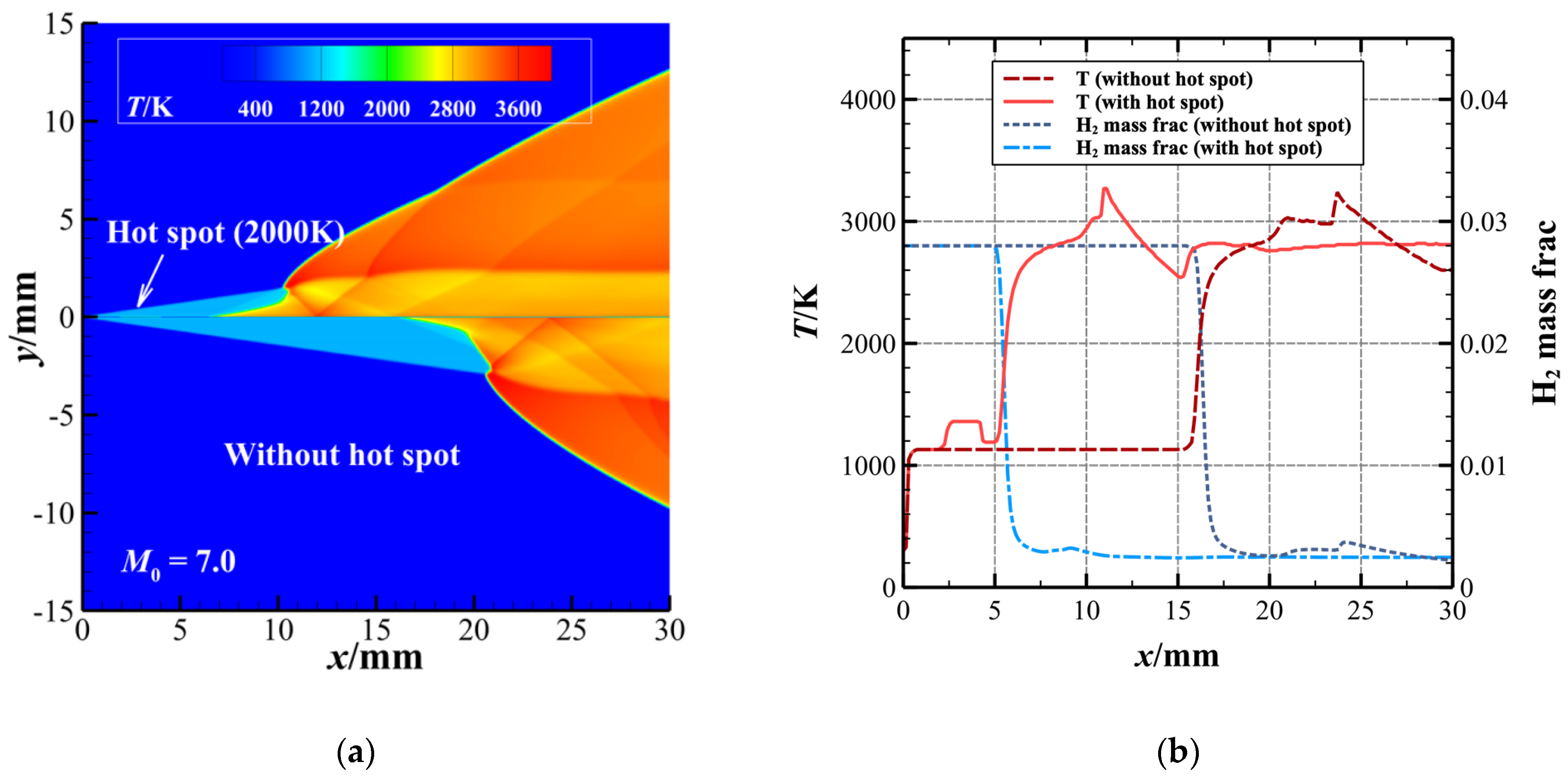
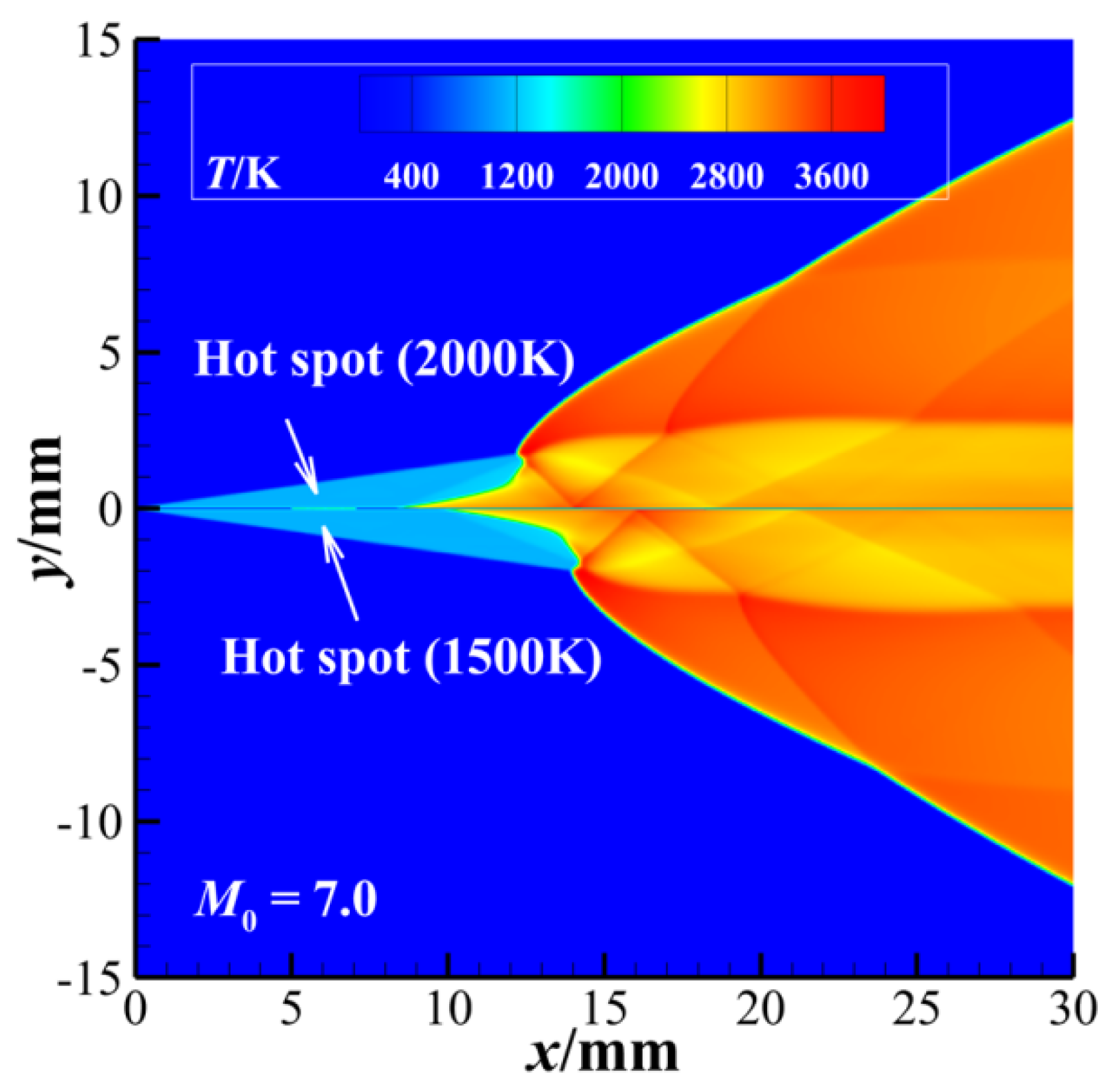
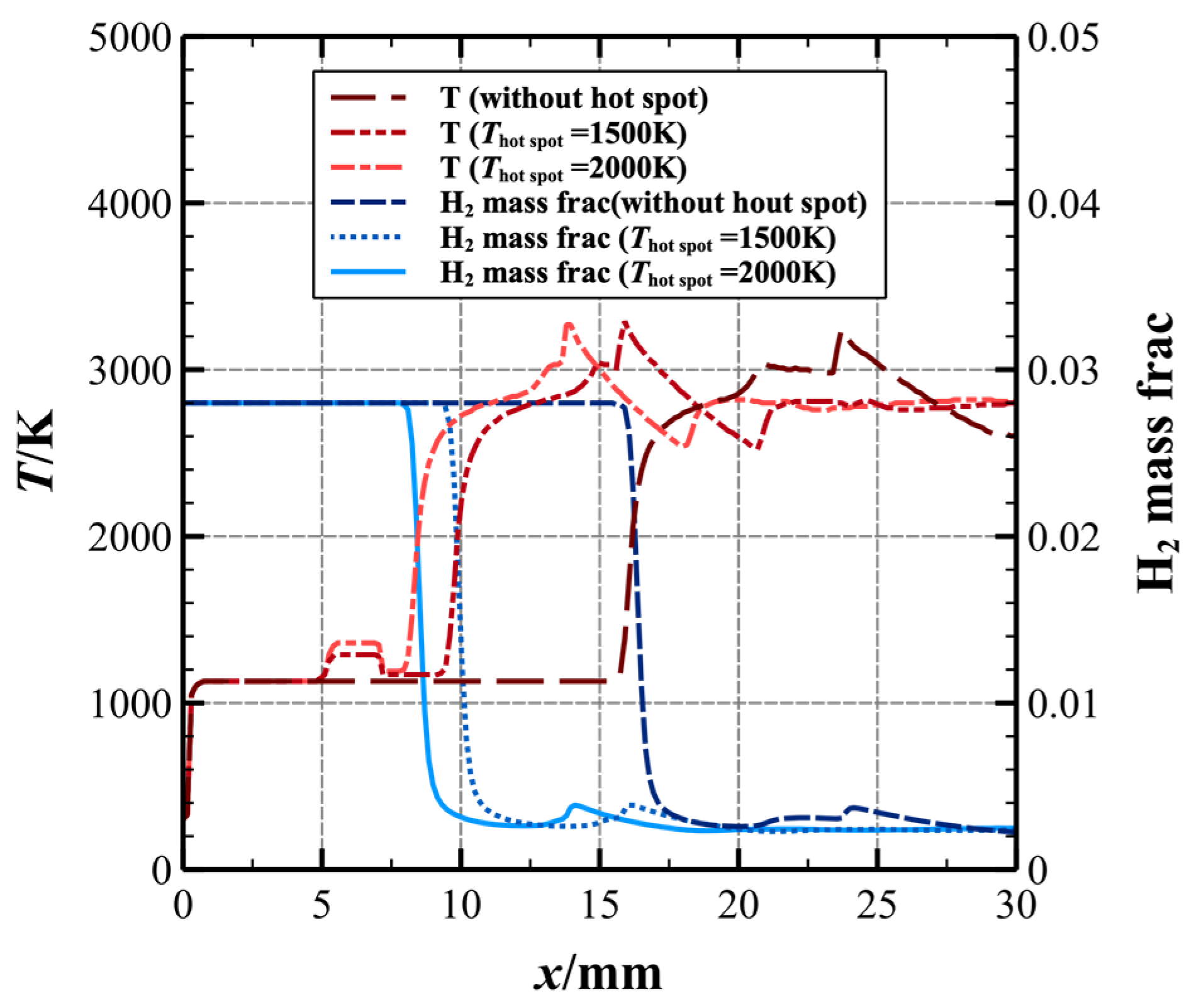
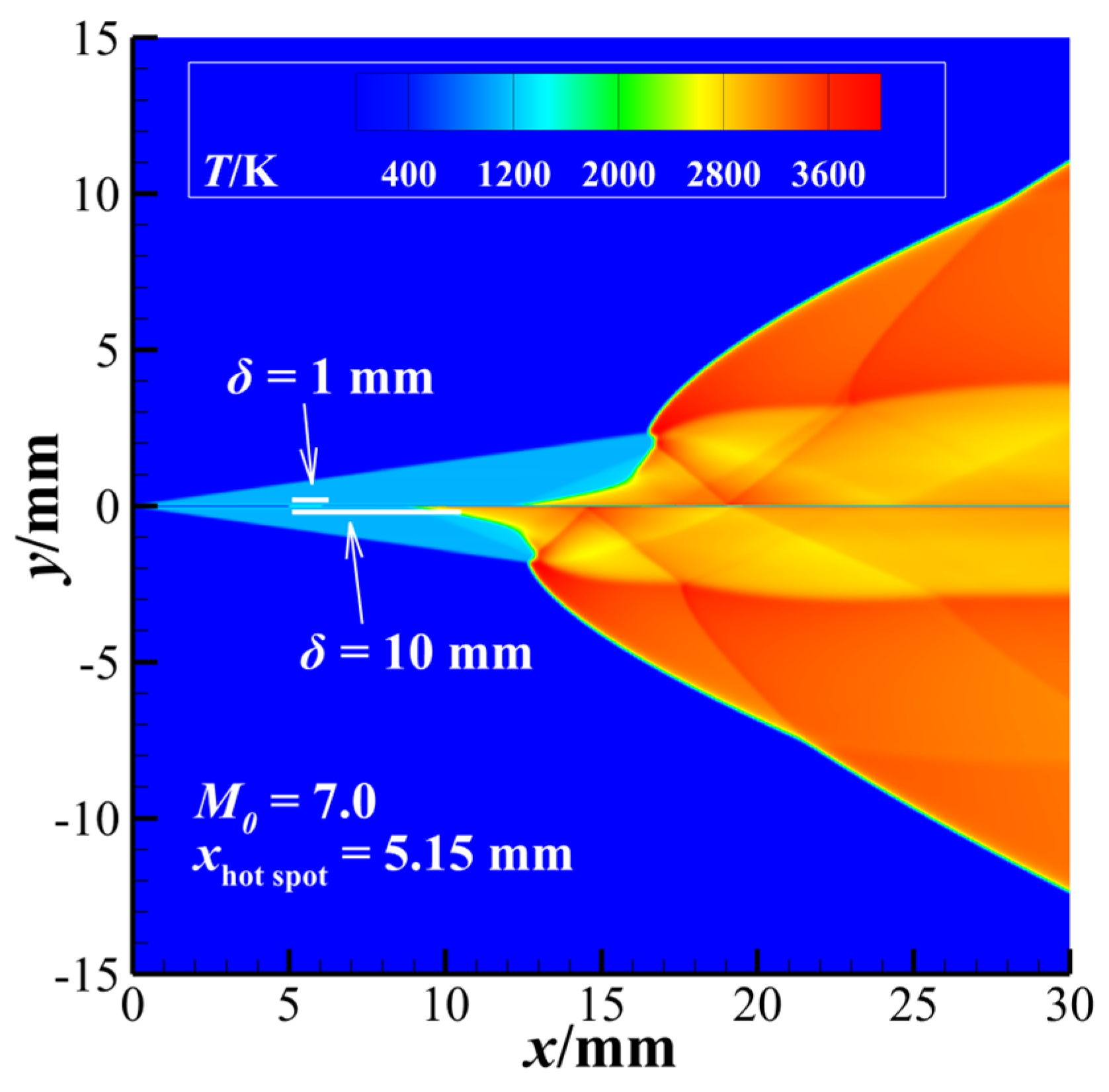
3.1. Initiation Characteristics of ODW Induced by a Hot-Spot
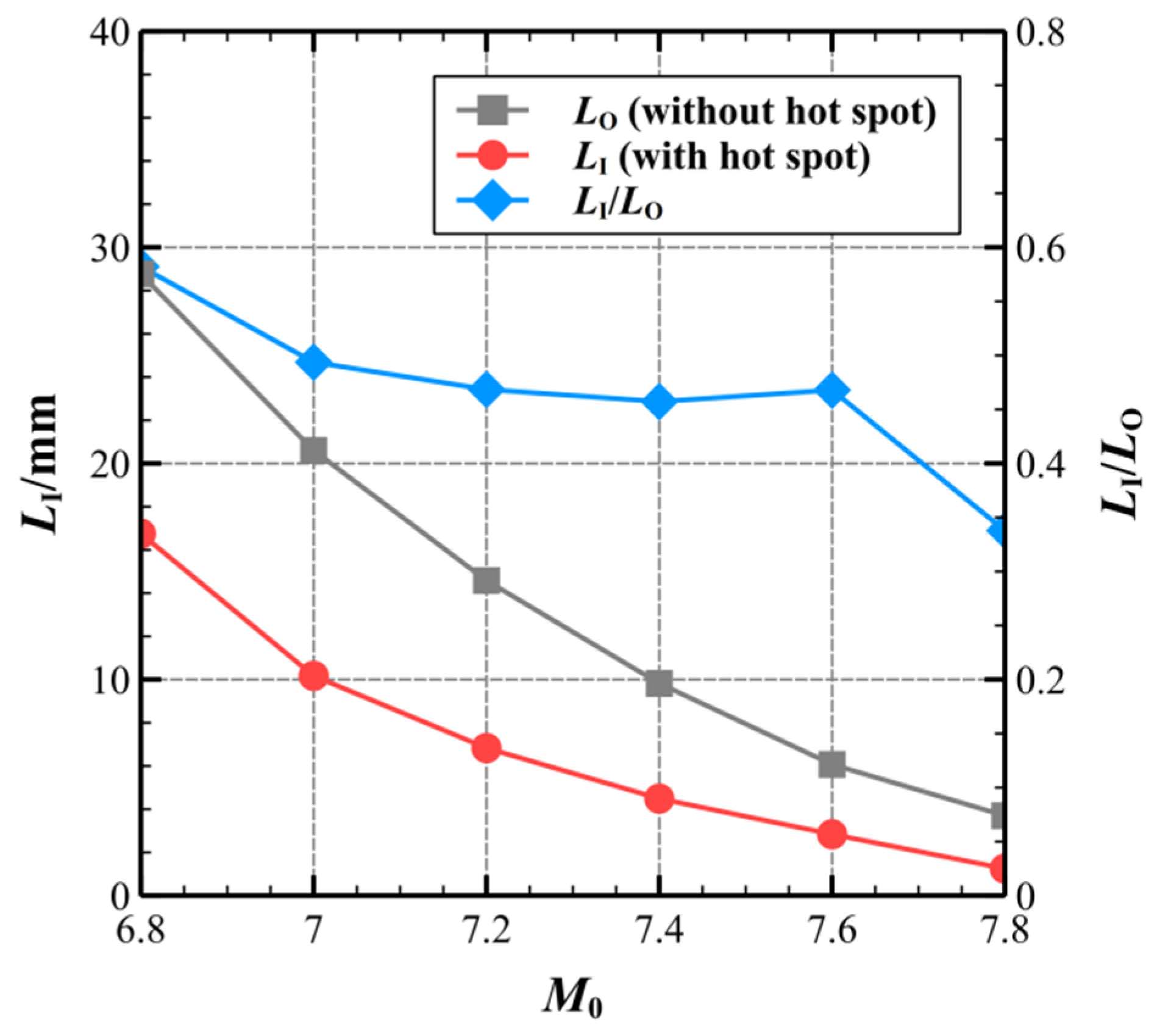
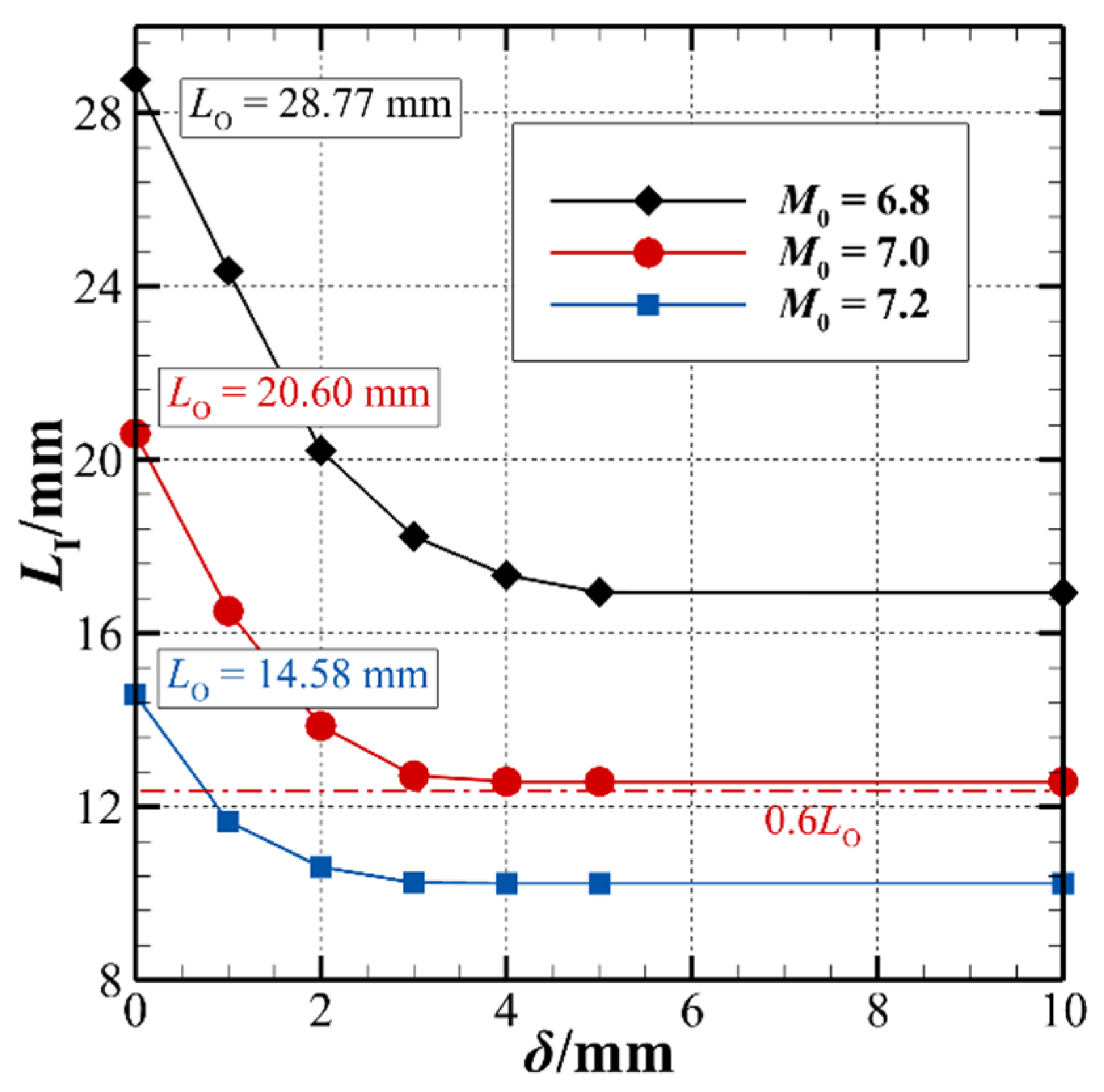
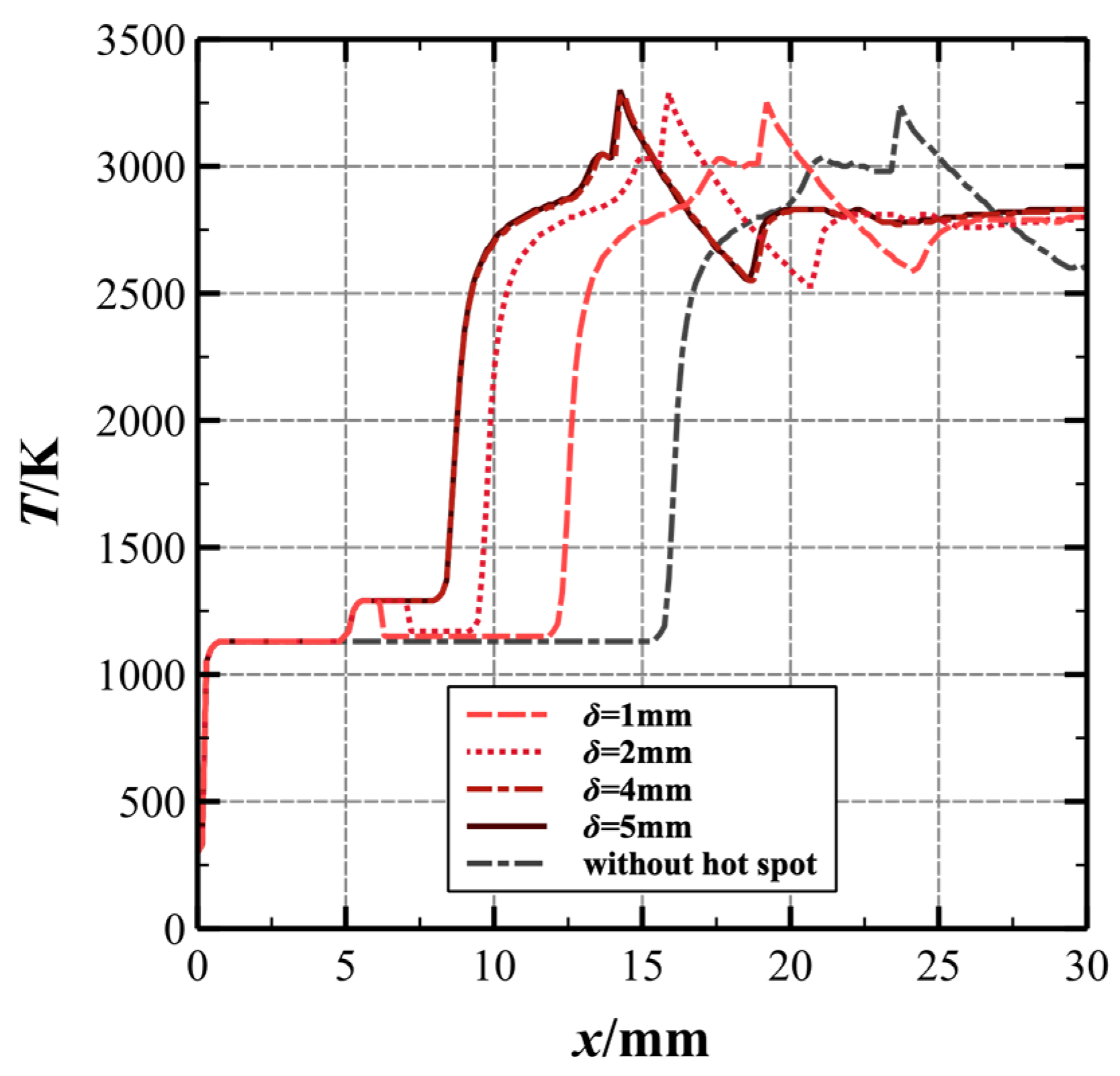
3.2. The Effects of Hot-Spot Parameters on ODW
4. Summary and Conclusions
- Laser-heating hot-spots are an effective method to accelerate the initiation of the ODW. They change the initiation mode of the ODW from no ignition to ignition. In the situation of a longer initiation length at a low flight Mach number or high altitude, this approach makes the initiation length shorter, broadening the engine’s working range of flight speed and height.
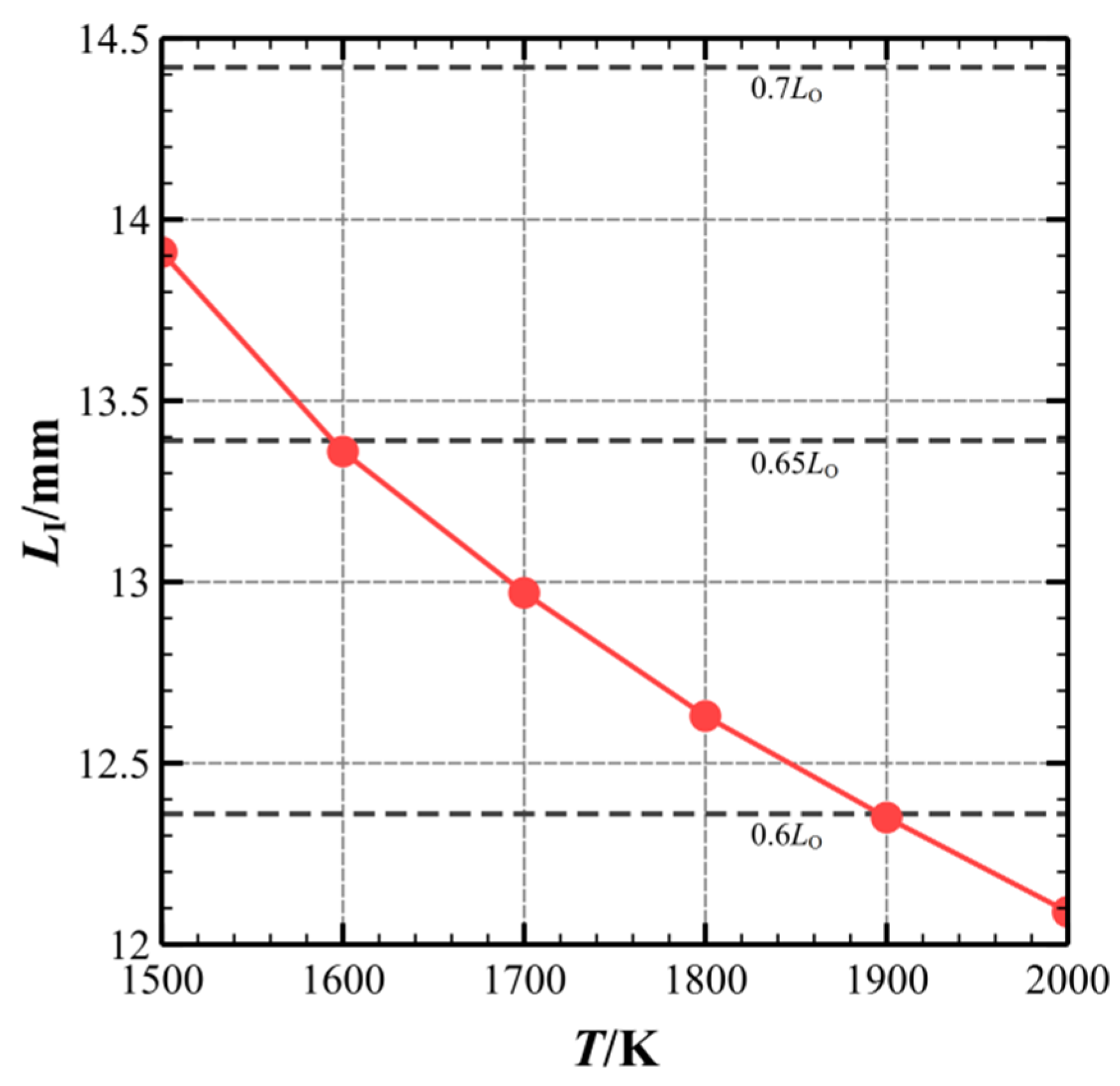
- Higher hot-spot temperatures are more conducive to the initiation of oblique detonation. With the start position of xhot-spot = 5.15 mm and the size of δ = 2 mm, the temperature of the hot-spot increases by 500 K, the initiation position of the ODW was moved about 13% upstream, and the characteristic length of the induction zone decreased from approximately 13.9 mm to about 12.1 mm.
- The larger the size of the hot-spot, the closer the oblique detonation initiation is upstream. There is a maximum hotspot size at different Mach numbers, beyond which the ignition is generated within the hotspot and the length of the induction zone does not change. The higher the Mach number, the smaller the maximum hotspot size. In addition, from the perspective of energy consumption, a small hot-spot at a high temperature is preferable for accelerating ODW initiation than a large hot-spot at a low temperature.
- The initiation of the oblique detonation is sensitive to the position of the laser-heating hot-spots. The closer the hot-spot is located upstream, the shorter the length of the induction zone of ODW. If a 2000 K hotspot is at the beginning of the wedge, then the ODW’s initiation distance will be reduced to about 30% of that without hotspot acceleration.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, K.; Teng, H.; Yang, P.; Ng, H.D. Numerical investigation of flow structures resulting from the interaction between an oblique detonation wave and an upper expansion corner. J. Fluid Mech. 2020, 903, A28. [Google Scholar] [CrossRef]
- Kailasanath, K. Review of propulsion applications of detonation waves. AIAA J. 2000, 38, 1698–1708. [Google Scholar] [CrossRef]
- Teng, H.H.; Jiang, Z.L. On the transition pattern of the oblique detonation structure. J. Fluid Mech. 2012, 713, 659–669. [Google Scholar] [CrossRef]
- Dunlap, R.; Brehm, R.L.; Nicholls, J.A. A preliminary study of the application of steady-state detonative combustion to a reaction engine. J. Jet Propuls. 1958, 28, 451–456. [Google Scholar] [CrossRef]
- Pratt, D.T.; Humphrey, J.W.; Glenn, D.E. Morphology of standing oblique detonation waves. J. Propuls. Power 1991, 7, 837–845. [Google Scholar] [CrossRef]
- Morrison, R.B. Oblique Detonation Wave Ramjet; NASA-CR-159192; NASA: Hampton, VA, USA, 1980. [Google Scholar]
- Zhang, B.; Liu, H.; Yan, B.; Ng, H.D. Experimental study of detonation limits in methane-oxygen mixtures: Determining tube scale and initial pressure effects. Fuel 2020, 259, 116220. [Google Scholar] [CrossRef]
- Yang, P.; Teng, H.; Jiang, Z. Effects of inflow Mach number on oblique detonation initiation with a two-step induction-reaction kinetic model. Combust. Flame 2018, 193, 246–256. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, B. Numerical and experimental analysis of detonation induced by shock wave focusing. Combust. Flame 2023, 251, 112691. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, B.; Ng, H.D.; Liu, H.; Wang, F. Effects of inert gas jet on the transition from deflagration to detonation in a stoichiometric methane-oxygen mixture. Fuel 2021, 285, 119237. [Google Scholar] [CrossRef]
- Li, C.; Kailasanath, K.; Oran, E.S. Detonation structures behind oblique shocks. Phys. Fluids 1994, 6, 1600–1611. [Google Scholar] [CrossRef]
- Li, C.; Kailasanath, K.; Oran, E.S. Effects of boundary layers on oblique-detonation structures. In Proceedings of the 31st Aerospace Sciences Meeting, Reno, NV, USA, 11–14 January 1993. AIAA Paper 1993-0450. [Google Scholar]
- Viguier, C.; Silva, L.F.; Desbordes, D.; Deshaies, B. Onset of oblique detonation waves: Comparison between experimental and numerical results for hydrogen-air mixtures. Symp. (Int.) Combust. 1996, 26, 3023–3031. [Google Scholar] [CrossRef]
- Desbordes, D.; Hamada, L.; Guerraud, C. Supersonic H2-air combustions behind oblique detonation waves. Shock Waves 1995, 4, 339–345. [Google Scholar] [CrossRef]
- Kamel, M.R.; Morris, C.I.; Stouklov, I.G.; Hanson, R.K. PLIF imaging of hypersonic reactive flow around blunt bodies. Symp. (Int.) Combust. 1996, 26, 2909–2915. [Google Scholar] [CrossRef]
- Qin, Q.; Zhang, X. Study on the effects of geometry on the initiation characteristics of the oblique detonation wave for hydrogen-air mixture. Int. J. Hydrogen Energy 2019, 44, 17004–17014. [Google Scholar] [CrossRef]
- Teng, H.; Zhang, Y.; Yang, P.; Jiang, Z. Oblique detonation wave triggered by a double wedge in hypersonic flow. Chin. J. Aeronaut. 2022, 35, 176–184. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiang, G.; Tu, Q.; Wang, Q.; Wei, H. The initiation characteristics of oblique detonation in acetylene-air mixtures in the finite wedge. Acta. Mech. Sin. 2023, 39, 122231. [Google Scholar] [CrossRef]
- Zhang, G.; Li, G.; Wang, K. Wave structure of oblique detonation disturbed by an expansion wave from a bended tunnel. Appl. Therm. Eng. 2020, 180, 115856. [Google Scholar] [CrossRef]
- Fang, Y.; Hu, Z.; Teng, H. Numerical investigation of oblique detonations induced by a finite wedge in a stoichiometric hydrogen-air mixture. Fuel 2018, 234, 502–507. [Google Scholar] [CrossRef]
- Cai, X.; Liang, J.; Deiterding, R.; Mahmoudi, Y.; Sun, M. Experimental and numerical investigations on propagating modes of detonations: Detonation wave/boundary layer interaction. Combust. Flame 2018, 190, 201–215. [Google Scholar] [CrossRef]
- Zhang, Y.; Fang, Y.; Ng, H.D.; Teng, H. Numerical investigation on the initiation of oblique detonation waves in stoichiometric acetylene—Oxygen mixtures with high argon dilution. Combust. Flame 2019, 204, 391–396. [Google Scholar] [CrossRef]
- Watanabe, H.; Matsuo, A.; Chinnayya, A.; Matsuoka, K.; Kasahara, J. Numerical analysis of the mean structure of gaseous detonation with dilute water spray. J. Fluid Mech. 2020, 887, A4. [Google Scholar] [CrossRef]
- Niu, S.; Yang, P.; Wang, K.; Teng, H. Unsteady Oblique Detonation Waves in a Tunnel Induced by Inflow Mach Number Variation. Aerospace 2023, 10, 330. [Google Scholar] [CrossRef]
- Fang, Y.; Hu, Z.; Teng, H.; Jiang, Z. Numerical study of the oblique detonation initiation induced by spheres. Chin. J. Theor. Appl. Mech. 2017, 49, 268–273. [Google Scholar]
- Han, X.; Zhang, W.; Zhang, Z.; Liu, Y.; Jiang, Z. Numerical Study of Oblique Detonation Waves Induced by a Bump. J. Propuls. Technol. 2022, 43, 200853. [Google Scholar]
- Xiang, G.; Zhang, Y.; Zhang, C.; Kou, Y. Study on initiation mechanism of oblique detonation induced by blunt bump on wedge surface. Fuel 2022, 323, 124314. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, B. Characteristics of flame acceleration and deflagration-to-detonation transition enhanced by SF6 jet-in-cross-flow/flame interaction. Aerosp. Sci. Technol. 2023, 140, 108451. [Google Scholar] [CrossRef]
- Wang, A.; Bian, J.; Teng, H. Numerical study on initiation of oblique detonation wave by hot jet. Appl. Therm. Eng. 2022, 213, 118679. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiang, G.; Gao, X.; Yu, J.; Hu, X.; Xin, Y.; Li, D.; Wang, Q. Study on initiation characteristics of oblique detonation induced by hydrogen jets in acetylene-air mixtures. Fuel 2023, 350, 128787. [Google Scholar]
- Daiber, J.W.; Thompson, H.M. Laser Driven Detonation Waves in Gases. Phys. Fluids 1967, 10, 1162. [Google Scholar] [CrossRef]
- Steverding, B. Ignition of laser detonation waves. J. Appl. Phys. 1974, 45, 3507. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Z.; Jiang, Z.; Han, X.; Liu, Y.; Wang, C. Numerical investigation of free oblique detonation wave induced by non-intrusive energy deposition. AIP Adv. 2021, 11, 125119. [Google Scholar] [CrossRef]
- Melguizo-Gavilanes, J.; Boeck, L.R.; Mével, R.; Shepherd, J. Hot surface ignition of stoichiometric hydrogen-air mixtures. Int. J. Hydrogen Energy 2017, 42, 7393–7403. [Google Scholar] [CrossRef]
- Kumar, R.K. Ignition of hydrogen-oxgen-diluent mixtures adjacent to a hot, nonreactive surface. Combust. Flame 1989, 75, 197–215. [Google Scholar] [CrossRef]
- Marengo, S.; Migliavacca, G.; Hugony, F.; Maggioni, A.; Morreale, C. Reactivity of H2/air mixtures over hot metal surfaces. Int. J. Hydrogen Energy 2010, 35, 10018–10023. [Google Scholar] [CrossRef]
- Ghermay, Y.; Mantzaras, J.; Bombach, R.; Boulouchos, K. Homogeneous combustion of fuel-lean H2/O2/N2 mixtures over platinum at elevated pressures and preheats. Combust. Flame 2011, 158, 1491–1506. [Google Scholar] [CrossRef]
- Jian, X.; Xu, R.; Shao, C.; Li, J. Thermal effect analysis of the interaction between laser and metal material. J. Shenyang Aerosp. Univ. 2014, 31, 33–36. [Google Scholar]
- Huang, J.; Shi, W.; Xie, Y.; An, F.; Li, Y. Numerical simulation of transient temperature field under the interaction between laser and metal materials. High Power Laser Part. Beams 2018, 30, 164–168. [Google Scholar]
- Xiang, G.; Zhang, Y.; Tu, Q.; Gao, Y.; Huang, X.; Peng, T. The initiation characteristics of oblique detonation waves induced by a curved surface. Aerosp. Sci. Technol. 2022, 128, 107743. [Google Scholar] [CrossRef]
- Darif, M.; Semmar, N. Numerical simulation of Si nanosecond laser annealing by COMSOL Multiphysics. In Proceedings of the COMSOL Conference 2008, Hannover, Germany, 4–6 November 2008; pp. 567–571. [Google Scholar]
- Hanon, M.M.; Akman, E.; Oztoprak, B.G.; Gunes, M.; Taha, Z.; Hajim, K.; Kacar, E.; Gundogdu, O.; Demir, A. Experimental and theoretical investigation of the drilling of alumina ceramic using Nd: YAG pulsed laser. Opt. Laser Technol. 2012, 44, 913–922. [Google Scholar] [CrossRef]
- Pei, X.; Wu, J. Numerical simulation of transient temperature field on metal material induced by pulse laser irradiation. Laser Technol. 2012, 36, 828–831. [Google Scholar]
- Sun, C.W. Effect of Laser Irradiation; National Defense Industry Press: Beijing, China, 2002. [Google Scholar]
- Rakic, A.D.; Djurisic, A.B.; Elazar, J.M.; Majewski, M.L. Optical properties of metallic films for vertical-cavity optoelectronic devices. Appl. Opt. 1998, 37, 5271–5283. [Google Scholar] [CrossRef]
- Genieys, T.; Sentis, M.; Utéza, O. Investigation of ultrashort laser excitation of aluminum and tungsten by reflectivity measurements. Appl. Phys. A 2020, 126, 263. [Google Scholar] [CrossRef]
- McBride, B.J.; Gordon, S.; Reno, M.A. Coefficients for Calculating Thermodynamic and Transport Properties of Individual Species; NASA: Hampton, VA, USA, 1993; TM-4513. [Google Scholar]
- Wilson, G.J.; MacCormack, R.W. Modeling supersonic combustion using a fully implicit numerical method. AIAA J. 1992, 30, 1008–1015. [Google Scholar] [CrossRef]
- Kim, K.H.; Kim, C.; Rho, O.H. Methods for the accurate computations of hypersonic flows: I. AUSMPW+ scheme. J. Comput. Phys. 2021, 174, 38–80. [Google Scholar] [CrossRef]
- Zhang, G.; Gao, S.; Xiang, G. Study on initiation mode of oblique detonation induced by a finite wedge. Phys. Fluids 2021, 33, 016102. [Google Scholar] [CrossRef]
- Teng, H.; Tian, C.; Zhang, Y.; Zhou, L.; Ng, H.D. Morphology of oblique detonation waves in a stoichiometric hydrogen-air mixture. J. Fluid Mech. 2021, 913, A1. [Google Scholar] [CrossRef]



| Properties | Values |
|---|---|
| Density (ρ) (g/cm3) | 19.3 |
| Heat conductivity (k) (W·m−1·K−1) | 174 |
| Specific heat (c) (J·kg−1·K−1) | 132 |
| Power Density (Q0) (W/cm2) | Temperature (T) (K) |
|---|---|
| 10,000 | 1217 |
| 16,000 | 1756 |
| 19,000 | 2021 |
| M0 | 6.8 | 7.0 | 7.2 | 7.4 | 7.6 |
|---|---|---|---|---|---|
| LI (mm) | 28.77 | 20.60 | 14.58 | 9.82 | 6.07 |
| xhot-spot (mm) | 2.88 | 2.06 | 1.46 | 0.98 | 0.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, Y.; Shang, J.; Xiang, G.; Wang, Q. Investigation on Accelerated Initiation of Oblique Detonation Wave Induced by Laser-Heating Hot-Spot. Aerospace 2024, 11, 485. https://doi.org/10.3390/aerospace11060485
Xin Y, Shang J, Xiang G, Wang Q. Investigation on Accelerated Initiation of Oblique Detonation Wave Induced by Laser-Heating Hot-Spot. Aerospace. 2024; 11(6):485. https://doi.org/10.3390/aerospace11060485
Chicago/Turabian StyleXin, Yirong, Jiahao Shang, Gaoxiang Xiang, and Qiu Wang. 2024. "Investigation on Accelerated Initiation of Oblique Detonation Wave Induced by Laser-Heating Hot-Spot" Aerospace 11, no. 6: 485. https://doi.org/10.3390/aerospace11060485
APA StyleXin, Y., Shang, J., Xiang, G., & Wang, Q. (2024). Investigation on Accelerated Initiation of Oblique Detonation Wave Induced by Laser-Heating Hot-Spot. Aerospace, 11(6), 485. https://doi.org/10.3390/aerospace11060485








