Numerical Study on Rotor–Building Coupled Flow Field and Its Influence on Rotor Aerodynamic Performance under an Atmospheric Boundary Layer
Abstract
:1. Introduction
2. Numerical Methods
2.1. CFD Solver
2.2. Atmospheric Boundary Layer
2.3. Physical Model and Mesh
3. Validation
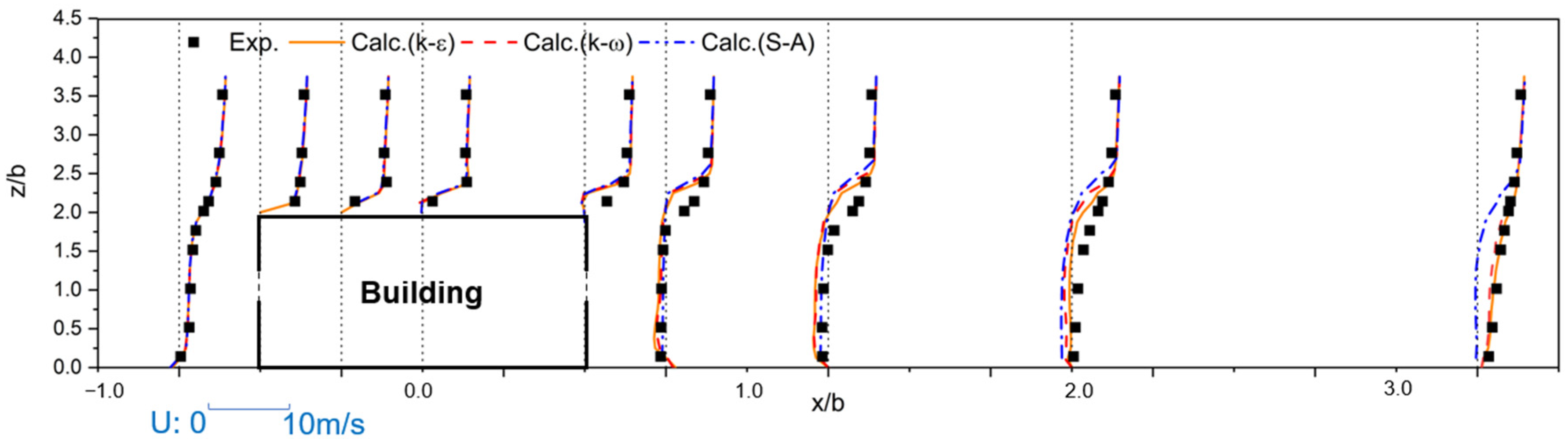
3.1. Validation of Building Flow Field
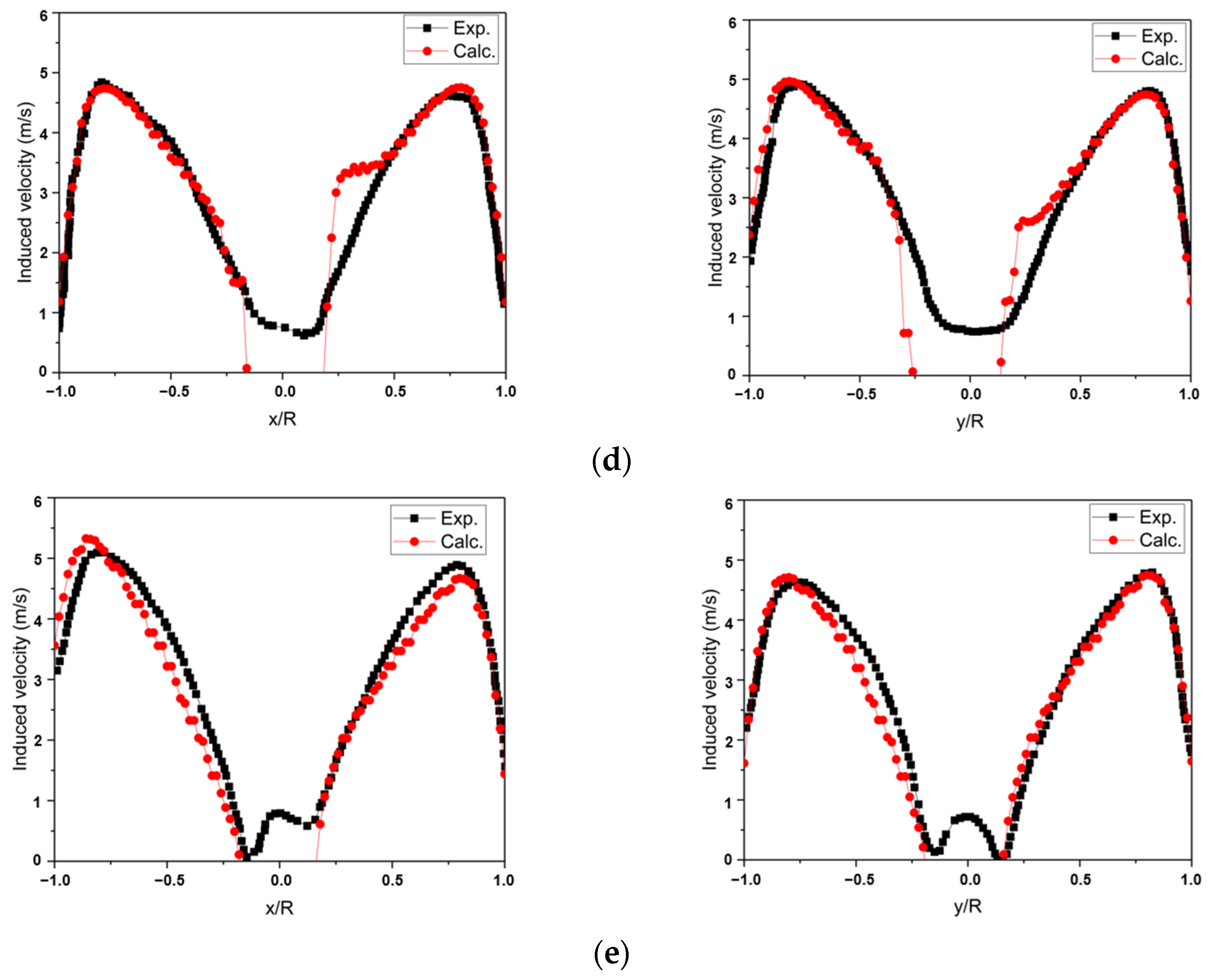
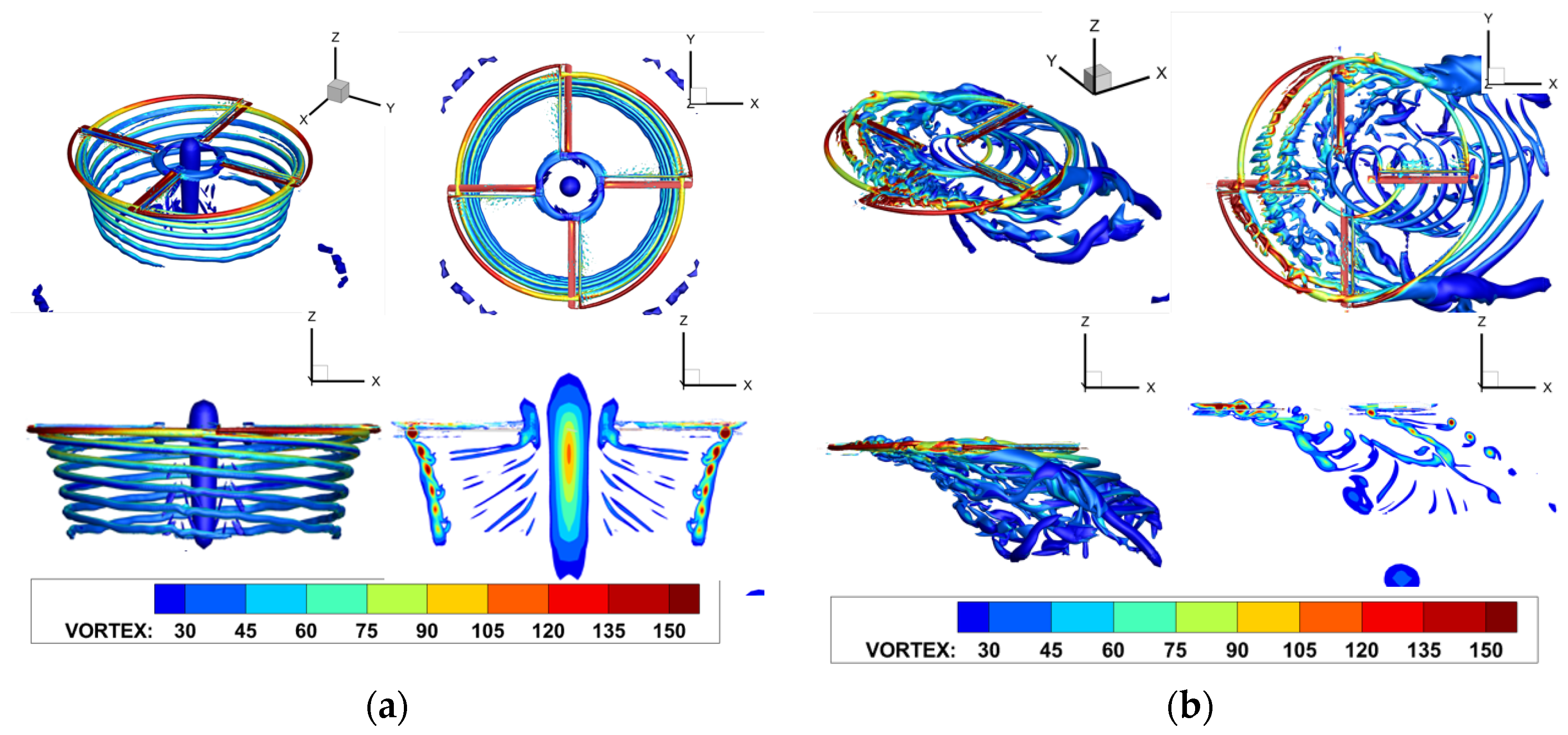
3.2. Validation in Rotor–Obstacle Interference Flow Field
4. Results
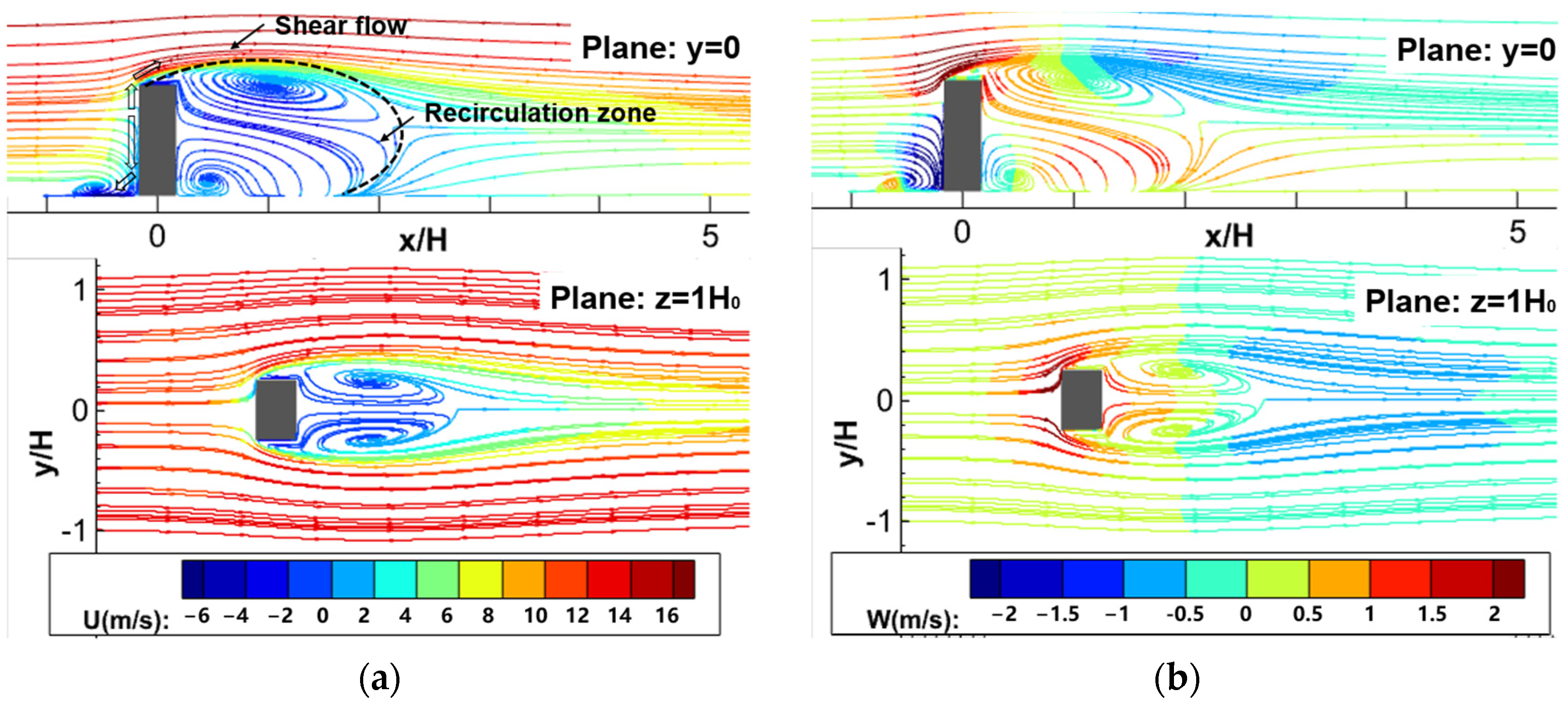
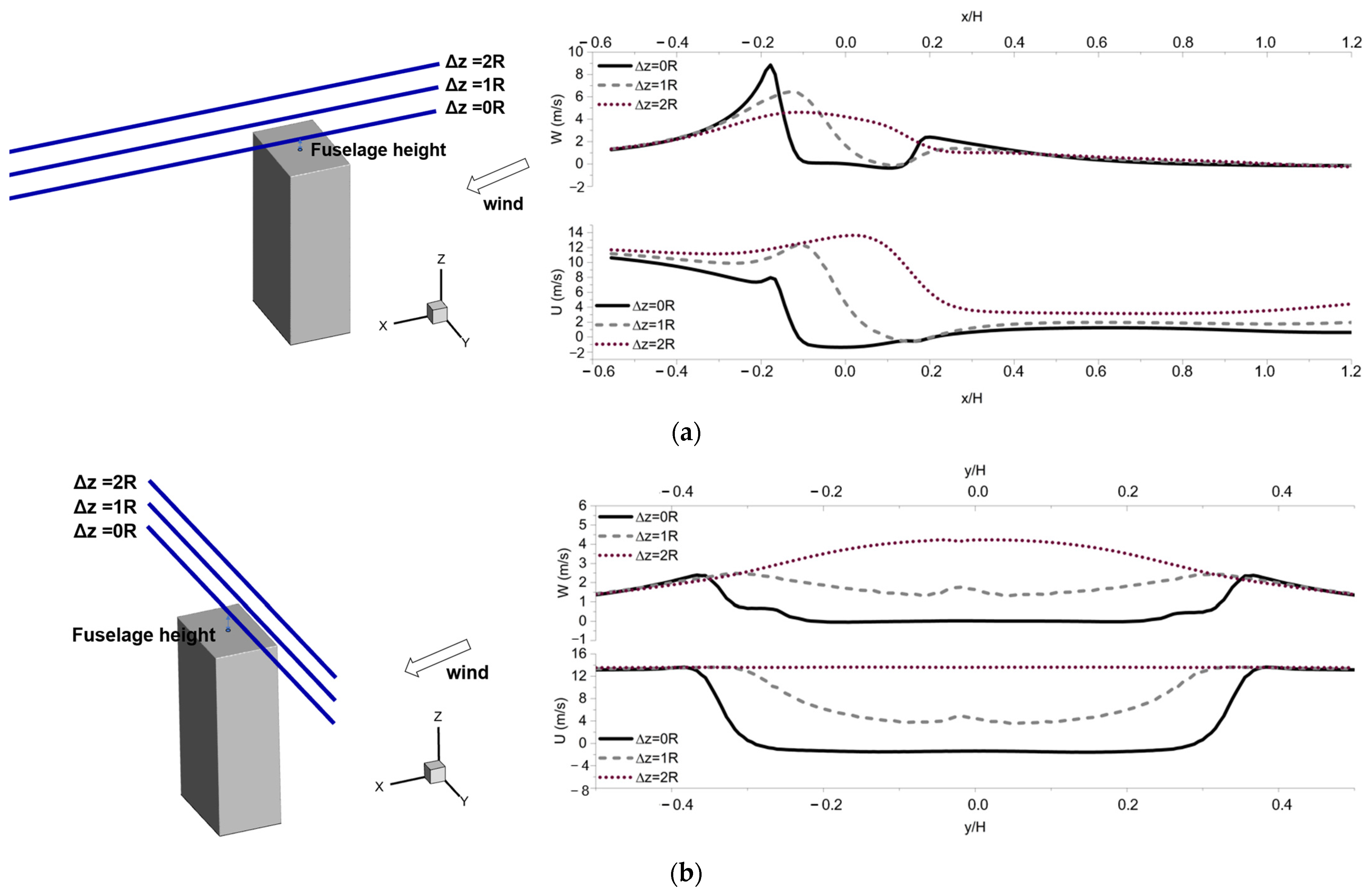
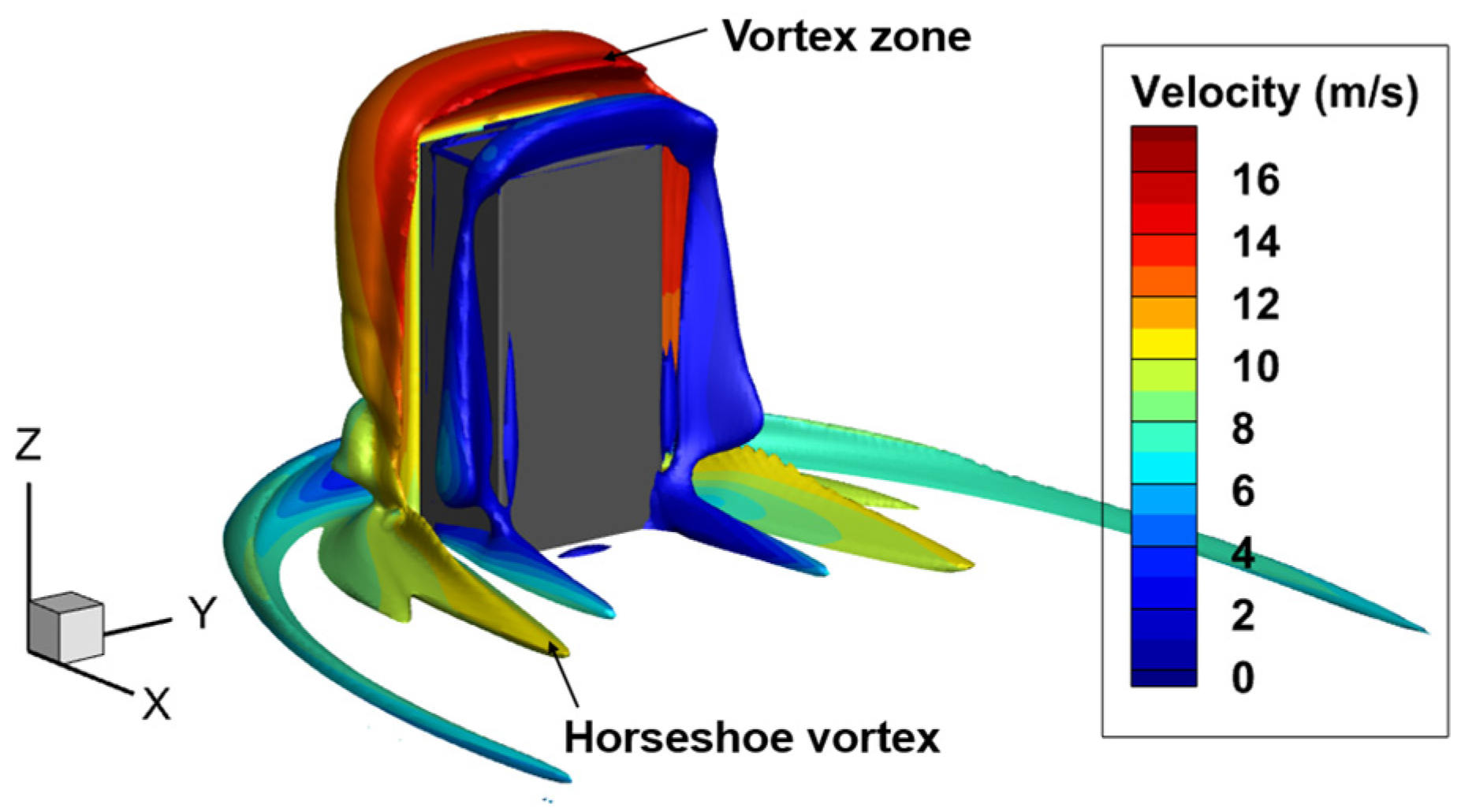
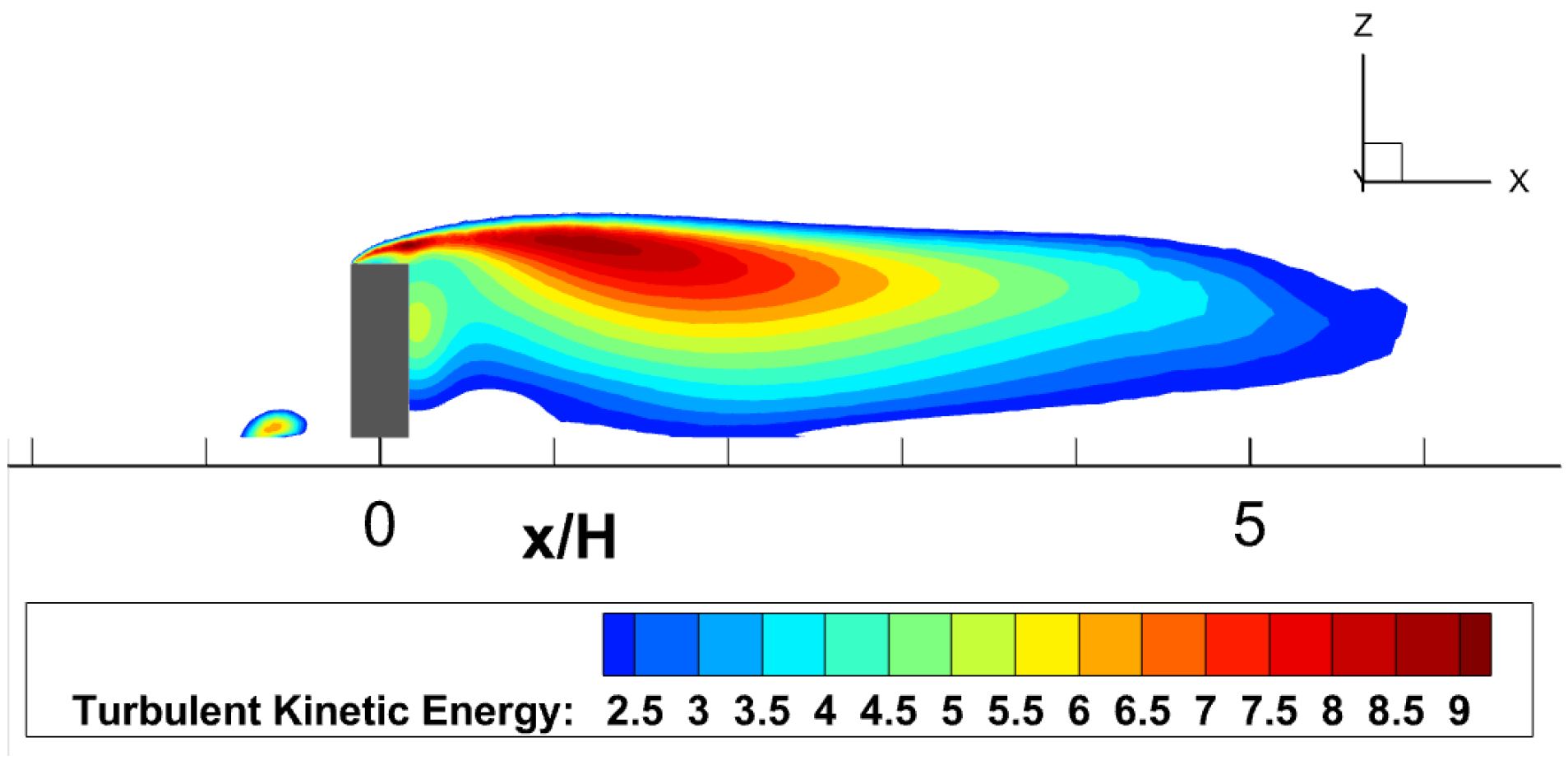
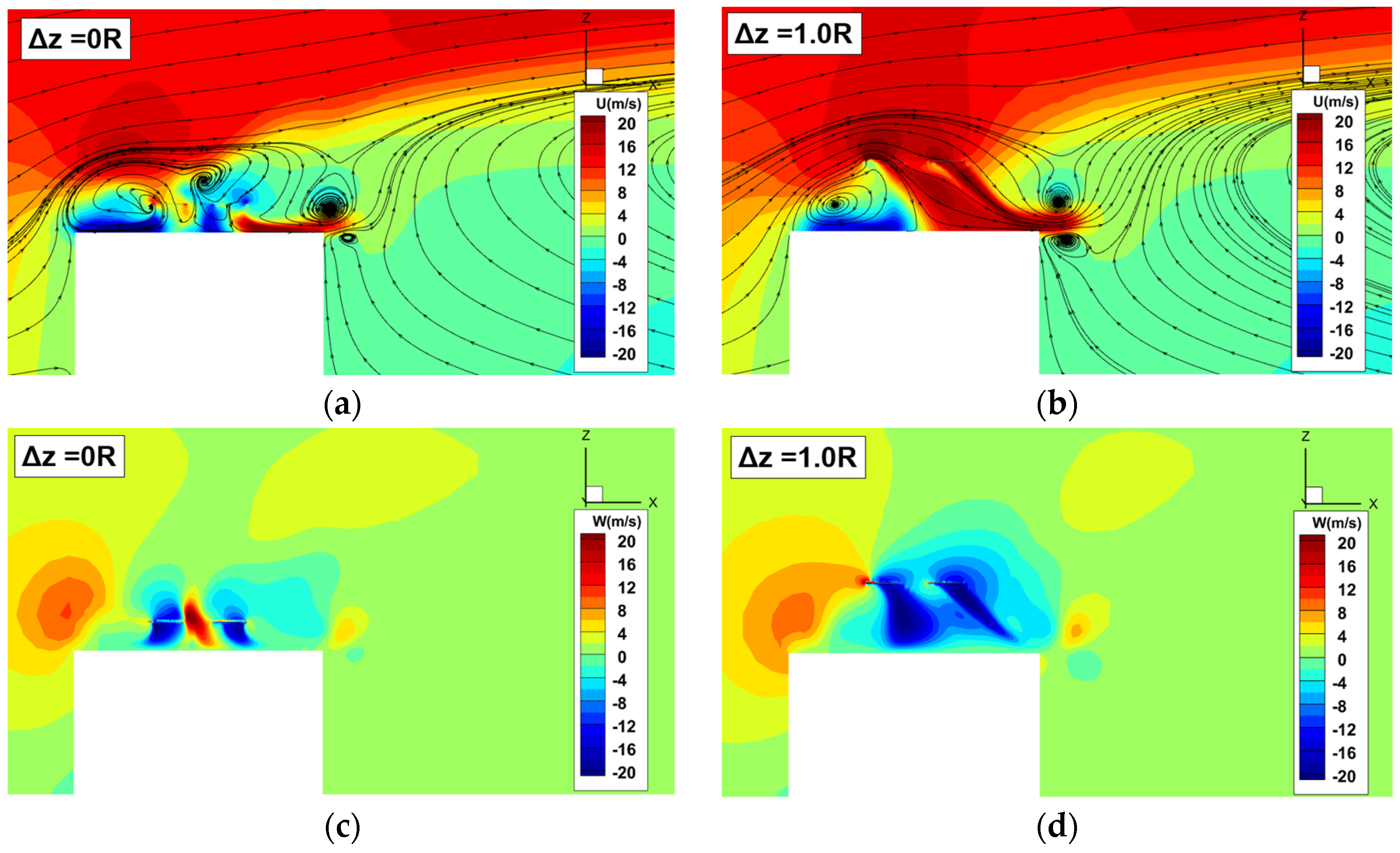
4.1. Isolated Building Flow Field
4.2. Rotor–Building Coupled Flow Field
5. Conclusions
- The numerical simulation method based on the RANS equations established in this study is suitable for calculating the coupled flow field disturbances between buildings and rotors. The overset grid method effectively handles the large-scale motion of rotors, while the Realizable model accurately captures the flow separation on building surfaces and the shear flow around buildings, enabling the precise prediction of rotor load variations under building disturbances.
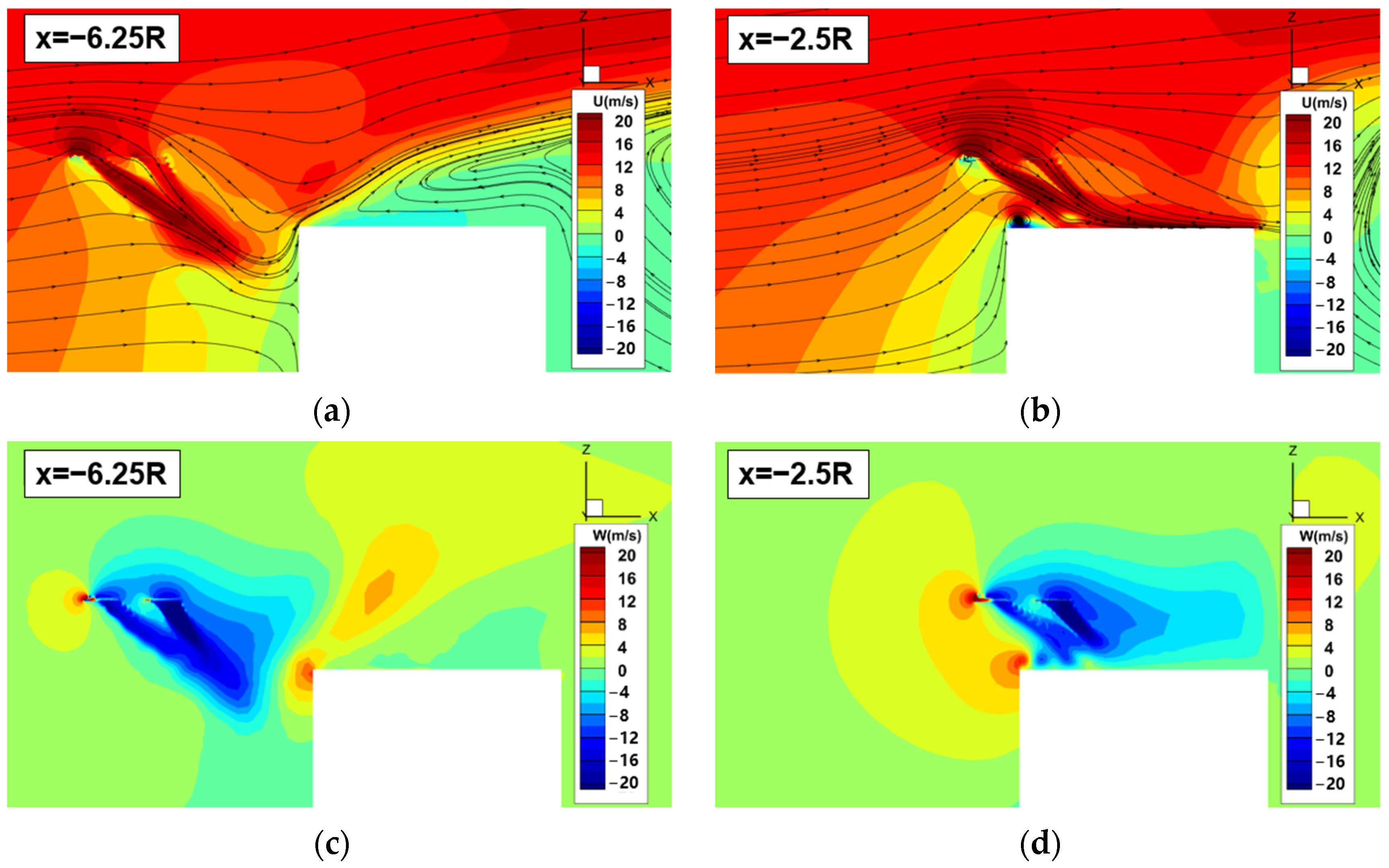
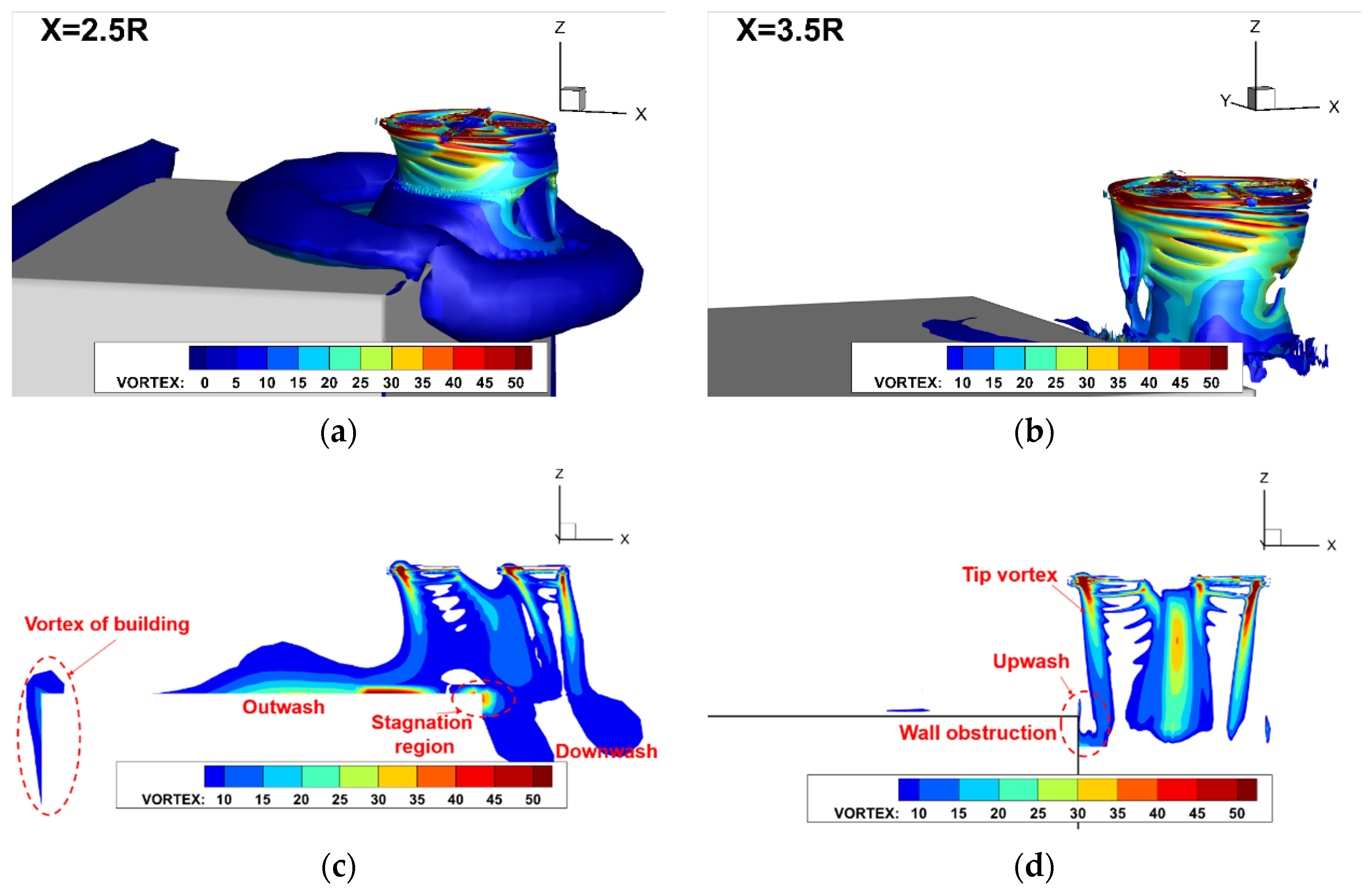
- Under atmospheric boundary conditions, extensive low-velocity vortex regions are observed at the rooftop, building sides, and in the wake region, with significant flow separation within two times the height of the building downstream of the rooftop position. On the Beaufort wind scale of 3–7, the building flow field operates within a self-similar Reynolds number region, where normalized flow velocities remain mostly constant. This characteristic provides a convenient approach for studying the safe flight envelope of helicopters around buildings.
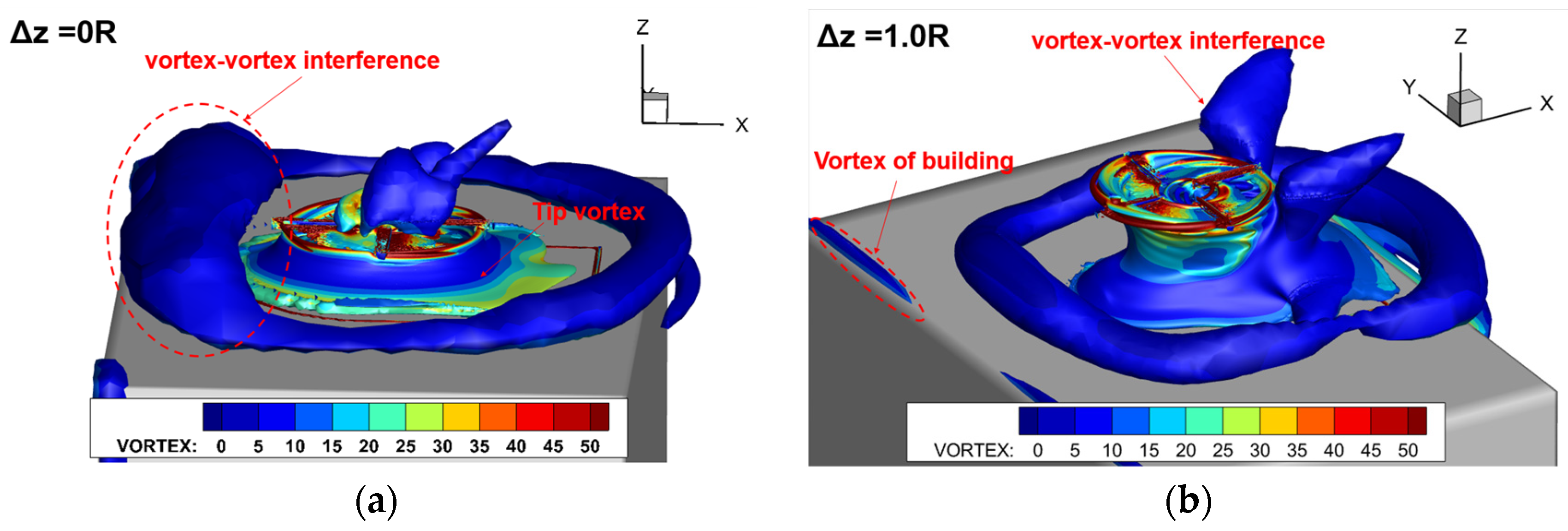
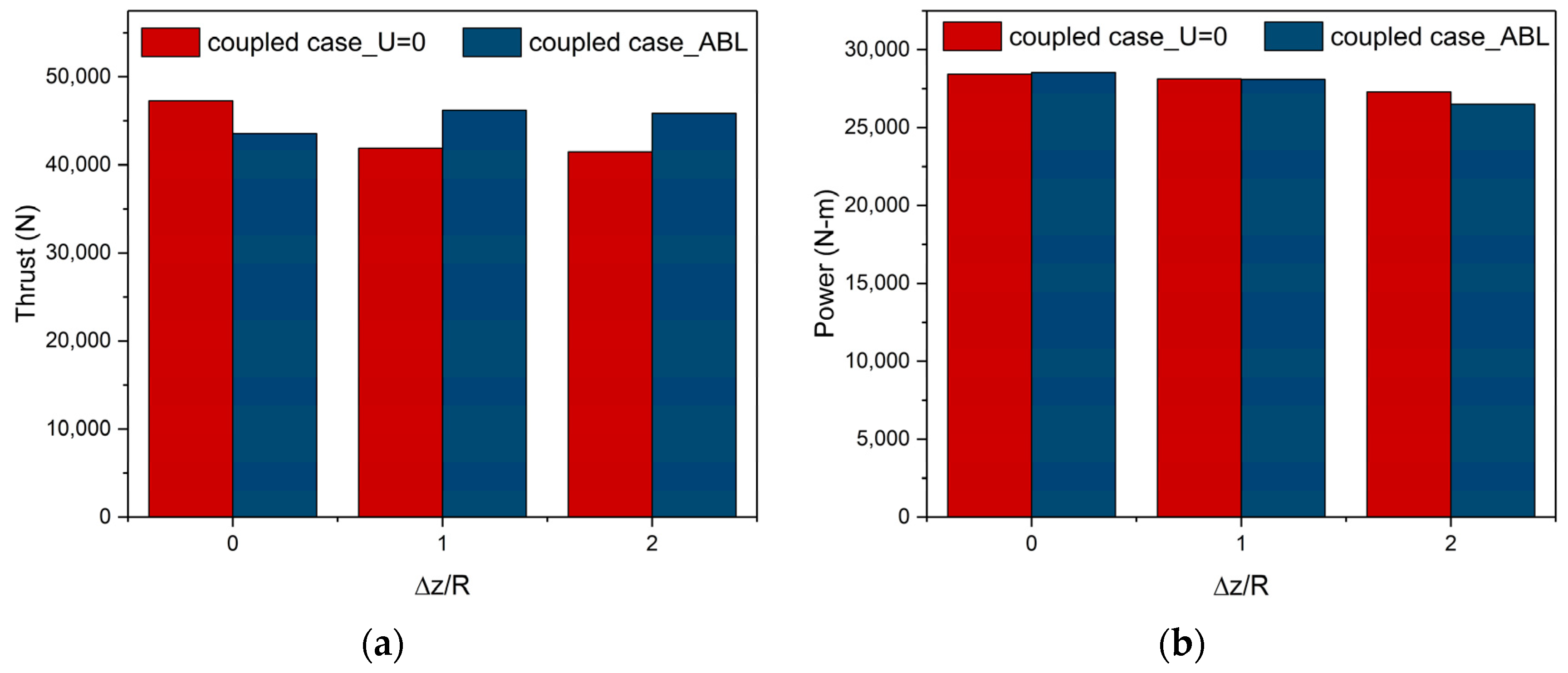
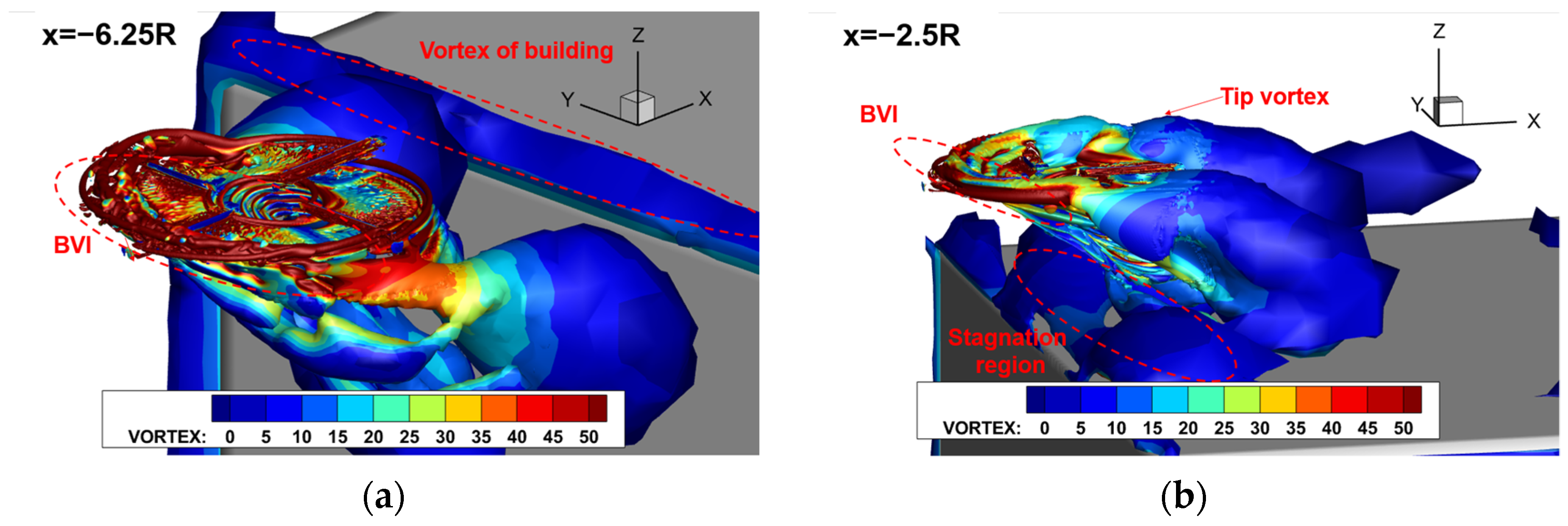
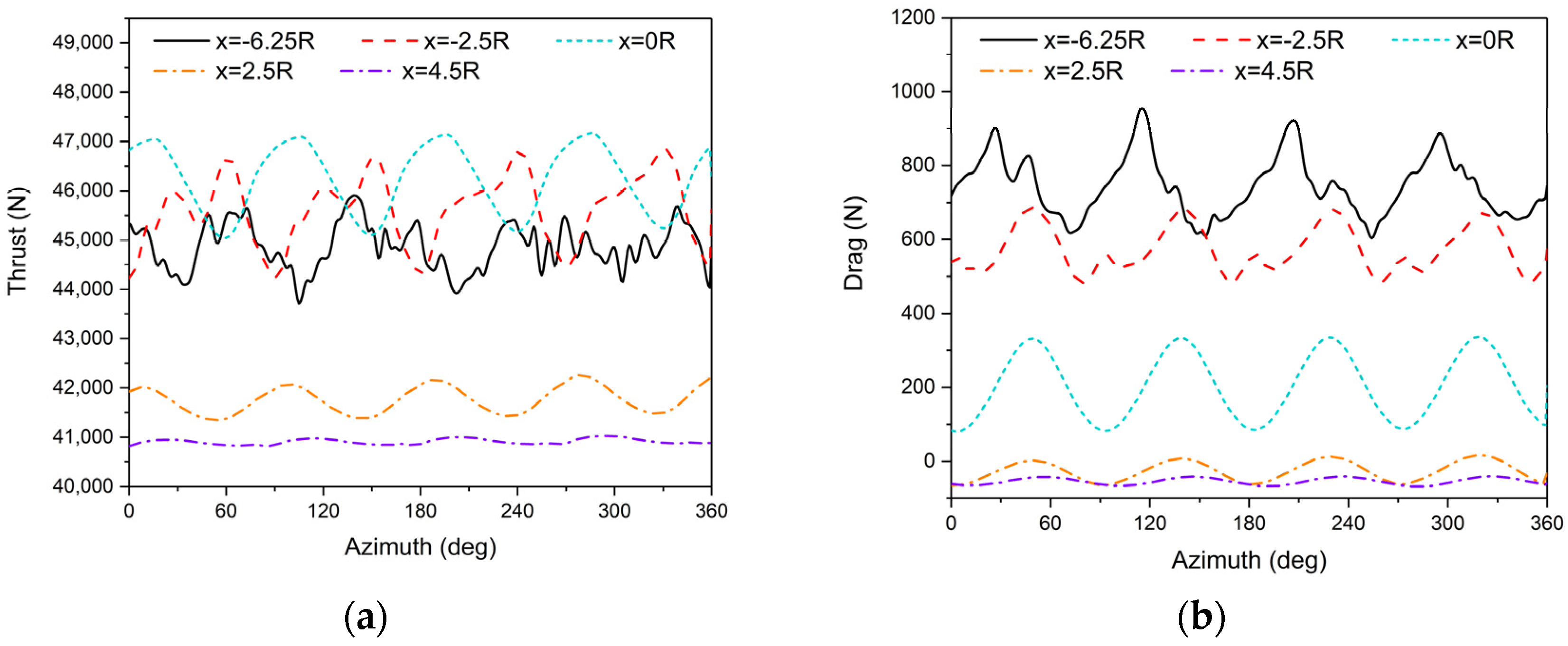
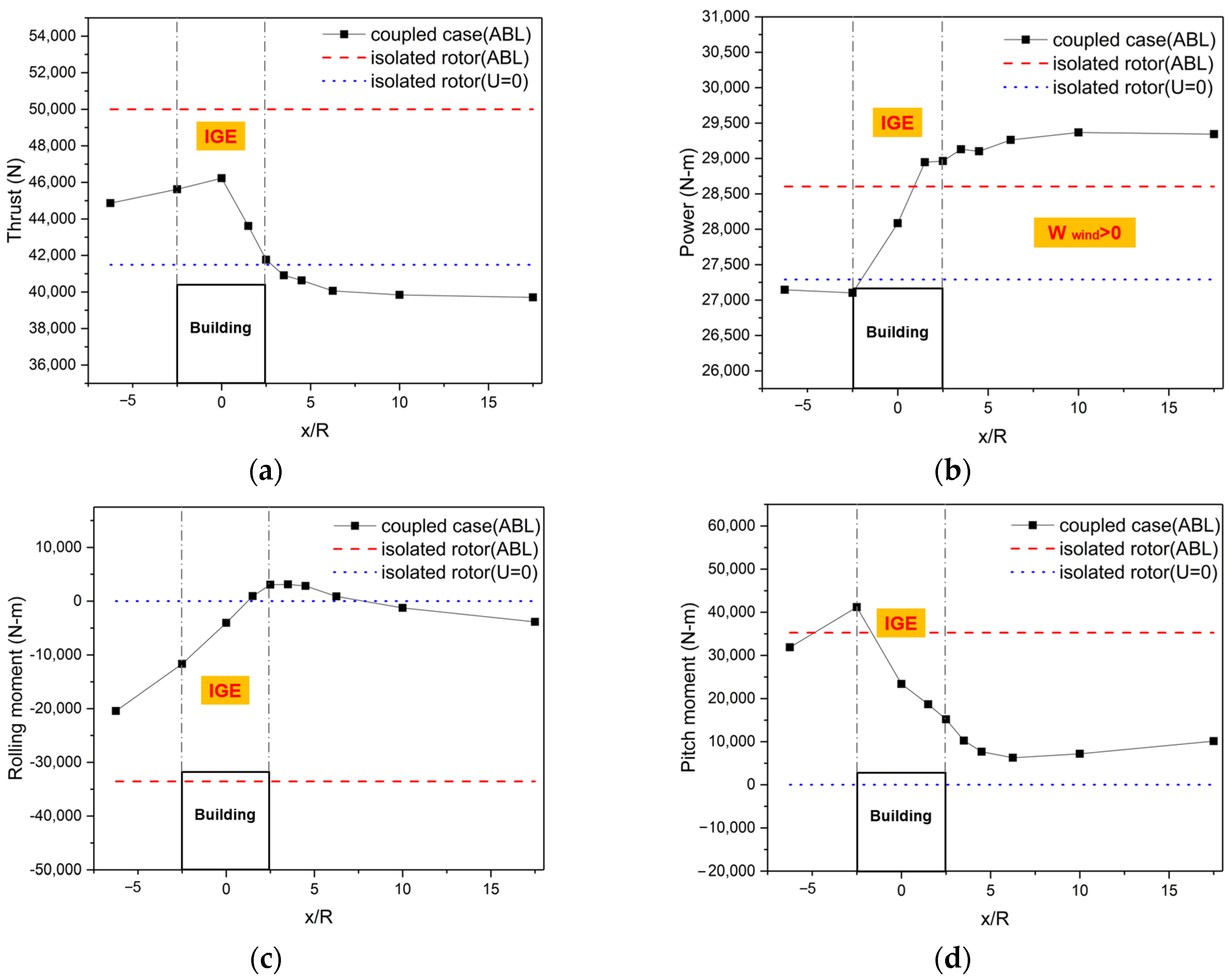
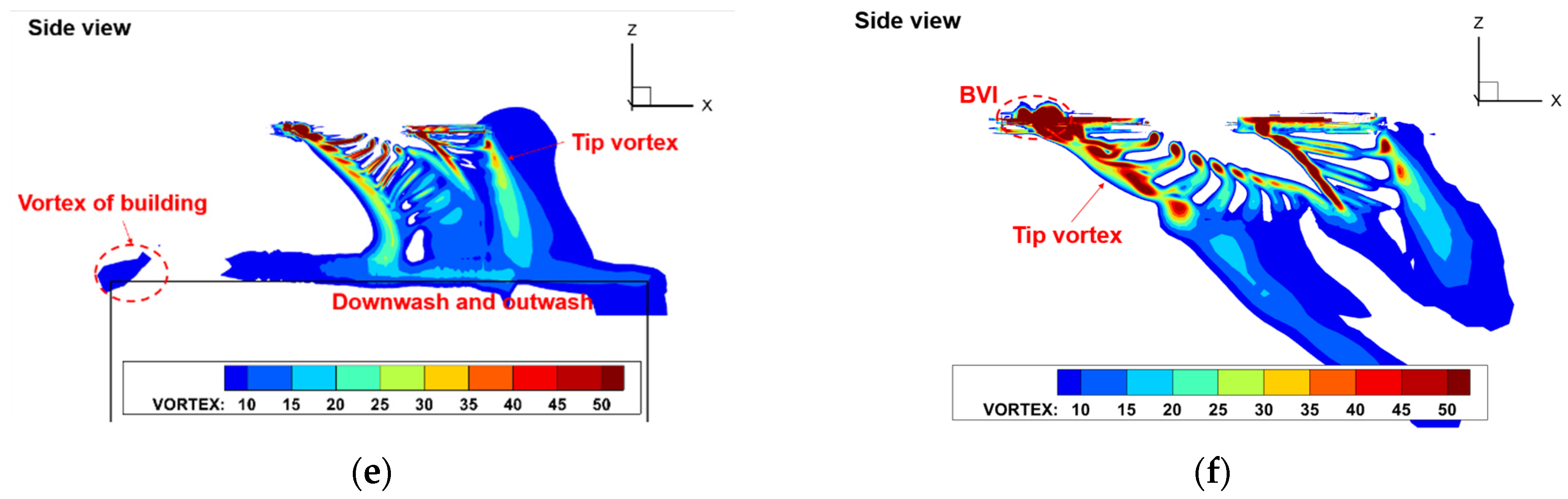
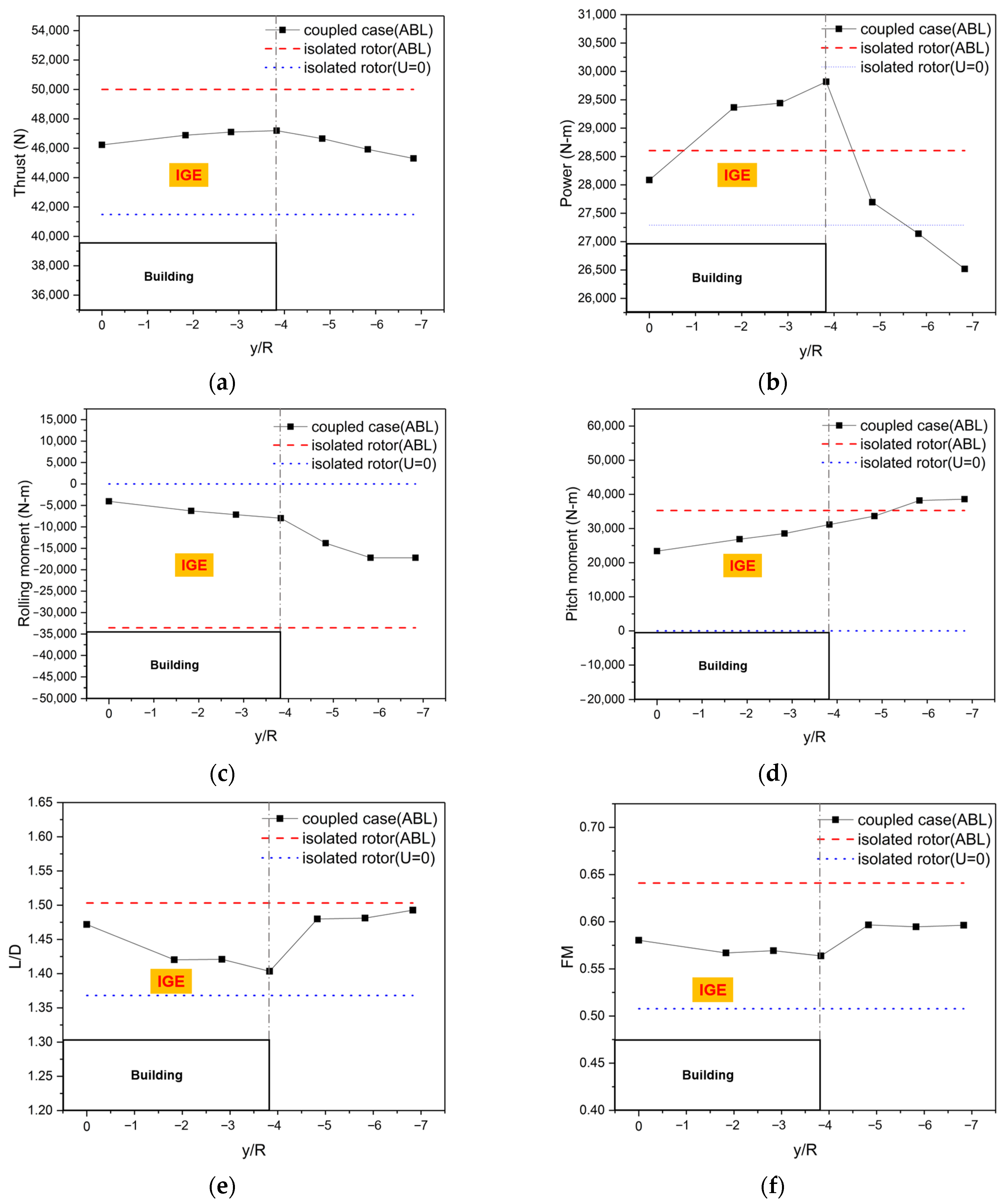
- During low-altitude hovering over building-induced turbulent airflow, the forward flow wakes mix with the building shed vortices, leading to flow circulation entering the rotor’s advancing side, resulting in a thrust loss of approximately 7.8% and generating a strong pitching moment. During rooftop takeoff, the rotor experiences an initial increase, followed by a decrease in thrust. Peak thrust is observed near the 1R position above the rooftop.
- Airflow on the headwind side of the building rises along the wall and impacts the rotor, leading to a 76% increase in pitching moment at the headwind eaves compared to the rearward positions. The area within 2R above the headwind eaves is identified as a hazardous region that must be avoided. The flow environment during the rearward approach is relatively stable, but the rotor consistently operates in a thrust loss state, with an average hover figure of merit loss of 11.4% in the wake region.
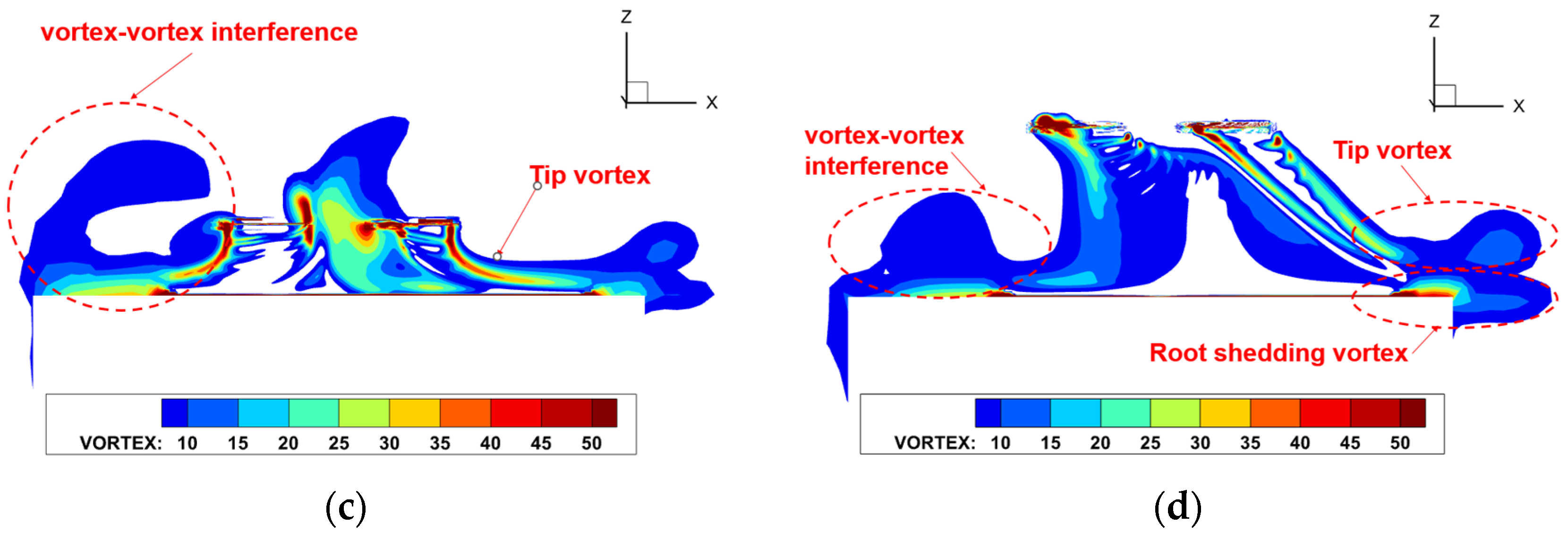
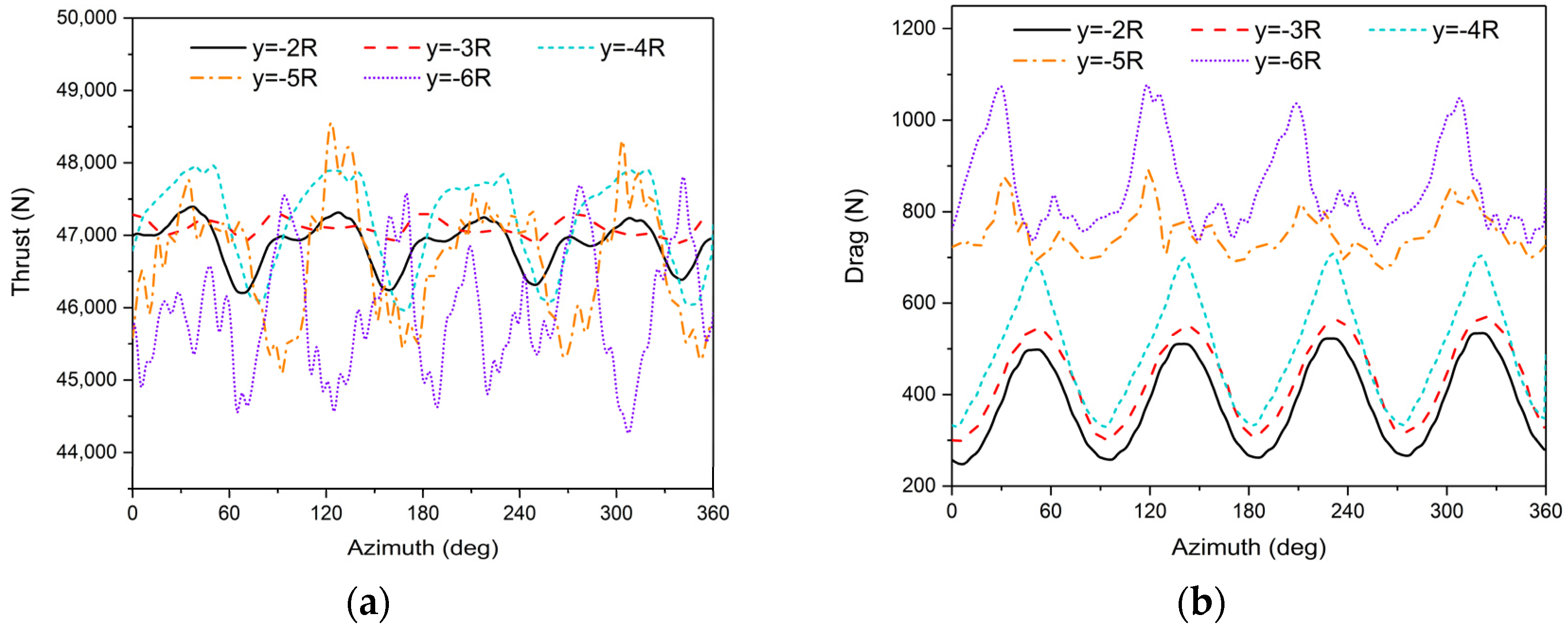
- During the crosswind approach, the wake experiences distortion, with radial contraction occurring as the age of the vortices increases. Strong vortex–vortex interactions occur as the root vortices converge below the rotor, leading to severe BVI and intense unsteady oscillations in rotor loads. When a counterclockwise rotating rotor adopts a left-side path during a crosswind approach, the semi-ground effect gain can increase the load concentration caused by non-uniform inflow velocities and reduce the sudden changes in roll moment that could lead to lateral overturning hazards.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yi, Z.; Li, R.; Feng, L.; Wu, Y.; Niu, J.; Gao, N. Boundary Layer Wind Tunnel Tests of Outdoor Airflow Field around Urban Buildings: A Review of Methods and Status. Renew. Sustain. Energy Rev. 2022, 167, 112717. [Google Scholar]
- U.S. Joint Helicopter Safety Analysis Team. The Compendium Report: The U.S. JHAST Baseline of Helicopter Accident Analysis; U.S.-JHSAT: Alexandria, VA, USA, 2011. [Google Scholar]
- Michael, J.B.; Lawson, R.E. Comparison of Centerline Velocity Measurements Obtained around 2d and 3d Building Arrays in a Wind Tunnel. In Proceedings of the International Society of Environmental Hydraulics Conference, Tempe, AZ, USA, 5–8 December 2001. [Google Scholar]
- Zhao, Y.H.; Liu, J.; Carmeliet, J. Physics-Based Stitching of Multi-Fov Piv Measurements for Urban Wind Fields. Build. Environ. 2021, 205, 108306. [Google Scholar]
- Yan, M.; Hibi, K. Turbulent Measurments of the Flow Field around a High-Rise Building. Wind Eng. JAWE 1998, 76, 55–64. [Google Scholar]
- Shreya, A.; Wong, J.K.; Song, J.; Mercan, O.; Kushner, P.J. Assessment of the Aerodynamic Performance of Unconventional Building Shapes Using 3d Steady Rans with Sst K-Ω Turbulence Model. J. Wind Eng. Ind. Aerodyn. 2022, 225, 104988. [Google Scholar]
- Yoshihide, T. Flow around a High-Rise Building Using Steady and Unsteady Rans Cfd: Effect of Large-Scale Fluctuations on the Velocity Statistics. J. Wind Eng. Ind. Aerodyn. 2015, 142, 10. [Google Scholar]
- Yoshihide, T.; Stathopoulos, T. Cfd Simulation of near-Field Pollutant Dispersion in the Urban Environment: A Review of Current Modeling Techniques. Atmos. Environ. 2013, 79, 716–730. [Google Scholar]
- Abiy, F.M.; Bitsuamlak, G.T. Prospect of Les for Predicting Wind Loads and Responses of Tall Buildings: A Validation Study. J. Wind Eng. Ind. Aerodyn. 2024, 244, 105613. [Google Scholar]
- Fei, D.; Kareem, A. A Multi-Fidelity Shape Optimization Via Surrogate Modeling for Civil Structures. J. Wind Eng. Ind. Aerodyn. 2018, 178, 49–56. [Google Scholar]
- Liu, Y.S.; Miao, S.G.; Zhang, C.L.; Cui, G.X.; Zhang, Z.S. Study on Micro-Atmospheric Environment by Coupling Large Eddy Simulation with Mesoscale Model. J. Wind. Eng. Ind. Aerodyn. 2012, 108, 106–117. [Google Scholar] [CrossRef]
- Bert, B. Les over Rans in Building Simulation for Outdoor and Indoor Applications: A Foregone Conclusion? Build. Simul. 2018, 11, 821–870. [Google Scholar]
- Juan, M.G.; Bre, F. Optimization of Rans Turbulence Models Using Genetic Algorithms to Improve the Prediction of Wind Pressure Coefficients on Low-Rise Buildings. J. Wind Eng. Ind. Aerodyn. 2019, 193, 103978. [Google Scholar]
- Giulia, C.; Szubert, D.; Vigevano, L.; Barakos, G.N. Numerical Modelling of the Aerodynamic Interference between Helicopter and Ground Obstacles. CEAS Aeronaut. J. 2017, 8, 589–611. [Google Scholar]
- Johnson, C.S.; Barakos, G.N. Optimizing Rotor Blades with Approximate British Experimental Rotor Programme Tips. J. Aircr. 2014, 51, 447–463. [Google Scholar] [CrossRef]
- Daniele, Z.; Gibertini, G.; Giuni, M.; Green, R. Experiments on the Helicopter-Obstacle Aerodynamic Interference in Absence of External Wind. In Proceedings of the 42nd European Rotorcraft Forum, Lille, France, 5–8 September 2016. [Google Scholar]
- Teresa, Q. Rotor Performance in the Wake of a Large Structure. In Proceedings of the American Helicopter Society 65th Annual Forun, Grapevine, TX, USA, 27–29 May 2009. [Google Scholar]
- Matthias, S. Simulation of Helicopter Aerodynamics in the Vicinity of an Obstacle Using a Free Wake Panel Method. In Proceedings of the 43rd European Rotorcraft Forum, Mailand, Italien, 12–15 September 2017. [Google Scholar]
- Feng, T.; Sun, Y.M.; Zhou, T.; Barakos, G.N.; Green, R. Simulation of the Aerodynamic Interaction between Rotor and Ground Obstacle Using Vortex Method. CEAS Aeronaut. J. 2018, 10, 733–753. [Google Scholar]
- Susan, P.; Wilkinson, C. A Computational Study of Outwash for a Helicopter Operating near a Vertical Face with Comparison to Experimental Data. In Proceedings of the AIAA Modeling and Simulation Technologies Conference 2009, Chicago, IL, USA, 10–13 August 2009. [Google Scholar]
- Bernardo, P.; Réamonn, M.R.; Patrick, Y.; Diarmuid, B.; Philip, C.; Jennifer, K. Investigation of Helicopter Downwash Effect on Pedestrian Comfort Using Cfd. Infrastruct. Asset Manag. 2019, 8, 7. [Google Scholar] [CrossRef]
- Adam, D. Cfd Analysis of Rotor Wake Influence on Rooftop Helipad Operations Safety. Trans. Inst. Aviat. 2016, 242, 7–22. [Google Scholar]
- James, S.F.; Owen, I. An Investigation of Ship Airwakes Using Detached-Eddy Simulation. Comput. Fluids 2010, 39, 656–673. [Google Scholar]
- Watson, N.A.; Kelly, M.F.; Owen, I.; Hodge, S.J.; White, M.D. Computational and Experimental Modelling Study of the Unsteady Airflow over the Aircraft Carrier Hms Queen Elizabeth. Ocean Eng. 2019, 172, 562–574. [Google Scholar] [CrossRef]
- Regis, T.; Murman, S.M.; Horn, J.; Schmitz, S. Effects of Atmospheric Turbulence Unsteadiness on Ship Airwakes and Helicopter Dynamics. J. Aircr. 2020, 57, 534–546. [Google Scholar]
- Shih, T.H.; Liou, W.W.; Shabbir, A.H.; Yang, Z.; Zhu, J. A New K-ϵ Eddy Viscosity Model for High Reynolds Number Turbulent Flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Smedman-Högström, A.S.; Högström, U. A Practical Method for Determining Wind Frequency Distributions for the Lowest 200 M from Routine Meteorological Data. J. Appl. Meteorol. Climatol. 1978, 17, 942–954. [Google Scholar] [CrossRef]
- Frank, B.; Werner, H.; Wengle, H. Numerical Simulation of Turbulent Flow over Surface-Mounted Obstacles with Sharp Edges and Corners. J. Wind Eng. Ind. Aerodyn. 1990, 35, 129–147. [Google Scholar]
- Oliveira Paulo, J.; Younis, B.A. On the Prediction of Turbulent Flows around Full-Scale Buildings. J. Wind Eng. Ind. Aerodyn. 2000, 86, 203–220. [Google Scholar] [CrossRef]
- Fan, X.H.; Ma, C.Y.; Su, B. Introduction and Comparison of Wind Load Codes for Advanced Structure between Chinese, American and British. Adv. Mater. Res. 2013, 700, 85–88. [Google Scholar]
- Philippe, R. Aerodynamic Design of the Aerospatiale Sa 365n Dauphin 2 Helicopter. J. Am. Helicopter Soc. 1982, 27, 27–33. [Google Scholar]
- Tamura, Y.; Kawai, H.; Uematsu, Y.; Marukawa, H.; Fujii, K.; Taniike, Y. Wind Load and Wind-Induced Response Estimations in the Recommendations for Loads on Buildings, Aij 1993. Eng. Struct. 1996, 18, 399–411. [Google Scholar] [CrossRef]
- Daniele, Z.; Giuni, M.; Green, R. Rotor-Obstacle Aerodynamic Interaction in Hovering Flight: An Experimental SurveyIn. In Proceedings of the AHS 72nd Annual Forum, West Palm Beach, FL, USA, 17–19 May 2016. [Google Scholar]
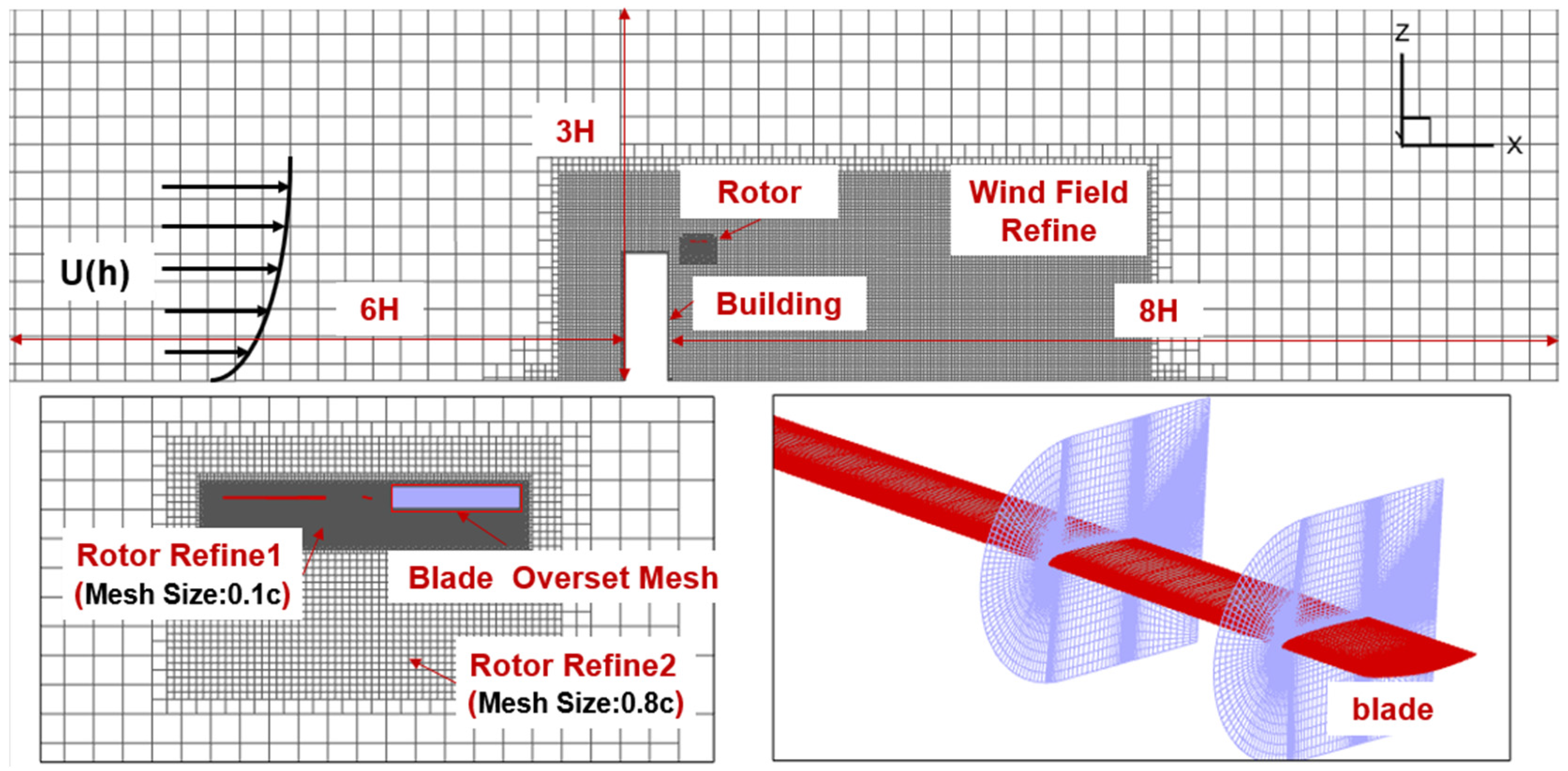
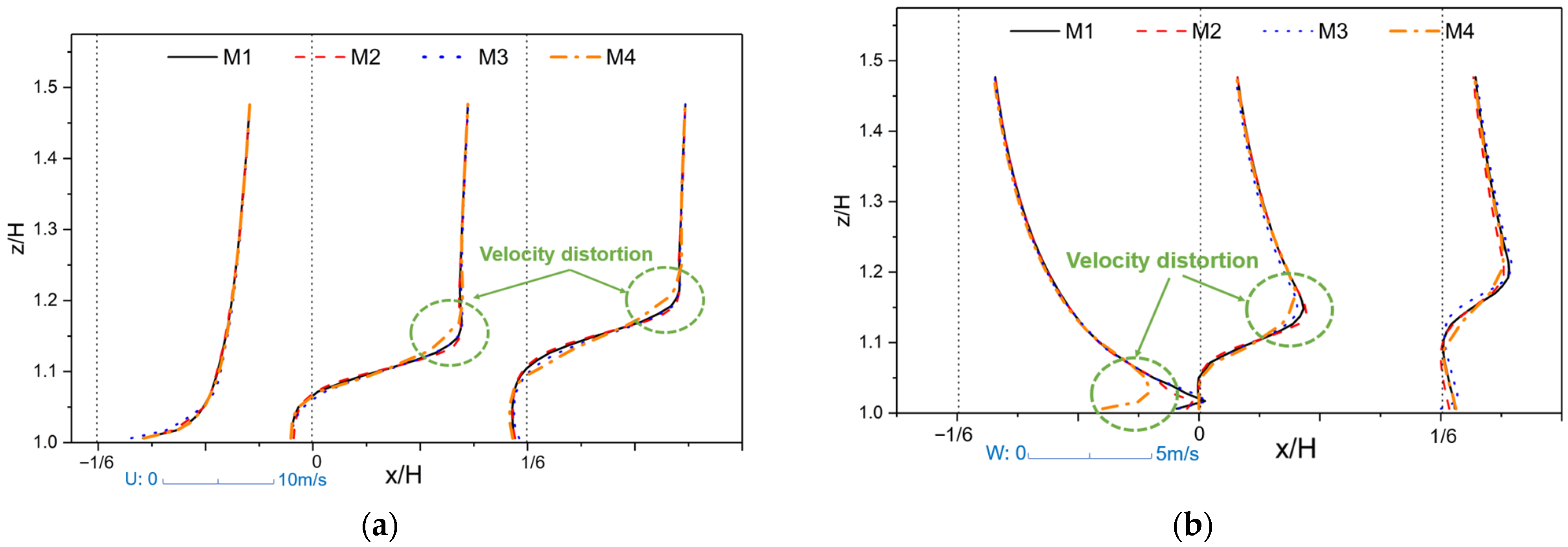








| Building | |
|---|---|
| Parameters | Value |
| 30.48 m × 45.72 m × 91.44 m | |
| Landform | D-type |
| Domain | 1400 m × 1000 m × 300 m |
| Rotor | |
| Parameters | Value |
| Number of blades | 4 |
| Diameter/m | 11.93 |
| Chord/m | 0.385 |
| Twist of blade/deg | −10 (linear) |
| rotational direction | clockwise |
| Airfoil | OA212, from 0.2R to 0.73R Linear tapering from 0.73R (OA212) to 0.88R (OA209) Linear tapering from 0.88R (OA209) to R (OA207) |
| Tip shape | 45° swept leading edge from 0.98R |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Shi, Y.; Aziz, A.; Xu, G. Numerical Study on Rotor–Building Coupled Flow Field and Its Influence on Rotor Aerodynamic Performance under an Atmospheric Boundary Layer. Aerospace 2024, 11, 521. https://doi.org/10.3390/aerospace11070521
Liu Y, Shi Y, Aziz A, Xu G. Numerical Study on Rotor–Building Coupled Flow Field and Its Influence on Rotor Aerodynamic Performance under an Atmospheric Boundary Layer. Aerospace. 2024; 11(7):521. https://doi.org/10.3390/aerospace11070521
Chicago/Turabian StyleLiu, Yang, Yongjie Shi, Aqib Aziz, and Guohua Xu. 2024. "Numerical Study on Rotor–Building Coupled Flow Field and Its Influence on Rotor Aerodynamic Performance under an Atmospheric Boundary Layer" Aerospace 11, no. 7: 521. https://doi.org/10.3390/aerospace11070521
APA StyleLiu, Y., Shi, Y., Aziz, A., & Xu, G. (2024). Numerical Study on Rotor–Building Coupled Flow Field and Its Influence on Rotor Aerodynamic Performance under an Atmospheric Boundary Layer. Aerospace, 11(7), 521. https://doi.org/10.3390/aerospace11070521







