Trajectory Design of Potentially Hazardous Asteroid Exploration with Reusable Probes from Cislunar Space
Abstract
:1. Introduction
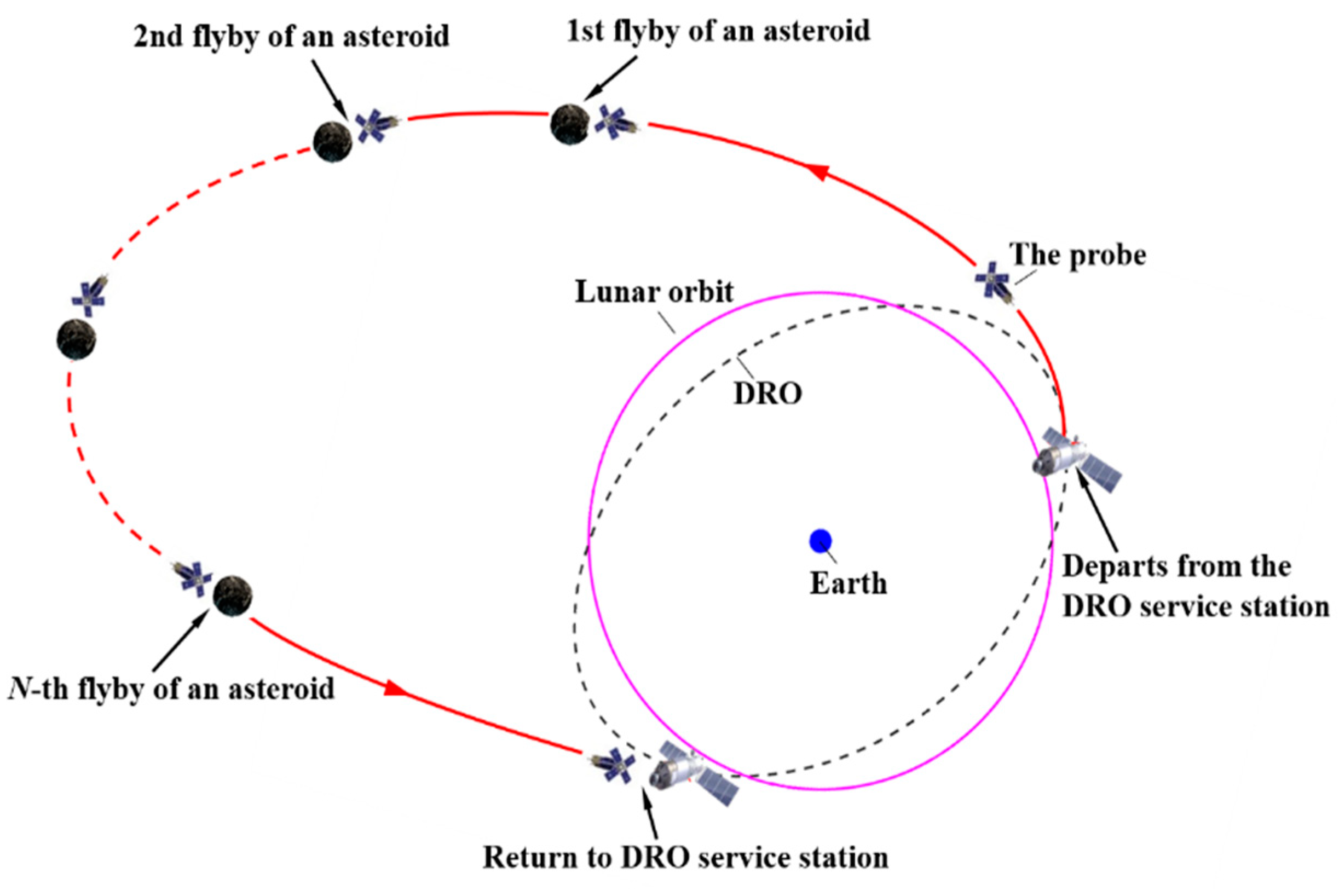
2. Problem Descriptions
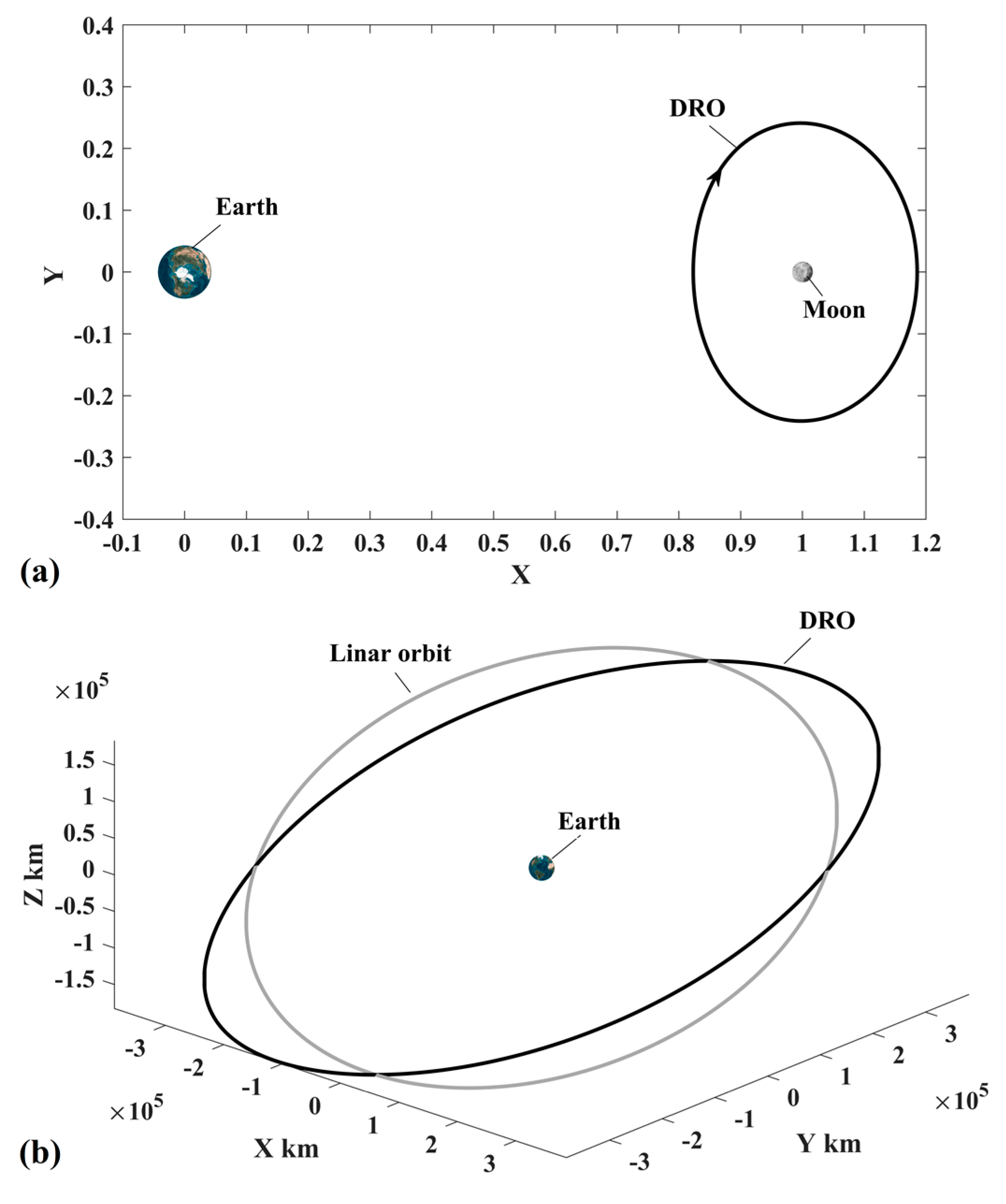
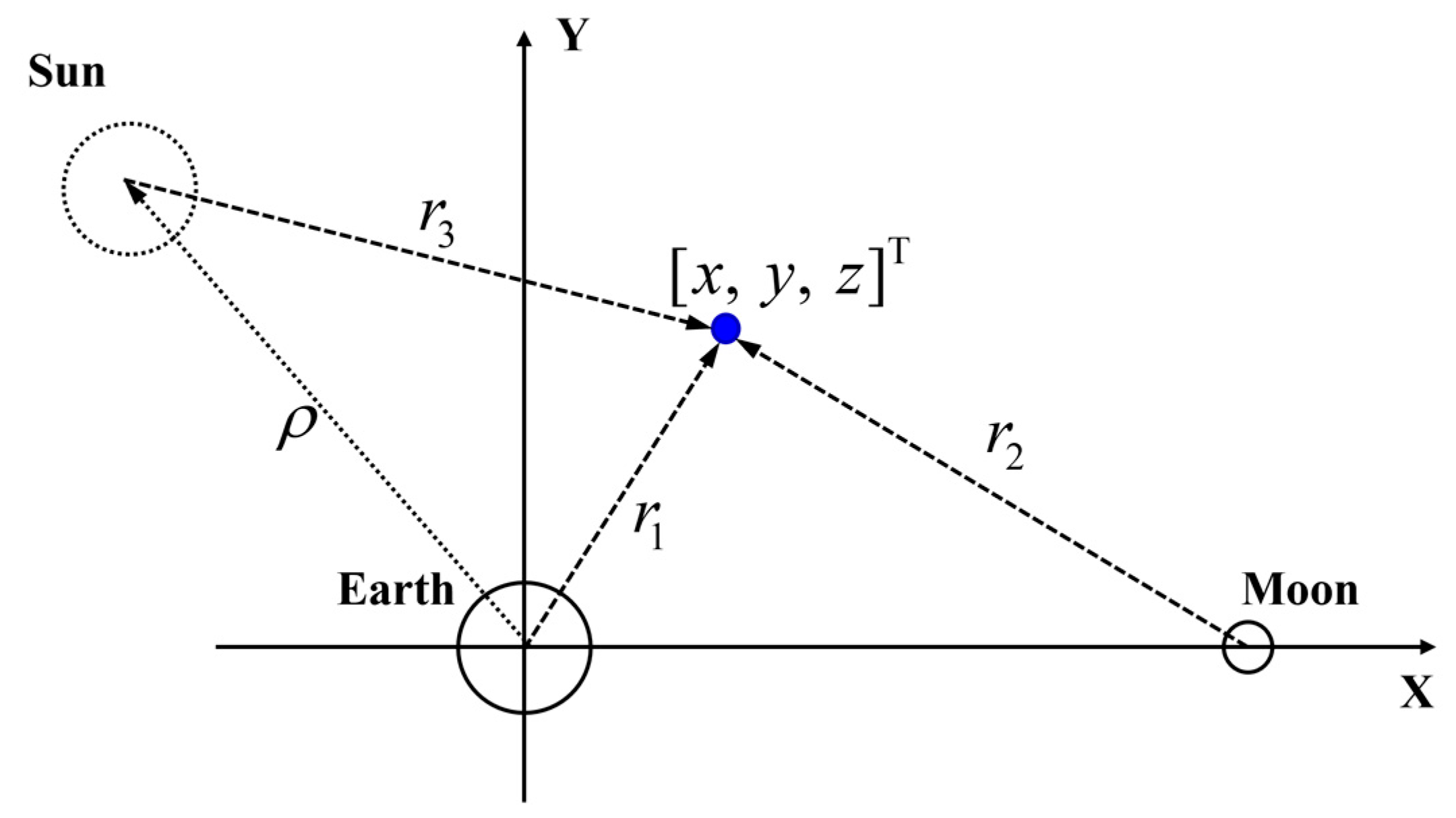
2.1. Orbital Dynamics
- (1)
- For the reusable probes
- (2)
- For the DSS
- (3)
- For the PHAs
2.2. Mission Constraints
2.3. Performance Indices
3. Trajectory Analysis
3.1. Simplified Orbital Dynamics
- (1)
- The two-body patched conics
- (2)
- The planar bicircular restricted four-body dynamics
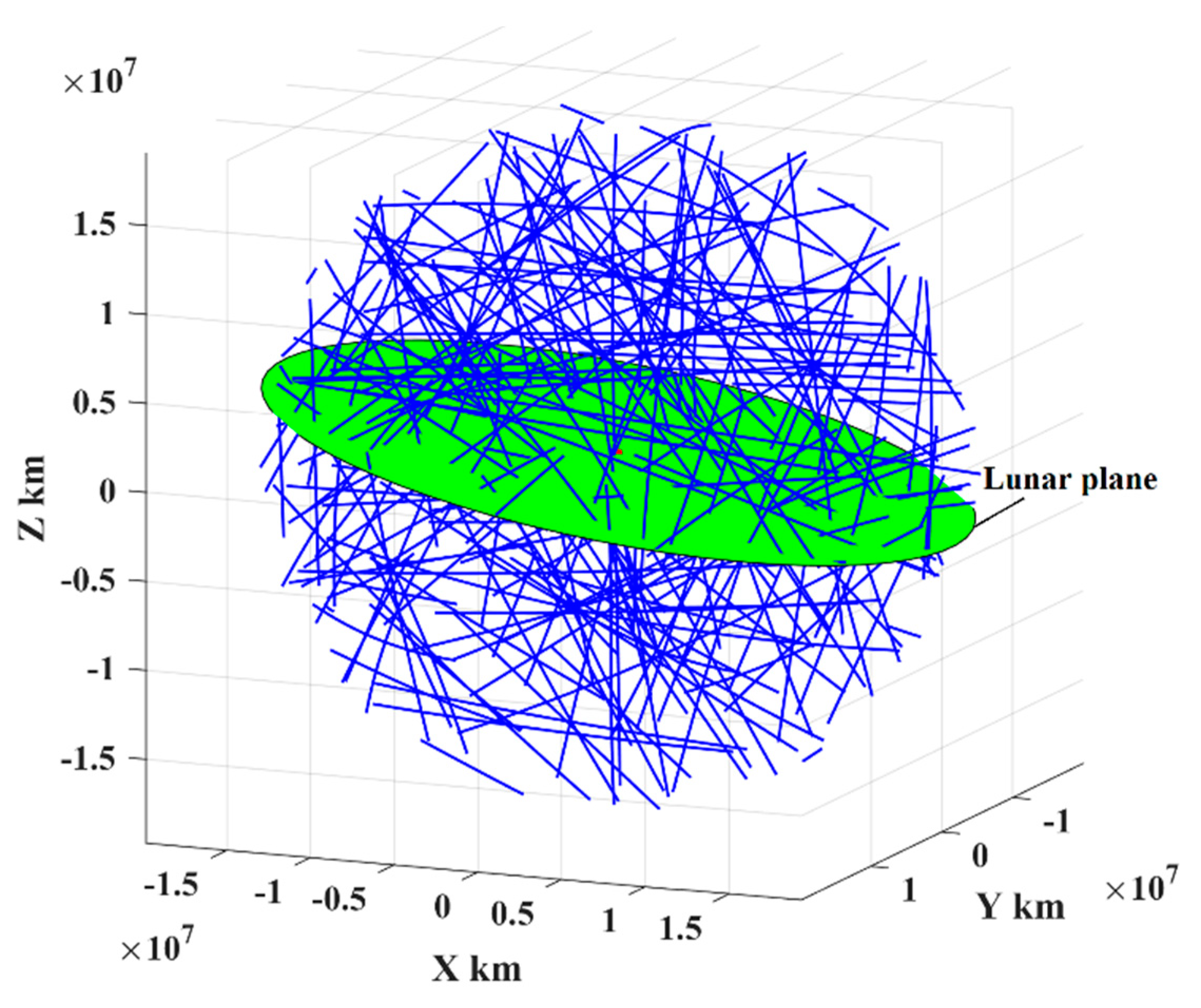
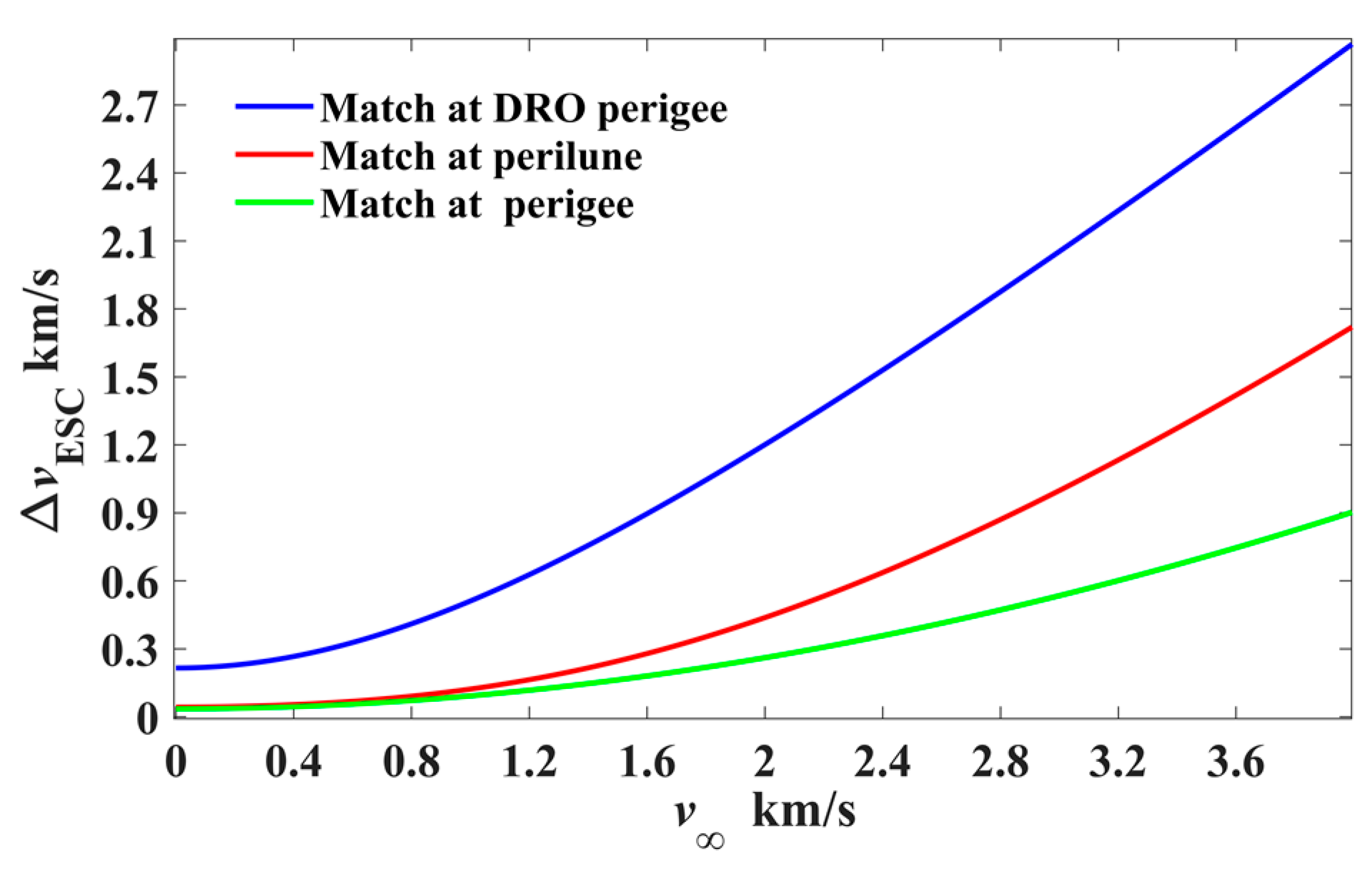
3.2. Analysis of Orbital Energy for Escape from the Cislunar Space
- 1.
- Direct escape
- 2.
- Perigee escape
- 3.
- Perilune escape
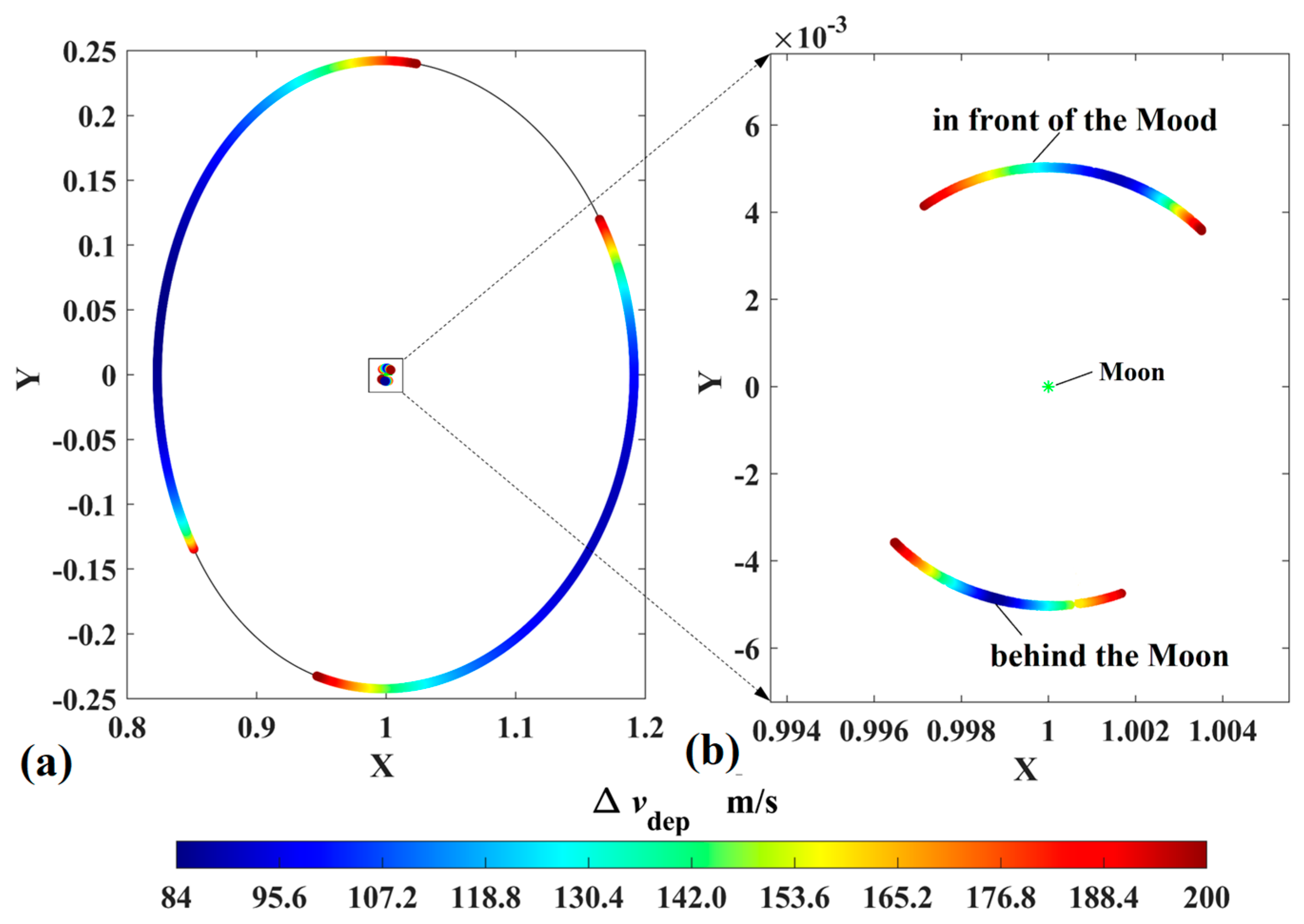
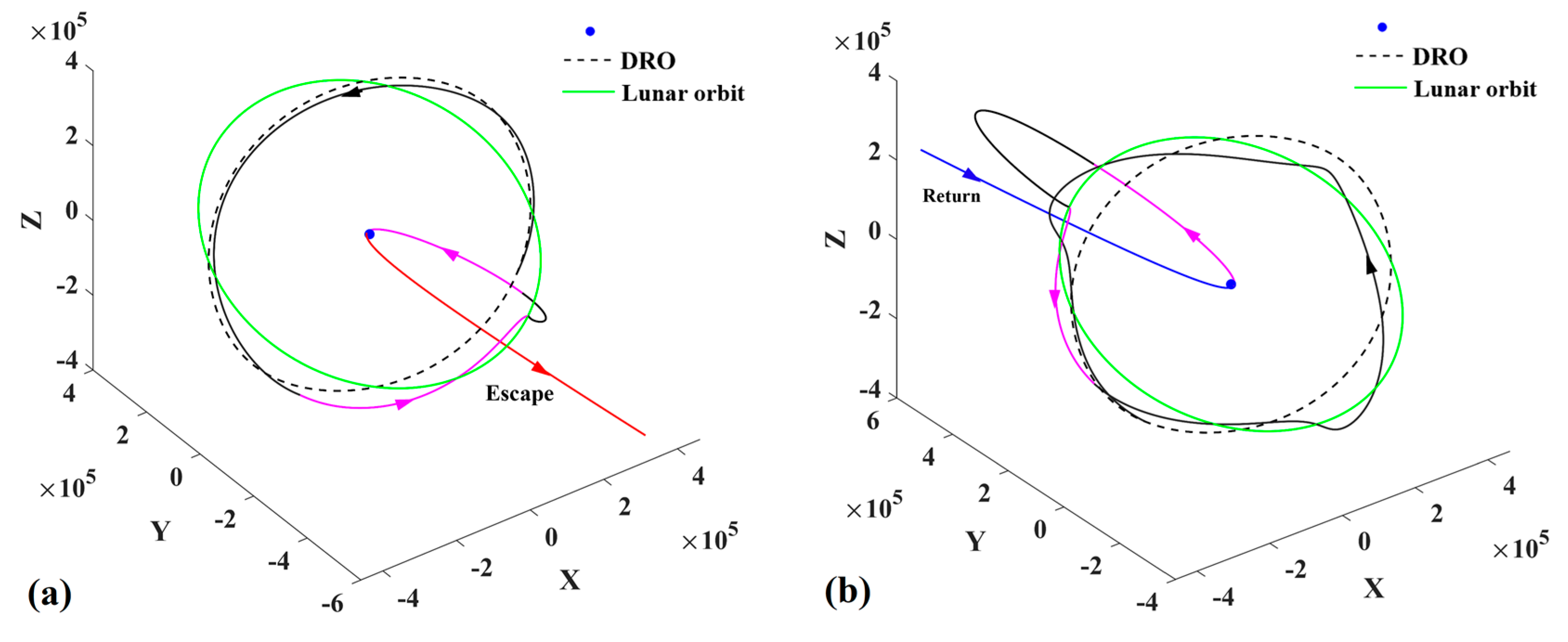
3.3. Analysis of Trajectories Reaching the Perilune and the Perigee from the DRO
- (1)
- Case 1
- (2)
- Case 2
- (3)
- Case 3
4. Trajectory Design
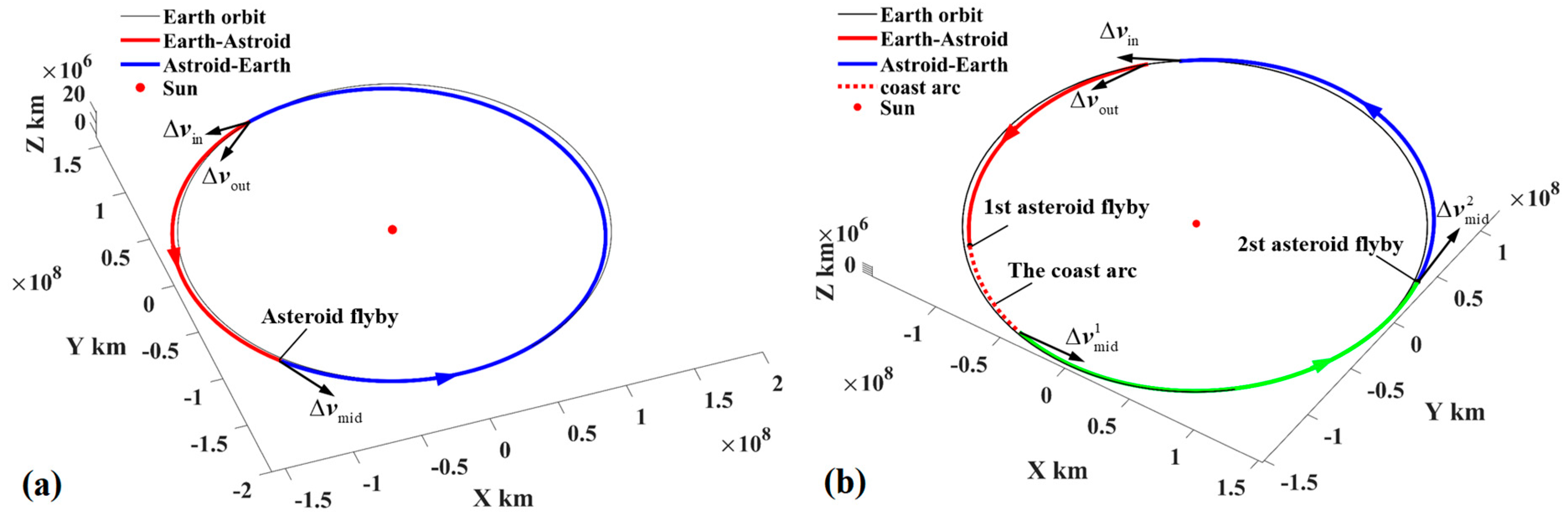
4.1. Constructing Earth–PHAs–Earth Interplanetary Trajectories Database
4.2. Constructing DSS−Perilune−Perigee Trajectory Database
4.3. Generating Round-Trip Trajectories
4.4. Allocating Round-Trip Trajectories
5. Trajectory Solutions
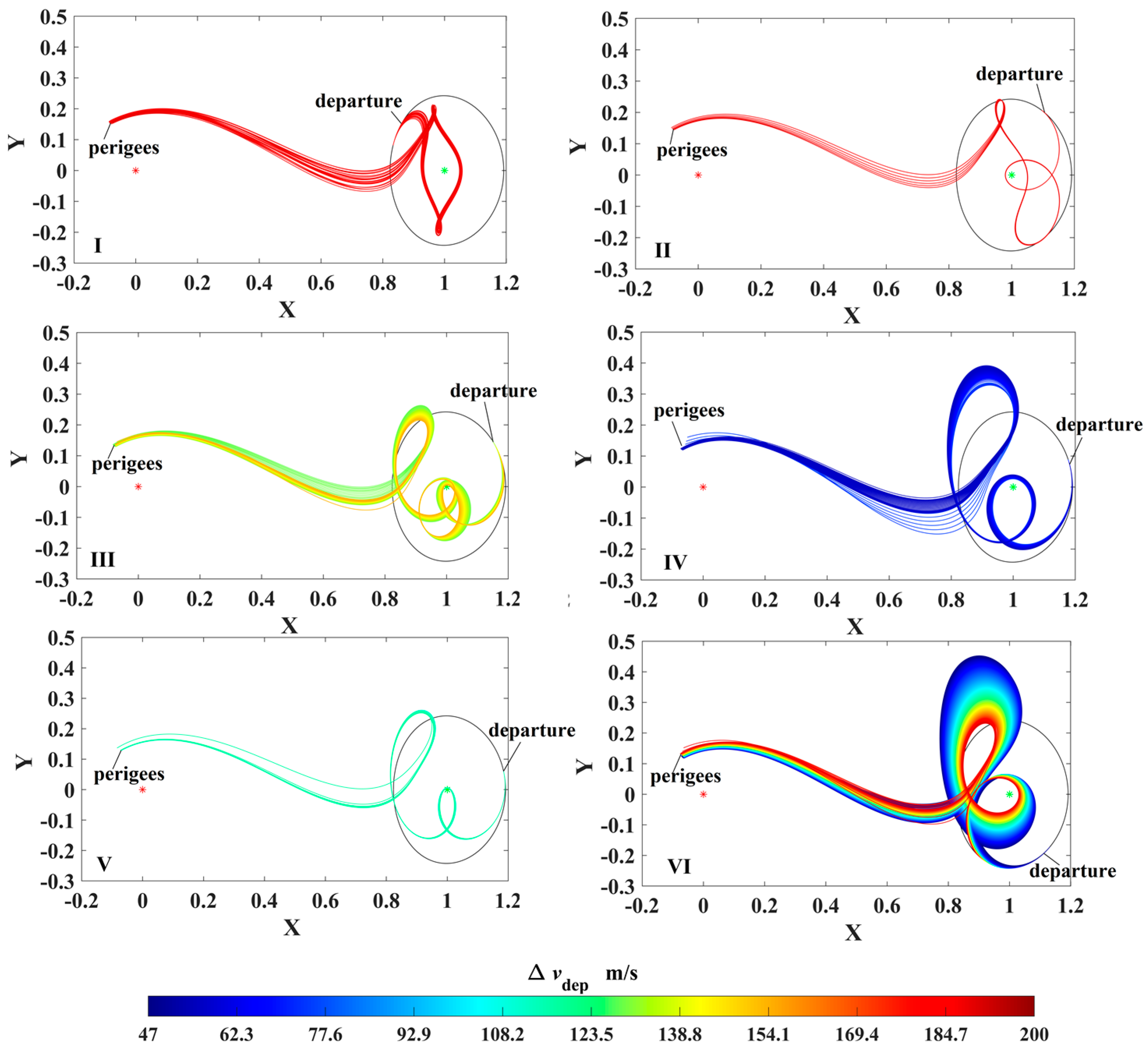
5.1. Solutions Designed in This Study and Submitted in the Competition
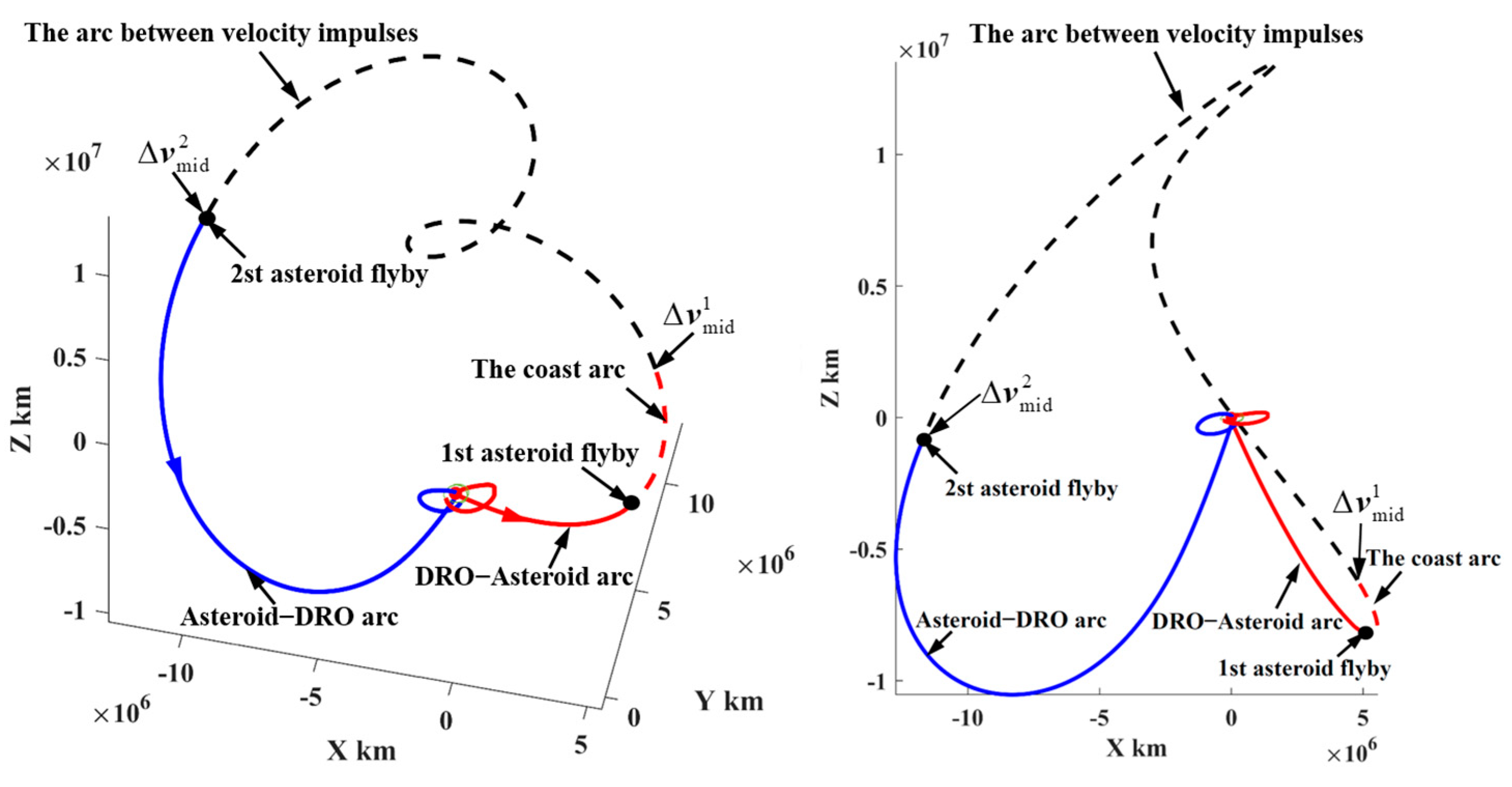
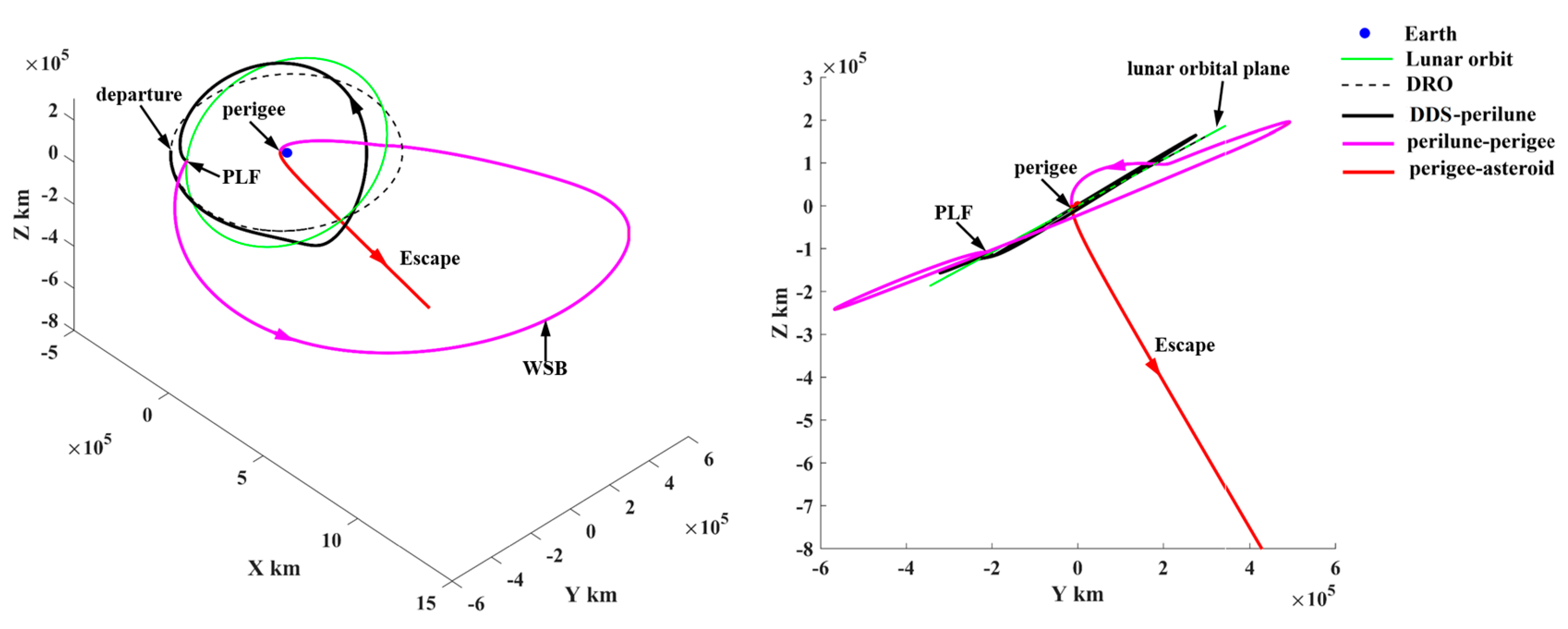
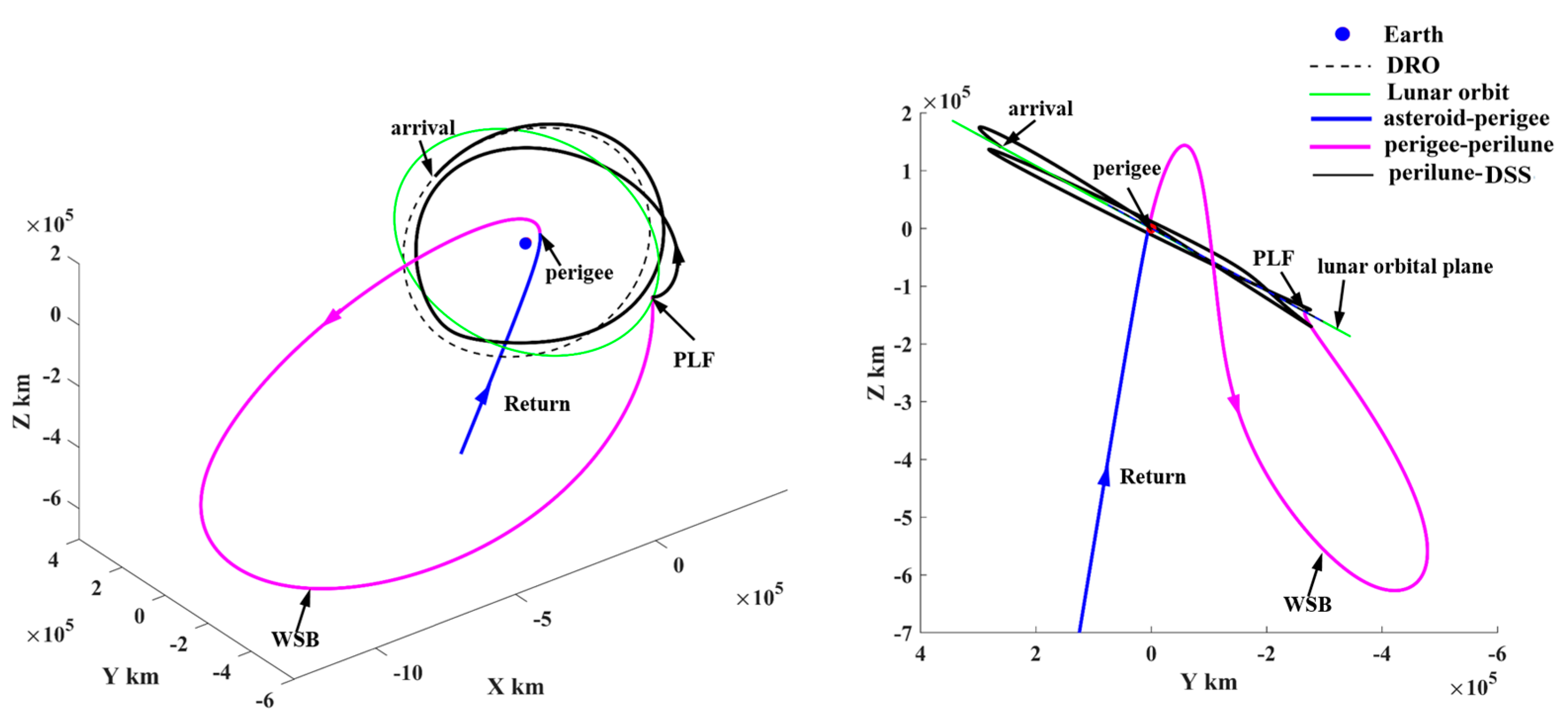
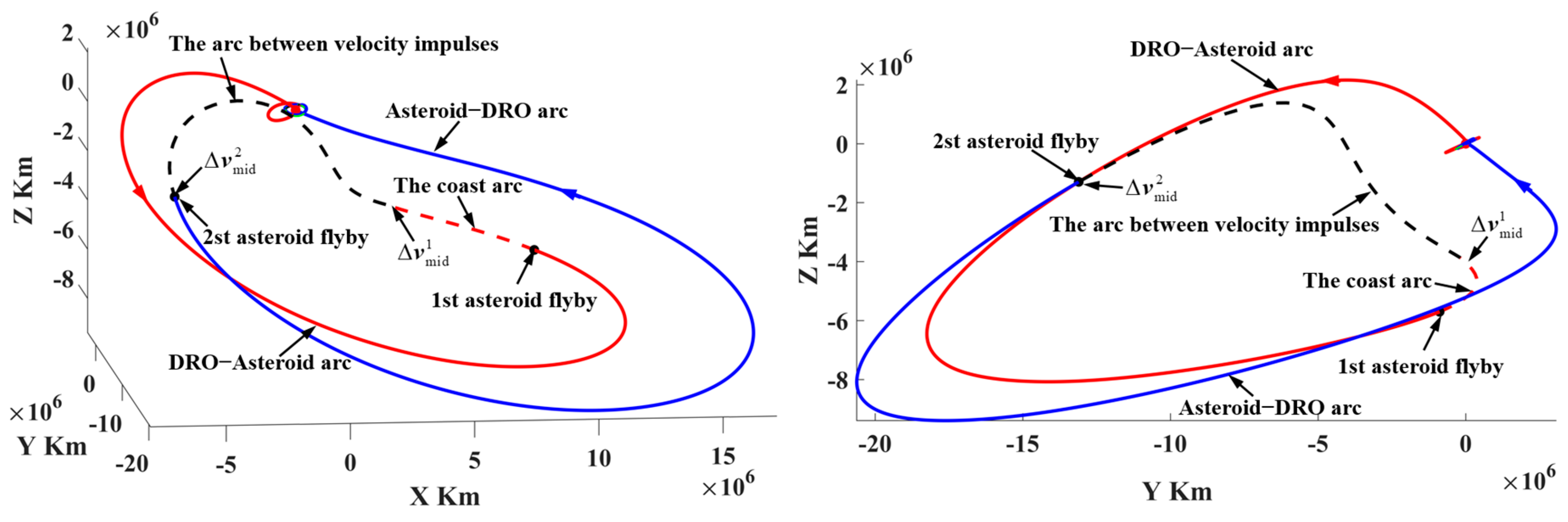
5.2. Representative Trajectories
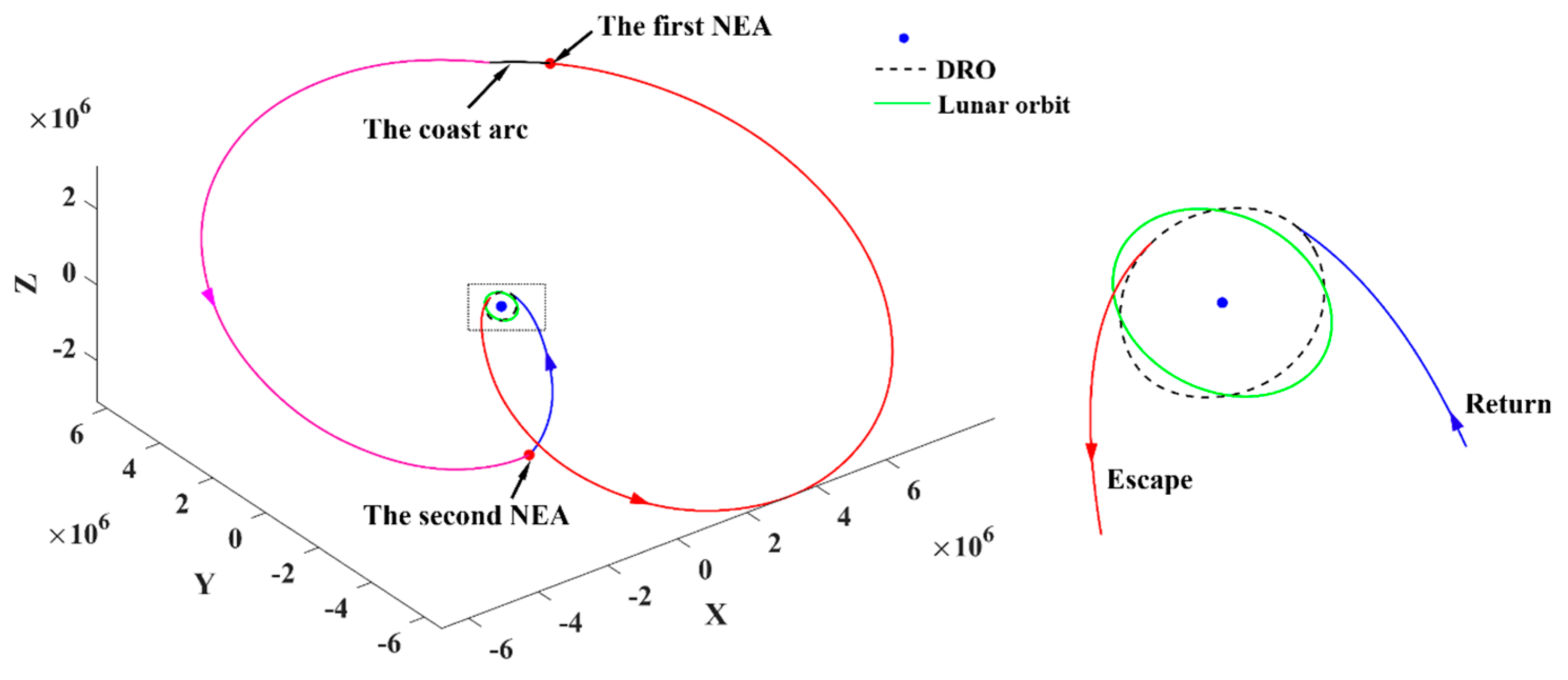
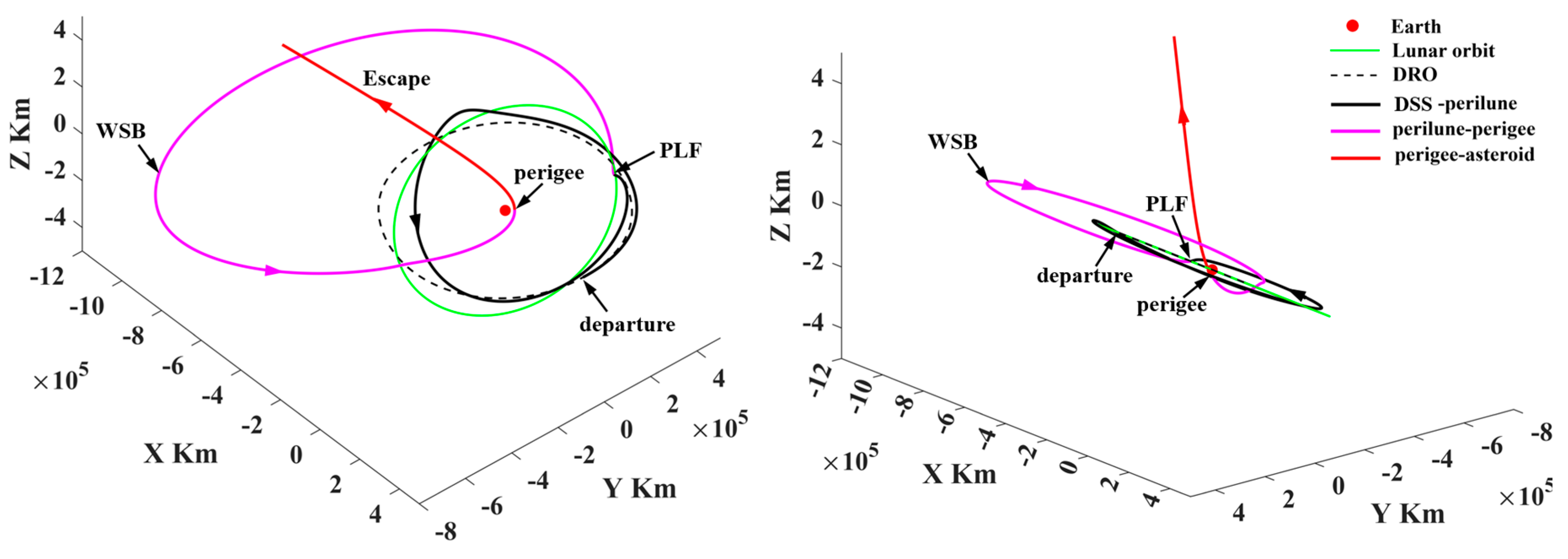
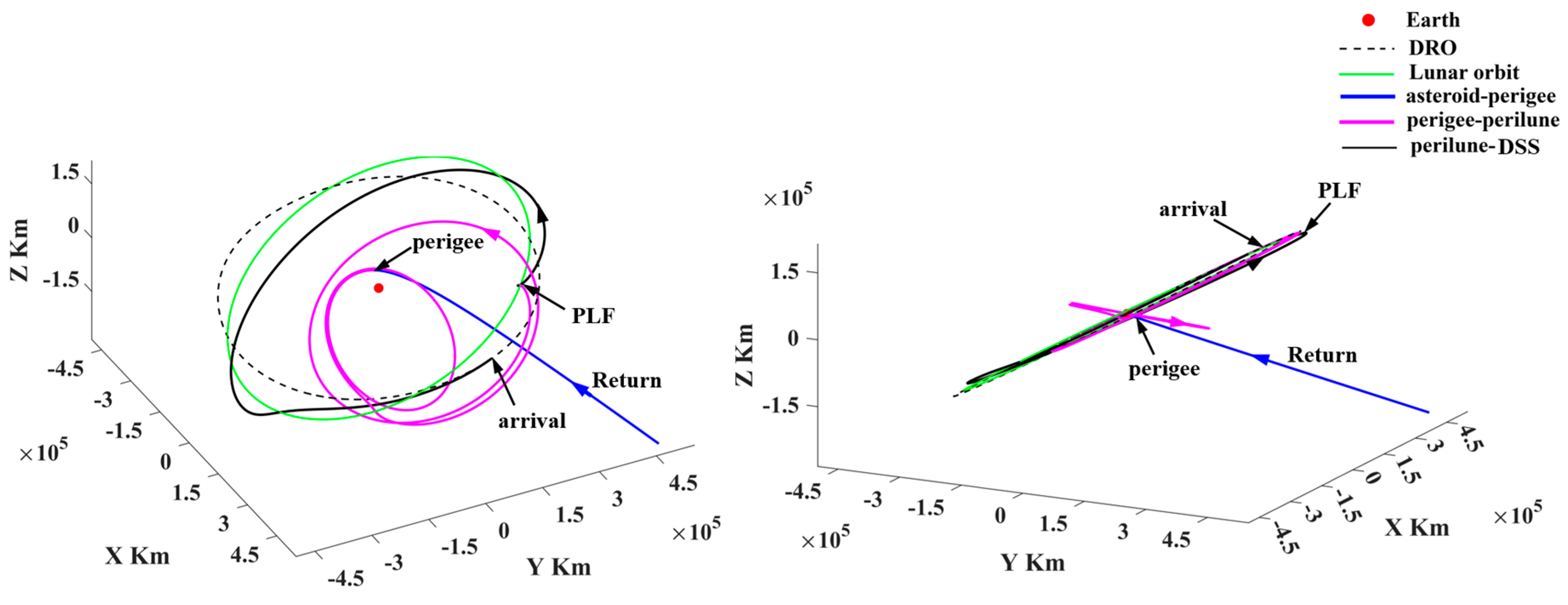
- (1)
- Representative trajectory I: the minimum-ΔV round trip exploring two PHAs
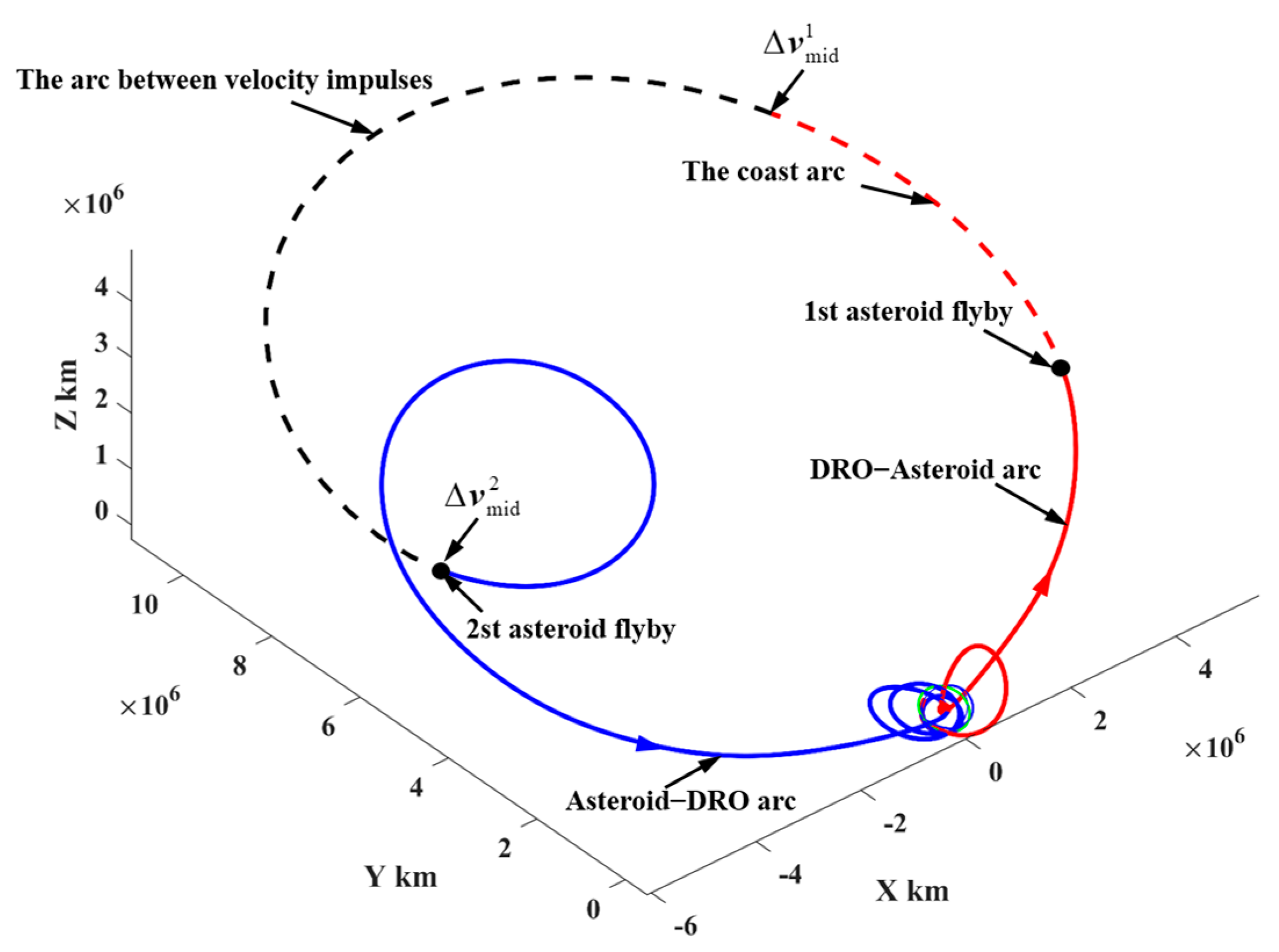
- (2)
- Representative trajectory II: the round trip exploring the PHA with a large inclination relative to the lunar orbital plane
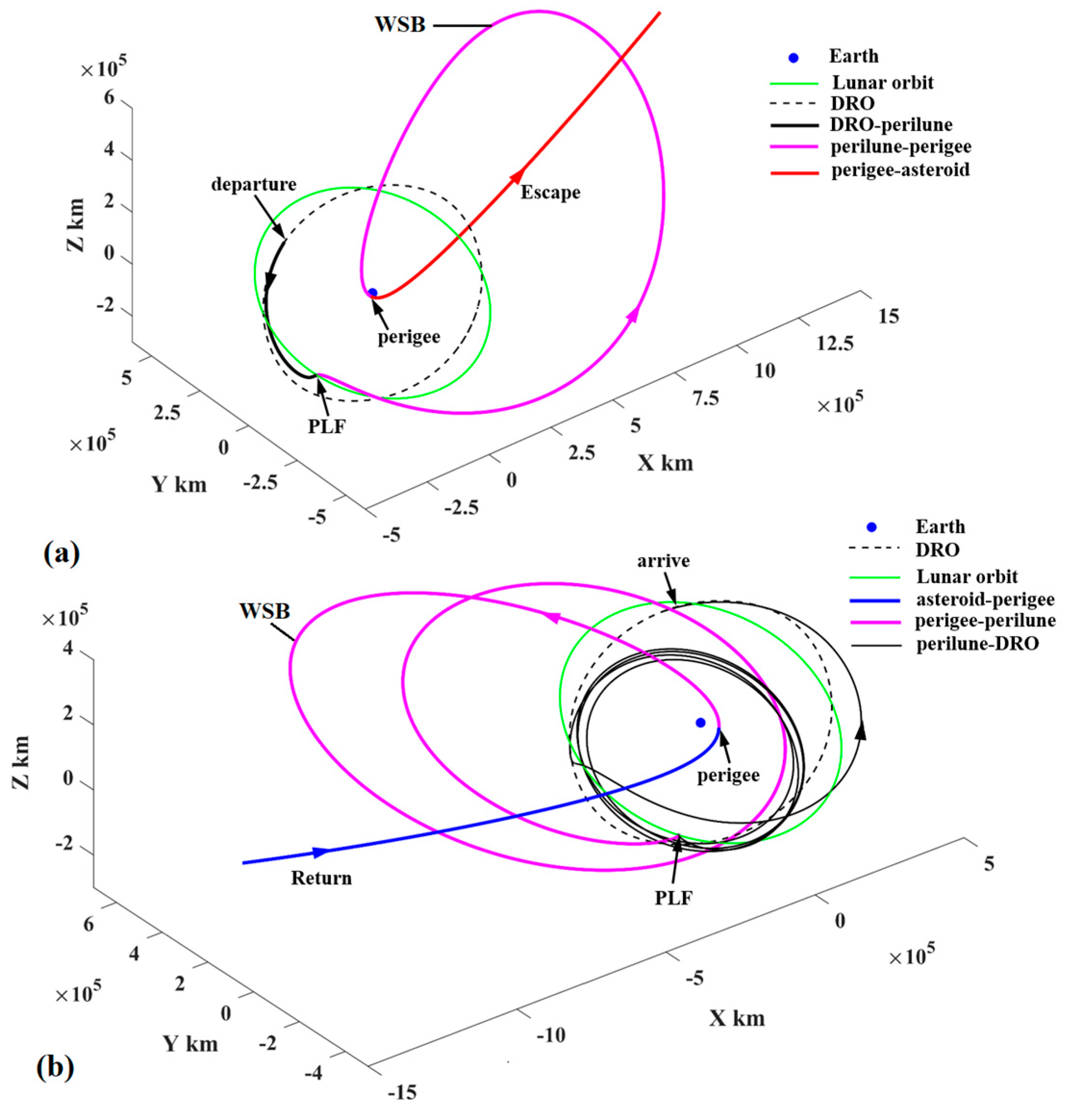
- (3)
- Representative trajectory III: the round trip with a single PLF to escape from (or return to) cislunar space
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Ephemerides of the Sun and the Moon
| Body | Sun | Moon |
|---|---|---|
| Epoch (MJD) | 60|676 | 60|676 |
| Semi-major axis/km | 149|735|127.038|2 | 391|655.927|755|148 |
| Eccentricity | 0.017|566|762|041 | 0.0 |
| Inclination/(°) | 23.436|367|962|048 | 28.443|269|963|777|8 |
| Right ascension of ascending node/(°) | 359.998|706|334|837 | 0.097|374|581|344|85 |
| Argument of perigee/(°) | 283.150|652|210|347 | 0.0 |
| Mean anomaly/(°) | 357.320|625|735|227 | 293.398|038|326|058 |
Appendix B. Ephemeris of the DSS
| 1.004416792940519 | |||||
| 0.318310613651114 | 0.636620862942161 | 0.954929789574872 | |||
| −0.181970920960444 | 0.002999214058291 | −0.001841735804046 | |||
| −0.000339694958002 | 0.000008393690079 | −0.000000619177065 | |||
| 0.318309134645416 | 0.636617759107742 | 0.954929213968546 | |||
| 0.000472036321598 | 0.000015290593321 | 0.000003018234912 | |||
| 0.244768639552355 | 0.002960758097617 | 0.002650026675994 | |||
| 0.318309196516475 | 0.636621150278213 | 0.954929177067250 | |||
| 0.000644080485616 | 0.000042417828521 | 0.000013643834980 | |||
| 0.363941953749817 | −0.011999166419257 | 0.011049154388712 | |||
| 0.318310565837136 | 0.636620009522340 | 0.954930966495610 | |||
| 0.489537961370538 | 0.011846929325199 | 0.015903320386205 | |||
| 0.000853780144252 | 0.000007209074015 | 0.000053373319044 |
Appendix C. Ephemerides of the Asteroids “2001 WN5” and “2009 WZ104”
| Asteroid Name | “2001 WN5” | “2009 WZ104” |
|---|---|---|
| Epoch (modified Julian day MJD) | 59,600 | 59,600 |
| Semi-major axis/km | 1.712 | 0.8554 |
| Eccentricity | 0.4672 | 0.1927 |
| Inclination/(°) | 1.92 | 9.83 |
| Right ascension of ascending node/(°) | 277.42 | 263.260 |
| Argument of perigee/(°) | 44.60 | 10.550 |
| Mean anomaly/(°) | 30.39 | 265.48 |
References
- Zhang, Y.; Michel, P. Shapes, structures, and evolution of small bodies. Astrodyn 2021, 5, 293–329. [Google Scholar] [CrossRef]
- Kawaguchi, J. The Hayabusa mission–its seven years flight. In Proceedings of the 2011 Symposium on VLSI Circuits-Digest of Technical Papers, Kyoto, Japan, 15–17 June 2011. [Google Scholar]
- Watanabe, S.-I.; Tsuda, Y.; Yoshikawa, M.; Tanaka, S.; Saiki, T.; Nakazawa, S. Hayabusa2 mission overview. Space Sci. Rev. 2017, 208, 3–16. [Google Scholar] [CrossRef]
- Lauretta, D.S.; Balram-Knutson, S.S.; Beshore, E.; Boynton, W.V.; D’aubigny, C.D.; DellaGiustina, D.N.; Enos, H.L.; Golish, D.R.; Hergenrother, C.W.; Howell, E.S.; et al. OSIRIS-REx: Sample return from asteroid (101955) Bennu. Space Sci. Rev. 2017, 212, 925–984. [Google Scholar] [CrossRef]
- Li, X.; Scheeres, D.J.; Qiao, D.; Liu, Z. Geophysical and orbital environments of asteroid 469219 2016 HO3. Astrodyn 2023, 7, 31–50. [Google Scholar] [CrossRef]
- Elvis, M. Let’s mine asteroids for science and profit. Nature 2012, 485, 549. [Google Scholar] [CrossRef] [PubMed]
- Gates, M.; Mazanek, D.; Muirhead, B.; Stich, S.; Naasz, B.; Chodas, P.; McDonald, M.; Reuter, J. NASA’s asteroid redirect mission concept development summary. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015. [Google Scholar]
- Brophy, J.; Culick, F.; Friedman, L.; Allen, C.; Baughman, D.; Bellerose, J. Asteroid Retrieval Feasibility Sstudy; Keck Institute for Space Studies, California Institute of Technology, Jet Propulsion Laboratory: Pasadena, CA, USA, 2012. [Google Scholar]
- García Yárnoz, D.; Sanchez, J.P.; McInnes, C.R. Easily retrievable objects among the NEA population. Celest. Mech. Dyn. Astron. 2013, 116, 367–388. [Google Scholar] [CrossRef]
- Lladó, N.; Ren, Y.; Masdemont, J.J.; Gómez, G. Capturing small asteroids into a Sun-Earth Lagrangian point. Acta Astronaut. 2014, 95, 176–188. [Google Scholar] [CrossRef]
- Baoyin, H.; Chen, Y.; Li, J. Capturing near Earth objects. Res. Astron. Astrophys. 2010, 10, 587–598. [Google Scholar] [CrossRef]
- Hasnain, Z.; Lamb, C.A.; Ross, S. Capturing near-Earth asteroids around Earth. Acta Astronaut. 2012, 81, 523–531. [Google Scholar] [CrossRef]
- Urrutxua, H.; Scheeres, D.; Bombardelli, C.; Gonzalo, J.L.; Peláez, J. What does it take to capture an asteroid? A case study on capturing asteroid 2006 RH120. In Proceedings of the 24th AAS/AIAA Space Flight Mechanics Meeting, San Diego, CA, USA, 26–30 January 2014. [Google Scholar]
- Stickle, A.; Rainey, E.; Syal, M.B.; Owen, J.; Miller, P.; Barnouin, O.; Ernst, C. Modeling impact outcomes for the Double Asteroid Redirection Test (DART) mission. Procedia Eng. 2017, 204, 116–123. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A. Rapid Solar Sail Rendezvous Missions to Asteroid 99942 Apophis. J. Spacecr. Rocket. 2009, 46, 134–140. [Google Scholar] [CrossRef]
- Quarta, A.; Mengali, G. Electric sail missions to potentially hazardous asteroids. Acta Astronaut. 2010, 66, 1506–1519. [Google Scholar] [CrossRef]
- Li, Q.; Tao, Y.; Jiang, F. Orbital Stability and Invariant Manifolds on Distant Retrograde Orbits around Ganymede and Nearby Higher-Period Orbits. Aerospace 2022, 9, 454. [Google Scholar] [CrossRef]
- Yin, Y.; Wang, M.; Shi, Y.; Zhang, H. Midcourse correction of Earth-Moon distant retrograde orbit transfer trajectories based on high-order state transition tensors. Astrodyn 2023, 7, 335–349. [Google Scholar] [CrossRef]
- Muralidharan, V.; Howell, K.C. Stretching directions in cislunar space: Applications for departures and transfer design. Astrodyn 2023, 7, 153–178. [Google Scholar] [CrossRef]
- Lopez, F.; Mauro, A.; Mauro, S.; Monteleone, G.; Sfasciamuro, D.E.; Villa, A. A Lunar-Orbiting Satellite Constellation for Wireless Energy Supply. Aerospace 2023, 10, 919. [Google Scholar] [CrossRef]
- Strange, N.; Landau, D.; McElrath, T.; Lantoine, G.; Lam, T. Overview of mission design for NASA asteroid redirect robotic mission concept. In Proceedings of the 33rd International Electric Propulsion Conference, Washington, DC, USA, 6–10 October 2013. [Google Scholar]
- Craig, D.; Herrmann, N.; Troutman, P. The evolvable Mars campaign-study status. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015. [Google Scholar]
- Whitley, R.; Martinez, R. Options for staging orbits in cislunar space. In Proceedings of the 2016 IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2016. [Google Scholar]
- McCarthy, B.; Howell, K. Leveraging quasi-periodic orbits for trajectory design in cislunar space. Astrodyn 2021, 5, 139–165. [Google Scholar] [CrossRef]
- Cavallari, I.; Petitdemange, R.; Lizy-Destrez, S. Transfer from a Lunar distant retrograde orbit to Mars through Lyapunov orbits. In Proceedings of the 27th International Symposium on Space Flight Dynamics, Melbourne, Australia, 24–28 February 2019. [Google Scholar]
- Zhang, G.; Pang, B.; Sun, Y.; Zhou, X.; Shang, Y.; Chen, C.; Lu, M.; Zhang, Y.; Jin, Z.; Zhang, Y.; et al. Optimal design of Mars immigration by using reusable transporters from the Earth-Moon system. Acta Astronaut. 2023, 207, 129–152. [Google Scholar] [CrossRef]
- Belbruno, E.; Miller, J. Sun-perturbed earth-to-moon transfers with ballistic capture. J. Guid. Control. Dyn. 1993, 16, 770–775. [Google Scholar] [CrossRef]
- Yamakawa, H.; Kawaguchi, J.; Ishii, N.; Matsuo, H. On Earth-Moon transfer trajectory with gravitational capture. Adv. Astronaut. Sci. 1993, 85, 397–416. [Google Scholar]
- Peng, C.; Zhang, H.; Wen, C.; Zhu, Z.; Gao, Y. Exploring More Solutions for Low-Energy Transfers to Lunar Distant Retrograde Orbits. Celest. Mech. Dyn. Astron. 2022, 134, 4. [Google Scholar] [CrossRef]




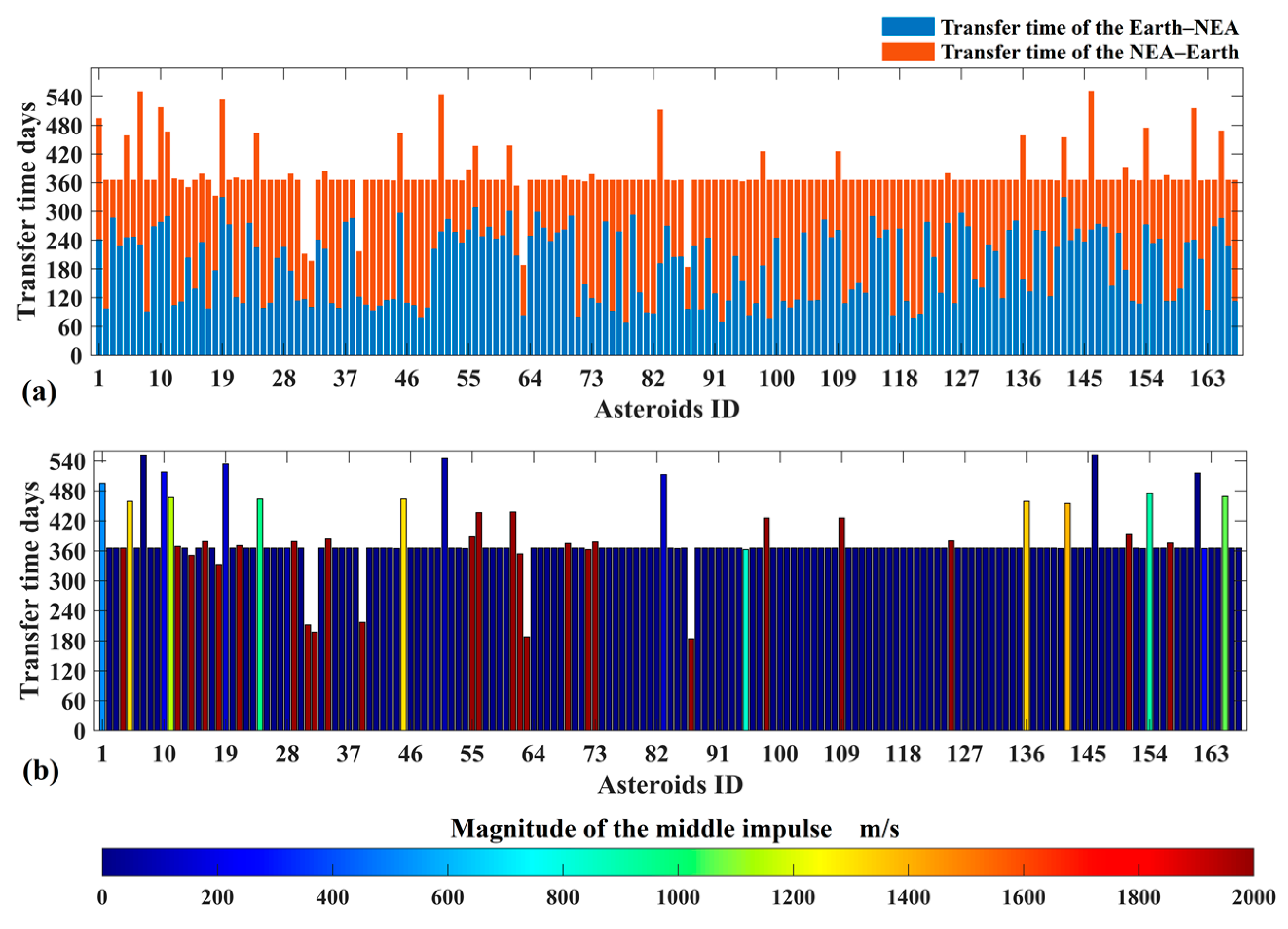



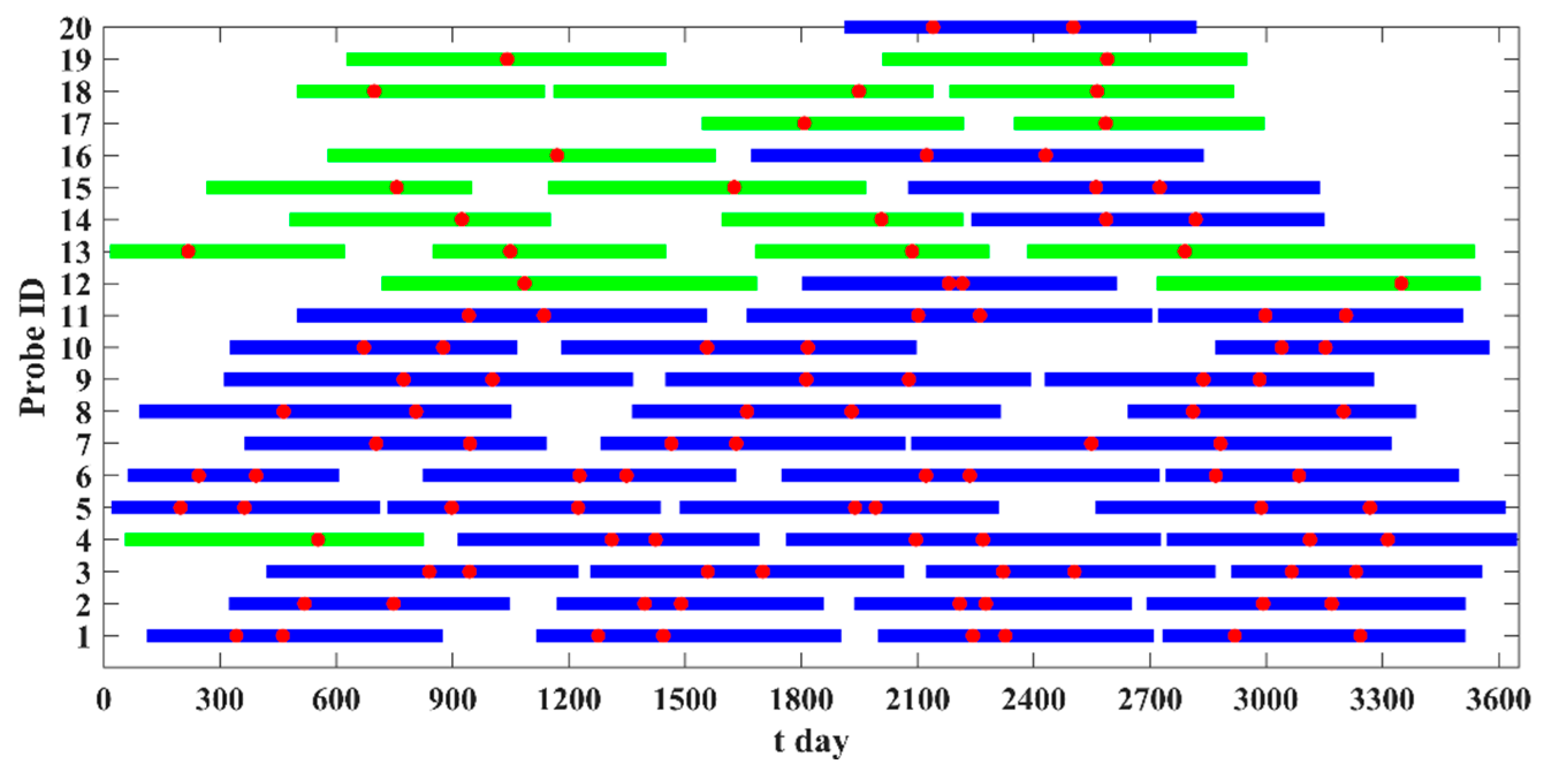
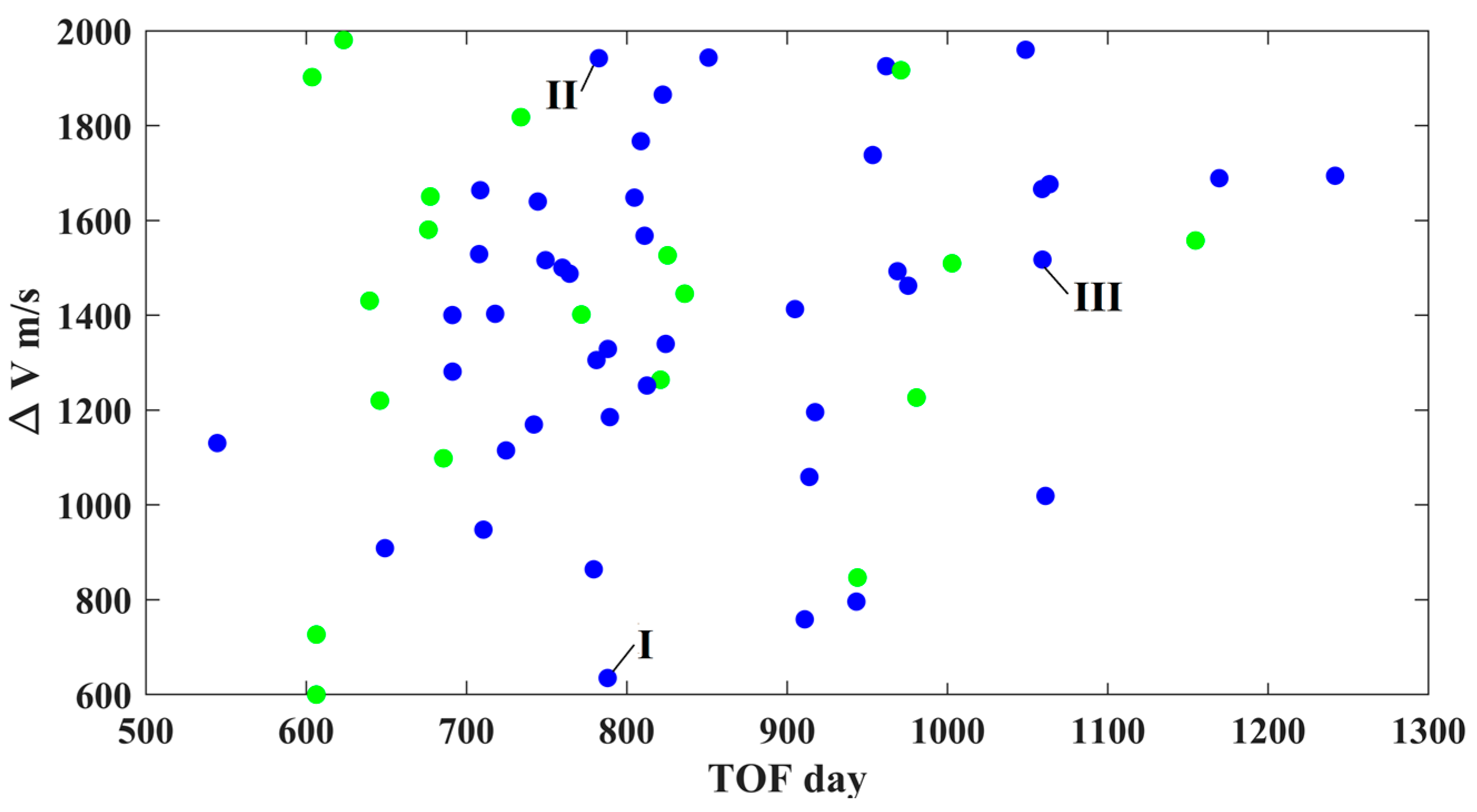
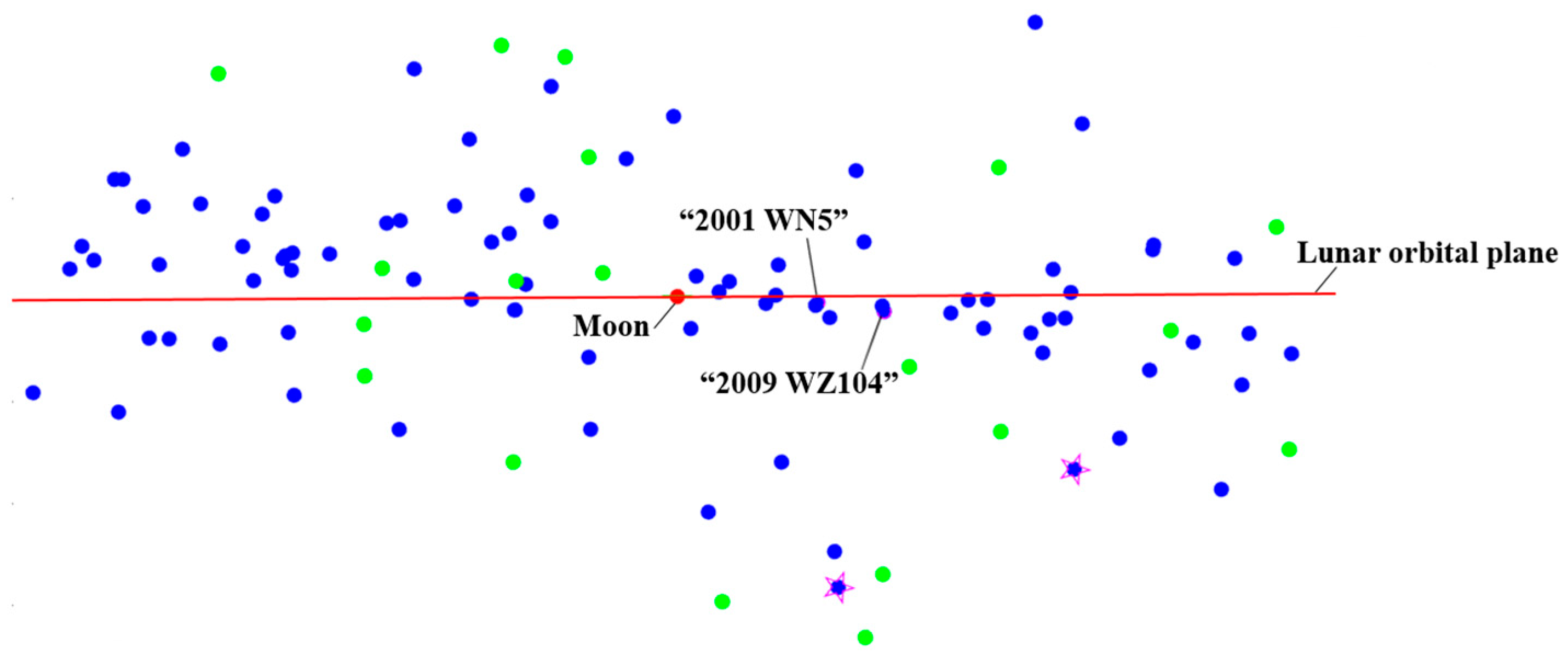
| Symbol | Numerical Value | Unit | Physical Meaning |
|---|---|---|---|
| 1.2300502 × 10−2 | — | Moon–Earth mass ratio | |
| 3.32946412 × 105 | DU3/TU2 | Normalized mass of the Sun | |
| DU | 391,655.927755 | km | Normalized distance unit |
| TU | 4.4933957 | day | Normalized time unit |
| VU | 1.00882606642 | km/s | Normalized velocity unit |
| Symbol | Value | Unit | Symbol | Value | Unit |
|---|---|---|---|---|---|
| [0, 3650] | Day | 1 | Day | ||
| [0, 179] | Deg | 1 | Deg | ||
| [0, 359] | Deg | 1 | Deg | ||
| [0, 100] | m/s | 1 | m/s | ||
| [−100, 100] | m/s | 1 | m/s |
| Ranking | Team Name | J1 | J2 | J3 |
|---|---|---|---|---|
| 1 | NSSC-BACC | 45 | 11 | 1.8025 km/s |
| 2 | NU-NAOC | 39 | 11 | 1.4239 km/s |
| 3 | BIT-CAST | 36 | 16 | 1.8724 km/s |
| 4 | SCU | 15 | 6 | 1.8188 km/s |
| 5 | NUAA-ASTL | 9 | 4 | 1.6599 km/s |
| Probe No. | Number of Round Trips | Number of Explored PHAs | Average Velocity Impulses | Probe No. | Number of Round Trips | Number of Explored PHAs | Average Velocity Impulse |
|---|---|---|---|---|---|---|---|
| 1 | 4 | 8 | 0.6266 km/s | 11 | 3 | 6 | 0.7771 km/s |
| 2 | 4 | 8 | 0.7081 km/s | 12 | 3 | 4 | 1.1535 km/s |
| 3 | 4 | 8 | 0.7051 km/s | 13 | 4 | 4 | 1.1967 km/s |
| 4 | 4 | 7 | 0.7388 km/s | 14 | 3 | 4 | 1.1550 km/s |
| 5 | 4 | 8 | 0.6610 km/s | 15 | 3 | 4 | 1.0097 km/s |
| 6 | 4 | 8 | 0.7325 km/s | 16 | 2 | 3 | 1.0662 km/s |
| 7 | 3 | 6 | 0.7215 km/s | 17 | 2 | 2 | 1.4352 km/s |
| 8 | 3 | 6 | 0.8838 km/s | 18 | 3 | 3 | 1.4916 km/s |
| 9 | 3 | 6 | 0.7343 km/s | 19 | 2 | 2 | 1.1866 km/s |
| 10 | 3 | 6 | 0.6715 km/s | 20 | 1 | 2 | 0.3794 km/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, C.; Zhang, R.; Gao, Y. Trajectory Design of Potentially Hazardous Asteroid Exploration with Reusable Probes from Cislunar Space. Aerospace 2024, 11, 546. https://doi.org/10.3390/aerospace11070546
Peng C, Zhang R, Gao Y. Trajectory Design of Potentially Hazardous Asteroid Exploration with Reusable Probes from Cislunar Space. Aerospace. 2024; 11(7):546. https://doi.org/10.3390/aerospace11070546
Chicago/Turabian StylePeng, Chao, Renyong Zhang, and Yang Gao. 2024. "Trajectory Design of Potentially Hazardous Asteroid Exploration with Reusable Probes from Cislunar Space" Aerospace 11, no. 7: 546. https://doi.org/10.3390/aerospace11070546
APA StylePeng, C., Zhang, R., & Gao, Y. (2024). Trajectory Design of Potentially Hazardous Asteroid Exploration with Reusable Probes from Cislunar Space. Aerospace, 11(7), 546. https://doi.org/10.3390/aerospace11070546





