Enhanced Computational Biased Proportional Navigation with Neural Networks for Impact Time Control
Abstract
:1. Introduction
2. Preliminaries
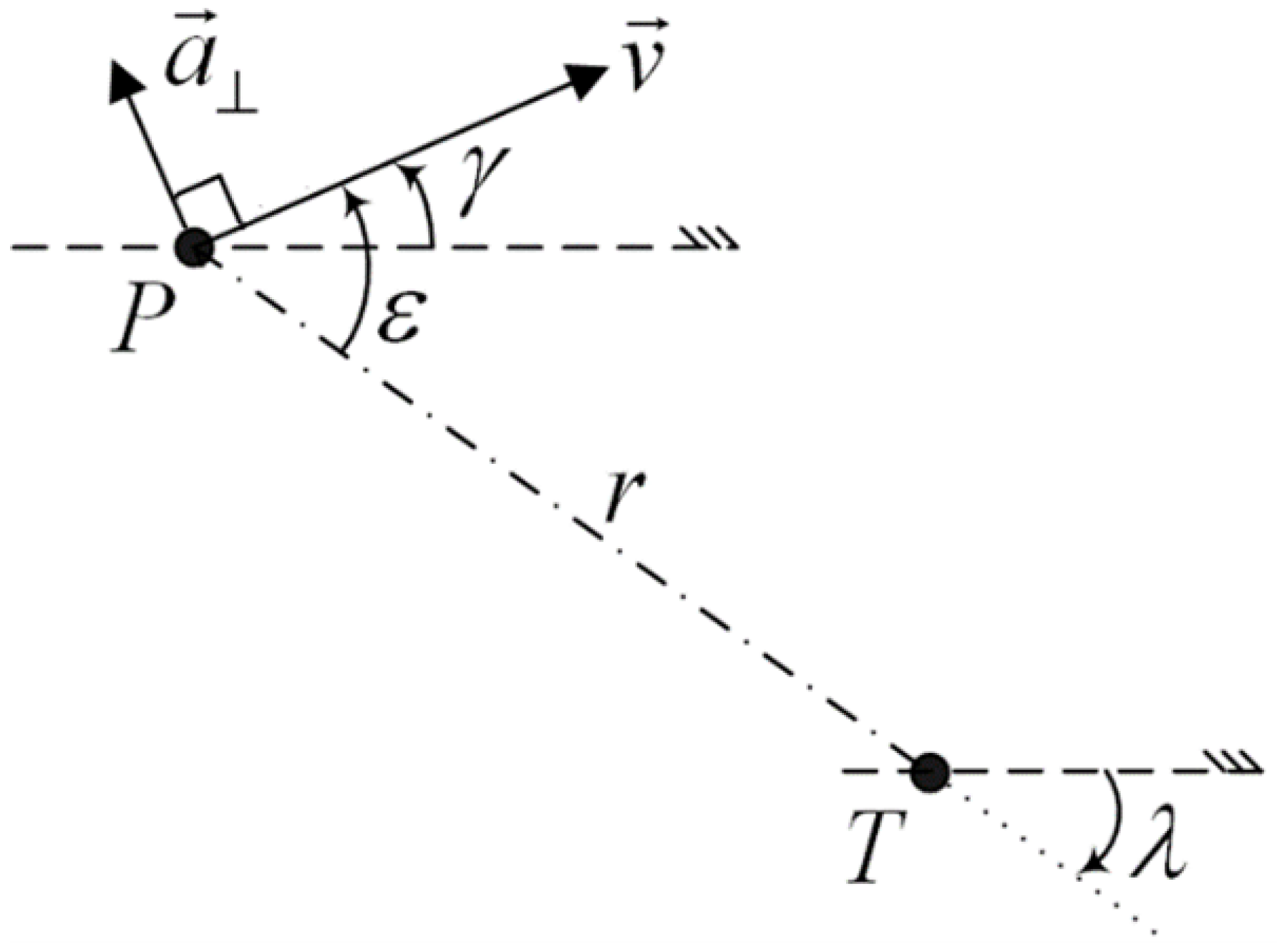
2.1. Engagement Geometry
2.2. Original Guidance Law
3. Real-Time Bias Computation by Neural Network
3.1. Neural Network Settings and Dataset Generation
3.2. Neural Network Training and Evaluation
4. Simulations
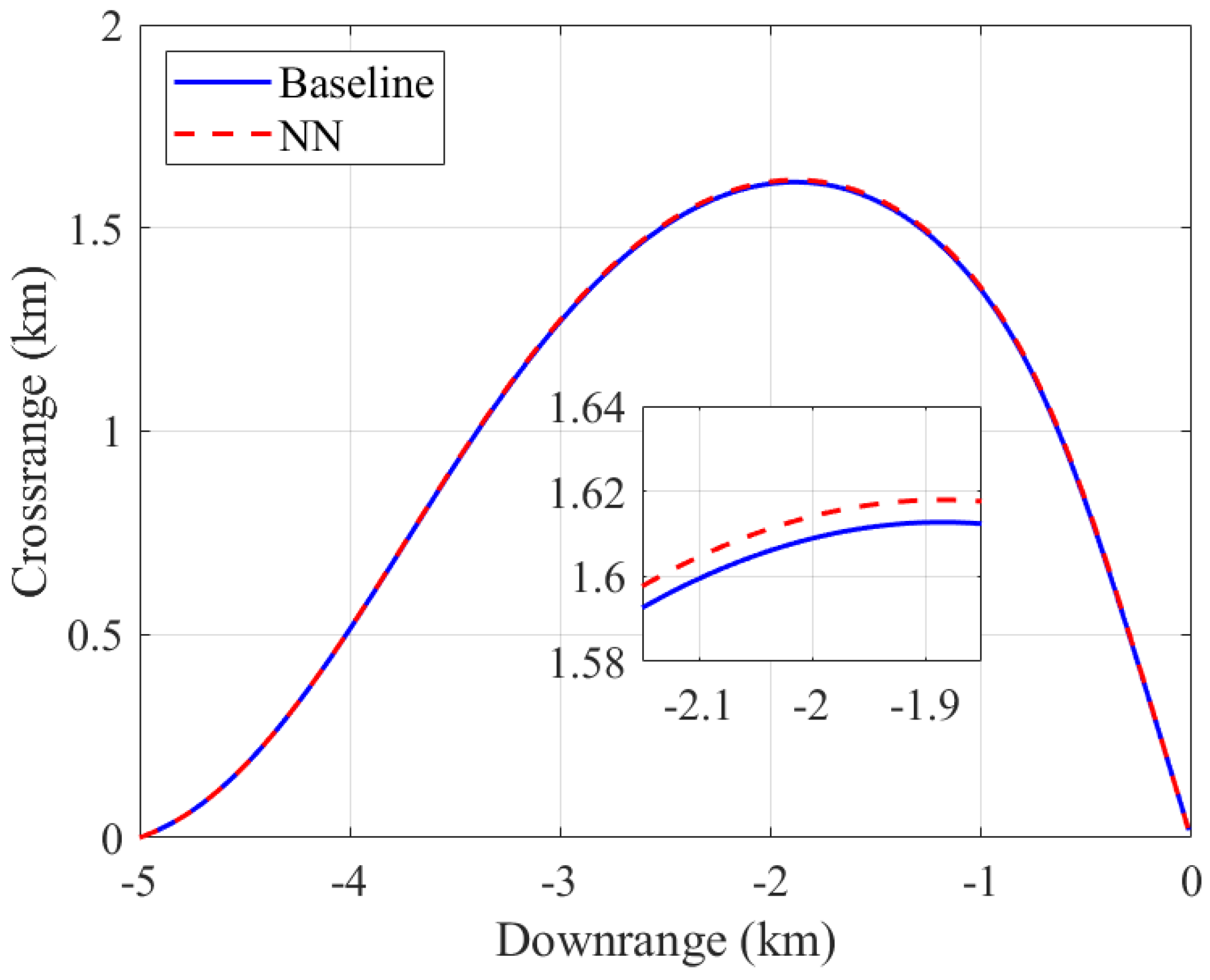
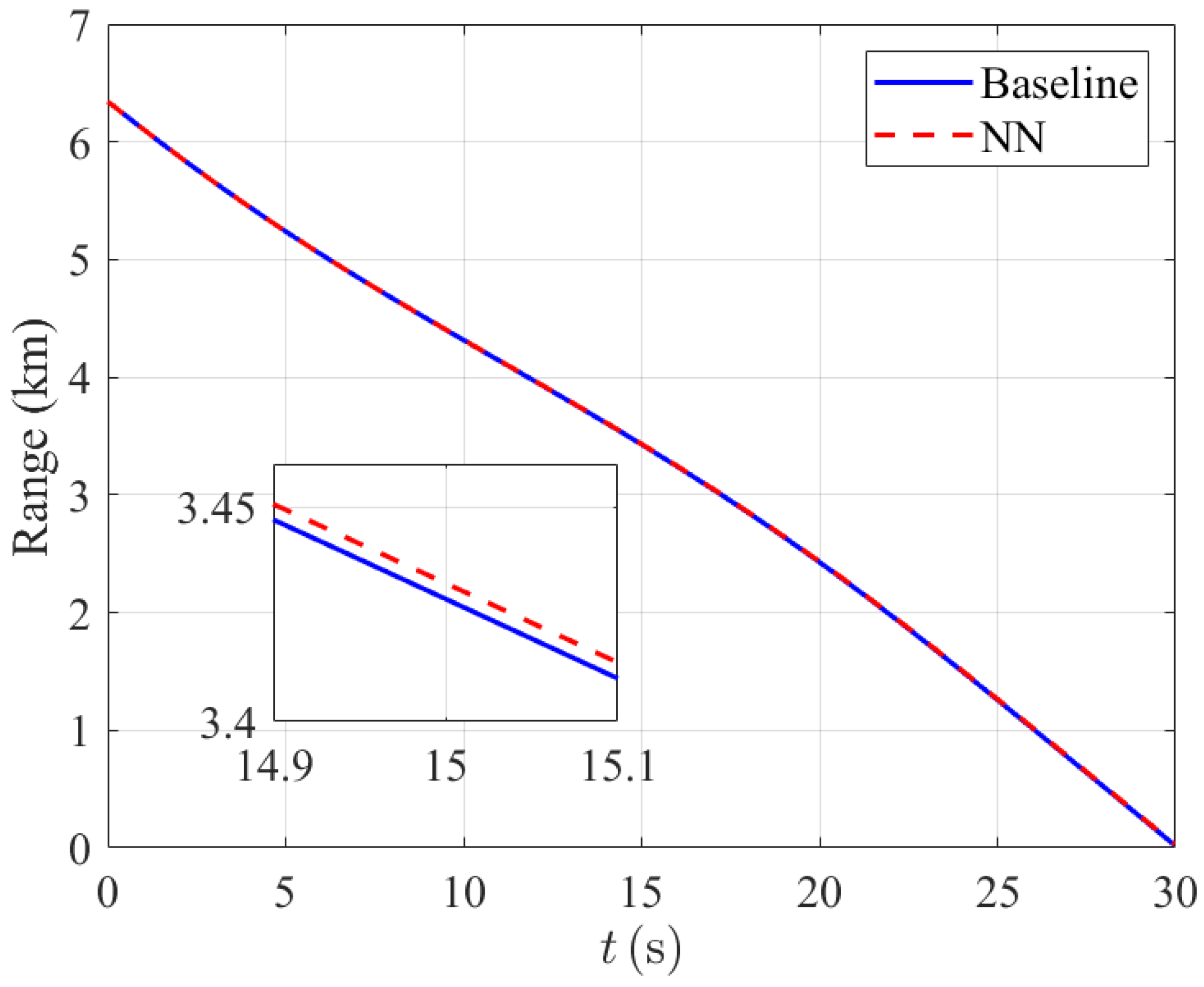
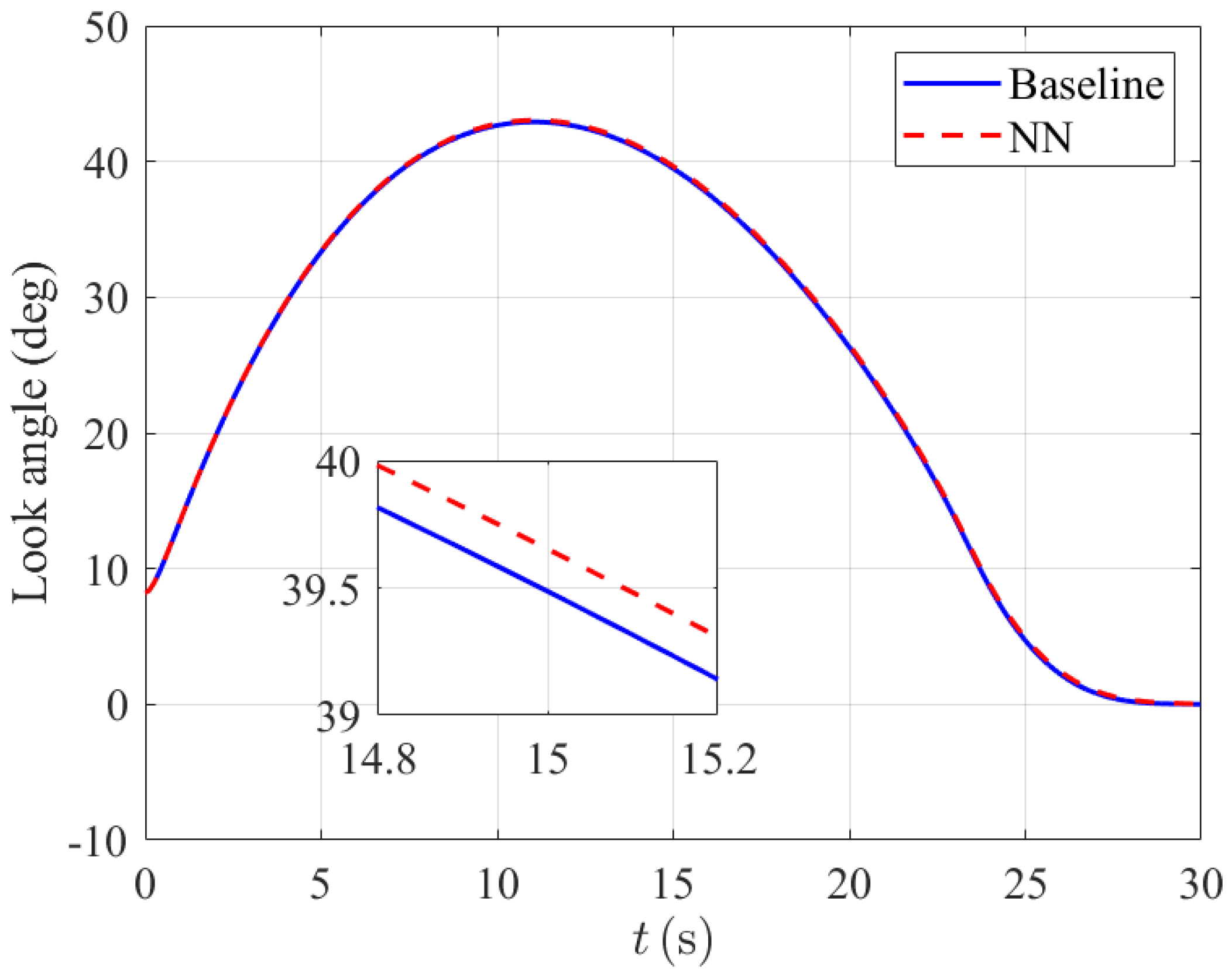
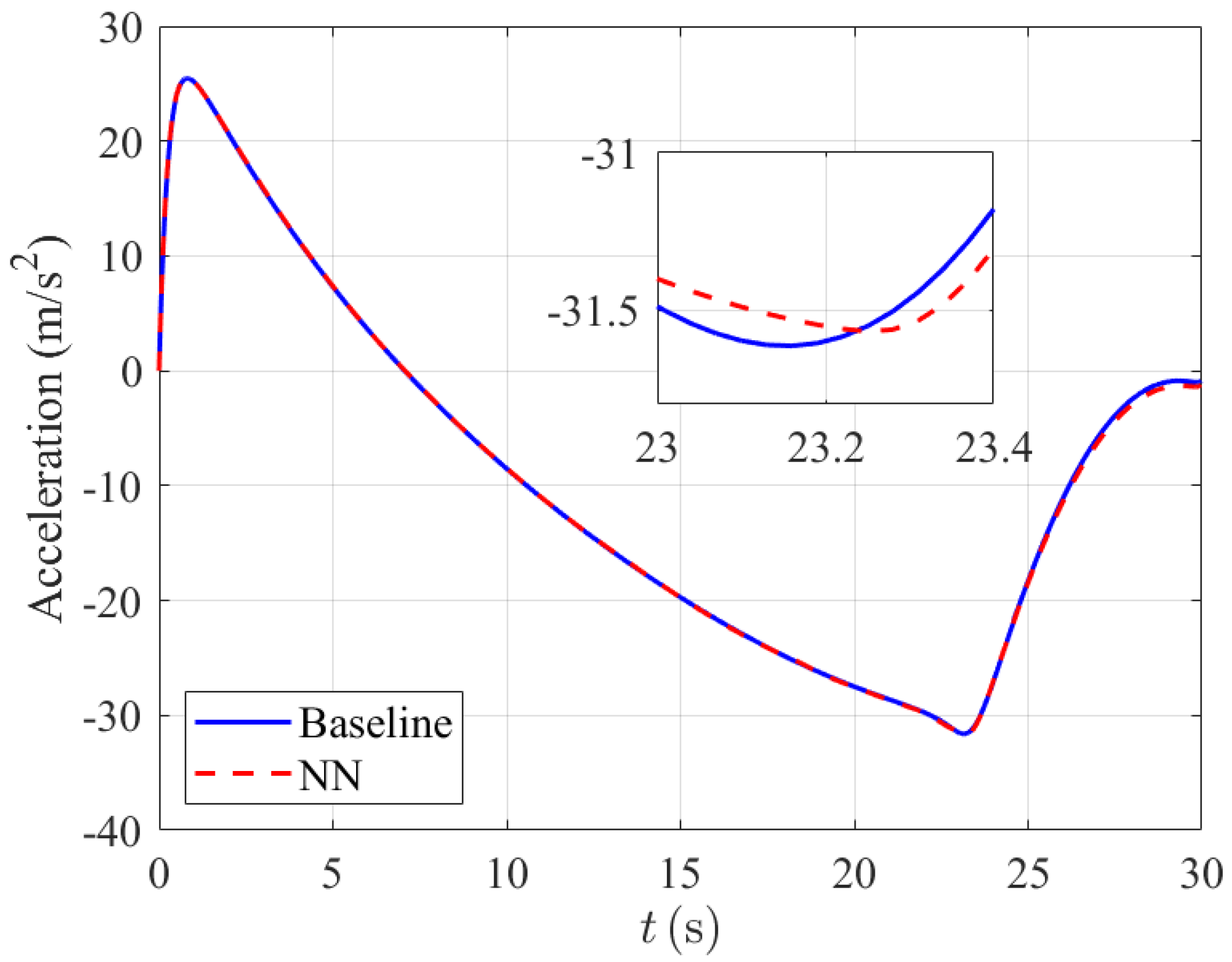
4.1. Trajectory Comparison
4.2. Time Consumption Comparison at Equal Update Frequency
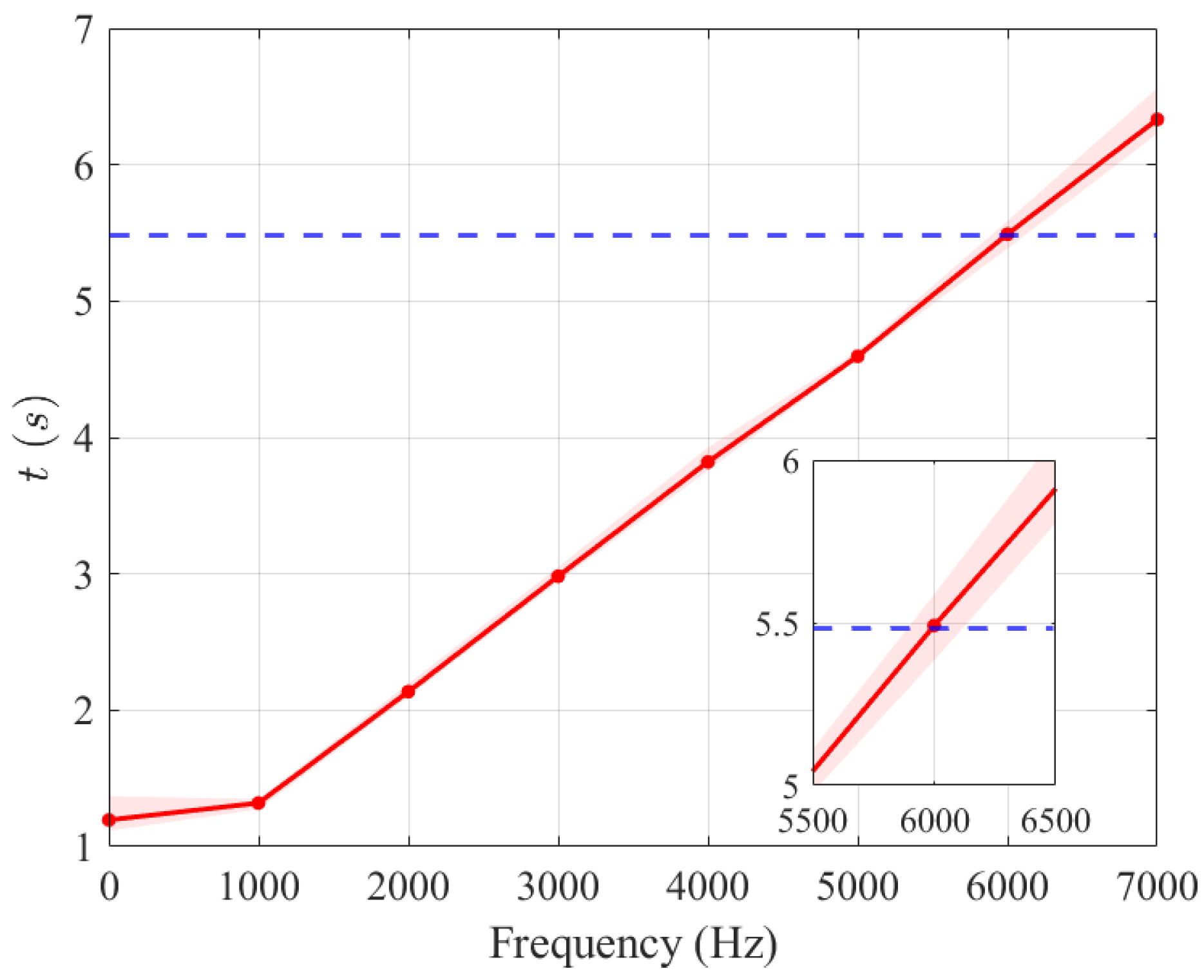
4.3. Update Frequency Comparison at Equal Real-World Time Usage
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, S.; Lee, C.H.; Shin, H.S.; Tsourdos, A. Optimal three-dimensional impact time guidance with seeker’s field-of-view constraint. Chin. J. Aeronaut. 2021, 34, 240–251. [Google Scholar] [CrossRef]
- Chai, R.; Guo, Y.; Zuo, Z.; Chen, K.; Shin, H.S.; Tsourdos, A. Cooperative motion planning and control for aerial-ground autonomous systems: Methods and applications. Prog. Aerosp. Sci. 2024, 146, 101005. [Google Scholar] [CrossRef]
- Narayanaswamy, S.; Damaren, C.J. Equinoctial Lyapunov control law for low-thrust rendezvous. J. Guid. Control Dyn. 2023, 46, 781–795. [Google Scholar] [CrossRef]
- Oguri, K.; McMahon, J.W. Robust spacecraft guidance around small bodies under uncertainty: Stochastic optimal control approach. J. Guid. Control Dyn. 2021, 44, 1295–1313. [Google Scholar] [CrossRef]
- Peterson, J.T.; Singh, S.K.; Junkins, J.L.; Taheri, E. Lyapunov guidance in orbit element space for low-thrust cislunar trajectories. In Proceedings of the AAS Guidance, Navigation and Control, Breckenridge, CO, USA, 30 January–5 February 2020; pp. 20–115. [Google Scholar]
- Tsalik, R.; Shima, T. Circular impact-time guidance. J. Guid. Control. Dyn. 2019, 42, 1836–1847. [Google Scholar] [CrossRef]
- Tekin, R.; Erer, K.S.; Holzapfel, F. Polynomial shaping of the look angle for impact-time control. J. Guid. Control. Dyn. 2017, 40, 2668–2673. [Google Scholar] [CrossRef]
- Hong, H.; Tekin, R.; Holzapfel, F. Guaranteed smooth trajectory generation for field-of-view constrained impact-time control. J. Guid. Control. Dyn. 2021, 44, 898–904. [Google Scholar] [CrossRef]
- Kim, H.G.; Lee, J.Y.; Kim, H.J.; Kwon, H.H.; Park, J.S. Look-angle-shaping guidance law for impact angle and time control with field-of-view constraint. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 1602–1612. [Google Scholar] [CrossRef]
- Ryoo, C.K.; Cho, H.; Tahk, M.J. Time-to-go weighted optimal guidance with impact angle constraints. IEEE Trans. Control. Syst. Technol. 2006, 14, 483–492. [Google Scholar] [CrossRef]
- Lee, C.H.; Kim, T.H.; Tahk, M.J. Effects of time-to-go errors on performance of optimal guidance laws. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 3270–3281. [Google Scholar] [CrossRef]
- Dhananjay, N.; Ghose, D. Accurate time-to-go estimation for proportional navigation guidance. J. Guid. Control. Dyn. 2014, 37, 1378–1383. [Google Scholar] [CrossRef]
- Tahk, M.J.; Shim, S.W.; Hong, S.M.; Choi, H.L.; Lee, C.H. Impact time control based on time-to-go prediction for sea-skimming antiship missiles. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2043–2052. [Google Scholar] [CrossRef]
- Jeon, I.S.; Lee, J.I.; Tahk, M.J. Impact-time-control guidance with generalized proportional navigation based on nonlinear formulation. J. Guid. Control Dyn. 2016, 39, 1885–1890. [Google Scholar] [CrossRef]
- Dong, W.; Wang, C.; Wang, J.; Xin, M. Varying-gain proportional navigation guidance for precise impact time control. J. Guid. Control Dyn. 2023, 46, 535–552. [Google Scholar] [CrossRef]
- Jiang, Z.; Ge, J.; Xu, Q.; Yang, T. Impact time control cooperative guidance law design based on modified proportional navigation. Aerospace 2021, 8, 231. [Google Scholar] [CrossRef]
- Saleem, A.; Ratnoo, A. Two stage proportional navigation guidance law for impact time control. In Proceedings of the 2018 Indian Control Conference (ICC), Kanpur, India, 4–6 January 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 312–317. [Google Scholar]
- Kumar, S.R.; Mukherjee, D. True-proportional-navigation inspired finite-time homing guidance for time constrained interception. Aerosp. Sci. Technol. 2022, 123, 107499. [Google Scholar] [CrossRef]
- Jeon, I.S.; Lee, J.I.; Tahk, M.J. Impact-time-control guidance law for anti-ship missiles. IEEE Trans. Control Syst. Technol. 2006, 14, 260–266. [Google Scholar] [CrossRef]
- Erer, K.S.; Tekin, R.; Hong, H. Computational Impact-Time Guidance with Biased Proportional Navigation. J. Guid. Control Dyn. 2024, 47, 1–7. [Google Scholar] [CrossRef]
- Jin, T.; He, S. Ensemble Transfer Learning Midcourse Guidance Algorithm for Velocity Maximization. J. Aerosp. Inf. Syst. 2023, 20, 204–215. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, J.; He, S.; Shin, H.S.; Tsourdos, A. Learning prediction-correction guidance for impact time control. Aerosp. Sci. Technol. 2021, 119, 107187. [Google Scholar] [CrossRef]
- Izzo, D.; Öztürk, E. Real-time guidance for low-thrust transfers using deep neural networks. J. Guid. Control Dyn. 2021, 44, 315–327. [Google Scholar] [CrossRef]
- Singh, S.K.; Junkins, J.L. Stochastic learning and extremal-field map based autonomous guidance of low-thrust spacecraft. Sci. Rep. 2022, 12, 17774. [Google Scholar] [CrossRef] [PubMed]
- Izzo, D.; Blazquez, E.; Ferede, R.; Origer, S.; De Wagter, C.; de Croon, G.C. Optimality principles in spacecraft neural guidance and control. Sci. Robot. 2024, 9, eadi6421. [Google Scholar] [CrossRef] [PubMed]
- He, S.; Shin, H.S.; Tsourdos, A. Computational missile guidance: A deep reinforcement learning approach. J. Aerosp. Inf. Syst. 2021, 18, 571–582. [Google Scholar] [CrossRef]
- Siddique, U.; Sinha, A.; Cao, Y. On Deep Reinforcement Learning for Target Capture Autonomous Guidance. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024; p. 0957. [Google Scholar]
- Sinha, A.; White, D.; Cao, Y. Deep Reinforcement Learning-based Optimal Time-constrained Intercept Guidance. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024; p. 2206. [Google Scholar]
- Erer, K.S.; Merttopçuoglu, O. Indirect impact-angle-control against stationary targets using biased pure proportional navigation. J. Guid. Control Dyn. 2012, 35, 700–704. [Google Scholar] [CrossRef]
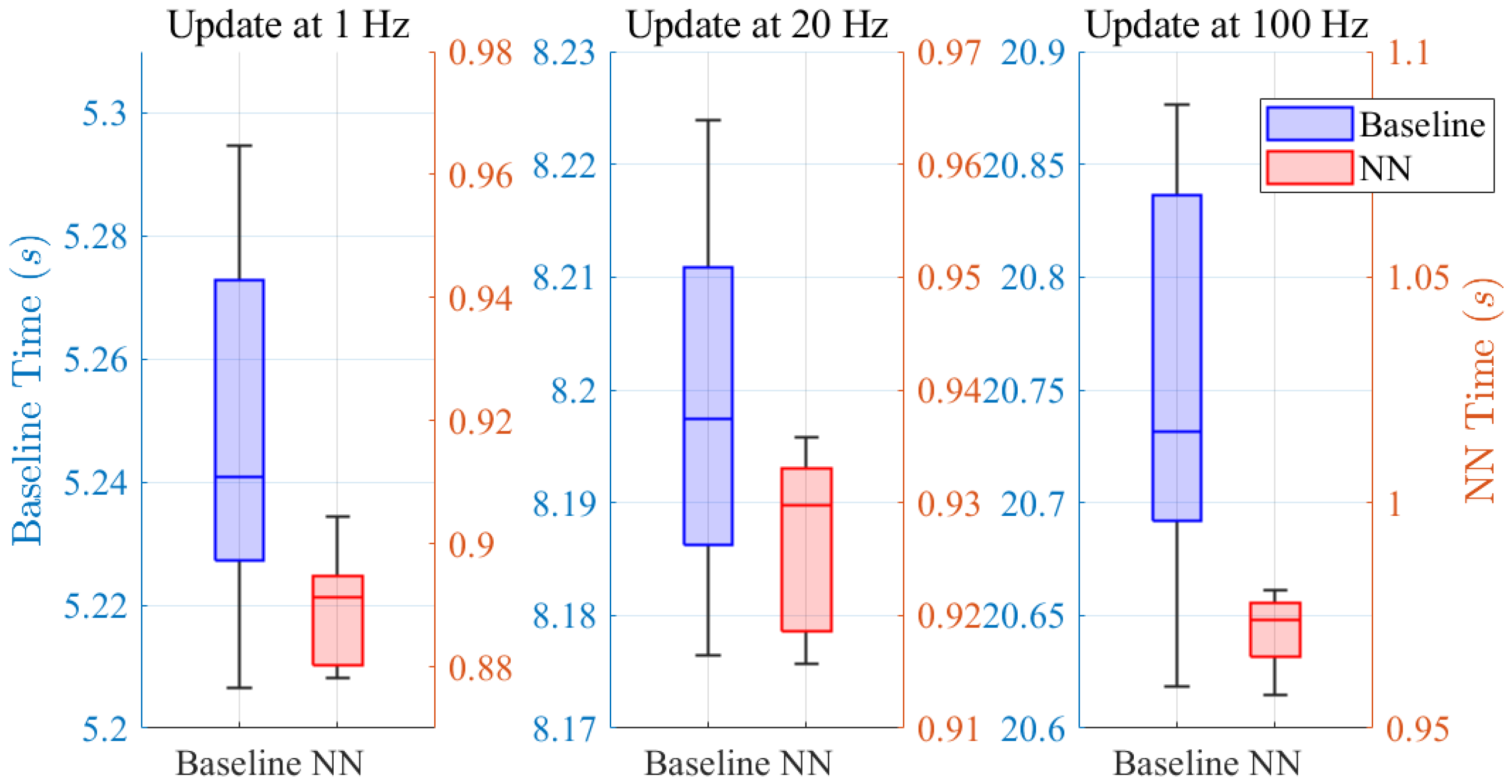

| Time Cost (s) | 1 Hz | 20 Hz | 100 Hz |
|---|---|---|---|
| Baseline method | 5.25 | 8.20 | 20.75 |
| Proposed method | 0.89 | 0.93 | 0.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Hong, H. Enhanced Computational Biased Proportional Navigation with Neural Networks for Impact Time Control. Aerospace 2024, 11, 670. https://doi.org/10.3390/aerospace11080670
Zhang X, Hong H. Enhanced Computational Biased Proportional Navigation with Neural Networks for Impact Time Control. Aerospace. 2024; 11(8):670. https://doi.org/10.3390/aerospace11080670
Chicago/Turabian StyleZhang, Xue, and Haichao Hong. 2024. "Enhanced Computational Biased Proportional Navigation with Neural Networks for Impact Time Control" Aerospace 11, no. 8: 670. https://doi.org/10.3390/aerospace11080670





