Adaptive Incremental Nonlinear Dynamic Inversion Control for Aerial Manipulators
Abstract
:1. Introduction
2. UAM Dynamic System Model
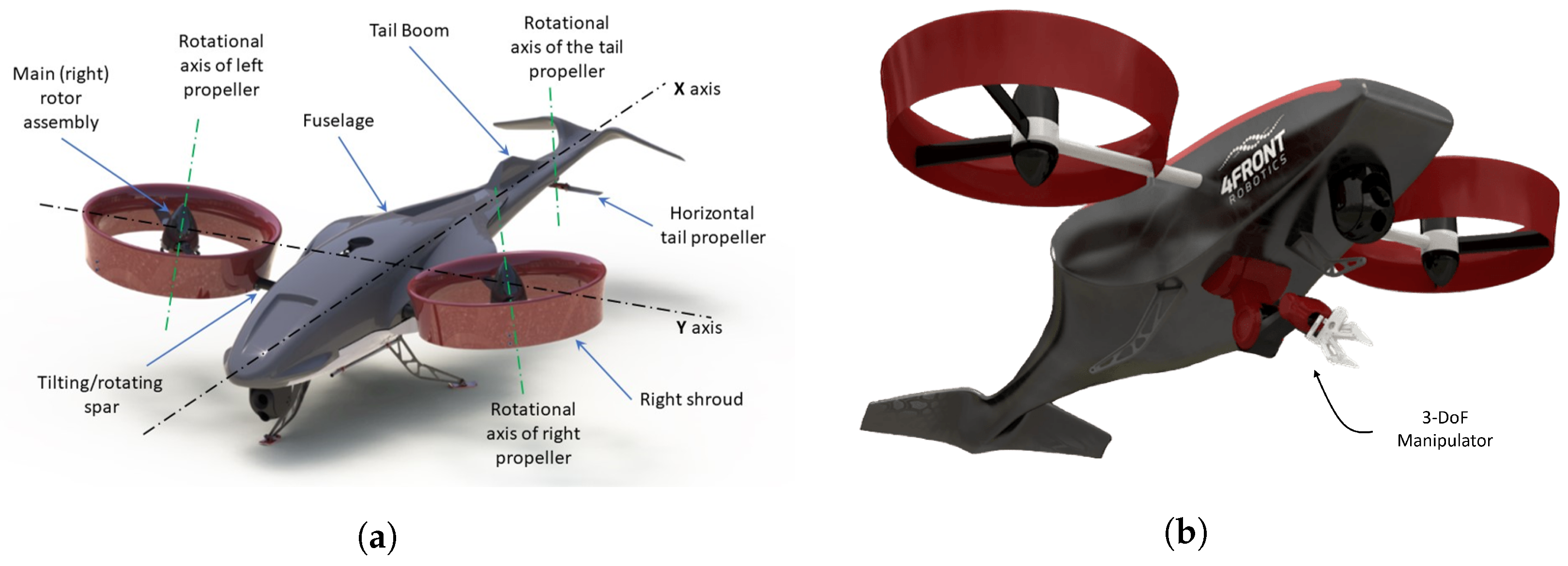
2.1. Navig8-UAM System
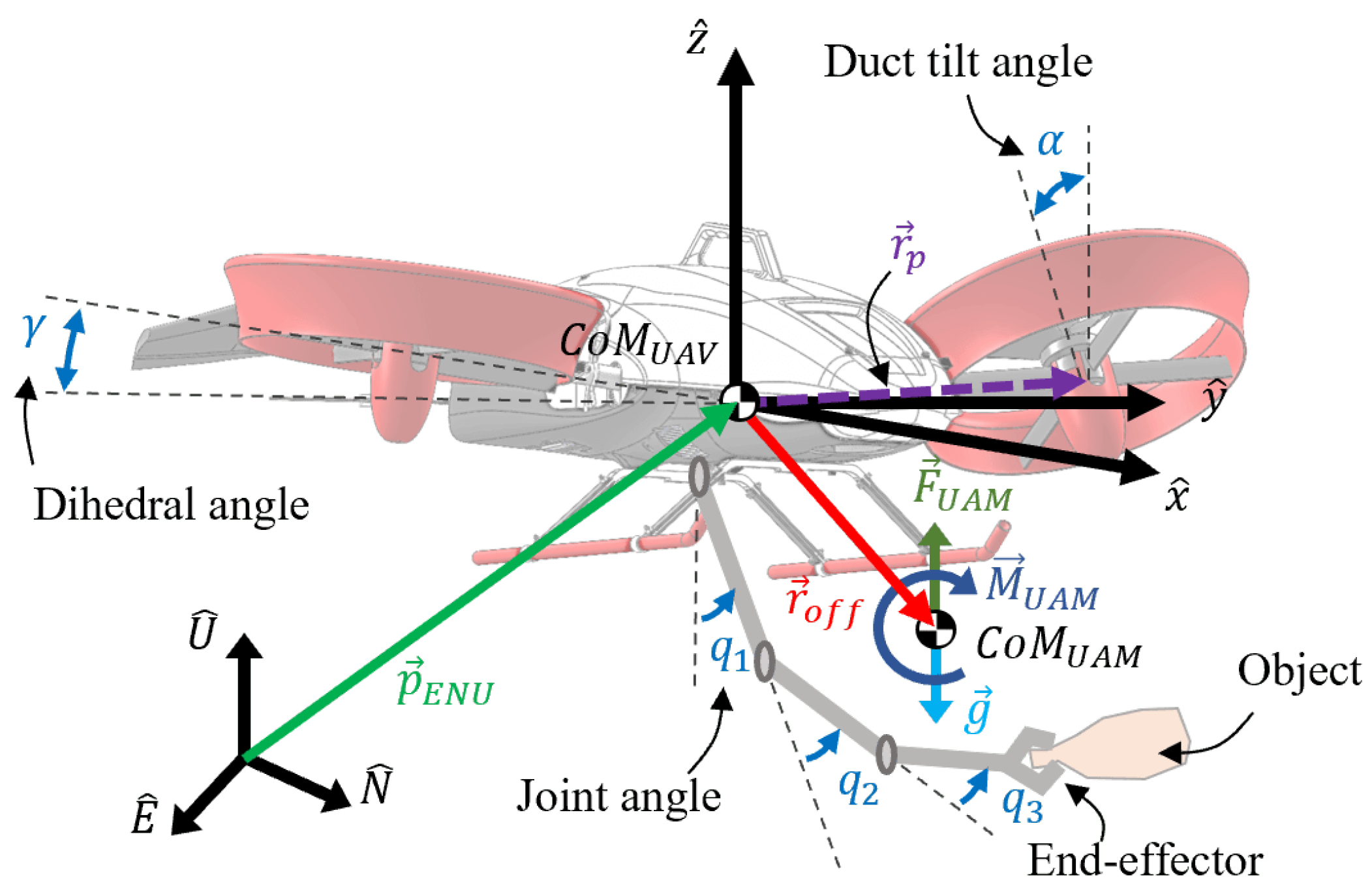
2.2. Force and Moment Equations for the Navig8-UAM
3. INDI for UAMs
3.1. Rotational Relationship
3.2. Translational Relationship
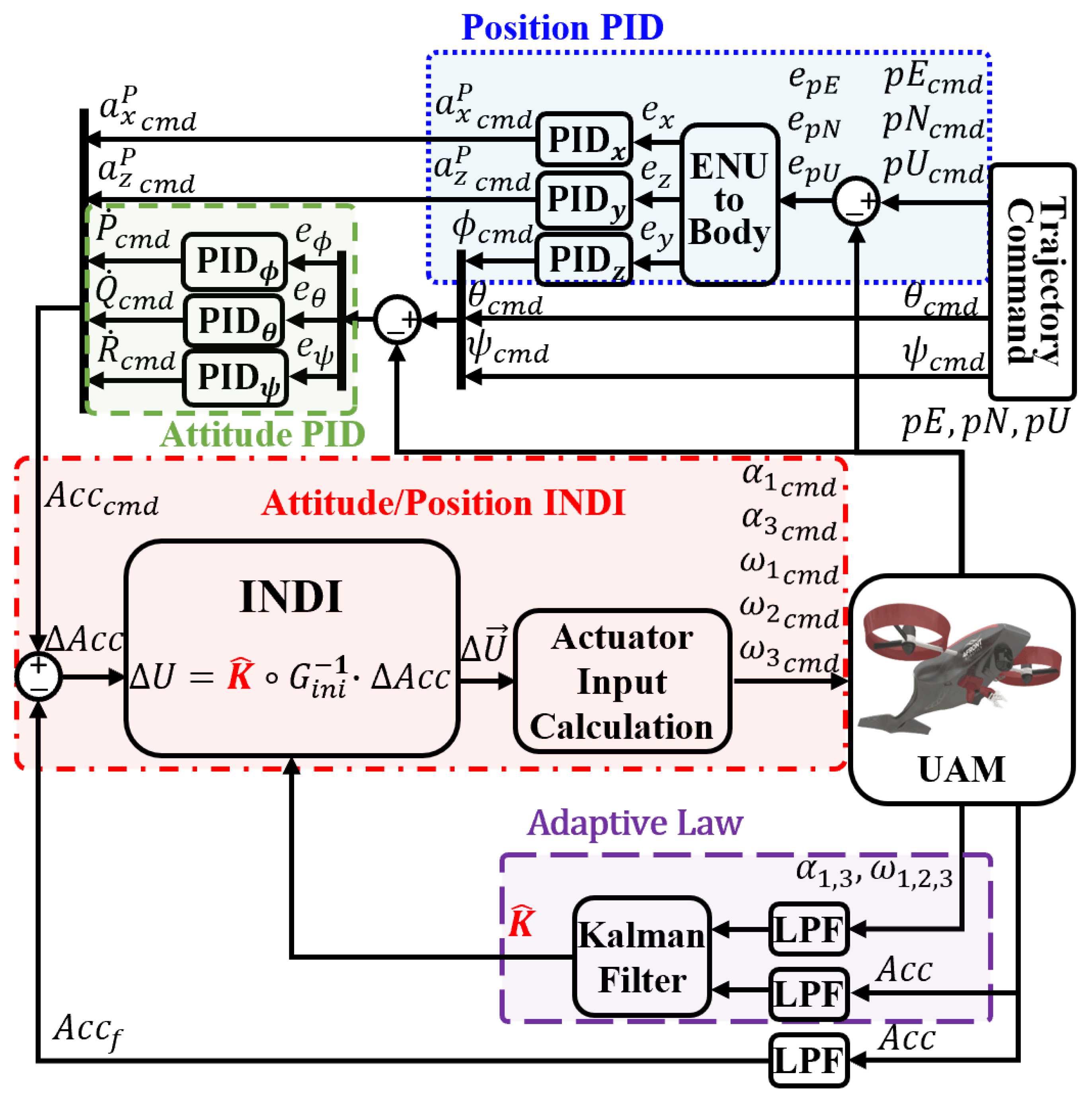
3.3. INDI Formulation
3.4. Control Effectiveness Matrix
4. Adaptive INDI for UAMs
4.1. Methodology
4.2. Analysis of the Inverse of the Control Effectiveness Matrix

4.3. Adaptation of Matrix
5. Simulation Results
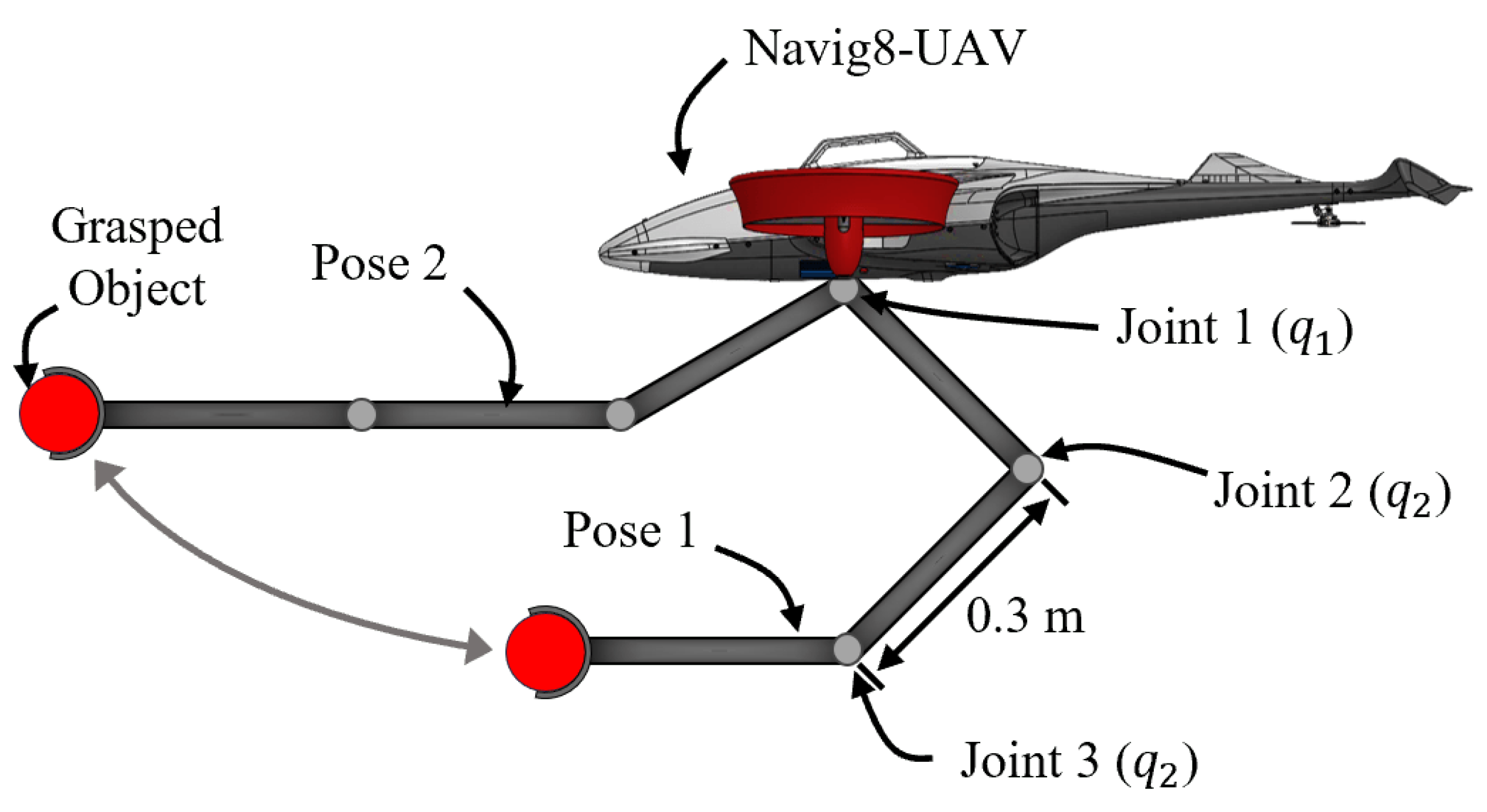
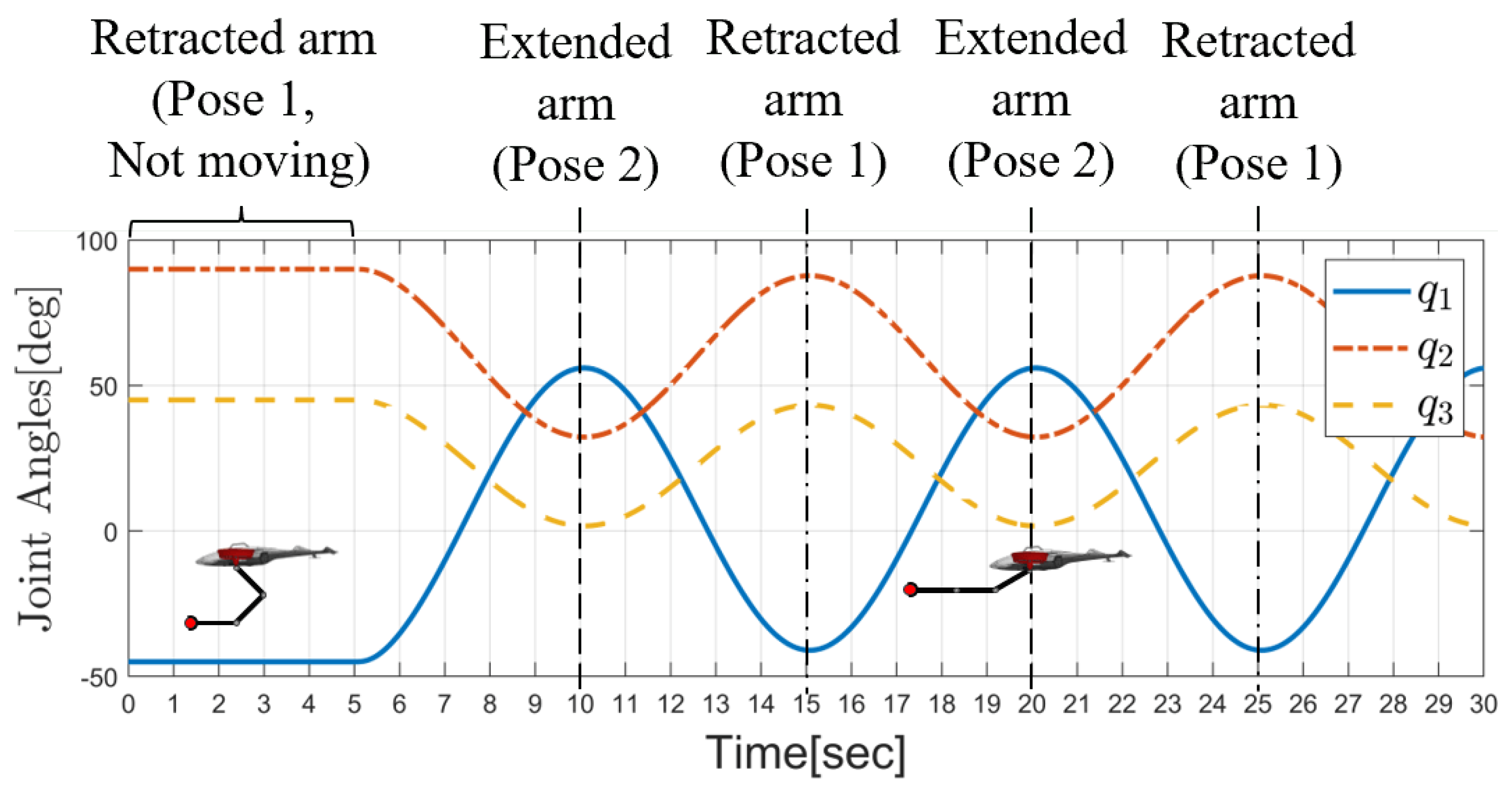
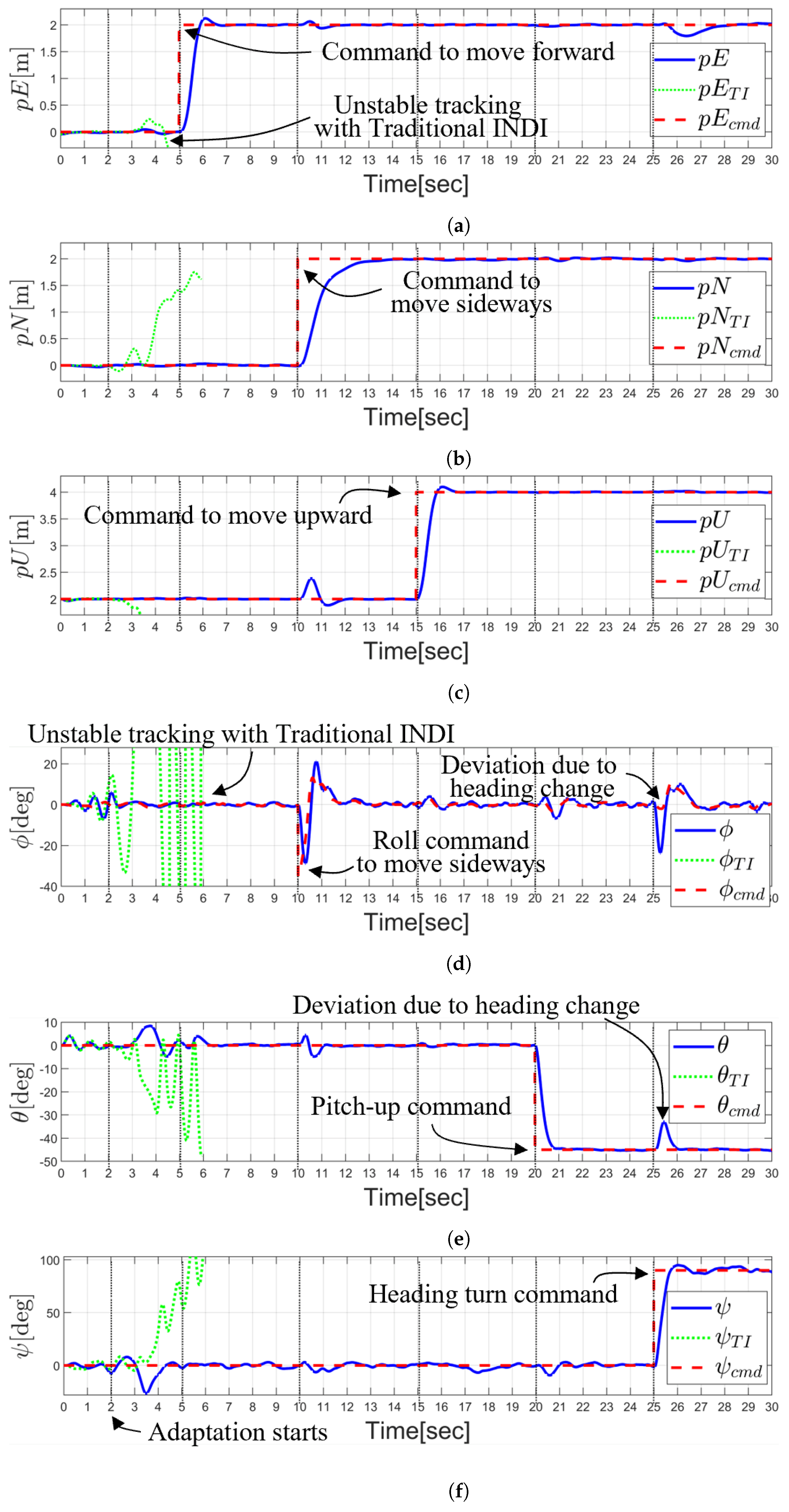
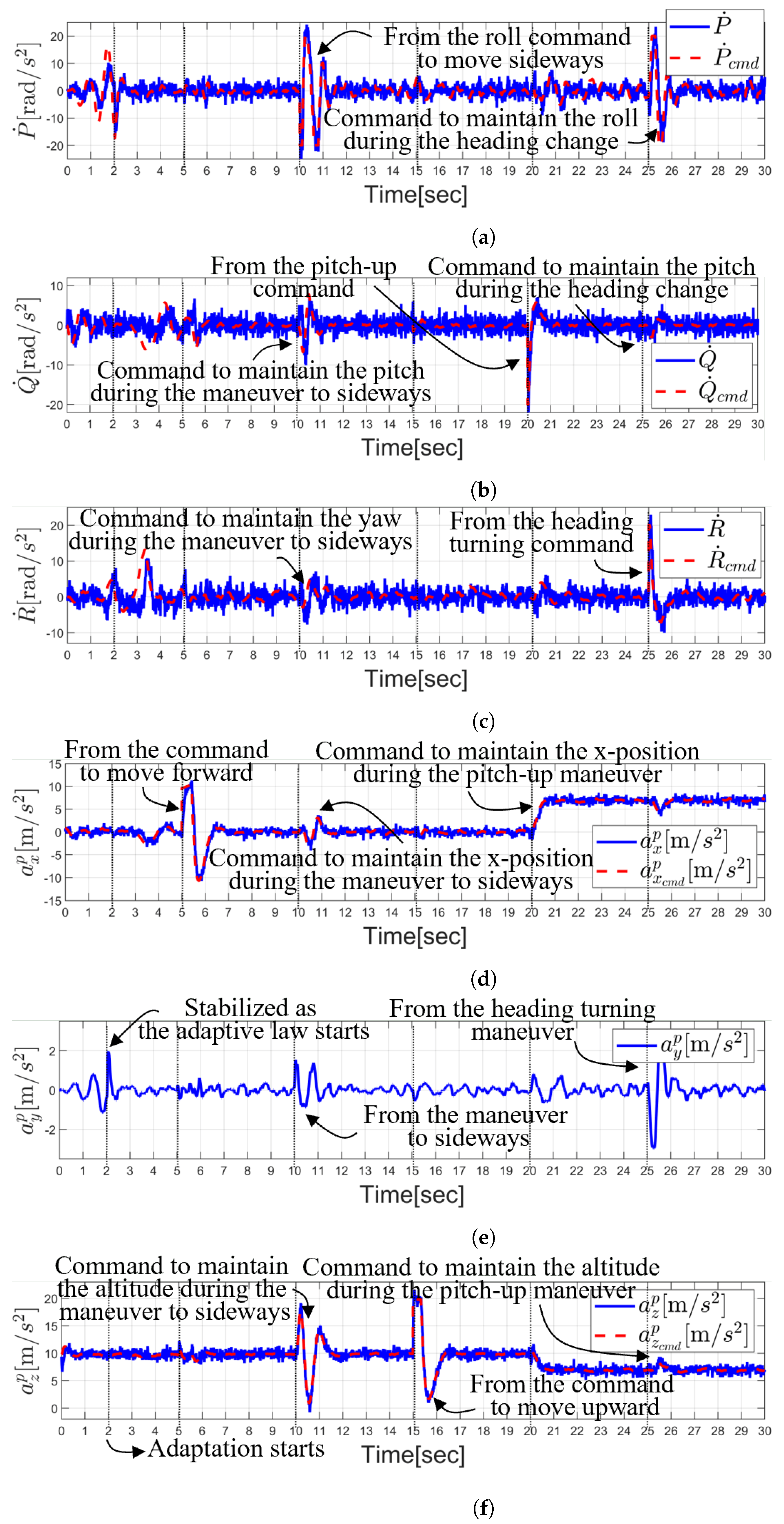
5.1. Step Response Simulation Test
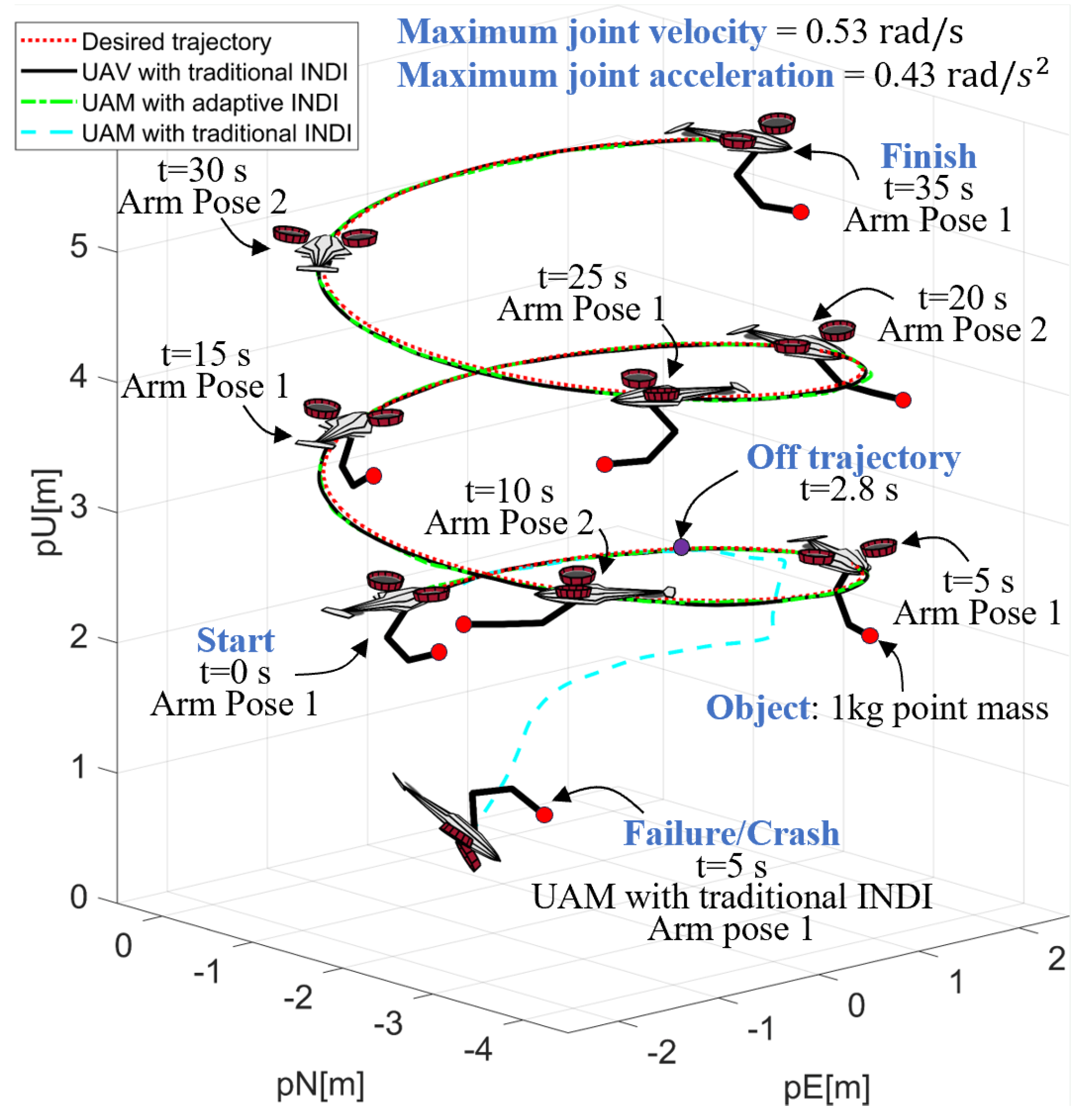
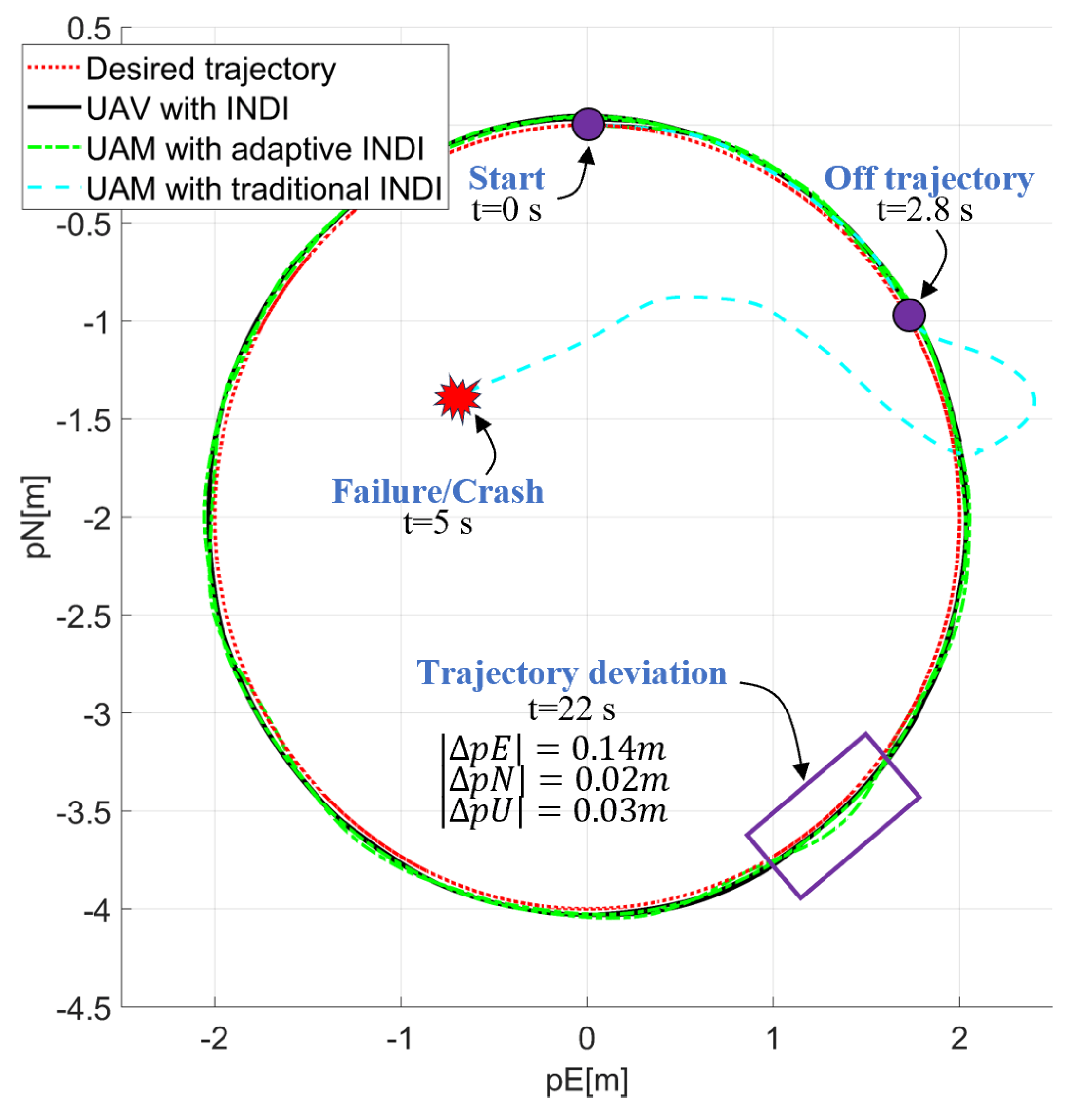
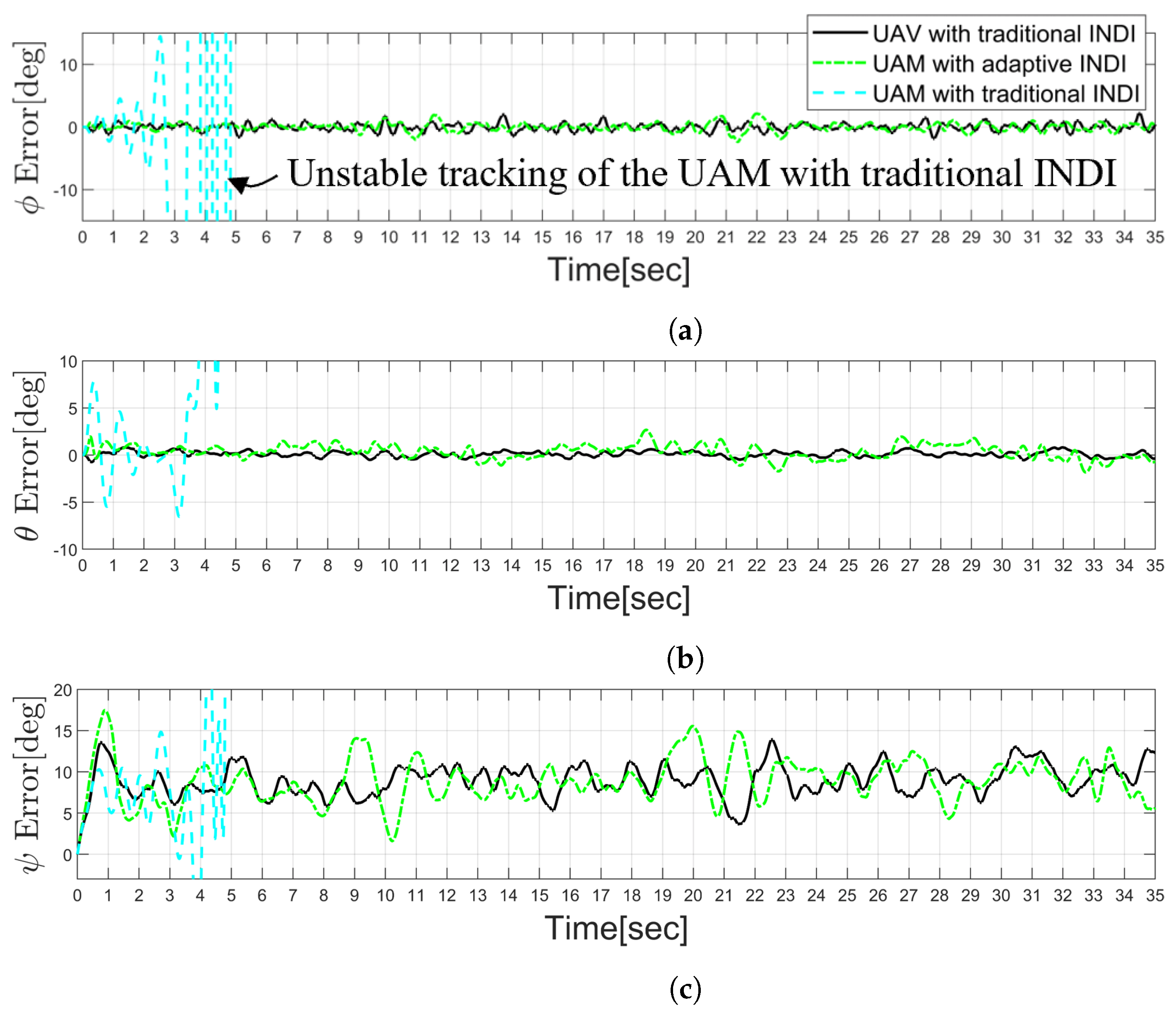
5.2. Helical Turn Climb Trajectory Tracking Flight Simulation
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Analytical Calculation of G
Appendix B. Example of the Analytical Calculation of G−1 for Navig8-UAM
References
- Konert, A.; Balcerzak, T. Military autonomous drones (UAVs)—From fantasy to reality. Legal and Ethical implications. Transp. Res. Procedia 2021, 59, 292–299. [Google Scholar] [CrossRef]
- Shakhatreh, H.; Sawalmeh, A.H.; Al-Fuqaha, A.; Dou, Z.; Almaita, E.; Khalil, I.; Othman, N.S.; Khreishah, A.; Guizani, M. Unmanned Aerial Vehicles (UAVs): A Survey on Civil Applications and Key Research Challenges. IEEE Access 2019, 7, 48572–48634. [Google Scholar] [CrossRef]
- Jimenez-Cano, A.E.; Martin, J.; Heredia, G.; Ollero, A.; Cano, R. Control of an aerial robot with multi-link arm for assembly tasks. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 4916–4921. [Google Scholar] [CrossRef]
- Orsag, M.; Korpela, C.; Oh, P. Modeling and control of MM-UAV: Mobile manipulating unmanned aerial vehicle. J. Intell. Robot. Syst. 2013, 69, 227–240. [Google Scholar] [CrossRef]
- Orsag, M.; Korpela, C.; Pekala, M.; Oh, P. Stability control in aerial manipulation. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 5581–5586. [Google Scholar] [CrossRef]
- Korpela, C.; Orsag, M.; Pekala, M.; Oh, P. Dynamic stability of a mobile manipulating unmanned aerial vehicle. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 4922–4927. [Google Scholar] [CrossRef]
- Orsag, M.; Korpela, C.; Bogdan, S.; Oh, P. Hybrid adaptive control for aerial manipulation. J. Intell. Robot. Syst. 2014, 73, 693–707. [Google Scholar] [CrossRef]
- Dief, T.N.; Yoshida, S. System identification and adaptive control of mass-varying quad-rotor. Evergreen 2017, 4, 58–66. [Google Scholar] [CrossRef]
- Garimella, G.; Sheckells, M.; Kim, S.; Kobilarov, M. A Framework for Reliable Aerial Manipulation. Unpublished 2018. Available online: https://asco.lcsr.jhu.edu/wp-content/uploads/2018/10/framework-reliable-aerial-1.pdf (accessed on 1 July 2022).
- Min, B.C.; Hong, J.H.; Matson, E.T. Adaptive robust control (ARC) for an altitude control of a quadrotor type UAV carrying an unknown payloads. In Proceedings of the 2011 11th International Conference on Control, Automation and Systems, Gyeonggi-do, Republic of Korea, 26–29 October 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1147–1151. [Google Scholar]
- Nicol, C.; Macnab, C.; Ramirez-Serrano, A. Robust adaptive control of a quadrotor helicopter. Mechatronics 2011, 21, 927–938. [Google Scholar] [CrossRef]
- Wang, C.; Nahon, M.; Trentini, M. Controller development and validation for a small quadrotor with compensation for model variation. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 902–909. [Google Scholar] [CrossRef]
- Wang, C.; Song, B.; Huang, P.; Tang, C. Trajectory tracking control for quadrotor robot subject to payload variation and wind gust disturbance. J. Intell. Robot. Syst. 2016, 83, 315–333. [Google Scholar] [CrossRef]
- Baraban, G.; Sheckells, M.; Kim, S.; Kobilarov, M. Adaptive parameter estimation for aerial manipulation. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 614–619. [Google Scholar] [CrossRef]
- Lee, H.; Kim, S.; Kim, H.J. Control of an aerial manipulator using on-line parameter estimator for an unknown payload. In Proceedings of the 2015 IEEE International Conference on Automation Science and Engineering (CASE), Gothenburg, Sweden, 24–28 August 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 316–321. [Google Scholar] [CrossRef]
- Lee, H.; Kim, H.J. Estimation, control, and planning for autonomous aerial transportation. IEEE Trans. Ind. Electron. 2016, 64, 3369–3379. [Google Scholar] [CrossRef]
- Park, C.; Ramirez-Serrano, A.; Bisheban, M. Estimation of Time-Varying Inertia of Aerial Manipulators Performing Manipulation of Unknown Objects. In Proceedings of the 10th International Conference of Control Systems, and Robotics (CDSR’23), Avestia, Ottawa, ON, Canada, 1–6 June 2023; p. 209. [Google Scholar] [CrossRef]
- Enns, D.; Bugajski, D.; Hendrick, R.; Stein, G. Dynamic inversion: An evolving methodology for flight control design. Int. J. Control. 1994, 59, 71–91. [Google Scholar] [CrossRef]
- Lombaerts, T.; Chu, P.; Mulder, J.A.; Joosten, D. Flight Control Reconfiguration based on a Modular Approach. IFAC Proc. Vol. 2009, 42, 259–264. [Google Scholar] [CrossRef]
- Simplício, P.; Pavel, M.; Van Kampen, E.; Chu, Q. An acceleration measurements-based approach for helicopter nonlinear flight control using incremental nonlinear dynamic inversion. Control. Eng. Pract. 2013, 21, 1065–1077. [Google Scholar] [CrossRef]
- Sun, S.; Romero, A.; Foehn, P.; Kaufmann, E.; Scaramuzza, D. A comparative study of nonlinear mpc and differential-flatness-based control for quadrotor agile flight. IEEE Trans. Robot. 2022, 38, 3357–3373. [Google Scholar] [CrossRef]
- Tal, E.; Karaman, S. Accurate tracking of aggressive quadrotor trajectories using incremental nonlinear dynamic inversion and differential flatness. IEEE Trans. Control. Syst. Technol. 2020, 29, 1203–1218. [Google Scholar] [CrossRef]
- Yang, J.; Cai, Z.; Zhao, J.; Wang, Z.; Ding, Y.; Wang, Y. INDI-based aggressive quadrotor flight control with position and attitude constraints. Robot. Auton. Syst. 2023, 159, 104292. [Google Scholar] [CrossRef]
- Smeur, E.J.; de Croon, G.C.; Chu, Q. Cascaded incremental nonlinear dynamic inversion for MAV disturbance rejection. Control. Eng. Pract. 2018, 73, 79–90. [Google Scholar] [CrossRef]
- Smeur, E.J.; Chu, Q.; De Croon, G.C. Adaptive incremental nonlinear dynamic inversion for attitude control of micro air vehicles. J. Guid. Control. Dyn. 2016, 39, 450–461. [Google Scholar] [CrossRef]
- Cao, S.; Shen, L.; Zhang, R.; Yu, H.; Wang, X. Adaptive Incremental Nonlinear Dynamic Inversion Control Based on Neural Network for UAV Maneuver. In Proceedings of the 2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Hong Kong, China, 8–12 July 2019; pp. 642–647. [Google Scholar] [CrossRef]
- Ahmadi, K.; Asadi, D.; Nabavi-Chashmi, S.Y.; Tutsoy, O. Modified adaptive discrete-time incremental nonlinear dynamic inversion control for quad-rotors in the presence of motor faults. Mech. Syst. Signal Process. 2023, 188, 109989. [Google Scholar] [CrossRef]
- Taherinezhad, M.; Ramirez-Serrano, A. An Enhanced Incremental Nonlinear Dynamic Inversion Control Strategy for Advanced Unmanned Aircraft Systems. Aerospace 2023, 10, 843. [Google Scholar] [CrossRef]
- Taherinezhad, M. Enhanced INDI+PID Control Strategy for Advanced Unmanned Aircraft Systems Having Highly Coupled Dynamics. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2023. [Google Scholar]
- Jansen, F.; Ramirez-Serrano, A. Agile unmanned vehicle navigation in highly confined environments. In Proceedings of the 2011 IEEE International Conference on Systems, Man, and Cybernetics, Anchorage, AK, USA, 9–12 October 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 2381–2386. [Google Scholar] [CrossRef]
- Amiri, N.; Ramirez-Serrano, A.; Davies, R.J. Integral backstepping control of an unconventional dual-fan unmanned aerial vehicle. J. Intell. Robot. Syst. 2013, 69, 147–159. [Google Scholar] [CrossRef]
- Majnoon, M.; Samsami, K.; Mehrandezh, M.; Ramirez-Serrano, A. Mobile-Target Tracking via Highly-Maneuverable VTOL UAVs with EO Vision. In Proceedings of the 2016 13th Conference on Computer and Robot Vision (CRV), Victoria, BC, Canada, 1–3 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 260–265. [Google Scholar] [CrossRef]
- Yavari, M.; Gupta, K.; Mehrandezh, M.; Ramirez-Serrano, A. Optimal real-time trajectory control of a pitch-hover UAV with a two link manipulator. In Proceedings of the 2018 International Conference on Unmanned Aircraft Systems (ICUAS), Dallas, TX, USA, 12–15 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 930–938. [Google Scholar] [CrossRef]
- Sieberling, S.; Chu, Q.; Mulder, J. Robust flight control using incremental nonlinear dynamic inversion and angular acceleration prediction. J. Guid. Control. Dyn. 2010, 33, 1732–1742. [Google Scholar] [CrossRef]
- Keesman, K.J.; Keesman, K.J. Time-varying Dynamic Systems Identification. In System Identification: An Introduction; Springer: London, UK, 2011; pp. 195–221. [Google Scholar] [CrossRef]
- Kalman, R.E.; Bucy, R.S. New results in linear filtering and prediction theory. J. Basic Eng. 1961, 83, 95–108. [Google Scholar] [CrossRef]

| 1st Column | 2nd Column | 3rd Column | 5th Column |
|---|---|---|---|
| Positive | ||||||||
| Negative |
| Size [m] | Mass [kg] | [kg·m2] | [kg·m2] | [kg·m2] | [kg·m2] | [kg·m2] | [kg·m2] | |
|---|---|---|---|---|---|---|---|---|
| Navig8-UAV | length: 1.0 | 5.0 | 0.0667 | 0.1492 | 0.2019 | 0.0147 | 0 | 0 |
| width: 0.8 | ||||||||
| height: 0.2 | ||||||||
| Each arm linkage | length: 0.3 | 0.5 | 0.0037 | 0.0037 | 0 | 0 | 0 | 0 |
| Object (sphere) | radius: 0.05 | 1.0 | 0.001 | 0.001 | 0.001 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, C.; Ramirez-Serrano, A.; Bisheban, M. Adaptive Incremental Nonlinear Dynamic Inversion Control for Aerial Manipulators. Aerospace 2024, 11, 671. https://doi.org/10.3390/aerospace11080671
Park C, Ramirez-Serrano A, Bisheban M. Adaptive Incremental Nonlinear Dynamic Inversion Control for Aerial Manipulators. Aerospace. 2024; 11(8):671. https://doi.org/10.3390/aerospace11080671
Chicago/Turabian StylePark, Chanhong, Alex Ramirez-Serrano, and Mahdis Bisheban. 2024. "Adaptive Incremental Nonlinear Dynamic Inversion Control for Aerial Manipulators" Aerospace 11, no. 8: 671. https://doi.org/10.3390/aerospace11080671
APA StylePark, C., Ramirez-Serrano, A., & Bisheban, M. (2024). Adaptive Incremental Nonlinear Dynamic Inversion Control for Aerial Manipulators. Aerospace, 11(8), 671. https://doi.org/10.3390/aerospace11080671







