A Peak-Finding Siamese Convolutional Neural Network (PF-SCNN) for Aero-Engine Hot Jet FT-IR Spectrum Classification
Abstract
:1. Introduction
- To achieve the classification of aero-engines, this paper employs an infrared spectroscopy detection method to measure the spectra of aero-engines’ hot jets, which are significant sources of aero-engines’ infrared radiation, using an FT-IR spectrometer. The infrared spectra measured using the FT-IR spectrometer offers characteristic molecular-level information about substances, thereby enhancing the scientific basis for classifying aero-engines based on their infrared spectra.
- This paper presents a SCNN for classifying the hot jet spectra of aero-engines using a data matching method. The network is based on 1DCNN, and feature similarity is calculated using the Euclidean distance metric. Subsequently, a spectral comparison method is employed for the purpose of performing spectrum classification.
- The objective of this paper is to propose an algorithm for identifying peaks that will optimize the training and prediction speed of the SCNN. The algorithm identifies the peak value in the mid-infrared spectrum data and quantifies the high-frequency peaks, which are subsequently employed as input for the SCNN.
2. Experimental Design and Data Set Production for Hot Jet Infrared Spectrum Measurement of Aero-Engines
2.1. Aero-Engine Spectrum Measurement Experiment Design
2.2. Spectrum Data Preprocessing and Data Set Production
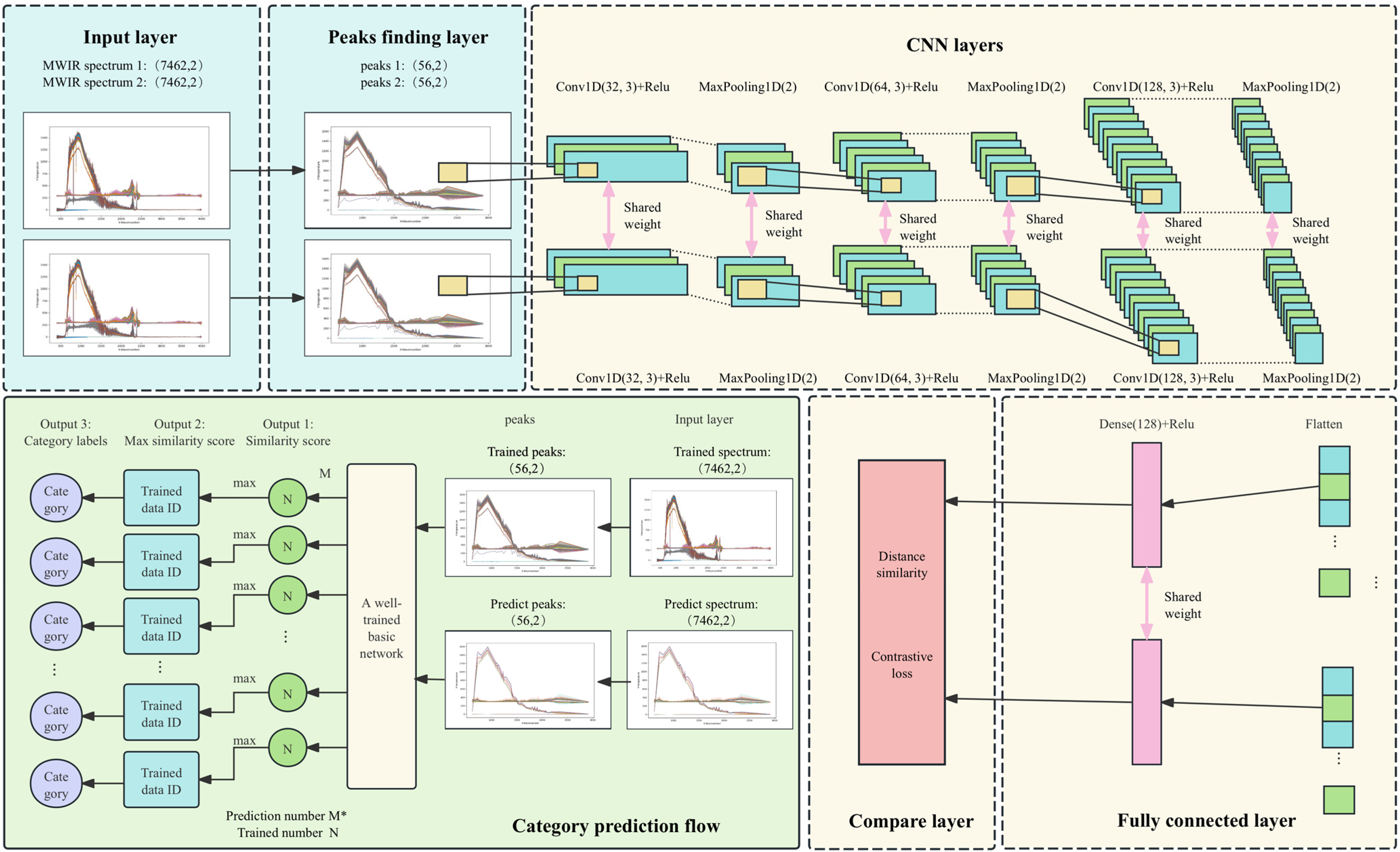
3. Architectural Design of Peak-Finding Siamese Convolutional Neural Network
3.1. Overall Network Structure Design
3.2. Base Network Architecture
3.2.1. One-Dimensional Convolutional Layer (Cov1D Layer)
3.2.2. Maximum Pooling Layer (MaxPool Layer)
3.2.3. Flattening Layer
3.2.4. Fully Connected Layer (FC Layer)
3.2.5. Comparison Layer
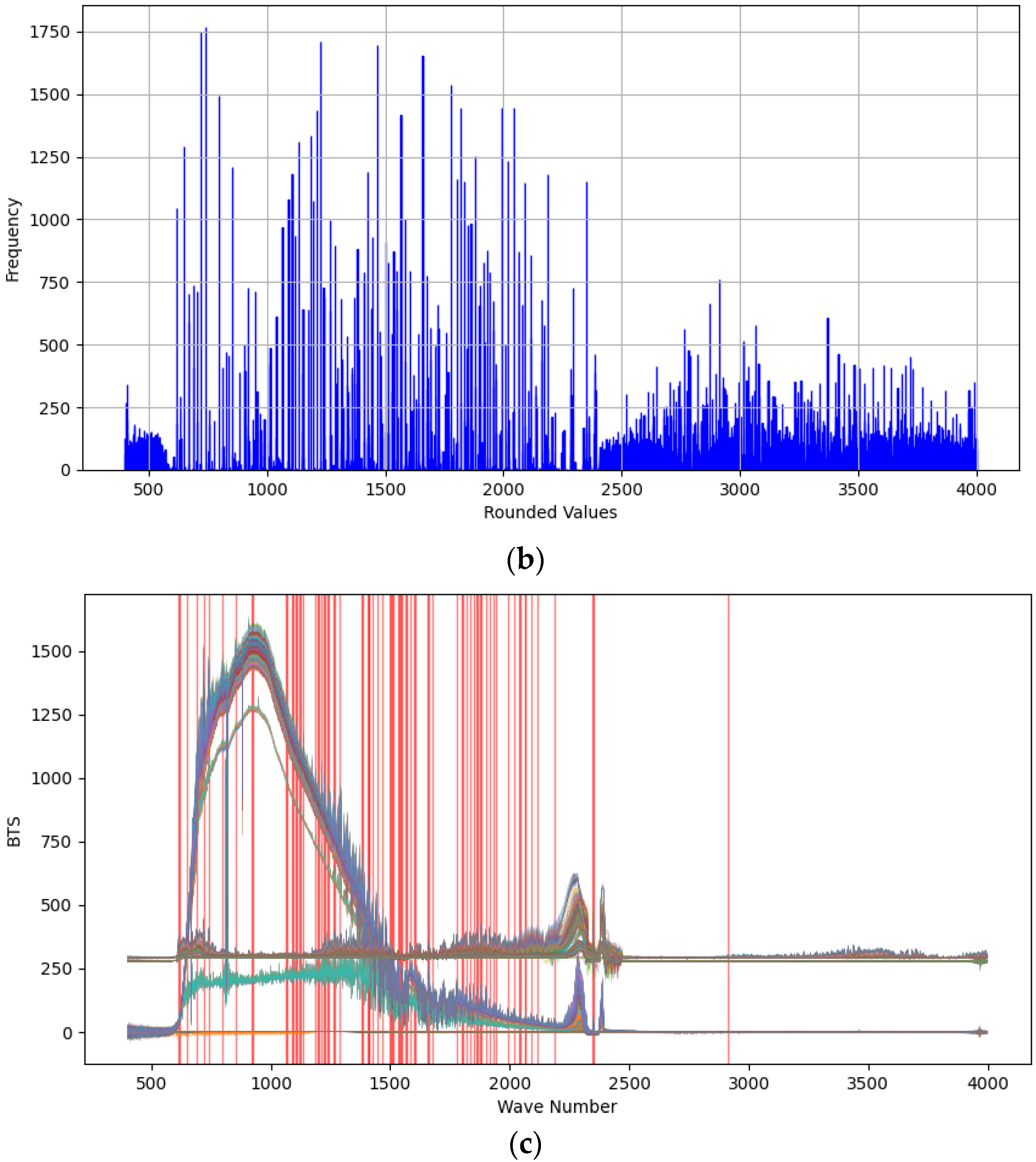
3.3. Peak-Finding Algorithm
| Algorithm 1: Peak-Finding and Peak Statistics Algorithm |
| Input: Spectrum data |
| Output: Peak data |
|
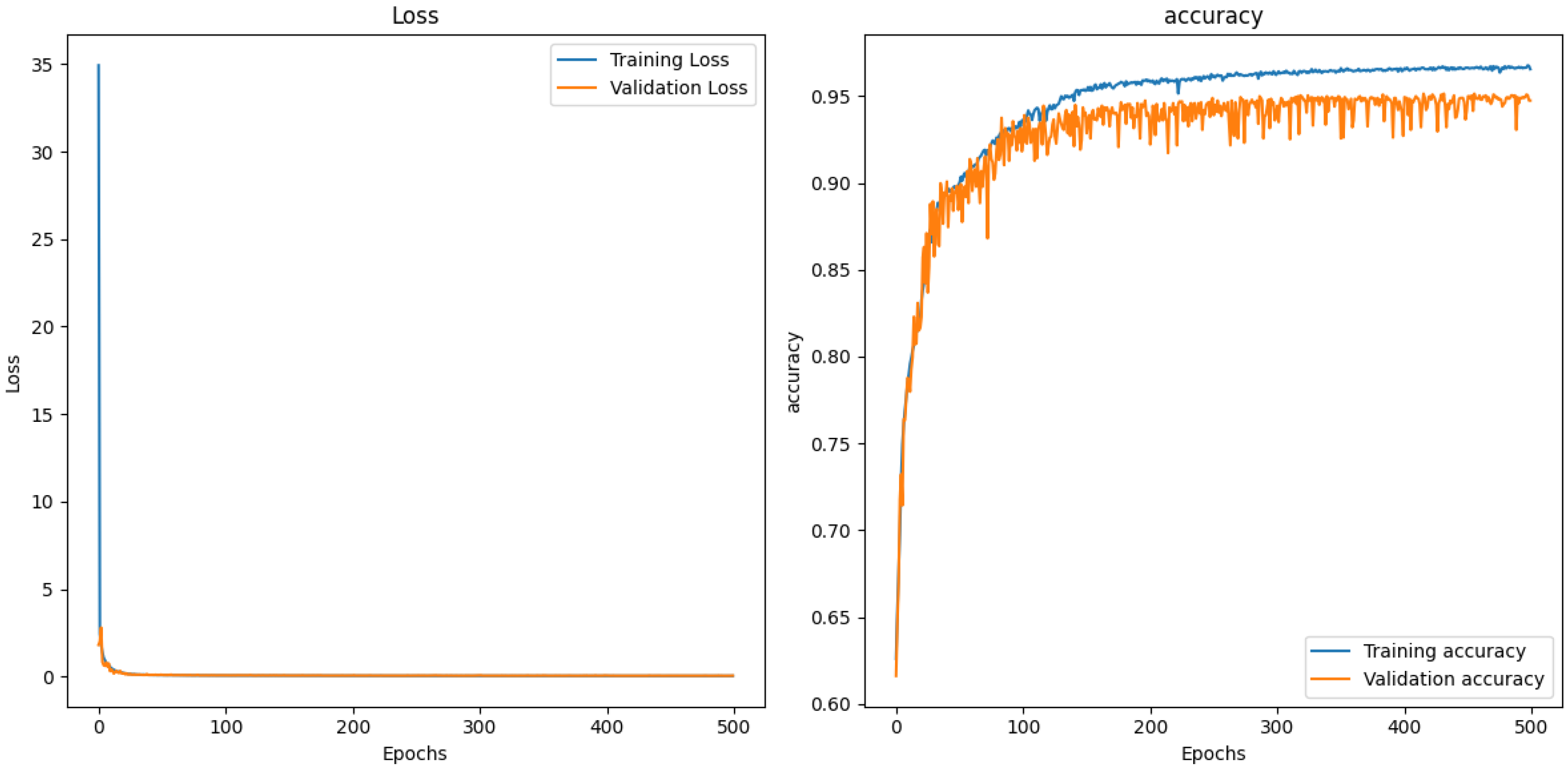
3.4. Network Training Methodology
3.4.1. Optimizer
3.4.2. Loss Function and Classification Accuracy
3.4.3. Similarity Score Function
4. Experiments and Results
4.1. Performance Measures and Experiment Results
4.2. The Traditional Method Classifies and Compares Experimental Results
4.3. Ablation Experiment Analysis
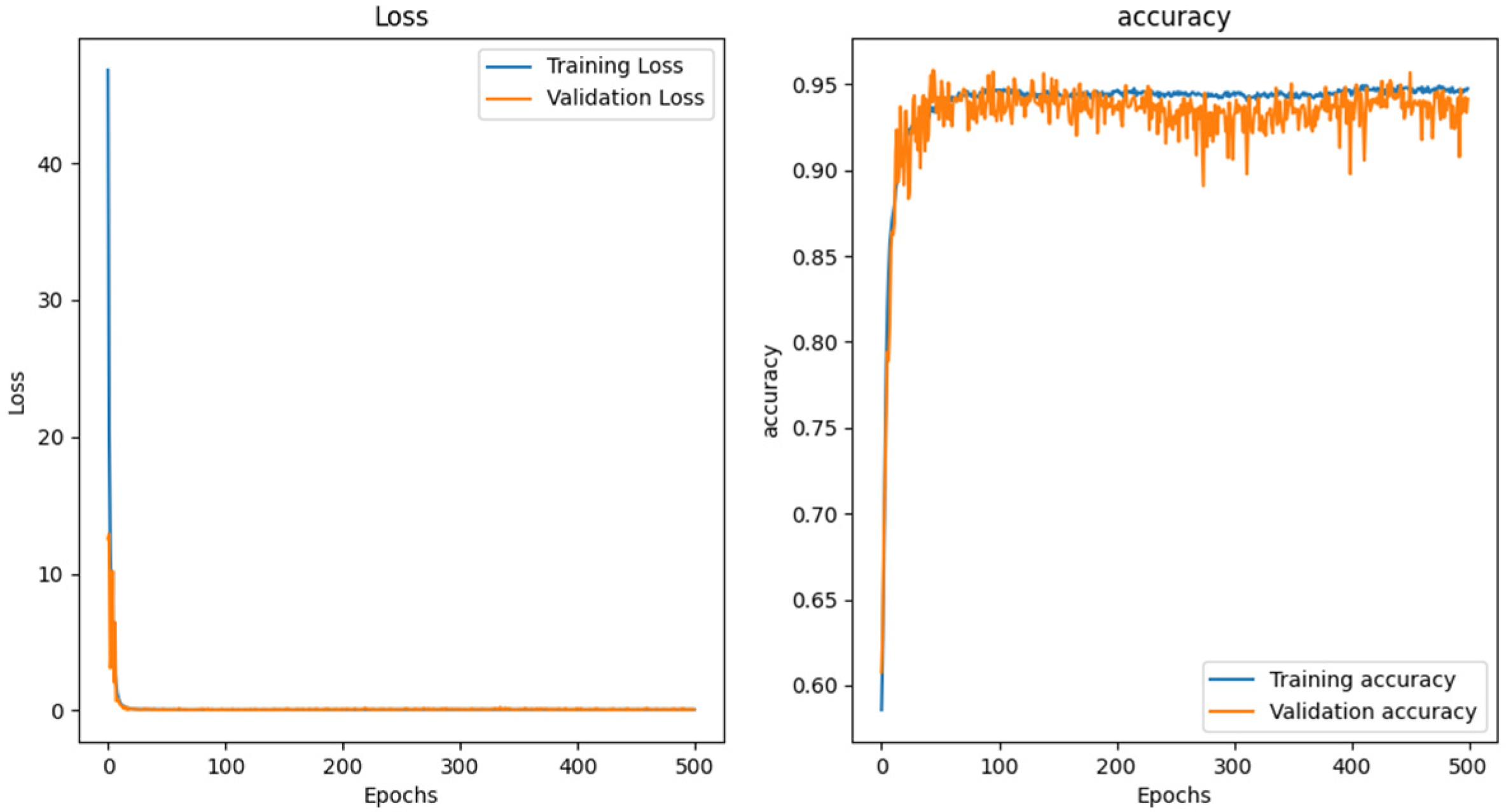
4.3.1. Peak Feature Effectiveness
4.3.2. SCNN Model
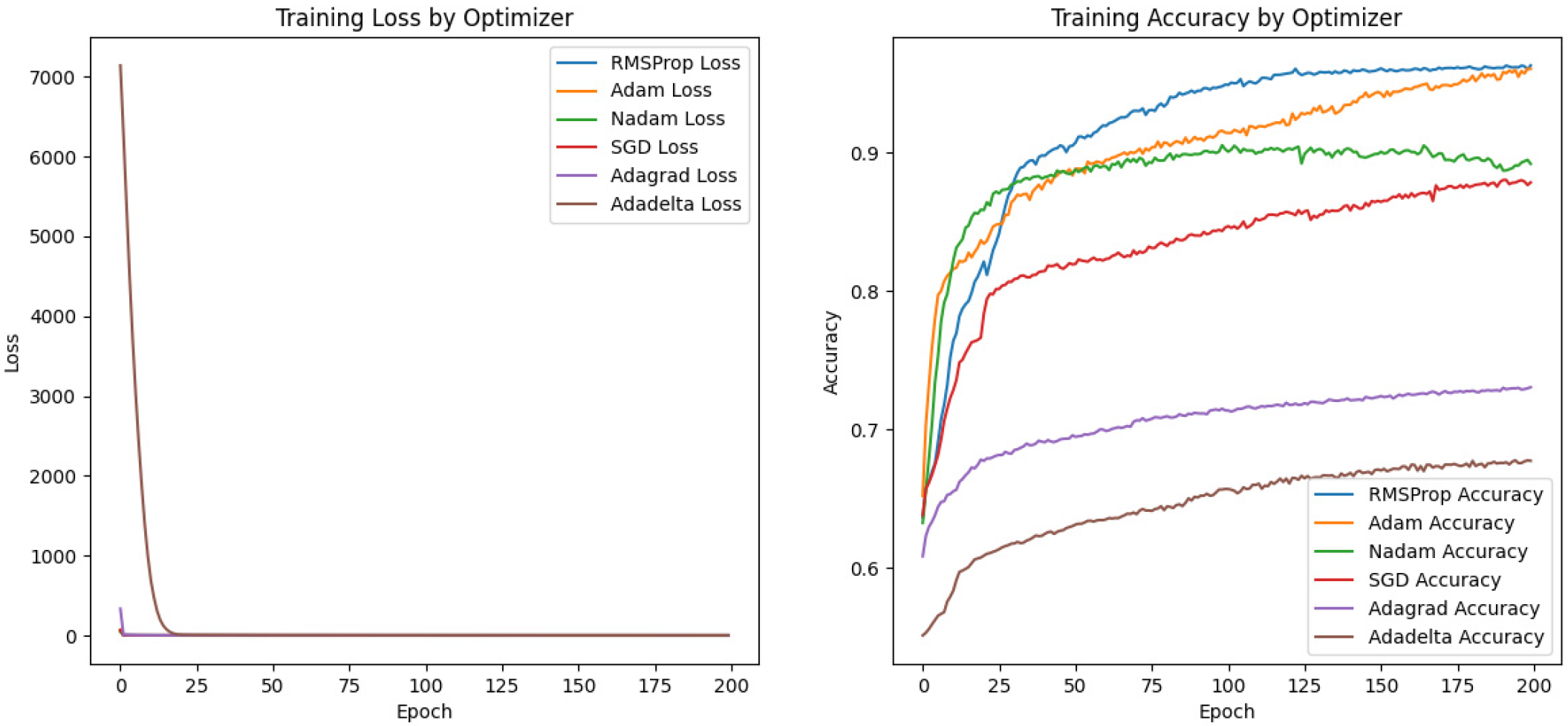
4.3.3. Optimizer Selection
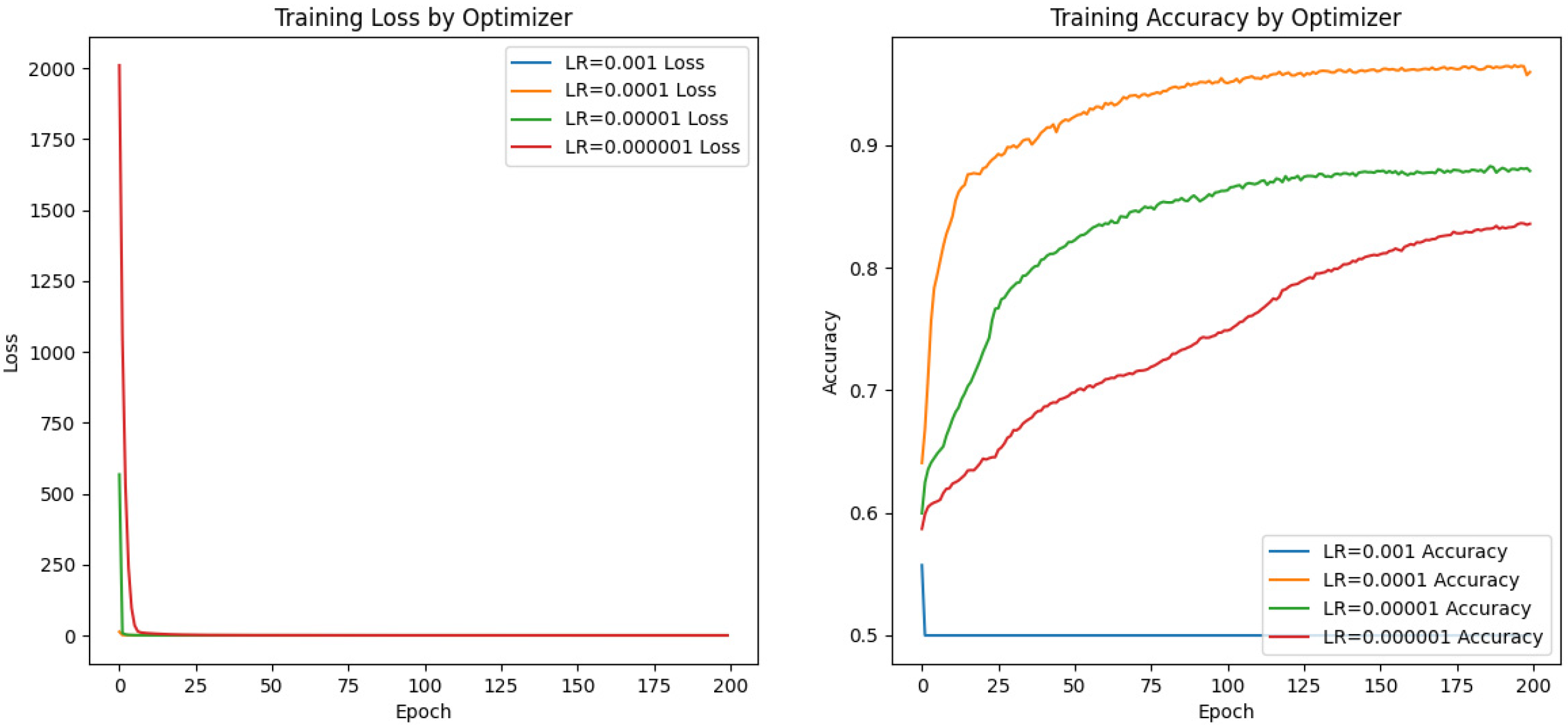
4.3.4. Learning Rate Selection
4.3.5. Running Time
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rozenstein, O.; Puckrin, E.; Adamowski, J. Development of a new approach based on midwave infrared spectroscopy for post-consumer black plastic waste sorting in the recycling industry. Waste Manag. 2017, 68, 38–44. [Google Scholar] [CrossRef] [PubMed]
- Hou, X.; Lv, S.; Chen, Z.; Xiao, F. Applications of Fourier transform infrared spectroscopy technologies on asphalt materials. Measurement 2018, 121, 304–316. [Google Scholar] [CrossRef]
- Ozaki, Y. Infrared Spectroscopy—Mid-infrared, Near-infrared, and Far-infrared/Terahertz Spectroscopy. Anal. Sci. 2021, 37, 1193–1212. [Google Scholar] [CrossRef]
- Jang, H.-D.; Kwon, S.; Nam, H.; Chang, D.E. Semi-Supervised Autoencoder for Chemical Gas Classification with FTIR Spectrum. Sensors 2024, 24, 3601. [Google Scholar] [CrossRef]
- Uddin, M.P.; Mamun, M.A.; Hossain, M.A. PCA-based Feature Reduction for Hyperspectral Remote Sensing Image Classification. IETE Tech. Rev. 2021, 38, 377–396. [Google Scholar] [CrossRef]
- Xia, J.; Bombrun, L.; Adali, T.; Berthoumieu, Y.; Germain, C. Spectral–Spatial Classification of Hyperspectral Images Using ICA and Edge-Preserving Filter via an Ensemble Strategy. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4971–4982. [Google Scholar] [CrossRef]
- Jia, S.; Zhao, Q.; Zhuang, J.; Tang, D.; Long, Y.; Xu, M.; Zhou, J.; Li, Q. Flexible Gabor-Based Superpixel-Level Unsupervised LDA for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 10394–10409. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, T. Three different SVM classification models in Tea Oil FTIR Application Research in Adulteration Detection. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2021; Volume 1748, p. 022037. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kumaravel, A.; Muthu, K.; Deenadayalan, N. A View of Artificial Neural Network Models in Different Application Areas. E3S Web Conf. 2021, 287, 03001. [Google Scholar]
- Li, X.; Li, Z.; Qiu, H.; Hou, G.; Fan, P. An overview of hyperspectral image feature extraction, classification methods and the methods based on small samples. Appl. Spectrosc. Rev. 2021, 58, 367–400. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Zhou, W.; Kamata, S.-I.; Wang, H.; Xue, X. Multiscanning-Based RNN–Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote. Sens. 2023, 61, 1–19. [Google Scholar] [CrossRef]
- Hu, H.; Xu, Z.; Wei, Y.; Wang, T.; Zhao, Y.; Xu, H.; Mao, X.; Huang, L. The Identification of Fritillaria Species Using Hyperspectral Imaging with Enhanced One-Dimensional Convolutional Neural Networks via Attention Mechanism. Foods 2023, 12, 4153. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Lan, Y.; Xie, Y.; Yu, L.; Chen, C.; Wu, Y.; Dai, X. A Spatial–Spectral Transformer for Hyperspectral Image Classification Based on Global Dependencies of Multi-Scale Features. Remote Sens. 2024, 16, 404. [Google Scholar] [CrossRef]
- Jia, S.; Jiang, S.; Lin, Z.; Xu, M.; Sun, W.; Huang, Q.; Zhu, J.; Jia, X. A Semisupervised Siamese Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote. Sens. 2021, 60, 1–17. [Google Scholar] [CrossRef]
- Ondrasovic, M.; Tarabek, P. Siamese Visual Object Tracking: A Survey. IEEE Access 2021, 9, 110149–110172. [Google Scholar] [CrossRef]
- Xu, T.; Feng, Z.; Wu, X.-J.; Kittler, J. Toward Robust Visual Object Tracking With Independent Target-Agnostic Detection and Effective Siamese Cross-Task Interaction. IEEE Trans. Image Process. 2023, 32, 1541–1554. [Google Scholar] [CrossRef]
- Wang, L.; Wang, L.; Wang, Q.; Atkinson, P.M. SSA-SiamNet: Spectral–Spatial-Wise Attention-Based Siamese network for Hyperspectral Image Change Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Melekhov, I.; Kannala, J.; Rahtu, E. Siamese network features for image matching. In Proceedings of the 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016. [Google Scholar]
- Li, Y.; Chen, C.L.P.; Zhang, T. A Survey on Siamese network: Methodologies, Applications, and Opportunities. IEEE Trans. Artif. Intell. 2022, 3, 994–1014. [Google Scholar] [CrossRef]
- Huang, L.; Chen, Y. Dual-Path Siamese CNN for Hyperspectral Image Classification With Limited Training Samples. IEEE Geosci. Remote Sens. Lett. 2021, 518–522. [Google Scholar] [CrossRef]
- Miao, J.; Wang, B.; Wu, X.; Zhang, L.; Hu, B.; Zhang, J.Q. Deep Feature Extraction Based on Siamese network and Auto-Encoder for Hyperspectral Image Classification. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019. [Google Scholar]
- Nanni, L.; Minchio, G.; Brahnam, S.; Maguolo, G.; Lumini, A. Experiments of Image Classification Using Dissimilarity Spaces Built with Siamese Networks. Sensors 2021, 21, 1573. [Google Scholar] [CrossRef]
- Liu, B.; Yu, X.; Zhang, P.; Yu, A.; Fu, Q.; Wei, X. Supervised Deep Feature Extraction for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1909–1921. [Google Scholar] [CrossRef]
- Rao, M.; Tang, P.; Zhang, Z. A Developed Siamese CNN with 3D Adaptive Spatial-Spectral Pyramid Pooling for Hyperspectral Image Classification. Remote Sens. 2020, 12, 1964. [Google Scholar] [CrossRef]
- Kruse, F.A.; Kierein-Young, K.S.; Boardman, J.W. Mineral mapping at Cuprite, Nevada with a 63-channel imaging spectrometer. Photogramm. Eng. Remote Sens. 1990, 56, 83–92. [Google Scholar]
- Bromley, J.; Bentz, J.W.; Bottou, L.; Guyon, I.; LeCun, Y.; Moore, C.; Sackinger, E.; Shah, R. Signature Verification using a "Siamese" Time Delay Neural Network. Int. J. Pattern Recognit. Artif. Intell. 1993, 7, 669–688. [Google Scholar] [CrossRef]
- Thenkabail, P.; GangadharaRao, P.; Biggs, T.; Krishna, M.; Turral, H. Spectral Matching Techniques to Determine Historical Land-use/Land-cover (LULC) and Irrigated Areas Using Time-series 0.1-degree AVHRR Pathfinder Datasets. Photogramm. Eng. Remote Sens. 2007, 73, 1029–1040. [Google Scholar]
- Sohn, K. Improved deep metric learning with multi-class N-pair loss objective. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2016; pp. 1857–1865. [Google Scholar]
- Homan, D.C.; Cohen, M.H.; Hovatta, T.; Kellermann, K.I.; Kovalev, Y.Y.; Lister, M.L.; Popkov, A.V.; Pushkarev, A.B.; Ros, E.; Savolainen, T. MOJAVE. XIX. Brightness Temperatures and Intrinsic Properties of Blazar Jets. Astrophys. J. 2021, 923, 67. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, J.; Jie, D. The research of near infrared spectral peak detection methods in big data era. In Proceedings of the 2016 ASABE International Meeting, Orlando, FL, USA, 17–20 July 2016. [Google Scholar]
- Tieleman, T.; Hinton, G. Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude. Coursera Neural Netw. Mach. Learn. 2012, 4, 26–31. [Google Scholar]





| Name | Measurement Pattern | Spectral Resolution (cm−1) | Spectral Measurement Range (μm) | Full Field of View Angle |
|---|---|---|---|---|
| EM27 | Active/Passive | Active: 0.5/1 Passive: 0.5/1/4 | 2.5~12 | 30 mrad (no telescope) (1.7°) |
| Telemetry Fourier Transform Infrared Spectrometer | Passive | 1 | 2.5~12 | 1.5° |
| Aero-Engine Serial Number | Environmental Temperature | Environmental Humidity | Detection Distance |
|---|---|---|---|
| Engine 1 (Turbofan) | 19 °C | 58.5% Rh | 5 m |
| Engine 2 (Turbofan) | 16 °C | 67% Rh | 5 m |
| Engine 3 (Turbojet) | 14 °C | 40% Rh | 5 m |
| Engine 4 (Turbojet UAV) | 30 °C | 43.5% Rh | 11.8 m |
| Engine 5 (Turbojet UAV with propeller at tail) | 20 °C | 71.5% Rh | 5 m |
| Engine 5 (Turbojet) | 19 °C | 73.5% Rh | 10 m |
| Number | Type | Number of Data Pieces | Number of Error Data | Full Band Data Volume | Mid-Infrared Range Data Volume |
|---|---|---|---|---|---|
| 1 | Engine 1 (Turbojet UAV) | 193 | 0 | 16,384 | 7464 |
| 2 | Engine 2 (Turbojet UAV with propeller at tail) | 48 | 0 | 16,384 | 7464 |
| 3 | Engine 3 (Turbojet) | 202 | 3 | 16,384 | 7464 |
| 4 | Engine 4 (Turbofan) | 792 | 17 | 16,384 | 7464 |
| 5 | Engine 5 (Turbofan) | 258 | 2 | 16,384 | 7464 |
| 6 | Engine 6 (Turbojet) | 384 | 4 | 16,384 | 7464 |
| Forecast Results | |||
|---|---|---|---|
| Positive Samples | Negative Samples | ||
| Real results | Positive samples | TP | TN |
| Negative samples | FP | FN | |
| Methods | Parameter Settings |
|---|---|
| PF-SCNN | Conv1D (32, 3), Conv1D (64, 3), Conv1D (128, 3), activation = ‘relu’ |
| MaxPooling1D (2) (x) | |
| Dense (128, activation = ‘relu’) | |
| Optimizers = RMSProp, (learning_rate = 0.0001) | |
| Loss = contrastive_loss, metrics = [accuracy] | |
| Epochs = 500 |
| Evaluation Criterion | Accuracy | Precision | Recall | Confusion Matrix | F1-Score |
|---|---|---|---|---|---|
| Data set | 99.46% | 99.77% | 99.56% | [27 0 0 0 0 0] [ 0 72 0 0 0 0] [ 0 0 21 0 0 0] [ 0 1 0 37 0 0] [ 0 0 0 0 20 0] [ 0 0 0 0 0 6] | 99.66% |
| Characteristic Peak Type | Emission Peak (cm−1) | Absorption Peak (cm−1) | ||
|---|---|---|---|---|
| Standard feature peak value | 2350 | 2390 | 720 | 667 |
| Feature peak range value | 2350.5–2348 | 2377–2392 | 722–718 | 666.7–670.5 |
| Methods | Parameter Settings |
|---|---|
| SVM | decision_function_shape = ‘ovr’, kernel = ‘rbf’ |
| XGBoost | objective = ‘multi:softmax’, num_classes = num_classes |
| CatBoost | loss_function = ‘MultiClass’ |
| Adaboost | n_estimators = 200 |
| Random Forest | n_estimators = 300 |
| LightGBM | objective’: ‘multiclass’, ‘num_class’: num_classes |
| Neural Network | hidden_layer_sizes = (100), activation = ‘relu’, solver = ‘adam’, max_iter = 200 |
| Evaluation Criterion | Accuracy | Precision Score | Recall | Confusion Matrix | F1-Score | |
|---|---|---|---|---|---|---|
| Classification Methods | ||||||
| CO2 feature vector + SVM | 59.78% | 44.15% | 47.67% | [ 8 0 3 0 0 0] [ 0 3 0 0 0 0] [ 9 1 12 0 0 0] [ 0 3 1 84 22 33] [ 0 0 0 0 0 0] [ 0 0 0 0 0 0] | 42.38% | |
| CO2 feature vector + XGBoost | 94.97% | 92.44% | 93.59% | [15 0 3 0 0 0] [ 0 7 0 0 0 0] [ 2 0 13 0 0 0] [ 0 0 0 83 3 0] [ 0 0 0 1 19 0] [ 0 0 0 0 0 33] | 92.95% | |
| CO2 feature vector + CatBoost | 94.41% | 90.35% | 93.52% | [15 0 2 0 0 0] [ 0 6 0 0 0 0] [ 2 0 14 0 0 0] [ 0 0 0 83 4 0] [ 0 1 0 1 18 0] [ 0 0 0 0 0 33] | 91.81% | |
| CO2 feature vector + AdaBoost | 79.89% | 63.66% | 71.49% | [17 5 6 0 0 0] [ 0 2 0 0 0 0] [ 0 0 10 0 0 0] [ 0 0 0 84 18 3] [ 0 0 0 0 0 0] [ 0 0 0 0 4 30] | 62.56% | |
| CO2 feature vector + Random Forest | 94.41% | 91.40% | 92.70% | [15 0 4 0 0 0] [ 0 7 0 0 0 0] [ 2 0 12 0 0 0] [ 0 0 0 83 3 0] [ 0 0 0 1 19 0] [ 0 0 0 0 0 33] | 91.91% | |
| CO2 feature vector + LightGBM | 94.41% | 90.68% | 92.40% | [14 0 2 0 0 0] [ 0 6 0 0 0 0] [ 3 0 14 0 0 0] [ 0 0 0 82 2 0] [ 0 1 0 2 20 0] [ 0 0 0 0 0 33] | 91.42% | |
| CO2 feature vector + Neural Networks | 84.92% | 76.79% | 76.57% | [17 0 2 0 0 0] [ 0 6 0 0 0 0] [ 0 0 12 0 0 0] [ 0 0 2 84 18 0] [ 0 1 0 0 0 0] [ 0 0 0 0 4 33] | 76.02% | |
| Methods | Accuracy | Precision | Recall | Confusion Matrix | F1-Score | Running Time |
|---|---|---|---|---|---|---|
| Peaks + SVM | 58.15 | 48.09 | 43.58 | [ 0 0 0 0 0 0] [13 42 0 0 0 0] [ 0 0 20 0 13 6] [14 30 0 38 0 0] [ 0 0 1 0 7 0] [ 0 0 0 0 0 0] | 41.02 | 0.54 |
| Peaks + XGBoost | 98.91 | 96.78 | 99.01 | [27 0 0 0 0 0] [ 0 72 0 1 0 0] [ 0 0 21 0 0 1] [ 0 0 0 37 0 0] [ 0 0 0 0 20 0] [ 0 0 0 0 0 5] | 97.76 | 1.27 |
| Evaluation Criterion | Accuracy | Precision | Recall | Confusion Matrix | F1-Score |
|---|---|---|---|---|---|
| Data set | 99.46% | 99.24% | 99.56% | [27 0 0 0 0 0] [ 0 72 0 0 0 0] [ 0 0 21 0 0 0] [ 0 0 1 37 0 0] [ 0 0 0 0 20 0] [ 0 0 0 0 0 6] | 99.39% |
| Methods | Parameter Settings |
|---|---|
| RMSProp | learning rate = 0.0001, clipvalue = 1.0 |
| Adam | learning rate = 0.0001, clipvalue = 1.0 |
| Nadam | learning rate = 0.0001, clipvalue = 1.0 |
| SGD | learning rate = 0.0001, clipvalue = 1.0 |
| Adagrad | learning rate = 0.0001, clipvalue = 1.0 |
| Adadelta | learning rate = 0.0001, clipvalue = 1.0 |
| Optimizers | Prediction Accuracy | Training Time/s |
|---|---|---|
| RMSProp | 96% | 1180.96 |
| Adam | 96% | 1014.82 |
| Nadam | 89% | 1523.14 |
| SGD | 88% | 1101.65 |
| Adagrad | 73% | 1021.90 |
| Adadelta | 68% | 991.90 |
| Learning Rate | Prediction Accuracy | Training Time/s |
|---|---|---|
| 0.001 | 0.50 | 1283.49 |
| 0.0001 | 0.96 | 1252.83 |
| 0.00001 | 0.88 | 1171.39 |
| 0.000001 | 0.84 | 1193.72 |
| Methods | Prediction Time |
|---|---|
| PF-SCNN | 71 s Each data; 3:44:17 total |
| SCNN | 79 s Each data; 4:30:45.78 total |
| CO2 feature vector + SVM | 0.12 s |
| CO2 feature vector + XGBoost | 0.30 s |
| CO2 feature vector + CatBoost | 4.74 s |
| CO2 feature vector + AdaBoost | 0.39 s |
| CO2 feature vector + Random Forest | 0.56 s |
| CO2 feature vector + LightGBM | 0.44 s |
| CO2 feature vector + Neural Networks | 0.85 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, S.; Han, W.; Kang, Z.; Luo, F.; Liao, Y.; Li, Z. A Peak-Finding Siamese Convolutional Neural Network (PF-SCNN) for Aero-Engine Hot Jet FT-IR Spectrum Classification. Aerospace 2024, 11, 703. https://doi.org/10.3390/aerospace11090703
Du S, Han W, Kang Z, Luo F, Liao Y, Li Z. A Peak-Finding Siamese Convolutional Neural Network (PF-SCNN) for Aero-Engine Hot Jet FT-IR Spectrum Classification. Aerospace. 2024; 11(9):703. https://doi.org/10.3390/aerospace11090703
Chicago/Turabian StyleDu, Shuhan, Wei Han, Zhenping Kang, Fengkun Luo, Yurong Liao, and Zhaoming Li. 2024. "A Peak-Finding Siamese Convolutional Neural Network (PF-SCNN) for Aero-Engine Hot Jet FT-IR Spectrum Classification" Aerospace 11, no. 9: 703. https://doi.org/10.3390/aerospace11090703
APA StyleDu, S., Han, W., Kang, Z., Luo, F., Liao, Y., & Li, Z. (2024). A Peak-Finding Siamese Convolutional Neural Network (PF-SCNN) for Aero-Engine Hot Jet FT-IR Spectrum Classification. Aerospace, 11(9), 703. https://doi.org/10.3390/aerospace11090703






