Impact of Pitch Angle Limitation on E-Sail Interplanetary Transfers
Abstract
:1. Introduction
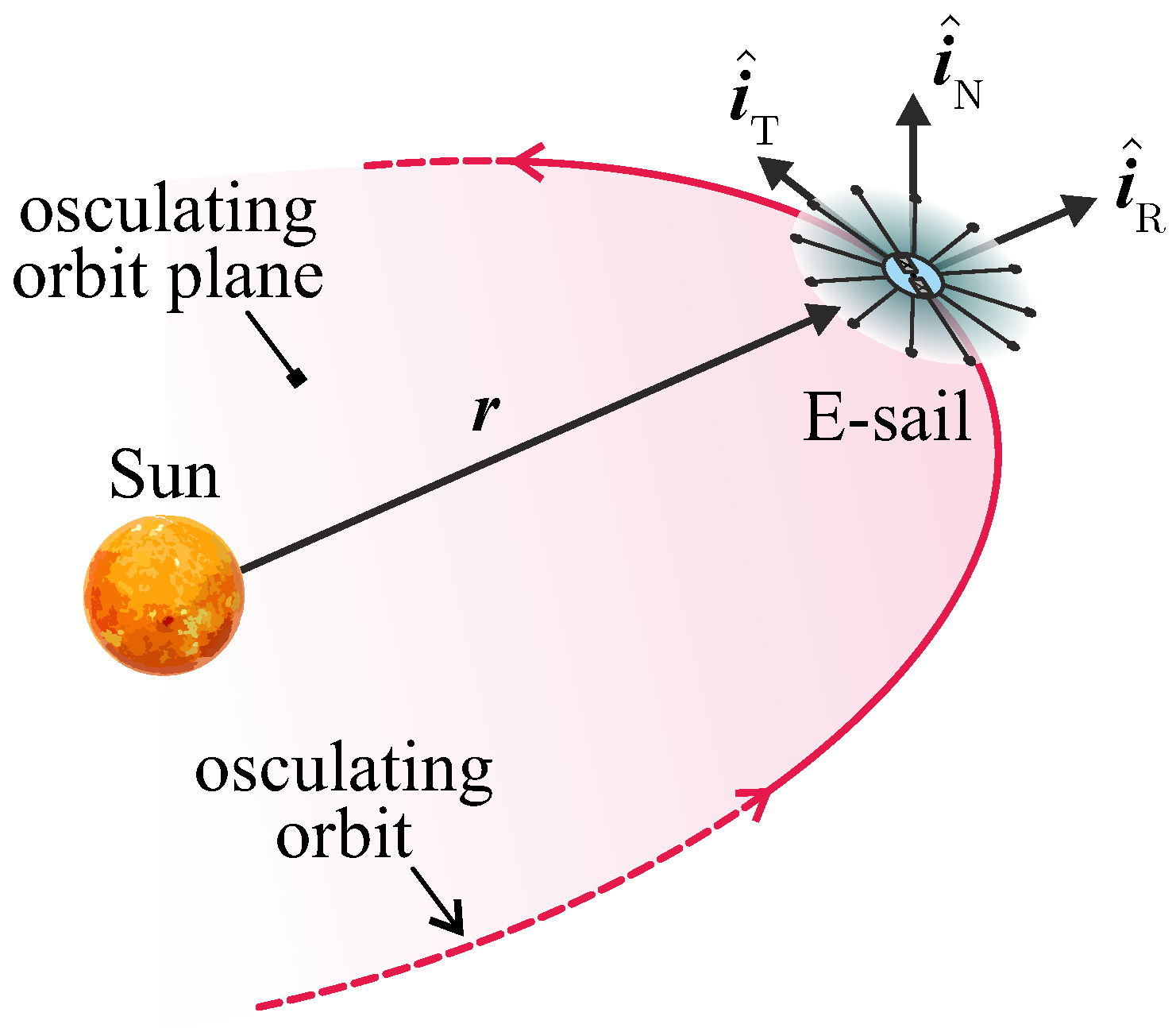
2. Mathematical Preliminaries and Thrust Vector Analytical Model
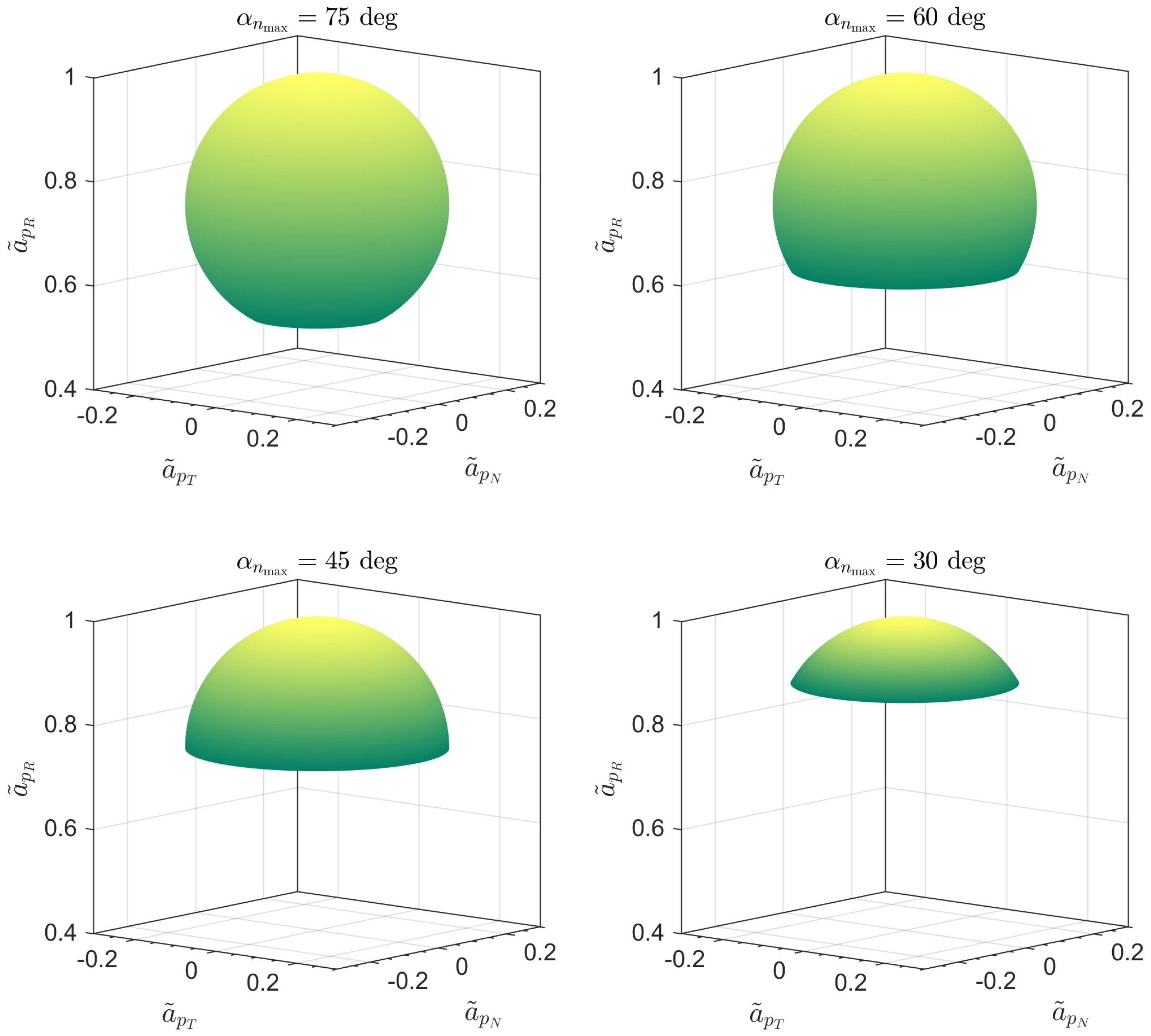
2.1. Analytical Model of the Propulsive Acceleration Vector
2.2. Brief Notes on Trajectory Optimization in Presence of Pitch Angle Constraint
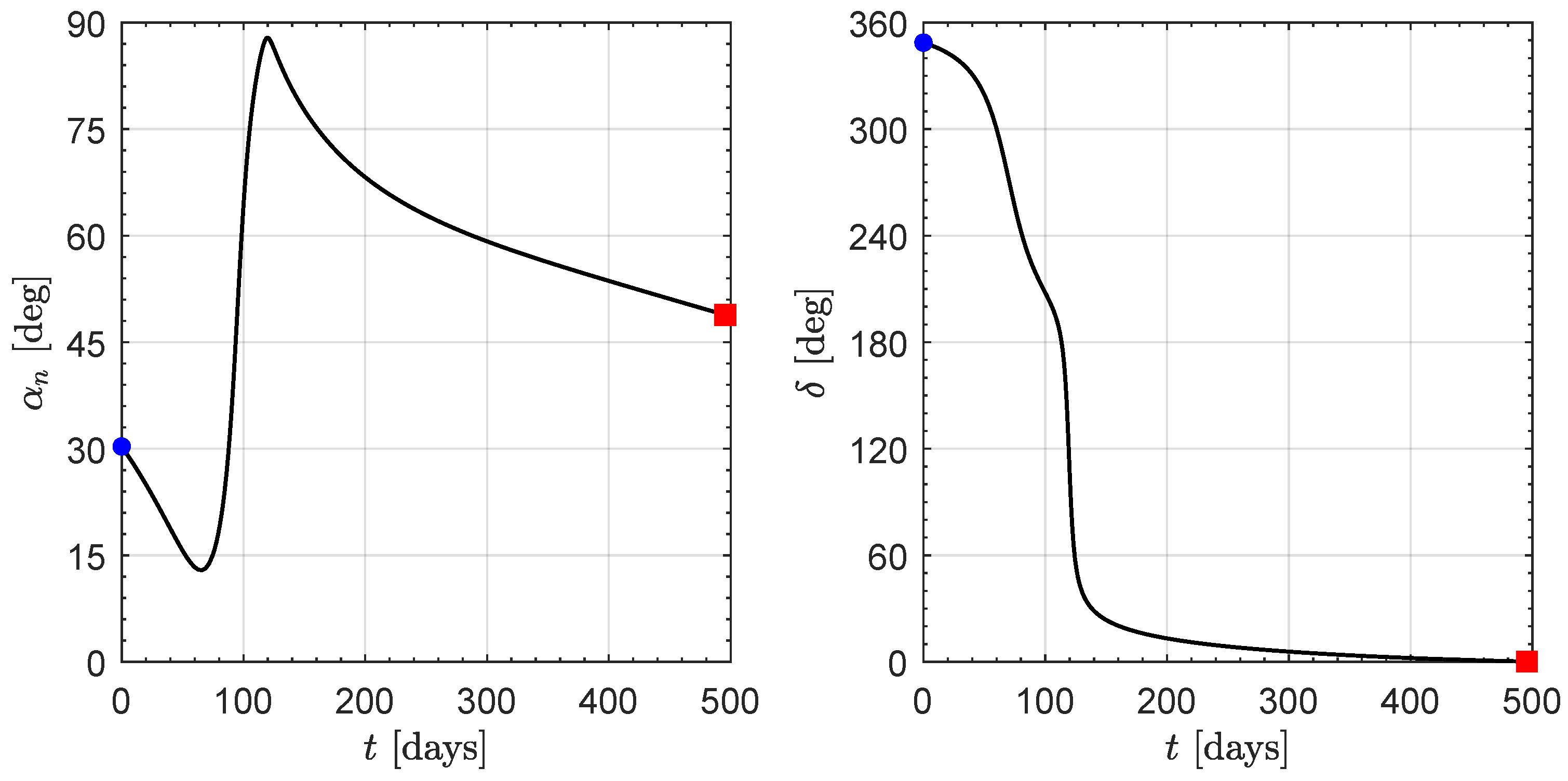
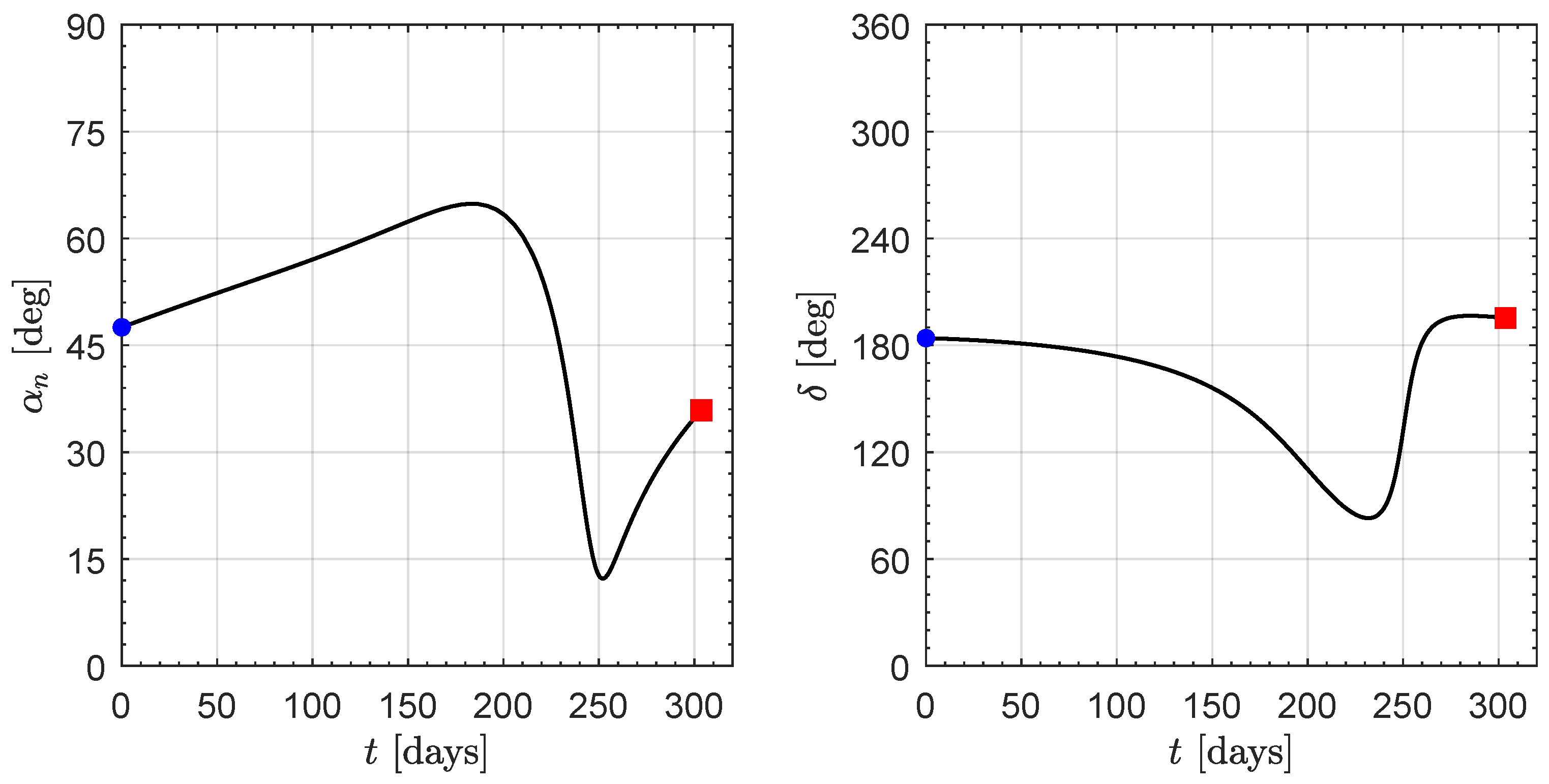
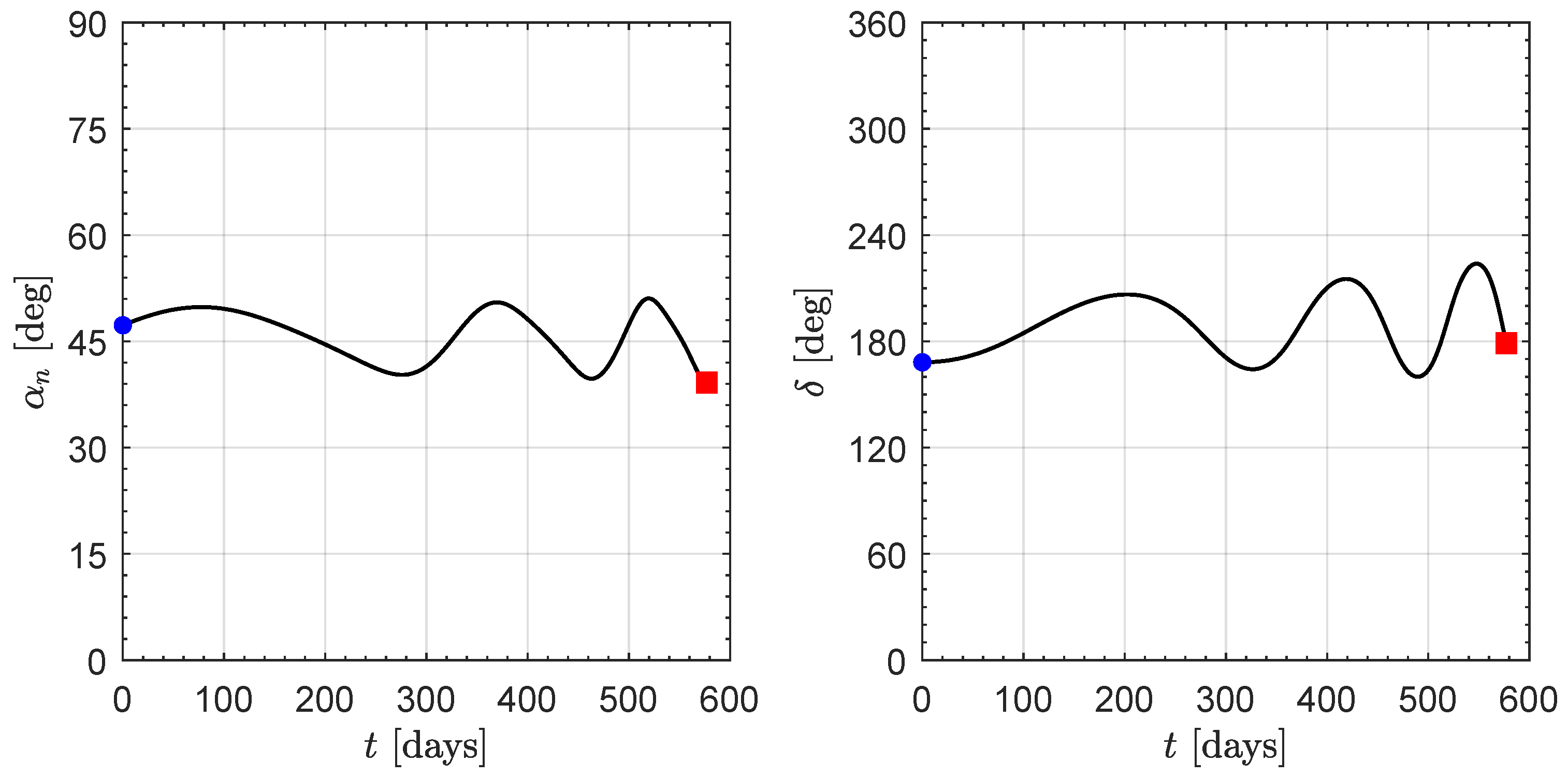
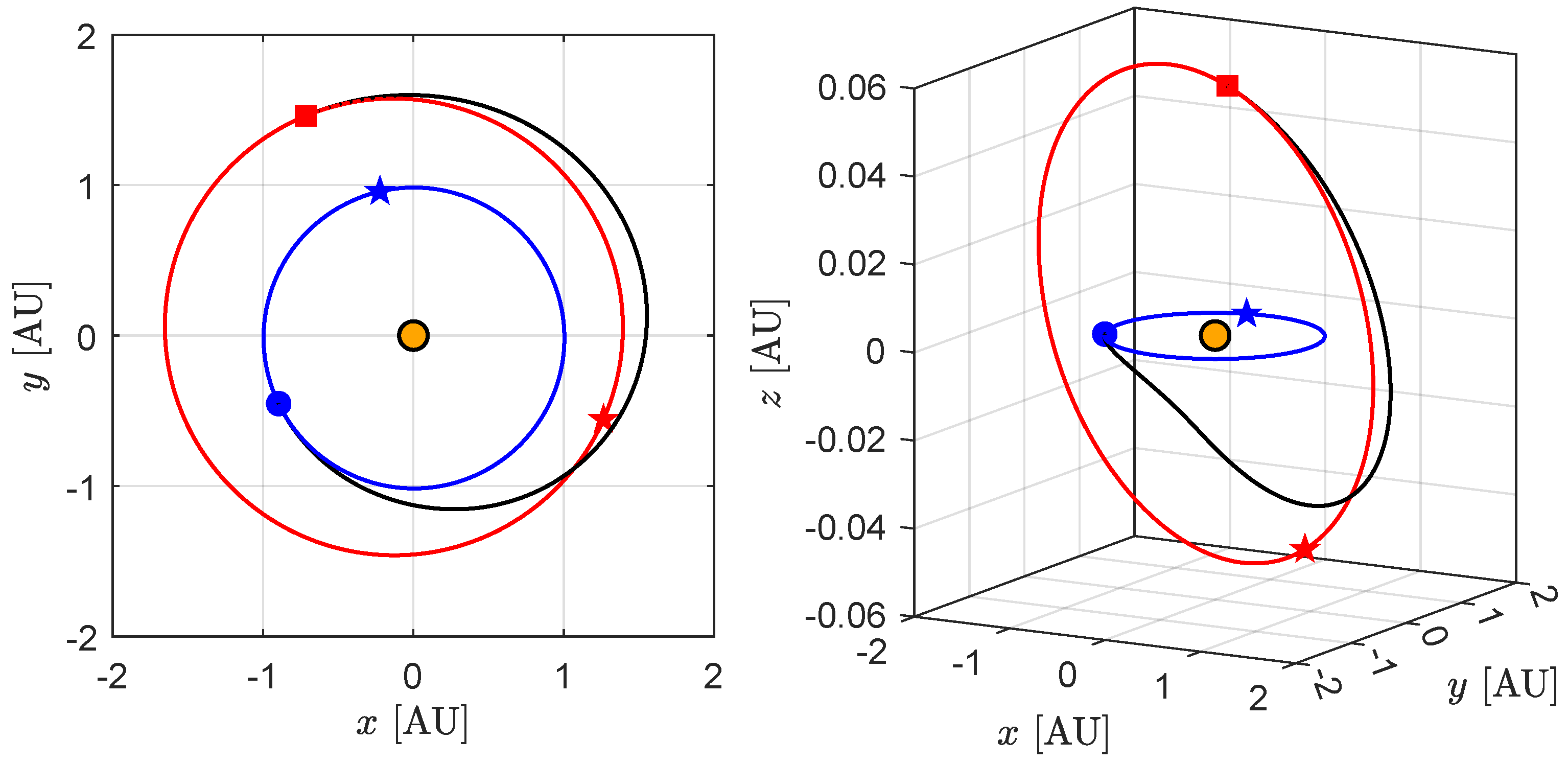
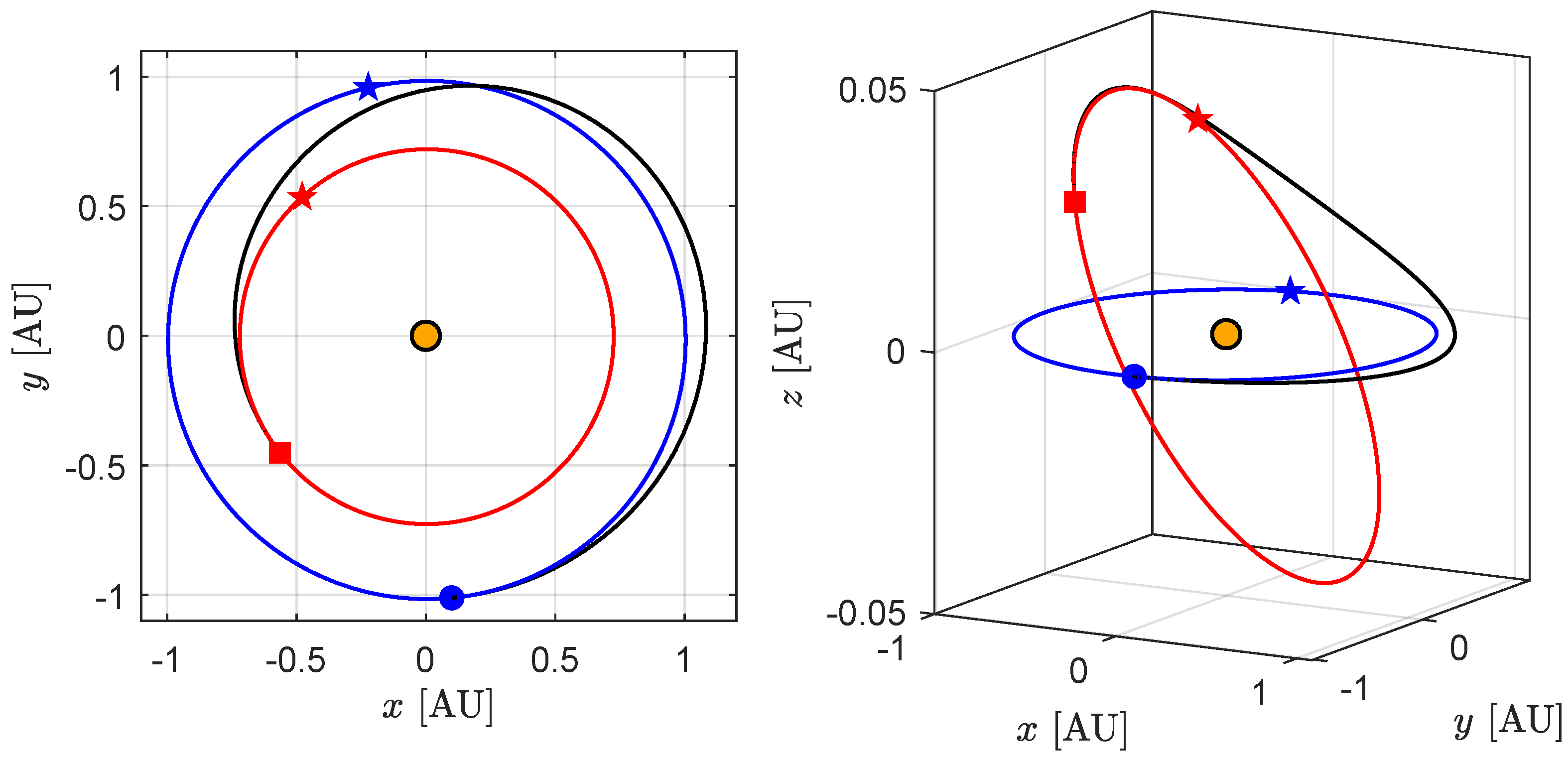
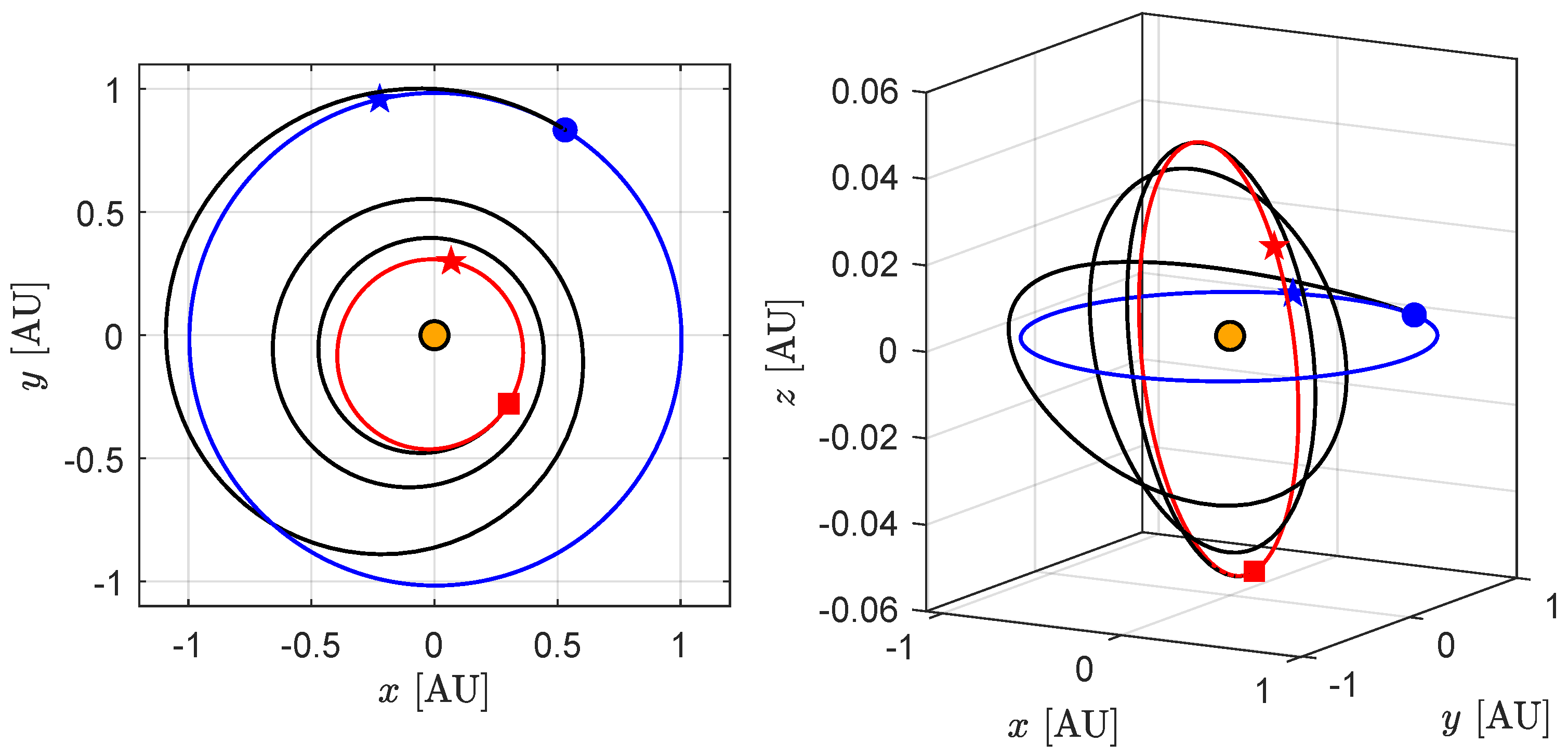
3. Orbital Simulations and Numerical Results
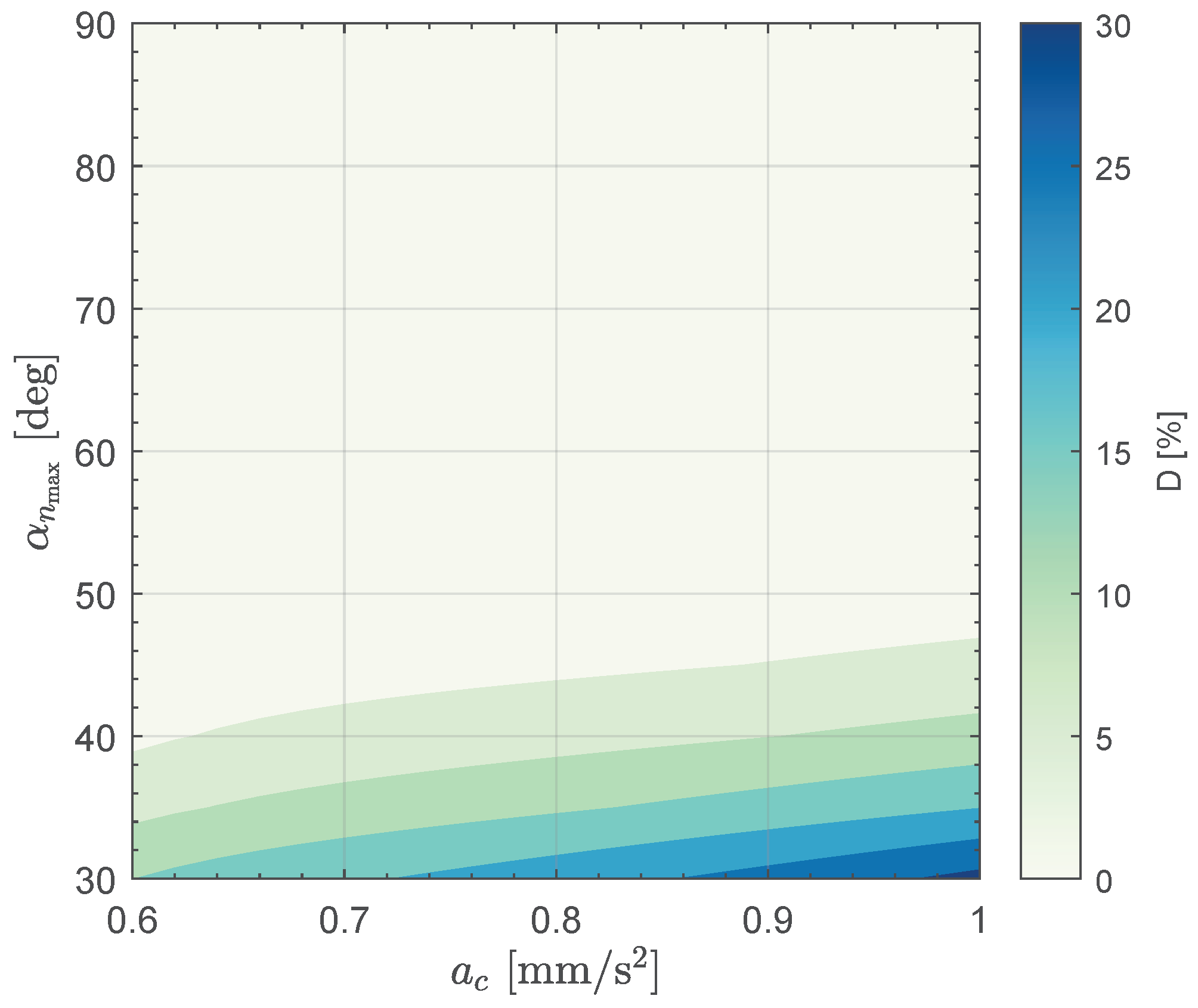
Effect of the Value of the Characteristic Acceleration
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Janhunen, P.; Toivanen, P.K.; Polkko, J.; Merikallio, S.; Salminen, P.; Haeggström, E.; Seppänen, H.; Kurppa, R.; Ukkonen, J.; Kiprich, S.; et al. Electric solar wind sail: Toward test missions. Rev. Sci. Instrum. 2010, 81, 111301. [Google Scholar] [CrossRef]
- Sanmartin, J.R. A review of electrodynamic tethers for science applications. Plasma Sources Sci. Technol. 2010, 19, 034022. [Google Scholar] [CrossRef]
- Seppänen, H.; Rauhala, T.; Kiprich, S.; Ukkonen, J.; Simonsson, M.; Kurppa, R.; Janhunen, P.; Hæggström, E. One kilometer (1 km) electric solar wind sail tether produced automatically. Rev. Sci. Instrum. 2013, 84, 095102. [Google Scholar] [CrossRef] [PubMed]
- Rauhala, T.; Seppänen, H.; Ukkonen, J.; Kiprich, S.; Maconi, G.; Janhunen, P.; Hæggström, E. Automatic 4-wire Heytether production for the electric solar wind sail. In Proceedings of the International Microelectronics Assembly and Packing Society Topical Workshop and Tabletop Exhibition on Wire Bonding, San Jose, CA, USA, 22–23 January 2013. [Google Scholar]
- Forward, R.L.; Hoyt, R.P. Failsafe multiline Hoytether lifetimes. In Proceedings of the 31st Joint Propulsion Conference and Exhibit, San Diego, CA, USA, 10–12 July 1995. [Google Scholar] [CrossRef]
- Forward, R.L.; Hoyt, R.P.; Uphoff, C.W. Terminator Tether: A spacecraft deorbit device. J. Spacecr. Rockets 2000, 37, 187–196. [Google Scholar] [CrossRef]
- Fulton, J.; Schaub, H. Dynamics and control of the flexible electrostatic sail deployment. In Proceedings of the 26th AAS/AIAA Space Flight Mechanics Meeting, Napa, CA, USA, 14–18 February 2016. [Google Scholar]
- Fulton, J.; Schaub, H. Fixed-axis electric sail deployment dynamics analysis using hub-mounted momentum control. Acta Astronaut. 2018, 144, 160–170. [Google Scholar] [CrossRef]
- Li, G.; Zhu, Z.H.; Du, C. Stability and control of radial deployment of electric solar wind sail. Nonlinear Dyn. 2021, 103, 481–501. [Google Scholar] [CrossRef]
- Toivanen, P.K.; Janhunen, P. Electric Solar Wind Sail: Deployment, Long-Term Dynamics, and Control Hardware Requirements. In Proceedings of the Advances in Solar Sailing, Glasgow, UK, 11–13 June 2013; Macdonald, M., Ed.; Springer: Chichester, UK, 2014; pp. 977–987. [Google Scholar] [CrossRef]
- Janhunen, P.; Quarta, A.A.; Mengali, G. Electric solar wind sail mass budget model. Geosci. Instrum. Methods Data Syst. 2013, 2, 85–95. [Google Scholar] [CrossRef]
- Boni, L.; Bassetto, M.; Mengali, G.; Quarta, A.A. Electric sail static structural analysis with Finite Element approach. Acta Astronaut. 2020, 175, 510–516. [Google Scholar] [CrossRef]
- Pacheco-Ramos, G.; Garcia-Vallejo, D.; Vazquez, R. Formulation of a high-fidelity multibody dynamical model for an electric solar wind sail. Int. J. Mech. Sci. 2023, 256, 108466. [Google Scholar] [CrossRef]
- Janhunen, P. Electric sail for spacecraft propulsion. J. Propuls. Power 2004, 20, 763–764. [Google Scholar] [CrossRef]
- Janhunen, P.; Sandroos, A. Simulation study of solar wind push on a charged wire: Basis of solar wind electric sail propulsion. Ann. Geophys. 2007, 25, 755–767. [Google Scholar] [CrossRef]
- Bassetto, M.; Niccolai, L.; Quarta, A.A.; Mengali, G. A comprehensive review of Electric Solar Wind Sail concept and its applications. Prog. Aerosp. Sci. 2022, 128, 100768. [Google Scholar] [CrossRef]
- Slavinskis, A.; Janhunen, P. Advances in CubeSat Sails and Tethers. 2023. Available online: https://www.mdpi.com/journal/aerospace/special_issues/2319OV36DR (accessed on 28 April 2024).
- Iakubivskyi, I.; Ehrpais, H.; Dalbins, J.; Oro, E.; Kulu, E.; Kütt, J.; Janhunen, P.; Slavinskis, A.; Ilbis, E.; Ploom, I.; et al. ESTCube-2 mission analysis: Plasma brake experiment for deorbiting. In Proceedings of the 67th International Astronautical Congress, Guadalajara, Mexico, 26–30 September 2016. [Google Scholar]
- Ofodile, I.; Kutt, J.; Kivastik, J.; Nigol, M.K.; Parelo, A.; Ilbis, E.; Ehrpais, H.; Slavinskis, A. ESTCube-2 Attitude Determination and Control: Step Towards Interplanetary CubeSats. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019. [Google Scholar] [CrossRef]
- Dalbins, J.; Allaje, K.; Iakubivskyi, I.; Kivastik, J.; Komarovskis, R.O.; Plans, M.; Sünter, I.; Teras, H.; Ehrpais, H.; Ilbis, E.; et al. ESTCube-2: The Experience of Developing a Highly Integrated CubeSat Platform. In Proceedings of the 2022 IEEE Aerospace Conference (AERO), Big Sky, MT, USA, 5–12 March 2022; pp. 1–16. [Google Scholar] [CrossRef]
- Kulu, E.; Slavinskis, A.; Kvell, U.; Pajusalu, M.; Kuuste, H.; Sünter, I.; Ilbis, E.; Eenmäe, T.; Laizans, K.; Vahter, A.; et al. ESTCube-1 nanosatellite for electric solar wind sail demonstration in low Earth Orbit. In Proceedings of the 64th International Astronautical Congress, Beijing, China, 23–27 September 2013. [Google Scholar]
- Lätt, S.; Slavinskis, A.; Ilbis, E.; Kvell, U.; Voormansik, K.; Kulu, E.; Pajusalu, M.; Kuuste, H.; Sünter, I.; Eenmäe, T.; et al. ESTCube-1 nanosatellite for electric solar wind sail in-orbit technology demonstration. Proc. Est. Acad. Sci. 2014, 63, 200–209. [Google Scholar] [CrossRef]
- Slavinskis, A.; Pajusalu, M.; Kuuste, H.; Ilbis, E.; Eenmäe, T.; Sünter, I.; Laizans, K.; Ehrpais, H.; Liias, P.; Kulu, E.; et al. ESTCube-1 in-orbit experience and lessons learned. IEEE Aerosp. Electron. Syst. Mag. 2015, 30, 12–22. [Google Scholar] [CrossRef]
- Praks, J.; Mughal, M.R.; Vainio, R.; Janhunen, P.; Envall, J.; Oleynik, P.; Näsilä, A.; Leppinen, H.; Niemelä, P.; Slavinskis, A.; et al. Aalto-1, multi-payload CubeSat: Design, integration and launch. Acta Astronaut. 2021, 187, 370–383. [Google Scholar] [CrossRef]
- Mughal, M.R.; Praks, J.; Vainio, R.; Janhunen, P.; Envall, J.; Näsilä, A.; Oleynik, P.; Niemelä, P.; Nyman, S.; Slavinskis, A.; et al. Aalto-1, multi-payload CubeSat: In-orbit results and lessons learned. Acta Astronaut. 2021, 187, 557–568. [Google Scholar] [CrossRef]
- Pascoa, J.C.; Teixeira, O.; Filipe, G. A Review of Propulsion Systems for CubeSats. In Proceedings of the ASME 2018 International Mechanical Engineering Congress and Exposition, Pittsburgh, PA, USA, 9–15 November 2018. [Google Scholar] [CrossRef]
- Francisco, C.; Henriques, R.; Barbosa, S. A Review on CubeSat Missions for Ionospheric Science. Aerospace 2023, 10, 622. [Google Scholar] [CrossRef]
- O’Reilly, D.; Herdrich, G.; Kavanagh, D.F. Electric Propulsion Methods for Small Satellites: A Review. Aerospace 2021, 8, 22. [Google Scholar] [CrossRef]
- Palos, M.F.; Janhunen, P.; Toivanen, P.; Tajmar, M.; Iakubivskyi, I.; Micciani, A.; Orsini, N.; Kütt, J.; Rohtsalu, A.; Dalbins, J.; et al. Electric Sail Mission Expeditor, ESME: Software Architecture and Initial ESTCube Lunar Cubesat E-sail Experiment Design. Aerospace 2023, 10, 694. [Google Scholar] [CrossRef]
- Dalbins, J.; Allaje, K.; Ehrpais, H.; Iakubivskyi, I.; Ilbis, E.; Janhunen, P.; Kivastik, J.; Merisalu, M.; Noorma, M.; Pajusalu, M.; et al. Interplanetary Student Nanospacecraft: Development of the LEO Demonstrator ESTCube-2. Aerospace 2023, 10, 503. [Google Scholar] [CrossRef]
- Bassetto, M.; Quarta, A.A.; Mengali, G. Analytical Tool for Thrust Vector Description of a Web-Shaped E-Sail. IEEE Trans. Aerosp. Electron. Syst. 2024; in press. [Google Scholar] [CrossRef]
- Bassetto, M.; Mengali, G.; Quarta, A.A. Thrust and Torque Vector Characteristics of Axially-symmetric E-Sail. Acta Astronaut. 2018, 146, 134–143. [Google Scholar] [CrossRef]
- Du, C.; Zhu, Z.H.; Li, G. Analysis of thrust-induced sail plane coning and attitude motion of electric sail. Acta Astronaut. 2021, 178, 129–142. [Google Scholar] [CrossRef]
- Quarta, A.A.; Mengali, G.; Bassetto, M.; Niccolai, L. Optimal circle-to-ellipse orbit transfer for Sun-facing E-sail. Aerospace 2022, 9, 671. [Google Scholar] [CrossRef]
- Bassetto, M. Tracking and Thrust Vectoring of E-Sail-Based Spacecraft for Solar Activity Monitoring. In Handbook of Space Resources; Badescu, V., Zacny, K., Bar-Cohen, Y., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2023; Chapter 3; pp. 167–228. [Google Scholar] [CrossRef]
- Du, C.; Zhu, Z.H.; Kang, J. Attitude Control and Stability Analysis of Electric Sail. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 5560–5570. [Google Scholar] [CrossRef]
- Montalvo, C.; Wiegmann, B. Electric sail space flight dynamics and controls. Acta Astronaut. 2018, 148, 268–275. [Google Scholar] [CrossRef]
- Toivanen, P.; Janhunen, P. Spin Plane Control and Thrust Vectoring of Electric Solar Wind Sail. J. Propuls. Power 2013, 29, 178–185. [Google Scholar] [CrossRef]
- Toivanen, P.; Janhunen, P. Thrust vectoring of an electric solar wind sail with a realistic sail shape. Acta Astronaut. 2017, 131, 145–151. [Google Scholar] [CrossRef]
- Du, C.; Zhu, Z.H. Dynamic characterization and sail angle control of electric solar wind sail by high-fidelity tether dynamics. Acta Astronaut. 2021, 189, 504–513. [Google Scholar] [CrossRef]
- Du, C.; Zhu, Z.H.; Wang, C.; Li, A.; Li, T. Evaluation of E-sail parameters on central spacecraft attitude stability using a high-fidelity rigid–flexible coupling model. Astrodynamics 2024, 8, 271–284. [Google Scholar] [CrossRef]
- Du, C.; Zhu, Z.H.; Li, G. Rigid-flexible coupling effect on attitude dynamics of electric solar wind sail. Commun. Nonlinear Sci. Numer. Simul. 2021, 95, 105663. [Google Scholar] [CrossRef]
- Lillian, T.D. Modal Analysis of Electric sail. Acta Astronaut. 2021, 185, 140–147. [Google Scholar] [CrossRef]
- Zeng, S.; Fan, W.; Ren, H. Attitude control for a full-scale flexible electric solar wind sail spacecraft on heliocentric and displaced non-Keplerian orbits. Acta Astronaut. 2023, 211, 734–749. [Google Scholar] [CrossRef]
- Urrios, J.; Pacheco-Ramos, G.; Vazquez, R. Optimal planning and guidance for Solar System exploration using Electric Solar Wind Sails. Acta Astronaut. 2024, 217, 116–129. [Google Scholar] [CrossRef]
- Huo, M.; Mengali, G.; Quarta, A.A.; Qi, N. Electric sail trajectory design with Bezier curve-based shaping approach. Aerosp. Sci. Technol. 2019, 88, 126–135. [Google Scholar] [CrossRef]
- Ogihara, M.; Kokubo, E.; Suzuki, T.K.; Morbidelli, A. Formation of the terrestrial planets in the solar system around 1 au via radial concentration of planetesimals. Astron. Astrophys. 2018, 612, L5. [Google Scholar] [CrossRef]
- Huo, M.Y.; Mengali, G.; Quarta, A.A. Electric sail thrust model from a geometrical perspective. J. Guid. Control Dyn. 2018, 41, 735–741. [Google Scholar] [CrossRef]
- Quarta, A.A. Optimal guidance for heliocentric orbit cranking with E-sail-propelled spacecraft. Aerospace 2024, 11, 490. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A.; Janhunen, P. Considerations of electric sailcraft trajectory design. JBIS-J. Br. Interplanet. Soc. 2008, 61, 326–329. [Google Scholar]
- McInnes, C.R. Solar Sailing: Technology, Dynamics and Mission Applications; Springer-Praxis Series in Space Science and Technology; Springer: Berlin/Heidelberg, Germany, 1999; Chapter 2; pp. 46–51. [Google Scholar] [CrossRef]
- Wright, J.L. Space Sailing; Gordon and Breach Science Publishers: Philadephia, PA, USA, 1992; pp. 223–233. [Google Scholar]
- Quarta, A.A.; Abu Salem, K.; Palaia, G. Solar sail transfer trajectory design for comet 29P/Schwassmann-Wachmann 1 rendezvous. Appl. Sci. 2023, 13, 9590. [Google Scholar] [CrossRef]
- Dachwald, B.; Seboldt, W.; Macdonald, M.; Mengali, G.; Quarta, A.; McInnes, C.; Rios-Reyes, L.; Scheeres, D.; Wie, B.; Görlich, M.; et al. Potential Solar Sail Degradation Effects on Trajectory and Attitude Control. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, CA, USA, 15–18 August 2005. [Google Scholar] [CrossRef]
- Walker, M.J.H.; Ireland, B.; Owens, J. A set of modified equinoctial orbit elements. Celest. Mech. 1985, 36, 409–419, Erratum in Celest. Mech. 1986, 38, 391–392. [Google Scholar] [CrossRef]
- Bryson, A.E.; Ho, Y.C. Applied Optimal Control; Hemisphere Publishing Corporation: New York, NY, USA, 1975; Chapter 2; pp. 71–89. ISBN 0-891-16228-3. [Google Scholar]
- Stengel, R.F. Optimal Control and Estimation; Dover Books on Mathematics; Dover Publications, Inc.: New York, NY, USA, 1994; pp. 222–254. [Google Scholar]
- Ross, I.M. A Primer on Pontryagin’s Principle in Optimal Control; Collegiate Publishers: San Francisco, CA, USA, 2015; Chapter 2; pp. 127–129. [Google Scholar]
- Quarta, A.A. Warm start for optimal transfer between close circular orbits with first generation E-sail. Adv. Space Res. 2024; in press. [Google Scholar] [CrossRef]
- Bate, R.R.; Mueller, D.D.; White, J.E. Fundamentals of Astrodynamics; Dover Publications: New York, NY, USA, 1971; Chapter 2; pp. 58–61. [Google Scholar]
- Quarta, A.A.; Mengali, G. Analysis of Electric Sail Heliocentric Motion under Radial Thrust. J. Guid. Control Dyn. 2016, 39, 1431–1435. [Google Scholar] [CrossRef]






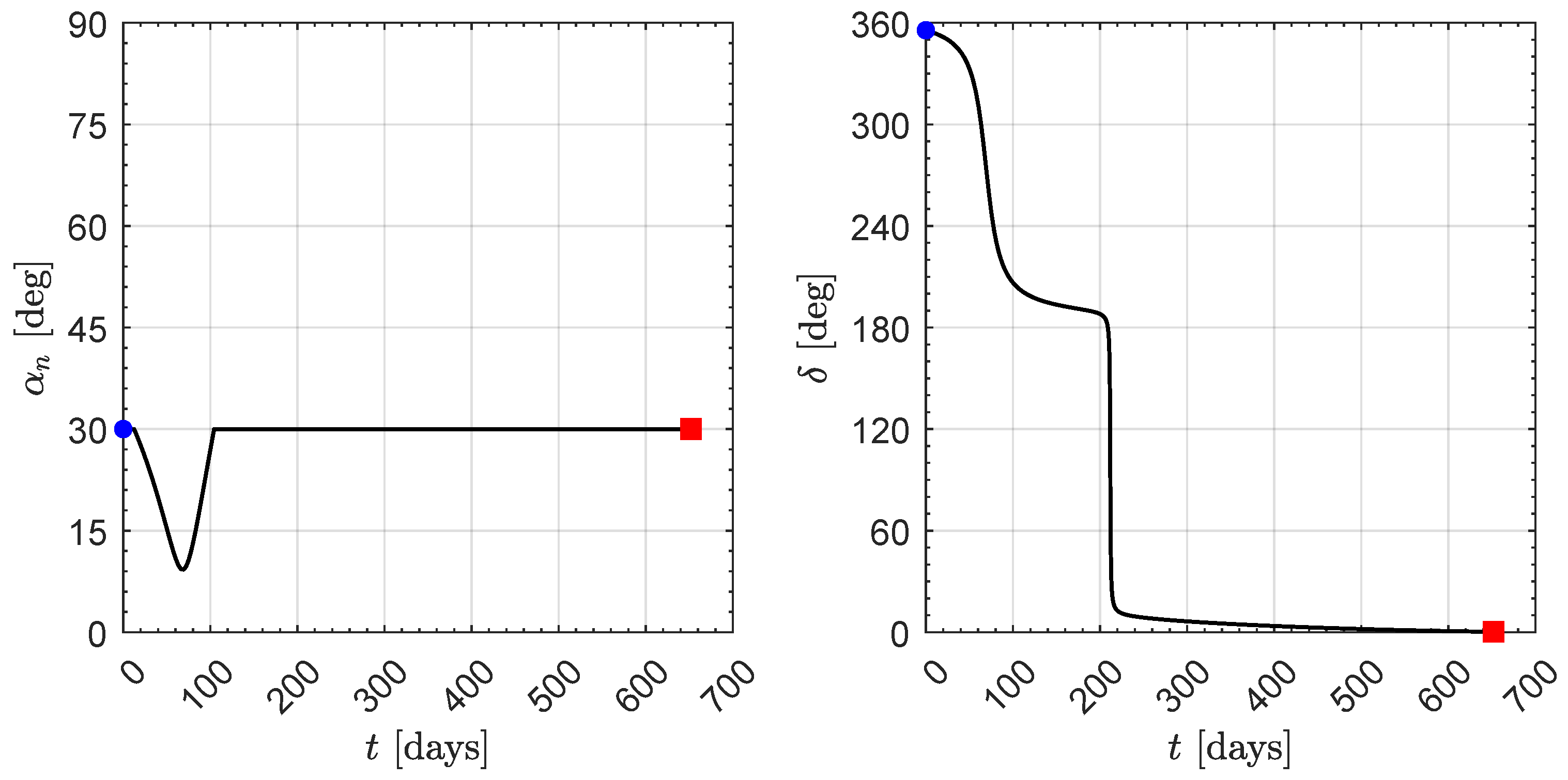

| Planet | Semi-Major Axis | Eccentricity | Inclination | Argument of Perihelion | RAAN |
|---|---|---|---|---|---|
| Earth | |||||
| Mars | |||||
| Venus | |||||
| Mercury |
| Scenario | |||
|---|---|---|---|
| Earth–Mars | |||
| Earth–Venus | |||
| Earth–Mercury |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quarta, A.A. Impact of Pitch Angle Limitation on E-Sail Interplanetary Transfers. Aerospace 2024, 11, 729. https://doi.org/10.3390/aerospace11090729
Quarta AA. Impact of Pitch Angle Limitation on E-Sail Interplanetary Transfers. Aerospace. 2024; 11(9):729. https://doi.org/10.3390/aerospace11090729
Chicago/Turabian StyleQuarta, Alessandro A. 2024. "Impact of Pitch Angle Limitation on E-Sail Interplanetary Transfers" Aerospace 11, no. 9: 729. https://doi.org/10.3390/aerospace11090729






