An Open-Source Code for High-Speed Non-Equilibrium Gas–Solid Flows in OpenFOAM
Abstract
:1. Introduction
2. Methodology
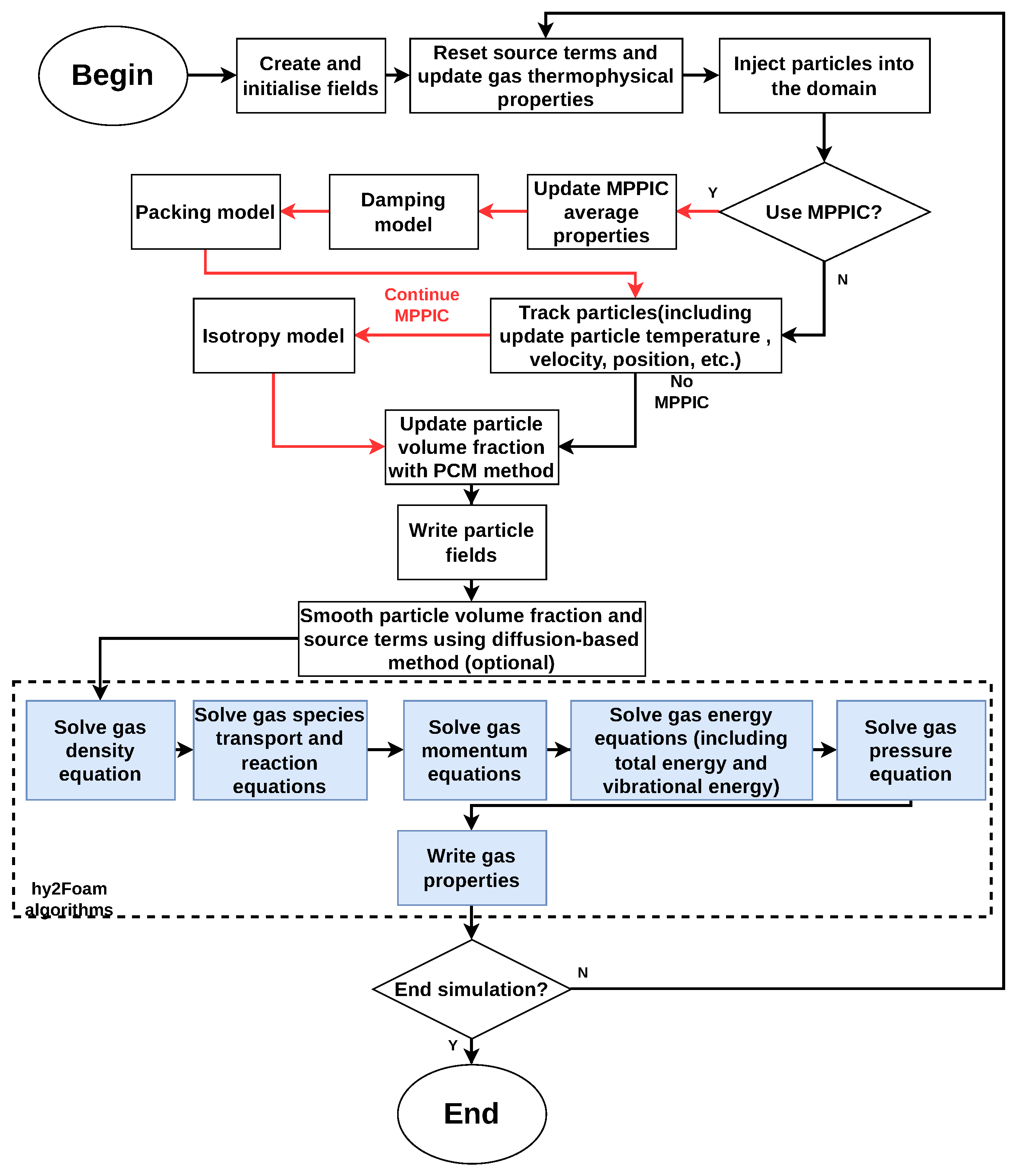
2.1. Algorithmic Overview
- Step 1: Calculation of the gas phase thermophysical properties necessary to calculate the particle drag force and reset the source terms of the particle phase.
- Step 2: Injection of particles from inlet boundaries.
- Step 3: Evolution of the disperse phase, including performing particle movements, updating temperatures, velocities and positions, and conducting Multi-Phase Particle-In-Cell (MPPIC) procedures (optional).
- Step 4: Sampling and calculation of discrete phase properties and returning the desired macroscopic fields, such as number density and surface heat flux.
- Step 5: Updating the particle volume fraction using the particle cell method.
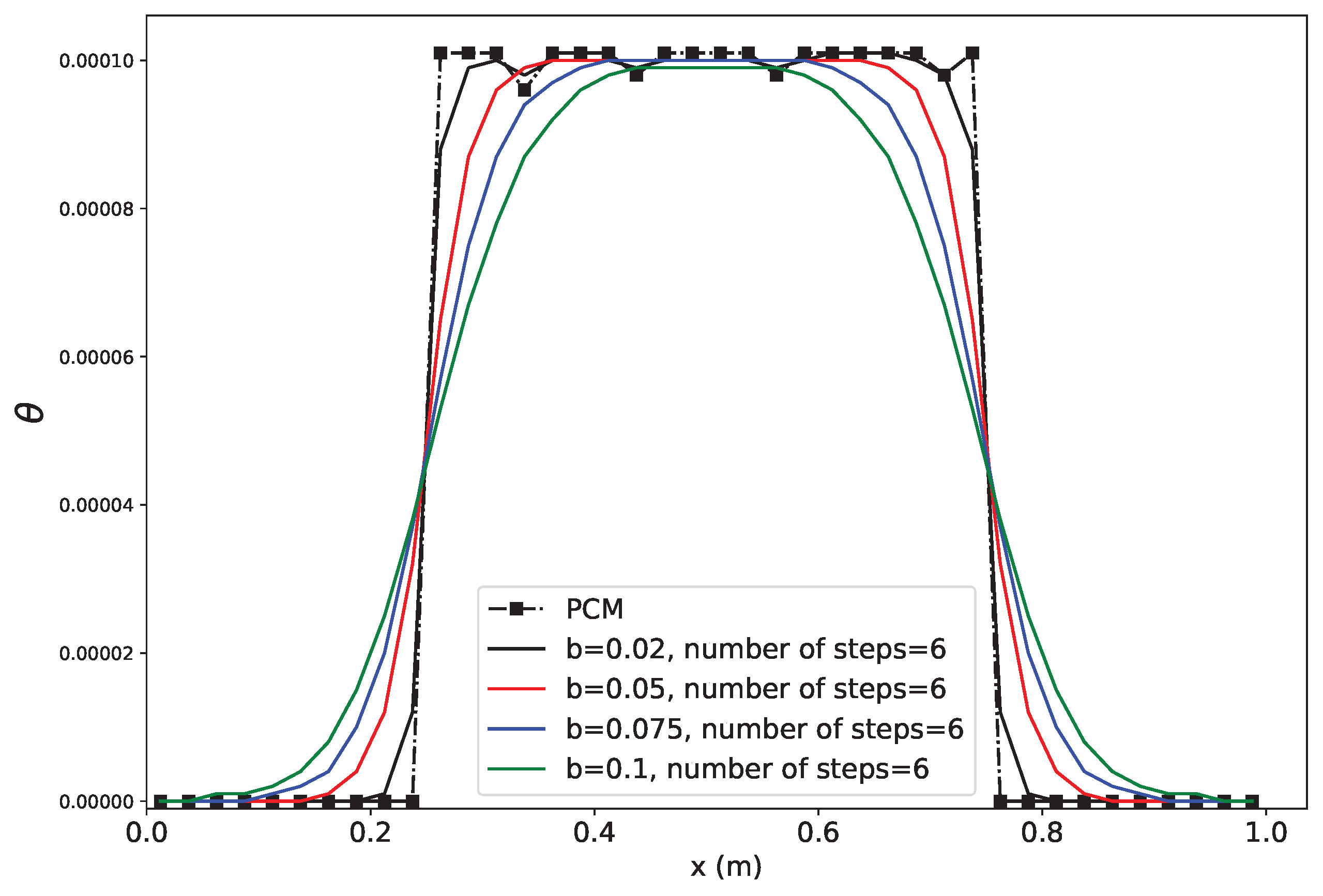
- Step 6: Smoothing the particle volume fraction and source terms using the diffusion-based method (optional).
- Step 7: Solving the continuity, momentum, and energy equations of the gas phase and entering the gas properties in the hy2Foam algorithm.
- Step 8: Return to Step 1 until the time reaches the final calculation time.
2.2. Governing Equations of Gas Phase
2.3. Governing Equations of Discrete Phase
- The solid particles are assumed to be perfectly spherical; for simplicity, the particle geometry effect is neglected during calculation of the gas–particle coupling.
- Because the dimension of particles in this work is small, there is no particle temperature gradient within the solid particles; thus, the particle temperature is spatially uniform.
- There is no mass exchange between the gas phase and solid phase.
- Particle forces such as the Magnus force, virtual mass force, and pressure gradient force are neglected, as particles in high-speed flows are dominated by the drag force.
- Gravitational and buoyancy forceThe particle gravitational and buoyancy force in the gas flow is calculated as follows:
- Drag forceThe drag force of a sphere is the most important force experienced by a particle, as it dominates the momentum exchange between the gas and the solid phase. Inaccurate calculation of the drag force leads to an uncertain particle distribution in space [26]. It is usually formulated aswhere and are the drag coefficient and the particle’s projected area (i.e., ). The drag coefficient formulations are continuously updated to adapting the new flow conditions, i.e., the Reynolds effect, Mach number effect, and Knudsen number effect. The drag force is expressed in OpenFOAM aswhere is the Reynolds number based on gas–particle relative velocity, expressed as follows:where is the dynamic viscosity of the gas.Except for the built-in Gidaspow drag model [27], which is named ErgunWenYuDrag in OpenFOAM, the drag models added in the solver are listed here:
- (1)
- Singh et al. drag correlation [28]:The particle drag coefficient model proposed by Singh and Kroells et al. [28] has recently achieved some acknowledgement [29,30,31,32] and yields good simulation results. A generalized physics-based spherical particle drag force model with satisfactory accuracy, it takes into account rarefaction effects and covers a wide range of supersonic and hypersonic flow regimes. The coefficients in Equation (18) are long expressions, and can be found in [28]. Note that and are the Mach number and Reynolds number, respectively, and are based on the gas velocity rather than the gas–particle relative velocity.
- (2)
- Henderson drag correlation [33]:Henderson [33] put forward a drag coefficient model for continuum and rarefied flows that has been extensively used in the simulation of high speed gas–particle flows. The expression of the drag coefficient is related to a Mach number based on the relative velocity between the particle and the gas. For < 1:where T is the gas temperature and is the particle temperature. For > 1.75:where S is the molecular speed ratio, and is equal to .Linear interpolation is used when is in the range of 1 and 1.75:
- (3)
- Clift and Gauvin drag correlation [34]:
- (4)
- Boiko et al. drag correlation [35]:
- Thermophoretic forceThe thermophoretic force is generated in regions characterized by significant temperature gradients, such as those present at the shock and within the thermal boundary layer. It is a result of collisions of molecules on a particle with greater energy on the high-temperature side compared to its low-temperature side [36]. Loth [36] proposed a thermophoretic force model, which is duplicated in the solver. When 0.01, the particle’s thermophoretic force is calculated as follows:where = 1.22 is the tangential momentum coefficient, is the temperature accommodation coefficient, which is approximately 2.18 [36], and is the thermal conductivity ratio of the gas and particle. When 0.01, the force is expressed as
- The MPPIC methodThe MPPIC method, first developed by Andrews and O’Rourke [42], is a highly efficient approach for handling the interactions of particles with moderate and high volume fractions during simulations of multiphase flows. The particle distribution function is obtained by solving the Liouville equation [42]:The particle’s total acceleration is equal to in Equation (13). The acceleration due to the enduring particle–particle contact iswhere is called the particle normal stress [19] or particle contact stress [20]. The Harris and Crighton model [43] and Lun’s model [44] are extensively used to model particle contact stress in the simulation of dense particle phases. After calculating the particle contact stress, the velocity of the solid particles in a cell is constrained and adjusted by increasing the particle contact stress to infinity, thereby preventing them from entering closely packed cells, which they may move towards in a packing model. The MPPIC method is improved by including the damping [20] and return-to-isotropy [21] models. For more detail on the derivation of the MPPIC method, see [19,20,21]. OpenFOAM includes a standard MPPIC method integrated into hy2PTFoam.
2.4. Interphase Coupling
3. Results and Discussions
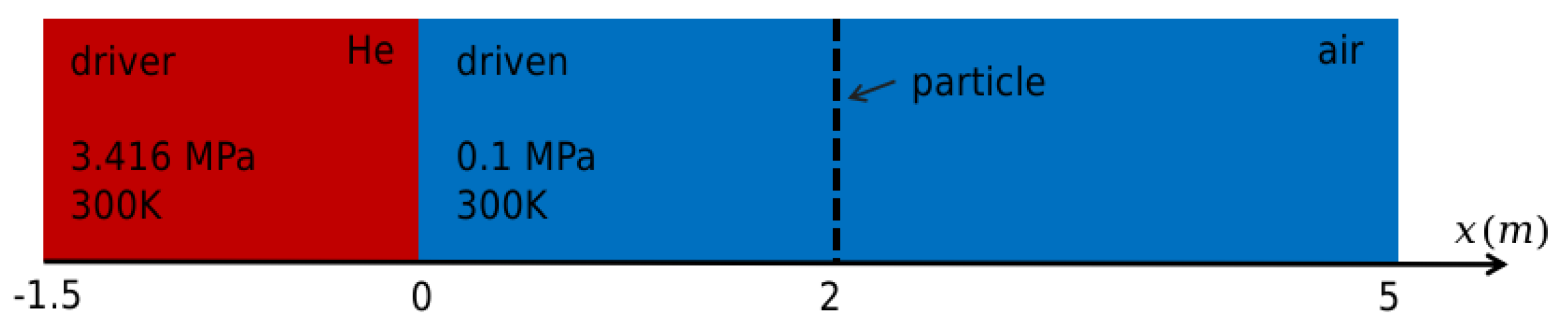
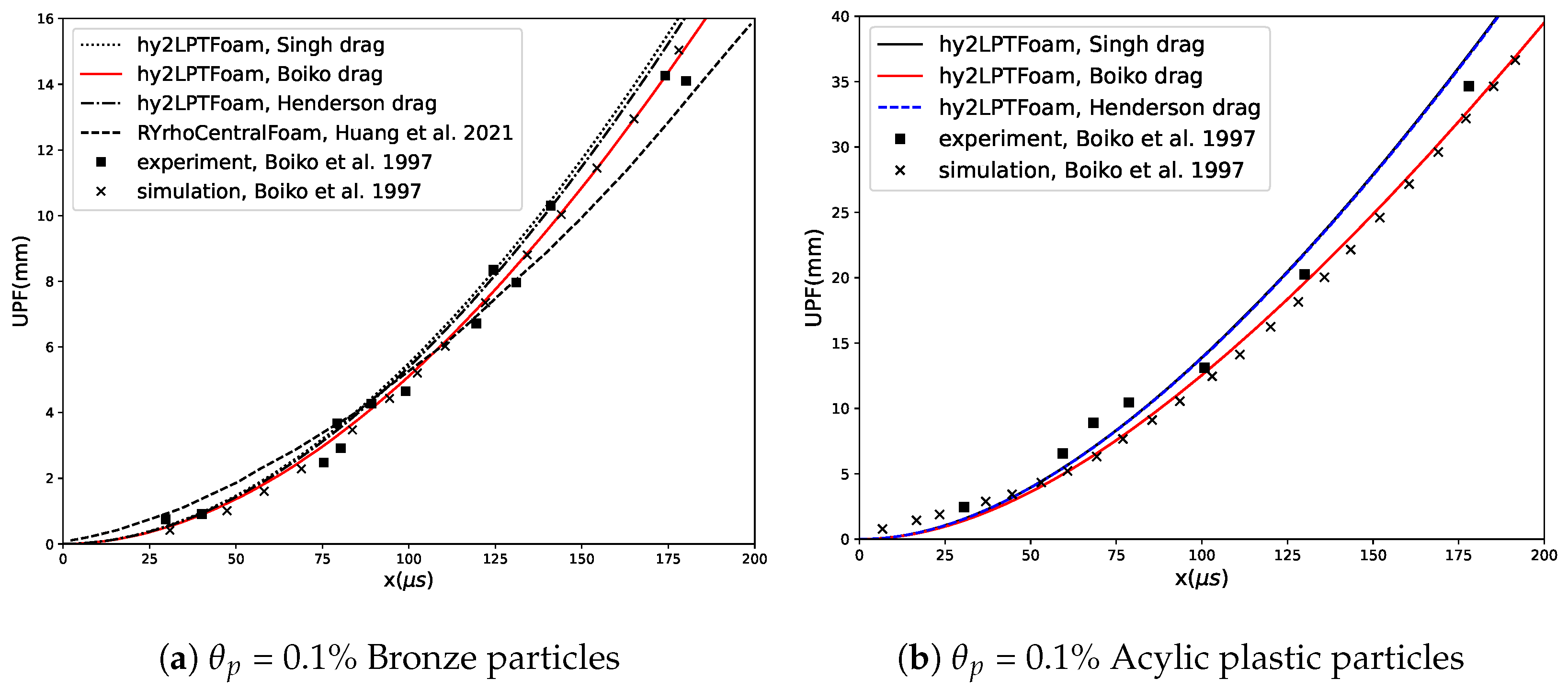
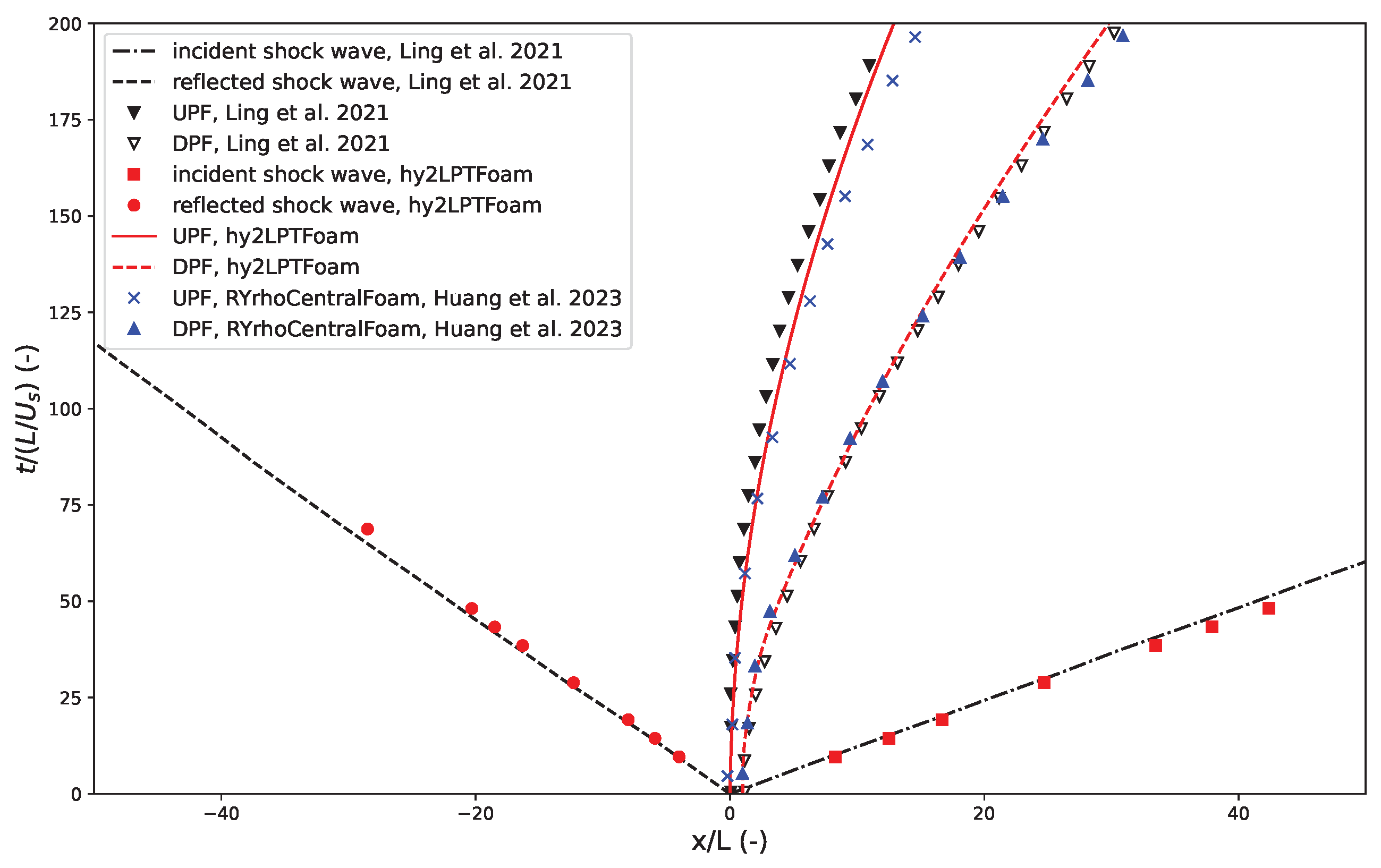
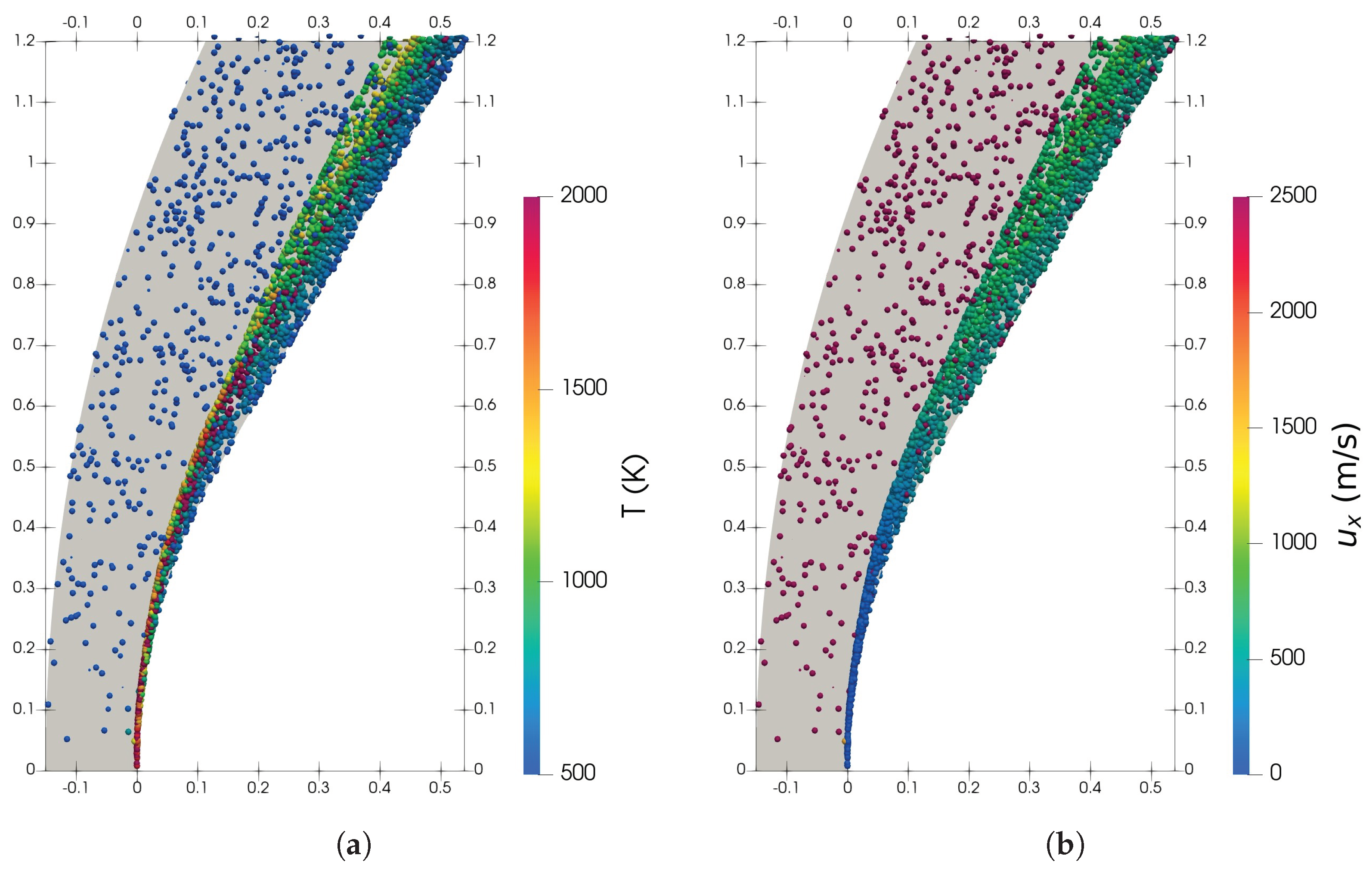
3.1. Shock–Particle Curtain Interaction
3.1.1. Low Particle Volume Fraction
3.1.2. Moderate Particle Volume Fraction = 21%
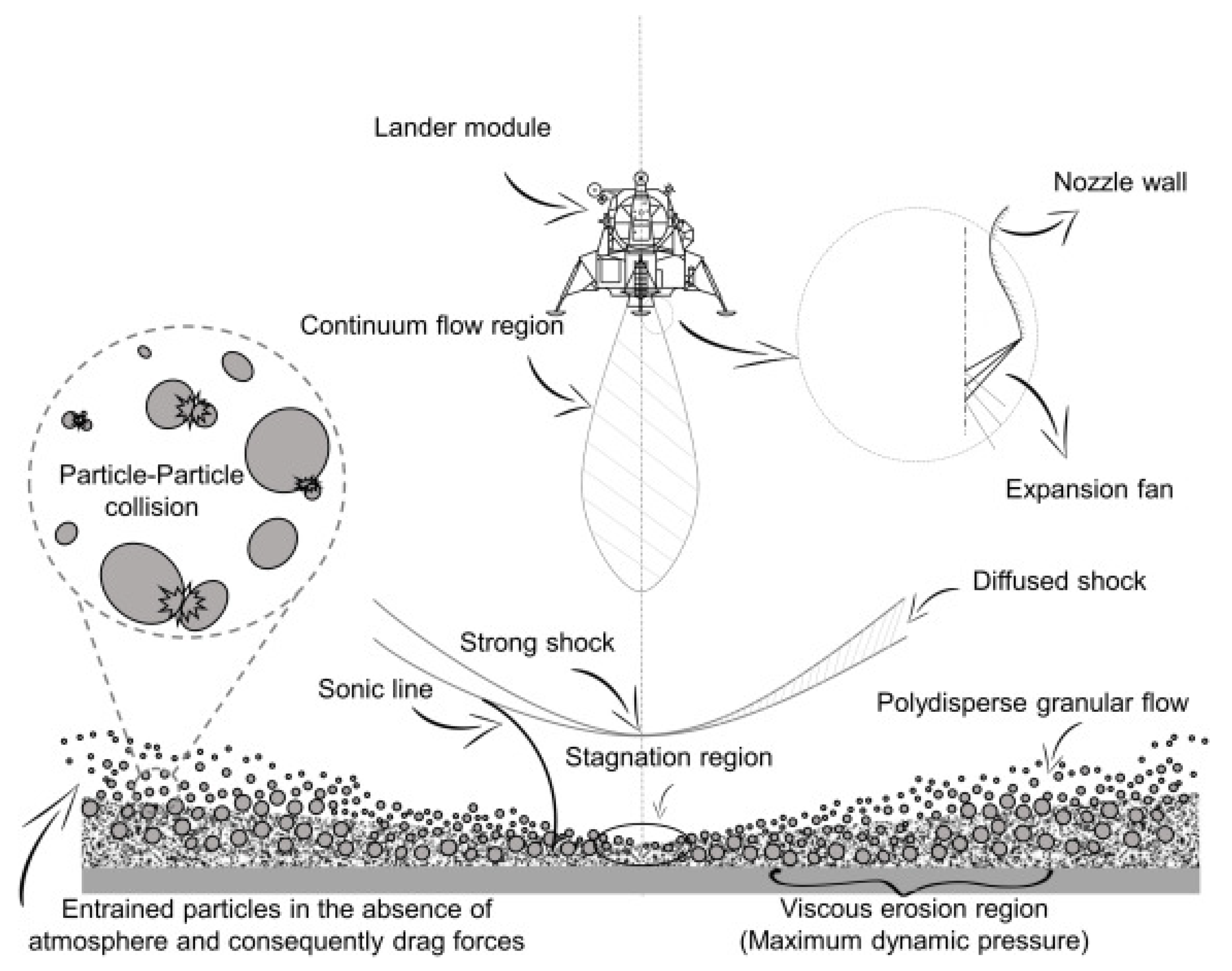
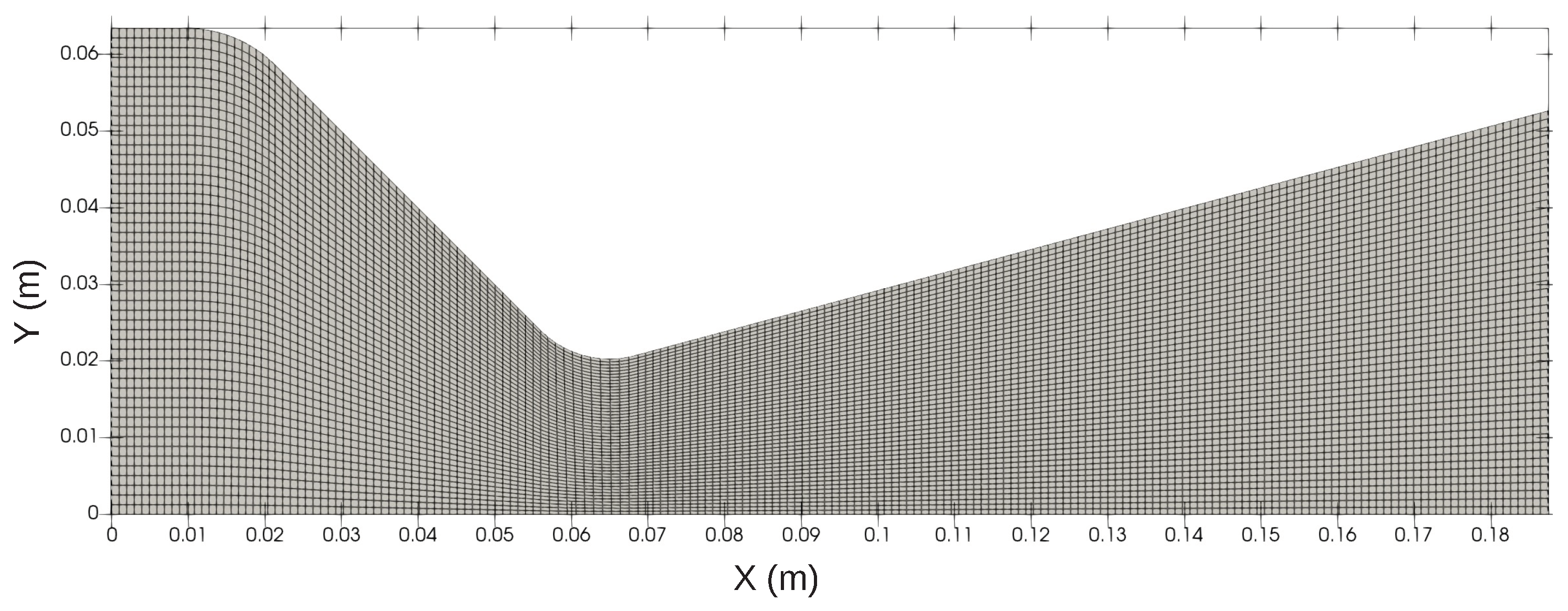
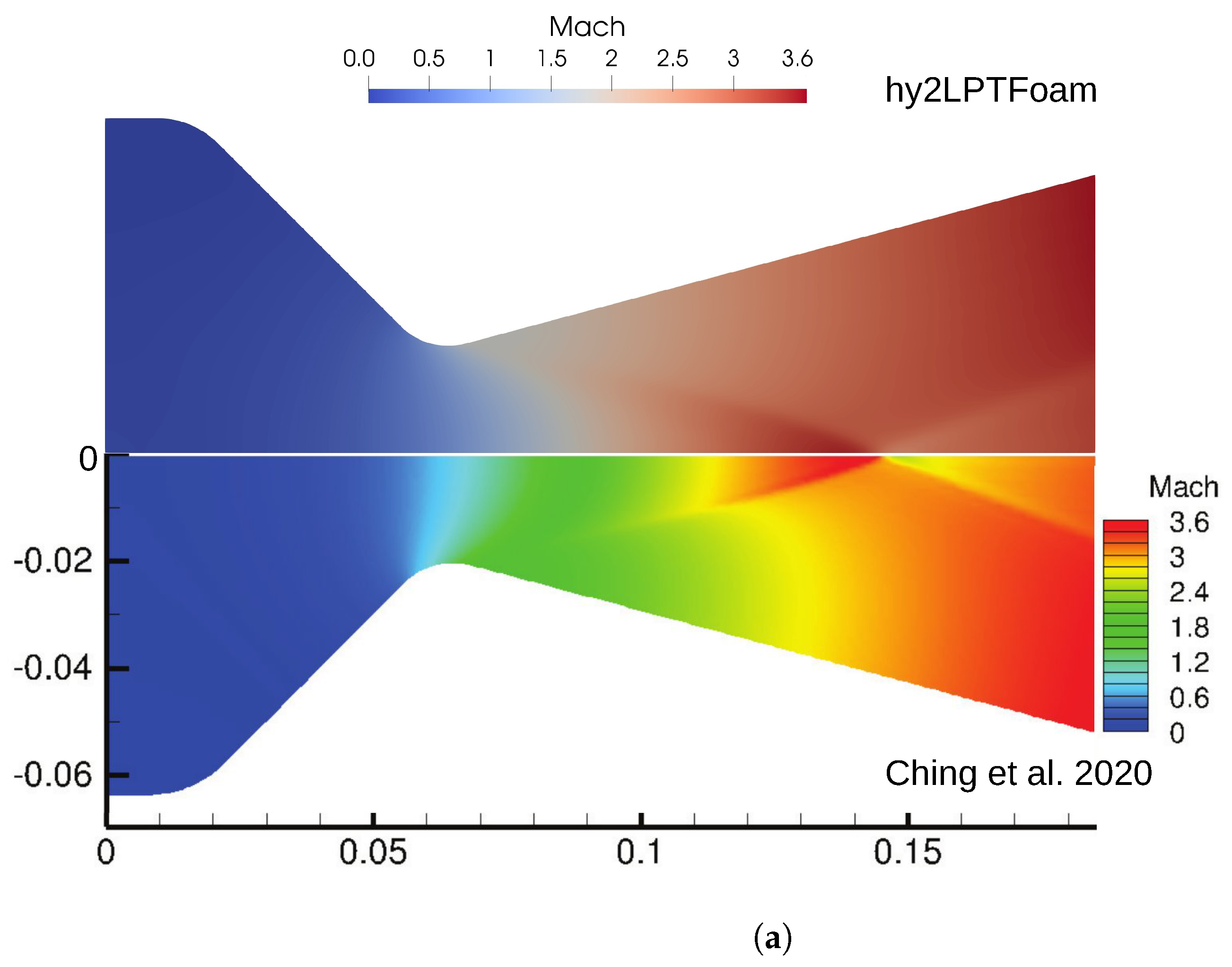
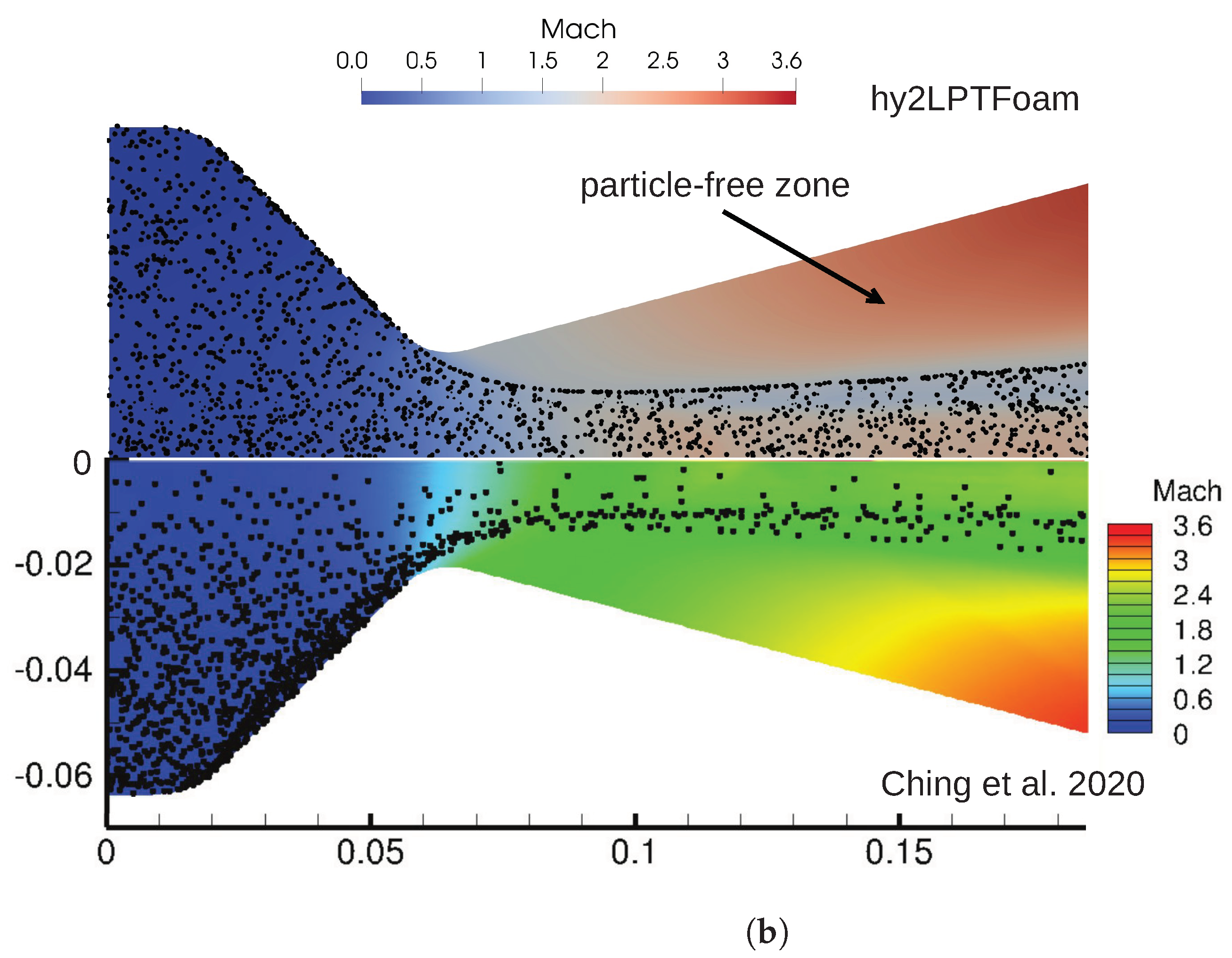
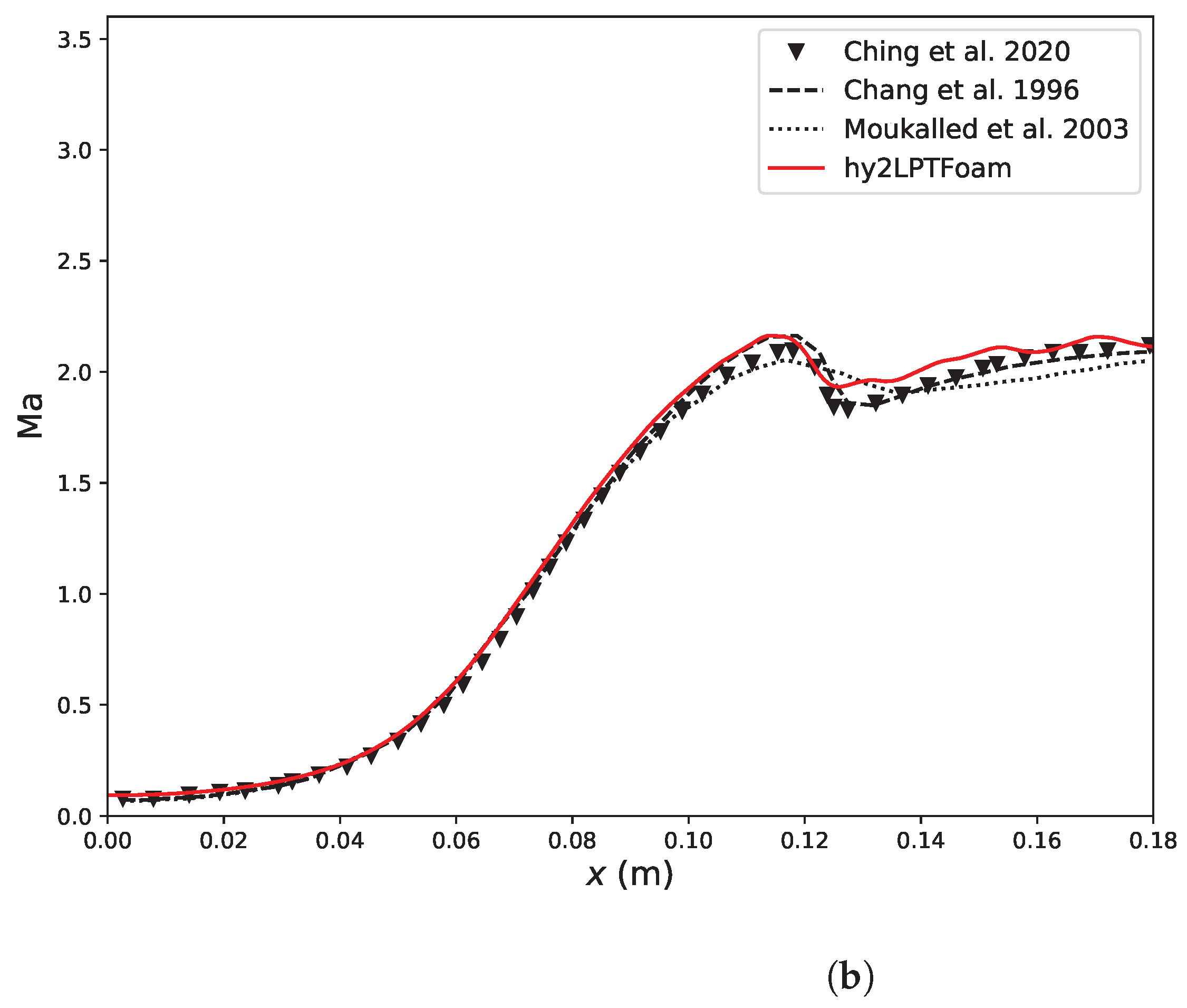
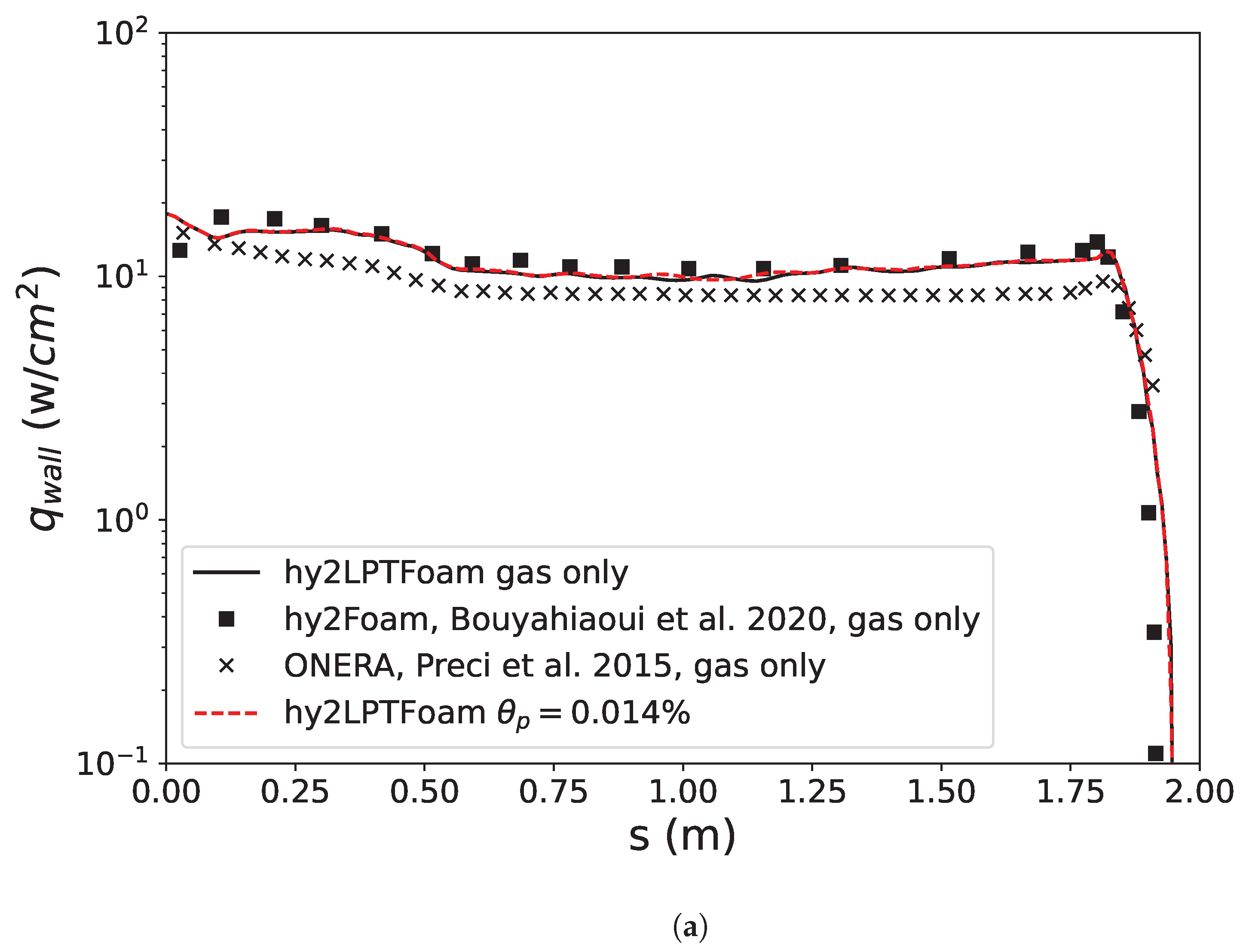
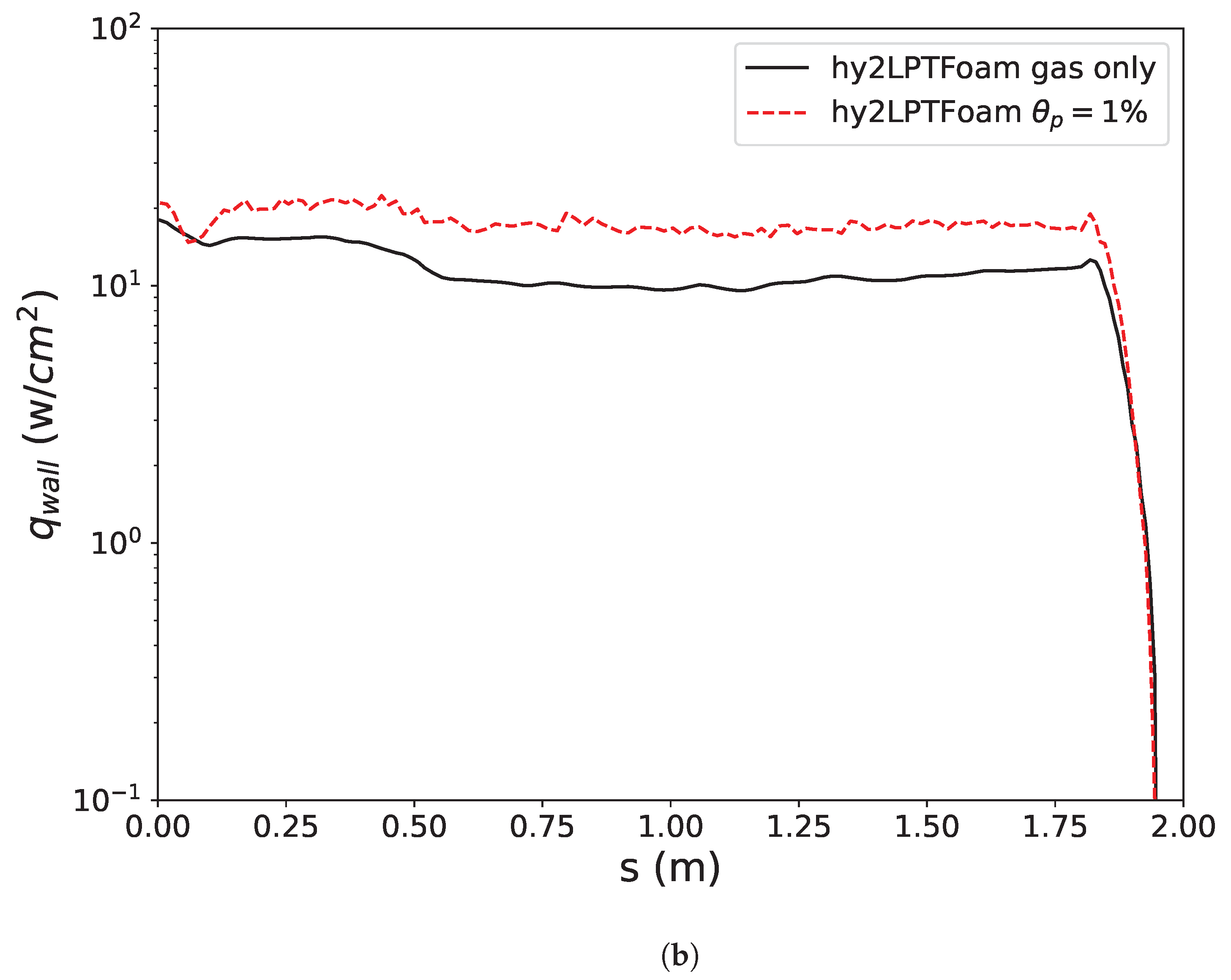
3.2. Two-Phase Flow in JPL Thruster
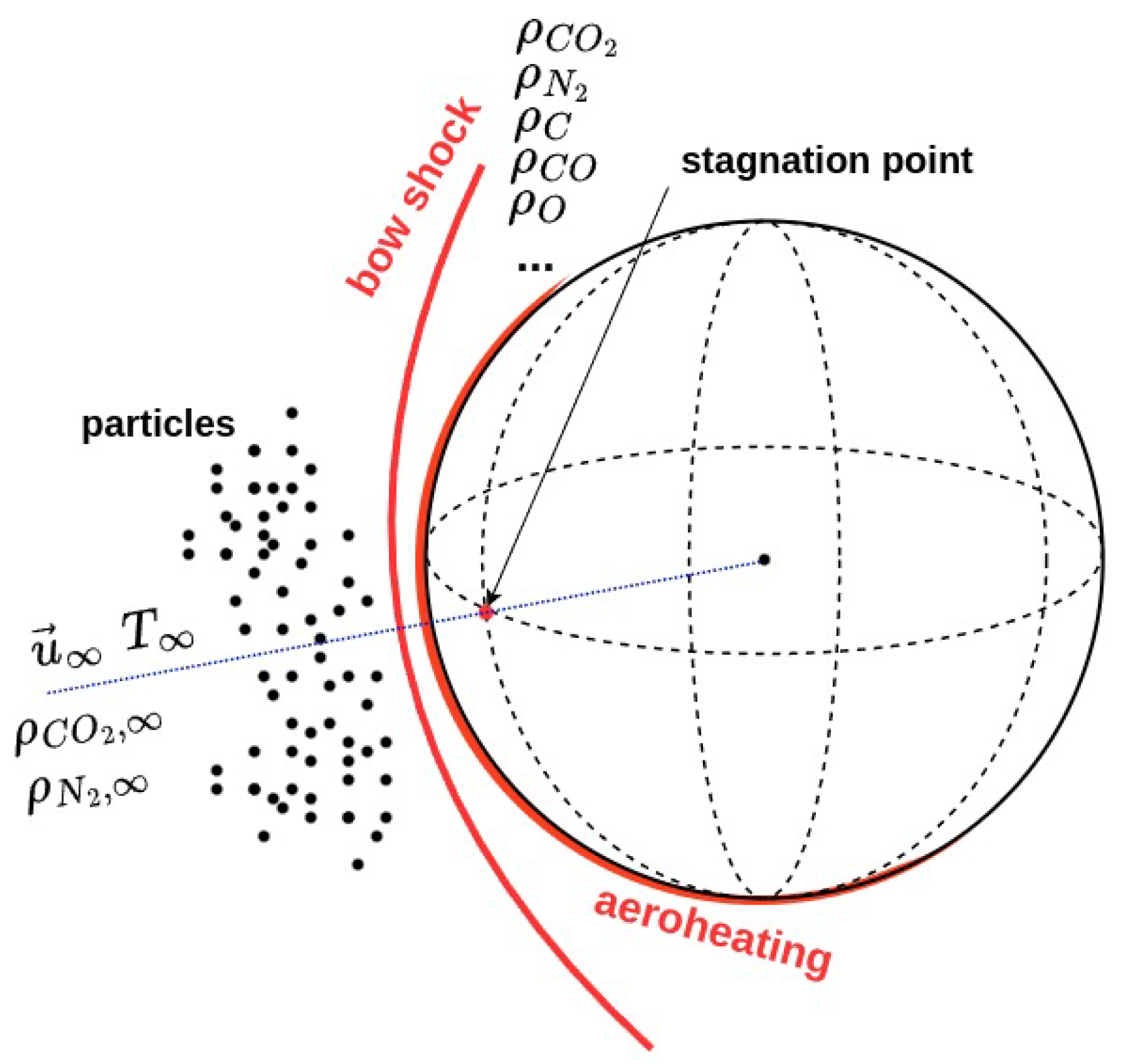
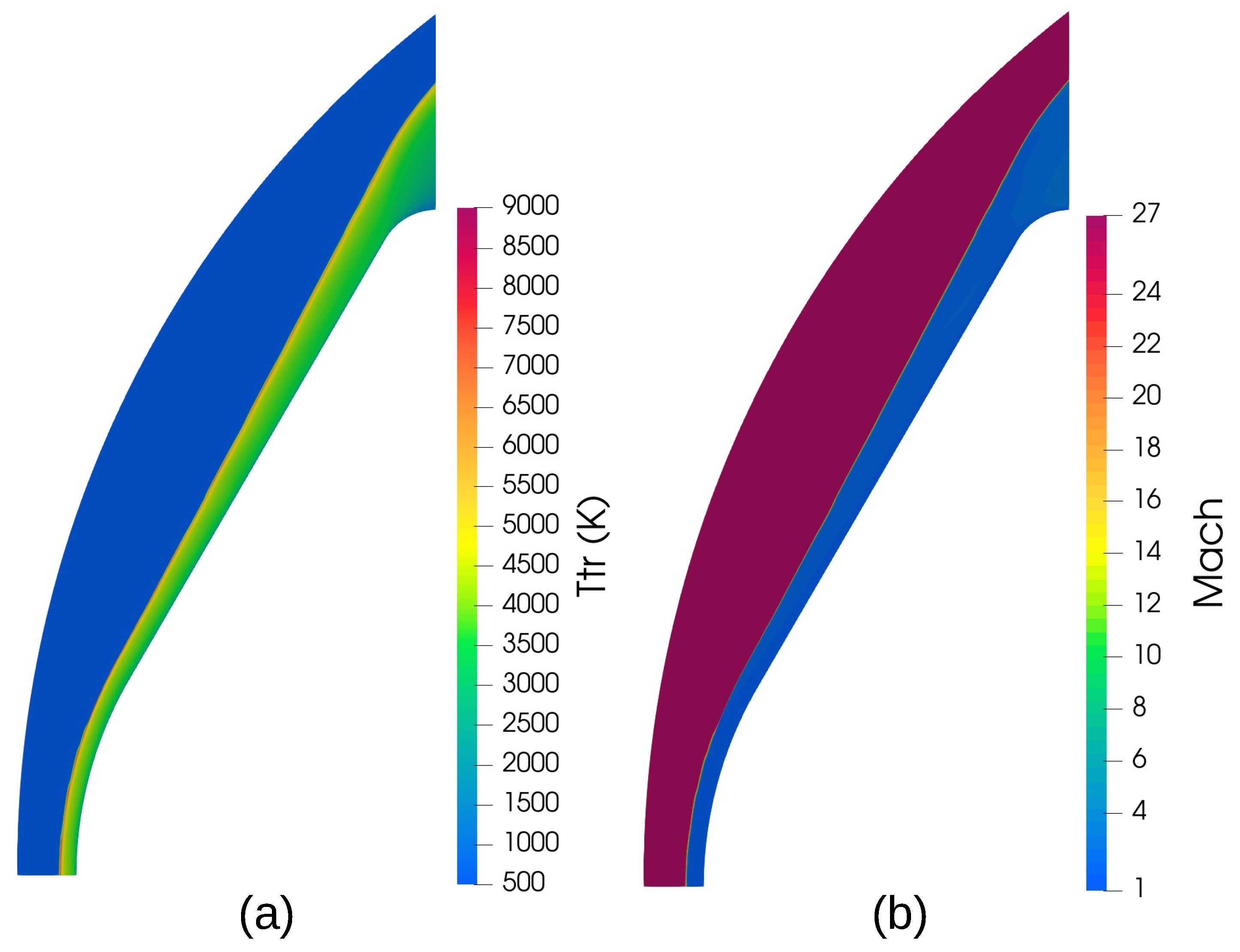
3.3. MSRO Body: Hypersonic Non-Equilibrium Flow during Mars Entry
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | |
| viscous stress tensor | |
| net mass production of gas species i | |
| sum of the vibrational source terms | |
| specific heat ratio | |
| heat transfer coefficient | |
| gas dynamic viscosity | |
| density | |
| volume fraction | |
| particle acceleration | |
| particle force | |
| gravitational and bouyancy force | |
| velocity | |
| particle position | |
| A | particle projection area |
| drag coefficient | |
| d | particle diameter |
| e | total energy per unit mass |
| J | diffusion flux |
| Knudsen number | |
| m | mass |
| Mach number | |
| Nusselt number | |
| p | pressure |
| Prandtl number | |
| Q | heat transferred from particle to gas |
| q | heat transfer |
| R | gas constant |
| Reynolds number | |
| energy exchange source | |
| momentum exchange source | |
| T | temperature |
| Y | gas species mass fraction |
| Subscripts | |
| ∞ | free stream properties |
| m | gas molecule |
| MPPIC | |
| p | particle properties |
| thermophoretic fortce | |
| trans-rotational energy mode | |
| vibro-electronic energy mode | |
| Acronyms | |
| DSMC | direct simulation Monte Carlo |
| MPPIC | multiphase particle-in-cell |
| OpenFOAM | Open Field Operation and Manipulation |
References
- Majid, A.; Bauder, U.; Herdrich, G.; Fertig, M. Two-Phase Flow Solver for Hypersonic Entry Flows in a Dusty Martian Atmosphere. J. Thermophys. Heat Transf. 2016, 30, 418–428. [Google Scholar] [CrossRef]
- Rahimi, A.; Ejtehadi, O.; Lee, K.; Myong, R. Near-field plume-surface interaction and regolith erosion and dispersal during the lunar landing. Acta Astronaut. 2020, 175, 308–326. [Google Scholar] [CrossRef]
- Park, C. Nonequilibrium Hypersonic Aerothermodynamics; Wiley: New York, NY, USA, 1989. [Google Scholar]
- Wright, M.J.; Candler, G.V.; Bose, D. Data-Parallel Line Relaxation Method for the Navier-Stokes Equations. AIAA J. 1998, 36, 1603–1609. [Google Scholar] [CrossRef]
- Gnoffo, P.A. An Upwind-Biased, Point-Implicit Relaxation Algorithm for Viscous, Compressible Perfect-Gas Flows; No. NASA-TP-2953; Hampton, VA, USA, 1990. Available online: https://ntrs.nasa.gov/citations/19900007726 (accessed on 9 August 2024).
- Daiß, A.; Schöll, E.; Frühauf, H.H.; Knab, O. Validation of the uranus navier-stokes code for high-temperature nonequilibrium flows. In Proceedings of the 5th International Aerospace Planes and Hypersonics Technologies Conference, Munich, Germany, 30 November–3 December 1993; p. 5070. [Google Scholar]
- Candler, G.V.; Johnson, H.B.; Nompelis, I.; Gidzak, V.M.; Subbareddy, P.K.; Barnhardt, M. Development of the US3D code for advanced compressible and reacting flow simulations. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015; p. 1893. [Google Scholar] [CrossRef]
- Haoui, R. Physico-chemical state of the air at the stagnation point during the atmospheric reentry of a spacecraft. Acta Astronaut. 2011, 68, 1660–1668. [Google Scholar] [CrossRef]
- Casseau, V. An Open-Source CFD Solver for Planetary Entry. Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 2017. [Google Scholar]
- Vatansever, D.; Celik, B. An open-source hypersonic solver for non-equilibrium flows. J. Aeronaut. Space Technol. 2021, 14, 35–52. [Google Scholar]
- Gibbons, N.N.; Damm, K.A.; Jacobs, P.A.; Gollan, R.J. Eilmer: An open-source multi-physics hypersonic flow solver. Comput. Phys. Commun. 2023, 282, 108551. [Google Scholar] [CrossRef]
- Bauder, U.; Fertig, M.; Auweter-Kurtz, M. Examination of the Coupling of the Loosely Coupled Sequential Navier-Stokes Code SINA. In Proceedings of the 40th Thermophysics Conference, Seattle, WA, USA, 23–26 June 2008; p. 3931. [Google Scholar]
- Sahai, A.; Palmer, G. Variable-fidelity Euler–Lagrange framework for simulating particle-laden high-speed flows. AIAA J. 2022, 60, 3001–3019. [Google Scholar] [CrossRef]
- Kroells, M.D.; Sahai, A.; Schwartzentruber, T.E. Sensitivity study of dust-induced surface erosion during Martian planetary entry. In Proceedings of the AIAA Scitech 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 0112. [Google Scholar]
- Greenshields, C.J.; Weller, H.G.; Gasparini, L.; Reese, J.M. Implementation of semi-discrete, non-staggered central schemes in a colocated, polyhedral, finite volume framework, for high-speed viscous flows. Int. J. Numer. Methods Fluids 2010, 63, 1–21. [Google Scholar] [CrossRef]
- Huang, Z.; Zhao, M.; Xu, Y.; Li, G.; Zhang, H. Eulerian-Lagrangian modelling of detonative combustion in two-phase gas-droplet mixtures with OpenFOAM: Validations and verifications. Fuel 2021, 286, 119402. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, H.; Zhang, Y.F.; Li, S.; Meng, Q. Modeling particle collisions in moderately dense curtain impacted by an incident shock wave. Phys. Fluids 2023, 35, 023327. [Google Scholar] [CrossRef]
- Ching, E.J.; Brill, S.R.; Barnhardt, M.; Ihme, M. A two-way coupled Euler-Lagrange method for simulating multiphase flows with discontinuous Galerkin schemes on arbitrary curved elements. J. Comput. Phys. 2020, 405, 109096. [Google Scholar] [CrossRef]
- Snider, D.M. An incompressible three-dimensional multiphase particle-in-cell model for dense particle flows. J. Comput. Phys. 2001, 170, 523–549. [Google Scholar] [CrossRef]
- O’Rourke, P.J.; Snider, D.M. An improved collision damping time for MP-PIC calculations of dense particle flows with applications to polydisperse sedimenting beds and colliding particle jets. Chem. Eng. Sci. 2010, 65, 6014–6028. [Google Scholar] [CrossRef]
- O’Rourke, P.J.; Snider, D.M. Inclusion of collisional return-to-isotropy in the MP-PIC method. Chem. Eng. Sci. 2012, 80, 39–54. [Google Scholar] [CrossRef]
- Marayikkottu Vijayan, A.; Levin, D.A. Study of shock interaction with a particle curtain using the Multiphase Particle in Cell (MP-PIC) approach. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023; p. 0281. [Google Scholar]
- Ranjbari, P.; Emamzadeh, M.; Mohseni, A. Numerical analysis of particle injection effect on gas-liquid two-phase flow in horizontal pipelines using coupled MPPIC-VOF method. Adv. Powder Technol. 2023, 34, 104235. [Google Scholar] [CrossRef]
- Vincent, C.; Daniel, E.; Thomas, S.; Richard, B. A Two-Temperature Open-Source CFD Model for Hypersonic Reacting Flows, Part Two: Multi-Dimensional Analysis. Aerospace 2016, 3, 45. [Google Scholar] [CrossRef]
- Cao, Z.; White, C.; Kontis, K. Numerical investigation of rarefied vortex loop formation due to shock wave diffraction with the use of rorticity. Phys. Fluids 2021, 33, 067112. [Google Scholar] [CrossRef]
- Cao, Z.; White, C.; Agir, M.B.; Kontis, K. Lunar plume-surface interactions using rarefiedMultiphaseFoam. Front. Mech. Eng. 2023, 9, 1116330. [Google Scholar] [CrossRef]
- Gidaspow, D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Singh, N.; Kroells, M.; Li, C.; Ching, E.; Ihme, M.; Hogan, C.J.; Schwartzentruber, T.E. General drag coefficient for flow over spherical particles. AIAA J. 2022, 60, 587–597. [Google Scholar] [CrossRef]
- Ching, E.J.; Singh, N.; Ihme, M. Simulations of Dusty Flows over Full-Scale Capsule During Martian Entry. J. Spacecr. Rocket. 2022, 59, 2053–2069. [Google Scholar] [CrossRef]
- Habeck, J.B.; Kroells, M.D.; Schwartzentruber, T.E.; Candler, G.V. Characterization of particle-surface impacts on a sphere-cone at hypersonic flight conditions. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023; p. 0205. [Google Scholar]
- Osnes, A.N.; Vartdal, M.; Khalloufi, M.; Capecelatro, J.; Balachandar, S. Comprehensive quasi-steady force correlations for compressible flow through random particle suspensions. Int. J. Multiph. Flow 2023, 165, 104485. [Google Scholar] [CrossRef]
- Boniou, V.; Fox, R.O. Shock–particle-curtain-interaction study with a hyperbolic two-fluid model: Effect of particle force models. Int. J. Multiph. Flow 2023, 169, 104591. [Google Scholar] [CrossRef]
- Henderson, C.B. Drag coefficients of spheres in continuum and rarefied flows. AIAA J. 1976, 14, 707–708. [Google Scholar] [CrossRef]
- Clift, R.; Gauvin, W. Motion of Particles in Turbulent Gas Streams. Br. Chem. Eng. 1971, 16, 229. [Google Scholar]
- Boiko, V.; Kiselev, V.; Kiselev, S.; Papyrin, A.; Poplavsky, S.; Fomin, V. Shock wave interaction with a cloud of particles. Shock Waves 1997, 7, 275–285. [Google Scholar] [CrossRef]
- Loth, E. Compressibility and Rarefaction Effects on Drag of a Spherical Particle. AIAA J. 2008, 46, 2219–2228. [Google Scholar] [CrossRef]
- Fox, T.W.; Rackett, C.W.; Nicholls, J.A. Shock wave ignition of magnesium powders. In Shock Tube and Shock Wave Research; Eleventh International Symposium. 1978. Available online: https://ntrs.nasa.gov/citations/19790031222 (accessed on 9 August 2024).
- Carlson, D.J.; Hoglund, R.F. Particle drag and heat transfer in rocket nozzles. AIAA J. 1964, 2, 1980–1984. [Google Scholar] [CrossRef]
- Tewfik, O.E. Discussion on G. C. Vliet and G. Leppert: ‘Forced convection heat transfer from an isothermal sphere to water’. J. Heat Transf. 1961, 83, 175. [Google Scholar] [CrossRef]
- Kavanau, L.L. Heat transfer from spheres to a rarefied gas in subsonic flow. Trans. Am. Soc. Mech. Eng. 1955, 77, 617–623. [Google Scholar] [CrossRef]
- Crowe, C.T.; Schwarzkopf, J.D.; Sommerfeld, M.; Tsuji, Y. Multiphase Flows with Droplets and Particles; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Andrews, M.J.; O’Rourke, P.J. The multiphase particle-in-cell (MP-PIC) method for dense particulate flows. Int. J. Multiph. Flow 1996, 22, 379–402. [Google Scholar] [CrossRef]
- Harris, S.; Crighton, D. Solitons, solitary waves, and voidage disturbances in gas-fluidized beds. J. Fluid Mech. 1994, 266, 243–276. [Google Scholar] [CrossRef]
- Lun, C.K.; Savage, S.B.; Jeffrey, D.; Chepurniy, N. Kinetic theories for granular flow: Inelastic particles in Couette flow and slightly inelastic particles in a general flowfield. J. Fluid Mech. 1984, 140, 223–256. [Google Scholar] [CrossRef]
- Are, S.; Hou, S.; Schmidt, D.P. Second-order spatial accuracy in Lagrangian–Eulerian spray calculations. Numer. Heat Transf. Part B 2005, 48, 25–44. [Google Scholar] [CrossRef]
- Sun, R.; Xiao, H. Diffusion-based coarse graining in hybrid continuum–discrete solvers: Theoretical formulation and a priori tests. Int. J. Multiph. Flow 2015, 77, 142–157. [Google Scholar] [CrossRef]
- Sun, R.; Xiao, H. Diffusion-based coarse graining in hybrid continuum–discrete solvers: Applications in CFD–DEM. Int. J. Multiph. Flow 2015, 72, 233–247. [Google Scholar] [CrossRef]
- Zhang, J.; Li, T.; Ström, H.; Wang, B.; Løvås, T. A novel coupling method for unresolved CFD-DEM modeling. Int. J. Heat Mass Transf. 2023, 203, 123817. [Google Scholar] [CrossRef]
- Ling, Y.; Wagner, J.; Beresh, S.; Kearney, S.; Balachandar, S. Interaction of a planar shock wave with a dense particle curtain: Modeling and experiments. Phys. Fluids 2012, 24, 113301. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, L.; Bai, L.; Shi, W.; Li, W.; Wang, C.; Agarwal, R. Experimental study and transient CFD/DEM simulation in a fluidized bed based on different drag models. RSC Adv. 2017, 7, 12764–12774. [Google Scholar] [CrossRef]
- Chang, H.T.; Hourng, L.W.; Chien, L.C.; Chien, L.C. Application of flux-vector-splitting scheme to a dilute gas–particle jpl nozzle flow. Int. J. Numer. Methods Fluids 1996, 22, 921–935. [Google Scholar] [CrossRef]
- Moukalled, F.; Darwish, M.; Sekar, B. A pressure-based algorithm for multi-phase flow at all speeds. J. Comput. Phys. 2003, 190, 550–571. [Google Scholar] [CrossRef]
- Maochang, D.; Xijun, Y.; Dawei, C.; Fang, Q.; Shijun, Z. Numerical Simulation of Gas-Particle Two-Phase Flow in a Nozzle with DG Method. Discret. Dyn. Nat. Soc. 2019, 2019, 7060481. [Google Scholar] [CrossRef]
- Cuffel, R.; Back, L.; Massier, P.F. Transonic flowfield in a supersonic nozzle with small throat radius of curvature. AIAA J. 1969, 7, 1364–1366. [Google Scholar] [CrossRef]
- Preci, A.; Auweter-Kurtz, M. Sensitivity analysis of non-equilibrium martian entry flow to chemical and thermal modelling. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015; p. 0982. [Google Scholar]
- Bouyahiaoui, Z.; Haoui, R.; Zidane, A.; Nouiri, A. Prediction of the flow field and convective heating during space capsule reentry using an open source solver. Int. J. Heat Mass Transf. 2020, 148, 119045. [Google Scholar] [CrossRef]
- Surzhikov, S.T. TC3: Convective and radiative heating of MSRO for simplest kinetic models. In Proceedings of the Radiation of High Temperature Gases in Atmospheric Entry, Porquerolles, France, 30 September–1 October 2004; Volume 583, p. 55. [Google Scholar]
- Prabhu, D.; Saunders, D. On heatshield shapes for Mars entry capsules. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012; p. 399. [Google Scholar]
- Blottner, F.G.; Johnson, M.; Ellis, M. Chemically Reacting Viscous Flow Program for Multi-Component Gas Mixtures; Technical report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 1971.
- Armaly, B.; Sutton, K. Viscosity of multicomponent partially ionized gas mixtures. In Proceedings of the 15th Thermophysics Conference, Snowmass, CO, USA, 14–16 July 1980; p. 1495. [Google Scholar]
- Landau, L. Theory of sound dispersion. Phys. Z. Der Sowjetunion 1936, 10, 34–43. [Google Scholar]
- Millikan, R.C.; White, D.R. Systematics of vibrational relaxation. J. Chem. Phys. 1963, 39, 3209–3213. [Google Scholar] [CrossRef]
- Oesterle, B.; Volkov, A.N.; Tsirkunov, Y.M. Numerical investigation of two-phase flow structure and heat transfer in a supersonic dusty gas flow over a blunt body. Prog. Flight Phys. 2013, 5, 441–456. [Google Scholar]
- Tsirkunov, Y.M.; Panfilov, S.; Klychnikov, M. Semiempirical model of impact interaction of a disperse impurity particle with a surface in a gas suspension flow. J. Eng. Phys. Thermophys. 1994, 67, 1018–1025. [Google Scholar] [CrossRef]
- Hinkle, A.; Hosder, S.; Johnston, C. Efficient Two-Way Coupled Analysis of Steady-State Particle-Laden Hypersonic Flows. J. Spacecr. Rocket. 2024, 61, 48–60. [Google Scholar] [CrossRef]






| gas total pressure (Pa) | 1.034 × |
| gas total temperature (K) | 555 |
| particle specific heat capacity (J/kg/K) | 1380 |
| particle density (kg/m3) | 4004.62 |
| particle diameter (m) | 2 × |
| particle inflow mass fraction | 0.3 |
| Wall Condition | Non-Catalytic |
|---|---|
| mass fraction | 1.0 |
| Wall temperature | 1500 |
| Gas velocity (m/s) | 5223 |
| Pressure (Pa) | 7.87 |
| Temperature (K) | 140 |
| particle density (kg/m3) | 2940 |
| particle diameter (m) | |
| particle specific heat capacity (J/kg/K) | 1000 |
| Reaction | ||||||
|---|---|---|---|---|---|---|
| −1.5 | 63,275 | −0.75 | 535 | |||
| −1.5 | 63,275 | −0.75 | 535 | |||
| −1.0 | 129,000 | −1.0 | 0 | |||
| −1.0 | 129,000 | −1.0 | 0 | |||
| −1.5 | 59,500 | −1.0 | 0 | |||
| −1.5 | 59,500 | −1.0 | 0 | |||
| 0.5 | 65,710 | −0.25 | 0 | |||
| −0.18 | 69,200 | −0.43 | 0 | |||
| 0 | 27,800 | 0.5 | 23,800 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Z.; Zhang, X.; Zhang, Y. An Open-Source Code for High-Speed Non-Equilibrium Gas–Solid Flows in OpenFOAM. Aerospace 2024, 11, 742. https://doi.org/10.3390/aerospace11090742
Cao Z, Zhang X, Zhang Y. An Open-Source Code for High-Speed Non-Equilibrium Gas–Solid Flows in OpenFOAM. Aerospace. 2024; 11(9):742. https://doi.org/10.3390/aerospace11090742
Chicago/Turabian StyleCao, Ziqu, Xiaofeng Zhang, and Yonghe Zhang. 2024. "An Open-Source Code for High-Speed Non-Equilibrium Gas–Solid Flows in OpenFOAM" Aerospace 11, no. 9: 742. https://doi.org/10.3390/aerospace11090742
APA StyleCao, Z., Zhang, X., & Zhang, Y. (2024). An Open-Source Code for High-Speed Non-Equilibrium Gas–Solid Flows in OpenFOAM. Aerospace, 11(9), 742. https://doi.org/10.3390/aerospace11090742






