Sensitivity Analysis of the Johnson-Cook Model for Ti-6Al-4V in Aeroengine Applications

Abstract

Titanium alloys, such as Ti-6Al-4V, are crucial for aeroengine structural integrity, especially during high-energy events like turbine blade-out scenarios. However, accurately predicting their behavior under such conditions requires the precise calibration of constitutive models. This study presents a comprehensive sensitivity analysis of the Johnson-Cook plasticity and progressive damage model parameters for Ti-6Al-4V in blade containment simulations. Using finite element models, key plasticity parameters (yield strength (A), strain-hardening constant (B), strain-rate sensitivity (C), thermal softening coefficient (m), and strain-hardening exponent (n)) and damage-related parameters (d1, d2, d3, d4, and d5) were systematically varied by ±5% to assess their influence on stress distribution, plastic deformation, and damage indices. The results indicate that the thermal softening coefficient (m) and the strain rate hardening coefficient (C) exhibit the most significant influence on the predicted casing damage, highlighting the importance of accurately characterizing these parameters. Variations in yield strength (A) and strain hardening exponent (n) also notably affect stress distribution and plastic deformation. While the damage evolution parameters (d1–d5) influence the overall damage progression, their individual sensitivities vary, with d1 and d4 showing more pronounced effects compared to others. These findings provide crucial guidance for calibrating the Johnson-Cook model to enhance aeroengine structural integrity assessments.

1. Introduction

Titanium alloys, such as Ti-6Al-4V, are essential in aerospace engineering due to their exceptional strength-to-weight ratio, corrosion resistance, and high-temperature capabilities [1,2,3,4,5,6,7]. These alloys represent 14% of the total weight of modern aircraft [8], with critical components like blades, casings, and compressors requiring their use [9,10]. However, accurately modeling the complex deformation and damage behavior of titanium alloys under the extreme conditions encountered in aeroengine applications remains a challenge [11,12,13,14].

The Johnson-Cook (J-C) plasticity and progressive damage model is widely used to simulate the high-strain-rate response of metallic materials [15,16,17,18], including titanium alloys [19,20,21,22,23,24,25,26,27]. This model accounts for the effects of strain, strain rate, stress triaxiality, and temperature on the material’s strength, damage evolution, and fracture [22,28,29,30]. Accurate calibration of the Johnson-Cook model parameters is crucial for reliable predictions of the structural integrity of aeroengine components during high-energy events, such as turbine blade-out scenarios [5,31,32].

While aircraft engine technology has advanced [33,34,35,36,37,38], engine failures, particularly from fan or compressor blade detachment, remain a critical safety concern. Two key challenges necessitate an integrated approach for improved engine design: accurately modeling the initial blade impact on the casing and understanding the complex interplay between dynamic strength, resistance, and subsequent vibrations that contribute to further engine damage [39,40]. This study addresses the first challenge by focusing on the structural integrity of the casing during a blade-out event. Specifically, it performs a sensitivity analysis of the Johnson-Cook plasticity and progressive damage model for Ti-6Al-4V, a crucial titanium alloy used in aeroengine components. Accurately capturing the material response during impact is essential for predicting damage and ensuring containment, directly contributing to improved safety. Future research should integrate this impact model with a comprehensive vibration analysis to fully address the second challenge and enable a more accurate and robust engine design, ultimately minimizing the risk of catastrophic failure.

Despite the extensive use of the Johnson-Cook model [14,15], comprehensive sensitivity analyses focused on aerospace-grade titanium alloys, particularly in the context of turbofan structural integrity, are scarce [31,32,41,42,43,44]. Uncertainties in the model parameters can lead to inaccurate predictions that result in over-design, premature failure, or even compromise operational safety. This research gap highlights the urgent need for a detailed and rigorous sensitivity analysis of the Johnson-Cook plasticity and damage model for titanium alloys.

This study presents a comprehensive sensitivity analysis of the Johnson-Cook plasticity and progressive damage models for Ti-6Al-4V alloy to identify the most critical parameters influencing aeroengine component structural response. Using finite element simulations of a full low-pressure compressor blade-out event within a Trent 1000-based aeroengine, this work systematically evaluates key plasticity and damage model parameters, prioritizing the most influential parameters and quantifying their impact on fan blade containment predictions. This detailed analysis provides robust guidance for model calibration, leading to more reliable assessments of aeroengine structural integrity.

2. Materials and Methods

Sensitivity analysis quantifies the influence of input parameter variations on model outputs [45,46,47]. While uncertainty quantification is a broad concern across various fields, it is particularly critical in engineering complex systems with multiple uncertainty sources [48,49] affecting simulation results. This study employs a local sensitivity analysis [50], investigating the impact of ±5% variations in J-C plasticity and damage parameters on the predicted structural response. A local sensitivity analysis evaluates the influence of deterministic model parameters on the responses of interest [46].

The chemical composition and mechanical behavior of the titanium alloy Ti-6Al-4V has been previously characterized in Tuninetti et al. [51,52]. The J-C model parameters were previously calibrated for plasticity using artificial neural networks [30], while damage and fracture were obtained through a combination of direct identification and finite element-based inverse calibration [22]. These parameters have been validated for temperatures between 25 °C and 400 °C and plastic strain rates up to 10⁻³ s⁻¹, ensuring their suitability for this study.

In explicit dynamics simulations, the Johnson-Cook model, incorporating plasticity, damage, and fracture, is a coupled constitutive framework where plastic deformation, damage evolution, and fracture are intrinsically linked through the damage variable and fracture strain. The governing constitutive model of Johnson-Cook [28] plasticity and progressive damage model are shown in Equations (1)–(3).

$$\sigma =\left(A+B{·\epsilon }^n\right)·\left(1+C·ln\left({\displaystyle \frac{\dot{\epsilon }}{\dot{{\epsilon }_{ref}}}}\right)\right)·\left(1-{\left(\left(T-T_{ref}\right)/\left(T_{melt}-T_{ref}\right)\right)}^m\right)$$

(1)

$${\epsilon }_f=\left(d_1+d_2·e^{{-d}_3\eta }\right)·\left(1+d_4·ln\left({\displaystyle \frac{\dot{\epsilon }}{\dot{{\epsilon }_{ref}}}}\right)\right)·\left(1+d_5·\left(T-T_{ref}\right)/\left(T_{melt}-T_{ref}\right)\right)$$

(2)

$$D=\int {\displaystyle \frac{d\epsilon }{{\epsilon }_f}}$$

(3)

The model predicts the von Mises equivalent stress ($\sigma )$, as a function of equivalent plastic strain ($\epsilon$), plastic strain rate ($\dot{\epsilon }$), and temperature ($T$), while damage is predicted with the index D, depending on the accumulative plastic strain $\left(d\epsilon \right)$ and fracture strain ${(\epsilon }_f)$. The latter depending on the stress triaxiality $\left(\eta \right)$, plastic strain rate, and temperature. The fracture in the material is reached for D = 1.

The Johnson-Cook model parameters considered for sensitivity analysis include yield stress (A), hardening constant (B), hardening exponent (n), strain rate sensitivity (C), thermal sensitivity (m), and damage model constants (d₁, d₂, d₃, d₄, and d₅). The control model parameters for the blade containment simulations, listed in

Table 1. Reference parameters for the J-C control model representing the plasticity and progressive damage of Ti-6Al-4V. The reference plastic strain rate, the melting temperature, and reference temperature are, respectively: $\dot{{\epsilon }_{ref}}$ = 0.001, $T_{melt}$ = 1660 °C, and $T_{ref}$ = 25 °C [22,30].

Plasticity Related Model Constants					Progressive Damage Model Constants
A (MPa)	B (MPa)	C	m	n	$d_1$	$d_2$	$d_3$	$d_4$	$d_5$
927.0	878.0	0.0137	0.594	0.795	0.246	186.0	$-$15.70	0.2582	1.206

[22,30], were subjected to ±5% variations to capture the model’s response to small parameter fluctuations, reflecting potential uncertainties in experimental calibration. The results from these variations were compared to the control model results (using the reference parameters from Table 1), and the percentage variation was calculated to assess the impact of these fluctuations on model performance.

The first full-computational model in the research literature giving qualitatively realistic results of the blade containment tests is reported in refs. [5,53]. The validation of a completely accurate model by academic research is clearly unfeasible due to the high cost of building the prototype model and the subsequent destruction under the containment test. Therefore, to reduce the uncertainty of computational results, the sensitivity analysis addressed here is a need. The aeroengine full turbofan model, analyzed within ANSYS Workbench Explicit Dynamics for sensitivity analysis of model parameters under containment testing, is given in Figure 1. Full constraints are given to the casing bores, while axial displacement constraint is applied in the fan disk. The fan included the detached blade and rotated at a maximum testing speed of 285 rad/s [54,55,56] with zero initial linear velocity (Figure 1a).

A predominantly hexahedral mesh, composed primarily of SOLID164 elements, was implemented for computational efficiency and stability, particularly in regions prone to large deformations and damage (e.g., fan blades). SOLID168 tetrahedral elements were strategically incorporated only where necessary, such as in the casing ribs and other complex features, to accommodate intricate geometries while minimizing their use and mitigating potential numerical issues associated with tetrahedral formulations. The casing was divided into six axial zones, with mesh refinement applied in areas expected to experience blade impact.

To ensure numerical accuracy and computational efficiency, a mesh convergence study was performed. This involved progressively refining the model mesh and balancing the mesh density with the computational cost. Three mesh configurations were used: 168,753 nodes and 240,994 elements (Figure 1b); 244,498 nodes and 295,838 elements (Figure 1c); and 331,759 nodes and 361,035 elements (Figure 1d). Element sizes were adjusted in key areas to better capture the system’s geometric and physical characteristics. The analysis aimed to identify a mesh providing an accurate representation while maintaining efficient simulation times. Refinement ceased upon achieving a suitable balance between accuracy and computational complexity.

To assess the sensitivity of the model to parameter variations, the equivalent plastic stress, damage index, and equivalent plastic strain at the last instance of impact simulation were selected as response metrics. These values, derived from turbofan simulations incorporating each parameter variation, were compared to the control model (Table 1) using relative error. The results of this sensitivity analysis are presented visually using star charts and, subsequently, ranked in order of importance.

3. Results

3.1. Mesh Convergence for Blade-Out Containment Simulation

To ensure numerical accuracy and computational efficiency, a mesh convergence study was conducted for the aeroengine blade-out containment simulation. A mesh quality assessment, using the orthogonal quality metric, yielded an average value of 0.81. This well-known metric quantifies the geometric deviation of individual elements from their ideal forms (e.g., rectangular prism or regular tetrahedron). The resultant value, approaching unity, signifies a high degree of shape conformity, suggesting the mesh’s suitability to generate accurate and numerically stable simulation results [57]. A mesh convergence analysis, considering three different configurations, demonstrated proper convergence with minimal variations in the results as the mesh was refined (Figure 2). For instance, in Figure 2a, the equivalent stress in the casing impact zone varied by 7.1% between the coarse and fine meshes, and only 2.6% between the medium and fine meshes. In the detached blade (hereafter referred to as “the blade”), the variation between coarse and medium meshes was 4.8%, decreasing to 0.8% between medium and fine meshes.

Additionally, a novel approach proposed by Tuninetti et al. [58] was employed to verify convergence through fractional error analysis, confirming that the fine mesh demonstrated convergence with negligible variation [58]. This approach verified a decreasing fractional error approaching zero with mesh refinement, confirming effective convergence (Figure 2b). Figure 2c shows the evolution of the impact, showing a detached blade and the casing deformations obtained with the refined meshed. The resulting impact dynamics and structural response of the turbofan system show nonlinear behavior characterized by rapid stress and deformation propagation in the casing and fan components. The detached blade was impacted with high energy, causing localized deformations in the casing and surrounding areas. Given the acceptable balance between numerical accuracy and computational cost, the fine mesh configuration was, therefore, selected for all subsequent simulations.

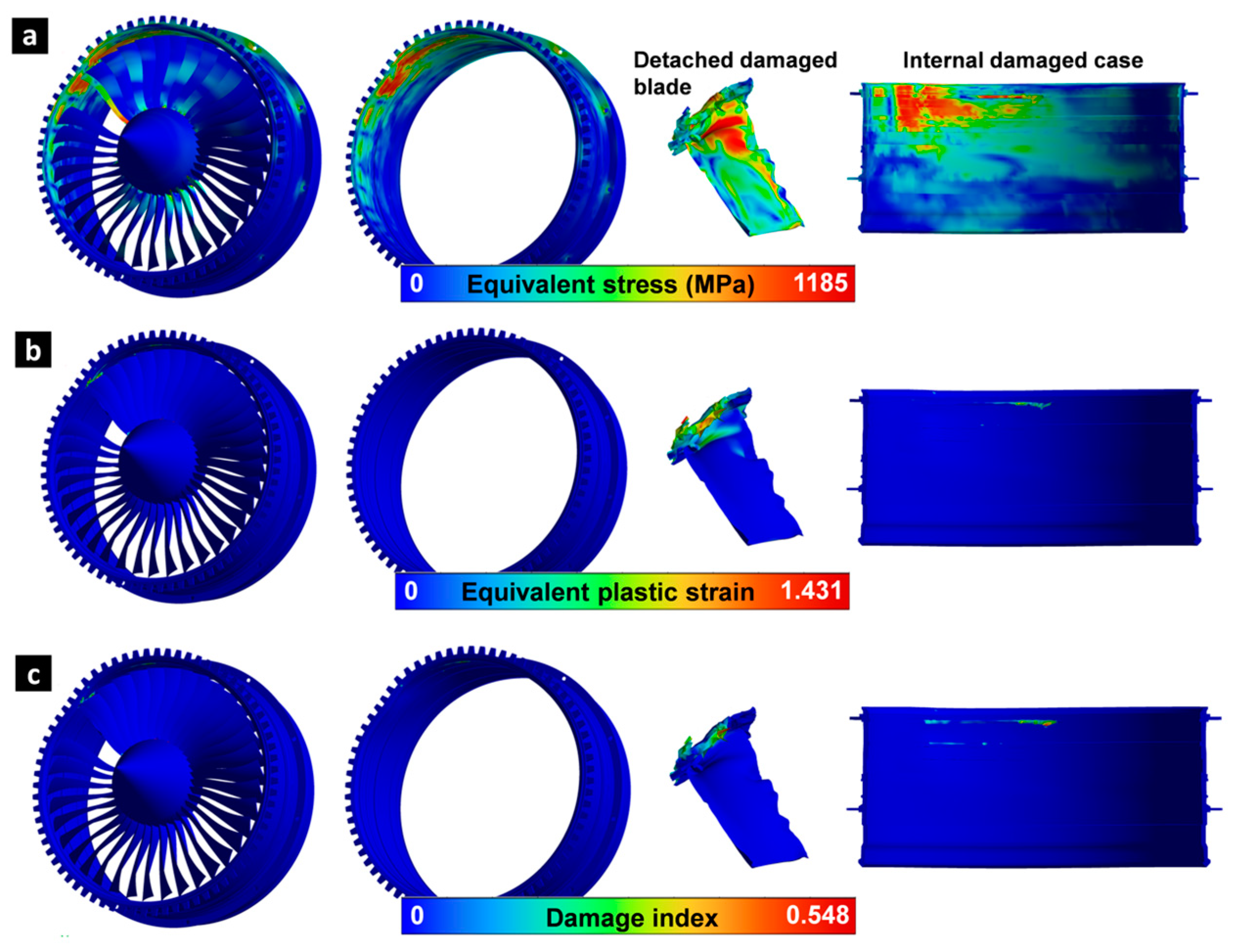
3.2. Aeroengine Blade-Out Containment Simulation Results Using the J-C Control Model

The blade-out containment simulation was conducted using the converged mesh and the Johnson-Cook control model parameters (Table 1). The structural response of key components, such as the detached blade, the casing, and the fan, was analyzed in terms of equivalent stress, equivalent plastic strain, and damage index. The results of the simulation are presented as contour plots in Figure 3 and summarized in

Table 2. Maximum reached values of the equivalent strain, stress, and damage index at the last simulated stage using the control model and the selected mesh.

Component	Stress (MPa)	Plastic Strain	Damage Index
Detached blade	1176	1.431	0.548
Case	1120	1.416	0.511
Fan	1185	0.728	0.179

, demonstrating the turbofan’s capacity to contain fan blades during impact. The simulation revealed that the detached blade exhibited localized plastic deformation, reaching a maximum equivalent plastic strain of 143% and a maximum stress of 1176 MPa. The casing successfully contained the blade, experiencing significant deformation near the impact region and reaching a maximum damage index of 0.55, suggesting compromised serviceability but no critical failure. The fan blades underwent plastic strain up to 0.73, with a maximum equivalent stress of 1185 MPa and a damage index of 0.179. While the casing experienced considerable deformation near the impact area, it successfully contained the blade. The fan and remaining blades deformed within acceptable limits, without fracture. The maximum damage index of 0.51 for the casing indicates that engine service was compromised but maintained a safety factor of approximately two for damage tolerance against explosion. These observations suggest a robust structural design capable of withstanding blade-out events without compromising overall aeroengine safety, providing a solid foundation for future research or design adjustments.

A sensitivity analysis is presented in the next section to ensure the result’s reliability. This sensitivity analysis considers the specific ranges of plastic strain rate, equivalent plastic strain, temperature, and stress triaxiality observed at critical points in the blade and the casing during a simulated blade detachment event under operational conditions. These ranges are plastic strain rate—0 to 1.2 × 10⁴ s⁻¹ (blade) and 0 to 1.1 × 10⁴ s⁻¹ (casing); temperature—25 °C to 700 °C (blade) and 25 °C to 400 °C (casing); and stress triaxiality—−0.6 to 0.5 (blade) and −2.7 to 0.7 (casing).

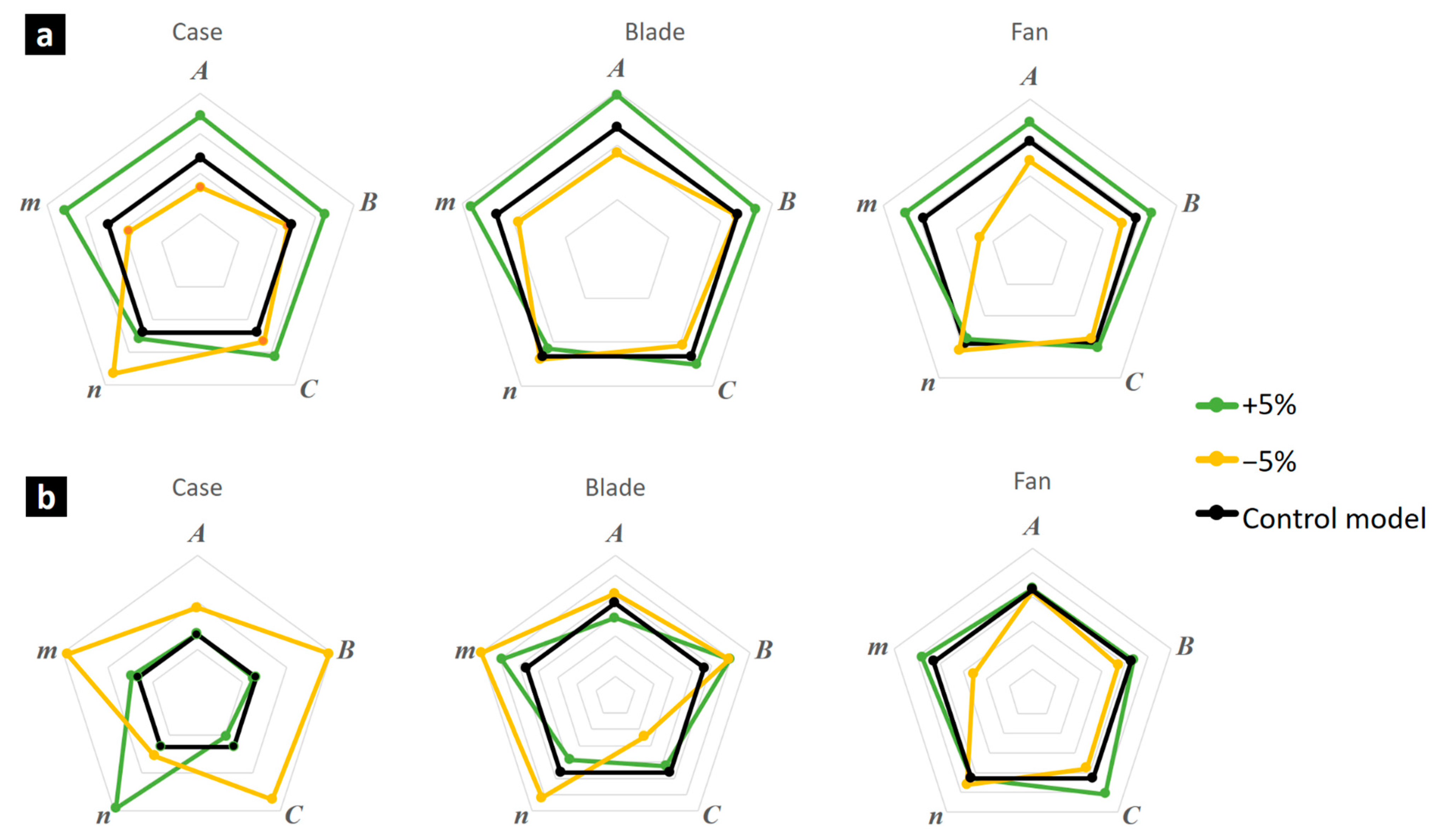
3.3. Influence of J-C Parameter Variation on Plasticity in a Aeroengine Blade-Out Scenario

Numerical simulations of a fan blade-out event in a full aeroengine model were conducted to assess the influence of Johnson-Cook plasticity parameters (A, B, n, C, and m) on equivalent stress and equivalent plastic strain at the last stage of the simulation. Each parameter was varied by ±5%, and the resulting percentage changes in stress and strain were recorded. The relative error between the results from the control model and the model with variations was calculated and presented in star plots to visualize the sensitivity of plasticity model parameters on the plastic stress and strain response (Figure 4). These observed changes in simulation results arise from the complex interplay between component impact interactions and altered stress/strain distributions due to variations in Johnson-Cook model parameters. In addition, the complex geometry leads to nonlinear interactions between the large deformations of the blade and the casing, making a precise explanation and quantification of parameter sensitivity challenging. While general trends are discernible (e.g., increasing A elevates stress), accurately determining the magnitude of these effects necessitates detailed simulations such as those presented here.

Analyzing the simulation results for parameter A, a 5% increase caused a general stress increase in all components, most notably in the case (4.58%). Strain changes were minimal. Conversely, a 5% decrease in A led to a stress reduction, with the largest decrease in the case (−3.26%). However, strain increased in the case (2.03%). These trends are explained by the nature of the material behavior and the resulting identified J-C model. Increasing the initial yield strength (A) directly elevates material strength, leading to higher stresses. Consequently, a stronger case (higher A) requires less strain to absorb the impact energy.

Parameters B and n govern strain hardening. Increasing either results in larger stress, increases strain, and potentially lowers strain accumulation, particularly in the case. This was observed when a 5% increase in B caused a stress increase in the case of 3.79%, and in the fan, it caused a stress increase of 1.73%. Strain showed a negative variation in the case (−0.2%) and increases in both the blade (4.62%) and the fan (1.33%). This increase may be explained by the fact that the casing becomes more rigid, forcing the blades to deform at a higher level. Decreasing B resulted in slight stress reductions across all components, with the case experiencing the largest decrease (−0.45%). The strain in the case, as expected, increased by 5.76%. In the variations in the hardening coefficient n, the 5% increase also produced higher stress in all components, as expected: 0.85% in the case and 0.6% in the fan. Decreasing n by 5% resulted in a stress increase in the case of 5.66%, along with minimal increases in the blade (0.33%) and in the fan (0.93%). This could be attributed to the higher localized impact, as the blade became stronger, producing a higher deformation in the case, and, consequently, higher stress than the effect of decreasing n. Strain increased in all components when decreasing n; 5.42% in the blade and 4.60% in the fan, with a lower effect in the case (0.85%).

Regarding m, a 5% increase led to increases in stress and strain, which were most pronounced in the case (which had a 5.01% stress increase and a 0.51% strain increase) and the blade (which had a 2.06% stress increase), along with a strain increase in the fan (7.12%). A 5% decrease in m caused stress to decrease in all components, most noticeably in the fan (−6.51%), while strain increased in the case (5.64%) and the blade (8.21%), and decreased significantly in the fan (−23.52%). Increasing the thermal softening exponent (m) clearly reduces strength at higher temperatures. Given the constant impact energy, which was absorbed as plastic energy and the consequent temperature increase in the softened material, the blade especially reached a higher level of plastic deformation compared to the case in all simulations, and, consequently, higher softening due to the m variation. This increases its sensitivity, exhibiting higher plastic strain during the impact.

Elevating the strain rate factor (C) strengthens the material, increasing stress, and localizing deformations. The 5% increase in C increased stress in the case, as expected, by 3.28% and, to a lesser extent, the blade by 0.78% and the fan by 0.46%. The strain decreased by −0.97% in the case, and in the blade, it decreased by −1.24% but increased significantly in the fan by 11.62%. Reducing C by 5% yielded mixed results for stress and strain. Case stress increased by 1.21%, while blade and fan stress decreased by −1.08% and −0.68%, respectively. The strain increased by 4.88% in the case, possibly due to the more localized impact; as in the blade it decreased by −7.61%, and in the fan, it decreased by −6.43%.

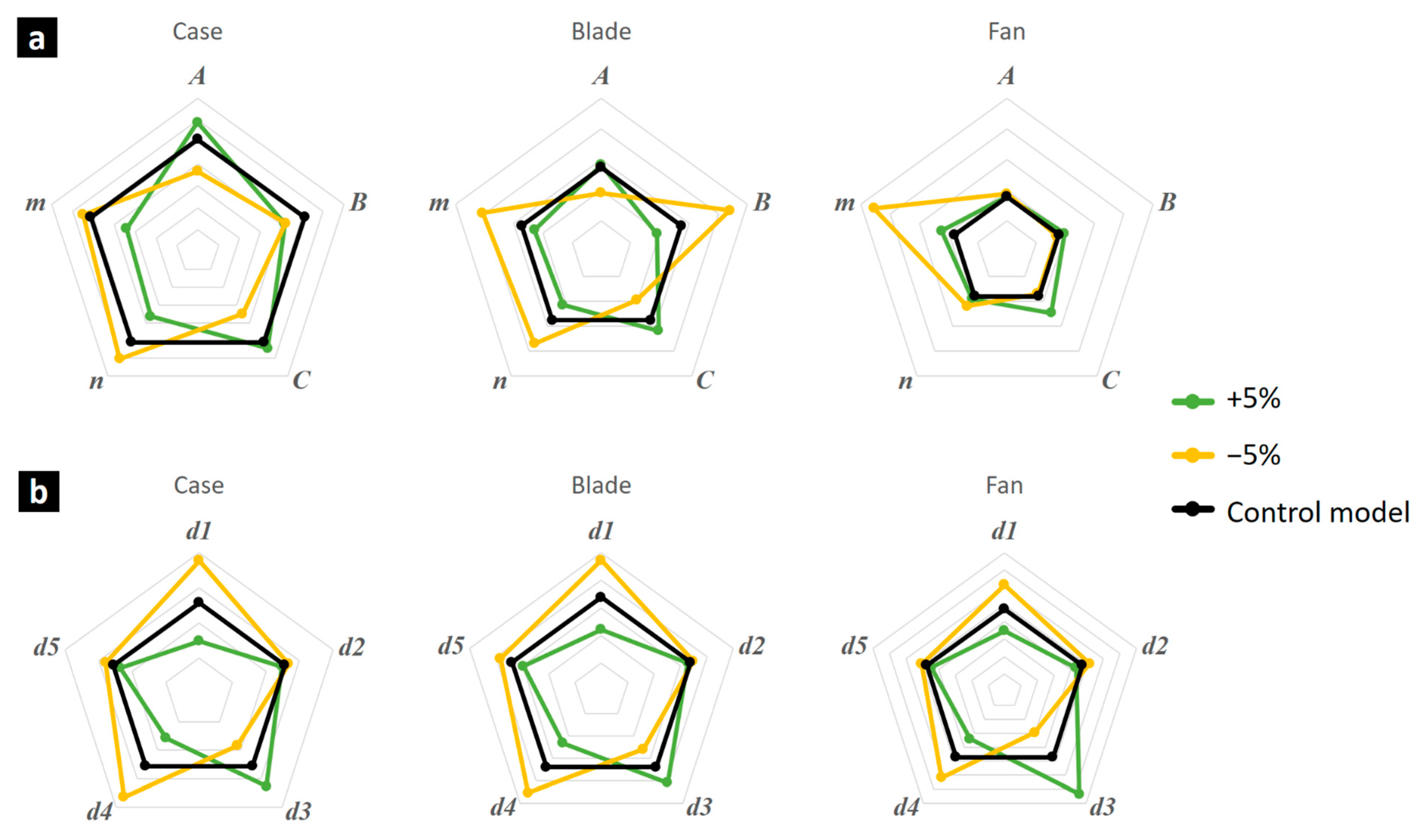
3.4. Influence of J-C Parameter Variation on Damage Evolution of Aeroengine Blade-Out

The sensitivity analysis assessing the impact of ±5% variations in Johnson-Cook parameters on damage in aeroengine components is shown in Figure 5 in two groups: plasticity model and damage model parameters. The results reveal that a 5% increase in parameter A caused a considerable damage increase in the casing (+15.48%), and minor increases in the blade (+3.4%) and fan (+0.73%). A 5% decrease drastically reduced damage in the casing (−28.28%) and the blade (−30.15%), slightly increasing fan damage (+5.63%). Parameter B, with the 5% increase, significantly increased fan damage (+10.34%), while reducing casing (−18.22%) and blade damage (−30.79%). Decreasing B had mixed effects, reducing casing damage (−17.79%) but significantly increasing blade damage (+60.79%).

Increasing C increased damage across all components, most notably in the fan (+38.08%). A 5% decrease substantially reduced casing (−31.43%) and blade damage (−28.64%).

In total, the 5% increase in both n (hardening coefficient) and m (thermal coefficient) significantly reduced casing and blade damage. Decreasing n increased blade and fan damage, while decreasing m, which substantially increased damage across all components, especially in the fan (+155.27%).

For the damage model parameters (d1–d5), d1 had the most pronounced effect on damage across all components, while d2 had the lowest effect. Parameter d3 strongly influenced fan damage, d4 caused similar changes across all components, and d5 had a minimal impact.

Figure 6 shows the influence of deterministic Johnson-Cook plasticity and damage model parameters on the damage index in order, from most influential to less influential in the fan, casing, and the blade (detached blade). Note that decreasing the thermal softening exponent (m) had a disproportionately large impact on fan damage. Because the initial damage index in the fan obtained with the J-C control model was very low (0.179), any increase appears as a large percentage change, even if the absolute change is relatively small. A 5% decrease in m accelerates thermal softening, leading to more extensive damage propagation in the fan during the blade-out event. While a 155.27% increase sounds dramatic, it represents an absolute increase of only 0.093 in the damage index. This seemingly small change is significant because the damage obtained from the control model is so low. Essentially, the sensitivity is amplified by the low initial value.

While fan damage is a major concern, the integrity of the casing is most critical to the safety of the aircraft, acting as the primary containment barrier during a blade-out or other engine failure event. In this critical component, the thermal coefficient (m) also had the largest influence on damage (±33%), followed by the strain rate hardening coefficient (C), and the strain hardening exponent (n), yield strength (A), and parameter B. Parameter d1 exhibited the most substantial effect on damage prediction; a 5% increase in d1 resulted in a decrease in predicted damage, while a 5% decrease led to an increase. Conversely, d2 demonstrated a minimal impact on damage (around ±0.4%). The parameters d4, d3, and d5 followed d1 in order of influence on both the case and the detached blade damage.

4. Conclusions

This study conducted a comprehensive local sensitivity analysis of the Johnson-Cook plasticity and the progressive damage model for Ti-6Al-4V titanium alloy, a crucial material constituting 14% of modern aircraft weight, and which is commonly used in aeroengine components. The analysis focused on identifying the most influential JC parameters affecting the predicted structural response of these components during a blade-out event. A preliminary mesh convergence study, using a fine mesh with an average orthogonal quality of 0.81, ensured the accuracy and reliability of the subsequent sensitivity analysis. The convergence study demonstrated an acceptable convergence of the maximum equivalent stress in both the casing impact zone (2.6% difference between medium and fine meshes) and the blade (0.8% difference between medium and fine meshes). A fractional error approach further validated the observed convergence.

The blade-out containment simulation, performed with the converged mesh, revealed key aspects of the structural behavior:

• Nonlinear behavior during blade detachment, characterized by rapid stress and deformation propagation, localized casing deformation due to the high-energy blade impact, and the maximum equivalent plastic strain of 143% in the detached blade, 142% in the casing, and 73% in the fan.
• A maximum damage index of 0.55 in the casing, indicating potential damage but below critical failure levels for affecting the structural integrity of the aircraft.

The sensitivity analysis, involving ±5% variations in JC parameters, revealed the following:

• A strong dependence of damage predictions on specific model parameters, particularly the thermal softening coefficient (m). Variations in m resulted in ±33% changes in casing damage, highlighting its critical role in accurate damage prediction.
• Other influential parameters, in decreasing order of importance, include the strain rate hardening coefficient (C), the strain hardening exponent (n), and yield strength (A). Parameters B, d1, d4, and d3 exhibited moderate to minor influence, while d5 and d2 showed a minimal impact on casing damage.

This work underscores the importance of precisely calibrating JC model parameters, especially m, for reliable assessments of aeroengine casing integrity during blade-out events. The identified sensitivities provide essential data for robust design and safety evaluations of aeroengine components. This local sensitivity analysis highlights the individual influence of Johnson-Cook model parameters. To further improve the accuracy and reliability of damage predictions in aeroengine applications, future research should investigate global sensitivity analyses that consider parameter interactions. Additionally, the coupled effects of temperature and strain rate, which are not captured by the standard J-C model, should be explored using modified models. This would provide a more comprehensive understanding of the model’s behavior and contribute to improved safety and performance in aeroengine design.