Analysis of Radio Science Data from the KaT Instrument of the 3GM Experiment During JUICE’s Early Cruise Phase
Abstract
:1. Introduction
2. 3GM Experiment
- The determination of Ganymede’s gravity field, at least to degree and order 30.
- The measurement of Ganymede complex tidal Love number with an accuracy better than 0.001 at the orbital frequency.
- The measurement of selected tidal Love numbers associated with inter-satellite tides.
- The measurement of Ganymede rotational state.
- Determination of Callisto’s tidal Love number k2 with an absolute uncertainty better than 0.06.
- The measurement of Callisto’s gravity field at least to degree and order 3 (with an accuracy for J3 better than 4 × 10−8).
- The determination of Europa’s unconstrained J2 and C22 gravity coefficients with 1–2% relative uncertainties.
- The improvement of the ephemerides of the Galilean moons [13].
2.1. Radio Tracking System and Links
2.2. Observation Campaigns
3. Orbit Determination Setup
3.1. Dynamical Model
3.2. Observational Model
3.3. Filter Setup and Estimated Parameters
4. Results
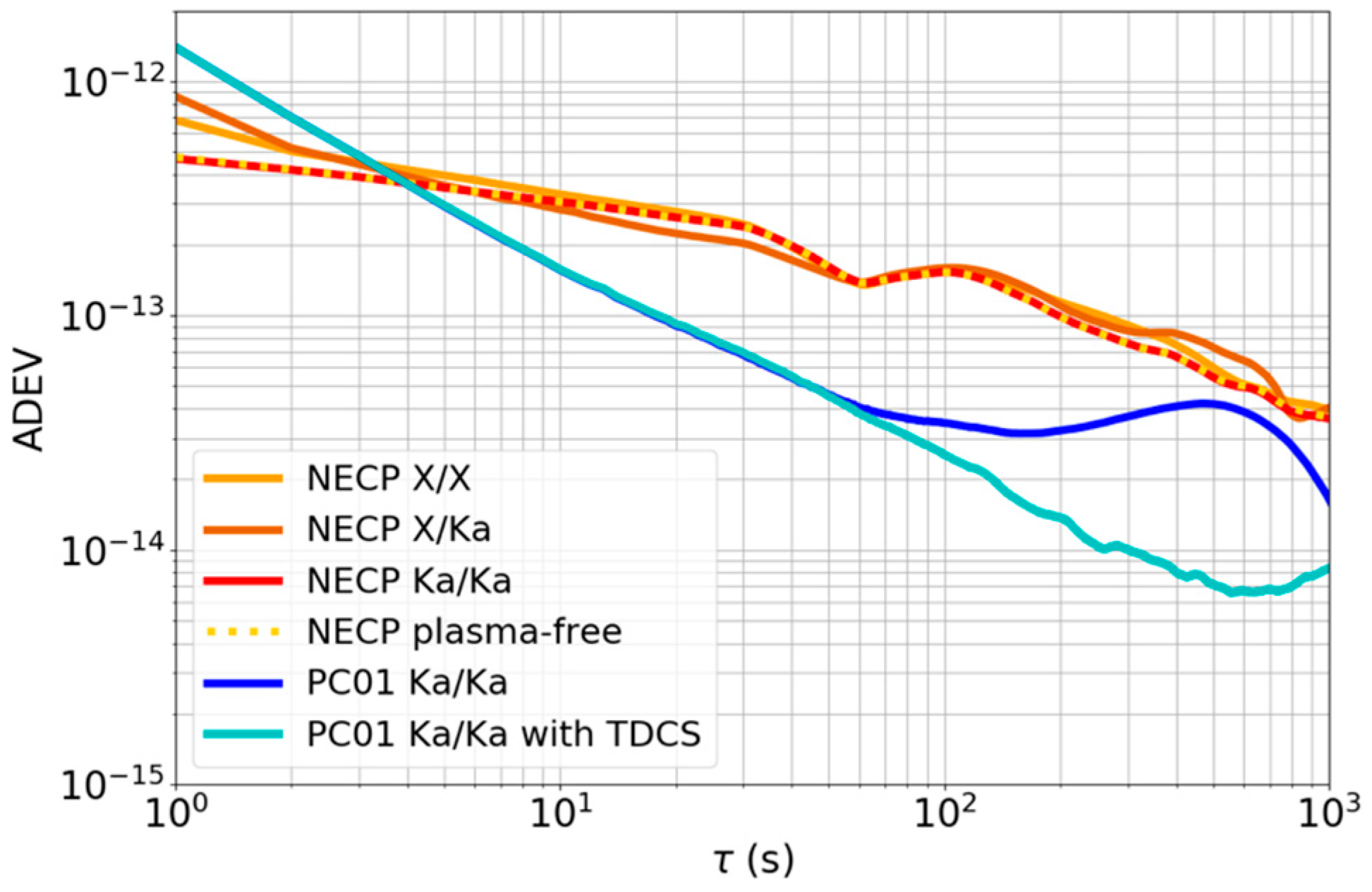
4.1. Orbit Determination Software Comparison
4.2. Data Quality
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grasset, O.; Dougherty, M.; Coustenis, A.; Bunce, E.; Erd, C.; Titov, D.; Blanc, M.; Coates, A.; Drossart, P.; Fletcher, L.; et al. JUpiter ICy moons Explorer (JUICE): An ESA mission to orbit Ganymede and to characterise the Jupiter system. Planet. Space Sci. 2013, 78, 1–21. [Google Scholar] [CrossRef]
- Tosi, F.; Roatsch, T.; Galli, A.; Hauber, E.; Lucchetti, A.; Molyneux, P.; Stephan, K.; Achilleos, N.; Bovolo, F.; Carter, J.; et al. Characterization of the Surfaces and Near-Surface Atmospheres of Ganymede, Europa and Callisto by JUICE. Space Sci. Rev. 2024, 220, 59. [Google Scholar] [CrossRef]
- Buccino, D.R.; Parisi, M.; Gramigna, E.; Gomez-Casajus, L.; Tortora, P.; Zannoni, M.; Caruso, A.; Park, R.S.; Withers, P.; Steffes, P.; et al. Ganymede’s Ionosphere Observed by a Dual-Frequency Radio Occultation With Juno. Geophys. Res. Lett. 2022, 49, e2022GL098420. [Google Scholar] [CrossRef]
- Fletcher, L.N.; Cavalié, T.; Grassi, D.; Hueso, R.; Lara, L.M.; Kaspi, Y.; Galanti, E.; Greathouse, T.K.; Molyneux, P.M.; Galand, M.; et al. Jupiter Science Enabled by ESA’s Jupiter Icy Moons Explorer. Space Sci. Rev. 2023, 219, 53. [Google Scholar] [CrossRef]
- Feltens, J.; Bellei, G.; Springer, T.; Kints, M.V.; Zandbergen, R.; Budnik, F.; Schönemann, E. Tropospheric and ionospheric media calibrations based on global navigation satellite system observation data. J. Space Weather Space Clim. 2018, 8, A30. [Google Scholar] [CrossRef]
- Lasagni Manghi, R.; Bernacchia, D.; Casajus, L.G.; Zannoni, M.; Tortora, P.; Martellucci, A.; De Vicente, J.; Villalvilla, J.; Maschwitz, G.; Cappuccio, P.; et al. Tropospheric Delay Calibration System Performance During the First Two BepiColombo Solar Conjunctions. Radio Sci. 2023, 58, e2022RS007614. [Google Scholar] [CrossRef]
- Lasagni Manghi, R.; Zannoni, M.; Tortora, P.; Martellucci, A.; De Vicente, J.; Villalvilla, J.; Mercolino, M.; Maschwitz, G.; Rose, T. Performance Characterization of ESA’s Tropospheric Delay Calibration System for Advanced Radio Science Experiments. Radio Sci. 2021, 56, e2021RS007330. [Google Scholar] [CrossRef]
- Evans, S.; Taber, W.; Drain, T.; Smith, J.; Wu, H.-C.; Guevara, M.; Sunseri, R.; Evans, J. MONTE: The next generation of mission design and navigation software. CEAS Space J. 2018, 10, 79–86. [Google Scholar] [CrossRef]
- Cappuccio, P.; Di Benedetto, M.; Durante, D.; Iess, L. Callisto and Europa Gravity Measurements from JUICE 3GM Experiment Simulation. Planet. Sci. J. 2022, 3, 199. [Google Scholar] [CrossRef]
- Cappuccio, P.; Hickey, A.; Durante, D.; Di Benedetto, M.; Iess, L.; De Marchi, F.; Plainaki, C.; Milillo, A.; Mura, A. Ganymede’s gravity, tides and rotational state from JUICE’s 3GM experiment simulation. Planet. Space Sci. 2020, 187, 104902. [Google Scholar] [CrossRef]
- Van Hoolst, T.; Tobie, G.; Vallat, C.; Altobelli, N.; Bruzzone, L.; Cao, H.; Dirkx, D.; Genova, A.; Hussmann, H.; Iess, L.; et al. Geophysical Characterization of the Interiors of Ganymede, Callisto and Europa by ESA’s JUpiter ICy moons Explorer. Space Sci. Rev. 2024, 220, 54. [Google Scholar] [CrossRef]
- Iafolla, V.; Fiorenza, E.; Lefevre, C.; Morbidini, A.; Nozzoli, S.; Peron, R.; Persichini, M.; Reale, A.; Santoli, F. Italian Spring Accelerometer (ISA): A fundamental support to BepiColombo Radio Science Experiments. Planet. Space Sci. 2010, 58, 300–308. [Google Scholar] [CrossRef]
- Fayolle, M.; Magnanini, A.; Lainey, V.; Dirkx, D.; Zannoni, M.; Tortora, P. Combining astrometry and JUICE-Europa Clipper radio science to improve the ephemerides of the Galilean moons. Astron. Astrophys. 2023, 677, A42. [Google Scholar] [CrossRef]
- De Marchi, F.; Gaetano, D.A.; Giuseppe, M.; Paolo, C.; Ivan, D.S.; Mauro, D.B.; Luciano, I. Observability of Ganymede’s gravity anomalies related to surface features by the 3GM experiment onboard ESA’s JUpiter ICy moons Explorer (JUICE) mission. Icarus 2021, 354, 114003. [Google Scholar] [CrossRef]
- De Marchi, F.; Cappuccio, P.; Mitri, G.; Iess, L. Frequency-dependent Ganymede’s tidal Love number k2 detection by JUICE’s 3GM experiment and implications for the subsurface ocean thickness. Icarus 2022, 386, 115150. [Google Scholar] [CrossRef]
- di Stefano, I.; Cappuccio, P.; Di Benedetto, M.; Iess, L. A test of general relativity with ESA’s JUICE mission. Adv. Space Res. 2022, 70, 854–862. [Google Scholar] [CrossRef]
- Cappuccio, P.; di Stefano, I.; Cascioli, G.; Iess, L. Comparison of light-time formulations in the post-Newtonian framework for the BepiColombo MORE experiment. Class. Quantum Gravity 2021, 38, 227001. [Google Scholar] [CrossRef]
- CCSDS Secretariat. PSEUDO-NOISE (PN) RANGING SYSTEMS. Washington, DC, USA. 2014. Available online: https://public.ccsds.org/Pubs/414x0g2.pdf (accessed on 10 October 2024).
- Bertotti, B.; Comoretto, G.; Iess, L. Doppler tracking of spacecraft with multi-frequency links. Astron. Astrophys. 1993, 269, 608–616. [Google Scholar]
- Iess, L.; Asmar, S.W.; Cappuccio, P.; Cascioli, G.; De Marchi, F.; di Stefano, I.; Genova, A.; Ashby, N.; Barriot, J.P.; Bender, P.; et al. Gravity, Geodesy and Fundamental Physics with BepiColombo’s MORE Investigation. Space Sci. Rev. 2021, 217, 21. [Google Scholar] [CrossRef]
- Cappuccio, P.; Notaro, V.; di Ruscio, A.; Iess, L.; Genova, A.; Durante, D.; di Stefano, I.; Asmar, S.W.; Ciarcia, S.; Simone, L. Report on first inflight data of bepicolombo’s mercury orbiter radio science experiment. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4984–4988. [Google Scholar] [CrossRef]
- Park, R.S.; Folkner, W.M.; Williams, J.G.; Boggs, D.H. The JPL Planetary and Lunar Ephemerides DE440 and DE441. Astron. J. 2021, 161, 105. [Google Scholar] [CrossRef]
- di Stefano, I.; Cappuccio, P.; Iess, L. Precise Modeling of Non-Gravitational Accelerations of the Spacecraft BepiColombo During Cruise Phase. J. Spacecr. Rocket. 2023, 60, 1625–1638. [Google Scholar] [CrossRef]
- ESA SPICE Service. JUICE SPICE Kernel Dataset; European Space Agency: Paris, France, 2024. [Google Scholar] [CrossRef]
- Moyer, T.D. Range and Doppler Tracking Observables 3.1 The Tracking Link. In JPL DEEP SPACE COMMUNICATIONS AND NAVIGATION SERIES; 2000. Available online: https://descanso.jpl.nasa.gov/monograph/series2/Descanso2_all.pdf (accessed on 27 September 2024).
- Springer, T.A.; Dow, J.M. NAPEOS: Mathematical Models and Algorithms; ESOC: Darmstadt, Germany, 2009. [Google Scholar]
- Petit, G.; Luzum, B. IERS Conventions (2010). 2010. Available online: https://www.iers.org/IERS/EN/Publications/TechnicalNotes/tn36.html (accessed on 21 May 2024).
- Wallace, P.T.; Capitaine, N. Precession-nutation procedures consistent with IAU 2006 resolutions. Astron. Astrophys 2007, 464, 793. [Google Scholar] [CrossRef]
- Moyer, T. Formulation for Observed and Computed Values of Deep Space Network Data Types for Navigation; John-Wiley & Sons, Inc.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Tapley, B.; Schutz, B.; Born, G.H. Statistical Orbit Determination; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Zannoni, M.; Tortora, P. Numerical error in interplanetary orbit determination software. J. Guid. Control Dyn. 2013, 36, 1008–1018. [Google Scholar] [CrossRef]
- Mariotti, G.; Tortora, P. Experimental validation of a dual uplink multifrequency dispersive noise calibration scheme for Deep Space tracking. Radio Sci. 2013, 48, 111–117. [Google Scholar] [CrossRef]
- Buccino, D.R.; Oudrhiri, K.; Parisi, M.; Park, R.S.; Mazarico, E.; Tortora, P.; Withers, P.; Genova, A.; Zannoni, M. Precision of Spacecraft Doppler Tracking at Low Signal-To-Noise Ratios. Radio Sci. 2023, 58, e2023RS007703. [Google Scholar] [CrossRef]
- Notaro, V.; Iess, L.; Armstrong, J.W.; Asmar, S.W. Reducing Doppler noise with multi-station tracking: The Cassini test case. Acta Astronaut. 2020, 173, 45–52. [Google Scholar] [CrossRef]
- Armstrong, J.W.; Estabrook, F.B.; Asmar, S.W.; Iess, L.; Tortora, P. Reducing antenna mechanical noise in precision spacecraft tracking. Radio Sci. 2008, 43, RS3010. [Google Scholar] [CrossRef]
- Papoulis, A.; Hoffman, J.G. Probability, Random Variables, and Stochastic Processes, 4th ed.; Papoulis, A., Pillai, S.U., Eds.; McGraw-Hill: Boston, MA, USA, 2002. [Google Scholar]
- Townsend, R.H.D. Fast calculation of the lomb-scargle periodogram using graphics processing units. Astrophys. J. Suppl. Ser. 2010, 191, 247–253. [Google Scholar] [CrossRef]
- Riley, W.J.; Howe, D. Handbook of Frequency Stability Analysis; National Institute of Standards and Technology: Boulder, CO, USA, 2008; Volume 31. [Google Scholar]
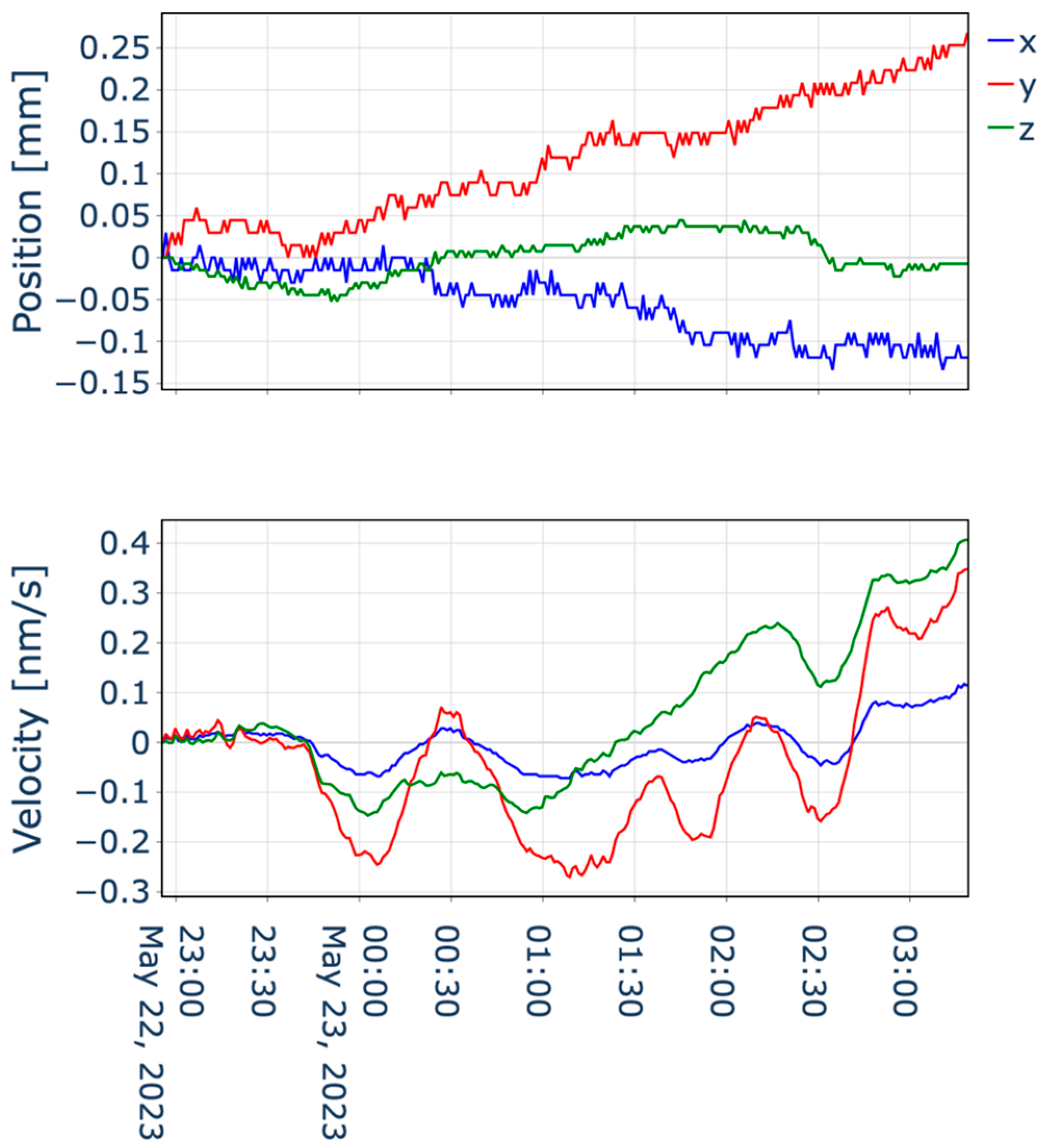

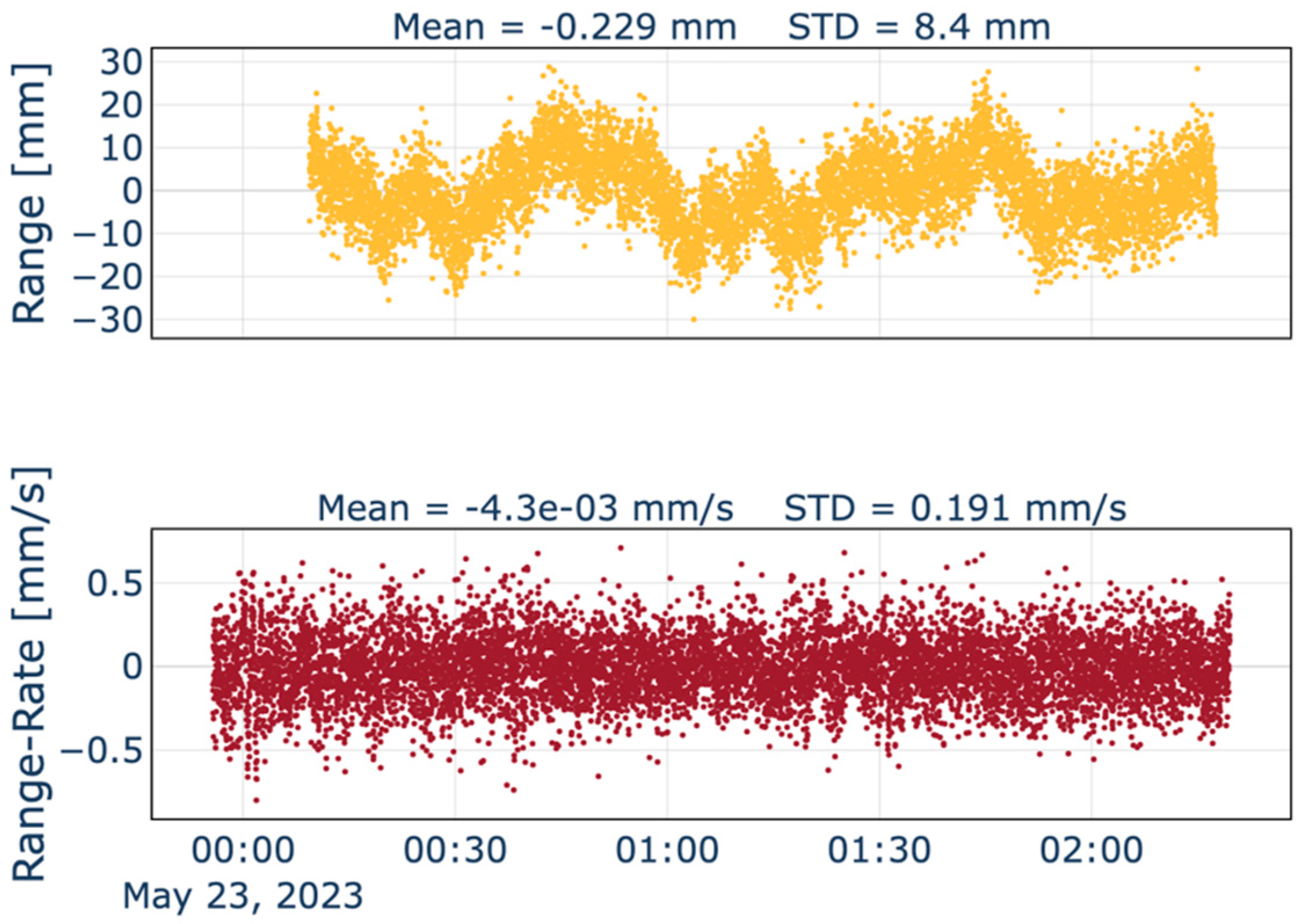

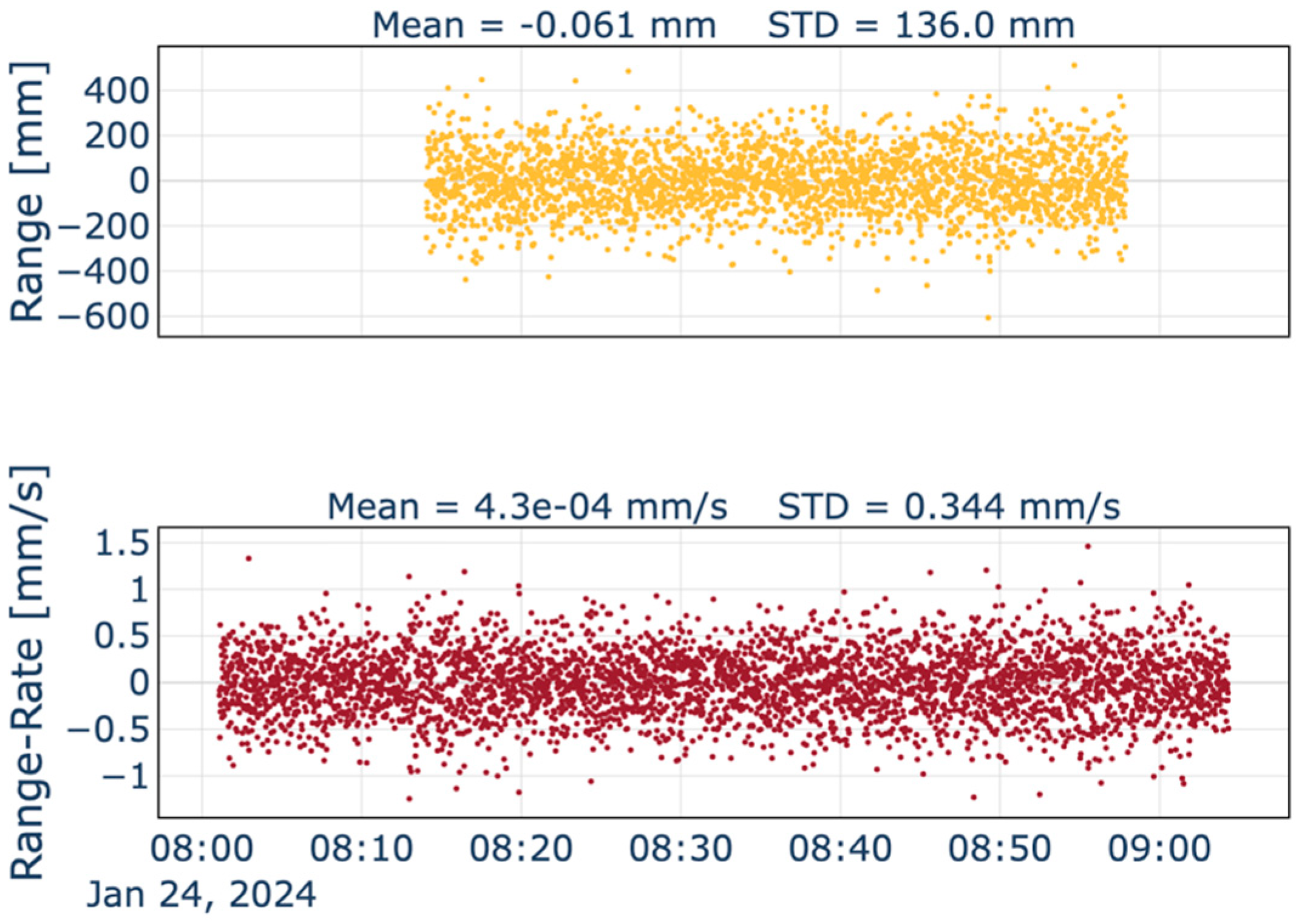
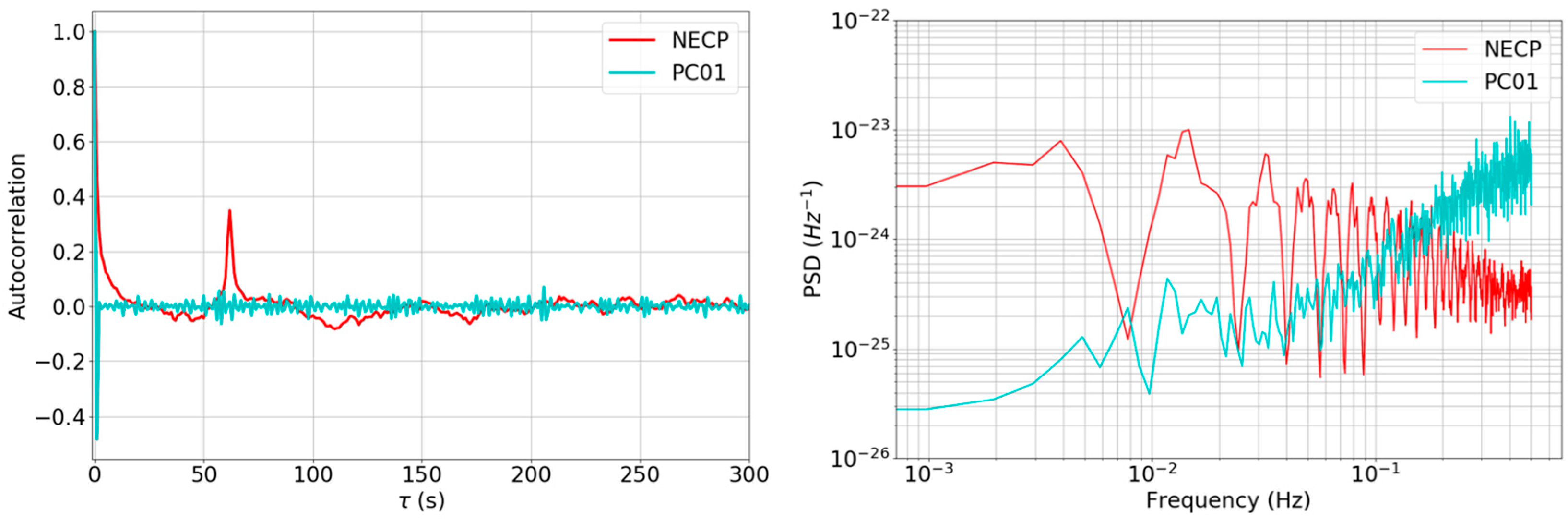
| Campaign | Test Duration | Link | Tropospheric Calibration | Earth-JUICE Distance | Sun-JUICE Distance | Round Trip Light Time |
|---|---|---|---|---|---|---|
| NECP | 125 min | Ka/Ka, X/X, X/Ka | GNSS | 0.06 AU | 1.05 AU | 62 s |
| PC01 | 65 min | Ka/Ka | TDCS and GNSS | 0.26 AU | 0.91 AU | 260 s |
| Surface Element | Effective Area | |
|---|---|---|
| Solar panel (x2) | 43.5 m2 | 0.19 |
| HGA | 5.1 m2 | 0.86 |
| Bus | 2.7 m2 | 0.48 |
| Parameter | Nominal Value | A Priori Uncertainty |
|---|---|---|
| JUICE position and velocity | From SPICE kernels [24] | 100 km and 1 m/s per component |
| Station location | From ESA database | 10 cm per component |
| Solar radiation pressure scale factor | 1.0 | 0.05 |
| Parameter | Difference Between Estimated Values | Formal Uncertainty |
|---|---|---|
| Spacecraft initial position [km] | X 0.006 Y 0.003 Z 0.079 | 7.6 1.9 82.7 |
| Spacecraft initial velocity [mm/s] | X 0.055 Y 0.017 Z 0.010 | 24 164 542 |
| Station location [mm] | X 0.001 Y 0.002 | 100 * 100 * 100 * |
| Solar radiation pressure scale factor | 0.05 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cappuccio, P.; Sesta, A.; Di Benedetto, M.; Durante, D.; De Filippis, U.; di Stefano, I.; Iess, L.; Mackenzie, R.; Godard, B. Analysis of Radio Science Data from the KaT Instrument of the 3GM Experiment During JUICE’s Early Cruise Phase. Aerospace 2025, 12, 56. https://doi.org/10.3390/aerospace12010056
Cappuccio P, Sesta A, Di Benedetto M, Durante D, De Filippis U, di Stefano I, Iess L, Mackenzie R, Godard B. Analysis of Radio Science Data from the KaT Instrument of the 3GM Experiment During JUICE’s Early Cruise Phase. Aerospace. 2025; 12(1):56. https://doi.org/10.3390/aerospace12010056
Chicago/Turabian StyleCappuccio, Paolo, Andrea Sesta, Mauro Di Benedetto, Daniele Durante, Umberto De Filippis, Ivan di Stefano, Luciano Iess, Ruaraidh Mackenzie, and Bernard Godard. 2025. "Analysis of Radio Science Data from the KaT Instrument of the 3GM Experiment During JUICE’s Early Cruise Phase" Aerospace 12, no. 1: 56. https://doi.org/10.3390/aerospace12010056
APA StyleCappuccio, P., Sesta, A., Di Benedetto, M., Durante, D., De Filippis, U., di Stefano, I., Iess, L., Mackenzie, R., & Godard, B. (2025). Analysis of Radio Science Data from the KaT Instrument of the 3GM Experiment During JUICE’s Early Cruise Phase. Aerospace, 12(1), 56. https://doi.org/10.3390/aerospace12010056








