New Transonic Tests of HB-2 Hypersonic Standard Models in the VTI T-38 Trisonic Wind Tunnel
Abstract
:1. Introduction
2. Materials and Methods
2.1. HB-2 Standard Model
2.2. Test Facility
2.3. Wind Tunnel Balances
2.4. Measurement Uncertainty
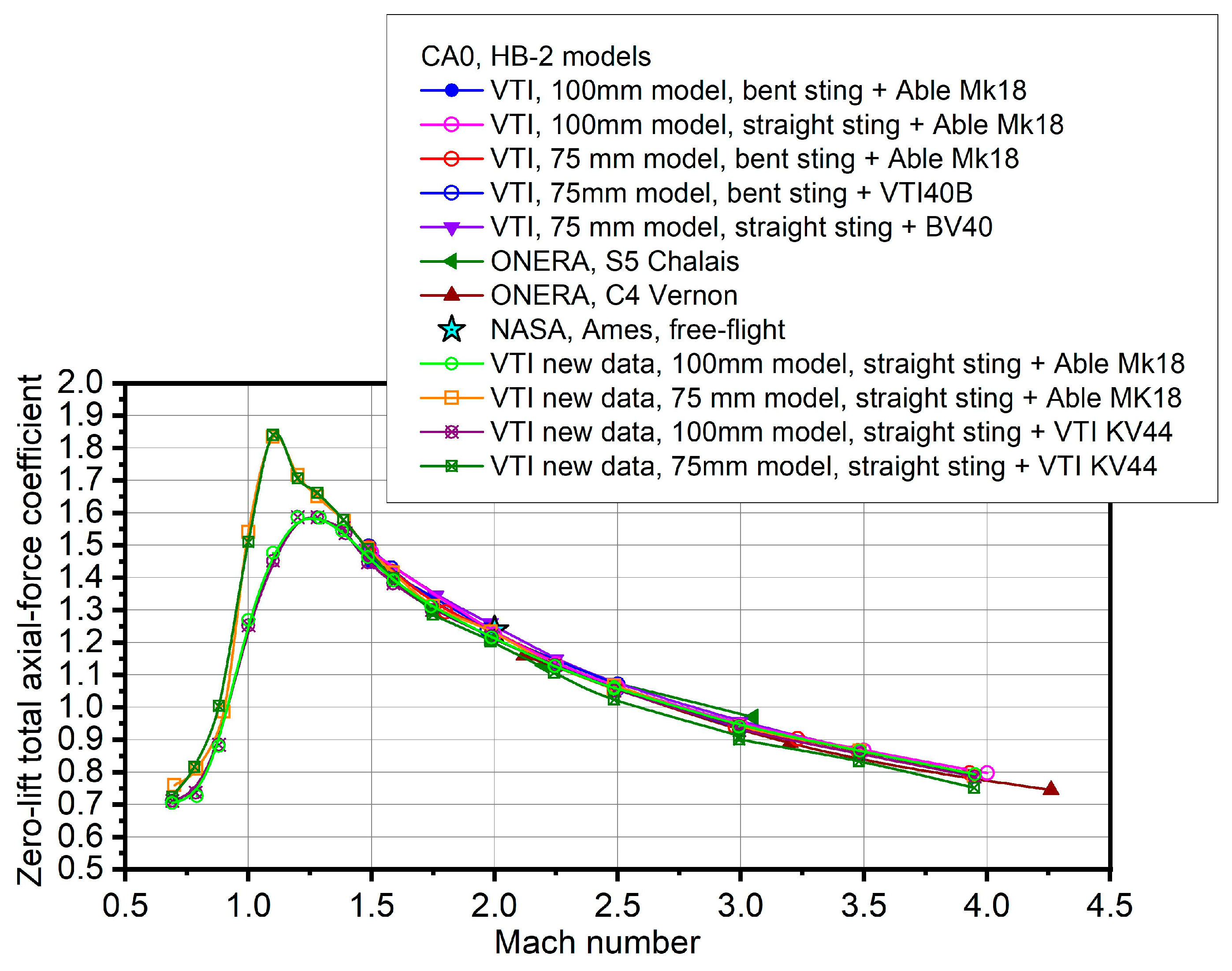
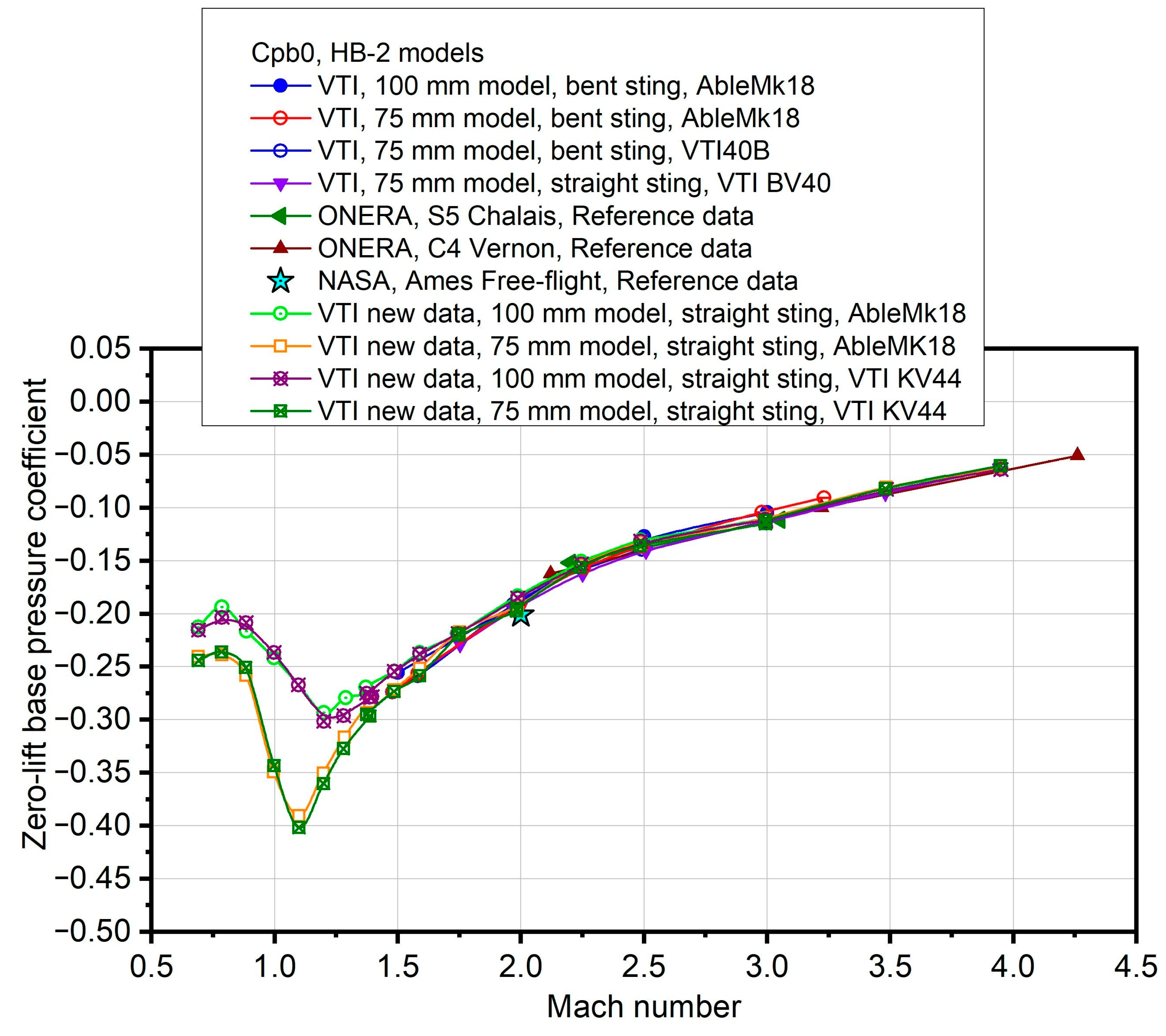
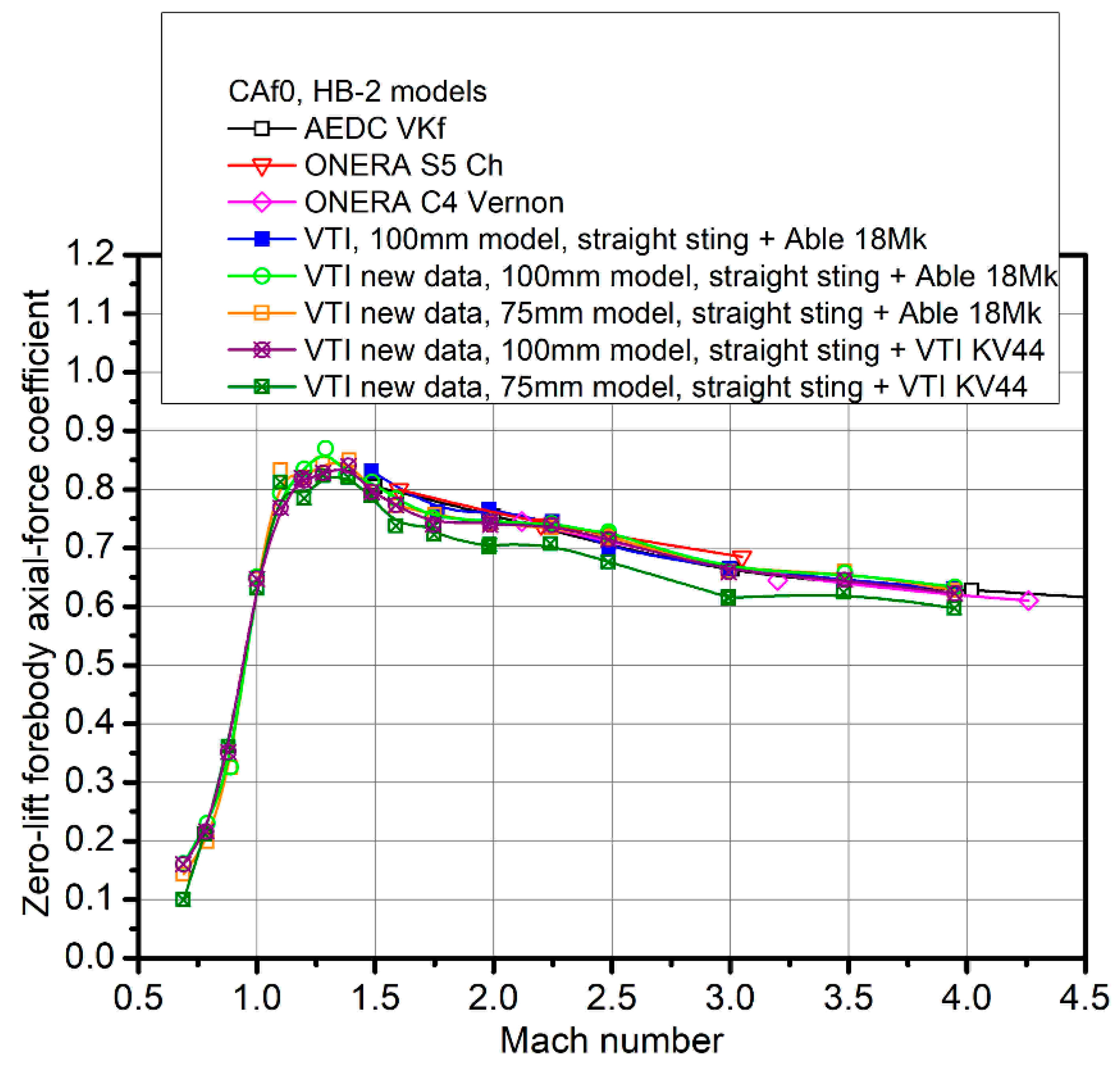
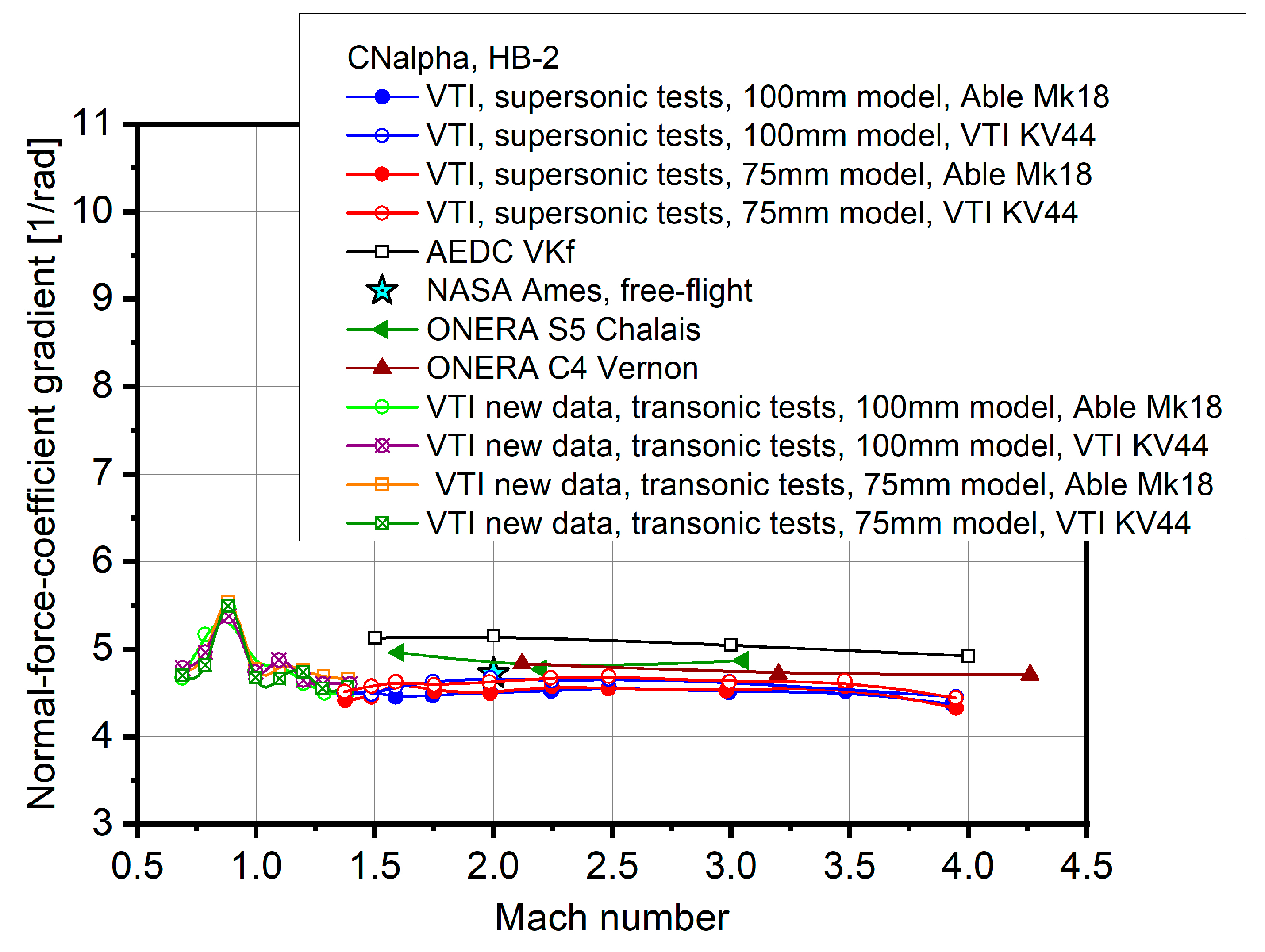
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Symbols
| D | Diameter of the model cylindrical forebody, m |
| M | Mach number |
| q | Dynamic pressure, bar, Pa |
| Re | Reynolds number, 1/m |
| Alpha | Total aerodynamic angle, ° |
| Phi | Aerodynamic roll angle, ° |
| σ | Standard deviation of the measured value |
| CNalpha | Normal-force-coefficient gradient, 1/rad |
| CA | Total-axial-force coefficient |
| CAf | Forebody-axial-force coefficient |
| CAb | Base-axial-force coefficient |
| Cpb | Base pressure coefficient |
| Sref | Model reference area, m2 |
| Sb | Model base area, m2 |
| Pst | Free-stream static pressure, bar, Pa |
| Pb | Base pressure, bar, Pa |
References
- Owen, F.K.; Owen, A.K. Measurement and Assessment of Wind Tunnel Flow Quality. Prog. Aerosp. Sci. 2008, 44, 315–348. [Google Scholar] [CrossRef]
- Philpott, D.R. Pressure Measurement in a Blowdown Wind Tunnel. Measurement 1985, 3, 107–114. [Google Scholar] [CrossRef]
- Reis, M.L.C.C.; Falcão Filho, J.B.P.; Moraes, L.F.G. The TTP Transonic Wind Tunnel Mach Number Uniformity Analysis. Measurement 2014, 51, 356–366. [Google Scholar] [CrossRef]
- Bobbit, C.; Everhart, J.; Foster, J.; Hill, J.; McHatton, R.; Tomek, W. National Transonic Facility Characterization Status. In Proceedings of the 38th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2000. [Google Scholar]
- Muylaert, J.; Walpot, L.; Haeuser, J.; Sagnier, P.; Devezeaux, D.; Papirnyk, O.; Lourme, D. Standard Model Testing in the European High Enthalpy Facility F4 and Extrapolation to Flight. In Proceedings of the 28th AIAA Joint Propulsion Conference and Exhibit, Nashville, TN, USA, 6–8 July 1992. [Google Scholar] [CrossRef]
- Hemsch, M.; Grubb, J.; Krieger, W.; Cler, D. Langley Wind Tunnel Data Quality Assurance: Check Standard Results. In Proceedings of the 21st AIAA Advanced Measurement Technology and Ground Testing Conference, Denver, CO, USA, 19–22 June 2000. [Google Scholar]
- DeLoach, R. Check-Standard Testing Across Multiple Transonic Wind Tunnels with the Modern Design of Experiments. In Proceedings of the 28th Aerodynamic Measurement Technology, Ground Testing, and Flight Testing Conference, New Orleans, LA, USA, 25–28 June 2012. [Google Scholar] [CrossRef]
- Ulbrich, N.M.; Amaya, M.A.; Flach, R. Use of the Ames Check Standard Model for the Validation of Wall Interference Corrections. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- Vassberg, J.; Dehaan, M.; Rivers, M.; Wahls, R. Development of a Common Research Model for Applied CFD Validation Studies. In Proceedings of the 26th AIAA Applied Aerodynamics Conference, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar] [CrossRef]
- Damljanović, D.; Vuković, Đ.; Ocokoljić, G.; Ilić, B.; Rašuo, B. Wind tunnel testing of standard models at off-design conditions. Aerospace 2021, 8, 275. [Google Scholar] [CrossRef]
- Damljanović, D.; Vuković, Đ.; Ilić, B.; Ocokoljić, G. Wind Tunnel Testing of HB-2 Hypersonic Standard Models in Non-Standard Transonic Conditions. In Proceedings of the 57th 3AF International Conference on Applied Aerodynamics, Bordeaux, France, 29–31 March 2023. [Google Scholar]
- Gray, J.D. Summary Report on Aerodynamic Characteristics of Standard Models HB-1 and HB-2; AEDC-TDR-64-137; Arnold Engineering Development Center: Tullahoma, TN, USA, 1964. [Google Scholar]
- Damljanović, D.; Rašuo, B.; Vuković, Ð.; Mandić, S.; Isaković, J. Hypervelocity ballistic reference models as experimental supersonic test cases. Aerosp. Sci. Technol. 2016, 52, 189–197. [Google Scholar] [CrossRef]
- Elfstrom, G.M.; Medved, B. The Yugoslav 1.5 m Trisonic Blowdown Wind Tunnel. In Proceedings of the 14th AIAA Aerodynamic Testing Conference, a Collection of Technical Papers, West Palm Beach, FL, USA, 5–7 March 1986. [Google Scholar]
- Elfstrom, G.M.; Medved, B.; Rainbird, W.J. Optimum porosity for an inclined-hole transonic test section wall treated for edgetone noise reduction. In Proceedings of the 15th Aerodynamic Testing Conference, San Diego, CA, USA, 18–20 May 1988. [Google Scholar]
- Damljanović, D.; Isaković, J.; Rašuo, B. T-38 Wind Tunnel Data Quality Assurance Based on Testing of a Standard Model. J. Aircr. 2013, 50, 1141–1149. [Google Scholar] [CrossRef]
- Gray, J.D.; Lindsay, E.E. Force Tests of Standard Hypervelocity Ballistic Models HB-1 and HB-2 at Mach 1.5 to 10; AEDC-TDR-63-137; Arnold Engineering Development Center: Tullahoma, TN, USA, 1963. [Google Scholar]
- Céresuéla, R. Mesurés d‘Efforts et de Pressions sur la Maquette Balistique Étalon H.B.2 (2 ≤ Mach ≤ 16.5); Note technique 13/1879 A; ONERA: Palaiseau, France, 1964. [Google Scholar]
- Malcolm, G.N.; Chapman, G.T. A Computer Program for Systematically Analyzing Free-Flight Data to Determine the Aerodynamics of Axisymmetric Bodies; NASA TN D-4766; NASA, Ames Research Center: Mountain View, CA, USA, 1968.
- Vuković, D.; Damljanović, D.; Ocokoljić, G.; Rašuo, B. Convergence of Transonic Wind Tunnel Test Results of the AGARD-B Standard Model. FME Trans. 2020, 48, 761–769. [Google Scholar]
- Kurn, A.G. Drag Measurements on a Series of Afterbodies at Transonic Speeds Showing the Effects of Sting Interference; C.P. No. 984; Aeronautical Research Council: Bedford, UK, 1968. [Google Scholar]
- Uselton, B.L.; Cyran, F.B. Critical Sting Length as Determined by the measurement of Pitch Damping Derivatives for Laminar, Transitional, and Tubulent Boundary Layers at Mach Number 3 for Reduced Frequencies 0.033 and 0.0056; AEDC-TR-77-66; Arnold Engineering Development Center: Tullahoma, TN, USA, 1977. [Google Scholar]
- Vuković, Ð.; Damljanović, D. HB-2 high-velocity correlation model at high angles of attack in supersonic wind tunnel tests. Chin. J. Aeronaut. 2019, 32, 1565–1576. [Google Scholar] [CrossRef]
- Lee, G.; Summers, J.L. Effects of Sting-Support Interference on the Drag of an Ogive-Cylinder Body with and Without a Boattail at 0.6 to 1.4 Mach Number; NACA RM A57109; Ames Aeronautical Laboratory: Moffet Field, CA, USA, 1957.
- Elsenaar, A.; Binion, T.W., Jr.; Stanewsky, E.; Hornung, H.G. (Eds.) Reynolds Number Effects in Transonic Flow; AGARDograph No.303; North Atlantic Treaty Organization: Washington, DC, USA, 1988. [Google Scholar]
- Mishra, R.; Neunaber, I.; Guilmineau, E.; Braud, C. Wind tunnel study: Is turbulent intensity a good candidate to help in bypassing low Reynolds number effects on 2d blade sections? J. Phys. 2022, 2265, 0220905. [Google Scholar] [CrossRef]
- Yao, J.; Lou, W.; Shen, G.; Guo, J.; Xing, Y. Influence of Inflow Turbulence on the Flow Characteristics around a Circular Cylinder. Appl. Sci. 2019, 9, 3595. [Google Scholar] [CrossRef]







| Measurement Uncertainties; Test Conditions | |||||||
|---|---|---|---|---|---|---|---|
| HB-2 Model Dia. | Conditions | 2σ M | 2σ Po Bar | 2σ q Bar | 2σ Re | 2σ Alpha ° | 2σ Phi ° |
| 75 mm | Mach 0.9 | ±0.00072 | ±0.0017 | ±0.0012 | ±3700 | ±0.043 | ±0.25 |
| Mach 1.4 | ±0.00063 | ±0.00076 | ±3300 | ||||
| Mach 2.0 | ±0.0012 | ±0.00031 | ±2900 | ||||
| 100 mm | Mach 0.9 | ±0.00072 | ±0.0017 | ±0.0012 | ±5000 | ±0.043 | ±0.25 |
| Mach 1.4 | ±0.00063 | ±0.00076 | ±4500 | ||||
| Mach 2.0 | ±0.0012 | ±0.00031 | ±3900 | ||||
| Measurement Uncertainties; 75 mm Diameter HB-2 Standard Model | |||||
|---|---|---|---|---|---|
| Balance | Conditions | 2σ CA | 2σ Cpb | 2σ CN | 2σ Cm |
| Able Mk18 | Mach 0.9 | ±0.0077 | ±0.00048 | ±0.046 | ±0.060 |
| Mach 1.4 | ±0.0059 | ±0.00027 | ±0.035 | ±0.047 | |
| Mach 2.0 | ±0.0064 | ±0.00087 | ±0.039 | ±0.041 | |
| VTI KV44 | Mach 0.9 | ±0.035 | ±0.00048 | ±0.014 | ±0.024 |
| Mach 1.4 | ±0.027 | ±0.00027 | ±0.011 | ±0.019 | |
| Mach 2.0 | ±0.030 | ±0.00087 | ±0.012 | ±0.021 | |
| Measurement Uncertainties; 100 mm Diameter HB-2 Standard Model | |||||
|---|---|---|---|---|---|
| Balance | Conditions | 2σ CA | 2σ Cpb | 2σ CN | 2σ Cm |
| Able Mk18 | Mach 0.9 | ±0.0045 | ±0.00048 | ±0.026 | ±0.026 |
| Mach 1.4 | ±0.0035 | ±0.00027 | ±0.020 | ±0.020 | |
| Mach 2.0 | ±0.0036 | ±0.00087 | ±0.022 | ±0.017 | |
| VTI KV44 | Mach 0.9 | ±0.02 | ±0.00048 | ±0.0079 | ±0.010 |
| Mach 1.4 | ±0.015 | ±0.00027 | ±0.0061 | ±0.008 | |
| Mach 2.0 | ±0.017 | ±0.00087 | ±0.0067 | ±0.0089 | |
| Transonic Test Results; 75 mm Diameter HB-2 Standard Model | |||||
|---|---|---|---|---|---|
| Balance | M | CA0 | CAf0 | Cpb0 | CNalpha |
| Able Mk18 | 0.70 | 0.759 | 0.143 | −0.241 | 4.74 |
| 0.79 | 0.810 | 0.199 | −0.239 | 4.96 | |
| 0.90 | 0.986 | 0.325 | −0.258 | 5.53 | |
| 1.00 | 1.541 | 0.647 | −0.349 | 4.78 | |
| 1.10 | 1.833 | 0.833 | −0.391 | 4.79 | |
| 1.19 | 1.716 | 0.820 | −0.350 | 4.76 | |
| 1.28 | 1.650 | 0.843 | −0.316 | 4.69 | |
| 1.39 | 1.575 | 0.850 | −0.283 | 4.66 | |
| VTI KV44 | 0.69 | 0.724 | 0.099 | −0.244 | 4.70 |
| 0.78 | 0.816 | 0.212 | −0.236 | 4.82 | |
| 0.88 | 1.004 | 0.361 | −0.251 | 5.49 | |
| 1.00 | 1.510 | 0.631 | −0.343 | 4.68 | |
| 1.10 | 1.841 | 0.812 | −0.402 | 4.66 | |
| 1.2 | 1.707 | 0.785 | −0.360 | 4.74 | |
| 1.28 | 1.661 | 0.823 | −0.327 | 4.55 | |
| 1.39 | 1.579 | 0.821 | −0.296 | 4.57 | |
| Transonic Test Results; 100 mm Diameter HB-2 Standard Model | |||||
|---|---|---|---|---|---|
| Balance | M | CA0 | CAf0 | Cpb0 | CNalpha |
| Able Mk18 | 0.69 | 0.705 | 0.161 | −0.212 | 4.67 |
| 0.79 | 0.726 | 0.230 | −0.194 | 5.17 | |
| 0.88 | 0.881 | 0.326 | −0.216 | 5.46 | |
| 1.00 | 1.27 | 0.651 | −0.242 | 4.76 | |
| 1.10 | 1.477 | 0.793 | −0.267 | 4.79 | |
| 1.19 | 1.586 | 0.835 | −0.293 | 4.76 | |
| 1.29 | 1.585 | 0.870 | −0.279 | 4.69 | |
| 1.38 | 1.546 | 0.825 | −0.276 | 4.66 | |
| VTI KV44 | 0.69 | 0.711 | 0.160 | −0.215 | 4.78 |
| 0.79 | 0.737 | 0.216 | −0.203 | 4.96 | |
| 0.88 | 0.885 | 0.352 | −0.208 | 5.37 | |
| 1.00 | 1.253 | 0.647 | −0.236 | 4.74 | |
| 1.10 | 1.452 | 0.769 | −0.267 | 4.88 | |
| 1.19 | 1.587 | 0.815 | −0.301 | 4.65 | |
| 1.28 | 1.586 | 0.828 | −0.296 | 4.60 | |
| 1.39 | 1.553 | 0.840 | −0.279 | 4.60 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Damljanović, D.; Vuković, Đ.; Ocokoljić, G.; Rašuo, B. New Transonic Tests of HB-2 Hypersonic Standard Models in the VTI T-38 Trisonic Wind Tunnel. Aerospace 2025, 12, 131. https://doi.org/10.3390/aerospace12020131
Damljanović D, Vuković Đ, Ocokoljić G, Rašuo B. New Transonic Tests of HB-2 Hypersonic Standard Models in the VTI T-38 Trisonic Wind Tunnel. Aerospace. 2025; 12(2):131. https://doi.org/10.3390/aerospace12020131
Chicago/Turabian StyleDamljanović, Dijana, Đorđe Vuković, Goran Ocokoljić, and Boško Rašuo. 2025. "New Transonic Tests of HB-2 Hypersonic Standard Models in the VTI T-38 Trisonic Wind Tunnel" Aerospace 12, no. 2: 131. https://doi.org/10.3390/aerospace12020131
APA StyleDamljanović, D., Vuković, Đ., Ocokoljić, G., & Rašuo, B. (2025). New Transonic Tests of HB-2 Hypersonic Standard Models in the VTI T-38 Trisonic Wind Tunnel. Aerospace, 12(2), 131. https://doi.org/10.3390/aerospace12020131






