A Combined Optimization Method for the Transition Control Schedules of Aero-Engines
Abstract
1. Introduction
2. Transition Optimization Problem of Aero-Engines
2.1. The Mathematical Formulation of the Transition Optimization Problem
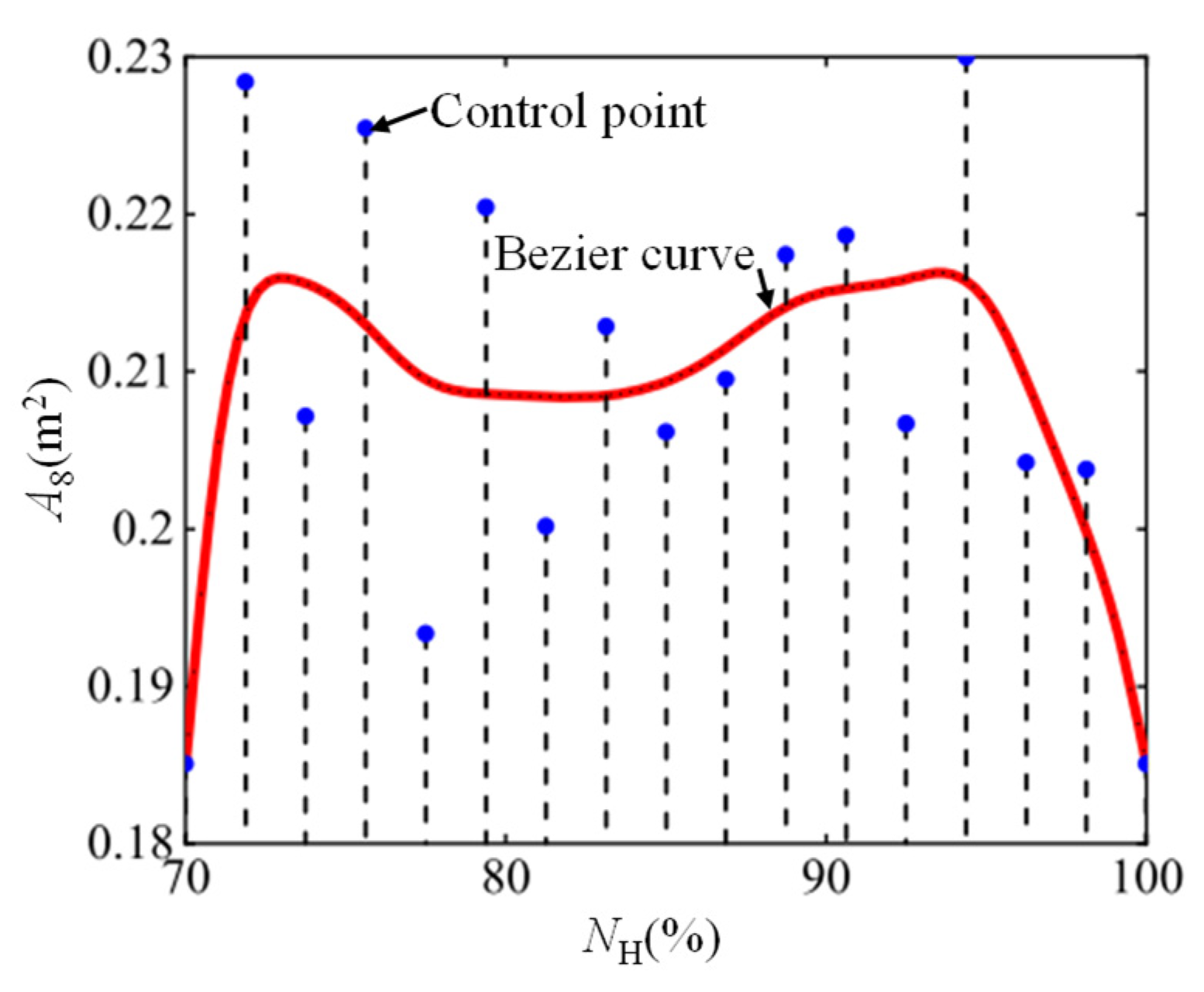
2.2. Traditional Optimization Methods for Transition Control Schedules
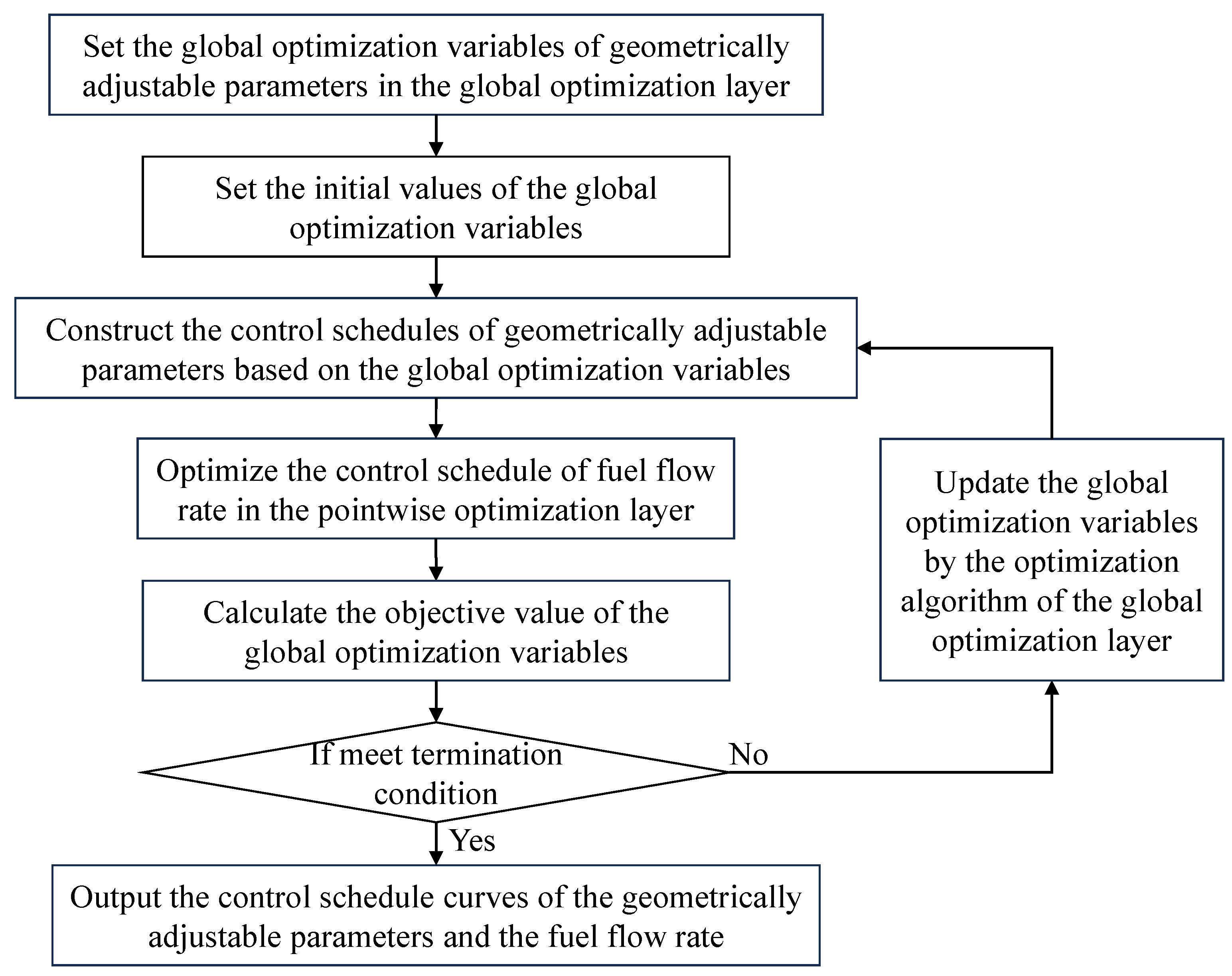
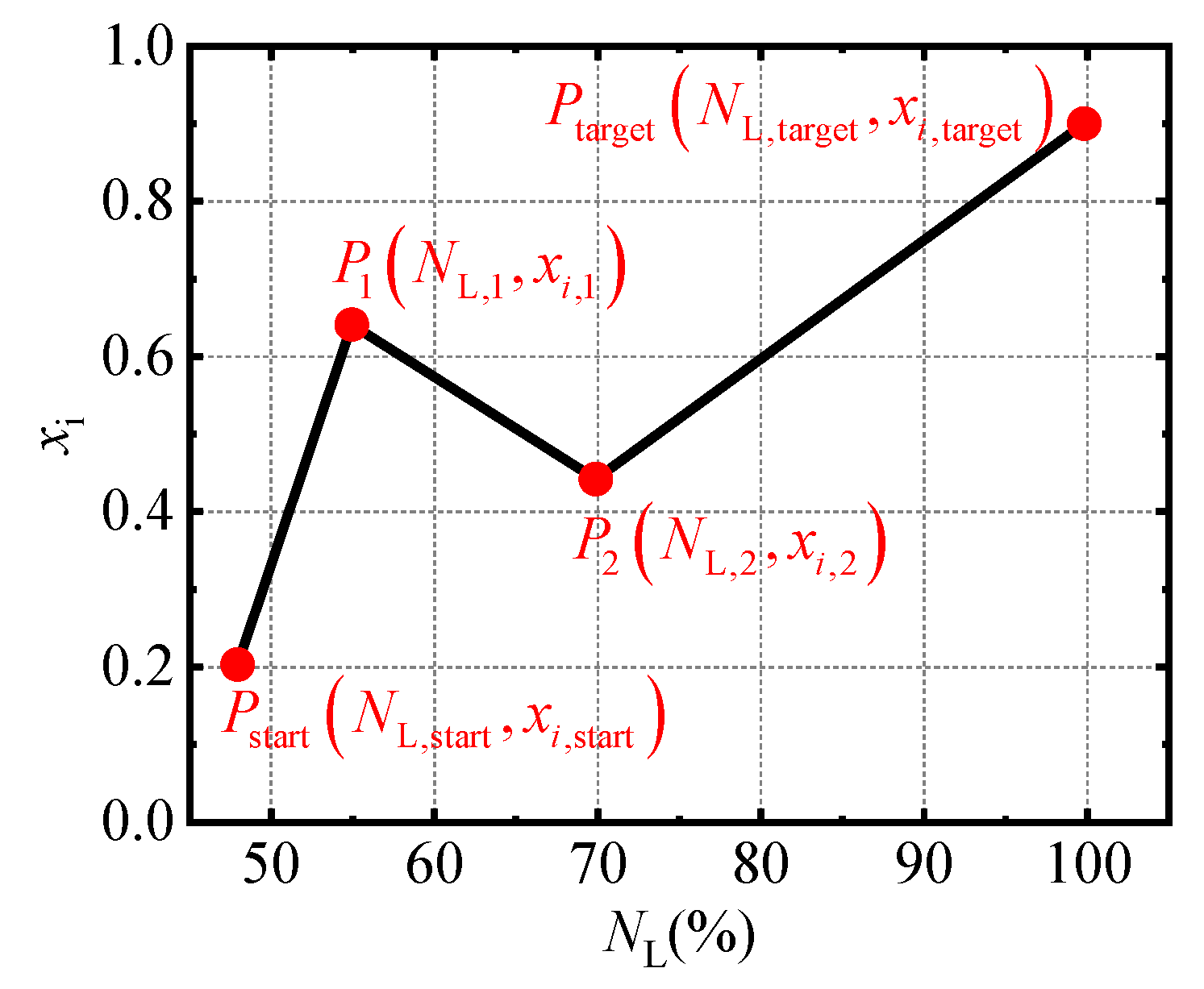
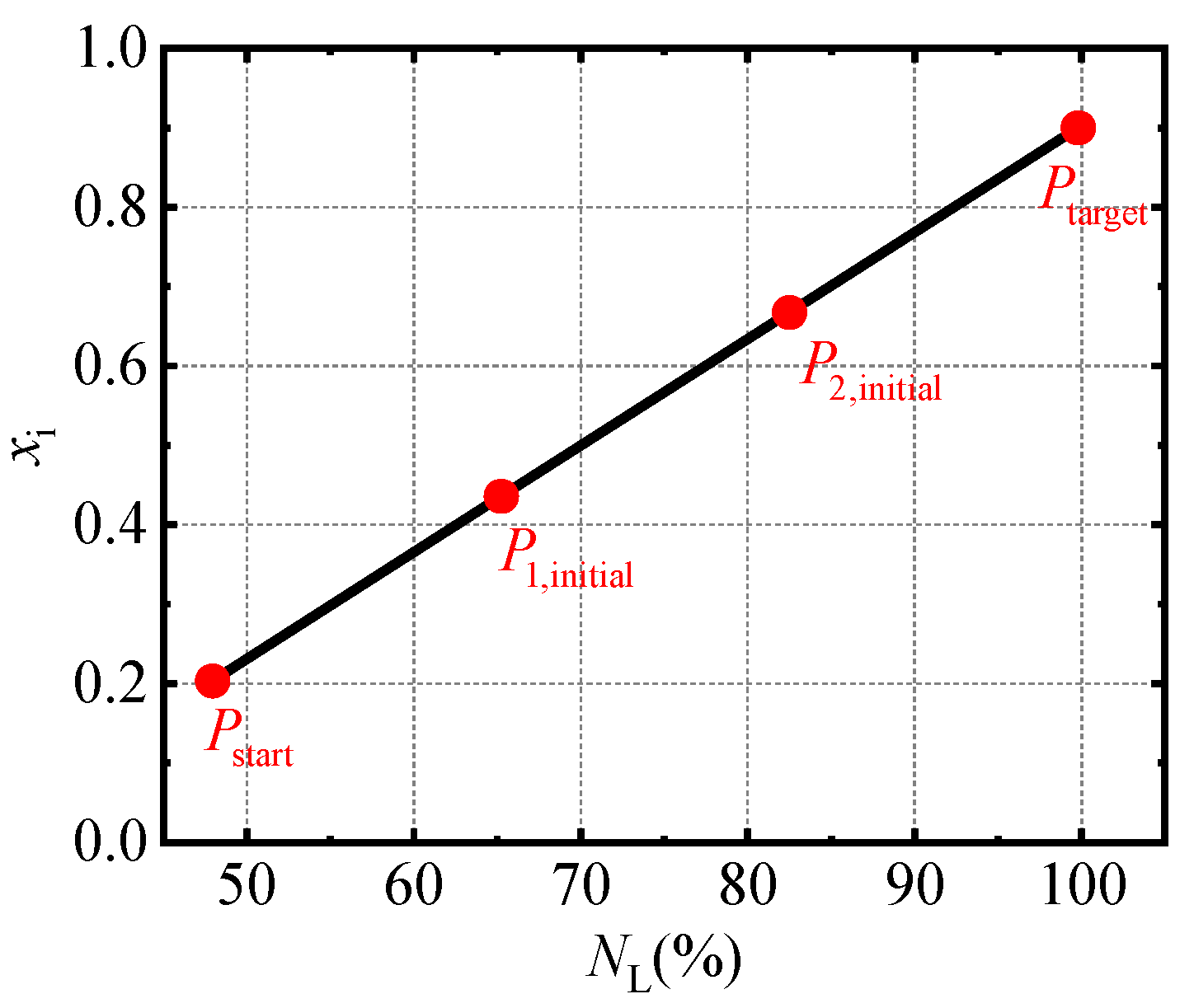
3. Combined Optimization Method
- (1)
- Set the global optimization variables of geometrically adjustable parameters in the global optimization layer.
- (2)
- Set the initial values of the global optimization variables.
- (3)
- Construct the control schedules of geometrically adjustable parameters based on the global optimization variables.
- (4)
- Optimize the control schedule of fuel flow rate in the pointwise optimization layer.
- (5)
- Calculate the objective value of the global optimization variables.
- (6)
- Check whether the termination condition of the global optimization layer is met.
4. Results and Discussion
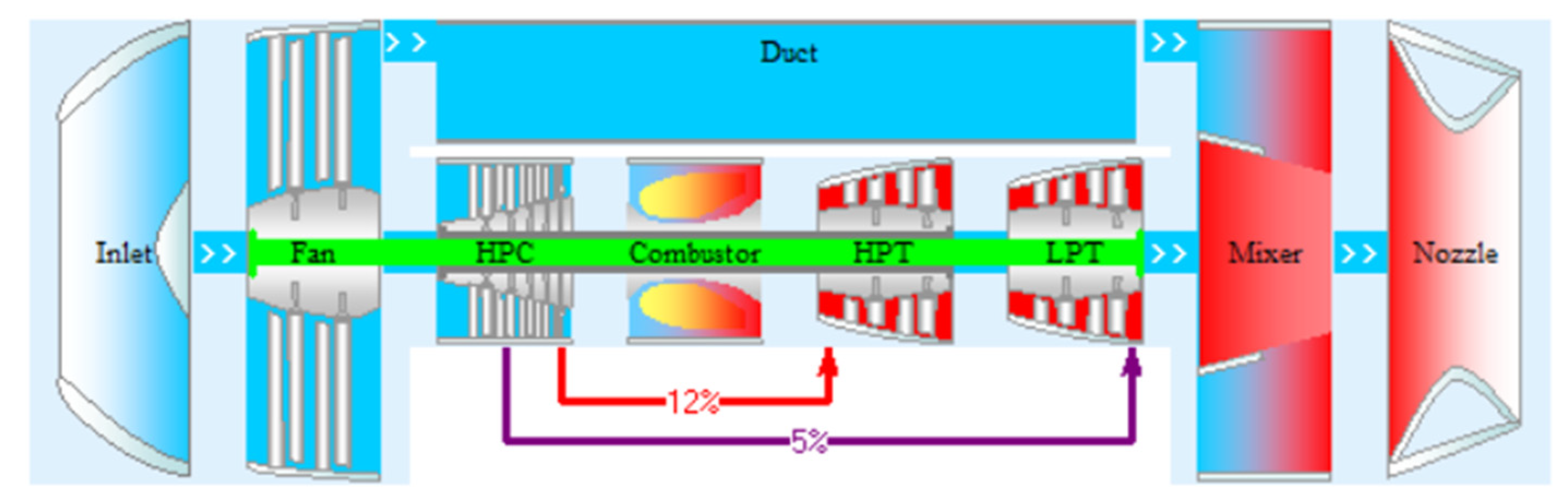
4.1. Simulation Model
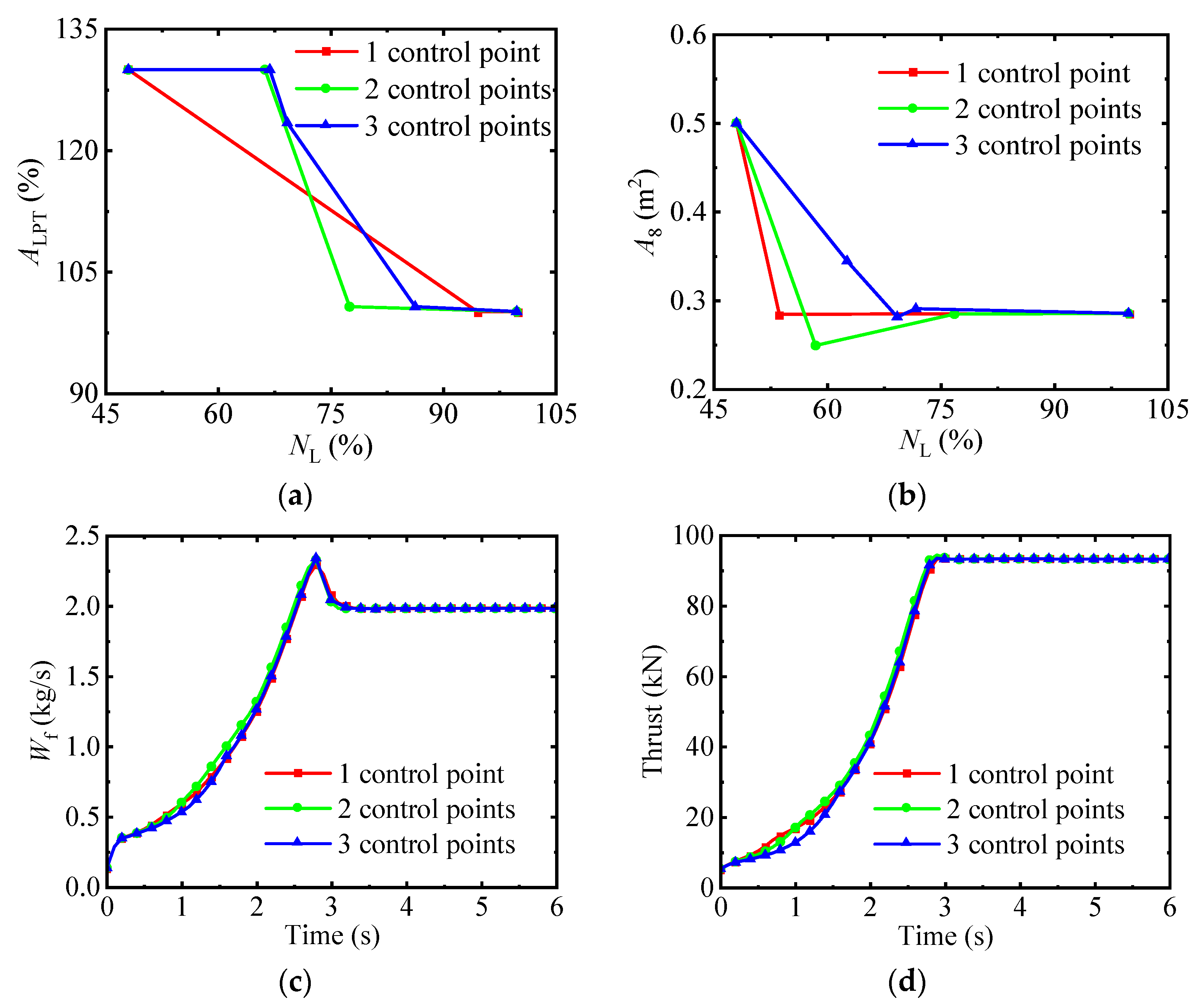
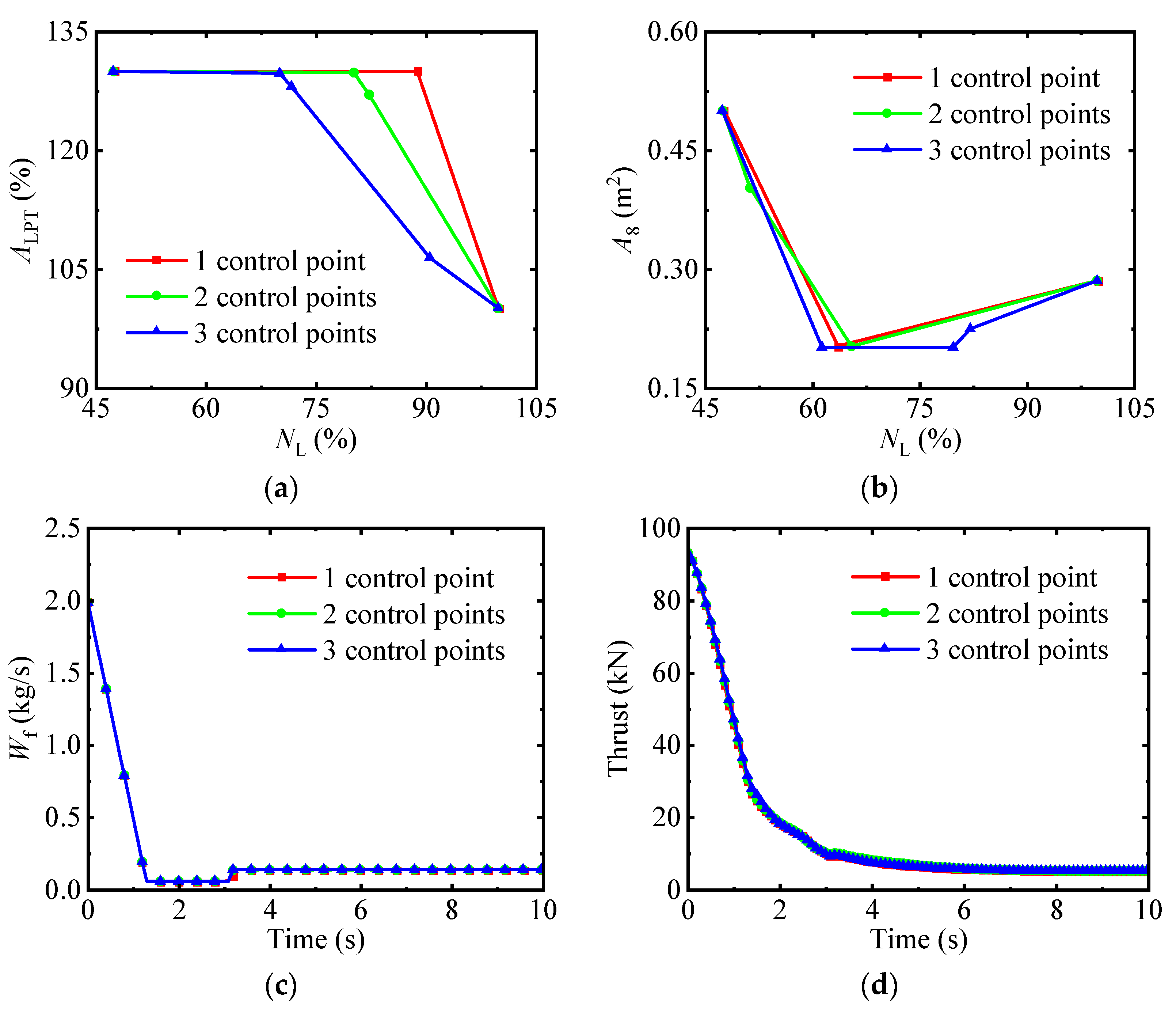
4.2. Research on the Number of Control Points
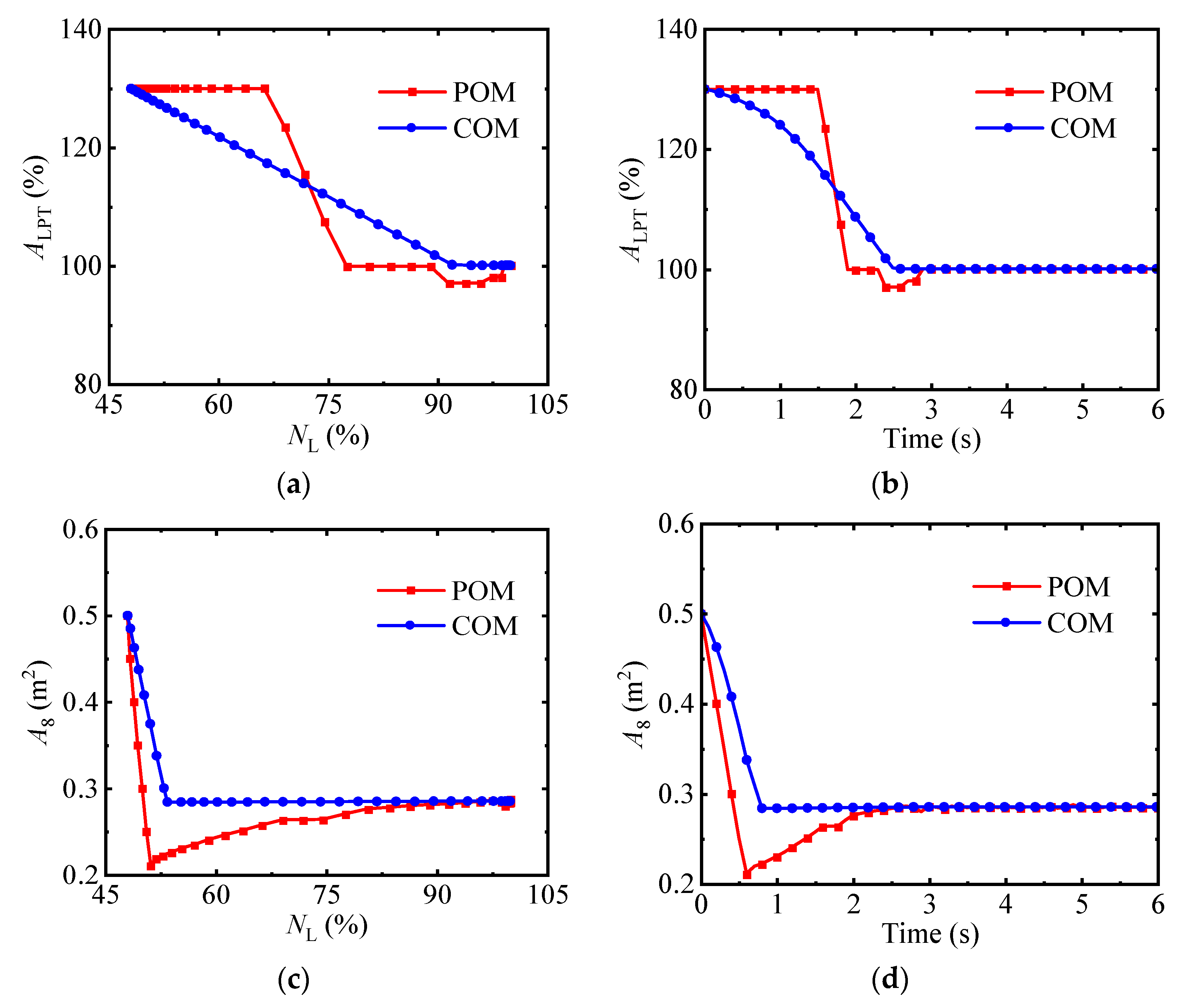
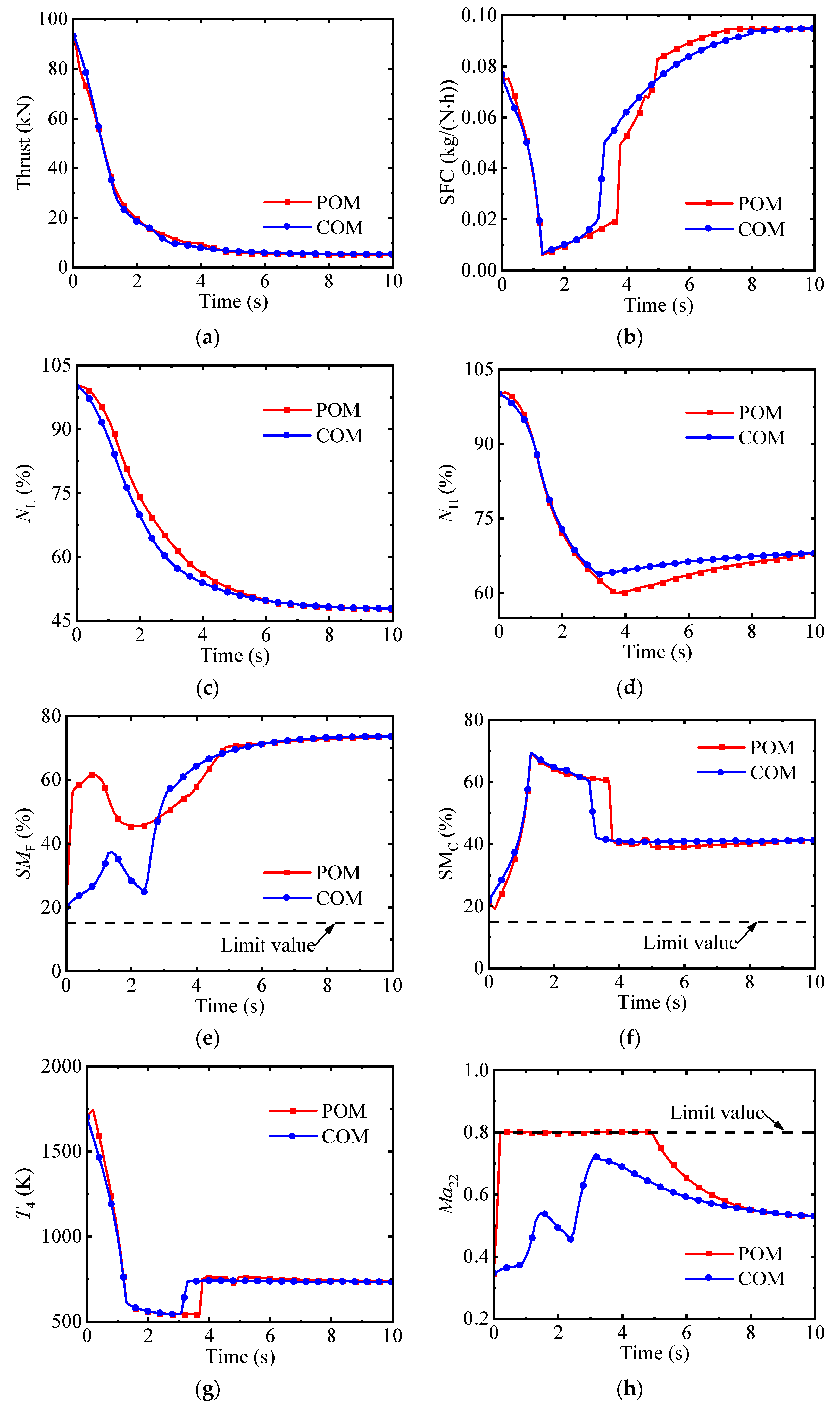
4.3. The Optimization Results of the Acceleration Process
4.4. The Optimization Results of the Deceleration Process
5. Conclusions
- (1)
- Compared with the fuel flow rate, geometrically adjustable parameters have a relatively minor impact on the transition process. Moreover, there exists a coupling relationship among geometrically adjustable parameters. That is, different combinations of these parameters can achieve the same control effect. This is the main reason why geometrically adjustable parameters obtained by traditional optimization methods tend to fluctuate. This is also the reason why the transition time does not change significantly after the smoothing technologies are applied to the control schedules.
- (2)
- In the global optimization layer of the combined optimization method, the number of control points has no obvious impact on the transition time. The fewer the number of control points, the more beneficial it is not only for reducing the optimization time but also for avoiding fluctuations in the control schedules.
- (3)
- There is no significant difference in the transition time optimized by the combined optimization method and the pointwise optimization method. However, the control schedules obtained by the combined optimization method are not only free from fluctuations but also simple, making them highly applicable in engineering.
- (4)
- Constrained by change rate constraints of the control points of geometrically adjustable parameters, the combined optimization method cannot adjust the geometrically adjustable parameters arbitrarily. This enables the optimized control schedules to prevent some components from becoming too close to their working boundaries, thus, enhancing the safety of the engine during the transition process.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| COM | Combined optimization method |
| HPC | High-pressure compressor |
| HPT | High-pressure turbine |
| LPT | Low-pressure turbine |
| SFC | Specific fuel consumption |
| POM | Pointwise optimization method |
| Adjustable parameters at time t | |
| The i-th adjustable parameter at time t | |
| Number of adjustable parameters | |
| Performance parameter of the engine | |
| Value of the performance parameter at the start of the transition process | |
| Target value of the performance parameter at the end of the transition process | |
| The j-th constraint condition | |
| Number of constraint conditions | |
| Fan surge margin | |
| HPC surge margin | |
| Low-pressure rotor speed | |
| High-pressure rotor speed | |
| Combustor outlet temperature | |
| Duct outlet Mach number | |
| Change rate of the adjustable parameters | |
| Objective function of the k-th time step | |
| Adjustable parameters at the end of the k-th time step | |
| The i-th adjustable parameter at the end of the k-th time step | |
| Target value of the i-th adjustable parameter at the end of the transition process | |
| Lower limits of the i-th adjustable parameter | |
| Upper limits of the i-th adjustable parameter | |
| Weight factor of the adjustable parameters | |
| Number of time steps | |
| Sequence of adjustable parameters over time | |
| Optimization variables of the global optimization methods | |
| Number of control points | |
| Serial number of the control point | |
| at the m-th control point | |
| The m-th dimensionless rotor speed increment | |
| Scaling factor | |
| Value of the i-th adjustable parameter of the m-th control point | |
| Optimization variables of the i-th adjustable parameter in the global optimization layer | |
| Optimization variables of adjustable parameters in the global optimization layer | |
| Fuel flow rate | |
| LPT throat area | |
| Nozzle throat area |
References
- Chen, H.; Li, Q.; Ye, Z.; Pang, S. Neural Network-Based Parameter Estimation and Compensation Control for Time-Delay Servo System of Aeroengine. Aerospace 2025, 12, 64. [Google Scholar] [CrossRef]
- Lian, X.C.; Wu, H. Aeroengine Principles; Northwestern Polytechnical University Press: Xi’an, China, 2005; p. 300. [Google Scholar]
- Hao, W.; Wang, Z.; Zhang, X.; Zhang, M. A New Design Method for Mode Transition Control Law of Variable Cycle Engine. In Proceedings of the AIAA 2018 Joint Propulsion Conference, Cincinnati, OH, USA, 9 July 2018. [Google Scholar]
- Zheng, J.; Luo, Y.; Tang, H.; Zhang, J.; Chen, M.; Zhang, Y. Design Method Research of Mode Switch Transient Control Schedule on Adaptive Cycle Engine. J. Propuls. Technol. 2022, 43, 49–58. [Google Scholar]
- Chen, Y.; Xu, S.; Cai, Y.; Tu, Q. Virtual Power Extraction Method of Designing Acceleration and Deceleration Control Law of Turbofan. In Proceedings of the 45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Denver, CO, USA, 2–5 August 2009. [Google Scholar]
- Chen, Y.; Xu, S.; Liu, Z.; Tu, Q.Y.; Yu, S.Z. Power Extraction Method for Acceleration and Deceleration Control Law Design of Turbofan Engine. J Aerosp. Power. 2009, 24, 867–874. [Google Scholar]
- Jia, L.Y.; Chen, Y.C.; Tan, T.; Tian, T.G. Analysis for Influence of Variable Geometry Parameters on Transition State Performance of Variable Cycle Engine. J. Propuls. Technol. 2020, 41, 1681–1691. [Google Scholar]
- Kurzke, J.; Halliwell, I. Propulsion and Power; Springer: Berlin, Germany, 2018; pp. 270–273. [Google Scholar]
- Jia, L.Y. Research on Variable Cycle Engine Control Schedule Design. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2017. [Google Scholar]
- Jia, L.Y.; Chen, Y.C.; Cheng, R.H.; Song, K.; Tan, T. Direct Simulation Method of Transient-State Performance of Variable Cycle Engines. J. Aeronaut. 2020, 41, 123901. [Google Scholar]
- Jia, L.; Chen, Y.; Cheng, R.; Tan, T.; Song, K. Designing Method of Acceleration and Deceleration Control Schedule for Variable Cycle Engine. Chin. J. Aeronaut. 2021, 34, 27–38. [Google Scholar] [CrossRef]
- Lu, J.; Guo, Y.Q.; Wang, L. A New Method for Designing Optimal Control Law of Aeroengine in Transient States. J. Aerosp. Power 2012, 27, 1914–1920. [Google Scholar]
- Qi, X.F.; Fan, D.; Chen, Y.C.; Li, W.G. Multivariable Optimal Acceleration Control of Turbofan Engine Based on FSQP Algorithm. J. Propuls. Technol. 2004, 25, 233–236. [Google Scholar]
- Li, J.; Fan, D.; Sreeram, V. Optimization of Aero Engine Acceleration Control in Combat State Based on Genetic Algorithms. Int. J. Turbo Jet-Eng. 2012, 29, 29–36. [Google Scholar] [CrossRef]
- Hu, H. Transient Control of Aeroengine Based on SQP Method. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2015. [Google Scholar]
- Jiang, T.M.; Zhang, X.B.; Wang, Z.X.; Liu, Y.Q. Design of Control Law Design of Lift Fan Starting Based on Time Prediction. J. Aerosp. Power 2023, 38, 2001–2014. [Google Scholar]
- Dai, A.N. Research on the On-Board Adaptive Model and Optimization Control of Aero-Engine. Master’s Thesis, Dalian University of Technology, Dalian, China, 2020. [Google Scholar]
- Liu, Z.H. Research on Optimizing Adaptive Acceleration and Deceleration Control Schedule of Turbofan Engine. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2021. [Google Scholar]
- Zhu, B.B. Design of Control Schedule and Control Algorithm for Triple Bypass Variable Cycle Engine. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2020. [Google Scholar]
- Zheng, Q.G.; Zhang, H.B. A Global Optimization Control for Turbo-Fan Engine Acceleration Schedule Design. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 308–316. [Google Scholar] [CrossRef]
- Zhao, L.; Fan, D.; Shan, W.W. A Global Optimization Approach to Aero-Engine Under Transient Conditions. J. Aerosp. Power 2007, 22, 1200–1203. [Google Scholar]
- Hao, W.; Wang, Z.X.; Zhang, X.B.; Li, Z.; Wang, J.K. Ground starting modeling and control law design method of variable cycle engine. J. Aerosp. Power 2022, 37, 152–164. [Google Scholar]
- Hao, W.; Wang, Z.X.; Zhang, X.B.; Li, Z.; Wang, J.K. Mode Transition Modeling and Control Law Design Method of Variable Cycle Engine. J. Propuls. Technol. 2022, 43, 78–87. [Google Scholar]
- Zhang, J.Y.; Dong, P.C.; Zheng, J.C.; Wang, J.; Chen, M. General Design Method of Control Law for Adaptive Cycle Engine Mode Transition. AIAA J. 2022, 60, 330–344. [Google Scholar] [CrossRef]
- Zhang, X.; Ye, Y.; Wang, Z.; Xiao, B. A Neural Network Learning-Based Global Optimization Approach for Aero-Engine Transient Control Schedule. Neurocomputing 2022, 469, 180–188. [Google Scholar] [CrossRef]
- Song, K.R.; Chen, Y.C.; Jia, L.Y.; Tan, T. Design of Variable Cycle Engine Acceleration Control Schedule Based on Gradient Method and Maximum Entropy Method. J. Propuls. Technol. 2022, 43, 55–63. [Google Scholar]
- Ye, Y.F.; Wang, Z.X.; Zhang, X.B. Cascade Ensemble-RBF-Based Optimization Algorithm for Aero-Engine Transient Control Schedule Design Optimization. Aerosp. Sci. Technol. 2021, 115, 106779. [Google Scholar] [CrossRef]
- Ye, Y.F.; Wang, Z.X.; Zhang, X.B. Multi-Surrogates Based Modelling and Optimization Algorithm Suitable for Aero-Engine. J. Propuls. Technol. 2021, 42, 2684–2693. [Google Scholar]
- Ye, Y.F.; Wang, Z.X.; Zhang, X.B. Sequential Ensemble Optimization Based on General Surrogate Model Prediction Variance and Its Application on Engine Acceleration Schedule Design. Chin. J. Aeronaut. 2021, 34, 16–33. [Google Scholar] [CrossRef]
- Yuan, X.Y.; Sun, W.Y. Optimal Theory and Methods; Beijing Science and Technology Press: Beijing, China, 2001. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution-A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Zhou, H. Research on Variable Cycle Engine Characteristics Analysis and Its Integration Design with Aircraft. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2016. [Google Scholar]
- Zhang, M.Y.; Wang, Z.X.; Zhang, X.B.; Zhou, L. Simulation of Windmilling-Ram Mode Performance for Tandem TBCC Engine. J. Aerosp. Power 2018, 33, 2939–2949. [Google Scholar]
- Hao, W.; Wang, Z.X.; Zhang, X.B.; Zhou, L. Acceleration Technique for Global Optimization of a Variable Cycle Engine. Aerosp. Sci. Technol. 2022, 129, 107792. [Google Scholar] [CrossRef]

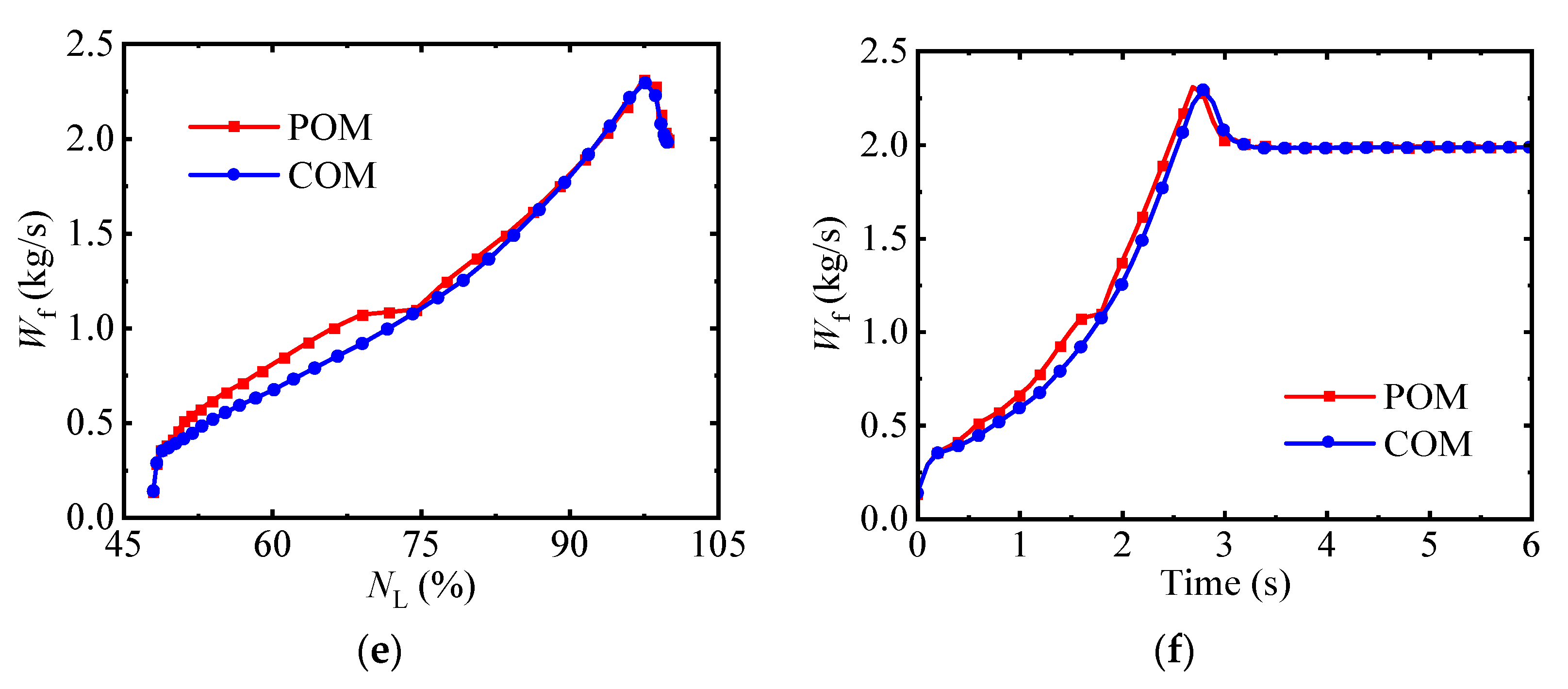
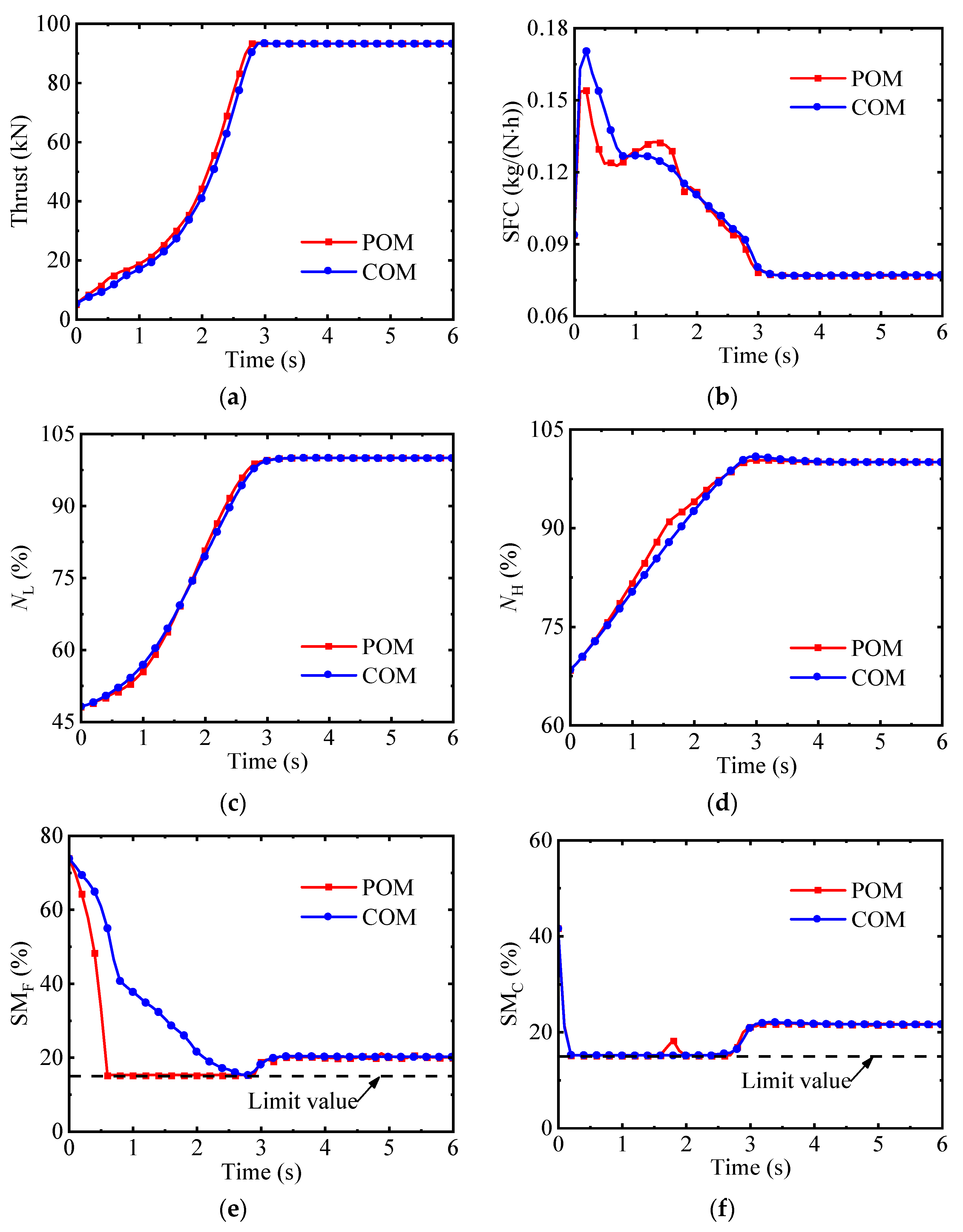
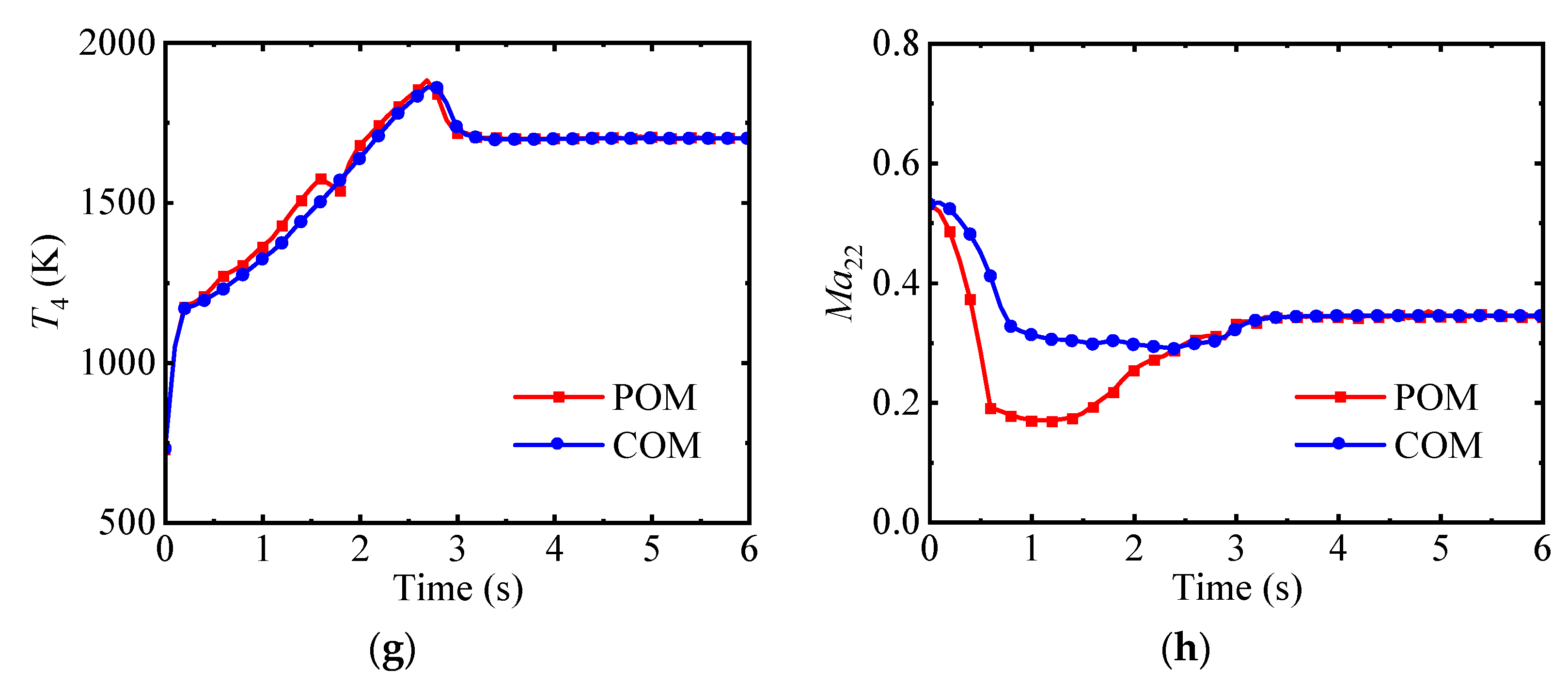
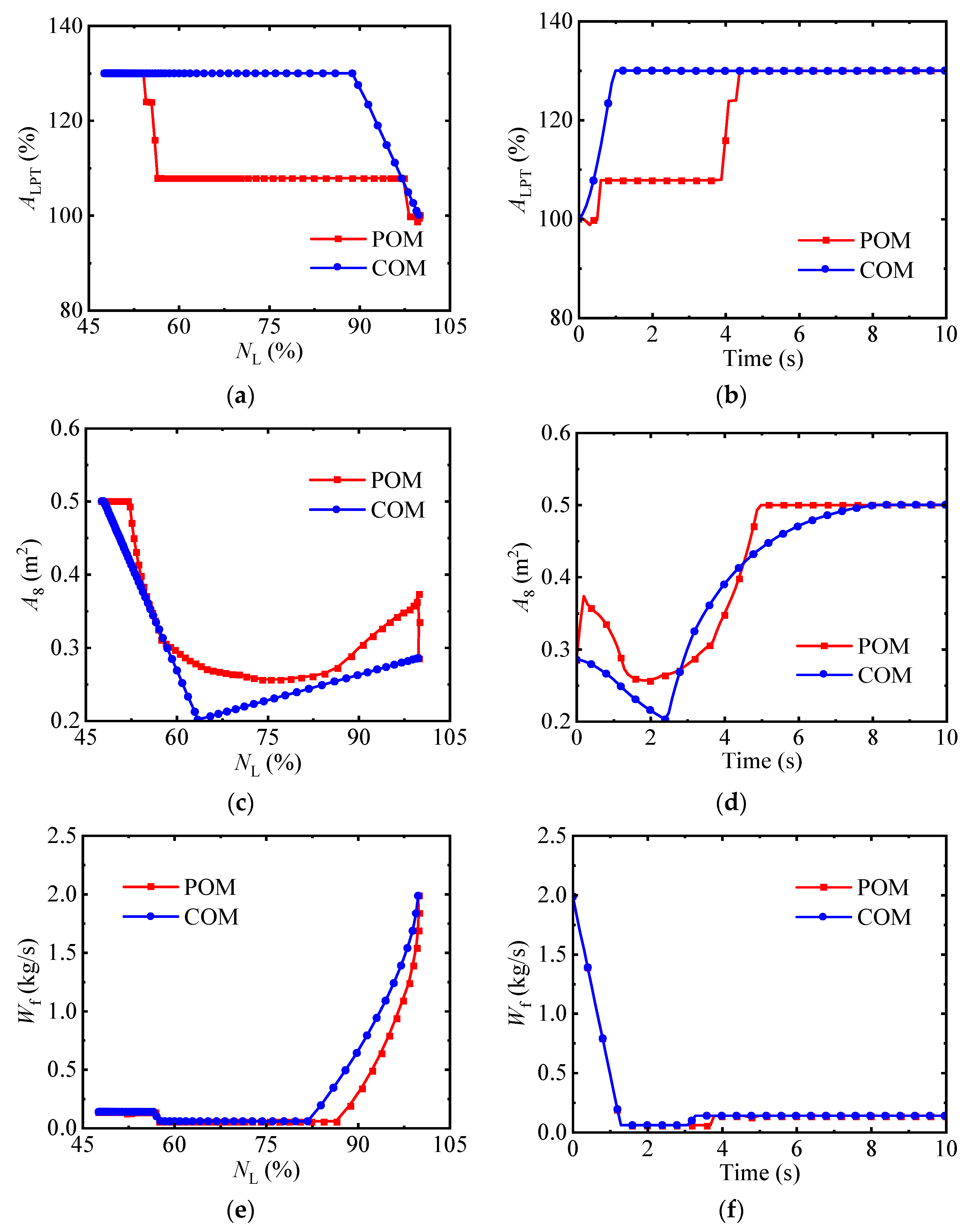
| Design Parameter | Value |
|---|---|
| Altitude (m) | 0 |
| Mach number | 0 |
| Inlet mass flow rate (kg/s) | 130 |
| Fan pressure ratio | 3.32 |
| Fan bypass ratio | 0.59 |
| HPC pressure ratio | 6.00 |
| Combustor outlet temperature (K) | 1976 |
| Thrust (kN) | 93.0 |
| Specific fuel consumption (kg/(N·h)) | 0.0767 |
| Parameter Name | Idle State | Maximum State |
|---|---|---|
| Altitude (m) | 0 | 0 |
| Mach number | 0 | 0 |
| (kg/s) | 0.1315 | 1.9854 |
| (%) | 130 | 100 |
| (m2) | 0.5 | 0.2846 |
| (%) | 48 | 100 |
| Thrust (kN) | 5.06 | 93.0 |
| Specific fuel consumption (kg/(N·h)) | 0.0936 | 0.0767 |
| Optimization Variable | Lower Limit | Upper Limit |
|---|---|---|
| (%) | 100 | 130 |
| (m2) | 0.2 | 0.5 |
| (kg/s) | 0.05 | 3 |
| Constraint Parameter | Lower Limit | Upper Limit |
|---|---|---|
| (%) | 15 | |
| (%) | 15 | |
| (%) | 102 | |
| (%) | 102 | |
| (K) | 2000 | |
| 0.8 | ||
| with respect to time (kg/s2) | 1.5 | |
| (%/%) | 20 | |
| (m2/%) | 0.5 |
| Optimization Case | Acceleration Optimization Time | Deceleration Optimization Time |
|---|---|---|
| Combined optimization with 1 control point | 2.5 h | 3.1 h |
| Combined optimization with 2 control points | 7.6 h | 9.6 h |
| Combined optimization with 3 control points | 20.0 h | 23.7 h |
| Pointwise optimization | 30 s | 37 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, W.; Zhang, X.; Li, B.; Wang, Z.; Li, D. A Combined Optimization Method for the Transition Control Schedules of Aero-Engines. Aerospace 2025, 12, 144. https://doi.org/10.3390/aerospace12020144
Hao W, Zhang X, Li B, Wang Z, Li D. A Combined Optimization Method for the Transition Control Schedules of Aero-Engines. Aerospace. 2025; 12(2):144. https://doi.org/10.3390/aerospace12020144
Chicago/Turabian StyleHao, Wang, Xiaobo Zhang, Baokuo Li, Zhanxue Wang, and Dawei Li. 2025. "A Combined Optimization Method for the Transition Control Schedules of Aero-Engines" Aerospace 12, no. 2: 144. https://doi.org/10.3390/aerospace12020144
APA StyleHao, W., Zhang, X., Li, B., Wang, Z., & Li, D. (2025). A Combined Optimization Method for the Transition Control Schedules of Aero-Engines. Aerospace, 12(2), 144. https://doi.org/10.3390/aerospace12020144





