Effects of the Position and Size of the Air Injection Holes in the Flow Structure of a Trapped-Vortex Combustor
Abstract
:1. Introduction
2. Materials and Methods
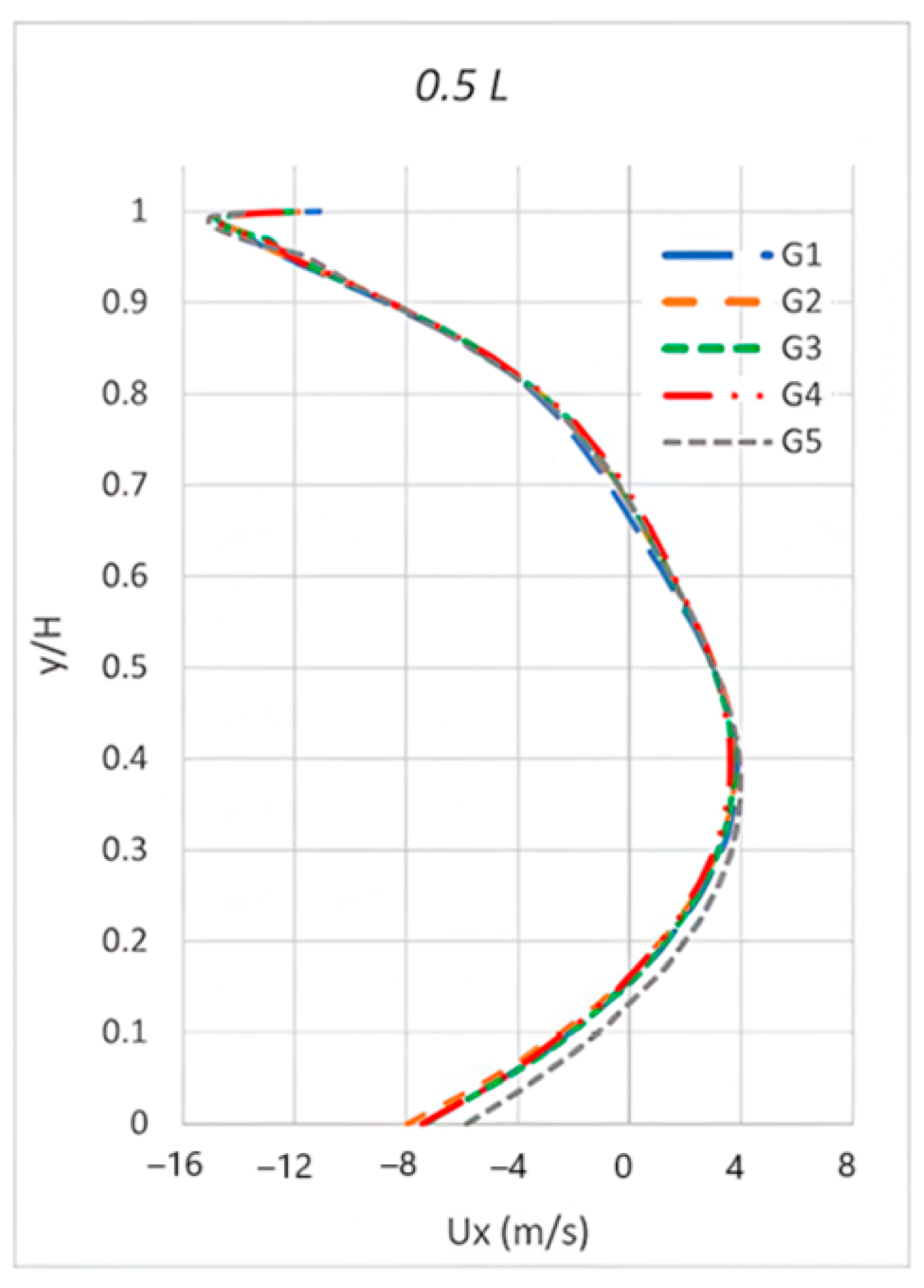
Numerical Methodology
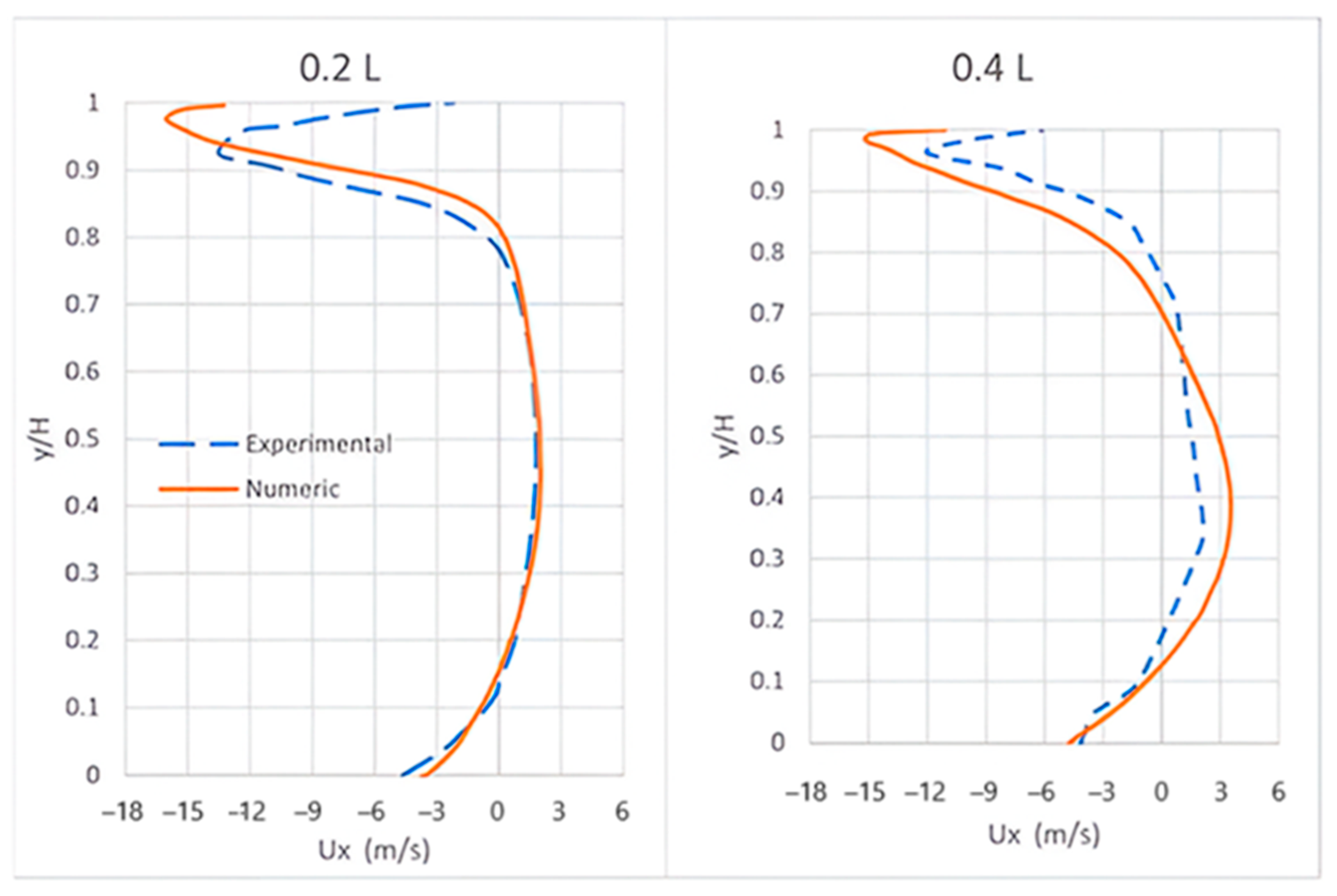
3. Results and Discussion
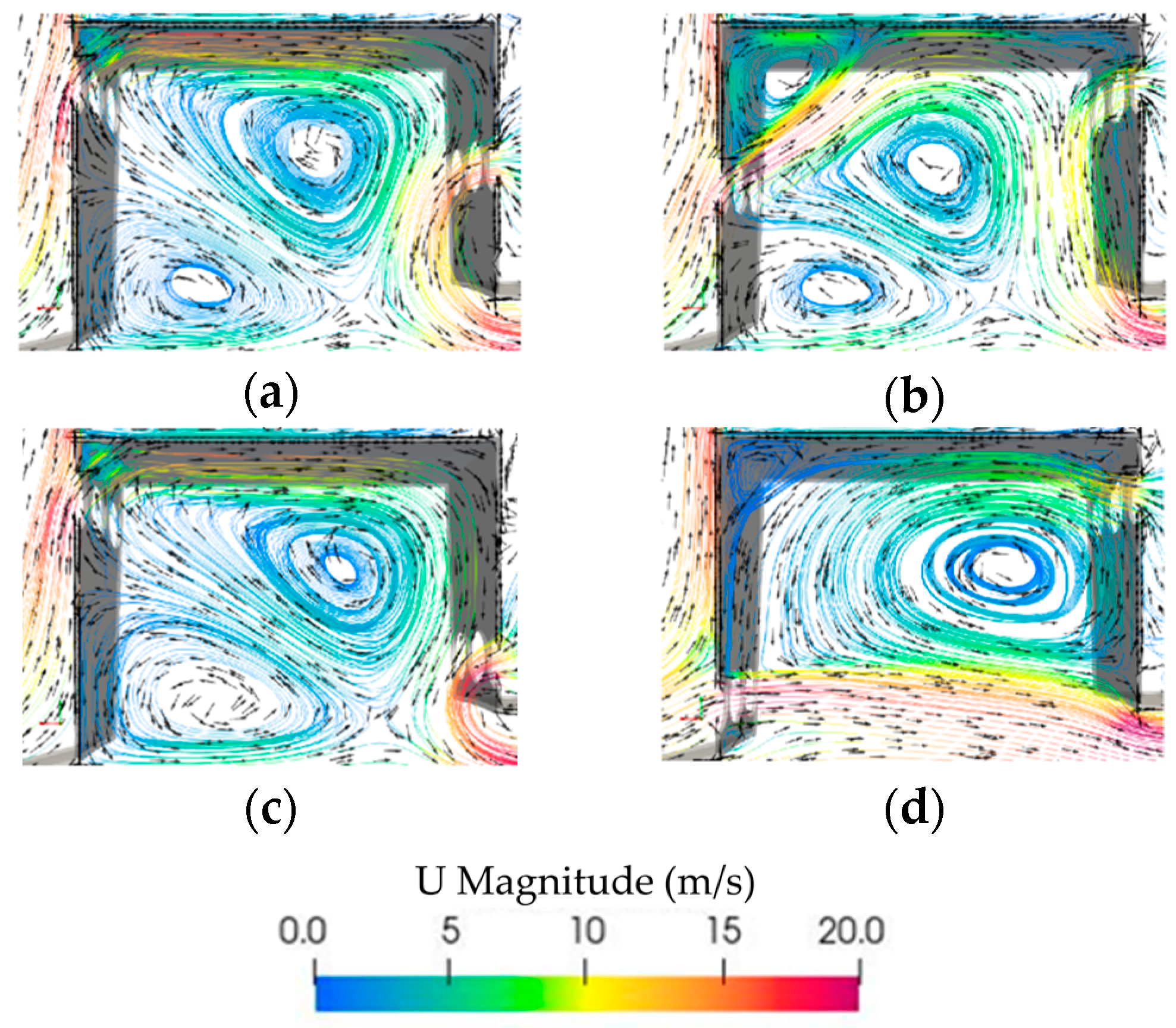
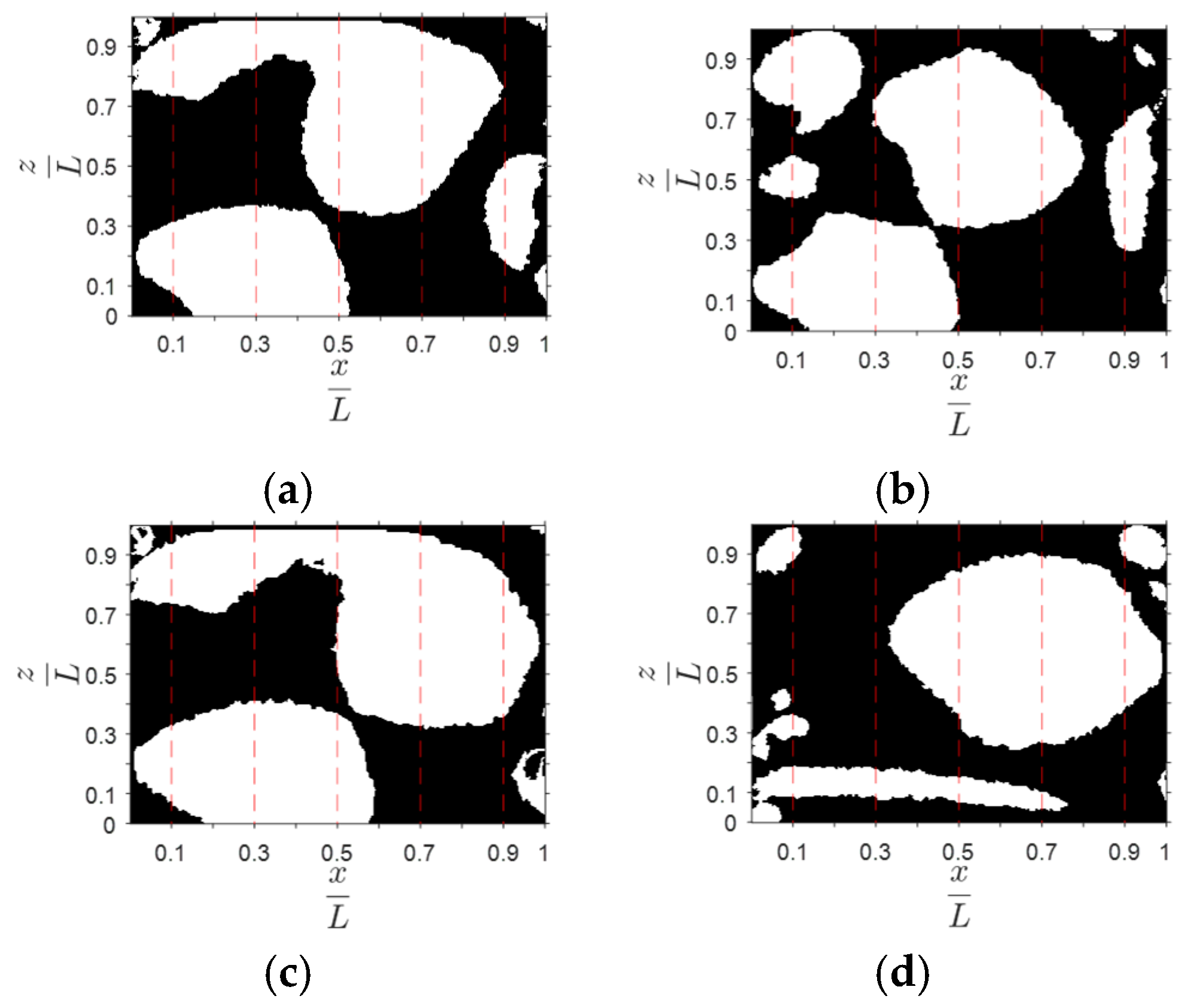
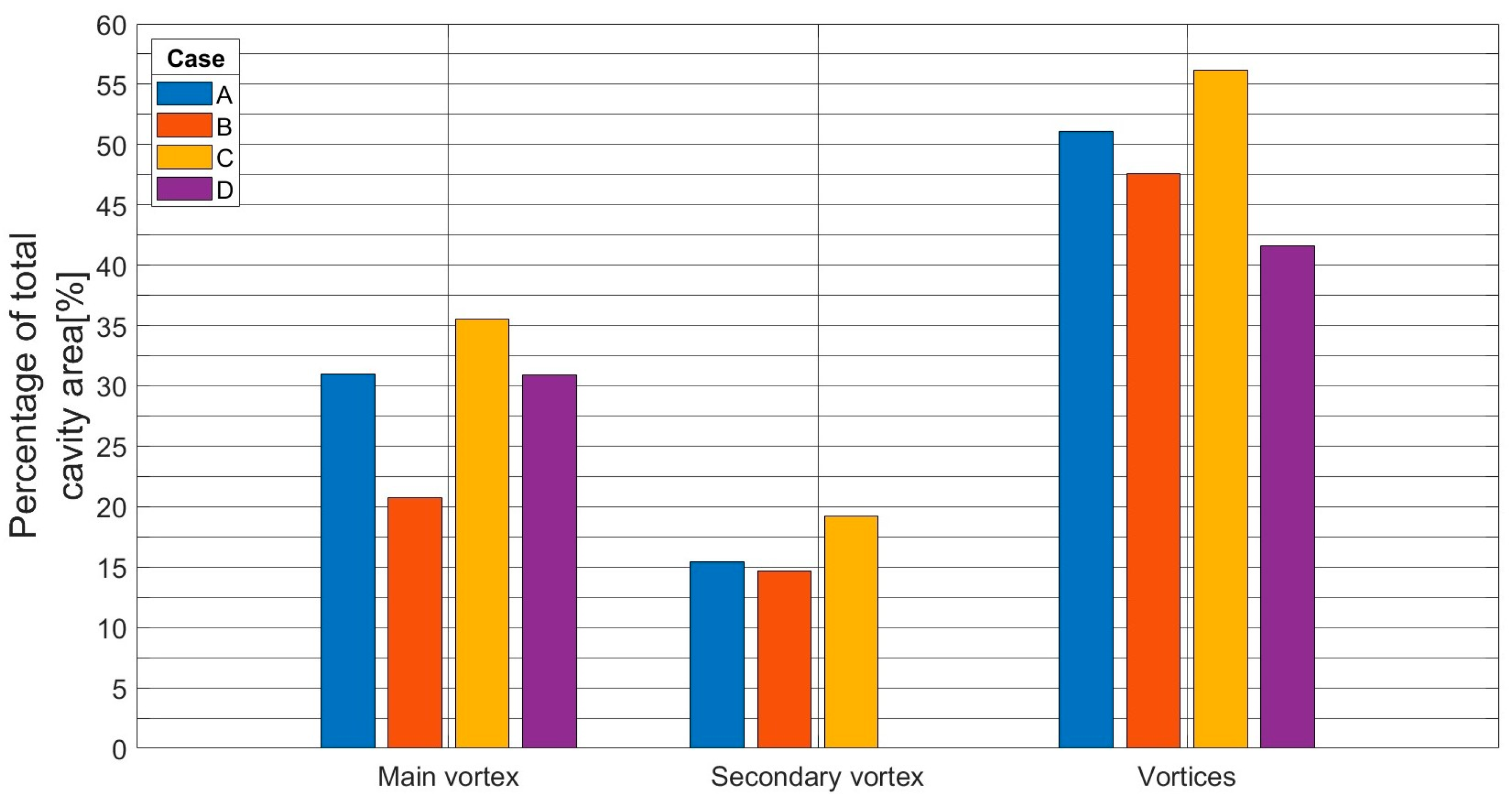
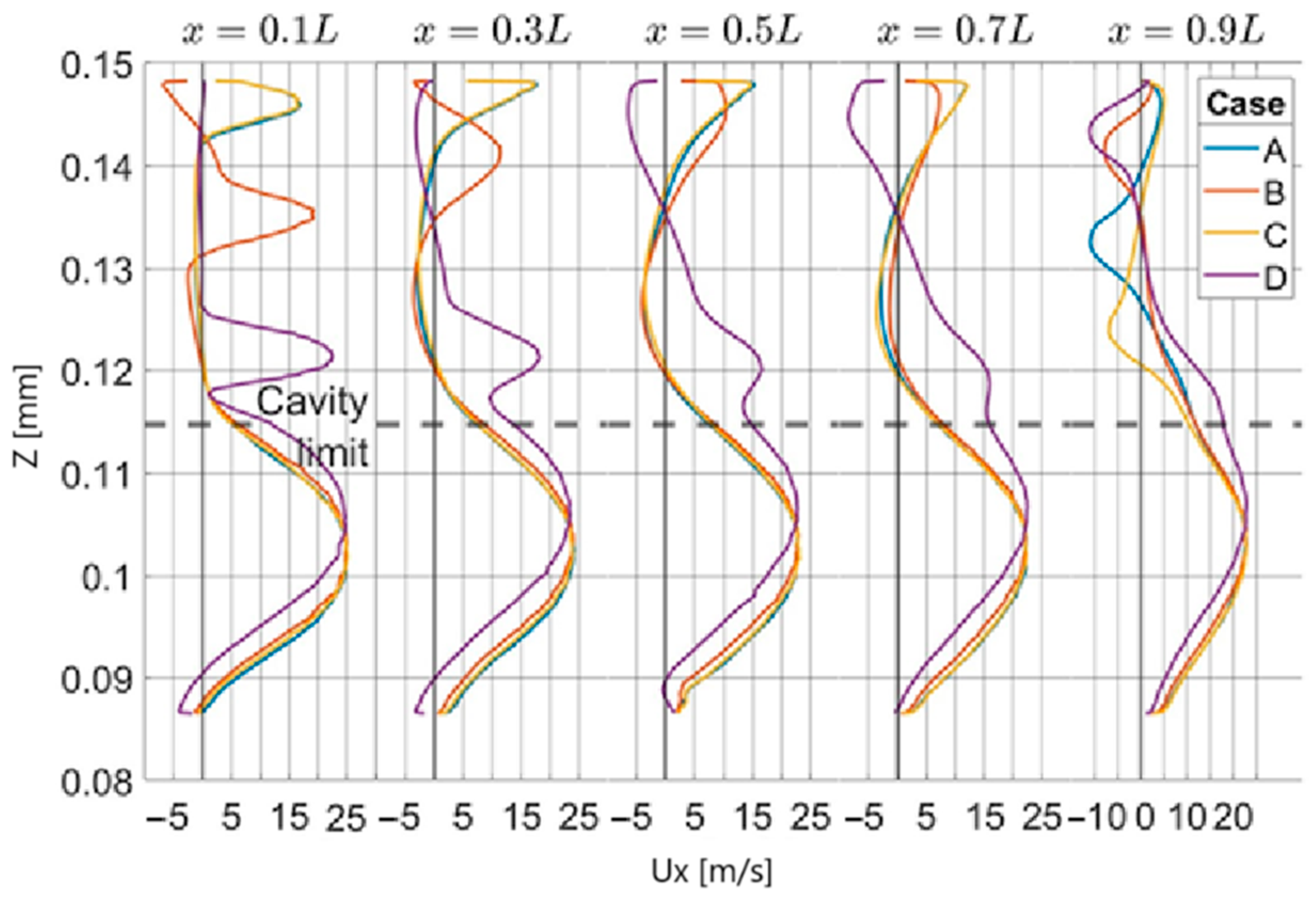
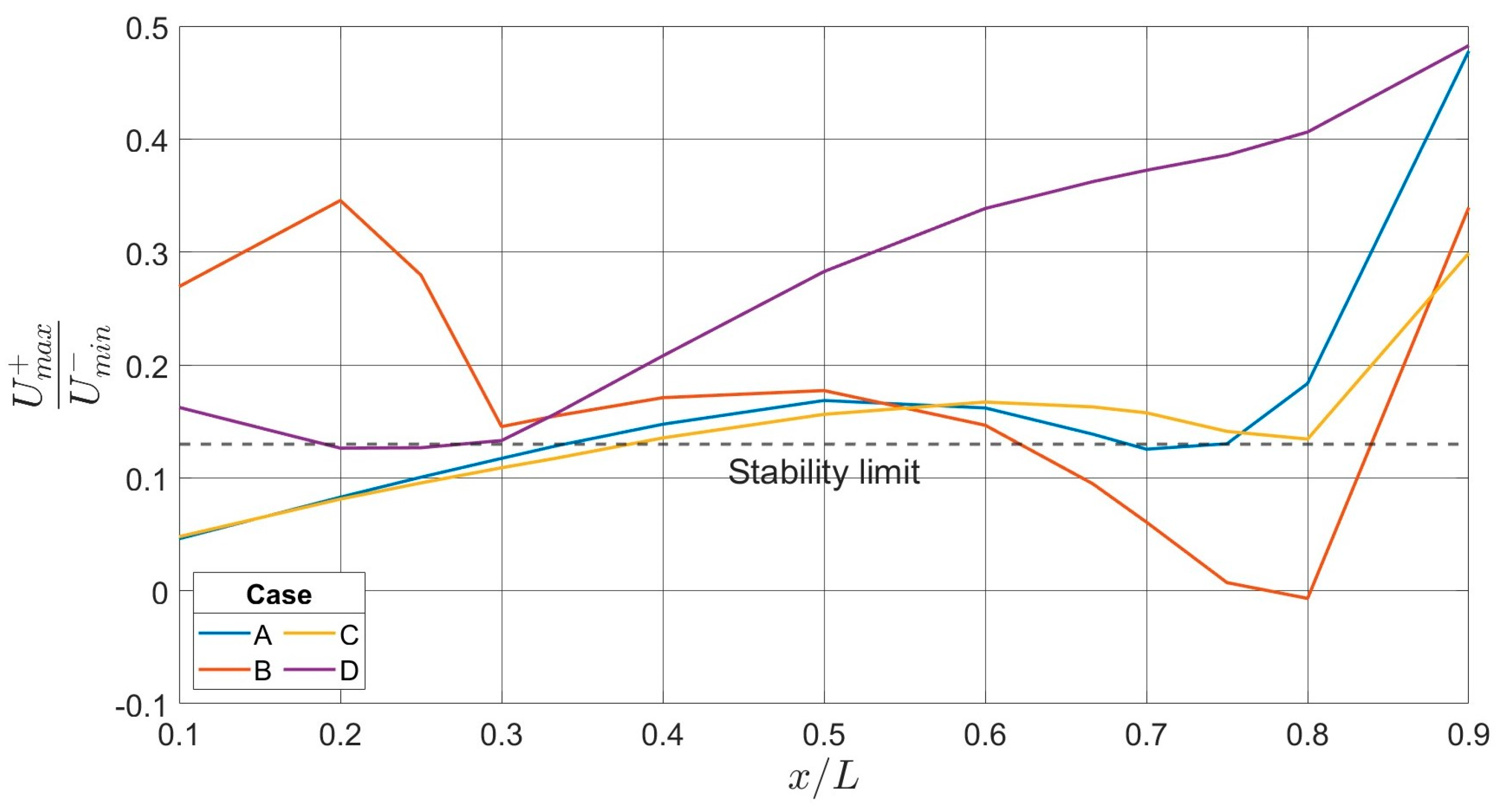
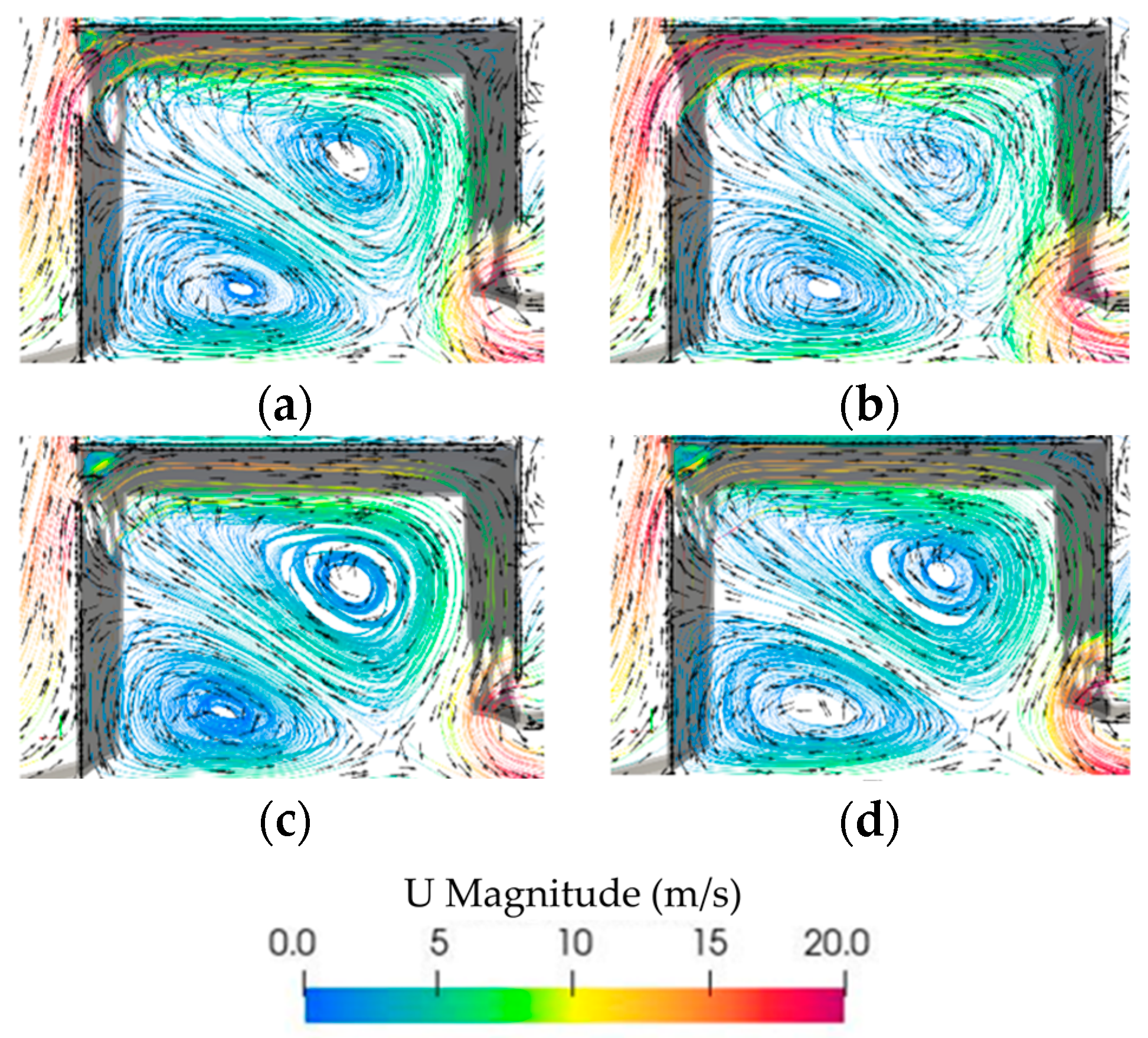
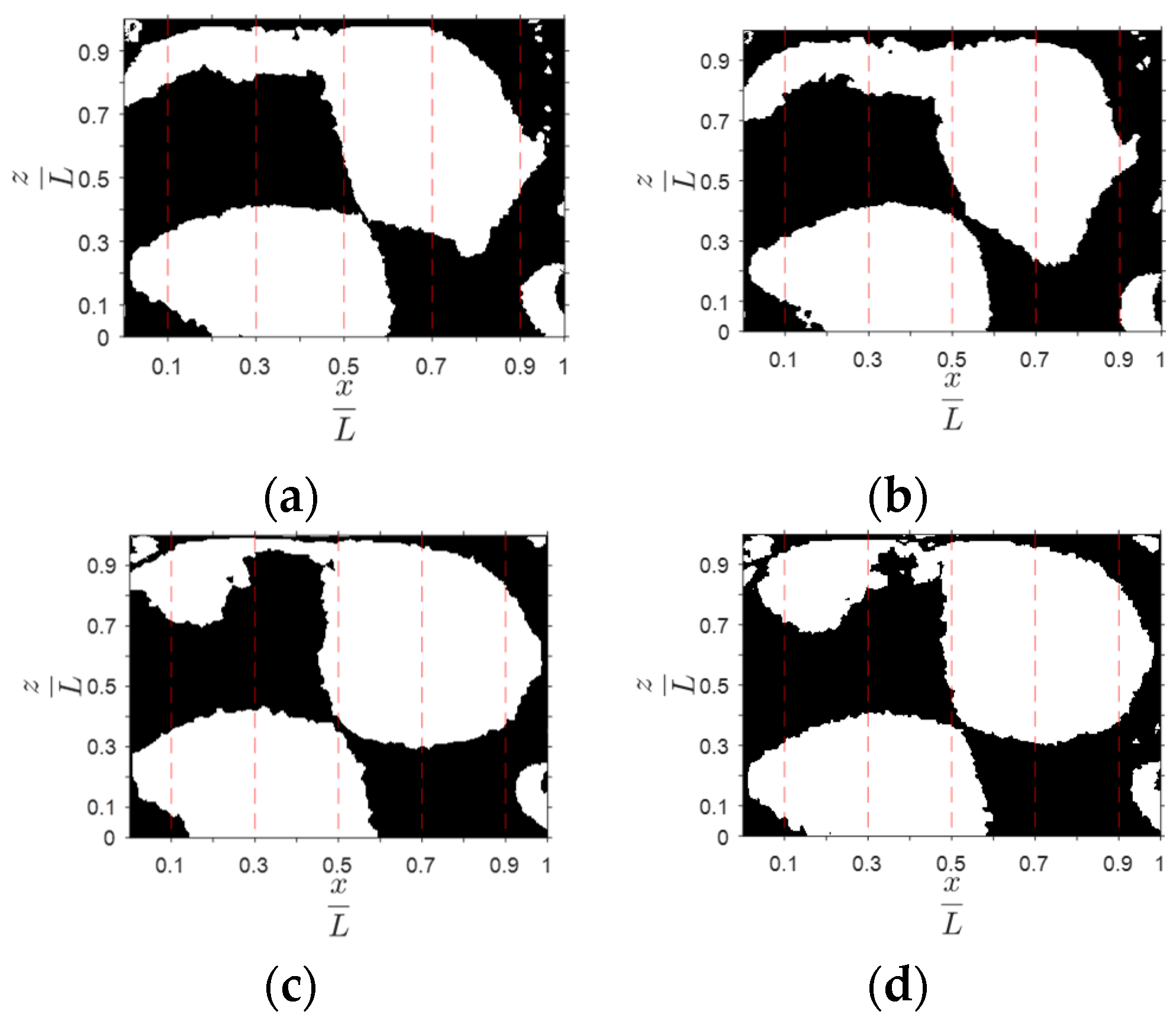
3.1. Results and Discussion for Cases A, B, C, and D
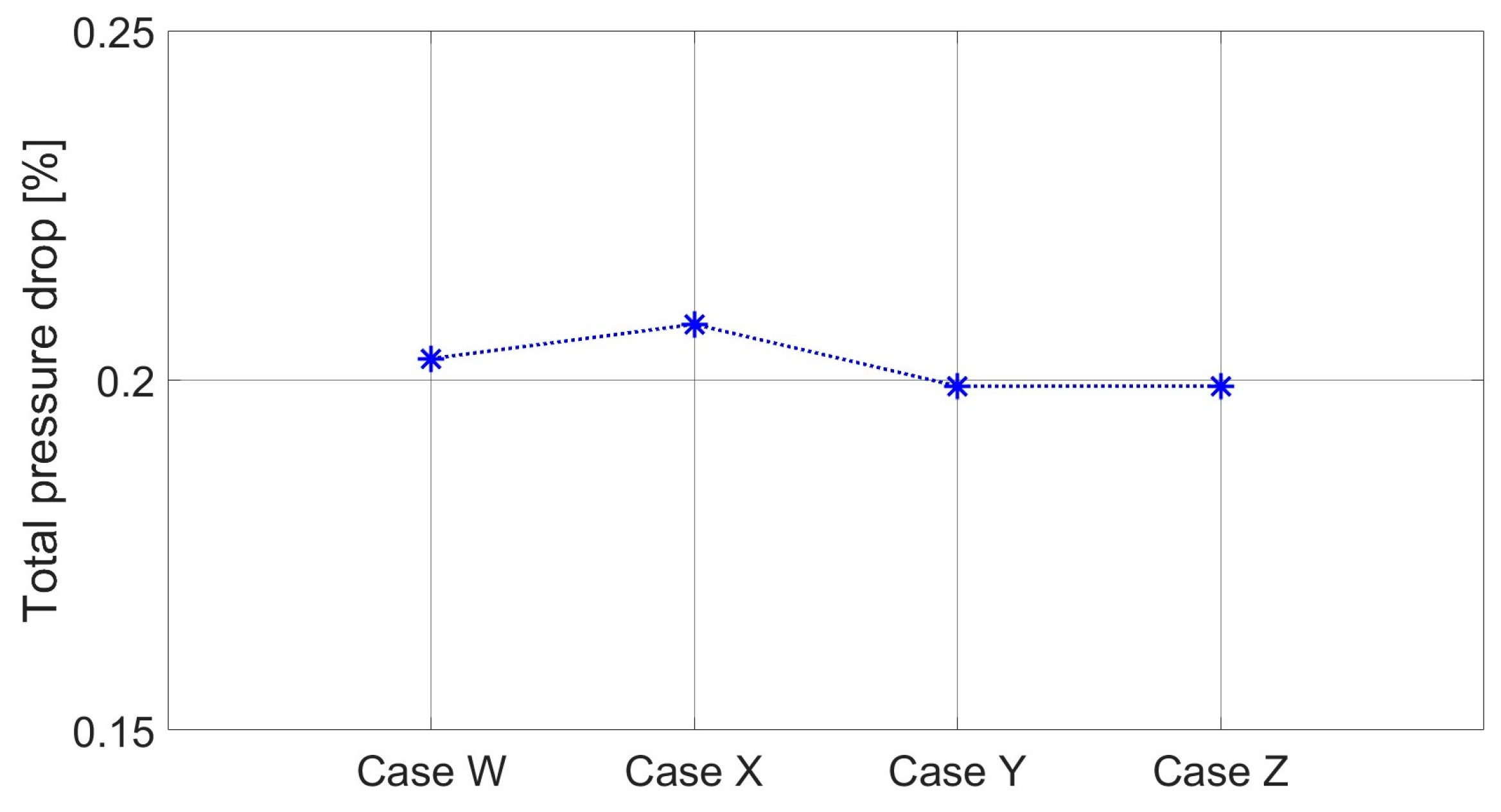
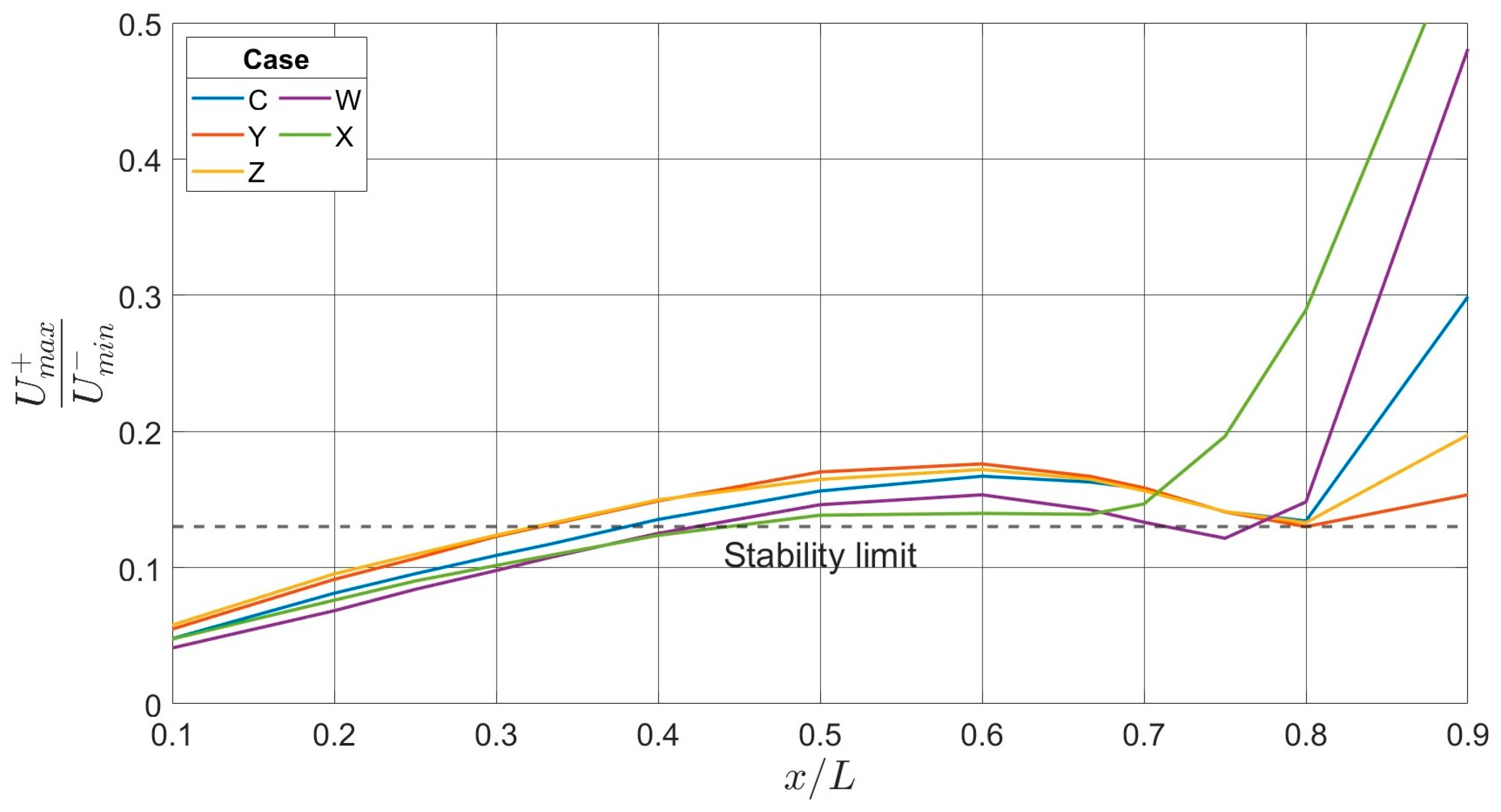
3.2. Results and Discussion for Cases W, X, Y, and Z
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| H | Cavity height |
| L | Cavity length |
| Air mass flow | |
| P | Pressure |
| T | Temperature |
| U | Axial velocity |
| x | Axial coordinate, axial direction |
| y | Vertical coordinate, vertical direction |
| z | Transverse coordinate, transverse direction |
| Subscripts | |
| At | Total area |
| max | Maximum |
| min | Minimum |
| t3 | Total at the combustor inlet |
| t4 | Total at the combustor outlet |
| Greek | |
| ϕ | Diameter |
References
- Jin, Y.; Li, Y.; He, X.; Zhang, J.; Jiang, B.; Wu, Z.; Song, Y. Experimental investigations of flow field and combustion characteristics of a model trapped vortex combustor. Appl. Energy 2014, 134, 257–269. [Google Scholar] [CrossRef]
- Xing, F.; Zhang, S.; Wang, P.; Fan, W. Experimental investigation of a single trapped-vortex combustor with a slight temperature raise. Aerosp. Sci. Technol. 2010, 14, 520–525. [Google Scholar] [CrossRef]
- Jin, Y.; He, X.; Zhang, J.; Jiang, B.; Wu, Z. Experimental study on emission performance of an LPP/TVC. Chin. J. Aeronaut. 2012, 25, 335–341. [Google Scholar] [CrossRef]
- Singhal, A.; Ravikrishna, R.V. Single cavity trapped vortex combustor dynamics-Part 1: Experiments. Int. J. Spray Combust. Dyn. 2011, 3, 23–44. [Google Scholar] [CrossRef]
- Katta, V.R.; Roquemore, W.M. Numerical studies on trapped-vortex concepts for stable combustión. In Proceedings of the ASME-Turbo Asia Conference, Jakarta, Indonesia, 5–7 November 1996. [Google Scholar]
- Li, M.; He, X.; Zhao, Y.; Jin, Y.; Yao, K.; Ge, Z. Performance enhancement of a trapped-vortex combustor for gas turbine engines using a novel hybrid-atomizer. Appl. Energy 2018, 216, 286–295. [Google Scholar] [CrossRef]
- Ezhil Kumar, P.K.; Mishra, D.P. Numerical simulation of cavity flow structure in an axisymmetric trapped vortex combustor. Aerosp. Sci. Technol. 2012, 21, 16–23. [Google Scholar] [CrossRef]
- Zhu, Y.; Jin, Y.; He, X. Effects of location and angle of primary injection on the cavity flow structure of a trapped vortex combustor model. Optik 2019, 180, 699–712. [Google Scholar] [CrossRef]
- Zhang, R.C.; Hao, F.; Fan, W.J. Combustion and stability characteristics of ultra-compact combustor using cavity for gas turbines. Appl. Energy 2018, 225, 940–954. [Google Scholar] [CrossRef]
- Zhang, R.; Fan, W. Experimental study of entrainment phenomenon in a trapped vortex combustor. Chin. J. Aeronaut. 2013, 26, 63–73. [Google Scholar] [CrossRef]
- Singhal, A.; Ravikrishna, R.V. Single cavity trapped vortex combustor dynamics-Part 2: Simulations. Int. J. Spray Combust. Dyn. 2011, 3, 45–62. [Google Scholar] [CrossRef]
- Zhao, D.; Gutmark, E.; Goey, P. A review of cavity-based trapped vortex, ultra-compact, high-g, inter-turbine combustors. Prog. Energy Combust. Sci. 2018, 66, 42–82. [Google Scholar] [CrossRef]
- Xing, F.; Wang, P.; Zhang, S.; Zou, J.; Zheng, Y.; Zhang, R.; Fan, W. Experiment and simulation study on lean blow-out of trapped vortex combustor with various aspect ratios. Aerosp. Sci. Technol. 2012, 18, 48–55. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Li, R.M.; Liu, H.X.; Yang, M.L. Effects of Fueling Scheme on the Performance of a Trapped Combustor Rig. In Proceedings of the 45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Denver, CO, USA, 2–5 August 2009. [Google Scholar]
- Ezhil Kumar, P.K.; Mishra, D.P. Flame Stability Characteristics of Two-Dimensional Trapped Vortex Combustor. Combust. Sci. Technol. 2016, 188, 1283–1302. [Google Scholar] [CrossRef]
- Ezhil Kumar, P.K.; Mishra, D.P. Numerical study of reacting flow characteristics of a 2D twin cavity trapped vortex combustor. Combust. Theory Model. 2017, 21, 658–676. [Google Scholar] [CrossRef]
- Guo, Y.; Gong, C.; Huang, Y.; Duan, F.; He, X. Combustion and emission performance of swirling-flow single trapped vortex combustor. Appl. Therm. Eng. 2017, 236, 121678. [Google Scholar] [CrossRef]
- Zhao, Y.; Gong, C.; Li, M. Effect of air-injection mode on mainstream-forced entrainment and combustion characteristics of a cavity-based combustor. Phys. Fluids 2024, 36, 087128. [Google Scholar] [CrossRef]
- Sharifzadeh, R.; Afshari, A. Numerical investigation of flow field effects on fuel–air mixing in a non-reacting trapped vortex combustor with different injection arrangements. Eur. J. Mech./B Fluids 2020, 82, 106–122. [Google Scholar] [CrossRef]
- Burrus, D.L.; Roquemore, W.M.; Johnson, A.W.; Shouse, D.T. Performance Assessment of a Prototype Trapped Vortex Combustor Concept for Gas Turbine Application. In Proceedings of the ASME-IGTI, New Orleans, LA, USA, 4–7 June 2001. [Google Scholar]
- Roquemore, W.; Shouse, D.; Burrus, D.; Johnson, A.; Cooper, C.; Duncan, B.; Hsu, K.-Y.; Katta, V.; Sturgess, G.; Vihinen, I. Trapped vortex combustor concept for gas turbine engines. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001. [Google Scholar] [CrossRef]
- Zhang, R.; Fan, W.; Shi, Q.; Tan, W. Structural design and performance experiment of a single vortex combustor with single-cavity and air blast atomisers. Aerosp. Sci. Technol. 2014, 39, 95–108. [Google Scholar] [CrossRef]
- Mishra, D.P.; Sudharshan, R. Numerical analysis of fuel-air mixing in a two-dimensional trapped vortex combustor. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2010, 224, 65–75. [Google Scholar] [CrossRef]
- Reddy, J.N.; Anand, N.K.; Roy, P. Finite Element and Finite Volume Methods for Heat Transfer and Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Roache, P.J. Quantification of uncertainty in computational fluid dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. Trans. ASME 2008, 130, 0780011–0780014. [Google Scholar] [CrossRef]
- Jin, Y.; He, X.; Zhang, J.; Jiang, B.; Wu, Z. Numerical investigation on flow structures of a laboratory-scale trapped vortex combustor. Appl. Therm. Eng. 2014, 66, 318–327. [Google Scholar] [CrossRef]
- Li, M.; He, X.; Zhao, Y.; Jin, Y.; Ge, Z.; Sun, Y. Dome structure effects on combustion performance of a trapped vortex combustor. Appl. Energy 2017, 208, 72–82. [Google Scholar] [CrossRef]
- Vengadesan, Y.; Sony, C. Enhanced vortex stability in trapped vortex combustor. Aeronaut. J. 2010, 114, 333–337. [Google Scholar]
- Lefebvre, A.H.; Ballal, D.R. Gas Turbine Combustions: Alternative Fuels and Emissions; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Agarwal, K.K.; Ravikrishna, R.V. Experimental and numerical studies in a compact trapped vortex combustor: Stability assessment and augmentation. Combust. Sci. Technol. 2011, 183, 1308–1327. [Google Scholar] [CrossRef]
- Zhan, J.M.; Li, Y.T.; Onyx Wai, W.H.; Hu, W.Q. Comparison between the Q criterion and Rortex in the application of an in-stream structure. Phys. Fluids 2019, 31, 121701-1–121701-7. [Google Scholar] [CrossRef]
- Elliott, G.S.; Samimy, M. Compressibility effects in free shear layers. Phys. Fluids A 1990, 2, 1231–1240. [Google Scholar] [CrossRef]
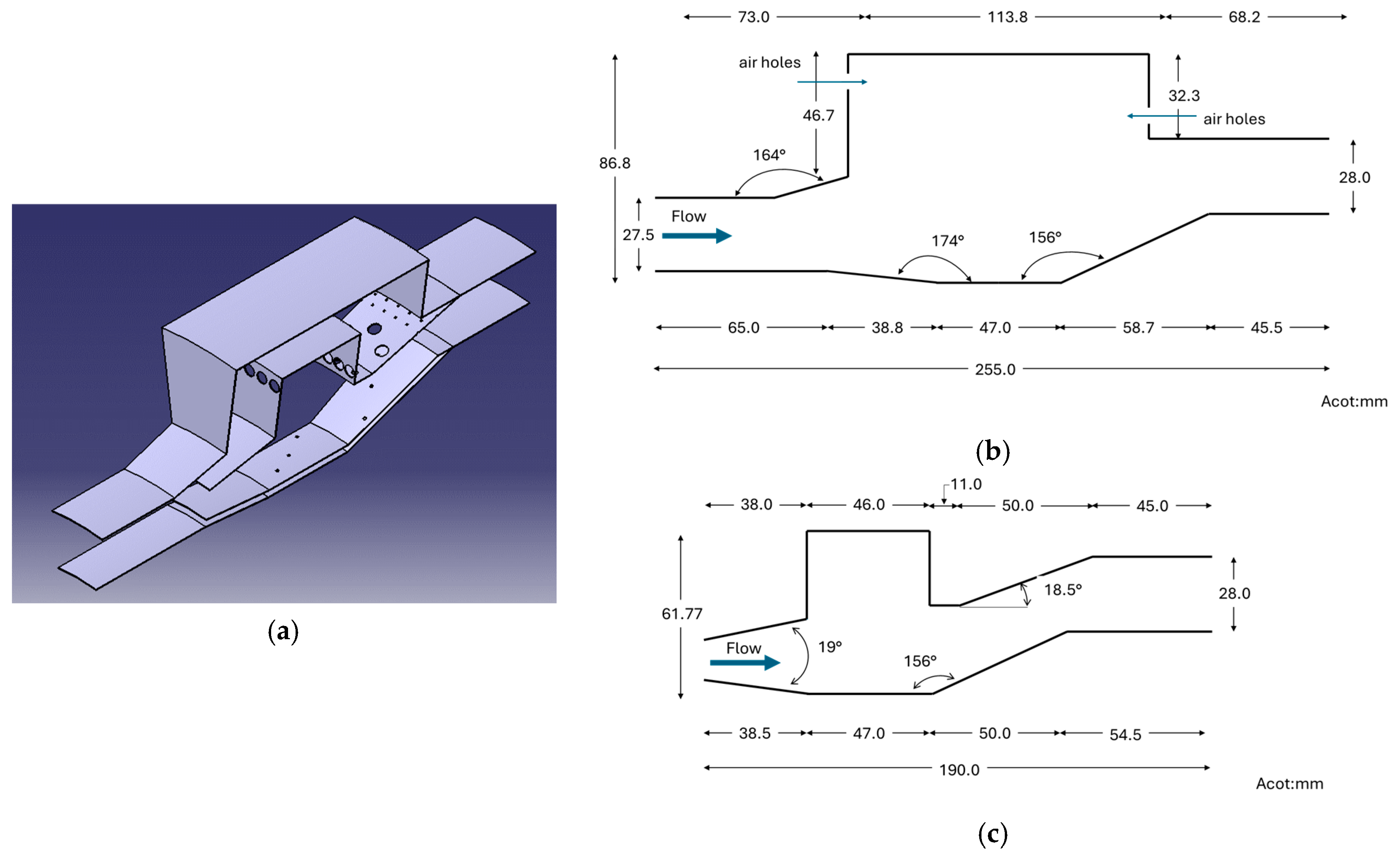
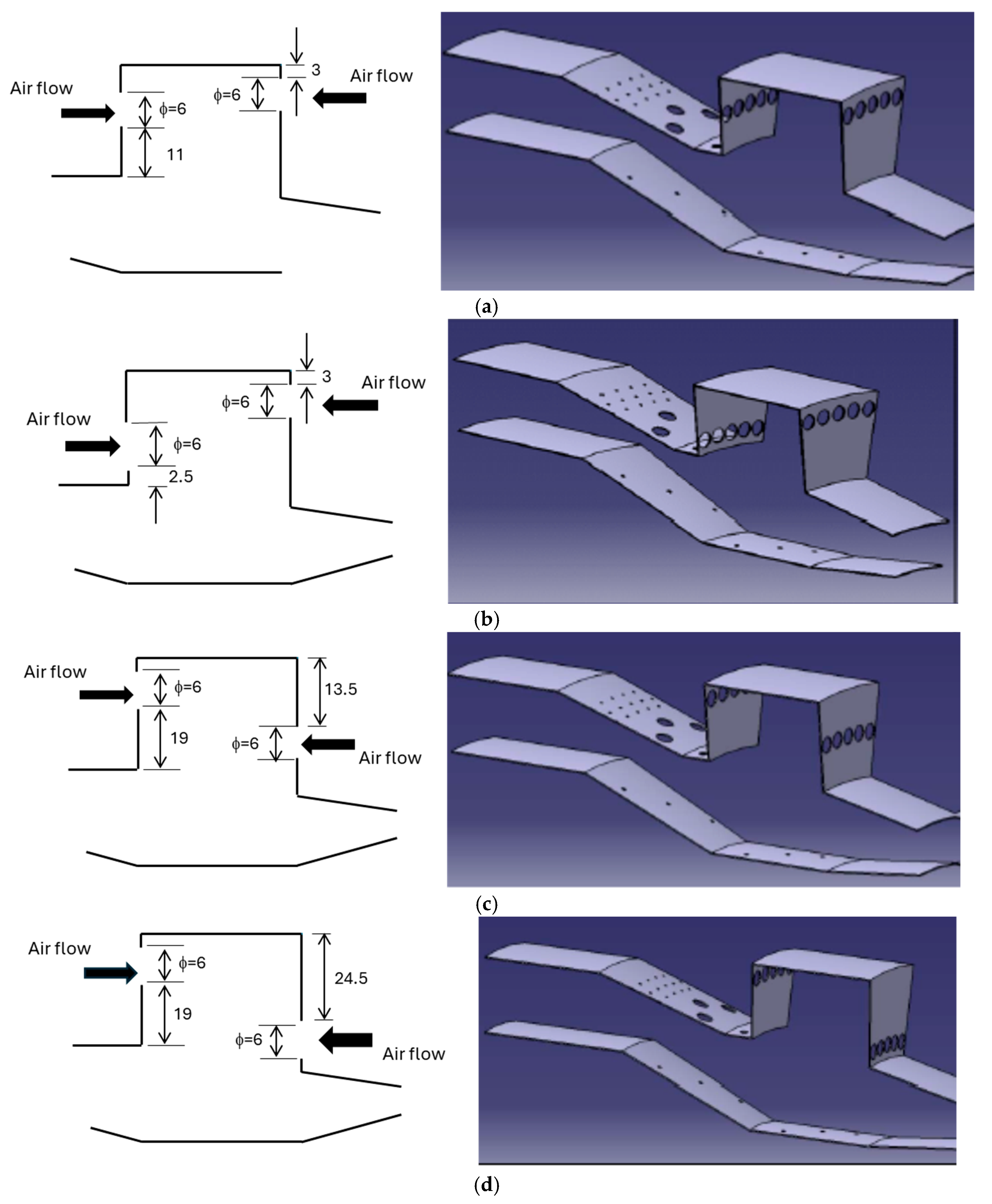




| Parameter | Value |
|---|---|
| Air mass flow | |
| Temperature at the combustor inlet | |
| Total pressure | |
| Temperature at the combustor outlet |
| Configuration | Holes by Row | |
|---|---|---|
| Original | ||
| W | ||
| X | ||
| Y | ||
| Z |
| Cells | |||||
| Negative cells | |||||
| Orthogonality | |||||
| Maximum skewness | |||||
| Computing time |
| Parameter | Value |
|---|---|
| Element size | |
| Growing rate | |
| Minimum number of cells in the aperture | |
| Skewness | |
| Inflation methods | |
| Inflation layers |
| Number of holes in the cavity | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreno Pacheco, L.A.; Barbosa Saldaña, J.G.; López Jarquín, E.G.; Martínez Trinidad, J.; García-León, R.A.; Toledo Velázquez, M. Effects of the Position and Size of the Air Injection Holes in the Flow Structure of a Trapped-Vortex Combustor. Aerospace 2025, 12, 264. https://doi.org/10.3390/aerospace12030264
Moreno Pacheco LA, Barbosa Saldaña JG, López Jarquín EG, Martínez Trinidad J, García-León RA, Toledo Velázquez M. Effects of the Position and Size of the Air Injection Holes in the Flow Structure of a Trapped-Vortex Combustor. Aerospace. 2025; 12(3):264. https://doi.org/10.3390/aerospace12030264
Chicago/Turabian StyleMoreno Pacheco, Luis Alfonso, Juan Gabriel Barbosa Saldaña, Edgar Geovany López Jarquín, José Martínez Trinidad, Ricardo Andrés García-León, and Miguel Toledo Velázquez. 2025. "Effects of the Position and Size of the Air Injection Holes in the Flow Structure of a Trapped-Vortex Combustor" Aerospace 12, no. 3: 264. https://doi.org/10.3390/aerospace12030264
APA StyleMoreno Pacheco, L. A., Barbosa Saldaña, J. G., López Jarquín, E. G., Martínez Trinidad, J., García-León, R. A., & Toledo Velázquez, M. (2025). Effects of the Position and Size of the Air Injection Holes in the Flow Structure of a Trapped-Vortex Combustor. Aerospace, 12(3), 264. https://doi.org/10.3390/aerospace12030264







