Autonomous Dogfight Decision-Making for Air Combat Based on Reinforcement Learning with Automatic Opponent Sampling
Abstract
:1. Introduction
2. Problem Statement
2.1. Dogfight Scenario
2.2. POMDP Formulation
2.2.1. State, Observation, and Action
2.2.2. Reward
3. AOS-PPO Algorithm
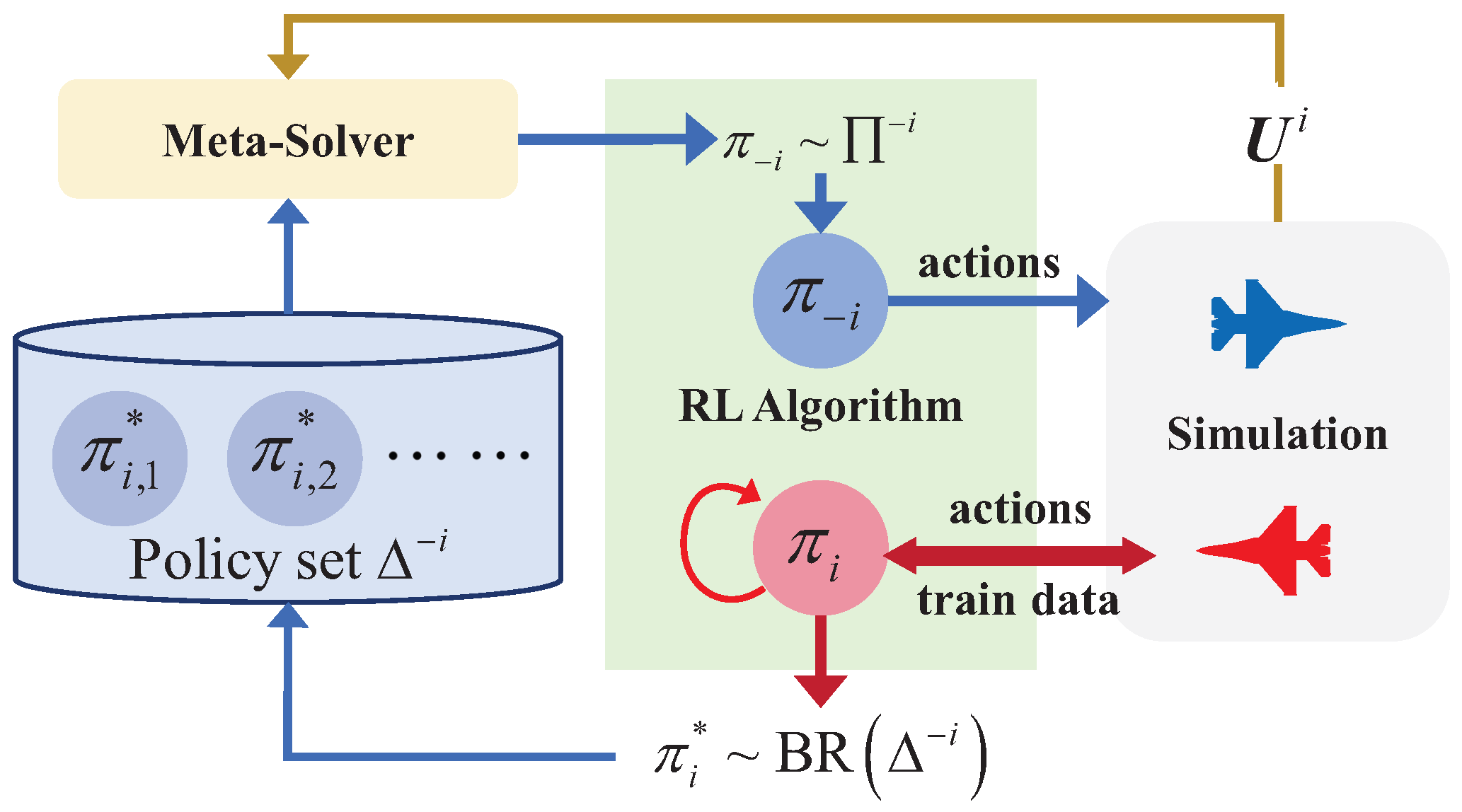
3.1. Self-Play Methods
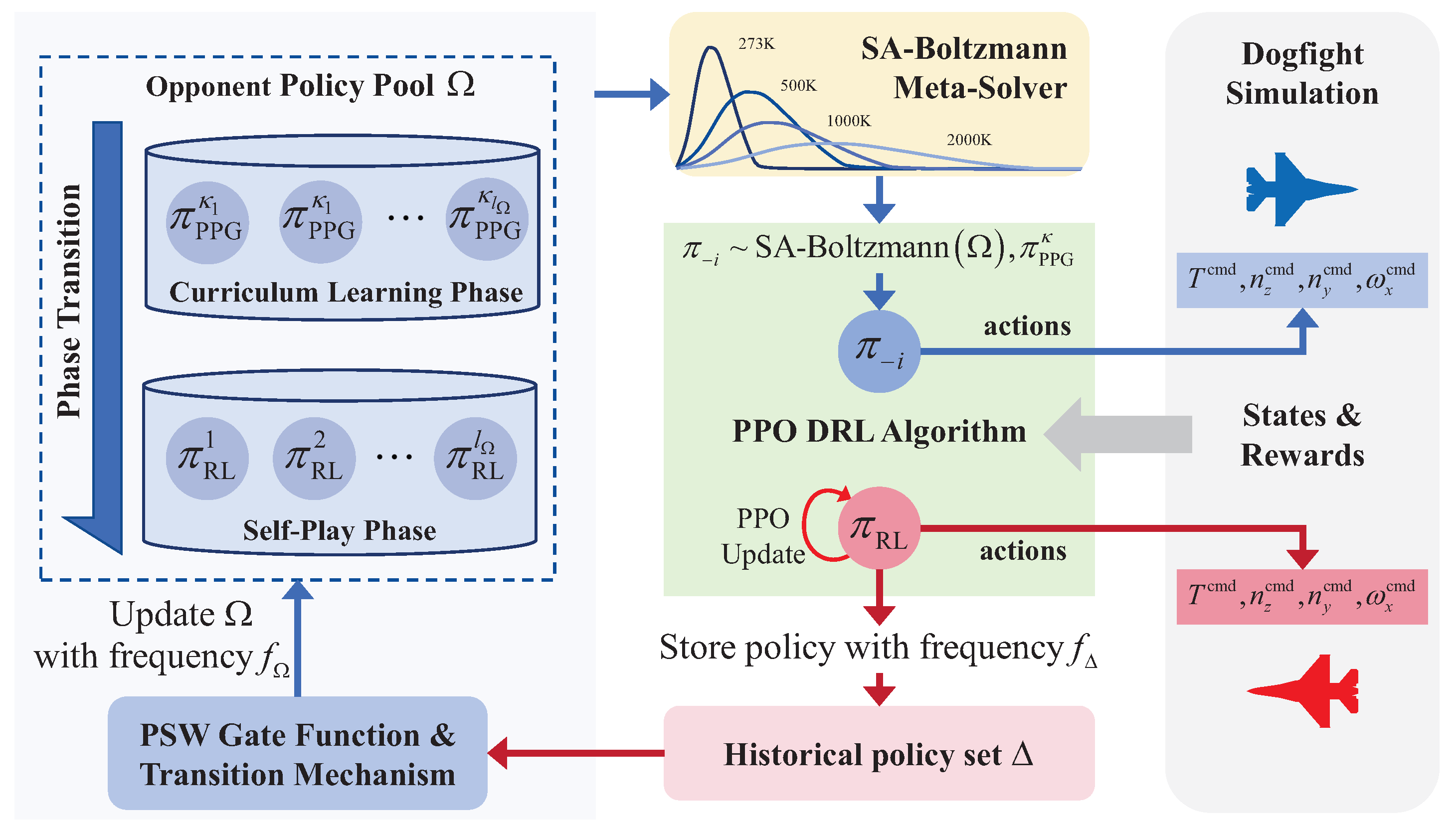
3.2. The Framework of AOS
3.3. The Components Constituting AOS
3.3.1. Phased Opponent Policy Pool
3.3.2. SA–Boltzmann Meta-Solver
| Algorithm 1 SA–Boltzmann Meta-Solver |
|
3.3.3. Priority Sliding Window Gate Function
| Algorithm 2 PSW-GF |
|
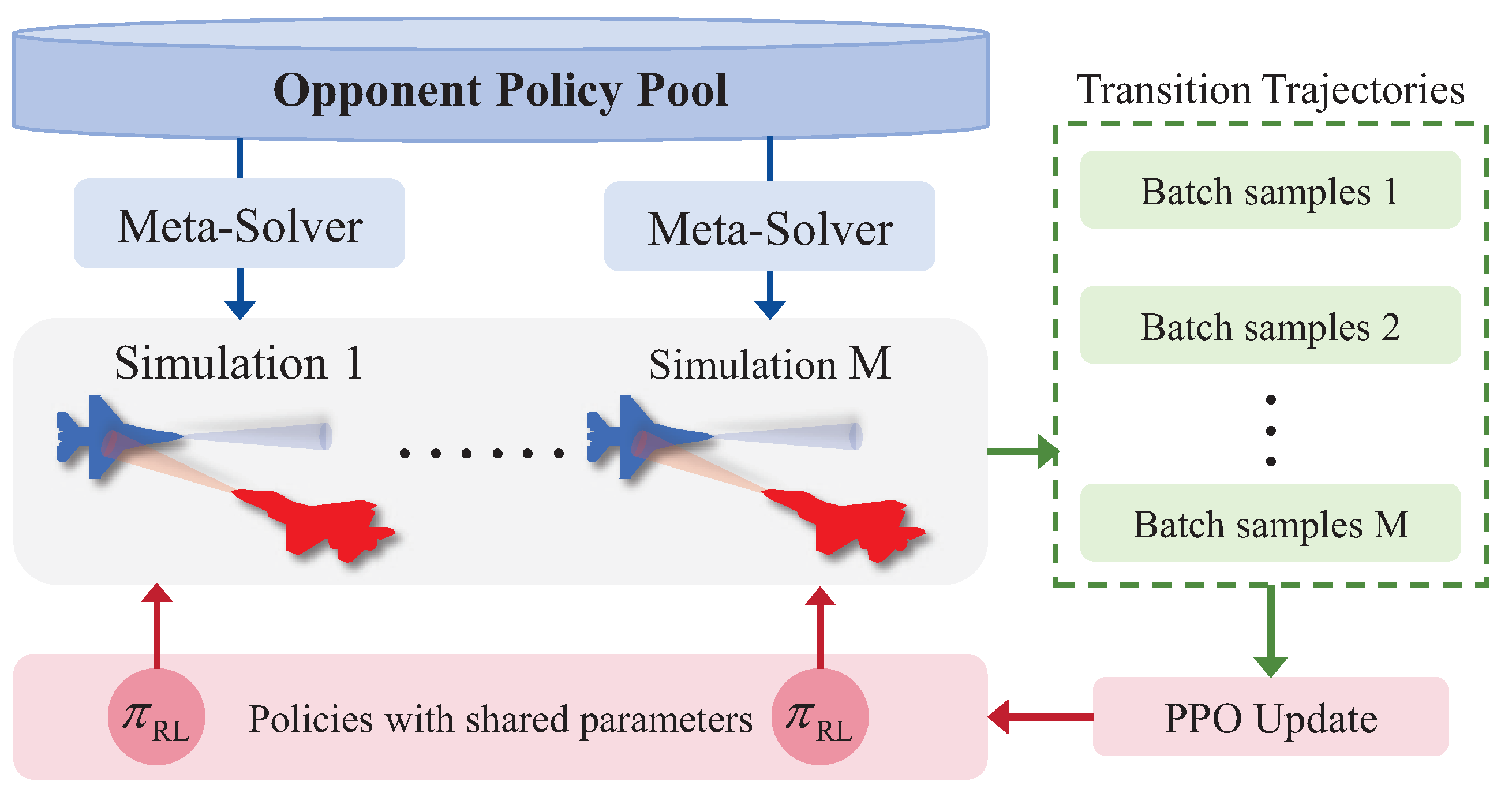
3.4. AOS-PPO with Distributed Training
| Algorithm 3 AOS-PPO. |
|
4. Results and Discussion
4.1. Experiment Settings
4.2. Training and Testing Comparisons
4.3. Ablation Study
4.4. Computational Efficiency
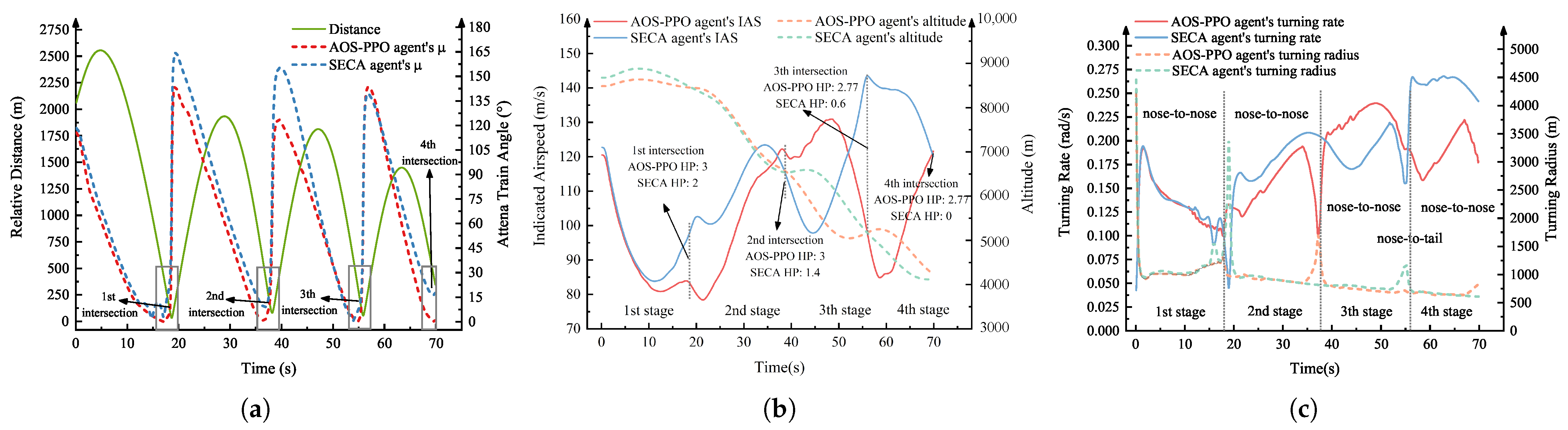
4.5. Simulation Analysis
4.6. Limitations and Future Works
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| RL | Reinforcement learning |
| AOS | Automatic opponent sampling |
| PPO | Proximal policy optimization |
| SA | Simulated annealing |
| SAC | Soft actor–critic |
| PFSP | Prioritized fictitious self-play |
| DOF | Degrees of freedom |
| PSRO | Policy Space Response Oracles |
| POMDP | Partially Observable Markov Decision Process |
| WEZ | Weapons Engagement Zone |
| HP | Health point |
| AWACS | Airborne warning and control |
| LOS | Line of sight |
| BR | Best response |
| SP | Self-play |
| CL | Curriculum learning |
| PPG | Pure Pursuit Guidance |
| WR | Win ratio |
| SDR | Shooting Down Ratio |
| TOW | Time of Win |
| SECA | State–event–condition–action |
| JPC | Joint policy correlation |
References
- Duan, H.; Lei, Y.; Xia, J.; Deng, Y.; Shi, Y. Autonomous Maneuver Decision for Unmanned Aerial Vehicle via Improved Pigeon-Inspired Optimization. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 3156–3170. [Google Scholar]
- Jing, X.; Cong, F.; Huang, J.; Tian, C.; Su, Z. Autonomous Maneuvering Decision-Making Algorithm for Unmanned Aerial Vehicles Based on Node Clustering and Deep Deterministic Policy Gradient. Aerospace 2024, 11, 1055. [Google Scholar] [CrossRef]
- Fan, Z.; Xu, Y.; Kang, Y.; Luo, D. Air Combat Maneuver Decision Method Based on A3C Deep Reinforcement Learning. Machines 2022, 10, 1033. [Google Scholar] [CrossRef]
- Zhu, J.; Kuang, M.; Zhou, W.; Shi, H.; Zhu, J.; Han, X. Mastering air combat game with deep reinforcement learning. Def. Technol. 2024, 34, 295–312. [Google Scholar] [CrossRef]
- Sun, Z.; Piao, H.; Yang, Z.; Zhao, Y.; Zhan, G.; Zhou, D.; Meng, G.; Chen, H.; Chen, X.; Qu, B. Multi-agent hierarchical policy gradient for Air Combat Tactics emergence via self-play. Eng. Appl. Artif. Intell. 2021, 98, 104112. [Google Scholar] [CrossRef]
- Choi, J.; Seo, M.; Shin, H.S.; Oh, H. Adversarial Swarm Defence Using Multiple Fixed-Wing Unmanned Aerial Vehicles. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 5204–5219. [Google Scholar]
- Ren, Z.; Zhang, D.; Tang, S.; Xiong, W.; Yang, S.H. Cooperative maneuver decision making for multi-UAV air combat based on incomplete information dynamic game. Def. Technol. 2023, 27, 308–317. [Google Scholar]
- Huang, L.; Zhu, Q. A Dynamic Game Framework for Rational and Persistent Robot Deception With an Application to Deceptive Pursuit-Evasion. IEEE Trans. Autom. Sci. Eng. 2022, 19, 2918–2932. [Google Scholar] [CrossRef]
- Wang, L.; Wang, J.; Liu, H.; Yue, T. Decision-Making Strategies for Close-Range Air Combat Based on Reinforcement Learning with Variable-Scale Actions. Aerospace 2023, 10, 401. [Google Scholar] [CrossRef]
- Li, Y.F.; Shi, J.P.; Jiang, W.; Zhang, W.G.; Lyu, Y.X. Autonomous maneuver decision-making for a UCAV in short-range aerial combat based on an MS-DDQN algorithm. Def. Technol. 2022, 18, 1697–1714. [Google Scholar]
- Singh, R.; Bhushan, B. Evolving Intelligent System for Trajectory Tracking of Unmanned Aerial Vehicles. IEEE Trans. Autom. Sci. Eng. 2022, 19, 1971–1984. [Google Scholar] [CrossRef]
- Durán-Delfín, J.E.; García-Beltrán, C.; Guerrero-Sánchez, M.; Valencia-Palomo, G.; Hernández-González, O. Modeling and Passivity-Based Control for a convertible fixed-wing VTOL. Appl. Math. Comput. 2024, 461, 128298. [Google Scholar] [CrossRef]
- Zhang, J.D.; Yu, Y.F.; Zheng, L.H.; Yang, Q.M.; Shi, G.Q.; Wu, Y. Situational continuity-based air combat autonomous maneuvering decision-making. Def. Technol. 2023, 29, 66–79. [Google Scholar] [CrossRef]
- Dong, Y.; Ai, J.; Liu, J. Guidance and control for own aircraft in the autonomous air combat: A historical review and future prospects. J. Aerosp. Eng. 2019, 233, 5943–5991. [Google Scholar] [CrossRef]
- Horie, K.; Conway, B. Optimal Fighter Pursuit-Evasion Maneuvers Found Via Two-Sided Optimization. J. Guid. Control. Dyn. 2006, 29, 105–112. [Google Scholar] [CrossRef]
- Taylor, L. Application of the epsilon technique to a realistic optimal pursuit-evasion problem. J. Optim. Theory Appl. 1975, 15, 685–702. [Google Scholar] [CrossRef]
- Anderson, G. A real-time closed-loop solution method for a class of nonlinear differential games. IEEE Trans. Autom. Control. 1972, 17, 576–577. [Google Scholar] [CrossRef]
- Jarmark, B.; Merz, A.; Breakwell, J. The variable-speed tail-chase aerial combat problem. J. Guid. Control. Dyn. 1981, 4, 323–328. [Google Scholar]
- Ramírez, L.; Żbikowski, R. Effectiveness of Autonomous Decision Making for Unmanned Combat Aerial Vehicles in Dogfight Engagements. J. Guid. Control. Dyn. 2018, 41, 1021–1024. [Google Scholar] [CrossRef]
- Wu, A.; Yang, R.; Liang, X.; Zhang, J.; Qi, D.; Wang, N. Visual Range Maneuver Decision of Unmanned Combat Aerial Vehicle Based on Fuzzy Reasoning. Int. J. Fuzzy Syst. 2022, 24, 519–536. [Google Scholar] [CrossRef]
- Hou, Y.; Liang, X.; Zhang, J.; Lv, M.; Yang, A. Hierarchical Decision-Making Framework for Multiple UCAVs Autonomous Confrontation. IEEE Trans. Veh. Technol. 2023, 72, 13953–13968. [Google Scholar]
- Li, K.; Liu, H.; Jiu, B.; Pu, W.; Peng, X.; Yan, J. Knowledge-Aided Model-Based Reinforcement Learning for Anti-Jamming Strategy Learning. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 2976–2994. [Google Scholar]
- Berner, C.; Brockman, G.; Chan, B.; Cheung, V.; Dębiak, P.; Dennison, C.; Farhi, D.; Fischer, Q.; Hashme, S.; Hesse, C.; et al. Dota 2 with Large Scale Deep Reinforcement Learning. arXiv 2019, arXiv:1912.06680. [Google Scholar]
- Vinyals, O.; Babuschkin, I.; Czarnecki, W.M.; Mathieu, M.; Dudzik, A.; Chung, J. Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature 2019, 575, 350–354. [Google Scholar]
- Peng, C.; Zhang, H.; He, Y.; Ma, J. State-Following-Kernel-Based Online Reinforcement Learning Guidance Law Against Maneuvering Target. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 5784–5797. [Google Scholar]
- Pope, A.P.; Ide, J.S.; Mićović, D.; Diaz, H.; Twedt, J.C.; Alcedo, K.; Walker, T.T.; Rosenbluth, D.; Ritholtz, L.; Javorsek, D. Hierarchical Reinforcement Learning for Air Combat At DARPA’s AlphaDogfight Trials. IEEE Trans. Artif. Intell. 2022, 4, 1371–1385. [Google Scholar]
- Bae, J.H.; Jung, H.; Kim, S.; Kim, S.; Kim, Y.D. Deep Reinforcement Learning-Based Air-to-Air Combat Maneuver Generation in a Realistic Environment. IEEE Access 2023, 11, 26427–26440. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, C. Maneuver Decision-Making of Deep Learning for UCAV Thorough Azimuth Angles. IEEE Access 2020, 8, 12976–12987. [Google Scholar]
- Yang, Q.; Zhang, J.; Shi, G.; Hu, J.; Wu, Y. Maneuver Decision of UAV in Short-Range Air Combat Based on Deep Reinforcement Learning. IEEE Access 2020, 8, 363–378. [Google Scholar]
- Bansal, T.; Pachocki, J.; Sidor, S.; Sutskever, I.; Mordatch, I. Emergent Complexity via Multi-Agent Competition. arXiv 2018, arXiv:1710.03748. [Google Scholar]
- Heinrich, J.; Lanctot, M.; Silver, D. Fictitious Self-Play in Extensive-Form Games. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 7–9 July 2015; Volume 37, pp. 805–813. [Google Scholar]
- Heinrich, J.; Silver, D. Deep Reinforcement Learning from Self-Play in Imperfect-Information Games. arXiv 2016, arXiv:1603.01121. [Google Scholar]
- Lanctot, M.; Zambaldi, V.; Gruslys, A.; Lazaridou, A.; Tuyls, K.; Pérolat, J.; Silver, D.; Graepel, T. A Unified Game-Theoretic Approach to Multiagent Reinforcement Learning. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Guyon, E.I., Ed.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. In Proceedings of the International Conference on Machine Learning, Pmlr, Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
- Stevens, B.; Lewis, F.; Johnson, E. Aircraft Control and Simulation: Dynamics, Controls Design, and Autonomous Systems, 3rd ed.; WILEY: Hoboken, NJ, USA, 2015. [Google Scholar]
- Mataric, M. Reward Functions for Accelerated Learning. In Machine Learning Proceedings 1994; Elsevier: Amsterdam, The Netherlands, 1994; pp. 181–189. [Google Scholar]
- Shaw, R. “Fighter Combat,” Tactics and Maneuvering; Naval Institute Press: Annapolis, MD, USA, 1986. [Google Scholar]
- Ulrich, B. Brown’s original fictitious play. J. Econ. Theory 2007, 135, 572–578. [Google Scholar]
- Hernandez, D.; Denamganai, K.; Devlin, S.; Samothrakis, S.; Walker, J.A. A Comparison of Self-Play Algorithms Under a Generalized Framework. IEEE Trans. Games 2022, 14, 221–231. [Google Scholar] [CrossRef]
- Bengio, Y.; Louradour, J.; Collobert, R.; Weston, J. Curriculum learning. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; pp. 41–48. [Google Scholar]
- Baker, B.; Kanitscheider, I.; Markov, T.; Wu, Y.; Powell, G.; McGrew, B.; Mordatch, I. Emergent Tool Use From Multi-Agent Autocurricula. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 30 April 2020. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]

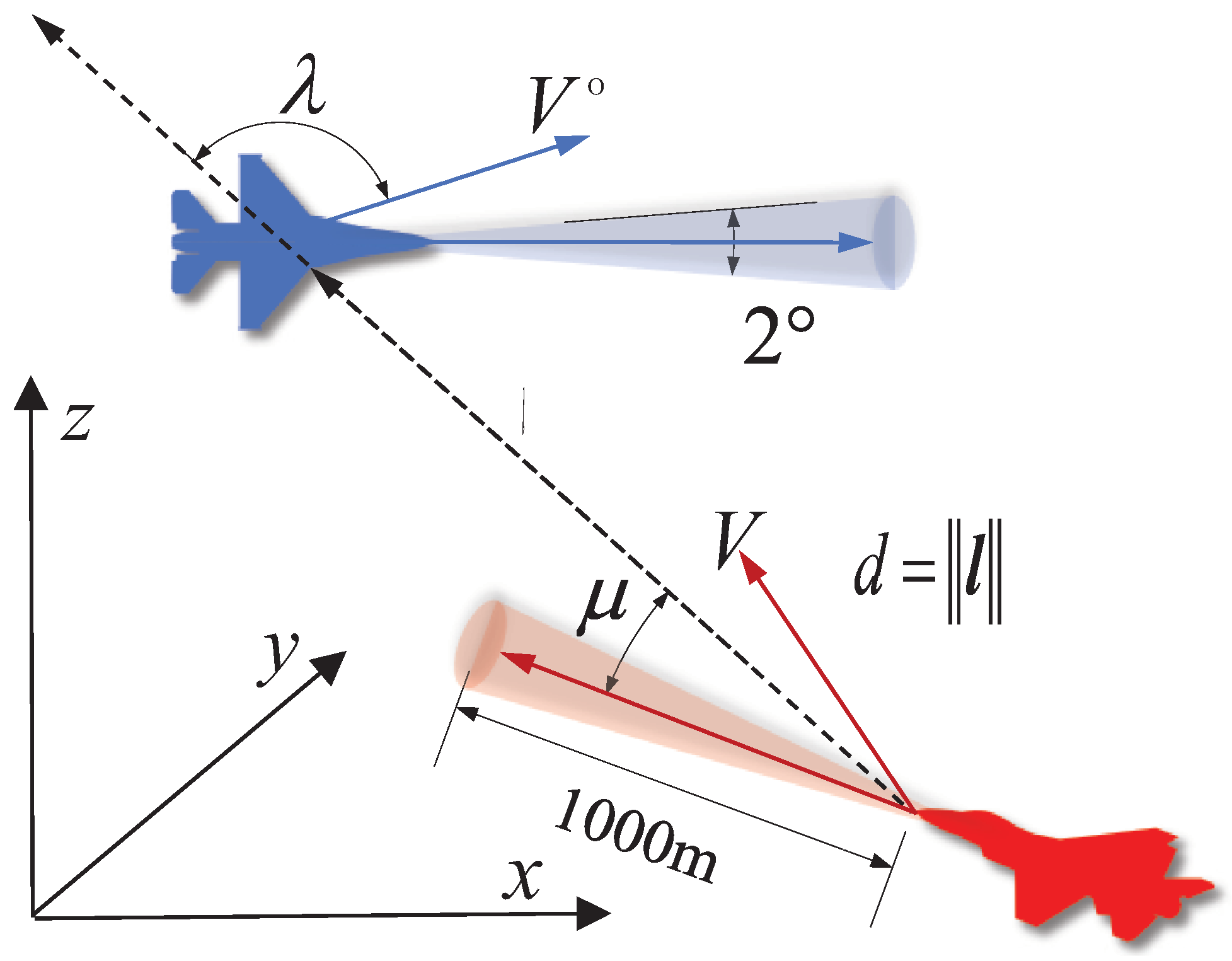



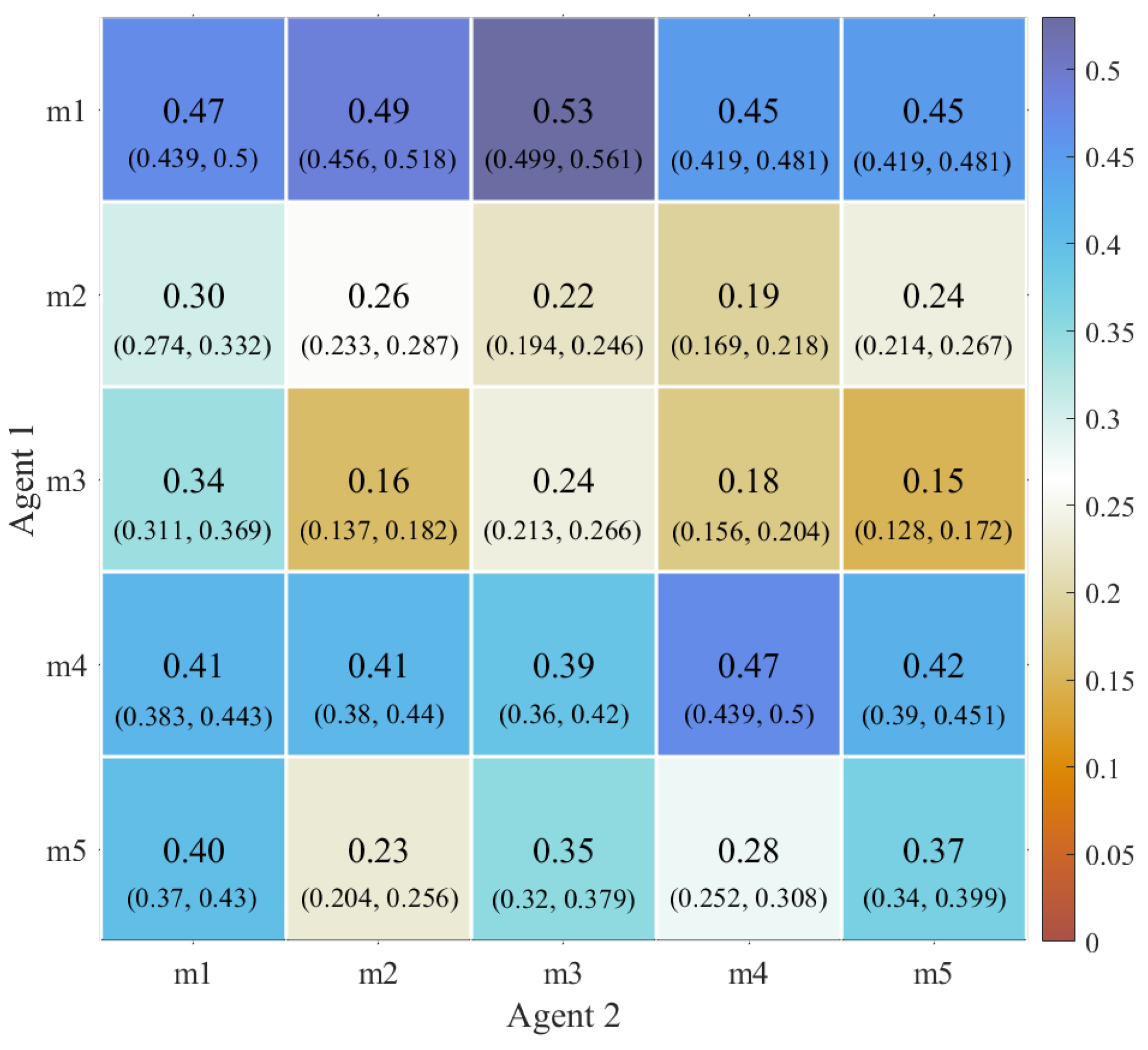
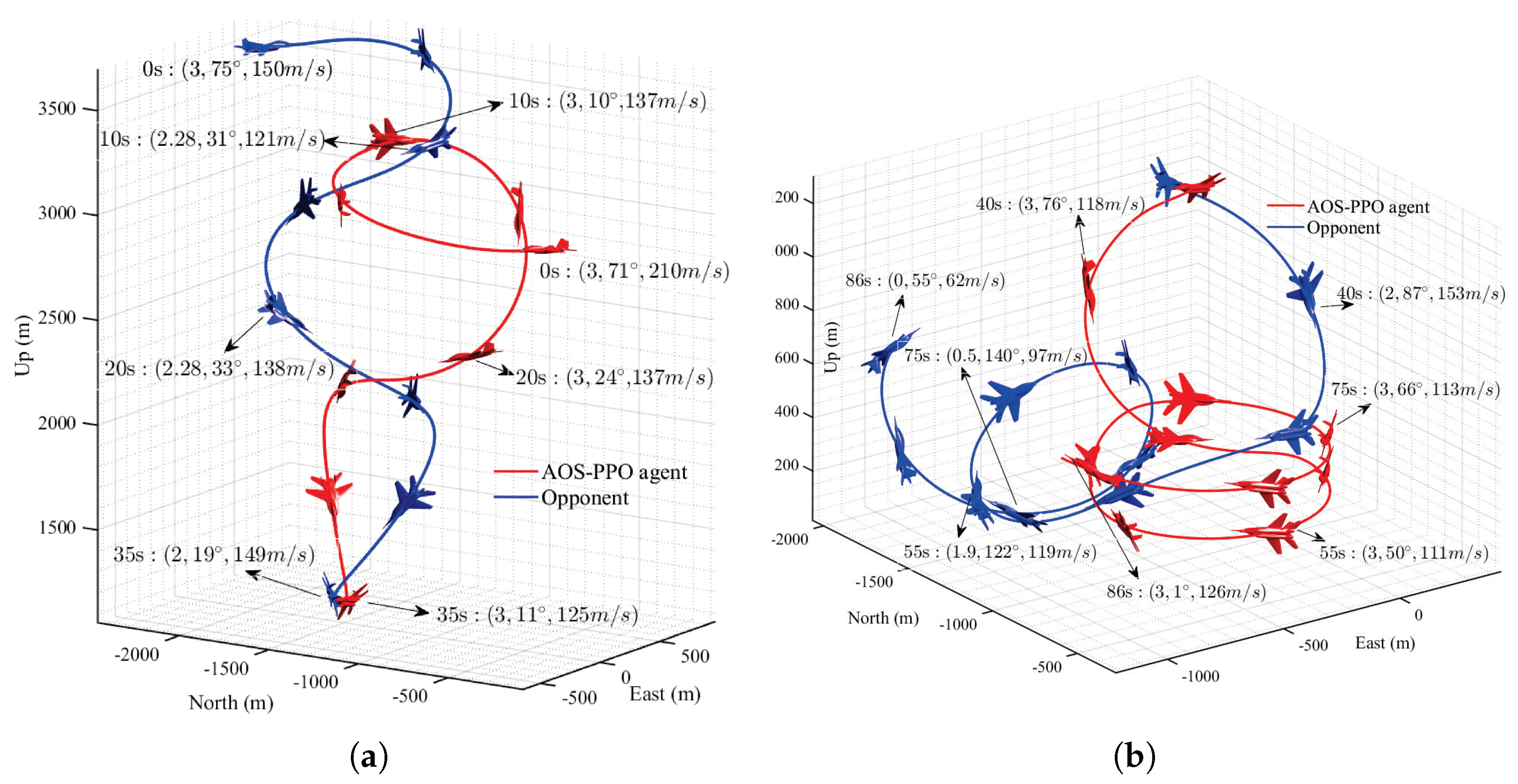
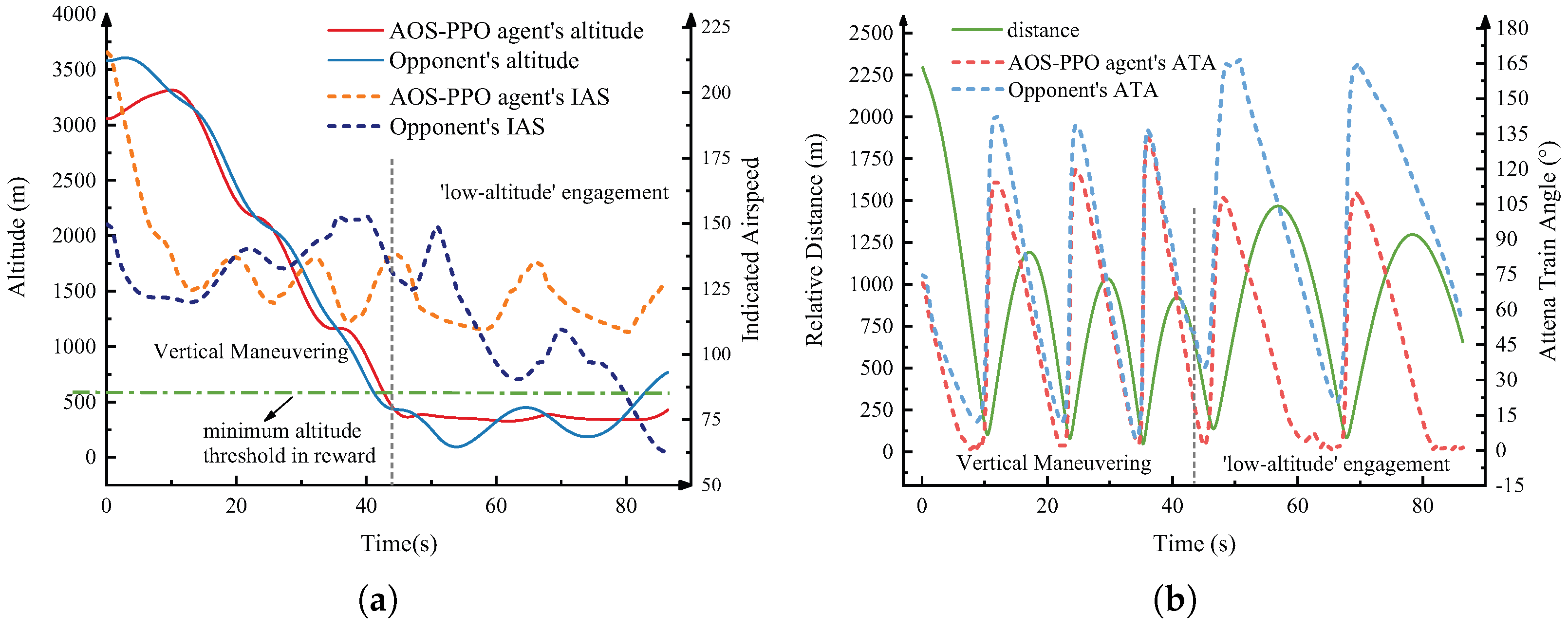
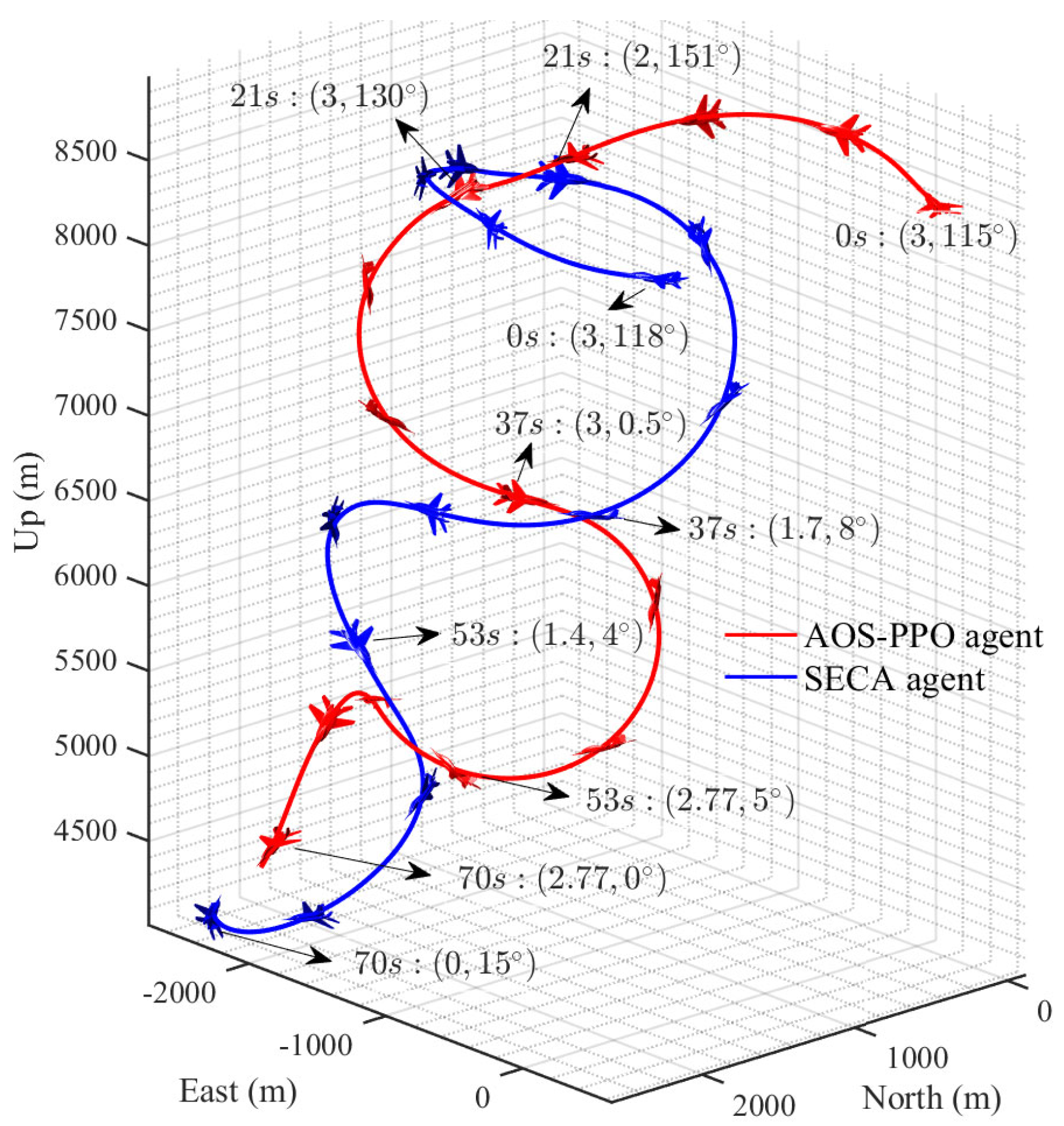
| Observations | Meaning |
|---|---|
| Agent’s indicated airspeed (IAS) | |
| V | Agent’s velocity in the reference frame |
| Opponent’s velocity in the reference frame | |
| Agent’s angle of attack | |
| Agent’s rolling angle | |
| Agent’s pitching angle | |
| Agent’s yawing angle | |
| d | Relative range between two fighters |
| Closing rate of the opponent | |
| h | Agent’s altitude |
| Opponent’s altitude | |
| Agent’s antenna train angle | |
| Opponent’s aspect angle |
| Action | Value Range | Meaning |
|---|---|---|
| Throttle command | ||
| −∼ | Normal acceleration command | |
| −∼ | Lateral acceleration command | |
| −4 rad/s ∼ 4 rad/s | Roll rate command |
| Parameter | Value |
|---|---|
| Length of opponent policy pool, | 8 |
| Frequency of storing historical policy, | 50 |
| Frequency of updating , | 50 |
| Initial temperature in SA–Boltzmann | 1700 K |
| Parameter | Value |
|---|---|
| Discount factor, | |
| Critic iteration times, | 20 |
| Policy iteration times, | 20 |
| Sampling batch size in one training epoch, | 40,000 |
| Number of distributed agents, M | 10 |
| Clip parameter, |
| Components | Layer Shape | Activation Function |
|---|---|---|
| Input layer | (1, 17) | Identity |
| Hidden layers | (4, 128) | Leaky Relu |
| Output layer of actor | (1, 4) | Tanh |
| Output layer of critic | (1, 1) | Identity |
| Parameter | Value |
|---|---|
| Initial pitch angle for the agent and the opponent, | |
| Initial roll angle for the agent and the opponent, | |
| Initial yaw angle for the agent and the opponent, | (, ) |
| Initial distance between the agent and the opponent, | (1000 m, 3000 m) |
| Initial altitude for the agent and the opponent, | (3000 m, 10,000 m) |
| Initial health point for the agent and the opponent, | 3 s |
| Initial antenna train angle for the agent, | (, ) |
| Opponents | Agent’s WR | Agent’s SDR | Agent’s TOW | Opponent’s WR | Opponent’s SDR |
|---|---|---|---|---|---|
| SAC-lstm | 0.545 | 0.115 | 289.3 | 0.341 | 0.027 |
| PPO | 0.722 | 0.383 | 266.5 | 0.187 | 0.004 |
| PFSP-PPO | 0.629 | 0.276 | 283.5 | 0.325 | 0.034 |
| SECA | 0.417 | 0.361 | 290.1 | 0.162 | 0.03 |
| w/o CL | 0.744 | 0.465 | 188.39 | 0.102 | 0.008 |
| w/o SA–Boltzmann | 0.754 | 0.281 | 275.3 | 0.135 | 0.02 |
| Methods | WR | SDR | TOW |
|---|---|---|---|
| AOS-PPO | 0.818 | 0.751 | 107.81 |
| w/o CL | 0.754 | 0.677 | 133.16 |
| w/o SA–Boltzmann | 0.758 | 0.683 | 131.1 |
| Algorithm | Computation Time per Decision |
|---|---|
| AOS-PPO | 0.028 s |
| PFSP-PPO | 0.029 s |
| SAC-lstm | 0.041 s |
| SECA | 0.012 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Song, T.; Mo, L.; Lv, M.; Lin, D. Autonomous Dogfight Decision-Making for Air Combat Based on Reinforcement Learning with Automatic Opponent Sampling. Aerospace 2025, 12, 265. https://doi.org/10.3390/aerospace12030265
Chen C, Song T, Mo L, Lv M, Lin D. Autonomous Dogfight Decision-Making for Air Combat Based on Reinforcement Learning with Automatic Opponent Sampling. Aerospace. 2025; 12(3):265. https://doi.org/10.3390/aerospace12030265
Chicago/Turabian StyleChen, Can, Tao Song, Li Mo, Maolong Lv, and Defu Lin. 2025. "Autonomous Dogfight Decision-Making for Air Combat Based on Reinforcement Learning with Automatic Opponent Sampling" Aerospace 12, no. 3: 265. https://doi.org/10.3390/aerospace12030265
APA StyleChen, C., Song, T., Mo, L., Lv, M., & Lin, D. (2025). Autonomous Dogfight Decision-Making for Air Combat Based on Reinforcement Learning with Automatic Opponent Sampling. Aerospace, 12(3), 265. https://doi.org/10.3390/aerospace12030265






