Heuristic Deepening of the Variable Cycle Engine Model Based on an Improved Volumetric Dynamics Method
Abstract
1. Introduction
- (1)
- A pressure ratio collaborative update method is proposed to address the oversight of the static pressure balance constraint at the mixer in conventional volumetric models.
- (2)
- An adaptive virtual volume method is proposed to improve the model’s real-time performance while preserving the dynamic advantages of the volumetric dynamic method.
- (3)
- Based on the proposed improved volumetric dynamic method, the component-level model of the variable cycle engine is established. The model can capture the actual physical characteristics of the VCE more accurately.
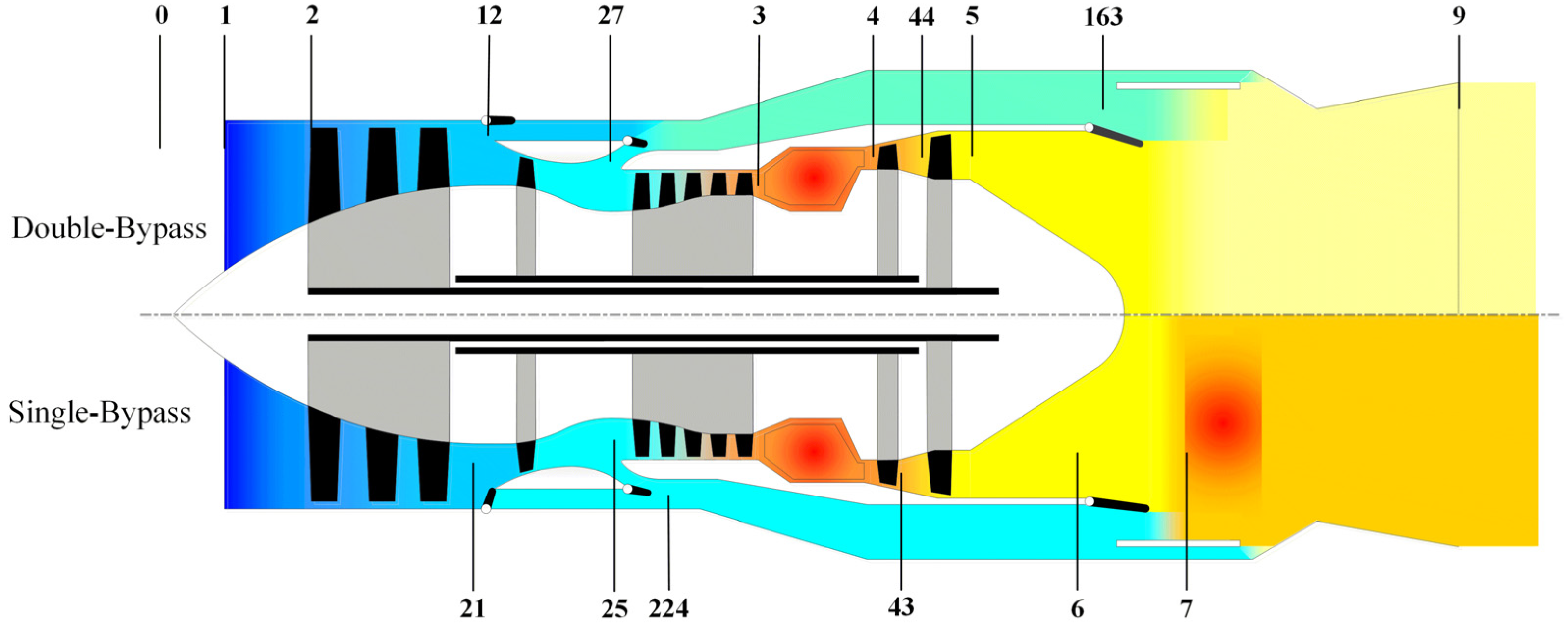
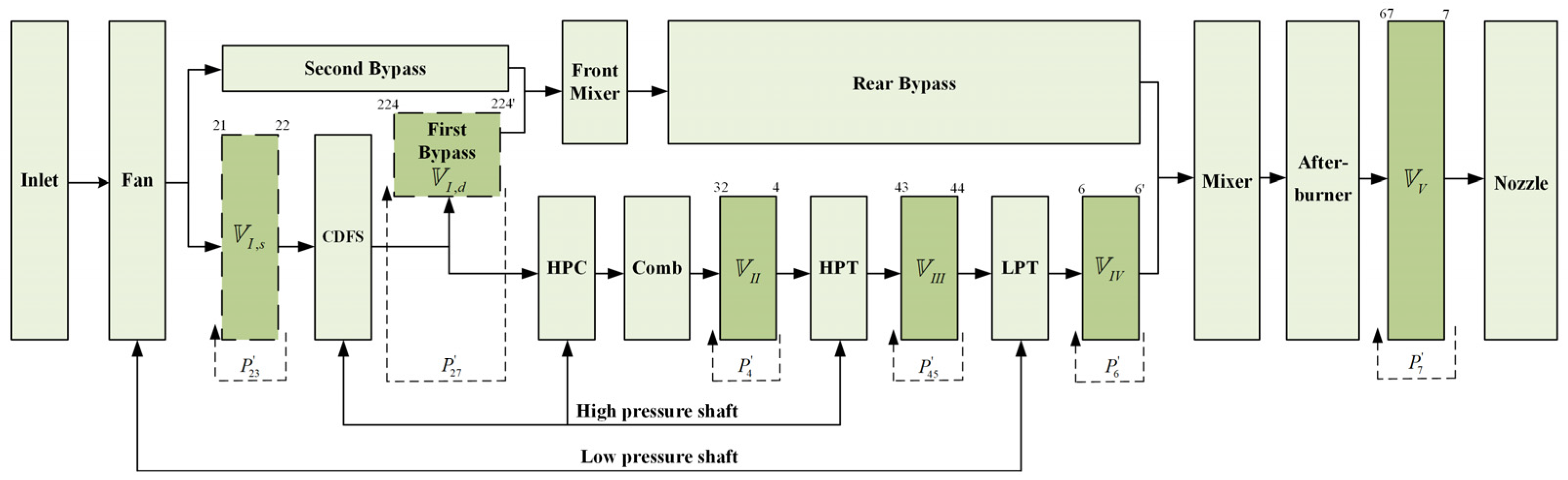
2. Component-Level Modeling
2.1. Modeling Hypothesis
- (1)
- The gas within the engine flow path is treated as a quasi one-dimensional flow.
- (2)
- The effects of variations in the gas Reynolds number on component characteristics are disregarded.
- (3)
- The adiabatic coefficient at each section of the engine is regarded as a function of total temperature and residual gas coefficient at that section.
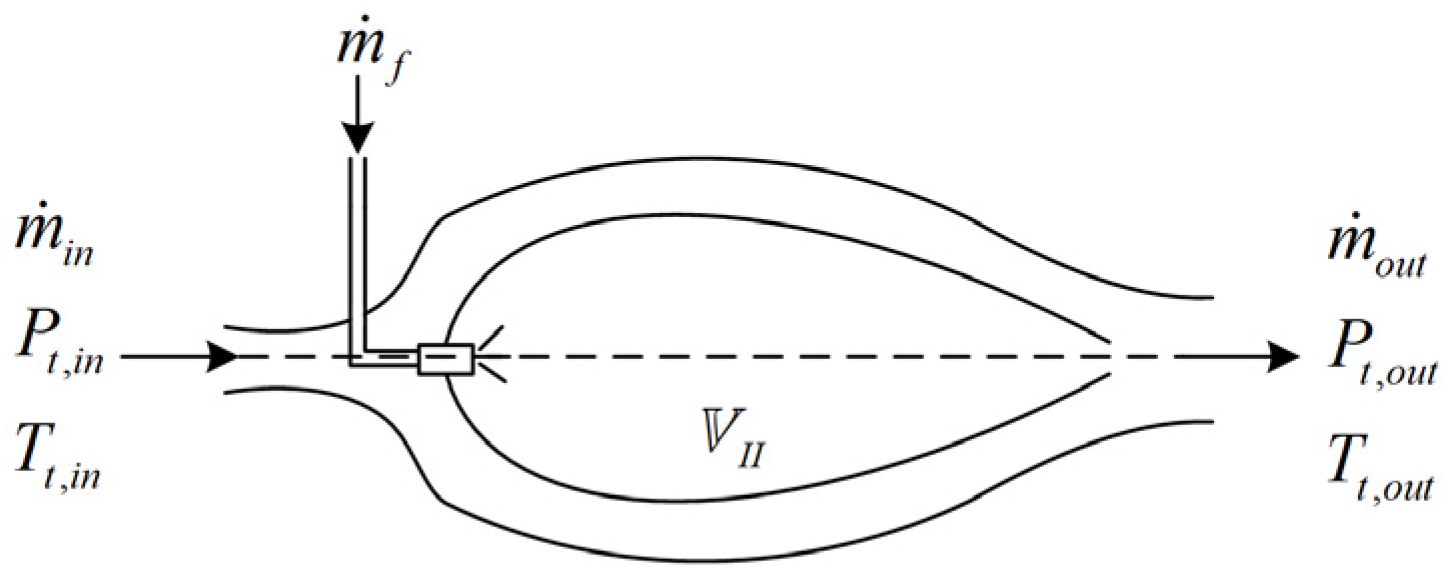
2.2. Volume Modeling
2.3. Component-Level Model
- (1)
- Can avoid the iteration solutions for related components’ outlet parameters;
- (2)
- Can accurately capture the high-frequency characteristics of the engine’s transient state processes;
- (3)
- Can reflect the accumulation effects resulting from mass and energy;
- (4)
- Can demonstrate the impact of actuator variations on engine performance.
3. Improved Volumetric Dynamics Method
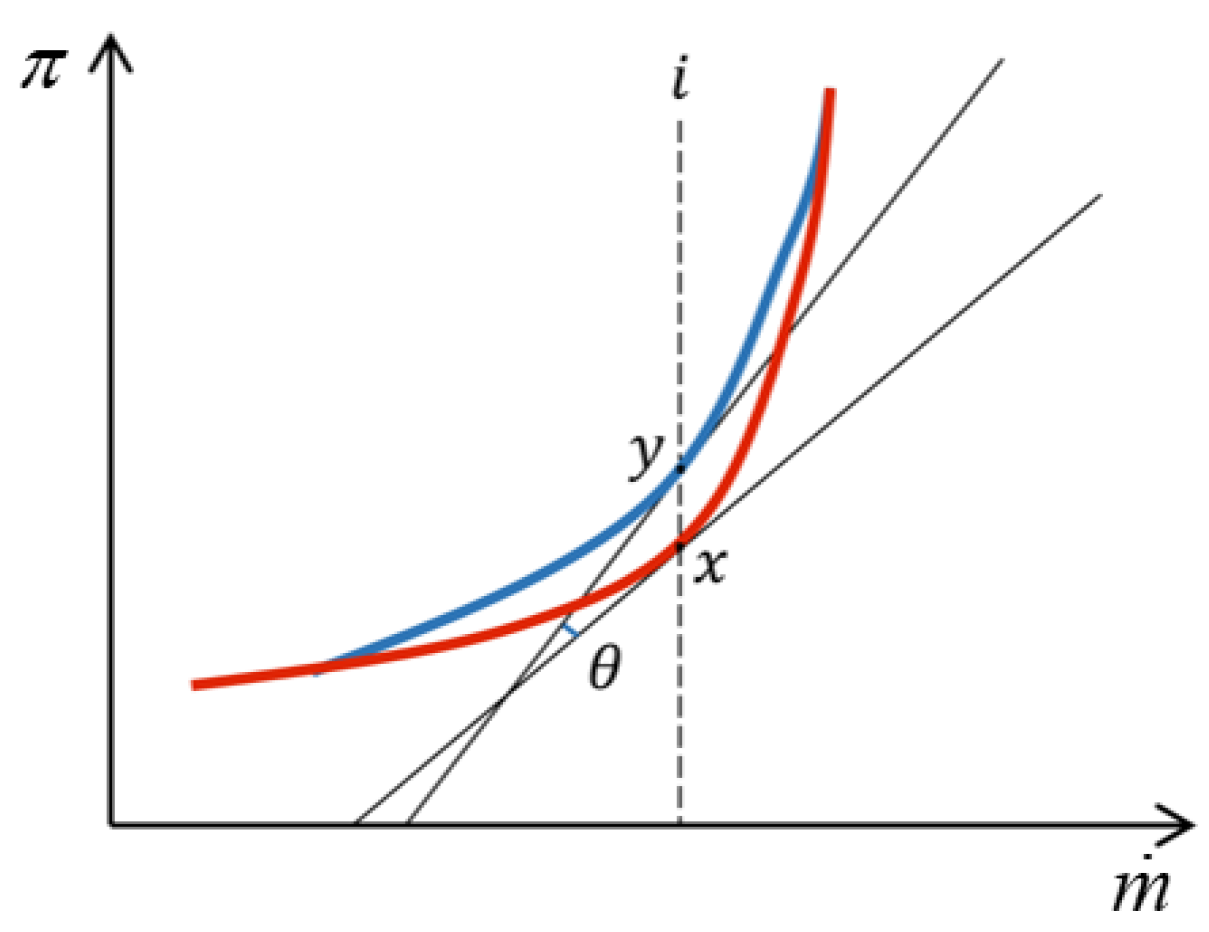
3.1. Pressure Ratio Collaborative Updating Method
3.2. Adaptive Virtual Volume Method
4. Simulation and Analysis
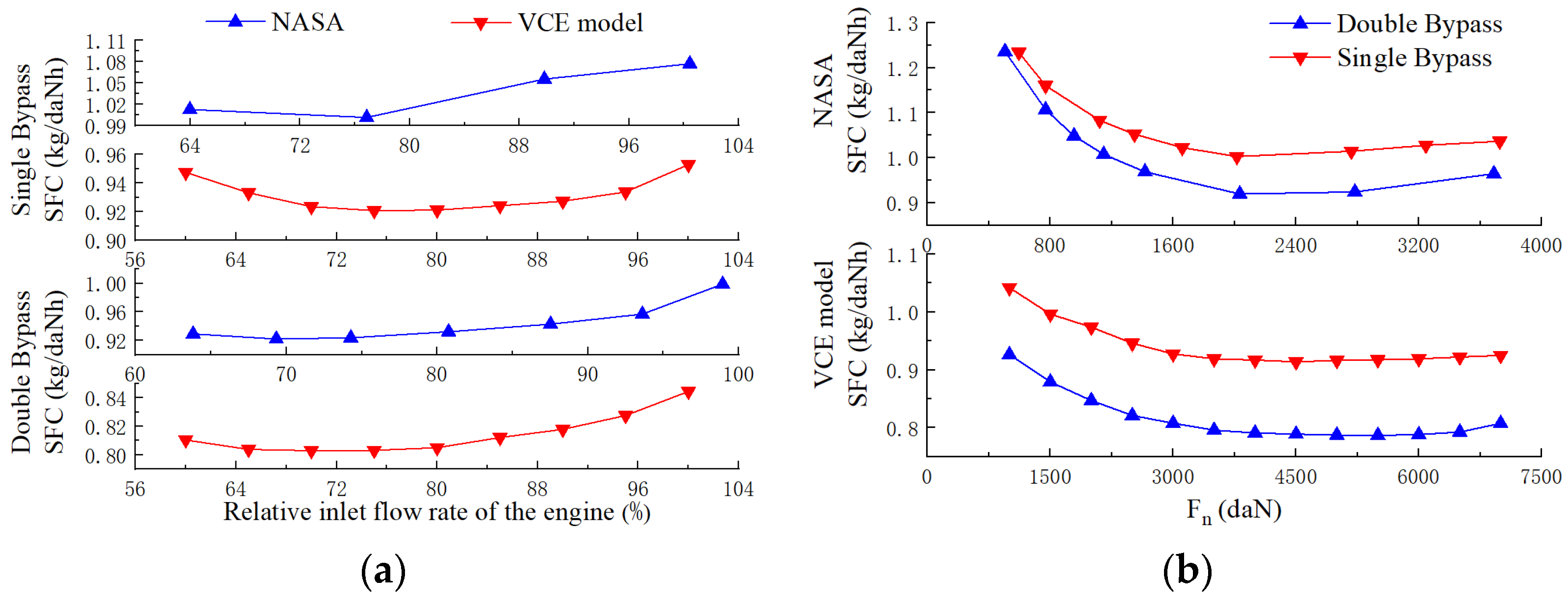
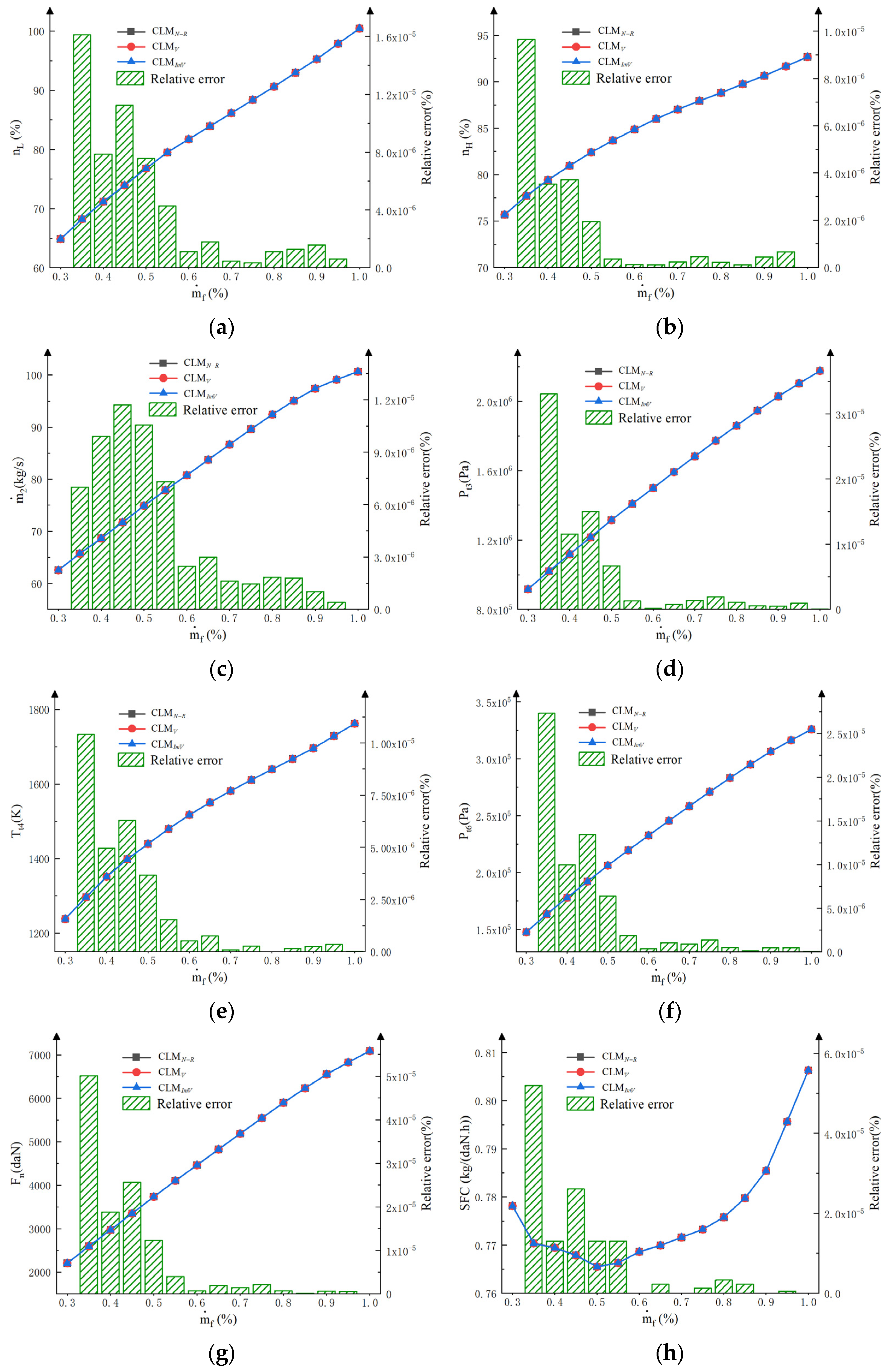
4.1. Comparison of Steady State
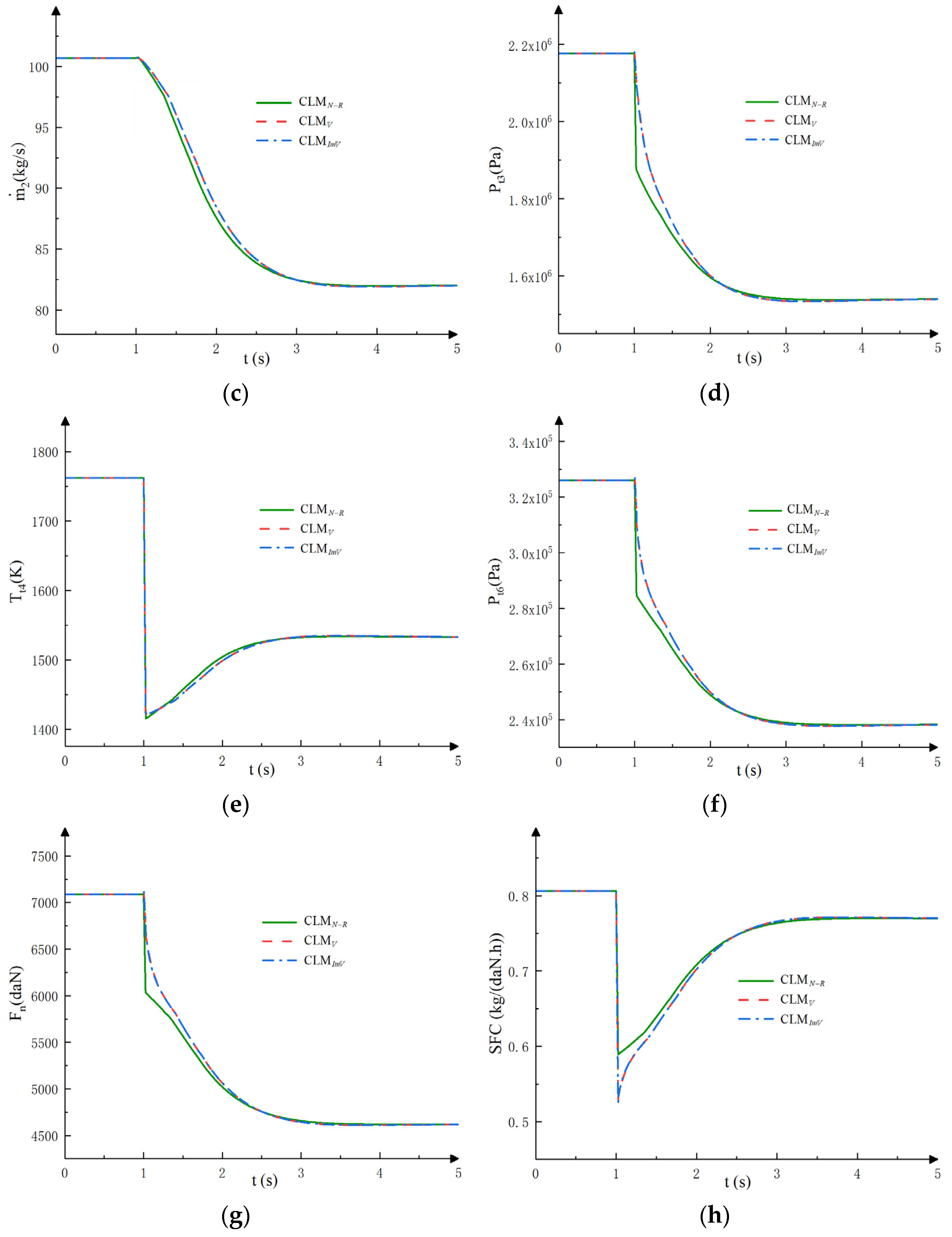
4.2. Comparison of Transition State
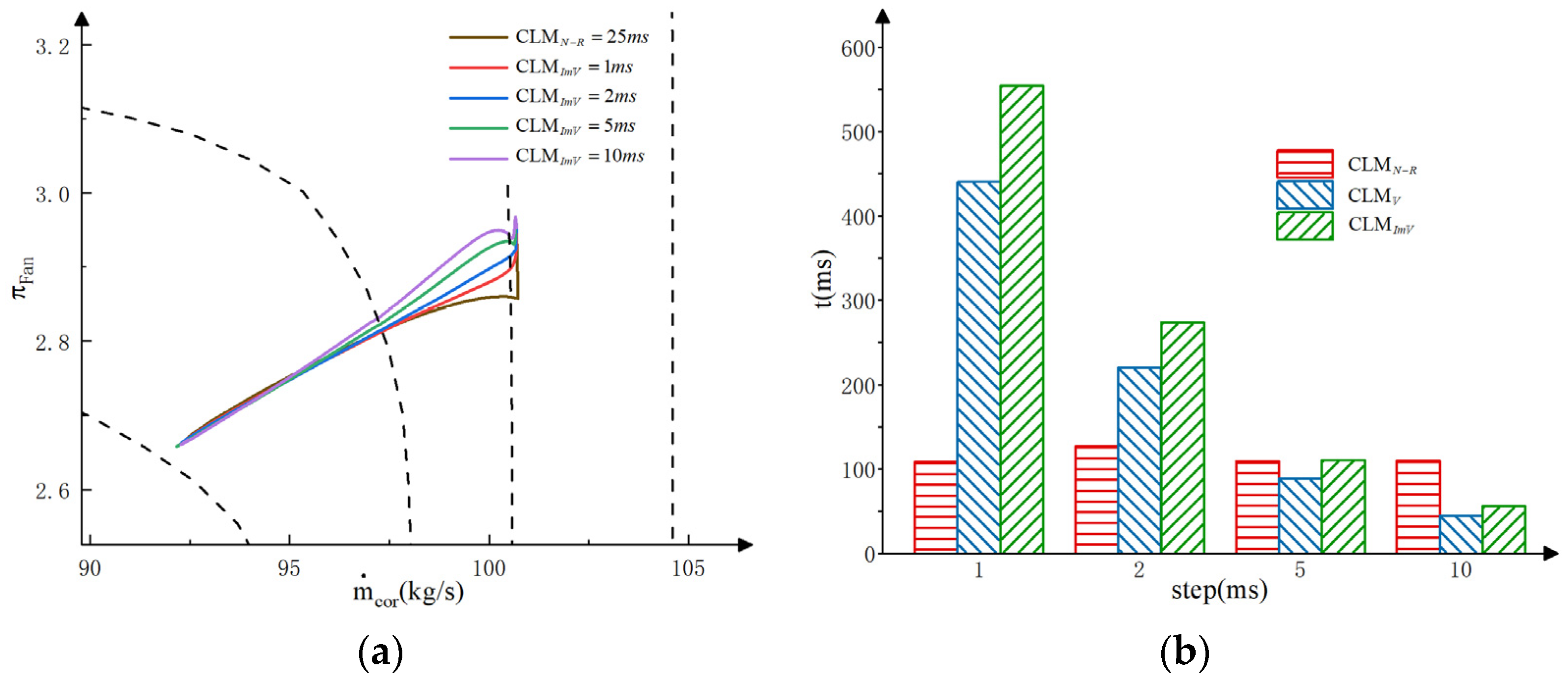
4.3. Simulation of Improved Volumetric Dynamics Model
5. Conclusions
- (1)
- Based on the systematic analysis of the volumetric dynamics modeling process and flow path updating mechanism, a complex configuration model of the VCE is established.
- (2)
- A pressure ratio collaborative update method is proposed to address the oversight of the static pressure balance constraint at the mixer in conventional volumetric models. This method also offers a more accurate simulation of the nozzle’s impact on engine dynamic performance matching.
- (3)
- An adaptive virtual volume method is proposed by using cosine similarity as the optimization criterion. This method improves the model’s real-time performance while preserving the dynamic advantages of the volumetric dynamic method.
- (4)
- The steady-state error of volumetric dynamics model is no greater than 0.0052%, and the transient state simulation curves are smoother, which means the model can capture the actual physical characteristics of VCE more accurately.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Meaning |
| area | |
| throat area of nozzle | |
| the guide area of low-pressure turbine | |
| enthalpy | |
| calorific value of fuel | |
| optimization criterion | |
| adiabatic coefficient | |
| mass flow rate | |
| rotor speed | |
| total pressure | |
| static pressure | |
| gas constant | |
| current moment | |
| total temperature | |
| volume of combustion chamber | |
| volume | |
| residual gas coefficient | |
| combustion efficiency | |
| velocity coefficient | |
| pressure ratio | |
| total pressure recovery coefficient of first bypass | |
| total pressure recovery coefficient of combustion chamber | |
| total pressure recovery coefficient between HPT and LPT | |
| total pressure recovery coefficient between LPT and mixer | |
| total pressure recovery coefficient of afterburner | |
| enthalpy coefficient | |
| momentum function | |
| Newton–Raphson iteration model | |
| volumetric dynamics model | |
| improved volumetric dynamics model | |
| subscript | |
| high-pressure shaft | |
| fuel | |
| low-pressure shaft | |
| inlet of volume | |
| outlet of volume |
References
- Aygun, H.; Turan, O. Exergetic sustainability off-design analysis of variable-cycle aero-engine in various bypass modes. Energy 2020, 195, 117008. [Google Scholar]
- Jia, X.; Zhou, D.; Wei, X.; Wang, H. A novel performance analysis framework for adaptive cycle engine variable geometry components based on topological sorting with rules. Aerosp. Sci. Technol. 2023, 141, 108579. [Google Scholar]
- Jia, X.; Zhou, D. Multi-variable anti-disturbance controller with state-dependent switching law for adaptive cycle engine. Energy 2024, 288, 129845. [Google Scholar] [CrossRef]
- Tahan, M.; Tsoutsanis, E.; Muhammad, M.; Karim, Z.A. Performance-based health monitoring, diagnostics and prognostics for condition-based maintenance of gas turbines: A review. Appl. Energy 2017, 198, 122–144. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, T.; Sheng, H. A novel aeroengine real-time model for active stability control: Compressor instabilities integration. Aerosp. Sci. Technol. 2024, 145, 108844. [Google Scholar] [CrossRef]
- Sheng, H.; Liu, T.; Zhao, Y.; Chen, Q.; Yin, B.; Huang, R. New model-based method for aero-engine turbine blade tip clearance measurement. Chin. J. Aeronaut. 2023, 36, 128–147. [Google Scholar] [CrossRef]
- Wei, Z.; Zhang, S.; Jafari, S.; Nikolaidis, T. Gas turbine aero-engines real time on-board modelling: A review, research challenges, and exploring the future. Prog. Aerosp. Sci. 2020, 121, 100693. [Google Scholar]
- Chen, J.; Hu, Z.; Wang, J. Aero-engine real-time models and their applications. Math. Probl. Eng. 2021, 2021, 9917523. [Google Scholar]
- Aliramezani, M.; Koch, C.R.; Shahbakhti, M. Modeling, diagnostics, optimization, and control of internal combustion engines via modern machine learning techniques: A review and future directions. Prog. Energy Combust. Sci. 2022, 88, 100967. [Google Scholar]
- Wang, J. Identification-based aeroengine nonlinear modeling: A comparative study. Simulation 2020, 96, 199–206. [Google Scholar]
- Villarreal-Valderrama, F.; Liceaga-Castro, E.; Hernandez-Alcantara, D.; Santana-Delgado, C.; Ekici, S.; Amezquita-Brooks, L. Control-Oriented System Identification of Turbojet Dynamics. Aerospace 2024, 11, 630. [Google Scholar] [CrossRef]
- Ma, Y.; Du, X.; Sun, X. Adaptive modification of turbofan engine nonlinear model based on LSTM neural networks and hybrid optimization method. Chin. J. Aeronaut. 2022, 35, 314–332. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, J.; Zhou, W.; Lu, F.; Xu, W. Neural network-based model predictive control with fuzzy-SQP optimization for direct thrust control of turbofan engine. Chin. J. Aeronaut. 2022, 35, 59–71. [Google Scholar] [CrossRef]
- Ren, L.-H.; Ye, Z.-F.; Zhao, Y.-P. A modeling method for aero-engine by combining stochastic gradient descent with support vector regression. Aerosp. Sci. Technol. 2020, 99, 105775. [Google Scholar] [CrossRef]
- Quevedo-Reina, R.; Álamo, G.M.; Padrón, L.A.; Aznárez, J.J. Surrogate model based on ANN for the evaluation of the fundamental frequency of offshore wind turbines supported on jackets. Comput. Struct. 2023, 274, 106917. [Google Scholar] [CrossRef]
- Luo, X.; Geng, J.; Li, M.; Liu, B.; Wang, L.; Song, Z. Research on Iterative Calculation and Optimization Methods of Aero-engine On-board Model. J. Syst. Simul. 2022, 34, 2649–2658. [Google Scholar]
- Pang, S.; Li, Q.; Feng, H. A hybrid onboard adaptive model for aero-engine parameter prediction. Aerosp. Sci. Technol. 2020, 105, 105951. [Google Scholar] [CrossRef]
- Cheng, X.; Zheng, H.; Yang, Q.; Zheng, P.; Dong, W. Surrogate model-based real-time gas path fault diagnosis for gas turbines under transient conditions. Energy 2023, 278, 127944. [Google Scholar] [CrossRef]
- Cai, W.; Zhao, Y.-P.; Zhu, Y.; Yin, J.; Xu, Z.-Y.; Liu, W.-M. A Novel Hybrid Aeroengine Modeling Method for Combining Data-Driven Modules. J. Aerosp. Eng. 2024, 37, 04024055. [Google Scholar] [CrossRef]
- Wang, B.; Xuan, Y. Heuristic deepening of aero engine performance analysis model based on thermodynamic principle of variable mass system. Energy 2024, 306, 132481. [Google Scholar] [CrossRef]
- Ozdemir, U. Comparison of the Newton–Raphson Method and genetic algorithm solutions for nonlinear aircraft trim analysis. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2023, 237, 725–740. [Google Scholar]
- Kong, X.; Wang, X.; Tan, D.; He, A. A non-iterative aeroengine model based on volume effect. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Portland, OR, USA, 8–11 August 2011; p. 6623. [Google Scholar]
- Jia, Z.; Tang, H.; Jin, D.; Xiao, Y.; Chen, M.; Li, S.; Liu, X. Research on the volume-based fully coupled method of the multi-fidelity engine simulation. Aerosp. Sci. Technol. 2022, 123, 107429. [Google Scholar]
- Palman, M.; Leizeronok, B.; Cukurel, B. Comparative study of numerical approaches to adaptive gas turbine cycle analysis. Int. J. Turbo Jet-Engines 2023, 40, 425–436. [Google Scholar]
- Zheng, Q.; Li, L.; Zhang, H.; Chen, J. Research on a high-precision real-time improvement method for aero-engine component-level model. Int. J. Turbo Jet-Engines 2024, 41, 293–305. [Google Scholar]
- Pang, S.; Li, Q.; Zhang, H. A new online modelling method for aircraft engine state space model. Chin. J. Aeronaut. 2020, 33, 1756–1773. [Google Scholar]
- Fawke, A.J.; Saravanamuttoo, H.I.H. Digital computer methods for prediction of gas turbine dynamic response. SAE Trans. 1971, 80, 1805–1813. [Google Scholar]
- Roberts, R.A.; Eastbourn, S.M. Modeling techniques for a computational efficient dynamic turbofan engine model. Int. J. Aerosp. Eng. 2014, 2014, 283479. [Google Scholar]
- Yepifanov, S.; Zelenskyi, R.; Sirenko, F.; Loboda, I. Simulation of pneumatic volumes for a gas turbine transient state analysis. Turbo Expo: Power for Land, Sea, and Air. Am. Soc. Mech. Eng. 2017, 50916, V006T05A037. [Google Scholar]
- Kurosaki, M.; Sasamoto, M.; Asaka, K.; Nakamura, K.; Kakiuchi, D. An efficient transient simulation method for a volume dynamics model. Turbo expo: Power for land, sea, and air. Am. Soc. Mech. Eng. 2018, 51128, V006T05A008. [Google Scholar]
- Liu, Y.; Chen, M.; Tang, H. A versatile volume-based modeling technique of distributed local quadratic convergence for aeroengines. Propuls. Power Res. 2024, 13, 46–63. [Google Scholar]
- Guo, C.; Sun, Y.; Li, L.; Zhu, X. High-Fidelity Simulation and Performance Analysis of Twin-Spool Turbofan Engine Based on Multi-dynamics Approach. Int. J. Aeronaut. Space Sci. 2024, 25, 1243–1256. [Google Scholar]
- Pan, M.X.; Chen, Q.L.; Zhou, Y.Q.; Zhou, W.; Huang, J. A multi-dynamics approach to turbofan engine modeling. Chin. J. Aeronaut 2019, 40, 99–110. [Google Scholar]
- Cai, C.; Zheng, Q.; Zhang, H. A new method to improve the real-time performance of aero-engine component level model. Int. J. Turbo Jet-Engines 2023, 40, 101–109. [Google Scholar]
- Hashmi, M.B.; Lemma, T.A.; Ahsan, S.; Rahman, S. Transient behavior in variable geometry industrial gas turbines: A comprehensive overview of pertinent modeling techniques. Entropy 2021, 23, 250. [Google Scholar] [CrossRef]
- French, M.; Allen, C. NASA VCE Test Bed Engine Aerodynamic Performance Characteristics and Test Results; AIAA Paper 1981–1594; NACA: Boston, MA, USA, 1981.




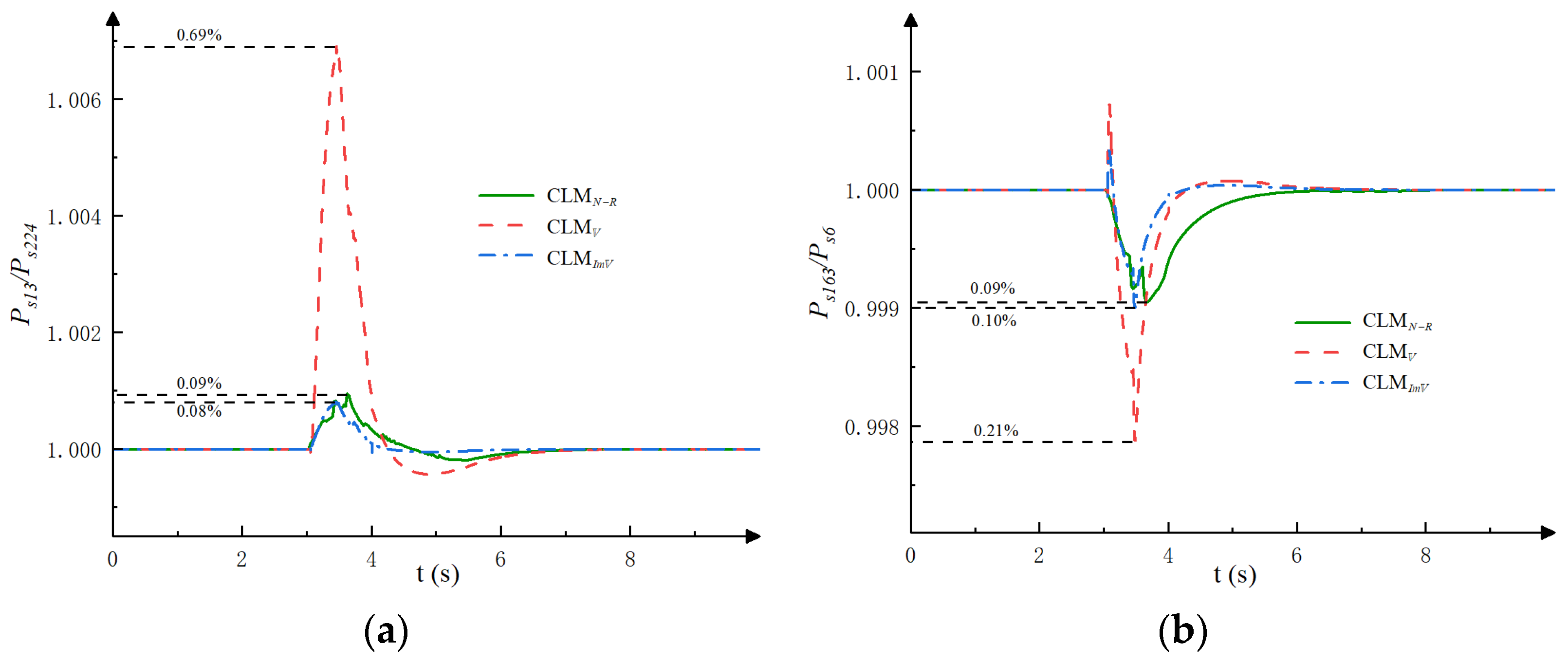
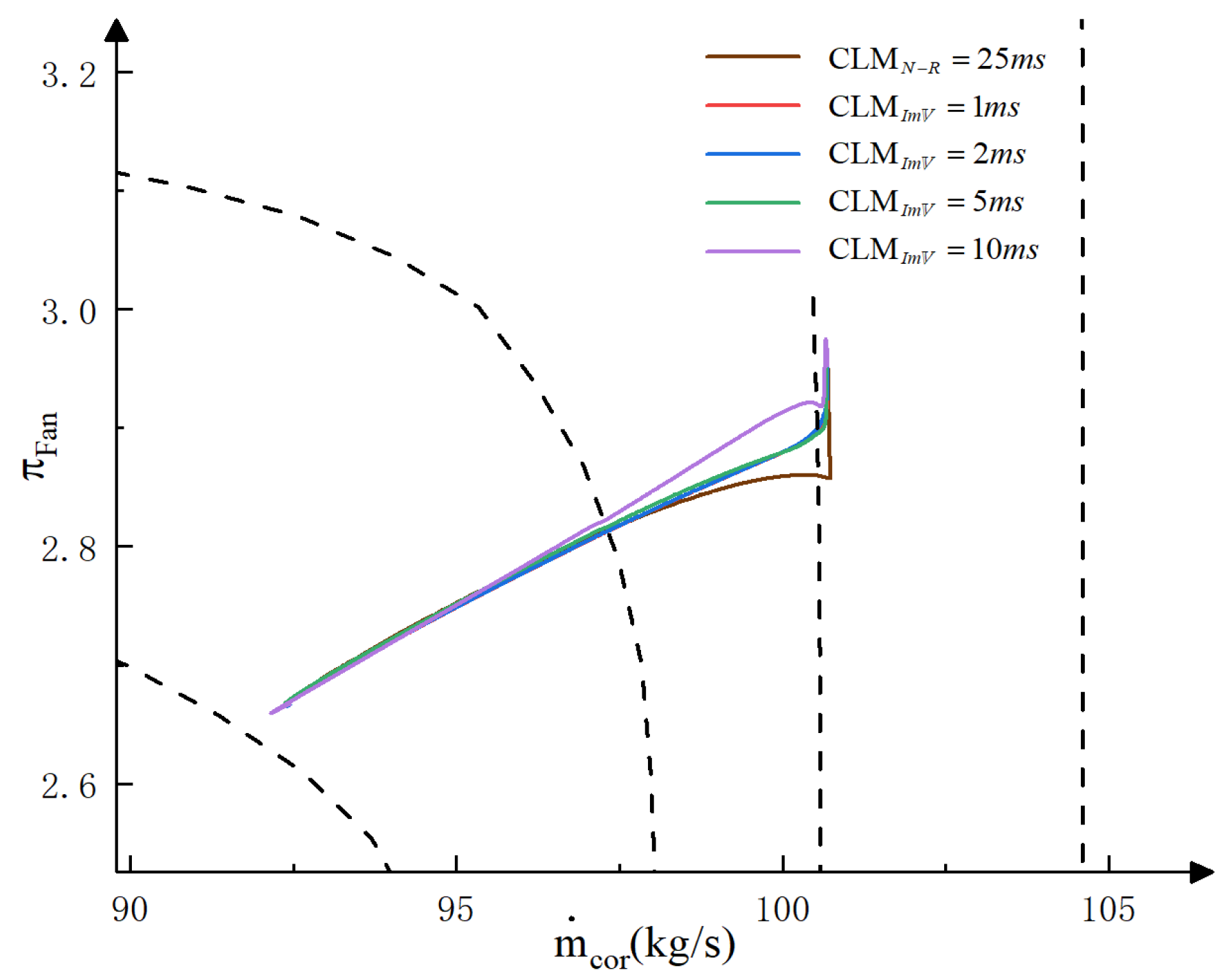

| Model | RMSE | RMSE | RMSE | RMSE | RMSE |
|---|---|---|---|---|---|
| 0.0035% | 0.0034% | 0.0041% | 0.0029% | 0.0025% | |
| 0.0034% | 0.0034% | 0.0040% | 0.0029% | 0.0018% |
| Model | Average Time of Single-Step | Total Time |
|---|---|---|
| 0.269 ms | 2.34 ms | |
| 0.105 ms | 3.65 ms | |
| 0.103 ms | 2.35 ms |
| Step | /m3 | /m3 | /m3 | /m3 | /m3 | t/ms | |
|---|---|---|---|---|---|---|---|
| 1 ms | 1 | 2 | 2 | 2 | 3 | 554.4 | 5.0000 |
| 2 ms | 5.50 | 1.01 | 1.94 | 9.70 | 3.07 | 273.6 | 4.9999 |
| 5 ms | 7.77 | 0.27 | 13.52 | 11.64 | 1.96 | 110.1 | 4.9995 |
| 10 ms | 12.82 | 0.45 | 7.67 | 14.10 | 1.95 | 55.8 | 4.9977 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Lu, S.; Guo, L.; Zhou, W.; Huang, J. Heuristic Deepening of the Variable Cycle Engine Model Based on an Improved Volumetric Dynamics Method. Aerospace 2025, 12, 274. https://doi.org/10.3390/aerospace12040274
Chen Y, Lu S, Guo L, Zhou W, Huang J. Heuristic Deepening of the Variable Cycle Engine Model Based on an Improved Volumetric Dynamics Method. Aerospace. 2025; 12(4):274. https://doi.org/10.3390/aerospace12040274
Chicago/Turabian StyleChen, Ying, Sangwei Lu, Lin Guo, Wenxiang Zhou, and Jinquan Huang. 2025. "Heuristic Deepening of the Variable Cycle Engine Model Based on an Improved Volumetric Dynamics Method" Aerospace 12, no. 4: 274. https://doi.org/10.3390/aerospace12040274
APA StyleChen, Y., Lu, S., Guo, L., Zhou, W., & Huang, J. (2025). Heuristic Deepening of the Variable Cycle Engine Model Based on an Improved Volumetric Dynamics Method. Aerospace, 12(4), 274. https://doi.org/10.3390/aerospace12040274





