Aerodynamic Prediction and Design Optimization Using Multi-Fidelity Deep Neural Network
Abstract
:1. Introduction
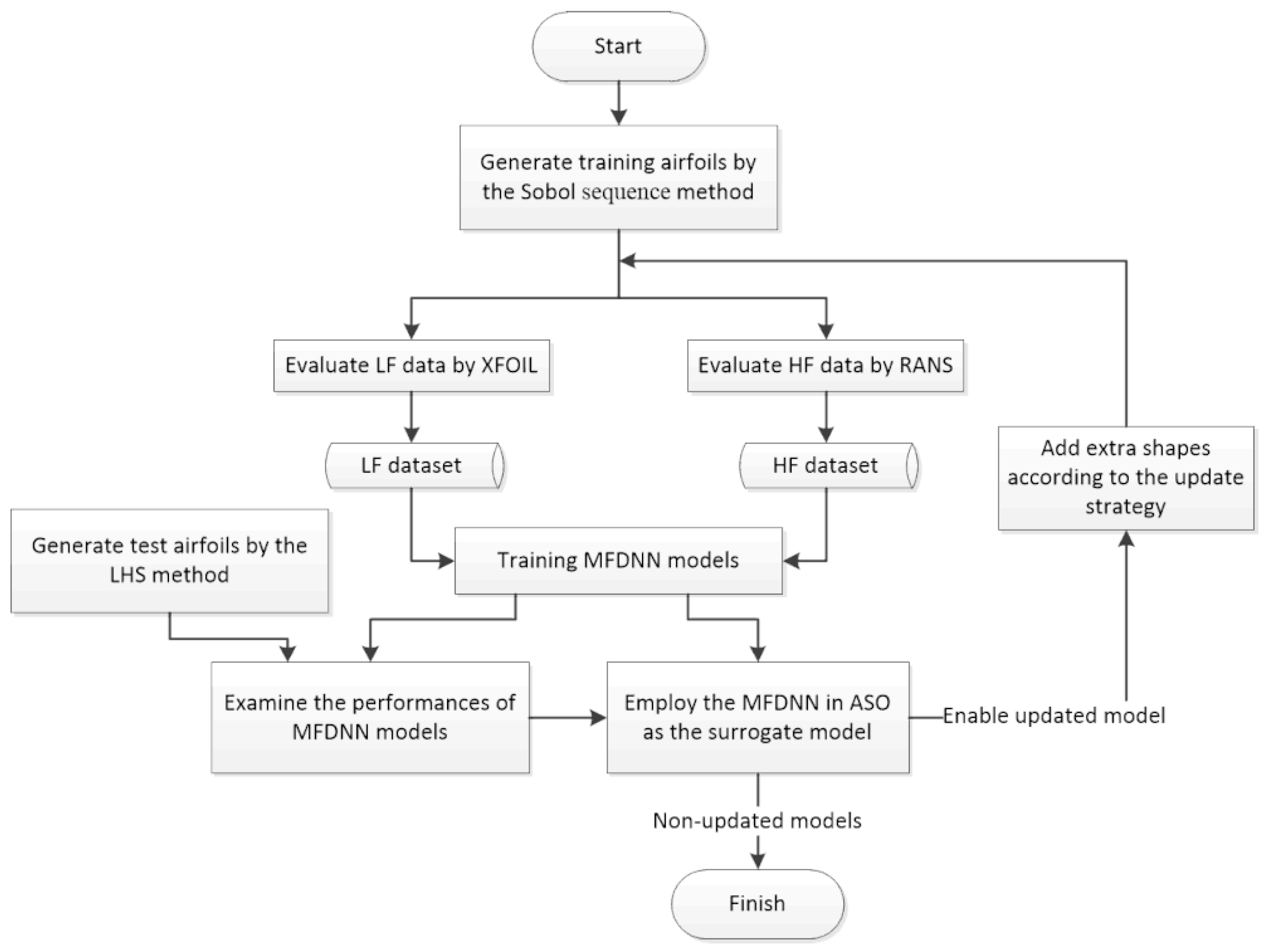
2. Methods
2.1. Construction of Datasets
2.1.1. Geometry Parameterization Method
2.1.2. Calculations of Aerodynamic Coefficients
2.1.3. Design of Experiment Method
2.2. Training of Multi-Fidelity Deep Neural Networks
2.3. The Global Optimization Algorithm
- (1)
- Initialize a population of particles with random positions and velocities within defined bounds.
- (2)
- Evaluate the objective function Fobj for each particle.
- (3)
- Update the personal best position of each particle.
- (4)
- Update the global best position of all particles.
- (5)
- Evaluate and update the velocity and position of the particles according to Equations (15) and (16).
- (6)
- Repeat steps 2–5 until the stopping criterion is met.
3. Aerodynamic Coefficient Predictions Using MFDNN Models
3.1. Description of the Aerodynamic Prediction Task
3.2. Training Results of the Models
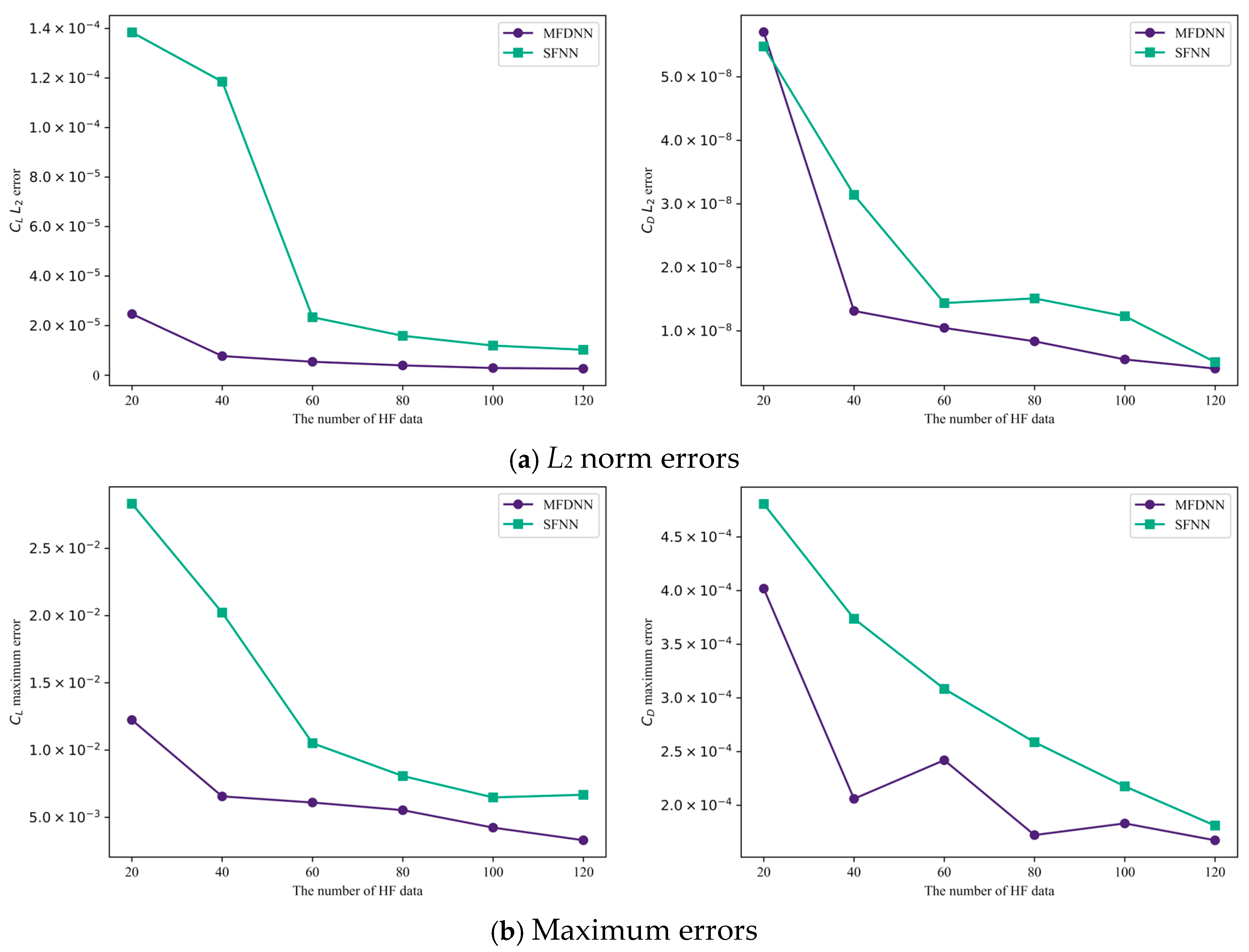
3.3. Examination of Accuracy and Efficiency
4. Aerodynamic Shape Optimization Using MFDNN Models
4.1. Description of the Aerodynamic Shape Optimization Problem
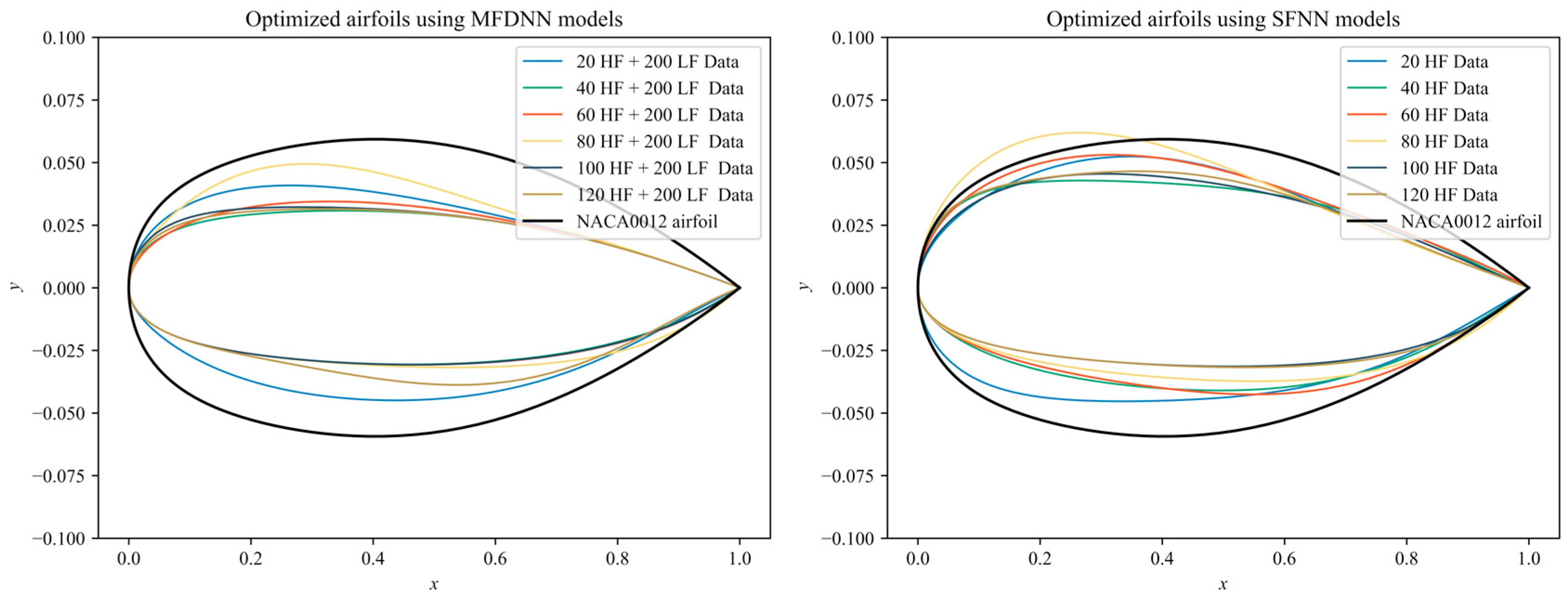
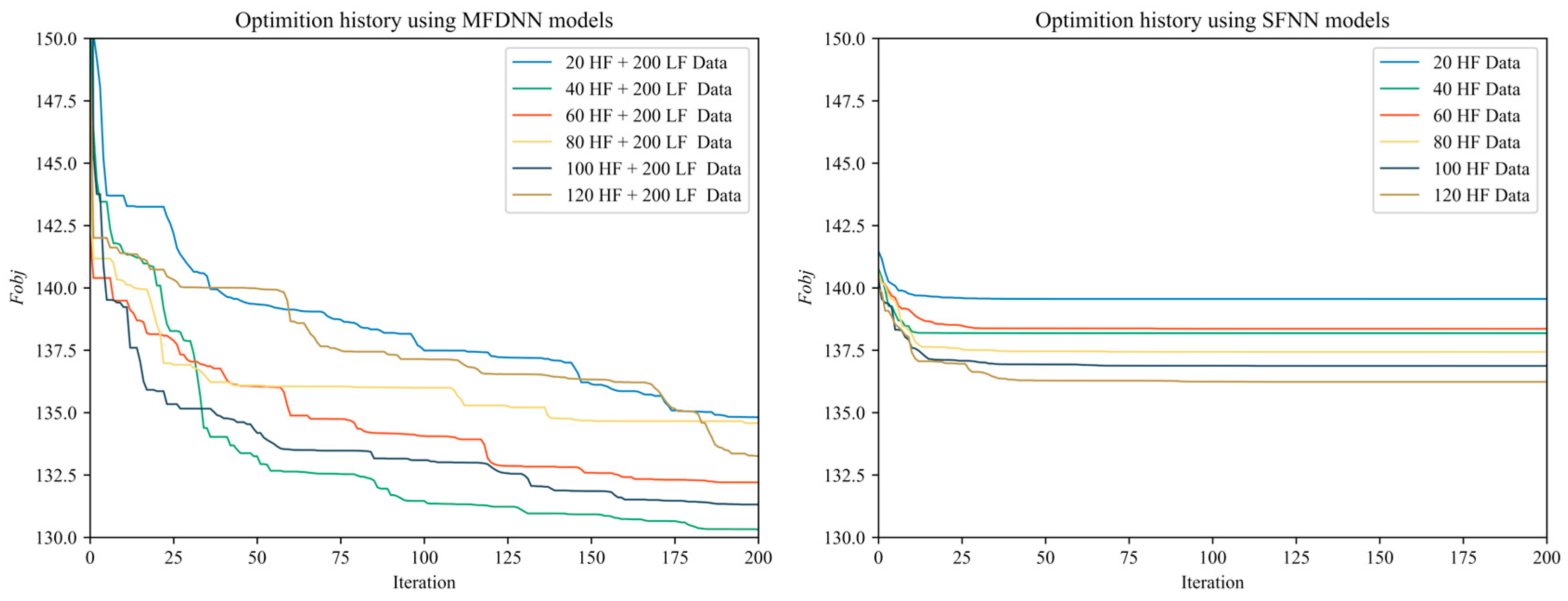
4.2. Optimization Results Using the Non-Updated MFDNN Models
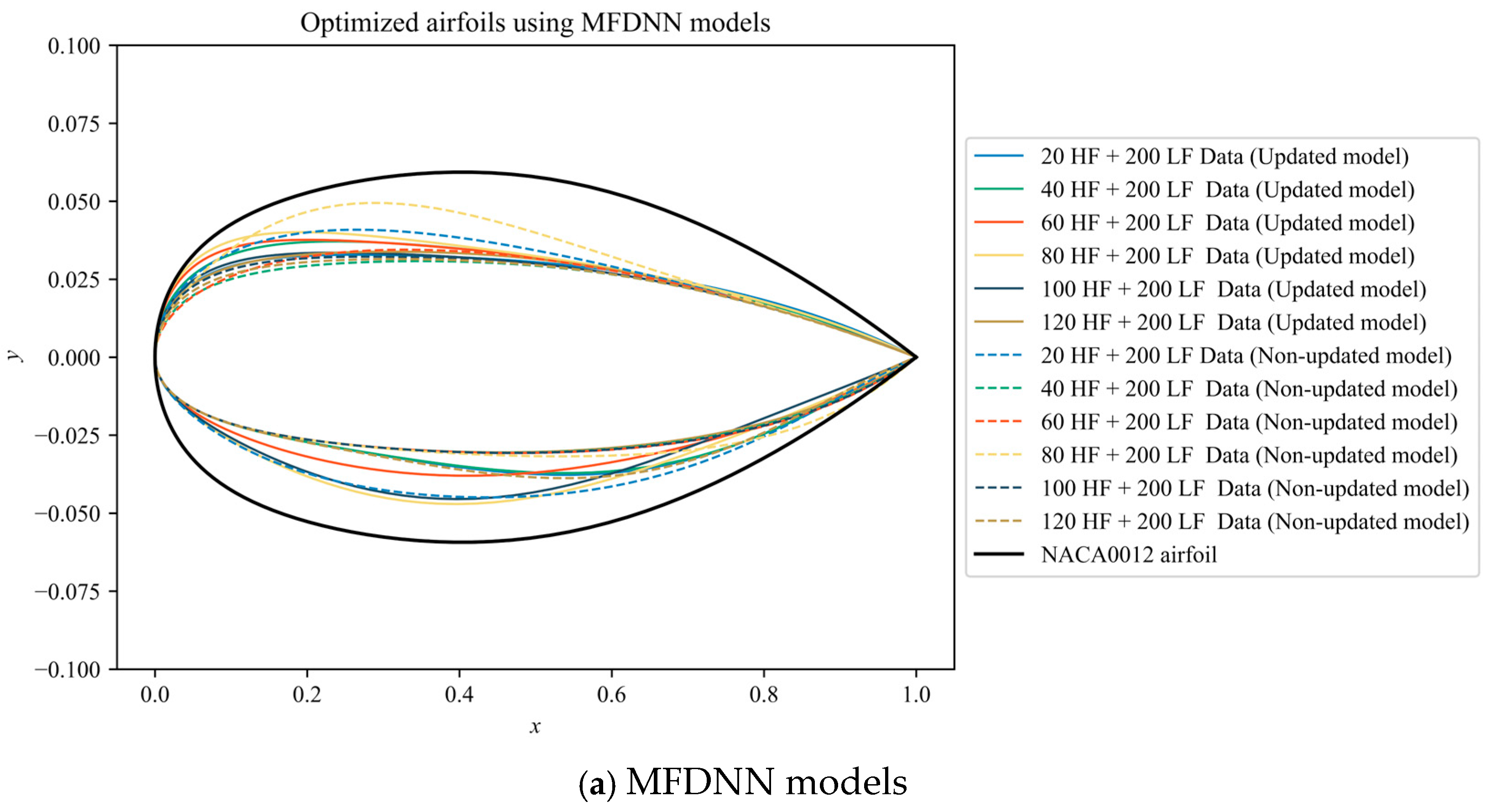
4.3. Optimization Results Using the Updated MFDNN Models
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MFDNN | Multi-fidelity Deep Neural Network |
| SFNN | Single-fidelity Neural Network |
| HF | High-fidelity |
| LF | Low-fidelity |
| ASO | Aerodynamic Shape Optimization |
| CFD | Computational Fluid Dynamics |
| SBO | Surrogate-based Optimization |
| PRM | Polynomial Regression Models |
| RBF | Radial Basis Function |
| MLP | Multi-layered Perceptron |
| CNN | Convolutional Neural Network |
| SVM | Support Vector Machines |
| GEANN | Gradient-enhanced Artificial Neural Networks |
| RNN | Recurrent Neural Networks |
| RANS | Reynolds-averaged Navier–Stokes |
| TL | Transfer Learning |
| CST | Class–Shape–Function Transformation |
| LHS | Latin Hypercube Sampling |
| DOE | Design of Experiment |
| IDW | Inverse Distance Weighting |
| DV | Design Variable |
| MSE | Mean Square Error |
| PSO | Particle Swarm Optimization |
| LD | Learning Rate |
| DT | Dual-threshold |
References
- Box, G.E.P.; Wilson, K.B. On the Experimental Attainment of Optimum Conditions. J. R. Stat. Soc. Ser. B Methodol. 1951, 13, 270–310. [Google Scholar] [CrossRef]
- Haftka, R.T.; Scott, E.P.; Cruz, J.R. Optimization and Experiments: A Survey. Appl. Mech. Rev. 1998, 51, 435–448. [Google Scholar] [CrossRef]
- Simpson, T.W.; Poplinski, J.D.; Koch, P.N.; Allen, J.K. Metamodels for computer-based engineering design: Survey and recommendations. J. Eng. Comput. 2001, 17, 129–150. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments; John Wiley & Sons: New York, NY, USA, 2016. [Google Scholar]
- Engelund, W.C.; Stanley, D.O.; Lepsch, R.A.; McMillin, M.M.; Unal, R. Aerodynamic configuration design using response surface methodology analysis. In Proceedings of the Aircraft Design, Systems, and Operations Meeting, Monterey, CA, USA, 1 August 1993; p. 10718. [Google Scholar]
- Vavalle, A.; Qin, N. Iterative Response Surface Based Optimization Scheme for Transonic Airfoil Design. J. Aircr. 2007, 44, 365–376. [Google Scholar] [CrossRef]
- Krige, D.G. A statistical approach to some basic mine valuation problems on the Witwatersrand. J. S. Afr. Inst. Min. Metall. 1951, 52, 119–139. [Google Scholar]
- Matheron, G. Principles of geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Simpson, T.W.; Mauery, T.M.; Korte, J.J.; Mistree, F. Kriging Models for Global Approximation in Simulation-Based Multidisciplinary Design Optimization. AIAA J. 2001, 39, 2233–2241. [Google Scholar] [CrossRef]
- Jeong, S.; Murayama, M.; Yamamoto, K. Efficient Optimization Design Method Using Kriging Model. J. Aircr. 2005, 42, 413–420. [Google Scholar] [CrossRef]
- Liu, W.; Batill, S. Gradient-Enhanced Response Surface Approximations Using Kriging Models. In Proceedings of the 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, GA, USA, 4–6 September 2002. [Google Scholar]
- Laurenceau, J.; Sagaut, P. Building Efficient Response Surfaces of Aerodynamic Functions with Kriging and Cokriging. AIAA J. 2008, 46, 498–507. [Google Scholar] [CrossRef]
- Chung, H.S.; Alonso, J. Using gradients to construct cokriging approximation models for high-dimensional design optimization problems. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002. [Google Scholar]
- Han, Z. Kriging surrogate model and its application to design optimization: A review of recent progress. Hangkong Xuebao/Acta Aeronaut. Astronaut. Sin. 2016, 37, 3197–3225. (In Chinese) [Google Scholar] [CrossRef]
- Buhmann, M.D. Radial basis functions. Acta Numer. 2000, 9, 1–38. [Google Scholar] [CrossRef]
- Wendland, H. Scattered Data Approximation; Cambridge University Press: Cambridge, UK, 2004; Volume 17, p. x+336. [Google Scholar]
- Tyagi, A.; Singh, P.; Rao, A.; Kumar, G.; Singh, R.K. A novel framework for optimizing Gurney flaps using RBF surrogate model and cuckoo search algorithm. Acta Mech. 2024, 235, 3385–3404. [Google Scholar] [CrossRef]
- Zhou, Z.; Ong, Y.S.; Nair, P.B.; Keane, A.J.; Lum, K.Y. Combining Global and Local Surrogate Models to Accelerate Evolutionary Optimization. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2007, 37, 66–76. [Google Scholar] [CrossRef]
- Queipo, N.V.; Haftka, R.T.; Shyy, W.; Goel, T.; Vaidyanathan, R.; Kevin Tucker, P. Surrogate-based analysis and optimization. Prog. Aerosp. Sci. 2005, 41, 1–28. [Google Scholar] [CrossRef]
- Yakowitz, S.J.; Szidarovszky, F. A comparison of kriging with nonparametric regression methods. J. Multivar. Anal. 1985, 16, 21–53. [Google Scholar] [CrossRef]
- Santos, M.; Mattos, B.; Girardi, R. Aerodynamic Coefficient Prediction of Airfoils Using Neural Networks. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, USA, 7–10 January 2008. [Google Scholar]
- Zhang, Y.; Sung, W.J.; Mavris, D.N. Application of Convolutional Neural Network to Predict Airfoil Lift Coefficient. In Proceedings of the 2018 AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Andrés-Pérez, E.; Carro-Calvo, L.; Salcedo-Sanz, S.; Martin-Burgos, M.J. Aerodynamic Shape Design by Evolutionary Optimization and Support Vector Machines; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Bouhlel, M.A.; He, S.; Martins, J.R.R.A. Scalable gradient–enhanced artificial neural networks for airfoil shape design in the subsonic and transonic regimes. Struct. Multidiscip. Optim. 2020, 61, 1363–1376. [Google Scholar] [CrossRef]
- Du, X.; He, P.; Martins, J.R.R.A. Rapid airfoil design optimization via neural networks-based parameterization and surrogate modeling. Aerosp. Sci. Technol. 2021, 113, 106701. [Google Scholar] [CrossRef]
- Li, J.; Du, X.; Martins, J.R.R.A. Machine learning in aerodynamic shape optimization. Prog. Aerosp. Sci. 2022, 134, 100849. [Google Scholar] [CrossRef]
- Forrester, A.I.J.; Sóbester, A.; Keane, A.J. Multi-fidelity optimization via surrogate modelling. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 3251–3269. [Google Scholar] [CrossRef]
- Kennedy, M.; O’Hagan, A. Predicting the output from a complex computer code when fast approximations are available. Biometrika 2000, 87, 1–13. [Google Scholar] [CrossRef]
- Han, Z.-H.; Görtz, S. Hierarchical Kriging Model for Variable-Fidelity Surrogate Modeling. AIAA J. 2012, 50, 1885–1896. [Google Scholar] [CrossRef]
- Han, Z.; Xu, C.; Zhang, L.; Zhang, Y.; Zhang, K.; Song, W. Efficient aerodynamic shape optimization using variable-fidelity surrogate models and multilevel computational grids. Chin. J. Aeronaut. 2020, 33, 31–47. [Google Scholar] [CrossRef]
- Shi, M.; Lv, L.; Sun, W.; Song, X. A multi-fidelity surrogate model based on support vector regression. Struct. Multidiscip. Optim. 2020, 61, 2363–2375. [Google Scholar] [CrossRef]
- Tao, J.; Sun, G. Application of deep learning based multi-fidelity surrogate model to robust aerodynamic design optimization. Aerosp. Sci. Technol. 2019, 92, 722–737. [Google Scholar] [CrossRef]
- Meng, X.; Karniadakis, G.E. A composite neural network that learns from multi-fidelity data: Application to function approximation and inverse PDE problems. J. Comput. Phys. 2020, 401, 109020. [Google Scholar] [CrossRef]
- Zhang, X.; Xie, F.; Ji, T.; Zhu, Z.; Zheng, Y. Multi-fidelity deep neural network surrogate model for aerodynamic shape optimization. Comput. Methods Appl. Mech. Eng. 2021, 373, 113485. [Google Scholar] [CrossRef]
- Yang, A.; Li, J.; Liem, R.P. Multi-fidelity Data-driven Aerodynamic Shape Optimization of Wings with Composite Neural Networks. In Proceedings of the AIAA AVIATION 2023 Forum, San Diego, CA, USA, 12–16 June 2023. [Google Scholar]
- Li, Z.; Montomoli, F.; Casari, N.; Pinelli, M. High-Dimensional Uncertainty Quantification of High-Pressure Turbine Vane Based on Multi-Fidelity Deep Neural Networks. In Proceedings of the ASME Turbo Expo 2023: Turbomachinery Technical Conference and Exposition, Boston, MA, USA, 26–30 June 2023. [Google Scholar]
- Wu, X.; Zuo, Z.; Ma, L.; Zhang, W. Multi-fidelity neural network-based aerodynamic optimization framework for propeller design in electric aircraft. Aerosp. Sci. Technol. 2024, 146, 108963. [Google Scholar] [CrossRef]
- Nagawkar, J.R.; Leifsson, L.T.; He, P. Aerodynamic Shape Optimization Using Gradient-Enhanced Multifidelity Neural Networks. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Tao, G.; Fan, C.; Wang, W.; Guo, W.; Cui, J. Multi-fidelity deep learning for aerodynamic shape optimization using convolutional neural network. Phys. Fluids 2024, 36, 056116. [Google Scholar] [CrossRef]
- Geng, X.; Liu, P.; Hu, T.; Qu, Q.; Dai, J.; Lyu, C.; Ge, Y.; Akkermans, R.A.D. Multi-fidelity optimization of a quiet propeller based on deep deterministic policy gradient and transfer learning. Aerosp. Sci. Technol. 2023, 137, 108288. [Google Scholar] [CrossRef]
- Liao, P.; Song, W.; Du, P.; Zhao, H. Multi-fidelity convolutional neural network surrogate model for aerodynamic optimization based on transfer learning. Phys. Fluids 2021, 33, 127121. [Google Scholar] [CrossRef]
- Kulfan, B.; Bussoletti, J. “Fundamental” Parameteric Geometry Representations for Aircraft Component Shapes. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Portsmouth, VI, USA, 6–8 September 2006. [Google Scholar]
- Kulfan, B. A Universal Parametric Geometry Representation Method—“CST”. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. [Google Scholar]
- van Ingen, J. The eN Method for Transition Prediction. Historical Review of Work at TU Delft. In Proceedings of the 38th Fluid Dynamics Conference and Exhibit, Seattle, WA, USA, 23 June–26 June 2008; Fluid Dynamics and Co-Located Conferences. American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2008. [Google Scholar]
- Zhou, D.; Lu, Z.; Guo, T.; Chen, G. Aeroelastic prediction and analysis for a transonic fan rotor with the “hot” blade shape. Chin. J. Aeronaut. 2021, 34, 50–61. [Google Scholar] [CrossRef]
- Bartier, P.M.; Keller, C.P. Multivariate interpolation to incorporate thematic surface data using inverse distance weighting (IDW). Comput. Geosci. 1996, 22, 795–799. [Google Scholar] [CrossRef]
- Zhao, Y.; Forhad, A. A general method for simulation of fluid flows with moving and compliant boundaries on unstructured grids. Comput. Methods Appl. Mech. Eng. 2003, 192, 4439–4466. [Google Scholar] [CrossRef]
- McGhee, R.J.; Bingham, G.J. Low-Speed Aerodynamic Characteristics of a 17-Percent-Thick Medium Speed Airfoil Designed for General Aviation Applications; NASA-TP-1786; NASA Langley Research Center: Hampton, VA, USA, 1973. [Google Scholar]
- Sobol, I.M. On the distribution of points in a cube and the approximate evaluation of integrals. USSR Comput. Math. Math. Phys. 1967, 7, 86–112. [Google Scholar] [CrossRef]
- Jin, R.; Chen, W.; Sudjianto, A. An efficient algorithm for constructing optimal design of computer experiments. J. Stat. Plan. Inference 2005, 134, 268–287. [Google Scholar] [CrossRef]
- Saves, P.; Lafage, R.; Bartoli, N.; Diouane, Y.; Bussemaker, J.; Lefebvre, T.; Hwang, J.T.; Morlier, J.; Martins, J.R.R.A. SMT 2.0: A Surrogate Modeling Toolbox with a focus on hierarchical and mixed variables Gaussian processes. Adv. Eng. Softw. 2024, 188, 103571. [Google Scholar] [CrossRef]
- Shalabi, L.A.; Shaaban, Z.; Kasasbeh, B. Data Mining: A Preprocessing Engine. J. Comput. Sci. 2006, 2, 735–739. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 1944, pp. 1942–1948. [Google Scholar]


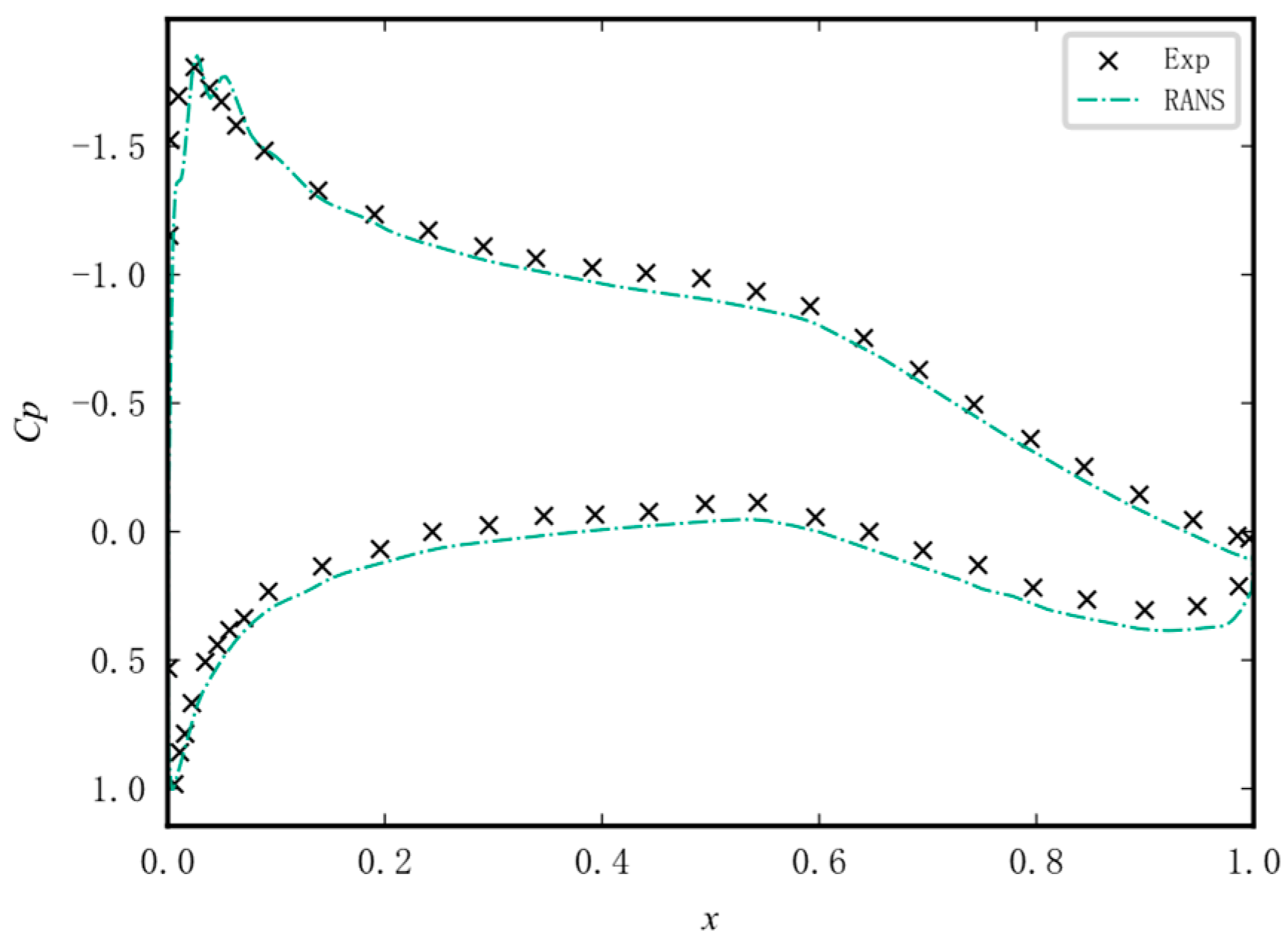
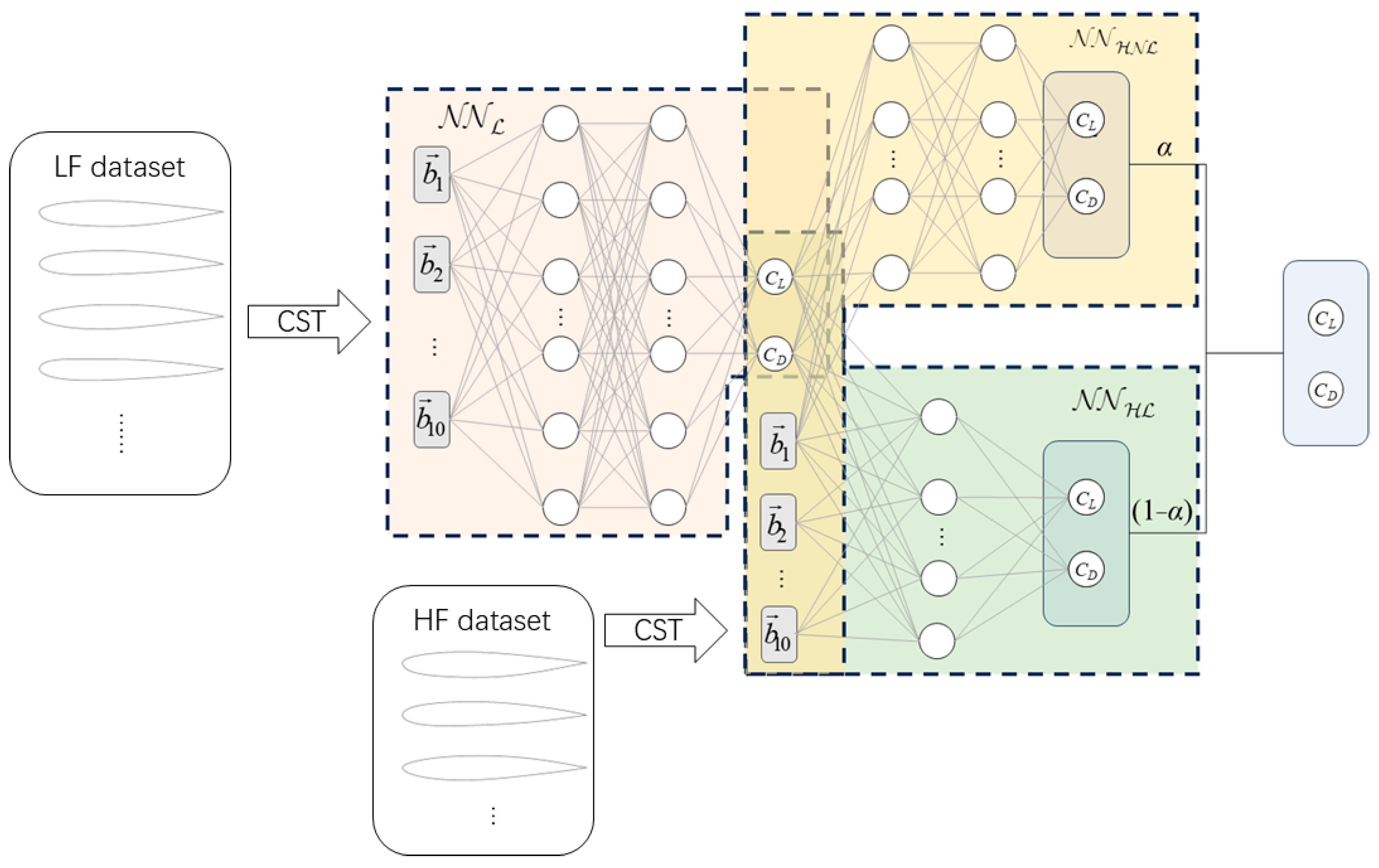



| Upper Surface | Lower Surface | |||||
|---|---|---|---|---|---|---|
| Baseline | Upper Bound | Lower Bound | Baseline | Upper Bound | Lower Bound | |
| b0 | 0.160612 | 0.240918 | 0.080306 | −0.160612 | −0.080306 | −0.240918 |
| b1 | 0.1200491 | 0.1800737 | 0.0600246 | −0.120049 | −0.060025 | −0.180074 |
| b2 | 0.1792529 | 0.2688794 | 0.0896265 | −0.179253 | −0.089627 | −0.268879 |
| b3 | 0.1776805 | 0.2665208 | 0.0888403 | −0.177681 | −0.088840 | −0.266521 |
| b4 | 0.1881634 | 0.2822451 | 0.0940817 | −0.188163 | −0.094082 | −0.282245 |
| (a) | ||||||
|---|---|---|---|---|---|---|
| Data (LF/HF) | λHF | |||||
| 0.01 | 0.001 | 0.0001 | 0.00001 | 0.000001 | 0.0000001 | |
| 200/20 | 3.35 × 10−5 | 2.47 × 10−5 | 1.24 × 10−5 | 1.60 × 10−5 | 1.47 × 10−5 | 1.27 × 10−5 |
| 200/40 | 1.18 × 10−5 | 1.13 × 10−5 | 3.87 × 10−6 | 7.09 × 10−6 | 9.30 × 10−6 | 8.00 × 10−6 |
| 200/60 | 1.03 × 10−5 | 1.03 × 10−5 | 1.06 × 10−5 | 3.94 × 10−6 | 2.72 × 10−6 | 6.14 × 10−6 |
| 200/80 | 1.05 × 10−5 | 9.99 × 10−6 | 8.87 × 10−6 | 2.17 × 10−6 | 1.99 × 10−6 | 8.96 × 10−6 |
| 200/100 | 1.05 × 10−5 | 9.56 × 10−6 | 9.39 × 10−6 | 1.45 × 10−6 | 1.54 × 10−6 | 4.36 × 10−6 |
| 200/120 | 1.08 × 10−5 | 9.83 × 10−6 | 1.00 × 10−5 | 1.32 × 10−6 | 2.11 × 10−6 | 2.37 × 10-−6 |
| (b) | ||||||
| Data (HF) | λHF | |||||
| 0.01 | 0.001 | 0.0001 | 0.00001 | 0.000001 | 0.0000001 | |
| 20 | 7.64 × 10−5 | 6.99 × 10−5 | 6.92 × 10−5 | 3.27 × 10−4 | 3.39 × 10−4 | 3.35 × 10−4 |
| 40 | 6.71 × 10−5 | 6.96 × 10−5 | 5.93 × 10−5 | 1.90 × 10−4 | 1.67 × 10−4 | 1.43 × 10−4 |
| 60 | 1.87 × 10−5 | 1.36 × 10−5 | 1.17 × 10−5 | 4.04 × 10−5 | 6.55 × 10−5 | 6.24 × 10−5 |
| 80 | 1.05 × 10−5 | 7.96 × 10−6 | 1.22 × 10−5 | 3.42 × 10−5 | 4.19 × 10−5 | 4.89 × 10−5 |
| 100 | 1.35 × 10−5 | 5.99 × 10−6 | 6.32 × 10−6 | 2.80 × 10−5 | 2.60 × 10−5 | 2.33 × 10−5 |
| 120 | 1.23 × 10−5 | 6.53 × 10−6 | 5.14 × 10−6 | 2.74 × 10−5 | 3.20 × 10−5 | 1.62 × 10−5 |
| MFDNN | SFNN | ||||
|---|---|---|---|---|---|
| Data (LF/HF) | Tanh | ReLU | Data (HF) | Tanh | ReLU |
| 200/20 | 3.31 × 10−5 | 1.24 × 10−5 | 20 | 1.11 × 10−4 | 6.92 × 10−5 |
| 200/40 | 1.22 × 10−5 | 3.87 × 10−6 | 40 | 6.46 × 10−5 | 5.93 × 10−5 |
| 200/60 | 7.40 × 10−6 | 2.72 × 10−6 | 60 | 2.55 × 10−5 | 1.17 × 10−5 |
| 200/80 | 9.55 × 10−6 | 1.99 × 10−6 | 80 | 1.88 × 10−5 | 7.96 × 10−6 |
| 200/100 | 4.82 × 10−5 | 1.45 × 10−6 | 100 | 7.59 × 10−6 | 5.99 × 10−6 |
| 200/120 | 1.41 × 10−6 | 1.32 × 10−6 | 120 | 6.55 × 10−6 | 5.14 × 10−6 |
| (a) | ||||||||
|---|---|---|---|---|---|---|---|---|
| HF Data | LR | λLF | λHF | |||||
| Layers | Neurons | Neurons | Layers | Neurons | ||||
| 20/40 | 0.01 | 0.001 | 1 × 10−4 | 2 | 60 | 50 | 5 | 40 |
| 60/80 | 0.01 | 0.001 | 1 × 10−6 | 2 | 60 | 50 | 5 | 40 |
| 100/120 | 0.01 | 0.001 | 1 × 10−5 | 2 | 60 | 50 | 5 | 40 |
| (b) | ||||||||
| HF Data | LR | λHF | Layers | Neurons | ||||
| 20/40/60/120 | 0.01 | 1 × 10−4 | 5 | 40 | ||||
| 80/100 | 0.01 | 1 × 10−3 | 5 | 40 | ||||
| Data (LF/HF) | MFDNN Time (Minutes) | Data (HF) | SFNN Time (Minutes) |
|---|---|---|---|
| 200/20 | 80.80 | 20 | 64.50 |
| 200/40 | 147.60 | 40 | 131.30 |
| 200/60 | 214.32 | 60 | 198.02 |
| 200/80 | 281.05 | 80 | 264.75 |
| 200/100 | 347.85 | 100 | 331.55 |
| 200/120 | 414.58 | 120 | 398.28 |
| Parameters | Values |
|---|---|
| Number of particles | 30 |
| Inertia | 0.5 |
| Global increment | 2 |
| Particle increment | 2 |
| Velocity limitation | 10% |
| Max iterations | 200 |
| MFDNN | SFNN | |||||
|---|---|---|---|---|---|---|
| CL (Counts) | CD (Counts) | Fobj | CL (Counts) | CD (Counts) | Fobj | |
| 200–20 | 52.0 | 134.65 | 134.65 | 52.0 | 139.56 | 139.56 |
| 200–40 | 52.0 | 130.25 | 130.25 | 52.0 | 138.18 | 138.18 |
| 200–60 | 52.0 | 131.81 | 131.81 | 52.0 | 138.36 | 138.36 |
| 200–80 | 52.0 | 131.23 | 131.23 | 52.0 | 137.43 | 137.43 |
| 200–100 | 52.0 | 131.18 | 131.18 | 52.0 | 136.87 | 136.87 |
| 200–120 | 52.0 | 132.71 | 132.71 | 52.0 | 136.23 | 136.23 |
| (a) | ||||||||
|---|---|---|---|---|---|---|---|---|
| CL (Counts) | CD (Counts) | Fobj | ||||||
| LF-HF Data | MFDNN | CFD | Error | MFDNN | CFD | Error | MFDNN | CFD |
| 200–20 | 52.00 | 50.26 | 1.74 | 134.65 | 133.55 | 1.09 | 134.65 | 3159.76 |
| 200–40 | 52.00 | 50.03 | 1.97 | 130.25 | 133.24 | 2.99 | 130.25 | 4010.26 |
| 200–60 | 52.00 | 50.17 | 1.83 | 131.81 | 133.89 | 2.08 | 131.81 | 3475.96 |
| 200–80 | 52.00 | 50.36 | 1.64 | 131.23 | 132.79 | 1.56 | 131.23 | 2811.38 |
| 200–100 | 52.00 | 50.35 | 1.65 | 131.18 | 131.76 | 0.58 | 131.18 | 2868.12 |
| 200–120 | 52.00 | 50.91 | 1.09 | 132.71 | 133.54 | 0.83 | 132.71 | 1331.05 |
| (b) | ||||||||
| CL (Counts) | CD (Counts) | Fobj | ||||||
| HF Data | SFNN | CFD | Error | SFNN | CFD | Error | SFNN | CFD |
| 20 | 52.00 | 51.16 | 0.84 | 139.56 | 137.34 | 2.21 | 139.56 | 846.17 |
| 40 | 52.00 | 51.29 | 0.71 | 138.18 | 135.00 | 3.19 | 138.18 | 642.12 |
| 60 | 52.00 | 51.66 | 0.34 | 138.36 | 135.70 | 2.66 | 138.36 | 249.02 |
| 80 | 52.00 | 51.64 | 0.36 | 137.43 | 136.05 | 1.38 | 137.43 | 267.28 |
| 100 | 52.00 | 52.77 | 0.77 | 136.87 | 133.30 | 3.57 | 136.87 | 720.42 |
| 120 | 52.00 | 51.93 | 0.07 | 136.23 | 133.92 | 2.31 | 136.23 | 138.99 |
| (a) | ||||||||
|---|---|---|---|---|---|---|---|---|
| CL (Counts) | CD (Counts) | Fobj | ||||||
| LF-HF Data | MFDNN | CFD | Error | MFDNN | CFD | Error | MFDNN | CFD |
| 200–20 | 52.00 | 51.95 | 0.05 | 133.60 | 133.59 | 0.01 | 133.61 | 135.91 |
| 200–40 | 51.99 | 51.99 | 0.00 | 132.58 | 132.66 | 0.07 | 132.78 | 132.83 |
| 200–60 | 52.00 | 51.89 | 0.11 | 133.01 | 132.94 | 0.07 | 133.01 | 144.77 |
| 200–80 | 52.01 | 52.05 | 0.04 | 134.60 | 134.67 | 0.07 | 134.66 | 137.25 |
| 200–100 | 51.98 | 51.92 | 0.06 | 133.91 | 134.05 | 0.14 | 134.21 | 139.92 |
| 200–120 | 52.00 | 51.95 | 0.05 | 131.80 | 132.56 | 0.77 | 131.80 | 135.22 |
| (b) | ||||||||
| CL (Counts) | CD (Counts) | Fobj | ||||||
| HF Data | SFNN | CFD | Error | SFNN | CFD | Error | SFNN | CFD |
| 20 | 52.00 | 52.27 | 0.27 | 137.97 | 136.40 | 1.57 | 137.97 | 210.99 |
| 40 | 52.00 | 52.08 | 0.08 | 137.34 | 135.96 | 1.38 | 137.34 | 141.62 |
| 60 | 52.00 | 51.98 | 0.02 | 139.22 | 137.40 | 1.82 | 139.22 | 137.97 |
| 80 | 52.00 | 51.90 | 0.10 | 137.46 | 136.86 | 0.60 | 137.46 | 147.45 |
| 100 | 52.00 | 52.17 | 0.17 | 137.82 | 137.60 | 0.22 | 137.84 | 167.35 |
| 120 | 51.98 | 52.01 | 0.03 | 136.39 | 136.39 | 0.00 | 136.92 | 136.42 |
| CL (Counts) | CD (Counts) | Fobj | ||||||
|---|---|---|---|---|---|---|---|---|
| HF Data | DTMFDNN | CFD | Error | DTMFDNN | CFD | Error | DTMFDNN | CFD |
| 20 | 51.99 | 51.97 | 0.03 | 132.74 | 133.65 | 0.92 | 132.80 | 134.77 |
| 40 | 52.01 | 51.97 | 0.04 | 133.67 | 133.58 | 0.09 | 133.74 | 134.76 |
| 60 | 52.00 | 51.96 | 0.04 | 132.83 | 132.97 | 0.14 | 132.85 | 134.50 |
| 80 | 52.00 | 52.04 | 0.04 | 131.72 | 133.80 | 2.08 | 131.72 | 135.64 |
| 100 | 52.00 | 51.96 | 0.04 | 131.97 | 133.65 | 1.68 | 131.97 | 135.64 |
| 120 | 51.99 | 51.92 | 0.07 | 135.41 | 135.86 | 0.45 | 135.46 | 142.17 |
| Single-Threshold Update Strategy | Dual-Threshold Update Strategy | |||
|---|---|---|---|---|
| LF-HF Data | CFD | XFOIL | CFD | XFOIL |
| 200–20 | 23 | 23 | 13 | 88 |
| 200–40 | 29 | 29 | 16 | 67 |
| 200–60 | 25 | 25 | 15 | 85 |
| 200–80 | 23 | 23 | 12 | 79 |
| 200–100 | 13 | 13 | 9 | 87 |
| 200–120 | 22 | 22 | 8 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, B.; Shen, E.; Wu, J.; Guo, T.; Lu, Z.; Zhou, D. Aerodynamic Prediction and Design Optimization Using Multi-Fidelity Deep Neural Network. Aerospace 2025, 12, 292. https://doi.org/10.3390/aerospace12040292
Du B, Shen E, Wu J, Guo T, Lu Z, Zhou D. Aerodynamic Prediction and Design Optimization Using Multi-Fidelity Deep Neural Network. Aerospace. 2025; 12(4):292. https://doi.org/10.3390/aerospace12040292
Chicago/Turabian StyleDu, Bingchen, Ennan Shen, Jiangpeng Wu, Tongqing Guo, Zhiliang Lu, and Di Zhou. 2025. "Aerodynamic Prediction and Design Optimization Using Multi-Fidelity Deep Neural Network" Aerospace 12, no. 4: 292. https://doi.org/10.3390/aerospace12040292
APA StyleDu, B., Shen, E., Wu, J., Guo, T., Lu, Z., & Zhou, D. (2025). Aerodynamic Prediction and Design Optimization Using Multi-Fidelity Deep Neural Network. Aerospace, 12(4), 292. https://doi.org/10.3390/aerospace12040292






