Online Estimation Method and Verification of Sampling Mass for Lunar Drilling in the Chang’E-6 Mission
Abstract
:1. Introduction
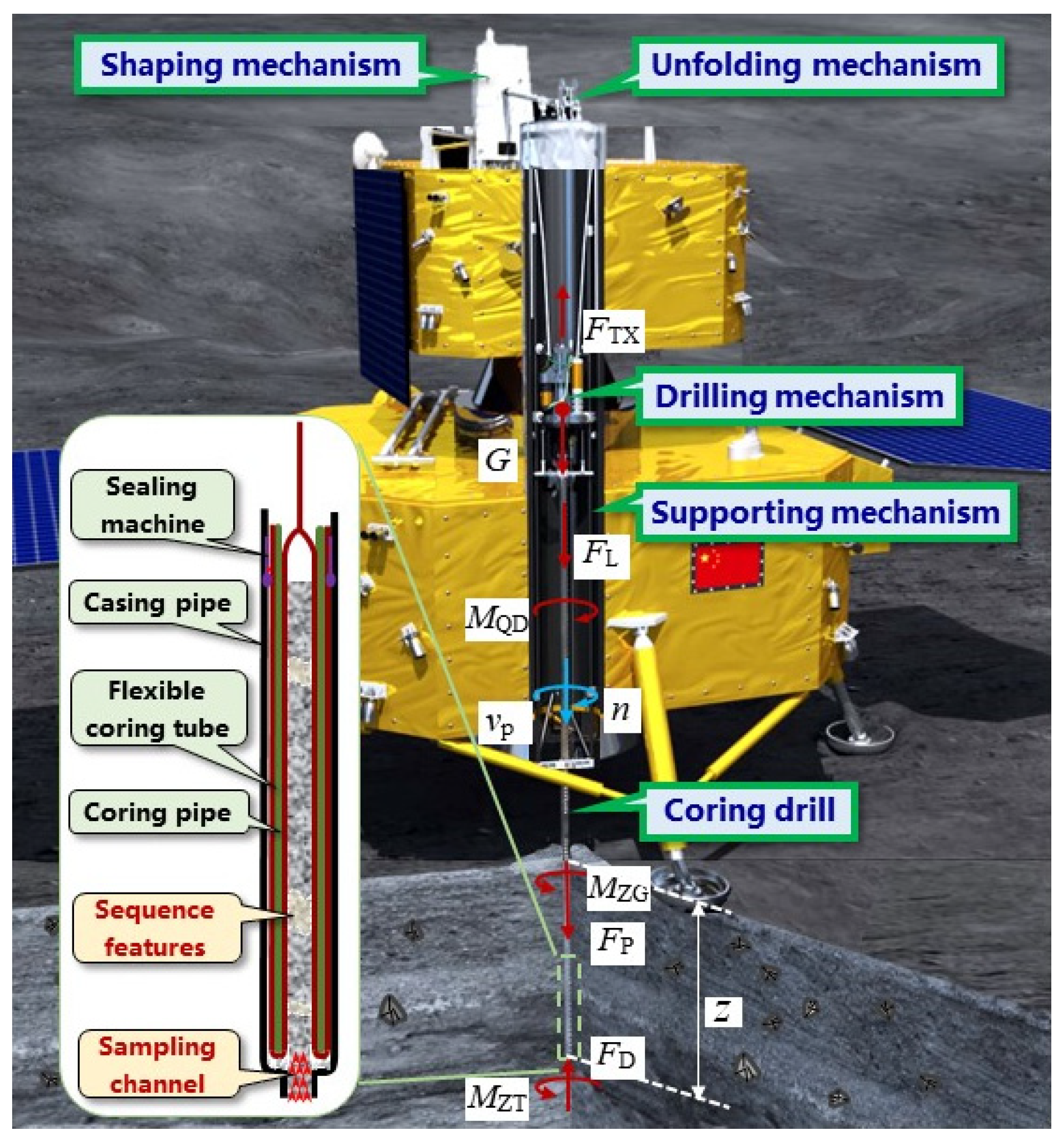
2. Drilling–Sampling Device System Structure and Principle
2.1. Drilling–Sampling Device System Structure
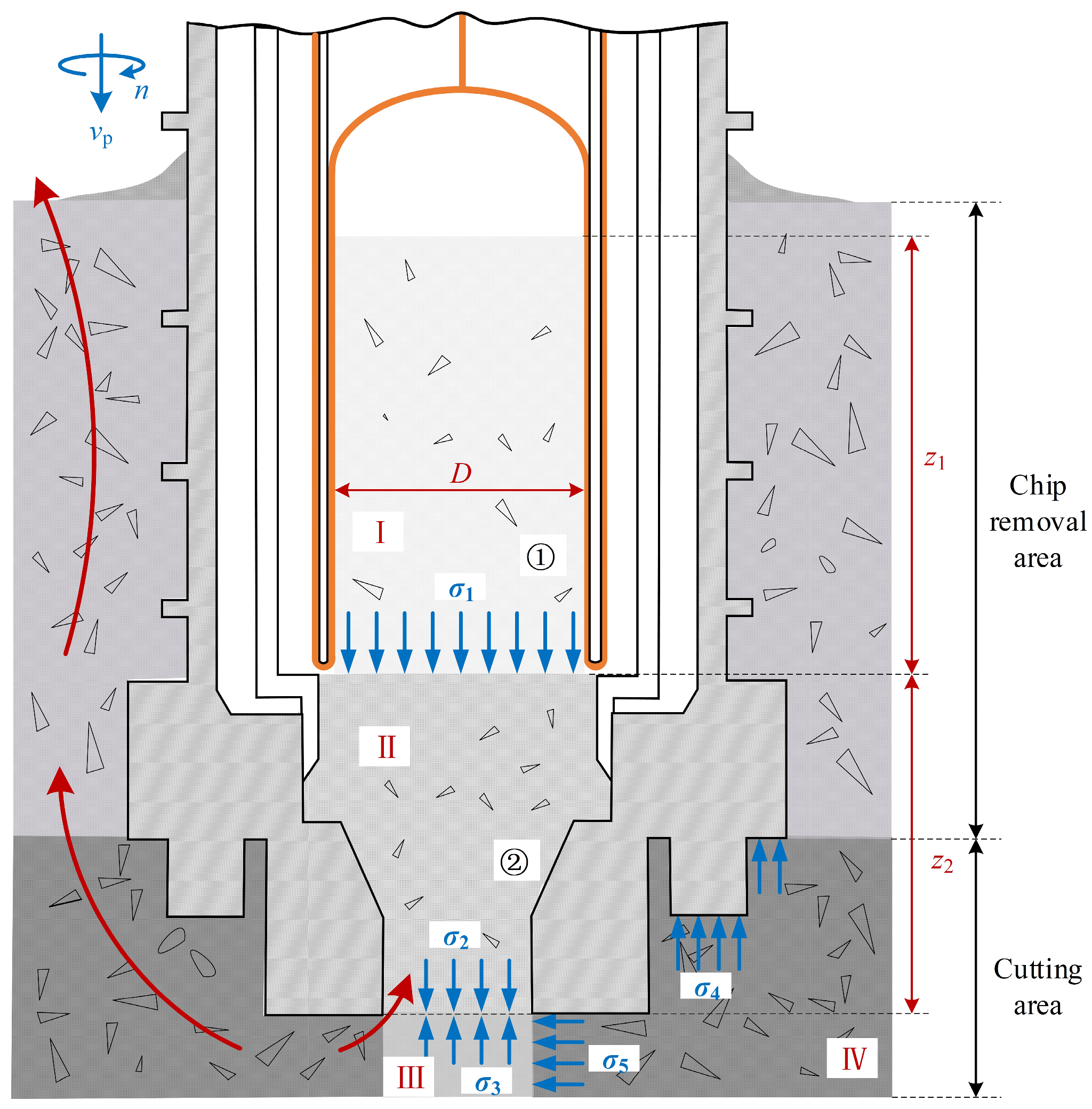
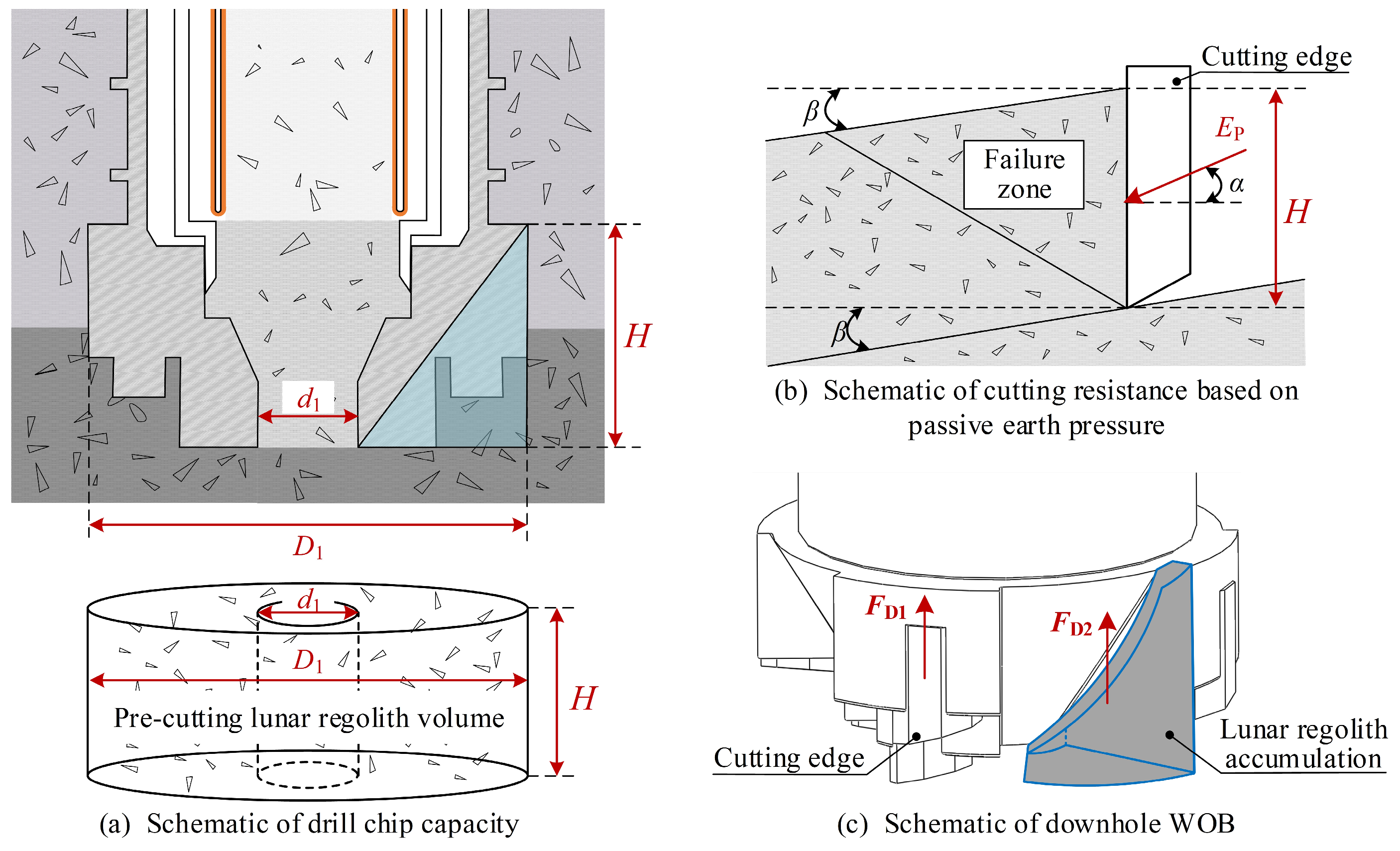
2.2. Analysis of Drilling–Coring Physical Model
3. Estimation Method and Validation of Sample Collection Quantity
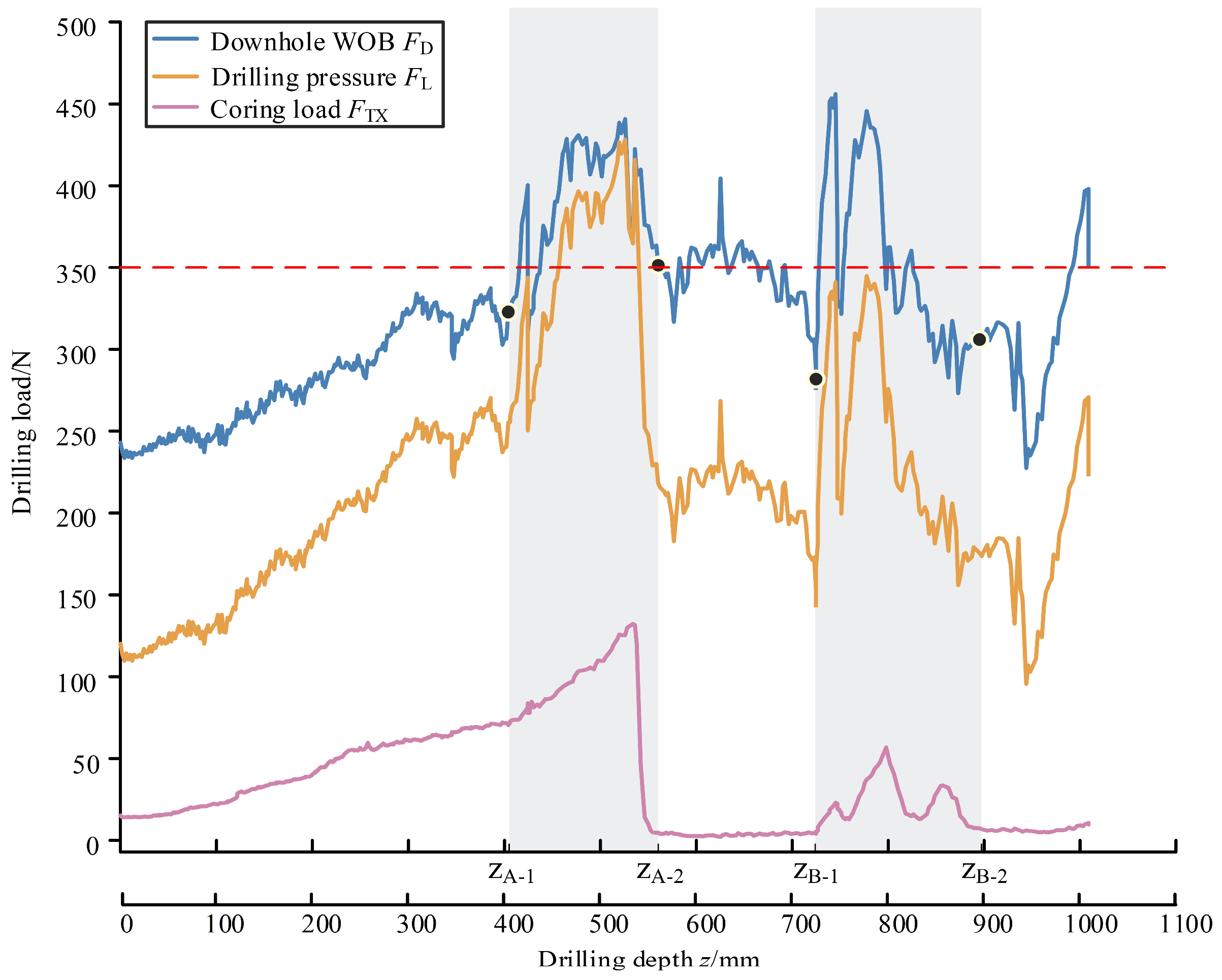
3.1. Analysis of Response Characteristics of Regolith–Machine Interaction
3.1.1. Correlation Analysis of Coring Load and Sampling Status
3.1.2. Correlation Analysis of Drilling Force and Sampling Status
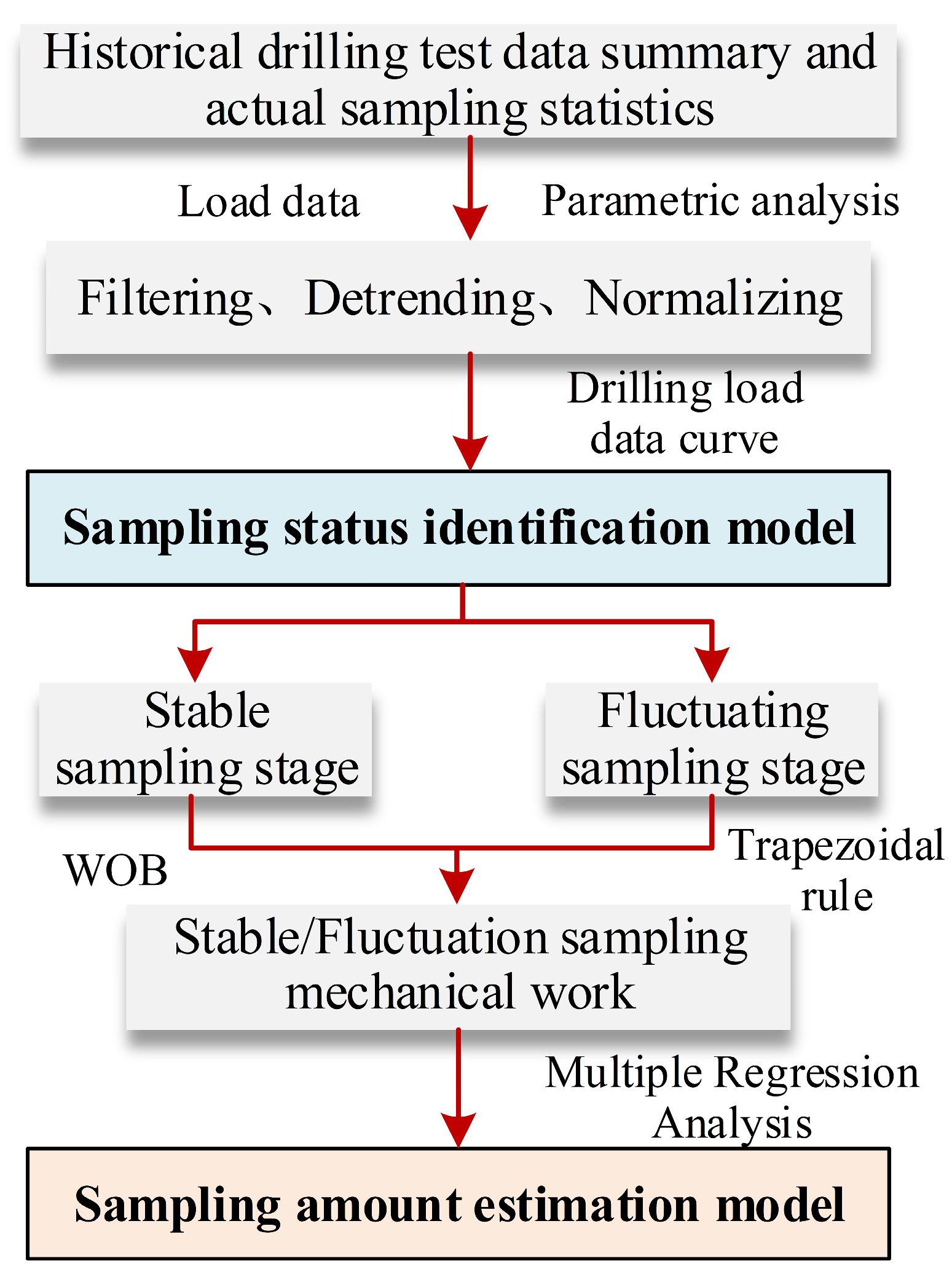
3.2. Construction of Sampling Status Identification Model
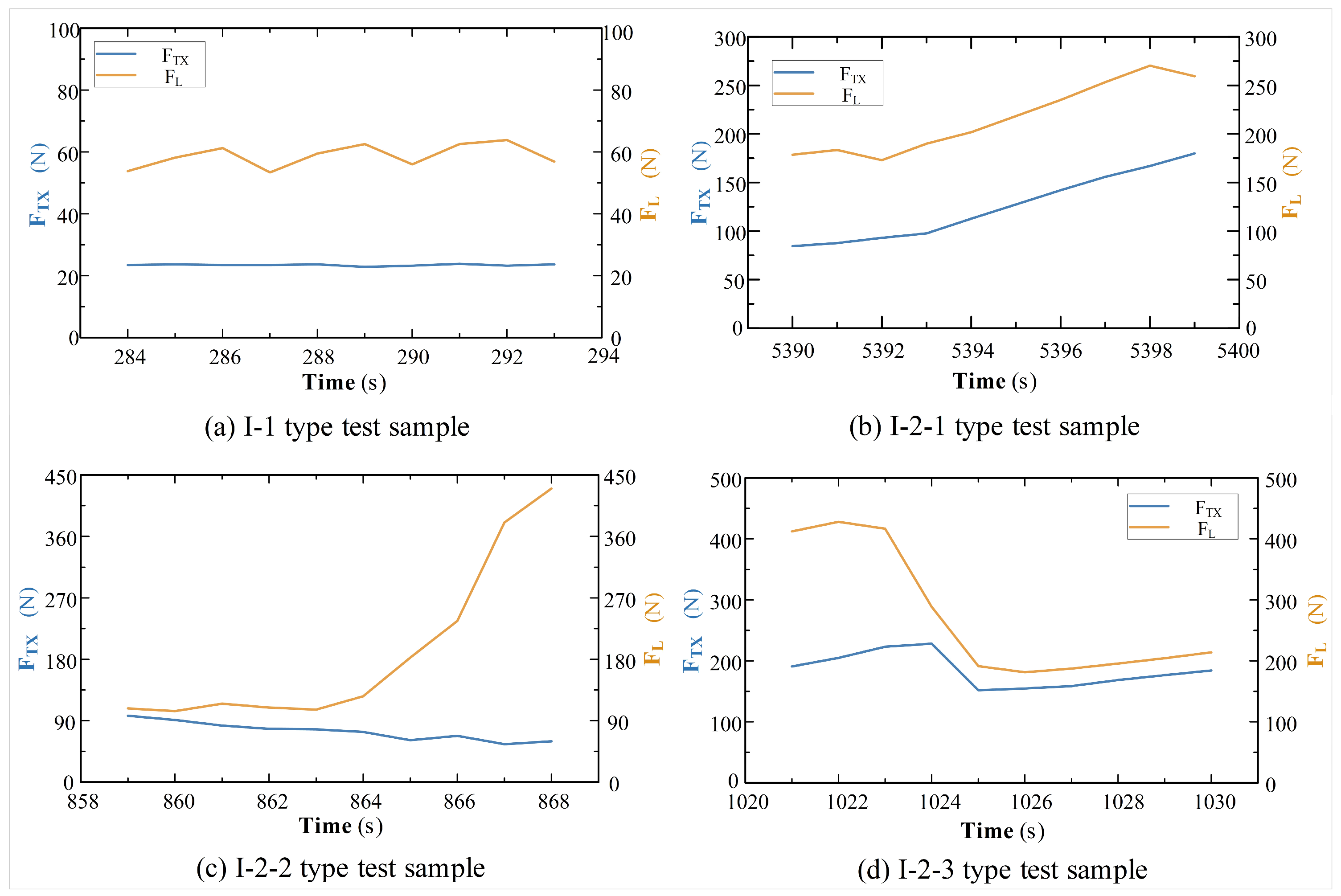
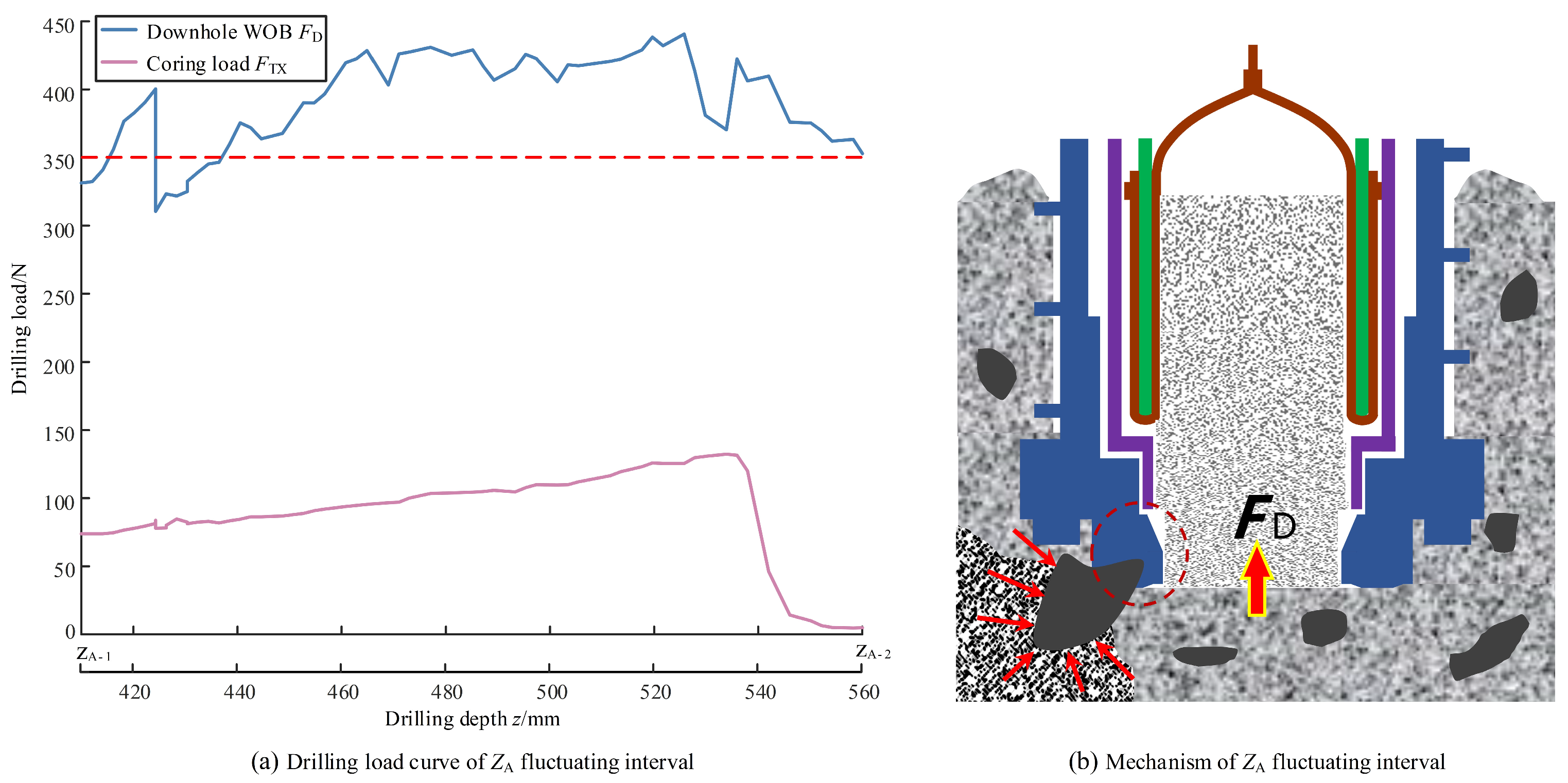
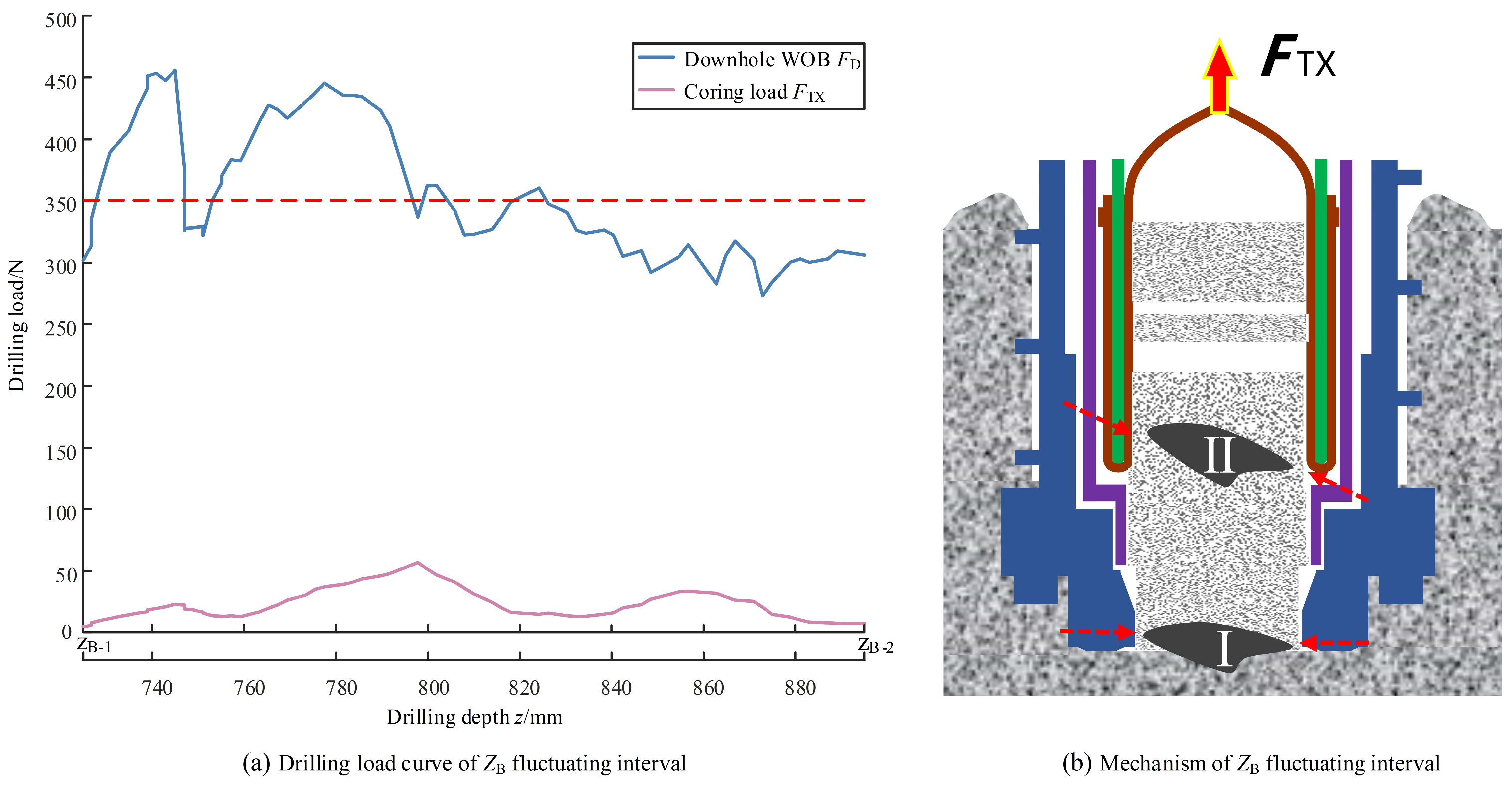
3.2.1. Selection of Sample Division
- I-level model of sampling status learning samples
- Type I-1 test sample: coring load stable stage.
- Type I-2 test sample: coring load fluctuating stage.
- 2.
- II-level model of sampling status learning samples
- Type II-1 test sample: coring load stable, drilling force stable stage.
- Type II-2 test sample: coring load stable, drilling force fluctuating stage.
3.2.2. Identification Model Construction
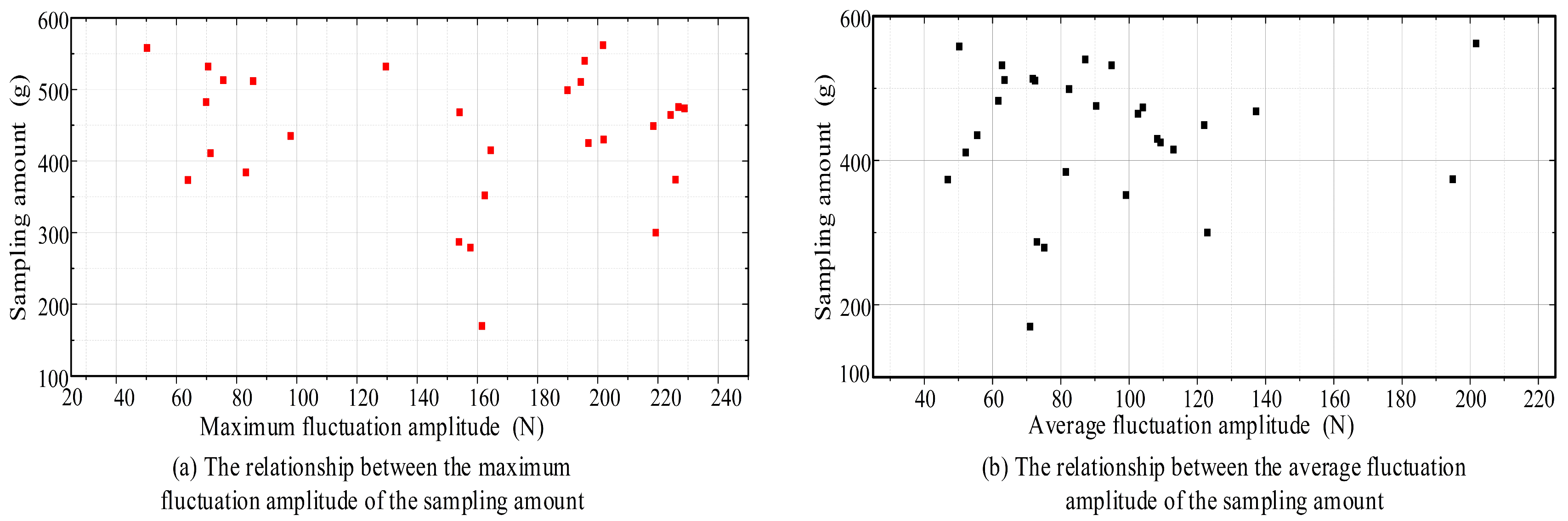
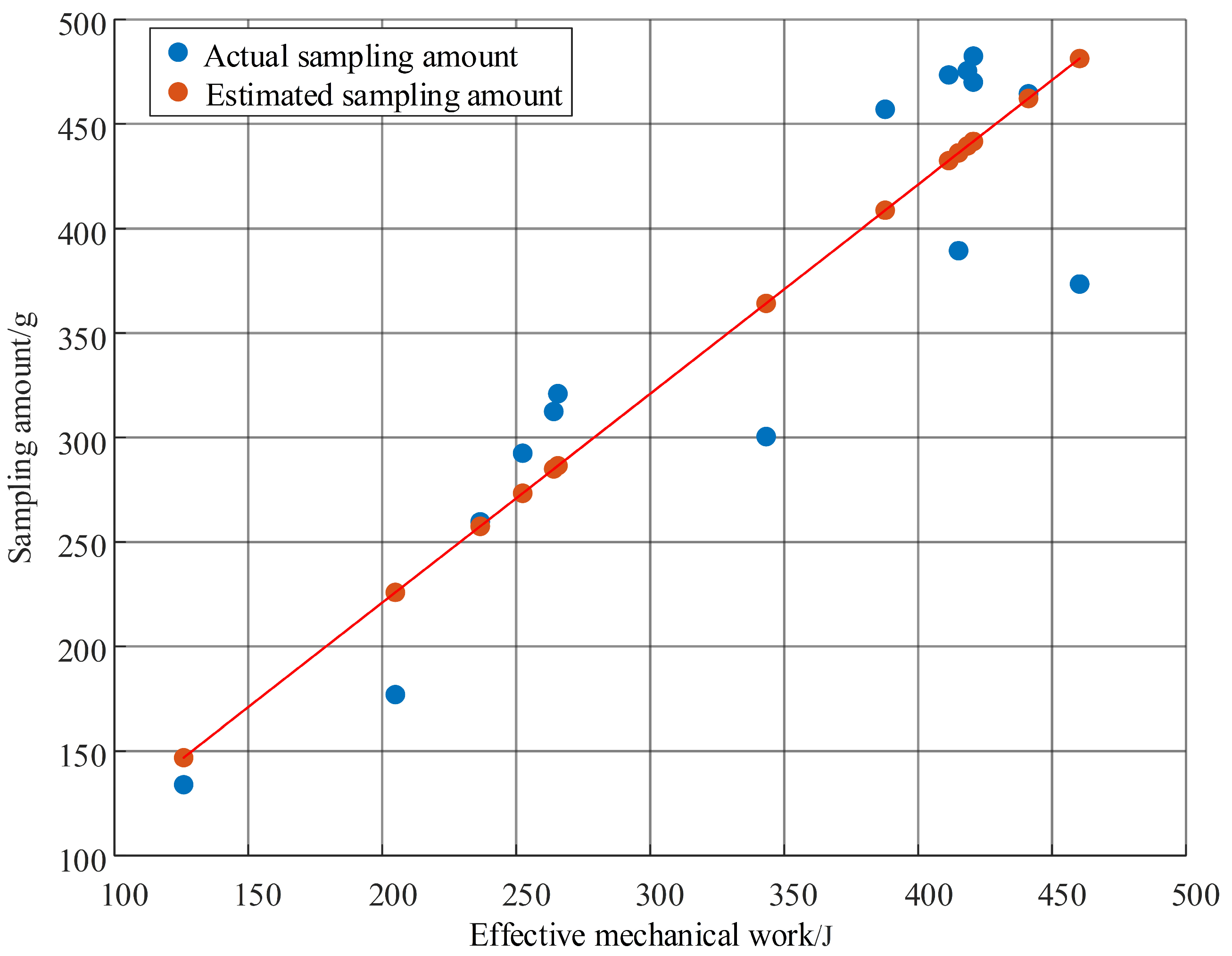
3.3. Analysis and Verification of Drilling–Sampling Mass Estimation Method
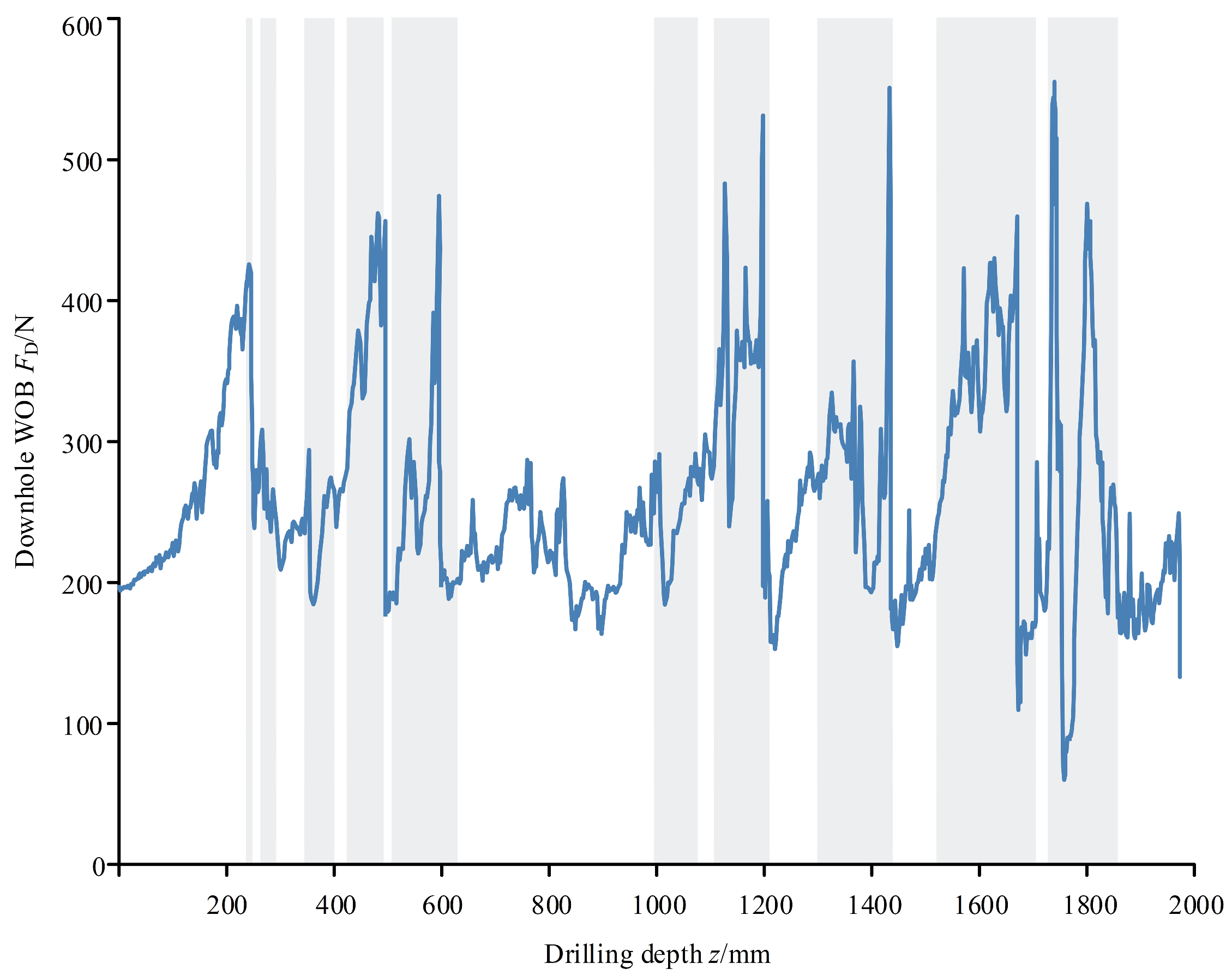
4. Analysis of On-Orbit Drilling Operation Status of Chang’E-6
4.1. On-Orbit Drilling–Sampling Mass Estimation
4.2. Response Analysis of Non-Nominal Conditions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| WOB | weight on bit |
| FL | drilling force |
| G | gravity of coring drill |
| FTX | coring load |
| FD | downhole WOB |
| FP | chip removal resistance |
| ρ | bulk density |
| μ | static friction coefficient |
| KP | steering coefficient, determined by the internal friction angle of soil |
| D | flexible coring tube diameter |
| Q0 | pressure at depth of z = 0 |
| A | horizontal contact area between drilling tool and lunar regolith |
References
- Li, C.; Su, Y.; Pettinelli, E.; Xing, S.; Ding, C.; Liu, J.; Ren, X.; Lauro, S.E.; Soldovieri, F.; Zeng, X. The Moon’s Farside Shallow Subsurface Structure Unveiled by Chang’E-4 Lunar Penetrating Radar. Sci. Adv. 2020, 6, eaay6898. [Google Scholar] [CrossRef] [PubMed]
- Hao, H.; Gao, M.; Wu, Y.; Gao, Z.; Li, Y.; Zhou, X.; Chu, P.; Wang, X.; Li, J.; Zhou, L. Design, Test, and Verification of in-Situ Condition Preserved Coring and Analysis System in Lunar-Based Simulation Environment. Int. J. Min. Sci. Technol. 2024, 34, 1259–1272. [Google Scholar] [CrossRef]
- Xu, J.; Ding, C.; Su, Y.; Ding, Z.; Yang, S.; Li, J.; Dong, Z.; Sharma, R.; Qiu, X.; Lei, Z. Lunar Exploration Based on Ground-Based Radar: Current Research Progress and Future Prospects. Remote Sens. 2024, 16, 3484. [Google Scholar] [CrossRef]
- Gaddis, L.R.; Joy, K.H.; Bussey, B.J.; Carpenter, J.D.; Crawford, I.A.; Elphic, R.C.; Halekas, J.S.; Lawrence, S.J.; Xiao, L. Recent Exploration of the Moon: Science from Lunar Missions since 2006. Rev. Mineral. Geochem. 2023, 89, 1–51. [Google Scholar] [CrossRef]
- Tian, H.-C.; Wang, H.; Chen, Y.; Yang, W.; Zhou, Q.; Zhang, C.; Lin, H.-L.; Huang, C.; Wu, S.-T.; Jia, L.-H. Non-KREEP Origin for Chang’e-5 Basalts in the Procellarum KREEP Terrane. Nature 2021, 600, 59–63. [Google Scholar] [CrossRef] [PubMed]
- Jayathilake, B.A.C.S.; Ilankoon, I.M.S.K.; Dushyantha, M.N.P. Assessment of Significant Geotechnical Parameters for Lunar Regolith Excavations. Acta Astronaut. 2022, 196, 107–122. [Google Scholar] [CrossRef]
- Ishida, T.; Fukuda, S.; Kariya, K.; Kamata, H.; Takadama, K.; Kojima, H.; Sawai, S.; Sakai, S. Vision-Based Navigation and Obstacle Detection Flight Results in SLIM Lunar Landing. Acta Astronaut. 2025, 226, 772–781. [Google Scholar] [CrossRef]
- Mathew, N.; Durga Prasad, K.; Prasad Vajja, D.; Aasik, V.; Mohammad, F.; Pramod, P.P.; Satheesh Chandran, M.; John Antony, K.; Ram Prabhu, M.; Dhanya, M.B. Chandra’s Surface Thermophysical Experiment (ChaSTE) Onboard Chandrayaan 3 Lander. Adv. Space Res. 2025, 75, 5936–5945. [Google Scholar] [CrossRef]
- Li, C.; Zuo, W.; Wen, W.; Zeng, X.; Gao, X.; Liu, Y.; Fu, Q.; Zhang, Z.; Su, Y.; Ren, X. Overview of the Chang’e-4 Mission: Opening the Frontier of Scientific Exploration of the Lunar Far Side. Space Sci. Rev. 2021, 217, 35. [Google Scholar] [CrossRef]
- Li, C.; Hu, H.; Yang, M.-F.; Liu, J.; Zhou, Q.; Ren, X.; Liu, B.; Liu, D.; Zeng, X.; Zuo, W. Nature of the Lunar Far-Side Samples Returned by the Chang’E-6 Mission. Natl. Sci. Rev. 2024, 11, nwae328. [Google Scholar] [CrossRef]
- Badescu, V. (Ed.) Moon: Prospective Energy and Material Resources; Springer: Berlin/Heidelberg, Germany, 2012; pp. 268–278. ISBN 978-3-642-27968-3. [Google Scholar]
- Ding, L.; Zhou, R.; Yuan, Y.; Yang, H.; Li, J.; Yu, T.; Liu, C.; Wang, J.; Li, S.; Gao, H. A 2-Year Locomotive Exploration and Scientific Investigation of the Lunar Farside by the Yutu-2 Rover. Sci. Robot. 2022, 7, eabj6660. [Google Scholar] [CrossRef] [PubMed]
- Yue, Z.; Gou, S.; Sun, S.; Yang, W.; Chen, Y.; Wang, Y.; Lin, H.; Di, K.; Lin, Y.; Li, X. Geological Context of the Chang’e-6 Landing Area and Implications for Sample Analysis. Innovation 2024, 5, 100663. [Google Scholar] [CrossRef] [PubMed]
- Gao, M.; Wang, X.; Zhang, G.; Li, M.; Liu, T.; Hao, H.; Li, C.; Xie, H. The Novel Idea and Technical Progress of Lunar In-Situ Condition Preserved Coring. Geomech. Geophys. Geo-Energ. Geo-Resour. 2022, 8, 46. [Google Scholar] [CrossRef]
- Knez, D.; Khalilidermani, M. A Review of Different Aspects of Off-Earth Drilling. Energies 2021, 14, 7351. [Google Scholar] [CrossRef]
- Zacny, K.; Paulsen, G.; Szczesiak, M.; Craft, J.; Chu, P.; McKay, C.; Glass, B.; Davila, A.; Marinova, M.; Pollard, W. LunarVader: Development and Testing of Lunar Drill in Vacuum Chamber and in Lunar Analog Site of Antarctica. J. Aerosp. Eng. 2013, 26, 74–86. [Google Scholar] [CrossRef]
- Lin, Y.; Yang, W.; Zhang, H.; Hui, H.; Hu, S.; Xiao, L.; Liu, J.; Xiao, Z.; Yue, Z.; Zhang, J. Return to the Moon: New Perspectives on Lunar Exploration. Sci. Bull. 2024, 69, 2136–2148. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Zhang, G.; Gao, M.; Zhang, X.; Xie, H. Advances in Drill-Based Sampling Technology for Extraterrestrial Bodies. Space Sci. Rev. 2024, 220, 66. [Google Scholar] [CrossRef]
- Robinson, M.S.; Plescia, J.B.; Jolliff, B.L.; Lawrence, S.J. Soviet Lunar Sample Return Missions: Landing Site Identification and Geologic Context. Planet. Space Sci. 2012, 69, 76–88. [Google Scholar] [CrossRef]
- Zhang, T.; Pang, Y.; Zeng, T.; Wang, G.; Yin, S.; Xu, K.; Mo, G.; Zhang, X.; Wang, L.; Yang, S. Robotic Drilling for the Chinese Chang’E 5 Lunar Sample-Return Mission. Int. J. Robot. Res. 2023, 42, 586–613. [Google Scholar] [CrossRef]
- Ivanov, M.A.; Head, J.W.; Hiesinger, H. New Insights into the Regional and Local Geological Context of the Luna 16 Landing Site. Icarus 2023, 400, 115579. [Google Scholar] [CrossRef]
- Wu, F.-Y.; Li, Q.-L.; Chen, Y.; Hu, S.; Yue, Z.-Y.; Zhou, Q.; Wang, H.; Yang, W.; Tian, H.-C.; Zhang, C. Lunar Evolution in Light of the Chang’e-5 Returned Samples. Annu. Rev. Earth Planet. Sci. 2024, 52, 159–194. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, Y.; Xu, K.; Ding, X.; Wei, H.; Chao, C.; Wang, B.; Wang, B. Robotic Drilling Tests in Simulated Lunar Regolith Environment. J. Field Robot. 2021, 38, 1011–1035. [Google Scholar] [CrossRef]
- Cannon, H.N.; Stoker, C.R.; Dunagan, S.E.; Davis, K.; Gómez-Elvira, J.; Glass, B.J.; Lemke, L.G.; Miller, D.; Bonaccorsi, R.; Branson, M. MARTE: Technology Development and Lessons Learned from a Mars Drilling Mission Simulation. J. Field Robot. 2007, 24, 877–905. [Google Scholar] [CrossRef]
- Glass, B.; Cannon, H.; Branson, M.; Hanagud, S.; Paulsen, G. DAME: Planetary-Prototype Drilling Automation. Astrobiology 2008, 8, 653–664. [Google Scholar] [CrossRef]
- Tang, J.-Y.; Deng, Z.-Q.; Chen, C.-B.; Wang, Y.-C.; Quan, Q.-Q.; Jiang, S.-Y.; Tang, D.-W. Review of Planetary Drilling & Coring Technologies Oriented Towards Deep Space Exploration. J. Astronaut. 2017, 38, 555. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, T.; Wei, H.; Liu, J.; Wang, W.; Yuan, X.; Pang, Y.; Guan, Y.; Hou, X.; Xu, K. Advances in Extraterrestrial Drilling Technology to Discover the Secrets Hidden Inside Celestial Bodies. Space Sci. Rev. 2022, 218, 47. [Google Scholar] [CrossRef]
- Huang, W.; Rong, W.; Liu, D.; Jiang, C.; Jia, H.; Bao, J.; Fang, J. Design and Realization of Recovery System of Chang’e-5 Reentry Spacecraft. Space Sci. Technol. 2021, 2021, 9898756. [Google Scholar] [CrossRef]
- Zheng, Y.; Yang, M.; Deng, X.; Jin, S.; Peng, J.; Su, Y.; Gu, Z.; Chen, L.; Pang, Y.; Zhang, N. Analysis of Chang’e-5 Lunar Core Drilling Process. Chin. J. Aeronaut. 2023, 36, 292–303. [Google Scholar] [CrossRef]
- Jiang, S.-Y.; Liang, J.-N.; Lai, X.-M.; Deng, X.-J.; Pang, Y.; Zhang, W.-W.; Tang, J.-Y.; Quan, Q.-Q.; Peng, J.; Zhang, G.; et al. Analysis on Drilling and Coring Process and Lunar Regolith Stratification State Interpretation in Chang’E-5. J. Mech. Eng. 2022, 58, 348–360. [Google Scholar] [CrossRef]
- Quan, Q.-Q.; Shi, X.-M.; Tang, D.-W.; Jiang, S.-Y.; Deng, Z.-Q. Analysis and test research on influencing factors of drilling and coring quantity of lunar soil simulant. J. Beijing Univ. Aeronaut. Astronaut. 2015, 41, 2052–2060. [Google Scholar] [CrossRef]
- Quan, Q.-Q.; Chen, C.-B.; Deng, Z.-Q.; Tang, J.-Y.; Tang, D.-W. On Modeling Drilling Load in Lunar Regolith Simulant. Chin. J. Mech. Eng. 2018, 31, 20. [Google Scholar] [CrossRef]
- Quan, Q.; Tang, J.; Yuan, F.; Jiang, S.; Deng, Z. Drilling Load Modeling and Validation Based on the Filling Rate of Auger Flute in Planetary Sampling. Chin. J. Aeronaut. 2017, 30, 434–446. [Google Scholar] [CrossRef]
- Fan, X.; Xu, C.; Liang, L.; Chen, Q.; Deng, J. Analytical Solution for Displacement-Dependent Passive Earth Pressure on Rigid Walls with Various Wall Movements in Cohesionless Soil. Comput. Geotech. 2021, 140, 104470. [Google Scholar] [CrossRef]
- Akbari Garakani, A.; Pirjalili, A.; Desai, C.S. An Effective Stress-Based DSC Model for Predicting the Coefficient of Lateral Soil Pressure in Unsaturated Soils. Acta Geotech. 2021, 16, 3813–3830. [Google Scholar] [CrossRef]




| Test Number | Percentage of the Stable Stage in Ι-Level Model | Percentage of the Stable Stage in II-Level Model | Percentage of Stable Stage for the Threshold Method | Decline Rate |
|---|---|---|---|---|
| 2017031702 | 90.1639% | 67.2131% | 92.58% | 34.54% |
| 2017053104 | 94.2308% | 77.8846% | 92.09% | 20.30% |
| 2017060302 | 100% | 91.4894% | 98.78% | 7.38% |
| 2023030101 | 85.2332% | 78.9474% | 96.76% | 30.45% |
| 20203042701 | 85.5932% | 78.8136% | 98.87% | 31.77% |
| 2023042702 | 94.1176% | 63.7255% | 96.17% | 37.63% |
| 2023042801 | 85.7143% | 65.9341% | 97.98% | 42.32% |
| Test Number | Estimated Sampling Mass (g) | Actual Sampling Mass (g) | Testing Set Error |
|---|---|---|---|
| 2024051001 | 462.2168 | 464.5 | 0.49% |
| 2023042710 | 481.3341 | 373.5 | 28.87% |
| 2023042714 | 439.4387 | 475.5 | 7.58% |
| 2023042809 | 432.4797 | 473.5 | 8.66% |
| 2023042812 | 441.6663 | 482.5 | 8.46% |
| 2023042816 | 285.0223 | 312.5 | 8.79% |
| 2023052301 | 146.8797 | 134 | 9.61% |
| 2023052401 | 364.2651 | 300.5 | 21.22% |
| 2023052402 | 256.6494 | 321 | 20.05% |
| 2023052403 | 225.9095 | 177 | 27.63% |
| 2023052501 | 441.6481 | 470 | 6.03% |
| 2023060101 | 408.6759 | 457 | 10.57% |
| 2023060102 | 273.3930 | 292.5 | 6.53% |
| 2023060201 | 436.1698 | 389.5 | 11.98% |
| 2020120201 | 257.5665 | 259.72 | 0.83% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Guo, L.; Zhang, W.; Jiang, S.; Deng, X.; Zhang, N.; Deng, Z. Online Estimation Method and Verification of Sampling Mass for Lunar Drilling in the Chang’E-6 Mission. Aerospace 2025, 12, 331. https://doi.org/10.3390/aerospace12040331
Zhang G, Guo L, Zhang W, Jiang S, Deng X, Zhang N, Deng Z. Online Estimation Method and Verification of Sampling Mass for Lunar Drilling in the Chang’E-6 Mission. Aerospace. 2025; 12(4):331. https://doi.org/10.3390/aerospace12040331
Chicago/Turabian StyleZhang, Gao, Lei Guo, Weiwei Zhang, Shengyuan Jiang, Xiangjin Deng, Nai Zhang, and Zongquan Deng. 2025. "Online Estimation Method and Verification of Sampling Mass for Lunar Drilling in the Chang’E-6 Mission" Aerospace 12, no. 4: 331. https://doi.org/10.3390/aerospace12040331
APA StyleZhang, G., Guo, L., Zhang, W., Jiang, S., Deng, X., Zhang, N., & Deng, Z. (2025). Online Estimation Method and Verification of Sampling Mass for Lunar Drilling in the Chang’E-6 Mission. Aerospace, 12(4), 331. https://doi.org/10.3390/aerospace12040331







