Numerical Analyses of Aerodynamic and Aeroacoustic Interaction Characteristics of Rear-Mounted Propeller on Highspeed Helicopter
Abstract
:1. Introduction
2. Numerical Method
2.1. Adaptive Boundary Method in the Hybrid Grid System
2.2. CFD Method
2.3. Aeroacoustic Analogy Method
3. Method Validation
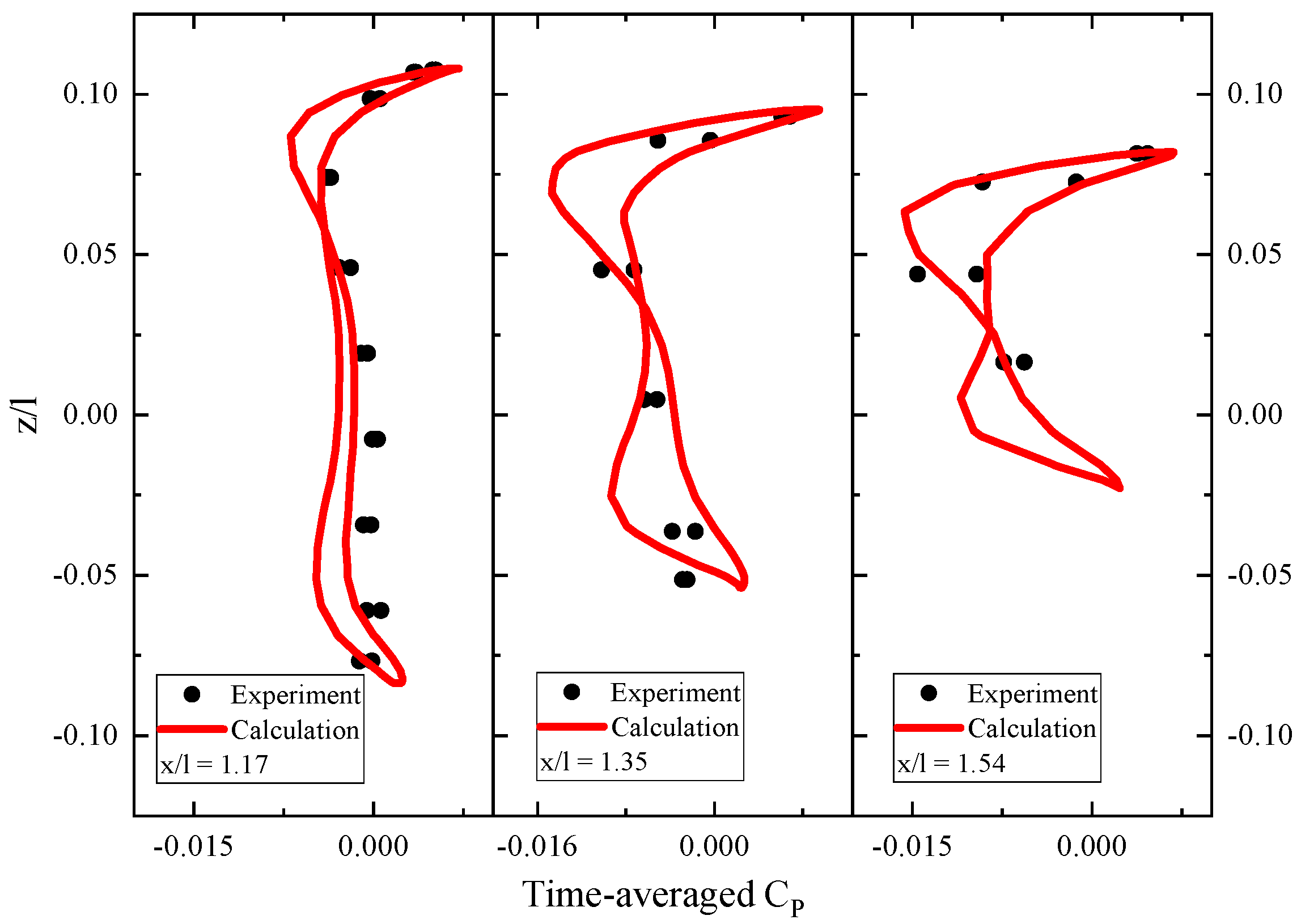
3.1. CFD Method Validation
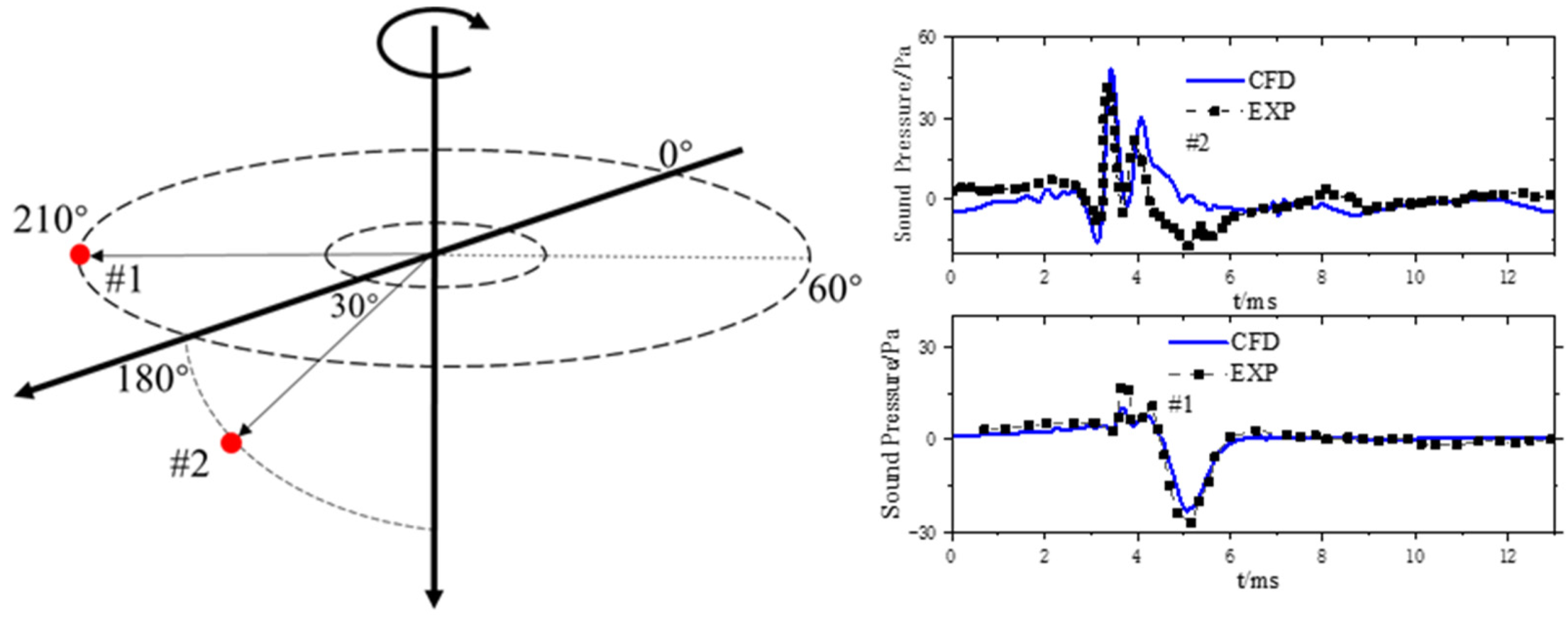
3.2. Aeroacoustic Prediction Method Validation
4. Numerical Results
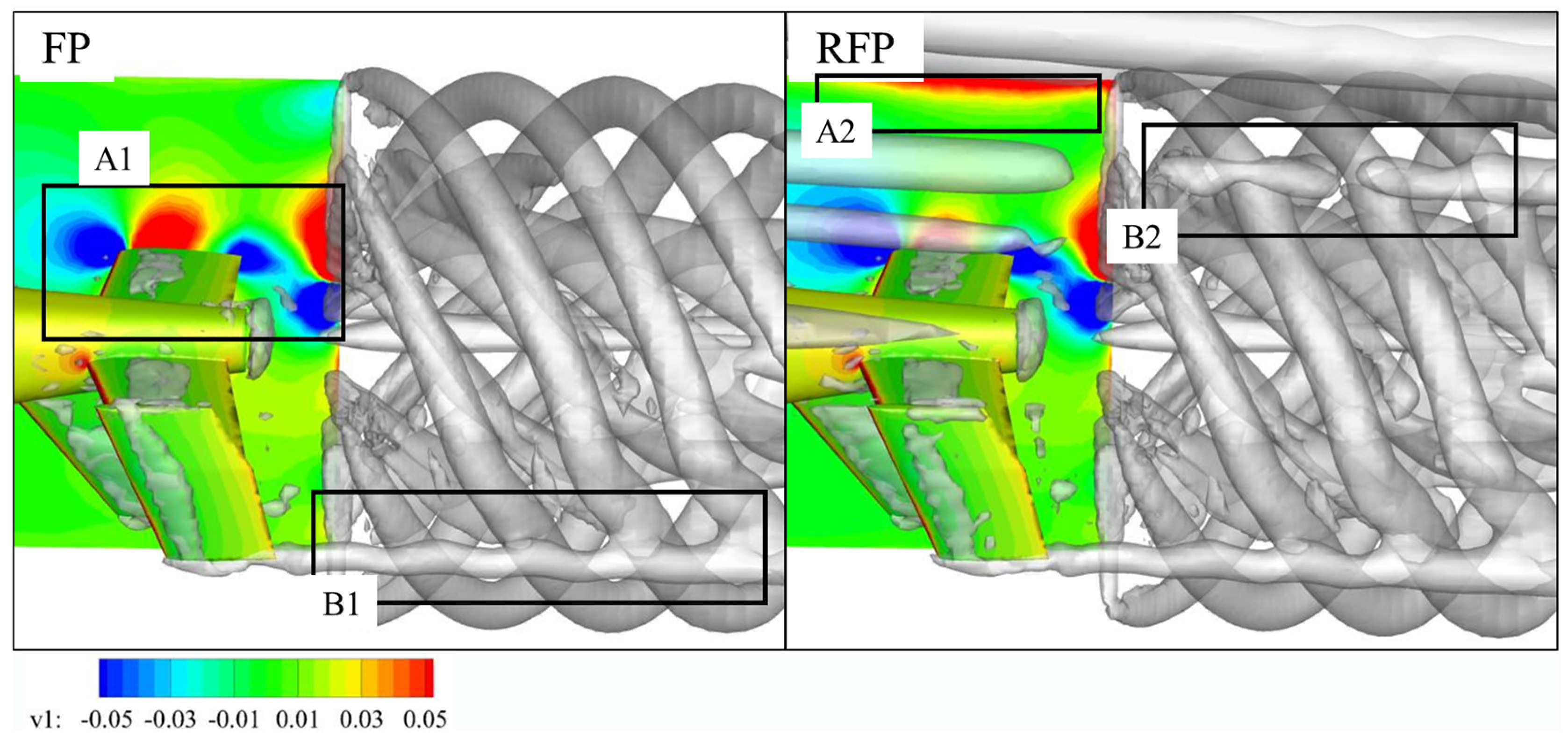
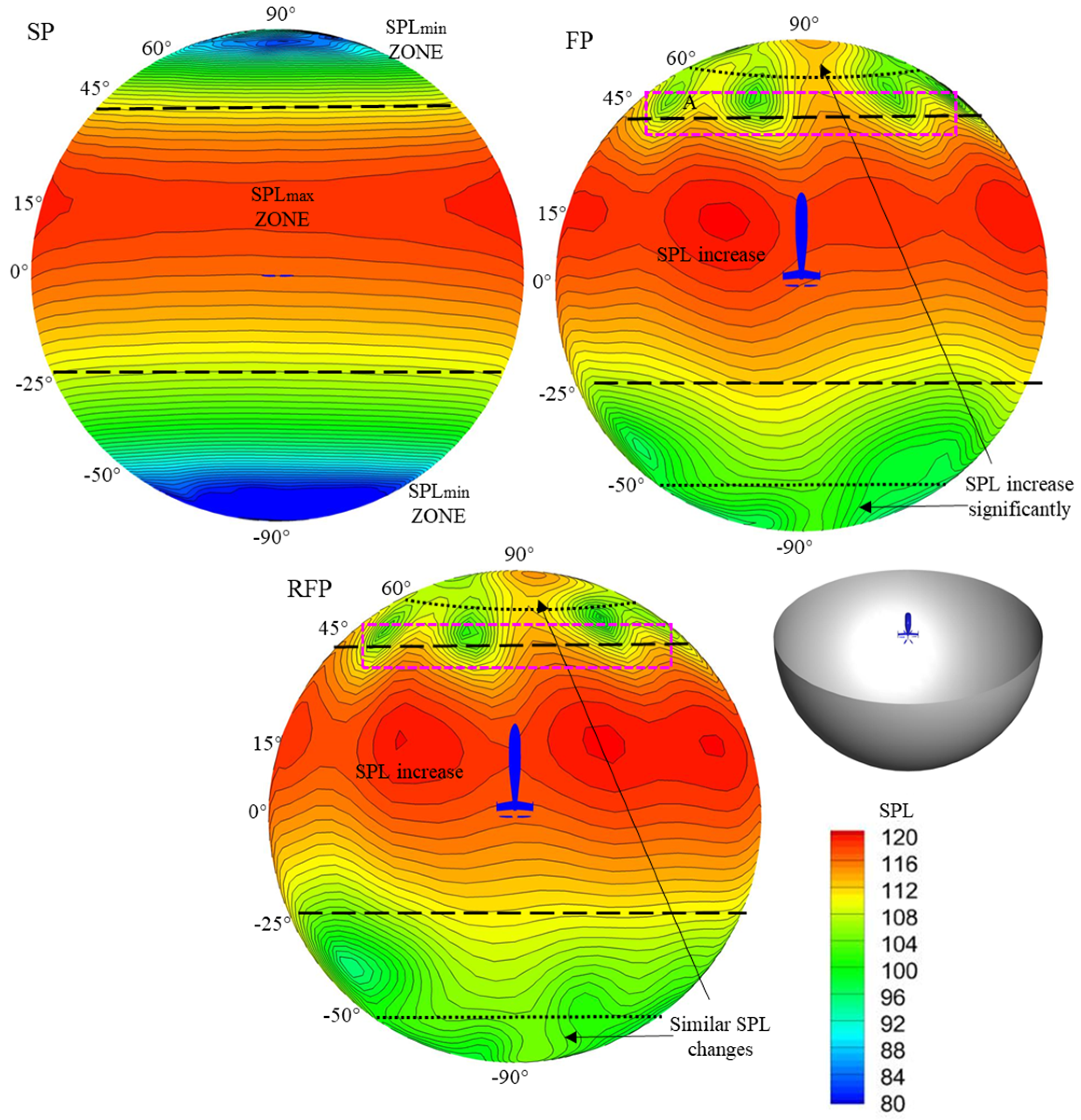
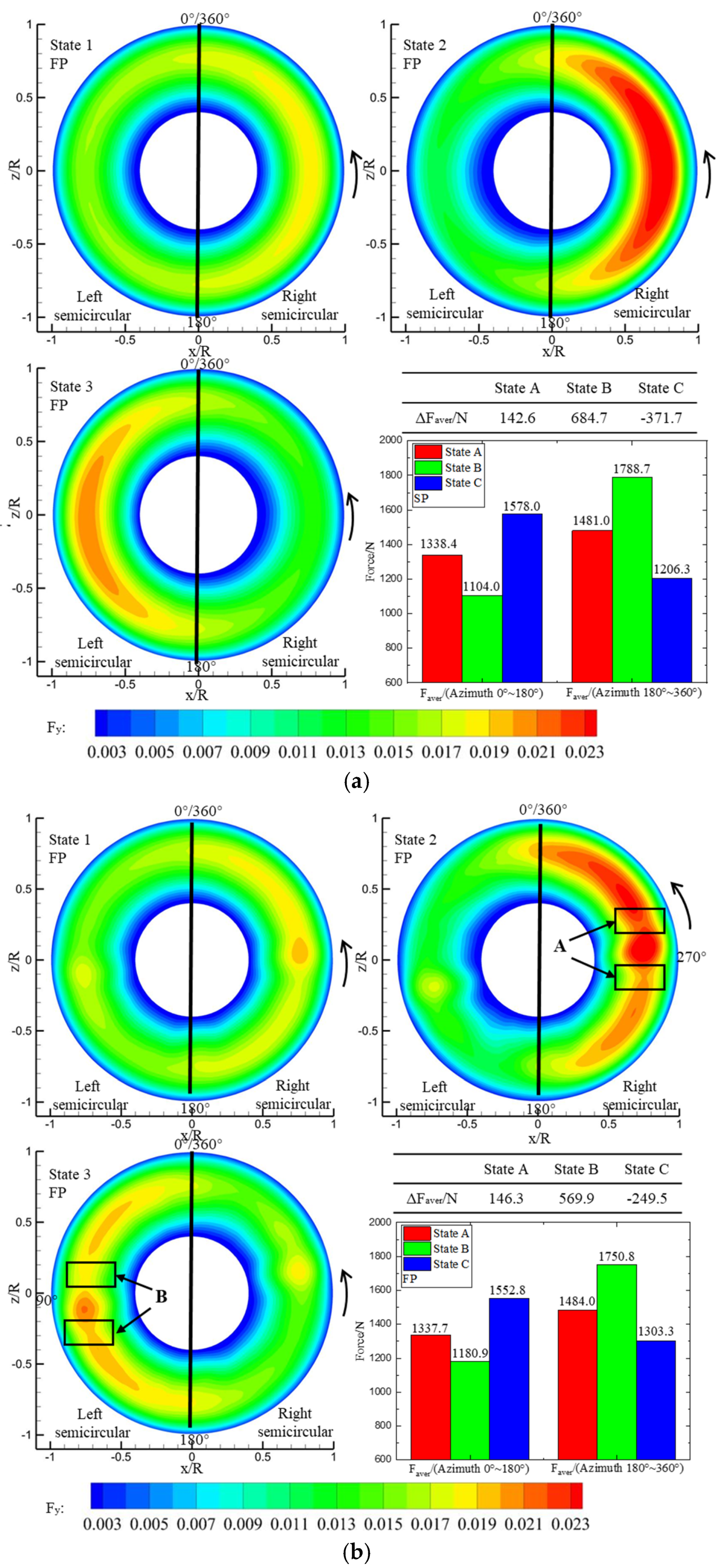
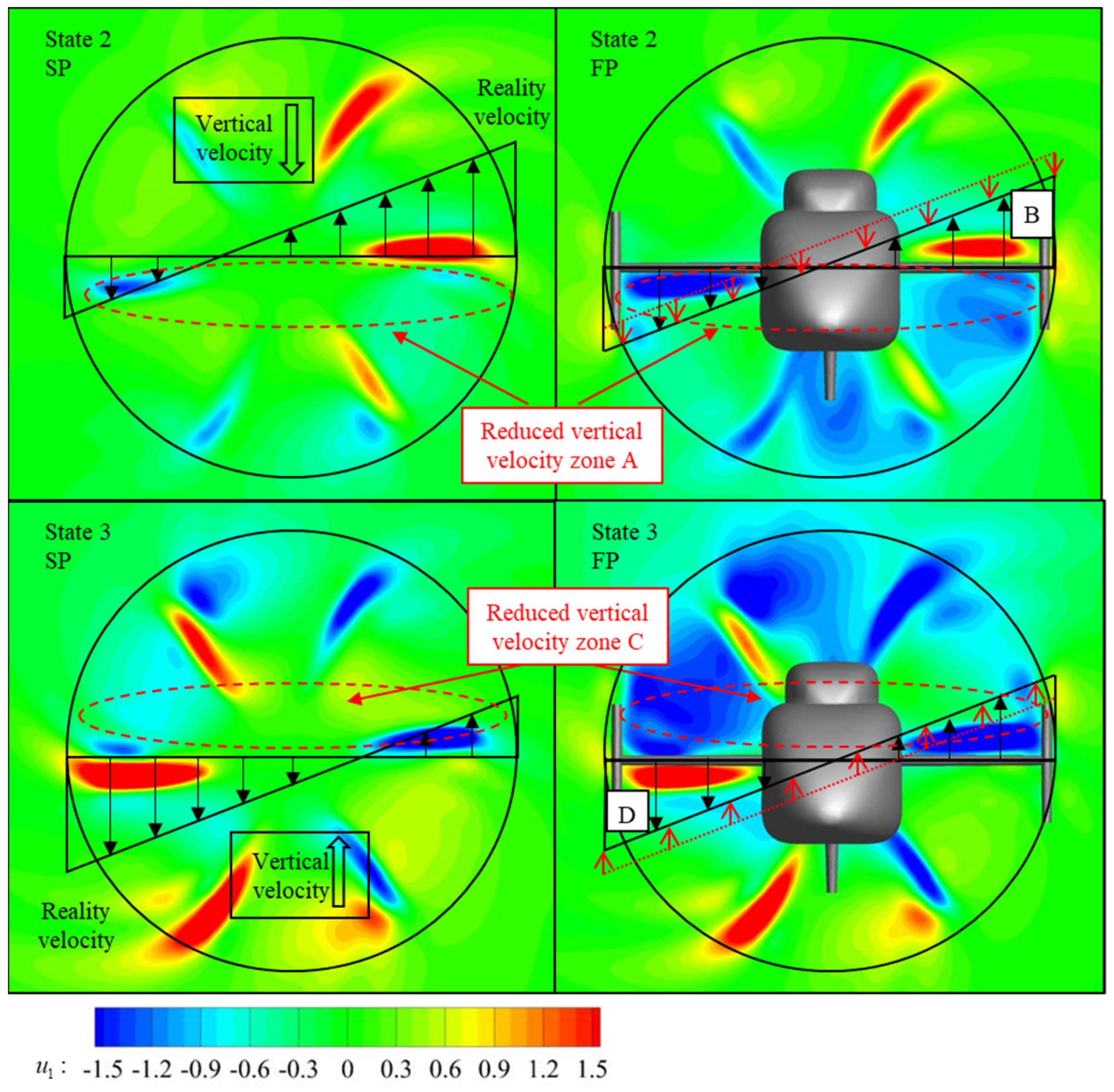
4.1. Forward Flight Case
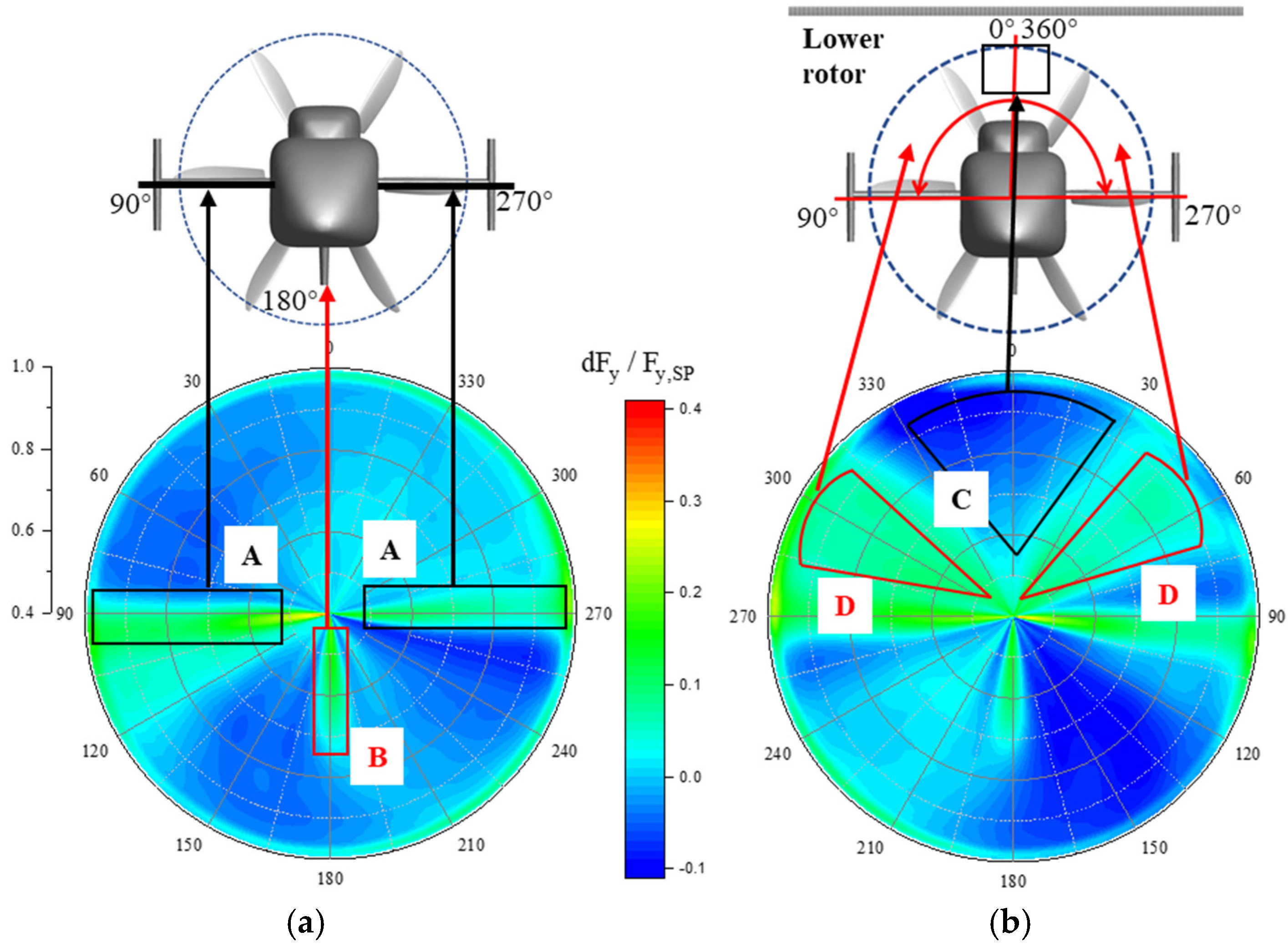
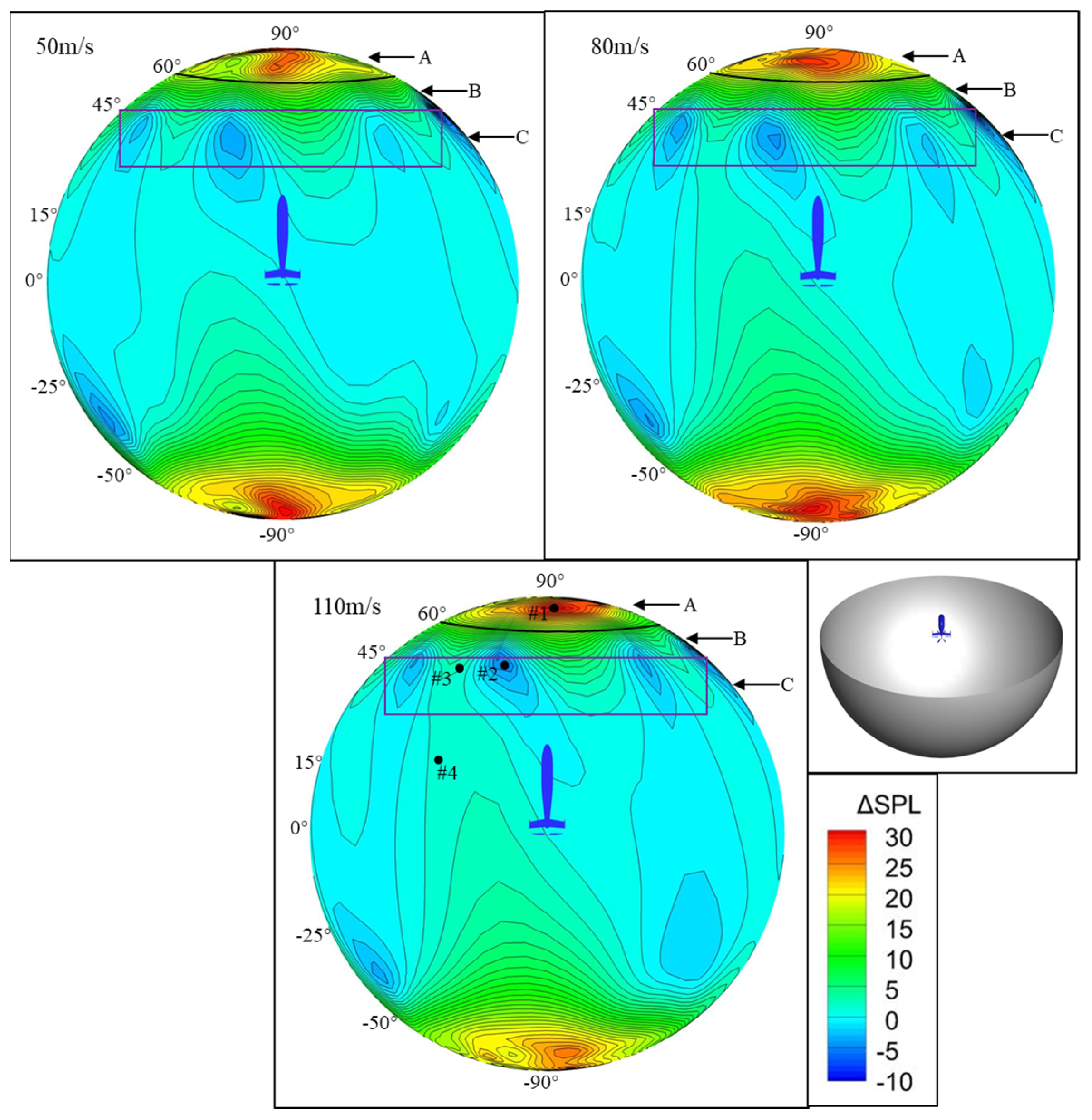
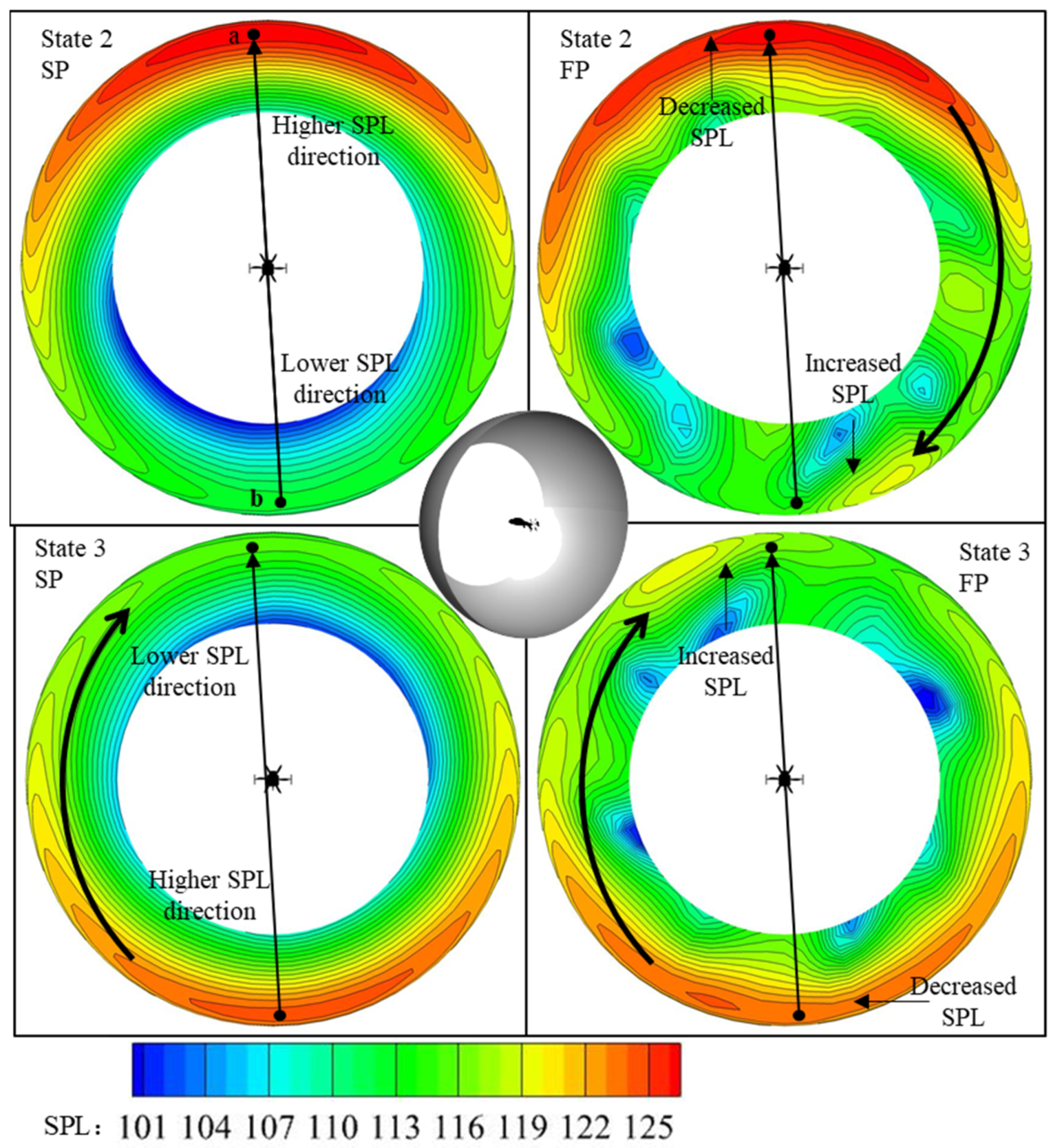
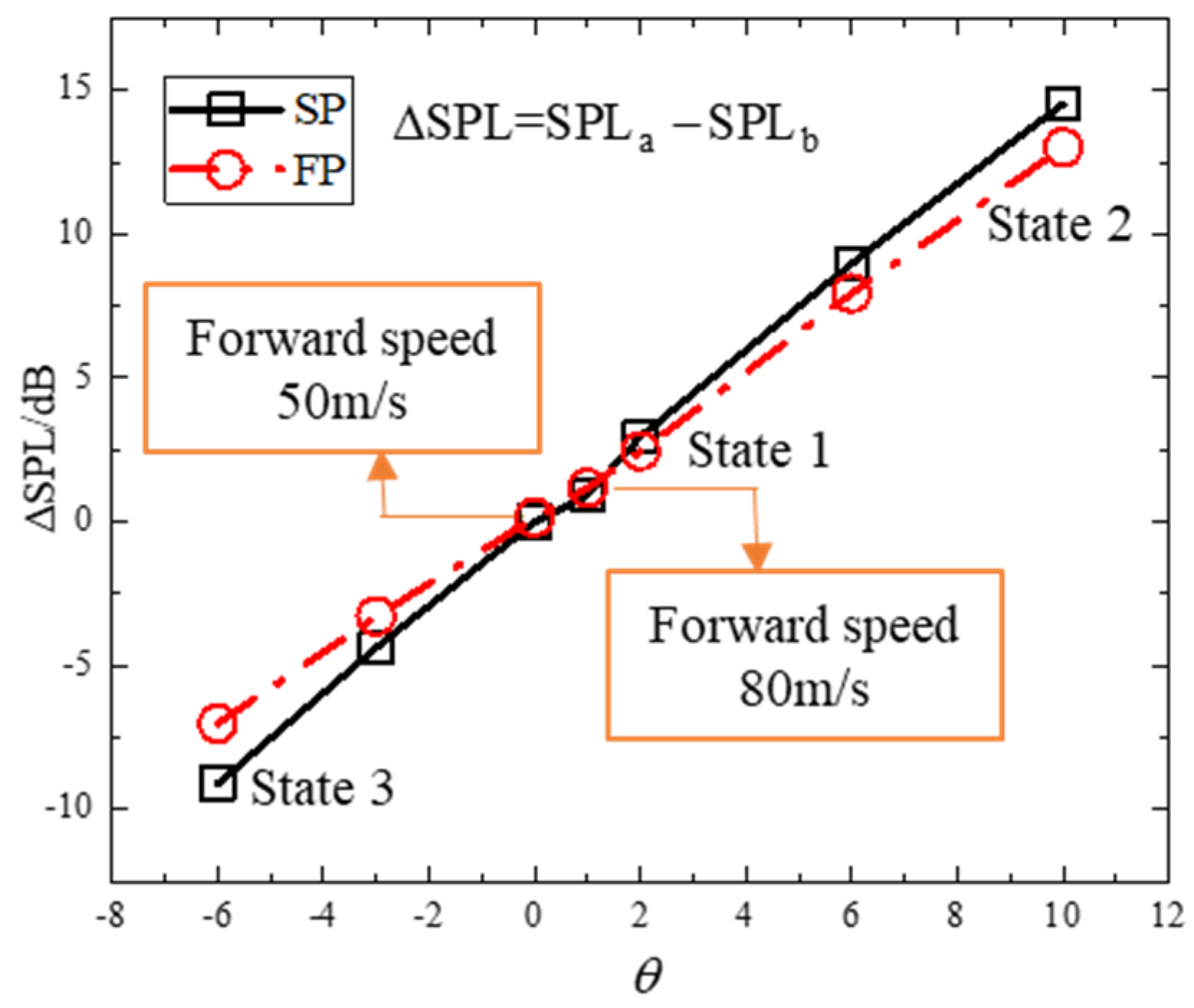
4.2. Effects of Horizontal Flight Speed
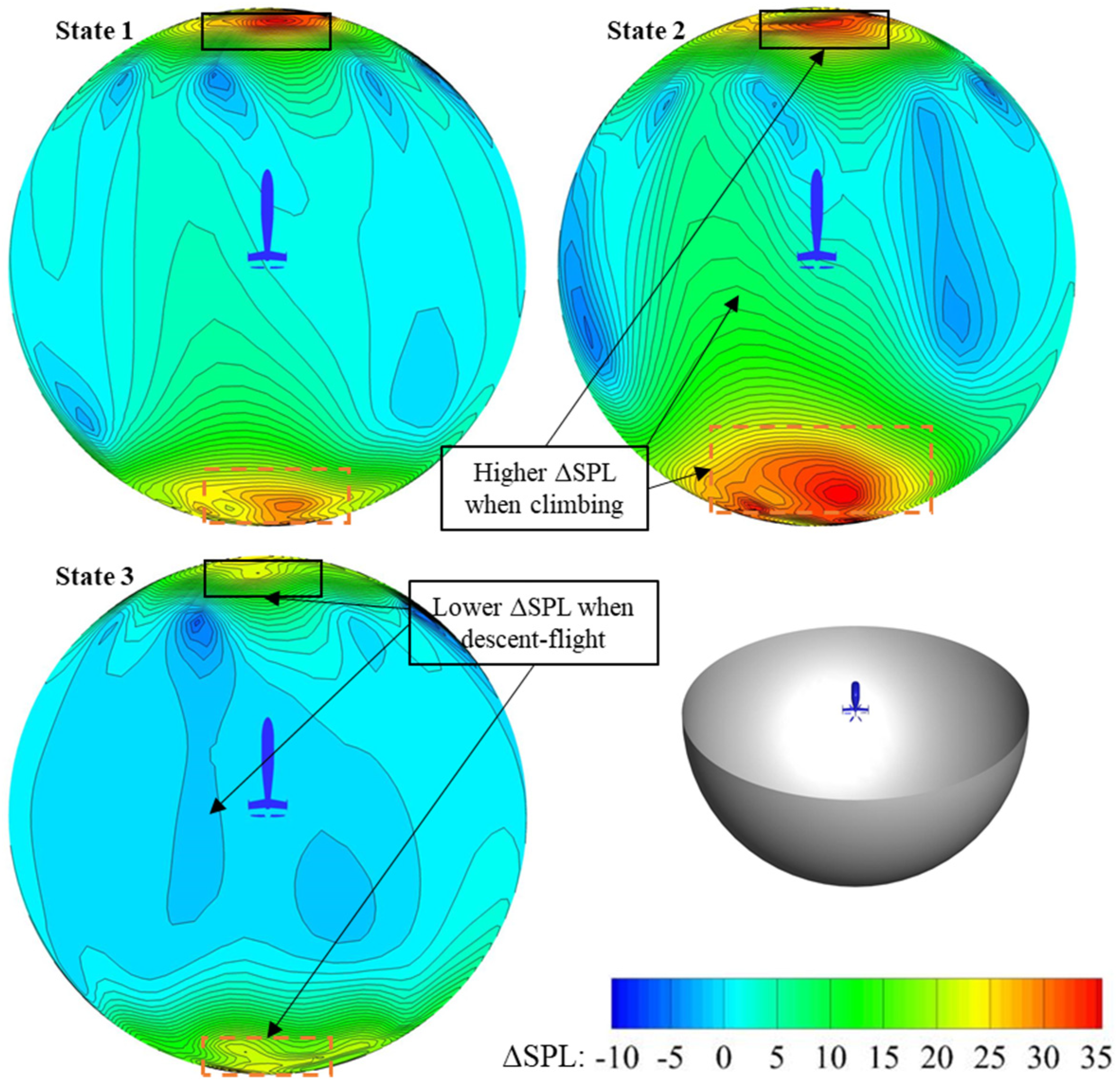
4.3. Effects of Vertical Flight Speed
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ruddell, A.J. Advancing blade concept (ABC) development. J. Am. Helicopter Soc. 1976, 22, 13–23. [Google Scholar] [CrossRef]
- Derosa, S.; Eadie, W.; Eller, E. S-97TM Adaptive Survivability; American Helicopter Society International Forum: Fairfax, VA, USA, 2013. [Google Scholar]
- Stokkermans, T.; Veldhuis, L.; Soemarwoto, B.; Fukari, R.; Eglin, P. Breakdown of aerodynamic interactions for the lateral rotors on a compound helicopter. Aerosp. Sci. Technol. 2020, 101, 105845. [Google Scholar] [CrossRef]
- Boisard, R. Numerical analysis of rotor/propeller aerodynamic interactions on a high-speed compound helicopter. J. Am. Helicopter Soc. 2022, 67, 012005. [Google Scholar] [CrossRef]
- Lorber, P.; Law, G.; O’neill, J.; Aircraft, S.; Bowles, P.; United Technologies Research Center. Overview of S-97 RAIDER scale model tests. In Proceedings of the 72nd Annual Forum of the American Helicopter Society, West Palm Beach, FL, USA, 17–19 May 2016. [Google Scholar]
- Bowles, P.O.; Matalanis, C.G.; Bbttisti, M. Full-configuration CFD analysis of the S-97 RAIDER. In Proceedings of the 75th Annual Forum of the Vertical Flight Society, Philadelphia, PA, USA, 3–16 May 2019. [Google Scholar]
- Fery, F.; Thiemeier, J.; Oehrle, C.; Keßler, M.; Krämer, E. Aerodynamic interactions on Airbus helicopters’ compound helicopter RACER in cruise flight. J. Am. Helicopter Soc. 2020, 65, 1–14. [Google Scholar] [CrossRef]
- Thiemeier, J.; Öhrle, C.; Frey, F.; Keßler, M.; Krämer, E. Aerodynamics and flight mechanics analysis of Airbus Helicopters’ compound helicopter RACER in hover under crosswind conditions. CEAS Aeronaut. J. 2020, 11, 49–66. [Google Scholar] [CrossRef]
- Blacha, M.; Fink, A. Clean Sky 2: Exploring new rotorcraft high speed configurations. In Proceedings of the 43rd European Rotorcraft Forum, Milan, Italy, 12–15 September 2017. [Google Scholar]
- Zhang, T.; Barakos, G.N.; Furqan. On the aerodynamic performance of redundant propellers for multi-rotor eVTOL in cruise. Aerosp. Sci. Technol. 2024, 145, 108846. [Google Scholar] [CrossRef]
- Zhang, T.; Barakos, G.N.; Furqan; Foster, M. High-fidelity aerodynamic and acoustic design and analysis of a heavy-lift eVTOL. Aerosp. Sci. Technol. 2023, 137, 108307. [Google Scholar] [CrossRef]
- Zhang, T.; Barakos, G.N.; Furqan; Foster, M. Multi-fidelity aerodynamic design and analysis of propellers for a heavy-lift eVTOL. Aerosp. Sci. Technol. 2023, 135, 108185. [Google Scholar] [CrossRef]
- Zhang, T.; Barakos, G.N. High-fidelity numerical investigations of rotor-propeller aerodynamic interactions. Aerosp. Sci. Technol. 2022, 124, 107517. [Google Scholar] [CrossRef]
- Steijl, R.; Barakos, G.N.; Badcock, K. A framework for CFD analysis of helicopter rotors in hover and forward flight. Int. J. Numer. Methods Fluids 2006, 51, 819–847. [Google Scholar] [CrossRef]
- Hu, Z.Y.; Xu, G.H.; Shi, Y.J. A robust overset assembly method for multiple overlapping bodies. Int. J. Numer. Methods Fluids 2020, 93, 653–682. [Google Scholar] [CrossRef]
- Hu, Z.Y.; Xu, G.H.; Shi, Y.J. A new study on the gap effect of an airfoil with active flap control based on the overset grid method. Int. J. Aeronaut. Space Sci. 2021, 22, 779–801. [Google Scholar] [CrossRef]
- Zou, D.; Bonfiglioli, A.; Paciorri, R.; Liu, J. An embedded shock-fitting technique on unstructured dynamic grids. Comput. Fluids 2021, 218, 104847. [Google Scholar] [CrossRef]
- Chang, X.; Ma, R.; Wang, N.; Zhao, Z.; Zhang, L. A parallel implicit hole-cutting method based on background mesh for unstructured Chimera grid. Comput. Fluids 2020, 198, 104403. [Google Scholar] [CrossRef]
- Champasak, P.; Panagant, N.; Pholdee, N.; Bureerat, S.; Rajendran, P.; Yildiz, A.R. Grid-based many-objective optimiser for aircraft conceptual design with multiple aircraft configurations. Eng. Appl. Artif. Intell. 2023, 126, 106951. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, Y.; Yang, A. Numerical simulations of complex aircraft configurations using structured overset grids with implicit hole-cutting. Aerosp. Sci. Technol. 2019, 94, 105402. [Google Scholar] [CrossRef]
- Liu, T.; Qu, K.; Cai, J.; Pan, S. A three-dimensional aircraft ice accretion model based on the numerical solution of the unsteady Stefan problem. Aerosp. Sci. Technol. 2019, 93, 105328. [Google Scholar] [CrossRef]
- Pang, C.; Gao, Z.; Yang, H.; Chen, S. An efficient grid assembling method in unsteady dynamic motion simulation using overset grid. Aerosp. Sci. Technol. 2021, 110, 106450. [Google Scholar] [CrossRef]
- Qi, H.; Xu, G.; Lu, C.; Shi, Y. A study of coaxial rotor aerodynamic interaction mechanism in hover with high-efficient trim model. Aerosp. Sci. Technol. 2019, 84, 1116–1130. [Google Scholar] [CrossRef]
- Hwang, Y.J.; Kwon, O.J. Assessment of S-76 rotor hover performance in ground effect using an unstructured mixed mesh method. Aerosp. Sci. Technol. 2019, 84, 223–236. [Google Scholar] [CrossRef]
- Oehrle, C.; Fery, F.; Thiemeier, J.; Manuel, K.; Ewald, K. Coupled and trimmed aerodynamic and aeroacoustic simulations for Airbus Helicopters’ compound helicopter RACER. J. Am. Helicopter Soc. 2019, 64, 1–14. [Google Scholar] [CrossRef]
- Chirico, G.; Barakos, G.N.; Bown, N. Propeller installation effects on turboprop aircraft acoustics. J. Sound Vib. 2018, 424, 238–262. [Google Scholar] [CrossRef]
- Higgins, R.J.; Barakos, G.N.; Shahpar, S.; Tristanto, I. A computational fluid dynamic acoustic investigation of a tiltwing eVTOL concept aircraft. Aerosp. Sci. Technol. 2021, 111, 106571. [Google Scholar] [CrossRef]
- Myers, M.K.; Hausmann, J.S. Computation of acoustic scattering from a moving rigid surface. J. Acoust. Soc. Am. 1992, 91, 2594–2605. [Google Scholar] [CrossRef]
- Chen, S.Y.; Zhao, Q.J.; Ma, Y.Y. An adaptive integration surface for predicting transonic rotor noise in hovering and forward flights. Chin. J. Aeronaut. 2019, 32, 2047–2058. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, K.; Zhao, Q.; Wang, W. Numerical analysis of rotor aeroacoustic characteristics during collective pitch aperiodic variation in hover. Aerosp. Sci. Technol. 2022, 124, 107411. [Google Scholar] [CrossRef]
- Li, P.; Zhao, Q.J.; Zhu, Q. CFD calculations on the unsteady aerodynamic characteristics of a tilt-rotor in a conversion mode. Chin. J. Aeronaut. 2015, 28, 1593–1605. [Google Scholar] [CrossRef]
- Zhao, Q.J.; Zhao, G.Q.; Wang, B. Robust Navier-Stokes method for predicting unsteady flowfield and aerodynamic characteristics of helicopter rotor. Chin. J. Aeronaut. 2018, 31, 214–224. [Google Scholar] [CrossRef]
- Meakin, R. A new method for establishing intergrid communication among systems of overset grids. In Proceedings of the 10th Computational Fluid Dynamics Conference, Honolulu, HI, USA, 24–27 June 1991. [Google Scholar]
- Farassat, F.; Succi, G.P. A review of propeller discrete frequency noise prediction technology with emphasis on two current methods for time domain calculations. J. Sound Vib. 1980, 71, 399–419. [Google Scholar] [CrossRef]
- Francescantonio, P.D. A new boundary integral formulation for the prediction of sound radiation. J. Sound Vib. 1997, 202, 491–509. [Google Scholar] [CrossRef]
- Roe, P.L. Approximate Riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- Raymond, E.M.; Susan, A.G. Steady and periodic pressure measurements on a generic helicopter fuselage model in the presence of a rotor. NASA Tech. Memo. 2000, 210286. [Google Scholar]
- Ho, J.C.; Yeo, H. Analytical study of an isolated coaxial rotor system with lift offset. Aerosp. Sci. Technol. 2020, 100, 105818. [Google Scholar] [CrossRef]
- Jia, Z.; Lee, S. Impulsive loading noise of a lift-offset coaxial rotor in high-speed forward flight. AIAA J. 2020, 58, 687701. [Google Scholar] [CrossRef]
- Hayami, K.; Sugawara, H.; Yumino, T.; Tanabe, Y.; Kameda, M. CFD analysis on the performance of a coaxial rotor with lift offset at high advance ratios. Aerosp. Sci. Technol. 2023, 135, 108194. [Google Scholar] [CrossRef]
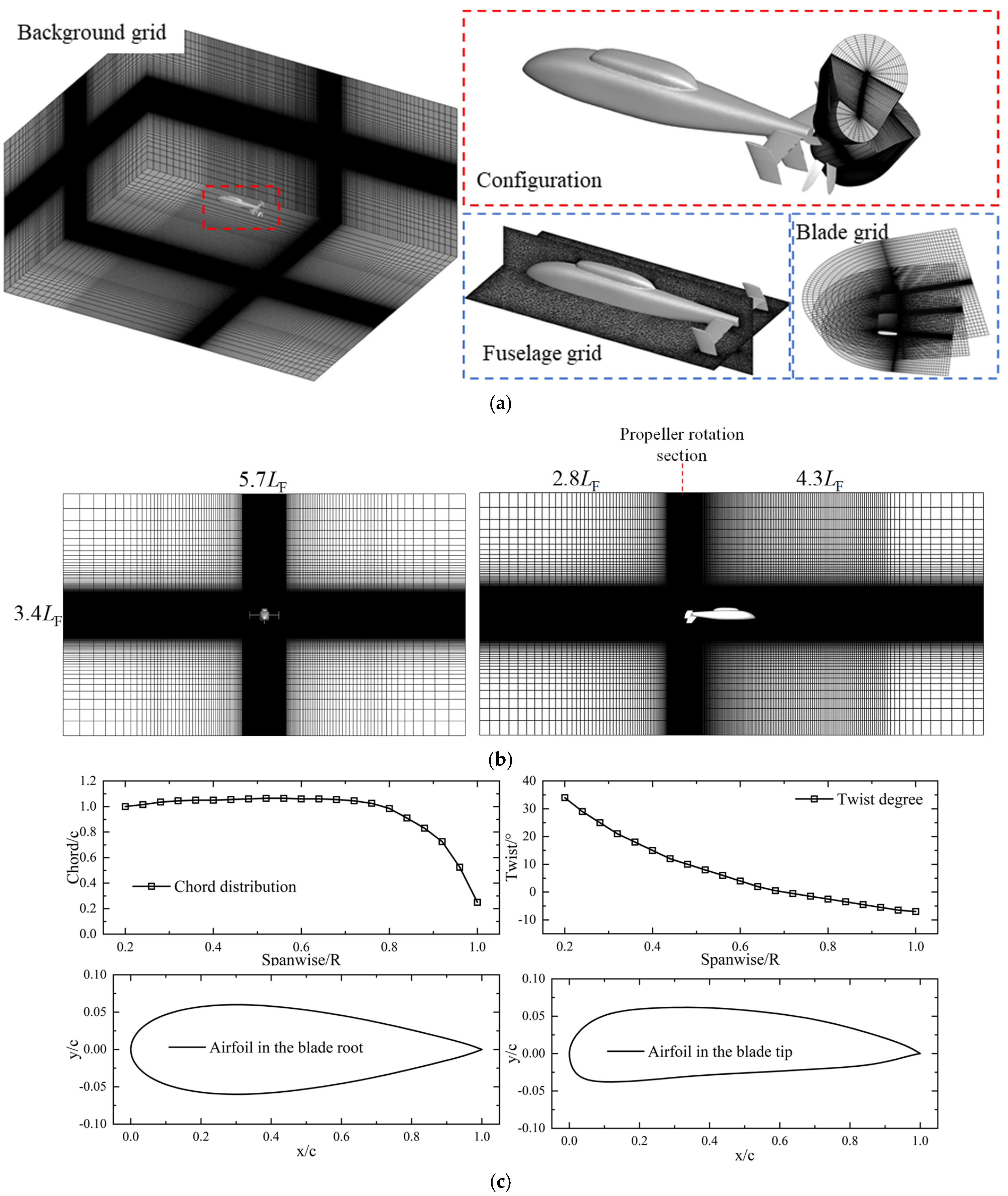
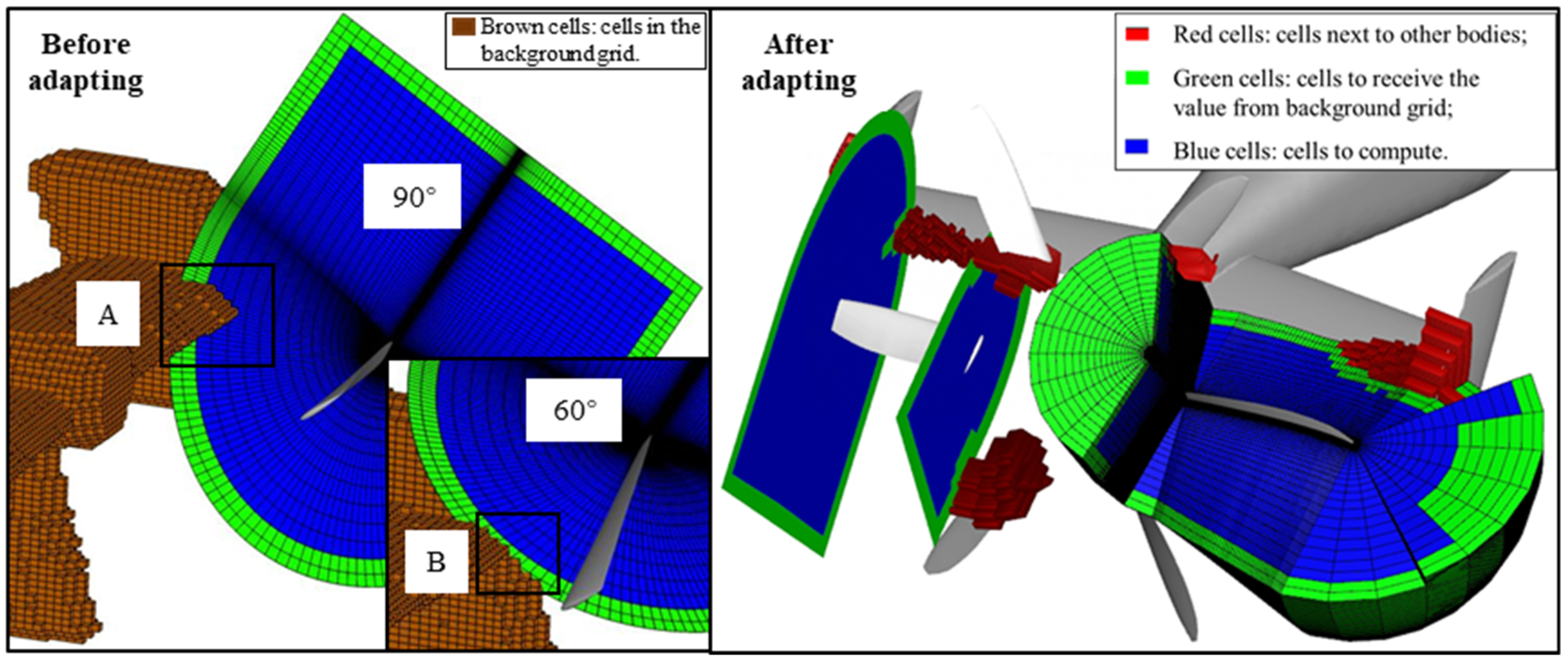


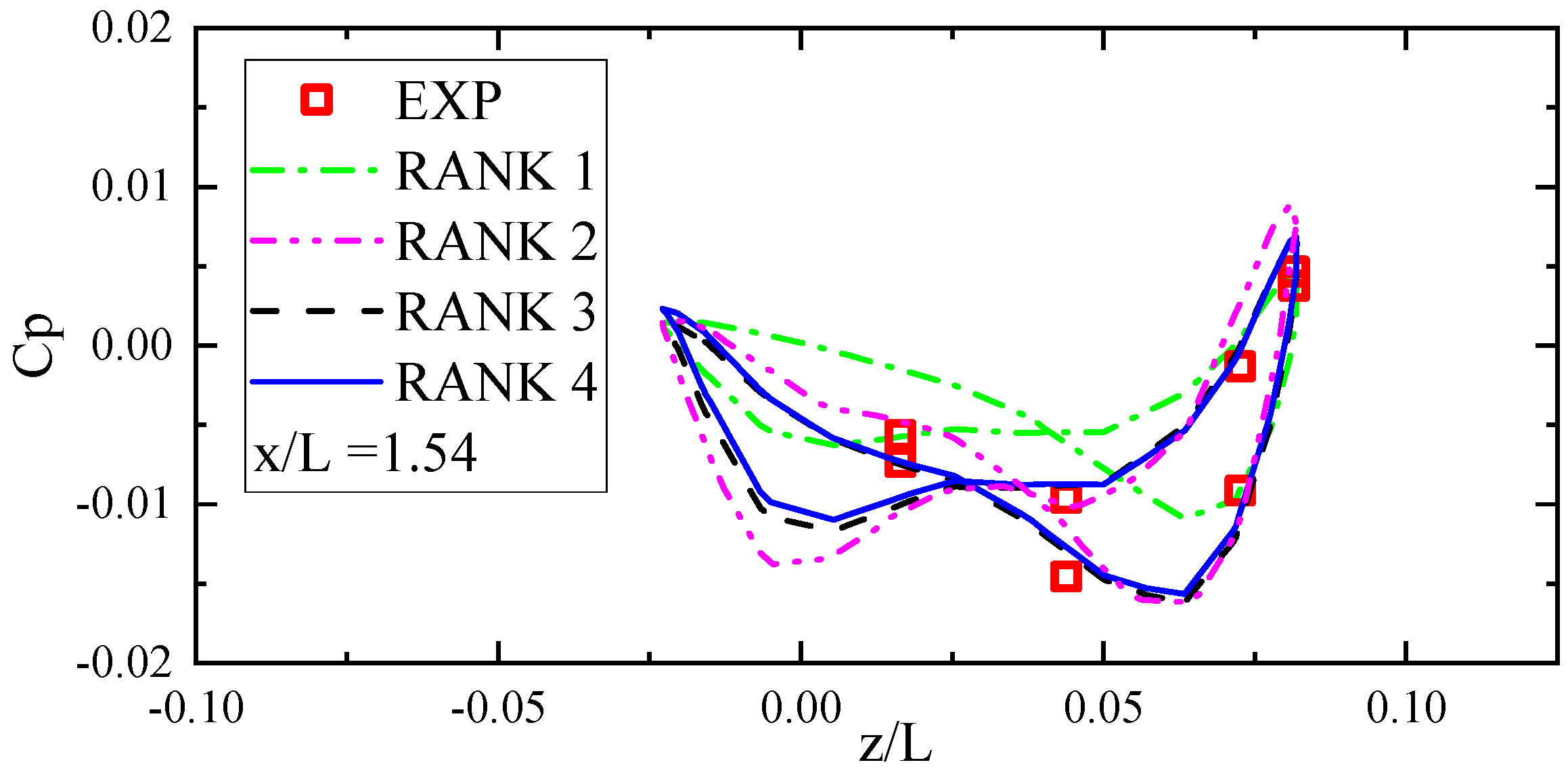





| Grid Quantity | Fuselage Grid/Million | Blade Grid/Million | Background Grid/Million | Total Grid/Million | Computational Time/Hour | Aerodynamic Pressure Error/% |
|---|---|---|---|---|---|---|
| RANK 1 | 1.9 | 2.4 | 14.2 | 18.5 | 245.7 | 0.88 |
| RANK 2 | 3.4 | 3.8 | 21.9 | 29.1 | 467.1 | 0.72 |
| RANK 3 | 4.0 | 4.6 | 30.8 | 39.4 | 594.5 | 0.59 |
| RANK 4 | 5.1 | 5.3 | 42.9 | 53.3 | 746.6 | 0.58 |
| Fuselage Length | Fuselage Width | Propeller Radius | Propeller Chord | Propeller RPM | Air Density |
|---|---|---|---|---|---|
| 5.46 m | 2.27 m | 1.0 m | 0.154 m | 2655 r/min | 1.225 kg/m3 |
| Boundary | Boundary Condition | |
|---|---|---|
| Numerical simulation (URANS) | Fuselage surface | Slip-free adiabatic boundary condition |
| Propeller blade surface | Slip-free adiabatic boundary condition | |
| Farfield boundary | Reflection-free boundary condition | |
| Noise prediction (FW-H equations) | Fuselage | Farassat1A |
| Propeller | FW-H_pds |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, D.; Chen, X.; Zhao, Q.; Bao, W. Numerical Analyses of Aerodynamic and Aeroacoustic Interaction Characteristics of Rear-Mounted Propeller on Highspeed Helicopter. Aerospace 2025, 12, 343. https://doi.org/10.3390/aerospace12040343
Sun D, Chen X, Zhao Q, Bao W. Numerical Analyses of Aerodynamic and Aeroacoustic Interaction Characteristics of Rear-Mounted Propeller on Highspeed Helicopter. Aerospace. 2025; 12(4):343. https://doi.org/10.3390/aerospace12040343
Chicago/Turabian StyleSun, Dazhi, Xi Chen, Qijun Zhao, and Weicheng Bao. 2025. "Numerical Analyses of Aerodynamic and Aeroacoustic Interaction Characteristics of Rear-Mounted Propeller on Highspeed Helicopter" Aerospace 12, no. 4: 343. https://doi.org/10.3390/aerospace12040343
APA StyleSun, D., Chen, X., Zhao, Q., & Bao, W. (2025). Numerical Analyses of Aerodynamic and Aeroacoustic Interaction Characteristics of Rear-Mounted Propeller on Highspeed Helicopter. Aerospace, 12(4), 343. https://doi.org/10.3390/aerospace12040343






