A Magnetometer-Only Attitude Determination Strategy for Small Satellites: Design of the Algorithm and Hardware-in-the-Loop Testing

Abstract

Attitude determination represents a fundamental task for spacecraft. Achieving this task on small satellites, and nanosatellites in particular, is further challenging, because the limited power and computational resources available on-board, together with the low development budget, set strict constraints on the selection of the sensors and the complexity of the algorithms. Attitude determination is obtained here from the only measurements of a three-axis magnetometer and a model of the Geomagnetic field, stored on the on-board computer. First, the angular rates are estimated and processed using a second-order low-pass Butterworth filter, then they are used as an input, along with Geomagnetic field data, to estimate the attitude matrix using an unsymmetrical TRIAD. The computational efficiency is enhanced by arranging complex matrix operations into a form of the Faddeev algorithm, which is implemented using systolic array architecture on the FPGA core of a CubeSat on-board computer. The performance and the robustness of the algorithm are evaluated by means of numerical analyses in MATLAB Simulink, showing pointing and angular rate accuracy below 10° and 0.2°/s. The algorithm implemented on FPGA is verified by Hardware-in-the-loop simulation, confirming the results from numerical analyses and efficiency.

1. Introduction

Mission operations often require the capability to orient the spacecraft in a specific direction. To perform these maneuvers, an adequately accurate knowledge of the spacecraft orientation in space, namely its attitude, is required, and this is the goal of attitude determination. The results from this process are input to attitude control, which produces, through the actuators, an adequate control torque driving the spacecraft to the desired attitude.

The problem of attitude determination has been extensively studied since the outset of space exploration, and consists of the determination of the rotation matrix $\mathit{A}$, which transforms any vector $v_b$, whose coordinates are expressed in a reference frame ${\mathcal{F}}_b$ rotating rigidly with the spacecraft, to the corresponding vector $v_i$, expressed in a reference coordinate system ${\mathcal{F}}_i$ [1]. Typically, the problem is solved using the Tri-axial Attitude Determination (TRIAD) algorithm which requires the knowledge of at least two couples of vectors in both ${\mathcal{F}}_b$ and ${\mathcal{F}}_i$ [2]. Similar methods, representing solutions to Wahba’s problem [3], have been widely applied and include the q-method by Davenport [1,4], Schuster’s QUaternion ESTimator (QUEST) algorithm [5,6] and the optimized TRIAD by Bar-Itzhack and Harman [7]. Other approaches produce attitude determination by direct quaternion estimation [8,9], and can be significantly faster than the other algorithms outlined but can show singularities, which occur when the attitude rotation axis lays on the plane of the unit vectors on which the estimation is based, as detail by Markley [10].

The above-mentioned algorithms require two vector measurements in two-body frames ${\mathcal{F}}_b$ and ${\mathcal{F}}_i$. In fact, the measurements in ${\mathcal{F}}_i$ can be replaced by predictions of the vector behavior in time and space; for instance, the International Geomagnetic Reference Field (IGRF) model can be used to estimate the values of the Geomagnetic field vector at any orbital coordinates of the spacecraft [11]. These models can be rather complex and accurate, and their selection is a crucial part of the design process. A similar approach is not effective for vectors in ${\mathcal{F}}_b$ because their prediction requires knowledge of the spacecraft attitude, which is instead the unknown of the attitude determination problem. As a result, on-board sensors must be used for vector measurements in ${\mathcal{F}}_b$, and their characteristics strongly determine the accuracy of the attitude determination algorithm. The use of star trackers can produce attitude determination with accuracy less than 0.01°. Nevertheless, these components are relatively expensive, power and memory consuming if compared to MEMS (Micro-Electro-Mechanical Systems) sensors, such as magnetometers, gyroscopes, and sun sensors, which, therefore, represent an attracting alternative for low-cost missions. MEMS gyroscopes are accurate angular rate sensors; nevertheless, because of technological limitations, they usually have structure defects which produce high drift and require compensation, thus opening to alternative methods of angular rate determination [12].

Gyroless attitude determination methods are of interest as backup solutions for small satellite missions that do not require high pointing accuracy for basic operations [13]. Such a solution can be effective when the above-mentioned measurement drift increases above a threshold level, in case of failure of the sensor and in the presence of an error in the algorithm which produces the interpretation of the signal. Several methods have been proposed based on the use of a three-axis magnetometer together either with other low-cost sensors or solar panels [14,15,16,17] or on their own.

Magnetometer-only attitude determination is a challenging task, mainly because the measurements from a three-axis magnetometer can provide information on only two axes of the spacecraft attitude. To resolve all three axes, either some constraints on the attitude motion or a filtering process is required. A first solution was proposed by Natanson et al. [18], whose DADMOD algorithm provided good results in the post-processing. A further implementation of the algorithm using DADMOD to initialize a Real-Time Sequential Filter (RTSF) extended it to real-time applications [19,20], with an accuracy of 2° on attitude and 0.01°/s on angular rates.

The most popular methods for three-axis magnetometer-only attitude determination are based on the Extended Kalman Filter (EKF) and can reach an accuracy below 5° on attitude and 0.01°/s on the angular rates [21,22,23]. Other solutions include the Unscented Kalman Filter (UKF) algorithm by Ma and Jiang [24], or the two-step EKF algorithm proposed by Searcy and Pernicka [25], which achieves accuracies of less than 1°, but is effective only if the angular rates along at least one axis exceeds 0.1°/s.

Despite their rather high accuracy, the mentioned algorithms either require sophisticate models for vector estimation, are effective only under some specific attitude control, or include complex vector and matrix operations. The latter can be rather complex to be implemented as the Field Programmable Gate Array (FPGA) core of an On-Board Computer (OBC). The use of FPGA-based OBC in small satellites, especially CubeSats, has grown in the last years. This trend is motivated by FPGA hardware and software flexibility, which allows on-ground and in-orbit risk-free reconfiguration, and by their capability to perform processes in parallel.

In this work, we propose a simple attitude determination strategy suitable to be implemented on an FPGA-based OBC. The solution does not require any Kalman Filter and is based only on the measurements of a three-axis magnetometer and the Geomagnetic field data stored on the OBC memory. Angular rates are determined independently from attitude, based on a method proposed previously by the same authors [26]. The Attitude matrix is then estimated by developing a form of the unsymmetrical TRIAD. All the complex matrix operations are arranged in the form of a Faddeev algorithm [27], which can be implemented on FPGA using one single compact systolic array architecture [28]. The use of the same architecture for all the complex matrix operations leads to an increase in the system and algorithm efficiency. The performance and robustness of the attitude determination strategy are verified by means of numerical analyses in MATLAB Simulink, showing an accuracy of 0.2°/s for angular rates and below 10° for the attitude. The results show how process delay, characterizing the algorithm, can be minimal when implemented on real hardware, as verified by Hardware-in-the-Loop (HiL) simulation.

The manuscript is organized as follows. In Section 2, the dynamical framework and the models used for the analysis are introduced. The design and implementation of the attitude determination algorithm is provided in Section 3, and its performance and robustness are verified by numerical analyses in Section 4. The analyses are performed simulating the detumbling and pointing of the satellite after deployment, assuming unknown initial conditions randomly selected. In Section 5 the algorithm is implemented on the FPGA core of a CubeSat OBC, and tested by HiL simulation as a preliminary verification of its suitability for implementation for real missions.

2. Dynamical Framework

The attitude determination strategy presented in this work is targeted to spacecraft orbiting in circular Low Earth Orbits (LEO) and does not require any a-priori knowledge of the Right Ascension of the Ascending Node (RAAN) $\mathsf{\Omega }$, orbit phase angle ${\varphi }_0$, attitude and angular rates.

The satellite is modeled as a rigid body, and its attitude is described using Euler angles $\left(\phi ,\theta ,\psi \right)$ and angular rates $\left(\omega ={\left[\begin{array}{ccc}{\omega }_x& {\omega }_y& {\omega }_z\end{array}\right]}^T\right)$, representing the angular velocity components of the reference frame ${\mathcal{F}}_b={\left[\begin{array}{ccc}{\widehat{x}}_b& {\widehat{y}}_b& {\widehat{z}}_b\end{array}\right]}^T$, attached to the satellite, with respect to the inertial reference frame ${\mathcal{F}}_i={\left[\begin{array}{ccc}{\widehat{x}}_i& {\widehat{y}}_i& {\widehat{z}}_i\end{array}\right]}^T$, here selected as the Geo-Centric Inertial (GCI) frame. Assuming ${\mathcal{F}}_b$ to be coincident with the principal axes of inertia of the satellite, then attitude dynamics can be expressed by the following set of equations [1]

$$\begin{array}{c}\{\begin{array}{c}\dot{\phi }={\omega }_x+\sin \phi \tan \theta {\omega }_y+\cos \phi \tan \theta {\omega }_z\\ \dot{\theta }=\cos \phi {\omega }_y-\sin \phi {\omega }_z\\ \dot{\psi }=\frac{\left(\sin \phi {\omega }_y-\cos \phi {\omega }_z\right)}{\cos \theta }\end{array}\\ \{\begin{array}{c}{\dot{\omega }}_x=\left(\frac{I_y-I_z}{I_x}\right){\omega }_y{\omega }_z+{\tau }_x\\ {\dot{\omega }}_y=\left(\frac{I_z-I_x}{I_y}\right){\omega }_x{\omega }_z+{\tau }_y\\ {\dot{\omega }}_z=\left(\frac{I_x-I_y}{I_z}\right){\omega }_x{\omega }_y+{\tau }_z\end{array}\end{array},$$

(1)

where $I_i$ and ${\tau }_i$ are, respectively, the moment of inertia and the external torque in the i-th direction of ${\mathcal{F}}_b$. It can be noticed that the third equation in system (1) shows a singularity for $\theta =\frac{\pi }{2}+k\pi k\in \mathrm{𝕫},$ and this can be avoided using quaternions instead of Euler angles to represent the attitude [1]. The attitude dynamics using the quaternion representation can be expressed by the following system:

$$\begin{array}{c}\{\begin{array}{c}\begin{array}{c}\dot{q_1}=\frac{1}{2}\left(q_4{\omega }_x+q_2{\omega }_z-q_3{\omega }_y\right)\\ \dot{q_2}=\frac{1}{2}\left(q_4{\omega }_y-q_1{\omega }_z+q_3{\omega }_x\right)\end{array}\\ \begin{array}{c}\dot{q_3}=\frac{1}{2}\left(q_4{\omega }_z+q_1{\omega }_y-q_2{\omega }_x\right)\\ \dot{q_4}=-\frac{1}{2}\left(q_1{\omega }_x+q_2{\omega }_y+q_3{\omega }_z\right)\end{array}\end{array}\\ \{\begin{array}{c}{\dot{\omega }}_x=\left(\frac{I_y-I_z}{I_x}\right){\omega }_y{\omega }_z+{\tau }_x\\ {\dot{\omega }}_y=\left(\frac{I_z-I_x}{I_y}\right){\omega }_x{\omega }_z+{\tau }_y\\ {\dot{\omega }}_z=\left(\frac{I_x-I_y}{I_z}\right){\omega }_x{\omega }_y+{\tau }_z\end{array}\end{array},$$

(2)

For the case examined here, the control torque is produced by three magnetorquers each one orthogonal to an axis of ${\mathcal{F}}_b$. Indicating with $\mathit{m}$ the magnetic dipole moment produced by the three magnetorquers, the control torque is given by:

$$\mathit{\tau }=\mathit{m}\times {\mathit{B}}_{\mathit{b}},$$

(3)

where ${\mathit{B}}_{\mathit{b}}={\left[\begin{array}{ccc}{B}_{b,x}& B_{b,y}& B_{b,z}\end{array}\right]}^{\mathit{T}}$ is the Geomagnetic field vector in ${\mathcal{F}}_b$.

Considering the worst-case scenario of a spacecraft deployed with unknown attitude and angular rates, equipped with only a three-axis magnetometer as an attitude sensor, then the only control actions that can be performed are stabilization and pointing with respect to the Geomagnetic field. A case of interest is that in which the satellite is stabilized to pure-spin around the i-th axis, with a desired angular rate ${\overline{\omega }}_i$ and, contemporarily, the i-th axis is redirected towards the Geomagnetic field vector. A suitable control law, leading to the mentioned result for ${\widehat{x}}_b$, is given by the following equations:

$$\mathit{m}={\mathit{m}}_{\mathit{d}}+{\mathit{m}}_{\mathit{p}}$$

(4a)

$$\{\begin{array}{c}{m}_{d,x}=k_1\dot{\beta }\\ m_{d,y}=\begin{array}{cc}-k_2\left({\omega }_x-{\overline{\omega }}_x\right)sign\left(B_{b,z}\right)& if\left|B_{b,z}\right|\ge \left|B_{b,y}\right|\\ 0& if\left|B_{b,z}\right|<\left|B_{b,y}\right|\end{array}\\ m_{d,z}=\begin{array}{cc}{k}_2\left({\omega }_x-{\overline{\omega }}_x\right)sign\left(B_{b,y}\right)& if\left|B_{b,z}\right|<\left|B_{b,x}\right|\\ 0& if\left|B_{b,z}\right|\ge \left|B_{b,x}\right|\end{array}\end{array}$$

(4b)

$${\mathit{m}}_{\mathit{p}}=k_p{\mathit{B}}_{\mathit{b}}\times \left({\widehat{x}}_b\times {\widehat{B}}_b\right)$$

(4c)

where the hat “ $\widehat{a}$” indicates the direction of the vector $\mathit{a}$, $\dot{\beta }=\mathrm{acos}\left({\widehat{B}}_{b,x}\right)$, k_p is the gain for the pointing control, and k_i are the gains for the stabilization law. It can be noticed that Equation (4a) is similar to the nadir-pointing control in [29], in which the nadir direction in Equation (4c) is replaced by ${\widehat{B}}_b$ and the damping term, originally given by the B-dot, has been changed to Equation (4b). Equation (4b) corresponds to a rearrangement of the Y-Thompson spin, where the spin axis is ${\widehat{x}}_b$ instead of ${\widehat{y}}_b$ [30]. In this arrangement, a magnetic torque along ${\widehat{x}}_b$ produces damping, which is inversely proportional to the angular displacement between ${\widehat{x}}_b$ and the magnetic field vector, in virtue of $\dot{\beta }=\mathrm{acos}\left({\widehat{B}}_{b,x}\right)$. Differently, the magnetic torques along ${\widehat{y}}_b$ and ${\widehat{z}}_b$ decrease as ${\omega }_x$ reaches the desired value ${\overline{\omega }}_i$ allowing non-zero spin stabilization. It is worth noting that, once solved the attitude determination problem, the same control law Equations (4a)–(4c) can be used to point towards the desired direction $\widehat{r}$, by simply replacing ${\widehat{B}}_b$ with $\widehat{r}$ in Equation (4c). The selection of the control gain represents a rather complex issue for both the control laws Equations (4b) and (4c). In fact, even though higher gains correspond to higher torques, these are typically limited by the threshold value of the magnetic dipole moments, which can be generated by the attitude control system. Some criteria for an optimal selection of these gains, in the presence of different constraints, have been developed [31,32,33].

In Section 4 and Section 5, numerical and HiL simulations are performed to verify the performance and robustness of the attitude determination algorithm.

3. Attitude Determination Algorithm

The design and implementation of the proposed magnetometer-only attitude determination algorithm are hereafter discussed. The spacecraft attitude and angular rates are determined in two different steps, thus limiting the size of the vectors and matrixes computed through the process to 3 × 1 and 3 × 3. All those vector and matrix operations that can be rearranged into the following form, a matrix equation of size 3:

$$U=W{X}^{-1}Y+Z,$$

(5)

can be implemented on FPGA by means of the Faddeev algorithm [34], using a single systolic array architecture. It means that the FPGA area dedicated to the systolic array can be used to calculate the results for any vector or matrix operation expressed in the form of Equation (5), taking advantage of parallel computing and reducing the usage on FPGA, thus increasing the efficiency of the algorithm [35,36,37]. This concept is now applied to implement the attitude determination algorithm.

The three-axis magnetometer operates at a fixed sampling frequency $f_k$, producing the measurement ${\mathit{B}}_{\mathit{b}}^{\left(\mathit{k}\right)}$. The time derivatives of ${\mathit{B}}_{\mathit{b}}$ can be approximated as ${\dot{\mathit{B}}}_{\mathit{b}}^{\left(\mathit{k}\right)}=f_k\left({\mathit{B}}_{\mathit{b}}^{\left(\mathit{k}\right)}-{\mathit{B}}_{\mathit{b}}^{\left(\mathit{k}-\mathbf{1}\right)}\right)$ and, as proved in a previous work by the authors [26], the angular rates can be estimated by processing with a second-order low-pass filter the results from the following equation:

$${\mathit{\omega }}^{\left(\mathit{k}\right)}\approx f_k\frac{{\dot{\mathit{B}}}_{\mathit{b}}^{\left(\mathit{k}\right)}\times {\dot{\mathit{B}}}_{\mathit{b}}^{\left(\mathit{k}-\mathbf{1}\right)}}{{\left|\left|{\dot{\mathit{B}}}_{\mathit{b}}^{\left(\mathit{k}\right)}\right|\right|}^2},$$

(6)

It is worth highlighting that Equation (6) requires three consecutive samplings ${\mathit{B}}_{\mathit{b}}^{\left(\mathit{k}\right)}$; therefore, it produces an estimation of the angular rates with a delay equal to three times the sampling time $\left(3/f_k\right)$. The effect of this delay will be examined in Section 4 and Section 5.

Equation (6) can be rearranged in a form suitable for systolic array implementation, which consists of the determination of the values of matrixes $\mathit{W}$, $\mathit{X}$, $\mathit{Y},$ and $\mathit{Z}$. A solution is given by the following set:

$$\mathit{U}=\mathit{\omega }$$

(7a)

$$\mathit{W}=\left({\dot{\mathit{B}}}_{\mathit{b}}^{\left(\mathit{k}\right)}\times {\dot{\mathit{B}}}_{\mathit{b}}^{\left(\mathit{k}-\mathbf{1}\right)}\right)\left[\begin{array}{ccc}1& 1& 1\end{array}\right]$$

(7b)

$$\mathit{X}={\dot{\mathit{B}}}_{\mathit{b}}^{\left(\mathit{k}\right)}{}^{\mathit{T}}{\dot{\mathit{B}}}_{\mathit{b}}^{\left(\mathit{k}\right)}\mathit{I}$$

(7c)

$$\mathit{Y}=\mathit{I}$$

(7d)

$$\mathit{Z}=\mathbf{0}$$

(7e)

where $\mathit{I}$ and $\mathbf{0}$ indicate the 3 × 3 identities and the 3 × 3 zero matrixes. If the mass distribution of the spacecraft is not spherical, such as in CubeSats, Equation (6) is affected by an error, that resembles a high-frequency noise [26], associated with the nonlinear terms $-\mathit{\omega }\times I\omega$. This can be removed using a second-order Butterworth low-pass filter [35,36], characterized by the following transfer function:

$$H\left(s\right)=\frac{K_0}{{\left(\frac{s}{f_{co}}\right)}^2+1.4142\left(\frac{s}{f_{co}}\right)+1}$$

(8)

where $K_0$ is the filter gain and $f_{co}$ is the cut-off frequency.

The estimated values of the angular rates and a model of the Geomagnetic field are now used to implement the unsymmetrical TRIAD and estimate the attitude matrix $\mathit{A}$. As discussed in Section 1, the TRIAD requires knowledge of at least two vectors in ${\mathcal{F}}_b$ and the corresponding values in ${\mathcal{F}}_i$. Each vector ${\mathit{v}}_{\mathit{b}}$ can be converted to the corresponding ${\mathit{v}}_{\mathit{i}}$ by applying the transformation ${\mathit{v}}_{\mathit{i}}=\mathit{A}{\mathit{v}}_{\mathit{b}}$, where the expression for the rotation matrix $\mathit{A}$ is given below:

$$\mathit{A}=\left[\begin{array}{ccc}\cos \psi \cos \theta & \cos \phi \sin \psi +\cos \psi \sin \phi \sin \theta & \sin \phi \sin \psi -\cos \phi \cos \psi \sin \theta \\ -\cos \theta \sin \psi & \cos \phi \cos \psi -\sin \phi \sin \psi \sin \theta & \cos \psi \sin \phi +\cos \phi \sin \psi \sin \theta \\ \sin \theta & -\cos \theta sin\phi & \cos \phi \cos \theta \end{array}\right],$$

(9)

According to Equation (9), $\mathit{A}$ depends on the Euler angles and; therefore, it changes in time with the attitude of the spacecraft. The value of $\mathit{A}$ is here estimated based on the values of ${\mathit{B}}_{\mathit{b}}^{\left(\mathit{k}\right)}$ which are provided at fixed sampling rates. The value of the attitude matrix is estimated corresponding to each sample k and indicated as ${\mathit{A}}^{\left(\mathit{k}\right)}$. The matrix is assumed constant in the interval between two consecutive samplings.

Based on these considerations, the Geomagnetic field vector and its derivative in the two reference frames can be related by the following equations:

$${\mathit{B}}_{\mathit{i}}^{\left(\mathit{k}\right)}={\mathit{A}}^{\left(\mathit{k}\right)}{\mathit{B}}_{\mathit{b}}^{\left(\mathit{k}\right)}$$

(10a)

$${\dot{{\mathit{B}}_{\mathit{i}}}}^{\left(\mathit{k}\right)}={\mathit{A}}^{\left(\mathit{k}\right)}\left({\dot{{\mathit{B}}_{\mathit{b}}}}^{\left(\mathit{k}\right)}+{\mathit{\omega }}^{\left(\mathit{k}\right)}\times {\mathit{B}}_{\mathit{b}}^{\left(\mathit{k}\right)}\right)$$

(10b)

If the inclination of the orbital plane $i$ and the altitude $h$ of the spacecraft are known, the IGRF model can be used to calculate the Geomagnetic field data to be stored on the OBC [11]. These data are selected and arranged into tables whose first entry is the true anomaly (ϑ) of the satellite (i.e., $\left[{\vartheta }^{\left(k\right)}{B}_{i,x}^{\left(k\right)}{B}_{i,y}^{\left(k\right)}{B}_{i,z}^{\left(k\right)}\right]$). When the satellite passes over the ground station, the value of ϑ at the passage is sent to the satellite and stored by the FPGA, which then propagates it in time. The value of ϑ triggers the reading of the table, producing the vector ${\mathit{B}}_{\mathit{i}}^{\left(\mathit{k}\right)}$. The derivative in time of ${\mathit{B}}_{\mathit{i}}^{\left(\mathit{k}\right)}$ can then be computed as ${\dot{\mathit{B}}}_{\mathit{i}}^{\left(\mathit{k}\right)}=f_k\left({\mathit{B}}_{\mathit{i}}^{\left(\mathit{k}\right)}-{\mathit{B}}_{\mathit{i}}^{\left(\mathit{k}-1\right)}\right)$.

Equation (6) could be used to solve the determination problem; nevertheless, a more accurate expression was developed based on the following result in [26]:

$${\mathit{\omega }}_{\perp }=\frac{{\dot{\mathit{B}}}_{\mathit{b}}\times {\mathit{B}}_{\mathit{b}}}{{\left|\left|{\mathit{B}}_{\mathit{b}}\right|\right|}^2}$$

(11)

The vector product $\mathit{\omega }\times {\mathit{B}}_{\mathit{b}}$ in Equation (10b) can be rearranged as follows:

$$\mathit{\omega }\times {\mathit{B}}_{\mathit{b}}=\Vert \mathit{\omega }\Vert \Vert {\mathit{B}}_{\mathit{b}}\Vert \sin \alpha \widehat{n}$$

where α is the angle between the vectors and $\widehat{n}$ is the direction orthogonal to the plane, which they define. Noting that $\Vert \mathit{\omega }\Vert \sin \alpha$ is the projection of $\mathit{\omega }$ orthogonal to ${\mathit{B}}_{\mathit{b}}$, then ${\mathit{\omega }}_{\perp }=\Vert \mathit{\omega }\Vert \sin \alpha$ and considering Equation (11) it follows that:

$$\mathit{\omega }\times {\mathit{B}}_{\mathit{b}}=\Vert \mathit{\omega }\Vert \Vert {\mathit{B}}_{\mathit{b}}\Vert \sin \alpha \widehat{n}={\mathit{\omega }}_{\perp }\times {\mathit{B}}_{\mathit{b}}=\frac{{\dot{\mathit{B}}}_{\mathit{b}}\times {\mathit{B}}_{\mathit{b}}}{{\left|\left|{\mathit{B}}_{\mathit{b}}\right|\right|}^2}\times {\mathit{B}}_{\mathit{b}}$$

(12)

Using the triple vector product properties $\frac{{\dot{\mathit{B}}}_{\mathit{b}}\times {\mathit{B}}_{\mathit{b}}}{{\left|\left|{\mathit{B}}_{\mathit{b}}\right|\right|}^2}\times {\mathit{B}}_{\mathit{b}}=\frac{\left[-\left({\mathit{B}}_{\mathit{b}}^{\mathit{T}}{\mathit{B}}_{\mathit{b}}\right){\dot{\mathit{B}}}_{\mathit{b}}+\left({\mathit{B}}_{\mathit{b}}^{\mathit{T}}{\dot{\mathit{B}}}_{\mathit{b}}\right){\mathit{B}}_{\mathit{b}}\right]}{{\left|\left|{\mathit{B}}_{\mathit{b}}\right|\right|}^2}=-{\dot{\mathit{B}}}_{\mathit{b}}+\frac{\left({\mathit{B}}_{\mathit{b}}^{\mathit{T}}{\dot{\mathit{B}}}_{\mathit{b}}\right){\mathit{B}}_{\mathit{b}}}{{\left|\left|{\mathit{B}}_{\mathit{b}}\right|\right|}^2}$, then Equation (10b) can be written as:

$$\begin{array}{c}{\dot{{\mathit{B}}_{\mathit{i}}}}^{\left(\mathit{k}\right)}={\mathit{A}}^{\left(\mathit{k}\right)}\left({\dot{{\mathit{B}}_{\mathit{b}}}}^{\left(\mathit{k}\right)}+{\mathit{\omega }}^{\left(\mathit{k}\right)}\times {\mathit{B}}_{\mathit{b}}^{\left(\mathit{k}\right)}\right)={\mathit{A}}^{\left(\mathit{k}\right)}\left({\dot{{\mathit{B}}_{\mathit{b}}}}^{\left(\mathit{k}\right)}-{\dot{{\mathit{B}}_{\mathit{b}}}}^{\left(\mathit{k}\right)}+\frac{{\mathit{B}}_{\mathit{b}}^{\left(\mathit{k}\right)}{\dot{\mathit{B}}}_{\mathit{b}}^{\left(\mathit{k}\right)}{}^{\mathit{T}}{\mathit{B}}_{\mathit{b}}^{\left(\mathit{k}\right)}}{{\left|\left|{\mathit{B}}_{\mathit{b}}^{\left(\mathit{k}\right)}\right|\right|}^2}\right)=\\ ={\mathit{A}}^{\left(\mathit{k}\right)}\left({\widehat{B}}_b^{\left(k\right)}{\dot{\mathit{B}}}_{\mathit{b}}^{\left(\mathit{k}\right)}{}^{\mathit{T}}{\widehat{B}}_b^{\left(k\right)}\right)\end{array}$$

(13)

For the sake of clearness, the following compact notation is introduced:

$$\{\begin{array}{c}{\widehat{b}}_1={\widehat{B}}_{\mathrm{b}}^{\left(k\right)}\\ {\widehat{b}}_2={\widehat{B}}_b^{\left(k\right)}{\widehat{\dot{B}}}_b^{\left(k\right)}{}^T{\widehat{B}}_b^{\left(k\right)}\\ {\widehat{b}}_3={\widehat{b}}_1\times {\widehat{b}}_2\\ {\widehat{b}}_4={\widehat{b}}_1\times {\widehat{b}}_3\end{array}\{\begin{array}{c}\begin{array}{c}{\widehat{r}}_1={\widehat{B}}_i^{\left(k\right)}\\ {\widehat{r}}_2={\widehat{\dot{B}}}_i^{\left(k\right)}\end{array}\\ \begin{array}{c}{\widehat{r}}_3={\widehat{r}}_1\times {\widehat{r}}_2\\ {\widehat{r}}_4={\widehat{r}}_1\times {\widehat{r}}_3\end{array}\end{array}$$

(14)

Based on Equation (14) the attitude matrix at time $k$ can be estimated as follows:

$${\mathit{A}}^{\left(\mathit{k}\right)}=\left[b_1⋮b_3⋮b_4\right]{\left[r_1⋮r_3⋮r_4\right]}^T$$

(15)

Equation (15) is equivalent to the unsymmetrical form of the TRIAD algorithm [10], in which the relative weight of the measurement $b_1$ is higher than that of $b_2$ in the estimation of ${\mathit{A}}^{\left(\mathit{k}\right)}$. This form was preferred because the accuracy on ${\mathit{B}}_{\mathit{b}}^{\left(\mathit{k}\right)}$, measured by on-board sensors, is reasonably higher than that of ${\mathit{\omega }}_{\perp }$, estimated during the process. It can be noticed that the matrix $\left[r_1⋮r_3⋮r_4\right]$ has a unit norm, and its transpose corresponds to the inverse. Therefore, Equation (15) can be set in the form Equation (6) of the Faddeev algorithm and solved through the systolic array architecture:

$$\mathit{U}={\mathit{A}}^{\mathit{k}}$$

(16a)

$$\mathit{W}=\left[b_1⋮b_3⋮b_4\right]$$

(16b)

$$\mathit{X}=\left[r_1⋮r_3⋮r_4\right]$$

(16c)

$$\mathit{Y}=\mathit{I}$$

(16d)

$$\mathit{Z}=\mathbf{0}$$

(16e)

4. Performance and Robustness Analysis

A preliminary analysis of the attitude determination algorithm is performed by numerical simulation on two Test Cases (TC), TC1 and TC2, which differ by the angular rates at the deployment. The simulations are performed considering the properties of the 3U CubeSat Tigrisat, launched by the School of Aerospace Engineering in 2014, with volume $340\times 100\times 100{\mathrm{mm}}^3$ and the total mass $m=4\mathrm{kg}$. The dynamic attitude equations are integrated using Matlab Simulink ode8 fixed-step solver, considering a time step of 1 s and for a total time corresponding to three orbital periods. For each step of the integration, the Geomagnetic field vector ${\mathit{B}}_{\mathit{i}}$ is calculated using the IGRF model and converted to ${\mathit{B}}_{\mathit{b}}$ as ${\mathit{B}}_{\mathit{b}}={\mathit{A}}^{-1}{\mathit{B}}_{\mathit{i}}$ [11].

The inertial properties of the satellite, the orbital elements and the filter and control parameters common to the two test cases are listed in

Table 1. Parameters for the simulations of Test Case 1 and Test Case2.

Moments of Inertia		Orbital Parameters
$I_x\left({\mathrm{kgm}}^2\right)$	0.0065	$h\left(\mathrm{km}\right)$	600
$I_y\left({\mathrm{kgm}}^2\right)$	0.0409	$i(°)$	87
$I_z\left({\mathrm{kgm}}^2\right)$	0.0409	$\mathsf{\Omega }(°)$	0
Coil number of Turns		Coil Area
$N_x$	320	$A_x\left({\mathrm{m}}^2\right)$	0.0032
$N_y$	220	$A_y\left({\mathrm{m}}^2\right)$	0.0149
$N_z$	220	$A_z\left({\mathrm{m}}^2\right)$	0.0149
Control Gains		Filter Cut-off Frequencies
$k_1$	1.8	$f_{co}{}_x\left(\mathrm{Hz}\right)$	0.0218
$k_2$	1	$f_{co}{}_y\left(\mathrm{Hz}\right)$	0.0017
$k_p$	500	$f_{co}{}_z\left(\mathrm{Hz}\right)$	0.0017
Filter Gains		Euler Angles at Deployment
$K_{0,x}$	1	$\phi$	0
$K_{0,y}$	1	$\theta$	0
$K_{0,z}$	1	$\psi$	0
Simulation Parameters
$f_k\left(\mathrm{Hz}\right)$	1
Solver	ODE8
$\mathrm{Total}\mathrm{time}($s$)$	17386
$\overline{{\omega }_x}\left(°/\mathrm{s}\right)$	2.5

, where the total time of the simulation corresponds to three orbital periods. The angular rates at the deployment for the two test cases are shown in

Table 2. Angular rates at deployment for Test Case 1 and Test Case 2.

TC1		TC2
${\omega }_x\left(°/\mathrm{s}\right)$	11	${\omega }_x\left(°/\mathrm{s}\right)$	5
${\omega }_x\left(°/\mathrm{s}\right)$	11	${\omega }_x\left(°/\mathrm{s}\right)$	3
${\omega }_x\left(°/\mathrm{s}\right)$	10	${\omega }_x\left(°/\mathrm{s}\right)$	−3

.

First, TC1 is examined. To investigate the accuracy of the attitude determination algorithm, the Mean Squared Error (MSE) between the actual $\mathit{A}$ and the estimated ${\mathit{A}}^{\mathit{k}}$ is calculated. The actual $\mathit{A}$ is calculated based on the Euler angles calculated during the numerical integration by means of Equation (9). Figure 1 shows that the MSE assumes a final value of 1.172 × 10⁻² end enters the $\pm 10\%$ error band (with respect to the final value) in 16680 s. The figure also reports the MSE calculated for $\mathit{A}$ considering a delay of 5 (dashed line) and 6 (dotted line) seconds. These are calculated comparing, for each sample, the actual $\mathit{A}$ with the same matrix at, respectively, the sample k-5 and k-6. The MSE for the 5 s and 6 s “delayed” $\mathit{A}$ reaches the final value of, respectively, 1.065 × 10⁻² and 1.533 × 10⁻², 10% lower and 23% higher than the MSE for TC1. This result indicates that the process suffers a delay, which is in the range 5–6 s, thus five to six times higher than the simulation time step. Such a process delay arises because both the estimation processes require the same systolic array architecture, and the attitude matrix is calculated after the angular rates, which require three consecutive samples ($3/f_k=3$ s), and filtering to produce the result. The delay is considerably reduced when the algorithm is implemented on real hardware with higher operating and sampling frequency.

For the sake of clarity, the accuracy of the attitude determination is also evaluated by comparing the “actual” Euler angles, resulting from the ODE8 solver to the estimated ones, computed from ${\mathit{A}}^{\mathit{k}}$. The difference between the estimated and the actual (from the integration) Euler angles is shown in Figure 2.

In particular, a highlight of Figure 2 from time 6000 s to the end of the simulation is reported in Figure 3, showing that the estimated $\phi$ and $\theta$ enter the $\pm 10°$ error band but the same is not verified for ψ. The Root Mean Square (RMS) values of the estimation errors for three different time windows are reported in

Table 3. Root Mean Square of attitude estimation errors for Test Case 1.

TC1
Time Window (s)	RMS φ (°)	RMS θ (°)	RMS ψ (°)
0–6000	17.99	22.80	42.62
6000–12,000	7.99	1.95	23.72
12,000–17,386 (end)	4.42	3.97	14.23

.

Figure 4 and Figure 5 show the comparison and the estimation error between the actual angular rates and the estimated ones.

It can be noticed that the angular rate ${\omega }_x$ reaches the target value of 2.5°, while ${\omega }_y$ and ${\omega }_z$ approach zero. The angular rates enter the $\pm 0.2$°/s error band in the times and with the RMS error indicated in

Table 4. Root Mean Square of the angular rates estimation error and settling times for Test Case 1.

TC1
RMS ${\omega }_x\left(°/\mathrm{s}\right)$	0.034	$t_{s,x}\left(\mathrm{s}\right)$	11707
RMS ${\omega }_y\left(°/\mathrm{s}\right)$	0.004	$t_{s,y}\left(\mathrm{s}\right)$	6639
RMS ${\omega }_z\left(°/\mathrm{s}\right)$	0.003	$t_{s,z}\left(\mathrm{s}\right)$	6697

.

Simulations results indicate that the control law Equations (4a)–(4c) is effective in producing the desired attitude, with the x-axis aligning to the Geomagnetic field vector, as shown in Figure 6.

The same analysis is repeated for the TC2, in which the satellite is supposed to be deployed at lower angular rates. The MSE between the actual $\mathit{A}$ and the estimated ${\mathit{A}}^{\left(\mathit{k}\right)}$ are plotted in Figure 7. In TC2, the MSE enters the ±10% error band with respect to the final value of 1.158 × 10⁻² in 12,111 s. The MSE for 5 s and 6 s delays are 1.071 × 10⁻² and 1.539 × 10⁻², respectively, the 8% lower and the 25% higher than the final MSE for TC2. Similar to TC1, this result indicates which the delay process is in the interval 5–6 s.

The estimation errors on the Euler angles show similar behavior in time, as reported in Figure 8, with $\phi$ and $\theta$ entering the ±10° error band in 4740 s and 5367 s, and $\psi$ settling between 10° and 15°. The RMS values for TC2 are reported in

Table 5. Root Mean Square of attitude estimation errors for Test Case 2.

TC2
Time Window (s)	RMS φ (°)	RMS θ (°)	RMS ψ (°)
0–6000	16.70	11.15	26.69
6000–12,000	4.69	5.61	14.41
12,000–17,386 (end)	3.77	4.03	13.76

.

With respect to the angular rates, the target values are reached, and the error band of $\pm 0.2$°/s is entered for all the axes in a time shorter than that for TC1. The results are shown in Figure 9 and in

Table 6. Root Mean Square of the angular rates estimation error and settling times for Test Case 2.

TC2
RMS ${\omega }_x\left(°/\mathrm{s}\right)$	0.014	$t_{s,x}\left(\mathrm{s}\right)$	7175
RMS ${\omega }_y\left(°/\mathrm{s}\right)$	0.001	$t_{s,y}\left(\mathrm{s}\right)$	5550
RMS ${\omega }_z\left(°/\mathrm{s}\right)$	0.002	$t_{s,z}\left(\mathrm{s}\right)$	5584

, including the RMS of angular rates estimation errors after settling time.

To evaluate the robustness of the algorithm, a total of 100 Test Cases (TC) is simulated, selecting random initial conditions for the orbital parameters, initial attitude, and initial angular rates. The values are selected within the following ranges:

$$\mathsf{\Omega },{\varphi }_0\in \left[\begin{array}{cc}-180& 180\end{array}\right]°$$

$$\mathsf{\phi },\mathsf{\theta },\mathsf{\psi }\in \left[\begin{array}{cc}-180& 180\end{array}\right]°$$

$${\mathsf{\omega }}_{\mathrm{x}},{\mathsf{\omega }}_{\mathrm{y}},{\mathsf{\omega }}_{\mathrm{z}}\in \left[\begin{array}{cc}-10& 10\end{array}\right]°$$

$$h\in \left[\begin{array}{cc}400& 700\end{array}\right]\mathrm{km}$$

$$i\in \left[\begin{array}{cc}80& 100\end{array}\right]°$$

There are different altitudes; therefore, the orbital period of the 100 TC will be different, therefore a unique total time for the simulation is selected, and it is set equal to 18,000 s, to be comparable with TC1 and TC2. To ensure that all the simulated TC converge within the mentioned time, the control gains were set to the following values k_p = 400, k₁ = 10, and k₂ = 1. The filter parameters are the same for all the TC and equal to the values reported in Table 1.

The MSE was calculated on ${\mathit{A}}^{\left(\mathit{k}\right)}$ for all the 100 TC, and it settles to a value ranging from 1.856 × 10⁻² to 2.505 × 10⁻², proving that the algorithm is robust with respect to the uncertain initial. For a clearer evaluation of the performance, the mean value for the RMS of the attitude estimation errors over the 100 TC was calculated and are reported in

Table 7. Mean Root Mean Square of the attitude estimation errors for the 100 Test Cases.

100 TC
Time Window (s)	RMS φ (°)	RMS θ (°)	RMS ψ (°)
0–6000	19.79	17.99	34.39
6000–12,000	11.35	9.52	25.07
12,000–18,000 (end)	5.65	6.55	18.06

. The results in the table are in agreement with those evaluated for TC1 and TC2, with the accuracy of attitude determination exceeding the threshold level only for ψ. Angular rates determination is verified as well, registering that all the TC enter the ±0.2°/s error band within 14,902 s. The mean value for the RMS of the angular rates estimation errors was calculated and are reported in

Table 8. Mean Root Mean Square of the angular rates estimation errors for the 100 Test Cases.

100 TC
Time Window (s)	$\mathbf{RMS}{\mathit{\omega }}_{\mathit{x}}(°/\mathbf{s})$	$\mathbf{RMS}{\mathit{\omega }}_{\mathit{x}}(°/\mathbf{s})$	$\mathbf{RMS}{\mathit{\omega }}_{\mathit{x}}(°/\mathbf{s})$
0–6000	1.21	1.49	1.49
6000–12,000	0.16	0.02	0.02
12,000–18,000 (end)	0.14	0.01	0.01

.

Numerical analyses here discussed represent only a preliminary result. The final validation of the algorithm is performed by HiL simulations, discussed in the following section.

5. Implementation of FPGA and Hardware-in-the-Loop Simulations

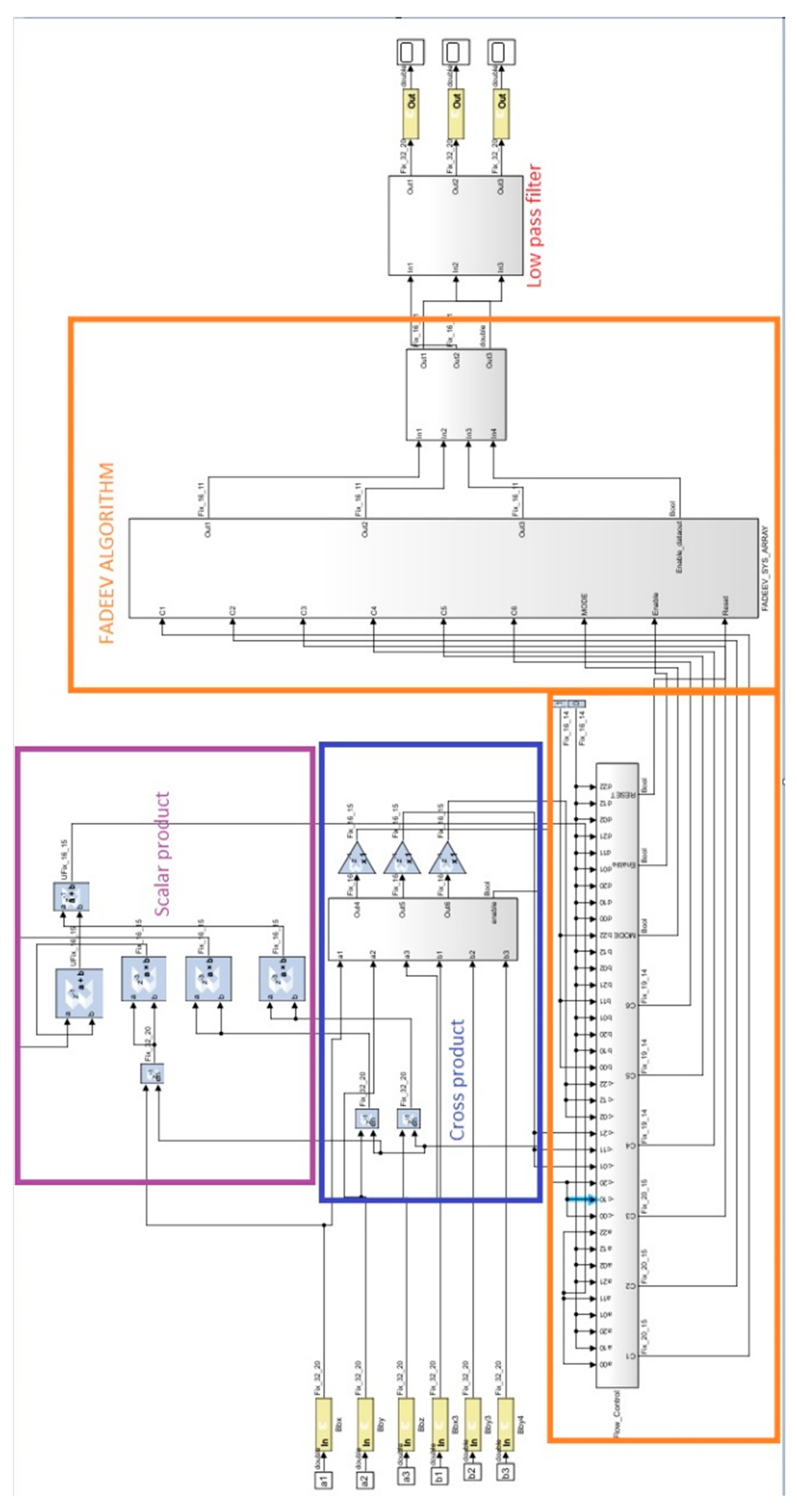
Once validated, the global behavior of the algorithm was implemented on an Artix-7 xc7a50t FPGA, which is a core of the OBC currently under development for STECCO (Space Traveling Egg-Controlled Catadioptric Object), the first PocketQube of the School of Aerospace Engineering. The main blocks of the algorithm are shown in Figure 10.

The Geomagnetic field is simulated using Matlab Simulink and sent to the FPGA for processing them. The Geomagnetic field data were processed to include the quantization error characterizing the 12-bit MEMS three-axis magnetometer and random white noise, considering a standard deviation of 2 × 10⁻⁷ T. The same systolic array architecture is used for both angular rates and attitude estimation, using Equations (7a)–(7d) and (16a)–(16d). The second-order Butterworth low-pass filter was implemented according to [38,39].

When implementing an algorithm on FPGA, its mathematical formulation is converted into several logical operations, which are stored into organized structures called Look Up Tables (LUT) and executed with desired time scheduling, under the control of Flip Flops (FF) [40]. The number of operators that can be stored in the LUT, as well as the total number of LUT and FF, is limited. Therefore, minimizing their utilization is a crucial task, and for this aim, systolic array architecture was considered [28]. It is worth highlighting that, as mentioned before, the use of the same architecture for both attitude matrix and angular rates estimation further increases the efficiency in terms of usage. Similar considerations apply for the total available memory (RAM) and the usage of the Digital Signal Processor, leading the logical process.

The resource utilization for the algorithm implemented on the FGPA is reported in

Table 9. Indicative values of the utilization and power required for the attitude determination algorithm.

Resource	Utilization	% Utilization
Look Up Table	4738	14.53
Flip Flop	2576	3.95
RAM	4.50	6
DSP	30	25
Power [W]	0.277
Digit representation	32-bit Fixed-point
No. clock cycles	53

. One run of the algorithm requires 53 clock cycles, 40 of which are addressed to the systolic array architecture, which, therefore, represents the most computationally demanding section.

The HiL simulations are performed based on the same data used for TC1, reported in Table 1 and Table 2. The high working frequency of the FPGA, equal to 50 MHz, allows reducing both the delay due to the filtering process, corresponding to a few clock cycles (2 × 10⁻⁸ s) and that related to the sampling frequency of the magnetometer, which is here increased to $f_k=100\mathrm{Hz}$, with benefit on the accuracy of the algorithm. In the selection of the sampling frequency, the Nyquist criterion must be considered to avoid aliasing and, therefore, loss of information. In particular, according to Fonod and Gill [33], the sampling frequency can be related to the maximum angular rate expected for the satellite as $f_k\ge \frac{{\omega }^{max}}{\pi }$, a condition which is verified for TC1 and $f_k=100\mathrm{Hz}$. The MSE for TC1 at 100 Hz sampling frequency is represented in Figure 11, finally showing that the impact of process delay is a major cause of the error and that this delay can be reduced to negligible values in real hardware implementation.

It can be noticed that when the algorithm converges, the MSE settles in the range from 1.056 × 10⁻² to 1.1805 × 10⁻², a value included between the MSE calculated for $\mathit{A}$ with 5 × 10⁻² s and 6 × 10⁻² s delay, respectively equal to 1.038 × 10⁻² and 1.2455 × 10⁻². The estimation errors on the Euler angles are shown in Figure 12.

The results obtained from the HiL simulations match those from numerical analysis in Section 4, with $\phi$, $\theta ,$ and $\psi$ entering the ±10° error band in 13,431 s, 12,655 s, and 4775 s. The RMS values of the attitude estimation error are reported in

Table 10. Root Mean Square of the attitude estimation errors for Hardware-in-the-Loop simulation of Test Case 1.

TC1
Time Window (s)	RMS φ (°)	RMS θ (°)	RMS ψ (°)
0–6000	17.99	22.80	23.72
6000–12,000	13.99	11.96	4.23
12,000–17,386 (end)	5.43	3.15	3.71

.

The time behavior of the estimation errors on the angular rates is reported in Figure 13, showing that ${\omega }_x$ reaches the target value of 2.5°, while ${\omega }_y$ and ${\omega }_z$ approach zero. The settling times and the RMS values of the estimation of the angular rates after settling are reported in

Table 11. Root Mean Square of angular rates estimation error and settling times for Hardware-in-the-Loop simulation of Test Case 1.

TC2
RMS ${\omega }_x\left(°/\mathrm{s}\right)$	0.034	$t_{s,x}\left(\mathrm{s}\right)$	7104
RMS ${\omega }_y\left(°/\mathrm{s}\right)$	0.004	$t_{s,y}\left(\mathrm{s}\right)$	7140
RMS ${\omega }_z\left(°/\mathrm{s}\right)$	0.003	$t_{s,z}\left(\mathrm{s}\right)$	7155

.

6. Discussion

After having verified the performance of the algorithm, it is worth to compare it to other magnetometer-only solutions available in the literature [19,20,21,22,23,24,25]. As mentioned in the introduction, these are typically based on the use of a Kalman filter (EKF or UKF) and can provide accuracy as good as 1° and 0.01°/s in the estimation of, respectively, the Euler angles and the angular rates. By comparison with the values reported in Table 10 and Table 11, it can be noticed that the accuracy of KF based algorithms is higher than that of the solution proposed. This result indicates that further investigation should be performed to improve the accuracy of the algorithm, but the output from HiL simulations is promising.

Nevertheless, the attitude matrix and angular rate estimation algorithm discussed here is proposed to be a backup solution to be activated in case of failure of the primary attitude determination system. Therefore, also other features, besides accuracy, should be taken into account to evaluate its suitability. In particular, two aspects are worth to be examined, which are power and area usage. The former should be limited to be compliant with realistic power limitations occurring when a backup mode is required. The latter represents a constraint for the implementation on the FPGA, as discussed in Section 5, and should be minimized. Using systolic array architecture represents our attempt to reduce both power and area usage. This task was achieved by designing the attitude and angular rate estimation algorithm to be implemented in the Faddeev form.

A detailed comparison in terms of power usage between the solution proposed and the KF based algorithms available in the literature would require the implementation of these onto microprocessors, which is beyond the scope of this work. Nevertheless, an estimation of power usage can be provided from the analysis by Mohd et al. [41], evaluating N × N matrix multiplication performance on FPGA, using a systolic array, and on two microprocessors. A comparison between the power usage by the two devices in terms of the size N of the matrix is reported in

Table 12. Comparison of the power usage between FPGA and microprocessor [41].

Matrix Size	Power Usage (mW)
	FPGA	Microprocessor
2 × 2	237.05	794.24
4 × 4	287.70	791.43
8 × 8	290.27	788.36
16 × 16	293.53	840.42

, considering the lowest value between the two microprocessors.

It can be noticed that the estimated power usage from the algorithm proposed, implementing 3 × 3 matrix operations, is equal to 277 mW, a value compatible with those in Table 12. If referring to the methods [20,21,22,23,24,25], the matrix size ranges from 6 × 6 to 9 × 9; therefore, their power usage can be estimated to approximately 2.7 times higher.

Recalling that the comparative analysis presented in this section represents only a preliminary result, it indicates that the attitude matrix and angular rate estimation strategy proposed can be a suitable option when the use of FPGA based OBC is preferred and lower accuracy can be accepted for the benefit of lower power usage.

7. Conclusions

We proposed a magnetometer-only attitude determination strategy tailored for implementation on the FPGA core of an OBC, using systolic array architecture to enhance the efficiency of the algorithm. The determination algorithm is aimed to be a backup solution in case of failure of the primary determination system.

The algorithm provides results with accuracy of $\pm 0.2°$/s on the angular rates and of $\pm 10$° on the Euler angles. The numerical analyses and HiL simulations indicate that the algorithm suffers some processing delay, introduced by the filtering process, and by the sampling frequency of the magnetometer. This delay reduces as the operating frequency of the FPGA and, especially, the sampling frequency of the magnetometer increase. Simulations performed considering a MEMS three-axis magnetometer with sampling frequency as high as 100 Hz and an FPGA running at 50 MHz, indicate that the processing delay can be reduced to 50–60 milliseconds.

Despite being compatible with several small satellite missions and applications, the algorithm proposed is less accurate than other magnetometer-only methods available in the literature. Nevertheless, its lower power usage can represent an advantage for some critical scenarios. Furthermore, the low resources required and the use of systolic array architecture allows implementing the algorithm on the OBC at minimal area usage, resulting in a suitable and versatile solution for the use in small satellite missions.