Beyond Contrail Avoidance: Efficacy of Flight Altitude Changes to Minimise Contrail Climate Forcing
Abstract
:1. Introduction
2. Data and Methodology
2.1. Aircraft Activity and Emissions
2.2. Contrail Simulation and Uncertainty
2.3. Climate Forcing of Contrails and CO2
2.4. Contrail Mitigation
2.5. Loss of Separation
3. Results and Discussion
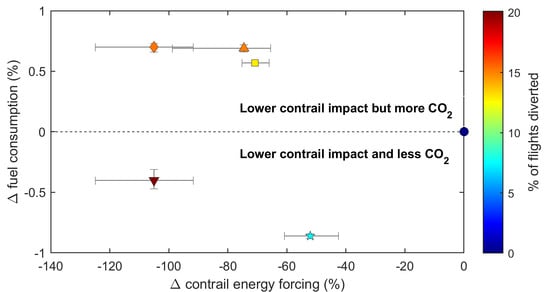
3.1. Efficacy of Flight Altitude Changes
3.1.1. Contrail Avoidance
3.1.2. Minimum Contrail RF’
3.1.3. Minimum EFcontrail
3.1.4. Minimum EFcontrail with No Fuel Penalty
3.1.5. Minimum EFtotal
3.2. Loss of Separation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kärcher, B.; Kleine, J.; Sauer, D.; Voigt, C. Contrail formation: Analysis of sublimation mechanisms. Geophys. Res. Lett. 2018, 45, 13547–13552. [Google Scholar] [CrossRef]
- Schumann, U. Formation, properties and climatic effects of contrails. Comptes Rendus Phys. 2005, 6, 549–565. [Google Scholar] [CrossRef]
- Schumann, U. On conditions for contrail formation from aircraft exhausts. Meteorol. Z. 1996, 5, 4–23. [Google Scholar] [CrossRef]
- Kärcher, B.; Yu, F. Role of aircraft soot emissions in contrail formation. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef] [Green Version]
- Schumann, U. A contrail cirrus prediction model. Geosci. Model Dev. 2012, 5, 543–580. [Google Scholar] [CrossRef] [Green Version]
- Kärcher, B. The importance of contrail ice formation for mitigating the climate impact of aviation. J. Geophys. Res. Atmos. 2016, 121, 3497–3505. [Google Scholar] [CrossRef] [Green Version]
- Jensen, E.; Toon, O.B.; Kinne, S.; Sachse, G.W.; Anderson, B.E.; Chan, K.R.; Twohy, C.H.; Gandrud, B.; Heymsfield, A.; Miake-Lye, R.C. Environmental conditions required for contrail formation and persistence. J. Geophys. Res. Space Phys. 1998, 103, 3929–3936. [Google Scholar] [CrossRef]
- Kärcher, B. Formation and radiative forcing of contrail cirrus. Nat. Commun. 2018, 9, 1824. [Google Scholar] [CrossRef] [PubMed]
- Vazquez-Navarro, M.; Mannstein, H.; Kox, S. Contrail life cycle and properties from 1 year of MSG/SEVIRI rapid-scan images. Atmos. Chem. Phys. 2015, 15, 8739–8749. [Google Scholar] [CrossRef] [Green Version]
- Schumann, U.; Graf, K.; Mannstein, H.; Mayer, B. Contrails: Visible aviation induced climate impact. In Atmospheric Physics; Springer: Berlin/Heidelberg, Germany, 2012; pp. 239–257. [Google Scholar] [CrossRef]
- Irvine, E.; Hoskins, B.J.; Shine, K.P. A simple framework for assessing the trade-off between the climate impact of aviation carbon dioxide emissions and contrails for a single flight. Environ. Res. Lett. 2014, 9, 064021. [Google Scholar] [CrossRef]
- Burkhardt, U.; Kärcher, B. Global radiative forcing from contrail cirrus. Nat. Clim. Chang. 2011, 1, 54–58. [Google Scholar] [CrossRef] [Green Version]
- Mannstein, H.; Schumann, U. Aircraft induced contrail cirrus over Europe. Meteorol. Z. 2005, 14, 549–554. [Google Scholar] [CrossRef] [Green Version]
- Duda, D.P.; Minnis, P.; Nguyen, L. Estimates of cloud radiative forcing in contrail clusters using GOES imagery. J. Geophys. Res. Space Phys. 2001, 106, 4927–4937. [Google Scholar] [CrossRef]
- Schumann, U.; Mayer, B.; Graf, K.; Mannstein, H. A parametric radiative forcing model for contrail cirrus. J. Appl. Meteorol. Clim. 2012, 51, 1391–1406. [Google Scholar] [CrossRef] [Green Version]
- Fuglestvedt, J.S.; Shine, K.P.; Berntsen, T.; Cook, J.; Lee, D.; Stenke, A.; Skeie, R.; Velders, G.J.M.; Waitz, I. Transport impacts on atmosphere and climate: Metrics. Atmos. Environ. 2010, 44, 4648–4677. [Google Scholar] [CrossRef] [Green Version]
- Meerkötter, R.; Schumann, U.; Doelling, D.R.; Minnis, P.; Nakajima, T.; Tsushima, Y. Radiative forcing by contrails. Ann. Geophys. 1999, 17, 1080–1094. [Google Scholar] [CrossRef]
- Schumann, U.; Graf, K. Aviation-induced cirrus and radiation changes at diurnal timescales. J. Geophys. Res. Atmos. 2013, 118, 2404–2421. [Google Scholar] [CrossRef] [Green Version]
- Newinger, C.; Burkhardt, U. Sensitivity of contrail cirrus radiative forcing to air traffic scheduling. J. Geophys. Res. Space Phys. 2012, 117, D10205. [Google Scholar] [CrossRef] [Green Version]
- Bock, L.; Burkhardt, U. The temporal evolution of a long-lived contrail cirrus cluster: Simulations with a global climate model. J. Geophys. Res. Atmos. 2016, 121, 3548–3565. [Google Scholar] [CrossRef] [Green Version]
- Schumann, U.; Penner, J.E.; Chen, Y.; Zhou, C.; Graf, K. Dehydration effects from contrails in a coupled contrail–climate model. Atmos. Chem. Phys. 2015, 15, 11179–11199. [Google Scholar] [CrossRef] [Green Version]
- Lee, D.; Pitari, G.; Grewe, V.; Gierens, K.; Penner, J.; Petzold, A.; Prather, M.; Schumann, U.; Bais, A.; Berntsen, T.; et al. Transport impacts on atmosphere and climate: Aviation. Atmos. Environ. 2010, 44, 4678–4734. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schumann, U.; Graf, K.; Mannstein, H. Potential to reduce the climate impact of aviation by flight level changes. AIAA paper 2011, 3376, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.-C.; Gettelman, A. Simulated radiative forcing from contrails and contrail cirrus. Atmos. Chem. Phys. 2013, 13, 12525–12536. [Google Scholar] [CrossRef] [Green Version]
- Yi, B.; Yang, P.; Liou, K.-N.; Minnis, P.; Penner, J.E. Simulation of the global contrail radiative forcing: A sensitivity analysis. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef] [Green Version]
- Minnis, P.; Palikonda, R.; Walter, B.J.; Ayers, J.K.; Mannstein, H. Contrail properties over the eastern North Pacific from AVHRR data. Meteorol. Z. 2005, 14, 515–523. [Google Scholar] [CrossRef]
- Schumann, U.; Heymsfield, A.J. On the life cycle of individual contrails and contrail cirrus. Meteorol. Monogr. 2017, 58, 3.1–3.24. [Google Scholar] [CrossRef]
- Teoh, R.; Schumann, U.; Majumdar, A.; Stettler, M.E. Mitigating the climate forcing of aircraft contrails by small-scale diversions and technology adoption. Environ. Sci. Technol. 2020, 54, 2941–2950. [Google Scholar] [CrossRef]
- Boies, A.M.; Stettler, M.E.J.; Swanson, J.J.; Johnson, T.J.; Olfert, J.; Johnson, M.; Eggersdorfer, M.L.; Rindlisbacher, T.; Wang, J.; Thomson, K.; et al. Particle emission characteristics of a gas turbine with a double annular combustor. Aerosol Sci. Technol. 2015, 49, 842–855. [Google Scholar] [CrossRef] [Green Version]
- Stickles, R.; Barrett, J. TAPS II Combustor Final Report. CLEEN Program; Federal Aviation Administration (FAA): Washington, DC, USA, 2013. [Google Scholar]
- Lobo, P.; Durdina, L.; Smallwood, G.J.; Rindlisbacher, T.; Siegerist, F.; Black, E.A.; Yu, Z.; Mensah, A.A.; Hagen, D.E.; Miake-Lye, R.C.; et al. Measurement of aircraft engine non-volatile pm emissions: Results of the aviation-particle regulatory instrumentation demonstration experiment (A-PRIDE) 4 campaign. Aerosol Sci. Technol. 2015, 49, 472–484. [Google Scholar] [CrossRef] [Green Version]
- Moore, R.; Thornhill, K.L.; Weinzierl, B.; Sauer, D.; D’Ascoli, E.; Kim, J.; Lichtenstern, M.; Scheibe, M.; Beaton, B.; Beyersdorf, A.J.; et al. Biofuel blending reduces particle emissions from aircraft engines at cruise conditions. Nature 2017, 543, 411–415. [Google Scholar] [CrossRef] [Green Version]
- Twomey, S. Pollution and the planetary albedo. Atmos. Environ. (1967) 1974, 8, 1251–1256. [Google Scholar] [CrossRef]
- Howe, S.; Kolios, A.; Brennan, F.P. Environmental life cycle assessment of commercial passenger jet airliners. Transp. Res. Part D Transp. Environ. 2013, 19, 34–41. [Google Scholar] [CrossRef]
- Dray, L.; Evans, A.; Reynolds, T.; Schäfer, A.W.; Vera-Morales, M.; Bosbach, W. Airline fleet replacement funded by a carbon tax: An integrated assessment. Transp. Policy 2014, 34, 75–84. [Google Scholar] [CrossRef]
- Chereau, D.; Kleffmann, K.; Callan, P. Dossier: Fuel for Thought | Airlines. Available online: https://airlines.iata.org/analysis/dossier-fuel-for-thought (accessed on 20 December 2019).
- Schäfer, A.W.; Waitz, I.A. Air transportation and the environment. Transp. Policy 2014, 34, 1–4. [Google Scholar] [CrossRef]
- Bock, L.; Burkhardt, U. Contrail cirrus radiative forcing for future air traffic. Atmos. Chem. Phys. 2019, 19, 8163–8174. [Google Scholar] [CrossRef] [Green Version]
- Caiazzo, F.; Agarwal, A.; Speth, R.L.; Barrett, S.R. Impact of biofuels on contrail warming. Environ. Res. Lett. 2017, 12, 114013. [Google Scholar] [CrossRef]
- Gierens, K.; Spichtinger, P. On the size distribution of ice-supersaturated regions in the upper troposphere and lowermost stratosphere. Ann. Geophys. 2000, 18, 499–504. [Google Scholar] [CrossRef]
- Spichtinger, P.; Gierens, K.; Leiterer, U.; Dier, H. Ice supersaturation in the tropopause region over Lindenberg, Germany. Meteorol. Z. 2003, 12, 143–156. [Google Scholar] [CrossRef]
- Dickson, N.C.; Gierens, K.M.; Rogers, H.L.; Jones, R.L. Probabilistic description of ice-supersaturated layers in low resolution profiles of relative humidity. Atmos. Chem. Phys. 2010, 10, 6749–6763. [Google Scholar] [CrossRef]
- Lim, Y.; Gardi, A.G.M.; Sabatini, R. Optimal aircraft trajectories to minimize the radiative impact of contrails and CO 2. Energy Procedia 2017, 110, 446–452. [Google Scholar] [CrossRef]
- Mannstein, H.; Spichtinger, P.; Gierens, K. A note on how to avoid contrail cirrus. Transp. Res. Part D Transp. Environ. 2005, 10, 421–426. [Google Scholar] [CrossRef]
- Williams, V.; Noland, R.B. Variability of contrail formation conditions and the implications for policies to reduce the climate impacts of aviation. Transp. Res. Part D Transp. Environ. 2005, 10, 269–280. [Google Scholar] [CrossRef]
- Avila, D.; Sherry, L.; Thompson, T. Reducing global warming by airline contrail avoidance: A case study of annual benefits for the contiguous United States. Transp. Res. Interdiscip. Perspect. 2019, 2, 100033. [Google Scholar] [CrossRef]
- Yin, F.; Grewe, V.; Frömming, C.; Yamashita, H. Impact on flight trajectory characteristics when avoiding the formation of persistent contrails for transatlantic flights. Transp. Res. Part D Transp. Environ. 2018, 65, 466–484. [Google Scholar] [CrossRef]
- Grewe, V.; Matthes, S.; Frömming, C.; Brinkop, S.; Jöckel, P.; Gierens, K.; Champougny, T.; Fuglestvedt, J.; Haslerud, A.; Irvine, E.; et al. Feasibility of climate-optimized air traffic routing for trans-Atlantic flights. Environ. Res. Lett. 2017, 12, 034003. [Google Scholar] [CrossRef]
- Rosenow, J.; Fricke, H.; Luchkova, T.; Schultz, M. Minimizing contrail formation by rerouting around dynamic ice-supersaturated regions. Aeronaut. Aerosp. Open Access J. 2018, 2, 1. [Google Scholar] [CrossRef] [Green Version]
- Filippone, A. Assessment of aircraft contrail avoidance strategies. J. Aircr. 2015, 52, 872–877. [Google Scholar] [CrossRef]
- Matthes, S.; Schumann, U.; Grewe, V.; Frömming, C.; Dahlmann, K.; Koch, A.; Mannstein, H. Climate Optimized Air Transport; Springer: Berlin/Heidelberg, Germany, 2012; pp. 727–746. [Google Scholar] [CrossRef]
- Myhre, G.; Stordal, F. On the tradeoff of the solar and thermal infrared radiative impact of contrails. Geophys. Res. Lett. 2001, 28, 3119–3122. [Google Scholar] [CrossRef]
- Stuber, N.; Forster, P.M.; Rädel, G.; Shine, K.P. The importance of the diurnal and annual cycle of air traffic for contrail radiative forcing. Nature 2006, 441, 864–867. [Google Scholar] [CrossRef]
- Stettler, M.E.; Eastham, S.; Barrett, S.R. Air quality and public health impacts of UK airports. Part I: Emissions. Atmos. Environ. 2011, 45, 5415–5424. [Google Scholar] [CrossRef]
- Nuic, A. User Manual for the Base of Aircraft Data (BADA) Revision 3.12.; Eurocontrol Experimental Centre: Les Bordes, France, 2014; Volume EEC. [Google Scholar]
- Schumann, U. Influence of propulsion efficiency on contrail formation. Aerosp. Sci. Technol. 2000, 4, 391–401. [Google Scholar] [CrossRef] [Green Version]
- Teoh, R.; Stettler, M.E.; Majumdar, A.; Schumann, U.; Graves, B.; Boies, A.M. A methodology to relate black carbon particle number and mass emissions. J. Aerosol Sci. 2019, 132, 44–59. [Google Scholar] [CrossRef]
- Jeßberger, P.; Voigt, C.; Schumann, U.; Sölch, I.; Schlager, H.; Kaufmann, S.; Petzold, A.; Schäuble, D.; Gayet, J.-F. Aircraft type influence on contrail properties. Atmos. Chem. Phys. 2013, 13, 11965–11984. [Google Scholar] [CrossRef] [Green Version]
- Schumann, U.; Jeßberger, P.; Voigt, C. Contrail ice particles in aircraft wakes and their climatic importance. Geophys. Res. Lett. 2013, 40, 2867–2872. [Google Scholar] [CrossRef]
- Schumann, U.; Baumann, R.; Baumgardner, D.; Bedka, S.T.; Duda, D.P.; Freudenthaler, V.; Gayet, J.-F.; Heymsfield, A.J.; Minnis, P.; Quante, M.; et al. Properties of individual contrails: A compilation of observations and some comparisons. Atmospheric Chem. Phys. 2017, 17, 403–438. [Google Scholar] [CrossRef] [Green Version]
- Voigt, C.; Schumann, U.; Jurkat, T.; Schäuble, D.; Schlager, H.; Petzold, A.; Gayet, J.-F.; Krämer, M.; Schneider, J.; Borrmann, S.; et al. In-situ observations of young contrails—Overview and selected results from the CONCERT campaign. Atmos. Chem. Phys. 2010, 10, 9039–9056. [Google Scholar] [CrossRef] [Green Version]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- ECMWF. Forecast User Guide—5.1 Generation of the Ensemble, Ensemble of Data Assimilations (EDA). Available online: https://confluence.ecmwf.int/display/FUG/Ensemble+of+Data+Assimilations+-+EDA (accessed on 7 August 2020).
- Gounou, A.; Hogan, R.J. A sensitivity study of the effect of horizontal photon transport on the radiative forcing of contrails. J. Atmos. Sci. 2007, 64, 1706–1716. [Google Scholar] [CrossRef] [Green Version]
- Forster, L.; Emde, C.; Mayer, B.; Unterstrasser, S. Effects of three-dimensional photon transport on the radiative forcing of realistic contrails. J. Atmos. Sci. 2012, 69, 2243–2255. [Google Scholar] [CrossRef] [Green Version]
- Rosenow, J.; Fricke, H. Individual condensation trails in aircraft trajectory optimization. Sustainability 2019, 11, 6082. [Google Scholar] [CrossRef] [Green Version]
- Bickel, M.; Ponater, M.; Bock, L.; Burkhardt, U.; Reineke, S. Estimating the effective radiative forcing of contrail cirrus. J. Clim. 2020, 33, 1991–2005. [Google Scholar] [CrossRef] [Green Version]
- Joos, F.; Roth, R.; Fuglestvedt, J.S.; Peters, G.G.; Enting, I.G.; Von Bloh, W.; Brovkin, V.; Burke, E.J.; Eby, M.; Edwards, N.R.; et al. Carbon dioxide and climate impulse response functions for the computation of greenhouse gas metrics: A multi-model analysis. Atmos. Chem. Phys. 2013, 13, 2793–2825. [Google Scholar] [CrossRef] [Green Version]
- Wilkerson, J.; Jacobson, M.Z.; Malwitz, A.; Balasubramanian, S.; Wayson, R.; Fleming, G.; Naiman, A.D.; Lele, S.K. Analysis of emission data from global commercial aviation: 2004 and 2006. Atmos. Chem. Phys. 2010, 10, 6391–6408. [Google Scholar] [CrossRef] [Green Version]
- NASA. By the Numbers | Earth—NASA Solar System Exploration. Available online: https://solarsystem.nasa.gov/planets/earth/by-the-numbers/ (accessed on 27 November 2019).
- Nuic, A.; Poles, D.; Mouillet, V. BADA: An advanced aircraft performance model for present and future ATM systems. Int. J. Adapt. Control. Signal Process. 2010, 24, 850–866. [Google Scholar] [CrossRef]
- Poll, D.; Schumann, U. An estimation method for the fuel burn and other performance characteristics of civil transport aircraft in the cruise. Part 1 fundamental quantities and governing relations for a general atmosphere. Aeronaut. J. 2020, 1–39. [Google Scholar] [CrossRef]
- Eurocontrol. BADA, ATM’s Most Comprehensive Aircraft Performance Model, Just Got Even Better | EUROCONTROL. Available online: https://www.eurocontrol.int/news/bada-atms-most-comprehensive-aircraft-performance-model-just-got-even-better (accessed on 27 July 2020).
- Tobaruela, G.; Schuster, W.; Majumdar, A.; Ochieng, W.Y.; Martínez, L.; Hendrickx, P. A method to estimate air traffic controller mental workload based on traffic clearances. J. Air Transp. Manag. 2014, 39, 59–71. [Google Scholar] [CrossRef]
- ICAO. Air Traffic Management—Procedures for Air Navigation Services, 16th ed.; International Civil Aviation Organisation: Montreal, QC, Canada, 2016; Volume Doc 4444. [Google Scholar]
- Tobaruela, G. A Framework to Assess the Ability of Automation to Deliver Capacity Targets in European Airspace; Center for Transport Studies; Imperial College London: London, UK, 2015. [Google Scholar]
- Graf, K.; Schumann, U.; Mannstein, H.; Mayer, B. Aviation induced diurnal North Atlantic cirrus cover cycle. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef] [Green Version]
- Haywood, J.; Allan, R.P.; Bornemann, J.; Forster, P.M.; Francis, P.N.; Milton, S.; Rädel, G.; Rap, A.; Shine, K.P.; Thorpe, R. A case study of the radiative forcing of persistent contrails evolving into contrail-induced cirrus. J. Geophys. Res. Space Phys. 2009, 114, 114. [Google Scholar] [CrossRef] [Green Version]
- Schumann, U.; Mayer, B. Sensitivity of surface temperature to radiative forcing by contrail cirrus in a radiative-mixing model. Atmos. Chem. Phys. 2017, 17, 13833–13848. [Google Scholar] [CrossRef] [Green Version]
- Klein, A.; Kavoussi, S.; Lee, R.S. Weather Forecast Accuracy: Study of Impact on Airport Capacity and Estimation of Avoidable Costs. In Proceedings of the Eighth USA/Europe Air Traffic Management Research and Development Seminar, Napa, CA, USA, 29 June–2 July 2009. [Google Scholar]
- Krozel, J.; Mitchell, J.; Polishchuk, V.; Prete, J. Capacity Estimation for Airspaces with Convective Weather Constraints. In Guidance, Navigation, and Control Conference; American Institute of Aeronautics and Astronautics (AIAA): Reston, VA, USA, 2007; p. 6451. [Google Scholar]
- Federal Aviation Administration. Modernization of U.S. Airspace. Available online: https://www.faa.gov/nextgen/ (accessed on 7 August 2020).
- SESAR. Delivering the Single European Sky—Environmental Benefits. Available online: http://www.sesarju.eu/node/718 (accessed on 7 August 2020).



| Initial Contrail Length (109 m) | Mean Contrail Segment Age (h) | Mean Contrail RF’ (W m−2) | EFcontrail (1018 J) | Total Fuel Consumption, TFC a (108 kg) | a,b (1018 J) | EFtotal b (1018 J; Contrails + CO2) | ||
| Baseline Scenario | 6.933 [6.813, 7.312] | 4.373 [4.126, 4.629] | 1.420 [0.940, 2.200] | 5.753 [4.119, 8.449] | 2.90716 [2.90710, 2.90721] | 3.4277 [1.7187, 5.0480] | 9.037 [6.468, 12.280] | |
| % of Flights Diverted | Percentage Difference Relative to the Baseline Scenario | |||||||
| Initial Contrail Length | Mean Contrail Segment Age | Mean Contrail RF’ | EFcontrail | Total Fuel Consumption, TFC | b | EFtotal b | ||
| Min. Contrail Length | 12.9% [12.8, 13.2%] | −66.6% [−67.0, −65.8%] | −3.61% [−5.54, −0.59%] | −29.2% [−63.2, −12.4%] | −70.8% [−75.3, −66.0%] | +0.57% [+0.55, +0.59%] | +0.24% [+0.23, +0.24%] | −45.0% [−55.9, −38.6%] |
| Min. Contrail RF’ | 15.0% [14.7, 15.3%] | −17.3% [−20.3, −13.5%] | −9.05% [−10.6, −7.21%] | −186% [−282, −122%] | −74.6% [−89.6, −65.4%] | +0.69% [+0.66, +0.72%] | +0.28% [+0.27, +0.30%] | −47.2% [−59.0, −40.5%] |
| Min. EFcontrail | 15.3% [15.0, 15.7%] | −23.1% [−27.6, −17.4%] | −13.9% [−16.4, −11.4%] | −185% [−279, −121%] | −105% [−125, −91.8%] | +0.70% [+0.66, 0.73%] | +0.29% [+0.27, +0.30%] | −66.7% [−83.7, −57.2%] |
| Min. EFcontrail (No Fuel Penalty) | 7.63% [7.47, 7.81%] | −8.64% [−10.7, −6.66%] | −4.90% [−6.06, −4.20%] | −75.7% [−119, −46.1%] | −52.1% [−60.8, −42.5%] | −0.86% [−0.88, −0.84%] | −0.36% [+0.27, +0.30%] | −32.4% [−41.7, −27.4%] |
| Min. EFtotal (CO2 + Contrail) | 20.1% [19.9, 20.3%] | −23.2% [−27.7, −17.4%] | −13.7% [−16.3, −11.3%] | −183% [−275, −120%] | −105% [−125, −91.8%] | −0.40% [−0.47, −0.31%] | −0.17% [−0.20, −0.13%] | −66.8% [−83.9, −57.4%] |
| Strategy | Total (and %) of Flights Diverted | Total No. of Aircraft Pairs in Conflict | Total No. of Flights in Conflict | Ratio of Flights in Conflict to the Total No. of Flights Diverted (%) |
|---|---|---|---|---|
| Small-scale diversions [28] | 2196 (1.47%) | 169 | 304 | 13.8% |
| Min EFcontrail | 22696 (15.2%) | 1181 | 2056 | 9.06% |
| Min EFcontrail (no fuel penalty) | 11386 (7.63%) | 678 | 1222 | 10.7% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teoh, R.; Schumann, U.; Stettler, M.E.J. Beyond Contrail Avoidance: Efficacy of Flight Altitude Changes to Minimise Contrail Climate Forcing. Aerospace 2020, 7, 121. https://doi.org/10.3390/aerospace7090121
Teoh R, Schumann U, Stettler MEJ. Beyond Contrail Avoidance: Efficacy of Flight Altitude Changes to Minimise Contrail Climate Forcing. Aerospace. 2020; 7(9):121. https://doi.org/10.3390/aerospace7090121
Chicago/Turabian StyleTeoh, Roger, Ulrich Schumann, and Marc E. J. Stettler. 2020. "Beyond Contrail Avoidance: Efficacy of Flight Altitude Changes to Minimise Contrail Climate Forcing" Aerospace 7, no. 9: 121. https://doi.org/10.3390/aerospace7090121
APA StyleTeoh, R., Schumann, U., & Stettler, M. E. J. (2020). Beyond Contrail Avoidance: Efficacy of Flight Altitude Changes to Minimise Contrail Climate Forcing. Aerospace, 7(9), 121. https://doi.org/10.3390/aerospace7090121