Mathematical Modelling of Gimballed Tilt-Rotors for Real-Time Flight Simulation
Abstract
:1. Introduction
1.1. Motivation for Research
1.2. Tilt-Rotor Real-Time Simulation
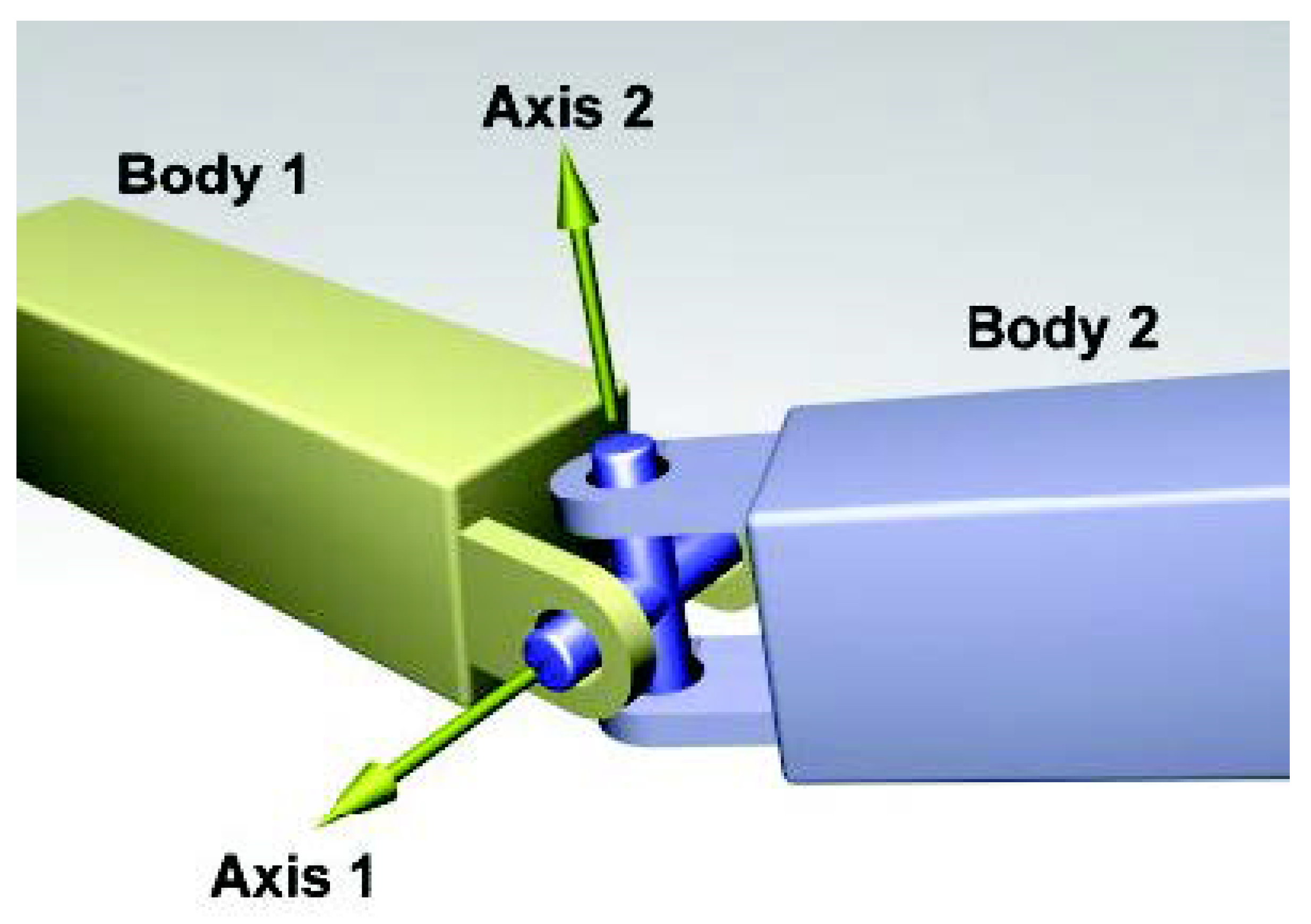
1.3. Gimballed Proprotors
2. Mathematical Model
2.1. Reference Frames
- Hub
- —Fixed, centered in the rotor hub, with:
- in the hub plane and positive forward;
- in the hub plane and positive outboard (starboard for the right rotor, port for the left rotor);
- perpendicular to the hub plane and positive downwards.
- Rotating
- —Centered in the rotor hub, rotating with angular speed equal to , and having:
- coincident with the projection of the blade axis on the hub plane and positive outwards;
- perpendicular to the hub plane and positive upwards;
- perpendicular to and (hence positive in the blade advancing direction).
- Tip-path-plane (TPP)
- —Centered in the rotor hub, rotating about with angular speed equal to ; its axes are:
- coincident with (perpendicular to the blade and positive in its advancing direction);
- perpendicular to the rotor tip-path-plane and positive upwards.
- perpendicular to and ;
- Blade
- —Centered in the blade flapping hinge, rotating with angular speed equal to ; its axes are:
- coincident with the blade axis and positive from the flapping hinge to the blade tip;
- coincident with and (perpendicular to the blade and positive in its advancing direction);
- perpendicular to and .
- From Blade system to TPP system:where both and are positive when the blade flaps upwards.
- From TPP system to Rotating system:
- From Rotating system to Hub system:where is the blade azimuth angle, that is, the angle between and the negative direction of , and is positive according to the direction of the rotor angular speed (counter-clockwise for the right rotor, clockwise for the left rotor).
2.2. Blade Position, Speed and Acceleration
- Relative speed of S with respect to the TPP system, due to blade rotation around the flapping hinge:
- Linear speed of the origin of the TPP system (due to aircraft motion):
- Tangential speed owing to reference frame rotation, which in turn is due to aircraft motion, gimbal motion and rotor spinning:where:
- relative acceleration of S (due to blade flapping) with respect to the TPP system, which in turn comprises a tangential and a centrifugal component:
- linear acceleration of the origin of the TPP system (due to aircraft motion):
- tangential acceleration owing to angular acceleration of the TPP reference frame:where:
- centrifugal acceleration, due to rotation of the TPP reference frame:
- Coriolis acceleration:
2.3. Rotor Aerodynamics
- is the twist angle, function of the position along ;
- , and are, respectively, the collective pitch, the lateral and the longitudinal cyclic;
- , being the pitch-flap coupling angle;
- is the zero-lift angle of attack;
- is the inflow angle.
- blade motion ;
- rotor inflow speedin which the three inflow states , and can be computed according to Pitt-Peters dynamic Model as described in Reference [19].
2.4. Aerodynamic Forces and Moments
- aerodynamic force along :
- aerodynamic force along :
- aerodynamic moment around :
- aerodynamic moment :
Airfoil Aerodynamic Coefficients
- The airfoil lift and drag coefficients are expressed by tables that are function of the angle of attack while for ranges of angle of attack outside available data the approximation proposed by Hoerner in Reference [20] is used:where the coefficients and are tuned to match the reference data in Reference [21].
- The missing portions of the polar curves are determined using Equation (46), and introducing corrections in order to best fit the available aerodynamic data.
- The derivatives of the aerodynamic coefficients with respect to the angle of attack ( and ) are computed using the centred difference method:
2.5. Flapping Dynamics Model for Gimballed Rotors
- The flapping angle of each blade is computed by adding to the gimbal attitude, , another contribution , representing the variations of flapping angle in each of the N blades due to the blade flexibility or to a coning hinge:
- The gimbal plane is assumed to be parallel to the rotor tip-path-plane, hence:
- the angles and in Equation (49) are the lateral and longitudinal attitudes of the TPP and are obtained using the multi-blade coordinate transformation (MBC) truncated to the first order, therefore
- m, c and are
- k contains the contributions of aerodynamic and inertial loads to system stiffness:In a generic flight condition, k, c and are in general different for each blade.
- takes into account the system structural damping. As evaluating the structural damping is extremely difficult, it is a common practice to express this term as a function of other system parameters. In the present model, has been expressed as a function of the viscous equivalent critical damping ratio, following the formulation proposed in Reference [22]:
- contains the contributions to system stiffness dependent on :where is the torsional stiffness of the gimbal joint and is z-component of acceleration seen by the blade due to the gimbal motion, function of the angular speed of the rotor and the yaw rate of the rigid body, in hub axes,
- can represent either the stiffness of the hub coning hinge (if present), or the structural stiffness.
- mass matrix:where is the identity matrix.
- damping matrix:with:
- Stiffness matrix:with:
- Non-homogeneous term:
2.6. Hub Loads
- aerodynamic loads;
- blade inertia;
- blade weight;
- forces and moments generated by the flapping hinge.
3. Software Implementation
3.1. Tilt-Rotor Simulation Model
3.2. Numerical Integration
3.3. Stand-Alone Model
4. Results and Discussion
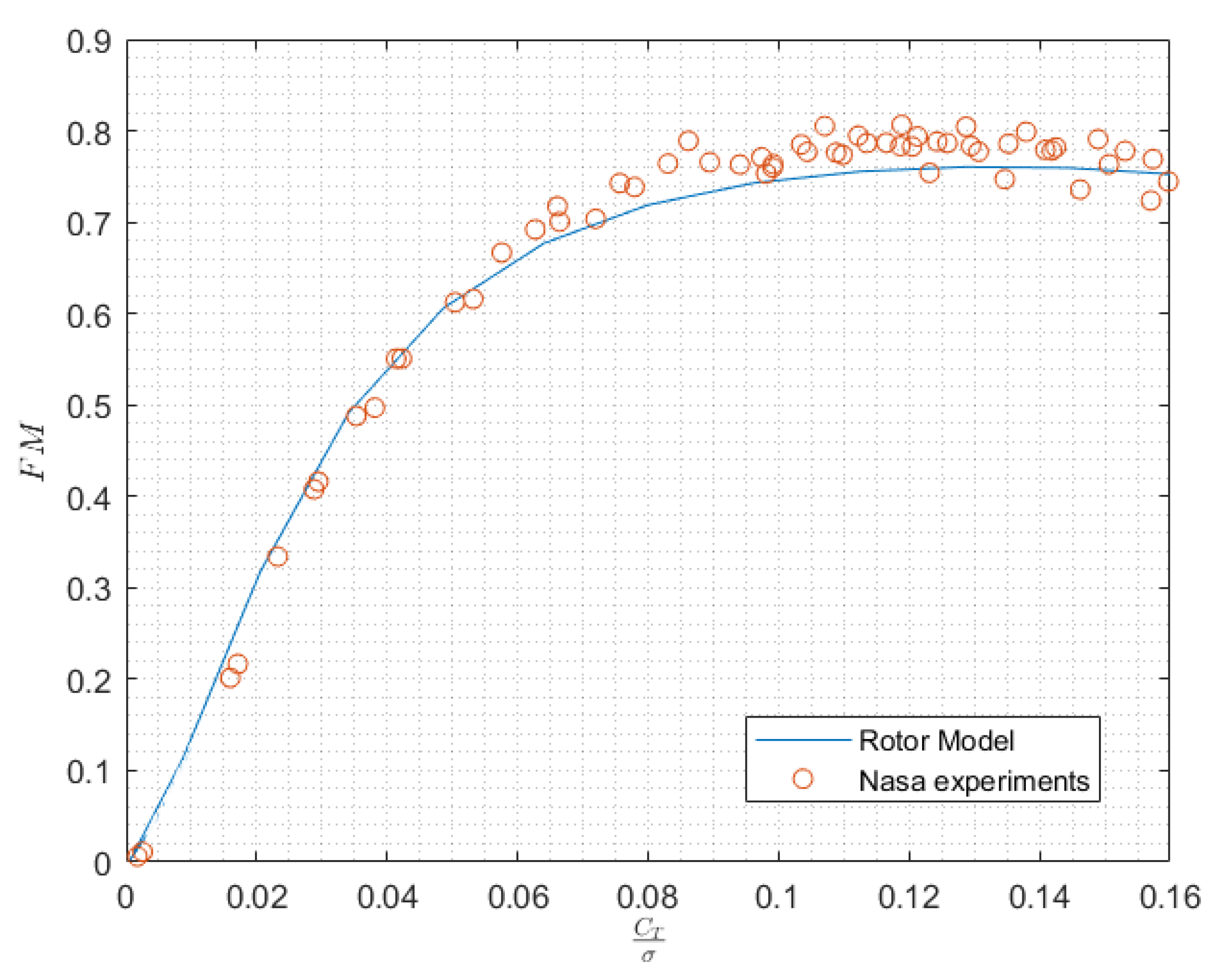
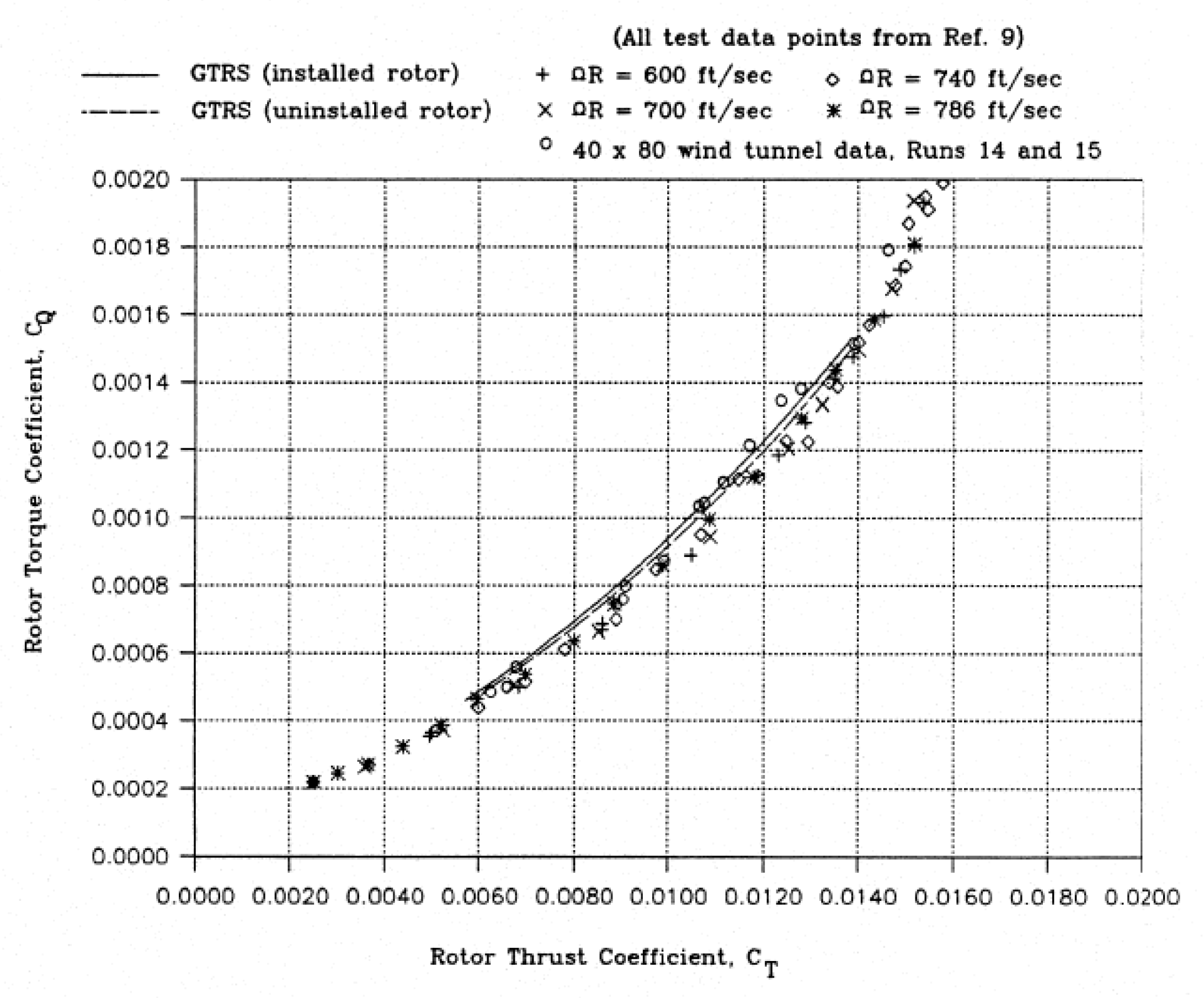
4.1. Rotor Performance
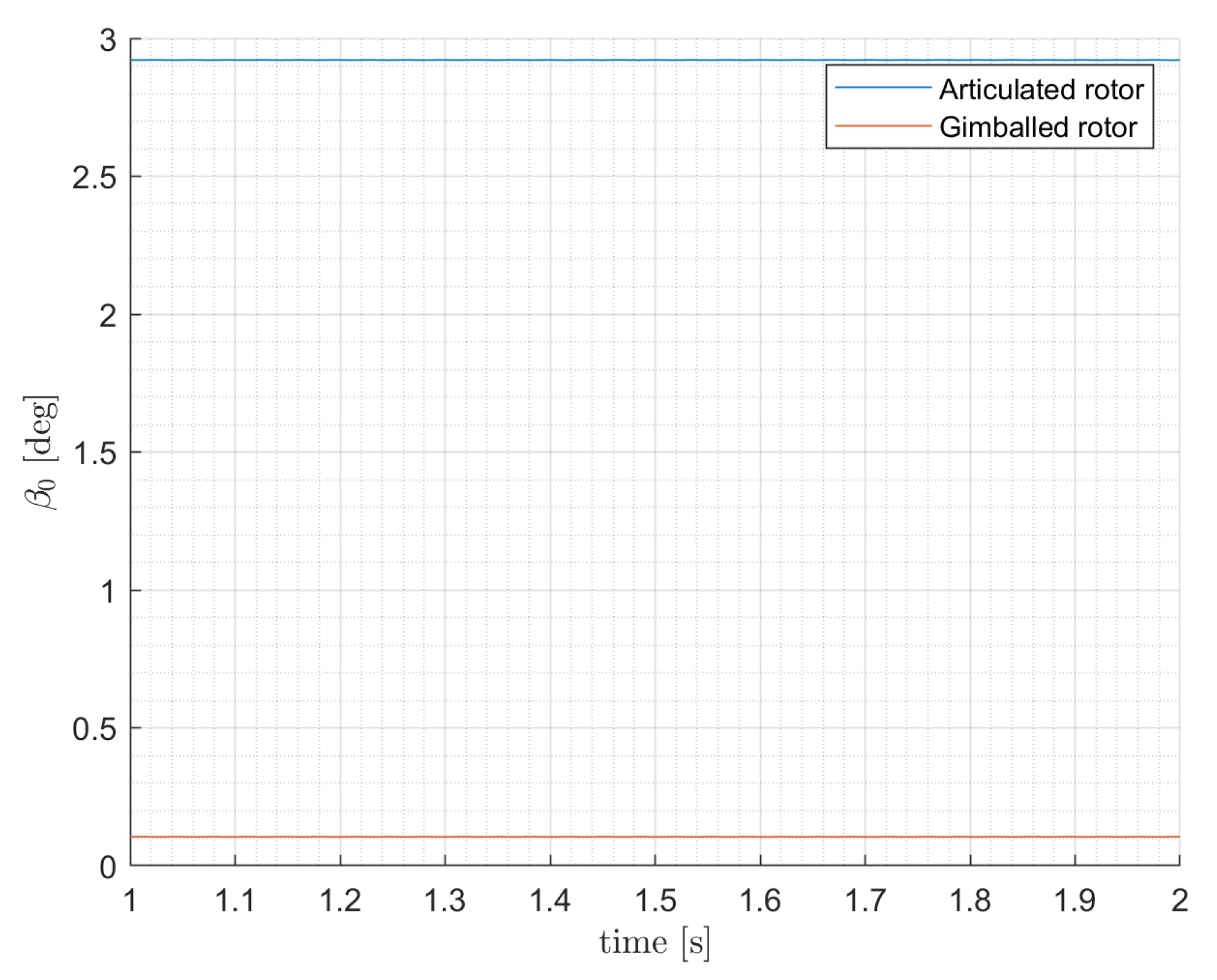
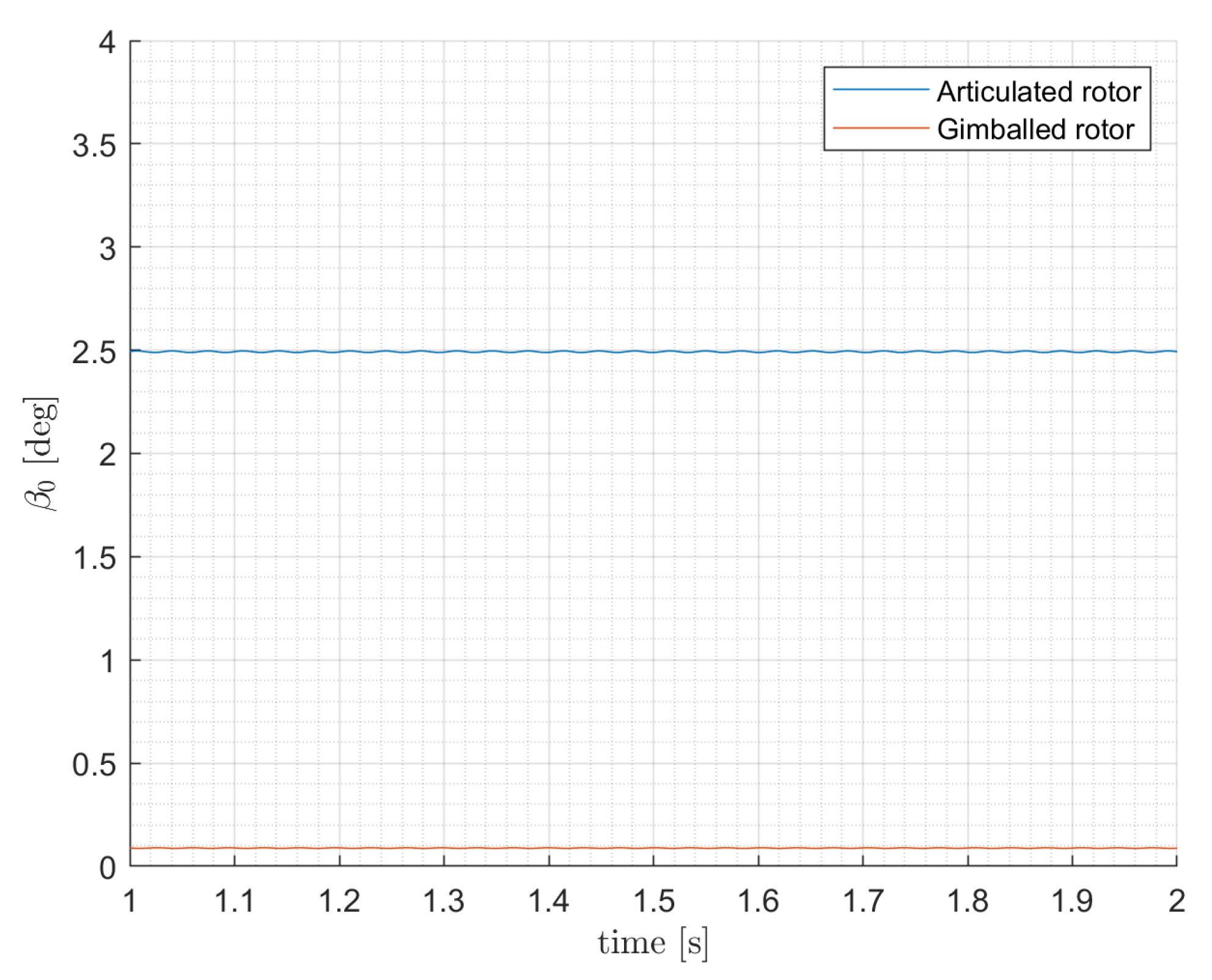
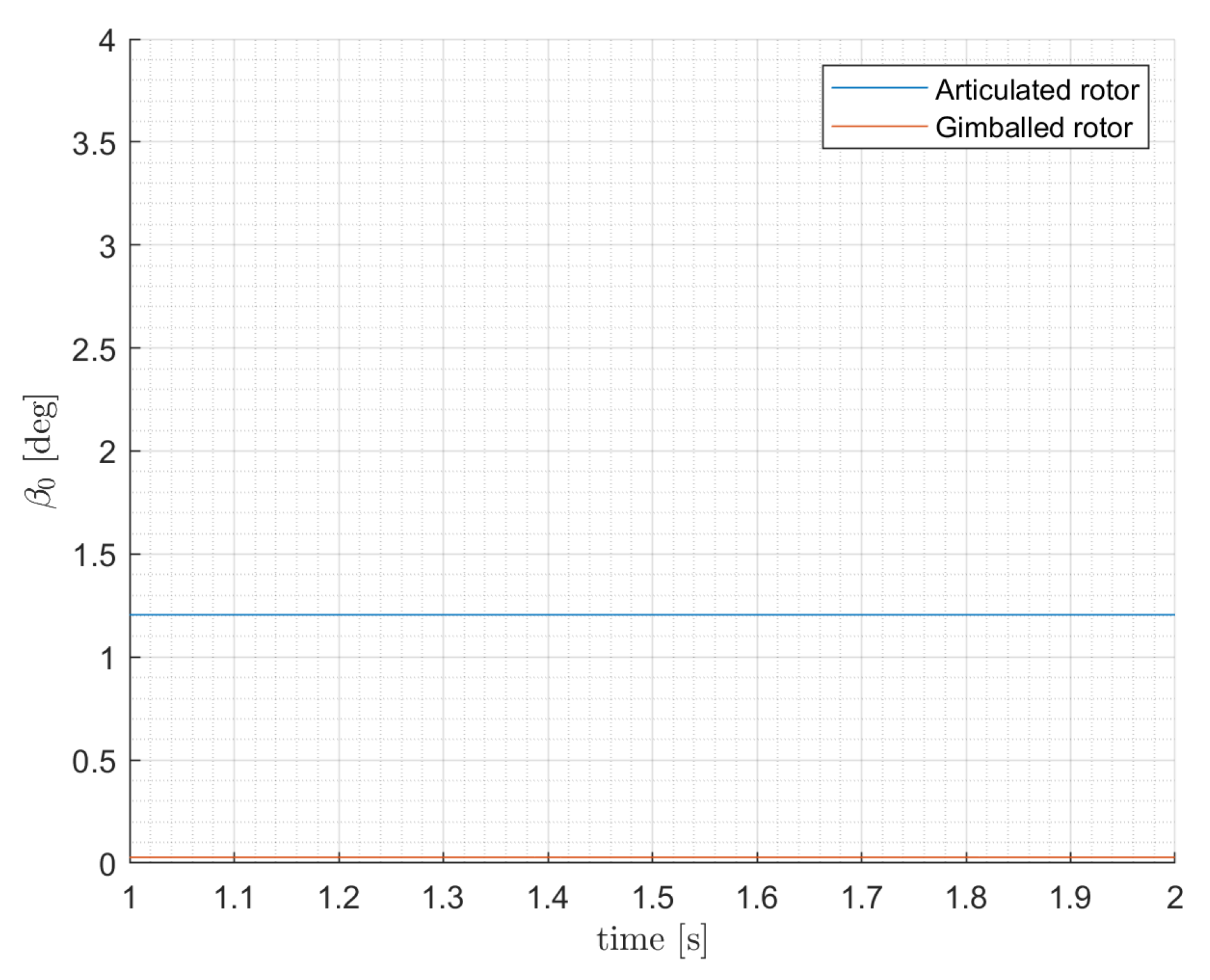
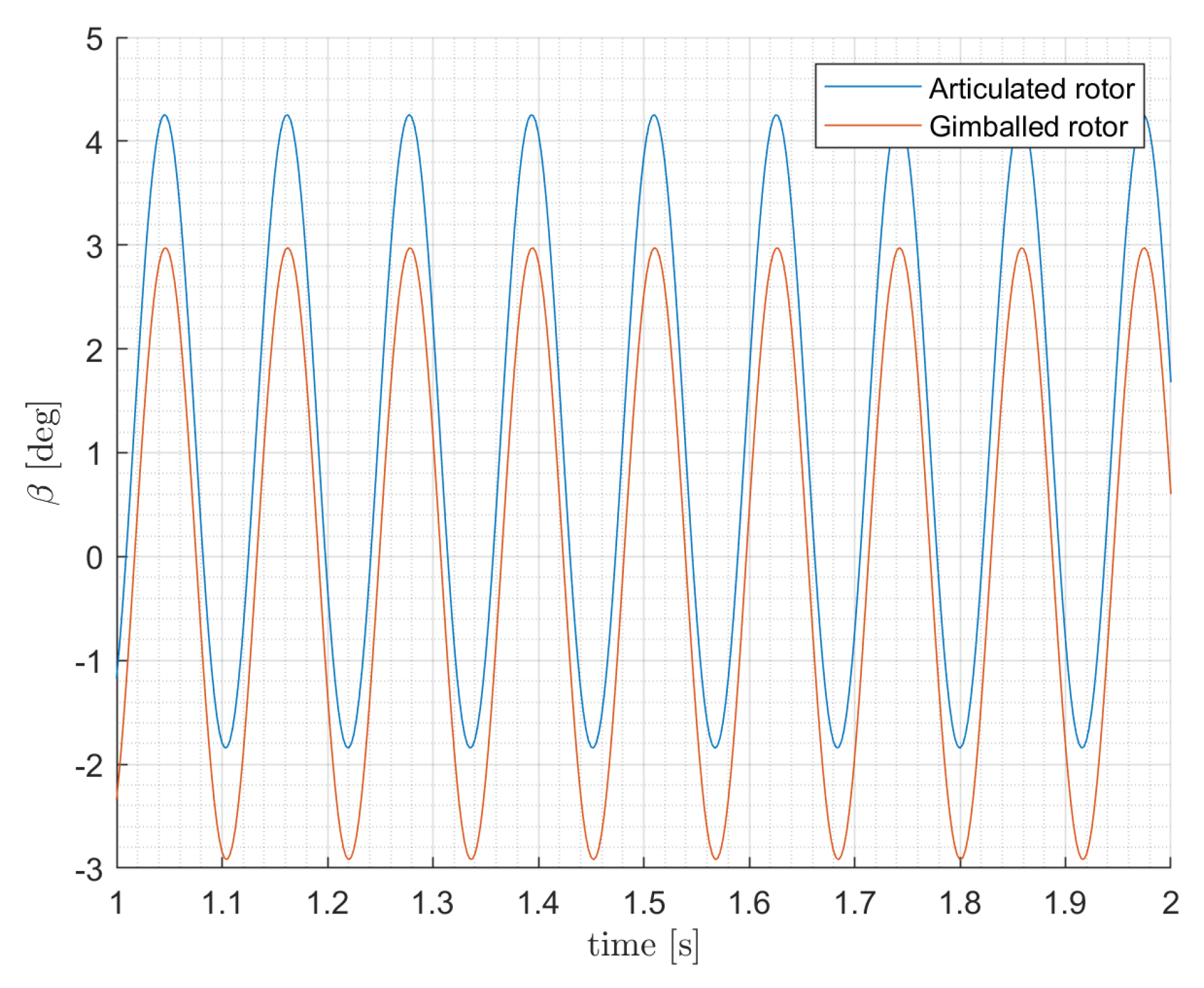
4.2. Blades Flapping Motion and Disk Coning
- Hover
- Low-speed flight in helicopter mode
- High-speed flight in airplane mode
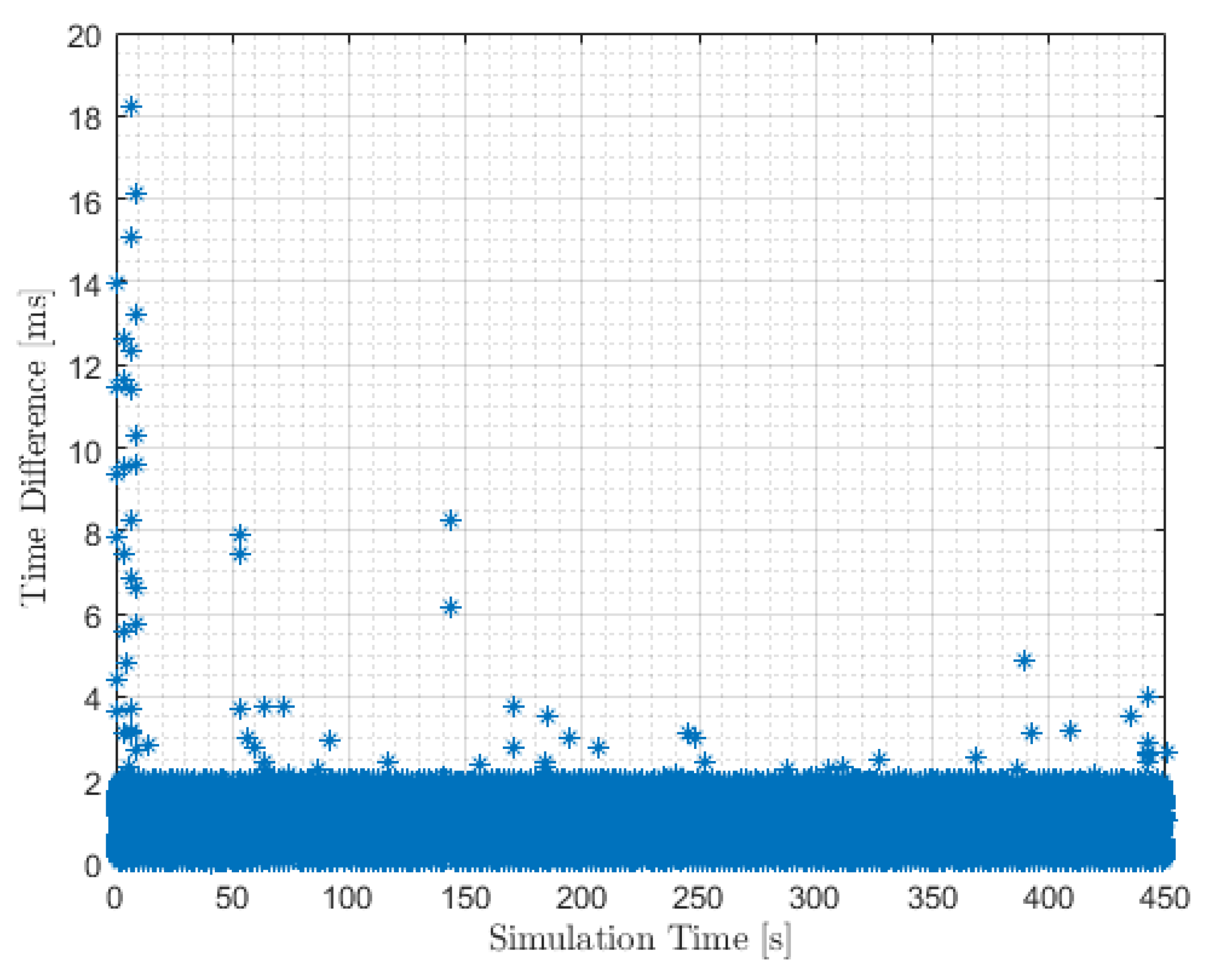
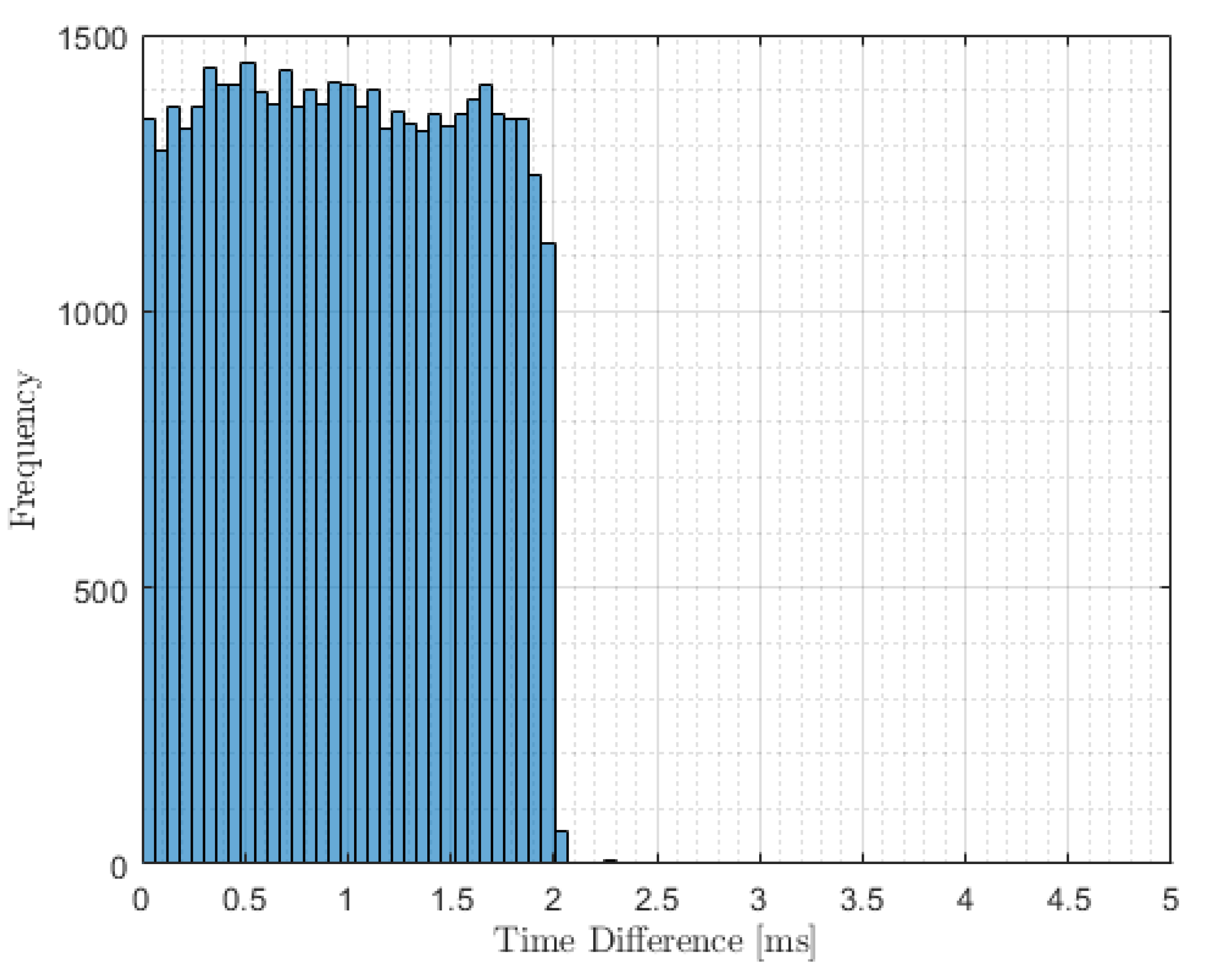
4.3. Code Performance in Pilot-In-The-Loop Simulations
5. Conclusions and Future Developments
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Anderson, S.B. Historical Overview of V/STOL Aircraft Technology; NASA TM81280; NASA: Washington, DC, USA, 1981.
- Harris, F.D. NASA/SP-2015-21259 Vol III. In Introduction to Autogyros, Helicopters, and Other V/STOL Aircraft; National Aeronautics and Space Administration: Washington, DC, USA; Ames Research Center: Mountain View, CA, USA; Moffet Field: Santa Clara, CA, USA, 2015; pp. 16–40. [Google Scholar]
- Maisel, M.D.; Giulianetti, D.J.; Dugan, D.C. NASA SP-2000-4517. In The History of the XV-15 Tilt Rotor Research Aircraft: From Concept to Flight; The NASA History Series; National Aeronautics and Space Administration, Office of Policy and Plans, NASA History Division: Washington, DC, USA, 2000. [Google Scholar]
- Rosenstein, H.; McVeigh, M.A.; Mollenkof, P.A. V/STOL Tilt Rotor Aircraft Study Mathematical Model for a Real Time Simulation of a Tilt Rotor Aircraft (Boeing Vertol Model 222); NASA: Washington, DC, USA, 1973; Volume VIII.
- Harendra, P.B.; Joglekar, M.J.; Gaffey, T.M.; Marr, R.L. V/STOL Tilt Rotor Study Volume V. A Mathematical Model For Real Time Flight Simulation of the Bell Model 301 Tilt Rotor Research Aircraft; Final Report; CR114614; NASA: Washington, DC, USA, 1973.
- Ferguson, S.W. A Mathematical Model for Real-Time Flight Simulation of a Generic Tilt-Rotor Aircraft; NASA CR166536; NASA: Washington, DC, USA, 1988.
- Carlson, R.G.; Miao, W.-L. Aeroelastic Analysis of the Elastic Gimbal Rotor; NASA CR166287; NASA: Washington, DC, USA, 1981.
- Padfield, G.D. Helicopter Flight Dynamics, including a treatment of Tiltrotor Aircraft, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Mattaboni, M.; Masarati, P.; Quaranta, G.; Mantegazza, P. Multibody Simulation of Integrated Tiltrotor Flight Mechanics, Aeroelasticity, and Control. J. Guid. Control. Dyn. 2012, 35, 5. [Google Scholar] [CrossRef]
- Nixon, M.W.; Kvaternik, R.G.; Settle, T.B. Tiltrotor Vibration Reduction Through Higher Harmonic Control. In Proceedings of the American Helicopter Society 53rd Annual Forum, Virginia Beach, VA, USA, 29 April–1 May 1997. [Google Scholar]
- Johnson, W. CAMRAD/JA A Comprehensive Analytical Model of Rotorcraft Aerodynamics and Dynamics; Johnson Aeronautics Version; User’s Manual: Palo Alto, CA, USA, 1988; Volume II. [Google Scholar]
- Barkai, S.M.; Rand, O.; Peyran, R.J.; Carlson, R.M. Modeling and Analysis of Tilt-Rotor Aeromechanical PhenomenaIn. Math. Comput. Model. 1998, 27, 17–43. [Google Scholar] [CrossRef]
- Hefflex, R.; Mnich, M.A. Minimum-Complexity Helicopter Simulation Math Model; NASA: Washington, DC, USA, 1988.
- Takahashi, M.D. A Flight-Dynamics Helicopter Mathematical Model with a Single Flap-Lag-Torsion Main Rotor; NASA TM102267; NASA: Washington, DC, USA, 1990.
- Barra, F.; Godio, S.; Guglieri, G.; Capone, P.; Monstein, R. Implementation of a Comprehensive Mathematical Model for Tilt-Rotor Real-Time Flight Simulation. In Proceedings of the 45th European Rotorcraft Forum, Warsaw, Poland, 17–20 September 2019. [Google Scholar]
- McVicair, J.; Scott, G. A Generic Tilt-Rotor Simulation Model with Parallel Implementation. Ph.D. Thesis, University of Glasgow, Glasgow, Scotland, 1993. [Google Scholar]
- Chen, R.T.N. Effects of Primary Rotor Parameters on Flapping Dynamics; NASA TP-1431; NASA: Washington, DC, USA, 1980.
- Johnson, W. Helicopter Theory; Dover Publications, Inc.: Mineola, NY, USA, 1980. [Google Scholar]
- Chen, R.T.N. A Survey of Nonuniform Inflow Models for Rotorcraft Flight Dynamics and Control Applications; NASA TM 102219; NASA: Washington, DC, USA, 1989.
- Hoerner, S.F. Fluid Dynamic; Lift, S.F., Ed.; Hoerner Fluid Dynamics: Brick Township, NJ, USA, 1975. [Google Scholar]
- Harris, F.D. Hover Performance of Isolated Proprotors and Propellers—Experimental Data; NASA CR 219486; NASA: Washington, DC, USA, 1988.
- Bielawa, R.L. Rotary Wing Structural Dynamics and Aeroelasticity, 2nd ed.; AIAA American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2006. [Google Scholar]
- Ferguson, S.W. Development and Validation of a Simulation for A Generic Tilt-Rotor Aircraft; NASA CR166537; NASA: Washington, DC, USA, 1989.









| Element | Simbol | Unit | Value | Reference |
|---|---|---|---|---|
| blade | [] | 244,047.23 | [6] | |
| gimbal | [] | 305.05 | [6] |
| Element | Symbol | Unit | Cond. 1 | Cond. 2 | Cond. 3 |
|---|---|---|---|---|---|
| True Air Speed | TAS | [] | 0 | 60 | 180 |
| Nacelle Angle | [] | 90 | 90 | 0 | |
| Rotor Angular speed | [] | 589 | 589 | 517 | |
| Hub Inlet X-Velocity | [] | 0 | 30.359 | −2.998 | |
| Hub Inlet Z-Velocity | [] | 0 | −5.359 | −92.551 | |
| Collective pitch input (after mixing unit) | [] | 6.98 | 4.82 | 28.26 | |
| Longitudinal cyclic pitch input (after mixing unit) | [] | −1.783 | 0.262 | 1.500 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abà, A.; Barra, F.; Capone, P.; Guglieri, G. Mathematical Modelling of Gimballed Tilt-Rotors for Real-Time Flight Simulation. Aerospace 2020, 7, 124. https://doi.org/10.3390/aerospace7090124
Abà A, Barra F, Capone P, Guglieri G. Mathematical Modelling of Gimballed Tilt-Rotors for Real-Time Flight Simulation. Aerospace. 2020; 7(9):124. https://doi.org/10.3390/aerospace7090124
Chicago/Turabian StyleAbà, Anna, Federico Barra, Pierluigi Capone, and Giorgio Guglieri. 2020. "Mathematical Modelling of Gimballed Tilt-Rotors for Real-Time Flight Simulation" Aerospace 7, no. 9: 124. https://doi.org/10.3390/aerospace7090124
APA StyleAbà, A., Barra, F., Capone, P., & Guglieri, G. (2020). Mathematical Modelling of Gimballed Tilt-Rotors for Real-Time Flight Simulation. Aerospace, 7(9), 124. https://doi.org/10.3390/aerospace7090124






