GA Optimization of Variable Angle Tow Composites in Buckling and Free Vibration Analysis through Layerwise Theory
Abstract
:1. Introduction
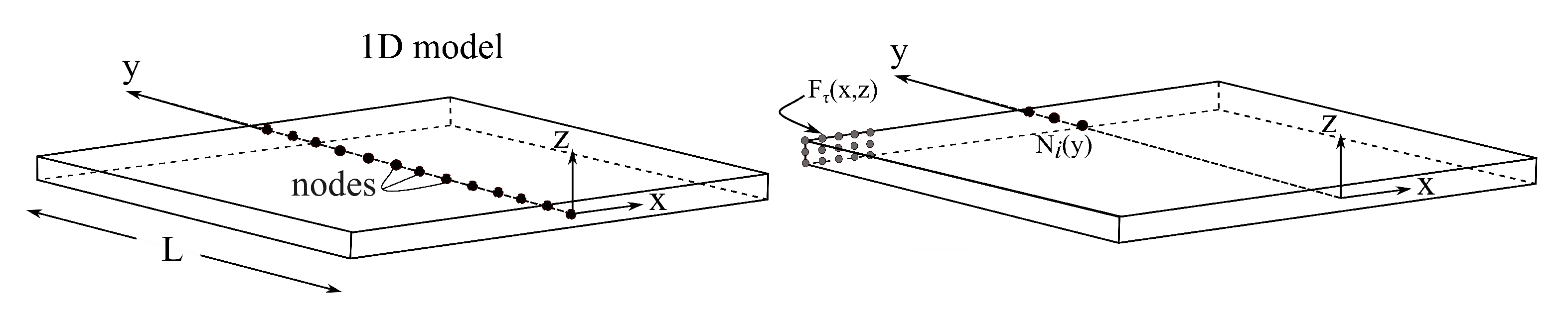
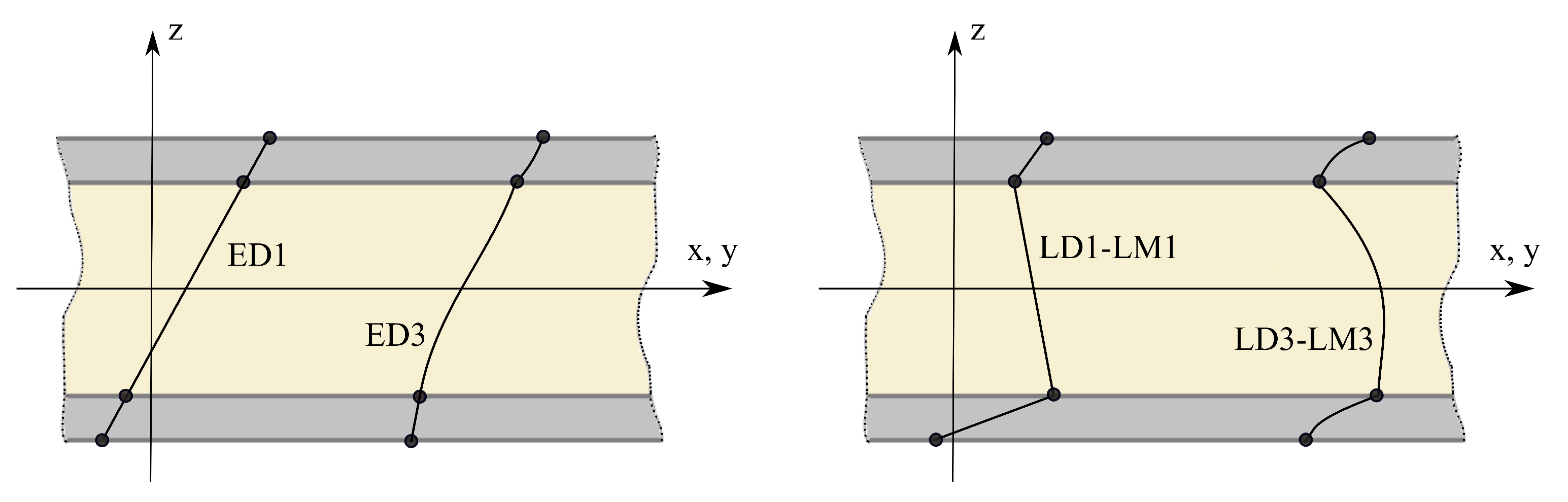
2. Carrera Unified Formulation for Beams
Preliminaries
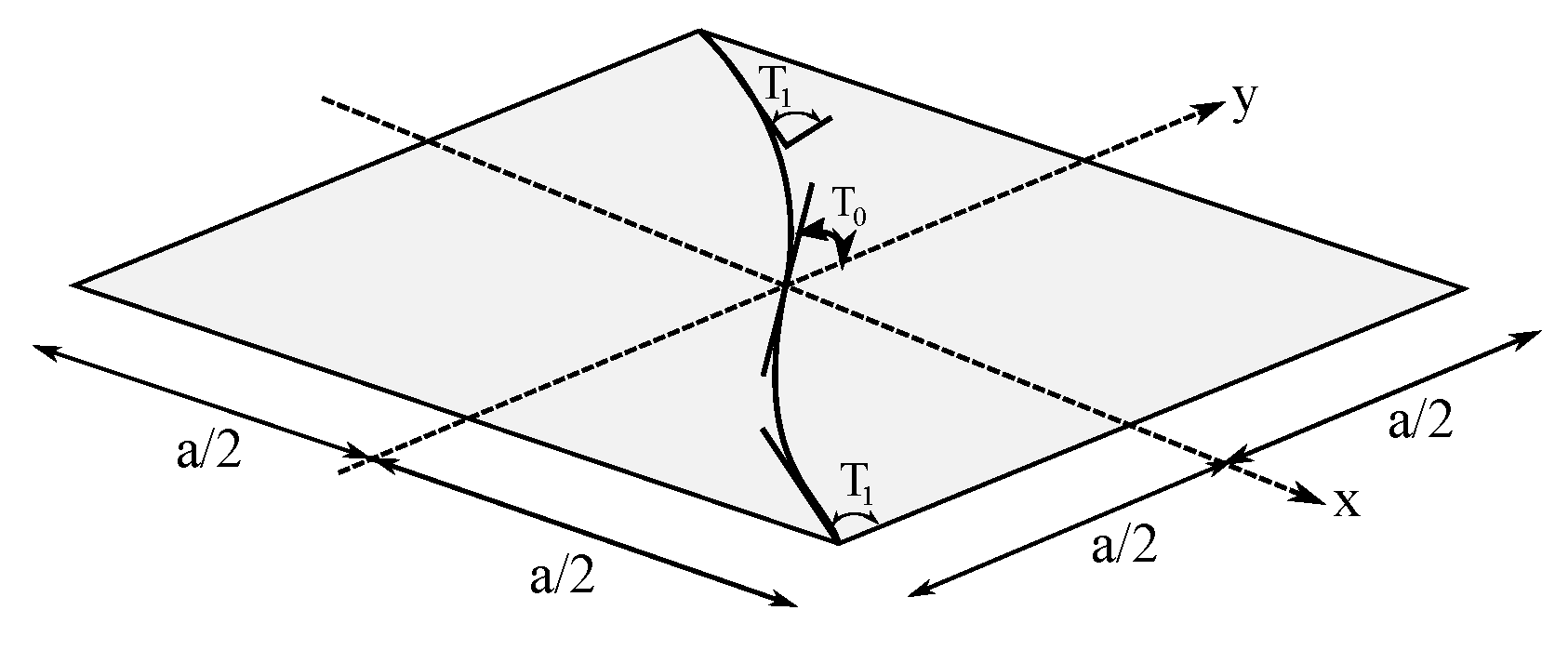
3. Constitutive Equations for VAT Laminates
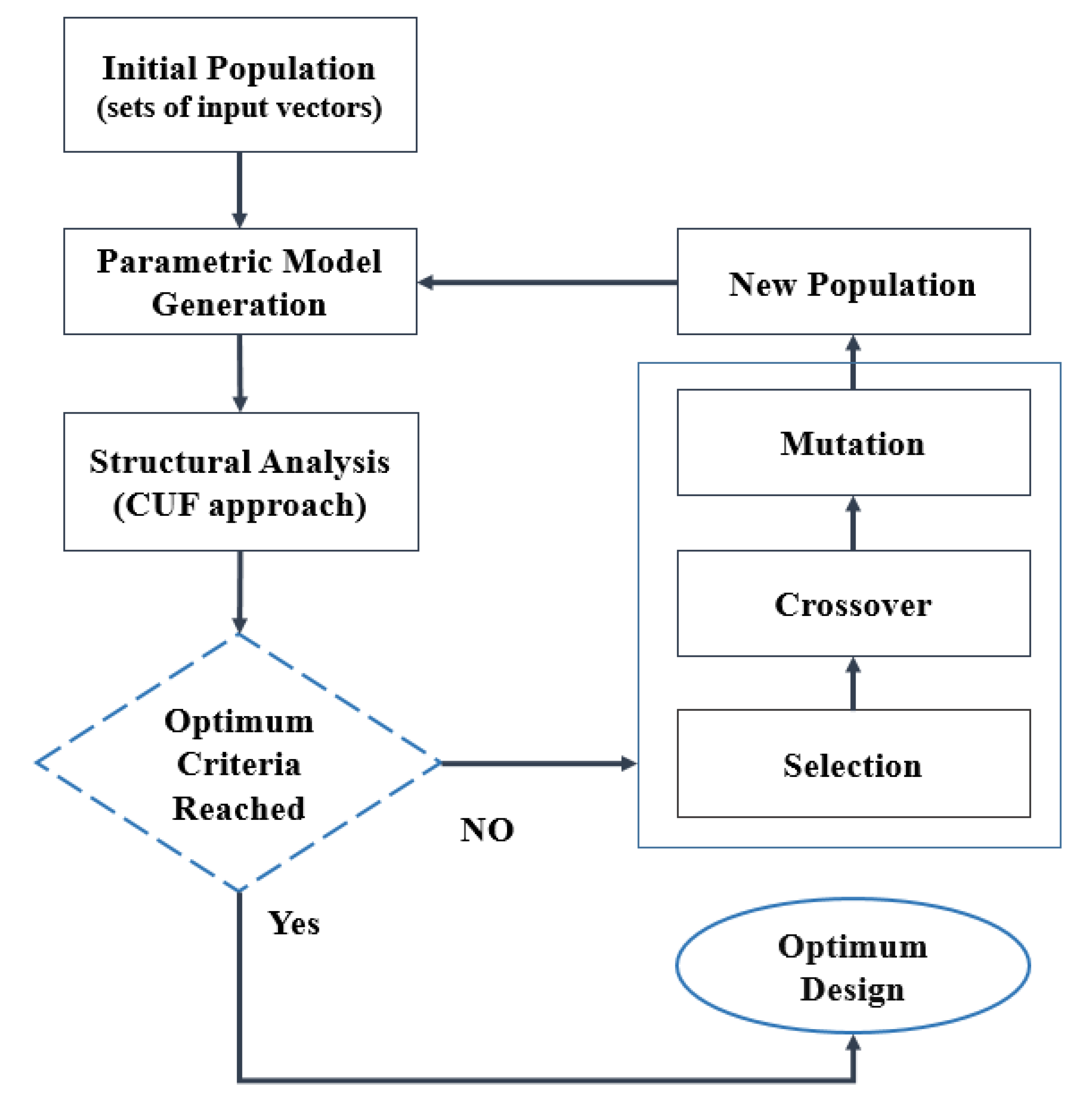
4. Optimization for VAT Composite Studies
4.1. Direct Search Stochastic Methods
4.2. Surrogate Model: Response Surface
4.3. Modeling of VAT Composite in Buckling Analysis
4.4. Modeling of VAT Composite in Free Vibration Analysis
5. Optimization Results and Discussion
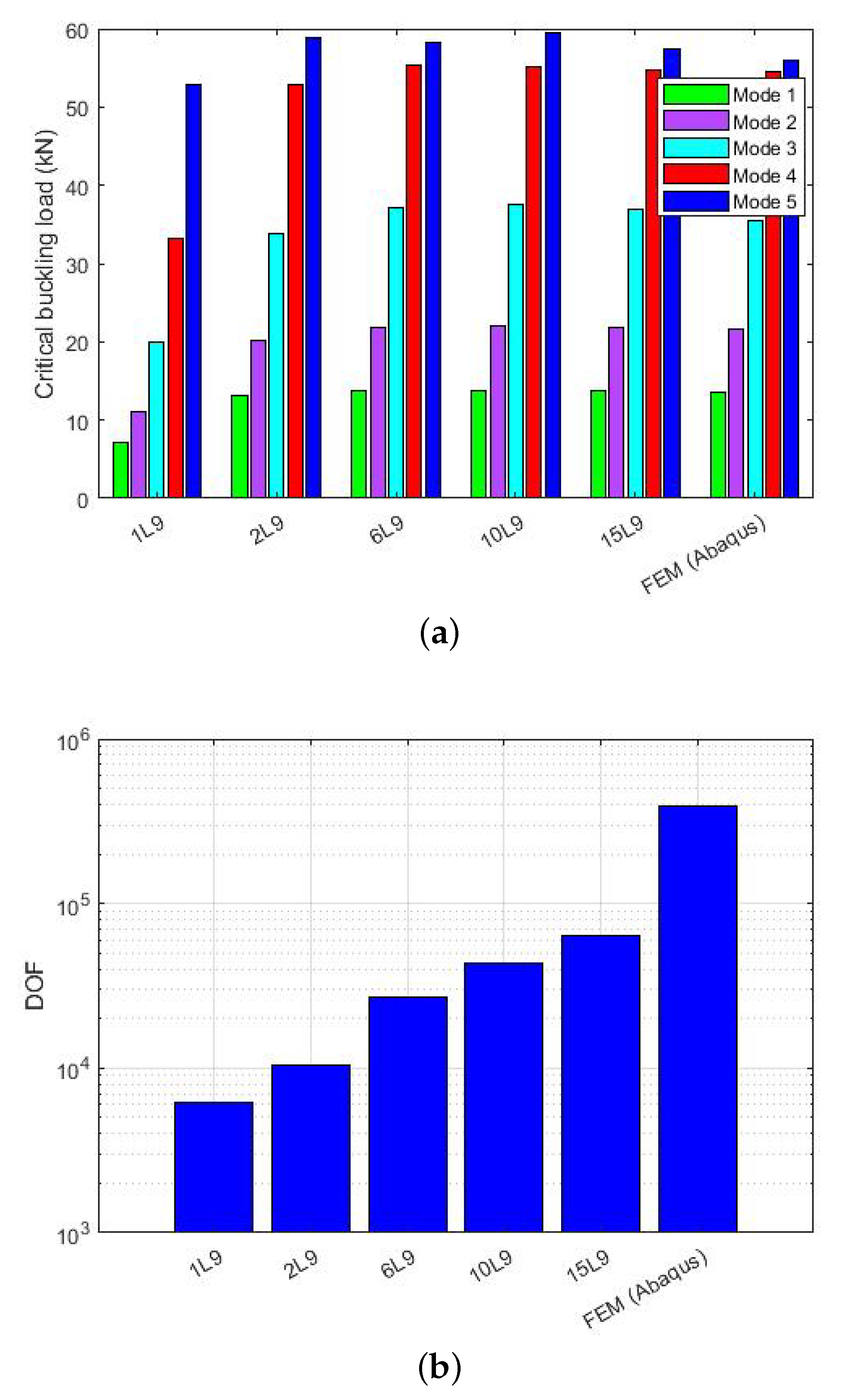
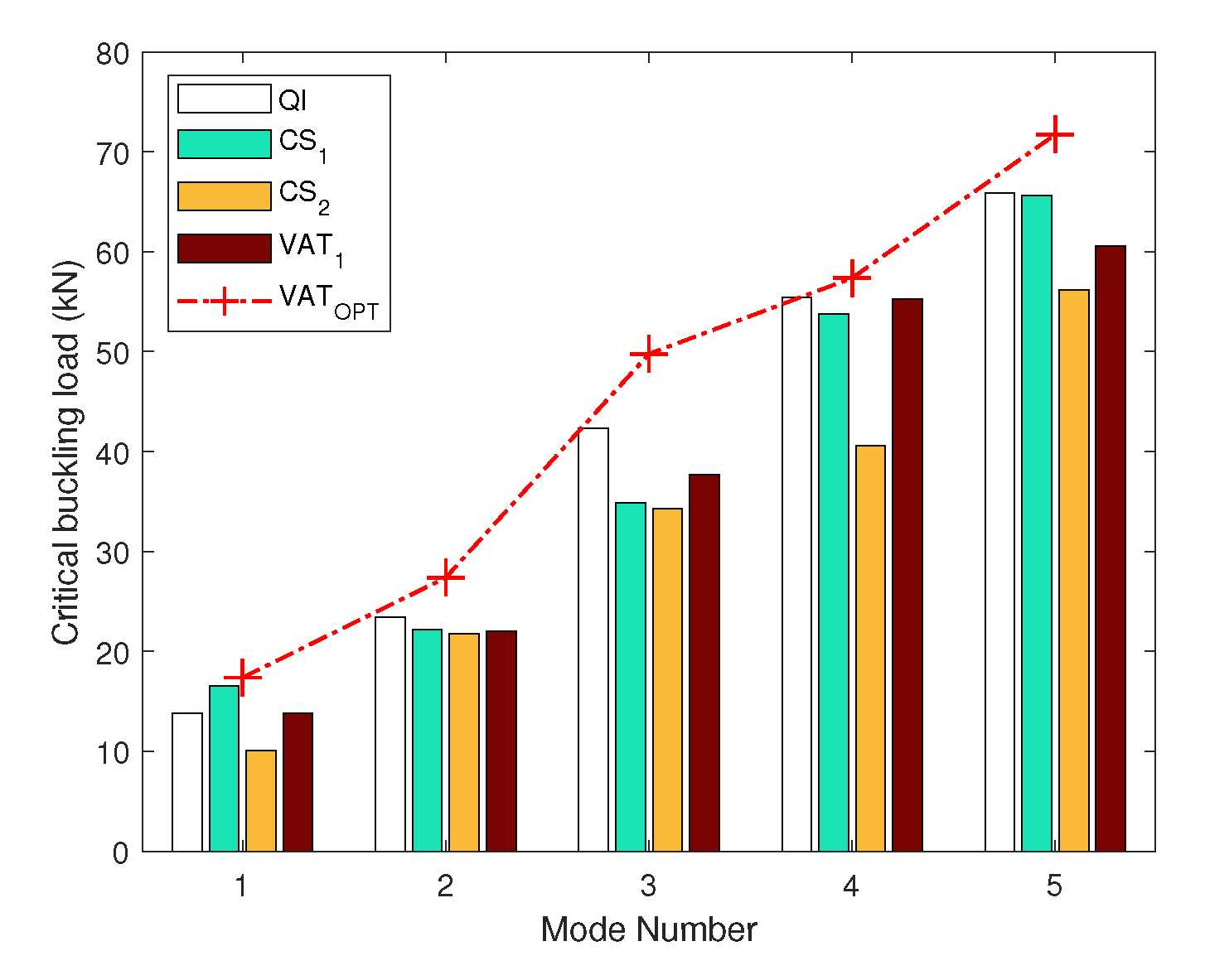
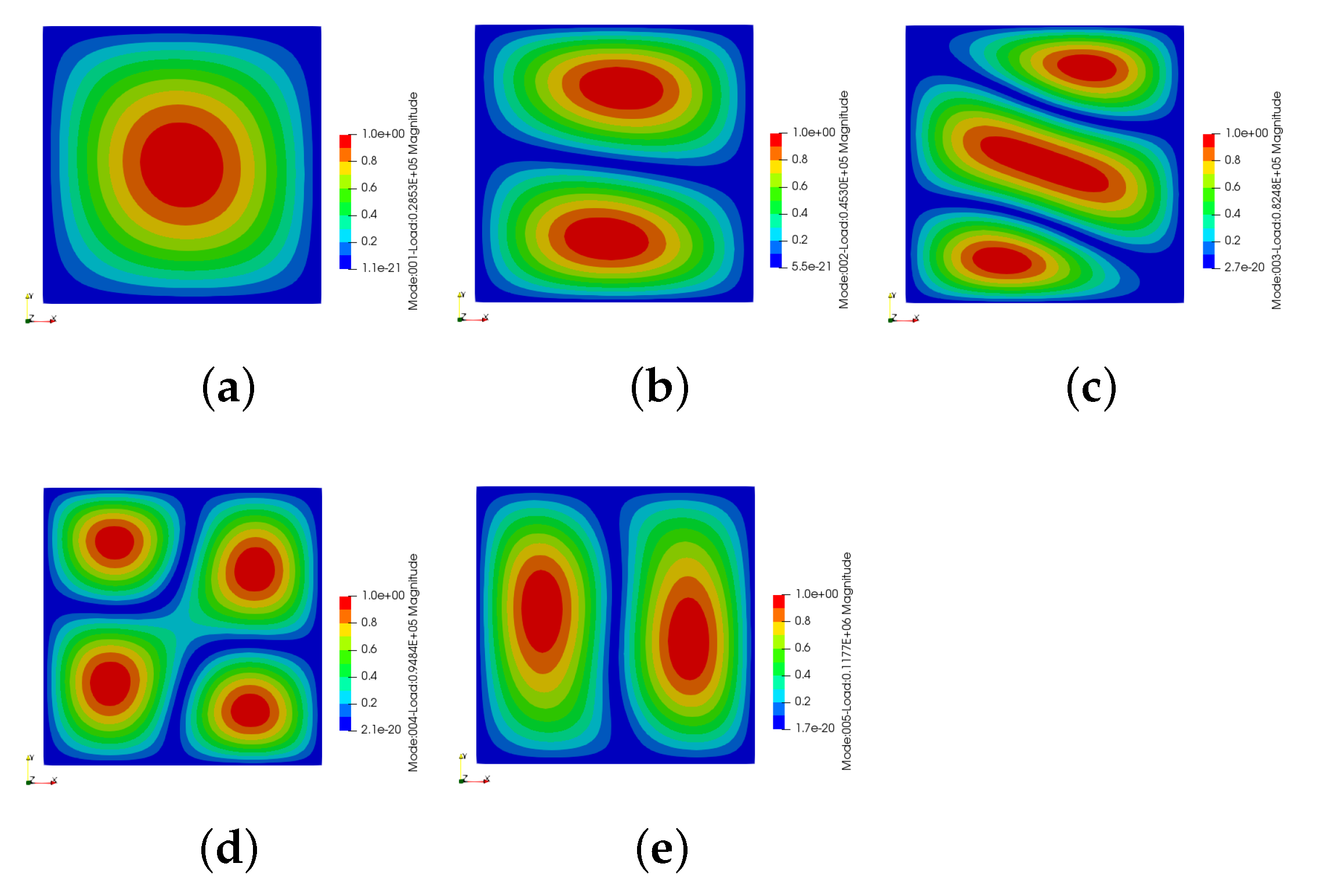
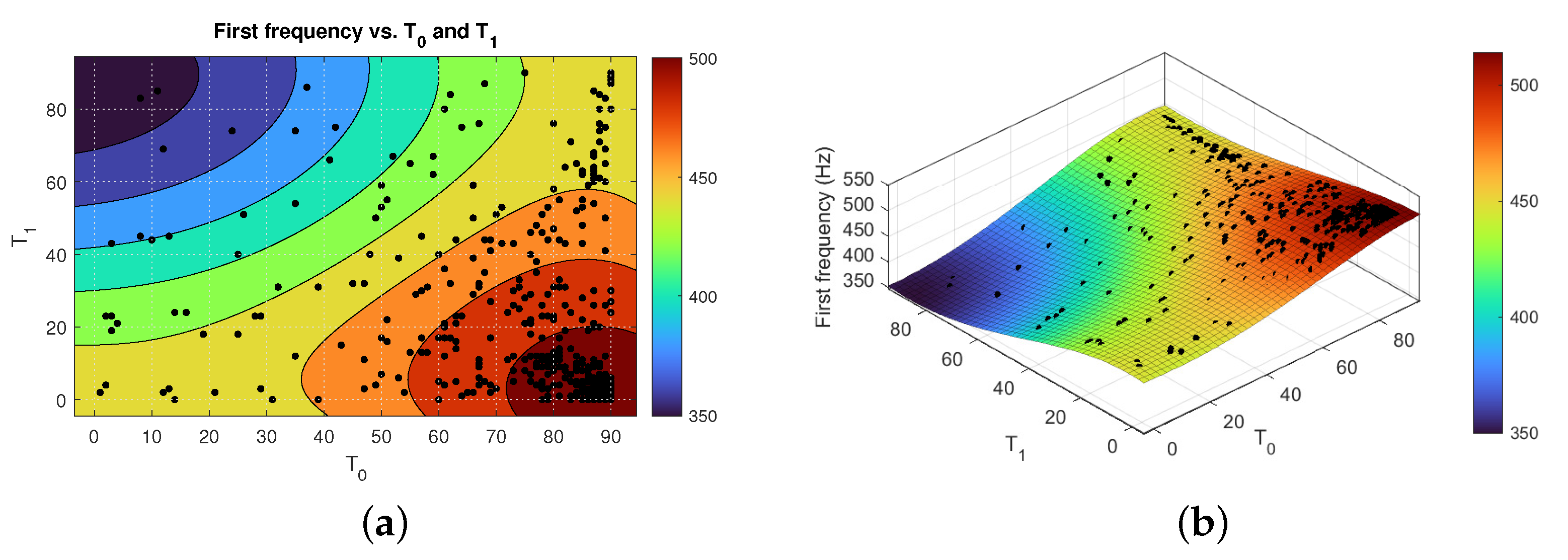
5.1. Buckling Results of VAT Laminate
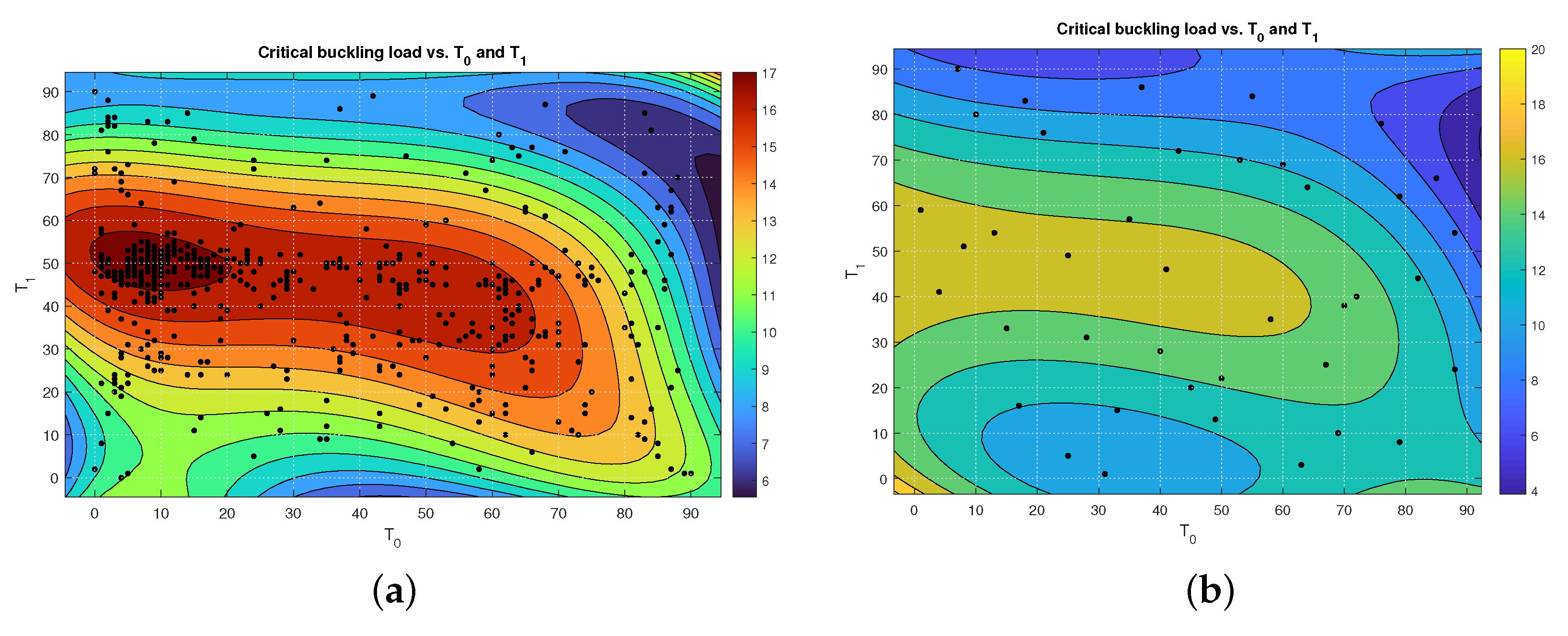
Reduction of Search Domain by Latin Hypercube Method
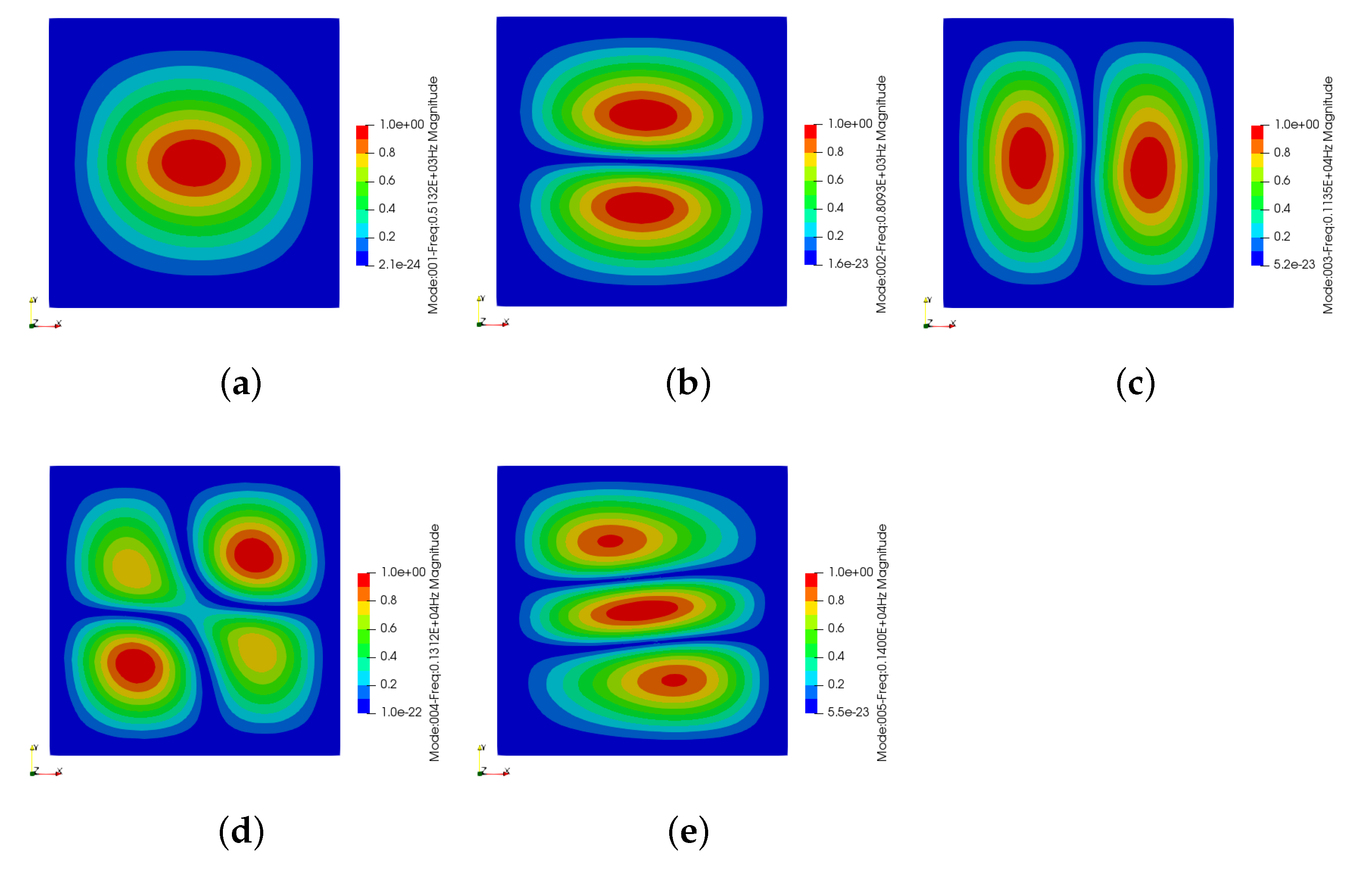
5.2. Results of VAT Laminate in Free Vibration
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 1D | One-Dimensional |
| CUF | Carrera Unified Formulation |
| VAT | Variable Angle Tow |
| LW | Layer Wise |
| GA | Genetic Algorithm |
| CLT | Classical Laminate Theory |
| DQM | Differential Quadrature Method |
| FEM | Finite Element Method |
| RS | Response Surface |
| LHS | Latin Hypercube Sampling |
| FN | Fundamental Nucleus |
| BC | Boundary Condition |
| QI | Quasi-Isotropic |
| CS | Constant Stiffness |
| DOF | Degree Of Freedom |
References
- Gürdal, Z.; Tatting, B.F.; Wu, C.K. Variable stiffness composite panels: Effects of stiffness variation on the in-plane and buckling response. Compos. Part A Appl. Sci. Manuf. 2008, 39, 911–922. [Google Scholar] [CrossRef]
- Hyer, W.M.; Lee, H.H. The use of curvilinear fiber format to improve buckling resistance of composite plates with central circular holes. Compos. Struct. 1991, 18, 239–261. [Google Scholar] [CrossRef]
- Gürdal, Z.; Olmedo, R. In-plane response of laminates with spatially varying fiber orientations—Variable stiffness concept. AIAA J. 1993, 31, 751–758. [Google Scholar] [CrossRef]
- Leissa, A.W.; Martin, A.F. Vibration and buckling of rectangular composite plates with variable fiber spacing. Compos. Struct. 1990, 14, 339–357. [Google Scholar] [CrossRef]
- Vescovini, R.; Dozio, L. A variable-kinematic model for variable stiffness plates: Vibration and buckling analysis. Compos. Struct. 2016, 142, 15–26. [Google Scholar] [CrossRef]
- Demasi, L.; Ashenafi, Y.; Cavallaro, R.; Santarpia, E. Generalized Unified Formulation shell element for functionally graded Variable-Stiffness Composite Laminates and aeroelastic applications. Compos. Struct. 2015, 133, 501–515. [Google Scholar] [CrossRef]
- Olmedo, R.; Gürdal, Z. Buckling response of laminates with spatially varying fiber orientations. Struct. Dyn. Mater. Conf. Struct. 1993, 1567. [Google Scholar] [CrossRef]
- Tatting, B.; Gürdal, Z. Analysis and design of tow-steered variable stiffness composite laminates. In Proceedings of the American Helicopter Society Hampton Roads Chapter, Structure Specialists’ Meeting, Williamsburg, VA, USA, 30 October–1 November 2001. [Google Scholar]
- Raju, G.; Wu, Z.; Kim, B.C.; Weaver, P.M. Prebuckling and buckling analysis of variable angle tow plates with general boundary conditions. Compos. Struct. 2012, 94, 2961–2970. [Google Scholar] [CrossRef] [Green Version]
- Raju, G.; Wu, Z.; Kim, B.C.; Weaver, P.M. Analysis of Tow-Placed, Variable-Stiffness Laminates. Master’s Thesis, Virginia Tech, Blacksburg, VA, USA, 1996. [Google Scholar]
- Chen, X.; Nie, G. Prebuckling and buckling analysis of moderately thick variable angle tow composite plates considering the extension-shear coupling. Compos. Struct. 2012, 242, 112093. [Google Scholar] [CrossRef]
- Coburn, B.H.; Wu, Z.; Weaver, P.M. Buckling analysis of stiffened variable angle tow panels. Compos. Struct. 2014, 111, 259–270. [Google Scholar] [CrossRef] [Green Version]
- Coburn, B.H.; Weaver, P.M. Buckling analysis, design and optimisation of variable-stiffness sandwich panels. Int. J. Solids Struct. 2016, 96, 217–228. [Google Scholar] [CrossRef] [Green Version]
- Hachemi, M.; Hamza-Cherif, S.M.; Houmat, A. Free vibration analysis of variable stiffness composite laminate plate with circular cutout. Aust. J. Mech. Eng. 2020, 18, 63–79. [Google Scholar] [CrossRef]
- Sciascia, G.; Oliveri, V.; Milazzo, A.; Weaver, P.M. Ritz Solution for Transient Analysis of Variable-Stiffness Shell Structures. Mech. Adv. Mater. Struct. 2020, 58, 1796–1810. [Google Scholar] [CrossRef]
- Carrera, E.; Cinefra, M.; Petrolo, M.; Zappino, E. Finite Element Analysis of Structures Through Unified Formulation. In Mechanics of Advanced Materials and Structures; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Carrera, E.; Giunta, G.; Petrolo, M. Beam Structures: Classical and Advanced Theories; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Carrera, E. Evaluation of Layerwise Mixed Theories for Laminated Plates Analysis. AIAA J. 1998, 36, 830–839. [Google Scholar] [CrossRef]
- Carrera, E.; Azzara, R.; Daneshkhah, E.; Pagani, A.; Wu, B. Buckling and post-buckling of anisotropic flat panels subjected to axial and shear in-plane loadings accounting for classical and refined structural and nonlinear theories. Int. J. Non-Linear Mech. 2021, 133, 103716. [Google Scholar] [CrossRef]
- Carrera, E.; Pagani, A.; Valvano, S. Shell elements with through-the-thickness variable kinematics for the analysis of laminated composite and sandwich structures. Compos. Part B Eng. 2017, 111, 294–314. [Google Scholar] [CrossRef] [Green Version]
- Pagani, A.; Valvano, S.; Carrera, E. Analysis of laminated composites and sandwich structures by variable-kinematic MITC9 plate elements. J. Sandw. Struct. Mater. 2018, 20, 4–41. [Google Scholar] [CrossRef] [Green Version]
- Pagani, A.; Daneshkhah, E.; Xu, X.; Carrera, E. Evaluation of geometrically nonlinear terms in the large-deflection and post-buckling analysis of isotropic rectangular plates. Int. J. Non-Linear Mech. 2020, 121, 103461. [Google Scholar] [CrossRef]
- Xu, X.; Fallahi, N.; Yang, H. Efficient CUF-based FEM analysis of thin-wall structures with Lagrange polynomial expansion. Mech. Adv. Mater. Struct. 2020, 1–22. [Google Scholar] [CrossRef]
- Tahani, M. Analysis of laminated composite beams using layerwise displacement theories. Compos. Struct. 2007, 79, 535–547. [Google Scholar] [CrossRef]
- Entezari, A.; Kouchakzadeh, M.A.; Carrera, E.; Filippi, M. A refined finite element method for stress analysis of rotors and rotating disks with variable thickness. Acta Mech. 2017, 228, 575–594. [Google Scholar] [CrossRef]
- Carrera, E.; Entezari, A.; Filippi, M.; Kouchakzadeh, M.A. 3D thermoelastic analysis of rotating disks having arbitrary profile based on a variable kinematic 1D finite element method. J. Therm. Stress. 2017, 39, 1572–1587. [Google Scholar] [CrossRef]
- Georgantzinos, S.K.; Giannopoulos, G.I.; Markolefas, S.I. Vibration Analysis of Carbon Fiber-Graphene-Reinforced Hybrid Polymer Composites Using Finite Element Techniques. Materials 2020, 13, 4225. [Google Scholar] [CrossRef]
- Georgantzinos, S.K.; Antoniou, P.A.; Giannopoulos, G.I.; Fatsis, A.; Markolefas, S.I. Design of Laminated Composite Plates with Carbon Nanotube Inclusions against Buckling: Waviness and Agglomeration Effects. Nanomaterials 2020, 11, 2261. [Google Scholar] [CrossRef] [PubMed]
- Uthale, S.A.; Dhamal, N.A.; Shinde, D.K.; Kelkar, A.D. Polymeric hybrid nanocomposites processing and finite element modeling: An overview. Sci. Prog. 2021, 18, 165–188. [Google Scholar] [CrossRef]
- Tsai, S.W.; Halpin, J.C.; Pagano, N.J. Composite Materials Workshop; Conn., Technomic Pub. Co.: St. Louis, MO, USA, 1968.
- Setoodeh, S.; Abdalla, M.M.; IJsselmuiden, S.T.; Gürdal, Z. Design of variable-stiffness composite panels for maximum buckling load. Compos. Struct. 2009, 87, 109–117. [Google Scholar] [CrossRef]
- Fukunag, H.; Vanderplaats, G.N. Stiffness optimization of orthotropic laminated composites using lamination parameters. AIAA J. 1991, 29, 641–646. [Google Scholar] [CrossRef]
- Liu, B.; Haftka, R.T.; Trompette, P. Maximization of buckling loads of composite panels using flexural lamination parameters. Struct. Multidiscip. Optim. 2004, 26, 28–36. [Google Scholar] [CrossRef]
- Bloomfield, M.W.; Herencia, J.E.; Weaver, P.M. Enhanced two-level optimization of anisotropic laminated composite plates with strength and buckling constraints. Thin-Walled Struct. 2009, 47, 1161–1167. [Google Scholar] [CrossRef]
- Tawfik, M.E.; Bishay, P.L.; Sadek, E.A. Neural Network-Based Second Order Reliability Method (NNBSORM) for Laminated Composite Plates in Free Vibration. Comput. Model. Eng. Sci. 2018, 115, 105–129. [Google Scholar]
- Alinejad, F.; Botto, D. Innovative adaptive penalty in surrogate-assisted robust optimization of blade attachments. Acta Mech. 2019, 230, 2735–2750. [Google Scholar] [CrossRef]
- Forrester, A.I.J.; Keane, A.J. Recent advances in surrogate-based optimization. Prog. Aerosp. Sci. 2009, 45, 50–79. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Ruan, X.; Gosling, P.D. Robust design optimization of variable angle tow composite plates for maximum buckling load in the presence of uncertainties. Compos. Struct. 2019, 223, 110985. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Nikbakt, S.; Kamarian, S.; Shakeri, M. A review on optimization of composite structures Part I: Laminated composites. Compos. Struct. 2018, 195, 158–185. [Google Scholar] [CrossRef]
- Esposito, M.; Gherlone, M. Material and strain sensing uncertainties quantification for the shape sensing of a composite wing box. Mech. Syst. Signal Process. 2021, 160, 107875. [Google Scholar] [CrossRef]
- Viglietti, A.; Zappino, E.; Carrera, E. Free vibration analysis of variable angle-tow composite wing structures. Aerosp. Sci. Technol. 2019, 92, 114–125. [Google Scholar] [CrossRef]
- Viglietti, A.; Zappino, E.; Carrera, E. Analysis of variable angle tow composites structures using variable kinematic models. Compos. Part B Eng. 2019, 171, 272–283. [Google Scholar] [CrossRef]
- Fallahi, N.; Viglietti, A.; Carrera, E.; Pagani, A.; Zappino, E. Effect of fiber orientation path on the buckling, free vibration, and static analyses of variable angle tow panels. Facta Univ. Ser. Mech. Eng. 2020, 18, 165–188. [Google Scholar] [CrossRef]
- Carrera, E.; Pagani, A.; Cabral, P.H.; Prado, A.; Silva, G. Component-Wise Models for the Accurate Dynamic and Buckling Analysis of Composite Wing Structures. In Proceedings of the ASME 2016 International Mechanical Engineering Congress and Exposition, Phoenix, AZ, USA, 11–17 November 2016. [Google Scholar]
- Carrera, E.; Petrolo, M. Refined beam elements with only displacement variables and plate/shell capabilities. Meccanica 2012, 47, 537–556. [Google Scholar] [CrossRef]
- Reddy, J.N. An evaluation of equivalent-single-layer and layerwise theories of composite laminates. Compos. Struct. 1993, 25, 21–35. [Google Scholar] [CrossRef]
- Borst, R.D.; Crisfield, M.A.; Remmers, J.J.C.; Verhoosel, C.V. Nonlinear Finite Element Analysis of Solids and Structures; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Tatting, B.F.; Gürdal, Z. Design and Manufacture of Elastically Tailored Tow Placed Plates. NASA/CR-2002-211919. 2020. Available online: https://ntrs.nasa.gov/citations/20020073162 (accessed on 7 September 2013).
- Hyer, M.W.; Charette, R.F. The use of curvilinear fiber format in composite structure design. In Proceedings of the 30th Conference on Structures, Structural Dynamics and Materials, Mobile, AL, USA, 3–5 April 1989. [Google Scholar]
- Hao, P.; Yuan, X.; Liu, H.; Wang, B.; Liu, C.; Yang, D.; Oan, S. Isogeometric buckling analysis of composite variable-stiffness panels. Compos. Struct. 2017, 165, 192–208. [Google Scholar] [CrossRef]
- Daneshkhah, E.; Nedoushan, R.J.; Shahgholian, D.; Sina, N. Cost-Effective Method of Optimization of Stacking Sequences in the Cylindrical Composite Shells Using Genetic Algorithm. Eur. J. Comput. Mech. 2020, 29-1, 115–138. [Google Scholar] [CrossRef]
- Ashenden, P.J.; Peterson, G.D.; Teegarden, D.A. Chapter twenty-five—Integrated System Modeling. In The System Designer’s Guide to VHDL-AMS, System and Silicon; Morgan Kaufmann: Burlington, MA, USA, 2003; pp. 735–750. [Google Scholar]
- Fan, Y.; Hu, W.; Li, G. Variable stiffness composite material design by using support vector regression assisted efficient global optimization method. Struct. Multidiscip. Optim. 1993, 56, 203–219. [Google Scholar]
- Arian Nik, M.; Fayazbakhsh, K.; Pasini, D.; Lessard, L. Surrogate-based multi-objective optimization of a composite laminate with curvilinear fibers. Compos. Struct. 2012, 94, 2306–2313. [Google Scholar] [CrossRef] [Green Version]
- Arian Nik, M.; Fayazbakhsh, K.; Pasini, D.; Lessard, L. Optimization of variable stiffness composites with embedded defects induced by Automated Fiber Placement. Compos. Struct. 2014, 107, 160–166. [Google Scholar] [CrossRef] [Green Version]
- Fallahi, N.; Carrera, E.; Pagani, A. Application of GA Optimization in Analysis of Variable Stiffness Composites. Facta Univ. Ser. Mech. Eng. 2021, 15, 65–70. [Google Scholar]
- Botto, D.; Alinejad, F. Innovative design of attachment for turbine blade rotating at high speed. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar]
- Alinejad, F.; Botto, D.; Gola, M.; Bessone, A. Reduction of the design space to optimize blade fir-tree attachments. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018; Volume 165, pp. 192–208. [Google Scholar]






| (GPa) | (GPa) | (GPa) | (GPa) | ||
|---|---|---|---|---|---|
| Material | 181 | 10.270 | 7.170 | 3.780 | 0.28 |
| Laminated Scheme | Layup Design | |
|---|---|---|
| [44,51] |
| Description | Maximum Number of Generation | Population Size | Crossover Percentage | Mutation Rate |
|---|---|---|---|---|
| Value | 20 | 50 | 0.8 | 0.04 |
| Laminated Scheme | First Natural Frequency (Hz) | |||
|---|---|---|---|---|
| 438.385 | ||||
| 433.064 | ||||
| 446.235 | ||||
| 438.659 | ||||
| 513.159 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fallahi, N. GA Optimization of Variable Angle Tow Composites in Buckling and Free Vibration Analysis through Layerwise Theory. Aerospace 2021, 8, 376. https://doi.org/10.3390/aerospace8120376
Fallahi N. GA Optimization of Variable Angle Tow Composites in Buckling and Free Vibration Analysis through Layerwise Theory. Aerospace. 2021; 8(12):376. https://doi.org/10.3390/aerospace8120376
Chicago/Turabian StyleFallahi, Nasim. 2021. "GA Optimization of Variable Angle Tow Composites in Buckling and Free Vibration Analysis through Layerwise Theory" Aerospace 8, no. 12: 376. https://doi.org/10.3390/aerospace8120376
APA StyleFallahi, N. (2021). GA Optimization of Variable Angle Tow Composites in Buckling and Free Vibration Analysis through Layerwise Theory. Aerospace, 8(12), 376. https://doi.org/10.3390/aerospace8120376





