An Explosion Based Algorithm to Solve the Optimization Problem in Quadcopter Control
Abstract
:1. Introduction
- There are multiple possible best solutions.
- There is information sharing between the multiple solutions that can assist each other to avoid local optima.
- Exploration in the search space of multiple solutions is more significant than a single solution.
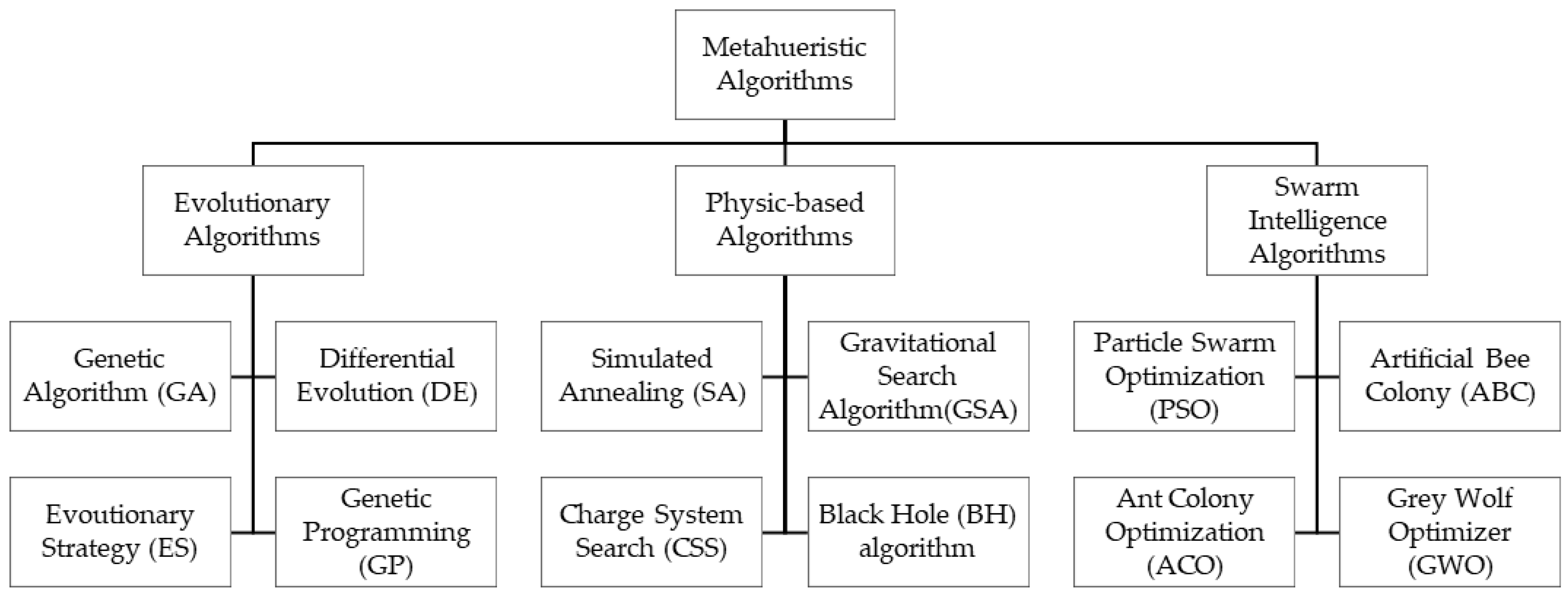
2. Random Explosion Algorithm (REA)
2.1. The Fundamental Concept
2.2. Design of the REA
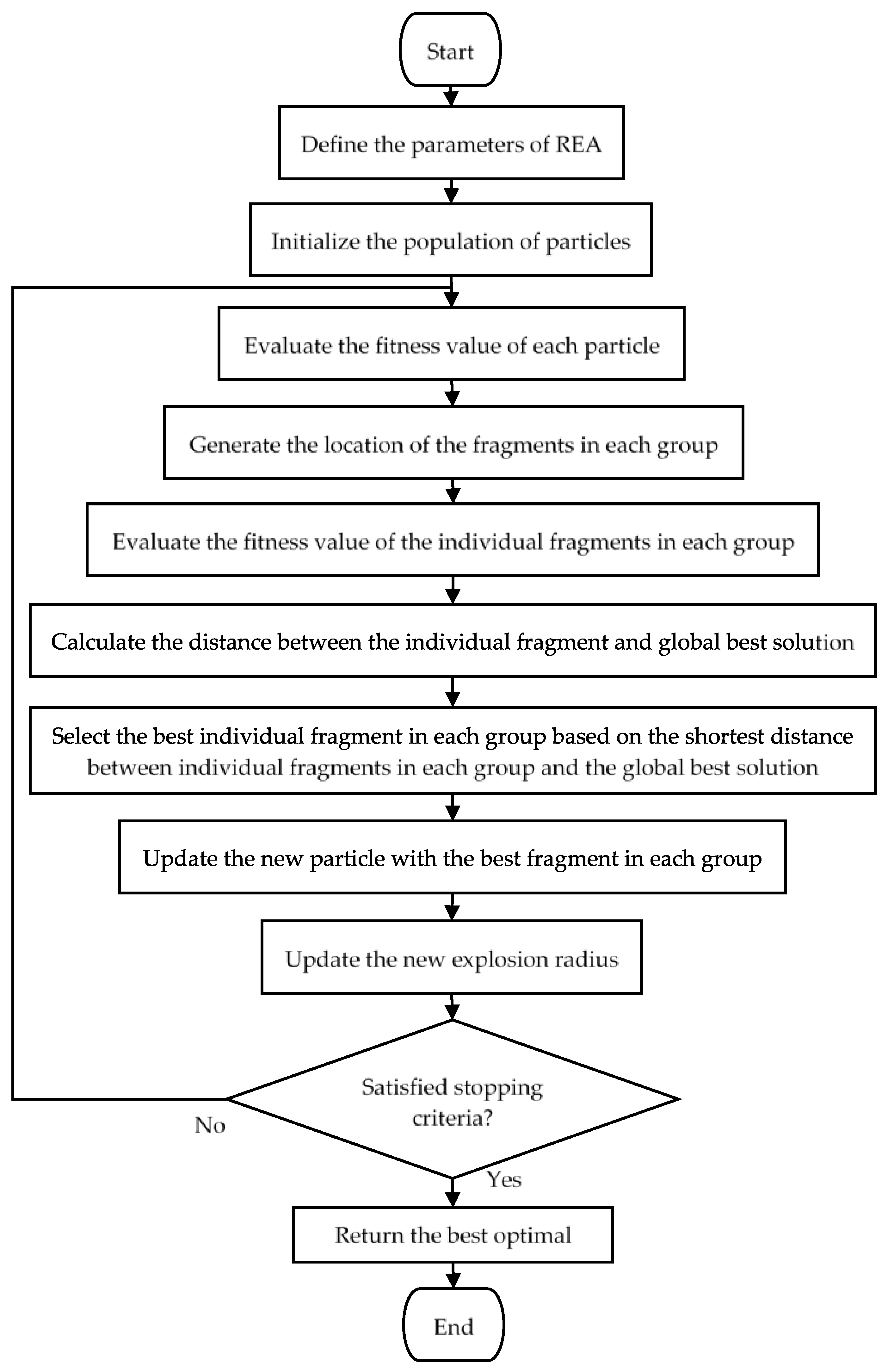
2.3. Steps of Implementation of REA
- Step 1:
- Define the parameters of REA (maximum iteration, number of particles, number of fragments, the radius of the explosion, c).
- Step 2:
- Initialize the particle population, , within the lower and upper bound of the search space, where i = 1, 2, 3, …, m.
- Step 3:
- Evaluate the fitness value of each particle.
- Step 4:
- Explosion: Generate the location of n-number of random fragments, , within the explosion radius, re, in each group (in the first explosion, an initial explosion radius is used; particle 1 will be group 1, particle 2 will be group 2, and so on).
- Step 5:
- Evaluate the fitness value of an individual fragment in each group.
- Step 6:
- Calculate the distance between individual fragments in each group and the global best solution.
- Step 7:
- Selection: Select the best fragment in each group which is the fragment that is nearest (minimum distance) to the global best solution.
- Step 8:
- Update the new particle with the best fragment in each group obtained in Step 7 to continue the next explosion.
- Step 9:
- Update the new explosion radius (explosion radius will be decreasing from the initial explosion radius to 0/~0).
- Step 10:
- If the stopping criterion is satisfied, then the algorithm will be stopped. Otherwise, return to Step 4.
- Step 11:
- Return the best optimal solution (after the stopping criteria are satisfied).
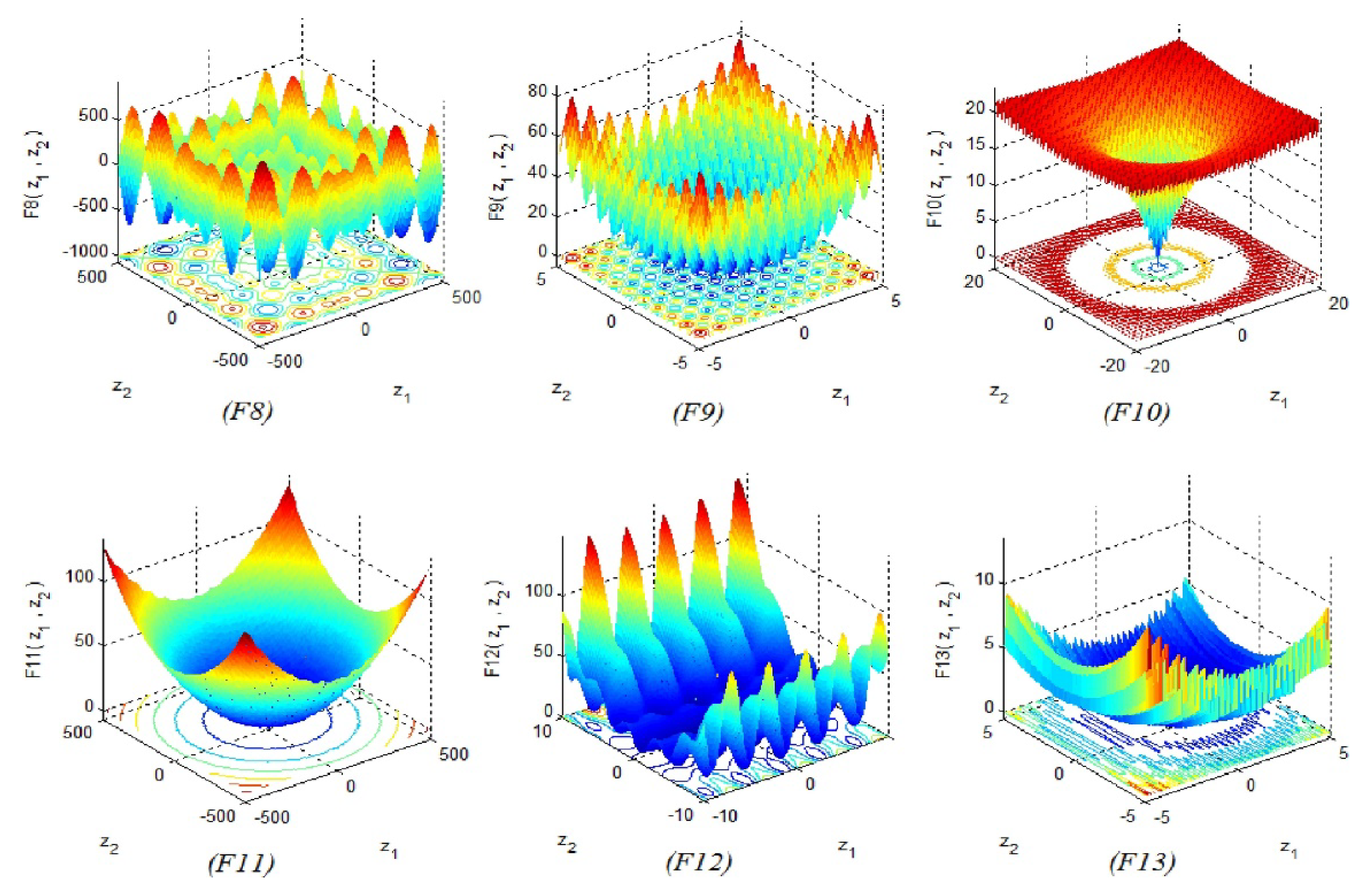
3. REA for the Benchmark Test Functions
4. REA for Quadrotor Control Application
4.1. Mathematical Model of The Quadrotor
4.2. A Hybrid PD2-LQR Controller
4.3. Objective Function
4.4. Experimental Setup
5. Results and Discussion
5.1. Performance Comparison of REA
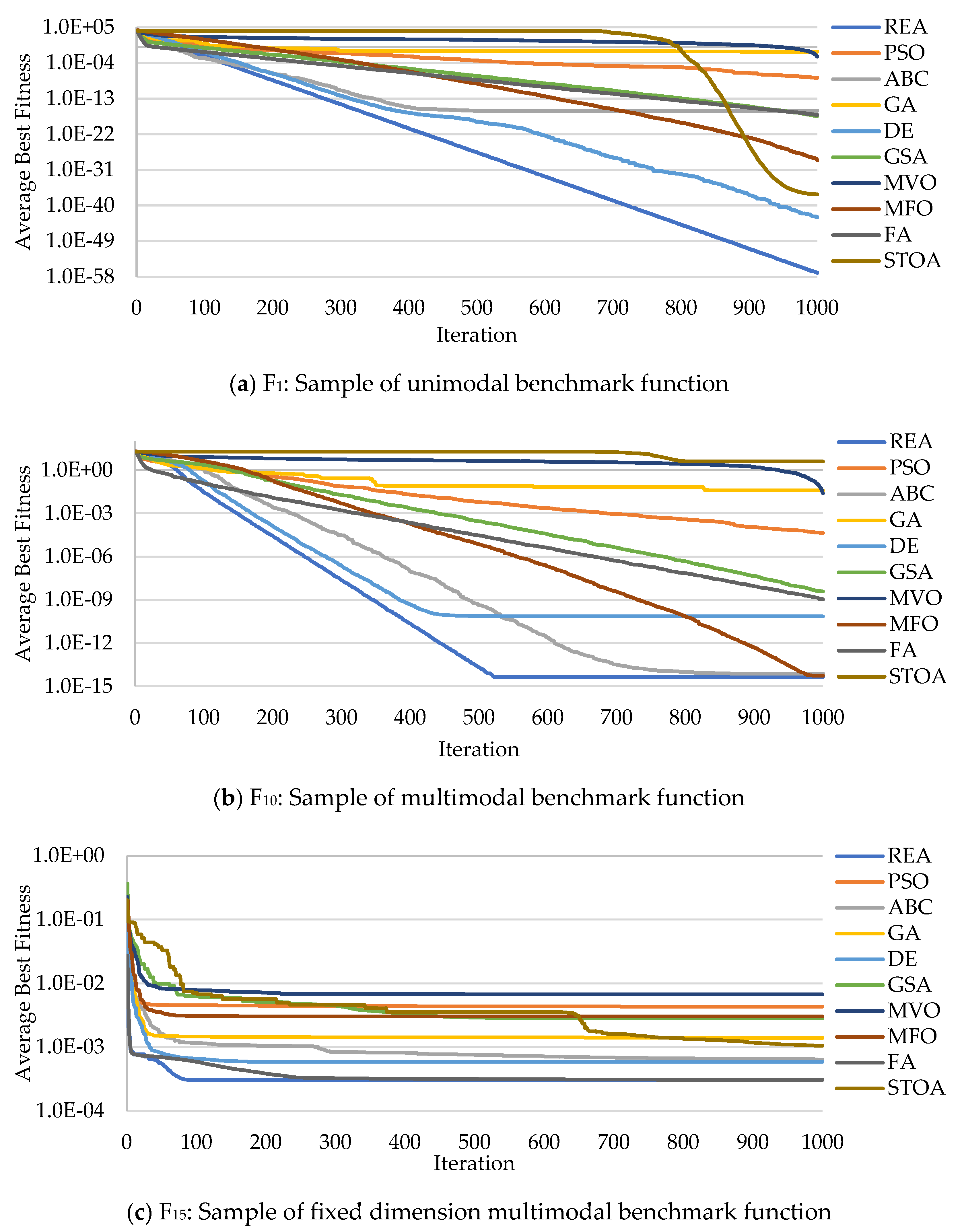
5.2. Convergence Analysis
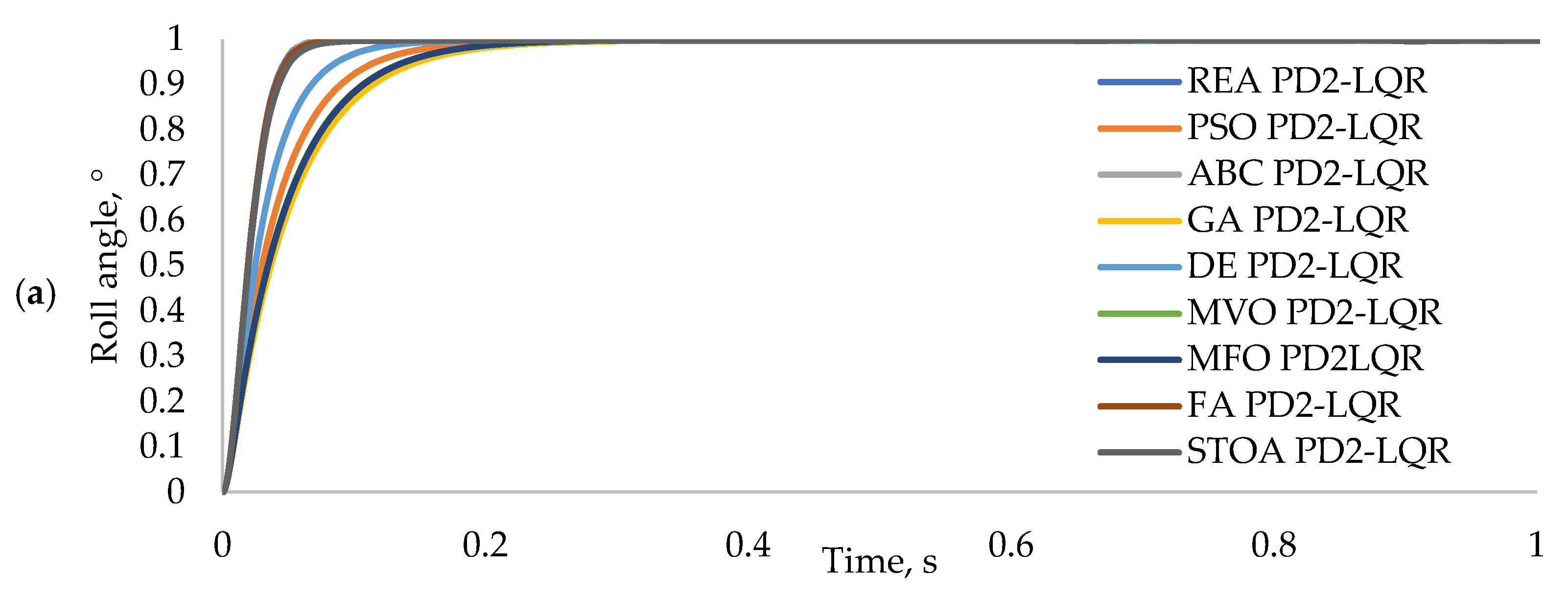
5.3. Performance Comparison of REA Based PD2-LQR Controller
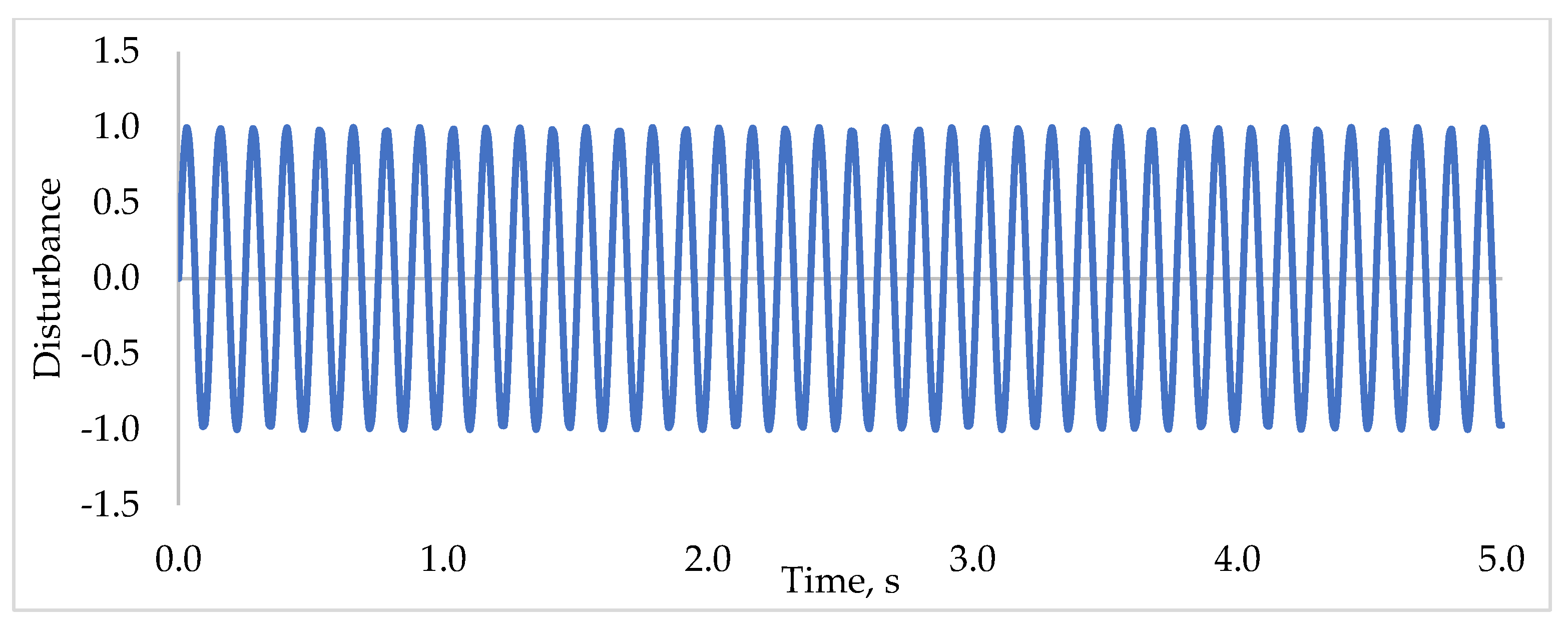
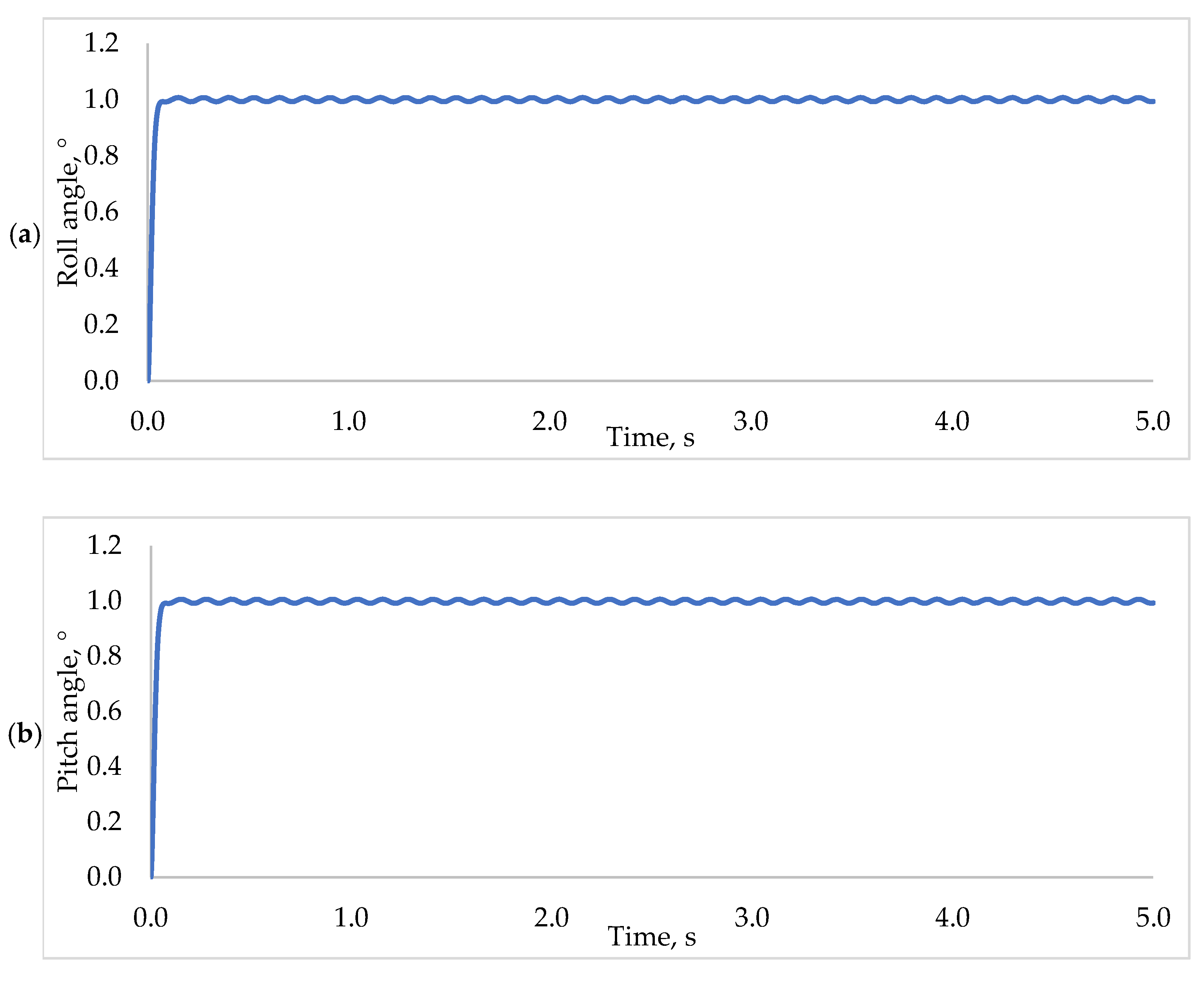
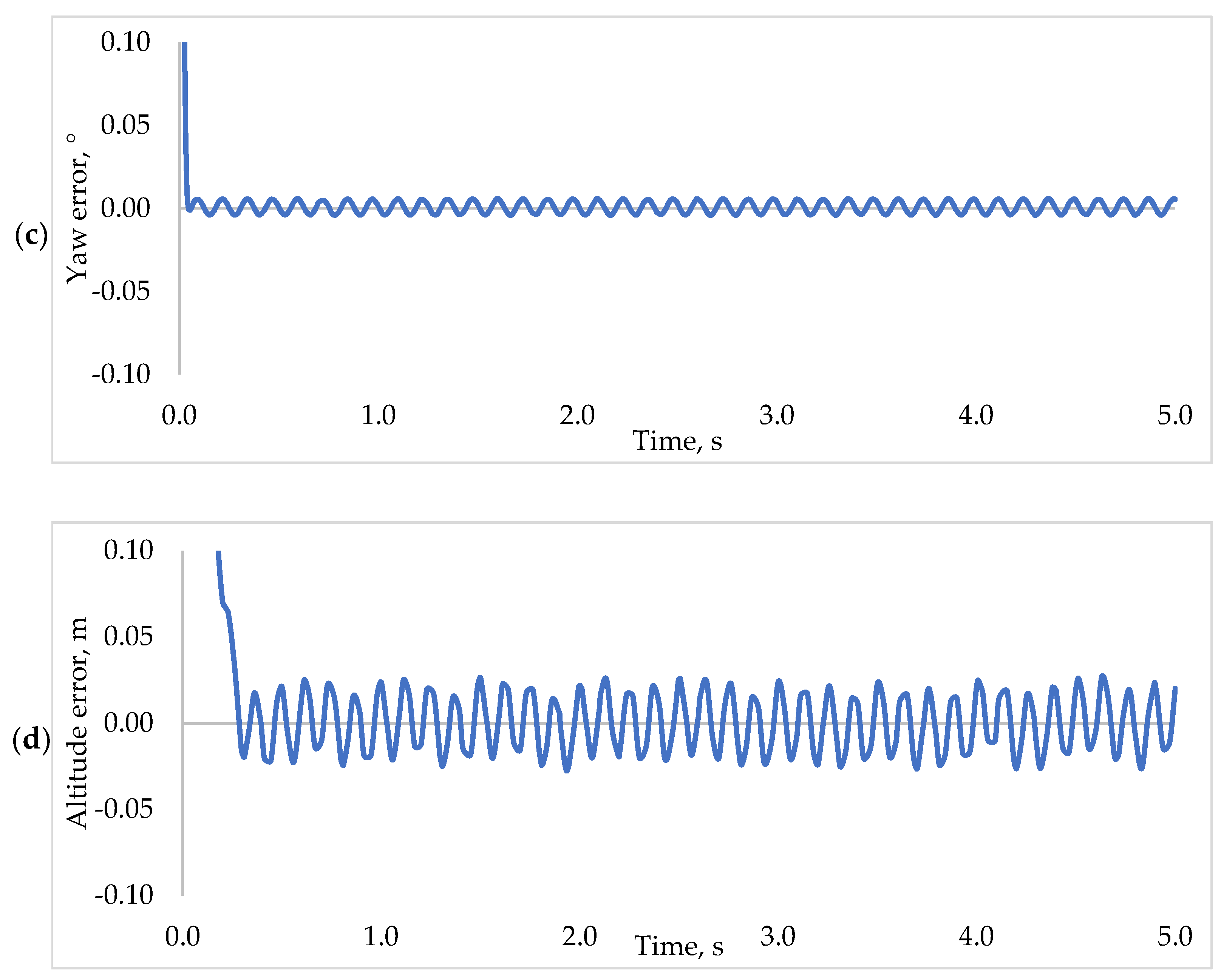
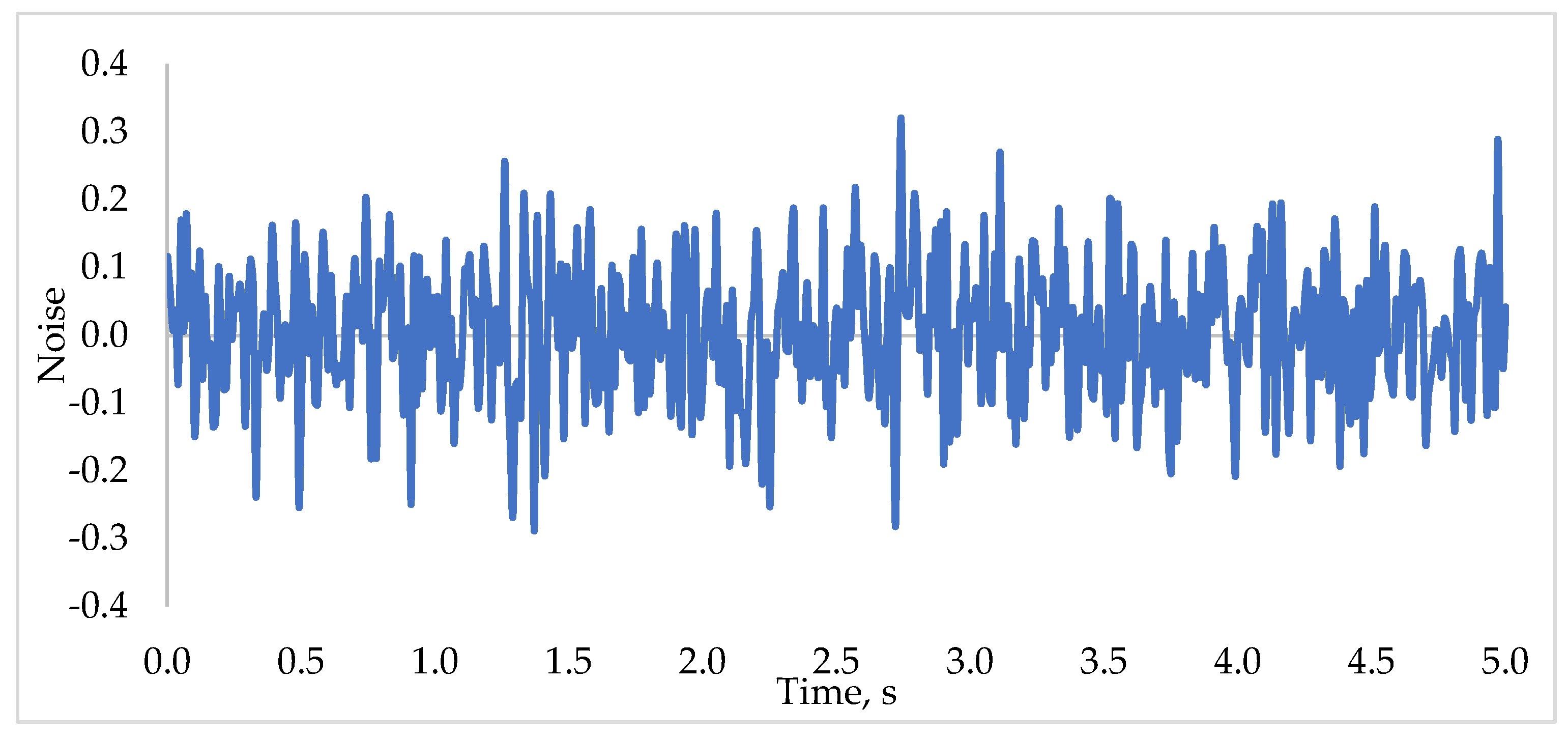
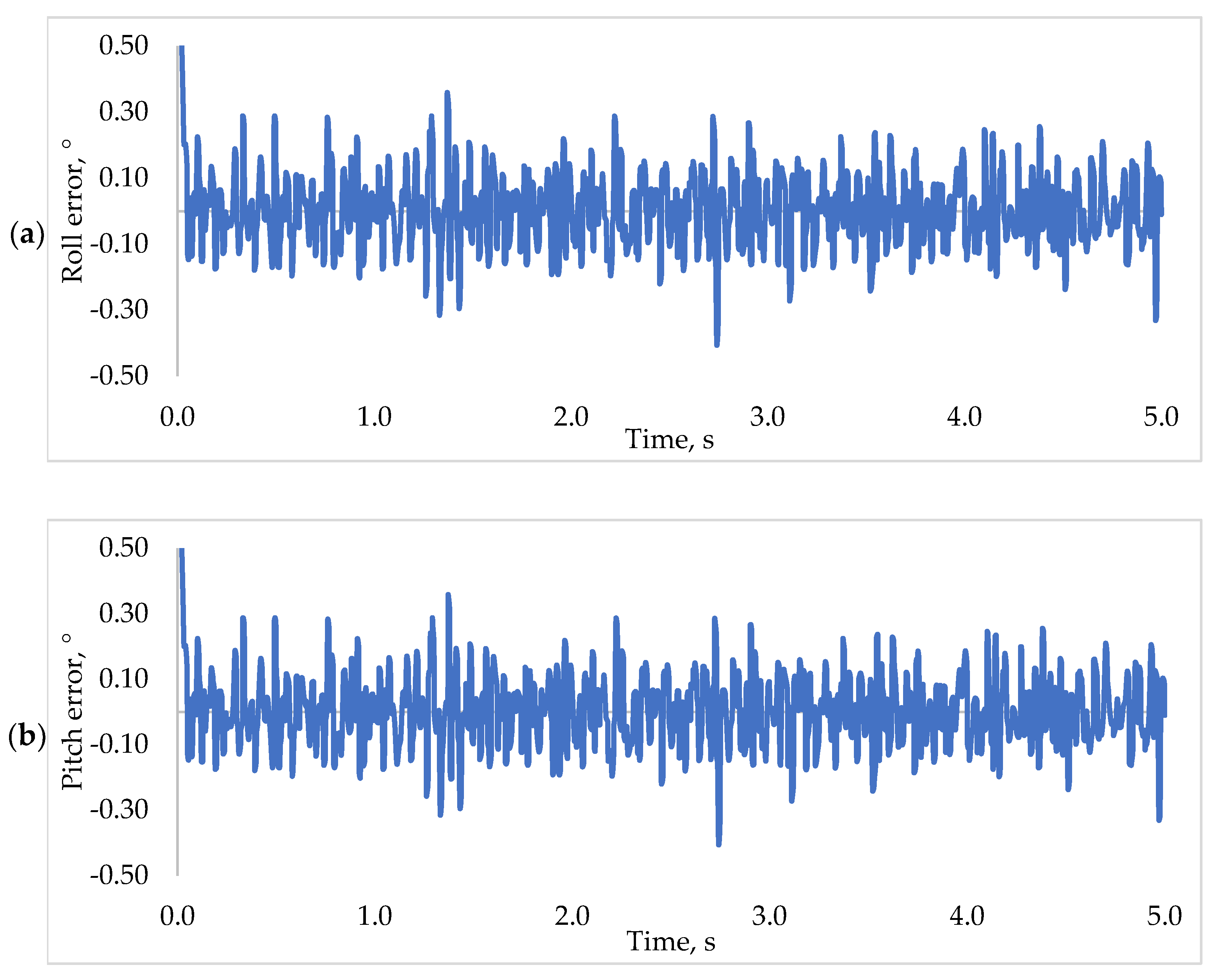
5.4. Robustness Test of REA Based PD2-LQR Controller
5.5. Summary
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Function | Dim | Range | fmin |
|---|---|---|---|
| 10 | (−100, 100) | 0 | |
| 10 | (−10, 10) | 0 | |
| 10 | (−100, 100) | 0 | |
| 10 | (−100, 100) | 0 | |
| 10 | (−30, 30) | 0 | |
| 10 | (−100, 100) | 0 | |
| 10 | (−1.28, 1.28) | 0 |
| Function | Dim | Range | fmin |
|---|---|---|---|
| 10 | (−500, 500) | −418.9829 × Dim | |
| 10 | (−5.12, 5.12) | 0 | |
| 10 | (−32, 32) | 0 | |
| 10 | (−600, 600) | 0 | |
| 10 | (−50, 50) | 0 | |
| 10 | (−50, 50) | 0 | |
| 10 | (0, π) | −4.687 | |
| 10 | (−20, 20) | −1 | |
| 10 | (−10, 10) | −1 |
| Function | Dim | Range | fmin |
|---|---|---|---|
| 2 | (−65.536, 65.536) | 1 | |
| 4 | (−5, 5) | 0.00030 | |
| 2 | (−5, 5) | −1.0316 | |
| 2 | (−5, 5) | 0.398 | |
| 2 | (−2, 2) | 3 | |
| 3 | (0, 1) | −3.86 | |
| 6 | (0, 1) | −3.32 | |
| 4 | (0, 10) | −10.1532 | |
| 4 | (0, 10) | −10.4029 | |
| 4 | (0, 10) | −10.5364 |
Appendix B
| F | REA | PSO | ABC | GA | DE | MVO | MFO | FA | STOA | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ave | Std | Ave | Std | Ave | Std | Ave | Std | Ave | Std | Ave | Std | Ave | Std | Ave | Std | Ave | Std | ||
| Unimodal | F1 | 9.72E-58 | 2.40E-58 | 1.82E-08 | 2.62E-08 | 8.79E-17 | 2.14E-17 | 6.76E-02 | 1.36E-01 | 1.13E-43 | 3.57E-43 | 4.08E-03 | 1.48E-03 | 2.52E-29 | 6.14E-29 | 7.58E-18 | 2.63E-18 | 6.58E-38 | 1.28E-37 |
| F2 | 7.91E-30 | 9.88E-31 | 6.42E-06 | 6.62E-06 | 3.12E-16 | 6.94E-17 | 3.71E-03 | 6.53E-03 | 2.01E-28 | 4.21E-28 | 1.69E-02 | 4.40E-03 | 1.32E-18 | 1.91E-18 | 6.80E-10 | 8.94E-11 | 5.21E-22 | 5.92E-22 | |
| F3 | 1.08E-57 | 1.81E-58 | 2.22E-02 | 2.21E-02 | 1.97E+01 | 1.64E+01 | 2.23E+02 | 1.19E+02 | 1.85E-04 | 3.46E-04 | 2.79E-02 | 1.93E-02 | 1.37E-06 | 2.29E-06 | 1.24E-17 | 3.71E-18 | 1.20E-23 | 2.88E-23 | |
| F4 | 1.81E-29 | 1.56E-30 | 2.00E-02 | 1.82E-02 | 5.97E-03 | 2.09E-03 | 1.19E+00 | 3.94E-01 | 1.47E+00 | 1.47E+00 | 4.66E-02 | 1.92E-02 | 2.53E-01 | 5.14E-01 | 1.62E-09 | 2.55E-10 | 2.45E-14 | 3.67E-14 | |
| F5 | 4.81E+00 | 1.71E+00 | 5.68E+00 | 1.62E+00 | 1.24E-01 | 1.51E-01 | 3.03E+01 | 2.80E+01 | 4.73E+00 | 2.44E+00 | 6.40E+01 | 9.78E+01 | 2.89E+01 | 5.21E+01 | 5.93E-01 | 1.51E+00 | 7.19E+00 | 4.23E-01 | |
| F6 | 0.00E+00 | 0.00E+00 | 6.83E-08 | 1.22E-07 | 9.84E-17 | 5.24E-17 | 2.20E-02 | 2.34E-02 | 9.27E-20 | 2.93E-19 | 3.97E-03 | 2.37E-03 | 9.49E-31 | 1.38E-30 | 8.23E-18 | 2.58E-18 | 1.25E-01 | 1.76E-01 | |
| F7 | 1.34E-04 | 6.06E-05 | 1.36E-03 | 6.20E-04 | 9.02E-03 | 4.40E-03 | 4.28E-03 | 5.70E-03 | 1.81E-03 | 6.87E-04 | 2.13E-03 | 1.13E-03 | 6.52E-03 | 4.18E-03 | 1.90E-04 | 2.23E-04 | 7.70E-04 | 6.85E-04 | |
| Multimodal | F8 | −3.10E+02 | 3.85E+02 | −2.78E+02 | 3.24E+02 | −4.19E+02 | 9.59E-13 | −3.67E+02 | 9.99E+01 | −3.80E+02 | 1.55E+02 | −3.00E+02 | 2.62E+02 | −3.30E+02 | 3.53E+02 | −3.55E+02 | 2.77E+02 | −2.64E+02 | 2.48E+02 |
| F9 | 1.60E+01 | 6.25E+00 | 6.88+E00 | 2.46E+00 | 0.00E+00 | 0.00E+00 | 2.31E-03 | 4.13E-03 | 3.29E+00 | 3.81E+00 | 1.56E+01 | 6.29E+00 | 1.91E+01 | 8.15E+00 | 8.16E+00 | 3.03E+00 | 6.97E-01 | 2.20E+00 | |
| F10 | 4.44E-15 | 0.00E+00 | 4.43E-05 | 3.12E-05 | 7.64E-15 | 2.02E-15 | 3.87E-02 | 5.68E-02 | 7.13E-11 | 2.25E-10 | 2.51E-02 | 5.34E-03 | 5.51E-15 | 1.72E-15 | 1.10E-09 | 1.84E-10 | 3.98E+00 | 8.40E+00 | |
| F11 | 2.62E-01 | 1.48E-01 | 1.69E-01 | 9.87E-02 | 1.72E-03 | 5.45E-03 | 6.11E-02 | 3.76E-02 | 3.72E-02 | 2.01E-02 | 3.61E-01 | 1.23E-01 | 2.13E-01 | 1.55E-01 | 6.08E-02 | 1.32E-02 | 2.25E-02 | 5.29E-02 | |
| F12 | 4.71E-32 | 1.15E-47 | 3.77E-10 | 4.12E-10 | 7.88E-17 | 2.13E-17 | 2.43E-04 | 2.01E-04 | 4.76E-32 | 1.23E-33 | 1.36E-04 | 7.16E-05 | 9.33E-02 | 2.10E-01 | 7.03E-20 | 1.97E-20 | 2.81E-02 | 1.50E-02 | |
| F13 | 1.35E-32 | 2.89E-48 | 3.49E-09 | 7.31E-09 | 9.41E-17 | 1.39E-17 | 4.71E-03 | 5.50E-03 | 1.40E-32 | 1.56E-33 | 1.82E-03 | 3.55E-03 | 4.39E-03 | 5.67E-03 | 3.99E-19 | 5.62E-20 | 1.33E-01 | 7.34E-02 | |
| Fixed-dimension Multimodal | F14 | 9.98E-01 | 0.00E+00 | 4.06E+00 | 2.52E+00 | 9.98E-01 | 1.05E-16 | 9.98E-01 | 1.44E-10 | 9.98E-01 | 0.00E+00 | 9.98E-01 | 4.70E-12 | 1.79E+00 | 1.30E+00 | 9.98E-01 | 2.67E-16 | 1.59E+00 | 9.58E-01 |
| F15 | 3.07E-04 | 5.71E-20 | 4.32E-03 | 8.46E-03 | 6.37E-04 | 9.97E-05 | 1.40E-03 | 5.48E-04 | 5.88E-04 | 4.32E-04 | 6.70E-03 | 9.43E-03 | 3.02E-03 | 6.10E-03 | 3.07E-04 | 1.86E-09 | 1.05E-03 | 3.74E-04 | |
| F16 | −1.03E+00 | 0.00E+00 | −1.03E+00 | 0.00E+00 | −1.03E+00 | 1.96E-16 | −1.03E+00 | 2.52E-06 | −1.03E+00 | 0.00E+00 | −1.03E+00 | 1.10E-07 | −1.03E+00 | 0.00E+00 | −1.03E+00 | 1.66E-16 | −1.03E+00 | 4.31E-07 | |
| F17 | 3.98E-01 | 0.00E+00 | 3.98E-01 | 0.00E+00 | 3.98E-01 | 0.00E+00 | 3.98E-01 | 3.54E-07 | 3.98E-01 | 0.00E+00 | 3.98E-01 | 2.10E-07 | 3.98E-01 | 0.00E+00 | 3.98E-01 | 0.00E+00 | 3.98E-01 | 2.04E-05 | |
| F18 | 3.00E+00 | 4.68E-16 | 3.00E+00 | 2.09E-16 | 3.00E+00 | 4.53E-06 | 3.00E+00 | 2.47E-07 | 3.00E+00 | 1.48E-15 | 3.00E+00 | 9.97E-07 | 3.00E+00 | 1.55E-15 | 3.00E+00 | 7.40E-16 | 3.00E+00 | 7.04E-06 | |
| F19 | −3.86E+00 | 4.68E-16 | −3.86E+00 | 8.24E-16 | −3.86E+00 | 5.34E-16 | −3.86E+00 | 1.01E-04 | −3.86E+00 | 9.36E-16 | −3.86E+00 | 2.85E-07 | −3.86E+00 | 9.36E-16 | −3.86E+00 | 4.91E-16 | −3.85E+00 | 2.31E-05 | |
| F20 | −3.20E+00 | 9.26E-08 | −3.29E+00 | 5.74E-02 | −3.32E+00 | 3.63E-16 | −3.07E+00 | 6.70E-01 | −3.26E+00 | 6.27E-02 | −3.25E+00 | 6.17E-02 | −3.23E+00 | 6.52E-02 | −3.27E+00 | 6.14E-02 | −3.01E+00 | 1.43E-01 | |
| F21 | −1.02E+01 | 1.87E-15 | −6.90E+00 | 3.54E+00 | −1.02E+01 | 1.87E-15 | −7.17E+00 | 3.86E+00 | −1.02E+01 | 5.92E-16 | −7.62E+00 | 2.67E+00 | −7.39E+00 | 3.01E+00 | −1.02E+01 | 2.37E-15 | −5.50E+00 | 4.31E+00 | |
| F22 | −1.04E+01 | 0.00E+00 | −7.67E+00 | 3.58E+00 | −1.04E+01 | 5.13E-12 | −8.11E+00 | 3.70E+00 | −1.04E+01 | 2.37E-15 | −7.81E+00 | 3.43E+00 | −8.21E+00 | 3.54E+00 | −1.04E+01 | 1.57E-15 | −6.45E+00 | 5.05E+00 | |
| F23 | −1.05E+01 | 0.00E+00 | −6.71E+00 | 4.05E+00 | −1.05E+01 | 3.19E-15 | −1.00E+01 | 1.70E+00 | −1.05E+01 | 1.87E-15 | −9.46E+00 | 2.27E+00 | −8.47E+00 | 3.39E+00 | −1.05E+01 | 1.32E-15 | −7.25E+00 | 4.38E+00 | |
Appendix C
| References | Sinusoidal Wind Gust Profile | |
|---|---|---|
| Amplitude | Frequency | |
| Yang and Yan [70] | 0.002–0.01 | π/100 |
| Khebbache and Tadjine [71] | 0.004–0.008 | 0.1 |
| Razmi and Afshinfar [72] | 0.01 | 0.01 |
| Dong and He [73] | 0.1–0.15 | 0.1π |
| Barikbin and Fakharian [56] | 0.1–0.2 | 0.3–0.5 |
| Alkamachi and Erçelebi [74] | 0.2 | 0.5 |
| Li, Ma [75] | 0.2 | 1.5–2 |
| Doukhi and Lee [49] | 0.8 | 0.6 |
| Zhen, Qi [76] | 1 | 1 |
| Nadda and Swarup [77] | 1 | 2 |
| Budiyono, Kang [78] | 1 | ≈0.16 |
| Luque-Vega, Castillo-Toledo [79] | 1 | 0.1 |
| Ru and Subbarao [80] | 1 | 10 |
| Fethalla, Saad [81] | 1–2.5 | 0.1–4 |
| Wang and Chen [82] | 10–60 | 1.2–3 |
| Ha and Hong [83] | (3t + 5), (2t) | 1–2 |
References
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Dhiman, G.; Kumar, V. Emperor penguin optimizer: A bio-inspired algorithm for engineering problems. Knowl. Based Syst. 2018, 159, 20–50. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Spotted hyena optimizer: A novel bio-inspired based metaheuristic technique for engineering applications. Adv. Eng. Softw. 2017, 114, 48–70. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution–A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Rechenberg, I. Evolutionsstrategien, in Simulationsmethoden in der Medizin und Biologie; Springer: Berlin/Heidelberg, Germany, 1978; pp. 83–114. [Google Scholar]
- Beyer, G.H.P.; Schwefel, H. Evolution strategies–A comprehensive introduction. Nat. Comput. 2002, 1, 3–52. [Google Scholar] [CrossRef]
- Koza, R.J.; Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992; Volume 1. [Google Scholar]
- Simon, D. Biogeography-Based Optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef] [Green Version]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Hatamlou, A. Black hole: A new heuristic optimization approach for data clustering. Inf. Sci. 2013, 222, 175–184. [Google Scholar] [CrossRef]
- Kaveh, A.; Khayatazad, M. A new meta-heuristic method: Ray Optimization. Comput. Struct. 2012, 112–113, 283–294. [Google Scholar] [CrossRef]
- Erol, K.O.; Eksin, I. A new optimization method: Big Bang–Big Crunch. Adv. Eng. Softw. 2006, 37, 106–111. [Google Scholar] [CrossRef]
- Formato, R.A. Central force optimization: A new deterministic gradient-like optimization metaheuristic. OPSEARCH 2009, 46, 25–51. [Google Scholar] [CrossRef]
- Kaveh, A.; Talatahari, S. A novel heuristic optimization method: Charged system search. Acta Mech. 2010, 213, 267–289. [Google Scholar] [CrossRef]
- Du, H.; Wu, X.; Zhuang, J. Small-World Optimization Algorithm for Function Optimization. In Advances in Natural Computation; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Alatas, B. ACROA: Artificial Chemical Reaction Optimization Algorithm for global optimization. Expert Syst. Appl. 2011, 38, 13170–13180. [Google Scholar] [CrossRef]
- Shah-Hosseini, H. Principal components analysis by the galaxy-based search algorithm: A novel metaheuristic for continuous optimisation. Int. J. Comput. Sci. Eng. 2011, 6, 132–140. [Google Scholar]
- Moghaddam, F.F.; Moghaddam, R.F.; Cheriet, M. Curved space optimization: A random search based on general relativity theory. arXiv 2012, arXiv:1208.2214. Available online: https://arxiv.org/pdf/1208.2214.pdf (accessed on 24 April 2021).
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Western Australia, 27 November–1 December 1995. [Google Scholar]
- Dorigo, M.; Birattari, M.; Stützle, T. Ant Colony Optimization: Artificial Ants as a Computational Intelligence Technique. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef] [Green Version]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Mucherino, A.; Seref, O. Monkey Search: A Novel Metaheuristic Search for Global Optimization. In AIP Conference Proceedings; American Institute of Physics: College Park, MA, USA, 2007. [Google Scholar]
- Yang, X.; Suash, D. Cuckoo Search via Lévy Flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009. [Google Scholar]
- Yang, X.-S. A New Metaheuristic Bat-Inspired Algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); González, J.R., Pelta, D.A., Cruz, C., Terrazas, G., Krasnogor, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar]
- Shiqin, Y.; Jianjun, J.; Guangxing, Y. A Dolphin Partner Optimization. In Proceedings of the 2009 WRI Global Congress on Intelligent Systems, Xiamen, China, 19–21 May 2009. [Google Scholar]
- Yang, X.-S. Firefly algorithm, stochastic test functions and design optimisation. Int. J. Bio-Inspired Comput. 2010, 2, 78–84. [Google Scholar] [CrossRef]
- Lu, X.; Zhou, Y. A Novel Global Convergence Algorithm: Bee Collecting Pollen Algorithm. In Advanced Intelligent Computing Theories and Applications. With Aspects of Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Abbass, H.A. MBO: Marriage in Honey Bees Optimization-A Haplometrosis Polygynous Swarming Approach. In Proceedings of the 2001 Congress on Evolutionary Computation (IEEE Cat. No. 01TH8546), Seoul, Korea, 27–30 May 2001. [Google Scholar]
- Alba, E.; Dorronsoro, B. The exploration/exploitation tradeoff in dynamic cellular genetic algorithms. IEEE Trans. Evol. Comput. 2005, 9, 126–142. [Google Scholar] [CrossRef] [Green Version]
- Olorunda, O.; Engelbrecht, A.P. Measuring Exploration/Exploitation in Particle Swarms Using Swarm Diversity. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), Hong Kong, 1–6 June 2008. [Google Scholar]
- Lozano, M.; García-Martínez, C. Hybrid metaheuristics with evolutionary algorithms specializing in intensification and diversification: Overview and progress report. Comput. Oper. Res. 2010, 37, 481–497. [Google Scholar] [CrossRef]
- Shanghooshabad, M.A.; Abadeh, M.S. Robust, interpretable and high quality fuzzy rule discovery using krill herd algorithm. J. Intell. Fuzzy Syst. 2016, 30, 1601–1612. [Google Scholar] [CrossRef]
- Ali, F.A.; Tawhid, M.A. Ahybrid cuckoo search algorithm with Nelder Mead method for solving global optimization problems. Springer Plus 2016, 5, 473. [Google Scholar] [CrossRef] [Green Version]
- Baer, K.; Ericson, L.; Krus, P. Robustness and performance evaluations for simulation-based control and component parameter optimization for a series hydraulic hybrid vehicle. Eng. Optim. 2020, 52, 446–464. [Google Scholar] [CrossRef] [Green Version]
- Wolpert, H.D.; Macready, W.G. Nofree lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Shehab, M.; Khader, A.T.; Al-Betar, M.A. A survey on applications and variants of the cuckoo search algorithm. Appl. Soft Comput. 2017, 61, 1041–1059. [Google Scholar] [CrossRef]
- Tangherloni, A.; Spolaor, S.; Cazzaniga, P.; Besozzi, D.; Rundo, L.; Mauri, G.; Nobile, M.S. Biochemical parameter estimation vs. benchmark functions: A comparative study of optimization performance and representation design. Appl. Soft Comput. 2019, 81, 105494. [Google Scholar] [CrossRef]
- Jamil, M.; Yang, X.-S. A literature survey of benchmark functions for global optimisation problems. Int. J. Math. Model. Numer. Optim. 2013, 4, 150–194. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.X.; He, X.-S.; Fan, Q.-W. Chapter 7-Mathematical framework for algorithm analysis. In Nature-Inspired Computation and Swarm Intelligence; Yang, X.S., Ed.; Academic Press: Cambridge, MA, USA, 2020; pp. 89–108. [Google Scholar]
- Digalakis, G.J.; Margaritis, K.G. On benchmarking functions for genetic algorithms. Int. J. Comput. Math. 2001, 77, 481–506. [Google Scholar] [CrossRef]
- Saud, L.; Hasan, A. Design of an Optimal Integral Backstepping Controller for a Quadcopter. J. Eng. 2018, 24, 46. [Google Scholar] [CrossRef]
- Erkol, H.O. Attitude controller optimization of four-rotor unmanned air vehicle. Int. J. Micro Air Veh. 2017, 10, 42–49. [Google Scholar] [CrossRef]
- Thanh, N.H.L.N.; Hong, S.K. Quadcopter Robust Adaptive Second Order Sliding Mode Control Based on PID Sliding Surface. IEEE Access 2018, 6, 66850–66860. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-Verse Optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Dhiman, G.; Kaur, A. STOA: A bio-inspired based optimization algorithm for industrial engineering problems. Eng. Appl. Artif. Intell. 2019, 82, 148–174. [Google Scholar] [CrossRef]
- Doukhi, O.; Lee, D.J. Neural Network-based Robust Adaptive Certainty Equivalent Controller for Quadrotor UAV with Unknown Disturbances. Int. J. Control. Autom. Syst. 2019, 17, 2365–2374. [Google Scholar] [CrossRef]
- Tanveer, M.H.; Hazry, D.; Ahmed, S.F.; Joyo, M.K.; Warsi, F.A.; Kamarudin, H.; Wan, K.; Razlan, Z.M.; Shahriman, A.B.; Hussain, A.T. Feedback sensor noise rejection control strategy for quadrotor UAV system. Aip Conf. Proc. 2015, 1660, 070053. [Google Scholar]
- Raza, S.; Gueaieb, W. Intelligent Flight Control of an Autonomous Quadrotor. In Motion Control; Casolo, F., Ed.; INTECH: Rijeka, Croatia, 2010; p. 580. [Google Scholar]
- Burggräf, P.; Martínez, A.R.P.; Roth, H.; Wagner, J. Quadrotors in factory applications: Design and implementation of the quadrotor’s P-PID cascade control system. SN Appl. Sci. 2019, 1, 722. [Google Scholar] [CrossRef] [Green Version]
- Rich, M.; Elia, N.; Jones, P. Design and Implementation of an H∞ Controller for a Quadrotor Helicopter. In Proceedings of the 21st Mediterranean Conference on Control and Automation, Crete, Greece, 25–28 June 2013. [Google Scholar]
- Hong, K.S.; Nguyen, N.P. Position control of a hummingbird quadcopter augmented by gain scheduling. Int. J. Eng. Res. Technol. 2018, 11, 1485–1498. [Google Scholar]
- Nelson, R.C. Flight Stability and Automatic Control, 2nd ed.; McGraw Hill: New York, NY, USA, 1998. [Google Scholar]
- Barikbin, B.; Fakharian, A. Trajectory tracking for quadrotor UAV transporting cable-suspended payload in wind presence. Trans. Inst. Meas. Control 2018, 41, 1243–1255. [Google Scholar] [CrossRef]
- Guo, Y.; Jiang, B.; Zhang, Y. A novel robust attitude control for quadrotor aircraft subject to actuator faults and wind gusts. IEEE/CAA J. Autom. Sin. 2018, 5, 292–300. [Google Scholar] [CrossRef]
- Li, J.; Li, Y. Dynamic Analysis and PID Control for a Quadrotor. In Proceedings of the 2011 IEEE International Conference on Mechatronics and Automation, Beijing, China, 7–10 August 2011. [Google Scholar]
- Fang, Z.; Gao, W. Adaptive backstepping control of an indoor micro-quadrotor. Res. J. Appl. Sci. Eng. Technol. 2012, 4, 4216–4226. [Google Scholar]
- Mohammadi, M.; Shahri, A.M. Adaptive Nonlinear Stabilization Control for a Quadrotor UAV: Theory, Simulation and Experimentation. J. Intell. Robot. Syst. 2013, 72, 105–122. [Google Scholar] [CrossRef]
- Tan, L.; Lu, L.; Jin, G. Attitude stabilization control of a quadrotor helicopter using integral backstepping. Iet Conf. Proc. 2012, 573–577. [Google Scholar]
- Kim, G.B.; Nguyen, T.K.; Budiyono, A.; Park, J.K.; Yoon, K.J.; Shin, J. Design and Development of a Class of Rotorcraft-Based UAV. Int. J. Adv. Robot. Syst. 2013, 10, 131. [Google Scholar] [CrossRef] [Green Version]
- Abbasi, E. Development and Implementation of a Adaptive Fuzzy Control System for a VTOL Vehicle in Hovering Mode. Int. J. Control Theory Comput. Modeling 2017, 7, 1–14. [Google Scholar] [CrossRef]
- Xuan-Mung, N.; Hong, S.-K. Improved Altitude Control Algorithm for Quadcopter Unmanned Aerial Vehicles. Appl. Sci. 2019, 9, 2122. [Google Scholar] [CrossRef] [Green Version]
- Martins, L.; Cardeira, C.; Oliveira, P. Linear Quadratic Regulator for Trajectory Tracking of a Quadrotor. Ifac Pap. Online 2019, 52, 176–181. [Google Scholar] [CrossRef]
- Wu, Y.; Hu, K.; Sun, X. Modeling and Control Design for Quadrotors: A Controlled Hamiltonian Systems Approach. IEEE Trans. Veh. Technol. 2018, 67, 11365–11376. [Google Scholar] [CrossRef]
- Choi, Y.; Ahn, H. Nonlinear Control of Quadrotor for Point Tracking: Actual Implementation and Experimental Tests. IEEE/ASME Trans. Mechatron. 2015, 20, 1179–1192. [Google Scholar] [CrossRef]
- Lu, H.; Liu, C.; Coombes, M.; Guo, L.; Chen, W. Online optimisation-based backstepping control design with application to quadrotor. IET Control Theory Appl. 2016, 10, 1601–1611. [Google Scholar] [CrossRef] [Green Version]
- Feng, B. Robust Control for Lateral and Longitudinal Channels of Small-Scale Unmanned Helicopters. J. Control Sci. Eng. 2015, 2015, 483096. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Yan, Y. Attitude regulation for unmanned quadrotors using adaptive fuzzy gain-scheduling sliding mode control. Aerosp. Sci. Technol. 2016, 54, 208–217. [Google Scholar] [CrossRef]
- Khebbache, H.; Tadjine, M. Robust fuzzy backstepping sliding mode controller for a quadrotor unmanned aerial vehicle. J. Control Eng. Appl. Inform. 2013, 15, 3–11. [Google Scholar]
- Razmi, H.; Afshinfar, S. Neural network-based adaptive sliding mode control design for position and attitude control of a quadrotor UAV. Aerosp. Sci. Technol. 2019, 91, 12–27. [Google Scholar] [CrossRef]
- Dong, J.; He, B. Novel Fuzzy PID-Type Iterative Learning Control for Quadrotor UAV. Sensors 2019, 19, 24. [Google Scholar]
- Alkamachi, A.; Erçelebi, E. H∞ control of an overactuated tilt rotors quadcopter. J. Cent. South Univ. 2018, 25, 586–599. [Google Scholar] [CrossRef]
- Li, Z.; Ma, X.; Li, Y. Robust tracking control strategy for a quadrotor using RPD-SMC and RISE. Neurocomputing 2019, 331, 312–322. [Google Scholar] [CrossRef]
- Zhen, H.; Qi, X.; Dong, H. An adaptive block backstepping controller for attitude stabilization of a quadrotor helicopter. WSEAS Trans. Syst. Control 2013, 8, 46–55. [Google Scholar]
- Nadda, S.; Swarup, A. Improved Quadrotor Altitude Control Design Using Second-Order Sliding Mode. J. Aerosp. Eng. 2017, 30, 04017065. [Google Scholar] [CrossRef]
- Budiyono, A.; Kang, T.; Dharmayanda, H.R. State space identification and implementation of H∞ control design for small-scale helicopter. Aircr. Eng. Aerosp. Technol. 2010, 82, 340–352. [Google Scholar]
- Luque-Vega, L.; Castillo-Toledo, B.; Loukianov, A.G. Robust block second order sliding mode control for a quadrotor. J. Frankl. Inst. 2012, 349, 719–739. [Google Scholar] [CrossRef]
- Ru, P.; Subbarao, K. Nonlinear Model Predictive Control for Unmanned Aerial Vehicles. Aerospace 2017, 4, 31. [Google Scholar] [CrossRef]
- Fethalla, N.; Saad, M.; Michalska, H.; Ghommam, J. Robust Observer-Based Dynamic Sliding Mode Controller for a Quadrotor UAV. IEEE Access 2018, 6, 45846–45859. [Google Scholar] [CrossRef]
- Wang, H.; Chen, M. Trajectory tracking control for an indoor quadrotor UAV based on the disturbance observer. Trans. Inst. Meas. Control 2015, 38, 675–692. [Google Scholar] [CrossRef]
- Ha, L.N.; Hong, S.K. Robust Dynamic Sliding Mode Control-Based PID–Super Twisting Algorithm and Disturbance Observer for Second-Order Nonlinear Systems: Application to UAVs. Electronics 2019, 8, 760. [Google Scholar] [CrossRef] [Green Version]





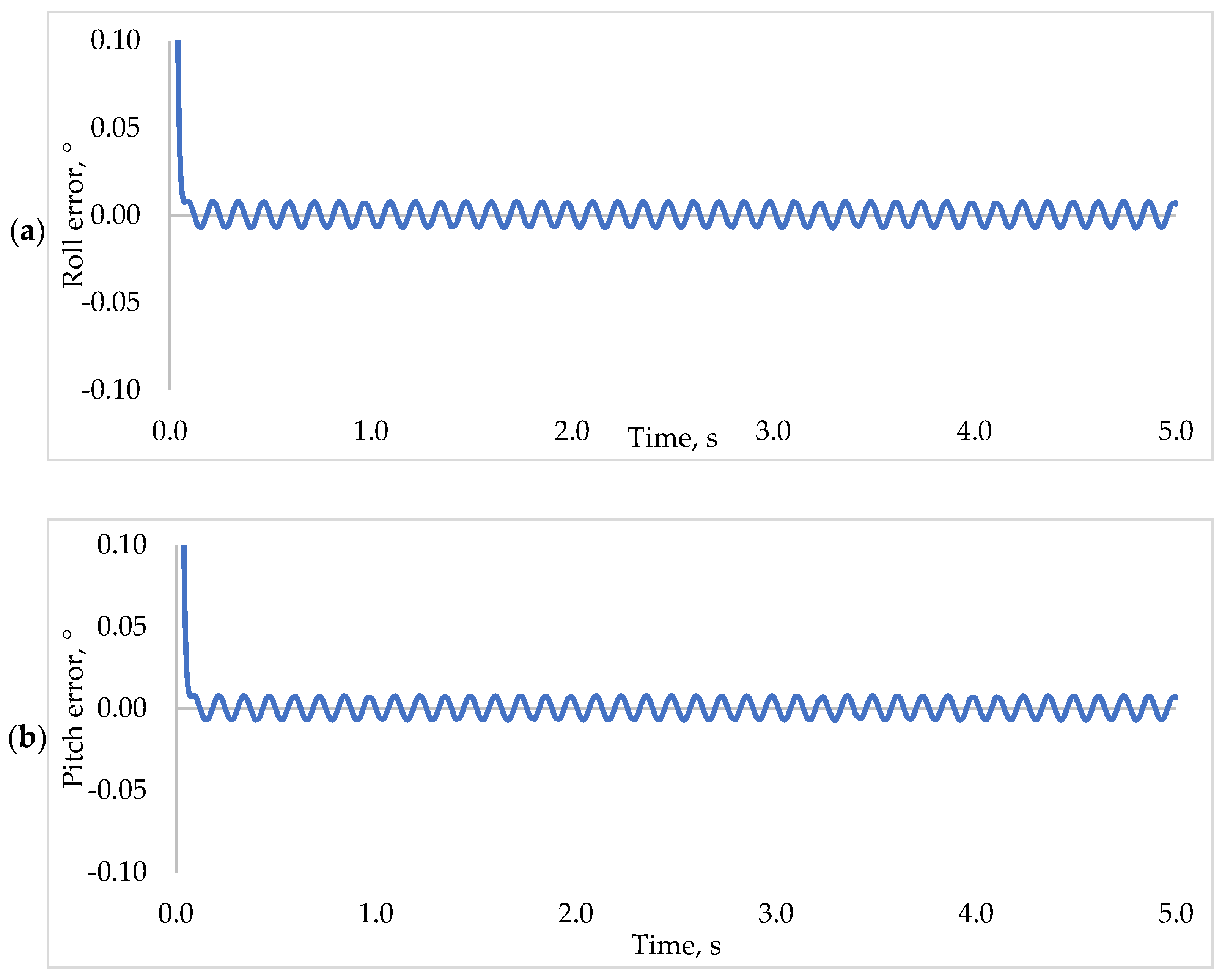



| Parameter | Value | Unit |
|---|---|---|
| Mass, m | 1.12 | Kg |
| Arm length, l | 0.23 | m |
| Inertia x-axis, Ix | 1.19 × 10−2 | Kgm2 |
| Inertia y-axis, Iy | 1.19 × 10−2 | Kgm2 |
| Inertia z-axis, Iz | 2.23 × 10−2 | Kgm2 |
| Rotor inertia, Jr | 8.50 × 10−4 | Kgm2 |
| Thrust coefficient, b | 7.73 × 10−6 | Ns2 |
| Drag coefficient, d | 1.28 × 10−7 | Nms2 |
| No. | Algorithms | Parameters | Value |
|---|---|---|---|
| 1 | Random Explosion Algorithm (REA) | No. of fragments, nF Explosion radius, re c | 90 (triple of the population size) (Ub, ~0) 70 |
| 2 | Particle Swarm Optimization (PSO) | Inertia coefficient, w Cognitive and social coefficient, c1, c2 | 0.75 1.8, 2 |
| 3 | Artificial Bee Colony (ABC) | Parameter limit | Number of food source × dimension, (number of food source = number of populations, dimension = dimension of solution) |
| 4 | Genetic Algorithm (GA) | Crossover Mutation | 0.9 0.05 |
| 5 | Differential Evolution (DE) | Crossover Scale factor | 0.9 0.5 |
| 6 | Multi-Verse Optimizer (MVO) | Wormhole existence probability Traveling distance rate | (0.2, 1) (0.6, 1) |
| 7 | Moth Flame Optimizer (MFO) | Convergence constant Logarithmic spiral | (−1, −2) 0.75 |
| 8 | Firefly Algorithm (FA) | Randomness factor, α Light absorption coefficient, γ | 0.2 1 |
| 9 | Sooty Tern Optimization Algorithm (STOA) | Controlling variable, Cf Sa | 2 (Cf, 0) |
| Motion | Algorithm | Rise Time, s | Settling Time, s | Overshoot, % | Steady-State error | RMSE |
|---|---|---|---|---|---|---|
| Roll | REA | 0.03361 | 0.05713 | 0.00000E+00 | 6.44466E-06 | 0.23449 |
| PSO | 0.08200 | 0.15520 | 0.00000E+00 | 3.20000E-03 | 0.22620 | |
| ABC | 0.03441 | 0.05765 | 0.00000E+00 | 5.65577E-04 | 0.24068 | |
| GA | 0.10570 | 0.19360 | 0.00000E+00 | 7.61930E-04 | 0.21840 | |
| DE | 0.06060 | 0.11330 | 0.00000E+00 | 7.05810E-04 | 0.22930 | |
| MVO | 0.09870 | 0.18210 | 0.00000E+00 | 1.50000E-03 | 0.21630 | |
| MFO | 0.09909 | 0.18101 | 2.32631E-02 | 1.73851E-04 | 0.21664 | |
| FA | 0.03422 | 0.05853 | 0.00000E+00 | 8.42488E-04 | 0.23436 | |
| STOA | 0.03677 | 0.06488 | 0.00000E+00 | 2.30451E-03 | 0.23422 | |
| Pitch | REA | 0.03361 | 0.05713 | 0.00000E+00 | 6.44466E-06 | 0.23449 |
| PSO | 0.08200 | 0.15520 | 0.00000E+00 | 3.20000E-03 | 0.22620 | |
| ABC | 0.03441 | 0.05765 | 0.00000E+00 | 5.65577E-04 | 0.24068 | |
| GA | 0.10570 | 0.19360 | 0.00000E+00 | 7.61930E-04 | 0.21840 | |
| DE | 0.06060 | 0.11330 | 0.00000E+00 | 7.05810E-04 | 0.22930 | |
| MVO | 0.09870 | 0.18210 | 0.00000E+00 | 1.50000E-03 | 0.21630 | |
| MFO | 0.09909 | 0.18101 | 2.32631E-02 | 1.73851E-04 | 0.21664 | |
| FA | 0.03422 | 0.05853 | 0.00000E+00 | 8.42488E-04 | 0.23436 | |
| STOA | 0.03677 | 0.06488 | 0.00000E+00 | 2.30451E-03 | 0.23422 | |
| Yaw | REA | 0.02294 | 0.03742 | 0.00000E+00 | 1.17230E-04 | 0.20431 |
| PSO | 0.08120 | 0.15000 | 0.00000E+00 | 2.40000E-03 | 0.18440 | |
| ABC | 0.02400 | 0.04160 | 0.00000E+00 | 6.79900E-04 | 0.20090 | |
| GA | 0.08390 | 0.15290 | 0.00000E+00 | 9.52840E-04 | 0.17360 | |
| DE | 0.11720 | 0.21080 | 4.50000E-03 | 1.34400E-04 | 0.16930 | |
| MVO | 0.03580 | 0.06770 | 0.00000E+00 | 1.60000E-03 | 0.19580 | |
| MFO | 0.05722 | 0.10487 | 1.55229E-02 | 9.20977E-05 | 0.18574 | |
| FA | 0.02437 | 0.04236 | 0.00000E+00 | 9.06897E-04 | 0.20156 | |
| STOA | 0.02537 | 0.04526 | 0.00000E+00 | 7.96213E-04 | 0.19670 | |
| Altitude | REA | 0.15748 | 0.26129 | 0.00000E+00 | 3.93389E-06 | 0.40235 |
| PSO | 0.16270 | 0.27240 | 1.71030E-05 | 8.18330E-10 | 0.39760 | |
| ABC | 0.15810 | 0.26280 | 0.00000E+00 | 1.81070E-04 | 0.40250 | |
| GA | 0.16879 | 0.28837 | 0.00000E+00 | 1.14450E-05 | 0.40447 | |
| DE | 0.16090 | 0.27070 | 0.00000E+00 | 1.92650E-04 | 0.40040 | |
| MVO | 0.15850 | 0.26310 | 2.94720E-06 | 6.36660E-11 | 0.39700 | |
| MFO | 0.16196 | 0.27312 | 0.00000E+00 | 7.35813E-05 | 0.40057 | |
| FA | 0.16110 | 0.26372 | 2.64186E-05 | 1.92583E-11 | 0.40152 | |
| STOA | 0.15958 | 0.26455 | 1.52380E-04 | 3.30136E-09 | 0.40270 |
| Motion | Algorithm | Rise Time | Settling Time | Overshoot | Steady-State Error | RMSE |
|---|---|---|---|---|---|---|
| Roll | PSO | −59.01713 | −63.19033 | - | −99.79860 | 3.66322 |
| ABC | −2.34674 | −0.90504 | - | −98.86052 | −2.57302 | |
| GA | −68.20629 | −70.49142 | - | −99.15417 | 7.36547 | |
| DE | −44.54463 | −49.57757 | - | −99.08691 | 2.26175 | |
| MVO | −65.95142 | −68.62789 | - | −99.57036 | 8.40786 | |
| MFO | −66.08584 | −68.43815 | −100.00000 | −96.29299 | 8.23617 | |
| FA | −1.79735 | −2.39915 | - | −99.23504 | 0.05346 | |
| STOA | −8.60110 | −11.94595 | - | −99.72035 | 0.11473 | |
| Pitch | PSO | −59.01713 | −63.19033 | - | −99.79860 | 3.66322 |
| ABC | −2.34674 | −0.90504 | - | −98.86052 | −2.57302 | |
| GA | −68.20629 | −70.49142 | - | −99.15417 | 7.36547 | |
| DE | −44.54463 | −49.57757 | - | −99.08691 | 2.26175 | |
| MVO | −65.95142 | −68.62789 | - | −99.57036 | 8.40786 | |
| MFO | −66.08584 | −68.43815 | −100.00000 | −96.29299 | 8.23617 | |
| FA | −1.79735 | −2.39915 | - | −99.23504 | 0.05346 | |
| STOA | −8.60110 | −11.94595 | - | −99.72035 | 0.11473 | |
| Yaw | PSO | −71.75218 | −75.05260 | - | −95.11540 | 10.79617 |
| ABC | −4.42820 | −10.04543 | - | −82.75771 | 1.69643 | |
| GA | −72.66123 | −75.52577 | - | −87.69674 | 17.68902 | |
| DE | −80.42898 | −82.24805 | −100.00000 | −12.77503 | 20.67817 | |
| MVO | −35.92952 | −44.72511 | - | −92.67310 | 4.34532 | |
| MFO | −59.91605 | −64.31817 | −100.00000 | 27.28919 | 9.99415 | |
| FA | −5.87671 | −11.66429 | - | −87.07347 | 1.36461 | |
| STOA | −9.58509 | −17.32273 | - | −85.27651 | 3.86803 | |
| Altitude | PSO | −3.21109 | −4.07913 | −100.00000 | 480,621.16279 | 1.19500 |
| ABC | −0.39497 | −0.57517 | - | −97.82742 | −0.03694 | |
| GA | −6.70340 | −9.39138 | - | −65.62806 | −0.52366 | |
| DE | −2.12831 | −3.47675 | - | −97.95801 | 0.48734 | |
| MVO | −0.64634 | −0.68854 | −100.00000 | 6,178,842.43626 | 1.34794 | |
| MFO | −2.77157 | −4.33162 | - | −94.65369 | 0.44420 | |
| FA | −2.25051 | −0.92294 | −100.00000 | 20,426,901.9929 | 0.20802 | |
| STOA | −1.31845 | −1.23301 | −100.00000 | 119,059.40416 | −0.08551 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shauqee, M.N.; Rajendran, P.; Suhadis, N.M. An Explosion Based Algorithm to Solve the Optimization Problem in Quadcopter Control. Aerospace 2021, 8, 125. https://doi.org/10.3390/aerospace8050125
Shauqee MN, Rajendran P, Suhadis NM. An Explosion Based Algorithm to Solve the Optimization Problem in Quadcopter Control. Aerospace. 2021; 8(5):125. https://doi.org/10.3390/aerospace8050125
Chicago/Turabian StyleShauqee, Mohamad Norherman, Parvathy Rajendran, and Nurulasikin Mohd Suhadis. 2021. "An Explosion Based Algorithm to Solve the Optimization Problem in Quadcopter Control" Aerospace 8, no. 5: 125. https://doi.org/10.3390/aerospace8050125
APA StyleShauqee, M. N., Rajendran, P., & Suhadis, N. M. (2021). An Explosion Based Algorithm to Solve the Optimization Problem in Quadcopter Control. Aerospace, 8(5), 125. https://doi.org/10.3390/aerospace8050125






