1. Introduction
Hypersonic vehicles refer to aircrafts, missiles, artillery shells and other vehicles with or without wings that travel at more than five times the speed of sound. Characterized by high penetration rate, hypersonic vehicles have great potential value both in military and economy. X-51, the first flight with an air-breathing scramjet engine in America, is a milestone in the development of hypersonic vehicle [
1]. A program named “Promethee” was launched in France to study hypersonic vehicles [
2]. In Banalor, India has made great efforts to hypersonic aerodynamics [
3]. And China has made huge progress in air-breathing systems in recent years [
4]. Hypersonic vehicle, for its important application value in the military field, has arisen extensive attention from a number of countries [
5]. It is of great importance to study the control of hypersonic vehicles.
Hypersonic vehicle is designed with complex stress conditions, and the applicability of mathematical model determines its control effect to a certain extent. In 2007, Parker put forward a control model of hypersonic vehicle [
6], which was made intuitively by abstracting formulas from various stress conditions. Fiorentini made some improvements to Parker’s model [
7]. In Fiorentini’s study, the model was further reduced to four formulas and some variables with little influence were omitted. However, both models are only applicable to rigid bodies. The high speed of hypersonic vehicle has certain influence on its elasticity. Zong put forward a hypersonic model that took elasticity into account [
8]. Liu developed a more accurate elastic replacement model [
9]. In the modeling, comprehensive algorithm [
10], quantitative echo [
11], two-stage orbit [
12] and other new methods based on the BGK scheme of gas dynamics were adopted. Today, the modeling of hypersonic vehicle is still a heated issue.
Hypersonic vehicle plays an important role in aircraft application, so that its security must be guaranteed. If a hypersonic vehicle is working in a tough environment, more uncertainties and a greater chance of failure may occur. Tang studied the fault tolerance of full state constrains [
13]. Sun studied methods for dealing with input saturation and state constraints [
14]. Cheng focused on the breakdown and rebound of the actuator [
15]. And An focused on the attack constraint [
16]. There are many methods used for fault-tolerant control. Some traditional control methods, such as PID, can tolerate failures, but only applicable for simple systems. Some advanced methods, such as Barrier Lyapunov function based adaptive finite time control [
17], second-class fuzzy technology and cuckoo search algorithm, have achieved good results in complex systems [
18].
adaptive control is usually not applied to fault-tolerant control, while
adaptive fault-tolerant control is usually applied to four-rotor vehicles, such as [
19,
20,
21,
22]. It is of great significance to apply
adaptive control in fault-tolerant control of hypersonic vehicles.
First, the hypersonic mathematical model is determined as a non-minimum phase flexible model in this paper. In order to simplify the structure of the controller and take the elastic model into consideration, a hypersonic model is established as a reference model [
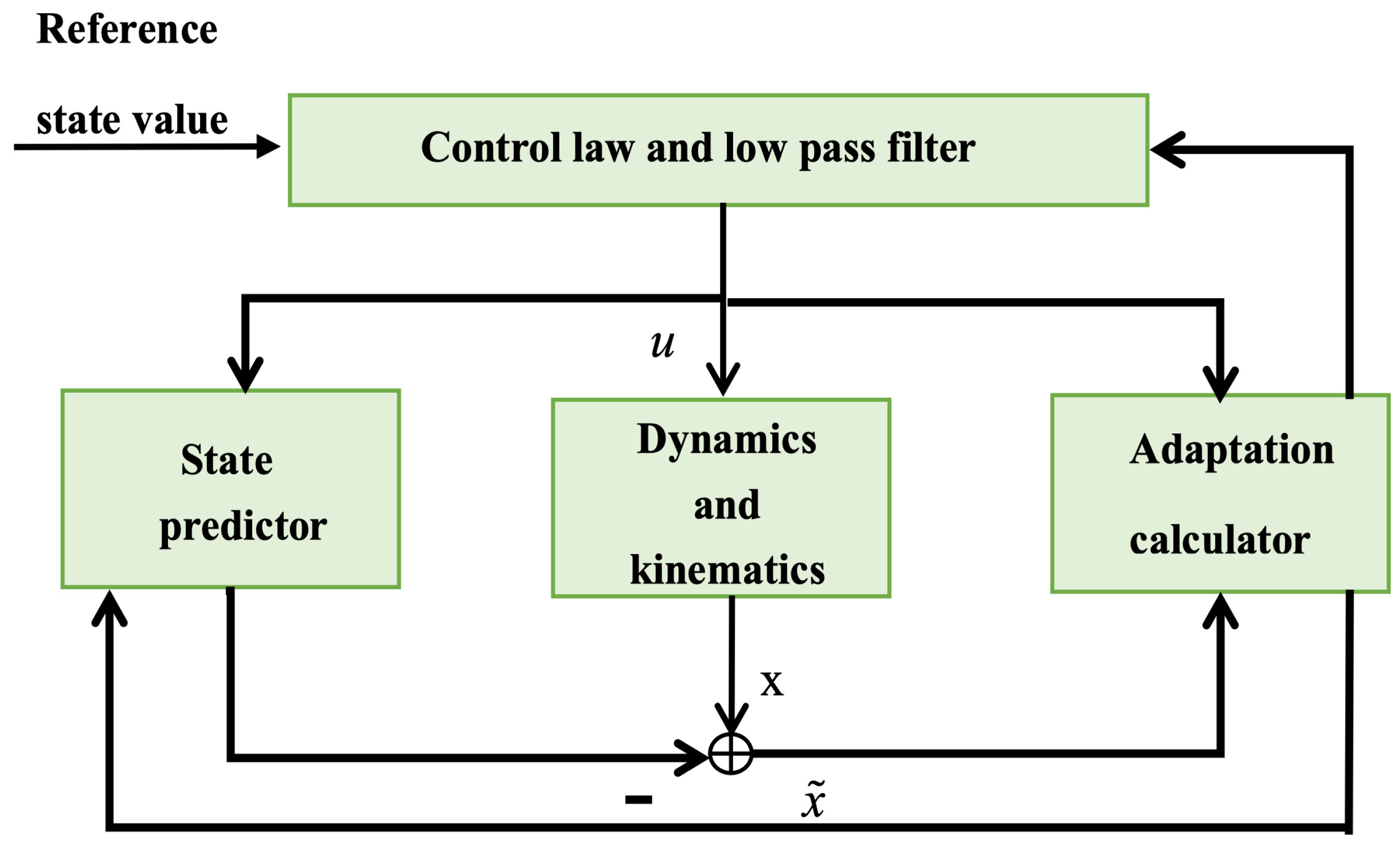
8]. The model contains not only elasticity but also uncertainty, so it is particularly important to study this model. As the modal frequency of aircraft structure is closer to the rigid modal frequency, the influence of elastic effect on the flight dynamics of elastic aircraft becomes increasingly significant. In particular, the processing and stability characteristics will become more complex and serious, and the "rigid aircraft" analysis method cannot be studied. Therefore, it is urgent to establish a multi-disciplinary coupling flight dynamics model of elastic vehicle. In this paper, the elastic engine model is taken as a part of the hypersonic vehicle model to make the mathematical model closer to the actual hypersonic vehicle dynamics. Second, the failure of the actuator is a loss failure. In reality, due to the wear and tear of the vehicle and the inherent age limit, loss failures often occur. Pneumatic rudder plays a decisive role in aircrafts, which is a guarantee to avoid loss failure. Proposed by Hovakimyan et al. in 2011,
adaptive control is a fast and robust adaptive control method as stated in [
23]. By adding a low-pass filter to the control law design, the separation of control law from adaptive law design is ensured. According to the particularity of the supersonic aircraft model, the height controller needs to derive the relationship between control value and state by backstepping. Then, in this paper, the
adaptive control method is introduced to control the hypersonic vehicle with elasticity and loss fault.
adaptive fault-tolerance control is an active fault-tolerant control that readjusts the parameters of the controller according to the fault, and can deal with the fault actively. Besides, the adaptive fault tolerance of fault occurrence amplitude is superior to passive fault tolerance control. In order to improve the performance of the control system to a greater extent, traditional
adaptive control needs to combine with fault tolerance control.
Since we consider aeroelastic model in this paper, the generalized aeroelastic force will affect the force and torque of the hypersonic vehicle. It makes the whole system more likely to get into an unstable state and increases the difficulty of control. When the faults of actuators occur the control ability will reduce significantly and the impact of elasticity on the system stability will be intensified. Therefore, to improve reliability of the control system, fault-tolerant controller with rapid response is necessary for the elastic hypersonic vehicle. We propose a adaptive fault-tolerant control method which combines the adaptive control method and fault-tolerant control theory. Firstly, adaptive control is a model following reconfiguration fault-tolerant control which does not require high linearity of the model and can be applied to nonlinear model like the hypersonic aircraft used in this paper. The internal structures of adaptive methods vary with model. The states, disturbances and reference trajectory of hypersonic vehicles can all be considered in designing adaptive parameters of controller. So adaptive control can have more targeted control effects for the specific aircraft. Secondly, as an improved method of adaptive control, adaptive fault-tolerance controller’s response speed is fast due to its structure of separating feedback control and adaptive law. For elastic hypersonic vehicle, the fast reaction rate is necessary. Besides that, it can also reduce the influence time of faults and improve flight quality. Finally, low-pass filters are designed to add into adaptive fault-tolerant controllers to restrain high frequency oscillation of control inputs. It can avoid the irreversible results produced by the interaction of high-frequency oscillation and aeroelasticity.
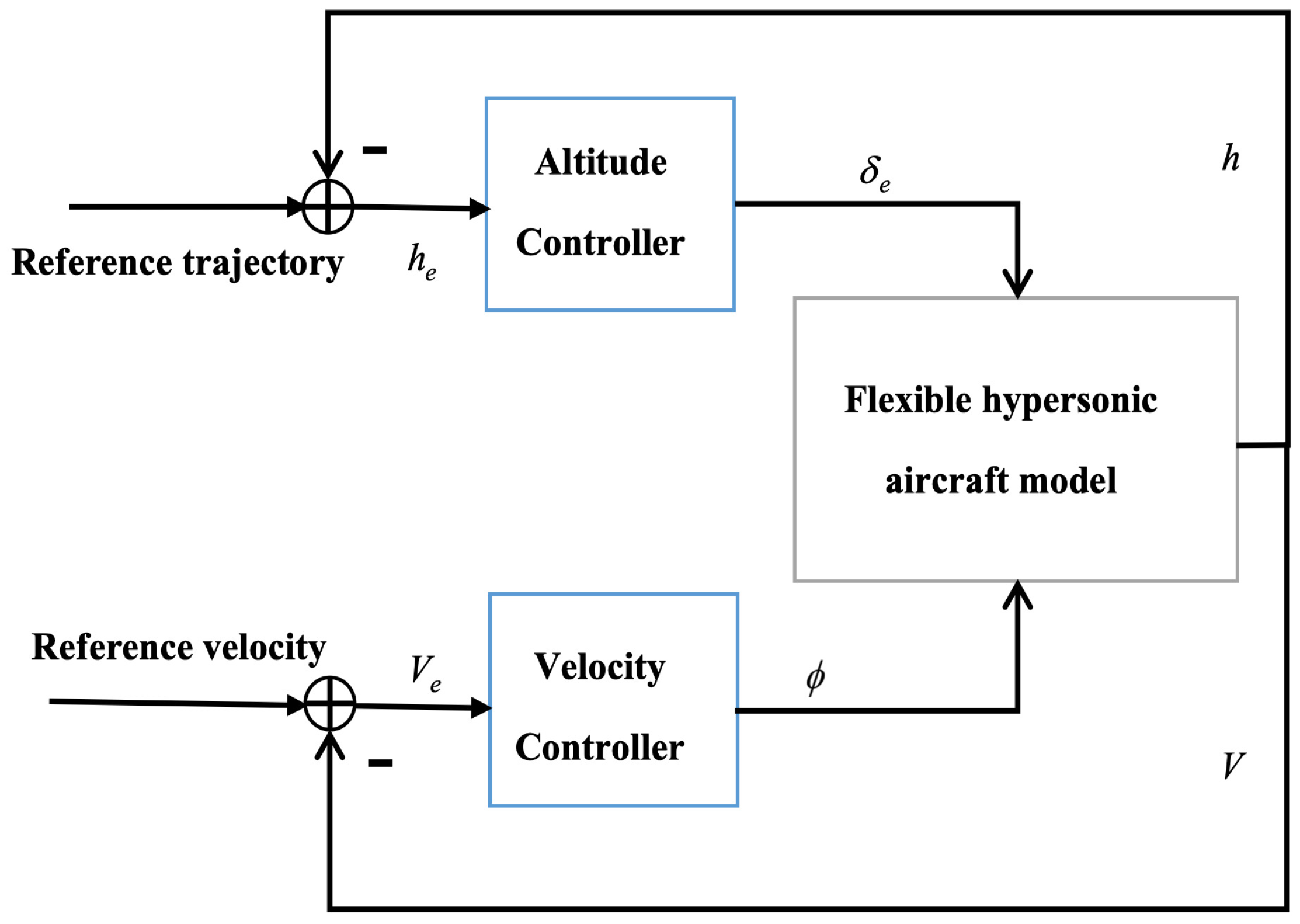
The paper is organized as follows. First, the dynamic model of the hypersonic aircraft is built in
Section 2. Then, the
adaptive controller is designed and the stability is proved in
Section 3. In
Section 4, the simulation results are shown and analyzed. Finally, conclusion of the whole paper is present in
Section 5.
The main contributions of this paper can be highlighted as follows.
(a) We build a hypersonic aircrafts model with loss fault and take elasticity into account. We simplify the model to a control-oriented model.
(b) We investigate the combination method of adaptive control and fault tolerance control. We propose two kinds of combination methods to suit different aircraft modeling situations.
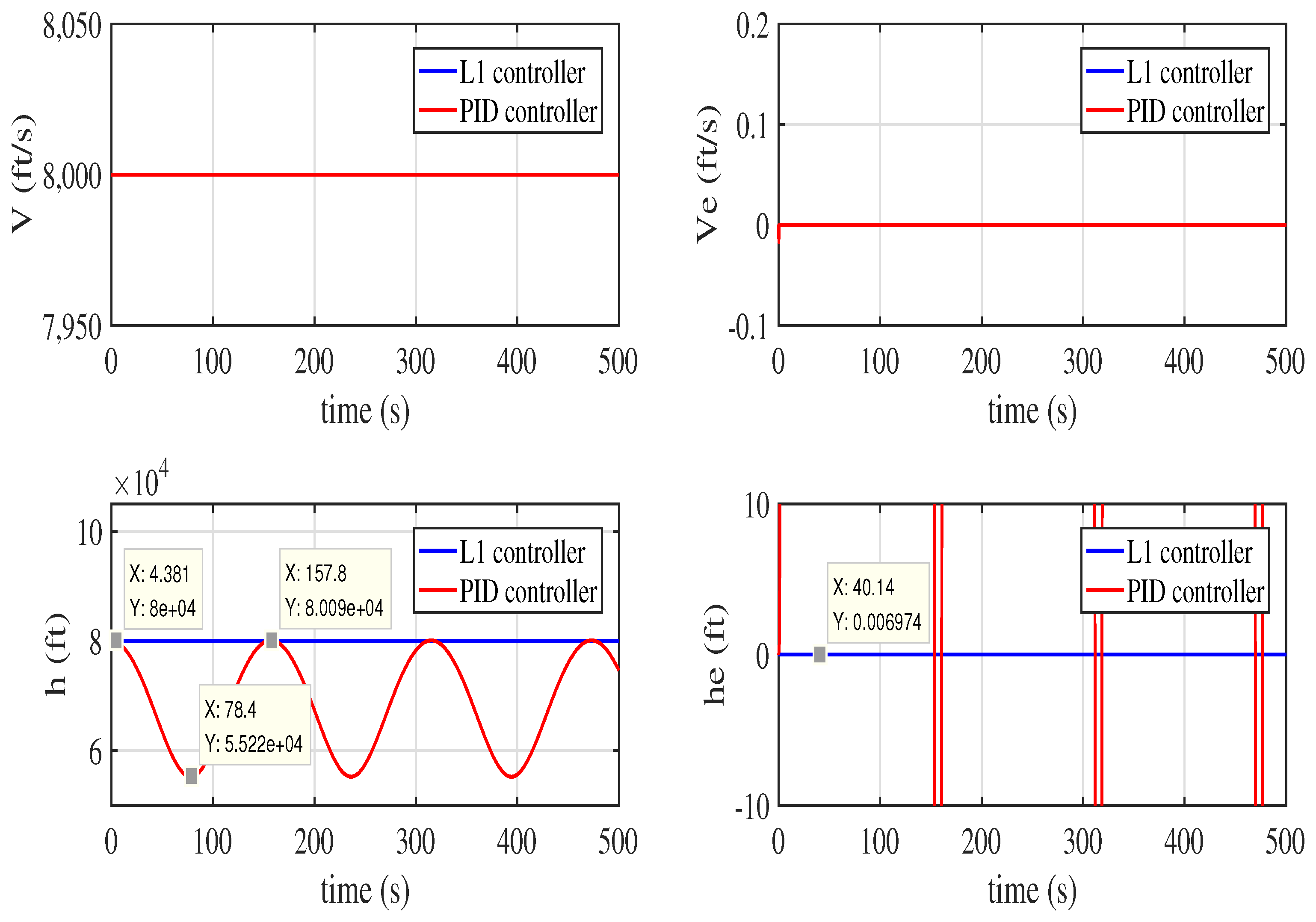
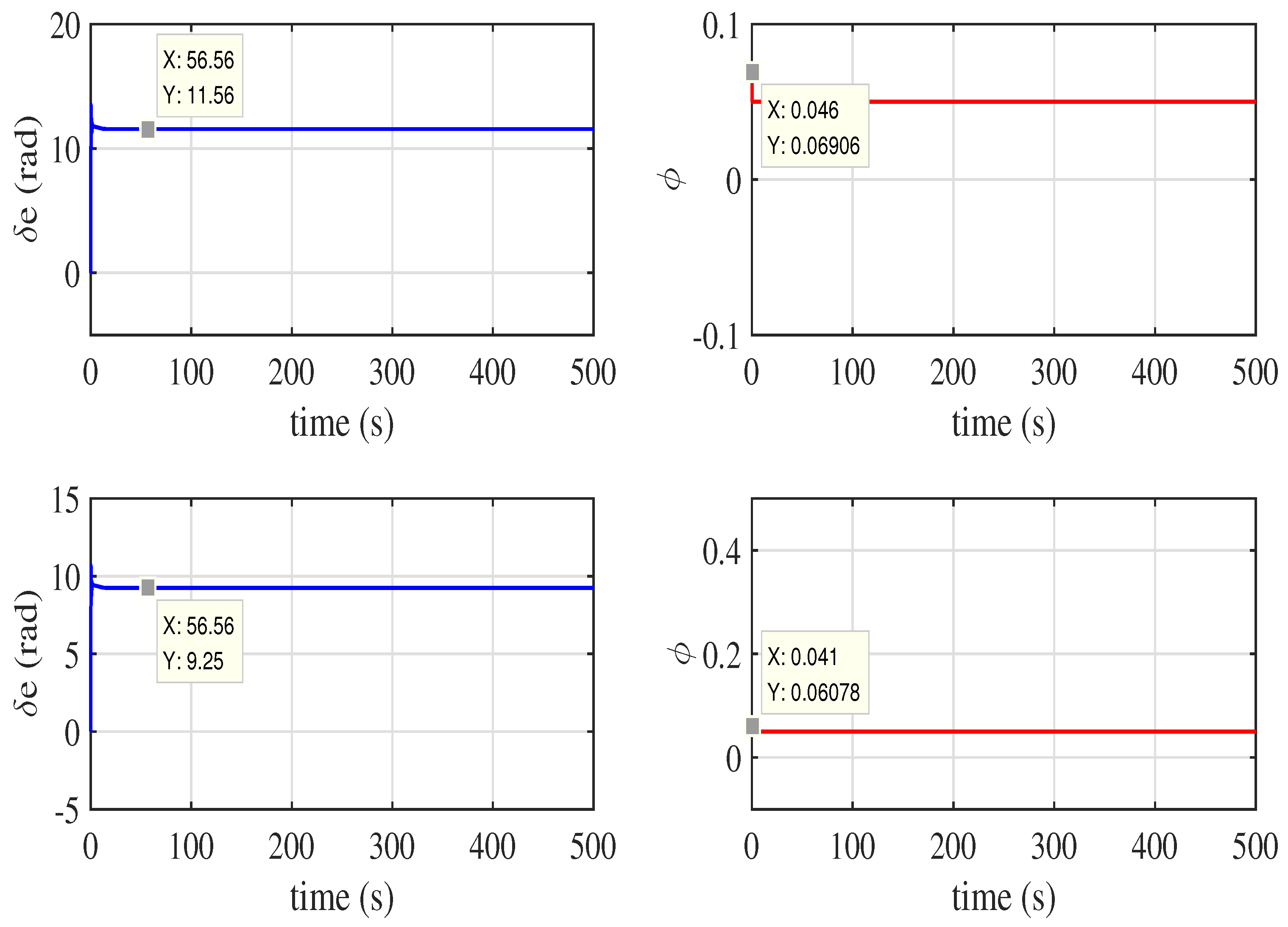
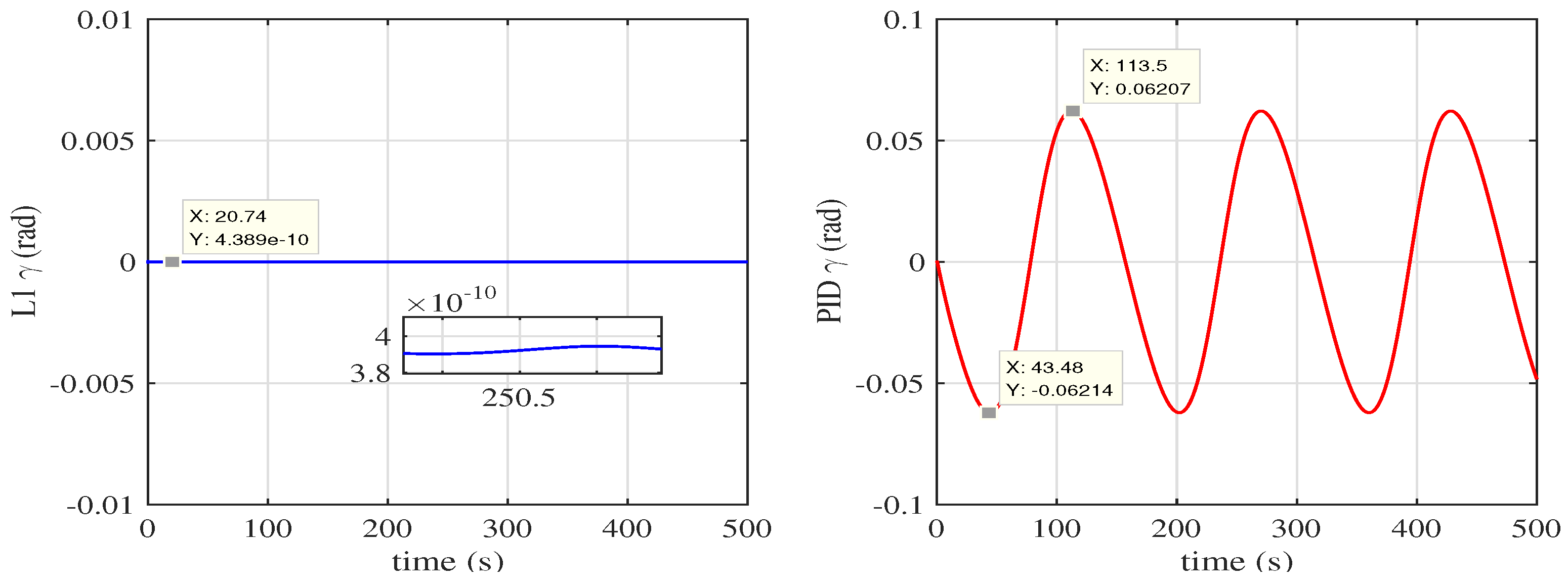
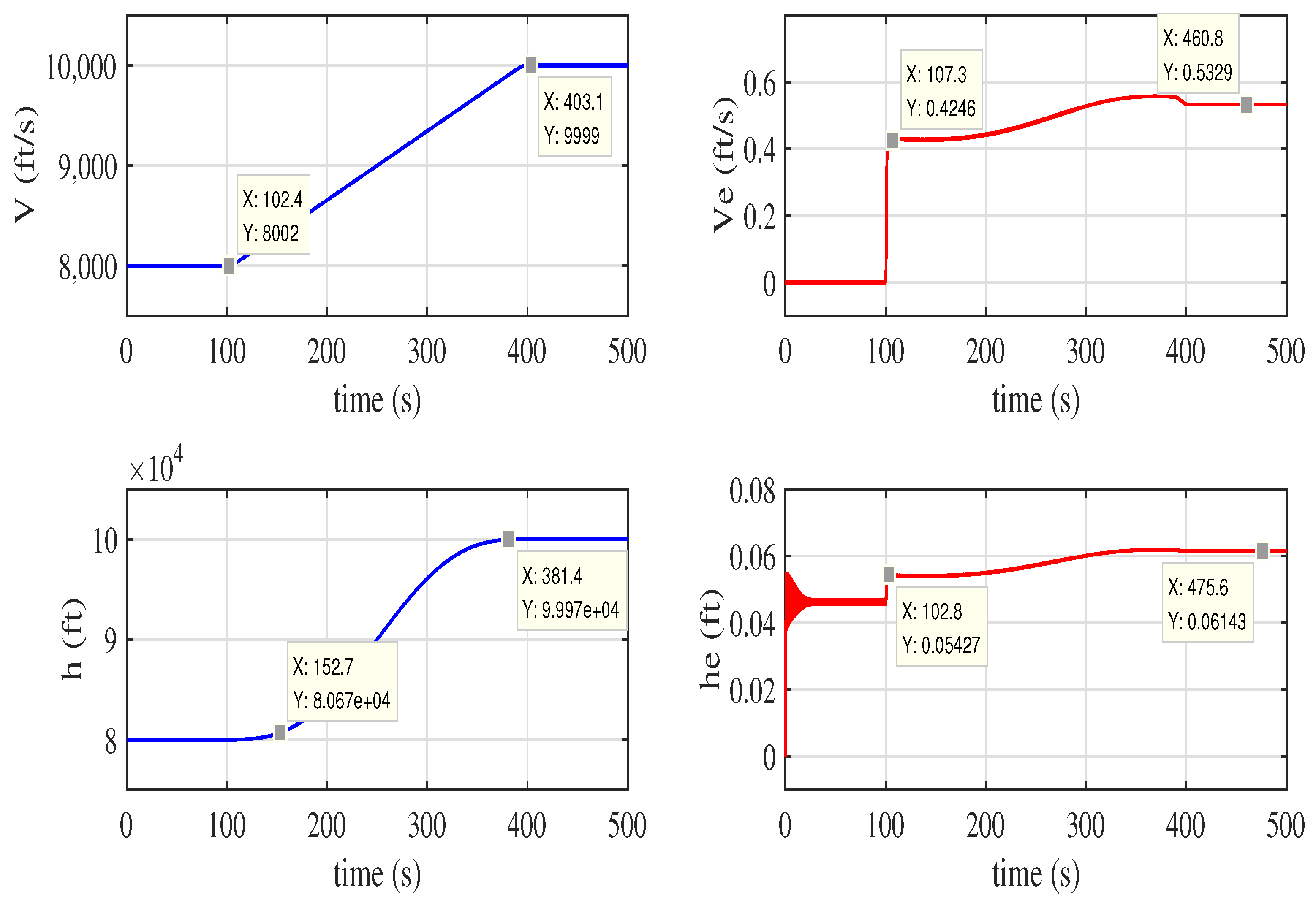
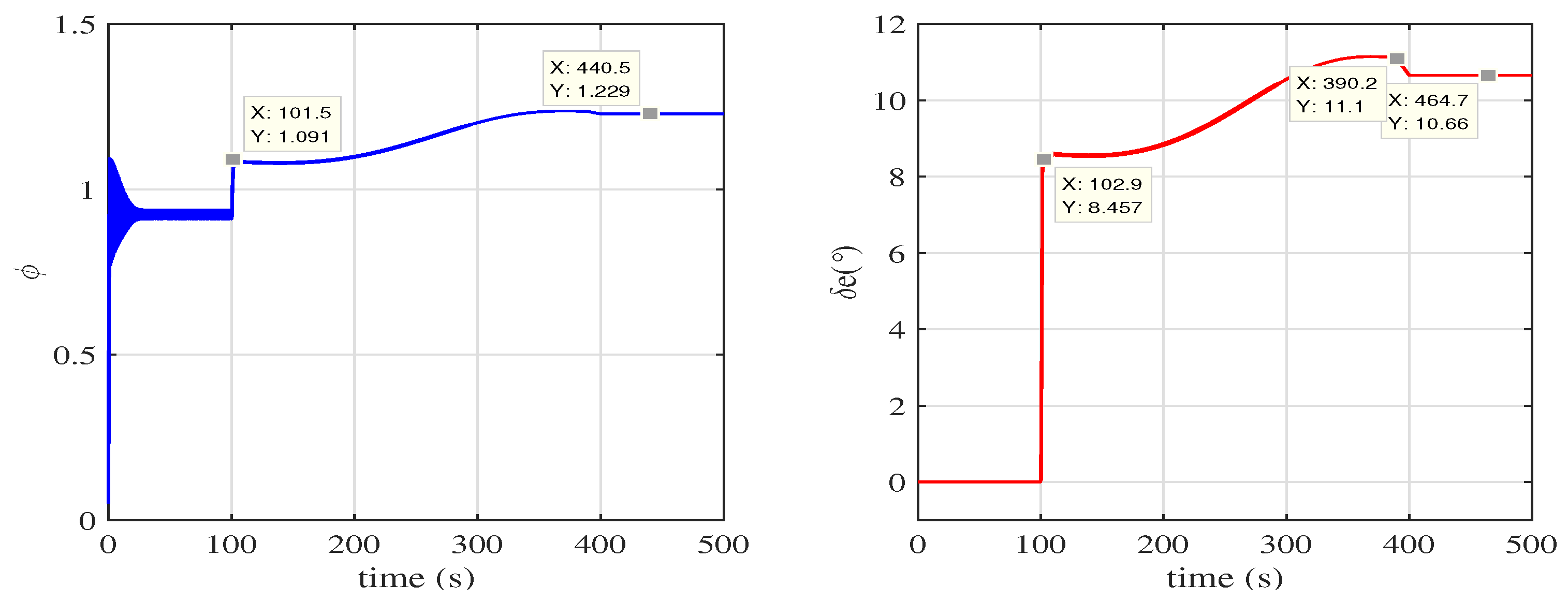
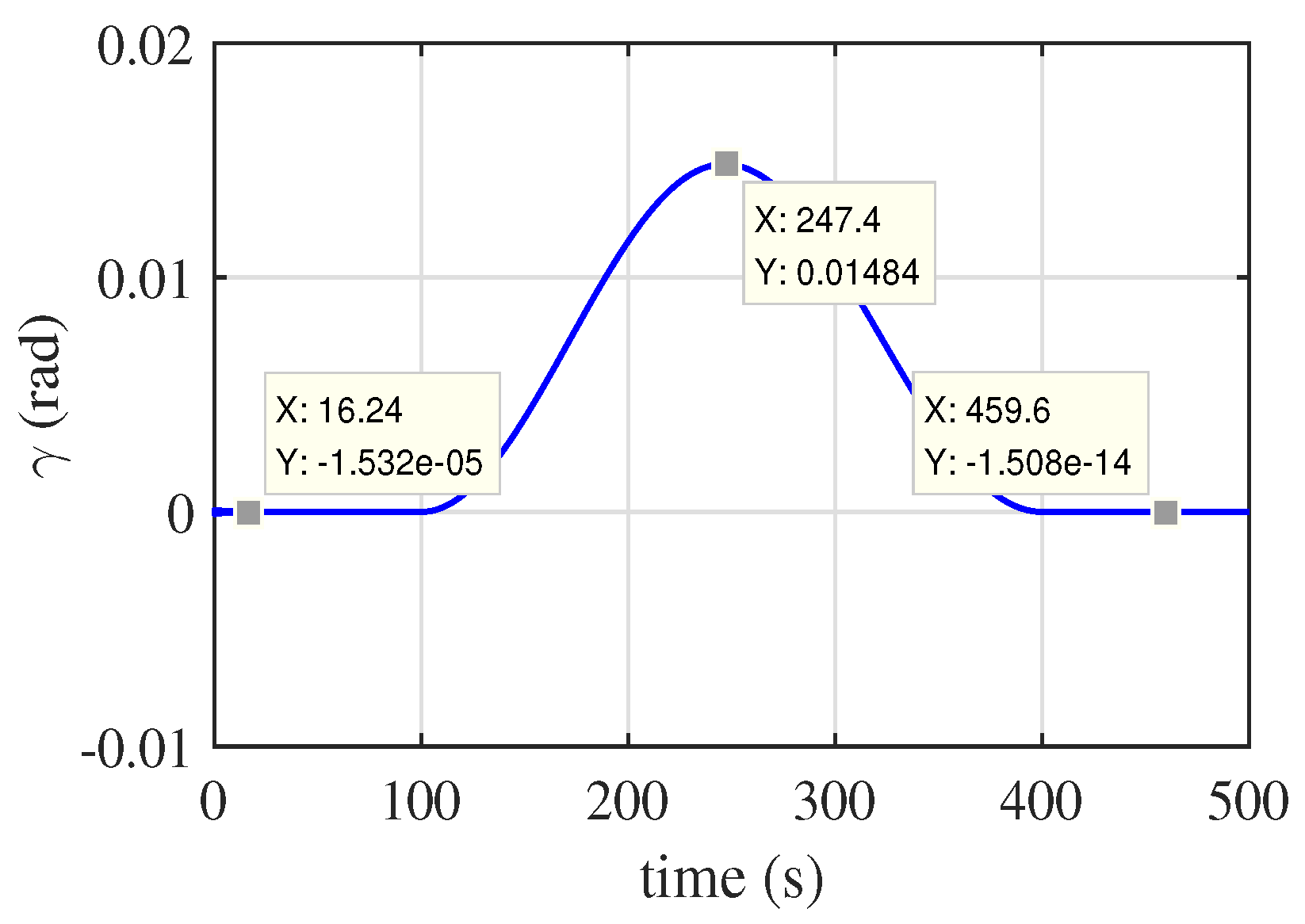
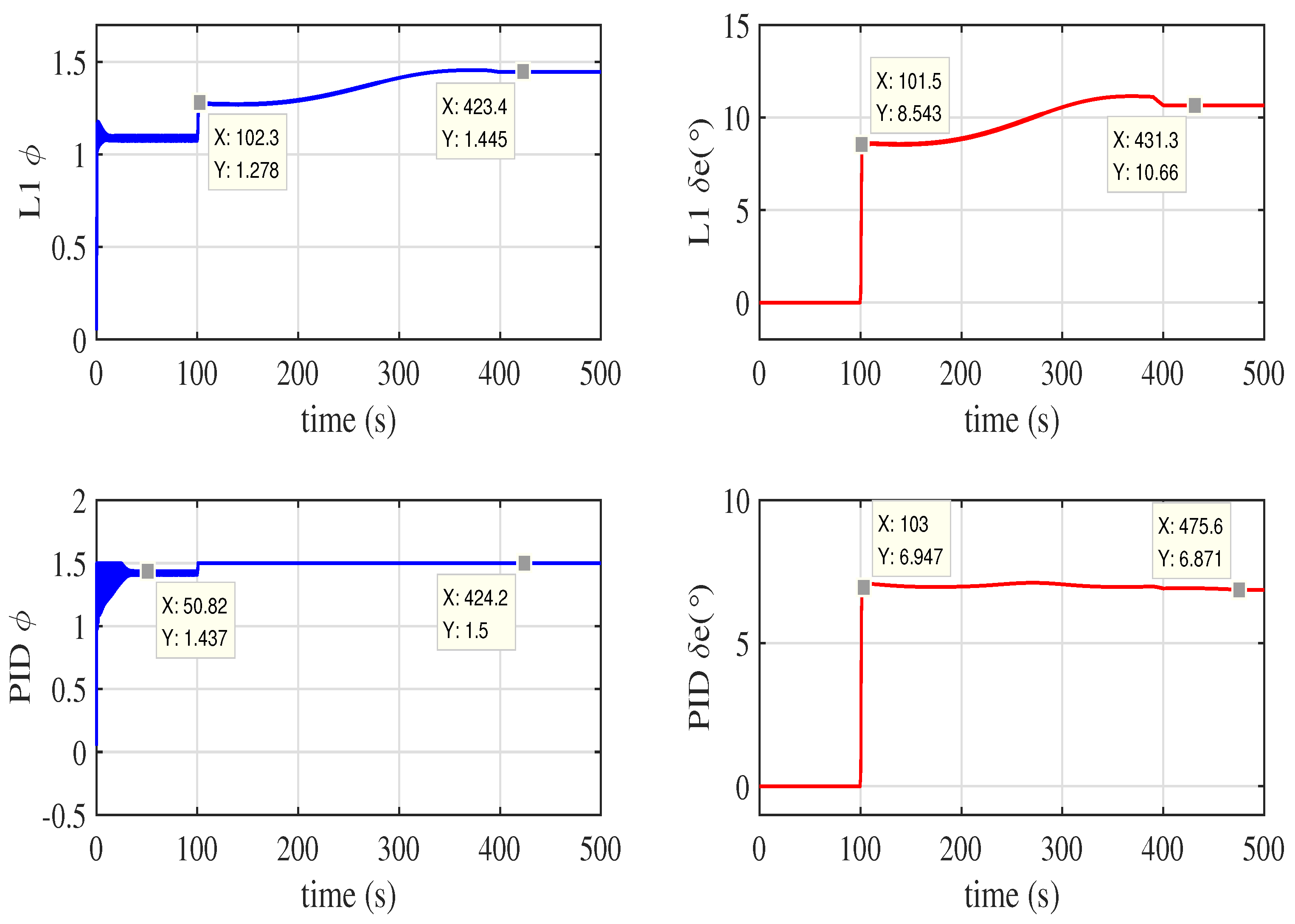
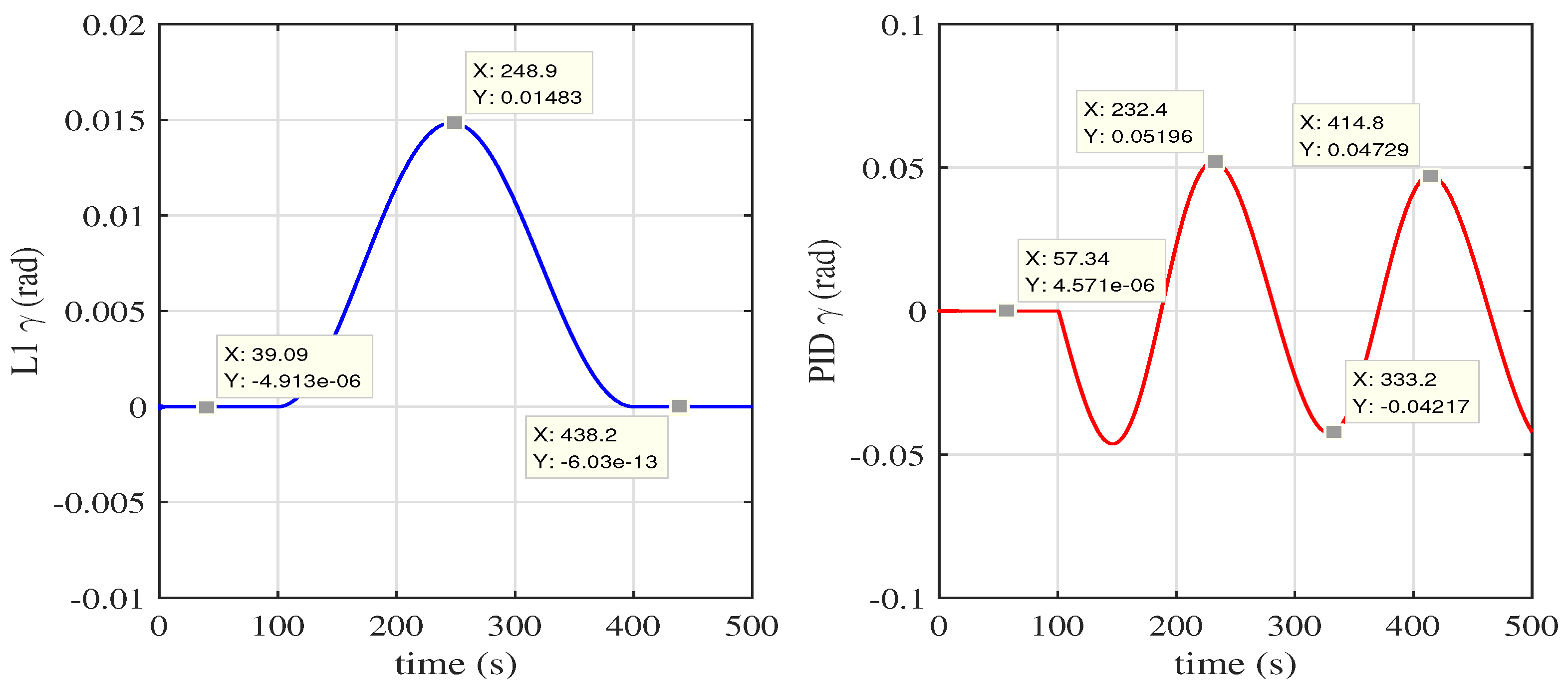
(c) We apply adaptive fault tolerance control method to hypersonic aircraft model and keep the hypersonic aircraft with elasticity tracking the reference longitudinal velocity and altitude in loss fault situations which have better performance than PID controller.
2. Problem Formulation
2.1. Dynamic Motion Equations
Assuming that the earth is flat, the earth coordinate system is chosen as the inertial seat. The frame beam is a free beam structure at both ends, and the first three elastic modes are considered. In [
7], a model of rigid-body vehicle dynamics is proposed.
Table 1 lists the meanings of each parameter appearing in the model.
Consider the decoupled longitudinal dynamic merely, the longitudinal rigid-body can be written as:
where
m is mass,
V,
h,
,
and
Q denote five rigid body states of the system, named velocity, altitude, track angle, pitch angle and pitch angle rate,
is attack angle,
T,
D,
L,
M present thrust, drag, lift and pitching torque,
g is acceleration due to gravity,
denotes moment of inertia along the longitudinal direction.
In Equation (
1), the forces and the torques are calculated as follow:
where
and
are control inputs, respectively fuel equivalent ratio and elevator deflection angle,
is mean aerodynamic chord,
S presents the reference area,
denotes the thrust-to-moment coupling coefficient,
is dynamic pressure and expressed as:
where
is air density,
is air density at nominal altitude,
presents nominal altitude and
denotes inverse of the air density exponential decay rate. Other coefficients
,
,
,
,
are given by:
For hypersonic vehicles, rigid-body dynamic model can not analogy the real dynamic situation of hypersonic vehicles. In order to obtain a more accurate result, the elasticity of hypersonic vehicles must be considered. The flexible engine model of air-breathing hypersonic aircraft with non-minimum phase shown in [
8] is presented as follow:
where
present generalized force,
and
present six elastic states,
is the damping factor,
is the natural oscillation frequency. In Equation (
5), the forces and the torques are calculated as follow:
The elasticity of hypersonic vehicles is relate to the attack angle. When hypersonic vehicle takes large maneuver, the elasticity makes great influence on stress situation. The model of hypersonic vehicle model becomes more accurate but more difficult to control.
According to Equation (
2), it can be seen that the coupling between elevator and lift affects the track angle, which causes a problem that the control law of elevator derived by standard inversion method based on the dynamics of altitude
h and track angle
makes the internal dynamic pitch angle and pitch angular velocity unstable. In order to solve this problem, the elevator deflection angle
in the track angle
is regarded as uncertainty so that the effect of
on altitude only appears in pitch angular velocity and the correlation of
h is improved. In addition, all items except pitch angle
are considered as uncertainties in the track angle formula. Besides, in order to decouple the longitudinal velocity and height in the controller, we consider the
in the longitudinal speed as uncertainty and ignore the effect of fuel equivalent in pitch angular velocity. Finally, the control oriented model is obtained by simplifying the model, which is written in the form of the sum of constant, control quantity and uncertainty in Equation (
7). The longitudinal velocity control logic can be set as fuel equivalent ratio-longitudinal thrust-longitudinal velocity and the altitude control logic is elevator deflection angle-pitching moment-pitch angular velocity-pitching angle-track angle-altitude.
2.2. Loss Fault and Model Simplification
For hypersonic aircrafts, when there’s a loss fault, it always comes to the pneumatic rudder. Specific to this paper, it is elevator deflection. Reflected on the model, it is a loss rate n acting on . According to Equations (1)–(4), each state is influenced by elevator deflection angle. It will cause plenty of extra calculation and deform the control effect if n is multiplied directly.
Treat
as an uncertainty in
V, ignore others except
in
and treat
an uncertainty in
Q as well. The model shown as Equation (
1) can be simplified as:
where
,
is the reference pitch angle and
present uncertainties. Although the control right is sacrificed after simplification, the designs of controllers become more convenient and increase the speed of fault tolerance control.
In aircraft control, the selected control variables are variables of actuator such as rudder deflection, motor speed, etc. or the variables that have operation relationship with the actuator such as force and torque. The fault mode selected in this paper is the loss fault acting on the actuator which makes the control value reduced in the simulation part. Then, the goal of fault tolerance control is to ensure that the final output control value is close to the output value of the fault-free state. The main methods are as follows:
1. Use the fault-tolerant ability of adaptive controller
In the formula , is an adaptive variable which is adjusted according to the error of the return controller outputs. When there is no fault in the actuator, the adaptive variable is affected by the error. In order to make the controller fault-tolerant, fault information is added into the adaptive variable to make it follow the fault of the actuator. The corresponding increase or decrease is made to ensure that the final control value remains unchanged. This method is suitable for the system whose control variable is the actuator variable and the system with simple structure.
2. Add compensators to the designed controller
Make the control quantity output under the non-fault state into the ideal control quantity. Under the loss fault condition, the ideal control quantity can be written as the sum of the failure control quantity and the compensation quantity. Then, in the process of modeling, the sum of failure control value and the compensation value can represent the ideal control quantity all the time. So the compensation value becomes a part of the control quantity with the design of the controller. This method is suitable for the system whose control variables are not actuator variables. Only a part of the control variables in this system are affected by the fault, and only the part responding to the fault needs to be fault tolerant.