Neural Nonlinear Autoregressive Model with Exogenous Input (NARX) for Turboshaft Aeroengine Fuel Control Unit Model †
Abstract
:1. Introduction
- Increased performance with the reduction in engine weight due to digital signaling, lower wire/connector count, reduced cooling need. 5% increase in thrust-to-weight ratio;
- Improved Mission Success: System availability improvement due to automated fault isolation, reduced maintenance time, and modular line-replaceable unit (LRU). 10% increase in system availability;
- Lower Life Cycle Cost: Reduced cycle time for design and manufacturing; reduced component and maintenance costs.
2. Materials and Methods
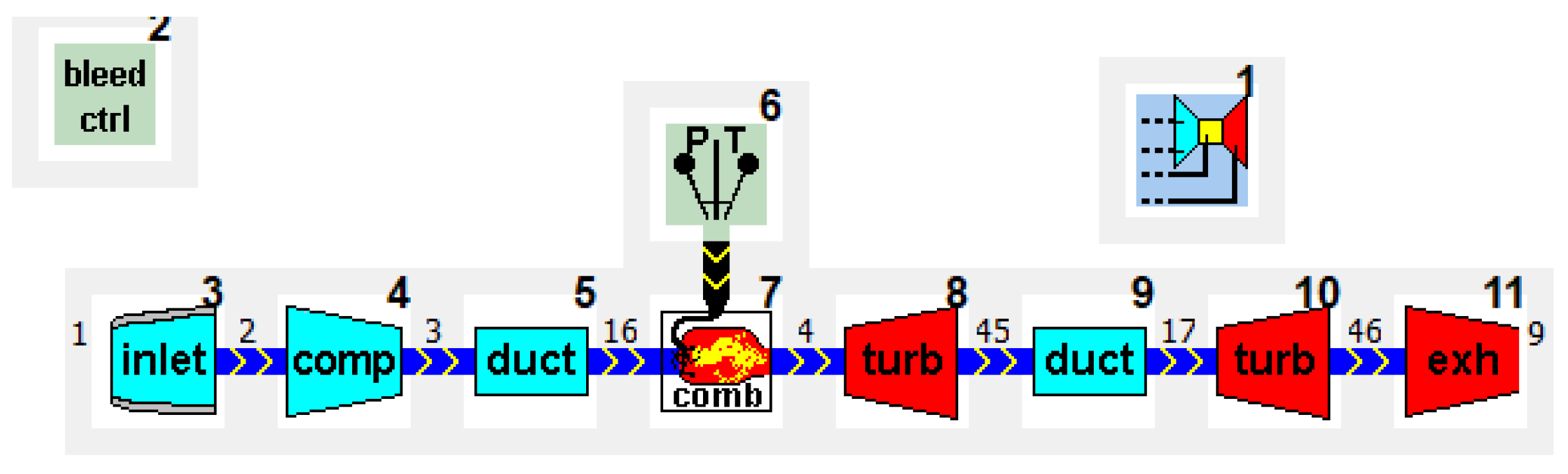
2.1. Gas Turbine Modelling
2.1.1. Design Point
2.1.2. Transient Simulations
2.1.3. Deteriorated Model
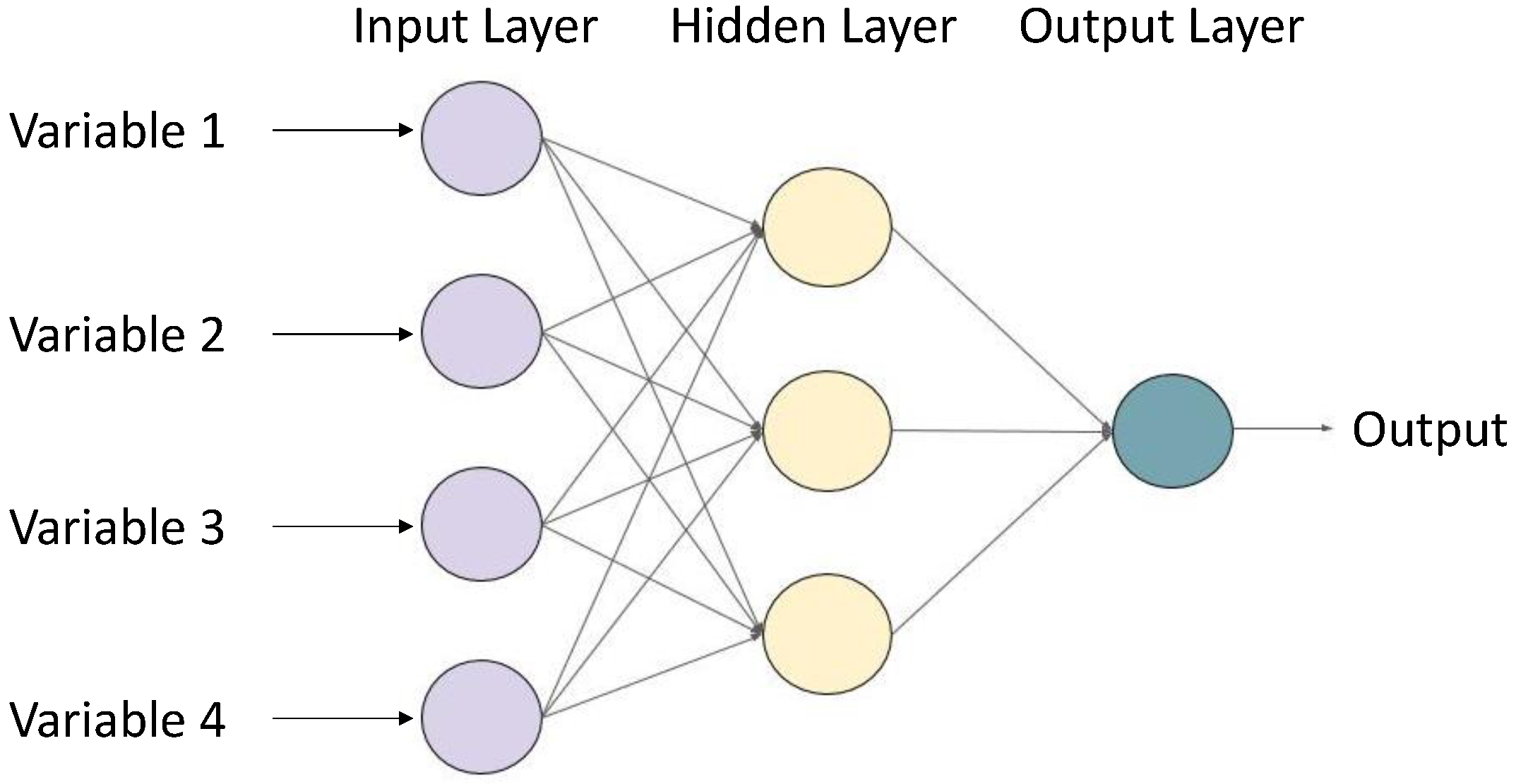
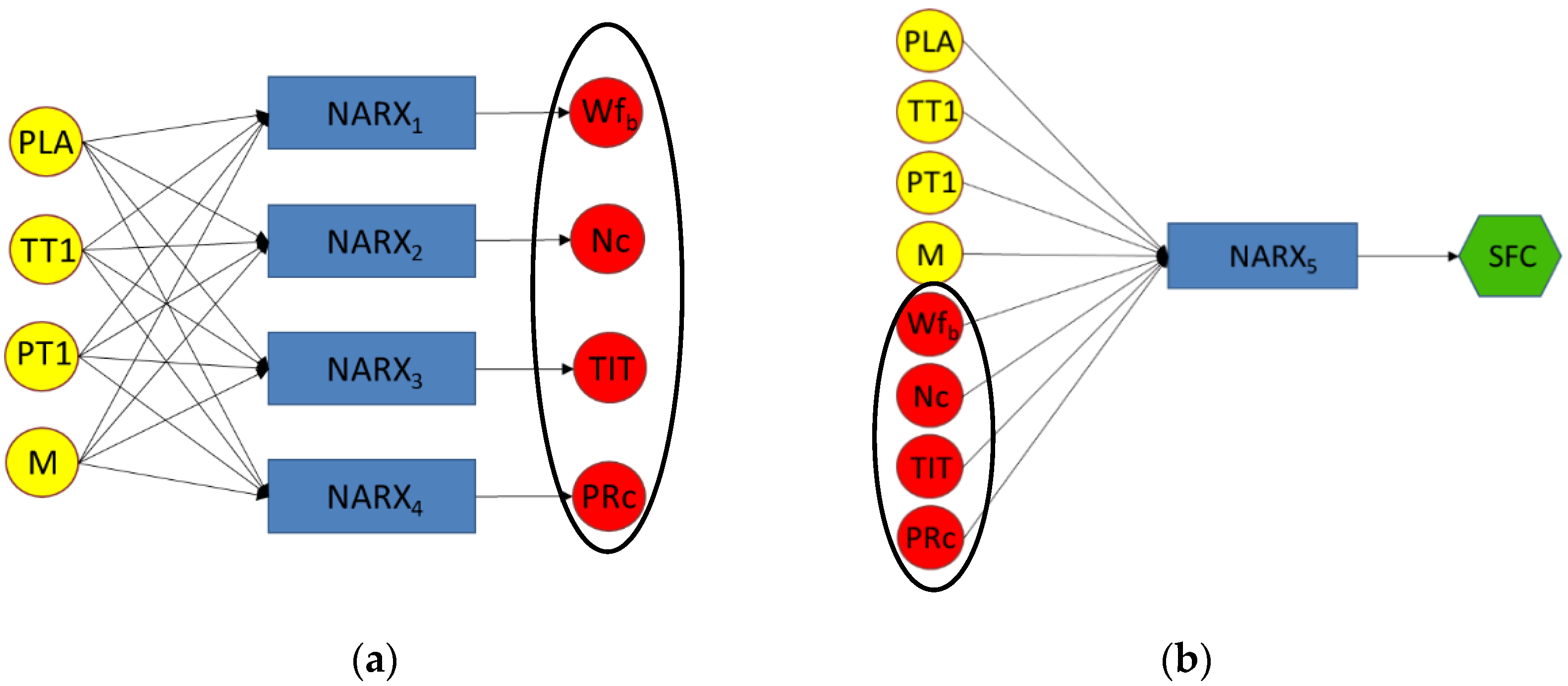
2.2. Neural Network Application to Transient Simulations
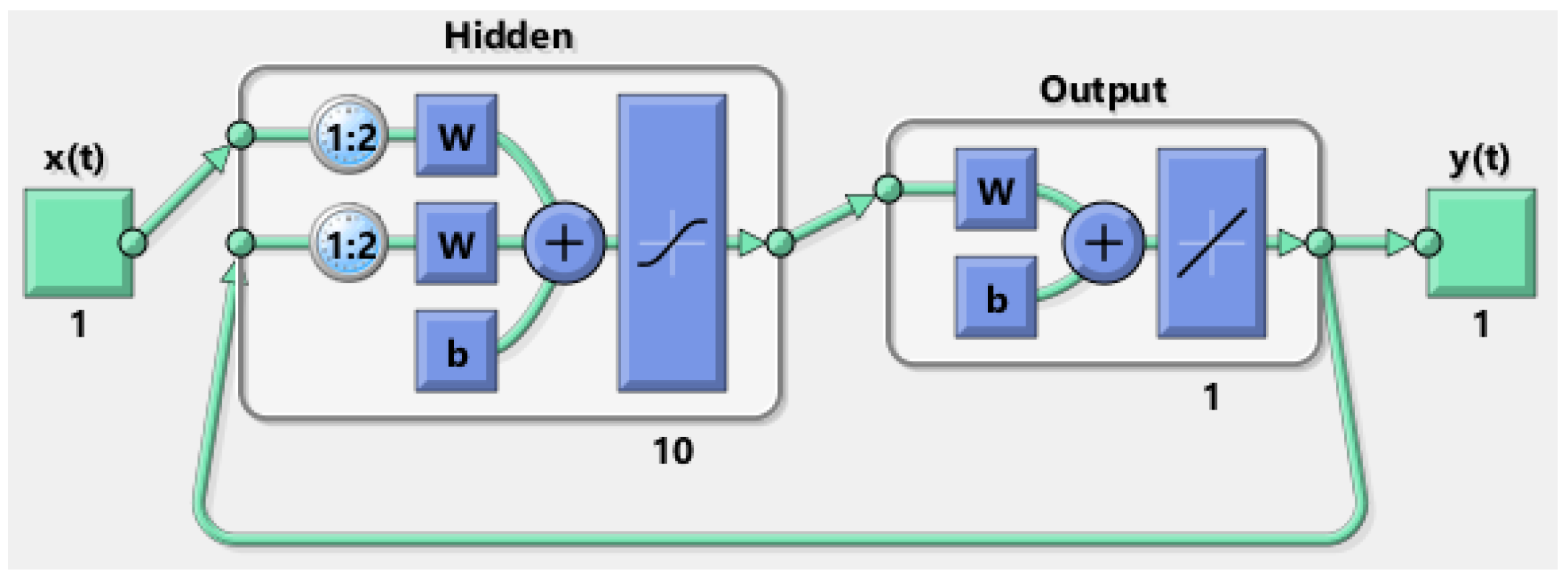
NARX Neural Network
- Mean-Square-Error (MSE) defined as follows:
- The Root-Mean-Square-Error (RMSE) defined as follows:
- The coefficient of determination R2 is defined as follows:where n is the number of data of each data set.
3. Results
- Engine parameters: shaft speed (Nc), turbine inlet total temperature (TIT), fuel mass flow rate (Wf_b), and compressor pressure ratio (PRc);
- Environment parameters: Mach number (M), atmospheric total temperature (TT1), and total pressure (PT1).
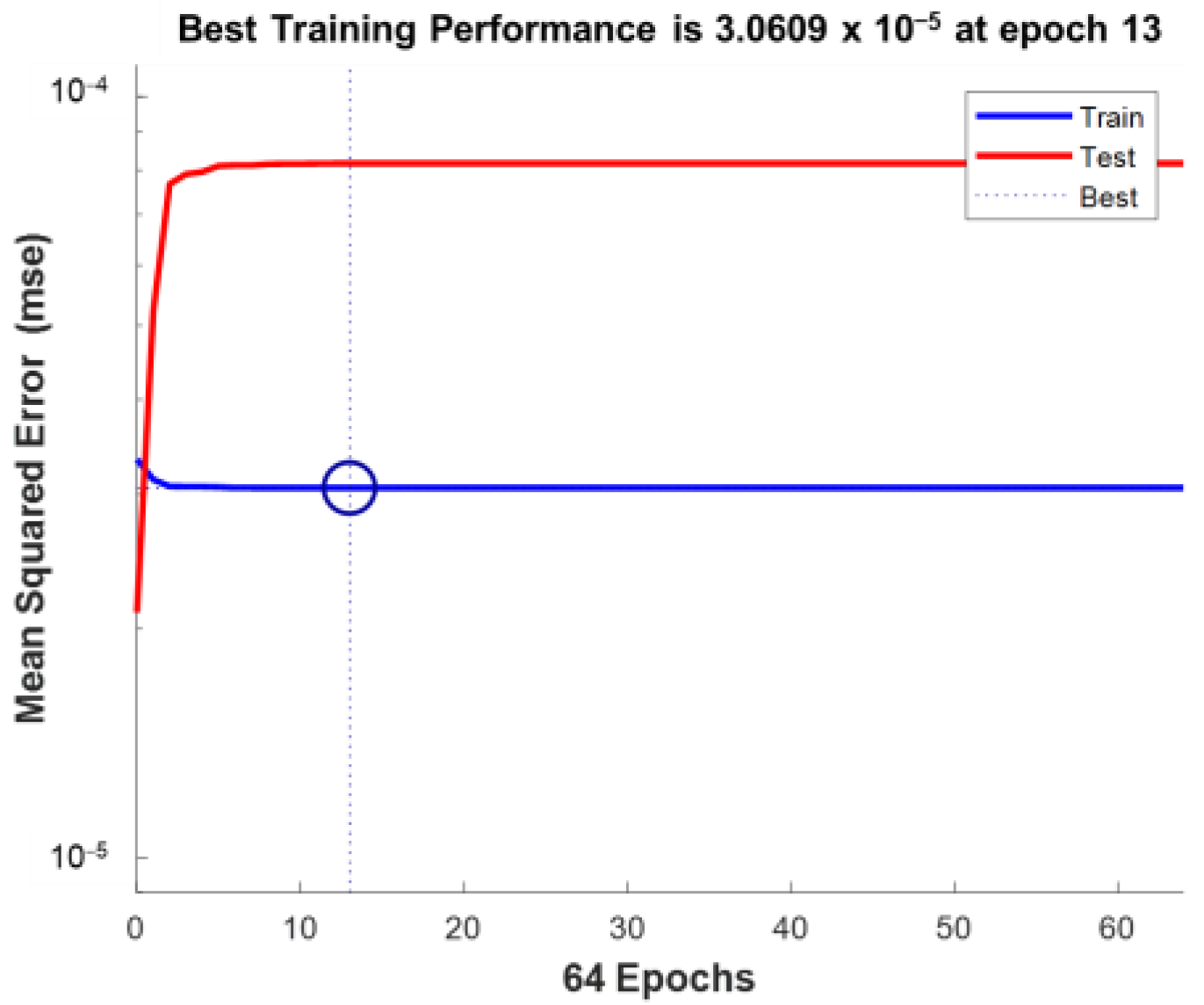
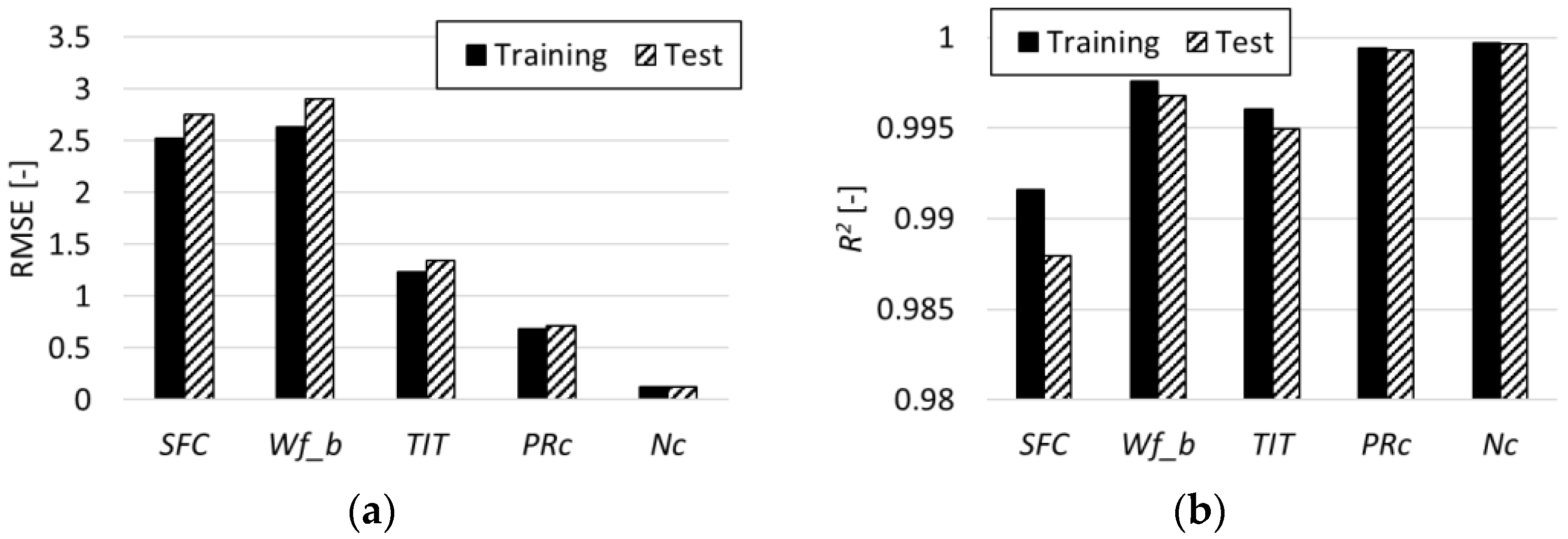
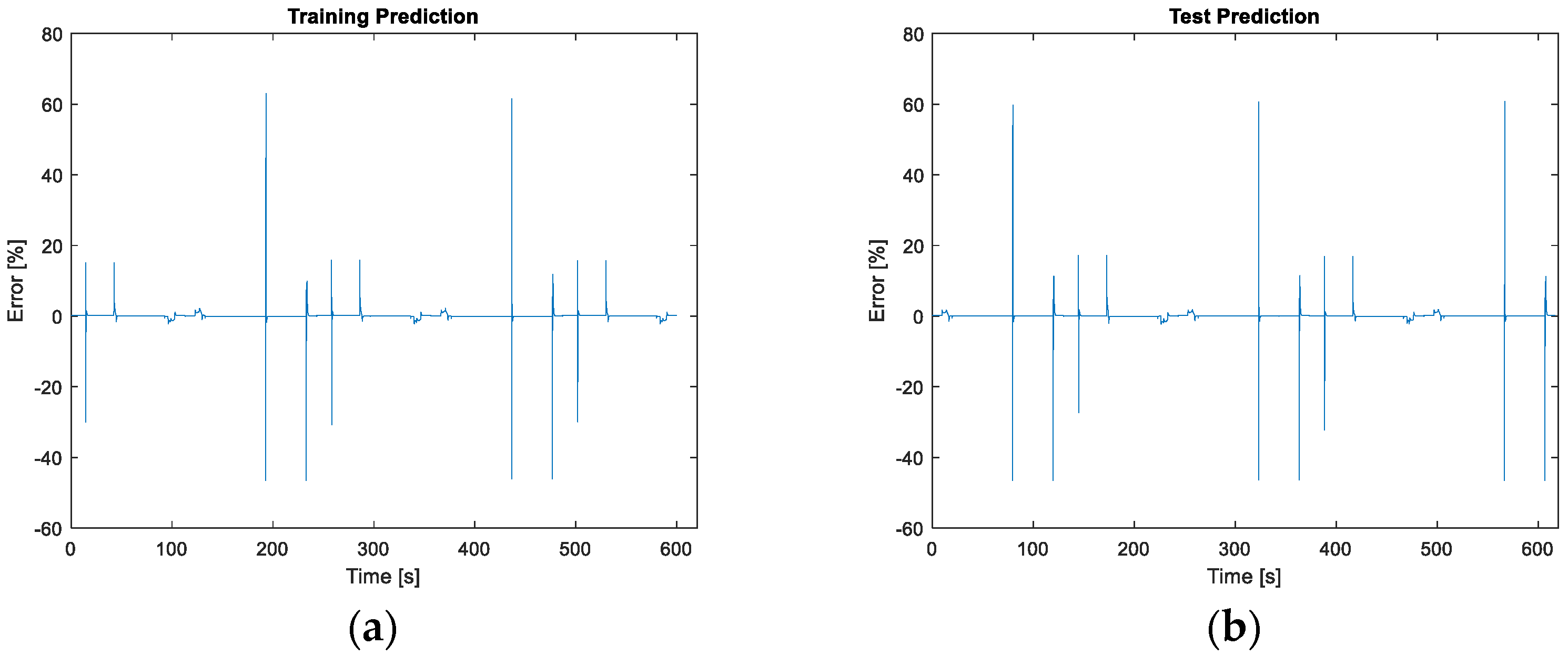
3.1. NARX Neural Networks Prediction Results
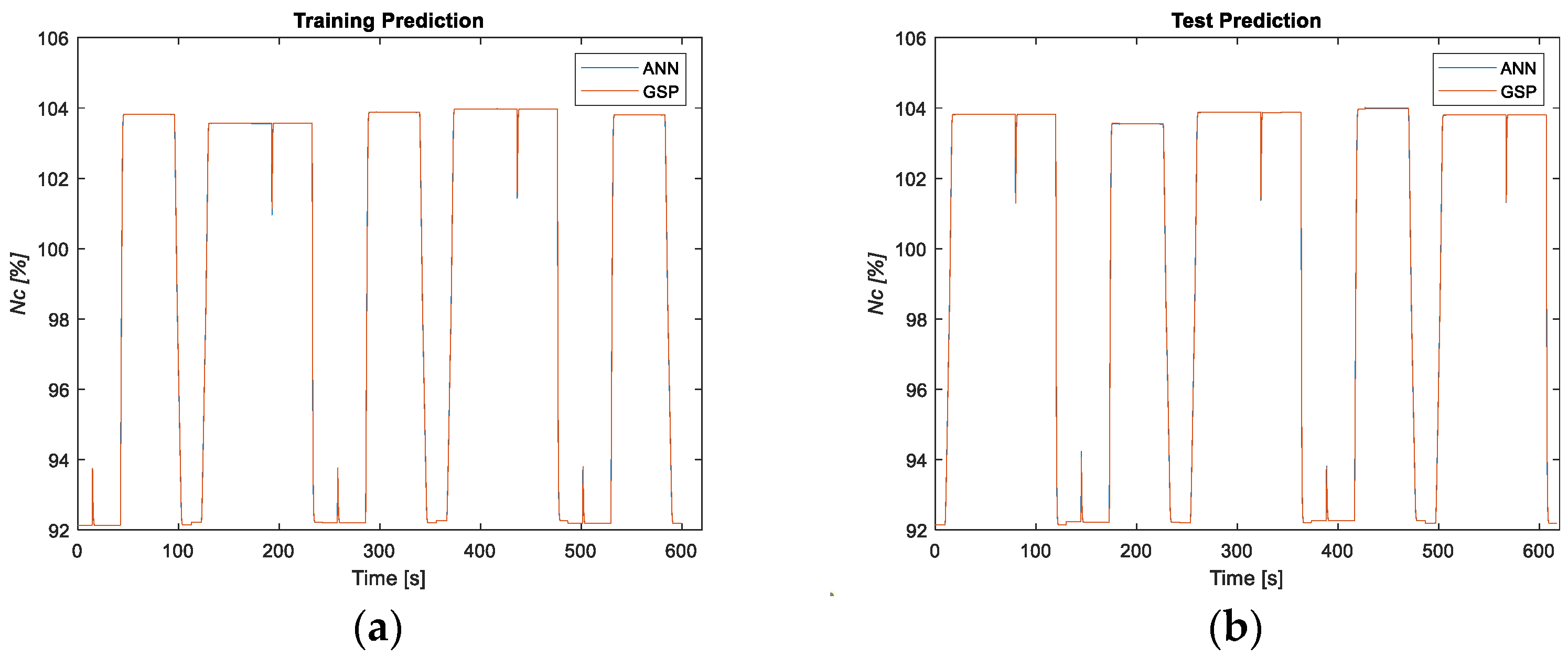
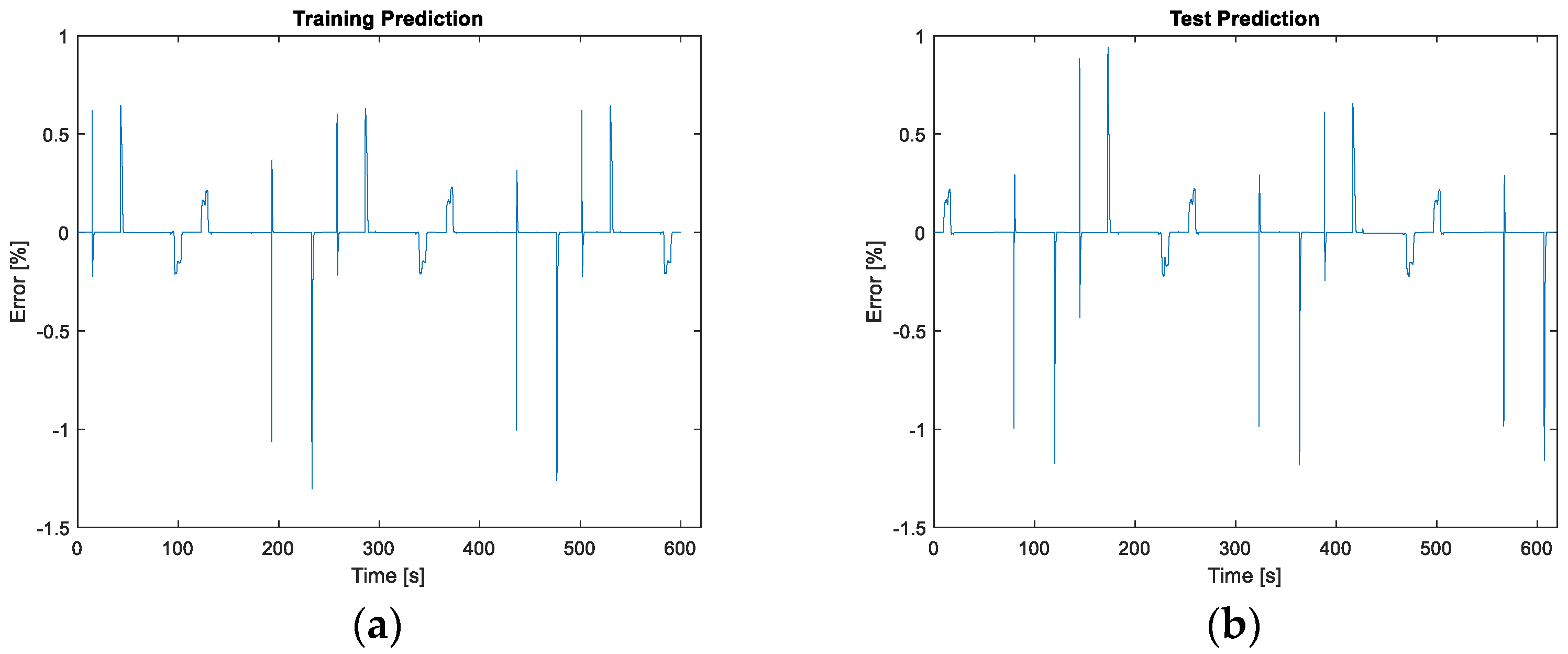
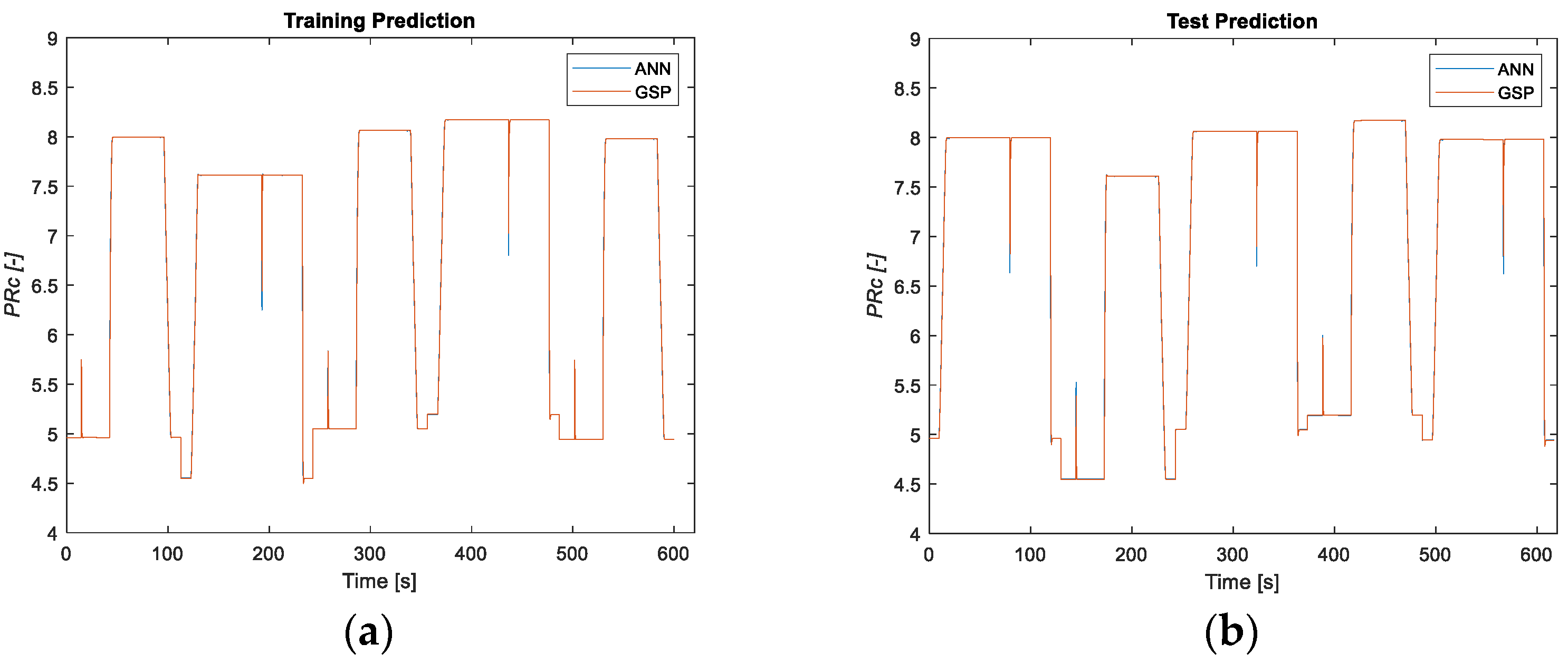
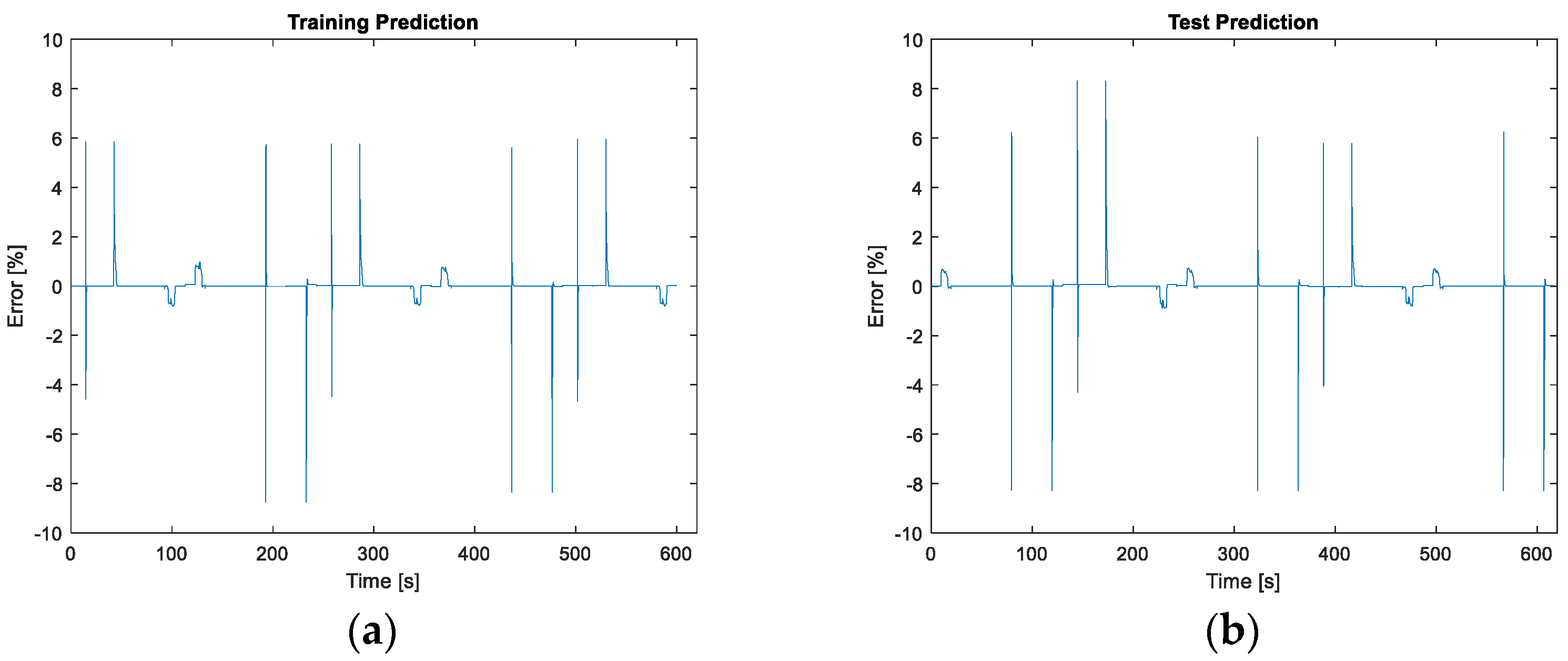
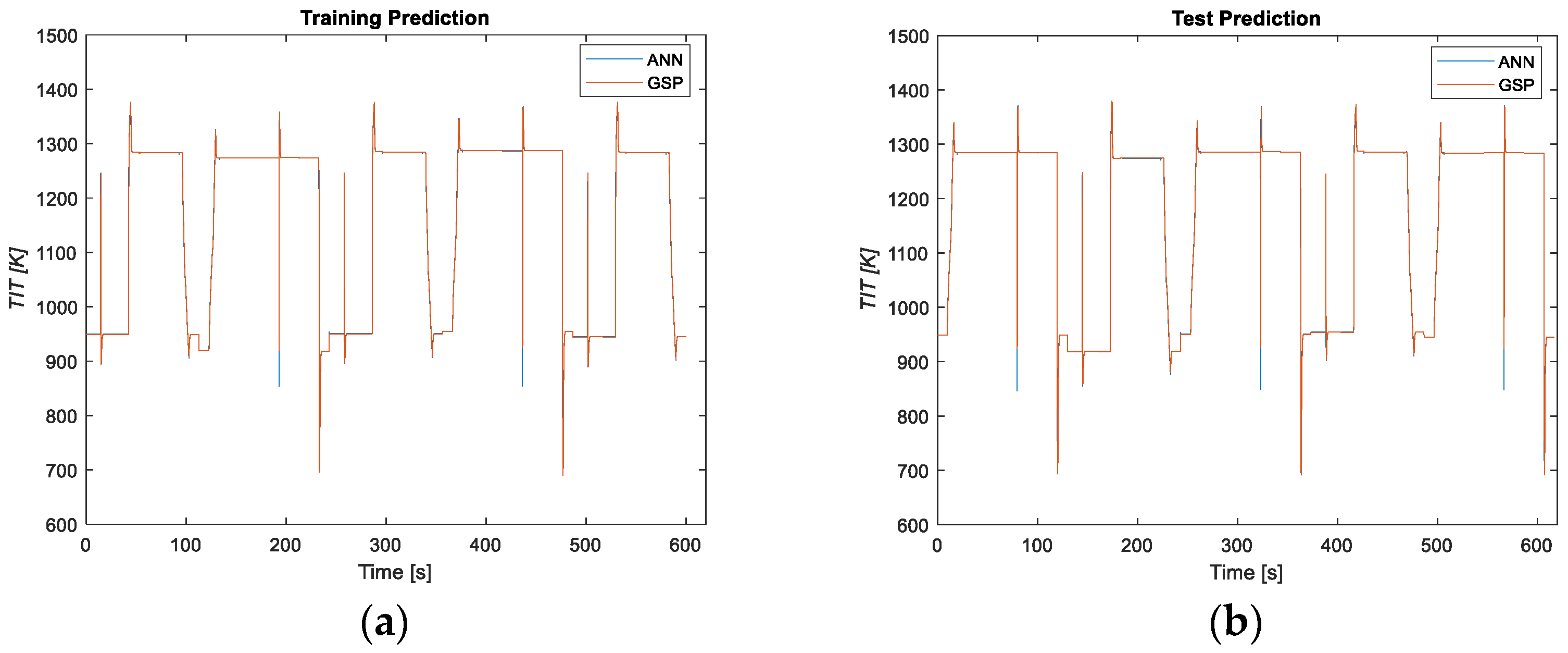
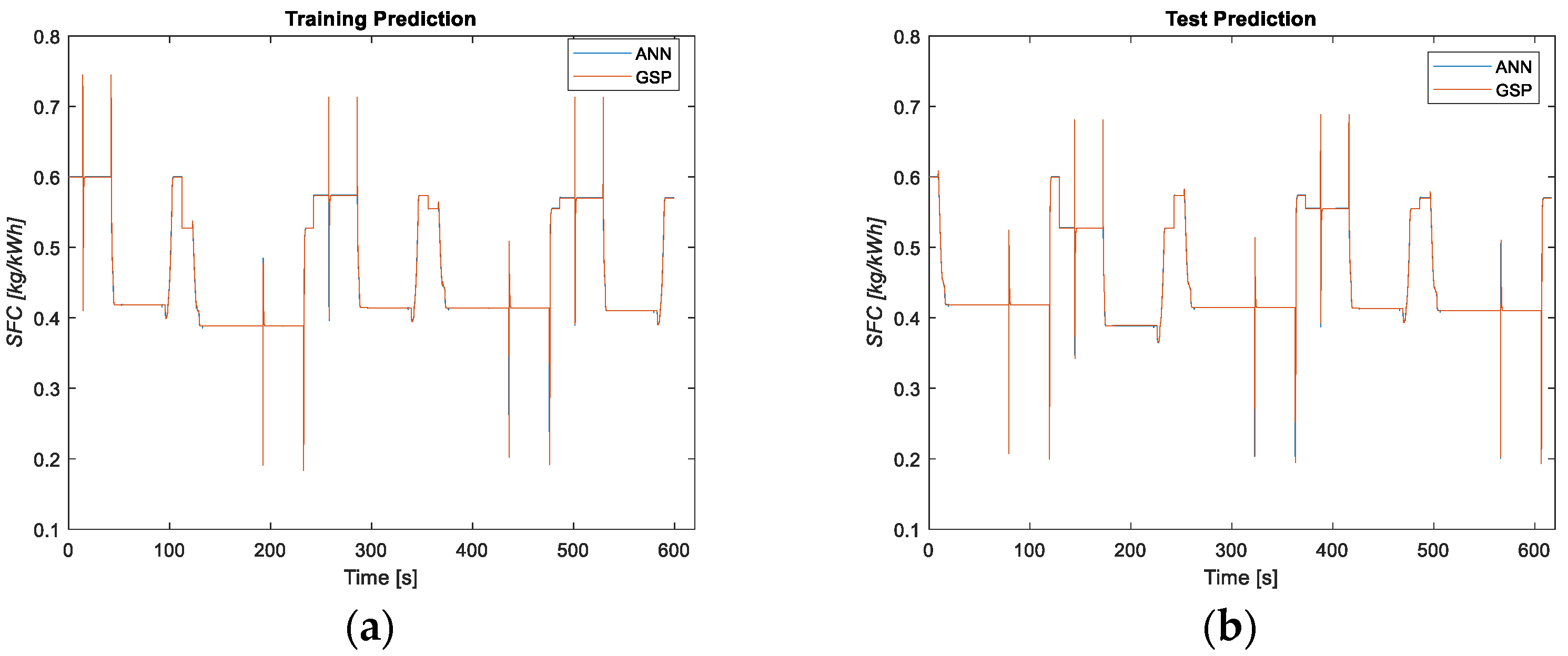
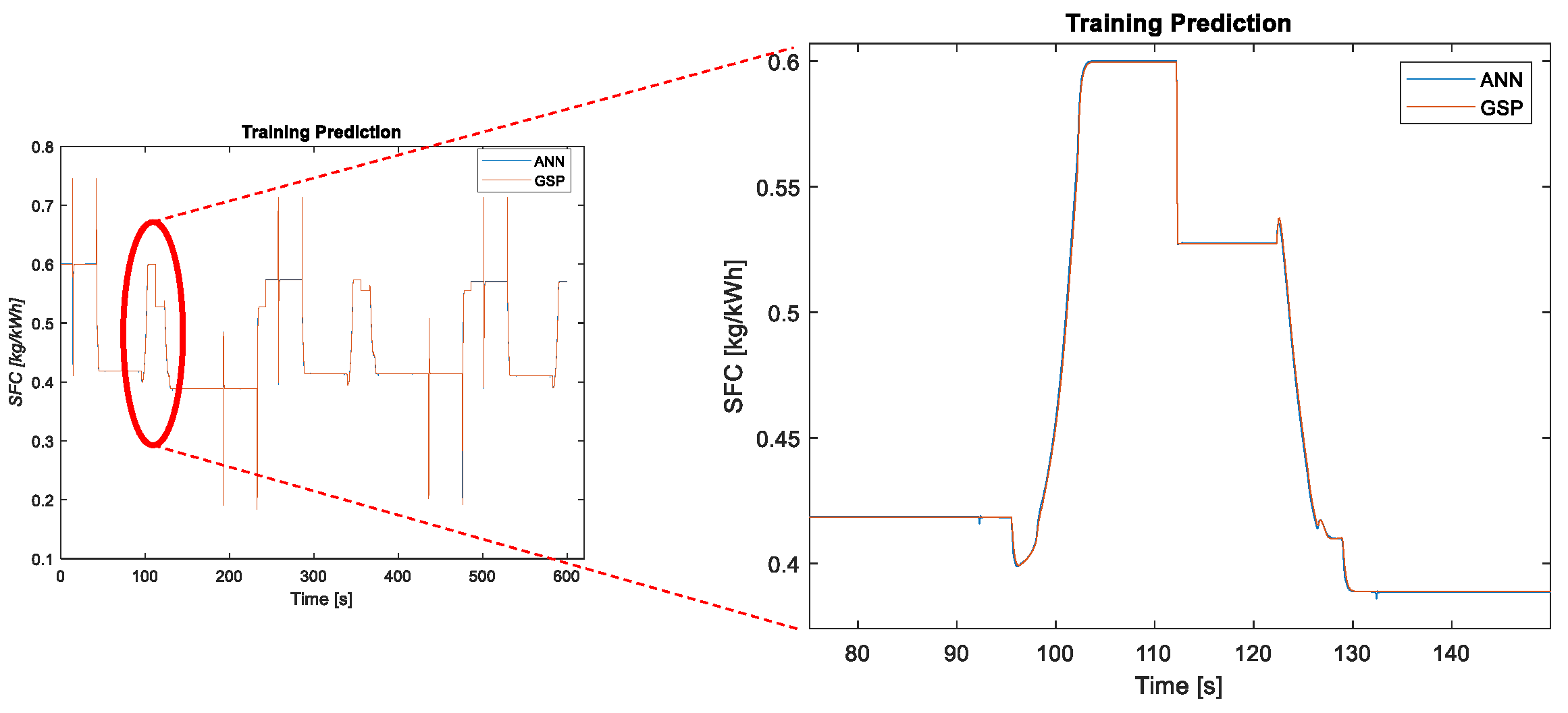
3.1.1. Healthy Results
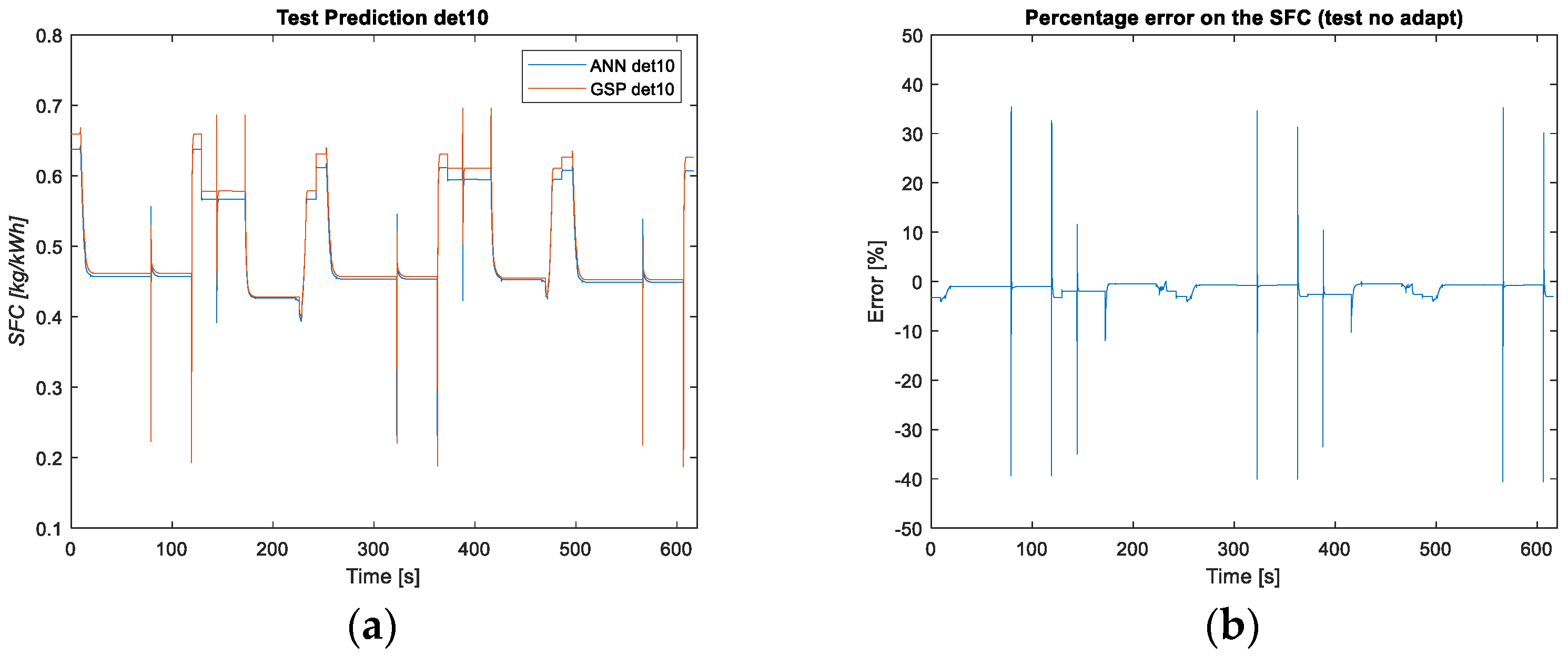
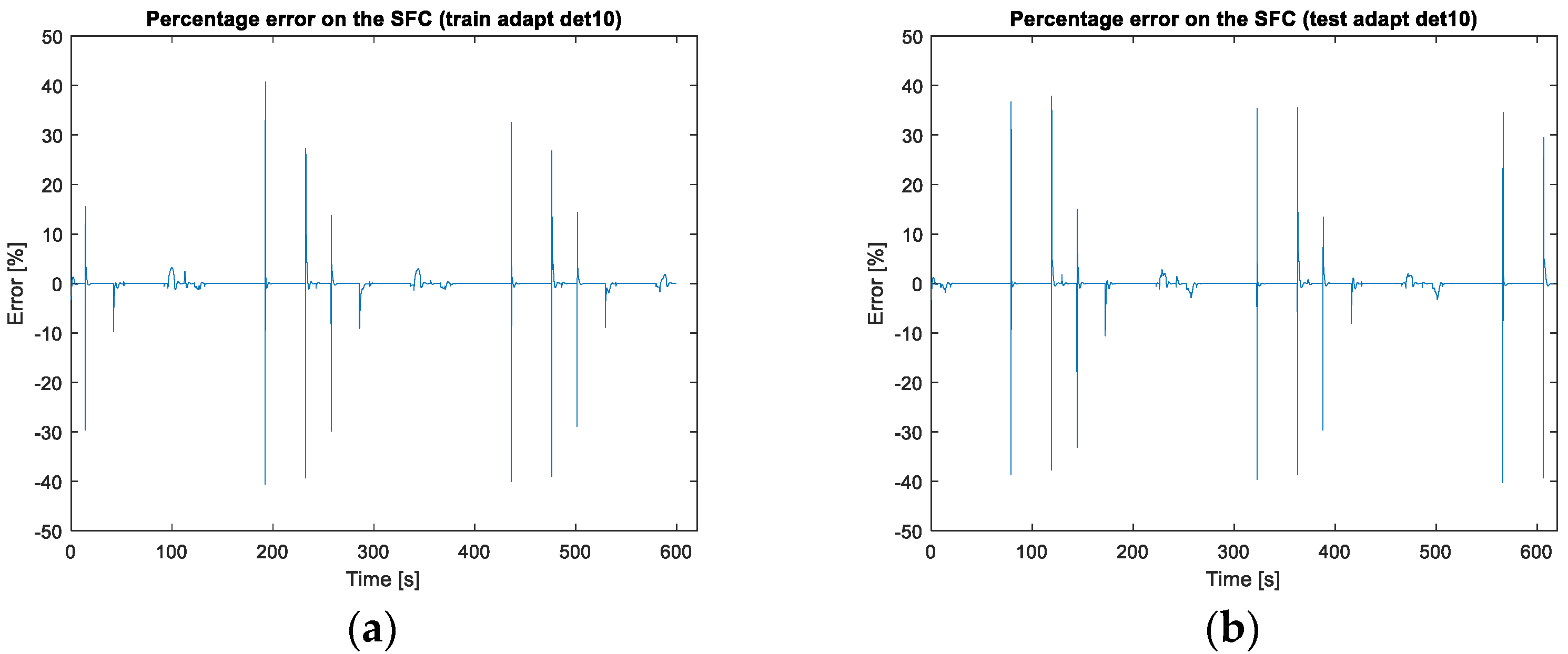
3.1.2. NARX Neural Networks Prediction Results Degraded Model
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Zheng, Q.; Zhang, H.; Li, Y.; Hu, Z. Aero-Engine On-Board Dynamic Adaptive MGD Neural Network Model within a Large Flight Envelope. IEEE Access 2018, 6, 45755–45761. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, Y.; Li, R. State Feedback Control for Partially Distributed Turboshaft Engine with Time Delay and Packet Dropouts. In Proceedings of the 37th Chinese Control Conference, Wuhan, China, 25–27 July 2018; pp. 25–27. [Google Scholar]
- Timothy, M.S.; Qwen, B.M.; Alireza, R.B.; Fouad, K. Development of Distributed Control Systems for Aircraft Turbo-Fan Engines. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, AIAA Propulsion and Energy Forum, American Institute of Aeronautics and Astronautics, Salt Lake City, UT, USA, 25–27 July 2016. [Google Scholar]
- Lee, S.M.; Roh, T.S.; Choi, D.W. Defect diagnostics of SUAV gas turbine engine using hybrid SVM-artificial neural network method. J. Mech. Sci. Technol. 2009, 23, 559–568. [Google Scholar] [CrossRef]
- Xia, T.; Xi, L.; Zhou, X. Modeling and optimizing maintenance schedule for energy systems subject to degradation. Comput. Ind. Eng. 2012, 63, 607.e14. [Google Scholar] [CrossRef]
- Li, Y.G.; Nilkitsaranont, P. Gas turbine performance prognostic for condition based maintenance. Appl. Energy 2009, 86, 2152–2161. [Google Scholar] [CrossRef]
- Biagetti, T.; Sciubba, E. Automatic diagnostics and prognostics of energy conversion processes via knowledge-based systems. Energy 2004, 29, 2553–2572. [Google Scholar] [CrossRef]
- Silva, J.A.M.; Venturini, O.J.; Lora, E.E.S.; Pinho, A.F.; Santos, J.J.C.S. Thermodynamic information system for diagnosis and prognosis of power plant operation condition. Energy 2011, 36, 4072–4079. [Google Scholar] [CrossRef]
- Volponi, A.J. Gas Turbine Engine Health Management Past, Present and Future Trends. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013. [Google Scholar]
- Wang, X.-Y.; Du, X.; Wang, X.-F.; Sun, X.-M.; Li, Y.-S. Controller Design of Aero-engines under the Distributed Architecture with Time Delays. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 6881–6886. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Campilongo, S.; Ficarella, A. A diagnostics tool for aero-engines health monitoring using machine learning technique. Energy Procedia 2018, 148, 860–867. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Ficarella, A.; De Carlo, L. Jet engine degradation prognostic using artificial neural networks. Aircr. Eng. Aerosp. Technol. 2019, 92, 296–303. [Google Scholar] [CrossRef]
- Wang, C.; Li, Y.G.; Yang, B.Y. Transient performance simulation of aircraft engine integrated with fuel and control systems. Appl. Therm. Eng. 2017, 114, 1029–1037. [Google Scholar] [CrossRef] [Green Version]
- Kordestani, M.; Saif, M.; Orchard, M.E.; Razavi-Far, R.; Khorasani, K. Failure Prognosis and Applications—A Survey of Recent Literature. IEEE Trans. Reliab. 2021, 70, 728–748. [Google Scholar] [CrossRef]
- Tsoumakas, G.; Katakis, I. Multi-Label Classification: An Overview; Department of Informatics, Aristotle University of Thessaloniki: Thessaloniki, Greece, 2006. [Google Scholar]
- Khorasani, K.; Kiakojoori, S. Dynamic neural networks for gas turbine engine degradation prediction, health monitoring and prognosis. Neural Comput. Appl. 2016, 27, 2157–2192. [Google Scholar]
- Asgari, H.; Chen, X.; Morini, M.; Pinelli, M.; Sainudiin, R.; Spina, P.R.; Venturini, M. NARX models for simulation of the start-up operation of a single-shaft gas turbine. Appl. Therm. Eng. 2016, 93, 368–376. [Google Scholar] [CrossRef]
- Kong, C.-D.; Ki, J.-Y.; Lee, C.-H. A Study on Fault Detection of a Turboshaft Engine Using Neural Network Method. Int. J. Aeronaut. Space Sci. Korean Soc. Aeronaut. Space Sci. 2008, 9, 100–110. [Google Scholar] [CrossRef] [Green Version]
- GSP 11 User Manual National Aerospace Laboratory NLR 2016. Available online: https://www.gspteam.com/Files/manuals/UM/GSP_UM_11.pdf (accessed on 1 July 2021).
- Janikovic, J. Gas Turbine Transient Performance Modeling for Engine Flight Path Cycle Analysis. Ph.D. Thesis, Cranfield University, Bedford, UK, 2010. [Google Scholar]
- Li, Y.G. Gas Turbine Diagnostics; Lecture Notes; Cranfield University: Bedford, UK, 2002. [Google Scholar]
- Zhao, N.-B.; Yang, J.-L.; Li, S.-Y.; Sun, Y.-W. A GM (1, 1) Markov Chain-Based Aeroengine Performance Degradation Forecast Approach Using Exhaust Gas Temperature. Math. Probl. Eng. 2014, 2014, 832851. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Quarta, M. Hybrid MultiGene Genetic Programming—Artificial neural networks approach for dynamic performance prediction of an aeroengine. Aerosp. Sci. Technol. 2020, 103, 105902. [Google Scholar] [CrossRef]

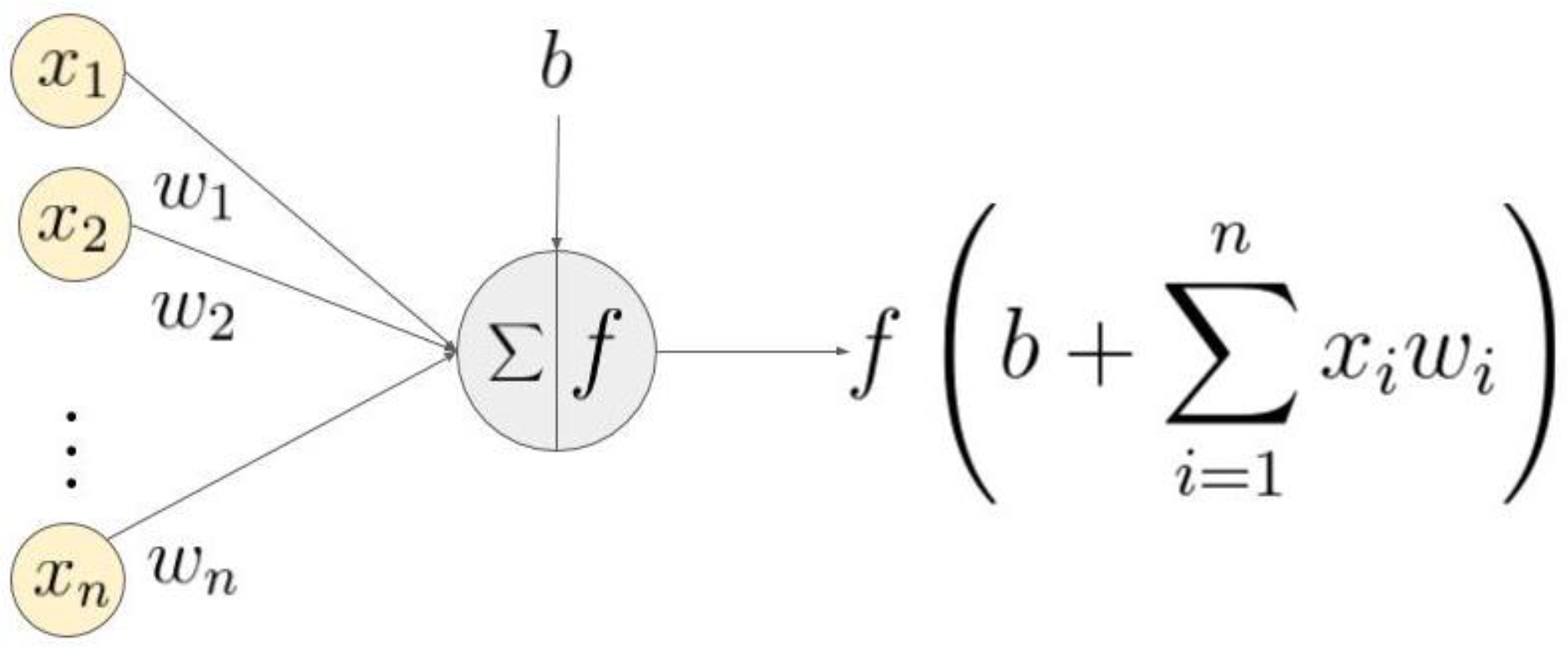






| Description | Value |
|---|---|
| Power | 200–400 (kW) |
| Weight | 110 (kg) |
| Pressure Ratio | 8:1 |
| Turbine Inlet Temp | 1173.15 (K) |
| SFC (Specific Fuel Consumption) | 0.426–0.33 (kg/kWh) |
| Compressor Configuration | 1 centrifugal |
| Turbine Configuration (one stage) | HPT, LPT |
| Description | Value | Unit |
|---|---|---|
| Power (POW) | 266 | (kW) |
| Intake Pressure ratio (PR) | 0.988 | (-) |
| Air Flow rate (Wa) | 2 | (kg/s) |
| Combustion efficiency (ηb) | 0.985 | (-) |
| Fuel Flow rate (Wfb) | 0.0315 | (kg/s) |
| Compressor Rotor Speed (n1) | 40,891 | (rpm) |
| Compressor Efficiency (ηc) | 0.825 | (-) |
| LPT Rotor Speed (n2) | 6000 | (rpm) |
| Turbine efficiency (ηt) | 0.88 | (-) |
| Spool Mechanical Efficiency (ηm) | 0.99 | (-) |
| h [m] | Mach Number | |
|---|---|---|
| TO (Take-Off) | 0 | 0 |
| CR1 (Cruise1) | 313.5 | 0.45 |
| CR2 (Cruise2) | 400 | 0.12 |
| CR3 (Cruise3) | 800 | 0.09 |
| CR4 (Cruise4) | 313.5 | 0.21 |
| Physical Fault | Flow Capacity Change | Isentropic Efficiency Change |
|---|---|---|
| Compressor Fouling | ηc↓ | |
| Compressor Erosion | ηc↓ | |
| Compressor Corrosion | ηc↓ | |
| Compressor Blade Rubbing | ηc↓ | |
| Turbine Fouling | ηt↓ | |
| Turbine Erosion | ηt↓ | |
| Turbine Corrosion | ηt↓ | |
| Turbine Blade Rubbing | ηt↓ | |
| Thermal Distortion | ηt↓ | |
| FOD (Foreign Object Damage) | and | ηc↓ and ηt↓ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Giorgi, M.G.; Strafella, L.; Ficarella, A. Neural Nonlinear Autoregressive Model with Exogenous Input (NARX) for Turboshaft Aeroengine Fuel Control Unit Model. Aerospace 2021, 8, 206. https://doi.org/10.3390/aerospace8080206
De Giorgi MG, Strafella L, Ficarella A. Neural Nonlinear Autoregressive Model with Exogenous Input (NARX) for Turboshaft Aeroengine Fuel Control Unit Model. Aerospace. 2021; 8(8):206. https://doi.org/10.3390/aerospace8080206
Chicago/Turabian StyleDe Giorgi, Maria Grazia, Luciano Strafella, and Antonio Ficarella. 2021. "Neural Nonlinear Autoregressive Model with Exogenous Input (NARX) for Turboshaft Aeroengine Fuel Control Unit Model" Aerospace 8, no. 8: 206. https://doi.org/10.3390/aerospace8080206
APA StyleDe Giorgi, M. G., Strafella, L., & Ficarella, A. (2021). Neural Nonlinear Autoregressive Model with Exogenous Input (NARX) for Turboshaft Aeroengine Fuel Control Unit Model. Aerospace, 8(8), 206. https://doi.org/10.3390/aerospace8080206








