Comparison of Tethered Post-Capture System Models for Space Debris Removal
Abstract
:1. Introduction
2. Dynamic Models of the Tethered System
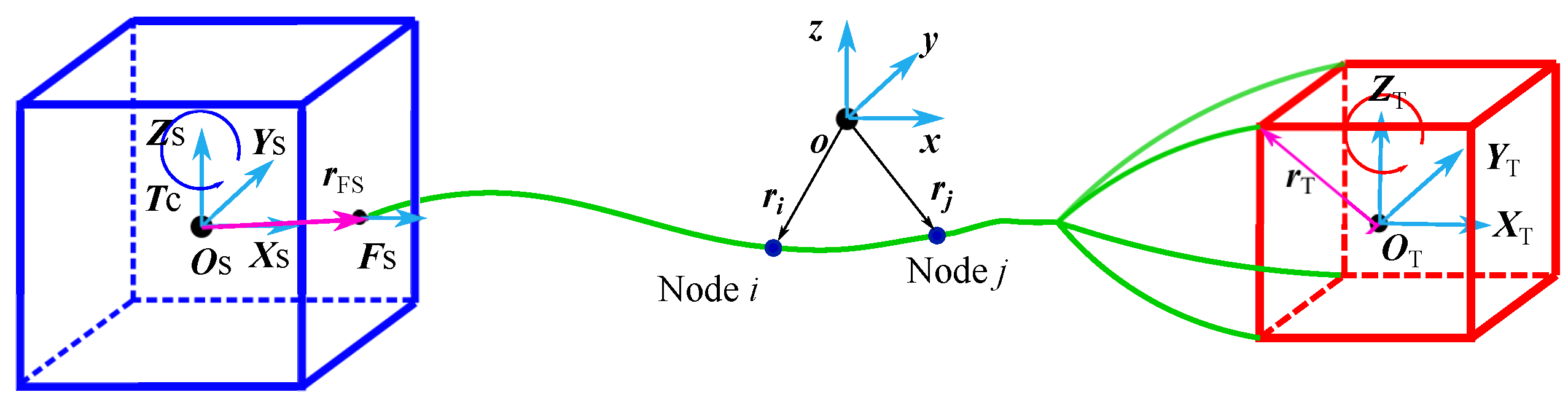
2.1. Configuration of Tethered System
2.2. Modified Dumbbell Model
2.2.1. Single Tether Configuration
2.2.2. Sub-Tether Configuration
2.3. Lumped-Mass Model
2.3.1. Single Tether Configuration
2.3.2. Sub-Tether Configuration
2.4. ANCF Model
2.4.1. Single Tether Configuration
2.4.2. Sub-Tether Configuration
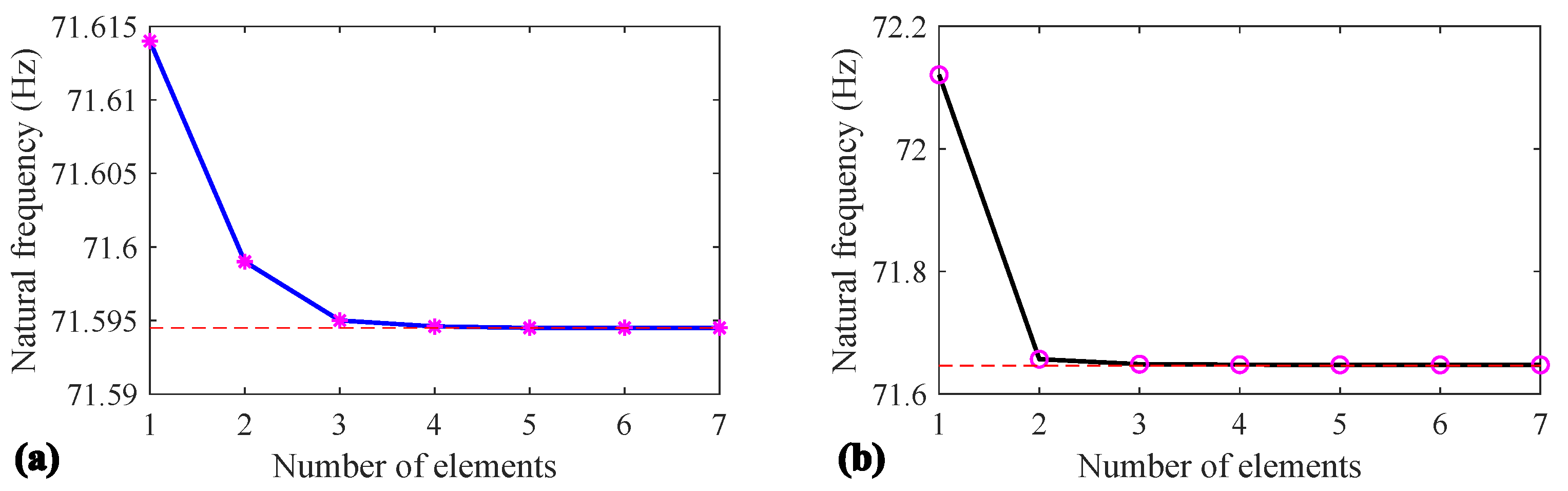
3. Modal Analysis of Tethered System
3.1. Analytical Results
3.2. Modified Dumbbell Model
3.3. Lumped-Mass Model
3.4. ANCF Model
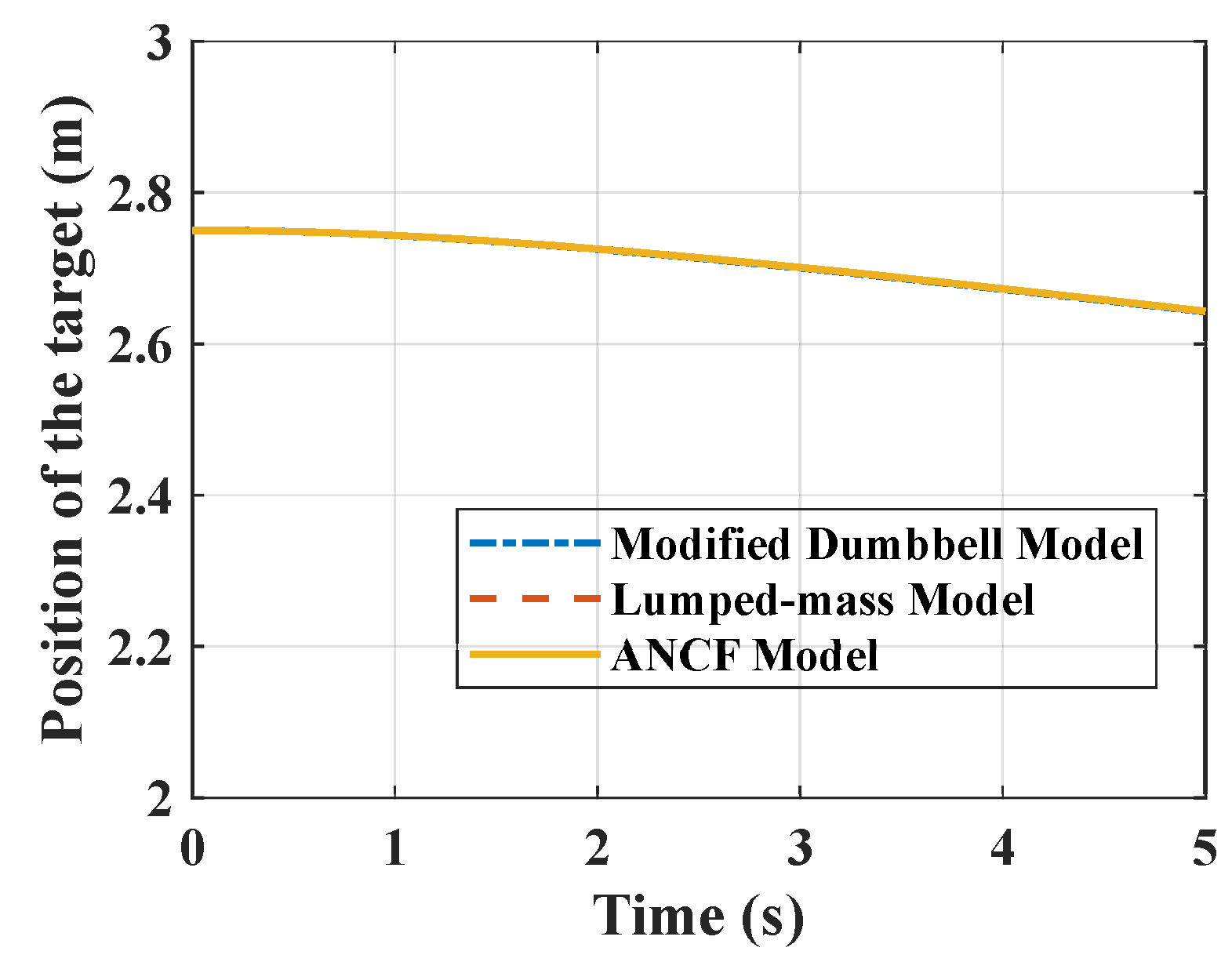
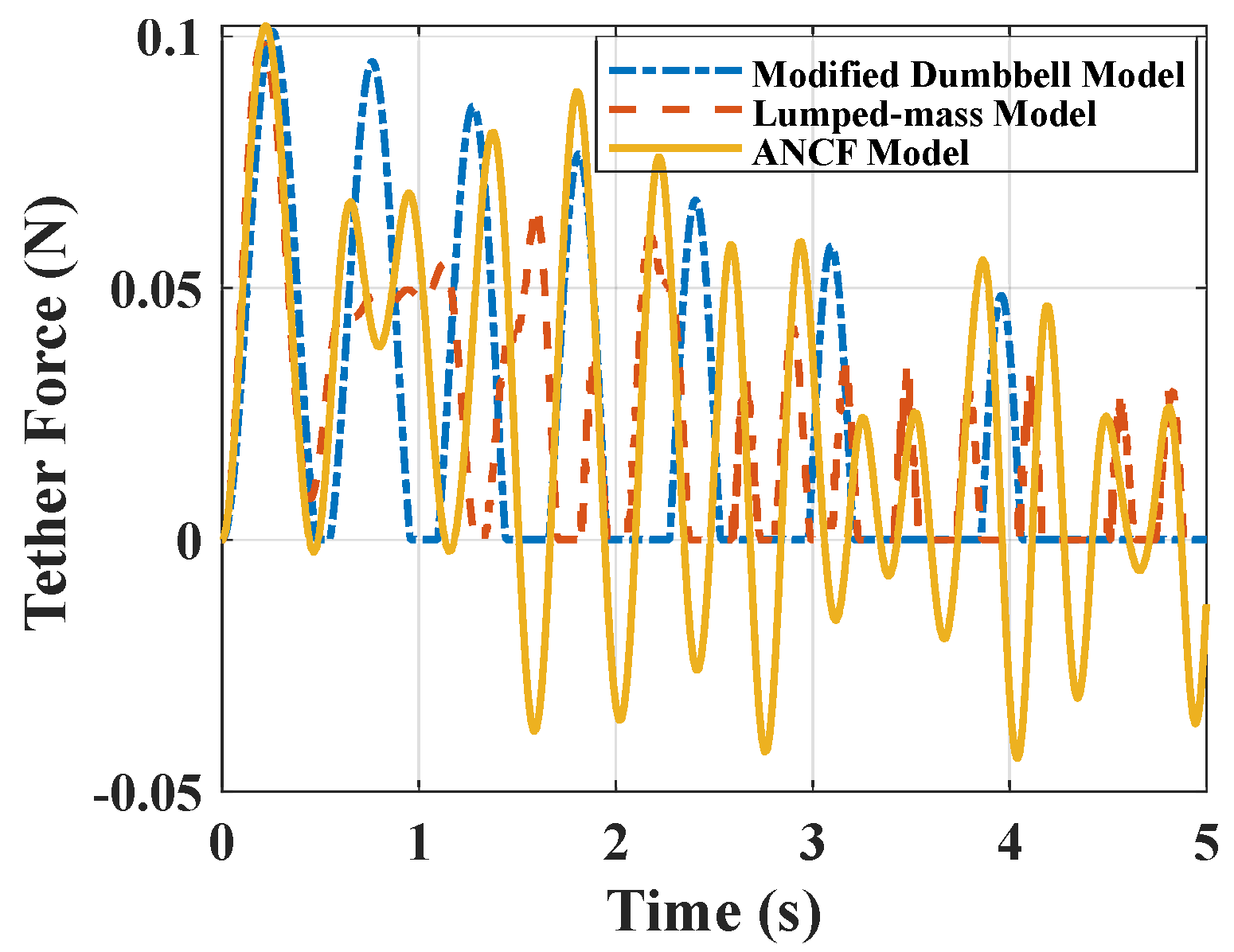
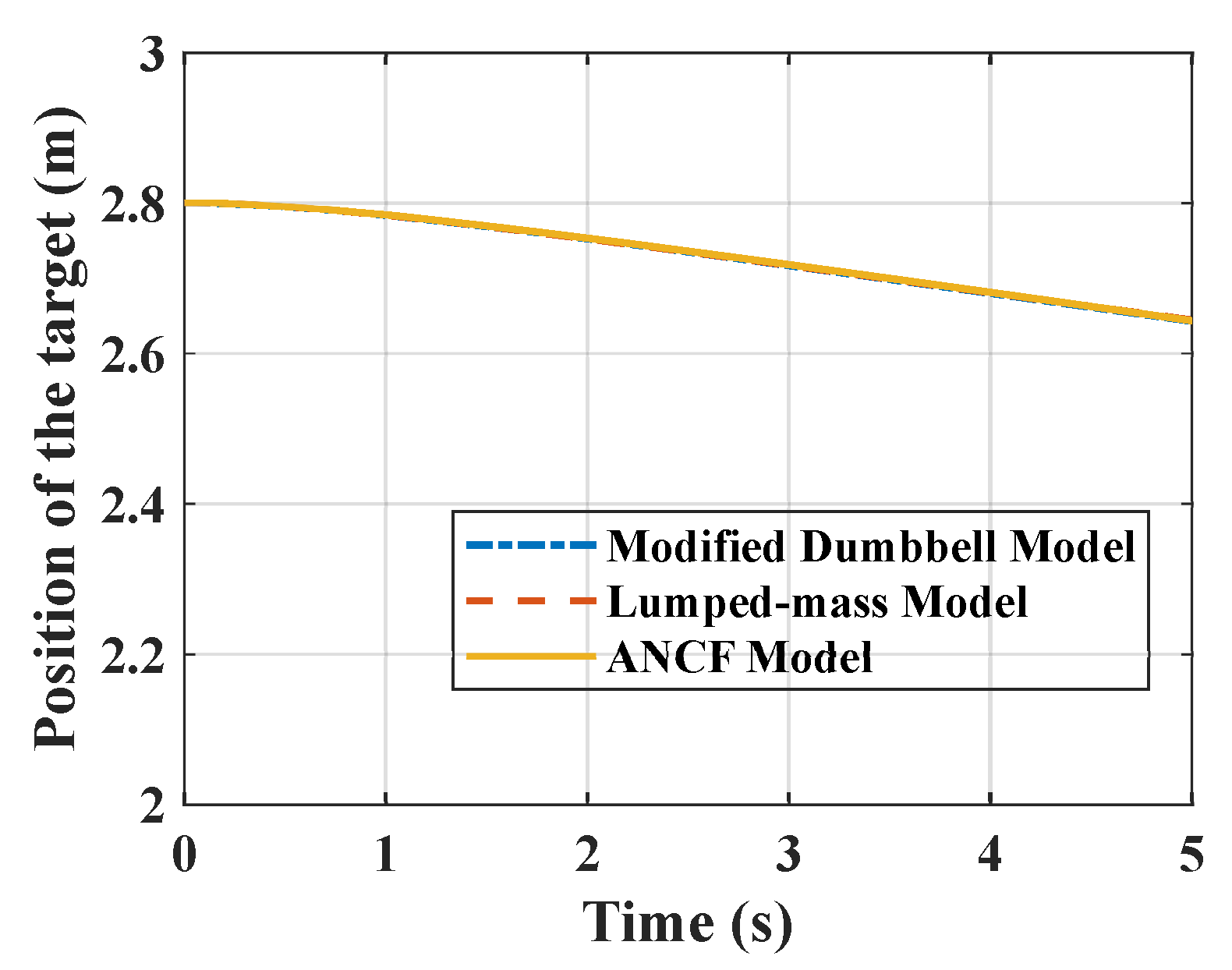
4. Comparison of Three Models
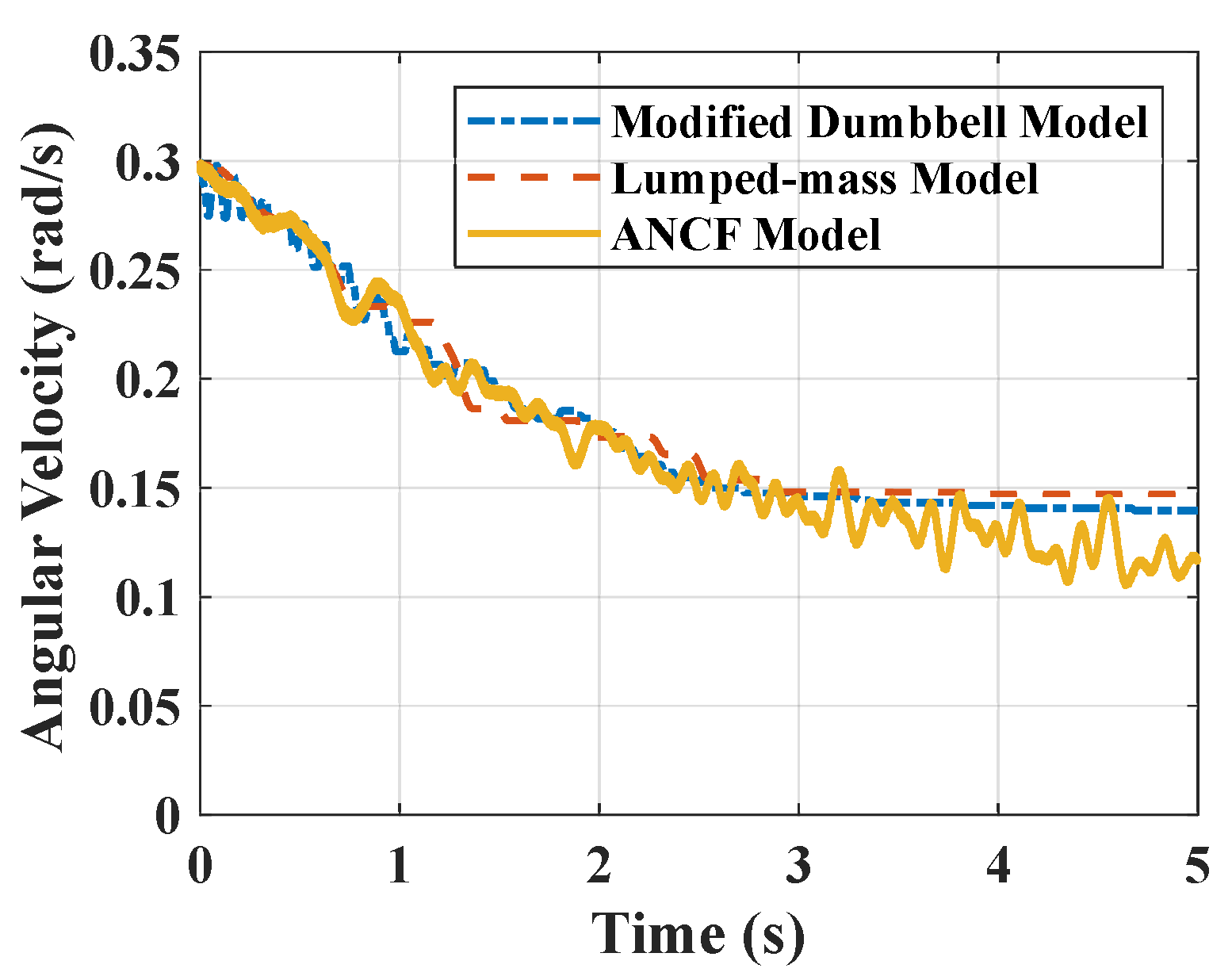
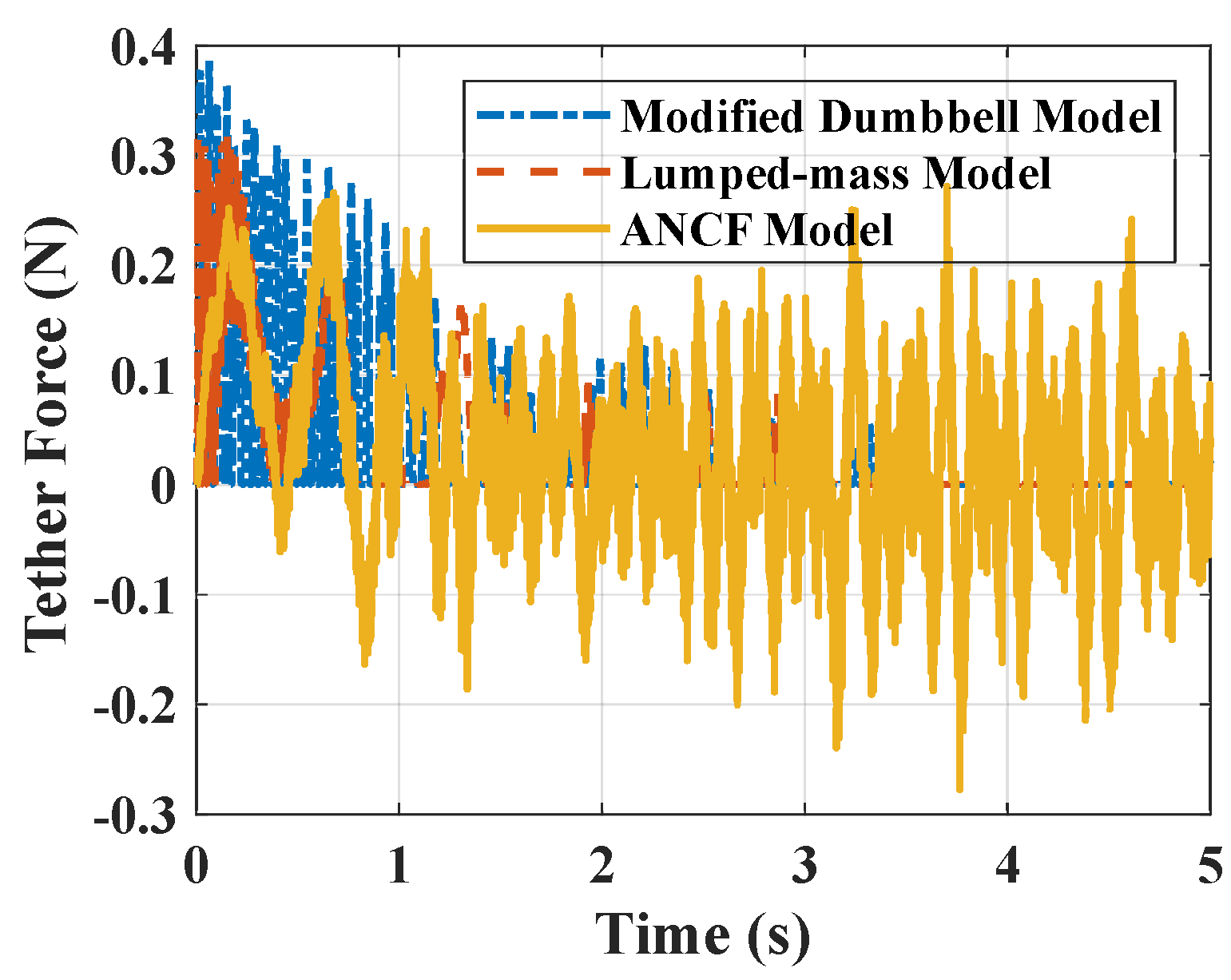
4.1. Single Tether Configuration
4.2. Sub-Tether Configuration
4.3. Comparison of Natural Frequency
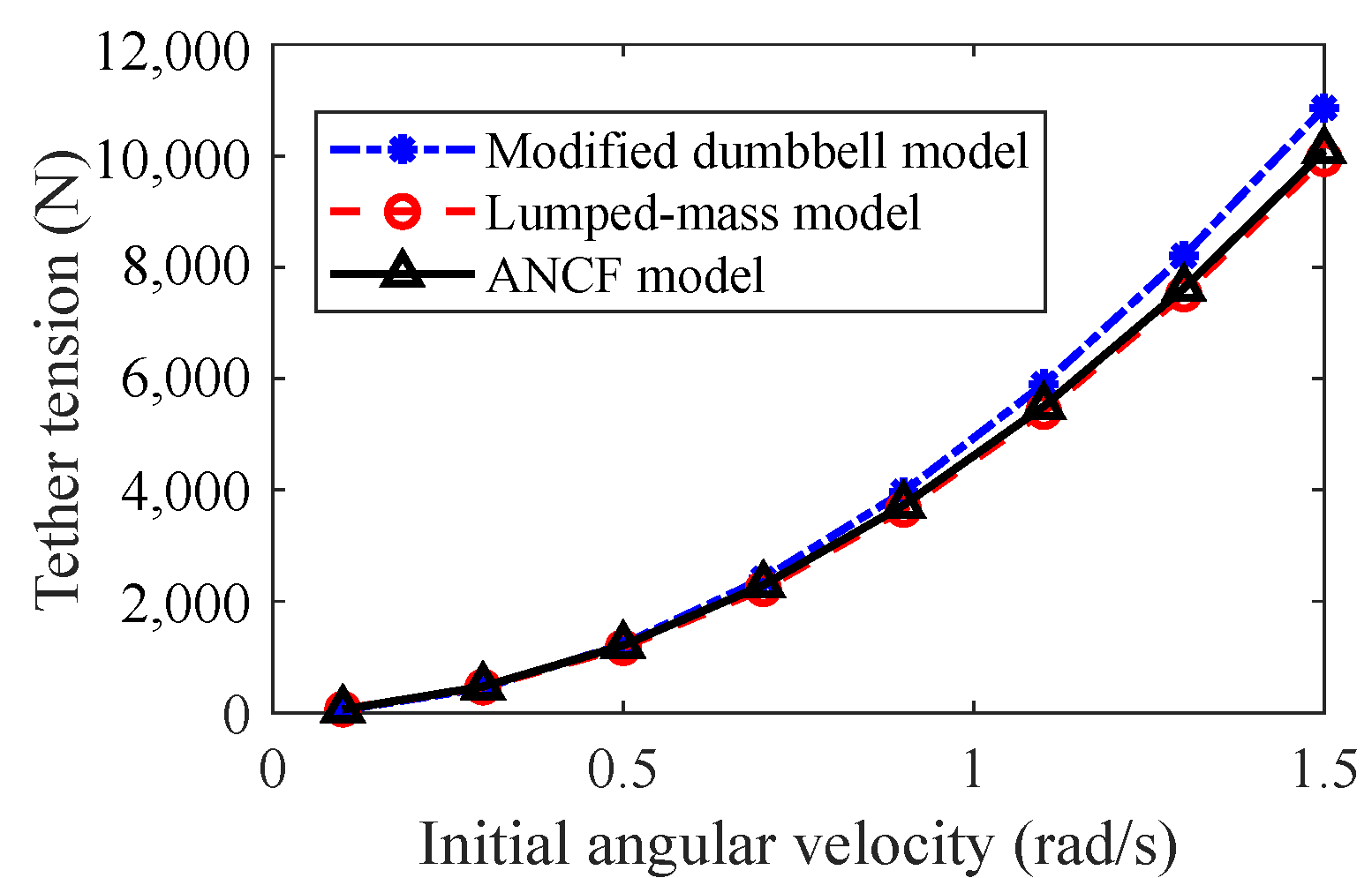
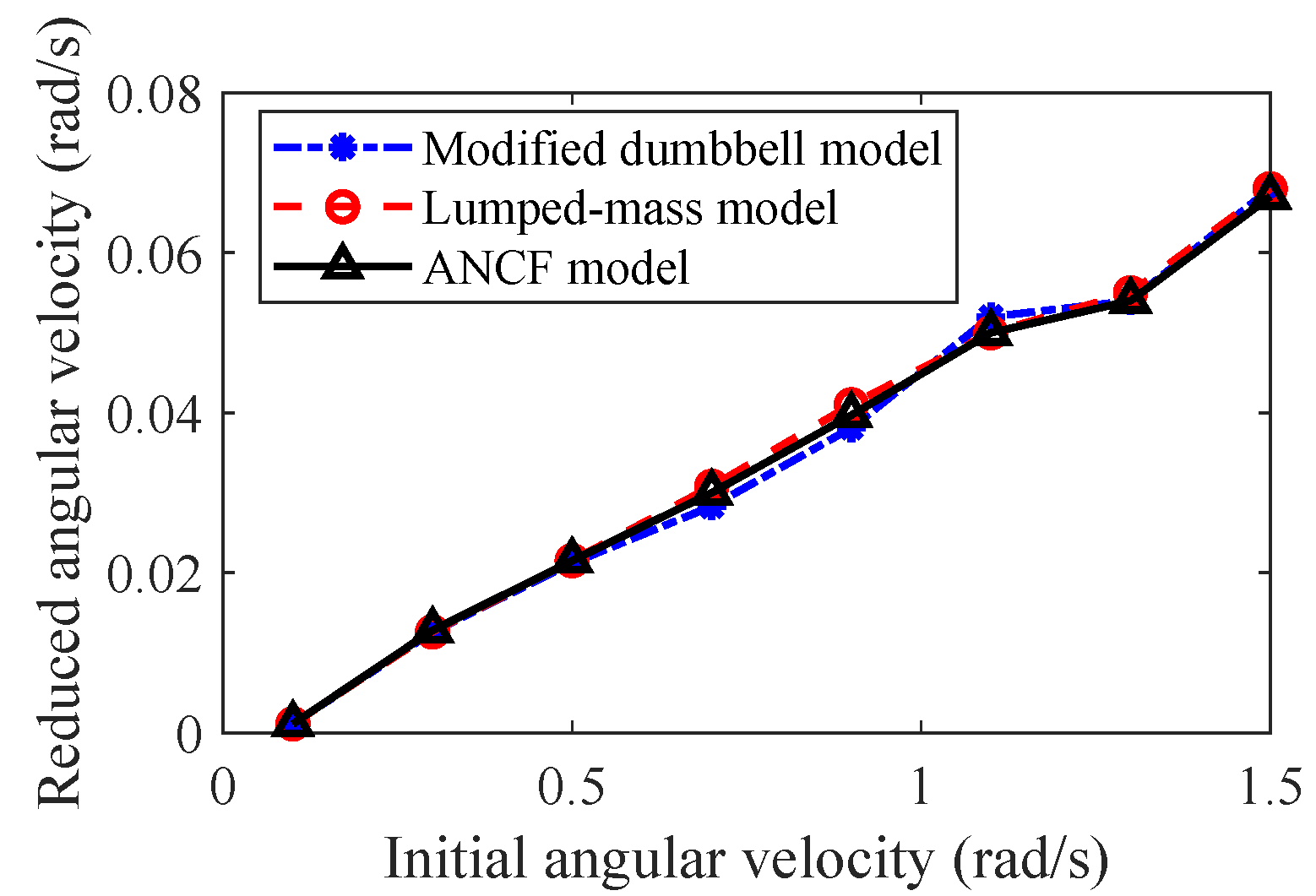
4.4. Influence by Initial Condition
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- NASA Orbital Debris Program Office. Orbital Debris Quaterly News; National Aeronautics and Space Administration: Washington, DC, USA, 2021; Volume 25, pp. 1–12. [Google Scholar]
- GlobalNews. Damage on Canadarm. 2021. Available online: https://globalnews.ca/news/7913922/canadarm2-damaged-international-space-station-junk/ (accessed on 7 June 2021).
- Shan, M.; Guo, J.; Gill, E. Review and comparison of active space debris capturing and removal methods. Prog. Aerosp. Sci. 2016, 80, 18–32. [Google Scholar] [CrossRef]
- Reed, J.; Barraclough, S. Development of harpoon system for capturing space debris. In Proceedings of the 6th European Conference on Space Debris, Darmstadt, Germany, 22–25 April 2013; Volume 723, p. 174. [Google Scholar]
- Bischof, B. ROGER-Robotic geostationary orbit restorer. In Proceedings of the 54th International Astronautical Congress of the International Astronautical Federation, Bremen, Germany, 29 September–3 October 2003. [Google Scholar]
- Tamaki, Y.; Tanaka, H. Penetration Characteristics of Metal Harpoons with Various Tip Shapes for Capturing Space Debris. In Proceedings of the 8th European Conference on Space Debris, Darmstadt, Germany, 20–23 April 2021. [Google Scholar]
- Sizov, D.A.; Aslanov, V.S. Space Debris Removal with Harpoon Assistance: Choice of Parameters and Optimization. J. Guid. Control. Dyn. 2020, 44, 767–778. [Google Scholar] [CrossRef]
- Cleary, S.; O’Connor, W.J. Control of space debris using an elastic tether and wave-based control. J. Guid. Control. Dyn. 2016, 39, 1392–1406. [Google Scholar] [CrossRef]
- Shan, M.; Guo, J.; Gill, E. Deployment Dynamics of Tethered-Net for Space Debris Removal. Acta Astronaut. 2017, 132, 293–302. [Google Scholar] [CrossRef]
- Botta, E.M.; Sharf, I.; Misra, A.K.; Teichmann, M. On the simulation of tether-nets for space debris capture with Vortex Dynamics. Acta Astronaut. 2016, 123, 91–102. [Google Scholar] [CrossRef]
- Benvenuto, R.; Salvi, S.; Lavagna, M. Dynamics analysis and GNC design of flexible systems for space debris active removal. Acta Astronaut. 2015, 110, 247–265. [Google Scholar] [CrossRef]
- Golebiowski, W.; Michalczyk, R.; Dyrek, M.; Battista, U.; Wormnes, K. Validated simulator for space debris removal with nets and other flexible tethers applications. Acta Astronaut. 2016, 129, 229–240. [Google Scholar] [CrossRef]
- Medina, A.; Cercós, L.; Stefanescu, R.M.; Benvenuto, R.; Pesce, V.; Marcon, M.; Lavagna, M.; González, I.; López, N.R.; Wormnes, K. Validation results of satellite mock-up capturing experiment using nets. Acta Astronaut. 2017, 134, 314–332. [Google Scholar] [CrossRef]
- Shan, M.; Guo, J.; Gill, E.; Golebiowski, W. Validation of Space Net Deployment Modeling Methods Using Parabolic Flight Experiment. J. Guid. Control. Dyn. 2017, 40, 3319–3327. [Google Scholar] [CrossRef]
- Aglietti, G.; Taylor, B.; Fellowes, S.; Ainley, S.; Tye, D.; Cox, C.; Zarkesh, A.; Mafficini, A.; Vinkoff, N.; Bashford, K.; et al. RemoveDEBRIS: An in-orbit demonstration of technologies for the removal of space debris. Aeronaut. J. 2020, 124, 1–23. [Google Scholar] [CrossRef]
- Benvenuto, R.; Lavagna, M.; Salvi, S. Multibody dynamics driving GNC and system design in tethered nets for active debris removal. Adv. Space Res. 2016, 58, 45–63. [Google Scholar] [CrossRef]
- Botta, E.M.; Sharf, I.; Misra, A.K. Contact Dynamics Modeling and Simulation of Tether Nets for Space-Debris Capture. J. Guid. Control. Dyn. 2016, 40, 110–123. [Google Scholar] [CrossRef]
- Zhang, F.; Huang, P. Releasing dynamics and stability control of maneuverable tethered space net. IEEE/ASME Trans. Mechatronics 2016, 22, 983–993. [Google Scholar] [CrossRef]
- Zhang, F.; Huang, P.; Meng, Z.; Zhang, Y.; Liu, Z. Dynamics analysis and controller design for maneuverable tethered space net robot. J. Guid. Control. Dyn. 2017, 40, 2828–2843. [Google Scholar] [CrossRef]
- Huang, P.; Wang, D.; Meng, Z.; Zhang, F.; Guo, J. Adaptive postcapture backstepping control for tumbling tethered space robot–target combination. J. Guid. Control. Dyn. 2015, 39, 150–156. [Google Scholar] [CrossRef]
- Pang, Z.; Yu, B.; Jin, D. Chaotic motion analysis of a rigid spacecraft dragging a satellite by an elastic tether. Acta Mech. 2015, 226, 2761–2771. [Google Scholar] [CrossRef]
- Forshaw, J.L.; Aglietti, G.S.; Fellowes, S.; Salmon, T.; Retat, I.; Hall, A.; Chabot, T.; Pisseloup, A.; Tye, D.; Bernal, C.; et al. The active space debris removal mission RemoveDebris. Part 1: From concept to launch. Acta Astronaut. 2020, 168, 293–309. [Google Scholar] [CrossRef] [Green Version]
- Aglietti, G.S.; Taylor, B.; Fellowes, S.; Salmon, T.; Retat, I.; Hall, A.; Chabot, T.; Pisseloup, A.; Cox, C.; Mafficini, A.; et al. The active space debris removal mission RemoveDebris. Part 2: In orbit operations. Acta Astronaut. 2020, 168, 310–322. [Google Scholar] [CrossRef] [Green Version]
- O’Connor, M.; Clearly, S.; Hayden, D. Debris de-tumbling and de-orbiting by elastic tether and wave-based control. In Proceedings of the 6th International Conference on Astrodynamics Tools and Techniques (ICATT), Darmstadt, Germany, 14–17 March 2016. [Google Scholar]
- Shan, M.; Shi, L. Post-capture control of a tumbling space debris via tether tension. Acta Astronaut. 2021, 180, 317–327. [Google Scholar] [CrossRef]
- Stadnyk, K.; Ulrich, S. Validating the Deployment of a Novel Tether Design for Orbital Debris Removal. J. Spacecr. Rocket. 2020, 57, 1335–1349. [Google Scholar] [CrossRef]
- Hovell, K.; Ulrich, S. Attitude stabilization of an uncooperative spacecraft in an orbital environment using visco-elastic tethers. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, San Diego, CA, USA, 4–8 January 2016; p. 0641. [Google Scholar]
- Hovell, K.; Ulrich, S. Postcapture dynamics and experimental validation of subtethered space debris. J. Guid. Control. Dyn. 2018, 41, 519–525. [Google Scholar] [CrossRef]
- Misra, A.; Nixon, M.; Modi, V. Nonlinear dynamics of two-body tethered satellite systems: Constant length case. J. Astronaut. Sci. 2001, 49, 219–236. [Google Scholar] [CrossRef]
- Shabana, A.A. Flexible multibody dynamics: Review of past and recent developments. Multibody Syst. Dyn. 1997, 1, 189–222. [Google Scholar] [CrossRef]
- Berzeri, M.; Shabana, A. Development of simple models for the elastic forces in the absolute nodal co-ordinate formulation. J. Sound Vib. 2000, 235, 539–565. [Google Scholar] [CrossRef]

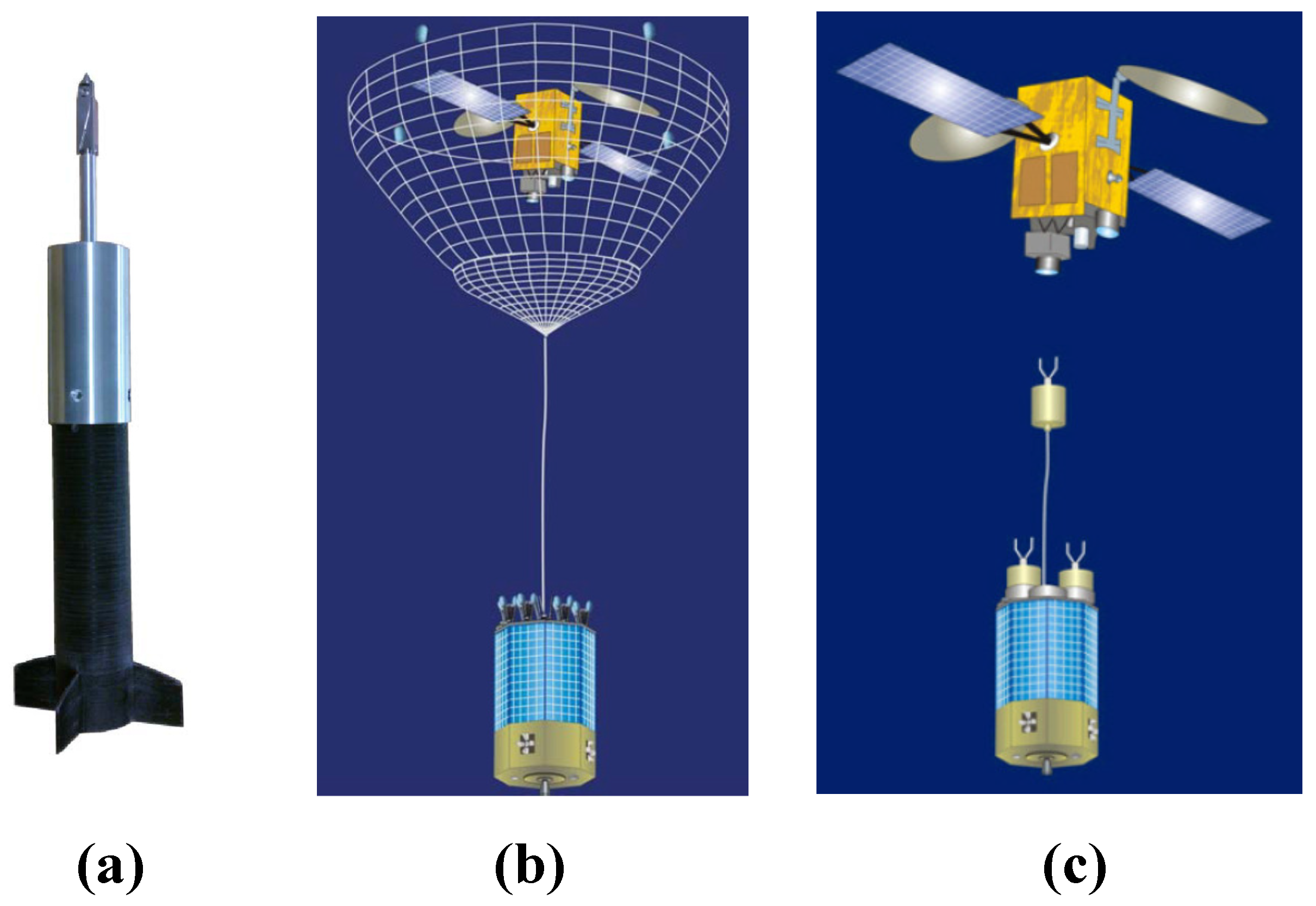

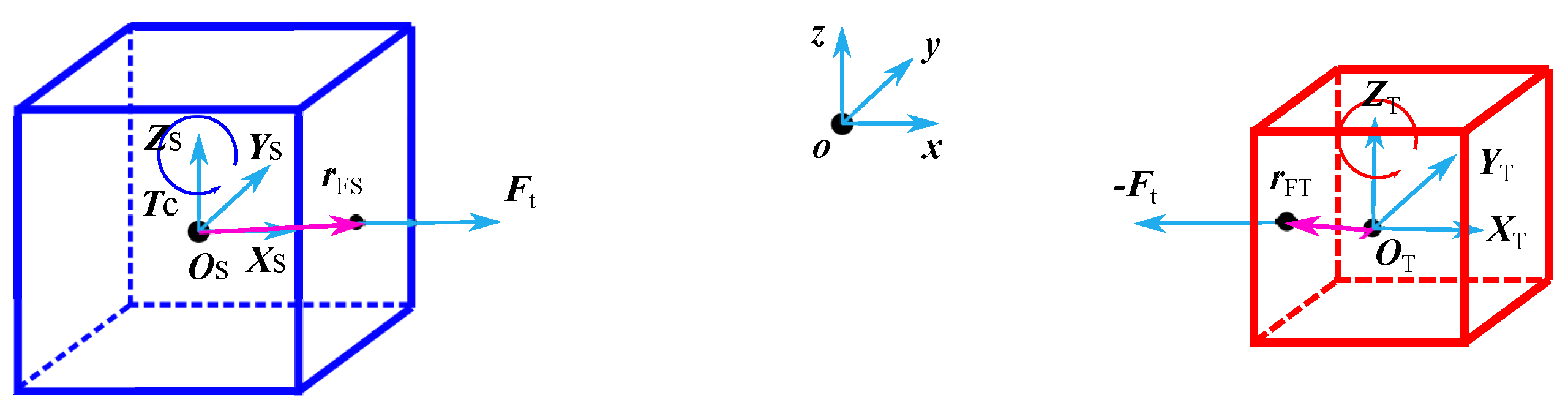

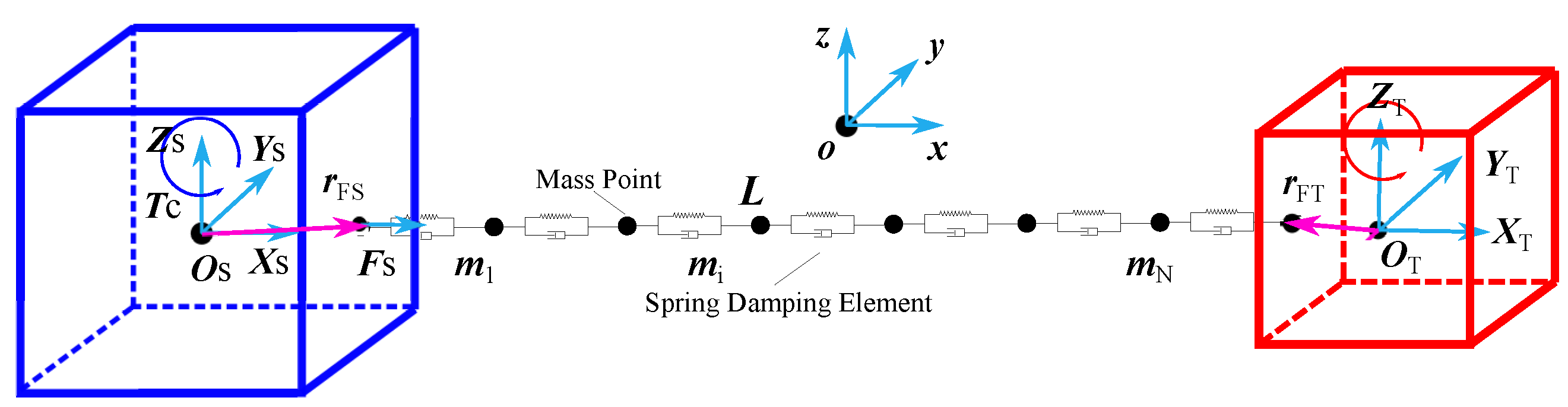

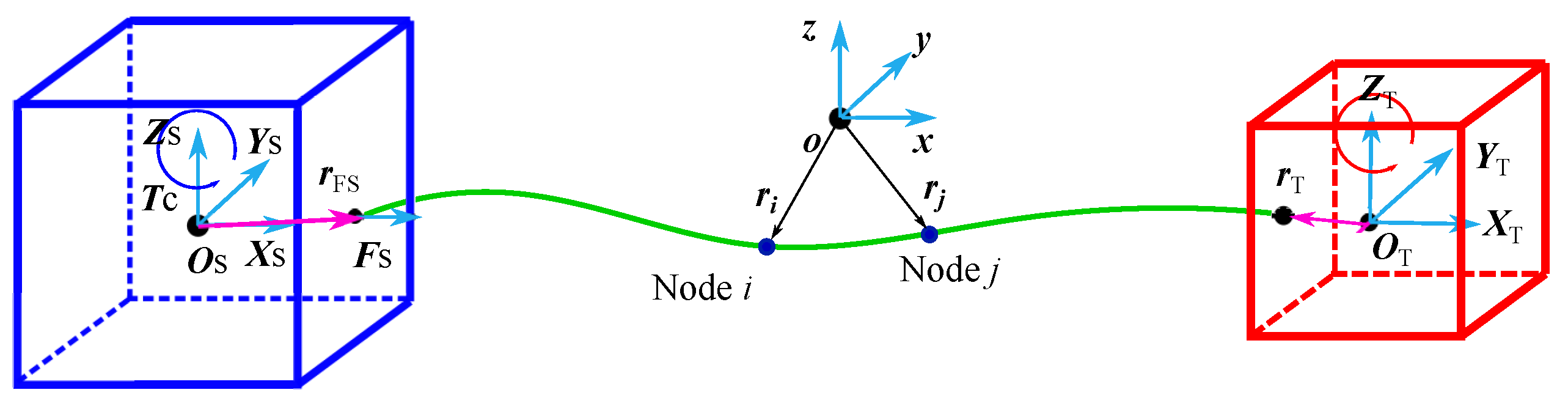


| Parameter | Value | |
|---|---|---|
| Service Satellite | Mass , (kg) | 10 |
| Dimensions −, (m) | 0.6 × 0.6 × 0.6 | |
| Target | Mass , (kg) | 3.5 |
| Dimensions −, (m) | 0.4 × 0.4 × 0.4 | |
| Tether | Main tether length L, (m) | 2.25 |
| Sub-tether length l, (m) | 0.4123 | |
| Tether diameter d, (mm) | 5 | |
| Damping coefficient c, (-) | 0.1 | |
| Young’s modulus E, (Pa) |
| Models | Screenshots of Animations |
|---|---|
| s s s | |
| Modified Dumbbell Model |  |
| Lumped-mass Model |  |
| ANCF Model |  |
| Models | Screenshots of Animations |
|---|---|
| s s s | |
| Modified Dumbbell Model |  |
| Lumped-mass Model |  |
| ANCF Model |  |
| Order | Analytical | Modified Dumbbell Model | Lumped-Mass Model | ANCF Model |
|---|---|---|---|---|
| 1 | 71.59 | 45.58 | 71.24 | 71.59 |
| 2 | 143.19 | - | 142.46 | 143.19 |
| 3 | 214.78 | - | 213.65 | 214.79 |
| 4 | 286.38 | - | 284.79 | 286.44 |
| 5 | 357.97 | - | 355.86 | 358.22 |
| Order | Analytical | Modified Dumbbell Model | Lumped-Mass Model | ANCF Model |
|---|---|---|---|---|
| 1 | 1.947 | 1.949 | 1.948 | 1.948 |
| 2 | 71.646 | - | 74.574 | 71.647 |
| 3 | 143.216 | - | 147.555 | 143.217 |
| 4 | 214.802 | - | 217.549 | 214.814 |
| 5 | 286.392 | - | 283.120 | 286.464 |
| Parameter | Value | |
|---|---|---|
| Service Satellite | Mass , (kg) | 500 |
| Dimensions −, (m) | 2.5 × 2.5 × 2.5 | |
| Target | Mass , (kg) | 8000 |
| Dimensions −, (m) | 5 × 5 × 5 | |
| Tether | Main tether length L, (m) | 100 |
| Tether diameter d, (mm) | 50 | |
| Damping coefficient c, (-) | 0.1 | |
| Young’s modulus E, (GPa) | 131 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, M.; Shi, L. Comparison of Tethered Post-Capture System Models for Space Debris Removal. Aerospace 2022, 9, 33. https://doi.org/10.3390/aerospace9010033
Shan M, Shi L. Comparison of Tethered Post-Capture System Models for Space Debris Removal. Aerospace. 2022; 9(1):33. https://doi.org/10.3390/aerospace9010033
Chicago/Turabian StyleShan, Minghe, and Lingling Shi. 2022. "Comparison of Tethered Post-Capture System Models for Space Debris Removal" Aerospace 9, no. 1: 33. https://doi.org/10.3390/aerospace9010033
APA StyleShan, M., & Shi, L. (2022). Comparison of Tethered Post-Capture System Models for Space Debris Removal. Aerospace, 9(1), 33. https://doi.org/10.3390/aerospace9010033






