Good Match between “Stop-and-Go” Strategy and Robust Guidance Based on Deep Reinforcement Learning
Abstract
:1. Introduction
- (1)
- The spacecraft can stop at any time during the process of approaching the asteroid to respond to an emergency or avoid hazards, giving the approach process more flexibility;
- (2)
- The original robust guidance can still work after the SaG point without the need to solve the guidance policy again, and therefore improve the real-time performance;
- (3)
- It can increase the AON observability in the range direction and therefore ensure the terminal accuracy of rendezvous guidance.
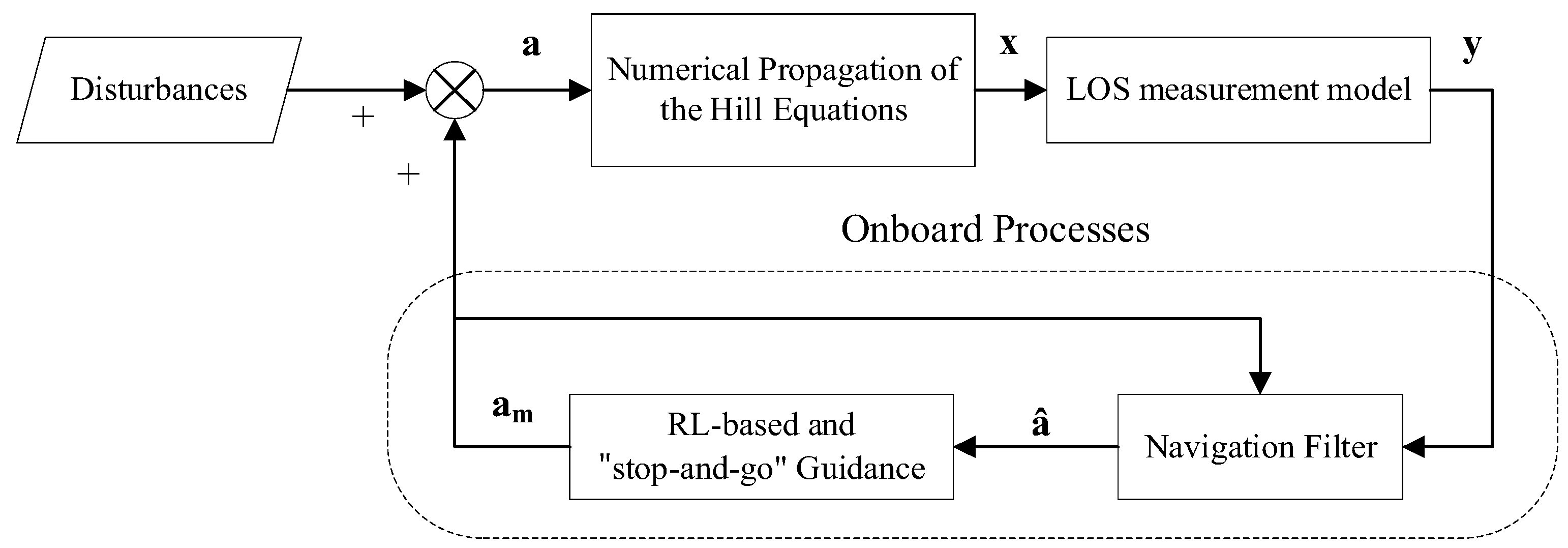
2. Robust Guidance Method with Enhanced AON Observability Based on DRL
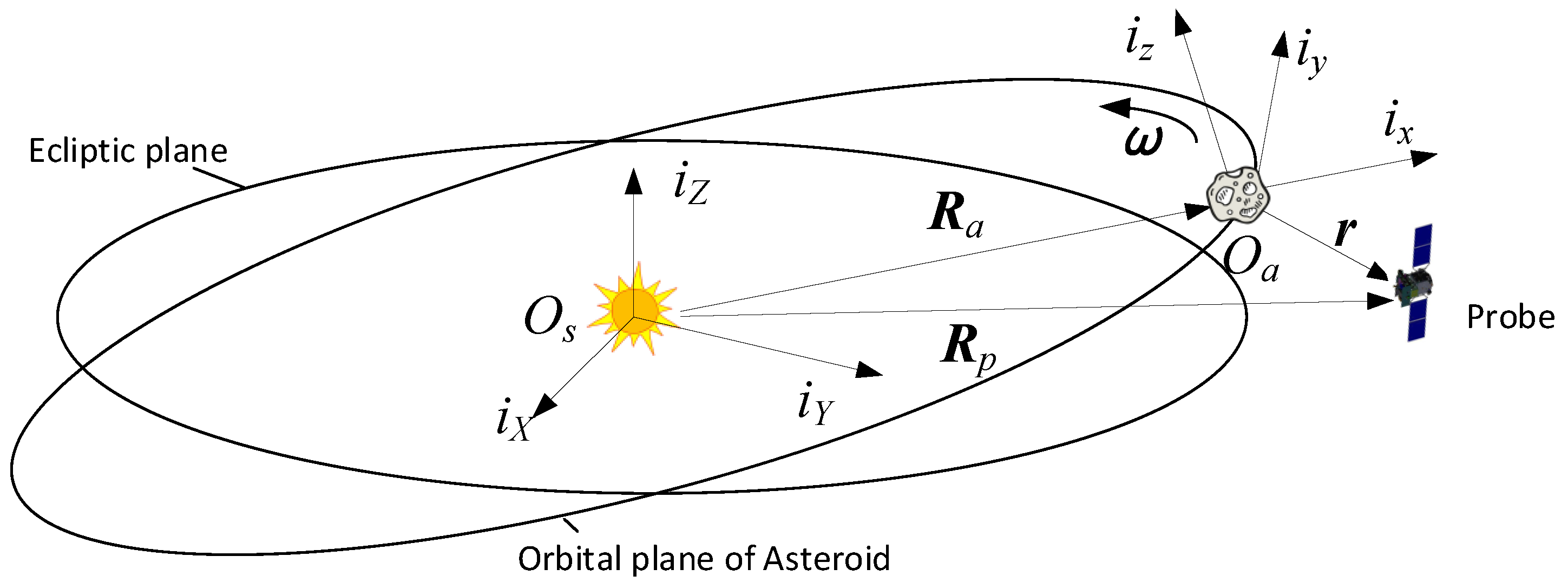
2.1. Close Approach Phase
- (1)
- The x axis is along the orbit radius.
- (2)
- The z axis follows the angular momentum direction of the asteroid’s orbit.
- (3)
- The y axis completes the right-handed coordinate system and is perpendicular to the x axis in the orbital plane.
2.2. Markov Decision Process (MDP)
2.3. Observation Uncertainty Analysis and Modeling
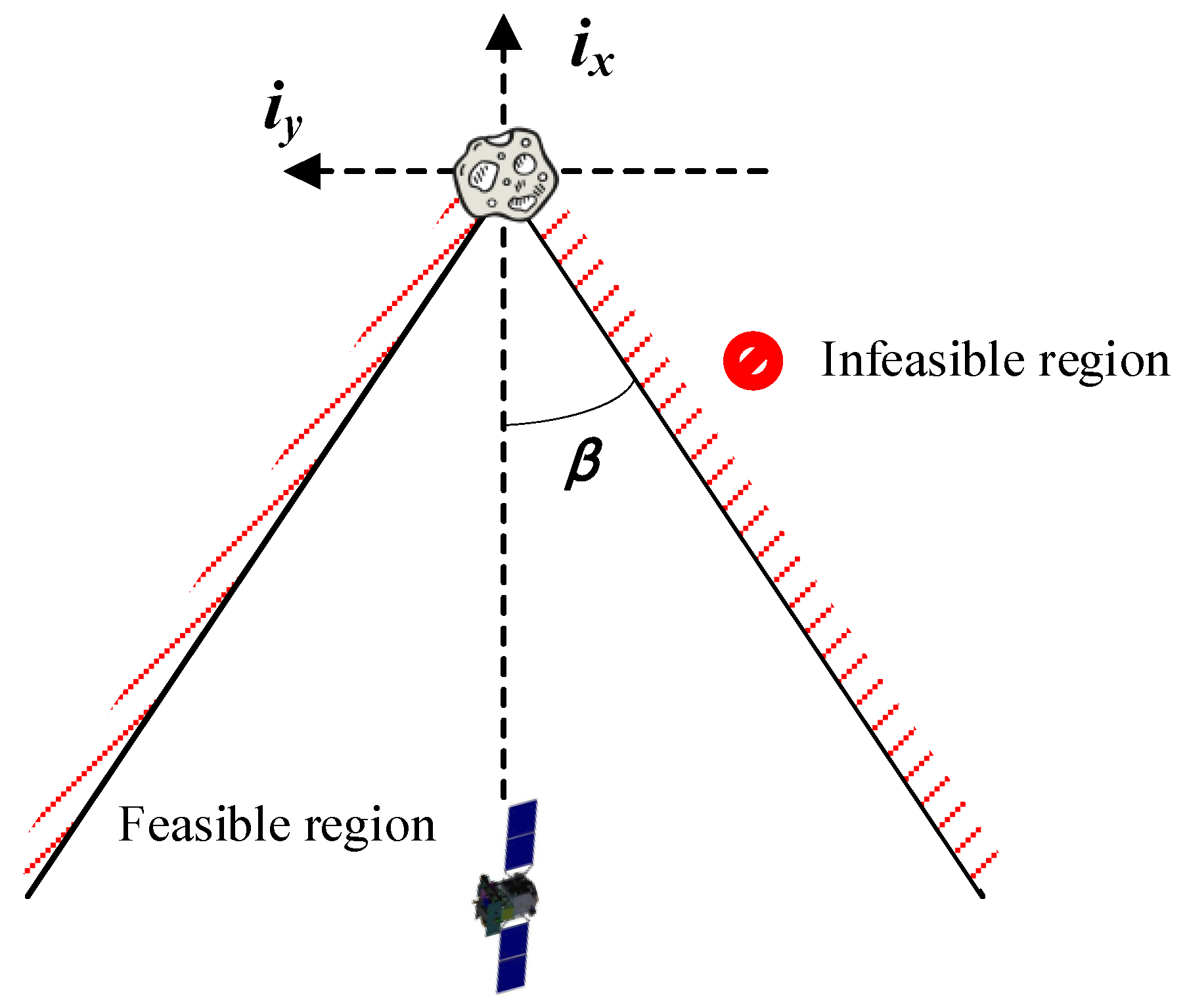
2.4. Constraints Analysis and Modeling
2.5. Reward Function Design
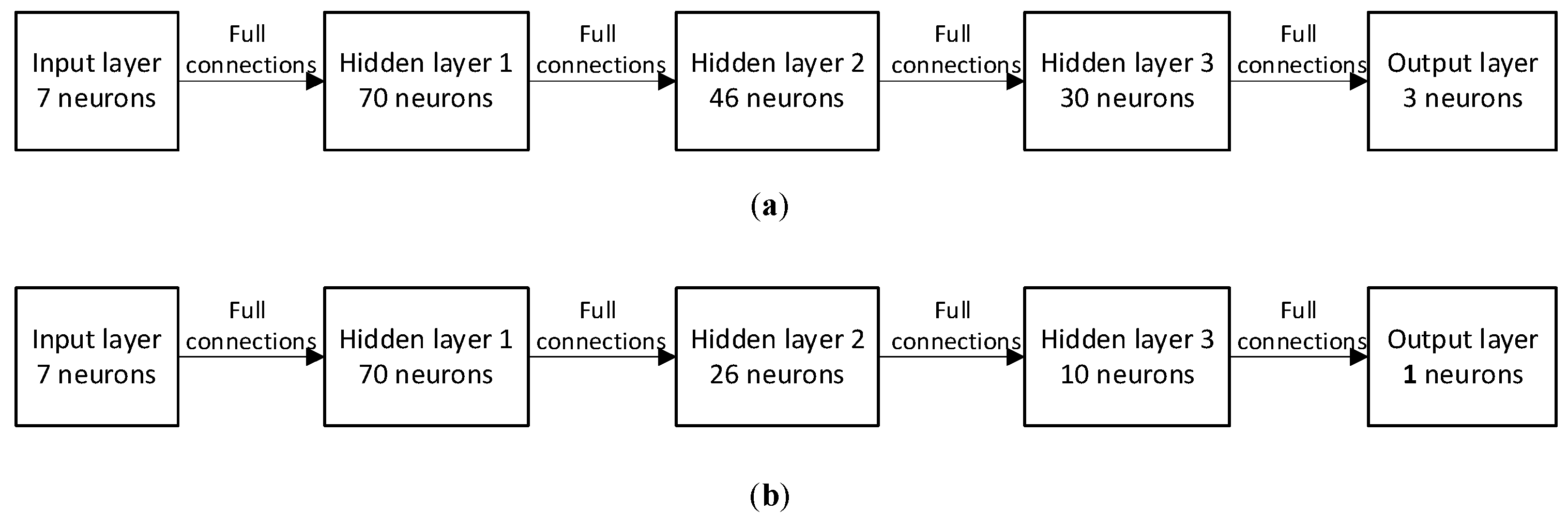
2.6. RL Algorithm
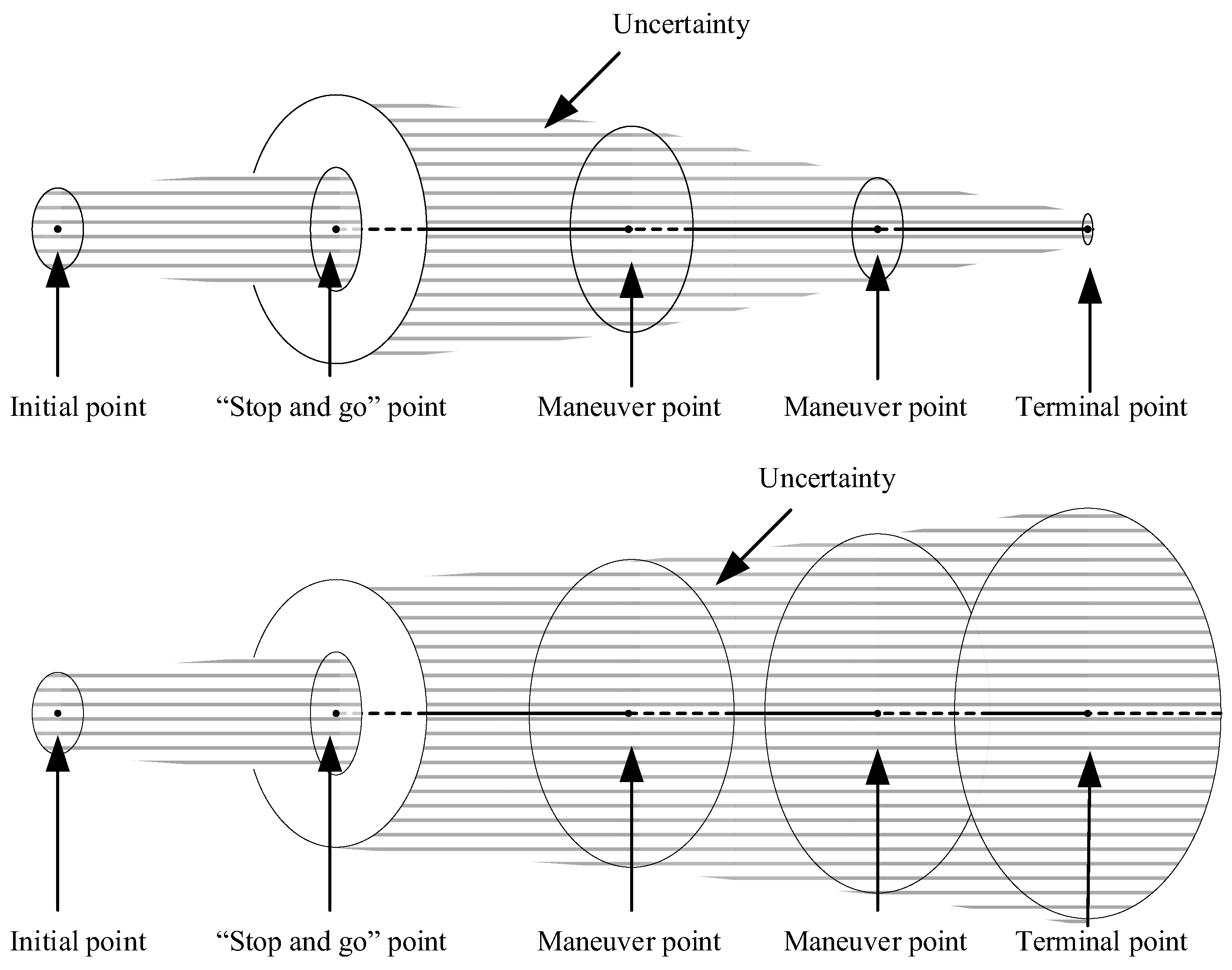
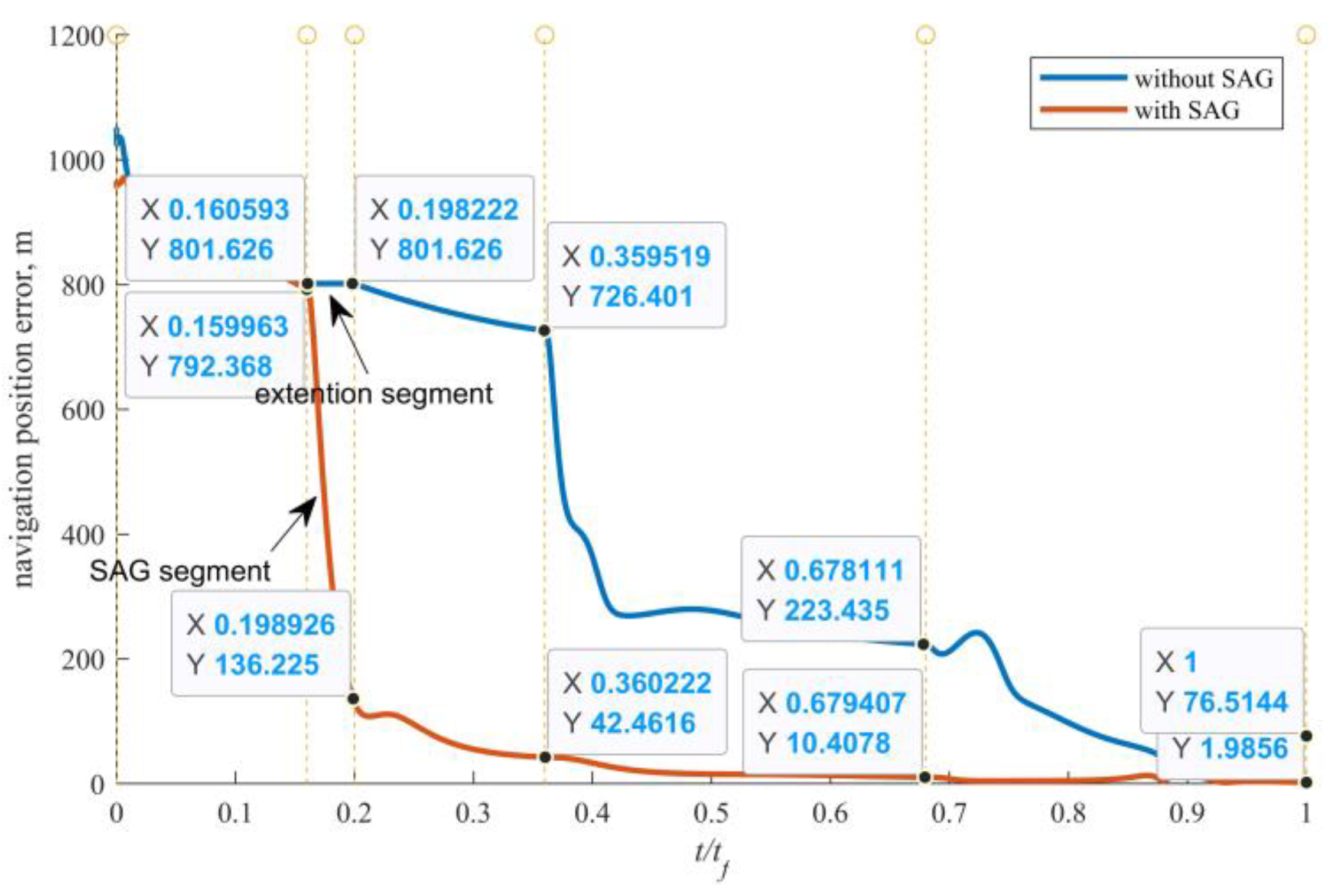
3. Flexible SaG Strategy
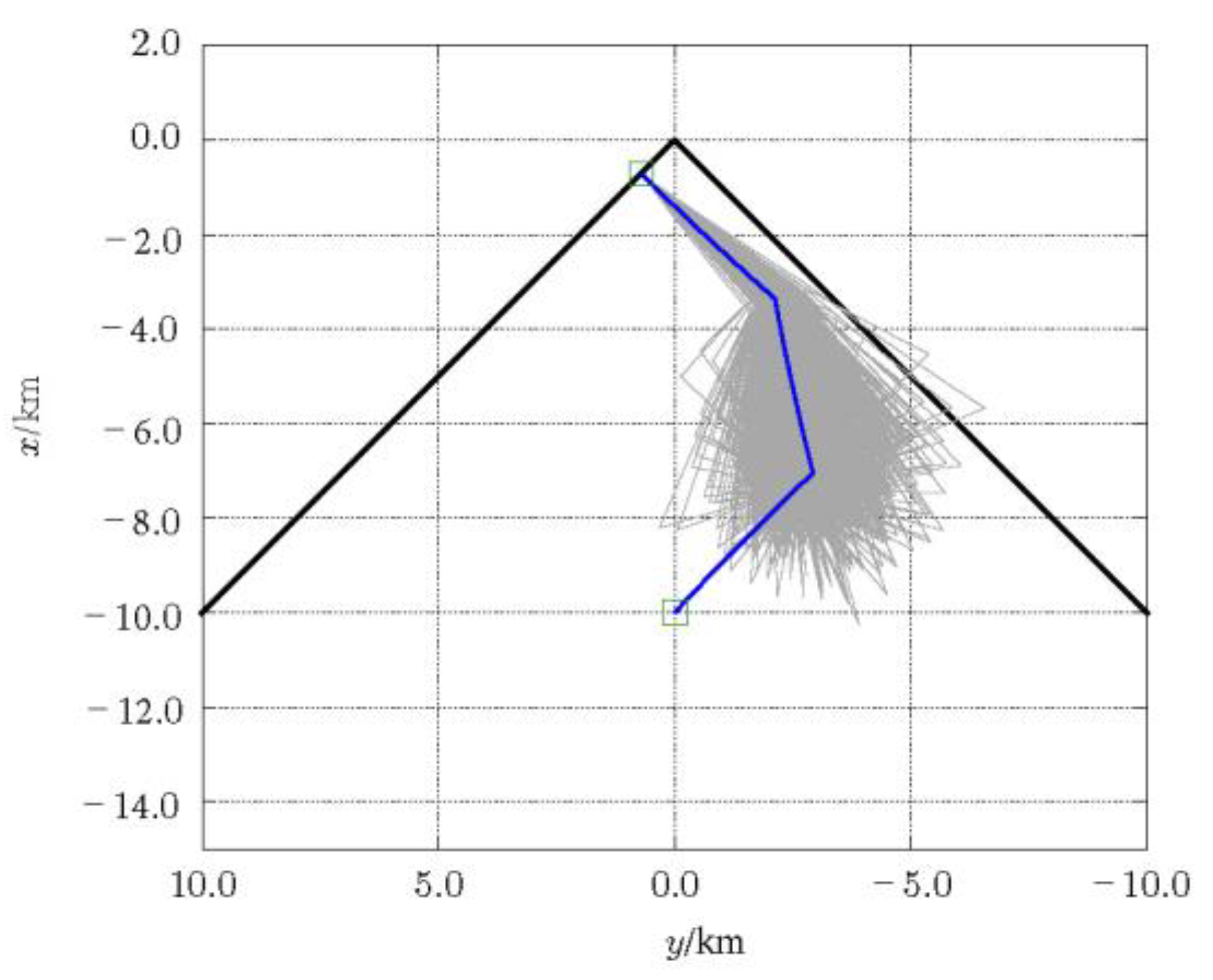
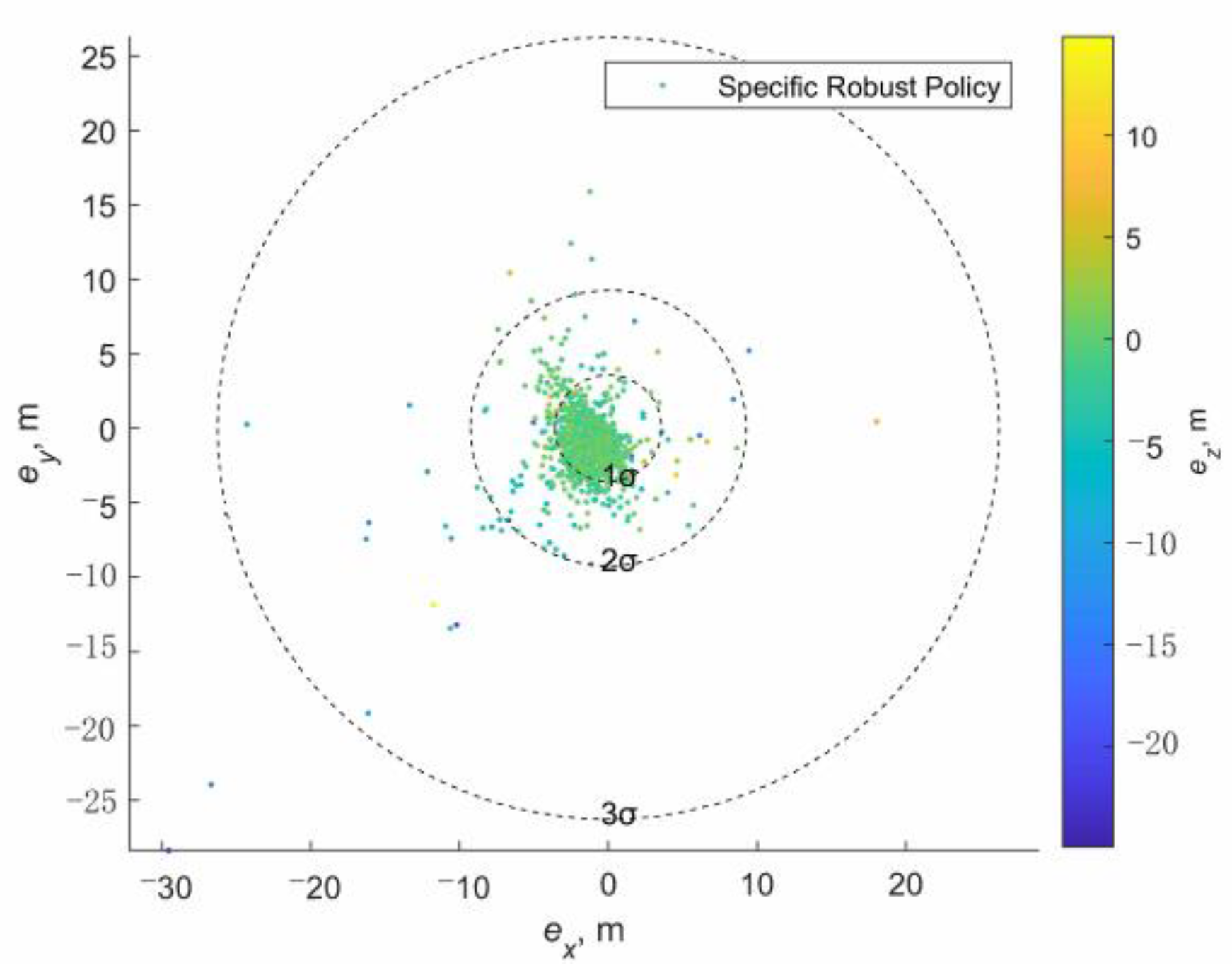
4. Numerical Simulation
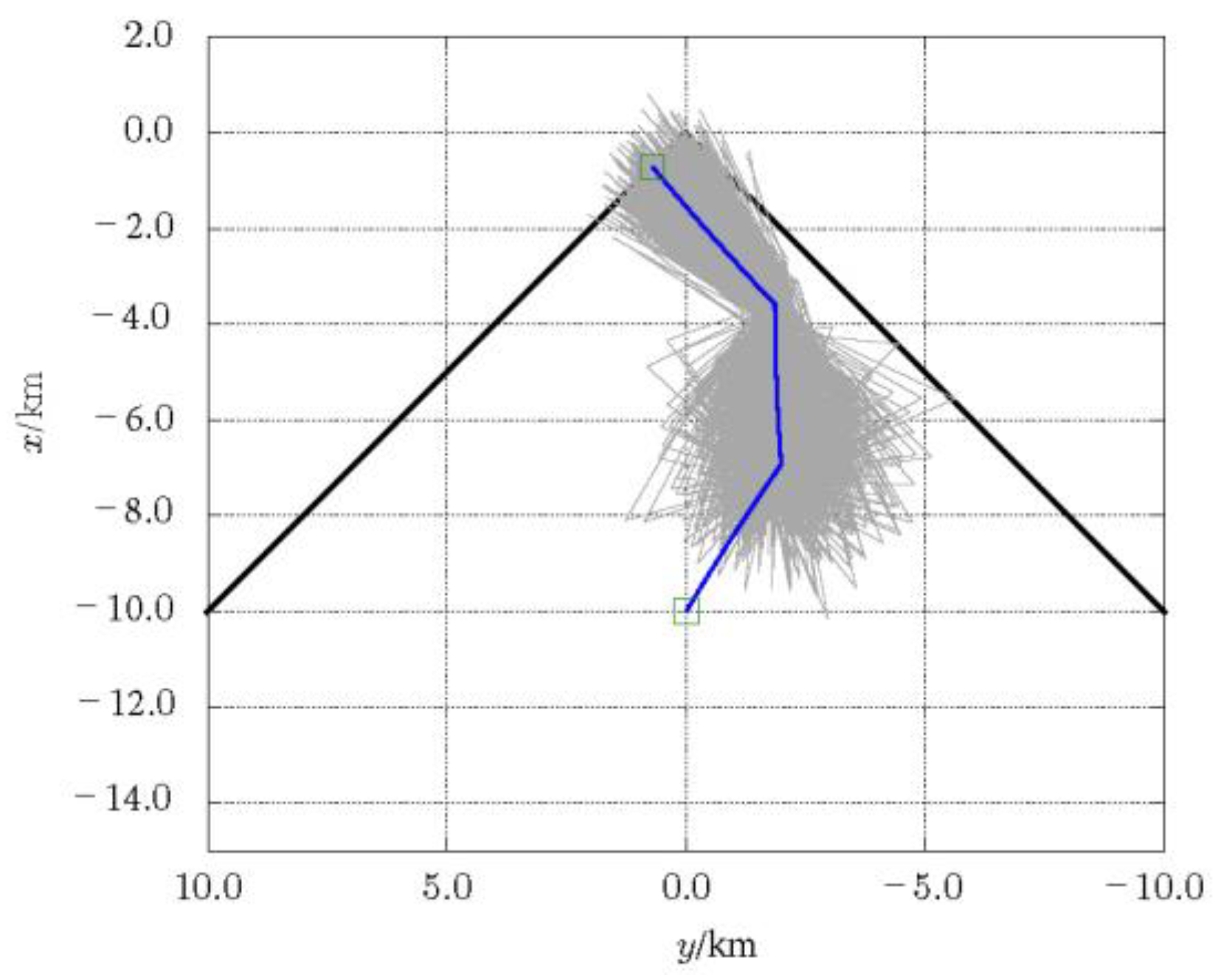
4.1. Simulation Conditions
4.2. AON Performance Improvement by SaG Strategy
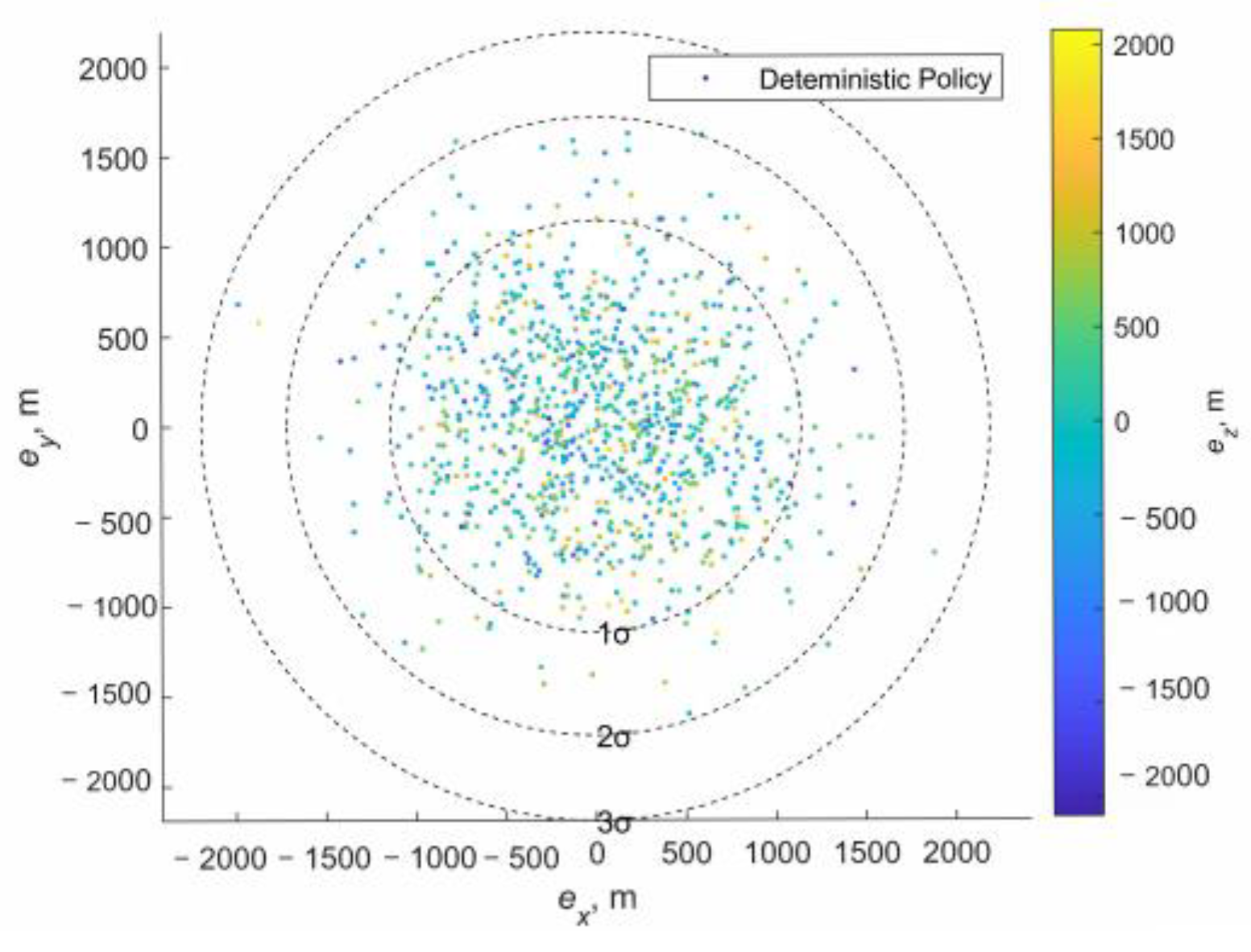
4.3. Deterministic Guidance Combined with SaG Strategy
4.4. Robust Guidance Combined with SaG Strategy
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tsuda, Y.; Yoshikawa, M.; Abe, M.; Minamino, H.; Nakazawa, S. System design of the Hayabusa 2—Asteroid sample return mission to 1999 JU3. Acta Astronaut. 2013, 91, 356–362. [Google Scholar] [CrossRef]
- Gal-Edd, J.; Cheuvront, A. The OSIRIS-REx asteroid sample return mission. In Proceedings of the Aerospace Conference, Big Sky, MT, USA, 2–9 March 2013. [Google Scholar]
- Vetrisano, M.; Branco, J.; Cuartielles, J.; Yárnoz, D.; Vasile, M.L. Deflecting small asteroids using laser ablation: Deep space navigation and asteroid orbit control for LightTouch2 Mission. In Proceedings of the AIAA Guidance, Navigation & Control Conference, Boston, MA, USA, 19–22 August 2013. [Google Scholar]
- Gil-Fernandez, J.; Prieto-Llanos, T.; Cadenas-Gorgojo, R.; Graziano, M.; Drai, R. Autonomous GNC Algorithms for Rendezvous Missions to Near-Earth-Objects. In Proceedings of the Aiaa/Aas Astrodynamics Specialist Conference & Exhibit, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar]
- Ogawa, N.; Terui, F.; Mimasu, Y.; Yoshikawa, K.; Tsuda, Y. Image-based autonomous navigation of Hayabusa2 using artificial landmarks: The design and brief in-flight results of the first landing on asteroid Ryugu. Astrodynamics 2020, 4, 15. [Google Scholar] [CrossRef]
- Ono, G.; Terui, F.; Ogawa, N.; Mimasu, Y.; Yoshikawa, K.; Takei, Y.; Saiki, T.; Tsuda, Y. Design and flight results of GNC systems in Hayabusa2 descent operations. Astrodynamics 2020, 4, 105–117. [Google Scholar] [CrossRef]
- Kominato, T.; Matsuoka, M.; Uo, M.; Hashimoto, T.; Kawaguchi, J.I. Optical hybrid navigation and station keeping around Itokawa. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Keystone, CO, USA, 18–21 August 2006; p. 6535. [Google Scholar]
- Tsuda, Y.; Takeuchi, H.; Ogawa, N.; Ono, G.; Kikuchi, S.; Oki, Y.; Ishiguro, M.; Kuroda, D.; Urakawa, S.; Okumura, S.-I. Rendezvous to asteroid with highly uncertain ephemeris: Hayabusa2’s Ryugu-approach operation result. Astrodynamics 2020, 4, 137–147. [Google Scholar] [CrossRef]
- Greco, C.; Carlo, M.; Vasile, M.; Epenoy, R. Direct Multiple Shooting Transcription with Polynomial Algebra for Optimal Control Problems Under Uncertainty. Astronaut. Acta 2019, 170, 224–234. [Google Scholar] [CrossRef]
- Greco, C.; Vasile, M. Closing the Loop Between Mission Design and Navigation Analysis. In Proceedings of the 71th International Astronautical Congress (IAC 2020)—The CyberSpace Edition, Virtual, 12–14 October 2020. [Google Scholar]
- Ozaki, N.; Campagnola, S.; Funase, R.; Yam, C.H. Stochastic Differential Dynamic Programming with Unscented Transform for Low-Thrust Trajectory Design. J. Guid. Control Dyn. 2017, 41, 377–387. [Google Scholar] [CrossRef]
- Ozaki, N.; Campagnola, S.; Funase, R. Tube Stochastic Optimal Control for Nonlinear Constrained Trajectory Optimization Problems. J. Guid. Control Dyn. 2020, 43, 1–11. [Google Scholar] [CrossRef]
- Oguri, K.; Mcmahon, J.W. Risk-aware Trajectory Design with Impulsive Maneuvers: Convex Optimization Approach. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Portland, ME, USA, 11–15 August 2019. [Google Scholar]
- Oguri, K.; Mcmahon, J.W. Risk-aware Trajectory Design with Continuous Thrust: Primer Vector Theory Approach. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Portland, ME, USA, 11–15 August 2019. [Google Scholar]
- Carlo, M.; Vasile, M.; Greco, C.; Epenoy, R. Robust Optimisation of Low-thrust Interplanetary Transfers using Evidence Theory. In Proceedings of the 29th AAS/AIAA Space Flight Mechanics Meeting, Ka’anapali, HI, USA, 13–17 January 2019. [Google Scholar]
- Izzo, D.; Mrtens, M.; Pan, B. A survey on artificial intelligence trends in spacecraft guidance dynamics and control. Astrodynamics 2019, 3, 287–299. [Google Scholar] [CrossRef]
- Izzo, D.; Sprague, C.; Tailor, D. Machine learning and evolutionary techniques in interplanetary trajectory design. In Modeling and Optimization in Space Engineering; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Sutton, R.; Barto, A. Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Kavukcuoglu, K. Asynchronous Methods for Deep Reinforcement Learning. arXiv 2016, arXiv:1602.01783. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Holt, H.; Armellin, R.; Scorsoglio, A.; Furfaro, R. Low-Thrust Trajectory Design Using Closed-Loop Feedback-Driven Control Laws and State-Dependent Parameters. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Zavoli, A.; Federici, L. Reinforcement Learning for Robust Trajectory Design of Interplanetary Missions. J. Guid. Control Dyn. 2021, 44, 1440–1453. [Google Scholar] [CrossRef]
- Arora, L.; Dutta, A. Reinforcement Learning for Sequential Low-Thrust Orbit Raising Problem. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Lafarge, N.B.; Miller, D.; Howell, K.C.; Linares, R. Guidance for Closed-Loop Transfers using Reinforcement Learning with Application to Libration Point Orbits. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Miller, D.; Englander, J.; Linares, R. Interplanetary Low-Thrust Design Using Proximal Policy Optimization. In Proceedings of the AAS 19-779, Portland, ME, USA, 11–15 August 2019. [Google Scholar]
- Silvestrini, S.; Lavagna, M.R. Spacecraft Formation Relative Trajectories Identification for Collision-Free Maneuvers using Neural-Reconstructed Dynamics. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Scorsoglio, A.; Furfaro, R.; Linares, R.; Massari, M. Actor-Critic Reinforcement Learning Approach to Relative Motion Guidance in Near-Rectilinear Orbit. In Proceedings of the 29th AAS/AIAA Space Flight Mechanics Meeting, Ka’anapali, HI, USA, 13–17 January 2019. [Google Scholar]
- Gaudet, B.; Linares, R.; Furfaro, R. Terminal Adaptive Guidance via Reinforcement Meta-Learning: Applications to Autonomous Asteroid Close-Proximity Operations. Acta Astronaut. 2020, 171, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Wang, J.; He, S.; Shin, H.-S.; Tsourdos, A. Learning prediction-correction guidance for impact time control. Aerosp. Sci. Technol. 2021, 119, 107187. [Google Scholar] [CrossRef]
- Federici, L.; Benedikter, B.; Zavoli, A. Deep Learning Techniques for Autonomous Spacecraft Guidance During Proximity Operations. J. Spacecr. Rocket. 2021, 58, 1774–1785. [Google Scholar] [CrossRef]
- Federici, L.; Scorsoglio, A.; Ghilardi, L.; D’Ambrosio, A.; Benedikter, B.; Zavoli, A.; Furfaro, R. Image-based Meta-Reinforcement Learning for Autonomous Terminal Guidance of an Impactor in a Binary Asteroid System. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Hovell, K.; Ulrich, S. Deep Reinforcement Learning for Spacecraft Proximity Operations Guidance. J. Spacecr. Rocket. 2021, 58, 254–264. [Google Scholar] [CrossRef]
- Gaudet, B.; Furfaro, R. Robust Spacecraft Hovering Near Small Bodies in Environments with Unknown Dynamics Using Reinforcement Learning. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, Minneapolis, MI, USA, 13–16 August 2012. [Google Scholar]
- Willis, S.; Izzo, D.; Hennes, D. Reinforcement Learning for Spacecraft Maneuvering Near Small Bodies. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, Napa, CA, USA, 14–18 February 2016. [Google Scholar]
- Furfaro, R.; Linares, R. Waypoint-Based generalized ZEM/ZEV feedback guidance for planetary landing via a reinforcement learning approach. In Proceedings of the 3rd International Academy of Astronautics Conference on Dynamics and Control of Space Systems, DyCoSS, Moscow, Russia, 30 May–1 June 2017. [Google Scholar]
- Gaudet, B.; Furfaro, R.; Linares, R. Reinforcement learning for angle-only intercept guidance of maneuvering targets. Aerosp. Sci. Technol. 2019, 99, 105746. [Google Scholar] [CrossRef]
- Furfaro, R.; Scorsoglio, A.; Linares, R.; Massari, M. Adaptive generalized ZEM-ZEV feedback guidance for planetary landing via a deep reinforcement learning approach. Acta Astronaut. 2020, 171, 156–171. [Google Scholar] [CrossRef]
- Scorsoglio, A.; D’Ambrosio, A.; Ghilardi, L.; Furfaro, R.; Curti, F. Safe lunar landing via images: A reinforcement meta-learning application to autonomous hazard avoidance and landing. In Proceedings of the 2020 AAS/AIAA Astrodynamics Specialist Conference—Lake Tahoe, Virtual, 9–12 August 2020. [Google Scholar]
- Scorsoglio, A.; Andrea, D.; Ghilardi, L.; Gaudet, B. Image-based Deep Reinforcement Meta-Learning for Autonomous Lunar Landing. J. Spacecr. Rocket. 2021, 59, 153–165. [Google Scholar] [CrossRef]
- Jiang, X.; Li, S.; Furfaro, R. Integrated guidance for Mars entry and powered descent using reinforcement learning and pseudospectral method. Acta Astronaut. 2019, 163, 114–129. [Google Scholar] [CrossRef]
- Gaudet, B.; Linares, R.; Furfaro, R. Adaptive Guidance and Integrated Navigation with Reinforcement Meta-Learning. Acta Astronaut. 2019, 169, 180–190. [Google Scholar] [CrossRef]
- Gaudet, B.; Furfaro, R.; Linares, R. A Guidance Law for Terminal Phase Exo-Atmospheric Interception Against a Maneuvering Target using Angle-Only Measurements Optimized using Reinforcement Meta-Learning. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- D’Amico, S.; Ardaens, J.S.; Gaias, G.; Benninghoff, H.; Schlepp, B.; Jorgensen, J.L. Noncooperative Rendezvous Using Angles-Only Optical Navigation: System Design and Flight Results. J. Guid. Control Dyn. 2013, 36, 1576–1595. [Google Scholar] [CrossRef]
- Grzymisch, J.; Fichter, W. Optimal Rendezvous Guidance with Enhanced Bearings-Only Observability. J. Guid. Control Dyn. 2015, 38, 1131–1140. [Google Scholar] [CrossRef]
- Mok, S.-H.; Pi, J.; Bang, H. One-step rendezvous guidance for improving observability in bearings-only navigation. Adv. Space Res. 2020, 66, 2689–2702. [Google Scholar] [CrossRef]
- Hou, B.; Wang, D.; Wang, J.; Ge, D.; Zhou, H.; Zhou, X. Optimal Maneuvering for Autonomous Relative Navigation Using Monocular Camera Sequential Images. J. Guid. Control Dyn. 2021, 44, 1947–1960. [Google Scholar] [CrossRef]
- Hartley, E.N.; Trodden, P.A.; Richards, A.G.; Maciejowski, J.M. Model predictive control system design and implementation for spacecraft rendezvous. Control Eng. Pract. 2012, 20, 695–713. [Google Scholar] [CrossRef]
- Hartley, E. A tutorial on model predictive control for spacecraft rendezvous. In Proceedings of the Control Conference, Linz, Austria, 15–17 July 2015. [Google Scholar]
- Vasile, M.; Maddock, C.A. Design of a Formation of Solar Pumped Lasers for Asteroid Deflection. Adv. Space Res. 2012, 50, 891–905. [Google Scholar] [CrossRef]
- Okasha, M.; Newman, B. Guidance, Navigation and Control for Satellite Proximity Operations using Tschauner-Hempel Equations. J. Astronaut. Sci. 2013, 60, 109–136. [Google Scholar] [CrossRef]
- Yuan, H.; Li, D.; Wang, J. Hybrid Guidance Optimization for Multipulse Glideslope Approach with Bearing-Only Navigation. Aerospace 2022, 9, 242. [Google Scholar] [CrossRef]
- Bhaskaran, S.; Nandi, S.; Broschart, S.; Wallace, M.; Cangahuala, L.A.; Olson, C. Small Body Landings Using Autonomous Onboard Optical Navigation. J. Astronaut. Sci. 2013, 58, 409–427. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Zhang, X. TensorFlow: A system for large-scale machine learning. USENIX Assoc. 2016, 16, 265–283. [Google Scholar]
- Hill, A.; Raffin, A.; Ernestus, M.; Gleave, A.; Kanervisto, A.; Traore, R.; Dhariwal, P.; Hesse, C.; Klimov, O.; Nichol, A.; et al. Stable Baselines. GitHub Repos. Available online: https://github.com/hill-a/stable-baselines (accessed on 5 May 2018).






| Super Parameter | Symbol | Value |
|---|---|---|
| Discount factor | 0.9999 | |
| GAE factor | 0.99 | |
| Learning rate | 2.5 × 10−4 | |
| Clip range | 0.3 | |
| Training step | 200 × 106 | |
| Parallel workers | 60 | |
| Episodes per batch | 4 | |
| SGA epochs per update | 30 |
| Epoch 2459600.5 (21 January 2022.0) TDB Reference: Heliocentric J2000 Ecliptic | ||
|---|---|---|
| Element | Value | Units |
| Semimajor axis | 1.001137344063433 | AU |
| Eccentricity | 0.1029843787386461 | |
| Inclination | 7.788928644671124 | deg |
| Longitude of the ascending node | 66.0142959682462 | deg |
| Perihelion argument angle | 305.6646720090911 | deg |
| Mean anomaly | 107.172338605596 | deg |
| Parameter | Value | Unit |
|---|---|---|
| Environment | ||
| Equivalent disturbance, 1σ | 1 × 10−7 | m/s2 |
| Measurement Noise, 1σ | 1 | mrad |
| Sample time | 10 | s |
| Rendezvous Mission | ||
| Initial condition, | m m m | |
| m/s m/s m/s | ||
| Target condition, | m m m | |
| m/s m/s m/s | ||
| Number of pulses, N | 3 | |
| Total time, T | 3 | day |
| Planned maneuver interval time, | 12 | hour |
| Start time of SaG | 12 | hour |
| Duration of SaG | 3 | hour |
| Navigation Initiation | ||
| Initial navigation error, 1σ | m m m | |
| mm/s mm/s mm/s |
| Policy Name | Environment Name | Observation Uncertainty |
|---|---|---|
| 0 | ||
| 0 | ||
| 1% range | ||
| 5 mm/s |
| Time Step | ||
|---|---|---|
| 0 | 0.022 | 18.35 |
| 1 | 0.015 | 18.48 |
| 2 | 0.017 | 121.21 |
| 3 | 0.023 | - |
| Time Step | ||
|---|---|---|
| 0 | 0.026 | 25.78 |
| 1 | 0.027 | 21.67 |
| 2 | 0.015 | 138.12 |
| 3 | 0.024 | - |
| Policy Name | Environment | ||||
|---|---|---|---|---|---|
| Mean | Std | Mean | Std | ||
| 0.07780 | - | 11.51 | - | ||
| 0.0825 | 0.0072 | 977.2 | 406.8 | ||
| 0.09175 | - | 2.123 | - | ||
| 0.0943 | 0.0046 | 3.578 | 3.436 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, H.; Li, D. Good Match between “Stop-and-Go” Strategy and Robust Guidance Based on Deep Reinforcement Learning. Aerospace 2022, 9, 569. https://doi.org/10.3390/aerospace9100569
Yuan H, Li D. Good Match between “Stop-and-Go” Strategy and Robust Guidance Based on Deep Reinforcement Learning. Aerospace. 2022; 9(10):569. https://doi.org/10.3390/aerospace9100569
Chicago/Turabian StyleYuan, Hao, and Dongxu Li. 2022. "Good Match between “Stop-and-Go” Strategy and Robust Guidance Based on Deep Reinforcement Learning" Aerospace 9, no. 10: 569. https://doi.org/10.3390/aerospace9100569
APA StyleYuan, H., & Li, D. (2022). Good Match between “Stop-and-Go” Strategy and Robust Guidance Based on Deep Reinforcement Learning. Aerospace, 9(10), 569. https://doi.org/10.3390/aerospace9100569







