Learning-Based Pose Estimation of Non-Cooperative Spacecrafts with Uncertainty Prediction
Abstract
:1. Introduction
- •
- We introduce the idea of region detection into the keypoint detection of spacecrafts, which can capture the feature of keypoints better;
- •
- We achieve effective uncertainty prediction for the detected keypoints, which can be used to automatically eliminate keypoints with low detection accuracy;
- •
- We conduct sufficient experiments on SPEED dataset [17]. Compared with previous methods, our method can reduce the average error of pose estimation by 53.3% while reducing the number of model parameters.
2. Related Work
2.1. Learning-Based Methods
2.2. Keypoint Detection
3. Method
3.1. 3D Wireframe Model Recovery
3.2. Spacecraft Detection Network (SDN)
3.3. Keypoints Detection Network (KDN)
3.4. Pose Estimation
| Algorithm 1 Keypoints selection strategy |
|
4. Experiments
4.1. Datasets and Implementation Details
4.2. Evaluation Metrics
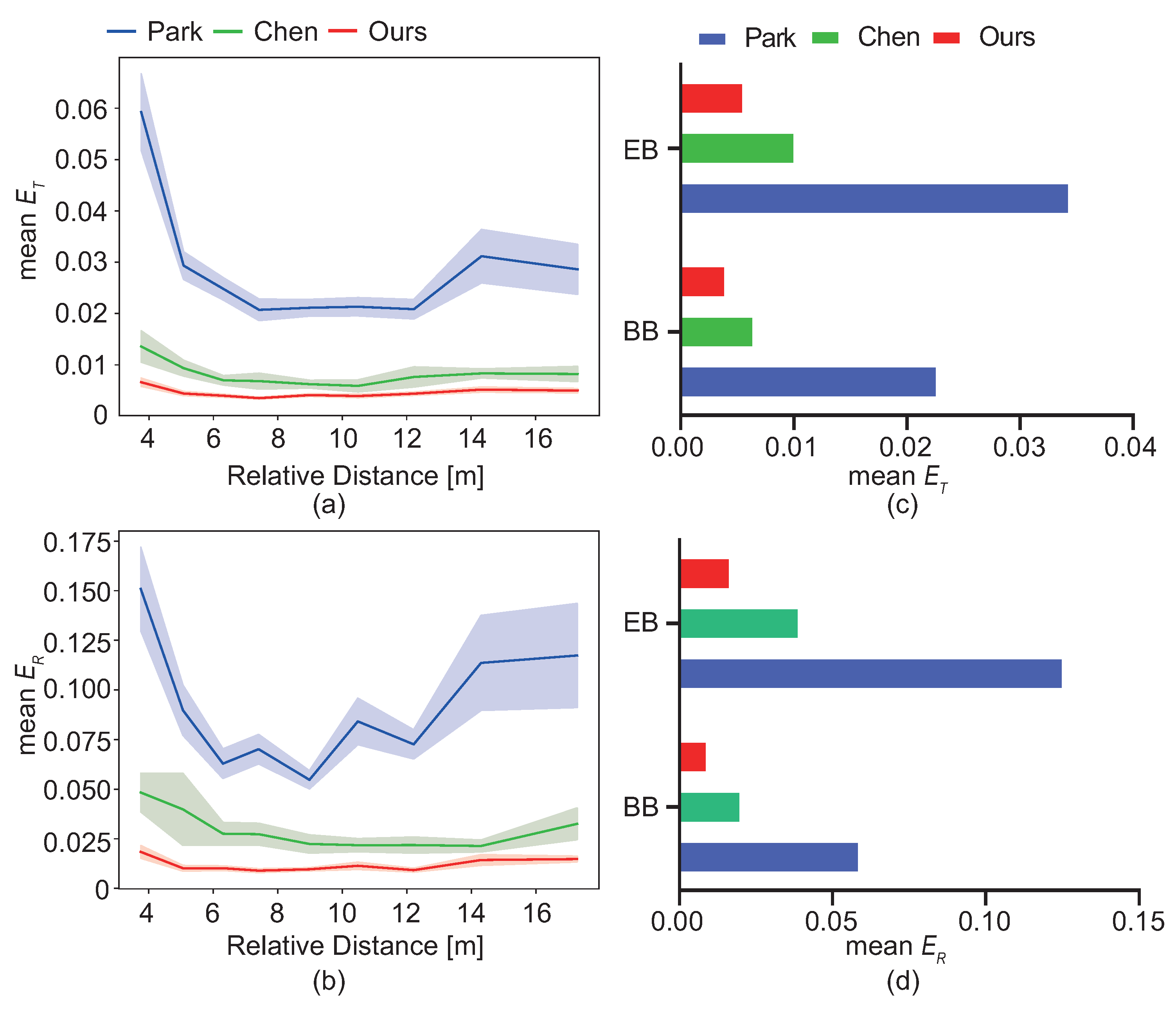
4.3. Comparison
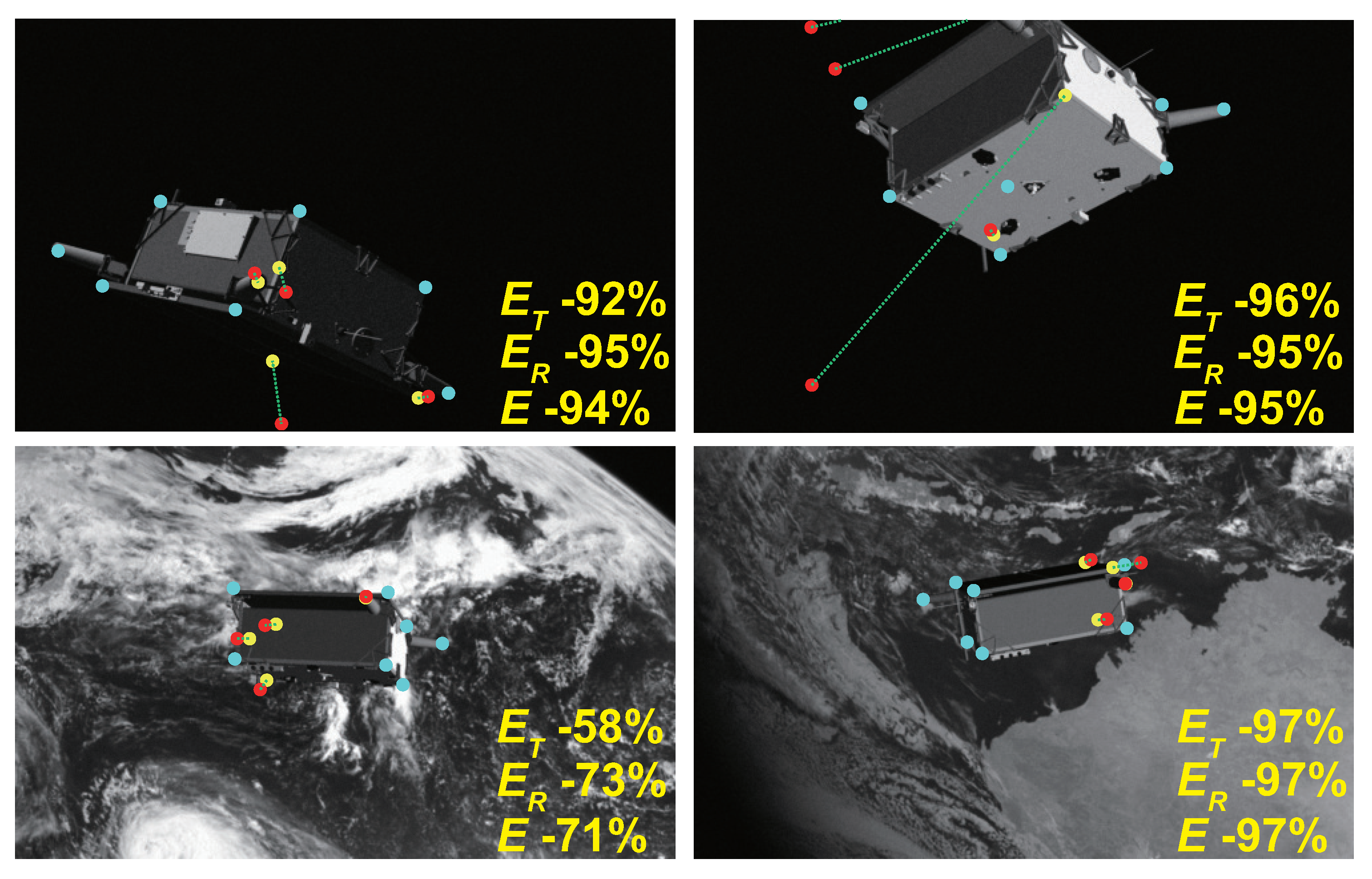
4.3.1. Comparison in Synthetic Images
4.3.2. Comparison in Real Images
4.4. Different Conditions for Pose Estimation
4.4.1. Performance with Different Background
4.4.2. Performance in Different Relative Distance
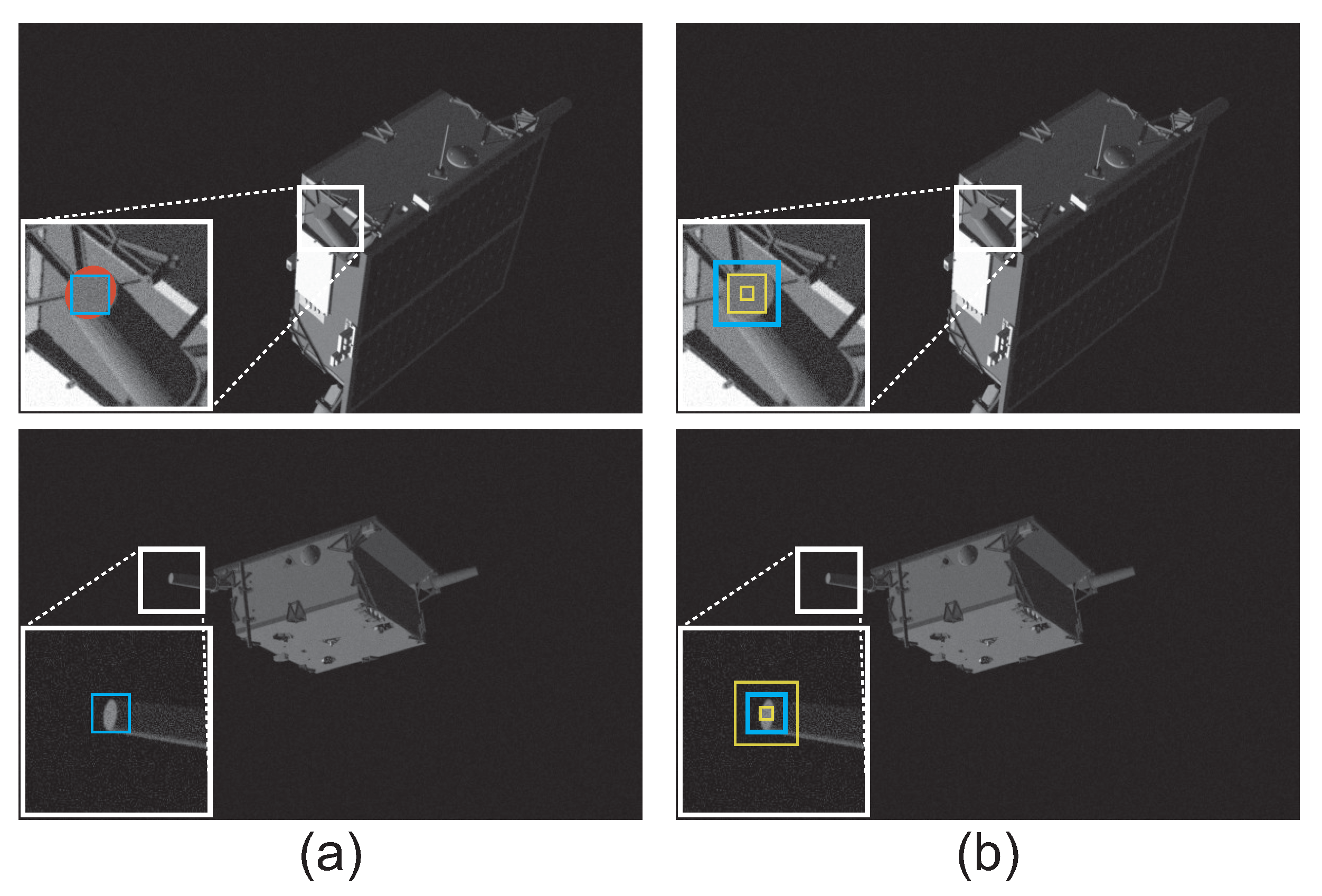
4.5. Effective Uncertainty Prediction
4.6. Comparison between SA and LS
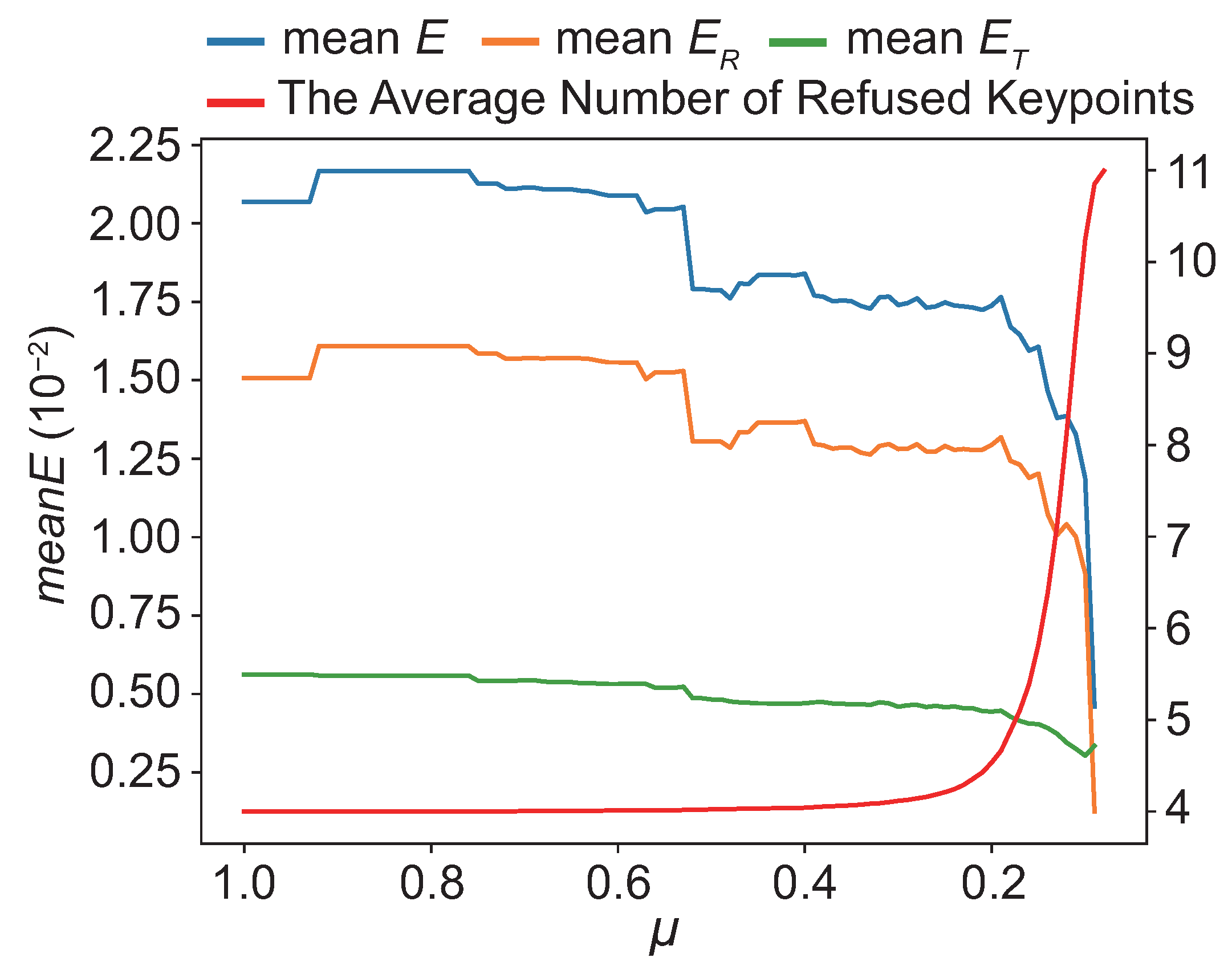
4.7. Hyperparameters Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| 2D homogenous coordinate of the i-th keipoint in the k-th image | |
| 3D homogenous coordinate of the i-th keipoint | |
| Internal parameter matrix of monocular camera | |
| Extrinsic matrix for rotation in the k-th image | |
| Extrinsic matrix for translation in the k-th image | |
| Scaling factor in the k-th image | |
| Predicted box in the k-th image | |
| Ground-truth box in the k-th image | |
| Predicted category in the k-th image | |
| Ground-truth category in the k-th image | |
| Predicted confidence in the k-th image | |
| Ground-truth confidence in the k-th image | |
| Predicted uncertainty in the k-th image | |
| Ground-truth uncertainty in the k-th image | |
| K | The number of keypoint categories |
| Uncertainty threshold | |
| C | Candidate keypoints set |
| D | Detected keypoints set |
| The number of keypoints used for pose estimation | |
| Predicted orientation in the k-th image | |
| Ground-truth orientation in the k-th image | |
| Predicted translation in the k-th image | |
| Ground-truth translation in the k-th image | |
| E | Error of pose estimation |
| Error of translation prediction | |
| Error of orientation prediction | |
| Average error of translation prediction | |
| Average error of orientation prediction | |
| Median error of translation prediction | |
| Median error of orientation prediction | |
| Acronyms | |
| SDN | Spacecraft Detection Network |
| KDN | Keypoint Detection Network |
| CNN | Convolutional Neural Network |
| FCN | Fully Convolutional Network |
| SA | Simulated Annealing |
| EB | Earth Background |
| BB | Black Background |
References
- Kassebom, M. Roger-an advanced solution for a geostationary service satellite. In Proceedings of the 54th International Astronautical Congress of the International Astronautical Federation, Bremen, Germany, 29 Septmber–3 October 2003; p. U-1. [Google Scholar]
- Saleh, J.H.; Lamassoure, E.; Hastings, D.E. Space systems flexibility provided by on-orbit servicing: Part 1. J. Spacecr. Rockets 2002, 39, 551–560. [Google Scholar] [CrossRef]
- Taylor, B.; Aglietti, G.; Fellowes, S.; Ainley, S.; Salmon, T.; Retat, I.; Burgess, C.; Hall, A.; Chabot, T.; Kanan, K.; et al. Remove debris mission, from concept to orbit. In Proceedings of the SmallSat 2018-32nd Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 4–9 August 2018; pp. 1–10. [Google Scholar]
- Andert, F.; Ammann, N.; Maass, B. Lidar-aided camera feature tracking and visual slam for spacecraft low-orbit navigation and planetary landing. Adv. Aerosp. Guid. Navig. Control. 2015, 605–623. [Google Scholar] [CrossRef]
- Gaudet, B.; Furfaro, R.; Udrea, B. Attitude estimation via LIDAR altimetry and a particle filter. In Proceedings of the 24th AAS/AIAA Space Flight Mechanics Meeting, Orlando, FL, USA, 26–30 January 2014; pp. 1449–1459. [Google Scholar]
- Axelrad, P.; Ward, L.M. Spacecraft attitude estimation using the Global Positioning System-Methodology and results for RADCAL. J. Guid. Control. Dyn. 1996, 19, 1201–1209. [Google Scholar] [CrossRef]
- Cassinis, L.P.; Fonod, R.; Gill, E. Review of the robustness and applicability of monocular pose estimation systems for relative navigation with an uncooperative spacecraft. Prog. Aerosp. Sci. 2019, 110, 100548. [Google Scholar] [CrossRef]
- Sharma, S.; Ventura, J. Robust Model-Based Monocular Pose Estimation for Noncooperative Spacecraft Rendezvous. J. Spacecr. Rockets 2017, 55, 1–35. [Google Scholar]
- Dhome, M.; Richetin, M.; Lapreste, J.T. Determination of the attitude of 3D objects from a single perspective view. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 1265–1278. [Google Scholar] [CrossRef]
- Kanani, K.; Petit, A.; Marchand, E.; Chabot, T.; Gerber, B. Vision based navigation for debris removal missions. In Proceedings of the 63rd International Astronautical Congress, Naples, Italy, 1–5 October 2012. [Google Scholar]
- Petit, A.; Marchand, E.; Kanani, K. Vision-based detection and tracking for space navigation in a rendezvous context. In Proceedings of the Artificial Intelligence, Robotics and Automation in Space, Turin, Italy, 4–6 September 2012. [Google Scholar]
- Sharma, S.; Ventura, J.; D’Amico, S. Robust model-based monocular pose initialization for noncooperative spacecraft rendezvous. J. Spacecr. Rockets 2018, 55, 1414–1429. [Google Scholar] [CrossRef] [Green Version]
- Augenstein, S.; Rock, S.M. Improved frame-to-frame pose tracking during vision-only SLAM/SFM with a tumbling target. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; IEEE: London, UK, 2011; pp. 3131–3138. [Google Scholar]
- Shi, J.; Ulrich, S.; Ruel, S. Spacecraft pose estimation using a monocular camera. In Proceedings of the 67th International Astronautical Congress, Guadalajara, Mexico, 26–30 September 2016. [Google Scholar]
- D’Amico, S.; Benn, M.; Jørgensen, J.L. Pose estimation of an uncooperative spacecraft from actual space imagery. Int. J. Space Sci. Eng. 2014, 2, 171–189. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–8 December 2012; Volume 25. [Google Scholar]
- Sharma, S.; D’Amico, S. Pose estimation for non-cooperative rendezvous using neural networks. In Proceedings of the 29th AIAA/AAS Space Flight Mechanics Meeting, Ka’anapali, HI, USA, 13–17 January 2019. [Google Scholar]
- Park, T.H.; Sharma, S.; D’Amico, S. Towards Robust Learning-Based Pose Estimation of Noncooperative Spacecraft. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Portland, ME, USA, 11–15 August 2019. [Google Scholar]
- Chen, B.; Cao, J.; Parra, A.; Chin, T.J. Satellite pose estimation with deep landmark regression and nonlinear pose refinement. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Park, T.H.; D’Amico, S. Robust Multi-Task Learning and Online Refinement for Spacecraft Pose Estimation across Domain Gap. In Proceedings of the the 11th International Workshop on Satellite Constellations & Formation Flying, Milan, Italy, 7–10 June 2022. [Google Scholar]
- Proença, P.F.; Gao, Y. Deep learning for spacecraft pose estimation from photorealistic rendering. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation, Online, 31 May 2020; IEEE: New York, NY, USA, 2020; pp. 6007–6013. [Google Scholar]
- Sharma, S.; Beierle, C.; D’Amico, S. Pose estimation for non-cooperative spacecraft rendezvous using convolutional neural networks. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2019; IEEE: New York, NY, USA, 2018; pp. 1–12. [Google Scholar]
- Sharma, S.; D’Amico, S. Neural network-based pose estimation for noncooperative spacecraft rendezvous. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4638–4658. [Google Scholar] [CrossRef]
- Lepetit, V.; Moreno-Noguer, F.; Fua, P. Epnp: An accurate o (n) solution to the pnp problem. Int. J. Comput. Vis. 2009, 81, 155–166. [Google Scholar] [CrossRef] [Green Version]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Lenc, K.; Vedaldi, A. Large scale evaluation of local image feature detectors on homography datasets. In Proceedings of the 29th British Machine Vision Conference, Newcastle, UK, 3–6 September 2018. [Google Scholar]
- Harris, C.; Stephens, M. A combined corner and edge detector. In Proceedings of the Alvey Vision Conference, Manchester, UK, 31 August–2 September 1988; Volume 15, pp. 147–151. [Google Scholar]
- Beaudet, P.R. Rotationally invariant image operators. In Proceedings of the 4th International Joint Conference Pattern Recognition, Kyoto, Japan, 7–10 November 1978. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; IEEE: New York, NY, USA, 2011; pp. 2564–2571. [Google Scholar]
- Matas, J.; Chum, O.; Urban, M.; Pajdla, T. Robust wide-baseline stereo from maximally stable extremal regions. Image. Vis. Comput. 2004, 22, 761–767. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Gool, L.V. Surf: Speeded up robust features. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 404–417. [Google Scholar]
- Rosten, E.; Drummond, T. Machine learning for high-speed corner detection. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 430–443. [Google Scholar]
- Rosten, E.; Porter, R.; Drummond, T. Faster and better: A machine learning approach to corner detection. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 32, 105–119. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leutenegger, S.; Chli, M.; Siegwart, R.Y. BRISK: Binary robust invariant scalable keypoints. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2548–2555. [Google Scholar]
- Verdie, Y.; Yi, K.; Fua, P.; Lepetit, V. Tilde: A temporally invariant learned detector. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5279–5288. [Google Scholar]
- Georgakis, G.; Karanam, S.; Wu, Z.; Ernst, J.; Košecká, J. End-to-end learning of keypoint detector and descriptor for pose invariant 3D matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1965–1973. [Google Scholar]
- Ono, Y.; Trulls, E.; Fua, P.; Yi, K.M. LF-Net: Learning local features from images. NeurIPS 2018, 31, 6234–6244. [Google Scholar]
- Sun, K.; Xiao, B.; Liu, D.; Wang, J. Deep high-resolution representation learning for human pose estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5693–5703. [Google Scholar]
- Xiang, Y.; Gubian, S.; Suomela, B.; Hoeng, J. Generalized simulated annealing for global optimization: The GenSA package. R J. 2013, 5, 13. [Google Scholar] [CrossRef]
- Ge, Z.; Liu, S.; Wang, F.; Li, Z.; Sun, J. Yolox: Exceeding yolo series in 2021. arXiv 2021, arXiv:2107.08430. [Google Scholar]
- Bochkovskiy, A.; Wang, C.Y.; Liao, H.Y.M. Yolov4: Optimal speed and accuracy of object detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1–13. [Google Scholar]
- Kelvins Pose Estimation Challenge 2019. Available online: https://kelvins.esa.int/satellite-pose-estimation-challenge/ (accessed on 4 July 2022).
- Kelvins Pose Estimation Challenge 2021. Available online: https://kelvins.esa.int/pose-estimation-2021/challenge/ (accessed on 14 July 2022).
- Gao, T.; Packer, B.; Koller, D. A segmentation-aware object detection model with occlusion handling. In Proceedings of the 24th IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 1361–1368. [Google Scholar]




| Method | Size [MB] | ||||||
|---|---|---|---|---|---|---|---|
| Park | 22.8 | 0.0198 | 0.0539 | 0.0783 | 0.0287 | 0.0929 | 0.1216 |
| Chen | 36.6 | 0.0047 | 0.0118 | 0.0172 | 0.0083 | 0.0299 | 0.0383 |
| Ours | 35.2 | 0.0036 | 0.0073 | 0.0116 | 0.0049 | 0.0129 | 0.0178 |
| Ours-small | 19.9 | 0.0041 | 0.0088 | 0.0138 | 0.0057 | 0.0235 | 0.029 |
| Ours-nano | 3.8 | 0.0048 | 0.0118 | 0.0175 | 0.0069 | 0.0270 | 0.0338 |
| Method | |||
|---|---|---|---|
| Park | 0.1135 | 0.1350 | 0.2485 |
| Chen | 0.1793 | 0.5457 | 0.7250 |
| Ours | 0.0414 | 0.0909 | 0.1323 |
| Ours-small | 0.1120 | 0.3689 | 0.4809 |
| Ours-nano | 0.1031 | 0.4883 | 0.5914 |
| Method | UTS | Top 7 | |||
|---|---|---|---|---|---|
| Ours | 0.0074 | 0.0216 | 0.0290 | ||
| ✓ | 0.0056 | 0.0151 | 0.0207 | ||
| ✓ | 0.0059 | 0.0179 | 0.0238 | ||
| ✓ | ✓ | 0.0049 | 0.0129 | 0.0178 |
| Method | SA/LS | ||||||
|---|---|---|---|---|---|---|---|
| Ours | SA | 0.0036 | 0.0073 | 0.0116 | 0.0049 | 0.0129 | 0.0178 |
| LS | 0.0058 | 0.0325 | 0.0407 | 0.0083 | 0.0422 | 0.0505 | |
| Ours-small | SA | 0.0041 | 0.0088 | 0.0138 | 0.0057 | 0.0235 | 0.0292 |
| LS | 0.0065 | 0.0334 | 0.0419 | 0.0093 | 0.0535 | 0.0628 | |
| Ours-nano | SA | 0.0048 | 0.0118 | 0.0175 | 0.0069 | 0.0270 | 0.0338 |
| LS | 0.0070 | 0.0364 | 0.0445 | 0.0095 | 0.0541 | 0.0636 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Zhang, H.; Hu, C. Learning-Based Pose Estimation of Non-Cooperative Spacecrafts with Uncertainty Prediction. Aerospace 2022, 9, 592. https://doi.org/10.3390/aerospace9100592
Li K, Zhang H, Hu C. Learning-Based Pose Estimation of Non-Cooperative Spacecrafts with Uncertainty Prediction. Aerospace. 2022; 9(10):592. https://doi.org/10.3390/aerospace9100592
Chicago/Turabian StyleLi, Kecen, Haopeng Zhang, and Chenyu Hu. 2022. "Learning-Based Pose Estimation of Non-Cooperative Spacecrafts with Uncertainty Prediction" Aerospace 9, no. 10: 592. https://doi.org/10.3390/aerospace9100592
APA StyleLi, K., Zhang, H., & Hu, C. (2022). Learning-Based Pose Estimation of Non-Cooperative Spacecrafts with Uncertainty Prediction. Aerospace, 9(10), 592. https://doi.org/10.3390/aerospace9100592







