A Novel Data-Driven-Based Component Map Generation Method for Transient Aero-Engine Performance Adaptation
Abstract
:1. Introduction
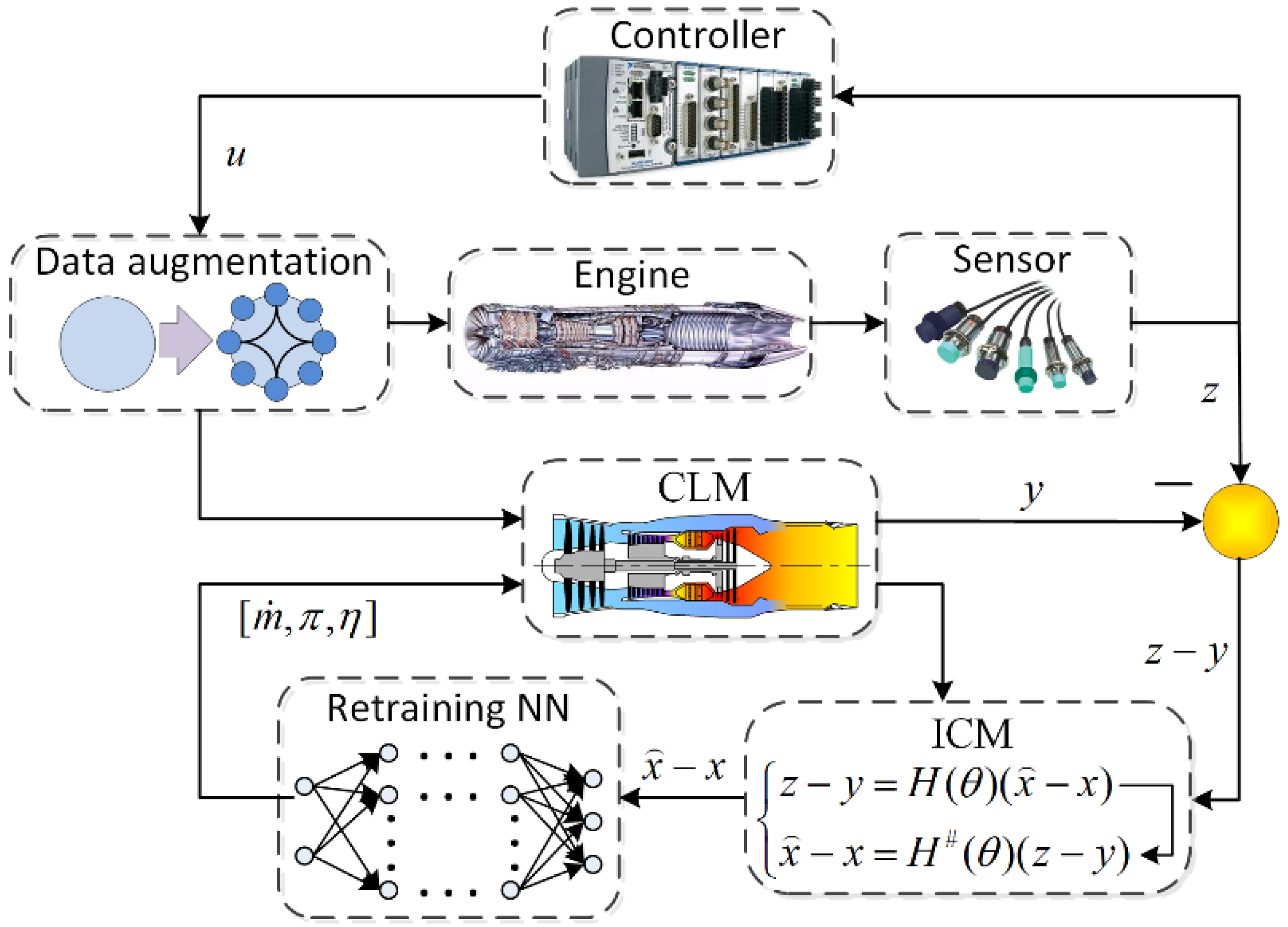
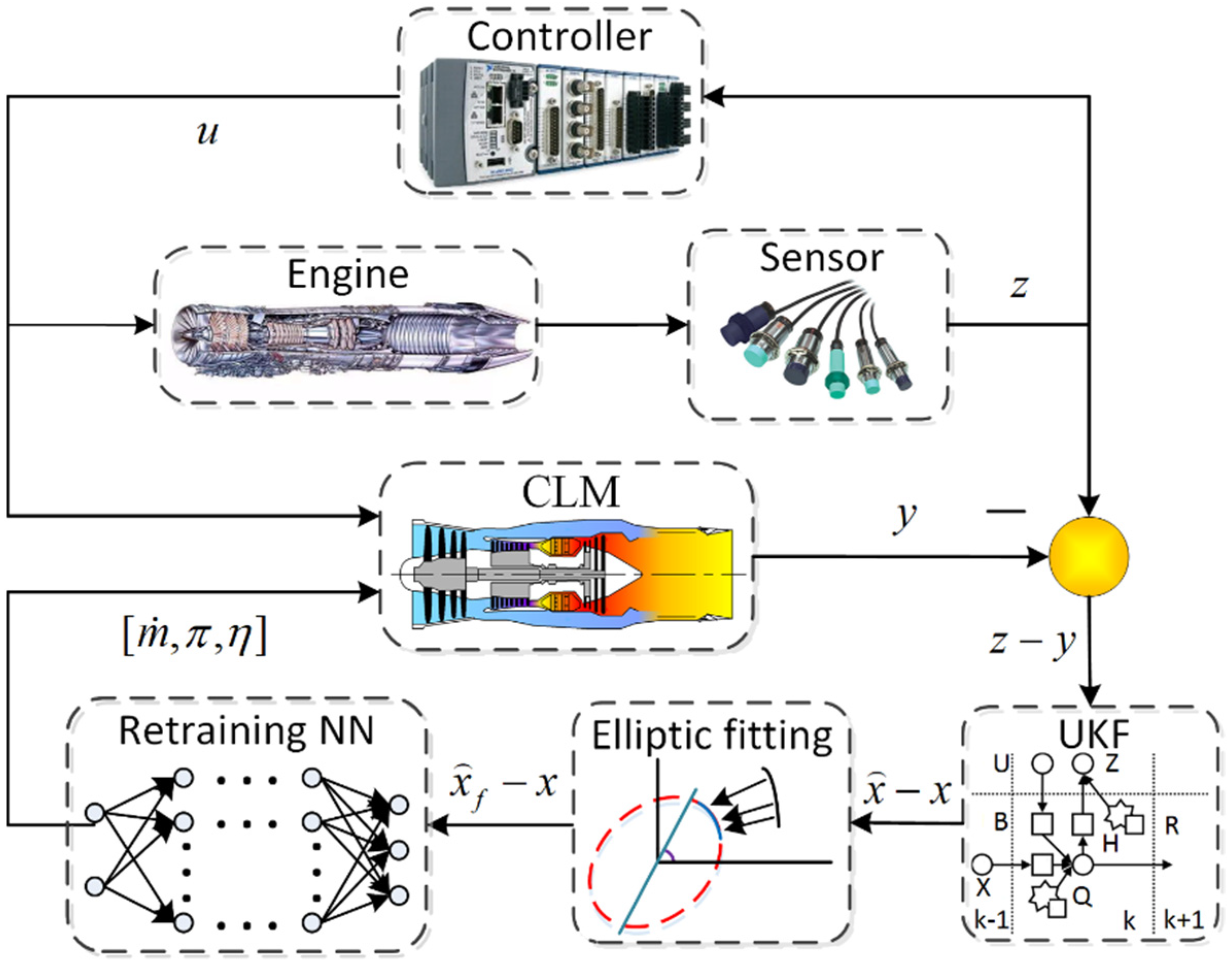
2. Formulation of the Proposed Adaptation Method
2.1. Performance Adaptation
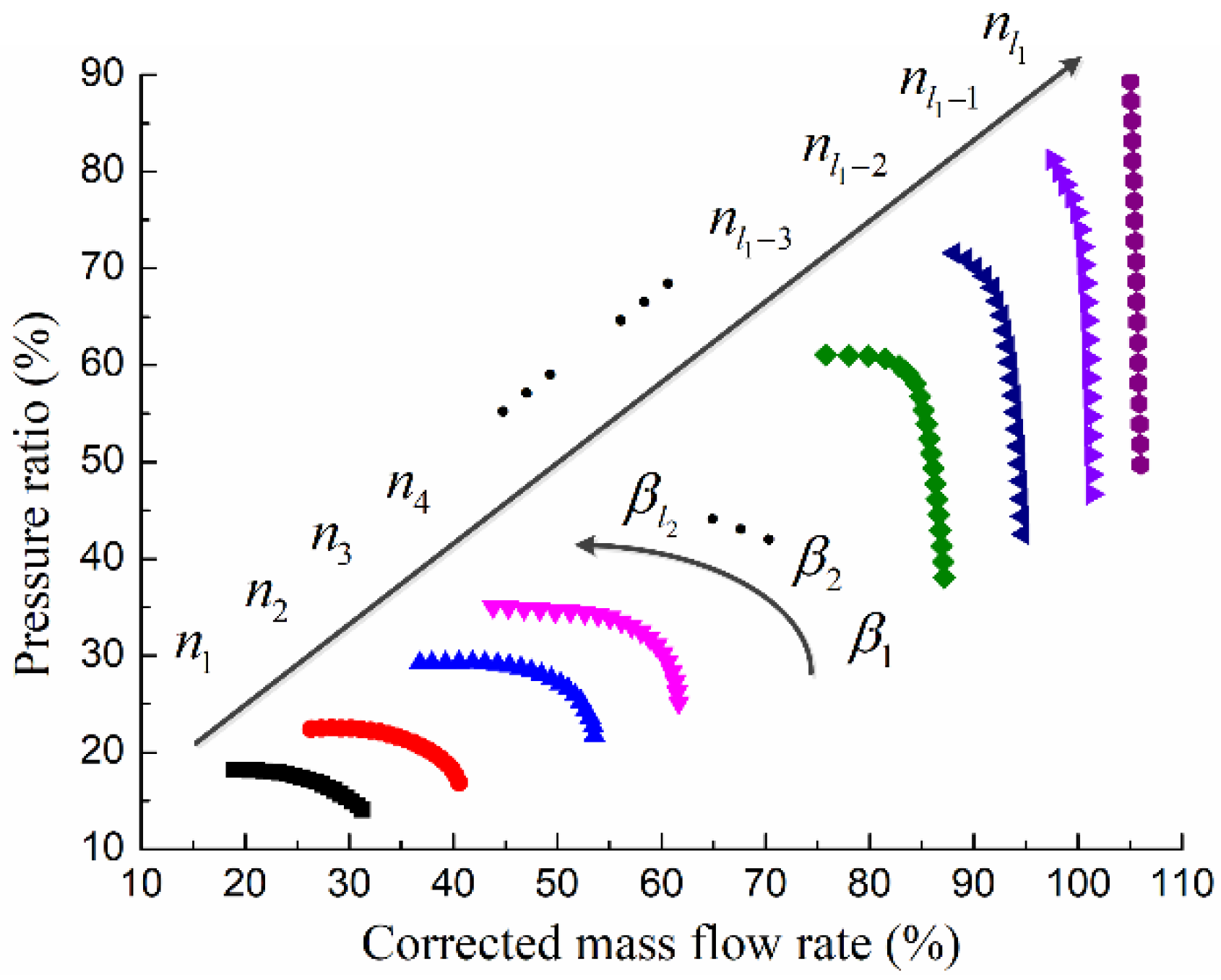
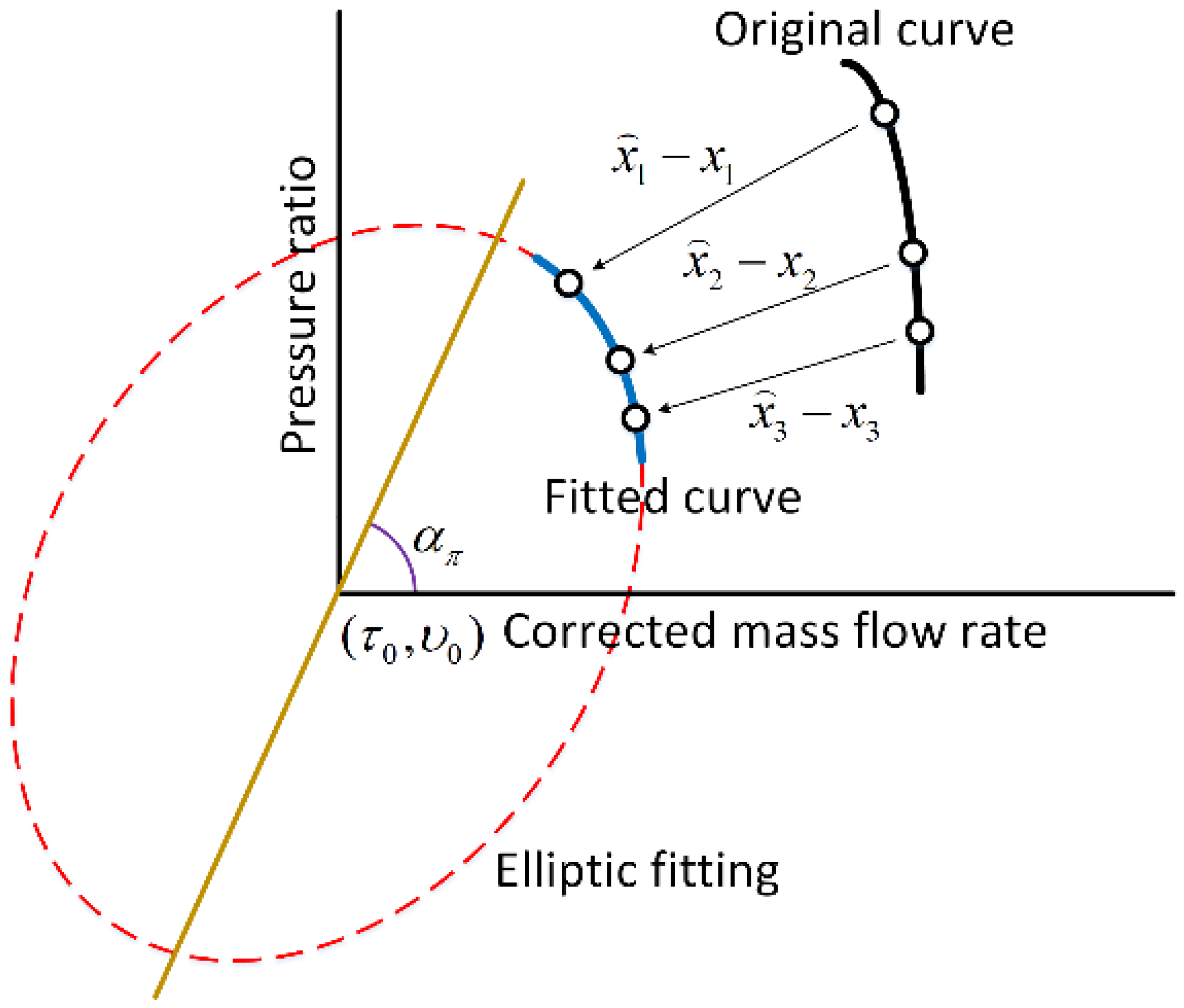
2.2. Compressor Neural Network
2.3. Steady State Adaptation Strategy
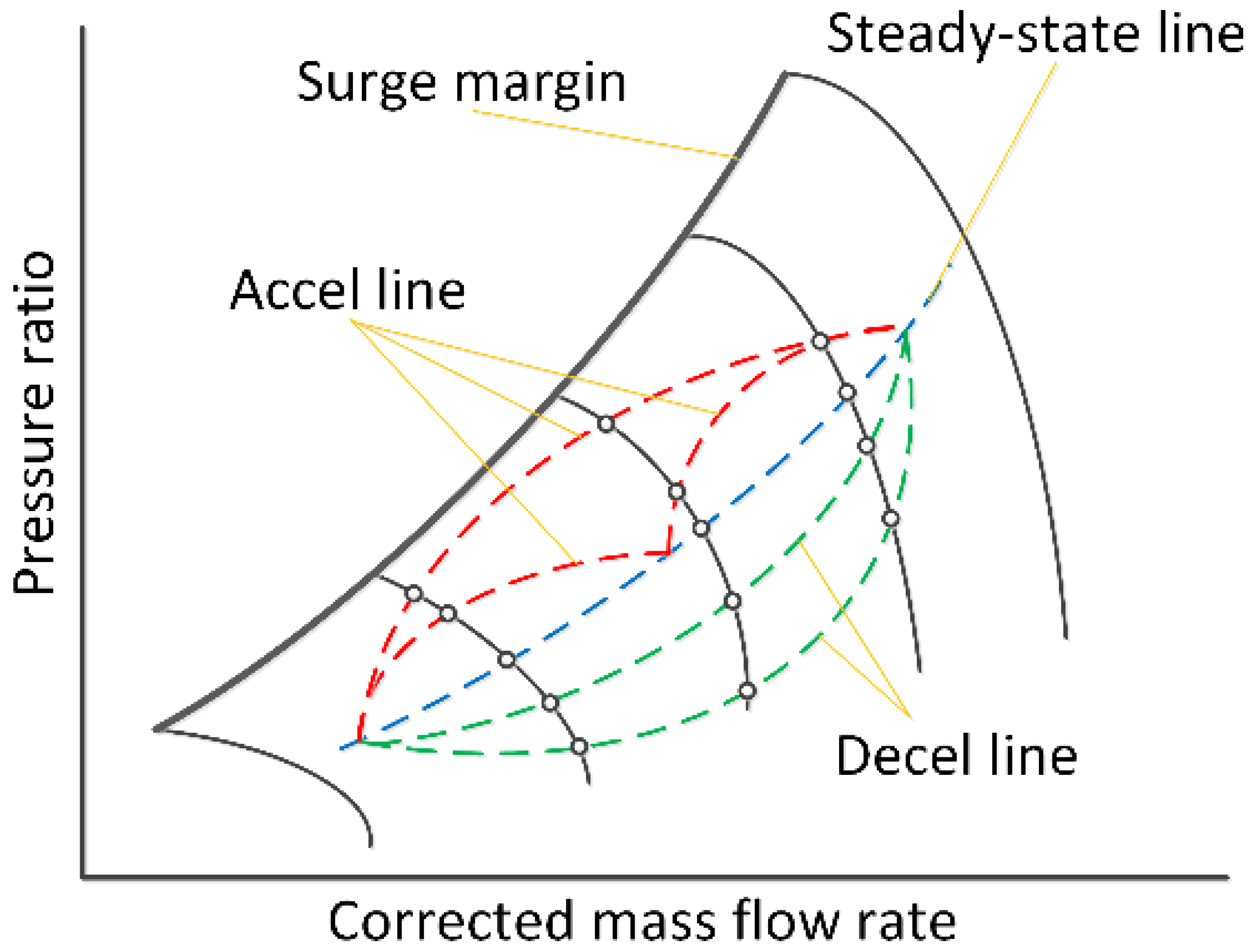
2.4. Transient Adaptation Strategy
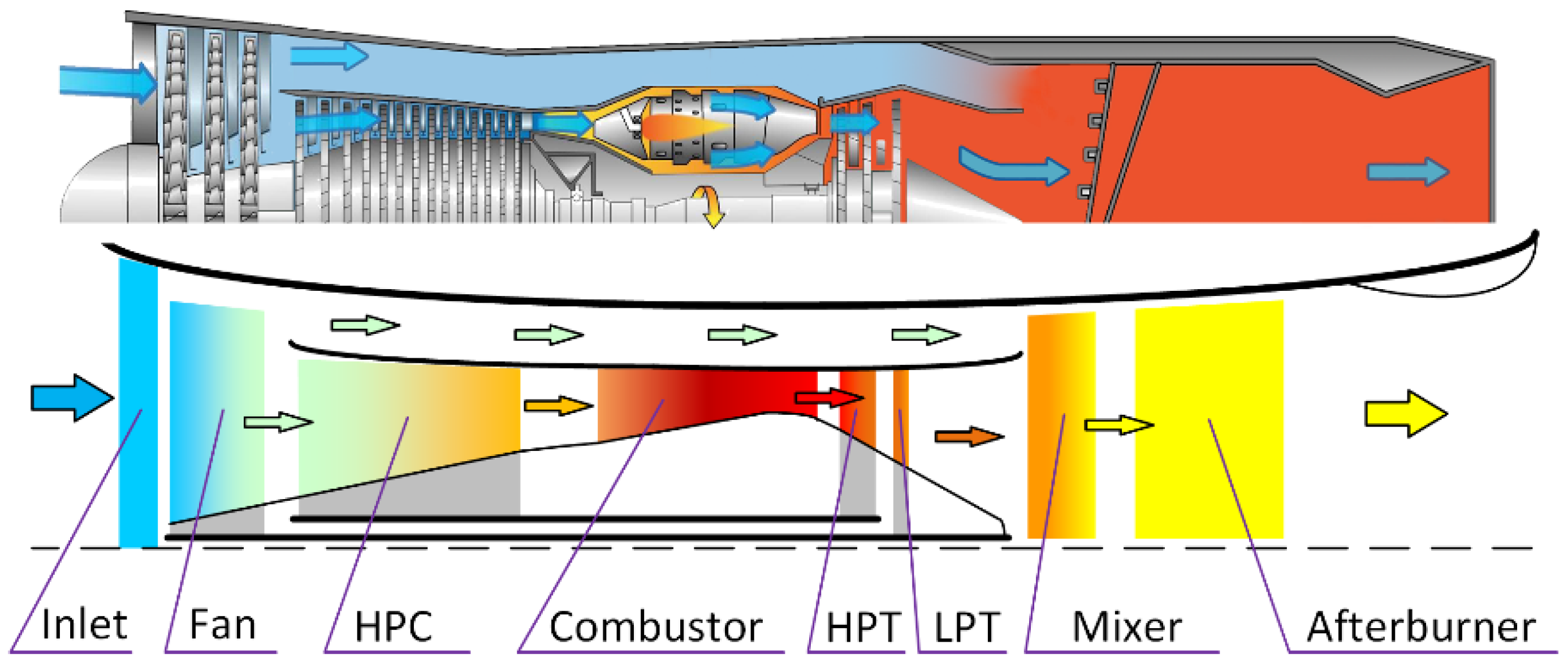
3. Application
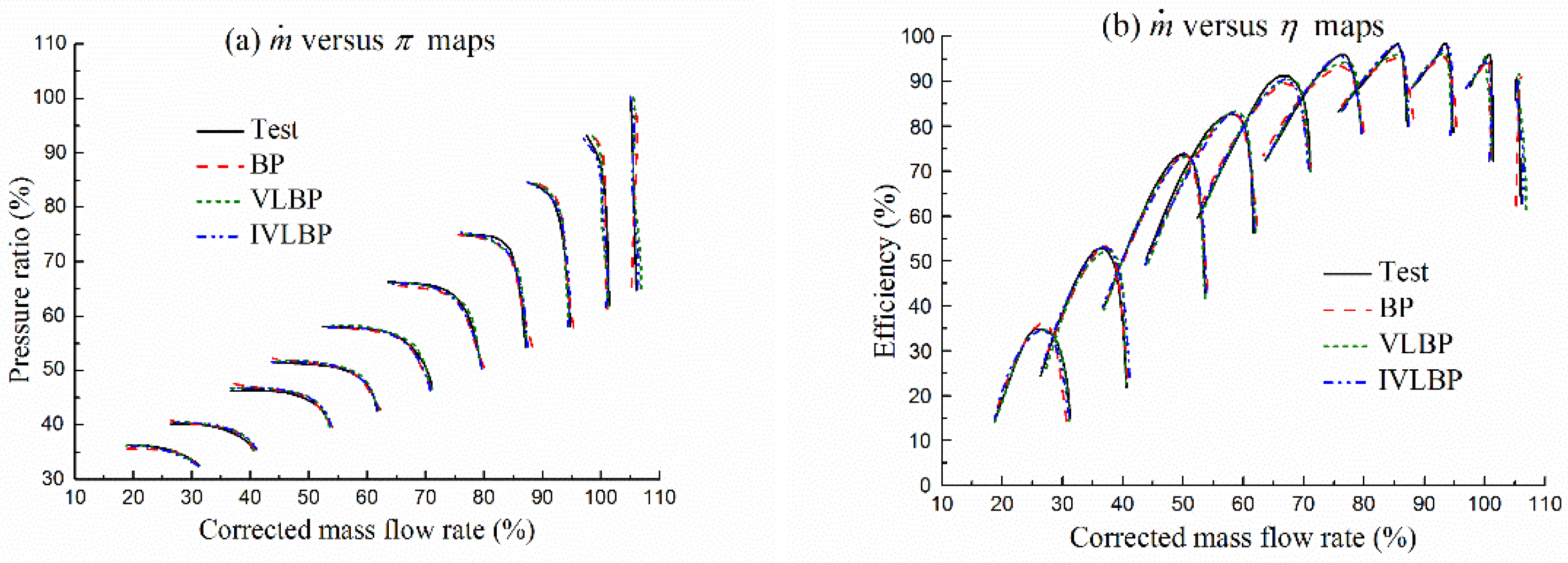
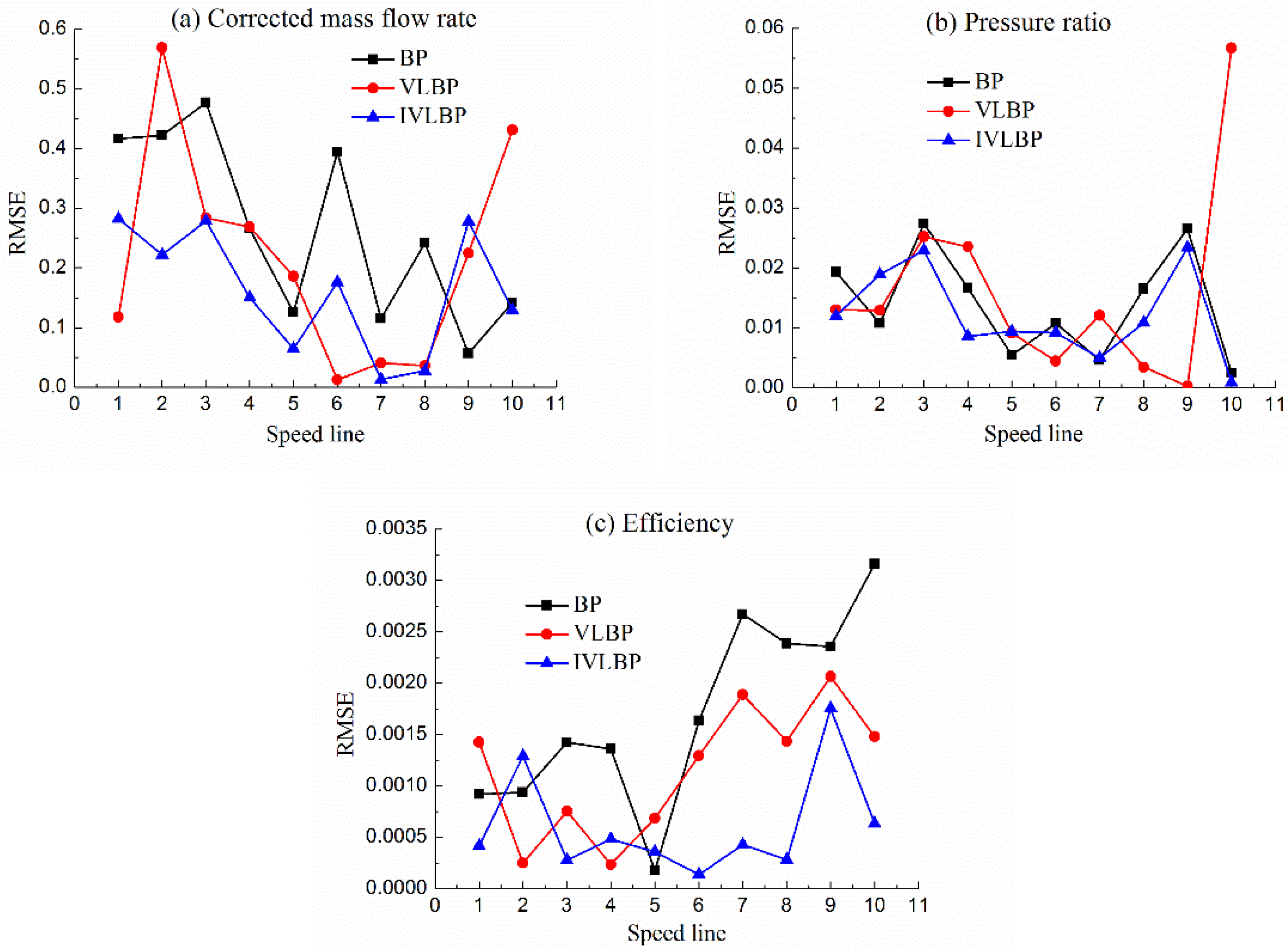
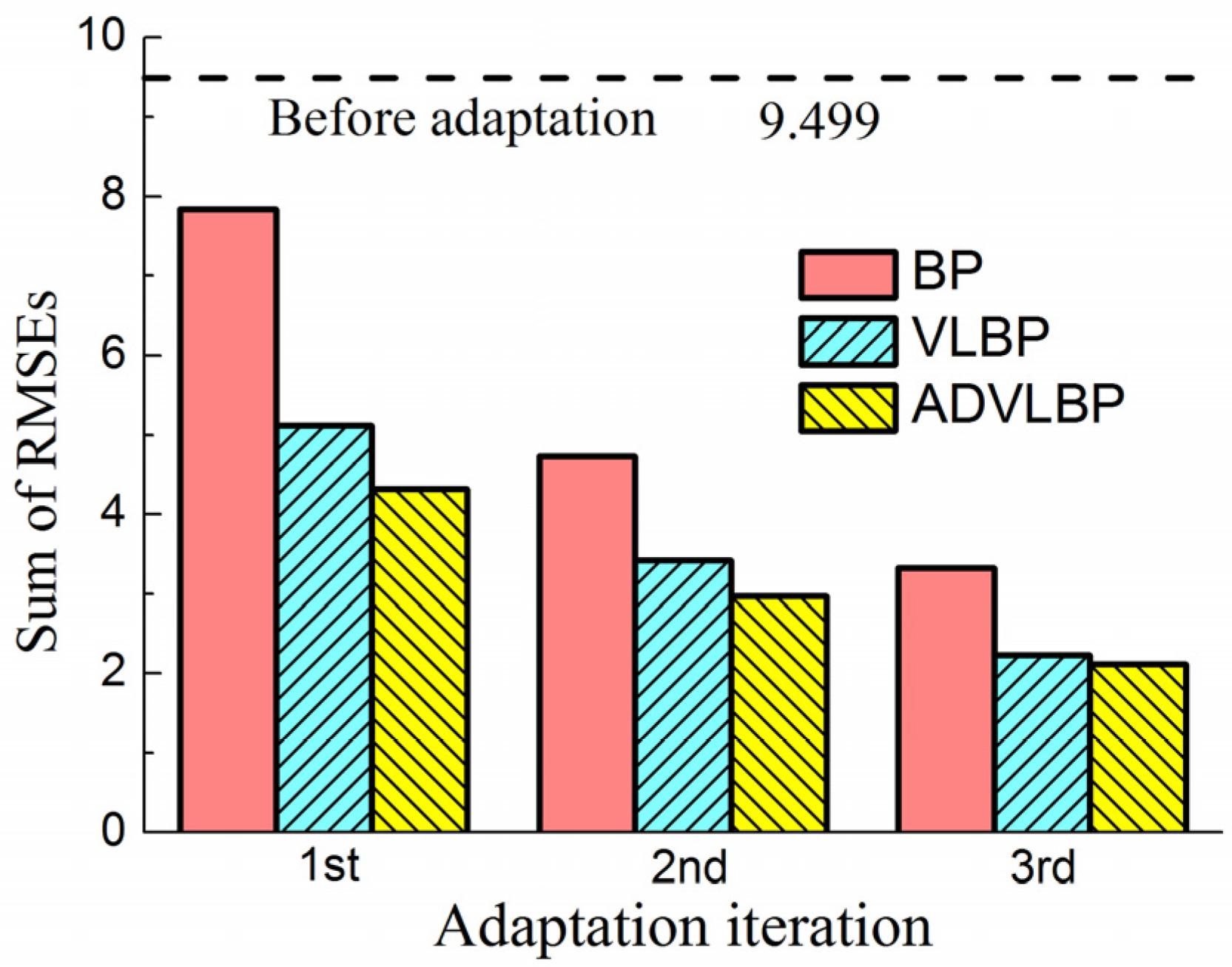
4. Results and Discussion
4.1. Case 1
4.2. Case 2
4.3. Case 3
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kurz, R.; Brun, K.; Wollie, M. Degradation effects on industrial gas turbines. J. Eng. Gas Turbines Power 2009, 131, 062401. [Google Scholar] [CrossRef]
- Fentaye, A.D.; Gilani, S.I.U.H.; Baheta, A.T. Gas turbine gas path diagnostics: A review. In Proceedings of the MATEC Web of Conferences, Kuantan, Malaysia, 18–19 August 2015; Volume 74, p. 5. [Google Scholar]
- Erario, M.L.; Giorgi, M.G.D.; Przysowa, R. Model-Based Dynamic Performance Simulation of a Microturbine Using Flight Test Data. Aerospace 2022, 9, 60. [Google Scholar] [CrossRef]
- Tsoutsanis, E.; Meskin, N.; Benammar, M.; Khorasani, K. An efficient component map generation method for prediction of gas turbine performance. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014; p. 45752. [Google Scholar]
- Stamatis, A.; Mathioudakis, K.; Papailiou, K.D. Adaptive simulation of gas turbine performance. J. Eng. Gas Turbines Power 1990, 112, 168–175. [Google Scholar] [CrossRef]
- Kong, C.; Ki, J.; Kang, M. A new scaling method for component maps of gas turbine using system identification. J. Eng. Gas Turbines Power 2003, 125, 979–985. [Google Scholar] [CrossRef]
- Lu, S.; Zhou, W.; Huang, J.; Lu, F.; Chen, Z. A Novel Performance Adaptation and Diagnostic Method for Aero-Engines Based on the Aerothermodynamic Inverse Model. Aerospace 2021, 9, 16. [Google Scholar] [CrossRef]
- Kong, C.; Kho, S.; Ki, J. Component map generation of a gas turbine using genetic algorithms. J. Eng. Gas Turbines Power 2004, 128, 92–96. [Google Scholar] [CrossRef]
- Qian, J.N.; Lu, F.; Qiu, X. Individual model identification for turbofan engine based on particle swarm optimization. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Dallas, TX, USA, 22–26 June 2015; p. 3363. [Google Scholar]
- Zhao, L.; Li, B.; Zhang, Y.; Yang, X. Nonlinear adaptation for performance model of an aero engine using QPSO. In Proceedings of the 2016 IEEE Information Technology, Networking, Electronic and Automation Control Conference, Chongqing, China, 20–22 May 2016; pp. 957–961. [Google Scholar]
- Li, Y.G.; Abdul Ghafir, M.F.; Wang, L. Non-Linear Multiple Points Gas Turbine Off-Design Performance Adaptation Using a Genetic Algorithm. J. Eng. Gas Turbines Power 2010, 133, 521–532. [Google Scholar]
- De Giorgi, M.G.; Strafella, L.; Menga, N.; Ficarella, A. Intelligent Combined Neural Network and Kernel Principal Component Analysis Tool for Engine Health Monitoring Purposes. Aerospace 2022, 9, 118. [Google Scholar] [CrossRef]
- Xu, M.; Wang, J.; Liu, J.; Li, M.; Geng, J.; Wu, Y.; Song, Z. An improved hybrid modeling method based on extreme learning machine for gas turbine engine. Aerosp. Sci. Technol. 2020, 107, 106333. [Google Scholar] [CrossRef]
- Gholamrezaei, M.; Ghorbanian, K. Application of integrated fuzzy logic and neural networks to the performance prediction of axial compressors. Proc. Inst. Mech. Eng. Part A J. Power Energy 2015, 229, 928–947. [Google Scholar] [CrossRef]
- Ebrahimi, S.H.; Afshari, A. An Artificial Neural Network Model for Prediction of the Operational Parameters of Centrifugal Compressors: An Alternative Comparison Method for Regression. J. Sci. Islamic Repub. Iran 2020, 31, 259–275. [Google Scholar]
- Ghorbanian, K.; Gholamrezaei, M. An artificial neural network approach to compressor performance prediction. Appl. Energy 2009, 86, 1210–1221. [Google Scholar] [CrossRef]
- Ghorbanian, K.; Gholamrezaei, M. Neural network modeling of axial flow compressor performance map. In Proceedings of the 45th AIAA Aerospace Science Meeting and Exhibit Reno, Reno, NV, USA, 8–11 January 2007. [Google Scholar]
- Ghorbanian, K.; Gholamrezaei, M. Axial compressor performance map prediction using artificial neural network. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Montreal, QC, Canada, 14–17 May 2007; Volume 47950, pp. 1199–1208. [Google Scholar]
- Ivanov, D.; Bestle, D.; Janke, C. Fast Compressor Map Computation by Utilizing Support Vector Machine and Response Surface Approximation. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Li, X.; Yang, C.; Wang, Y.; Wang, H.; Zu, X.; Sun, Y.; Hu, S. Compressor map regression modelling based on partial least squares. R. Soc. Open Sci. 2018, 5, 172454. [Google Scholar] [CrossRef]
- Tian, Z.; Gu, B.; Yang, L.; Lu, Y. Hybrid ANN–PLS approach to scroll compressor thermodynamic performance prediction. Appl. Therm. Eng. 2015, 77, 113–120. [Google Scholar] [CrossRef]
- Fei, J.; Zhao, N.; Shi, Y.; Feng, Y.; Wang, Z. Compressor performance prediction using a novel feed-forward neural network based on Gaussian kernel function. Adv. Mech. Eng. 2016, 8, 1687814016628396. [Google Scholar] [CrossRef]
- Volponi, A.; Simon, D.L. Enhanced Self Tuning On-Board Real-Time Model (eSTORM) for Aircraft Engine Performance Health Tracking; No. NASA/CR-2008-215272; NASA: Washington, DC, USA, 2008.
- Volponi, A. Data Fusion for Enhanced Aircraft Engine Prognostics and Health Management; No. NASA/CR-2005-214055; NASA: Washington, DC, USA, 2005.
- Volponi, A.; Brotherton, T. A bootstrap data methodology for sequential hybrid engine model building. In Proceedings of the 2005 IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2005; pp. 3463–3471. [Google Scholar]
- Ma, Y.-H.; DU, X.; Sun, X.-M. Adaptive modification of the turbofan engine nonlinear model based on LSTM neural networks and hybrid optimization method. Chin. J. Aeronaut. 2021, 35, 314–332. [Google Scholar] [CrossRef]
- Volponi, A.; Brotherton, T.; Luppold, R. Empirical tuning of an on-board gas turbine engine model for real-time module performance estimation. J. Eng. Gas Turbines Power 2008, 130, 021604. [Google Scholar] [CrossRef]
- Zhou, D.; Yao, Q.; Wu, H.; Ma, S.; Zhang, H. Fault diagnosis of gas turbine based on partly interpretable convolutional neural networks. Energy 2020, 200, 117467. [Google Scholar] [CrossRef]
- Kurzke, J. How to get component maps for aircraft gas turbine performance calculations. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Birmingham, UK, 10–13 June 1996; Volume 78767, p. V005T16A001. [Google Scholar]
- Yang, Q.; Li, S.; Cao, Y. A new component map generation method for gas turbine adaptation performance simulation. J. Mech. Sci. Technol. 2017, 31, 1947–1957. [Google Scholar] [CrossRef]
- Li, Y.G.; Pilidis, P.; Newby, M.A. An Adaptation Approach for Gas Turbine Design-Point Performance Simulation. In Proceedings of the ASME Turbo Expo 2005: Power for Land, Sea, and Air, Reno, NV, USA, 6–9 June 2005; pp. 95–105. [Google Scholar]
- Li, Y.G.; Pilidis, P. GA-based design-point performance adaptation and its comparison with ICM-based approach. Appl. Energy 2010, 87, 340–348. [Google Scholar] [CrossRef]
- Tsoutsanis, E.; Meskin, N.; Benammar, M.; Khorasani, K. Transient Gas Turbine Performance Diagnostics Through Nonlinear Adaptation of Compressor and Turbine Maps. J. Eng. Gas Turbines Power 2015, 137, 091201. [Google Scholar] [CrossRef]
- Kandepu, R.; Foss, B.; Imsland, L. Applying the unscented Kalman filter for nonlinear state estimation. J. Process Control 2008, 18, 753–768. [Google Scholar] [CrossRef]
- Dewallef, P.; Romessis, C.; Le´onard, O.; Mathioudakis, K. Combining Classification Techniques with Kalman Filters for Aircraft Engine Diagnostics. J. Eng. Gas Turbines Power 2006, 128, 595–603. [Google Scholar] [CrossRef]
- Tsoutsanis, E.; Li, Y.-G.; Pilidis, P.; Newby, M. Non-linear model calibration for off-design performance prediction of gas turbines with experimental data. Aeronaut. J. 2017, 121, 1758–1777. [Google Scholar] [CrossRef]
- Tsoutsanis, E.; Li, Y.G.; Pilidis, P.; Newby, M. Nonlinear model-based adaptation for off-design performance prediction of gas turbines. ISABE 2017, 2017, 21436. [Google Scholar]
- Zhou, W.; Huang, J.; Dou, J.; Shen, F. Object oriented simulation platform for turbofan engine and its control system. J. Aerosp. Power 2007, 22, 119–125. [Google Scholar]
- McCartney, M.; Haeringer, M.; Polifke, W. Comparison of Machine Learning Algorithms in the Interpolation and Extrapolation of Flame Describing Functions. J. Eng. Gas Turbines Power 2020, 142, 061009. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Vogl, T.P.; Mangis, J.K.; Rigler, A.K.; Zink, W.T.; Alkon, D.L. Accelerating the convergence of the back propagation method. Biol. Cybern. 1988, 59, 257–263. [Google Scholar] [CrossRef]













| Measurement | Symbol | Unit | Standard Deviation |
|---|---|---|---|
| Low-pressure rotating speed | nL | rpm | 0.0015 |
| High-pressure rotating speed | nH | rpm | 0.0015 |
| HPC inlet total temperature | Tt25 | K | 0.002 |
| HPC outlet total pressure | Pt3 | kPa | 0.0015 |
| Mixer inner inlet total pressure | Pt6 | kPa | 0.0015 |
| Mixer inner inlet total temperature | Tt6 | K | 0.002 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; Lu, S.; Huang, J.; Pan, M.; Chen, Z. A Novel Data-Driven-Based Component Map Generation Method for Transient Aero-Engine Performance Adaptation. Aerospace 2022, 9, 442. https://doi.org/10.3390/aerospace9080442
Zhou W, Lu S, Huang J, Pan M, Chen Z. A Novel Data-Driven-Based Component Map Generation Method for Transient Aero-Engine Performance Adaptation. Aerospace. 2022; 9(8):442. https://doi.org/10.3390/aerospace9080442
Chicago/Turabian StyleZhou, Wenxiang, Sangwei Lu, Jinquan Huang, Muxuan Pan, and Zhongguang Chen. 2022. "A Novel Data-Driven-Based Component Map Generation Method for Transient Aero-Engine Performance Adaptation" Aerospace 9, no. 8: 442. https://doi.org/10.3390/aerospace9080442
APA StyleZhou, W., Lu, S., Huang, J., Pan, M., & Chen, Z. (2022). A Novel Data-Driven-Based Component Map Generation Method for Transient Aero-Engine Performance Adaptation. Aerospace, 9(8), 442. https://doi.org/10.3390/aerospace9080442






