Aerodynamic Characteristics of Bristled Wings in Flapping Flight

Abstract

This study focuses on the aerodynamics of the smallest flying insects’ bristled wings. We measured and analyzed wing morphological data from 38 specimens of Mymaridae. Bristled wing flight was numerically simulated at Reynolds numbers from 1 to 80. The aerodynamic force, power, and efficiency of bristled wings using lift-based stroke, drag-based stroke, and clap-and-fling mechanism were evaluated. An unusual clap-and-fling pattern considering bristle crossing was first proposed. Our study shows that with a reduction in the wingspan of Mymaridae, the proportion of the wingtip bristled area increases. A lift-based stroke is superior to a drag-based stroke in terms of vertical force production and aerodynamic efficiency at 5 ≤ Re ≤ 20. Bristled wings employing the clap-and-fling mechanism achieve both vertical force and efficiency augmentation, while bristle crossing incurs a substantial horizontal force and contributes little to vertical force augmentation.

1. Introduction

When considering flying insects, people usually think of macroscopic insects such as dragonflies, honeybees, and butterflies. However, the body size of the vast majority of insects is no greater than a few millimeters [1]. Parasitic wasps from the families Mymaridae and Trichogrammatidae (termed “micro-wasps” throughout the rest of this paper) are the tiniest known flying insects [2] (e.g., Kikiki huna recorded as 158 μm in size [3] and Megaphragma amalphitanum recorded as 225 μm in size [4]). These minute insects are commonly encountered parasitoids of pest species, and have been widely used as biological control agents [5]. Elucidating the flight mechanism of these minute insects helps understand their dispersal strategies and provides valuable insight into the scale limits of biological flapping wing flight. Recent developments in microfabrication have made minuscule artificial flyers [6,7,8] or swimmers [9] with a wingspan of O(10⁻² m) or O(10⁻³ m) possible. Understanding the aerodynamic characteristics of these minute insects provides essentials for the miniaturization design of future bio-inspired micro-robots.

Unlike macroscopic flying insects’ solid wings, the smallest flying insects’ bristled wings are narrow and bare, with dozens of setae surrounding the wing margins. The cycle-averaged Reynolds number (Re) of these insects in flight is around 10 [10], at which viscous effects are significant. Previous aerodynamic research on minute insects’ bristled wings mainly considered simple kinematics, such as translation [11,12,13,14,15] and rotation [11] with constant velocity. In recent years, the aerodynamics of bristled wings in flapping motion began to receive attention. Numerical analyzes [16,17,18] and mechanical model experiments [19,20,21] have been used to investigate the “clap-and-fling” motion of the bristled wings. Lee et al. [22] numerically studied the formation and development of bristled wings’ gap flow. Capturing free-flying video of minute bristled-wing insects is difficult. The tiny size of bristled-wing insects makes them vulnerable and elusive, posing a considerable challenge for biomechanical measurements. Recently, Farisenkov et al. [10] made the first complete kinematic observation of the miniature bristled-wing beetle Paratuposa placentis’ flapping flight. They found that the flapping wing kinematics of P. placentis is similar to the kinematics of swimming in miniature aquatic crustaceans. Some fruit flies [23] also have been observed to use a drag-based swimming-like mode in forward flight. These drag-based swimming-like locomotion mechanisms are usually regarded as an aquatic phenomenon [24]. Conversely, lift-based mechanisms are common in the flight of larger insects, birds, and bats. A computational study compared the vertical forces generated by a solid wing using lift-based and drag-based strategies, suggesting that at Re < 20, the difference between these two strategies in the average vertical force and horizontal force coefficients is small [25]. An aerodynamic comparison of lift-based and drag-based flapping flight using bristled wings can certainly yield important design cues of flapping strategy for future minuscule artificial flyers. Engels et al. [26] analyzed the aerodynamics of two bristled wing kinematics (namely, horizontal flapping kinematics based on lift mechanism, and figure-of-eight flapping kinematics with vertical forces provided by a mixture of drag and lift mechanisms, where the drag mechanism dominates) at Re = 4, 14, and 57. A detailed comparative analysis of lift mechanism flapping versus pure drag mechanism flapping of bristled wings over a larger range of Reynolds numbers would be valuable.

One of the predominant lift-augmenting mechanisms is the “clap-and-fling” mechanism, proposed by Weis-Fogh [27] based on observations of Encarsia Formosa hovering. Clap-and-fling appears to be an obligate behavior for tiny insects [28], including thrips [29,30] and some parasitoid wasps [31]. These insects fly with nearly maximal wing amplitude, clap their wings together at the end of the upstroke, and fling their wings apart during pronation. Santhanakrishnan et al. [16] used porous wings to imitate the “leakiness” of thrips’ wings, and compared the aerodynamics of solid wings and porous wings during clap-and-fling. The study of Jones et al. [17] on the “fling” process of bristled wings indicated that the bristled wing reduces the drag required to “fling” wings apart. The clap-and-fling mechanism has some variants, such as the “partial clap-and-fling” [30], “near clap-and-fling” [32], and “clap-and-peel” [33]. Since the setal fringes of bristled wings are sparsely distributed, the left and right bristled wings may intersect in the clap-and-fling process [10]. Whether this “interlacing clap-and-fling” will have an impact on lift augmentation is worth exploring.

This paper aimed to investigate the aerodynamic performance of the smallest flying insects’ bristled wings in flapping flight, and to compare it with that of solid wings. The immersed boundary method was applied to simulate incompressible flows around the wing. The proposed study covers two main aspects: the aerodynamic force and efficiency of bristled wings using lift-based stroke, drag-based stroke, and clap-and-fling mechanisms; the effect of bristle crossing and the inter-wing gap on the vertical force augmentation of bristled wing clap-and-fling. We investigated the effect of the Re (ranges from 1 to 80) on the aerodynamic performance of bristled wings in different flapping modes, and compared them to obtain which flapping mode exhibits better aerodynamic performance at different Re. To the best of our knowledge, analysis of the aerodynamic effects of the crossover of the bristles on the left and right wings in the clap-and-fling process has not been pursued so far. The comparative study of this paper shows that bristle crossing incurs a substantial horizontal force, and contributes little to vertical force augmentation.

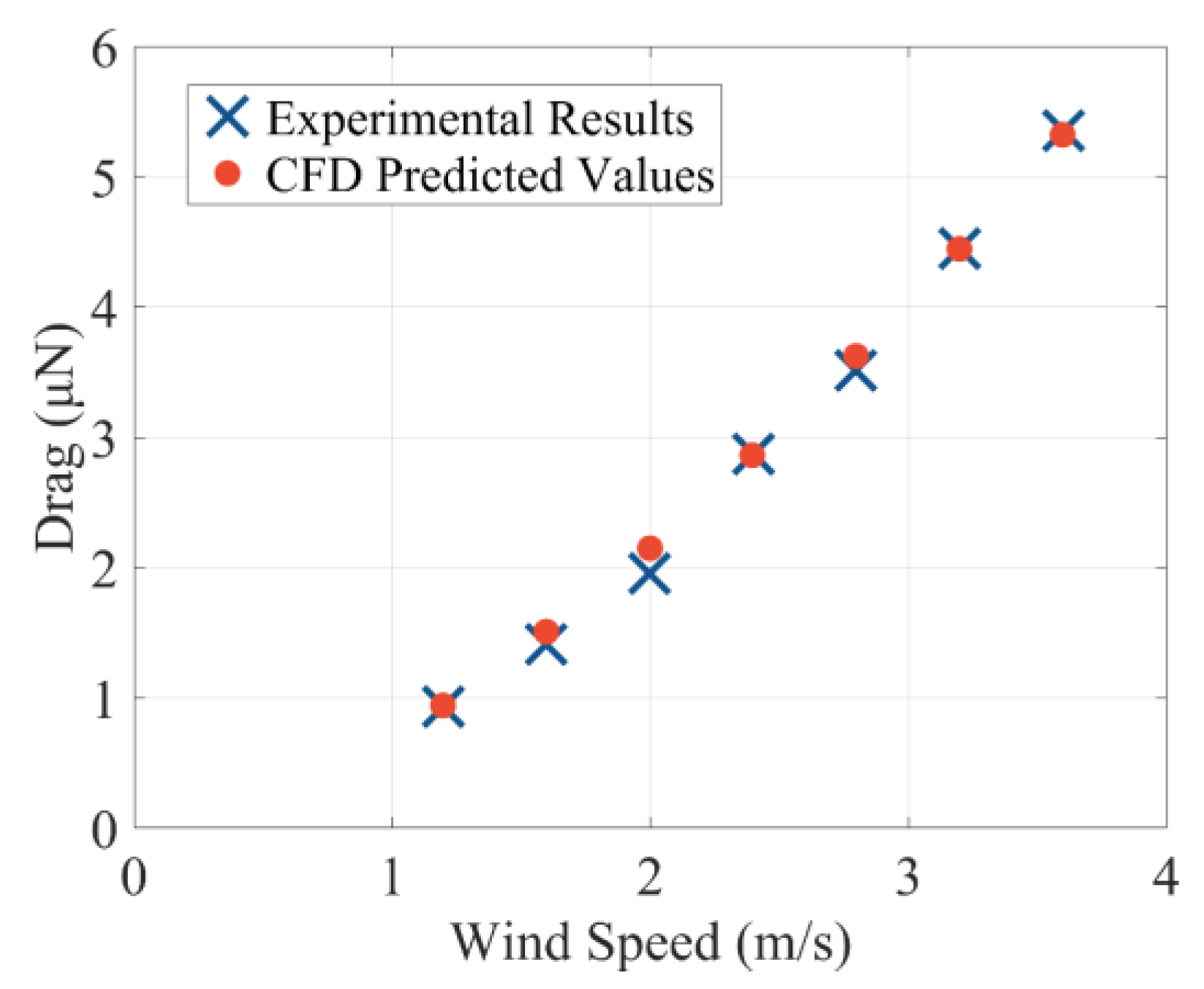
2. Materials and Methods

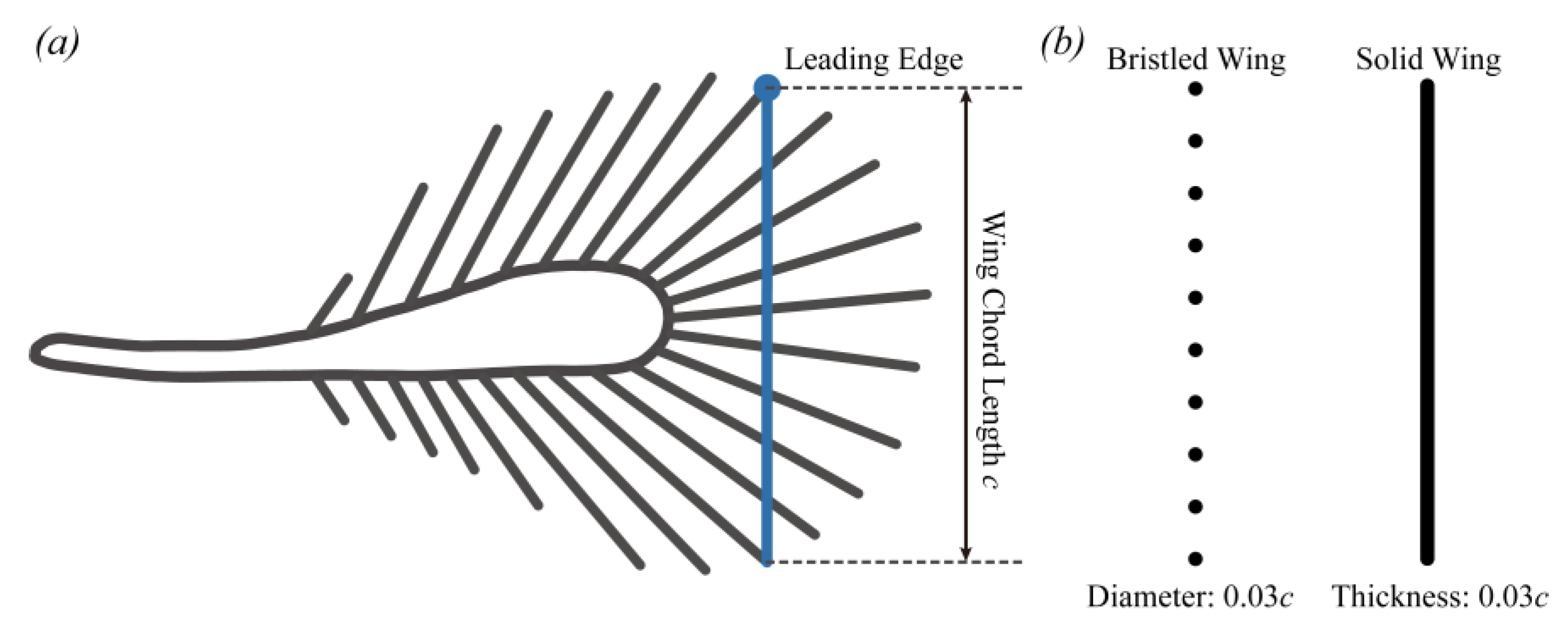
2.1. Research Subject and Morphology Measurement

Insects from the family Mymaridae were chosen as the research subject. Figure 1a shows the typical morphology of their bristled wing [34]. We collected wing morphological data on 38 specimens from the family Mymaridae using previously published [34,35,36,37,38,39] high-quality images. The selected samples were all female because the females are better at flying than the males [40]. The images were analyzed using ImageJ software (NIH, Bethesda, MD, USA) and calibrated against the known length of the scale bar. For each species, a single wing (forewing) was analyzed.

We measured the wingspan (defined as the maximum length from the wing root to the wingtip), the whole wing area $S_1$, the bristled portion area $S_2$ and the wingtip bristled area $S_3$ (defined as the bristled area around the wingtip in a 10% wingspan range) (Figure 1b). The ratio of $S_2$ to $S_1$ (proportion of the bristled portion area) and the ratio of $S_3$ to $S_2$ (proportion of the wingtip bristled area) vary with wingspan, as plotted in Figure 1c and d, respectively. With wingspan reduction, a clear upward trend in the proportion of the bristled portion area and the proportion of the wingtip bristled area is observed, indicating that their aerodynamic contributions are increasing.

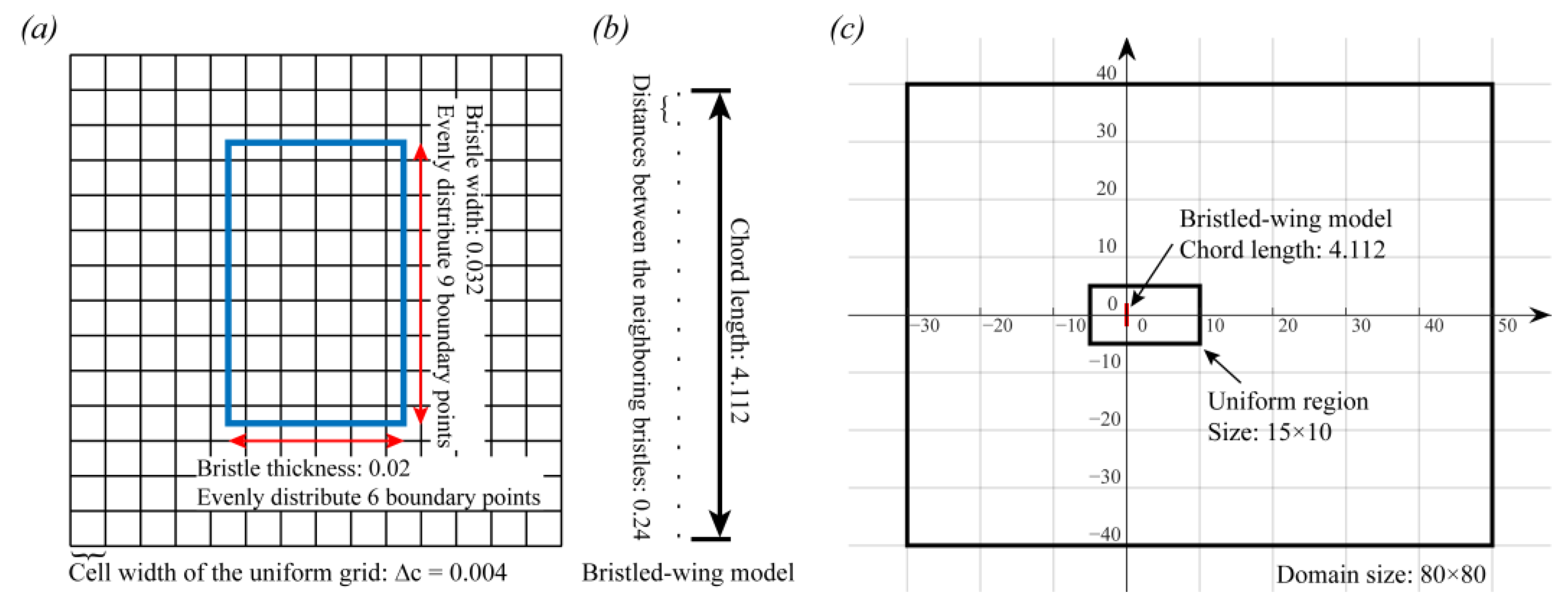
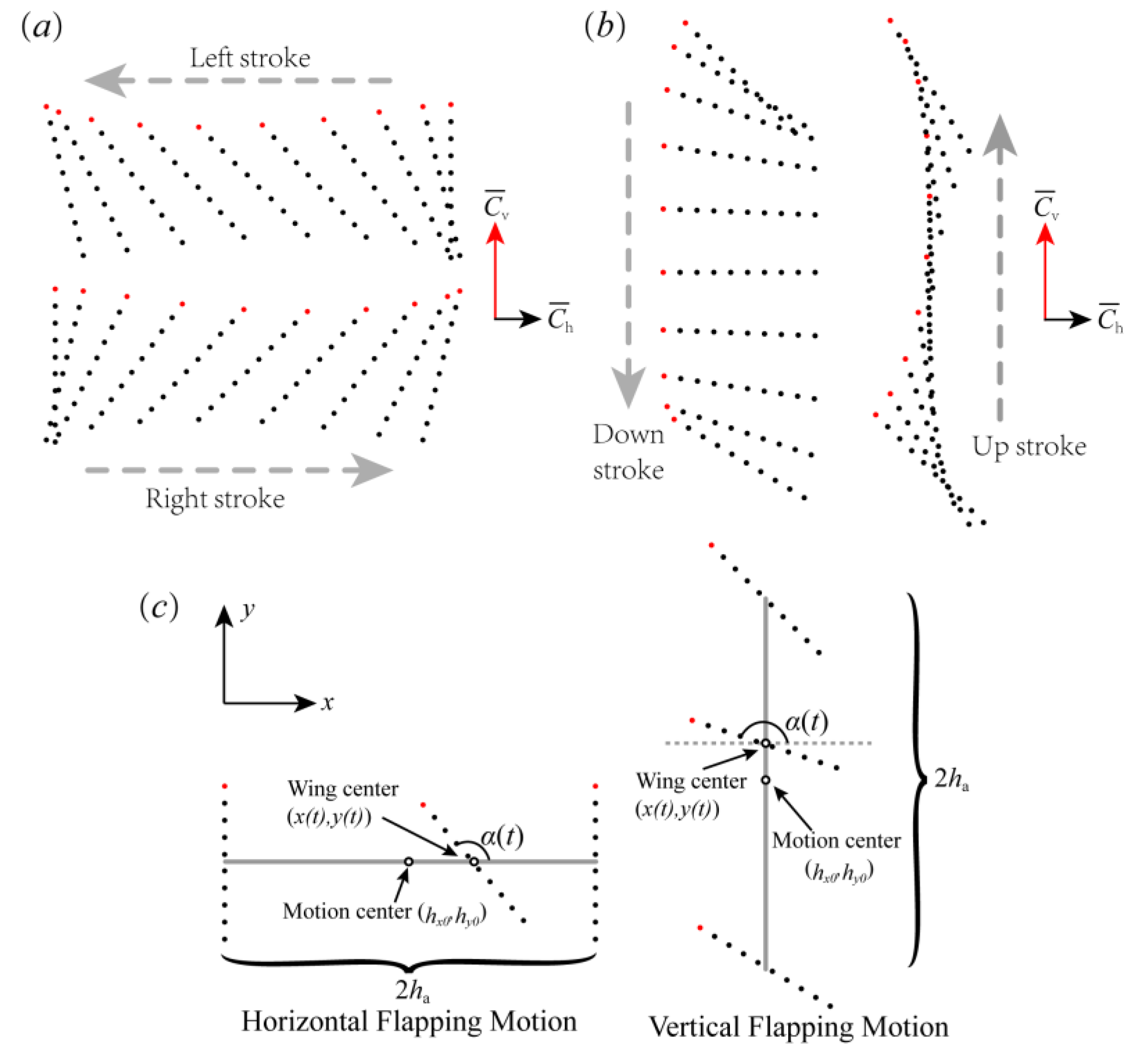
2.2. Bristled Wing Model and Kinematics

In order to perform accurate simulations of the flow field during bristled wings flapping, a very fine grid near the bristles is required, which poses a significant challenge for three-dimensional (3D) computation. Most of the relevant numerical studies in recent years have adopted two-dimensional (2D) simplified bristled wing models [17,18,22]. Liu and Sun [41] recently performed the CFD simulation of bristled wings in steady translational motion at AOA = 90°, showing that at Re = 10, the 3D effect appears in the wingtip region, resulting in a higher drag coefficient in this region than the 2D wing model. The length of this region is about 0.23 times the chord length, and both the region length and the drag increment almost do not vary with the aspect ratio. Although the study is not based on real flapping motions, its conclusions are instructive, implying that the 3D effects of flapping wings at low Re are less complex than those at high Re. Our study focuses on the comparison of the aerodynamic performance of bristled wings in different flapping motions, and the aforementioned 3D effects will not have a significant impact on the conclusions of the comparison.

When flapping wing motion is 2D simplified, the chord profiles of the wing are usually taken as a simplified wing model. As shown in Figure 1d, a large proportion of the Mymaridae’s bristles are radially distributed around the wingtip. Chord profiles near the wingtip can accurately reflect the structural features of these bristled wings. Thus, we chose chord profiles near the wingtip to construct the simplified 2D bristled wing model.

Let the chord length of the bristled wing be c (Figure 2a). In the flapping flight cases of this paper, all bristled wings are composed of 10 evenly arranged circles 0.03c in diameter, which resembles the actual average distribution density of the bristles on the Mymaridae’s bristled wing. To explore the aerodynamic differences between bristled wings and solid wings, we compared them in the following simulations, where the solid wing had rounded leading and trailing edges, with a length of c and a thickness of 0.03c. The simplified 2D models of the bristled wing and the solid wing are shown in Figure 2b. The cross-sectional area of the bristled wing model is $10\times \pi \times {\left(0.03c/2\right)}^2$ ≈ $7.069\times {10}^{-3}{c}^2$, while the cross-sectional area of the solid wing model is $0.03c^2-{\left(0.03c\right)}^2+\pi \times {\left(0.03c/2\right)}^2$ ≈ $2.981\times {10}^{-2}{c}^2$. The area of the bristled wing model is 23.7% of the solid wing model.

To study the aerodynamic differences of bristled wings flapping with a lift-based mechanism versus a drag-based mechanism, we assume two idealized stroke kinematics—horizontal flapping (HF) motion and vertical flapping (VF) motion. HF motion (Figure 3a) approximates the wing kinematics of some larger fly insects (e.g., the fruit fly), and both the left and right strokes provide a vertical force during flapping. VF motion (Figure 3b) is a theoretical flapping mode that is more common in the swimming of marine life. In VF motion, the windward area of the wing on the down stroke is larger than that on the up stroke; therefore, the average drag of the entire stroke points upward and provides a vertical force.

The motion of the wing is governed by the following kinematics:

$$x\left(t\right)=h_{\mathrm{x}0}+h_{\mathrm{a}}\sin \left(2\pi ft+\phi \right)\cos \left(\beta \right)$$

(1)

$$y\left(t\right)=h_{\mathrm{y}0}+h_{\mathrm{a}}\sin \left(2\pi ft+\phi \right)\sin \left(\beta \right)$$

(2)

$$\mathsf{\alpha }\left(t\right)={\alpha }_0+{\alpha }_{\mathrm{a}}\sin \left(2\pi ft\right)$$

(3)

where $\left(x\left(t\right),y\left(t\right)\right)$ is the position of the wing center,$\left(h_{\mathrm{x}0},h_{\mathrm{y}0}\right)$ is the position of the flapping wing motion center, $h_a$ is the amplitude of translation, $f$ is the flapping frequency, $\beta$ is the stroke plane angle, $\phi$ is the phase between translation and rotation, $\mathsf{\alpha }\left(t\right)$ is the AOA of the wing, ${\alpha }_0$ is the mean AOA, and ${\alpha }_a$ is the amplitude of rotation. Figure 3c presents a schematic diagram of some of the kinematic parameters.

Re is defined as follows:

$$Re=\frac{U_{\mathrm{mean}}c}{\nu }=\frac{4f{h}_{\mathrm{a}}c}{\nu }$$

(4)

where $U_{\mathrm{mean}}$ is the time-averaged velocity of the wing center in a whole stroke cycle. In the following simulations, Re ranges from 1 to 80, which is adjusted by changing the kinematic viscosity $\nu$ and keeping the other parameters constant.

2.3. Methodology

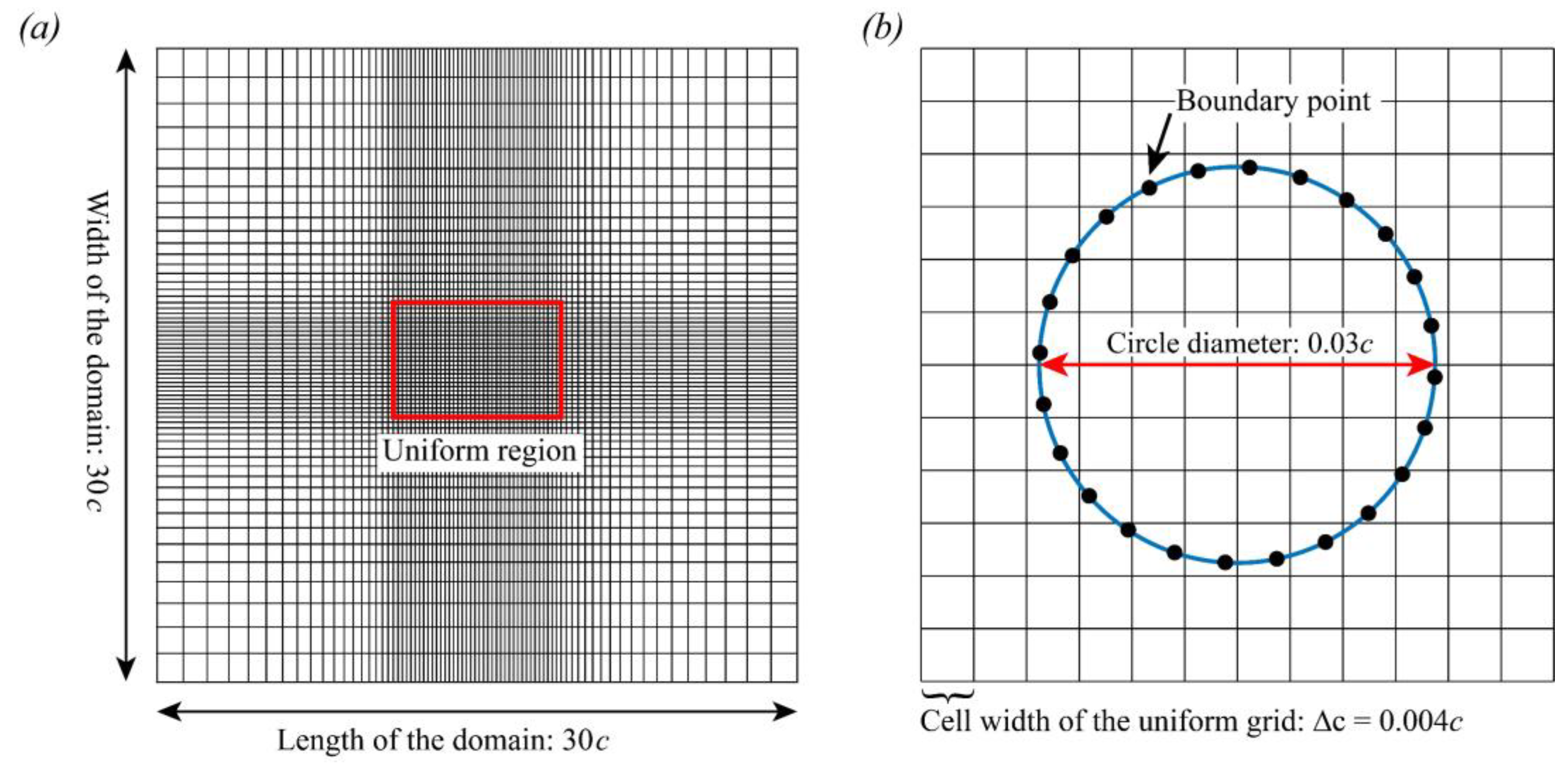
2.3.1. Immersed Boundary Method

We used the open-source immersed boundary method (IBM) code cuIBM [42] to simulate bristled wing flight in a viscous incompressible fluid. The projection-based formulation proposed by Taira and Colonius [43] was used to perform finite difference discretization of the system of equations. An explicit Adams–Bashforth time-stepping scheme was adopted for the convection terms, with a Crank–Nicolson scheme used for the diffusion terms.

A scaled Cartesian grid was used to discretize the flow field. The wings were placed in the center of a 30c × 30c flow field. The grid was uniform in a rectangular region near the wing model, with a uniform cell width of ∆c. Outside this region, the grid was exponentially stretched to the boundary of the flow field, with a stretching ratio of 1.01 (Figure 4a). The size of the uniform region varied in different cases (

Table 1. Size of the uniform region in different cases.

Cases	Size of Uniform Region
HF motion	3.5c × 2c
VF motion	2c × 4c
Clap-and-fling	6c × 2c

).

To test the convergence of the grid, we compared three different grid resolutions, in which ∆c was 0.002c, 0.004c, and 0.008c. The aerodynamic forces of a bristled wing in HF motion were solved at Re = 10.

Table 2. Grid independency test.

$\mathbf{\Delta }\mathit{c}$	0.002c	0.004c	0.008c
Grid Number	2594 × 1854	1583 × 1220	1012 × 834
${\overline{F}}_{\mathrm{V}}$(Re = 10)	0.8821	0.9072	0.9481
$\Delta {\overline{F}}_{\mathrm{V}}/{\overline{F}}_{\mathrm{V}}$ (Re = 10)	--	2.85%	4.51%

shows the average vertical forces ${\overline{F}}_{\mathrm{V}}$ under the three grid resolutions and the percent difference in the average vertical force $\Delta {\overline{F}}_{\mathrm{V}}/{\overline{F}}_{\mathrm{V}}$ between the current grid and the next denser grid. In this instance, “∆c = 0.004c” was used to calculate the subsequent simulations because the percentage difference between the “∆c = 0.004c” case and the “∆c = 0.002c” case was less than 3%. To prevent fluid leakage due to insufficient boundary points, the distance between adjacent boundary points should be close to the cell width of the near-body grid. Therefore, we set 24 boundary points on the circular bristle (Figure 4b). The time precision was set to 0.001.

The IBM code was validated [44] by simulating the flapping motion of an insect wing and comparing the result with the computational and experimental results presented by Wang et al. [45]. The results agreed reasonably well. To verify the effectiveness of our method in solving the bristled wing problem, we compared our numerical results with wind tunnel data [12]. The shape of the bristled wing was set according to the type-4 piezoelectric bristled wing [12]. To obtain the predicted drag, we assumed that the aerodynamic force of the piezoelectric wing was the same on the different cross-sections and multiplied the drag computed by the 2D model by the width of the piezoelectric wing (see Appendix A for details). The predicted drag and the experimental results show great consistency (Figure 5).

2.3.2. Aerodynamic Force, Power, and Efficiency in Flapping Flight

The lift-based and drag-based flapping flights of the bristled wing were compared in this paper. To avoid terminology confusion, we define the vertical component and horizontal component of the total aerodynamic force as the vertical force $F_{\mathrm{V}}$ and the horizontal force $F_{\mathrm{H}}$, respectively. These definitions are adhered to throughout this paper. The corresponding non-dimensionalized vertical and horizontal aerodynamic coefficients are defined as

$$C_{\mathrm{V}}=\frac{F_{\mathrm{V}}}{0.5\rho U_{\mathrm{rms}}^{2}c}$$

(5)

$$C_{\mathrm{H}}=\frac{F_{\mathrm{H}}}{0.5\rho U_{\mathrm{rms}}^{2}c}$$

(6)

where ρ is the fluid density and $U_{\mathrm{rms}}$ is the root mean square of the velocity of the wing center.

The aerodynamic power coefficient is calculated as

$$C_{\mathrm{P}}=\frac{\overrightarrow{F}·\overrightarrow{u}+\overrightarrow{M}·\overrightarrow{\omega }}{0.5\rho U_{\mathrm{rms}}^{3}c}$$

(7)

where $\overrightarrow{F}$ and $\overrightarrow{u}$ are the instantaneous total aerodynamic force and the velocity of the wing center, respectively. $\overrightarrow{M}$ and $\overrightarrow{\omega }$ are the instantaneous aerodynamic torque and the wing rotational velocity, respectively.

Each flapping simulation in this work consisted of four stroke cycles. The fourth cycle was used to analyze the aerodynamic performance and calculate the time-averaged vertical force coefficient ${\overline{C}}_{\mathrm{V}}$, horizontal force coefficient ${\overline{C}}_{\mathrm{H}}$, and aerodynamic power ${\overline{C}}_{\mathrm{P}}$. The power economy is an important measure of flapping flight performance. In this work, we defined ${\overline{C}}_{\mathrm{V}}/{\overline{C}}_{\mathrm{P}}$ as the aerodynamic efficiency metric of different flapping motions.

3. Results and Discussion

3.1. Lift-Based and Drag-Based Flapping of the Bristled Wing

HF and VF motions were set as two typical flapping motions to investigate the bristled wing performance under various Re. For all simulations in Section 3.1, $h_{\mathrm{a}}=1.25\mathrm{c}$, $f=0.1$, $\phi =\pi /2$, ${\alpha }_{\mathrm{a}}=\pi /4$, and $h_{\mathrm{x}0}=h_{\mathrm{y}0}=0$. For HF motion simulation, $\beta =0$ and ${\alpha }_0=\pi /2$. For VF motion simulation, $\beta =\pi /2$ and ${\alpha }_0=3\pi /4$.

3.1.1. The Instantaneous Force Production of the Bristled Wing in HF and VF Motion

The dimensionless time evolution curves of $C_{\mathrm{V}}$ and $C_{\mathrm{H}}$ for these two flapping motions (Re = 1, 5, 10, and 80) are shown in Figure 6. For both the HF and VF motions, the magnitudes of the $C_{\mathrm{V}}$ and $C_{\mathrm{H}}$ variation increase with Re reduction.

For HF motion (Figure 6a), $C_{\mathrm{V}}$ is positive for most of the stroke and peaks during the mid-left stroke and mid-right stroke. For Re = 1, 5, and 10, $C_{\mathrm{V}}$ drops to a small negative value between the two half-strokes because the deceleration of the wing causes it to be pushed by the flow on its upper side. For Re = 80, the crests and troughs of the $C_{\mathrm{V}}$ and $C_{\mathrm{H}}$ curves are much weaker than those of the strokes for Re = 1, 5, and 10, whereas their respective evolution laws are identical. At the same Re, the magnitude of the C_H curve is larger than that of the $C_{\mathrm{V}}$ curve.

For the VF motion (Figure 6b), the peak of C_V appears during the mid-down stroke as the wing’s translational velocity and windward area both reach their maximum values. For Re = 80, $C_{\mathrm{V}}$ is near the zero line during the mid-up stroke because the Re is higher and the wing chord is approximately parallel to its translation direction, which leads to a small windward area. For Re < 10, $C_{\mathrm{V}}$ shows obvious fluctuation during the up stroke and reaches the minimum near the point of the maximum upward velocity because the viscous effect becomes more dominant at Re < 10. Compared with $C_{\mathrm{V}}$, the $C_{\mathrm{H}}$ of VF motion is lower in magnitude and more changeable. Such variation in $C_{\mathrm{H}}$ is mainly associated with the change in the wing’s translational velocity and AOA.

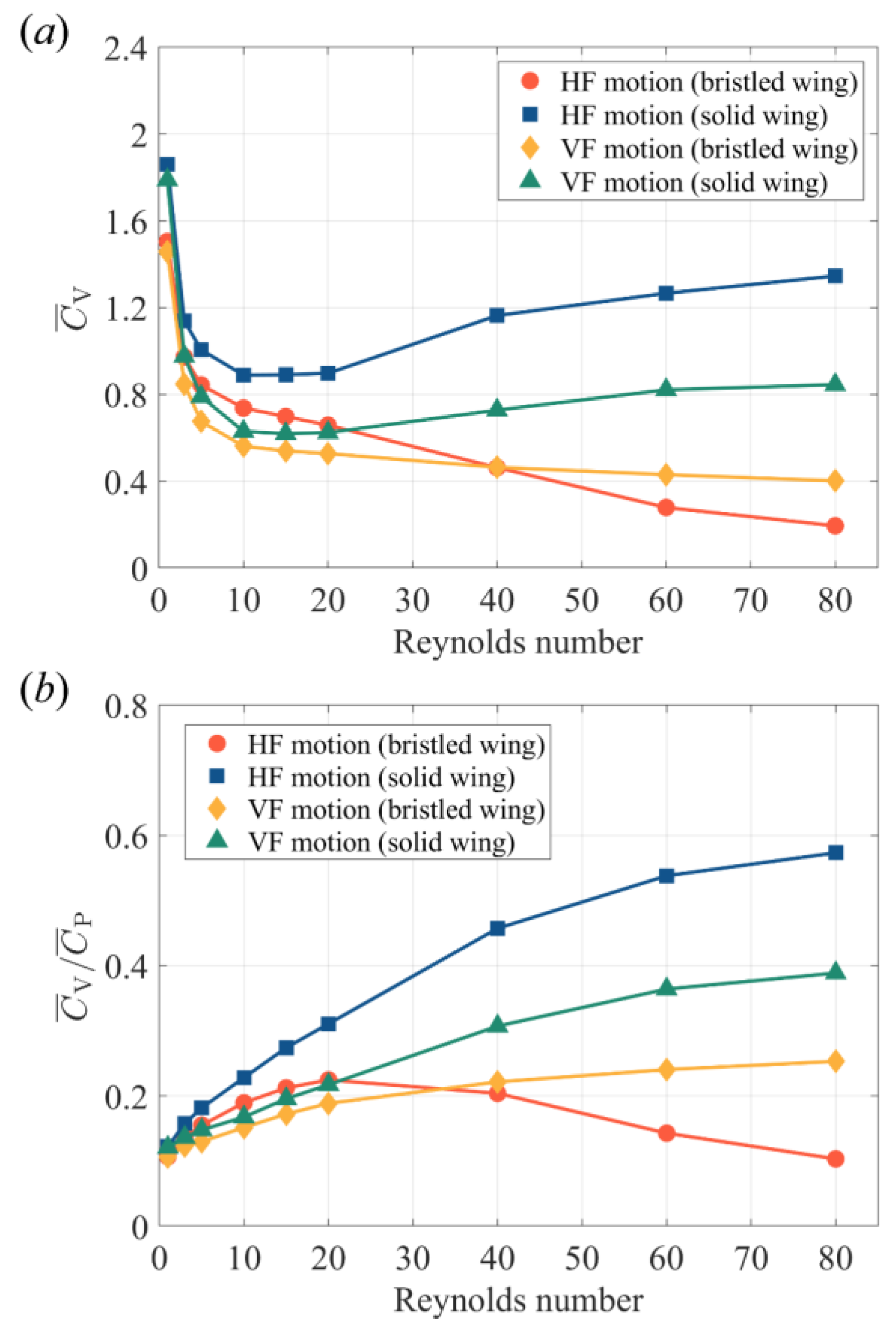
3.1.2. Air Leakage and the Effect of Re

By comparing the flow field vorticity plots of bristled wings at Re = 5 and Re = 80 (Figure 7), we can gain a deeper understanding of the aerodynamic differences at various Re. For all the flapping motions and Re investigated, a pair of counter-rotating vortices were attached to each bristle of the wing. Similar alternately arranged vortex structures also appeared in previous experiments of a translating bristled wing [20]. Part of the oncoming air flowed through the adjacent bristles. Such “air leakage” reduces the aerodynamic pressure on the windward side of the bristled wing, resulting in a wing force lower than that of the solid wing. Additionally, a higher Re leads to more obvious air leakage, and thus, greater loss of aerodynamic force. Aside from the air leakage phenomenon, for both HF and VF motion, no distinct leading edge vortex (LEV) or trailing edge vortex (TEV) was generated at Re = 80 (Figure 7c,d), whereas at Re = 5 (Figure 7a,b), an LEV and a TEV were attached to the bristled wing in the whole translation process and created a lower-pressure region above the wing. In addition, as the Re decreases, the viscous force gradually dominates. When the Reynolds number is sufficiently small, the aerodynamic force asymptotically becomes linearly proportional to the Re. For all these reasons, the instantaneous aerodynamic coefficient of the bristled wing was much higher at Re < 10 than at a relatively high Re (Re = 80).

3.1.3. Comparison between Bristled Wing and Solid Wing in HF and VF Motion

In order to analyze the aerodynamic difference of the bristled wing and the solid wing, we compared the ${\overline{C}}_{\mathrm{V}}$ (Figure 8a) and ${\overline{C}}_{\mathrm{V}}/{\overline{C}}_{\mathrm{P}}$ (Figure 8b) of these two types of wing at Re from 1 to 80. Both HF and VF motions were evaluated.

For the bristled wing in both VF and HF motion, ${\overline{C}}_{\mathrm{V}}$ increased monotonically as Re decreased from 80 to 1. A dramatic increase in ${\overline{C}}_{\mathrm{V}}$ appeared at Re < 10. The VF motion generated a greater ${\overline{C}}_{\mathrm{V}}$ than the HF motion for the bristled wing at Re = 80. However, when Re dropped to below 40, the ${\overline{C}}_{\mathrm{V}}$ generated by HF motion overtook that by VF motion. At Re = 10, the ${\overline{C}}_{\mathrm{V}}$ generated by HF motion is 1.312 times that by VF motion. For the solid wing from Re = 80 to Re = 1, the ${\overline{C}}_{\mathrm{V}}$ values generated by the VF and HF motions both experienced a process of slight decline followed by a dramatic increase. For all Re investigated, the solid wing generated a marginally higher ${\overline{C}}_{\mathrm{V}}$ than the bristled wing under the same flapping mode. At Re < 10, the gaps among the four curves in Figure 8a significantly narrowed. At Re = 5, the bristled wing in HF motion produced 83.9% of the ${\overline{C}}_{\mathrm{V}}$ produced by the solid wing in the same flapping mode, while the cross-sectional area of the bristled wing model is only 23.7% of that of the solid wing model.

For the bristled wing in VF motion, and for the solid wing in VF and HF motion, ${\overline{C}}_{\mathrm{V}}/{\overline{C}}_{\mathrm{P}}$ continually decreased as Re dropped from 80 to 1. In contrast, the ${\overline{C}}_{\mathrm{V}}/{\overline{C}}_{\mathrm{P}}$ for the bristled wing in HF motion first rose and then declined. The peak was located at approximately Re = 20. In the same flapping mode, ${\overline{C}}_{\mathrm{V}}/{\overline{C}}_{\mathrm{P}}$ was consistently higher for the solid wing than for the bristled wing; however, as Re decreased, the four curves in Figure 8b tended to converge at one point.

3.2. Wing–Wing Interactions of the Bristled Wing

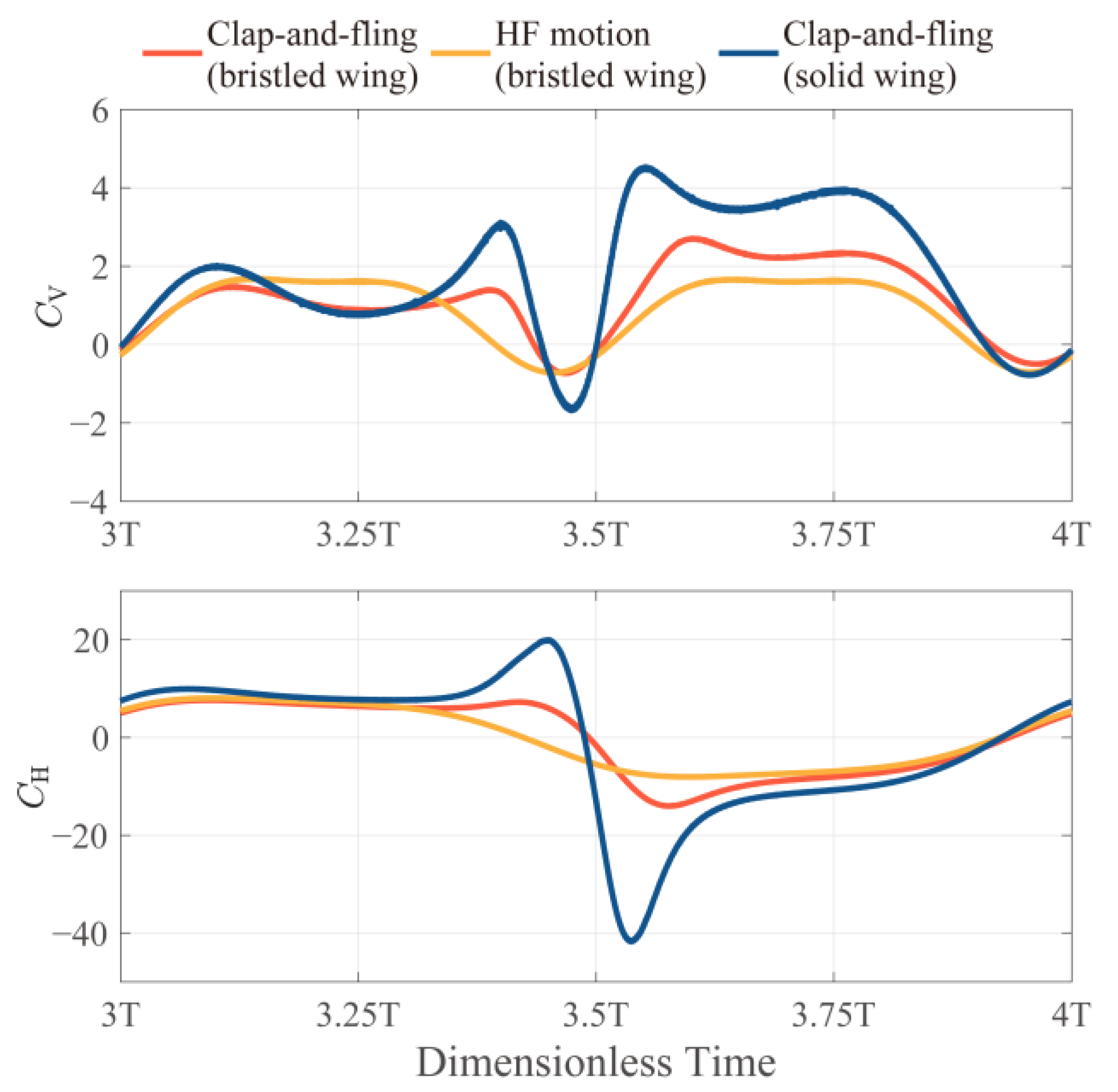
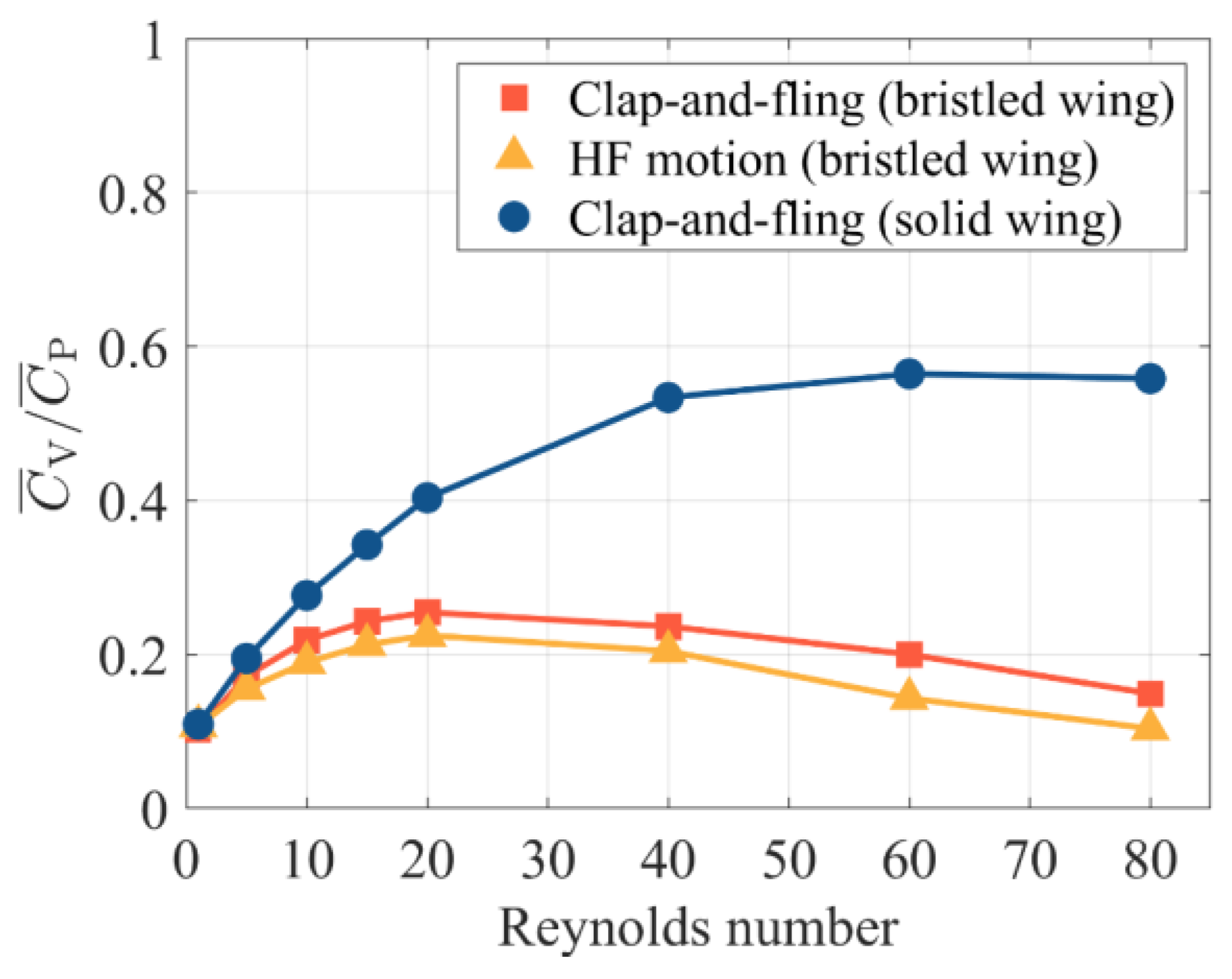
3.2.1. ${\overline{C}}_{\mathrm{V}}$ Augmentation of the Bristled Wing in Clap-And-Fling

To investigate the ${\overline{C}}_{\mathrm{V}}$ augmentation of bristled wings with a clap-and-fling mechanism, we simulated the clap-and-fling process for bristled wings and solid wings. As an idealization of clap-and-fling, two wings perform a mirror-like HF motion. The left and right wings are parallel at the end of the clap. We defined this parallel distance as the inter-wing gap δ. In Section 3.2.1, the inter-wing gap δ was set to 0.2c. For the left wing in clap-and-fling, $h_{\mathrm{a}}=1.25\mathrm{c}$, $f=0.1$, $\phi =-\pi /2$, ${\alpha }_{\mathrm{a}}=-\pi /4$, $\beta =0$, ${\alpha }_0=\pi /2$, $h_{\mathrm{x}0}=-1.35\mathrm{c}$, and $h_{\mathrm{y}0}=0$. The aerodynamic force and efficiency of the left wing in clap-and-fling were obtained.

We defined $\mathsf{\xi }$ (the ${\overline{C}}_{\mathrm{V}}$ in clap-and-fling minus the ${\overline{C}}_{\mathrm{V}}$ in HF motion) as the ${\overline{C}}_{\mathrm{V}}$ augmentation metric of the clap-and-fling motion. For all values of Re investigated, the $\mathsf{\xi }$ of bristled wings was greater than 0.1, and rose steadily as Re decreased from 40 to 1 (Figure 9), suggesting that the clap-and-fling mechanism can enhance the ${\overline{C}}_{\mathrm{V}}$ of bristled wings. However, due to “air leakage”, $\mathsf{\xi }$ was much lower for bristled wings than for solid wings. The wing surface of solid wings is continuous, forcing the air to flow out from below when “clapping” together and flow in from above when “flinging” apart. In contrast, the surface of the bristled wings is non-continuous. Part of the air will leak through the bristle clearances during clap-and-fling, leading to pressure loss and weaker ${\overline{C}}_{\mathrm{V}}$ enhancement.

To provide greater detail about bristled wings in clap-and-fling, we compared the instantaneous $C_{\mathrm{V}}$ and $C_{\mathrm{H}}$ traces of bristled wings and solid wings in clap-and-fling as well as those of a single bristled wing in HF motion at Re = 5 (Figure 10). In contrast to the bristled wing in HF motion, the $C_{\mathrm{V}}$ and $C_{\mathrm{H}}$ of the bristled wings in the clap-and-fling process peaked twice, which occurred within the time interval of t = 3.25 T–3.75 T. The first $C_{\mathrm{V}}$ and $C_{\mathrm{H}}$ peaks corresponded to the clapping motion, and the second $C_{\mathrm{V}}$ and $C_{\mathrm{H}}$ peaks corresponded to the flinging motion. The $C_{\mathrm{V}}$ and $C_{\mathrm{H}}$ peaks of the solid wings were both higher than those of the bristled wings in clap-and-fling. Considering the higher magnitude of the $C_{\mathrm{H}}$ peaks than the $C_{\mathrm{V}}$ peaks and the high flexibility of micro-insects’ flapping wings, the excessive $C_{\mathrm{H}}$ not only increases the energy consumption of the flapping motion but also causes over-deformation of the wing surface. In contrast, the bristled wings with relatively low $C_{\mathrm{H}}$ peaks have the potential to alleviate the above two issues.

A comparison of ${\overline{C}}_{\mathrm{V}}/{\overline{C}}_{\mathrm{P}}$ between bristled wings and solid wings in clap-and-fling as well as a bristled wing in HF motion is shown in Figure 11. As Re dropped from 80 to 1, for the bristled wings in both clap-and-fling and HF motion, ${\overline{C}}_{\mathrm{V}}/{\overline{C}}_{\mathrm{P}}$ first rose and then descended, and the peak was located at approximately Re = 20. In comparison, the ${\overline{C}}_{\mathrm{V}}/{\overline{C}}_{\mathrm{P}}$ of the solid wings in clap-and-fling continually decreased and was greater than that of the bristled wings in HF motion and in clap-and-fling at 5 ≤ Re ≤ 80. Notably, although clap-and-fling induces substantial instantaneous $C_{\mathrm{H}}$, the aerodynamic efficiency of bristled wings in clap-and-fling is higher than that of a single bristled wing in HF motion. At Re = 10, clap-and-fling brings about a 15.5% efficiency augmentation for bristled wings.

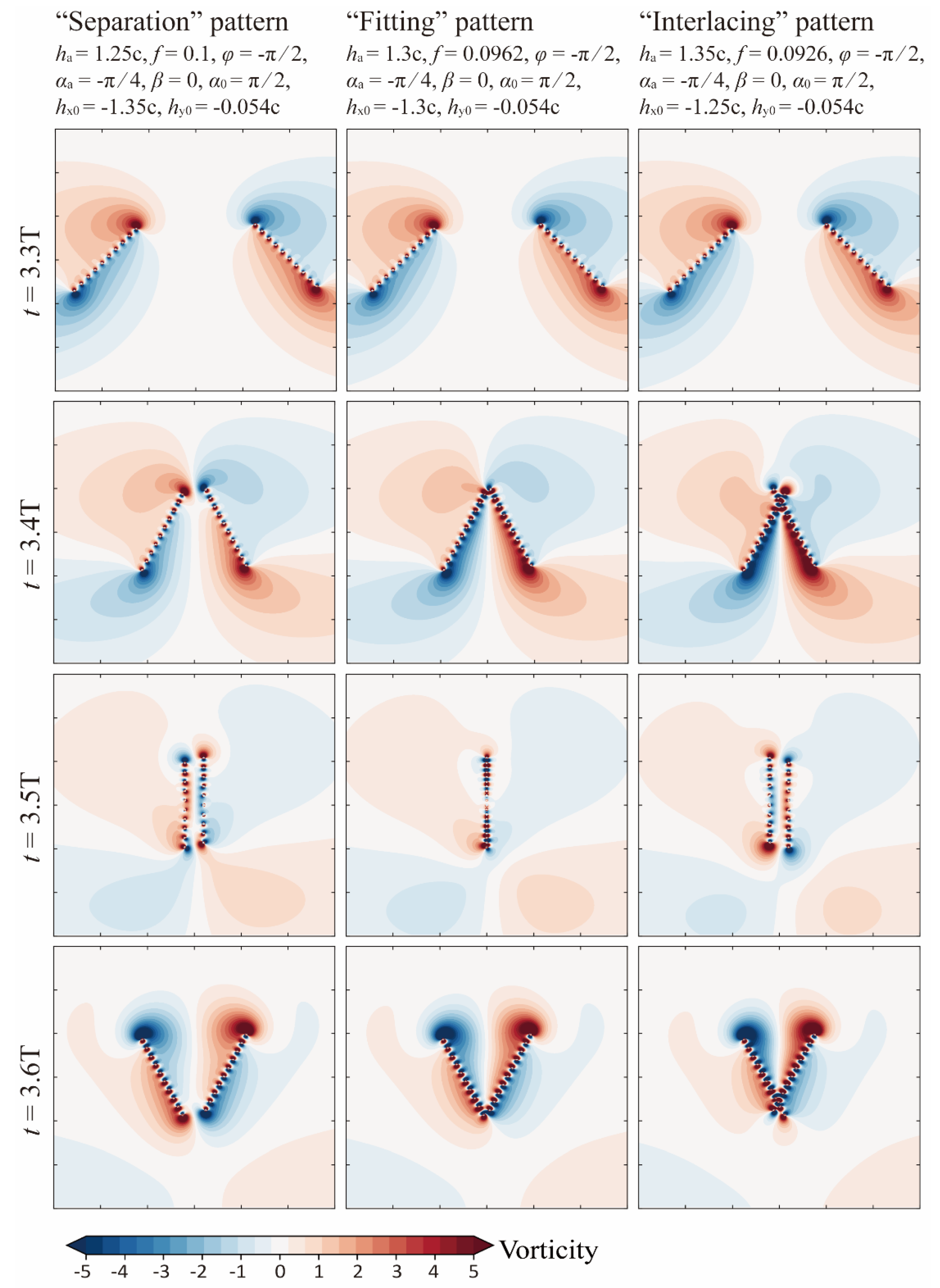
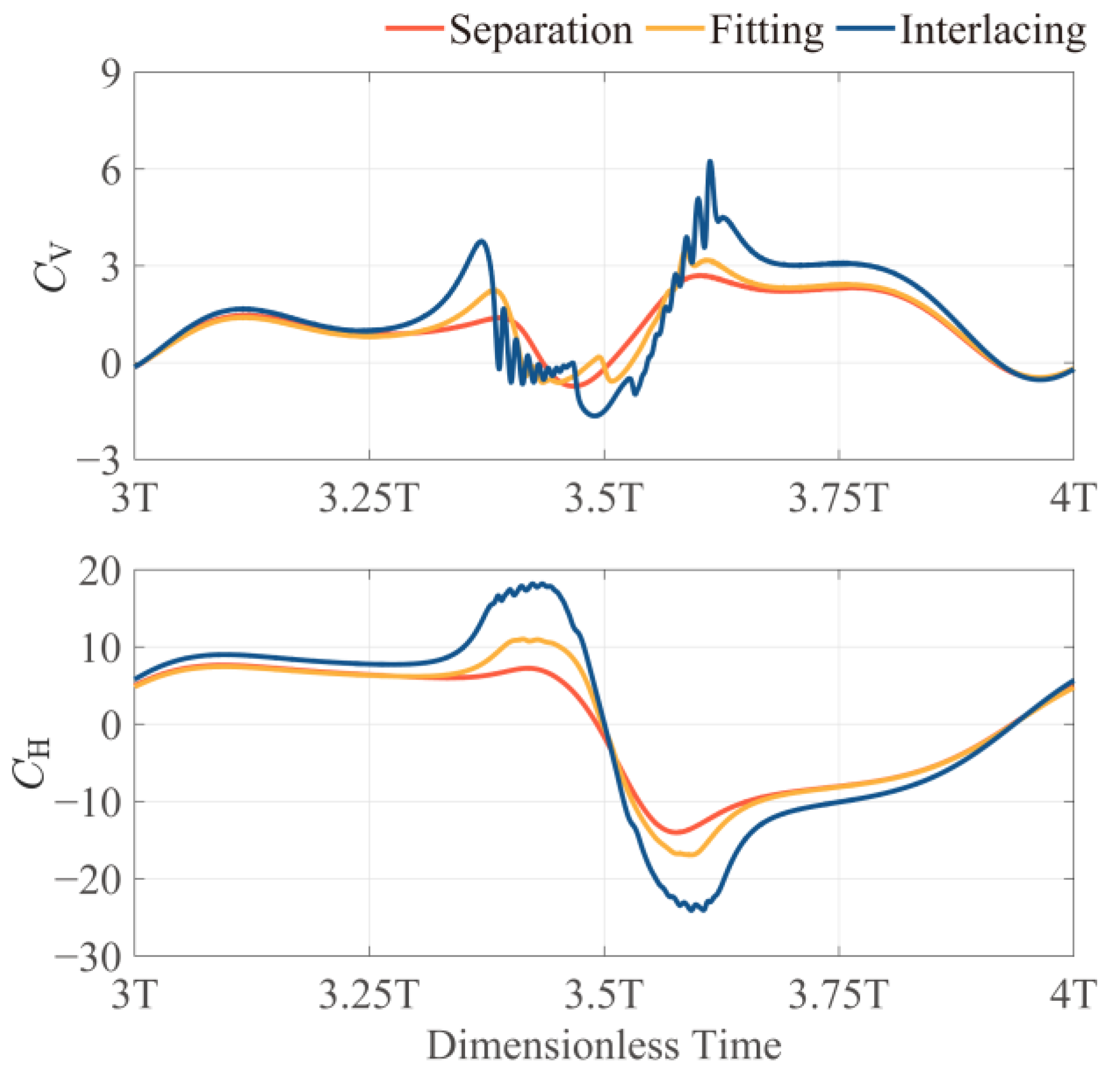
3.2.2. Effect of Bristle Crossing and Inter-Wing Gap Reduction

According to previous studies of solid wings in clap-and-fling [46], narrowing the inter-wing gap can help enhance the lift. Since the solid wing’s surface is continuous, the limit of the inter-wing gap is 0 (when two wings fit together). For the minute insects’ bristled wing, the interval distance between adjacent bristles is 4 to 10 times their diameter [15]. The bristles on the left and right wings may cross each other in the clap-and-fling process, which means that the inter-wing gap can be negative. This section studies the effect of bristle crossing and inter-wing gap δ on the bristled wing aerodynamics in clap-and-fling. Three clap-and-fling patterns (1 ≤ Re ≤ 80) with δ = +0.2c, 0.0c and −0.2c were set (Figure 12). These three patterns are referred to as the “separation”, “fitting”, and “interlacing” clap-and-fling patterns, respectively, hereinafter. To avoid bristles on the left and right wings colliding with each other and causing calculation errors in the “fitting” pattern, the left wing was shifted down by 0.054c. The same dislocation treatment was also performed for the other two patterns to ensure consistency.

Figure 13 illustrates the $C_{\mathrm{V}}$ and $C_{\mathrm{H}}$ changes of bristled wings in these three patterns at Re = 5. Compared with the “separation” pattern, the $C_{\mathrm{V}}$ and $C_{\mathrm{H}}$ curves of the “fitting” and “interlacing” patterns oscillate at high frequency as the two wings become close and separate. This effect occurs because the vortices attached to the bristles collide and integrate when the left and right wings cross each other. Additionally, the $C_{\mathrm{H}}$ peak of the bristled wing not only increases as δ decreases from +0.2c to 0.0c, but also continues to increase as δ decreases from 0.0c to −0.2c.

Although the instantaneous aerodynamic coefficients are significantly different, the ${\overline{C}}_{\mathrm{V}}$ values of bristled wings in these three patterns are close to each other. The variation in the bristled wing aerodynamic efficiency with Re for these three patterns is shown in Figure 14. At 1 ≤ Re ≤ 40, The aerodynamic efficiencies of the “separation” and “fitting” patterns are relatively close.

Table 3. The comparison of the aerodynamic efficiency of the “interlacing” pattern with that of the “separation” and “fitting” patterns.

Re		1	10	20	40	60
${\overline{C}}_{\mathrm{V}}/{\overline{C}}_{\mathrm{P}}$ of three patterns	“Interlacing”	0.0871	0.2007	0.2465	0.2335	0.1946
	“Separation”	0.1021	0.2185	0.2545	0.2364	0.2000
	“Fitting”	0.0954	0.2147	0.2584	0.2401	0.2064
Ratio of “interlacing” pattern’s ${\overline{C}}_{\mathrm{V}}/{\overline{C}}_{\mathrm{P}}$ to that of other two patterns	Ratio to “separation”	85.3%	91.9%	96.8%	98.8%	97.3%
	Ratio to “fitting”	91.3%	93.4%	95.3%	97.2%	94.2%

presents the comparison of the aerodynamic efficiency of the “interlacing” pattern with that of the other two patterns. When Re ≤ 60, the aerodynamic efficiency of the “interlacing” pattern is always the lowest, and the aerodynamic efficiency of the “interlacing” pattern is only 85.3% of that of the “separation” pattern at Re = 1. This is because δ decreases to −0.2c, $C_{\mathrm{H}}$ increases more sharply than $C_{\mathrm{V}}$, meaning that a higher aerodynamic power is needed to overcome the excess $C_{\mathrm{H}}$ generated by wing crossing.

4. Conclusions

In this paper, we studied the flapping flight of minute bristled-wing insects. Wing morphological data on 38 specimens of Mymaridae were measured and analyzed. Bristled wing flight was numerically simulated using the IBM. In assessing the merits of different flapping modes, the average vertical force coefficient ${\overline{C}}_{\mathrm{V}}$ and aerodynamic efficiency ${\overline{C}}_{\mathrm{V}}/{\overline{C}}_{\mathrm{P}}$ are two major indicators. The results of this study show the following:

• A bristled wing has higher ${\overline{C}}_{\mathrm{V}}$ and ${\overline{C}}_{\mathrm{V}}/{\overline{C}}_{\mathrm{P}}$ when using a lift-based mechanism than when using a drag-based mechanism at 5 < Re < 40. This Re range covers the most probable flight Re of minute bristled-wing insects. If Re < 5, for both mechanisms, ${\overline{C}}_{\mathrm{V}}$ rapidly increases and ${\overline{C}}_{\mathrm{V}}/{\overline{C}}_{\mathrm{P}}$ drops, and tends to converge at one point. When 1 < Re < 80, regardless of the mechanism used, the ${\overline{C}}_{\mathrm{V}}$ and ${\overline{C}}_{\mathrm{V}}/{\overline{C}}_{\mathrm{P}}$ of a bristled wing are lower than those of a solid wing with the same mechanism. Nevertheless, as Re declines, the aerodynamic differences between the bristled wing and solid wing decrease. At Re < 10, a bristled wing can produce more than 80% of the ${\overline{C}}_{\mathrm{V}}$ produced by a solid wing in the same flapping mode, while the cross-sectional area of the bristled wing model is only 23.7% of that of the solid wing model.
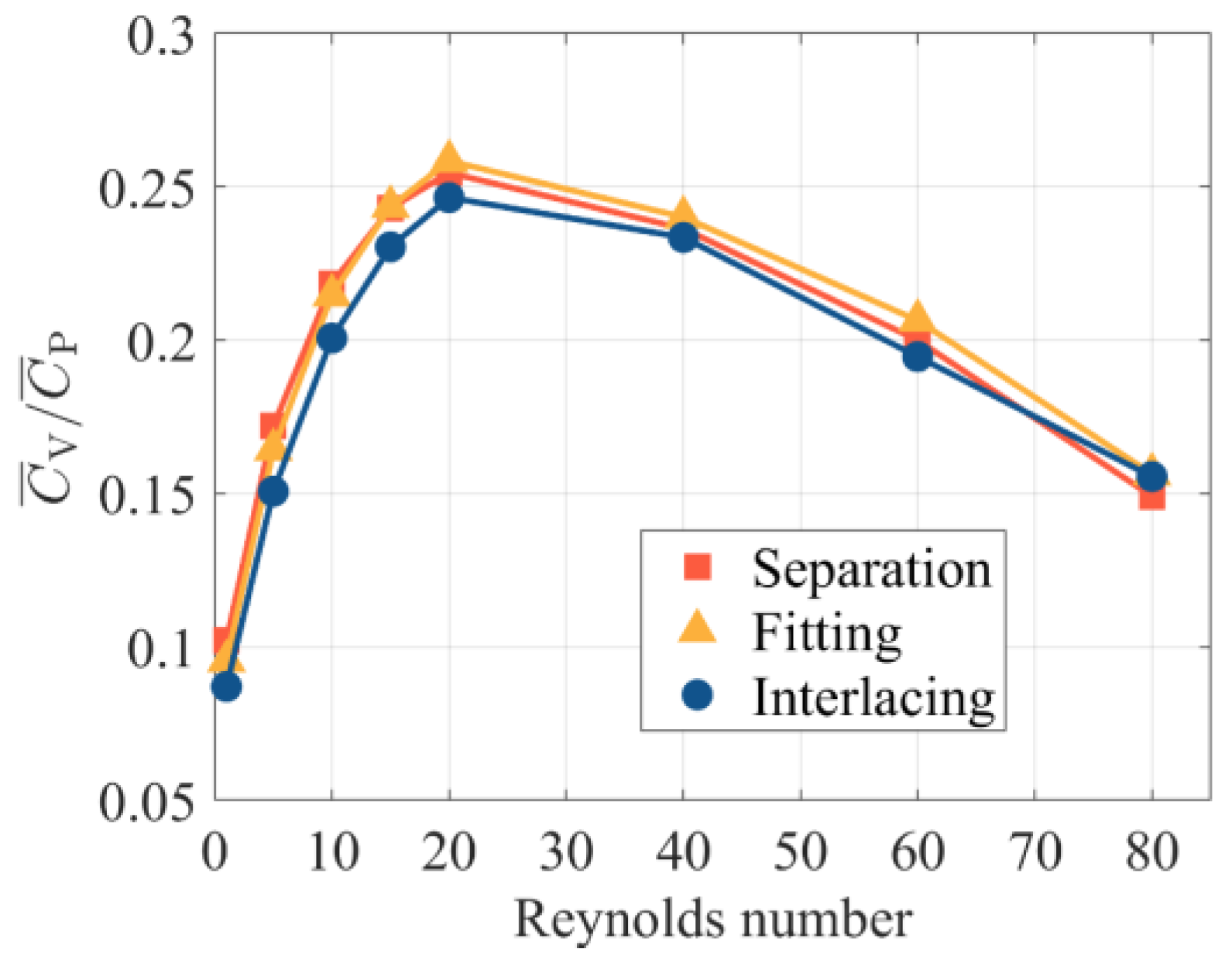
• When Re < 40, bristled wings in clap-and-fling motion can achieve ${\overline{C}}_{\mathrm{V}}$ augmentation of more than 30%. Particularly, when Re = 5, which approaches the flight Re of minute bristled-wing insects, the ${\overline{C}}_{\mathrm{V}}$ augmentation can be up to 50%. In contrast, when 5 < Re < 20, the ${\overline{C}}_{\mathrm{V}}$ augmentation of solid wings in clap-and-fling is close to 70%, but at the expense of a higher $C_{\mathrm{H}}$. Due to the unique morphology of bristled wings, they may cross each other when they “clap” together. We envisaged three clap-and-fling patterns with different inter-wing gaps, namely, “separation”, “fitting”, and “interlacing” clap-and-fling. The simulation results indicate that the ${\overline{C}}_V$ values of these three patterns are very close. At Re < 60, “interlacing” clap-and-fling produces substantial $C_{\mathrm{H}}$, resulting in a lower aerodynamic efficiency than the other two patterns.

This study compares the aerodynamic force and efficiency of the bristled wing and the solid wing in different flapping motions in detail. We performed a total of 68 simulation runs. Note that the wing model used for the simulations is rigid. It would be a logical future direction to investigate the effect of bristled wing flexibility on the aerodynamic characteristics under different flapping motions, which will facilitate a deeper understanding of the aerodynamic mechanisms behind the real flapping motion adopted by bristled-wing insects.