Advanced Control of an Electric Fuel-Oil Pump for Small Turbojet Engines
Abstract
:1. Introduction
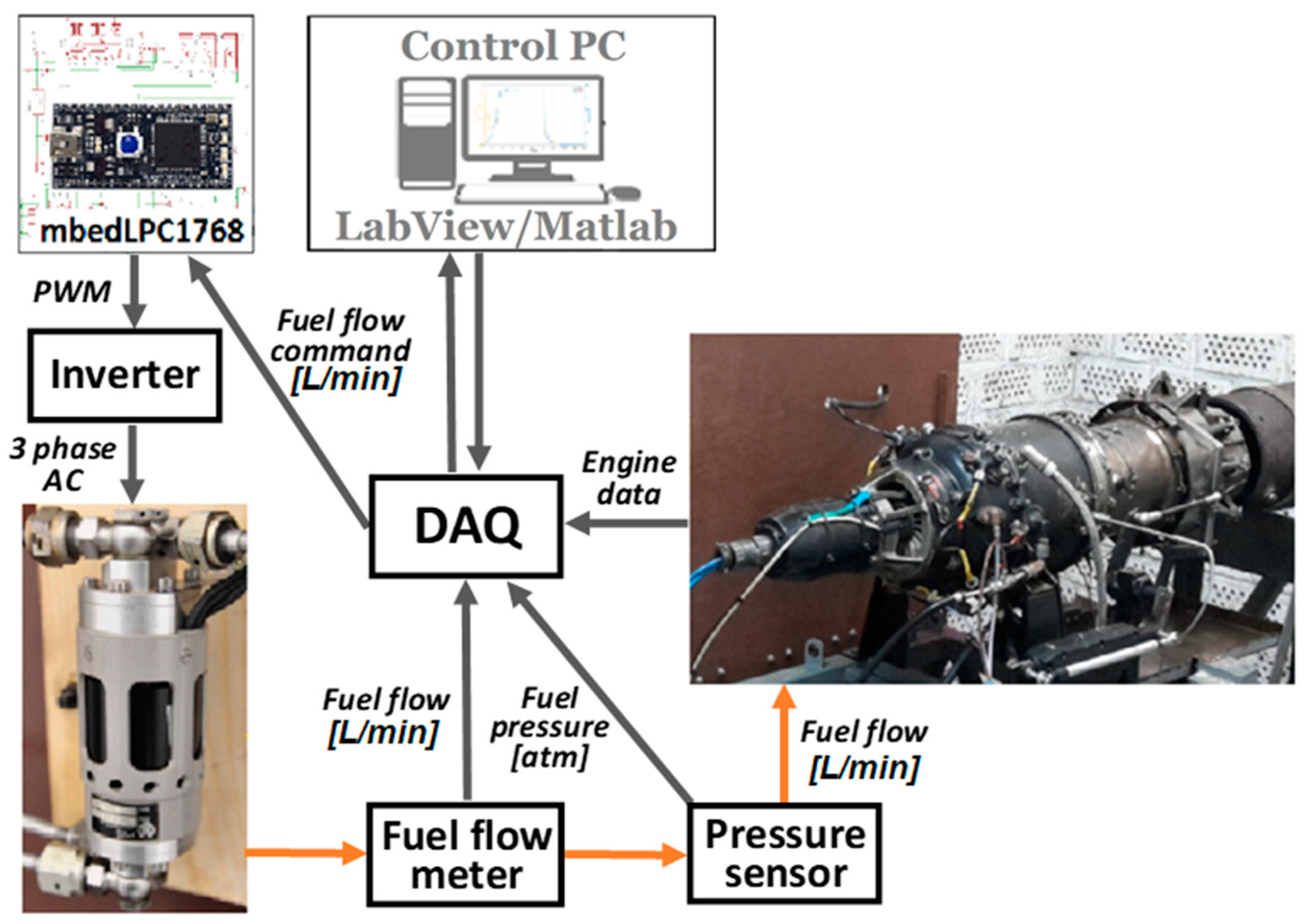
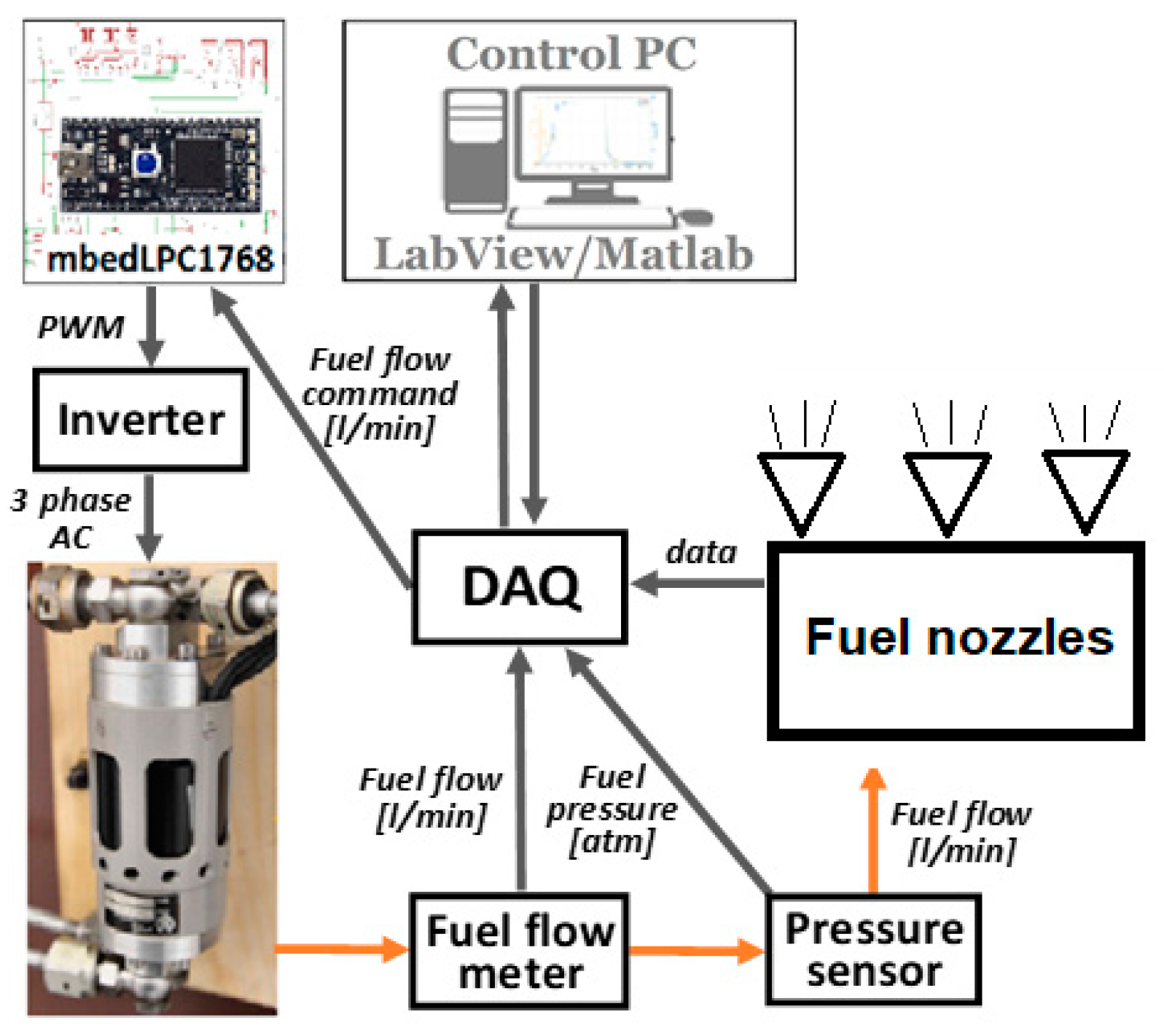
2. Hardware Used in the Study
- NI 9263—100 kHz Voltage Output Module, used for the control of analog engine systems;
- NI 9472—8-Channel, Digital I/O Module, used for the control of digital engine systems;
- NI 9205—±10 V, 250 kHz, 16-Bit, 32-Channel C Series Voltage Input Module, used for the measurement of analog sensors which, in this case, was QBE2002-P10;
- NI 9423—8 Channel Sinking Input, C Series Digital Module, used for the measurement of frequency signals which, in this case, was optical speed sensors;
- NI 9213—16-channel, Thermocouple Input Module, used for the measurement of thermocouples which, in this case, was K-thermocouple EGT sensors.
- Fuel-oil pump—a sensor-less BLDC motor, the rotor of which drives the fuel pump on one end and the oil pump on the other.
- Flow meter—Badger Meter, model MN2 SSPI-1, is an oval gear flow meter which measures the volumetric flow rate of fuel passing through the meter by repeatedly entrapping it with rotating parts. Its flow range is from 15 to 500 l/h, with a maximal temperature of 120 °C, accuracy of ±1% and maximal pressure of 5.5 MPa.
- Fuel pressure sensor—Siemens, model QBE 2002-P10 is suitable for the measurement of static and dynamic positive pressure. Its pressure range is from 0 to 1 MPa, temperature range from −40 to 80 °C and response time <5 ms.
- Inverter—three-phase inverter FOXY, model G2 R-60SB. Pulses are generated 50 times in a second and their width, which is directly proportional to the motor speed, can be in range of 1 ms to 2 ms.
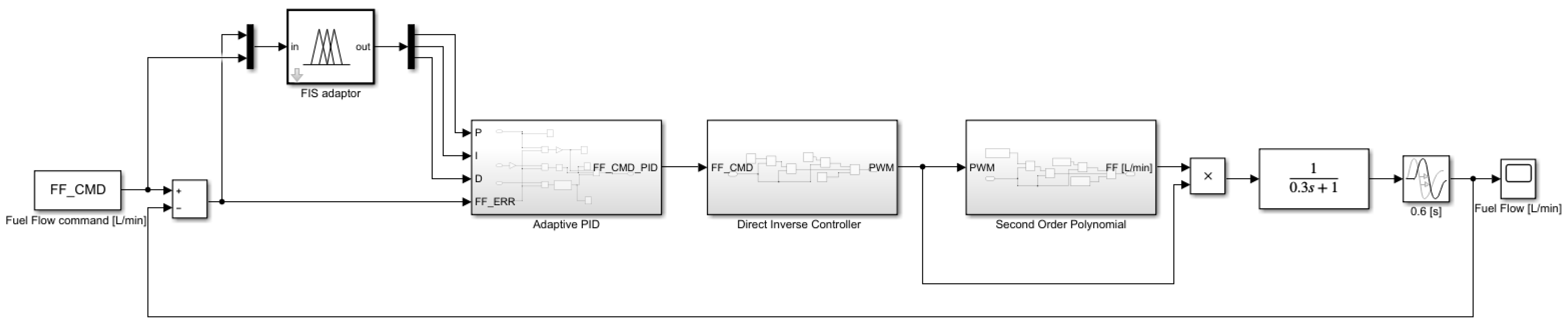
3. Design of the Fuel-Flow Control Algorithms
- Direct inverse controller—the computationally simplest control algorithm,
- PID—the traditional proportionate–integral–derivative controller,
- Fuzzy PID controller—PID controller, the coefficients of which are adapted by a fuzzy inference system.
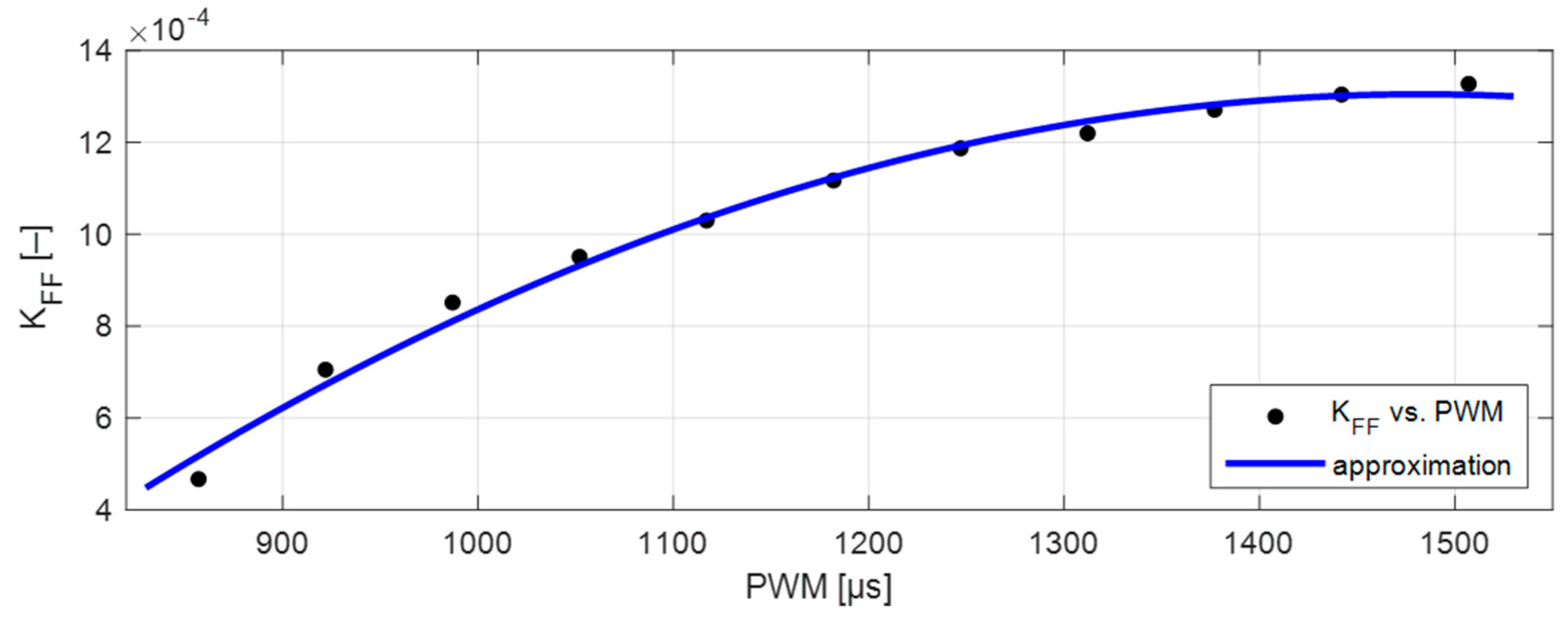
3.1. Dynamic Model of the Fuel System
- s—Laplace operator variable
- FF—Fuel flow [L/min]
- PWM—Pulse width modulation [μs]
- T—Time constant [s]
- KFF—Gain of the transfer function
- Td—Time delay constant [s].
3.2. Direct Inverse Control Design
3.3. PID Controller Design
3.4. Fuzzy Adaptive PID Controller Design
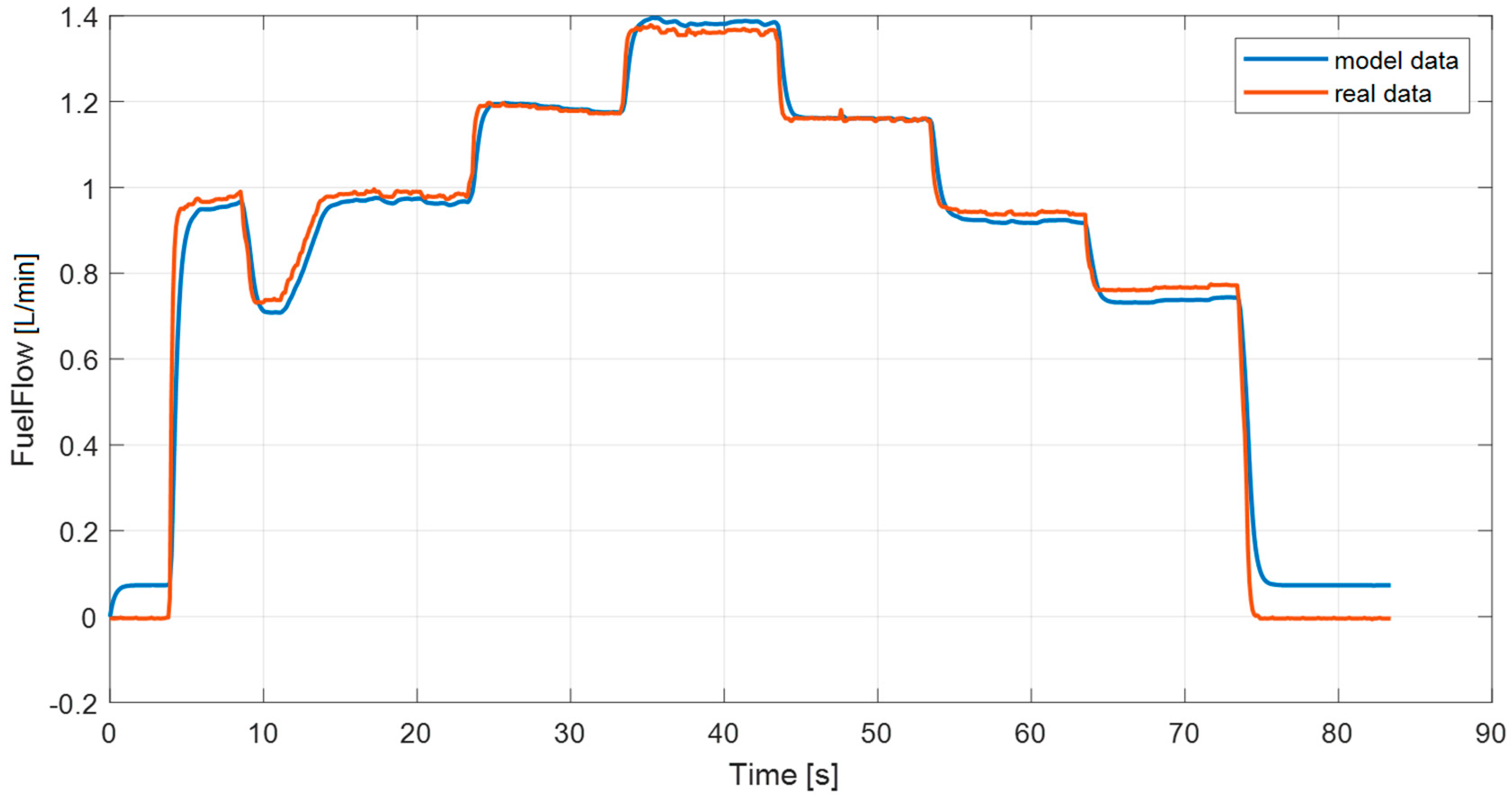
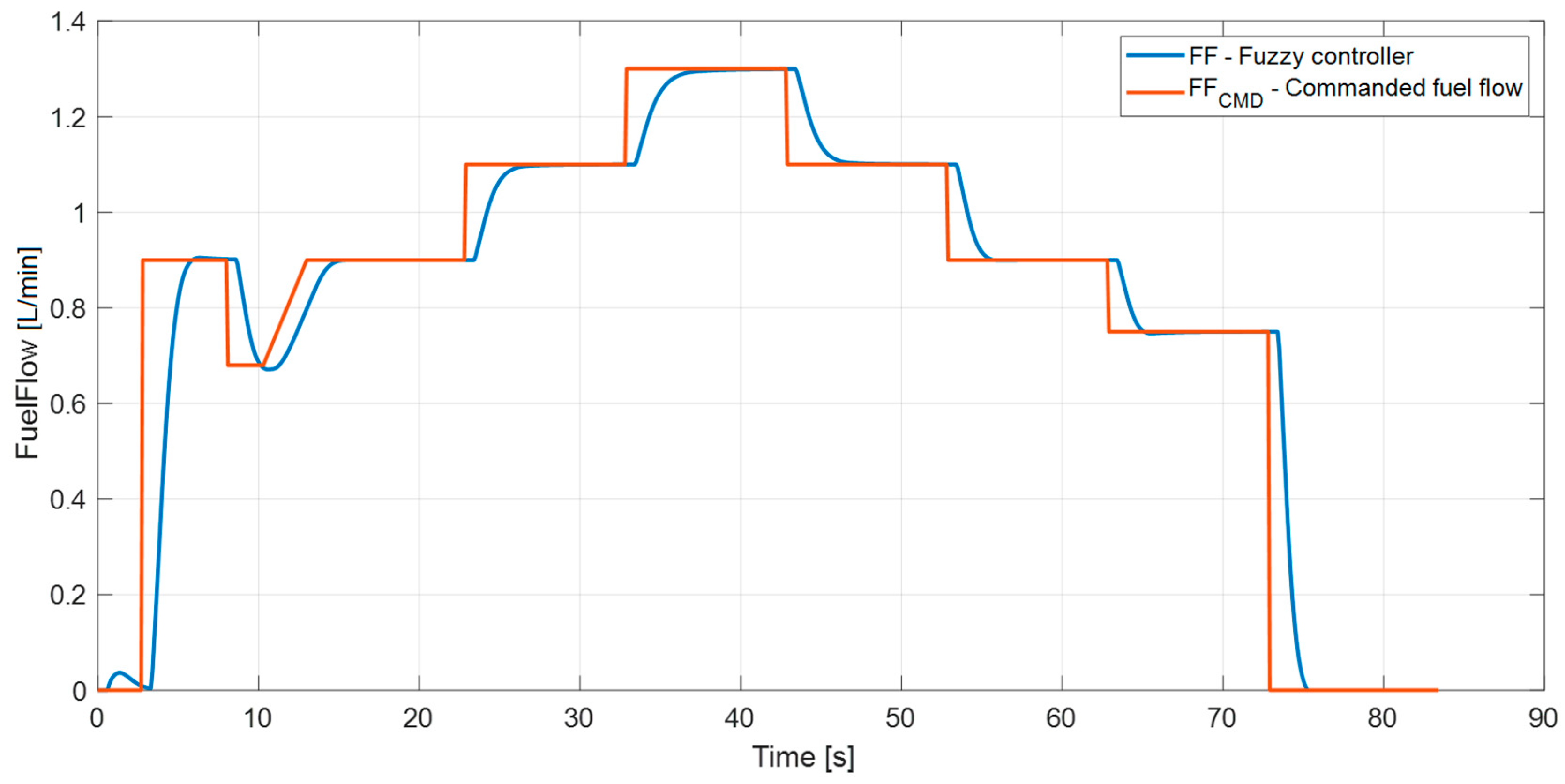
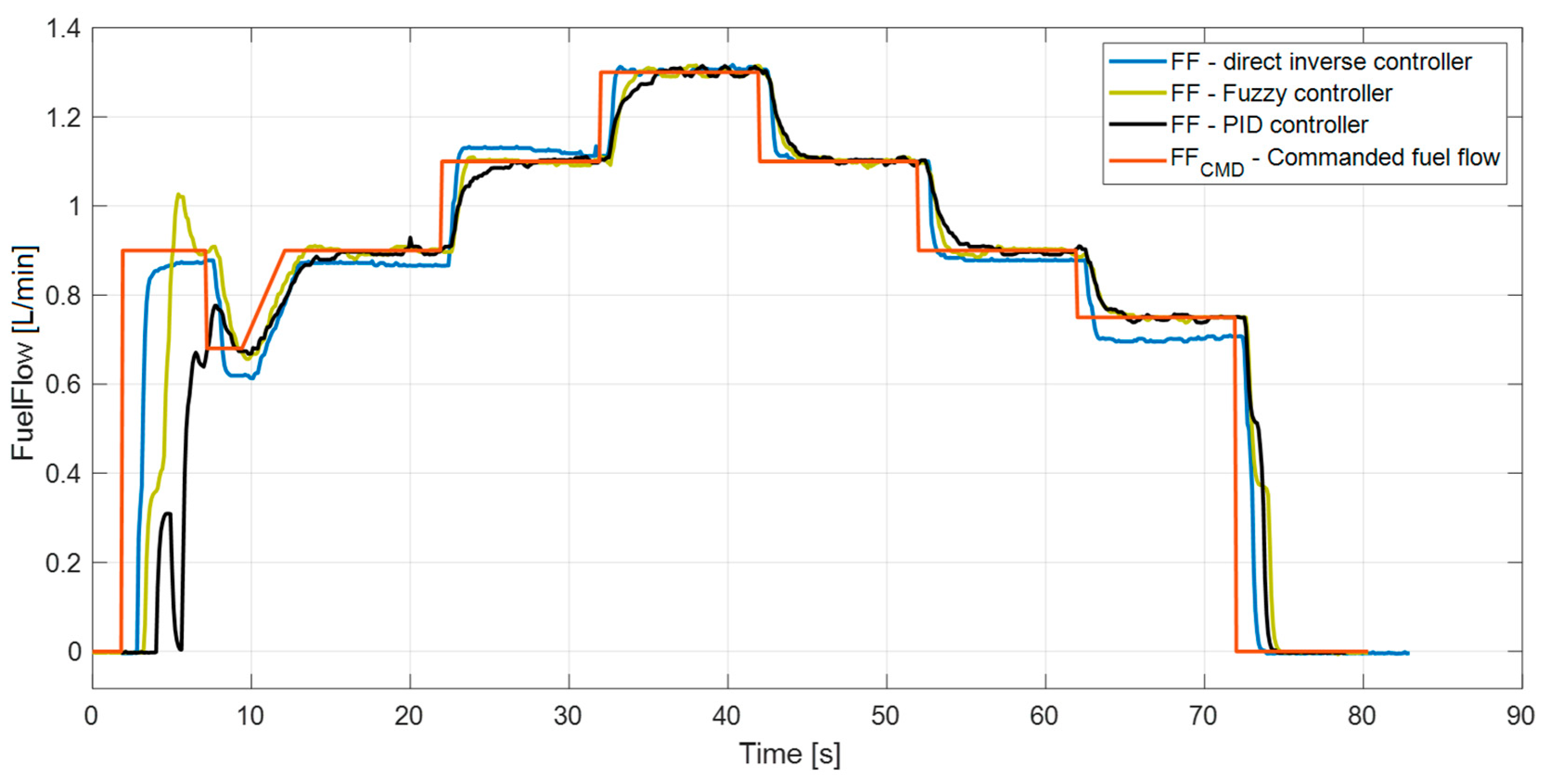
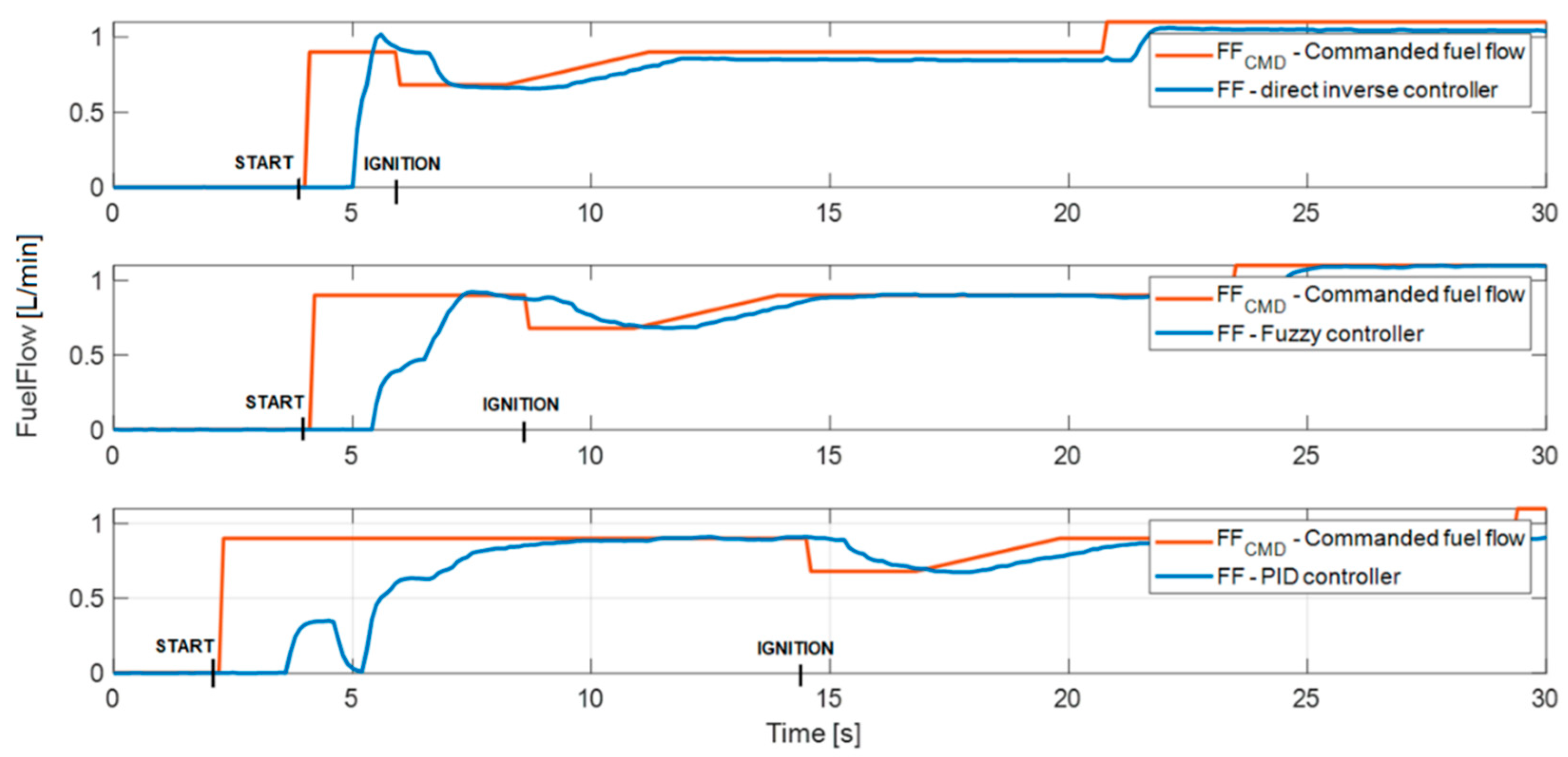
4. Experimental Testing
- t0—time of the fuel-low command start (ignition)
- tf—time of the fuel-flow command end (shutdown).
4.1. Tests on the Test Bench with Fuel Nozzles Only
4.2. Tests with a Working Engine iSTC-21v
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rezaei, A.; Dadouche, A. Development of a turbojet engine gearbox test rig for prognostics and health management. Mech. Syst. Signal Process. 2012, 33, 299–311. [Google Scholar] [CrossRef]
- Scholz, D.; Seresinhe, R.; Staack, I.; Lawson, C. Fuel consumption due to shaft power off-takes from the engine. In Proceedings of the 4th International Workshop on Aircraft System Technologies, Hamburg, Germany, 23–24 April 2013; Shaker Verlag: GmbH, Germany, 2013. [Google Scholar] [CrossRef]
- Cao, W.; Mecrow, B.C.; Atkinson, G.J.; Bennett, J.W.; Atkinson, D.J. Overview of electric motor technologies used for more electric aircraft (MEA). IEEE Trans. Ind. Electron. 2011, 59, 3523–3531. [Google Scholar] [CrossRef]
- Newman, R. The more electric engine concept. SAE Trans. J. Aerosp. 2004, 113, 1656–1661. [Google Scholar] [CrossRef]
- Beneda, K. Development of a modular FADEC for small scale turbojet engine. In Proceedings of the 2016 IEEE 14th International Symposium on Applied Machine Intelligence and Informatics (SAMI), Herlany, Slovakia, 21–23 January 2016; pp. 51–56. [Google Scholar] [CrossRef]
- Morioka, N.; Oyori, H. Fuel system design for the more electric engine. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2012; Volume 44670, pp. 767–774. [Google Scholar] [CrossRef]
- Sarala, P.; Kodad, S.F.; Sarvesh, B. Analysis of closed loop current controlled BLDC motor drive. In Proceedings of the 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016; pp. 1464–1468. [Google Scholar] [CrossRef]
- Gamazo-Real, J.C.; Vázquez-Sánchez, E.; Gómez-Gil, J. Position and speed control of brushless DC motors using sensorless techniques and application trends. Sensors 2010, 10, 6901–6947. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mamadapur, A.; Mahadev, G.U. Speed Control of BLDC Motor Using Neural Network Controller and PID Controller. In Proceedings of the 2019 2nd International Conference on Power and Embedded Drive Control (ICPEDC), Chennai, India, 21–23 August 2019; pp. 146–151. [Google Scholar] [CrossRef]
- Ramachandran, R.; Ganeshaperumal, D.; Subathra, B. Closed-Loop Control of BLDC Motor in Electric Vehicle Applications. In Proceedings of the 2019 IEEE International Conference on Clean Energy and Energy Efficient Electronics Circuit for Sustainable Development (INCCES), Krishnankoil, India, 18–20 December 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Gobi, R.; Raja, S. Closed loop speed control of sensorless BLDC drive using direct BEMF method with PI controller. Int. Res. J. Eng. Technol. 2018, 5, 168–174. [Google Scholar]
- Kandiban, R.; Arulmozhiyal, R. Design of adaptive fuzzy PID controller for speed control of BLDC motor. Int. J. Soft Comput. Eng. 2012, 2, 386–391. [Google Scholar]
- Neethu, K.; Boopathi, M.; Mannayee, G.; Kanish, T.C. Fuzzy logic based speed control of BLDC motor on sensorless technique for space applications. Indian J. Sci. Technol. 2016, 9, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Ch, L.; Palakeerthi, R. BLDC Drive Control using Artificial Intelligence Technique. Int. J. Comput. Appl. 2015, 118, 5–9. [Google Scholar] [CrossRef]
- Ramírez-Cárdenas, O.D.; Trujillo-Romero, F. Sensorless speed tracking of a brushless DC motor using a neural network. Math. Comput. Appl. 2020, 25, 57. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Design of Adaptive Controller Exploiting Learning Concepts Applied to a BLDC-Based Drive System. Energies 2020, 13, 2512. [Google Scholar] [CrossRef]
- Huh, N.; Park, H.S.; Lee, M.H.; Kim, J.M. Hybrid PWM Control for Regulating the High-Speed Operation of BLDC Motors and Expanding the Current Sensing Range of DC-link Single-Shunt. Energies 2019, 12, 4347. [Google Scholar] [CrossRef] [Green Version]
- Shao, J.; Nolan, D.; Teissier, M.; Swanson, D. A novel microcontroller-based sensorless brushless DC (BLDC) motor drive for automotive fuel pumps. IEEE Trans. Ind. Appl. 2003, 39, 1734–1740. [Google Scholar] [CrossRef]
- Liu, Q.; Ma, R.; Han, W.; Zhang, Q. A reliable starting method of sensorless brushless DC motor for aviation fuel pumps. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 4740–4744. [Google Scholar] [CrossRef]
- Tsai, C.C.; Lin, S.C.; Huang, H.C.; Cheng, Y.M. Design and control of a brushless DC limited-angle torque motor with its application to fuel control of small-scale gas turbine engines. Mechatronics 2009, 19, 29–41. [Google Scholar] [CrossRef]
- Andrs, O.; Vetiska, J.; Holub, M.; Kovar, J. Model Based Design of Fuel Pump Control. Appl. Mech. Mater. 2016, 821, 601–607. [Google Scholar] [CrossRef]
- Ding, R.; Xiao, L.; Jin, X. Robust Control for Electric Fuel Pump with Variant Nonlinear Loads Based on a New Combined Sliding Mode Surface. Int. J. Control Autom. Syst. 2019, 17, 716–728. [Google Scholar] [CrossRef]
- De Cesare, M.; Parotto, M.; Covassin, F.; Sgatti, S. Electric low pressure fuel pump control for fuel saving (No. 2013-01-0339). In Proceedings of the SAE 2013 World Congress & Exhibition, Detroit, MI, USA, 16–18 April 2013. [Google Scholar] [CrossRef]
- Montazeri-Gh, M.; Yousefpour, H.; Jafari, S. Fuzzy logic computing for design of gas turbine engine fuel control system. In Proceedings of the 2010 2nd International Conference on Computer and Automation Engineering (ICCAE), Singapore, 26–28 February 2010; Volume 5, pp. 723–727. [Google Scholar] [CrossRef]
- Andoga, R.; Főző, L.; Judičák, J.; Bréda, R.; Szabo, S.; Rozenberg, R.; Džunda, M. Intelligent situational control of small turbojet engines. Int. J. Aerosp. Eng. 2018, 2018, 8328792. [Google Scholar] [CrossRef]






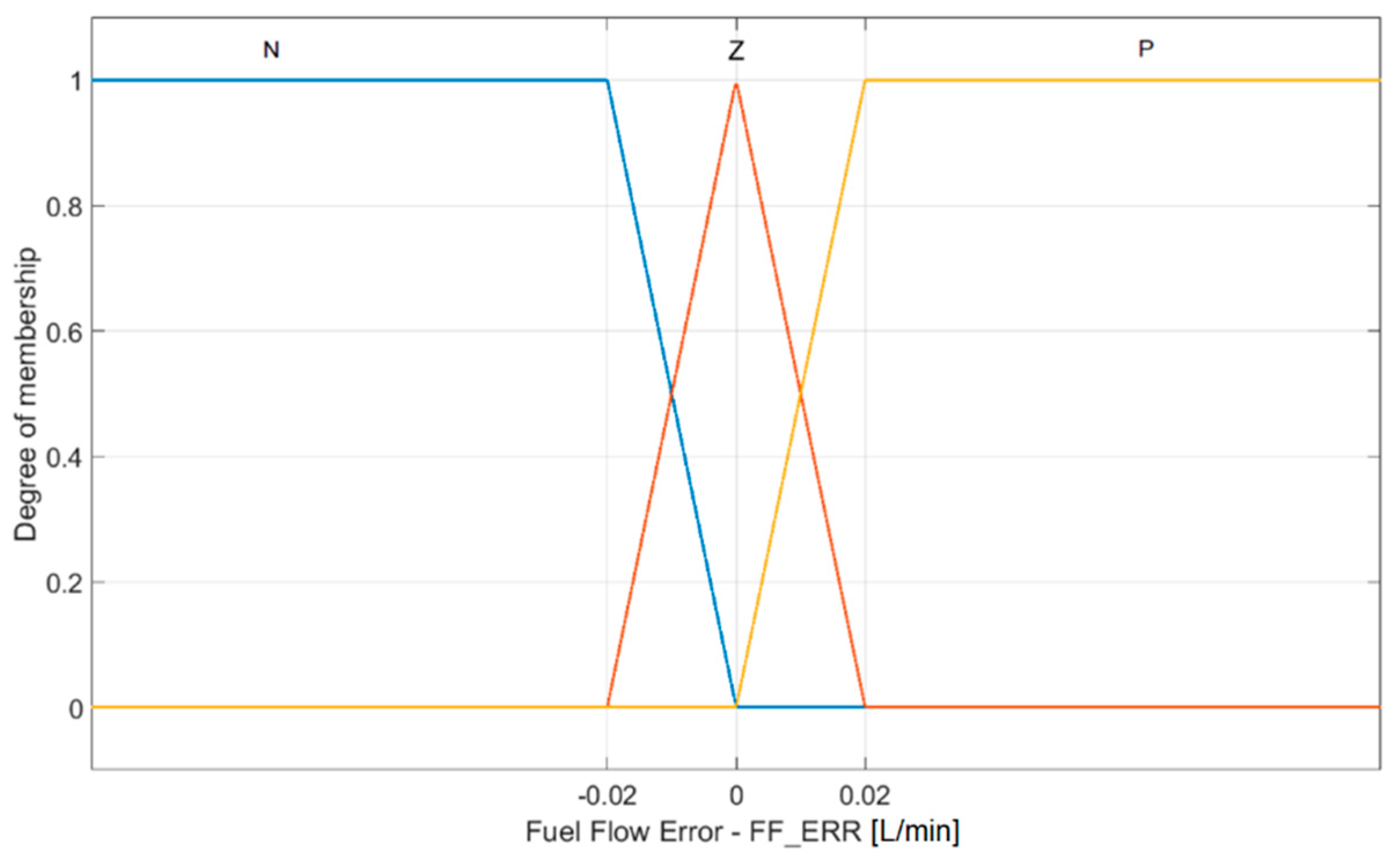
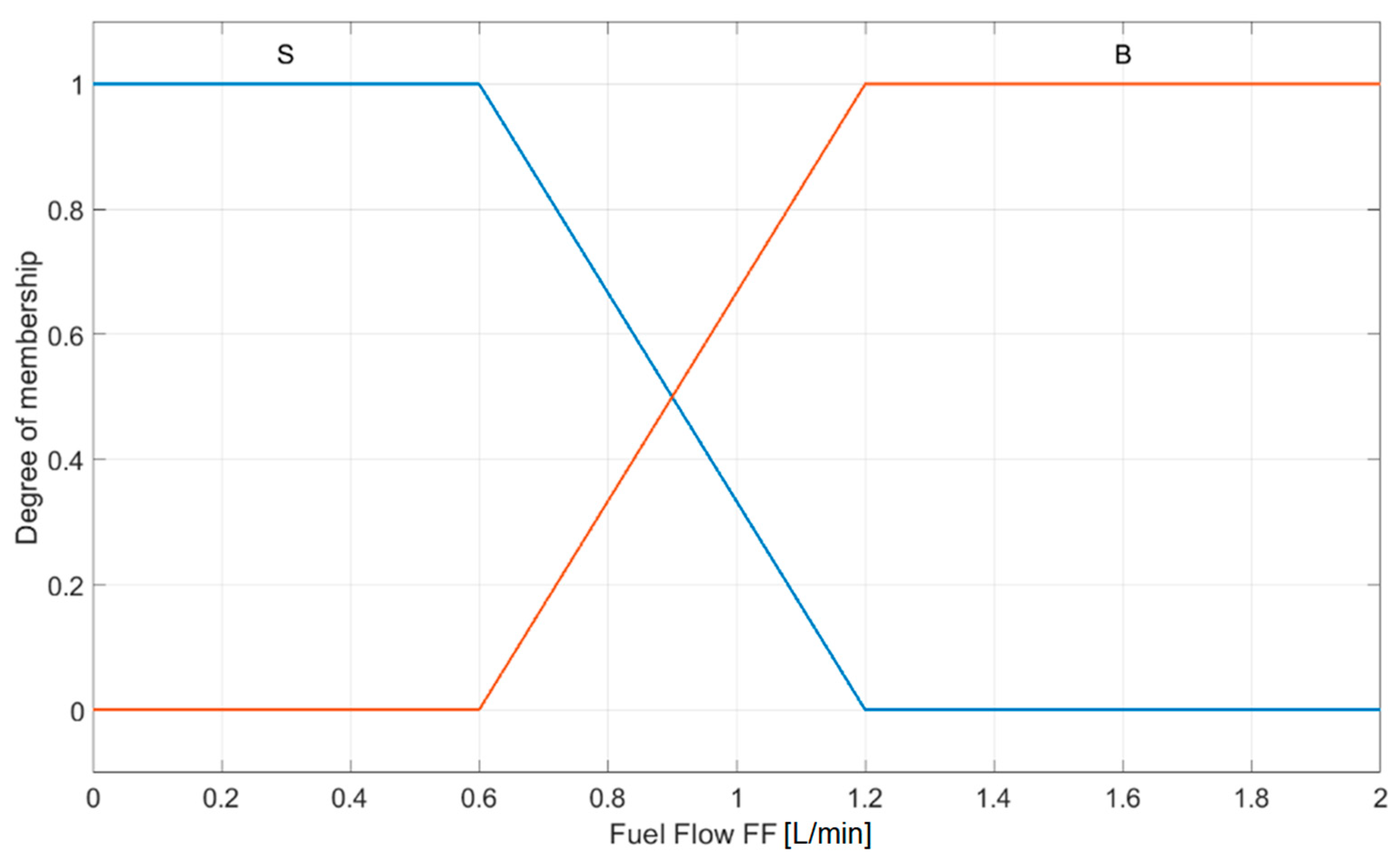


| P | I | D | |
|---|---|---|---|
| Z | 0 | 0 | 0 |
| PS | 0.17 | 0.6 | 0.05 |
| PM | 0.37 | 1.2 | - |
| PB | 0.6 | 1.8 | - |
| Inputs | Outputs | |||||
|---|---|---|---|---|---|---|
| Linguistic Variable | FFERR | FF | P | I | D | |
| Rule No. | ||||||
| 1 | N | S | PB | PB | Z | |
| 2 | P | S | PB | PB | Z | |
| 3 | N | B | PM | PM | Z | |
| 4 | P | B | PM | PM | Z | |
| 5 | Z | - | PS | PS | PS | |
| Controller | Average Rise Time (s) | Absolute Error Surface |
|---|---|---|
| Direct inverse model | 0.4 | 0.33 |
| PID controller | 2.1 | 0.3 |
| Fuzzy PID controller | 1.15 | 0.26 |
| Inputs | Outputs | |||||
|---|---|---|---|---|---|---|
| Linguistic Variable | FFERR | FF | P | I | D | |
| Rule No. | ||||||
| 1 | N | S | PB | PS | Z | |
| 2 | P | S | PB | PS | Z | |
| 3 | N | B | PM | PM | Z | |
| 4 | P | B | PM | PM | Z | |
| 5 | Z | - | PS | PS | PS | |
| Controller | Average Rise Time (s) | Absolute Error Surface |
|---|---|---|
| Direct inverse model | - | 0.9 |
| PID controller | 3.1 | 0.36 |
| Fuzzy PID controller | 2.26 | 0.29 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Főző, L.; Andoga, R. Advanced Control of an Electric Fuel-Oil Pump for Small Turbojet Engines. Aerospace 2022, 9, 607. https://doi.org/10.3390/aerospace9100607
Főző L, Andoga R. Advanced Control of an Electric Fuel-Oil Pump for Small Turbojet Engines. Aerospace. 2022; 9(10):607. https://doi.org/10.3390/aerospace9100607
Chicago/Turabian StyleFőző, Ladislav, and Rudolf Andoga. 2022. "Advanced Control of an Electric Fuel-Oil Pump for Small Turbojet Engines" Aerospace 9, no. 10: 607. https://doi.org/10.3390/aerospace9100607
APA StyleFőző, L., & Andoga, R. (2022). Advanced Control of an Electric Fuel-Oil Pump for Small Turbojet Engines. Aerospace, 9(10), 607. https://doi.org/10.3390/aerospace9100607







