Numerical Study on the Rebound of Low-Velocity Impact-Induced Indentation in Composite Laminate
Abstract
:1. Introduction
2. Materials and Methodology
2.1. Viscoelastic Constitutive Equations for a UD Laminae Ply
2.2. Failure Law of UD Laminae Ply
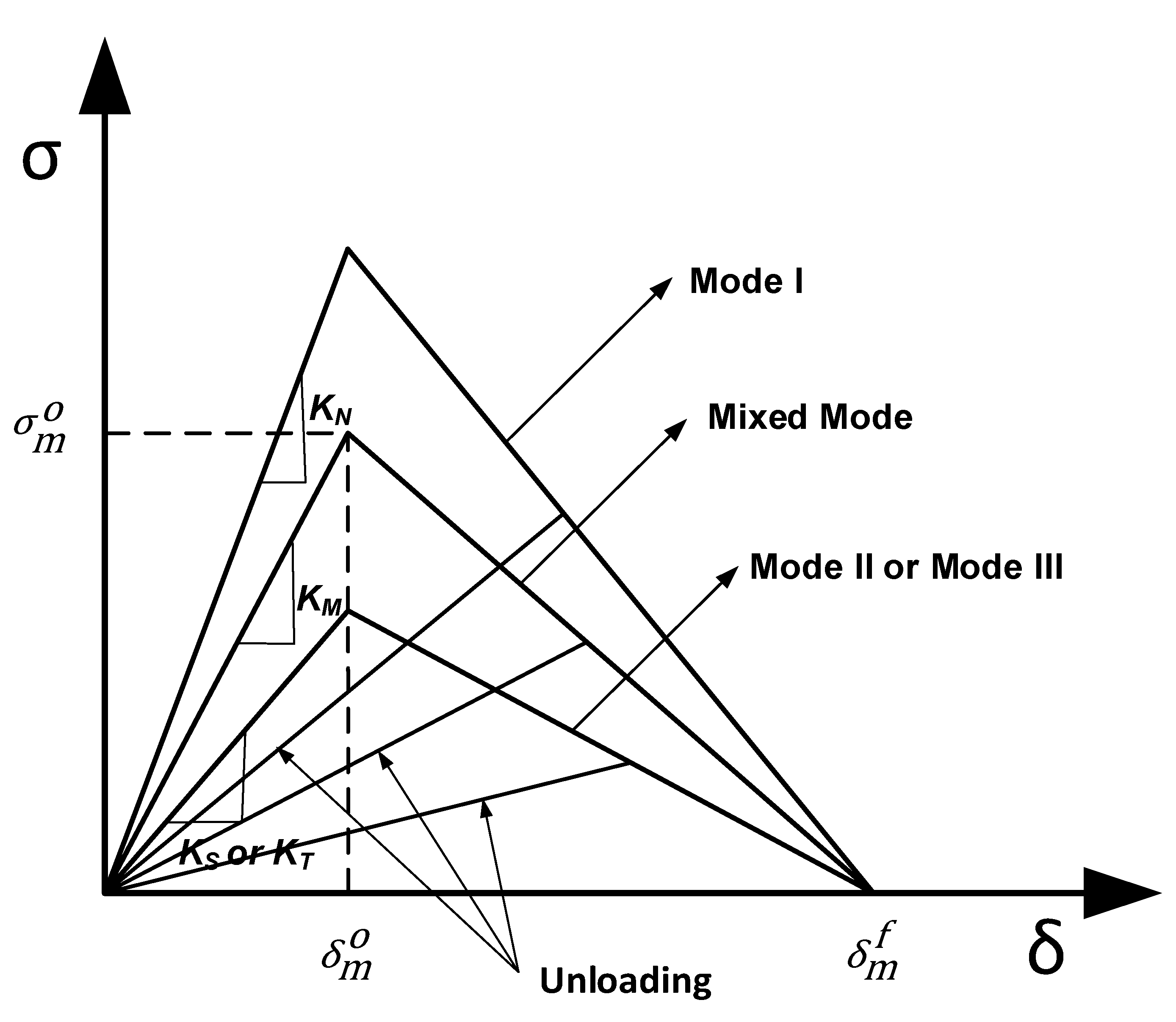
2.3. Viscoelastic Constitutive Equations for Cohesive Interface
2.4. Damage Law of Cohesive Interface
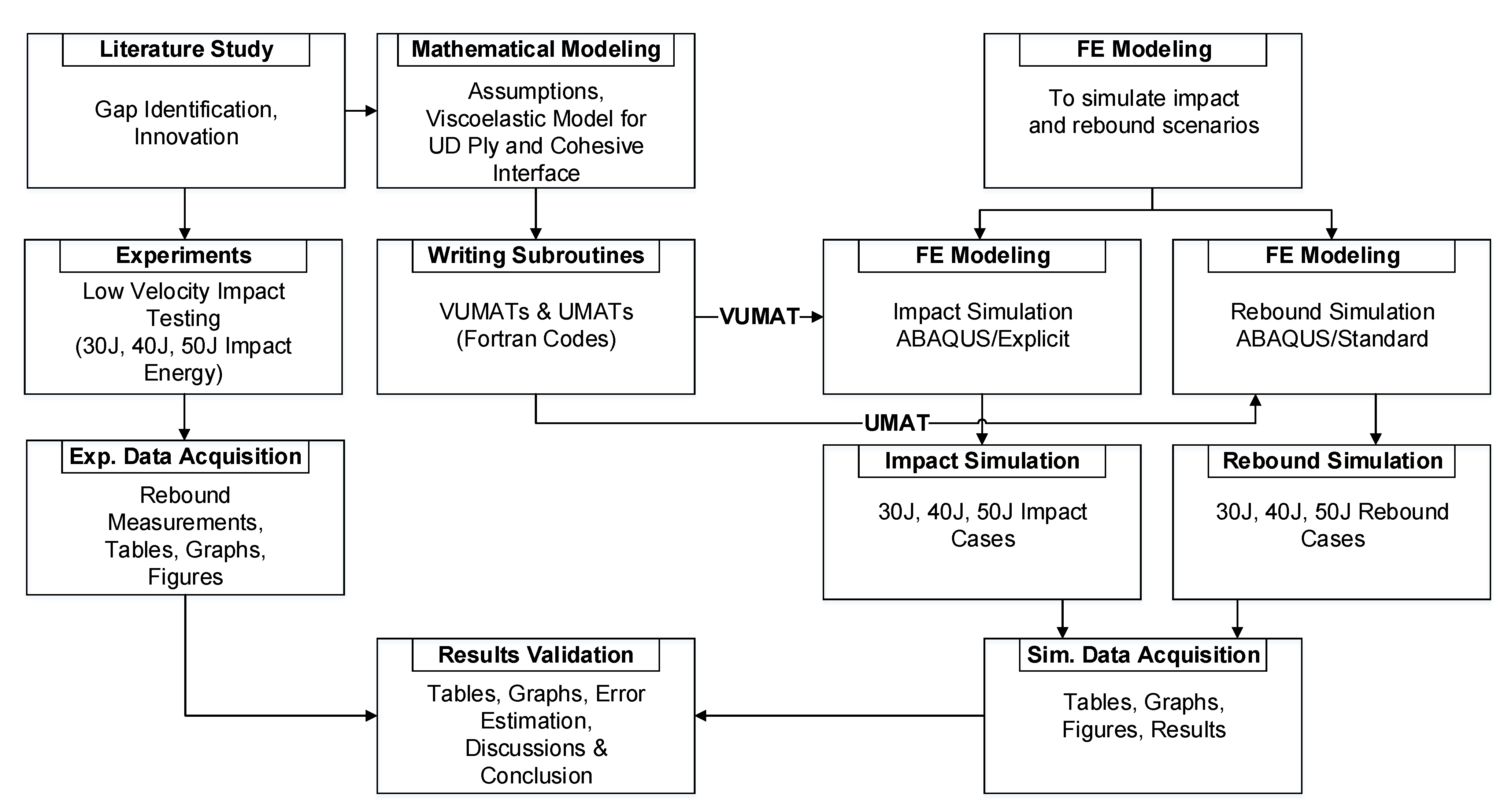
3. Experiment and FEM Simulation
3.1. Experimental Methodology
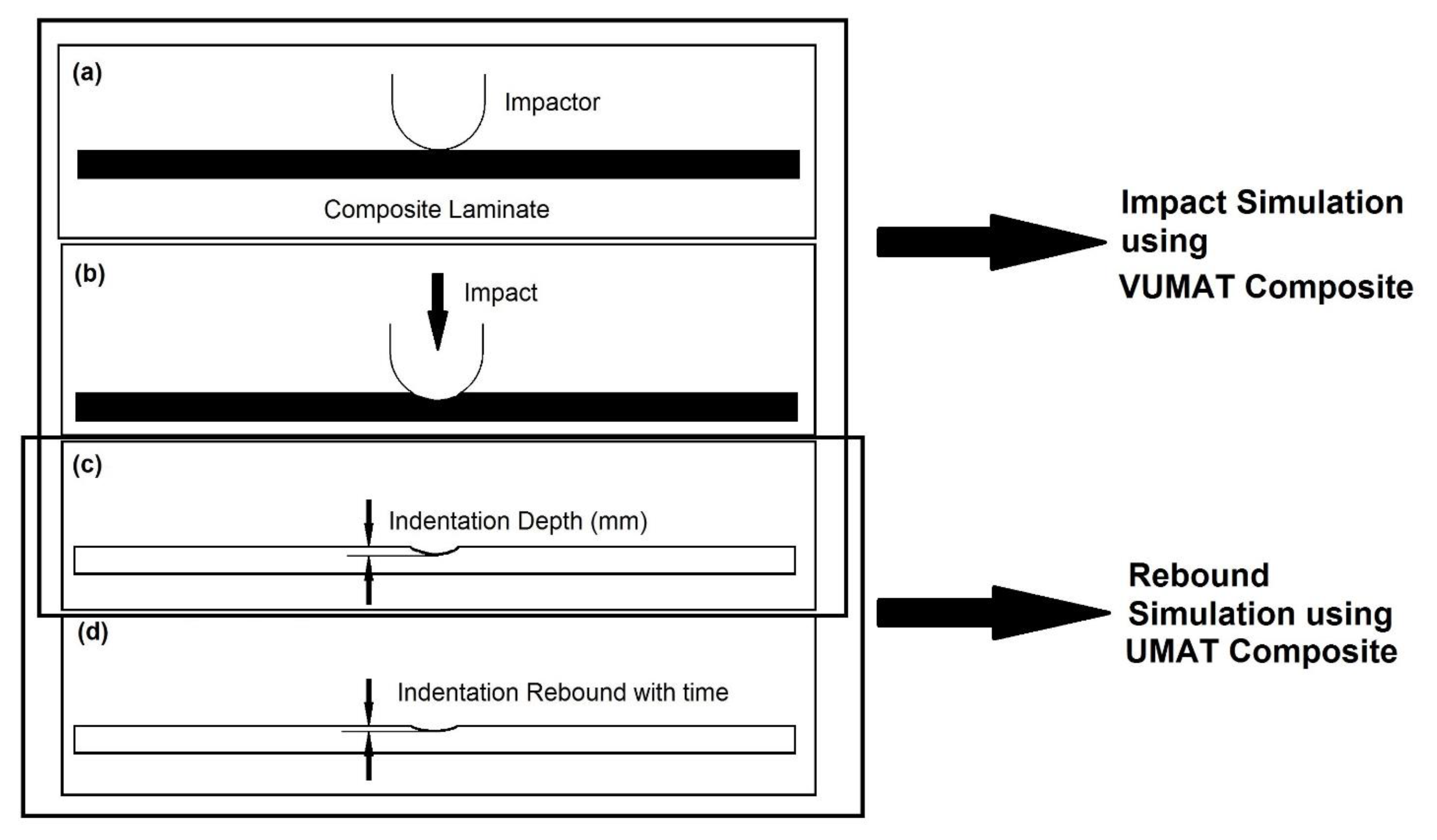
3.2. Simulation Methodology
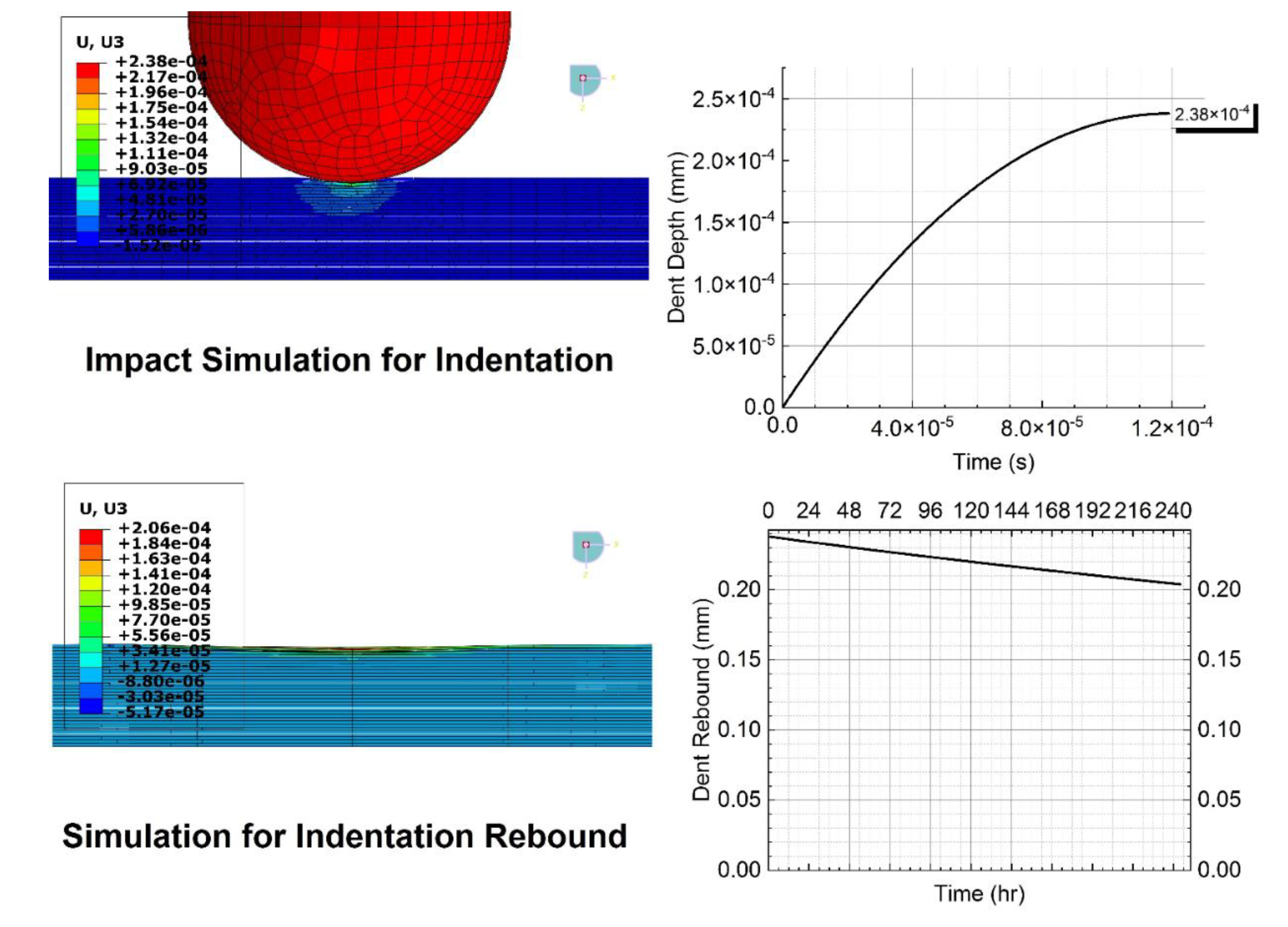
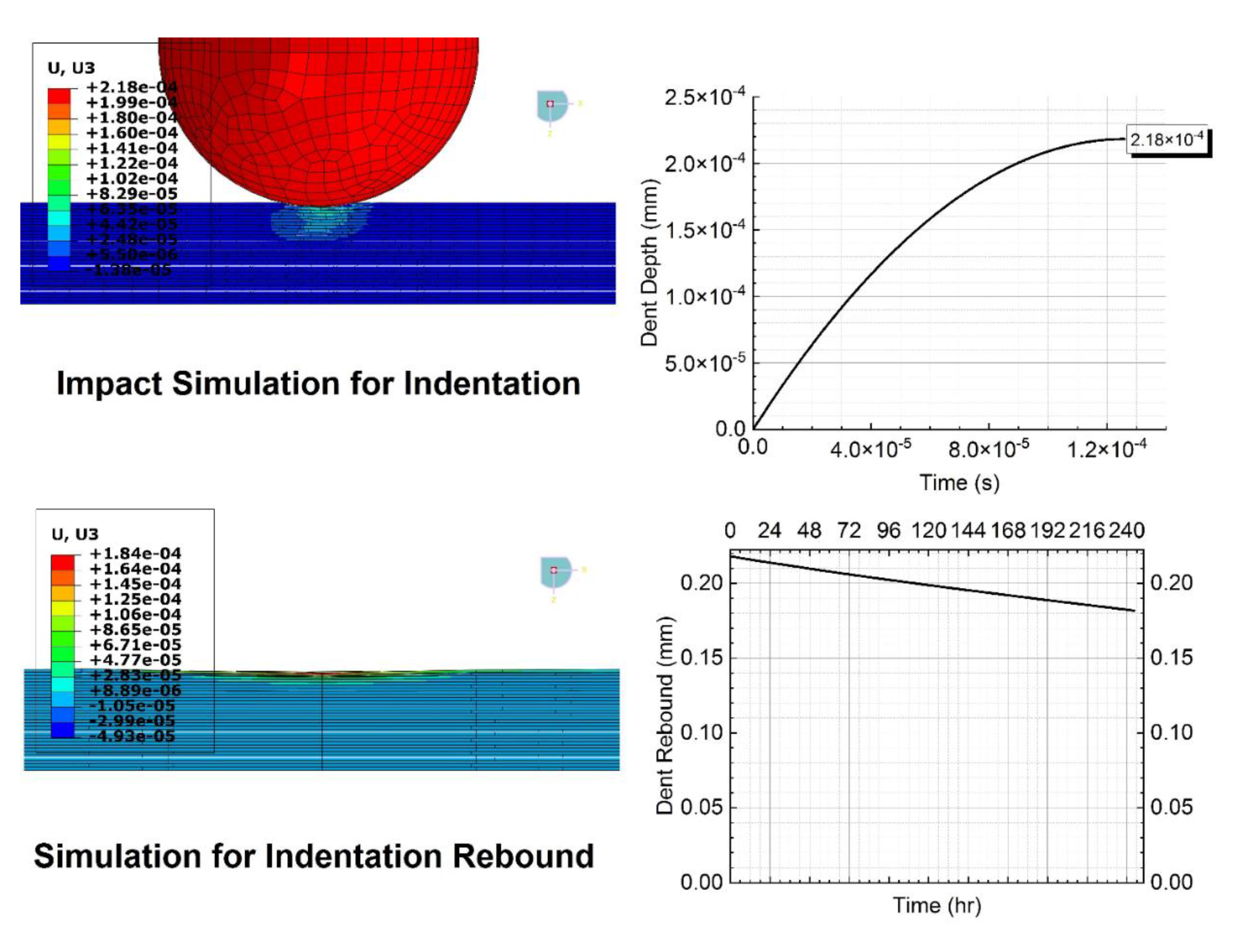
3.2.1. Simulation for Impact Case
3.2.2. Simulation for Rebound Case
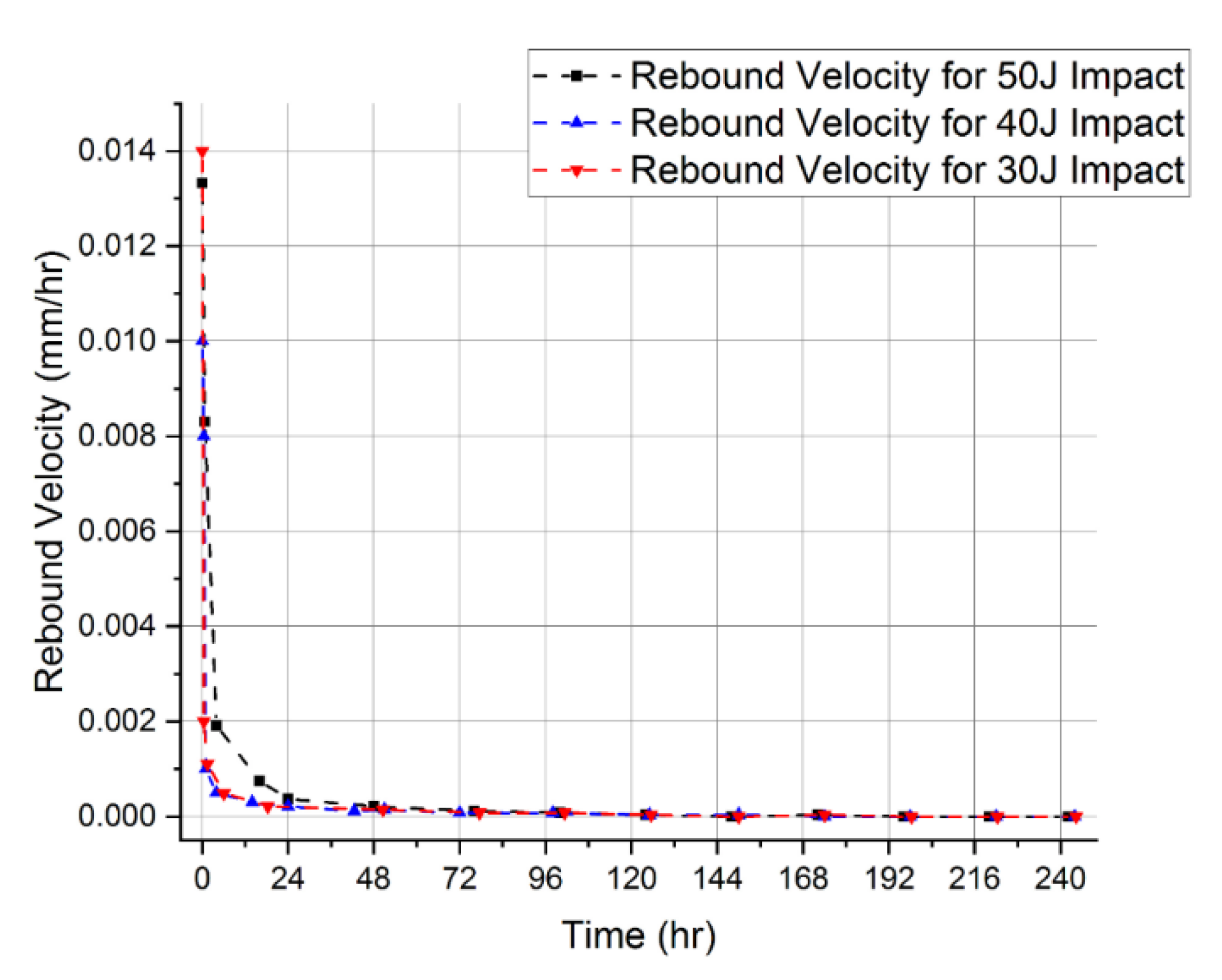
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LVI | Low-Velocity Impact |
| PMC | Polymer Matrix Composite |
| BK | Benzeggagh–Kenane |
| UMAT | User Material Subroutine for ABAQUS Standard |
| VUMAT | User Material Subroutine for ABAQUS Explicit |
| CFRP | Carbon Fiber-Reinforced Polymer |
| CZM | Cohesive Zone Modelling |
| VCCT | Virtual Crack Closure Technique |
| CDM | Continuum Damage Mechanics |
| UD | Unidirectional |
Appendix A [35]
Appendix B [35]
References
- Choi, H.Y.; Chang, F.K. A model for predicting damage in graphite/epoxy laminated composites resulting from low-velocity point impact. J. Compos. Mater. 1992, 26, 2134–2169. [Google Scholar] [CrossRef]
- Brewer, J.C.; Lagace, P.A. Quadratic stress criterion for initiation of delamination. J. Compos. Mater. 1988, 22, 1141–1155. [Google Scholar] [CrossRef]
- Tita, V.; Carvalho, J.; Vandepitte, D. Failure analysis of low velocity impact on thin composite laminates: Experimental and numerical approaches. Compos. Struct. 2008, 83, 413–428. [Google Scholar] [CrossRef]
- Farooq, U.; Myler, P. Efficient computational modelling of carbon fibre reinforced laminated composite panels subjected to low velocity drop-weight impact. Mater. Des. 2014, 54, 43–56. [Google Scholar] [CrossRef]
- Fleming, D.C. Delamination Modeling of Composites for Improved Crash Analysis; NASA/CR-1999-209725; National Aeronautics and Space Administration, Langley Research Center: Hampton, VA, USA, 1999. [Google Scholar]
- Ronald, K. Virtual crack closure technique: History, approach, and applications. Appl. Mech. Rev. 2004, 57, 109–143. [Google Scholar]
- Aymerich, F.; Dore, F.; Priolo, P. Prediction of impact-induced delamination in cross-ply composite laminates using cohesive interface elements. Compos. Sci. Technol. 2008, 68, 2383–2390. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Soutis, C. A finite element analysis of impact damage in composite laminates. Aeronaut. J. 2012, 116, 1131–1147. [Google Scholar] [CrossRef]
- Caputo, F.; De Luca, A.; Lamanna, G.; Borrelli, R.; Mercurio, U. Numerical study for the structural analysis of composite laminates subjected to low velocity impact. Compos. Part B 2014, 67, 296–302. [Google Scholar] [CrossRef]
- Bouvet, C.; Castanié, B.; Bizeul, M.; Barrau, J.J. Low velocity impact modelling in laminate composite panels with discrete interface elements. Int. J. Solids Struct. 2009, 46, 2809–2821. [Google Scholar] [CrossRef] [Green Version]
- Donadon, M.; Iannucci, L.; Falzon, B.; Hodgkinson, J.; Almeida, S. A progressive failure model for composite laminates subjected to low velocity impact damage. Comput. Struct. 2008, 86, 1232–1252. [Google Scholar] [CrossRef]
- Kim, E.H.; Rim, M.S.; Lee, I.; Hwang, T.-K. Composite damage model based on continuum damage mechanics and low velocity impact analysis of composite plates. Compos. Struct. 2013, 95, 123–134. [Google Scholar] [CrossRef]
- Riccio, A.; De Luca, A.; Di Felice, G.; Caputo, F. Modelling the simulation of impact induced damage onset and evolution in composites. Compos. Part B 2014, 66, 340–347. [Google Scholar] [CrossRef]
- Batra, R.C.; Gopinath, G.; Zheng, J.Q. Damage and failure in low energy impact of fiber-reinforced polymeric composite laminates. Compos. Struct. 2012, 94, 540–547. [Google Scholar] [CrossRef]
- Zubillaga, L.; Turon, A.; Maimi, P.; Costa, J.; Mahdi, S.; Linde, P. An energy based failure criterion for matrix crack induced delamination in laminated composite structures. J. Compos. Struct. 2014, 112, 339–344. [Google Scholar] [CrossRef]
- Bouvet, C.; Rivallant, S. Damage tolerance of composite structures under low-velocity impact. In Dynamic Deformation, Damage and Fracture in Composite Materials and Structures; Woodhead Publishing: Sawston, UK, 2016. [Google Scholar] [CrossRef]
- Karakuzu, R.; Erbil, E.; Aktas, M. Impact characterization of glass/epoxy composite plates: An experimental and numerical study. Compos. Part B 2010, 41, 388–395. [Google Scholar] [CrossRef]
- Caprino, G.; Langella, A.; Lopresto, A. Indentation and penetration of carbon fibre reinforced plastic laminates. Compos. Part B 2003, 34, 319–325. [Google Scholar] [CrossRef]
- He, W.; Guan, Z.; Li, X.; Liu, D. Prediction of permanent indentation due to impact on laminated composites based on an elasto-plastic model incorporating fiber failure. Compos. Struct. 2013, 96, 232–242. [Google Scholar] [CrossRef]
- Luo, G.M.; Lee, Y.J. Quasi-static simulation of constrained layered damped laminated curvature shells subjected to low-velocity impact. Compos. Part B 2011, 42, 1233–1243. [Google Scholar] [CrossRef]
- Sutherland, L.S.; Guedes Soares, C. The use of quasi-static testing to obtain the low-velocity impact damage resistance of marine GRP laminates. Compos. Part B 2012, 43, 1459–1467. [Google Scholar] [CrossRef]
- Yokozeki, T.; Kuroda, A.; Yoshimura, A.; Ogasawara, T.; Aoki, T. Damage characterization in thin-ply composite laminates under out-of-plane transverse loadings. Compos. Struct. 2010, 93, 49–57. [Google Scholar] [CrossRef]
- Brindle, A.R.; Zhang, X. Predicting the compression-after-impact performance of carbon fibre composites based on impact response. In Proceedings of the 17th International Conference on Composite Materials (ICCM17), Edinburgh, UK, 27–31 July 2009. [Google Scholar]
- Zhou, J.; Liu, B.; Wang, S. Finite element analysis on impact response and damage mechanism of composite laminates under single and repeated low-velocity impact. Aerosp. Sci. Technol. 2022, 129, 107810. [Google Scholar] [CrossRef]
- Xiao, L.; Wang, G.; Qiu, S.; Han, Z.; Lia, X.; Zhang, D. Exploration of energy absorption and viscoelastic behavior of CFRPs subjected to low velocity impact. Compos. Part B Eng. 2018, 165, 247–254. [Google Scholar] [CrossRef]
- Fazal, A.; Fancey, K.S. Viscoelastically prestressed polymeric matrix composites—Effects of test span and fiber volume fraction on Charpy impact characteristics. Compos. Part B 2013, 44, 4729. [Google Scholar] [CrossRef] [Green Version]
- Zobeiry, N.; Malek, S.; Vaziri, R.; Poursartip, A. A differential approach to finite element modelling of isotropic and transversely isotropic viscoelastic materials. Mech. Mater. 2016, 97, 76–91. [Google Scholar] [CrossRef]
- Kaliske, M.; Rothert, H. Formulation and implementation of three-dimensional viscoelasticity at small and finite strains. Comput. Mech. 1997, 19, 228–239. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Table 1, Conversion from tensor to matrix indices for the Voigt notation, Page 30, Chapter 2, Fundamentals of Aerospace Composite Materials. In Structural Health Monitoring of Aerospace Composites; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X. An efficient approach for predicting low-velocity impact force and damage in composite laminates. Compos. Struct. 2015, 130, 85–94. [Google Scholar] [CrossRef]
- Benzeggagh, M.L.; Kenane, M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus. J. Compos. Sci. Technol. 2003, 56, 439–449. [Google Scholar] [CrossRef]
- Camanho, P.P.; D_avila, C.G.; de Moura, M.F. Numerical simulation of mixed-mode progressive delamination in composite materials. J. Compos. Mater. 2003, 37, 1415–1438. [Google Scholar] [CrossRef]
- ASTM D7136; Standard Test Method for Measuring the Damage Resistance of a Fiber Reinforced Polymer Matrix Composite to a Drop-Weight Impact Event. ASTM International: West Conshohocken, PA, USA, 2015; pp. 1–16.
- Lu, T.; Chen, X.; Wang, H.; Zhang, L.; Zhou, Y. Comparison of low-velocity impact damage in thermoplastic and thermoset composites by non-destructive three-dimensional X-ray microscope. Polym. Test. 2020, 91, 106730. [Google Scholar] [CrossRef]
- Sirimontree, S.; Thongchom, C.; Saffari, P.R.; Refahati, N.; Jearsiripongkul, T.; Keawsawasvong, S. Effects of thermal environment and external mean flow on sound transmission loss of sandwich functionally graded magneto-electro-elastic cylindrical nanoshell. Eur. J. Mech.-A/Solids 2023, 97, 104774. [Google Scholar] [CrossRef]

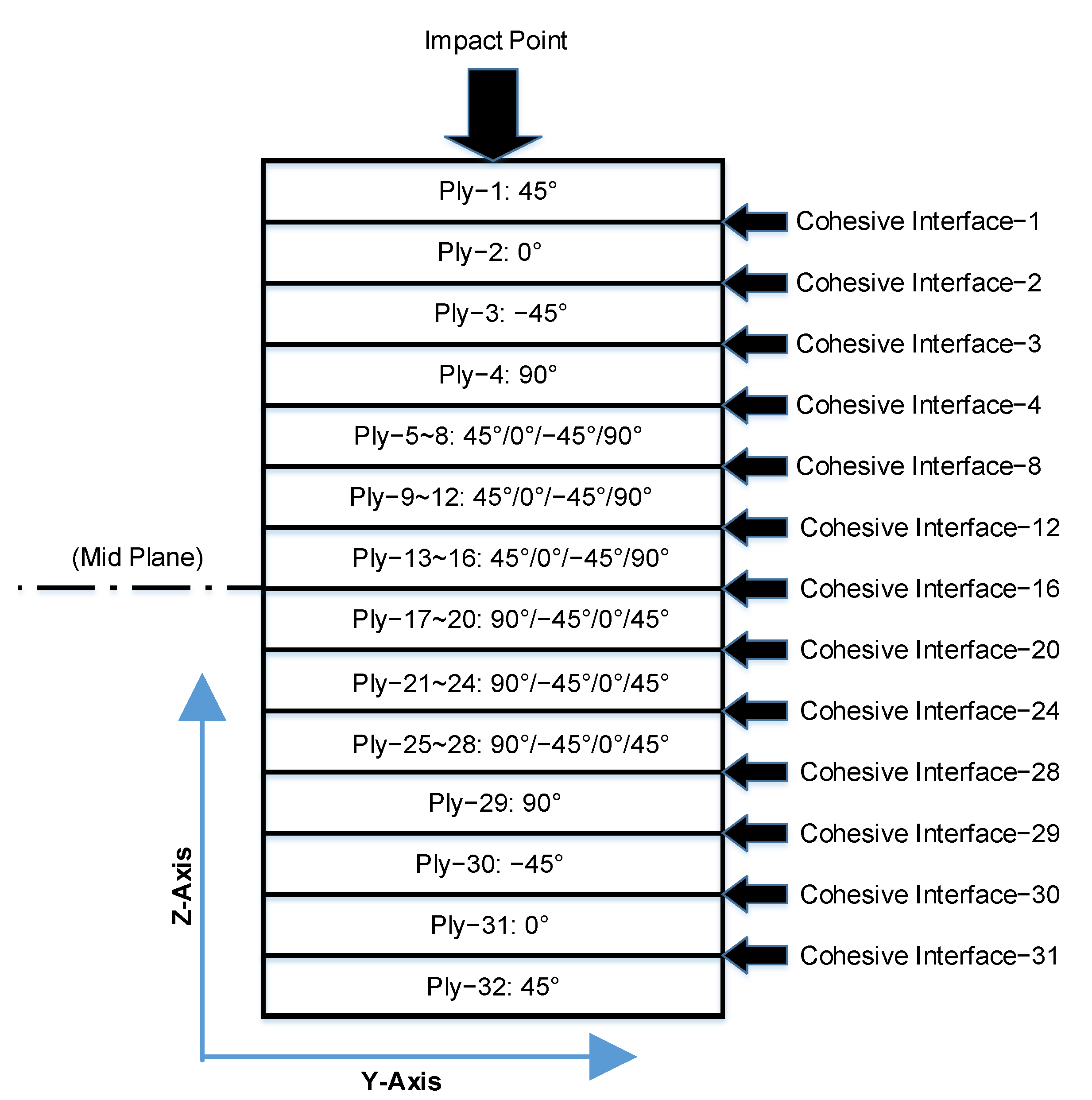

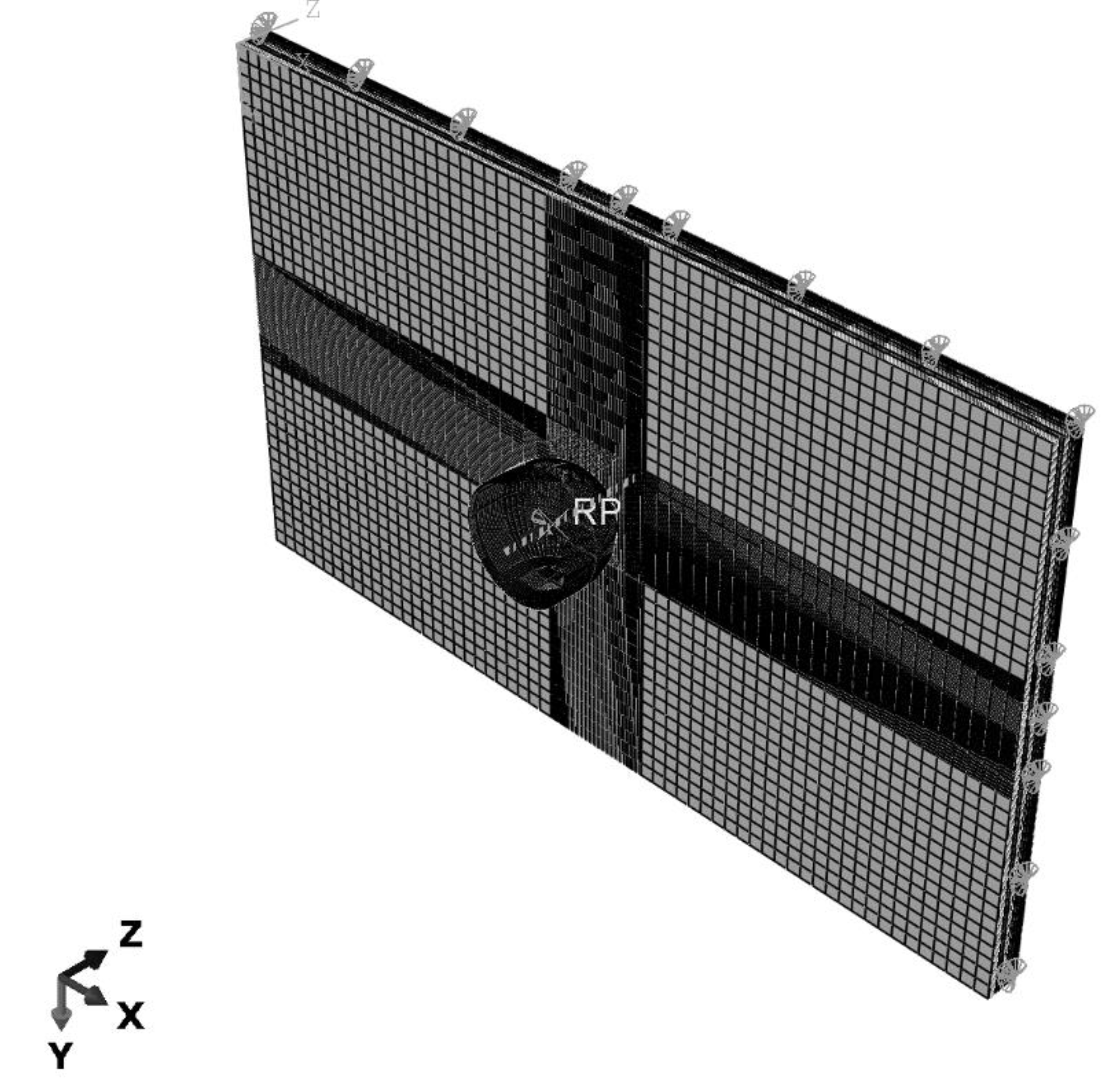
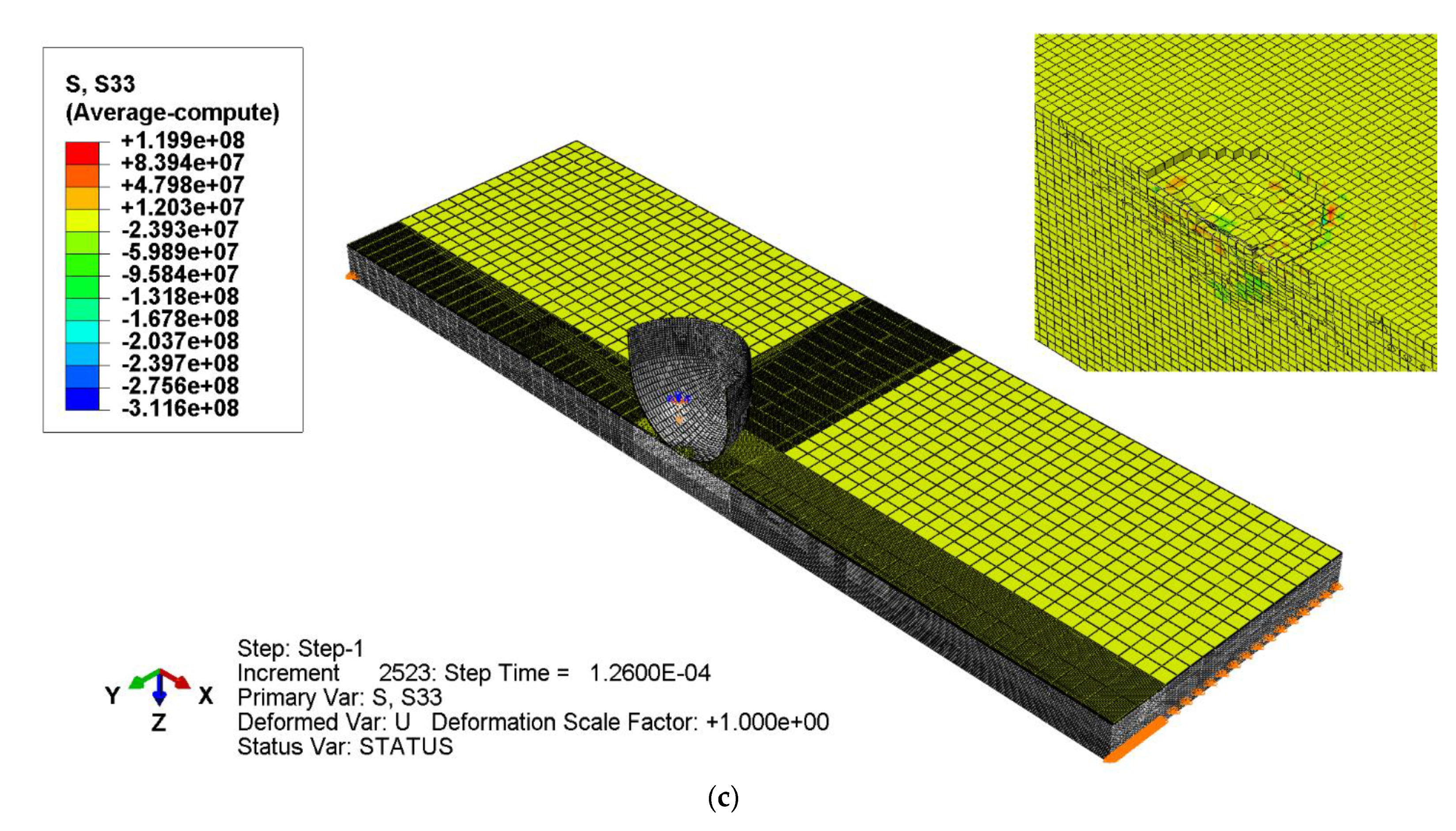



| Damage Type | Failure Mode | Damage Initiation | |
|---|---|---|---|
| Lamina Ply Level | Matrix | Tension Cracking | |
| Compression Cracking | |||
| Fiber | Tension Failure | ||
| Compression Failure | |||
| Elastic Constants of a Single UD Ply | Strength of a Single UD Ply |
|---|---|
| E1 = 144.62 GPa | = 2612.24 MPa |
| E2 = 9.76 GPa | = 1583.47 MPa |
| G12 = 5.44 GPa | = 58.25 MPa |
| G23 = 3.92 GPa | = 161.76 MPa |
| v12 = 0.31 | = 126.79 MPa |
| v23 = 0.46 | = 91.84 MPa |
| Damage Type | Damage Initiation | Damage Propagation |
|---|---|---|
| Cohesive Layer Interface | Linear Softening Mixed-Mode BK Law |
(GPa/mm) | (GPa/mm) | (MPa) | (MPa) | (mm) | (mm) | (GPa/mm) | (mm) |
|---|---|---|---|---|---|---|---|
| 1390.0 | 510.0 | 65.5 | 95.5 | 0.014 | 0.025 | 26.5 | 0.043 |
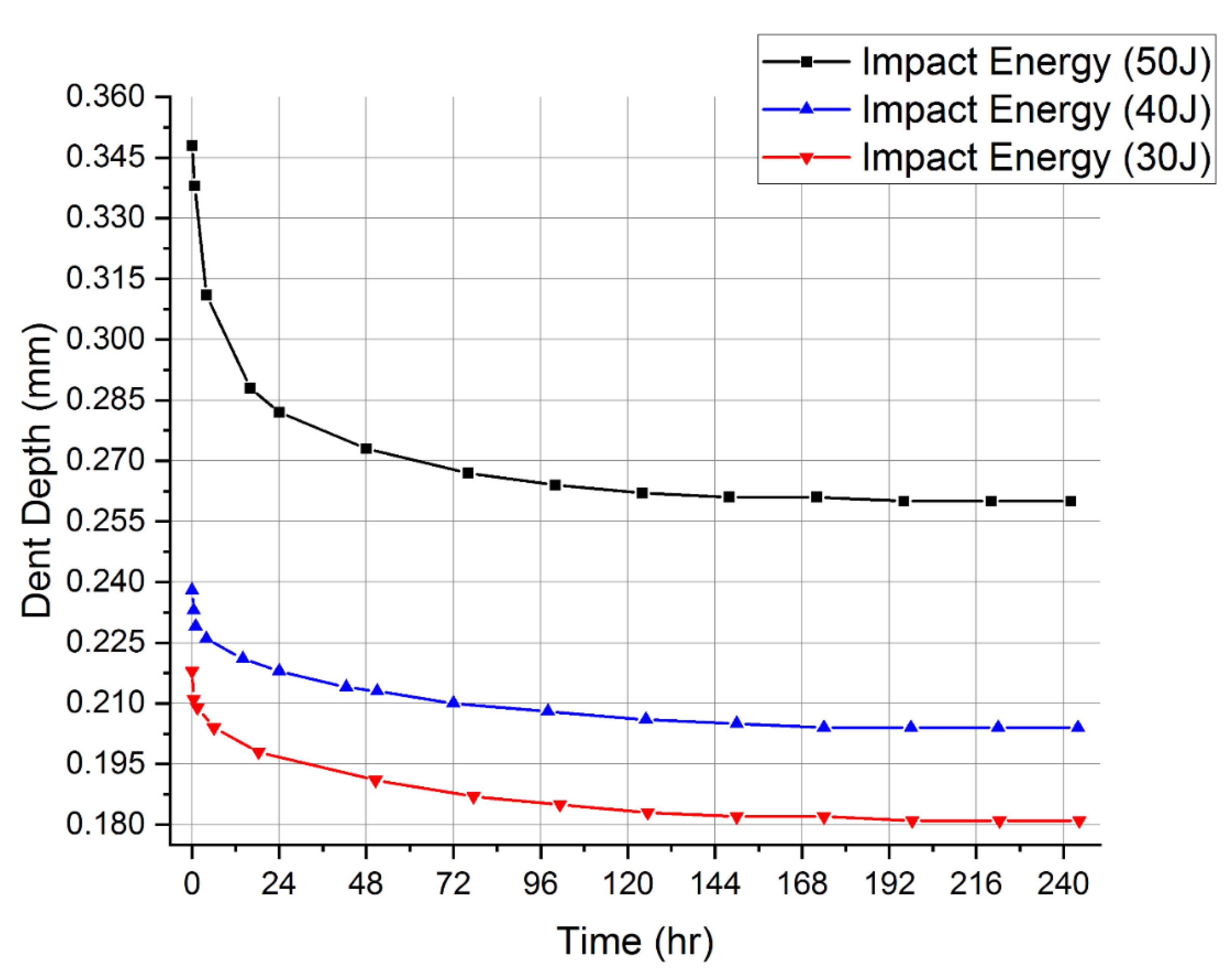
| Case I: 50 J | Case II: 40 J | Case III: 30 J | ||||
|---|---|---|---|---|---|---|
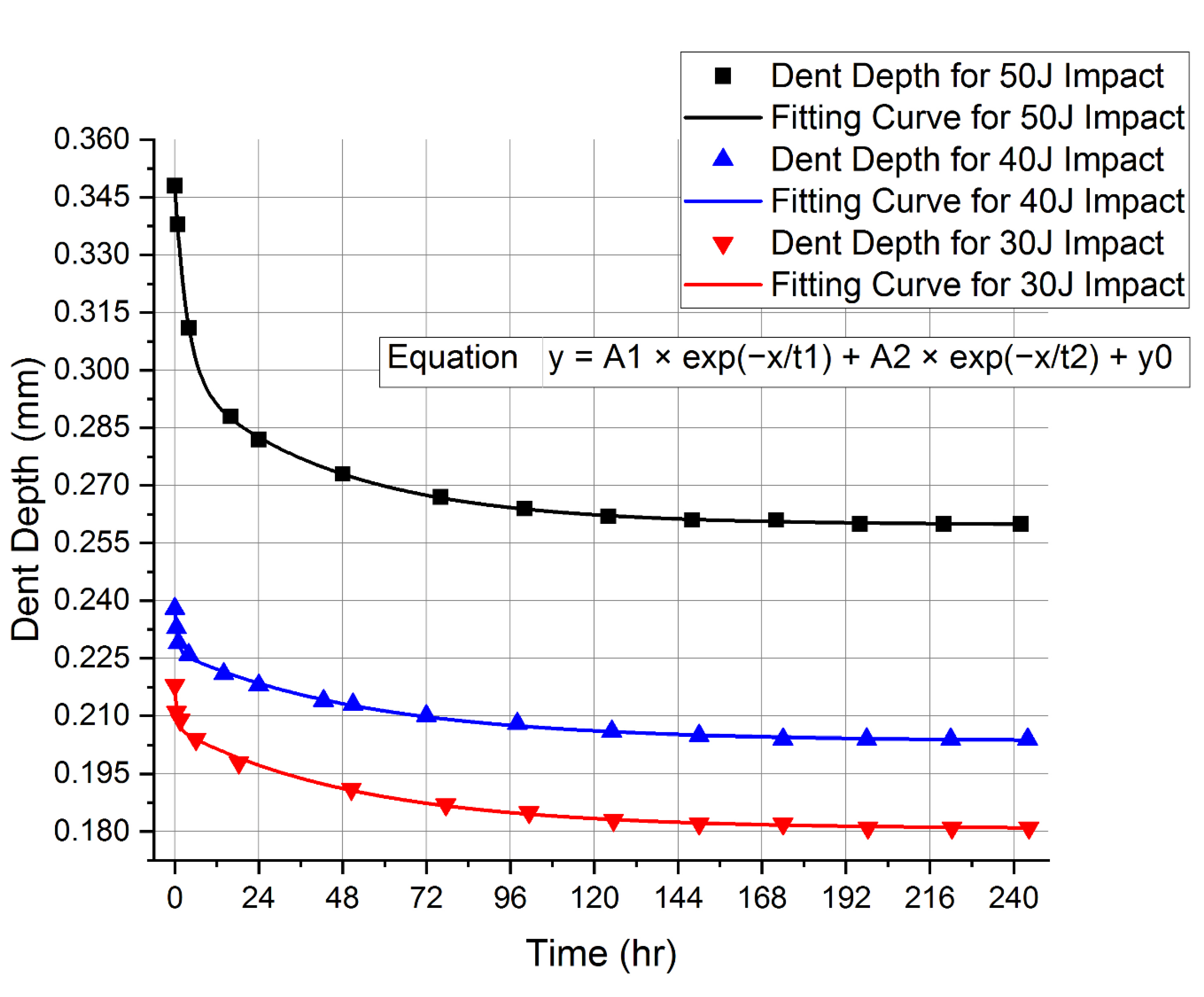
| Time (Hour) | Depth (mm) | Time (Hour) | Depth (mm) | Time (Hour) | Depth (mm) | |
| 0 | 0.348 | 0 | 0.238 | 0 | 0.218 | , Initial Indentation Depth |
| 0.75 | 0.338 | 0.5 | 0.233 | 0.5 | 0.211 | |
| 4 | 0.311 | 1 | 0.229 | 1.5 | 0.209 | |
| 16 | 0.288 | 4 | 0.226 | 6 | 0.204 | |
| 24 | 0.282 | 14 | 0.221 | 18.33 | 0.198 | |
| 48 | 0.273 | 24 | 0.218 | 50.5 | 0.191 | |
| 76 | 0.267 | 42.5 | 0.214 | 77.5 | 0.187 | |
| 100 | 0.264 | 51 | 0.213 | 101.33 | 0.185 | |
| 124 | 0.262 | 72 | 0.21 | 125.5 | 0.183 | |
| 148 | 0.261 | 98 | 0.208 | 150 | 0.182 | |
| 172 | 0.261 | 125 | 0.206 | 174 | 0.182 | |
| 196 | 0.26 | 150 | 0.205 | 198.33 | 0.181 | |
| 174 | 0.204 | |||||
| 220 | 0.26 | 198 | 0.204 | 222.33 | 0.181 | |
| 222 | 0.204 | |||||
| 242 | 0.26 | 244 | 0.204 | 244.33 | 0.181 | , Final Indentation Depth |
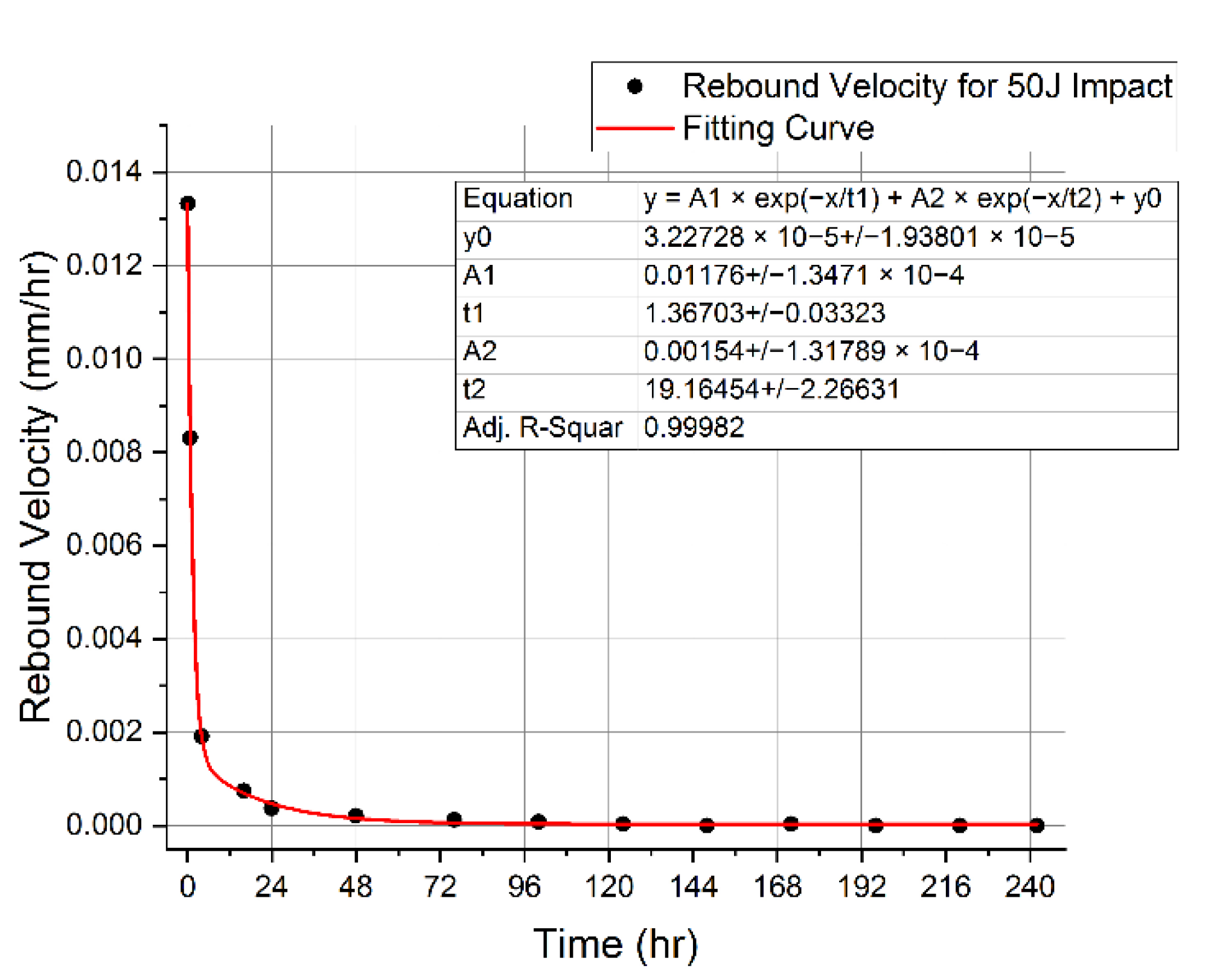
| Impact Energy | A1 | t1 | A2 | t2 | y0 | Adj. R-Squared |
|---|---|---|---|---|---|---|
| 50 J Case | 0.04918 | 3.48385 | 0.03910 | 44.22815 | 0.25979 | 0.99989 |
| 40 J Case | 0.01135 | 0.78406 | 0.02320 | 54.84134 | 0.20355 | 0.99823 |
| 30 J Case | 0.01074 | 0.74417 | 0.02614 | 52.47742 | 0.18074 | 0.99644 |
| Impact Energy (J) | |||
|---|---|---|---|
| 50 | 40 | 30 | |
| Velocity (m/s) | 4.472135955 | 4.00 | 3.464101615 |
| Impact Case | ABAQUS Explicit Analysis | ABAQUS Standard Analysis | |||
|---|---|---|---|---|---|
| Loading Step Time (ms) | Max Pressure (Pa) | Initial Indentation Depth (mm) | Rebound Step Time (h) | Final Indentation Depth (mm) | |
| Case I: 50 J | 0.155 | 4.8 × 108 | 0.348 | 242 | 0.260 |
| Case II: 40 J | 0.119 | 4.4 × 108 | 0.238 | 244 | 0.204 |
| Case III: 30 J | 0.126 | 4.1 × 108 | 0.218 | 244.33 | 0.181 |
| Impact Case | Material Type | 1st Maxwell Chain | 2nd Maxwell Chain | ||||
|---|---|---|---|---|---|---|---|
| Time 1 (h) | Value 1 (GPa) | Time 2 (h) | Value 2 (GPa) | ||||
| Case I: 50 J | UD Laminae Ply | 240 | 100 | 14 | 2 × 107 | ||
| Cohesive Interface | 240 | Value 1 | Value 1 | 14 | Value 2 | Value 2 | |
| 55.208 | 9.331 | 1.68 × 108 | 2.85 × 107 | ||||
| Case II: 40 J | UD Laminae Ply | 240 | 100 | 21 | 2 × 107 | ||
| Cohesive Interface | 240 | 55.208 | 9.331 | 21 | 1.93 × 108 | 3.27 × 107 | |
| Case III: 30 J | UD Laminae Ply | 240 | 100 | 16 | 2 × 107 | ||
| Cohesive Interface | 240 | 55.208 | 9.331 | 16 | 2.15 × 108 | 3.64 × 107 | |
| Impact Energy Case | Total Dent Rebound (mm) | Way Out | Experimental Result | Simulation Result | Prediction Accuracy |
|---|---|---|---|---|---|
| Case I: 50 J | 0.088 | Initial and Final Dent Depths | Matched | Matched | Accurately predicted |
| Dent Rebound Path | The curve decays at a faster rate and soon stops decaying before the final point | The curve decays at a slower rate and never stops decaying until the final point | Poor prediction Max error: 19.35% | ||
| Case II: 40 J | 0.034 | Initial and Final Dent Depths | Matched | Matched | Accurately predicted |
| Dent Rebound Path | The curve decays at a faster rate and soon stops decaying before the final point | The curve decays at a slower rate and never stops decaying until the final point | Fairly Iinaccurate Prediction Max error: 7.97% | ||
| Case III: 30 J | 0.037 | Initial and Final Dent Depths | Matched | Matched | Accurately predicted |
| Dent Rebound Path | The curve decays at a faster rate and soon stops decaying before the final point | The curve decays at a slower rate and never stops decaying until the final point | Fairly inaccurate prediction Max error: 9.88% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yousaf, M.; Zhou, C. Numerical Study on the Rebound of Low-Velocity Impact-Induced Indentation in Composite Laminate. Aerospace 2022, 9, 651. https://doi.org/10.3390/aerospace9110651
Yousaf M, Zhou C. Numerical Study on the Rebound of Low-Velocity Impact-Induced Indentation in Composite Laminate. Aerospace. 2022; 9(11):651. https://doi.org/10.3390/aerospace9110651
Chicago/Turabian StyleYousaf, Muhammad, and Chuwei Zhou. 2022. "Numerical Study on the Rebound of Low-Velocity Impact-Induced Indentation in Composite Laminate" Aerospace 9, no. 11: 651. https://doi.org/10.3390/aerospace9110651
APA StyleYousaf, M., & Zhou, C. (2022). Numerical Study on the Rebound of Low-Velocity Impact-Induced Indentation in Composite Laminate. Aerospace, 9(11), 651. https://doi.org/10.3390/aerospace9110651