Deep-Learning-Based Satellite Relative Pose Estimation Using Monocular Optical Images and 3D Structural Information
Abstract
:1. Introduction
- We propose a novel CNN-based satellite pose estimation method. The method takes full advantage of CNN and combines the spatial structure a priori information in the form of point clouds and accomplishes the task of estimating the relative pose of a satellite from a single monocular optical image with a high precision.
- We design a loss function that is suitable for satellite pose estimation. The loss function can guide the network training process and make the pose estimation results more accurate.
- We build an open-source simulation dataset called BUAA-SID-POSE 1.0. The dataset contains more than 250,000 images of five types of satellites in different poses, providing a large amount of data for relevant research.
2. Related Work
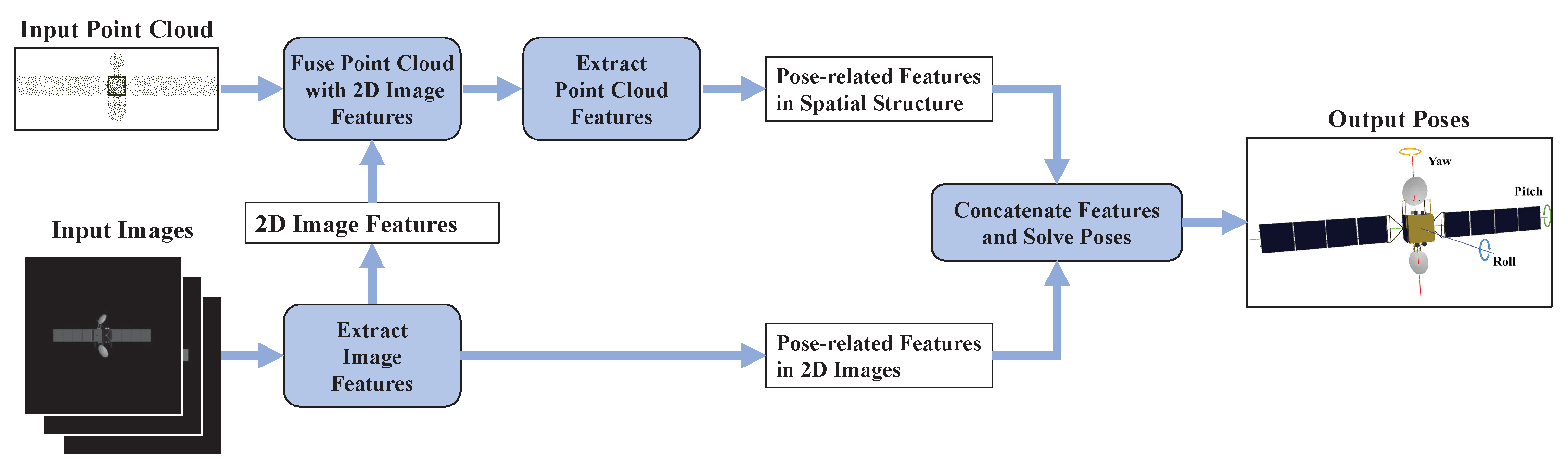
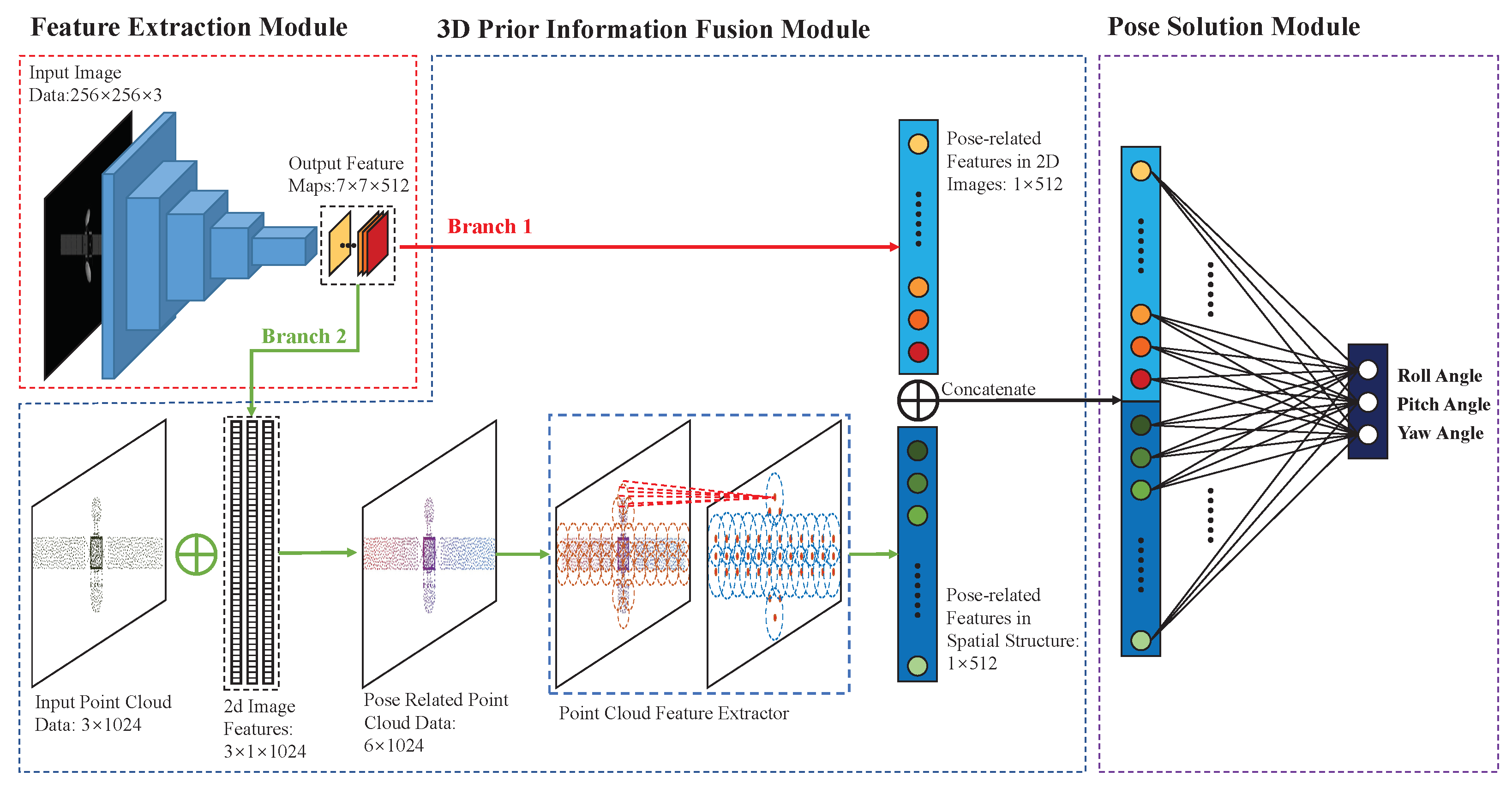
3. Method
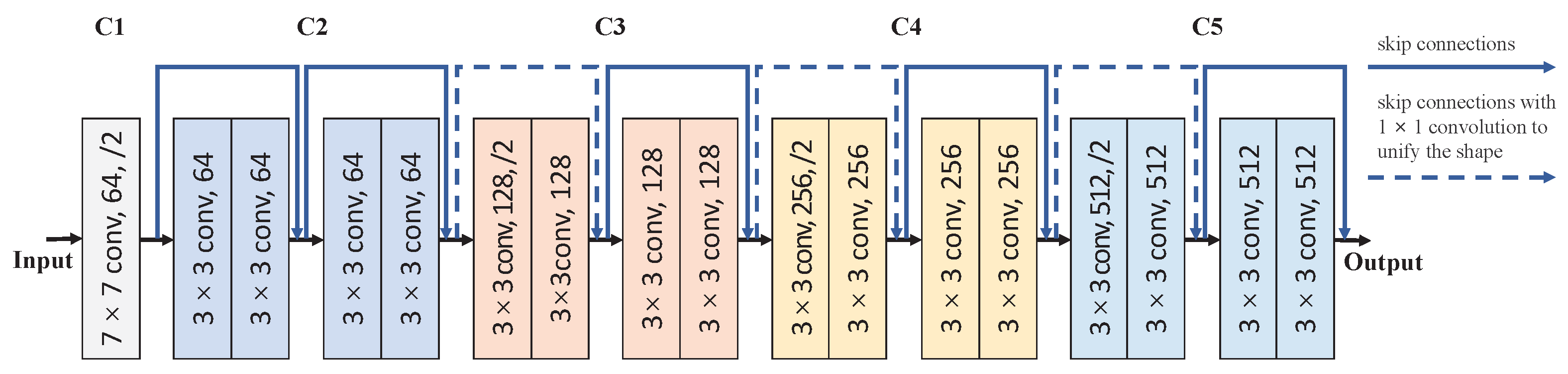
3.1. Feature Extraction Module
3.2. Three-Dimensional Prior Information Fusion Module
3.3. Pose Solution Module
4. Experiment Settings
4.1. Dataset
4.2. Experimental Environment
4.3. Evaluation Metrics
- Mean Absolute Error (MAE): MAE evaluates the mean error between the predicted pose and the ground truth. The calculation formula is shown as follows,
- Accuracy Rate (ACC): ACC evaluates the accuracy of the results under different accuracy requirements, including the ACC with the absolute error of less than and less than 5 denoted by and . AE is the absolute value of the difference between the predicted value and the true value. Considering the reasonableness of the absolute error threshold size settings in the metric, we examined the relevant literature. Ref. [21] uses a classification scheme to estimate the pose with a resolution much greater than in yaw angle, pitch angle, and roll angle; Ref. [9] also estimates attitude using a classification scheme with a resolution of in each dimension. In summary, the absolute error threshold chosen for the evaluation metrics is quite accurate when comparing existing algorithms for space object pose estimation.
4.4. Training Strategy
5. Experimental Results
5.1. Experimental Results of the Loss Function
5.2. Experimental Results of Model Structure and Initialization Mode
5.3. Experimental Results from the Structures of 3D Prior Information Fusion Module
5.4. Pose Estimation Results on BUAA-SID-POSE 1.0
5.5. Comparison
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Zhang, S.; Yang, H.; Cai, H.; Qian, S. Relative attitude and position estimation for a tumbling spacecraft. Aerosp. Sci. Technol. 2015, 42, 97–105. [Google Scholar] [CrossRef]
- Flores-Abad, A.; Ma, O.; Pham, K.; Ulrich, S. A review of space robotics technologies for on-orbit servicing. Prog. Aerosp. Sci. 2014, 68, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Long, A.; Richards, M.; Hastings, D.E. On-Orbit Servicing: A New Value Proposition for Satellite Design and Operation. J. Spacecr. Rocket. 2007, 44, 964–976. [Google Scholar] [CrossRef] [Green Version]
- Ambrose, R.; Nesnas, I.; Chandler, F.; Allen, B.; Fong, T.; Matthies, L.; Mueller, R. NASA Technology Roadmaps: TA 4: Robotics and Autonomous Systems; NASA: Washington DC, USA, 2015; pp. 50–51. [Google Scholar]
- Li, Y.; Zhang, A. Observability analysis and autonomous navigation for two satellites with relative position measurements. Acta Astronaut. 2019, 163, 77–86. [Google Scholar] [CrossRef]
- Pinard, D.; Reynaud, S.; Delpy, P.; Strandmoe, S.E. Accurate and autonomous navigation for the ATV. Aerosp. Sci. Technol. 2007, 11, 490–498. [Google Scholar] [CrossRef]
- Xing, Y.; Cao, X.; Zhang, S.; Guo, H.; Wang, F. Relative position and attitude estimation for satellite formation with coupled translational and rotational dynamics. Acta Astronaut. 2010, 67, 455–467. [Google Scholar] [CrossRef]
- De Jongh, W.; Jordaan, H.; Van Daalen, C. Experiment for pose estimation of uncooperative space debris using stereo vision. Acta Astronaut. 2020, 168, 164–173. [Google Scholar] [CrossRef]
- Cassinis, L.P.; Fonod, R.; Gill, E.; Ahrns, I.; Gil-Fernández, J. Evaluation of tightly-and loosely-coupled approaches in CNN-based pose estimation systems for uncooperative spacecraft. Acta Astronaut. 2021, 182, 189–202. [Google Scholar] [CrossRef]
- Guthrie, B.; Kim, M.; Urrutxua, H.; Hare, J. Image-based attitude determination of co-orbiting satellites using deep learning technologies. Aerosp. Sci. Technol. 2022, 120, 107232. [Google Scholar] [CrossRef]
- Ventura, J. Autonomous Proximity Operations for Noncooperative Space Targets. Ph.D. Thesis, Technische Universität München, Munich, Germany, 2016. [Google Scholar]
- Sharma, S.; Ventura, J.; D’Amico, S. Robust model-based monocular pose initialization for noncooperative spacecraft rendezvous. J. Spacecr. Rocket. 2018, 55, 1414–1429. [Google Scholar] [CrossRef]
- Pesce, V.; Haydar, M.F.; Lavagna, M.; Lovera, M. Comparison of filtering techniques for relative attitude estimation of uncooperative space objects. Aerosp. Sci. Technol. 2019, 84, 318–328. [Google Scholar] [CrossRef]
- Petit, A.; Marchand, E.; Kanani, K. Vision-based detection and tracking for space navigation in a rendezvous context. In Proceedings of the International Symposium on Artificial Intelligence, Robotics and Automation in Space i-SAIRAS 2012, Turin, Italy, 4–6 September 2012. [Google Scholar]
- Opromolla, R.; Fasano, G.; Rufino, G.; Grassi, M. A model-based 3D template matching technique for pose acquisition of an uncooperative space object. Sensors 2015, 15, 6360–6382. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Opromolla, R.; Fasano, G.; Rufino, G.; Grassi, M. Pose estimation for spacecraft relative navigation using model-based algorithms. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 431–447. [Google Scholar] [CrossRef]
- Yin, F.; Chou, W.; Wu, Y.; Dong, M. Relative pose determination of uncooperative known target based on extracting region of interest. Meas. Control 2020, 53, 589–600. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, Z.; Elgammal, A. Vision-based pose estimation for cooperative space objects. Acta Astronaut. 2013, 91, 115–122. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, Z. Multi-view space object recognition and pose estimation based on kernel regression. Chin. J. Aeronaut. 2014, 27, 1233–1241. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Jiang, Z.; Yao, Y.; Meng, G. Vision-based pose estimation for space objects by Gaussian process regression. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015; pp. 1–9. [Google Scholar]
- Sharma, S.; Beierle, C.; D’Amico, S. Pose estimation for non-cooperative spacecraft rendezvous using convolutional neural networks. In Proceedings of the 2018 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2018; pp. 1–12. [Google Scholar]
- Phisannupawong, T.; Kamsing, P.; Torteeka, P.; Channumsin, S.; Sawangwit, U.; Hematulin, W.; Jarawan, T.; Somjit, T.; Yooyen, S.; Delahaye, D.; et al. Vision-Based Spacecraft Pose Estimation via a Deep Convolutional Neural Network for Noncooperative Docking Operations. Aerospace 2020, 7, 126. [Google Scholar] [CrossRef]
- Oumer, N.W.; Kriegel, S.; Ali, H.; Reinartz, P. Appearance learning for 3D pose detection of a satellite at close-range. ISPRS J. Photogramm. Remote. Sens. 2017, 125, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Cao, J.; Parra, A.; Chin, T.J. Satellite Pose Estimation with Deep Landmark Regression and Nonlinear Pose Refinement. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop, Seoul, Republic of Korea, 27–28 October 2019; pp. 2816–2824. [Google Scholar]
- Huo, Y.; Li, Z.; Zhang, F. Fast and accurate spacecraft pose estimation from single shot space imagery using box reliability and keypoints existence judgments. IEEE Access 2020, 8, 216283–216297. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, Z.; Zhang, H.; Wei, Q. Vision-Based Pose Estimation for Textureless Space Objects by Contour Points Matching. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2342–2355. [Google Scholar] [CrossRef]
- Pasqualetto Cassinis, L.; Menicucci, A.; Gill, E.; Ahrns, I.; Sanchez-Gestido, M. On-ground validation of a CNN-based monocular pose estimation system for uncooperative spacecraft: Bridging domain shift in rendezvous scenarios. Acta Astronaut. 2022, 196, 123–138. [Google Scholar] [CrossRef]
- Li, K.; Zhang, H.; Hu, C. Learning-Based Pose Estimation of Non-Cooperative Spacecrafts with Uncertainty Prediction. Aerospace 2022, 9, 592. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, T.S.; Faugeras, O.D. Determination of camera location from 2-D to 3-D line and point correspondences. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 28–37. [Google Scholar] [CrossRef]
- Shiu, Y.C.; Ahmad, S. 3D location of circular and spherical features by monocular model-based vision. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, Cambridge, MA, USA, 14–17 November 1989; pp. 576–581. [Google Scholar]
- Meng, C.; Xue, J.; Hu, Z. Monocular Position-Pose Measurement Based on Circular and Linear Features. In Proceedings of the 2015 International Conference on Digital Image Computing: Techniques and Applications (DICTA), Adelaide, Australia, 23–25 November 2015; pp. 1–8. [Google Scholar]
- Meng, C.; Li, Z.; Sun, H.; Yuan, D.; Bai, X.; Zhou, F. Satellite Pose Estimation via Single Perspective Circle and Line. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 3084–3095. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 5105–5114. [Google Scholar]
- Manhardt, F.; Kehl, W.; Navab, N.; Tombari, F. Deep model-based 6d pose refinement in rgb. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 800–815. [Google Scholar]
- Wang, Y.; Tan, X.; Yang, Y.; Liu, X.; Ding, E.; Zhou, F.; Davis, L.S. 3d pose estimation for fine-grained object categories. In Proceedings of the European Conference on Computer Vision Workshops, Munich, Germany, 8–14 September 2018; pp. 619–632. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Zhang, H.; Liu, Z.; Jiang, Z.; An, M.; Zhao, D. BUAA-SID1.0 space object image dataset. Spacecr. Recovery Remote. Sens. 2010, 31, 65–71. [Google Scholar]
- Meng, G.; Jiang, Z.; Liu, Z.; Zhang, H.; Zhao, D. Full-viewpoint 3D Space Object Recognition Based on Kernel Locality Preserving Projections. Chin. J. Aeronaut. 2010, 23, 563–572. [Google Scholar]
- Corsini, M.; Cignoni, P.; Scopigno, R. Efficient and flexible sampling with blue noise properties of triangular meshes. IEEE Trans. Vis. Comput. Graph. 2012, 18, 914–924. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Red Hook, NY, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]



| Type | Apperance |
|---|---|
| A2100 | Has a pair of solar wings, which are symmetrically placed on both sides of the cube’s body |
| COBE | Has three solar wings, which are placed around the cylindrical body evenly. |
| EARLY-BIRD | Has two solar wings, which are distributed on the same side of the body. |
| FENGYUN | Has an entirely cylindrical satellite. |
| GALILEO | Has three long pole structures distributed around the body. |
| N.O. | ||||
|---|---|---|---|---|
| L1 | 1 | 1 | 1 | |
| L2 | 1 | 1 | 1 | |
| L3 | 1 | 1 | 1 | |
| L4 | 1.3 | 0.4 | 1.3 |
| Evaluation Metric | Experimental Setting | |||
|---|---|---|---|---|
| L1 | L2 | L3 | L4 | |
| 0.220 ± 0.036 | 0.495 ± 0.028 | 0.550 ± 0.032 | 0.557 ± 0.028 | |
| 0.388 ± 0.020 | 0.883 ± 0.009 | 0.912 ± 0.012 | 0.737 ± 0.023 | |
| 0.292 ± 0.042 | 0.522 ± 0.068 | 0.560 ± 0.061 | 0.648 ± 0.052 | |
| 0.637 ± 0.046 | 0.941 ± 0.009 | 0.936 ± 0.021 | 0.941 ± 0.016 | |
| 0.967 ± 0.007 | 0.999 ± 0.000 | 0.999 ± 0.000 | 0.998 ± 0.000 | |
| 0.600 ± 0.028 | 0.924 ± 0.018 | 0.925 ± 0.030 | 0.948 ± 0.014 | |
| 6.27 ± 0.53 | 2.31 ± 0.243 | 2.32 ± 0.59 | 2.22 ± 0.35 | |
| 1.72 ± 0.11 | 0.56 ± 0.02 | 0.51 ± 0.03 | 0.81 ± 0.05 | |
| 7.91 ± 0.40 | 3.12 ± 0.45 | 3.05 ± 0.85 | 2.32 ± 0.45 | |
| Experimental Setting | Evaluation Metric | ||||||
|---|---|---|---|---|---|---|---|
| Model Size | |||||||
| Copy one-channel image to generate three-channel image | 0.941 ± 0.016 | 0.998 ± 0.000 | 0.948 ± 0.014 | 2.223 ± 0.352 | 0.806 ± 0.050 | 2.316 ± 0.452 | 42.70 MB |
| Input one-channel image and customize layer C1 | 0.938 ± 0.022 | 0.995 ± 0.001 | 0.944 ± 0.019 | 2.333 ± 0.587 | 0.919 ± 0.612 | 2.560 ± 0.548 | 42.68 MB |
| Evaluation Metric | Experimental Setting * | |||||
|---|---|---|---|---|---|---|
| ResNet18 Setting 1 | ResNet18 Setting 2 | ResNet18 Setting 3 | ResNet50 Setting 1 | ResNet50 Setting 2 | ResNet50 Setting 3 | |
| 0.557 ± 0.028 | 0.474 ± 0.024 | 0.388 ± 0.021 | 0.623 ± 0.079 | 0.403 ± 0.063 | 0.337 ± 0.061 | |
| 0.737 ± 0.023 | 0.630 ± 0.033 | 0.559 ± 0.024 | 0.786 ± 0.072 | 0.513 ± 0.108 | 0.256 ± 0.114 | |
| 0.648 ± 0.052 | 0.591 ± 0.118 | 0.558 ± 0.057 | 0.649 ± 0.193 | 0.187 ± 0.099 | 0.238 ± 0.073 | |
| 0.941 ± 0.016 | 0.897 ± 0.019 | 0.884 ± 0.010 | 0.971 ± 0.005 | 0.907 ± 0.032 | 0.828 ± 0.064 | |
| 0.998 ± 0.000 | 0.995 ± 0.002 | 0.985 ± 0.002 | 0.998 ± 0.000 | 0.990 ± 0.075 | 0.785 ± 0.287 | |
| 0.948 ± 0.014 | 0.906 ± 0.036 | 0.905 ± 0.011 | 0.975 ± 0.010 | 0.392 ± 0.293 | 0.458 ± 0.328 | |
| 2.223 ± 0.352 | 3.248 ± 0.647 | 3.912 ± 0.265 | 1.588 ± 0.226 | 2.616 ± 0.547 | 4.815 ± 2.546 | |
| 0.806 ± 0.050 | 1.035 ± 0.077 | 1.323 ± 0.078 | 0.725 ± 0.104 | 1.330 ± 0.301 | 7.448 ± 13.529 | |
| 2.316 ± 0.452 | 3.353 ± 1.148 | 3.955 ± 0.346 | 1.392 ± 0.458 | 45.055 ± 41.092 | 43.644 ± 43.736 | |
| N.O. | Structure of Point Cloud Convolution Network | Structure of Spatial Related Features Extractor |
|---|---|---|
| S1 | PointNet | , , = 3, 2, 3 , , = 3, 2, 3 , , = 3, 2, 3 |
| S2 | PointNet++ (SSG) | , , = 3, 2, 3 , , = 3, 2, 3 , , = 3, 2, 3 |
| S3 | PointNet++ (SSG) | , , = 3, 1, 5 , , = 3, 1, 5 , , = 3, 1, 5 |
| S4 | PointNet++ (SSG) | , , = 3, 1, 5 , , = 5, 1, 3 , , = 7, 1, 1 |
| S5 | PointNet++ (MSG) | , , = 3, 2, 3 , , = 3, 2, 3 , , = 3, 2, 3 |
| S6 | PointNet++ (MSG) | , , = 3, 1, 5 , , = 5, 1, 3 , , = 7, 1, 1 |
| Evaluation Metric | Experimental Setting | ||||||
|---|---|---|---|---|---|---|---|
| Compare | S1 | S2 | S3 | S4 | S5 | S6 | |
| 0.278 ± 0.034 | 0.306 ± 0.043 | 0.331 ± 0.019 | 0.335 ± 0.011 | 0.294 ± 0.035 | 0.364 ± 0.065 | 0.386 ± 0.033 | |
| 0.369 ± 0.024 | 0.350 ± 0.120 | 0.448 ± 0.030 | 0.445 ± 0.022 | 0.371 ± 0.048 | 0.483 ± 0.049 | 0.454 ± 0.035 | |
| 0.370 ± 0.060 | 0.439 ± 0.066 | 0.645 ± 0.073 | 0.458 ± 0.064 | 0.350 ± 0.072 | 0.563 ± 0.056 | 0.560 ± 0.06 | |
| 0.699 ± 0.317 | 0.730 ± 0.050 | 0.745 ± 0.024 | 0.756 ± 0.012 | 0.711 ± 0.032 | 0.765 ± 0.043 | 0.773 ± 0.019 | |
| 0.849 ± 0.017 | 0.785 ± 0.162 | 0.901 ± 0.027 | 0.893 ± 0.021 | 0.864 ± 0.025 | 0.892 ± 0.017 | 0.891 ± 0.014 | |
| 0.714 ± 0.056 | 0.769 ± 0.042 | 0.782 ± 0.043 | 0.782 ± 0.044 | 0.666 ± 0.109 | 0.831 ± 0.029 | 0.839 ± 0.022 | |
| _MAE | 9.55 ± 1.41 | 8.16 ± 1.01 | 7.94 ± 1.00 | 7.48 ± 0.74 | 9.49 ± 1.61 | 7.54 ± 1.18 | 7.40 ± 0.75 |
| _MAE | 4.86 ± 0.49 | 5.12 ± 1.14 | 3.91 ± 0.65 | 4.02 ± 0.50 | 4.77 ± 0.49 | 4.34 ± 0.66 | 4.26 ± 0.30 |
| _MAE | 11.48 ± 1.56 | 9.96 ± 0.48 | 9.63 ± 1.64 | 9.61 ± 1.50 | 13.35 ± 3.49 | 9.05 ± 2.09 | 8.29 ± 1.04 |
| Evaluation Metric | A2100 | COBE | EARLY-BIRD | FENGYUN | GALILEO | MEAN |
|---|---|---|---|---|---|---|
| 0.437 | 0.132 | 0.414 | 0.317 | 0.350 | 0.330 | |
| 0.495 | 0.643 | 0.608 | 0.745 | 0.324 | 0.563 | |
| 0.630 | 0.879 | 0.725 | 0.821 | 0.799 | 0.771 | |
| 0.803 | 0.404 | 0.860 | 0.720 | 0.783 | 0.714 | |
| 0.893 | 0.996 | 0.972 | 0.996 | 0.851 | 0.942 | |
| 0.856 | 0.981 | 0.966 | 0.990 | 0.962 | 0.951 | |
| 6.23 | 20.46 | 5.36 | 9.17 | 8.02 | 9.85 | |
| 4.01 | 1.01 | 1.26 | 0.83 | 7.29 | 2.88 | |
| 7.36 | 1.05 | 1.69 | 0.92 | 1.80 | 2.56 |
| Evaluation Metric | Benchmark Method | Our Method |
|---|---|---|
| 0.274 | 0.330 | |
| 0.418 | 0.563 | |
| 0.614 | 0.771 | |
| 0.680 | 0.714 | |
| 0.885 | 0.942 | |
| 0.893 | 0.951 | |
| 10.43 | 9.85 | |
| 3.80 | 2.88 | |
| 4.26 | 2.56 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, S.; Zhang, H.; Meng, G.; An, M.; Xie, F.; Jiang, Z. Deep-Learning-Based Satellite Relative Pose Estimation Using Monocular Optical Images and 3D Structural Information. Aerospace 2022, 9, 768. https://doi.org/10.3390/aerospace9120768
Qiao S, Zhang H, Meng G, An M, Xie F, Jiang Z. Deep-Learning-Based Satellite Relative Pose Estimation Using Monocular Optical Images and 3D Structural Information. Aerospace. 2022; 9(12):768. https://doi.org/10.3390/aerospace9120768
Chicago/Turabian StyleQiao, Sijia, Haopeng Zhang, Gang Meng, Meng An, Fengying Xie, and Zhiguo Jiang. 2022. "Deep-Learning-Based Satellite Relative Pose Estimation Using Monocular Optical Images and 3D Structural Information" Aerospace 9, no. 12: 768. https://doi.org/10.3390/aerospace9120768
APA StyleQiao, S., Zhang, H., Meng, G., An, M., Xie, F., & Jiang, Z. (2022). Deep-Learning-Based Satellite Relative Pose Estimation Using Monocular Optical Images and 3D Structural Information. Aerospace, 9(12), 768. https://doi.org/10.3390/aerospace9120768


_Zhu.png)



