Numerical Research of an Ice Accretion Delay Method by the Bio-Inspired Leading Edge
Abstract
:1. Introduction
2. Numerical Simulation Methods
2.1. Governing Equations
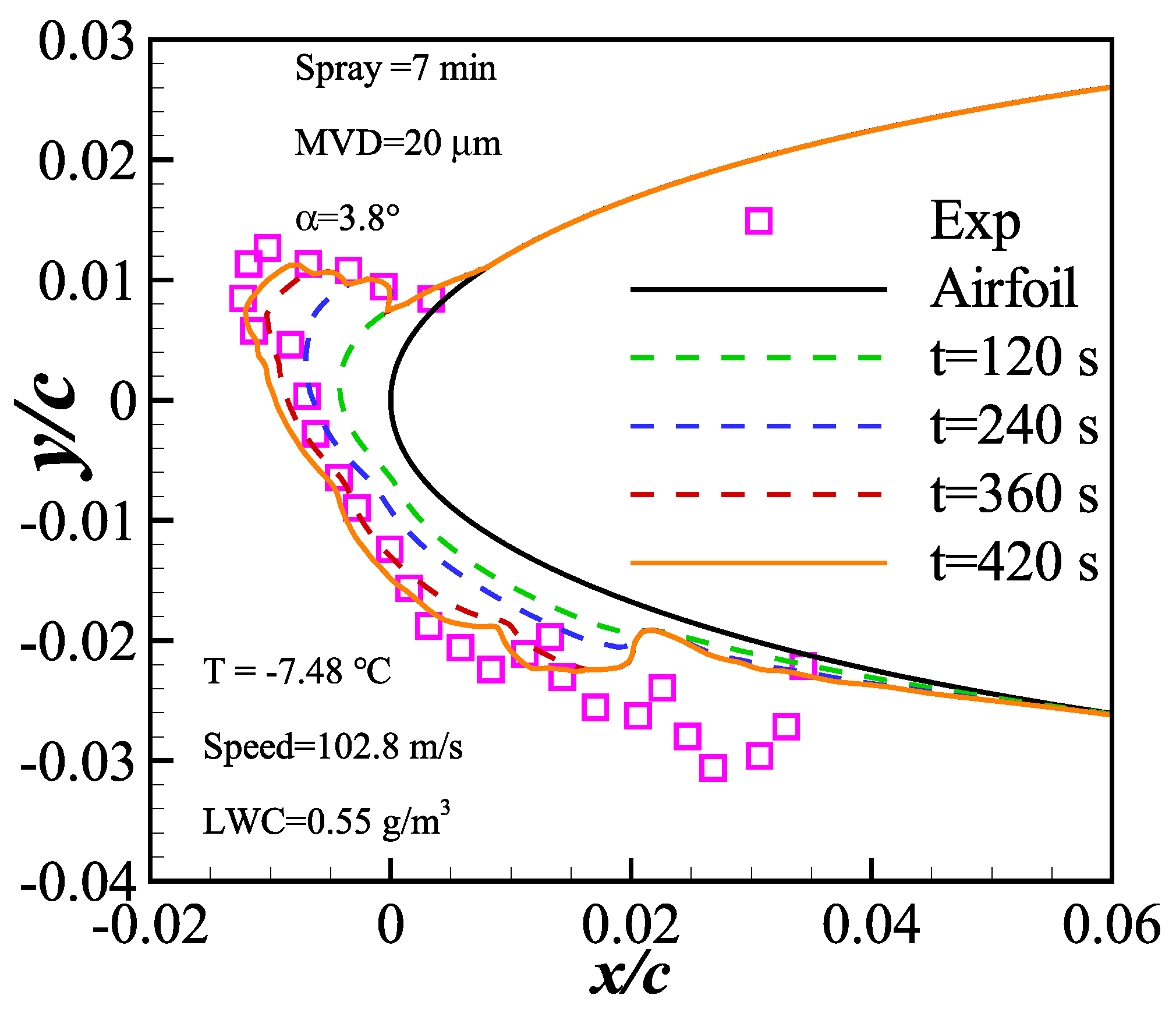
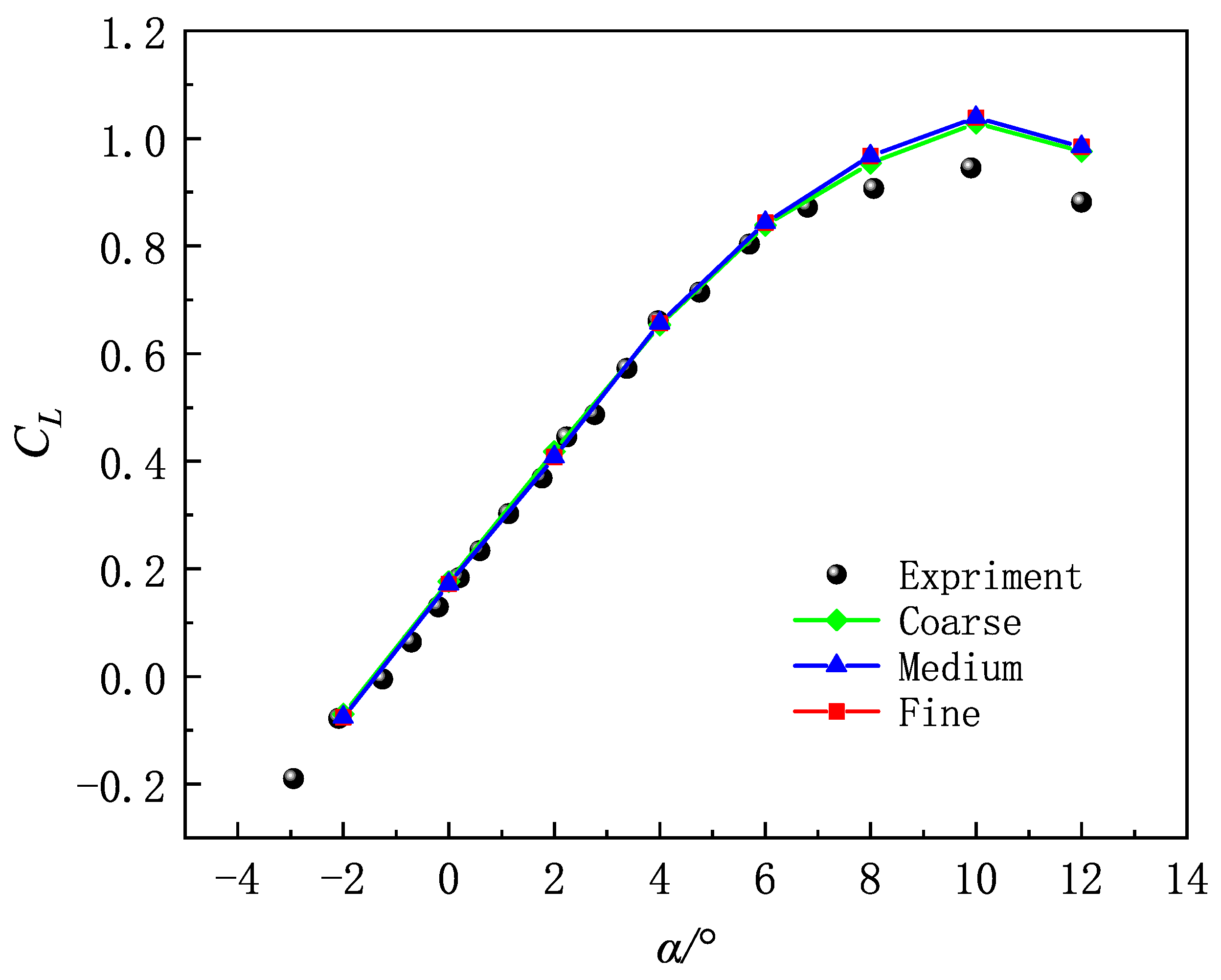
2.2. Method Verification
3. Results and Discussion
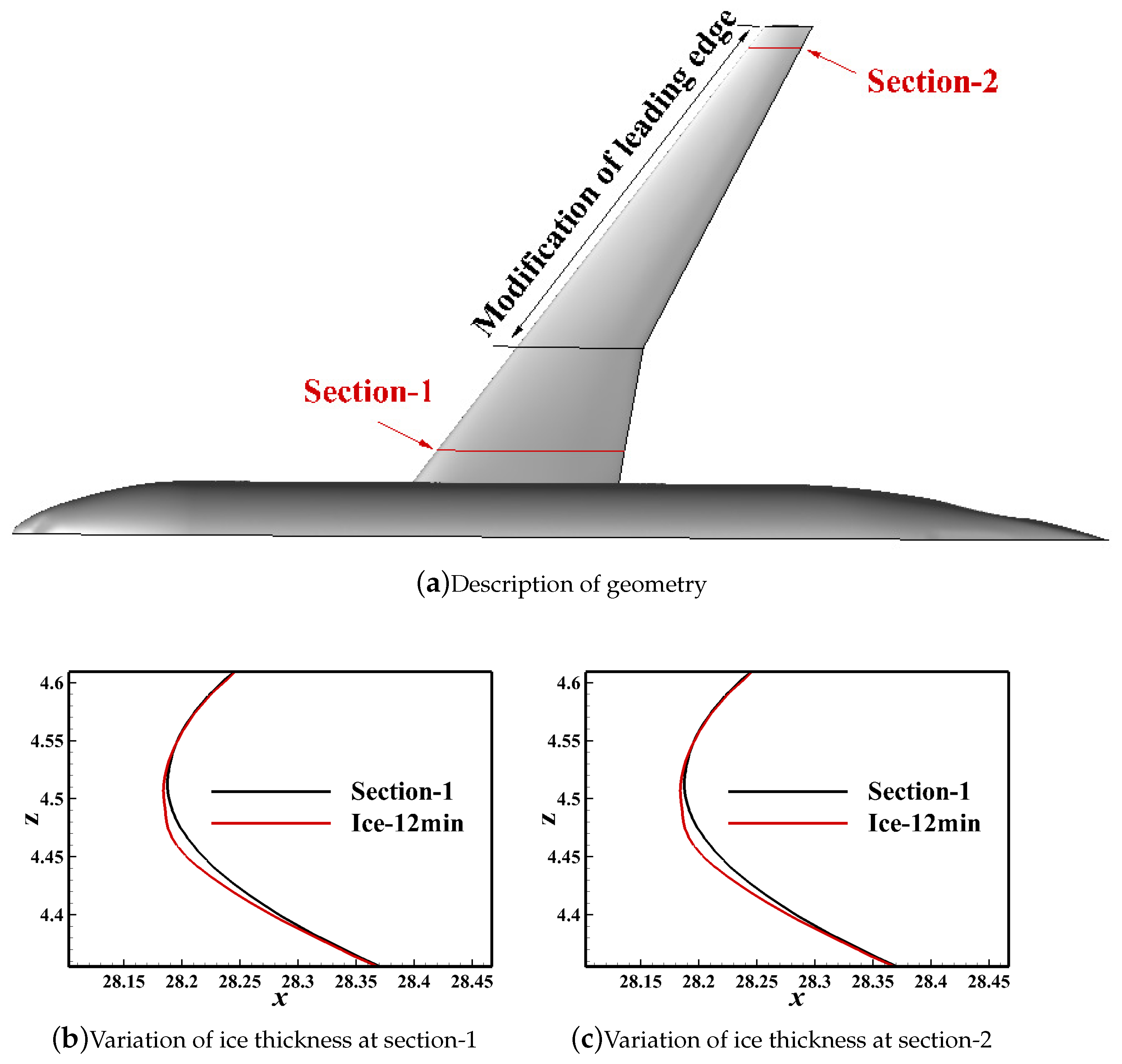
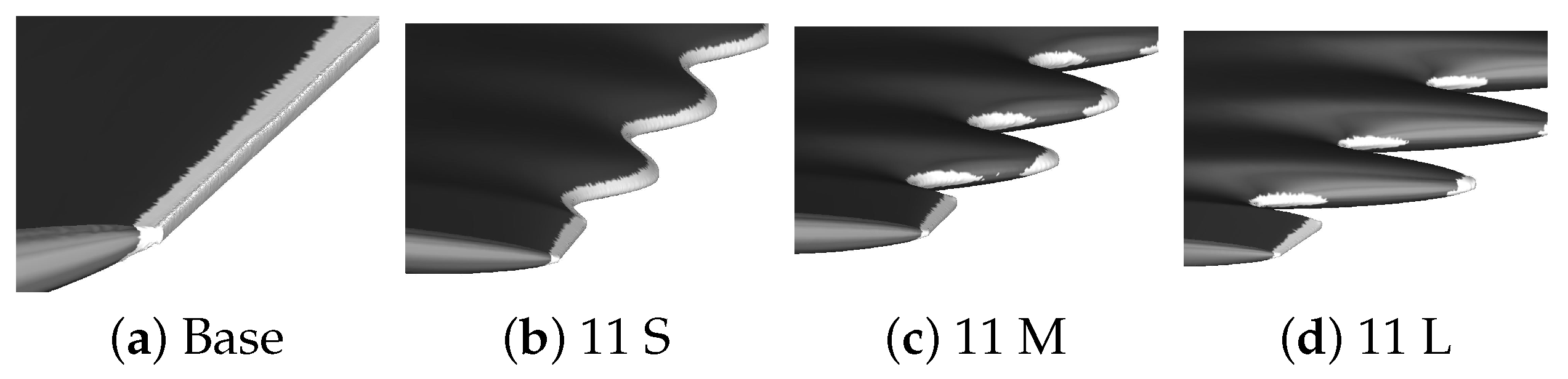
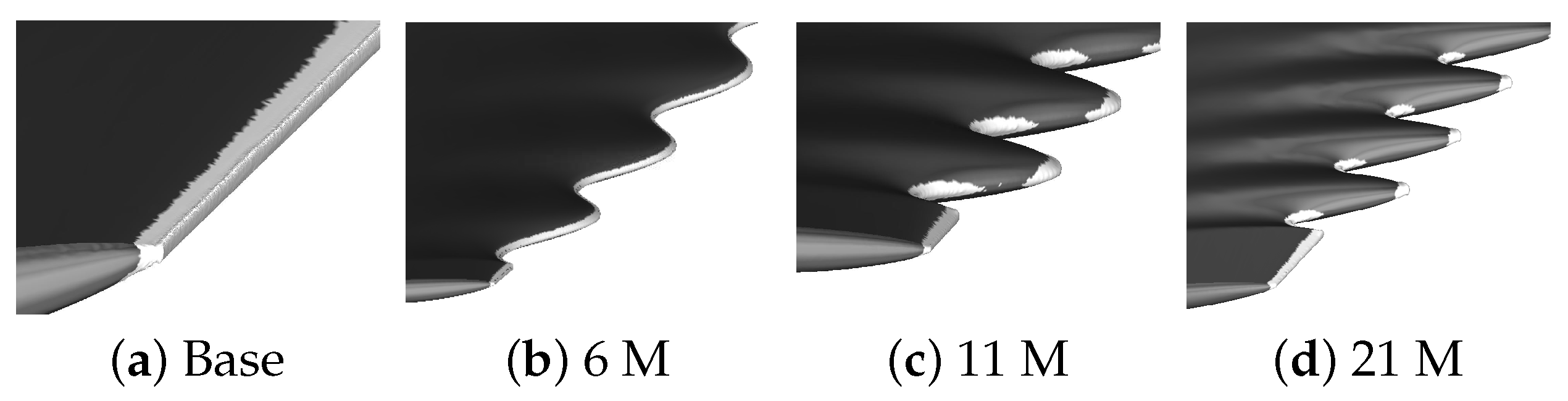
3.1. Geometry Description
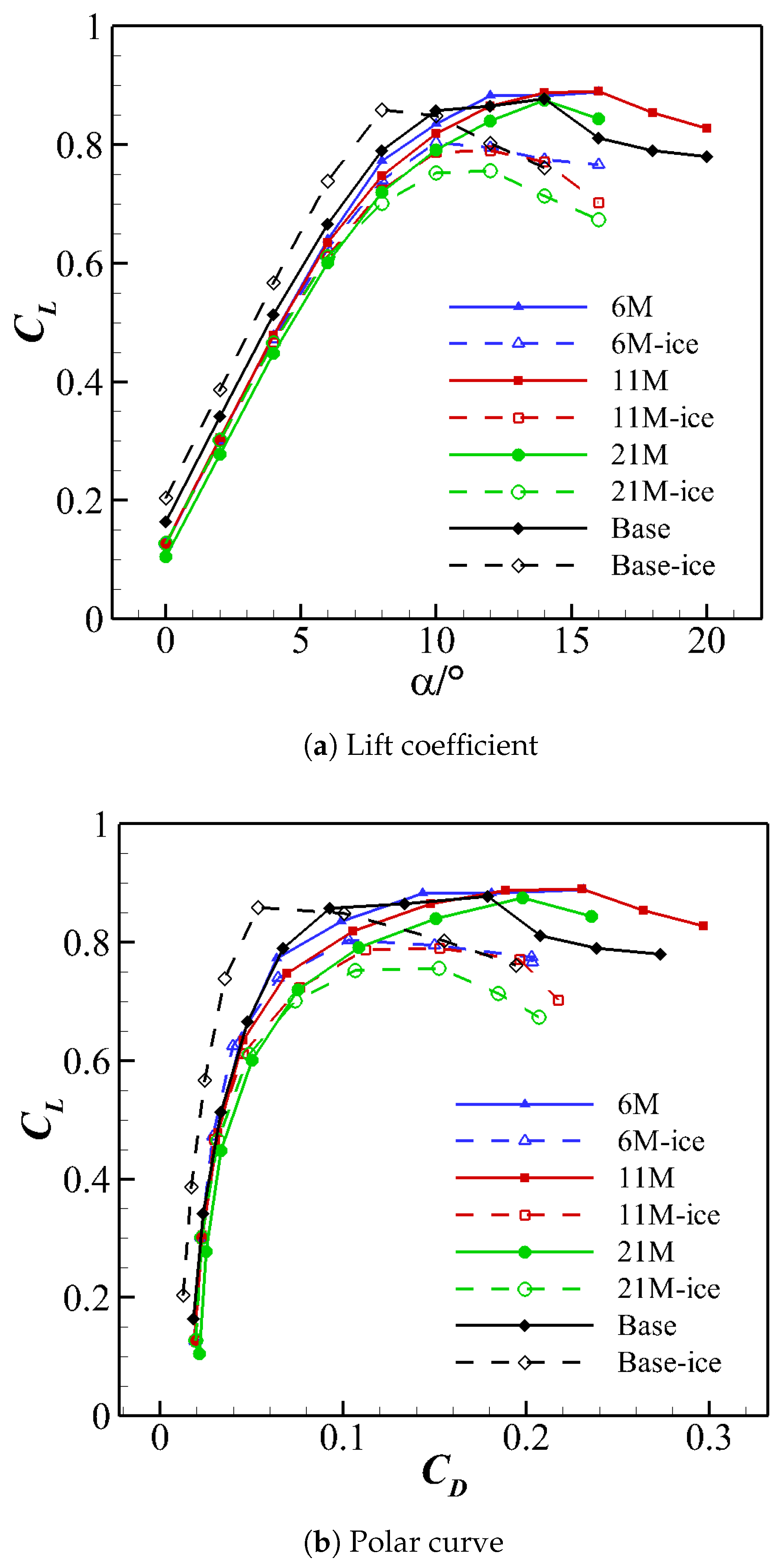
3.2. Effect of Amplitude
3.3. Effect of Wavelength
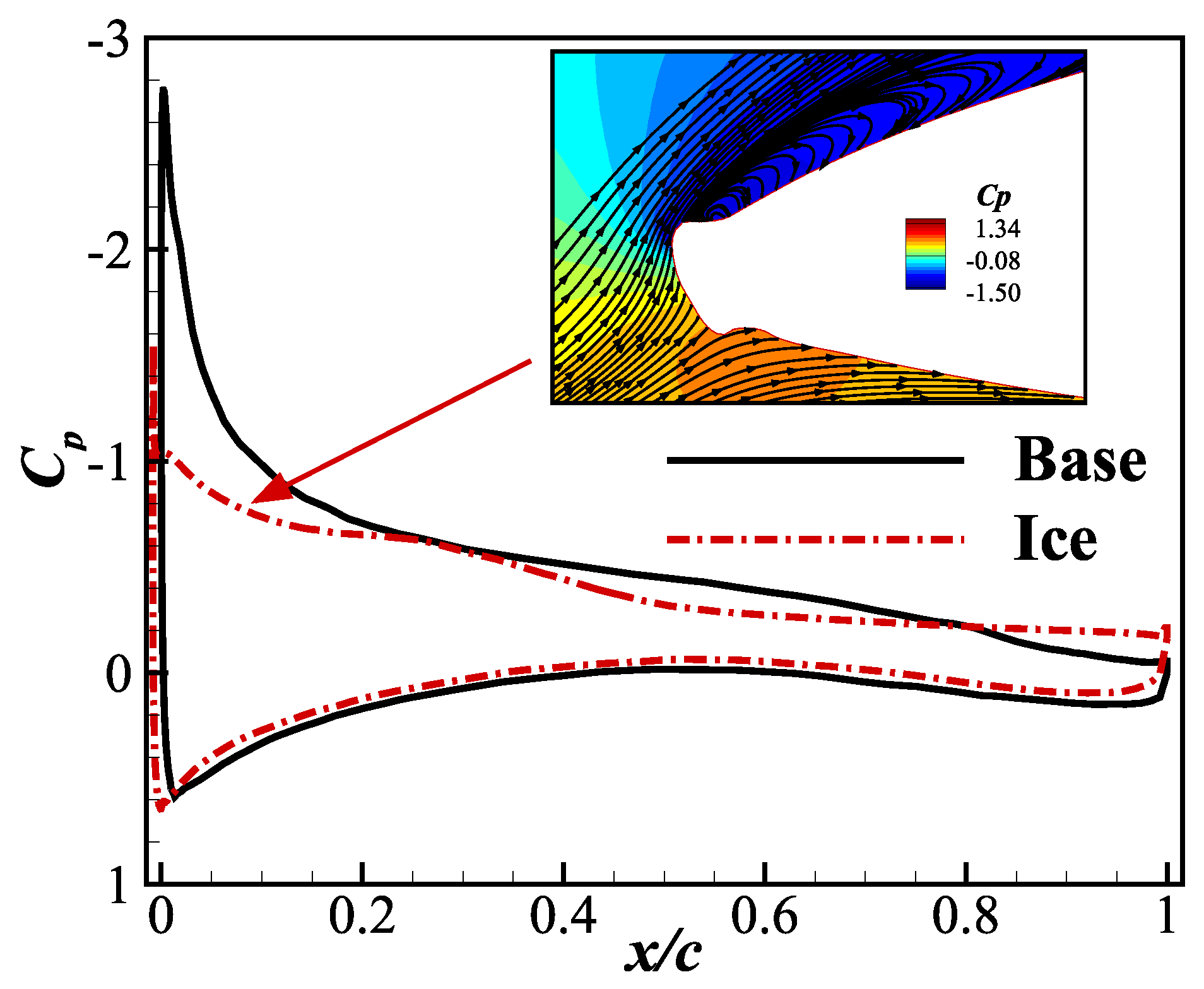
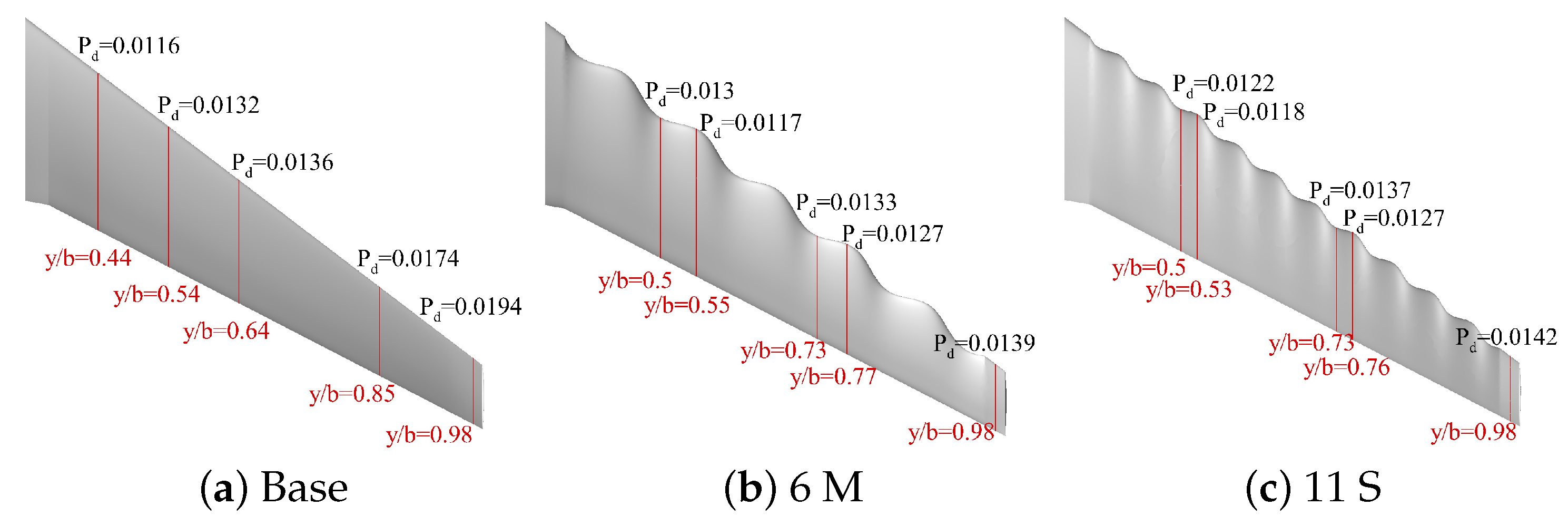
3.4. Analysis of Flow Field
3.5. Procrustes Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| WCA | Water contact angle |
| CRM | Common research model |
| LWC | Liquid water droplet content |
References
- Addy, H.E. Ice Accretions and Icing Effects for Modern Airfoils; National Aeronautics Administration, Glenn Research Center: Washington, DC, USA, 2000. [Google Scholar]
- Hassan, N.; Lu, S.; Xu, W.; He, G.; Faheem, M.; Ahmad, N.; Khan, M.A.; Butt, B.Z. Fabrication of a Pt nanoparticle surface on an aluminum substrate to achieve excellent superhydrophobicity and catalytic activity. New J. Chem. 2019, 43, 6069–6079. [Google Scholar] [CrossRef]
- Annavarapu, R.K.; Kim, S.; Wang, M.; Hart, A.J.; Sojoudi, H. Explaining evaporation-triggered wetting transition using local force balance model and contact line-fraction. Sci. Rep. 2019, 9, 405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khadak, A.; Subeshan, B.; Asmatulu, R. Studies on de-icing and anti-icing of carbon fiber-reinforced composites for aircraft surfaces using commercial multifunctional permanent superhydrophobic coatings. J. Mater. Sci. 2021, 56, 3078–3094. [Google Scholar] [CrossRef]
- Ma, L.; Li, H.; Hu, H. An Experimental Study on the Dynamics of Water Droplets Impingement onto a Goose Feather. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; p. 442. [Google Scholar]
- Alizadeh-Birjandi, E.; Tavakoli-Dastjerdi, F.; Leger, J.S.; Faull, K.F.; Davis, S.H.; Rothstein, J.P.; Pirouz Kavehpour, H. Delay of ice formation on penguin feathers. Eur. Phys. J. Spec. Top. 2020, 229, 1881–1896. [Google Scholar] [CrossRef]
- Diebold, J.M.; Broeren, A.P.; Bragg, M. Aerodynamic classification of swept-wing ice accretion. In Proceedings of the 5th AIAA Atmospheric and Space Environments Conference, San Diego, CA, USA, 24–27 June 2013; p. 2825. [Google Scholar]
- Broeren, A.P. Swept-Wing Ice Accretion Characterization and Aerodynamics: Research Plans and Current Status. In Proceedings of the 2011 Annual Technical Meeting, St. Louis, MO, USA, 10–12 May 2011. [Google Scholar]
- Li, H.R.; Zhang, Y.F.; Chen, H.X. Optimization design of airfoils under atmospheric icing conditions for UAV. Chin. J. Aeronaut. 2022, 35, 118–133. [Google Scholar]
- Li, H.; Zhang, Y.; Chen, H. Optimization of supercritical airfoil considering the ice-accretion effects. AIAA J. 2019, 57, 4650–4669. [Google Scholar] [CrossRef]
- Yirtici, O.; Tuncer, I.H.; Ozgen, S. Aerodynamic shape optimization of wind turbine blades for reducing power production losses due to ice accretion. In Proceedings of the 35th Wind Energy Symposium, Grapevine, TX, USA, 9–13 January 2017; p. 1850. [Google Scholar]
- Zhang, Y.; Zhang, X.; Li, Y.; Chang, M.; Xu, J.K. Aerodynamic performance of a low-Reynolds UAV with leading-edge protuberances inspired by humpback whale flippers. Chin. J. Aeronaut. 2021, 34, 415–424. [Google Scholar] [CrossRef]
- Chen, H.; Pan, C.; Wang, J. Effects of sinusoidal leading edge on delta wing performance and mechanism. Sci. China Technol. Sci. 2013, 56, 772–779. [Google Scholar] [CrossRef]
- Gopinathan, V.; Bruce Ralphin Rose, J. Aerodynamics with state-of-the-art bioinspired technology: Tubercles of humpback whale. Proc. Inst. Mech. Eng. Part J. Aerosp. Eng. 2021, 235, 2359–2377. [Google Scholar] [CrossRef]
- Johari, H.; Henoch, C.; Custodio, D.; Levshin, A. Effects of leading-edge protuberances on airfoil performance. AIAA J. 2007, 45, 2634–2642. [Google Scholar] [CrossRef]
- Cai, C.; Zuo, Z.; Maeda, T.; Kamada, Y.; Li, Q.; Shimamoto, K.; Liu, S. Periodic and aperiodic flow patterns around an airfoil with leading-edge protuberances. Phys. Fluids 2017, 29, 115110. [Google Scholar] [CrossRef]
- Miklosovic, D.S.; Murray, M.M.; Howle, L.E. Experimental evaluation of sinusoidal leading edges. J. Aircr. 2007, 44, 1404–1408. [Google Scholar] [CrossRef]
- Gower, J.C. Generalized procrustes analysis. Psychometrika 1975, 40, 33–51. [Google Scholar] [CrossRef]
- Meyners, M.; Kunert, J.; Qannari, E.M. Comparing generalized procrustes analysis and STATIS. Food Qual. Prefer. 2000, 11, 77–83. [Google Scholar] [CrossRef] [Green Version]
- Bourgault, Y.; Beaugendre, H.; Habashi, W.G. Development of a shallow-water icing model in FENSAP-ICE. J. Aircr. 2000, 37, 640–646. [Google Scholar] [CrossRef]
- Beaugendre, H.; Morency, F.; Habashi, W. ICE3D, FENSAP-ICE’S 3D in-flight ice accretion module. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002; p. 385. [Google Scholar]
- Morency, F.; Beaugendre, H.; Habashi, W. FENSAP-ICE: A Navier-Stokes Eulerian Droplet Impingement Approach for High-Lift Devices. CASI Conf. 2001, 15, 16. [Google Scholar]
- Ozcer, I.A.; Baruzzi, G.S.; Reid, T.; Habashi, W.G.; Fossati, M.; Croce, G. Fensap-Ice: Numerical Prediction of Ice Roughness Evolution, and Its Effects on Ice Shapes; SAE Technical Paper, 2011-38-0024; SAE International: Warrendale, PA, USA, 2011. [Google Scholar] [CrossRef]
- Pena, D.; Hoarau, Y.; Laurendeau, E. A single step ice accretion model using Level-Set method. J. Fluids Struct. 2016, 65, 278–294. [Google Scholar] [CrossRef] [Green Version]
- Vassberg, J.; Dehaan, M.; Rivers, M.; Wahls, R. Development of a common research model for applied CFD validation studies. In Proceedings of the 26th AIAA Applied Aerodynamics Conference, Honolulu, HI, USA, 18–21 August 2008; p. 6919. [Google Scholar]
- Çakir, T. Evaluation of Ice Accretion on a 2D Airfoil Using Commercial and Open Software. 2018. Available online: http://essay.utwente.nl/85119/ (accessed on 30 January 2018).
- Bolzon, M.; Kelso, R.; Arjomandi, M. The effects of tubercles on swept wing performance at low angles of attack. In Proceedings of the 19th Australasian Fluid Mechanics Conference, Melbourne, Australia, 8–11 December 2014; pp. 8–11. [Google Scholar]
- Pillai, S.N.; Sundaresan, A.; Gopal, R.; Priya, S.; Pasha, A.A.; Hameed, A.Z.; Jameel, A.G.A.; Reddy, V.M.; Juhany, K.A. Estimation of Chaotic Surface Pressure Characteristics of Ice Accreted Airfoils–A 0–1 Test Approach. IEEE Access 2021, 9, 114441–114456. [Google Scholar] [CrossRef]






| Type | Value |
|---|---|
| Reference area (S) | 383.6896 m2 |
| Reference chord length (c) | 7 m |
| Reference spanwise length (b) | 58.8137 m |
| Label | Amplitude (A) | Wavelength () |
|---|---|---|
| 6 M | 5 c | 3.5 m |
| 11 S | 2.5 c | 2.1 m |
| 11 M | 5 c | 2.1 m |
| 11 L | 10 c | 2.1 m |
| 21 M | 5 c | 1.05 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Wang, T.; Fu, Y.; Zhang, Y.; Chen, G. Numerical Research of an Ice Accretion Delay Method by the Bio-Inspired Leading Edge. Aerospace 2022, 9, 774. https://doi.org/10.3390/aerospace9120774
Xu X, Wang T, Fu Y, Zhang Y, Chen G. Numerical Research of an Ice Accretion Delay Method by the Bio-Inspired Leading Edge. Aerospace. 2022; 9(12):774. https://doi.org/10.3390/aerospace9120774
Chicago/Turabian StyleXu, Xiaogang, Tianbo Wang, Yifan Fu, Yang Zhang, and Gang Chen. 2022. "Numerical Research of an Ice Accretion Delay Method by the Bio-Inspired Leading Edge" Aerospace 9, no. 12: 774. https://doi.org/10.3390/aerospace9120774
APA StyleXu, X., Wang, T., Fu, Y., Zhang, Y., & Chen, G. (2022). Numerical Research of an Ice Accretion Delay Method by the Bio-Inspired Leading Edge. Aerospace, 9(12), 774. https://doi.org/10.3390/aerospace9120774








