Initial Assessment of a Fuel Cell—Gas Turbine Hybrid Propulsion Concept

Abstract

A fuel cell—gas turbine hybrid propulsion concept is introduced and initially assessed. The concept uses the water mass flow produced by a hydrogen fuel cell in order to improve the efficiency and power output of the gas turbine engine through burner steam injection. Therefore, the fuel cell product water is conditioned through a process of condensation, pressurization and re-vaporization. The vaporization uses the waste heat of the gas turbine exhaust. The functional principles of the system concept are introduced and discussed, and appropriate methodology for an initial concept evaluation is formulated. Essential technology fields are surveyed in brief. The impact of burner steam injection on gas turbine efficiency and sizing is parametrically modelled. Simplified parametric models of the fuel cell system and key components of the water treatment process are presented. Fuel cell stack efficiency and specific power levels are methodically derived from latest experimental studies at the laboratory scale. The overall concept is assessed for a liquid hydrogen fueled short-/medium range aircraft application. Block fuel savings of up to 7.1% are found for an optimum design case based on solid oxide fuel cell technology. The optimum design features a gas turbine water-to-air ratio of 6.1% in cruise and 62% reduced high-level NO_x emissions.

1. Introduction

Driven by the drastic need for decarbonization in aviation, hydrogen as a zero in-flight CO₂ emissions fuel has recently experienced a great revival in aeronautical research and development. Beyond the well-known and demonstrated option of hydrogen combustion in classic gas turbine (GT) engines, significant technological progress in electrochemical conversion systems adds to the dynamic development of hydrogen-based visions for future air transport. However, the application of fuel cells (FCs) in the scheme of propulsion and power for transport category aircraft holds great challenges, and classic GT engines still feature significant advantages in power-specific weight over future FC systems. At the same time, further efficiency improvements and significant NO_x emission reduction will be required for future aero engines. The injection of water in the compression section or the combustion chamber of a GT engine is well-known for its enhancement of cycle-specific work and efficiency, as well as its potential for significant cuts in NO_x emissions.

In this paper, a synergistic concept for a FC–GT hybrid aircraft propulsion system is introduced and initially assessed. A basic functional schematic of concept is presented in Figure 1. The concept utilizes the product water of the FC in order to improve the performance and emission characteristics of the GT engine. The FC product water is first condensed and separated from the FC residual air mass flow, then pressurized and re-evaporated before being injected in the GT engine. This treatment process allows for minimum work effort for the water pressurization—due to the incompressibility of liquid water—while the energy required for its re-evaporation is drawn from the GT exhaust heat. The electric power produced by the FC is available as a convenient source for on-board electric customers, including aircraft subsystems and possibly decentralized or distributed propulsors. Operational flexibility may be enhanced through an intermediate storage possibility for the liquefied water, in order to decouple the GT steam injection from the FC power setting.

At first, important developments in the key field of the technology relevant for the studied FC–GT hybrid propulsion system type are reviewed in the paper. Subsequently, the methodological foundation for the conceptual assessment is formulated and discussed, before the results obtained from isolated power system and aircraft-integrated design studies are presented and examined.

2. Review of Key Technologies

The presented study is motivated by and based upon a number of key technological developments in different fields, including hydrogen as an alternative fuel option for aviation, significant advances in FC technology, high-performance heat exchangers (HEXs) and advanced GT technology involving steam injection in the thermodynamic cycle. In this section, relevant aspects of technological progress in those fields are surveyed in brief.

2.1. Hydrogen Fuel in Aviation

Combustion and electrochemical conversion of hydrogen do not create carbon emissions. In a recent well-to-wake analysis of CO₂ equivalent emissions, green hydrogen by far outperformed conventional jet fuel as well as all other considered synthetic fuel options [1]. As a typical intermediate product along many production pathways for alternative hydrocarbon-based fuels, minimum fuel selling prices of liquid hydrogen (LH₂) are likely to be more affordable than most synthetically produced sustainable drop-in fuels [2]. Due to a different stoichiometry of the chemical reaction, the use of hydrogen fuel yields a water production rate that is approximately 2.5 times as high as the one obtained from the combustions of kerosene fuel. The effect of the resulting water vapor emissions on climate change is not yet fully understood—the debate mainly centers around conditions for the formation and avoidance of persistent contrails [3].

For commercial air transport, hydrogen as a fuel poses significant challenges for vehicular design [4] as well as in terms of ground infrastructural prerequisites [5]. The amounts of energy required for typical commercial transport aircraft missions require hydrogen fuel to be stored in its most compact form, i.e., as LH₂. The cryogenic temperature levels associated with LH₂, combined with a persisting low volumetric energy density in comparison to hydrocarbon fuels, require unconventional and complex onboard storage solutions that involve considerable structural mass and aerodynamic drag penalties.

Nevertheless, hydrogen-based aircraft designs have been considered in both theoretical and experimental studies throughout the history of commercial aviation. Famous hydrogen-fuelled flight tests were performed in the 1950s on a modified Martin B-57 “Canberra” and later in the 1980s on the Tupolev Tu-155, a modified version of the commercial Tu-154. Extensive preliminary design studies were performed in the 1970s by Boeing [6] and Lockheed [7,8] under NASA contract as well as during the European Commission (EC) funded CryoPlane project led by Airbus in the early 2000s. Since then, the topic of hydrogen-fuelled aircraft has been continuously investigated as part of academic research, for example at Cranfield University, yielding a series of doctoral theses on hydrogen-fuelled aero-engine and aircraft systems (e.g., [9,10], as well as the ongoing EC-funded project ENABLEH2 [11]).

A multitude of advanced hydrogen-fuelled aircraft concepts have recently been published by research organisations (e.g., NASA’s N3-X [12], Bauhaus Luftfahrt’s Hyliner2.0 [13], FlyZero [14]) and announced as technology concept planes by the industry (e.g., Airbus ZeroE [15], Do228 FC demonstrator [16]). A broad overview on hydrogen technology, economics and climate impact by 2050 is provided by a study issued by the European “CleanSky” and “Fuel Cells and Hydrogen” Joint Undertakings in 2020 [17]. As a first key technology brick in the context of the present paper, a brief overview of advanced fuel cell concepts is provided in the next section.

2.2. Advanced Fuel Cell Concepts

An FC is an electrochemical energy conversion device, which enables the direct conversion of chemical energy stored in a fuel to electricity. The fuel, typically hydrogen, is oxidized at the anode, while ambient oxygen is reduced at the cathode. In the process, water—and in the case of fuels other than hydrogen—additional by-products are formed and released from the cell (cf. Equation (1)):

$$H_2+0.5O_2\to H_{2}O.$$

(1)

The voltage that could theoretically be drawn from this reaction is 1.23 V at room temperature [18], however, various voltage losses occur in the cell, e.g., due to hindered mass transport, electrical resistance, fuel crossover or sluggish kinetics. Consequently, the practically achievable voltages U_Cell are significantly lower, the electrical efficiency η_Stack of the cell stack in reference to the heating value per mol of fuel FHV_mol (cf. Equation (2)) is diminished and the surplus energy is released as heat:

$${\eta }_{Stack}=\frac{2·F·U_{Cell}}{FH{V}_{mol}},$$

(2)

where F is the Faraday constant.

In an effort to find FCs applicable to versatile operating environments and application demands, various cell types have been developed. Out of these, the polymer electrolyte FC (PEFC), which is schematically depicted in Figure 2a, is the current state-of-the-art FC for transportation applications due to its comparably high specific power and quick load response. Therefore, most hydrogen-electric aircraft designs based on FC-electric propulsion rely on the PEFC (e.g., research projects Go4Hy2, BALIS, BILBO). This is comprised of a proton-conducting membrane, most commonly a perfluorosulfonic acid (PFSA) polymer that transports the protons formed on the anode over to the cathode while avoiding gas crossover and preventing short-circuiting due to its electrically insulating properties. As these functionalities are only maintained when the membrane’s water content is high enough, inlet gases are typically humidified. Generally, water management is crucial for successful PEFC operation in order to balance sufficient humidification on the one hand and the avoidance of excess amounts of (product) water causing pore flooding and mass transport losses on the other. Gas-diffusion layers (GDLs) are employed to aid water removal and gas transport to the catalytically active sites in the catalyst layer (CL). Catalysts are required to enhance the reaction kinetics of the hydrogen oxidation reaction and the oxygen reduction reaction (HOR and ORR); state-of-the-art high-performance materials are based on the noble metal Pt. It should be briefly noted that the schematics in Figure 2 only depict the core components of FCs. One individual cell would deliver a relatively small voltage as discussed above, which is why typically numerous cells are connected in series through bipolar plates, or so-called interconnects for higher temperature applications, to obtain an FC stack with technically usable output voltage. The stack itself is accompanied by balance-of-plant components such as compressors, humidifiers, thermal management, etc. The entire assembly will, in the following, be termed “FC system”.

The standard operating temperature of the PEFC is between 60 and 90 °C, which is a range in which reaction kinetics employing the above-mentioned catalysts are high enough to yield technically feasible current densities and the membrane is stable and (when humidified) well-conductive, while material degradation is limited. While PEFC systems are continuously further developed to match performance, cost and weight targets for various propulsion applications, they have already reached a high technological maturity and are utilized in commercial applications at the 100 kW scale [19].

Another FC type that has been developed to a high technological readiness level (TRL) is the solid oxide FC (SOFC) [20]. In contrast to the PEFC, the SOFC employs a solid ceramic electrolyte, typically yttria-stabilized zirconia (YSZ), which conducts O²⁻-ions (cf. OCC, oxygen-conducting ceramic in Figure 2d). In these cells, particularly high electrical efficiency can be achieved as gas crossover is mostly avoided. Furthermore, for sufficient electrolyte conductivity, high operating temperatures (>650 °C and up to 1200 °C) are needed, which enhance the reaction kinetics, minimize activation losses and further improve electrical efficiency, even when fully non-noble metal catalysts are employed. Drawbacks for transportation applications of the SOFC are the brittleness of the ceramic materials used, challenges related to the operating temperature (e.g., unsuitability of metallic interconnects, difficulty to find adequate sealing materials), limited specific power and a slow start up time. Recent lab-scale developments, however, show significant progress of both planar and microtubular designs, reaching stack power densities of up to 17 kW/L and start-up times well below 10 min [20,21,22,23,24].

To overcome the temperature-related struggles described for the low- and high-temperature FCs introduced above, i.e., the need for noble-metal catalysts, humidification issues and difficulty in thermal management of the PEFC on the one hand, and material-related challenges in sealing and interconnecting as well as thermal degradation for the SOFC on the other hand, intermediate temperature approaches are of interest. These can be realized by a change of electrolyte and a concomitant adaption of the catalysts in either the ceramic or the polymeric FC type.

For the former, instead of an OCC, proton-conducting ceramics (PCC) have also been developed. These materials’ ion conductivity reaches technically usable values at a significantly lower temperature, starting at around 300 °C [25]. With that, so-called proton-ceramic FCs (PCFCs, cf. Figure 2c) provide a much wider choice of materials for sealing, interconnecting and balance-of-plant components that can sustain the respectable temperature range than SOFCs do [26,27].

When it comes to polymeric electrolytes, a variety of membranes have been proposed, which are mostly phosphoric acid-doped such as PA-PBI (phosphoric acid-doped benzimidazoles) [28]. These cover operating temperatures ranging from 140 to 200 °C (cf. HT-PEFC, Figure 2b) and are proton-conductive without external humidification. Therefore, they alleviate the stringent requirements on the operating conditions that the PFSA membranes pose [29].

It should be noted that the latter two FC types are not at a development stage comparable to the PEFC or the SOFC. Scalability, especially close to the MW-scale as required for aviation, has not yet been shown, neither have standardized accelerated stress tests been systematically performed to assess the durability. Moreover, the bulk of related publications uses the power per electrode area as a means of comparison, whereas stack and system specific power are not specified for the often only lab-scale sized devices. Nevertheless, for the present work, all four cell types have been taken under consideration, aiming at exploring the application potential of each for the proposed hybrid concept for propulsion application in aviation. Forming the complement of the investigated hybrid propulsion concept, the effects of water/steam injection in GT engines are reviewed in brief below.

2.3. Water/Steam Injection in Gas Turbine Engines

The idea of improving the performance of GT engines through water or steam injection has been known at least since the publication of a British patent from 1944 [30]. The performance impact of water injection on the compressors of turbojet engines was analysed by Wilcox and Trout in 1950 [31]. The primary effects obtainable by GT water/steam injection—depending on the injection location and the condition of the injected water—include an increased cycle specific work and enhanced thermodynamic efficiency, as well as the reduction of NO_x emissions during the combustion process. Typical locations for water/steam injection in a GT engine include the air inlet as well as the compression combustion and turbine sections. Inlet and compressor water injection was applied to a number of the first generation, low-bypass ratio turbofan engines in the 1950s in order to enhance engine thrust for an improved take-off performance (e.g., J57 engine on the B-52 and KC-135 aircraft, JT3C engine on Boeing 707, JT9D engine on Boeing 747-100/200 and RR Spey engine on BAC 1–11 aircraft).

The injection of steam into the GT cycle is commonly used in stationary power plant technology (cf. [32,33,34]) in order to enhance both power output and thermodynamic efficiency. So-called “Steam-Injected Gas turbine” (STIG) power plants, with the steam typically produced using the GT exhaust heat, have been offered as commercial product solutions (cf. [33]) since 1987 [35].

Cheng demonstrated efficiency increases of up to 40% over a comparable simple GT cycle with a simultaneously enhanced power output by 70% for a steam injection rate of approximately 20% [32]. Noticeable efficiency gains may already be expected at much lower steam injection rates [36,37]. A consolidated overview of proposed and implemented GT cycles featuring water/steam injection is provided by Jonsson and Yan [38]. Daggett et al. have shown the significant cuts in NO_x emissions from kerosene combustion due to water injection in the compression section of turbofan engines [39,40]. The emission effects due to the ultra-wet combustion of natural gas and hydrogen have been numerically and experimentally studied by Göke et al., showing significant NO_x reductions for both types of fuel [41,42]. The most recent concept of a “Water-Enhanced Turbofan” (WET) engine, featuring in-flight water-recovery from the GT exhaust flow [43], has been initially assessed by Pouzolz et al. [44] and is currently under technology demonstration [45].

2.4. Advanced Heat Exchangers for Aeronautical Application

High-performance Heat Exchangers (HEXs) play a key role in the investigated propulsion system concept. This includes the HEX applications as part of the water treatment process as well as the HEXs required for the FC thermal management. HEXs are well-known from stationary applications as bulky and heavy components, especially when large amounts of heat need to be transferred. Therefore, HEX applications onboard transport category aircraft today refer exclusively to heat exchange tasks associated with engine auxiliaries and aircraft subsystems, such as air or fuel cooled oil coolers, or as part of the aircraft environmental control system, for instance.

The main heat management of classic GT based propulsion systems is intrinsically alleviated by the fact that most of the waste heat produced by the thermodynamic cycle is rejected at a relatively high temperature level via the core nozzle exit mass flow. This highly efficient heat rejection mechanism, at the same time, represents a significant source of losses in the power plant system. Therefore, significant research and development efforts have been invested over the last three decades in order to tackle the thermal losses in the GT exhaust flow. Common technical concepts include bottoming cycles that take the GT exhaust heat as a source of power, the utilization of the exhaust heat for the generation of steam and GT internal exhaust heat recuperation. For the latter concept, ultra-compact, high temperature resistant air-air HEX components have been developed and demonstrated for aero-engine integration [46,47]. Further advanced HEX configurations have been conceptually elaborated for an improved integration in the nozzle section of aircraft engines [48,49] as well as for secondary fluid recuperation based on multi-fluid HEXs [50]. In parallel, light-weight compact HEX designs for an application as compressor intercoolers have been developed [51,52] in order to increase the achievable fuel optimum cycle pressure ratios. Even more specialized high-performance microchannel HEXs originally developed for intercooling tasks in high-speed propulsion application are available [53].

Further momentum in the development of more advanced HEX technology certainly results from the thermal management demands posed by electrical components used in hybrid electric propulsion and power systems (cf. e.g., [54,55]). The need for rejecting significant amounts of waste heat at low temperature levels is also particularly relevant in the context of low-temperature FC application (cf. Section 2.2 above). Moreover, thermal management systems including various kinds of HEX will be crucial for the use of LH₂ systems for aircraft propulsion, as is reflected in ongoing research [56,57].

Existing empirical data for compact HEX designs are documented in [58,59], allowing the derivation of customized empirical correlations for HEX key performance for propulsion system conceptual design purposes.

2.5. Fuel Cell—Gas Turbine Hybrid Systems

In the quest for high system efficiencies, a number of studies have investigated the possibility of combining FCs with heat engines, typically GTs. While mostly developed for power generation applications in stationery use, these systems have also been proposed as (auxiliary) power units in aircraft and unmanned aerial vehicles [60,61,62].

Due to their similar operating temperature range, GTs are typically coupled with SOFCs, whereby two general concepts are distinguished: FC topping cycles versus FC bottoming cycles, i.e., energy conversion in the FC occurs upstream or downstream of the turbine [63]. A comprehensive review of past publications related to FC–GT hybrids is beyond the scope of this work and can be found elsewhere (cf. e.g., [60,64,65]). Nevertheless, some noteworthy examples in the context of the present work shall be briefly described in the following.

As mentioned above, one key aspect of the present concept is the use of the FC’s product water to enhance the performance of the turbine and benefit from the concomitantly reduced emissions. Utilizing the product water for various purposes in the aircraft, e.g., cabin humidity, grey water or even drinking water, has been proposed in several patents owned by aerospace companies, including Boeing, Airbus and Liebherr Aerospace [66,67,68,69]. A direct interaction between an FC and a turbofan engine in order to enhance the engine’s efficiency was, to the best of our knowledge, first described in 2016 by General Electric [70]. Amongst other approaches to efficiency enhancement, the author here puts forward the utilization of the FC product water for cooling of the turbofan engine as well as its direct injection into the core air flow path to alter temperature and/or compressibility properties. A suitable conditioning path for the FC product water that is required in order to minimize energy penalties for the water pressurization to relevant GT cycle pressure levels, and to exploit system synergies such as the GT waste heat utilization for the water vaporization, was very recently proposed as part of a patent application by Bauhaus Luftfahrt (BHL) [71].

FC technology as an option for the primary power supply on transport category aircraft, i.e., for the purpose of propulsion, has just very recently picked up momentum, together with the debate on hydrogen as an alternative fuel in aviation (cf. e.g., [72]). A hybrid system employing an SOFC, GTs and lithium ion batteries in order to boost take-off power was conceptually designed and assessed to be initially viable in larger aircraft applications by Collins et al. [73].

Lastly, it has been established that a high-pressure operation (up to 50 bar) could theoretically enhance the overall system efficiencies of FC–GT hybrids [74]. This is based on the fact that, theoretically, FC performance should increase with higher pressure due to an increased Nernst voltage and lower voltage losses [74,75,76,77]. Furthermore, the need for auxiliary components of FC–GT hybrid systems could simultaneously be lowered. These pressure levels have, however, not yet been practically realized as state-of-the-art FC technology cannot sustain the mechanical forces induced by these operating conditions. Even to realize operation at intermediate pressures (up to 15 bar [75,77]) the FCs are placed into pressure vessels designed to minimize fluctuations of pressure and consequently the mechanical strain on the FCs components.

3. Concept Evaluation Methodology

In this section, the methodological foundation of the aspired initial concept assessment is formulated and discussed. This includes the definition of system efficiencies and control volumes as well as the specification of key figures of merit for concept performance assessment at power system and aircraft level. Beyond this, the modelling of the power system’s key components is presented, the derivation of lab-scale FC technology properties is discussed and a simplified aircraft scaling approach for the integrated concept assessment at the vehicular level is introduced.

3.1. System Definition and Efficiency Formulation

Following the definition of the Thrust Specific Fuel Consumption (TSFC) as fuel flow per unit net thrust produced, the overall efficiency η_ov of aero propulsion systems is given by the ratio of fuel supply power P_supply, i.e., the product of fuel mass flow ${\dot{m}}_f$ and its heating value FHV, and the effective propulsive power P_thrust (cf. e.g., [78]):

$${\eta }_{ov}=\frac{P_{thrust}}{P_{supply}}=\frac{V_0·F_N}{{\dot{m}}_f·FHV},$$

(3)

where V₀ represents the flight velocity and F_N denotes the streamtube net thrust.

For the purpose of the present conceptual investigation, the classic breakdown of η_ov into the product of the core efficiency η_co, the transmission efficiency η_tr and the propulsive efficiency η_pr, is conveniently reorganized to yield η_ov as the product of the effective core engine efficiency η_co,eff and the effective propulsive device efficiency η_pd,eff (cf. [79]):

$${\eta }_{ov}={\eta }_{co}·{\eta }_{tr}·{\eta }_{pr}={\eta }_{co,eff}·{\eta }_{pd,eff},$$

(4)

where η_pd,eff relates the propulsive power demand in terms of F_N and V₀ to the effective core engine exit power P_co,eff, and η_co,eff forms the ratio of P_co,eff and P_supply [79]:

$$\begin{array}{cc}{\eta }_{pd,eff}=\frac{V_0·F_N}{P_{co,eff}},& {\eta }_{co,eff}=\frac{P_{co,eff}}{{\dot{m}}_f·FHV}\end{array}.$$

(5)

In GT power plants, P_co,eff is composed by the free shaft power extracted from the LPT in order to drive the propulsor P_co,sht and the residual excess power in the core flow at the LPT exit (Station 5) P_co,res (cf. [79]):

$$P_{co,eff}=P_{co,sht}+P_{co,res}.$$

(6)

For turbofan engines P_co,sht and P_co,res are thermodynamically expressed as (cf. [79]):

$$P_{co,sht,GT}={\dot{m}}_{co}·\mathsf{\Delta }{h}_{LPT,free}=\frac{P_{Fan,o}}{{\eta }_{mech,LP}}=\frac{{\dot{m}}_{bp}·\mathsf{\Delta }{h}_{Fan,o}}{{\eta }_{mech,LP}},$$

(7)

$$P_{co,res,GT}={\dot{m}}_{co}·\left(\mathsf{\Delta }{h}_{is,5\to amb}-\frac{V_0^2}{2}\right),$$

(8)

where $\mathsf{\Delta }{h}_{LPT,free}$ denotes the effective specific free work of the LPT and $\mathsf{\Delta }{h}_{Fan,o}$ is the effective specific work of the outer fan. The term $\mathsf{\Delta }{h}_{is,5\to amb}$ represents the ideal residual work remaining after the turbine expansion process. The core and bypass mass flows are indicated by ${\dot{m}}_{co}$ and ${\dot{m}}_{bp}$, respectively, while ${\eta }_{mech,LP}$ denotes the low pressure spool mechanical efficiency. The efficiency-optimal ratio between $P_{co,sht,GT}$ and $P_{co,res,GT}$ can be determined based on ideality conditions for turbofan engines [80] as well as for turboprop engines [81].

In the case of a combined power system, such as the considered FC–GT hybrid, P_co,eff equals the sum of the effective core engine exit powers for the installed GT engines, P_co,eff,GT, and the correspondingly equivalent effective power output of the FC power train, P_co,eff,FC:

$$P_{co,eff}=P_{co,eff,GT}+P_{co,eff,FC}.$$

(9)

The primary power output of the FC power train is the shaft power delivered by the electric motor, P_sht,eMot, which is driven by the FC system (FCS) electric power output. It is correlated to the fuel power supplied to the FC, namely ${\left({\dot{m}}_f·FHV\right)}_{FC}$, via the chain of electric component efficiencies:

$$P_{sht,eMot}={\left({\dot{m}}_f·FHV\right)}_{FC}·{\eta }_{FCS}·{\eta }_{PMAD}·{\eta }_{eMot},$$

(10)

where η_FCS represents the FC system electric efficiency, η_PMAD refers to the efficiency of the Power Management And Distribution (PMAD) system and η_eMot denotes the efficiency of the controlled electric motor.

Beside its (primary) electric power output, an FC delivers thermo-kinetic power via the stack outflow. The usefulness of this thermo-kinetic power strongly depends on the FC type and operating conditions, namely temperature and pressure. In case of high temperature and/or high pressure FCs, the stack outflow is typically expanded through a turbine in order to provide power for system internal customers such as the inlet air compressor. The residual thermo-kinetic power at the exit of the FC system, P_co,res,FC, eventually adds to the effective electric shaft power delivery:

$$P_{co,eff,FC}=P_{sht,eMot}+P_{co,res,FC}.$$

(11)

As part of the present power system concept, the FC exit mass flow is routed through a condenser HEX in order to extract liquid water from it. While the extracted liquid water is pressurized and piped to the GT, the residual of the FC exit mass flow ${\dot{m}}_{FC,res,dry}$ and its remaining ideal work potential at the condenser exit $\mathsf{\Delta }{h}_{is|Cond,ex,dry\to amb}$ define $P_{co,res,FC}$ analogously to Equation (8):

$$P_{co,res,FC}={\dot{m}}_{FC,res,dry}·\left(\mathsf{\Delta }{h}_{is|Cond,ex,dry\to amb}-\frac{V_0^2}{2}\right).$$

(12)

Applying the definition of η_co,eff (cf. Equation (5))to the FC power train yields:

$${\eta }_{co,eff,FC}=\frac{P_{co,eff,FC}}{P_{supply,FC}}=\frac{P_{sht,eMot}+P_{co,res,FC}}{{\left({\dot{m}}_f·FHV\right)}_{FC}}$$

(13)

and for the GT, respectively:

$${\eta }_{co,eff,GT}=\frac{P_{co,sht,GT}+P_{co,res,GT}}{{\left({\dot{m}}_f·FHV\right)}_{GT}}.$$

(14)

With this, the effective core efficiency for a FC–GT hybrid power system can be formulated as a power weighted superimposition of the GT and FC power train:

$${\eta }_{co,eff}=\frac{P_{co,eff}}{P_{supply}}=\frac{P_{co,eff,GT}+P_{co,eff,FC}}{{\left({\dot{m}}_f·FHV\right)}_{GT}+{\left({\dot{m}}_f·FHV\right)}_{FC}}.$$

(15)

While for GT engines, the lower heating value of the supplied fuel is used, it should be noted that in the case of low temperature FCs, the water contained in the product mass flow at the fuel exit might be condensed, i.e., in a liquid state, therefore requiring the application of the higher heating value of the fuel.

As can be seen from the equations above, the specific control volume definition of the effective core efficiency η_co,eff ensures a direct consistency of the main power outputs of both parts of the FC–GT hybrid power system, namely the free shaft power available from the GT LPT(s), P_co,sht,GT, and the shaft power delivered by the FC electric power train(s) $P_{sht,eMot}$, while also catering for the residual powers that are available for the conversion to propulsive thrust.

A key design and performance descriptor for FC–GT hybrid power systems is the power split parameter PS, which can be defined as follows:

$$PS=\frac{P_{sht,emot}}{P_{co,eff}}=\frac{P_{co,eff,FC}}{P_{co,eff,GT}+P_{co,eff,FC}}.$$

(16)

As can be seen from Equation (16), the PS parameter expresses the share of the FC power train output relative to the total power system output, based on the η_co,eff control volume.

For the fuel burn assessment, the Breguet-Coffin equation in integral form is solved for consumed fuel mass m_f as a function of aircraft instantaneous gross weight m_A/C,end at the end of a considered range segment ΔR:

$$m_f=m_{A/C,end}·\left(e^{\frac{\mathsf{\Delta }R·g}{FHV·L/D·{\eta }_{ov}}}-1\right),$$

(17)

where L/D refers to the aircraft’s aerodynamic efficiency, namely the ratio of lift-to-drag, and g represents the gravity constant. FHV is the effective fuel heating value of the hybrid power system, averaged according to the supply power split between the GT and FC power train parts. For all three parameters, FHV, L/D and η_ov, representative value for the considered flight segment should be used when evaluating Equation (17).

3.2. Mapping of Key Power System Component Properties

In order to facilitate an initial performance and emissions assessment of the investigated power system concept, the efficiency and mass properties of all key components are estimated using suitably simplified methods. All thermodynamic data for mass flows of semi-ideal gases are based on NASA’s Chemical Equilibrium with Applications (CEA) database [82], while all thermodynamic data for air-water mixtures are read from a real gas database based on the IAPWS IF-97 standard [83]. The used hydrogen-specific thermodynamic data also refer to [82]. Important assumptions and model paradigms for the individual power system components are documented in the following.

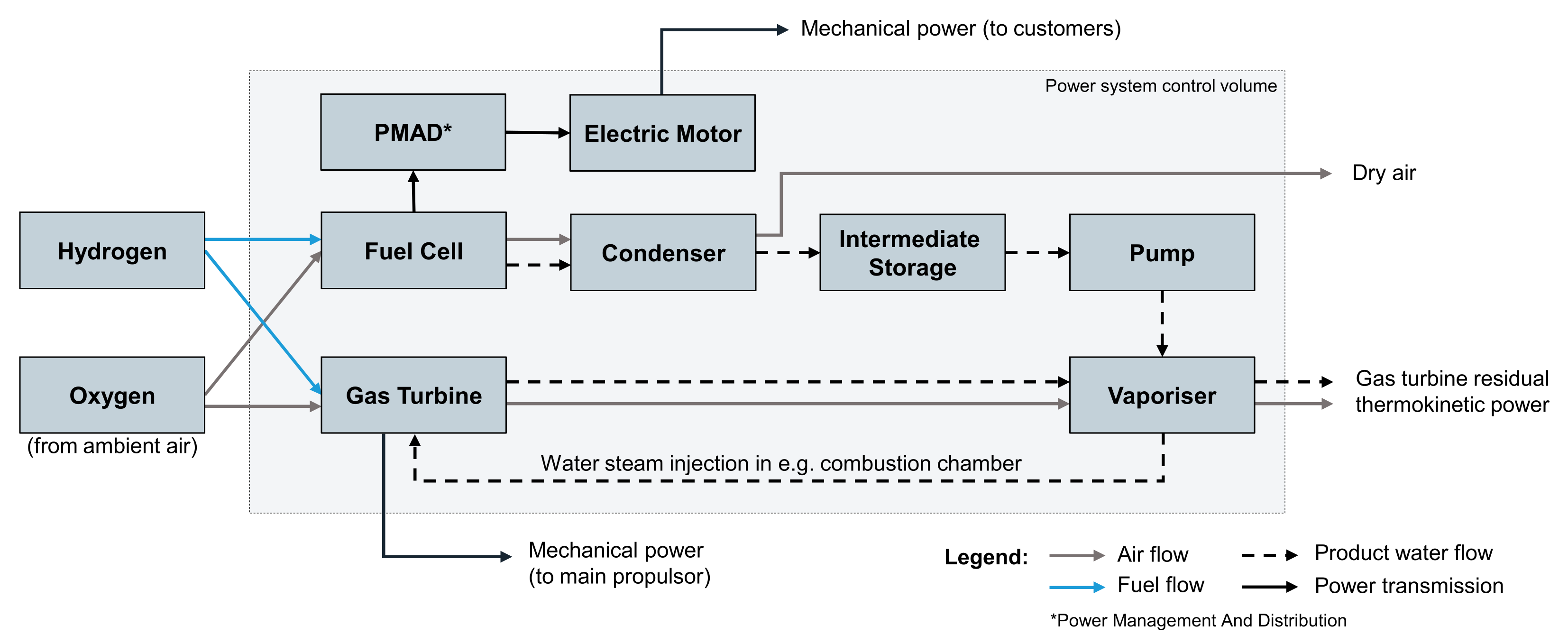
3.2.1. Fuel Cell

The FC as a system includes the cell stack as well as a variety of auxiliary systems, including balance of plant and thermal management systems in often complex arrangements. The objective of the FC modelling in this paper is an appropriately simplified representation of aspects relevant for the hybrid power system concept. This includes the water production rate obtainable from the FC, but also the mapping of the FC system efficiency η_FCS (cf. Equation (10)). Moreover, for the estimation of the overall system mass, the thermal household requires suitable consideration.

The FC system efficiency η_FCS describes the ratio of net electric power delivered by the FC system P_FCS,el to the system power supply via fuel flow, i.e., the product of fuel mass flow required for the cell redox reaction and its heating value ${\left(\dot{m}·FHV\right)}_{H_2}$:

$${\eta }_{FCS}=\frac{P_{FCS,el}}{{\left(\dot{m}·FHV\right)}_{H_2}}=\frac{P_{Stack,el}-P_{Aux,el}}{{\left(\dot{m}·FHV\right)}_{H_2}},$$

(18)

where P_FCS,el equals the stack electric power output P_Stack,el, reduced by all electric power demands P_Aux of the FC auxiliary systems including balance of plant and thermal management. It should be noted that, given the considered FC operating conditions in the present study, the lower heating value LHV is used for all FC efficiency evaluations.

Now, with ${\eta }_{Stack}$ (cf. Equation (2)) rewritten as:

$${\eta }_{Stack}=\frac{P_{Stack,el}}{{\left(\dot{m}·FHV\right)}_{H_2}}.$$

(19)

η_FCS can be expressed in a factorized form:

$${\eta }_{FCS}={\eta }_{Stack}·f_{\eta ,BoP,TMS},$$

(20)

with an efficiency factor $f_{\eta ,BoP,TMS}$ capturing all auxiliary electric power demands within the FC system being defined as:

$$f_{\eta ,BoP,TMS}=1-\frac{P_{Aux,el}}{P_{Stack,el}}.$$

(21)

Typical customers of P_Aux,el amongst the FC auxiliary systems mainly focus on the reactant supply units, i.e., pumps and compressors, and electric controllers. It should be noted that the residual effective excess power of the FC power train $P_{co,res,FC}$ (cf. Equation (12)) is conservatively neglected when evaluating ${\eta }_{co,eff,FC}$ acc. to Equation (13).

While for the present study, fuel supply pressure is assumed to be provided through an active regulation of the LH₂ fuel tank delivery pressure, the FC inlet air supply requires active pressurization. This is realized by a turbo compressor. For low temperature FCs without sufficient thermo-kinetic power at the exit of a FC stack, the inlet air compressor requires an electric drive. The correspondingly required power for the compression of inlet air mass flow ${\dot{m}}_{air}$ to the stack operating pressure is calculated as follows:

$$P_{comp,air}=\frac{{\dot{m}}_{air}·{\overline{c}}_p·T_{in}}{{\eta }_{Comp,air}}·\left({\left(\frac{p_{out}}{p_{in}}\right)}^{\frac{\gamma -1}{\gamma }}-1\right),$$

(22)

where ${\overline{c}}_p$ and $\gamma$ are the representative isobaric specific heat and isentropic exponents for the air compression process. The compressor inlet total pressure $p_{in}$ results from the freestream total pressure with an inlet pressure ratio of 99% assumed for the study. The compressor outlet total pressure $p_{out}$ corresponds to the FC operating pressure. The efficiency ${\eta }_{Comp,air}$ includes the isentropic efficiency of the turbo compressor, the mechanical efficiency of its shaft and bearing system and its electric drive unit. It should be noted that in the case of high temperature and/or high pressure FCs, the stack outflow is typically expanded through a turbine in order to drive the inlet air compressor, thereby reducing $P_{comp,air}$ to zero.

In order to obtain the value of P_Aux,el, and thus $f_{\eta ,BoP,TMS}$, the power requirements of all customers need to be added together. Beside $P_{comp,air}$, this also includes the power required in order to drive the liquid water pump within the product water treatment process (see Section 3.2.2). The electric power demand for the FC electric controller and auxiliary pumps and blowers within the balance of plant is assumed to be 3% of P_{Stack, el}.

The water mass flow ${\dot{m}}_{Stack,H2O}$ produced by an FC can be expressed as a function of P_Stack,el, η_Stack, the heating value per mol of fuel FHV_mol and the product water’s molar Mass $M_{H2O}$:

$${\dot{m}}_{Stack,H2O}=\frac{P_{Stack,el}·M_{H2O}}{{\eta }_{Stack}·FH{V}_{mol}}.$$

(23)

A parametric study of Equation (23) for a hydrogen FC is presented in Figure 3 below. As can be seen, the expectable water mass flows for typical stack efficiencies range from approximately 0.10 kg/s to 0.18 kg/s per MW of stack electric power.

All FC stacks considered in the study are assumed to be technically operated at an excess supply of reactants. While the excess air is simply passed through the stack, the unused fuel is assumed to be recirculated to the stack inlet without leakage.

While for the efficiency formulation above only the net mass flow rate of fuel that is effectively participating in the cell redox reaction was relevant, the thermal balance requires a more careful consideration of the actual mass flow rate of the reactants. In order to simplify the modelling of this, the stack is embedded in an auxiliary control volume that internalizes the recycling of unused fuel as well as any potentially required preheating of the fuel prior to entering the stack. A schematic representation of the stack and the auxiliary control volume referred to as “FC module” is presented in Figure 4.

The thermal balance of the FC module in Figure 4 is given by the heat production rate due to the redox reaction in stack ${\dot{Q}}_{Stack,prod}$, the net enthalpy flow across the FC due to its reactants net mass inflows, i.e., fuel and air supply, and its product mass outflow $\mathsf{\Delta }{\dot{H}}_{FC}$ and the residual waste heat to be removed from the cell ${\dot{Q}}_{FC,cool}$. The stack internal heat source term can be calculated from the stack efficiency:

$${\dot{Q}}_{Stack,prod}={\left(\dot{m}·FHV\right)}_{H_2}-P_{Stack,el}=P_{Stack,el}·\left(\frac{1}{{\eta }_{Stack}}-1\right).$$

(24)

The heat transfer terms result from the mass flows entering and exiting the control volume of the FC module:

$$\mathsf{\Delta }{\dot{H}}_{FC}={\left(\dot{m}·h\right)}_{H_2}+{\left(\dot{m}·h\right)}_{air}-{\left(\dot{m}·h\right)}_{FC,prod},$$

(25)

$${\dot{Q}}_{FC,cool}={\left(\dot{m}·h\right)}_{cool,in}-{\left(\dot{m}·h\right)}_{cool,out}.$$

(26)

As discussed above, ${\left(\dot{m}·h\right)}_{air}$ represents the enthalpy of the gross stack inlet air flow, while ${\left(\dot{m}·h\right)}_{H_2}$ refers to the enthalpy of the net fuel inflow. For a stationary equilibrium stack operating temperature, the following balance must be reached:

$$\mathsf{\Delta }{\dot{H}}_{FC}+{\dot{Q}}_{Stack,prod}+{\dot{Q}}_{FC,cool}=0.$$

(27)

while the FC heat production rate ${\dot{Q}}_{FC,prod}$ is always positive, the sign and absolute value of $\mathsf{\Delta }{\dot{H}}_{FC}$ depend on the inflow temperatures of the reactants, the stack operating temperature and the effective operating stoichiometry, i.e., the excess air supply ratio.

In a case where $\mathsf{\Delta }{\dot{H}}_{FC}$ is negative and its value exceeds ${\dot{Q}}_{Stack,prod}$ this would mean residual waste heat to be removed from the FC becomes negative, i.e., the cell needs to be heated in order to maintain its operating temperature. While this may be less relevant for low temperature FCs, this may often be the case for highly efficient high-temperature FCs. High temperature cell operation also increases the demand for a preheating of the reactants prior to entering the stack in order to reduce local thermal stresses. While preheating of the pre-compressed inlet air is often not applicable, fuel preheating is often required. In practice, both requirements are tackled by utilising the heat contained in the stack’s product exit mass flow to preheat the fuel inlet mass flow [18,60].

In order to emulate this for the present study, heat is transferred from the stack product mass flow to the fuel inflow via an FC internal HEX until $\mathsf{\Delta }{\dot{H}}_{FC}$ equals ${\dot{Q}}_{Stack,prod}$, in cases where ${\dot{Q}}_{FC,cool}$ would otherwise be <0. As a result in these cases, the temperature of the product mass flow leaving the FC is reduced relative to the stack operating temperature. The total pressure of the product outflow is assumed to be sufficiently close to the stack operating pressure.

The hydrogen fuel is preheated from the fuel supply temperature at the FC entry. Prior to entering the control volume of the FC, the hydrogen fuel mass flow from the LH₂ storage in the fuel tank is assumed to have absorbed a certain amount of heat due to its function as a cryogenic heat sink, e.g., used for the electric power train components as well as non-perfect thermal insulation of the fuel transmission system. A fuel supply temperature to the FC of 200 K is assumed for the present study.

3.2.2. Water Treatment Process

In order to allow for an efficient injection of the FC product water as superheated steam in the GT combustion chamber, the water first needs to be extracted from the FC product outflow, then pressurized in liquid form and re-vaporized. The basic thermodynamic implications of such a water treatment process are illustrated in Figure 5 based on a temperature entropy diagram for water. The water treatment process examples illustrated in the figure refer to the water released by a typical PEMFC and a typical SOFC, respectively.

An SOFC releases its product water at the anode (cf. Figure 2) while all other considered FC types release the water at the cathode, together with the excess mass flow from the cells’ oxidant supply. With the hydrogen fuel recirculated inside the FC, this means a pure water condenser for SOFCs. For all other FC types, the condenser sees a mixture of the FC product water mass flow and the residual air fraction of FC oxidant supply. Consequently, the partial pressure of the PEMFC’s product water in Figure 5 is significantly lower than that of the SOFC, resulting in a larger removal of heat required for the condensation process. At the same time, the condensation process of the PEMFC product water takes place at a lower temperature. The precooling of the FC product mass flow before condensation starts obviously requires more effort for the SOFC example due to the higher release temperature at the FC system exit.

For all studies presented in this paper, a liquid recovery of ≥90% of the FC product water can be assumed. The corresponding heat exchanger design modelling is discussed in Section 3.2.4. The liquefied fraction of the FC product water is subsequently pressurized by a water pump to a pressure level suitably above the total pressure in the GT combustion chamber and is then piped to the gas turbine core exhaust locations where the high-pressure water is reheated, vaporized and superheated using the residual GT exhaust heat. The power input required for the water pressurization is expressed as follows:

$$P_{Pump}=\frac{{\dot{m}}_{H_{2}O}}{{\rho }_{H_{2}O,liquid}}·\frac{P_{out}-P_{in}}{{\eta }_{Pump}}.$$

(28)

where ${\dot{m}}_{H_{2}O}$ is the liquid water mass flow through the pump and ${\rho }_{H_{2}O,liquid}$ refers to the corresponding fluid density. The pump system efficiency η_Pump includes the hydraulic efficiency of the pump as well as the involved mechanical, electric drive and power system efficiencies. A typical pump-delivered pressure level p_out would be 80 bar. The water inlet pressure level to the pump system, P_in, is defined by the FC operating pressure reduced by all pressure losses along the water treatment process between the FC stack and the pump inlet. Assuming P_in of 1.5 bar and η_Pump to be 0.5, the resultant water mass flow specific power input to the water pump system yields 15.7 kW/(kg/s). Extracted from the FC system this equals less than 0.2% of its electric power output. This low pumping power requirement is also reflected the water T-s diagram (cf. Figure 5) where the condenser outlet conditions (in case of full water recovery) are in immediate proximity of the vaporizer inlet conditions.

The mass of the water pump is calculated from a reference pump given in [61] using water mass flow-based proportional mass scaling. The mass of the required water piping system is derived in analogy to the aircraft fuel system. As a reference point, fuel system mass and throughput characteristics similar to an Airbus A320 aircraft are assumed. Piping system mass is then estimated via mass flow scaling using the liquid water throughput. An optional water tank acting as an intermediate reservoir of liquid water for increased operational flexibility of the overall system is not yet considered in the modelling.

3.2.3. Gas Turbine Engine

For the present study, the GT water injection is assumed to be realized via superheated steam injection into the combustion chamber. The resulting immediate effects on the thermodynamic cycle include an additional turbine mass flow due to injected water/steam and an increased mass flow-specific heat capacity in turbine, as well as a reduced compressor mass flow for a given power demand. A key descriptor for the implications of GT water/steam injection is the water-air-ratio (WAR), being defined as the ratio of steam mass flow ${\dot{m}}_{Steam}$ to compressor delivery mass flow at the combustor inlet ${\dot{m}}_{31}$, in the present study:

$$WAR=\frac{{\dot{m}}_{Steam}}{{\dot{m}}_{31}}.$$

(29)

The increased heat capacity in the turbine section for different levels of temperature and WAR is displayed in Figure 6a, while Figure 6b shows the reduction of core compressor mass flow against increasing steam injection.

As can be seen from the figure above, the specific work potential enhancement due to change of thermodynamic fluid properties is significant, e.g., approximately 25% at WAR = 0.3 for a typical average temperature level in the turbine section. At the same time, the core compressor mass flow reduces at a steep rate of approximately 1.8% per percent WAR increase, if a constant cycle output power is prescribed. This over-proportional compressor mass flow decrease results from the combined effect of the increased specific heat capacity in turbine flow and the added steam mass flow acting in the turbine section only. In this case, the required cycle output power is additionally reduced by the power produced through water supplying FC and the core compressor mass flow is reduced by more than 50% at WAR = 0.1.

Assuming the steam production from the liquefied FC product water mass flow to be performed using heat from the GT exhaust mass flow, the presence of the HEX in the core engine exhaust section will cause a pressure loss as a function of the amount of heat to be exchanged and as a trade-off with HEX size and mass.

In order to appropriately capture these main effects on the GT’s effective core efficiency, a simplified formulation approach is used for the present study. Accordingly, all the primary effects due to the steam injection are combined in the efficiency factor $f_{\eta ,co,eff,WAR}$. The GT effective core efficiency η_co,eff,GT is obtained when multiplying the steam injection efficiency factor with a baseline efficiency value ${\eta }_{co,eff,base}$:

$${\eta }_{co,eff,GT}=f_{\eta ,co,eff,WAR}·{\eta }_{co,eff,base}\left(P_{co,eff,GT}\right).$$

(30)

It should be noted that the baseline efficiency ${\eta }_{co,eff,base}$ will strongly depend on GT size effects. In order to also allow for technological sensitivity, the modelling of ${\eta }_{co,eff,base}$ is factorised into two parameters, and a technology factor $f_{\eta ,co,eff,tech}$ is used to emulate the η_co,eff,GT impact of advanced technology status and a true reference efficiency ${\eta }_{co,eff,ref}$, which is modelled as a function of $P_{co,eff,GT}$:

$${\eta }_{co,eff,base}=f_{\eta ,co,eff,tech}·{\eta }_{co,eff,ref}\left(P_{co,eff,GT}\right).$$

(31)

For ${\eta }_{co,eff,ref}$, a simple data fitting based on BHL-internal models of existing aircraft GT engines of different power classes typical for the year 2000 in service technology is employed in this paper:

$${\eta }_{co,eff,ref}=0.5089-5.0654·{\left(P_{co,eff,GT}\left[MW\right]+3.8\right)}^{-1.9}.$$

(32)

Based on its regression input data set, the validity of the ${\eta }_{co,eff,ref}$ correlation ranges from $P_{co,eff,GT}$≈ 1.5 MW up to $P_{co,eff,GT}$≈ 30 MW in cruise. Throughout the studies presented in this paper, a value of 1.2 is chosen for $f_{\eta ,co,eff,tech}$ in order to represent an appropriately advanced technology level.

For the $f_{\eta ,co,eff,WAR}$ factor, a simple heuristic based on published data and in-house performance synthesis computations was derived. The data basis for the heuristic law is visualized in Figure 7 below.

Roumeliotis and Mathioudakis [37] investigated the effects of water injection on GTs more generally, taking varying injection locations and conditions into account. For water steam injection in the combustion chamber, a potential for core efficiency enhancement of approximately 4% per 1% WAR is stated for low WAR injection rates and constant turbine inlet temperature operation. In Figure 7, data points for 2% and 4% WAR are depicted. Jonsson and Yan [38] collected data for various GT water/steam injection options. Again, a relevant data point derived from efficiency values provided for steam injection in the combustion chamber is annotated in Figure 7. Finally, Cheng and Nelson predicted a potential for an efficiency increase of up to 43% at WAR slightly above 20% while using exhaust gas recuperation for steam generation.

In order to supplement the data obtained from the literature, a number of GT cycle design points were computed for the present study using BHL’s in-house “Aircraft Propulsion System Simulation” (APSS) framework (cf. e.g., [84,85,86]). For these in-house simulated data points (black circles in Figure 7), steam injection in the combustion chamber of a 2-spool turbofan engine architecture was modelled using constant core turbo component polytropic efficiencies of 90%, a cycle featuring a burner exit temperature T₄ of 1700 K at an Overall Pressure Ratio (OPR) of 40 and a constant turbine cooling air supply of 25% of the high pressure compressor exit mass flow. Secondary customer offtakes including power and bleed air were set to zero. The vaporization and superheating of the recovery FC product water mass flow were modelled via a turbine exit duct-mounted vaporizer assuming a water heating up to LPT exit temperature T₅-50 K (=steam injection temperature in burner). To reflect the increasing heating effort required for the water vaporization and superheating as the water to GT exhaust air flow ratio grows, a linear correlation of core nozzle pressure loss against WAR was assumed that yields 5% at WAR = 0.15. For a given ideal nozzle exit velocity ratio according to Gasparovic [80], this effectively equals an increased back pressure for the cycle, hence reduced turbine expansion capacity. As such, the efficiency implication of the water vaporizer behind the LPT is effectively mapped to the effective core efficiency of the GT.

The heuristic correlation for $f_{\eta ,co,eff,WAR}$ derived from the data collected in Figure 7 yields:

$$f_{\eta ,co,eff,WAR}=1+0.21·\ln \left(30·WAR+1\right).$$

(33)

As can be seen in Figure 7, the correlation is supported by reference data up to WAR values of approximately 20%. As a first indication for the correlation’s confidence level, the logarithmic upper and linear lower bounds of the reference data basis are indicated as dashed lines in the figure.

The impact of steam injection in the GT combustion chamber on cruise NO_x emissions is estimated based on the experimental results for ultra-wet hydrogen combustion published by Göke et al. in their Figure 8 [42]. Therefore, quadratic data fittings for the NO_x concentrations measured in the combustion products under water-to-air ratios between 0% and 30% were produced at relevant combustion temperature levels. For a given WAR, an average NO_x concentration can be calculated from the set of data fittings. Absolute GT NO_x emissions obtained as the product of NO_x concentration and actual fuel flow can then be related to the NO_x emissions at WAR = 0 in order to evaluate the NO_x reduction potentials. Assuming zero NO_x emissions from the FC system, GT-produced NO_x represents the total NO_x emissions of the propulsion system.

3.2.4. Heat Exchangers

While for the efficiency of the FC module internal HEX used for the preheating of fuel (cf. Section 3.2.1), a prescribed value of 90% is assumed, the HEXs involved in the water treatment process require a more detailed consideration: The first one along the process is a HEX (condenser) required for water recovery from the FC product mass flow. It should be noted that the composition and thermal conditions of the relevant part of the FC outflow strongly depend on the FC type (cf. Section 3.2.2).

The condenser is modelled to be operated with freestream air as a coolant. The freestream mass flow rate is tailored to ensure a sufficient pinch point temperature difference between hot and cold HEX sides of 40 K at design point conditions (FL350, M0.78, ISA+10). The HEX performance calculation is therefore divided into two steps:

• temperature reduction down to saturation conditions; and,
• subsequent further cooling for latent heat transfer during phase change.

A second HEX (vaporizer) uses the GT exhaust gas mass flow for the vaporization and superheating of the pressurized water. The heat transfer of this HEX is segmented in three parts:

• heating the liquid water to boiling temperature;
• water vaporization; and,
• subsequent superheating of the water steam.

For sufficient thermodynamic conservatism in the studies presented in Section 4, steam superheating was limited to T₅ − 50 K. Both HEXs are modelled as counter flow HEXs with assumptions on pressure losses as summarized in

Table 1. Summary of key assumptions taken for the initial estimation of HEX properties within the water treatment process.

HEX	Property	Value
Condenser	Pressure Ratio (cold side)	0.95
	Pressure Ratio (hot side)	0.96
	Pinch Point Temperature Distance	40 K
Vaporizer	Pressure Ratio (cold side)	0.9 *
	Pressure Ratio (hot side)	f(WAR)
	Superheating Limitation	T5 − 50K

* compensated by water pump with very low effort due to incompressibility.

.

HEX efficiency ${\eta }_{HEX}$ for the condenser and vaporizer components is defined by the ratio of realized temperature difference between inlet to outlet and the theoretically maximum temperature difference between HEX hot side and cold side inlet:

$${\eta }_{HEX,Cond}=\frac{T_{Cond,in,h}-T_{Cond,out,h}}{T_{Cond,in,h}-T_{Cond,in,c}}, {\eta }_{HEX,Vap}=\frac{T_{Vap,out,c}-T_{Vap,in,c}}{T_{Vap,in,h}-T_{Vap,in,c}} .$$

(34)

HEX mass estimation is based on a semi-empirical method for air-air HEX acc. to Grieb [59]. Therefore, data for mass flow-specific matrix weights of exhaust recuperators versus HEX efficiency ${\eta }_{HEX}$ provided in [59] were fitted and scaled by a constant factor representing GT exhaust recuperator HEX installation weight effects $f_{m,HEX,inst}$, yielding the following correlation:

$$m_{HEX}=f_{m,HEX,inst}·82·{\dot{m}}_{air}·{\left({\eta }_{HEX}+0.2\right)}^{8.1} ,$$

(35)

where ${\dot{m}}_{air}$ is the representative air mass flow through the HEX matrix. Taking into account the specific matrix weight data used for the regression, the validity of Equation (34) ranges from ${\eta }_{HEX}$ ≈ 0.6 up to ${\eta }_{HEX}$ ≈ 0.9. For all HEX weight estimates in the present paper, a value of 1.6 is assumed for $f_{m,HEX,inst}$ (cf. also [59]).

In order to emulate the sizing of the multi-fluid, multi-phase HEXs involved in the water treatment process, the correlation in Equation (35) is applied using an equivalent air mass flow derived from the actually required heat capacity flows in the condenser and vaporiser HEXs. The respective equivalent air mass flows are tailored to facilitate the same amounts of heat transfer at the same temperature differences as the real multi-fluid, phase-changing condensers and vaporizers.

3.2.5. Electric Power Train

The electric power train represents the link between the net electric output power of the FC system and the mechanical shaft power absorbed by the targeted onboard customers. As such, it is constituted by a Power Management And Distribution (PMAD) system and a dedicated number of controlled electric motors. In the studies presented in this paper, as a first approach, the FC electric power is used to assist in driving the installed propulsive devices on the aircraft. Owing to the presence of the onboard LH₂ fuel storage as a convenient low-temperature heat sink, the employment of cryogenic technologies for key components of the electric power train seems warranted. This is reflected in a PMAD system efficiency η_PMAD of 99%, as well as the assumption of a High Temperature Superconducting (HTS) electric motor design paradigm also featuring 99% controlled efficiency (cf. e.g., [78]). Correspondingly, an advanced specific power target of 10 kW/kg is assumed for the overall electric power train.

3.2.6. Propulsive Devices

The propulsive device represents the assembly of the ducted fan, including the fan module, the fan drive gear system and the nacelle system. For all propulsive devices in the study, an effective propulsive device efficiency of 75% during typical cruise is assumed. This corresponds to a classic propulsive efficiency of approximately 88%, representing an advanced low specific thrust fan design.

Propulsive device mass is modelled based on a prescribed thrust-to-weight ratio in cruise. For the study, a cruise thrust-to-weight ratio of 1.7 is assumed, which is approximately 3 times the cruise thrust-to-weight ratio estimated for the advanced turbofan-type power plant systems.

3.3. Derivation of Lab-Scale Fuel Cell Technology Properties

In an attempt to evaluate the application potential of several FC types as introduced in Section 2.2 for the hybrid-concept presented herein, a number of recent publications on FC developments were taken into consideration [21,23,24,29,73,87,88,89,90]. Note that the focus lies on power performance only—other considerations of employing an FC in an aircraft (e.g., vibration tolerance, transient performance, etc.) go beyond the scope of this evaluation (cf. Appendix A.1).

As the polarization curves of novel FC developments are typically quoted per electrode area (i.e., in W/cm²), a number of assumptions (e.g., on thickness and weight share of cell components) were made in order to estimate the respective specific power in kW/kg as required for an assessment of the presented hybrid concept. For each FC type, a value for a conservative and a more aggressive estimation is specified in

Table A1. Summary of the performance characteristics of lab-stage FC developments. Values in grey italic font have been calculated/estimated using the assumptions described above, while values in standard font have been taken directly from the cited publications.

Cell Type	Estimation Type	Electrode Power Density +	Stack Specific Power *+x	Operating Pressure	Operating Temperature	Notes	Ref.
		W/cm2	kW/kg	Bar	°C	-	-
PEFC	conservative	1.33	4.20 (6.01)x	1.7	80	H2/O2	[87]
PEFC	aggressive	1.33	9.86 (14.09) x	1.7	80	H2/O2	[87]
HT-PEFC	-	~0.7	3	n.a.	160		[91]
HT-PEFC	conservative	0.512	1.55 (2.22) x	1 (100 sscm H2, 200 sscm O2)	120	H2/O2	[88]
HT-PEFC	aggressive	0.512	2.77 (3.96) x	1 (100 sscm H2, 200 sscm O2)	120	H2/O2	[88]
HT-PEFC	conservative	0.91	2.58 (3.69) x	1.47	240	H2/air	[29]
HT-PEFC	aggressive	0.91	6.2 (8.86) x	1.47	240	H2/air	[29]
PCFC	conservative	0.535	0.33	n.a.	500	Planar	[89]
PCFC	conservative	1.61	0.99	n.a.	650	Planar	[89]
PCFC	aggressive	0.535	0.63	n.a.	500	Planar	[89]
PCFC	aggressive	1.61	1.90	n.a.	650	Planar	[89]
PCFC	conservative	0.548	0.15	n.a.	500	Planar	[90]
PCFC	conservative	1.4	0.38	n.a.	650	Planar	[90]
PCFC	aggressive	0.548	0.38	n.a.	500	Planar	[90]
PCFC	aggressive	1.4	0.97	n.a.	650	Planar	[90]
SOFC	-	n.a.	1.88 (at 0.785 V)	5.07	750	Planar, including pressure vessel	[73]
SOFC	-	n.a.	4.6 (at 0.785 V)	5.07	750	Monolithic, incl. pressure vessel	[73]
SOFC	-	n.a.	2.5	n.a.	850	Planar	[24]
SOFC		1.27	2.7–4.7	n.a. (30 sscm)	800	Micro-monolithic, allows fast startup	[21]
SOFC	conservative	3.13	4.2	n.a. (1000 sscm H2, 2000 sscm O2)	800	Anode supported	[23]
SOFC SOFC	conservative	1.96	2.6	n.a. (1000 sscm H2, 2000 sscm O2)	650	Anode supported	[23]
	aggressive	3.13	5.4	n.a. (1000 sscm H2, 2000 sscm O2)	800	Anode supported	[23]
SOFC	aggressive	1.96	3.4	n.a. (1000 sscm H2, 2000 sscm O2)	650	Anode supported	[23]

⁺ peak power unless stated otherwise. * cell block components only. ^x for (HT-)PEFCs, additional hardware e.g., for compression is needed in the stack. This is estimated to result in a ca. 30% reduced stack specific power. The values in parenthesis refer to the corresponding specific power of the cell block.

.

All corresponding assumptions, technical details and references are given in Appendix A.2 to Appendix A.4. After recalculating the polarization curve in terms of stack specific power by normalizing with the derived peak power tabulated in Appendix A.5, the two best performing candidates were identified. Figure 8 displays the so-calculated performance characteristics of both cases based on the aggressive assumptions introduced in Appendix A.

For a given electric power output requirement and a specified operating point along the polarization curve, FC stack mass $m_{Stack}$ can be calculated from the data provided in Figure 8. In order to obtain the total mass of the FC system $m_{FCS}$ including its balance of plant and auxiliaries, the following correlation is used:

$$m_{FCS}=m_{Stack}+m_{Stack}·\left(f_{m,BoP,TMS}+f_{m,BoP,Aircomp}+f_{m,BoP,Res}\right) ,$$

(36)

where the additive mass factors $f_{m,BoP}$ indicate typical masses of key component groups of the balance of plant in relation to the stack mass. A synopsis of the factors used for the estimation of the FC system masses associated with the PEMFC and SOFC technology cases in Figure 8 is provided in

Table 2. Synopsis of FC system balance of plant additive mass factors PEMFC and SOFC technology cases.

Additive Mass Factors Relative to Stack	PEFC	SOFC
Thermal management ($f_{m,BoP,TMS}$)	1.61 *	0.39
Air compression system ($f_{m,BoP,Aircomp}$)	0.12	0.11
Other ($f_{m,BoP,Res}$)	0.16 *	0.21 **

* Based on HyPoint “Technical White Paper” [91]. ** Based on Tornabene et al. [61].

.

For the FC system mass calculation, three main component groups of the balance of plants and auxiliaries are distinguished: for the FC thermal management ($f_{m,BoP,TMS}$), the air compression system ($f_{m,BoP,Aircomp}$) and the residual of all other components ($f_{m,BoP,Res}$). As can be seen from Table 2, the values of the individual additive mass factors strongly depend on the FC type and its typical operating conditions, namely temperature and pressure. In particular, the significant additional mass connected to the thermal management system of the low-temperature FC technology option, namely the PEMFC, should be noted.

3.4. Simplified Aircraft Scaling Approach

Aircraft conceptual design and sizing for the integrated power system assessment studies presented in Section 4 of the paper is realized using a simplified discipline-oriented set of analysis modules based on Seitz [92]. Starting from the definition of the configurational setup of the aircraft and the integrated propulsion system, the design synthesis procedure includes

• the basic geometric description of the aircraft and its components primarily relevant for the study;
• the estimation of key aircraft component masses based on the underlying simplified geometric descriptions;
• the computation of aircraft aerodynamics during high-speed operation using the pre-calculated geometric and weight properties; and,
• the analysis of aircraft design mission performance based on the system weights, the aerodynamic properties and the energy and propulsion system efficiency characteristics.

During aircraft sizing, these disciplinary modules are consecutively evaluated. The required feedback correlations during the iterative aircraft scaling procedure are handled using a gradient-free iteration strategy as described and validated in [92]. Further verification and validation of the aircraft scaling approach were performed by Seitz and Engelmann [93]. For the present study, the pre-existing set of methods was supplemented in order to appropriately facilitate the aspired design studies for an LH₂-fuelled short-/medium range aircraft, with the cryogenic fuel storage accommodated in the fuselage. In the following, key relevant modelling aspects are discussed along the main disciplinary modules.

3.4.1. Geometry

Lifting surfaces are represented by simple trapezoidal planforms. Wing reference area scaling is performed for a prescribed wing loading at maximum landing weight in order to ensure appropriate low speed performance without detailed modelling of high-lift performance. Wing sweep is determined based on the simple sweep theory, i.e., employing cosine correction of the design cruise Mach number, applied to the aerodynamic center line at 25% chord length. Here, the effective design incidence Mach number for the wing airfoils is used as in input. Wing taper ratio is balanced to approximate elliptical spanwise lift distribution as a function of aircraft design cruise Mach number, wing aspect ratio and sweep angle according to Torenbeek [94]. Tail plane sizes are mapped as functions of wing reference area through prescribed volume coefficients. The wetted areas of lifting surfaces are determined based on the exposed regions of the component planform, translated using an empirical correlation given by McCormick [95]. Fuselage dimensioning in terms of diameter and overall length is performed under consideration of the design payload capacity and volumetric requirement associated with the accommodation of the onboard LH₂ fuel storage. The assumed LH₂ tank shape features spherically shaped heads that enclose an optional cylindrical center section. For the presented studies, an inner tank volume utilization of 87% is assumed, which corresponds to a 1.2 bar filling pressure and a venting pressure of 4 bar [9]. The corresponding gravimetric density of LH₂ is read from [9]. An additional allowance of 4% for trapped and unusable fuel in the tank is taken into account. A volumetric ratio of the tank walls to the inner storage volume of 40% is assumed based on results presented by Winnefeld et al. [96]. In summary, this yields a volumetric efficiency of the LH₂ storage, i.e., ratio of design mission fuel volume to the external displacement volume of the LH₂ tank in the fuselage, of 64%. During parametric studies with constant design passenger payload, fuselage diameter is retained constant, setting an upper limit to the allowable outer tank diameter. Hence, variations in required LH₂ tank size are accommodated via stretching or shrinking the length of the cylindrical fuselage center section.

3.4.2. Weights

The mapping of aircraft component masses is based on a combination of suitable textbook methods. The selection of the employed handbook methods for the individual components is made in order to secure appropriate functional sensitivity for essential physical effects connected to the aspired conceptual design study at aircraft level. A compact overview of the weight prediction methods for key aircraft components is given as follows: Wing and fuselage structural masses are calculated according to [97]. For LH₂ tank mass estimation a constant gravimetric tank efficiency as defined by Verstraete [9] of 50% is assumed, i.e., the tank’s structural mass equals the stored fuel mass. The mass of the LH₂-specific onboard fuel system is considered as a constant fraction (2.5%) of aircraft Maximum Take-Off Weight (MTOW). All other airframe components, systems and equipment masses are summarized in a residual share of MTOW. Optimized mass and balance for aircraft with fuselage stored LH₂ tanks is neglected, in the first instance.

3.4.3. Aerodynamics

The mapping of aircraft aerodynamics is based on handbook methods (cf. [95,98,99,100]). A simple symmetric polar approach is used with the induced drag share modelled based on the wing’s geometric properties using a correlation for Oswald’s efficiency factor given by [100]. Skin friction and form drag for the wing and fuselage components are determined according to [95]. For wing aerodynamic mapping, the Mean Aerodynamic Chord (MAC) is treated as representative. The flow around the fuselage is assumed to be fully turbulent. The relative chordwise transition point from laminar to turbulent flow along the wing’s MAC is prescribed by a free input parameter. The skin friction and form drags of all other aircraft components, including the empennage and propulsion system nacelles, are directly geared to the wing’s drag using a constant factor. The wave drag of the overall aircraft is prescribed as a constant share of its total drag. The additional drag due to the rejection of water condenser as well as the FC waste heat is estimated as a delta in drag coefficient based on a change in drag counts per rejected heat load given by Pratt et al. [101]. Trim drag (typically 1–2% of aircraft total drag) is not explicitly modelled, but is considered as part of the induced drag share.

3.4.4. Performance

The performance mapping of the study aircraft is based on the performance formulation presented in Section 3.1. For the mission, fuel burn calculation during aircraft sizing is evaluated using the Breguet-Coffin equation as provided in Equation (17). Mission trip fuel is computed solely based on the performance properties for a typical cruise point. As such, the transversal flight phases are averaged as part of the considered cruise segment. Mission block fuel is obtained by adding a mass fraction of 1% of aircraft MTOW for LTO cycle and taxi fuel to the calculated trip fuel mass. For the computation design loaded fuel, the design stage length is increased by an additional 800 nmi as a convenient means of incorporating the required contingencies and reserves.

4. Concept Evaluation Results

In this section, the evaluation results for the investigated hybrid propulsion and power system concept are presented. Therefore, initial design studies at the isolated power system level and at the integrated vehicular level are introduced and discussed, before the impact of two selected scenarios of lab-scale FC technology on the potential aircraft design fuel and in-flight NO_x emission savings is assessed. To round off, more advanced integration options for the investigated technology concept are discussed in brief. The power system layout considered throughout the initial assessment features one FC system driving an electrically powered fan and two under-wing installed turbofan-type GT power plants. Specific aircraft-level integration implications of a third propulsive device, such as geometric integration aspects, changed structural load paths and local aerodynamic interference drag effects, as well as center of gravity shifts, control surface sizing impacts and changed OEI climb gradients during aircraft sizing, are not taken account in the first instance. Instead, the shaft power absorbed, the thrust produced and the mass added by the electrically driven fan is simply added to the propulsive devices of the turbofan power plants, thereby emulating a twin-engine aircraft configuration. All system and component sizing during the concept evaluation studies presented in the following are purely based on representative cruise conditions with typical margins built in for key high-power and low-speed operating points.

4.1. Initial Power System Design Study

In order to gauge the basic behavior of key design properties of the investigated hybrid power system concept, a variation of the design power split PS_des between the FC based and the GT based branches of the overall power train (cf. Equation (16)) is studied in this section. The study is conducted at typical cruise conditions, with the components of the two parallel branches of the power system and the water treatment process sized for a range of PS_des between 0 (all GT powered) and 0.7 (70% FC, 30% GT powered), assuming a constant P_co,eff of 10 MW for the overall system. All water recovered from the fuel cell exit is immediately applied to the GT cycle, i.e., no intermediate water storage is considered. For the study, an advanced FC system operating at 80 °C and 2 bar is assumed featuring a specific power of 2 kW/kg at a constant efficiency of 60% in cruise. The FC system efficiency includes a constant efficiency factor for auxiliary electric power customers assumed to be 0.9 in the first instance, meaning 10% of the stack electric power output would be absorbed by the balance of plant. The water treatment process is sized for a 95% recovery of FC product water. Electric power train and propulsive device settings refer to Section 3.2.5 and Section 3.2.6, respectively. The primary figures of merit targeted in the study include the power system total effective core efficiency η_co,eff and the overall mass of the power system plus propulsive devices. The results obtained from the study are presented in Figure 9, including an annotation of key relevant settings.

Inspection of the effective core efficiency trends displayed in Figure 9 reveals how the effective core efficiency of the overall power system results from the power split-based superimposition of the efficiency trending behaviors of its two parallel branches. While the η_co,eff,FC appears constant against PS_des, η_co,eff,GT is strongly affected by both the increasing water-air-ratio and reducing size as effective core excess power is incrementally shifted over to the FC branch via the PS_des descriptor. Given the decreasing positive gradient of $f_{\eta ,co,eff,WAR}$ as WAR incrementally rises (cf. Equation (33)) and the simultaneously increasing negative gradient of ${\eta }_{co,eff,ref}$ as $P_{co,eff,GT}$ diminishes (cf. Equation (32)), a maximum of ${\eta }_{co,eff,GT}$ is formed at PS_des = 0.45. In consequence, an optimum of the complete power system effective core efficiency η_co,eff is obtained in the middle ground between η_co,eff,GT and η_co,eff,FC. In the studied case with η_co,eff,FC exceeding the maximum value of ${\eta }_{co,eff,GT}$, η_co,eff for the complete power system occurs at a larger design power split than for the GT branch alone, i.e., PS_des = 0.56.

Figure 9 also shows the trending behaviour of the overall propulsion system normalized mass stack-up as PS_des is varied. Starting from the pure turbofan baseline arrangement at PS_des = 0, the GT masses reduce constantly as PS_des increases. The simultaneously rising masses of the FC power train and water treatment process components, however, lead to a monotonic increase of the overall propulsion system mass. The linear behavior of the GT, FC and the electrically powered propulsor (propulsive device including electric drive motor and PMAD system) results from the constant specific power assumptions for the individual components. The study behaviour of the HEX component masses is mainly driven by linear scaling effects of the involved HEX fluid mass flows, such as the linear increase in FC product water mass flow as PS_des is raised. A synopsis of relevant design performance and mass data for the key design cases of the study is provided in

Table 3. Summary of power system performance and mass properties for selected design cases.

Property	Unit	PSdes = 0	PSdes = 0.45 1	PSdes = 0.56 2
${\eta }_{co,eff}$	[-]	0.515	0.569	0.571
${\eta }_{co,eff,GT}$	[-]	0.515	0.554	0.550
${\eta }_{co,eff,FC}$	[-]	0.588	0.588	0.588
${\eta }_{Stack}$	[-]	0.667	0.667	0.667
$P_{Stack,el}$	[kW]	0	5100	6300
${\dot{Q}}_{Stack,prod}$	[kW]	0	2550	3150
${\dot{Q}}_{FC,cool}$	[kW]	0	2042	2522
$P_{sht,eMot}$	[kW]	0	4499	5557
${\dot{m}}_{Stack,H2O}$	[kg/s]	0.000	0.569	0.703
${\dot{Q}}_{Cond}$	[kW]	0	1884	2327
${\eta }_{HEX.Cond}$	[-]	0.581	0.581	0.581
$P_{Pump}$	[kW]	0.0	8.5	10.5
${\dot{Q}}_{Vap}$ (both engines)	[kW]	0	1093	1270
${\eta }_{HEX,Vap}$	[-]	0.871	0.882	0.889
$P_{co,eff,GT}$ (per engine)	[MW]	5.000	2.751	2.221
${\dot{m}}_{Steam}$	[kg/s]	0.000	0.540	0.668
$WAR$	[%]	0.0	8.0	13.3
$f_{\eta ,co,eff,WAR}$	[-]	1.000	1.257	1.338
${\eta }_{co,eff,ref}$	[-]	0.515	0.441	0.411
GT mass 3 (both engines)	[kg]	5863	3228	2607
Electric propulsor mass	[kg]	0	1330	1643
FC system mass	[kg]	0	2295	2835
Condenser mass	[kg]	0	529	654
Water transmission system mass	[kg]	0	208	257
Vaporiser mass (both engines)	[kg]	0	650	716
Overall propulsion system mass	[kg]	5863	8240	8711

¹ η_co,eff,GT = maximum; ² η_co,eff = maximum; ³ including propulsive devices.

.

Table 3 shows that for the ${\eta }_{co,eff}$ optimum design at PS_des = 0.56, the total mass of the overall propulsion system is increased by 49% over the baseline design purely featuring turbofan engines. The corresponding relative improvement ${\eta }_{co,eff}$ amounts to 11% with a WAR in the GT cycle of 13.3%. The water treatment in this case is sized for an FC product water mass flow of approximately 0.7 kg/s, yielding a share of 19% of the overall propulsion system mass. The pumping power required for the pressurisation of the water mass flow is only 0.17% of the electric power output of the FC stack. It can be seen that the heat transfer required for the water condensation ${\dot{Q}}_{HEX,Cond}$ clearly exceeds the heat transfer during steam production ${\dot{Q}}_{HEX,Vap}$.

The ratio between the heat produced by the FC stack ${\dot{Q}}_{Stack,prod}$ and its residual waste heat to be removed by the thermal management system ${\dot{Q}}_{FC,cool}$ indicates that in the study case, approximately 20% of ${\dot{Q}}_{Stack,prod}$ is rejected from the FC through the net balance of its reactants and product enthalpy flows $·{\dot{H}}_{FC}$.

4.2. Initial Aircraft-Integrated Assessment

In order to obtain an initial aircraft-integrated fuel burn assessment of the FC–GT hybrid power system concept, the previously presented propulsion system study is transferred to the vehicular level. As a relevant and convenient technology application case, a generic LH₂-fuelled short-/medium-range transport task is selected featuring a design payload capacity of 180 passengers on a 3000 nmi stage length. Key characteristics of the corresponding advanced baseline aircraft are listed in

Table 4. Key characteristics of baseline aircraft for aircraft-integrated concept assessment studies.

Property	Value
Design Range	3000 nmi
Fuel Type	LH2
Cruise Condition	ISA, M0.78, FL350
Lift/Drag	18.0
Fuel Heating Value	120.9 MJ/kg (LHV)
TSFC *	4.83 g/kN/s
ηco,eff	53%
ηpd,eff	75%
OEW	49,000 kg
Payload	18,000 kg
Design Loaded Fuel	6300 kg
MTOW	73,300 kg
MTOW/Sref,Wing	650 kg/m2

* Corresponds to 13.5 g/kN/s based on FHV 43 MJ/kg.

below.

The baseline aircraft characterised in Table 4 is powered by turbofan-type GT engines without hybridization. The efficiency properties given in the table, namely Lift/Drag, TSFC and propulsion system efficiency figures, refer to typical (mid-)cruise conditions. The additional structural and systems masses intrinsic to the use of LH₂ as the onboard fuel are reflected in the OEW which is considerably higher than for a kerosene fueled aircraft with similar MTOW. The effective MTOW mass shares for the baseline aircraft’s airframe structure and for its systems and equipment are 30% and 15%, respectively. The baseline aircraft’s increased fuselage size and corresponding drag characteristics due to the internal LH₂ fuel storage are additionally reflected in the aircraft’s aerodynamic efficiency, which might otherwise be interpreted as relatively low for a highly advanced short-/medium-range aircraft.

Similarly to the power system level study, the design power split parameter PS_des in cruise is investigated as part of the aircraft integrated sizing study targeting design mission block fuel as the central figure of merit. In order to ensure first order consistency against the investigated aircraft design variations, a number of basic aircraft scaling laws are followed throughout the study: The aircraft lifting surfaces are scaled at a constant maximum loading. Correspondingly, the maximum loading of the wing, i.e., aircraft MTOW per wing reference area S_ref,Wing, is retained at a constant of 650 kg/m² in order to ensure appropriate low-speed aerodynamic performance. Propulsion system scaling is performed based on the P_co,eff design requirement obtained from the aircraft during cruise. Identical design specific thrust settings are adopted for all aircraft designs. The scaling implications of the onboard LH₂ infrastructure refer to the description provided in Section 3.4.

Together with the PS_des parameter, the study includes sensitivities for key FC system design and performance figures, namely FC system efficiency η_FCS,cr and specific power SP_FCS,cr in cruise. For the study, again, a low temperature FC type is assumed, operating at a temperature of 80°C and pressure of 2 bar. An FC product water recovery of 90% in the condenser is assumed. The results of the aircraft-integrated sizing study in terms of design mission block fuel are summarised in Figure 10, where Figure 10a shows the η_FCS,cr and Figure 10b displays the sensitivity with regard to SP_FCS,cr.

As expected, the block fuel saving potential of the FC–GT hybrid propulsion concept increases with both, improving FC system efficiency and FC system specific power (cf. Figure 10). Design fuel savings may generally be expected when η_FCS,cr and SP_FCS,cr lie above 60% and 1500 W/kg, respectively. Above these values, improving FC efficiency and specific power continuously enhances the potential for fuel burn reduction while simultaneously shifting the fuel-optimum design cruise power splits to higher values. It should be noted, however, that the lever for further improvement through additional enhancement of SP_FCS,cr progressively diminishes as the FC system mass share of the aircraft gross weight declines. Further improvements in FC system efficiency, in contrast, may open the potential for significant further fuel savings. For a selected representative scenario of η_FCS,cr and SP_FCS,cr from the performed study, a more detailed view is presented in Figure 11 below.

Beside the characteristic design block fuel trend versus design cruise power split, Figure 11 also displays the associated nonlinear increase in GT water-to-air ratio as design power is shifted more and more to the FC branch of the overall power system. In the region of low block fuel designs, GT WAR notably ranges from 5% to 10%. The corresponding implications can be exemplified for the fuel optimum design at PS_des,cr ≈ 0.42 as highlighted in

Table 5. Summary of key characteristics for block optimum aircraft from Figure 11.

Property	Value [%]
Design cruise power split PSdes,cr	41.5
GT WAR	5.72
Change in ηco,eff *	12.8
Change in aircraft $c_{D0}$ due to system waste heat rejection *	2.26
Change in propulsion system mass *	35.0
Change in aircraft OEW *	6.40
Change in aircraft MTOW *	3.78
Change in design block fuel *	−6.18
Change in GT fuel flow *	−44.1
Change in NOx emissions *	−61.2

* relative to baseline aircraft (PS_des,cr = 0).

.

As can be seen from the table above, the selected fuel optimum aircraft design from Figure 11 features a η_co,eff improvement of 12.8% at an increase of the overall propulsion system mass of 35% compared to the non-hybrid baseline aircraft design. The aerodynamic drag penalty calculated for the propulsion system heat rejection expressed in terms of the aircraft zero-drag coefficient $c_{D0}$ yields approximately 2.3%. In summary, a design block reduction of 6.2% is obtained. Together with the GT fuel flow reduction of 44.1% at the given PS_des,cr the WAR in the GT engines of approximately 5.7% leads to a calculated NO_x emission reduction of approximately 61%.

4.3. Introduction of Lab-Scale Fuel Cell Technology

In an important final step of the initial assessment of the investigated FC–GT hybrid propulsion concept, the generic assumptions regarding FC design characteristics from the previous studies are replaced by lab-scale experimental data of pre-selected low- and high-temperature FC technology concepts taken from the technology survey presented in Section 2.2 (corresponding assumptions in Appendix A). Therefore, suitable cruise operating points are selected from the performance curves of the PEMFC and SOFC stacks characterised in Section 3.3 (cf. Figure 8). In the first instance, cruise operation of both the stack technologies is considered to be at 40% of maximum loading, thereby ensuring adequate power reserves for high-power low-speed operations such as take-off and go-around (cf. [78]). Nevertheless, it should be noted that the present study is a purely stationary consideration, i.e., no transient implications are taken into account in the first instance. In order to meet rapid transient response time requirements, the SOFC-based hybrid power system would be expected to necessitate, for example, an additional high specific power battery and/or enhanced operational characteristics of the involved GT engines.

The cruise operating points deliver both the design specific powers and the efficiencies of PEMFC and SOFC stacks. The balance of plant efficiency factors $f_{\eta ,BoP,TMS}$ for both FC system cases are predicted as described in Section 3.2.1. The FC system masses are calculated from the stack specific powers at cruise conditions (cf. Figure 8) using the additive mass factors for the balance of plant items provided in Table 2. A summary of the resulting FC cruise efficiency and specific power metrics at stack and system level is provided in

Table 6. Cruise efficiency and specific power characteristics calculated for selected PEMFC and SOFC technology cases.

FC Cruise Property	Unit	PEMFC Case	SOFC Case
${\eta }_{Stack}$	[-]	0.58 *	0.74 *
$f_{\eta ,BoP,TMS}$	[-]	0.77	0.97
${\eta }_{FCS}$	[-]	0.45	0.72
$P/W_{Stack}$	[kW/kg]	3.94 *	2.16 *
$P/W_{FCS}$	[kW/kg]	1.03	1.26

* at 40% peak power, based on Figure 8.

below.

The SOFC technology case in the table above features a higher system efficiency ${\eta }_{FCS}$ than the PEMFC concept. This is rooted in both, a higher stack efficiency and lower losses associated with the balance of plant systems, as the air supply compressor is driven by an exhaust turbine. With regard to the calculated stack specific powers P/W_Stack the PEMFC case shows clear advantages over the SOFC. The significant masses added by the balance of plant, especially by the thermal management system, however, diminish this advantage of the low temperature technology case, when benchmarking the specific powers at FC system level P/W_FCS. The resulting aircraft design block fuel trends of both FC technology cases is plotted versus the PS_des,cr parameter in Figure 12.

While hybridization based on the selected PEMFC technology case does not lead to a design fuel reduction, Figure 12 displays a clear opportunity for fuel savings for the studied SOFC case. This is primarily due to the higher system efficiency, but also due to the slightly lower masses at FC system level and for the HEXs within the water treatment process. As a result of this, a full FC product water recovery is numerically achieved in contrast to a best and balanced 90% recovery in the PEMFC case. A brief characterization of the optimum fuel design for the SOFC technology case is given in

Table 7. Summary of key characteristics of block fuel optimum aircraft design based on selected SOFC technology case.

Property	Value [%]
Design cruise power split PSdes,cr	42.8
GT WAR	6.11
Change in ηco,eff *	18.3
Change in GT fuel flow *	−44.4
Change in propulsion system mass *	64.9
Change in aircraft MTOW *	8.70
Change in design block fuel *	−7.07
Change in NOx emissions *	−62.4

* relative to baseline aircraft (PS_des,cr = 0).

.

Minimum design block fuel for the SOFC case is obtained at PS_des,cr ≈ 0.43, equivalent to an improvement of approximately 7.1% over the turbofan powered baseline aircraft. The corresponding cruise NO_x emission benefit of the optimum hybrid design is calculated to approximately 62%.

4.4. Discussion of Advanced Integration Options

The initial concept assessment studies presented earlier in this section were performed for a most simplistic implementation option for the proposed FC–GT hybrid power system. However, a number of more advanced conceptual implementation options are very well conceivable that could feature an even more synergistic integration of technologies at the aircraft level. A few important aspects with regard to advanced technology integration opportunities based on the studied hybrid power system are briefly discussed here.

Depending on the effectively achievable design power split values for the hybrid power system, there are multiple potential onboard customers for the FC system electric power output. These include the electric subsystems of the aircraft as well as distributed propulsion systems and advanced aircraft annexed technologies such as wing tip propellers for vortex drag improvements, wing hybrid laminar flow control or the possibility of emission free ground operation.

The presence of an onboard cryogenic heat sink due to the LH₂ fuel storage certainly is a key enabler for the consideration of superconducting technology as part of the fuel cell based electric power train. Beyond this, the inevitable boil-off from the LH₂ storage might be an attractive source of power for independent ground operations. While a purely LH₂-based fuel supply appears most attractive for the proposed hybrid propulsion concepts, a dual-fuel configuration is also conceivable with the FC operated on hydrogen while the GT engines remain fueled by a sustainable drop-in fuel.

The FC system itself could be strategically decentralized through distributed stacks and structurally embedded HEXs, thereby enhancing structural load alleviation of the dry wing design in case of LH₂-fuelled aircraft and tapping the potential for efficient heat rejection through aircraft external surfaces without dedicated radiator devices [102,103].

From the investigation of lab-scale FC technologies, the benefits of high-temperature SOFC technology for the use in the presented hybrid have been clearly identified in this assessment focusing on specific power performance only. The key issue of SOFC operational limitations due to very slow transient responses is certainly alleviated through the combination with GT engines in a hybrid concept when compared to a fully SOFC based propulsion system. However, further work will be required to investigate the transient operational implications of FC–GT hybrid system designs with a special focus on SOFC technology options.

An intermediate storage capability for the liquefied FC product water will facilitate new opportunities for optimally tailored system performance characteristics within the entire flight envelope, and for minimized local NO_x emissions.

The GT performance benefits obtainable from a given fuel product water mass flow depend on the engine size and the specific work capacity of the underlying cycle. For an increased specific work capacity of the baseline cycle, a predefined water mass flow translated to a higher water-to-air ratio in the cycle. Therefore, the hybrid combination of advanced FC technology with high specific work GT cycles, for example through topping cycles such as that realized in a Composite Cycle Engine [84,104,105] seems to be most beneficial. First steps towards the evaluation of hydrogen-fueled Composite Cycle Engine concepts are presented in [106].

A particularly synergistic technology configuration becomes obvious when combining the proposed LH₂-fuelled FC–GT hybrid power system with fuselage boundary layer ingesting propulsion as implemented by the recently proven Propulsive Fuselage Concept [107].

5. Conclusions and Further Work

In the present paper, a FC–GT hybrid propulsion concept was introduced and initially assessed. The studied concept uses the by-product of one central system element, i.e., the water mass flow released by a hydrogen FC while producing electric power, in order to improve the efficiency and power output of another key system element, namely a GT engine enhanced by a steam-injected thermodynamic cycle. The FC product water is conditioned through a process of condensation, pressurization and re-vaporization prior to its GT injection. The water vaporization is performed using the waste heat in the GT core exhaust.

The concept assessment was performed for an LH₂ fueled short-/medium range transport task featuring a design of 180 passengers on a 3000 nmi stage length. The assessment included design studies for the isolated propulsion system as well as at the integrated aircraft level. Therefore, appropriate methodology was formulated, and parametric modelling of all key components was performed. As a key power system parameter, the impact of the design power split ratio, i.e., the ratio between the power delivered by the FC branch and the total power delivery of the hybrid power system, was investigated.

At the power system level, an increasing design power split ratio at constant total power output has two main effects on the efficiency of the involved GT engines: (1) The FC product water mass flow increases proportionately with the increasing power output of the FC stack. Together with the simultaneously reducing size and power output target of the GT engines, the ratio of injected water mass flow to the GT air mass flow, i.e., the water-to-air-ratio, rises non-linearly and causes significant enhancements of the cycle efficiency. (2) The shrinking GT size diminishes the associated baseline efficiency. The resulting GT efficiency trending behavior against the design power split ratio, when superimposed with the more constant efficiency scaling behavior of the FC, forms a distinct efficiency optimum of the hybrid power system sized for a total power output of 10 MW. The pumping power required for the pressurization of the water mass flow is lower than 0.2% of the electric power output of the FC stack, and thus has only a minor impact on power system efficiency.

Despite monotonic increases in overall propulsion mass due to the components of the FC and water treatment process as design power split is shifted more to the FC branch, the optimal behavior of the power system efficiency basically translates also to the vehicular level. For the studied aircraft application case, design fuel savings were found as soon as the efficiency of the FC system in cruise reached 60% and higher at simultaneous cruise-specific powers of 1.5 kW/kg or above.

These findings were completed by the investigation of two distinct study cases based on selected lab-scale PEMFC and SOFC technology, which showed that a propulsion system hybridization using the selected PEMFC technology case does not lead to design fuel reductions for the air transport task considered. In contrast, the studied SOFC technology case displayed a clear opportunity for design fuel savings. This was primarily due to the higher system efficiency for the SOFC case in cruise when compared to the selected PEMFC concept. It should be noted, however, that no transient operation was considered, which represents one of the operational advantages of the PEFC.

Specifically, minimum design block fuel for the SOFC case was identified at a design power split ratio of approximately 43%, yielding an improvement of 7.1% over the turbofan powered baseline aircraft. The corresponding water-to-air ratio of approximately 6.1% in the GT cycle and the simultaneous design fuel flow reduction of 44% in the GT combustion chambers translated to a cruise NO_x emission benefit of approximately 62%.

The conceptual design evaluation studies presented in this paper were performed for a most simplistic architectural implementation of the proposed hybrid propulsion concept, featuring two under-wing podded turbofan engines and an electric ducted fan driven by a central FC power train. Specific aircraft-level integration implications of a third propulsive device were not taken into account. All water recovered from the FC exit was immediately applied to the GT cycle, i.e., no intermediate water storage was considered. The system and component sizing was mainly based on representative cruise conditions without detailed consideration of key high-power and low-speed operating points. Therefore, further work needs to exhaustively analyse all relevant operating conditions within the design and sizing of the hybrid propulsion system concept. This particularly includes the consideration of the aircraft’s overall thermal household and abnormal operating modes, e.g., under partial system failure, as well as optimized operations featuring an intermediate storage of the liquefied FC product water, which will need to be explored and reflected in order to obtain best and balanced design solutions.

For a broader evaluation of the efficiency and emission-saving potentials associated with the presented concept, further studies should also include synergistically annexed technologies combined in consistent overall aircraft technology configurations. Therefore, the compatibility of the FC product water utilization in advanced high specific power heat engine cycles needs to be explored. Among various potential customers for the electric power produced by the FC branch of the hybrid power system, the fuselage boundary layer ingesting propulsor of a propulsive fuselage concept aircraft certainly represents a particularly attractive option.

To summarize, the performed initial assessment demonstrates the potential of future SOFC technology synergistically combined with GT engines for application in transport aircraft propulsion and power systems. Exploiting the synergies of the key components within the presented hybrid concept enables promising opportunities for relevant emission reductions and, consequently, a reduced climate impact of aviation.