Low Speed Aerodynamic Analysis of the N2A Hybrid Wing–Body
Abstract
:1. Introduction
2. Related Work
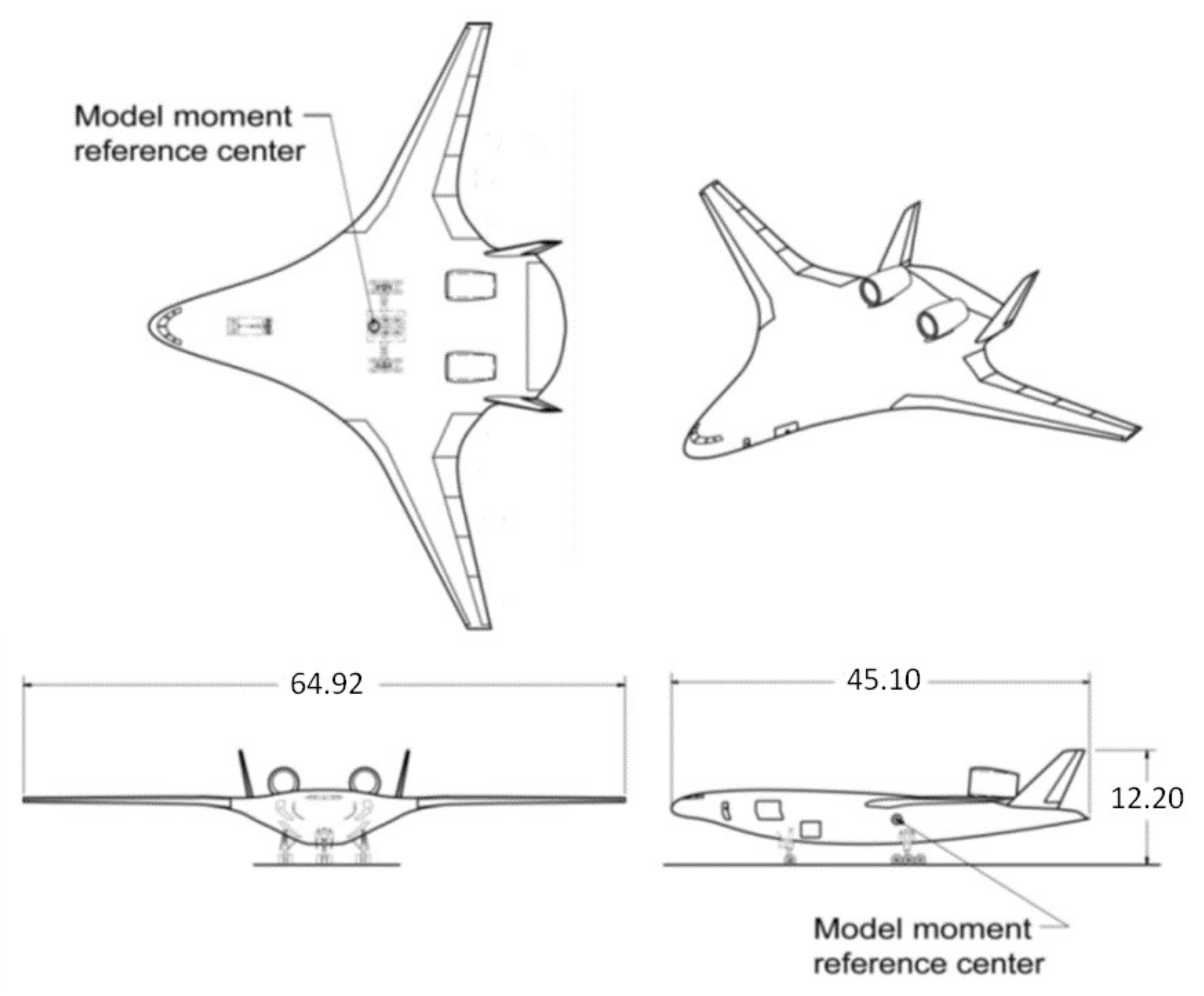
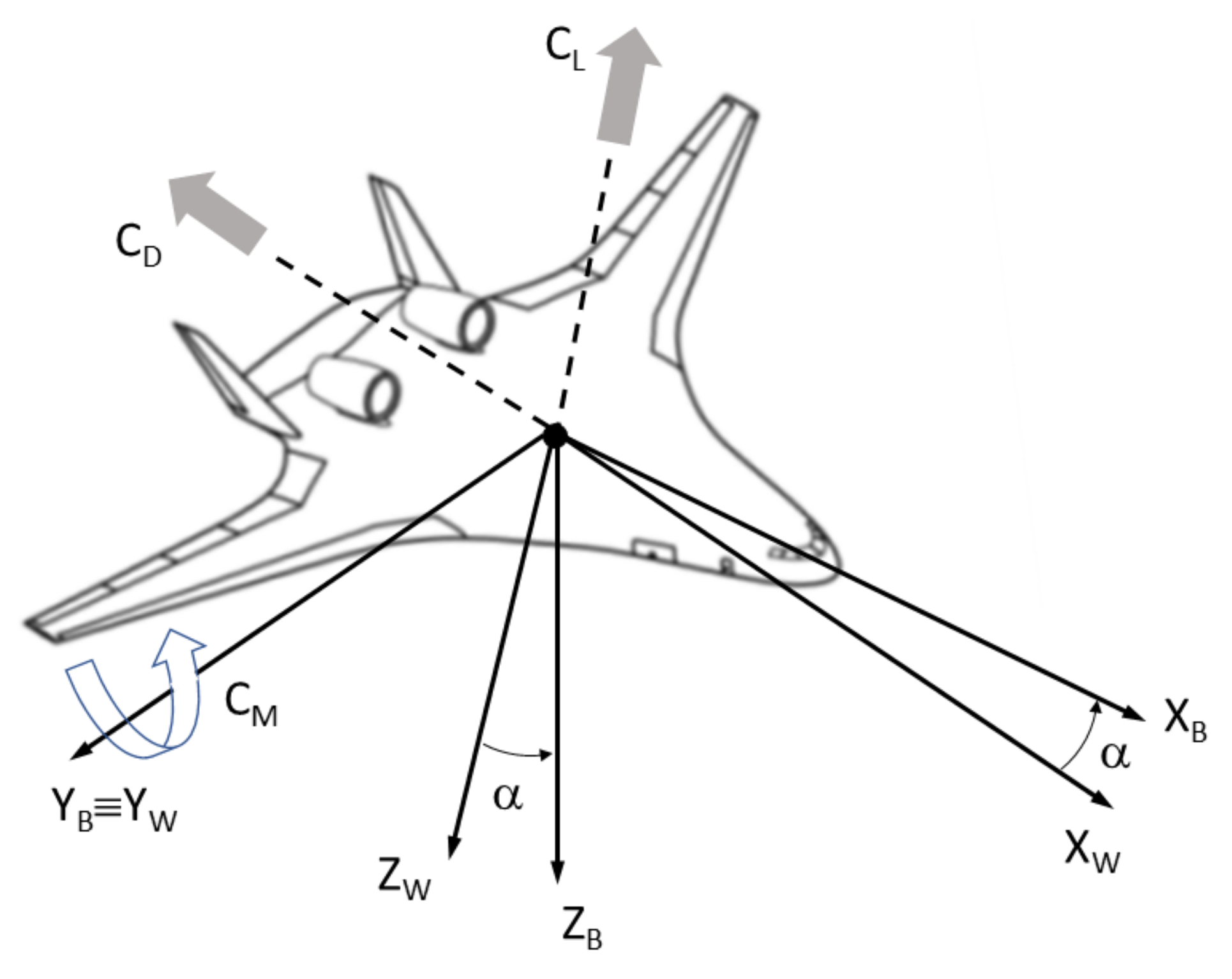
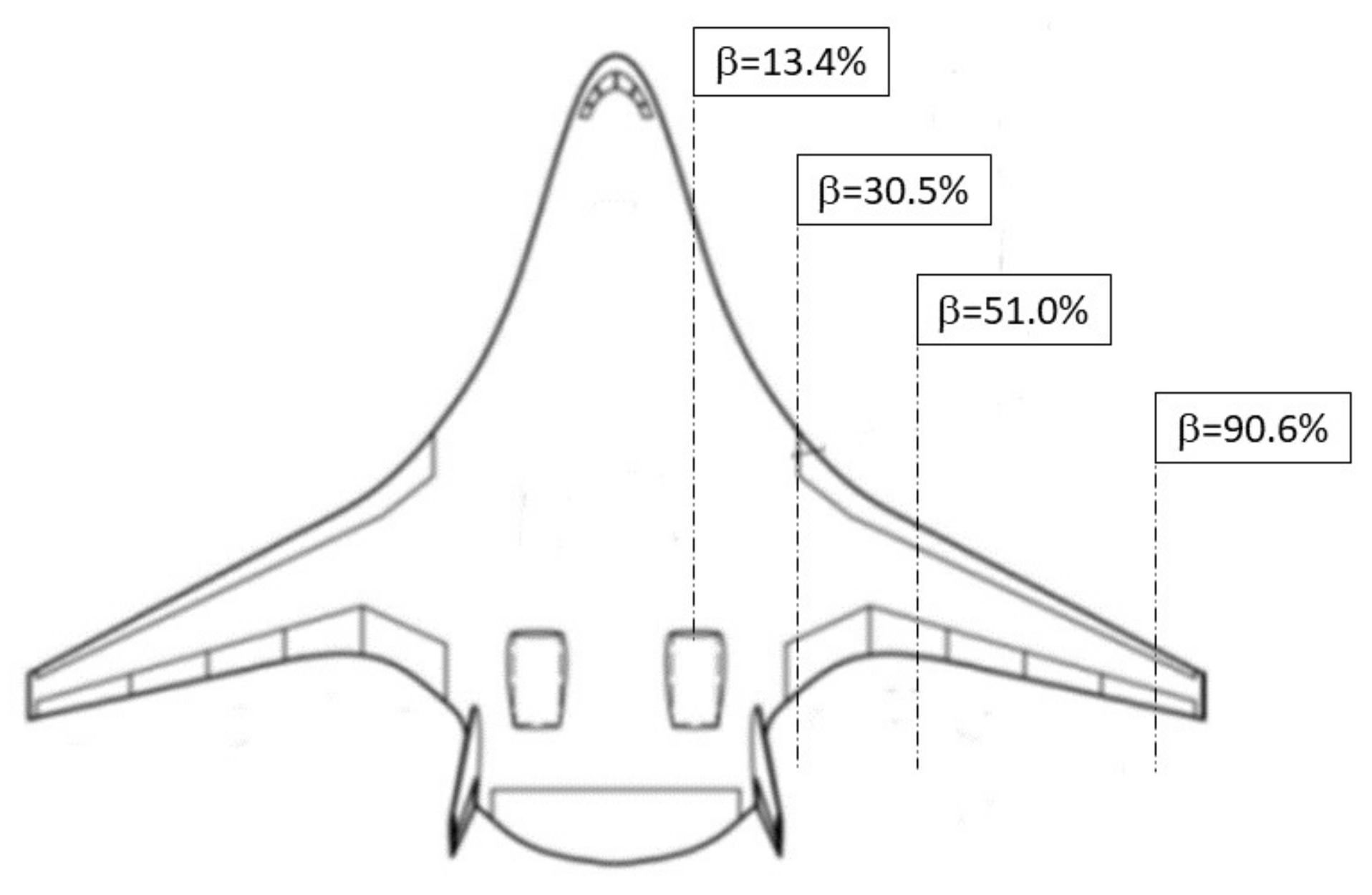
3. Aircraft Aeroshape and Aerodynamics
4. CFD Simulation of the N2A Configuration
4.1. CFD Test Matrix
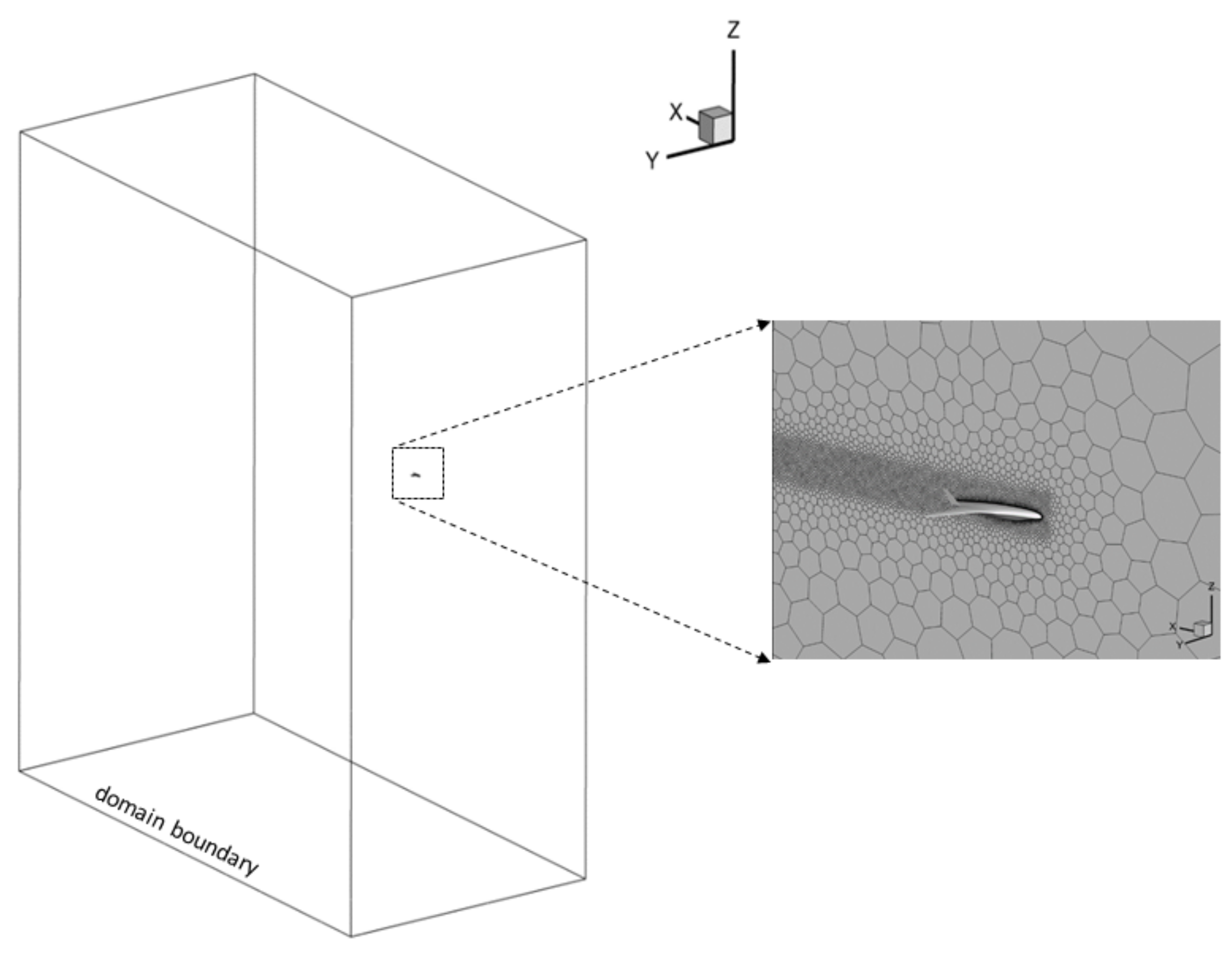
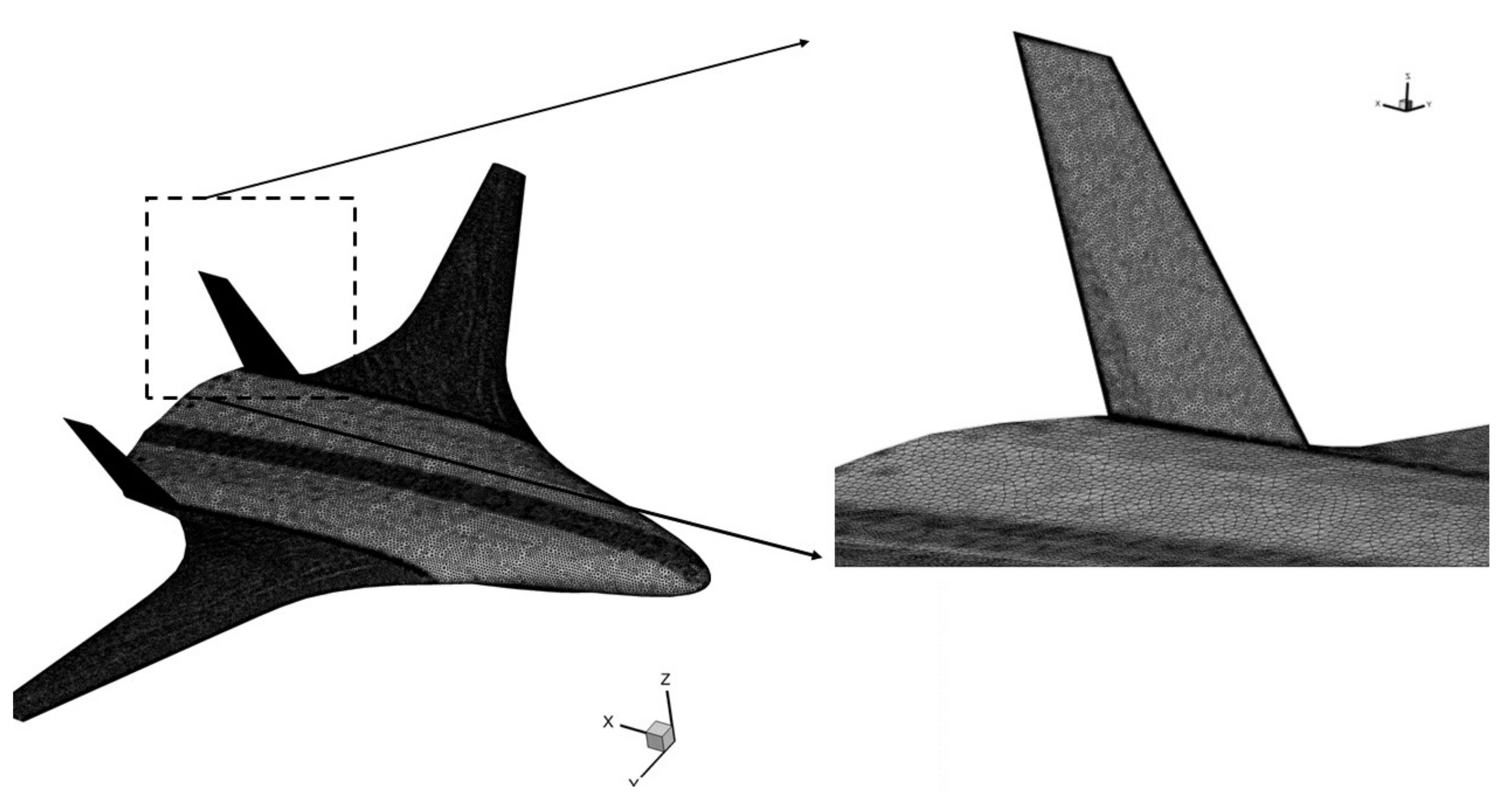
4.2. CFD Mesh Domain
5. Fluent Solver
6. SU2 Solver
6.1. Solution Methodology
6.2. Numerical Schemes Adopted
7. Result Discussions with Experimental Data Comparisons
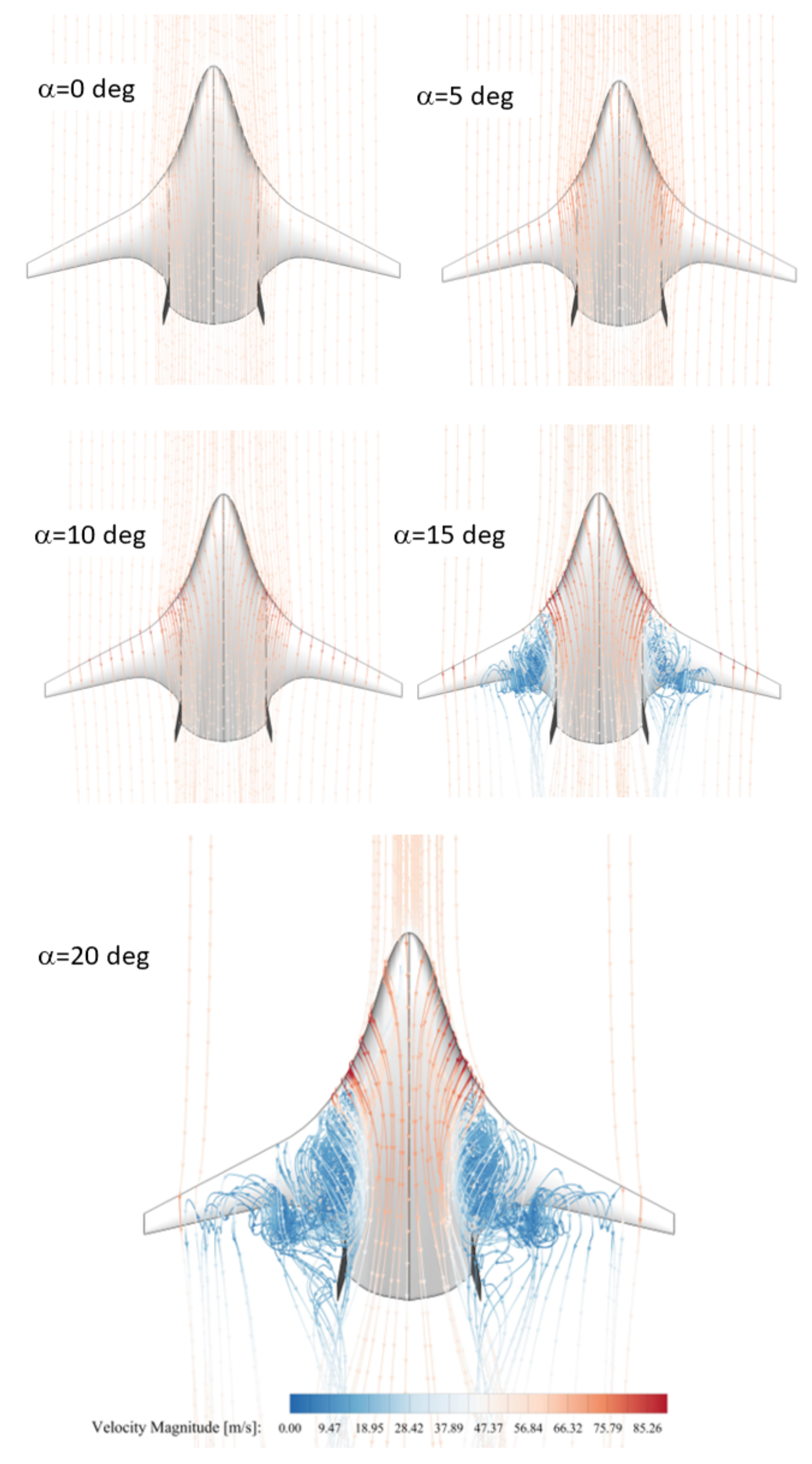
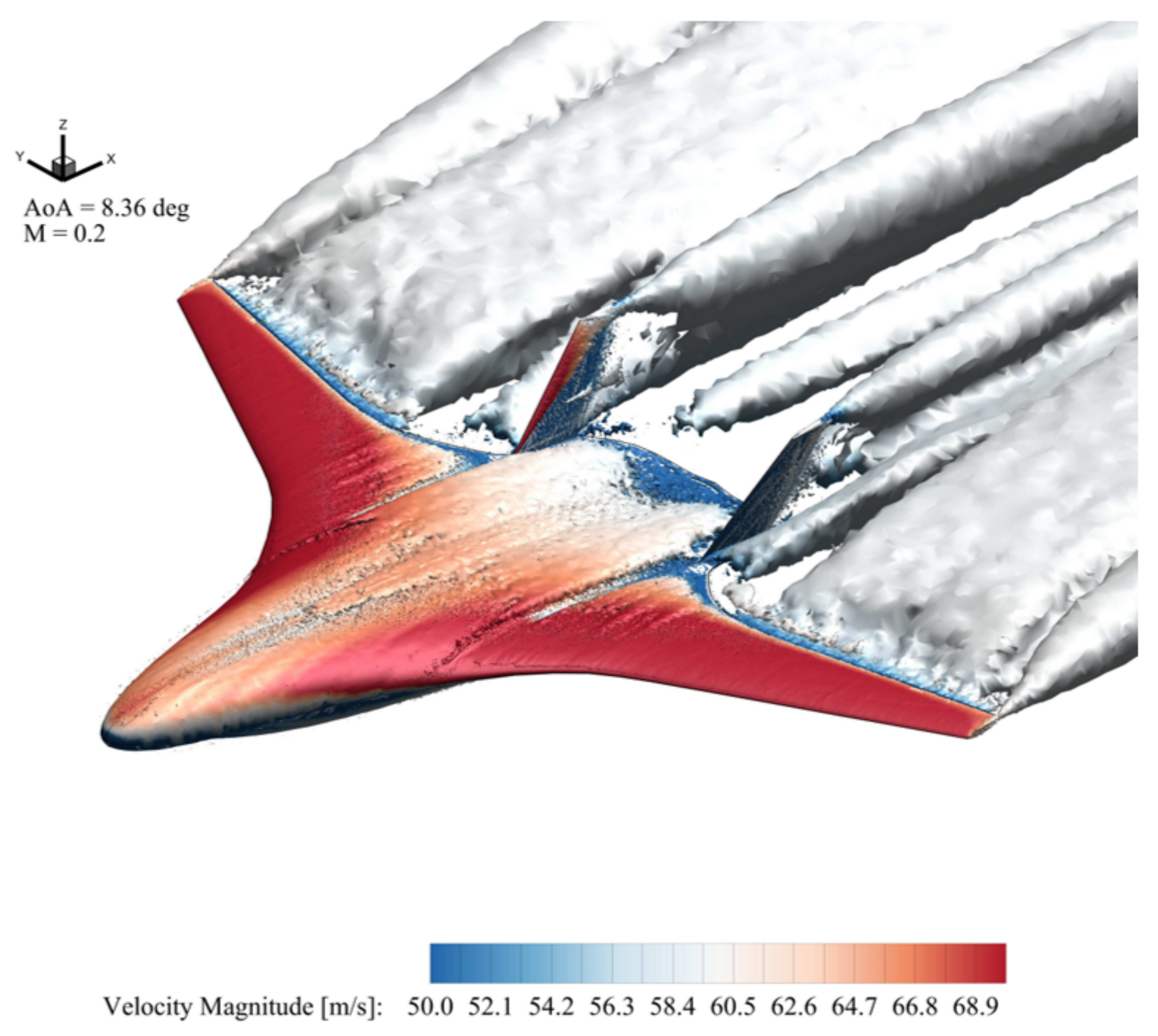
7.1. Flowfield Visualisation
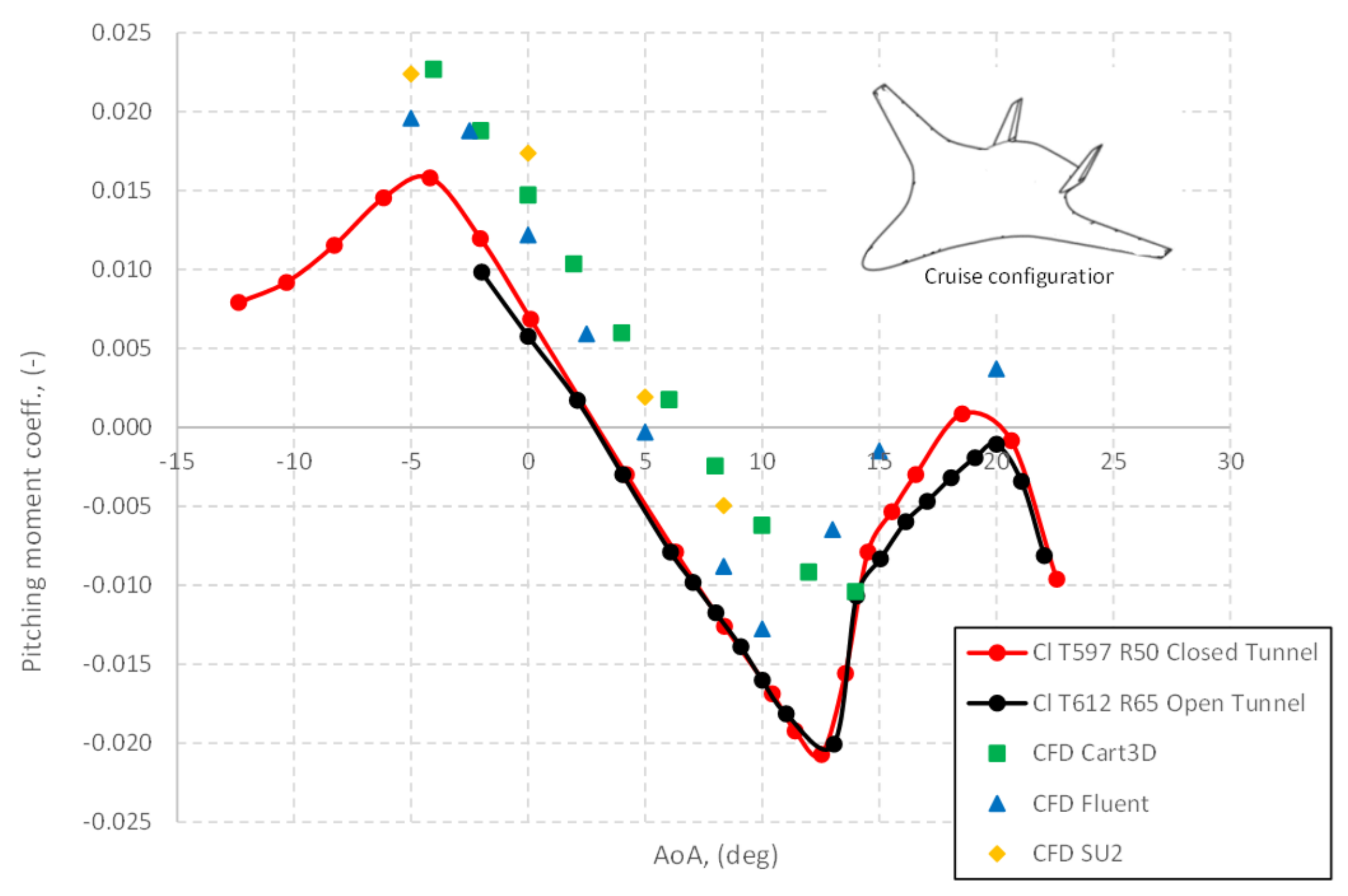
7.2. Aerodynamic Coefficients
7.3. Pressure Coefficient Distributions
7.4. Reynolds Number Effect on Aircraft Aerodynamic Coefficients
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FF | Free-Flight |
| WT | Wind tunnel |
| TAW | Tube-And-Wing |
| FW | Flying Wing |
| BWB | Blended Wing Body |
| IWB | Integrated Wing-Body |
| HWB | Hybrid Wing Body |
| M | Million |
| MDPI | Multidisciplinary Digital Publishing Institute |
References
- Chen, Z.; Zhang, M.; Chen, Y.; Sang, W.; Tan, Z.; Li, D.; Zhang, B. Assesment on critical technologies for conceptual design of blended-wing-body civil aircraft. Chin. J. Aeronaut. 2019, 32, 1797–1827. [Google Scholar] [CrossRef]
- Ikeda, T.; Bill, C. Aerodynamic performance of a Blended Wing Body Configuration Aircraft. In Proceedings of the International Congress of Aeronautical Sciences (ICAS), Hamburg, Germany, 3–8 September 2006. [Google Scholar]
- Qin, N.; Vavalle, A.; Le Moigne, A.; Hackett, K.; Weinerfelt, P. Aerodynamic considerations of blended wing body aircraft. Prog. Aerosp. Sci. 2004, 40, 321–343. [Google Scholar] [CrossRef]
- Lyu, Z.; Martins, J.R.R.A. Aerodynamic design optimization studies of a blended wing body aircraft. J. Aircr. 2014, 51, 1604–1617. [Google Scholar] [CrossRef] [Green Version]
- Karpuk, S.; Yaolong, L.; Ehlam, A. Multi-fidelity design optimization of a Long-Range blended wing body aircraft with new aiframe technologies. Aerospace 2020, 7, 87. [Google Scholar] [CrossRef]
- Almosnino, D. A Low Subsonic Study of the NASA N2A Hybrid Wing-Body Using an Inviscid Euler-Adjoint Solver. In Proceedings of the 34th Applied Aerodynamics Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar]
- Aprovitola, A.; Iuspa, L.; Pezzella, G.; Viviani, A. Phase-A design of a reusable re-entry vehicle. Acta Astronaut. 2021, 187, 141–155. [Google Scholar] [CrossRef]
- Economon, T.D.; Palacios, F.; Copeland, S.R.; Lukaczyk, T.W.; Alonso, J.J. SU2: An Open-SOurce suite for multiphysics simulation and design. AIAA J. 2016, 54, 828–846. [Google Scholar] [CrossRef]
- Aprovitola, A.; Di Nuzzo, P.E.; Pezzella, G.; Viviani, A. Aerodynamic Analysis of a Supersonic Transport Aircraft at Landing Speed Conditions. Energies 2021, 14, 6615. [Google Scholar] [CrossRef]
- Kontogianniss, A.; Parenteau, M. Viscous-Inviscid Analysis of Transonic Swept Wings using 2.5D RANS and Parametric Shapes. In Proceedings of the AIAA Scitech, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Liebeck, R.H. Design of the blended wing body subsonic transport. J. Aircr. 2004, 41, 10–25. [Google Scholar] [CrossRef] [Green Version]
- Liebeck, R.H.; Page, M.A.; Rawdon, B.K. Blended-wing-body subsonic commercial transport. In Proceedings of the 36th Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 12–15 January 1998. [Google Scholar]
- Deere, K.A.; Luckring, J.M.; McMillin, S.N.; Flamm, J.D.; Roman, D. CFD predictions for transonic performance of the ERA hybrid wing-body configuration (invited). In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Gatlin, G.M.; Vicroy, D.D.; Carter, M.B. Experimental Investigation of the Low-Speed Aerodynamic Characteristics of a 5.8-Percent Scale Hybrid Wing Body Configuration. In Proceedings of the 30th AIAA Applied Aerodynamics Conference, New Orleans, LA, USA, 25–28 June 2012; Volume 1. [Google Scholar]
- Vicroy, D.D. Blended-Wing-Body Low-Speed Flight Dynamics: Summary of Ground Tests and Sample Results (Invited). In Proceedings of the 47th AIAA Aerospace Sciences Meeting and Exhibit, Orlando, FL, USA, 5–8 January 2009. [Google Scholar]
- Vicroy, D.D.; Gatlin, G.M.; Jenkins, L.N.; Murphy, P.C.; Carter, M.B. Low-Speed Aerodynamic Investigations of a Hybrid Wing Body Configuration. In Proceedings of the 32th Applied Aerodynamics Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- NASA N2A Hybrid Wing Body. Available online: http://hangar.openvsp.org/vspfiles/349 (accessed on 1 December 2021).
- Dowling, A.; Greitzer, E. The Silent Aircraft Initiative—Overview. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, 2007-0452CP, Reno, NV, USA, 8–11 January 2006. [Google Scholar]
- Ansys Fluent User’s Guide 2019R1; ANSYS, Inc.: Canonsburg, PA, USA, 2019.
- Vitale, S.; Pini, M.; Colonna, P.; Gori, G.; Guardone, A.A.; Economon, T.D.; Palacios, F.; Alonso, J.J. Extension of the SU2 Open Source CFD code to the simulation of turbulent flows of fluids modelled with complex thermophysical laws. In Proceedings of the AIAA Aviation, Dallas, TX, USA, 22–26 June 2015. [Google Scholar]
- Ravishanara, A.K.; Ozdemir, H.; van der Weide, E. Implementation of a pressure based incompressible flow solver in SU2 for wind turbine applications. In Proceedings of the AIAA Scitech, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Molina, E.; Alonso, J.J. Scale-Resolving simulations in SU2. In Proceedings of the 1st SU2 Conference, Princeton, NJ, USA, 10–12 June 2020. [Google Scholar]
- Duraisamy, K. Entropy-Stable Schemes in the Low-Mach-Number regime: Flux preconditioning, entropy breakdowns, and entropy transfers. arXiv 2021, arXiv:2110.11941. [Google Scholar]
- SU2 Website Documentation. Available online: https://su2code.github.io (accessed on 21 December 2021).
- Vleer, B. Towards the Ultimate Conservative Difference Scheme III. Upstream-centered Finite Difference Schemes for Ideal Compressible Flow. J. Comput. Phys. 1977, 23, 263–275. [Google Scholar]
- Viviani, A.; Aprovitola, A.; Iuspa, L.; Pezzella, G. Low Speed Longitudinal Aerodynamics of a Blended Wing-Body Re-Entry Vehicle. Aerosp. Sci. Technol. 2020, 107, 106303. [Google Scholar] [CrossRef]




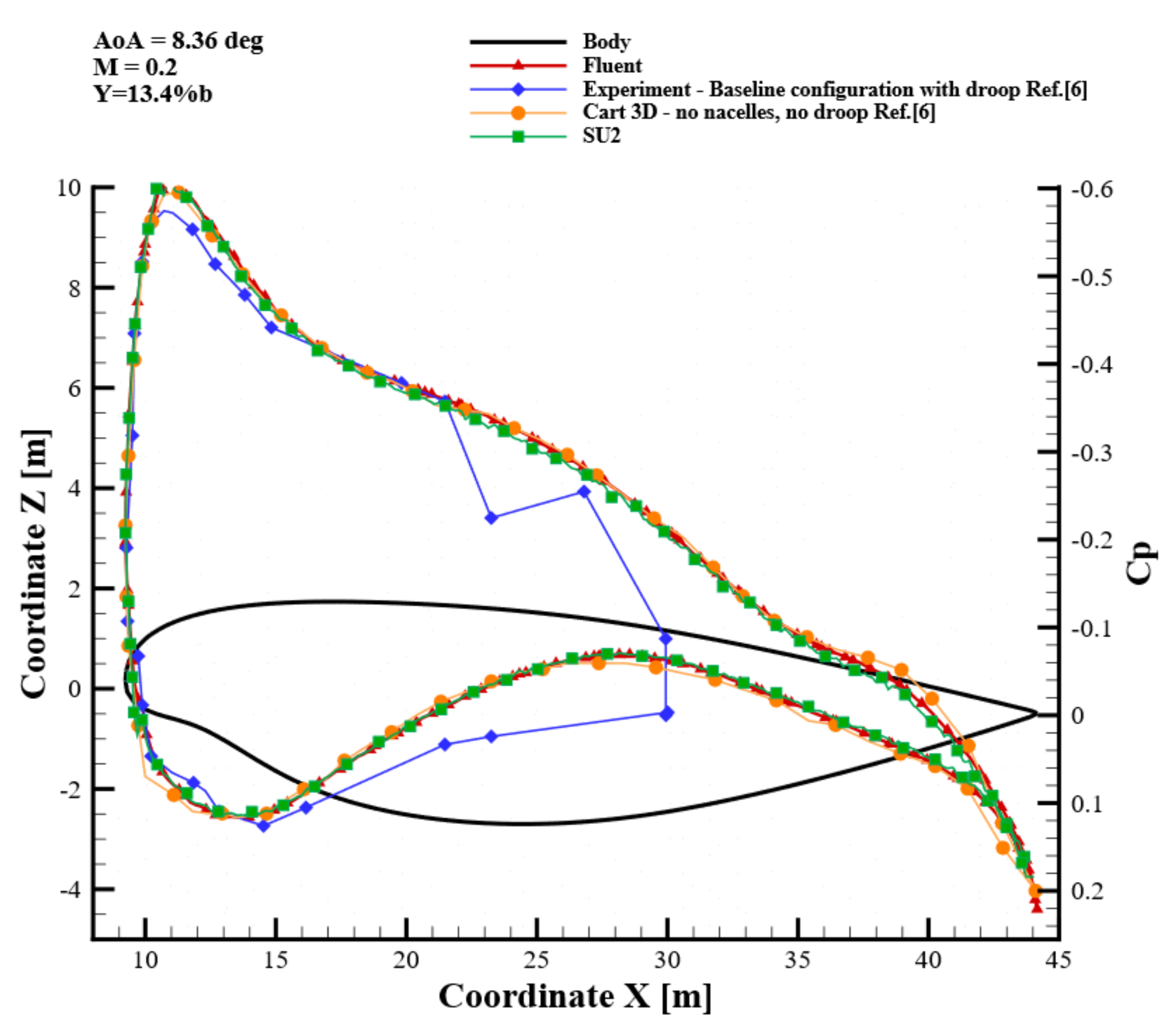
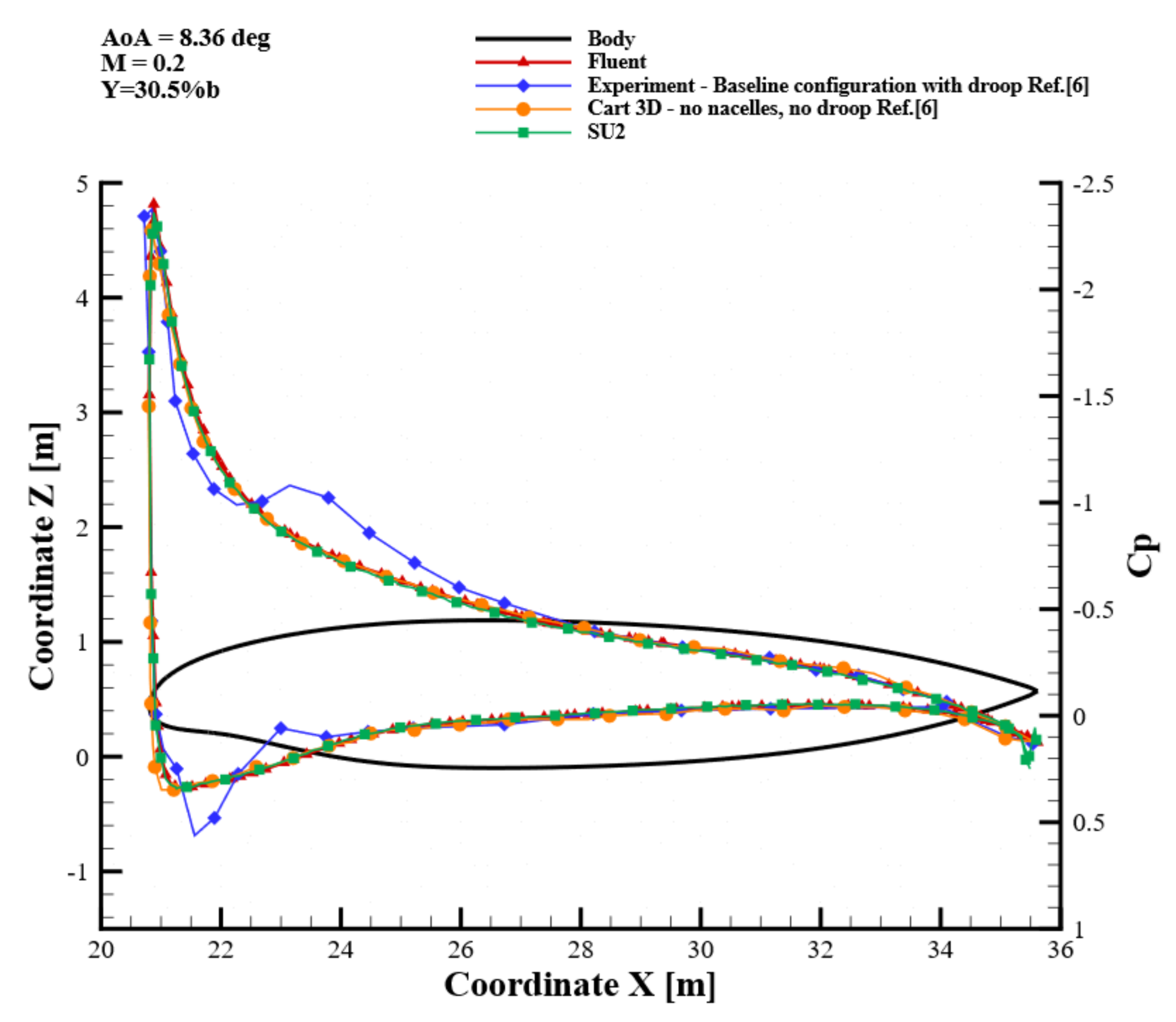
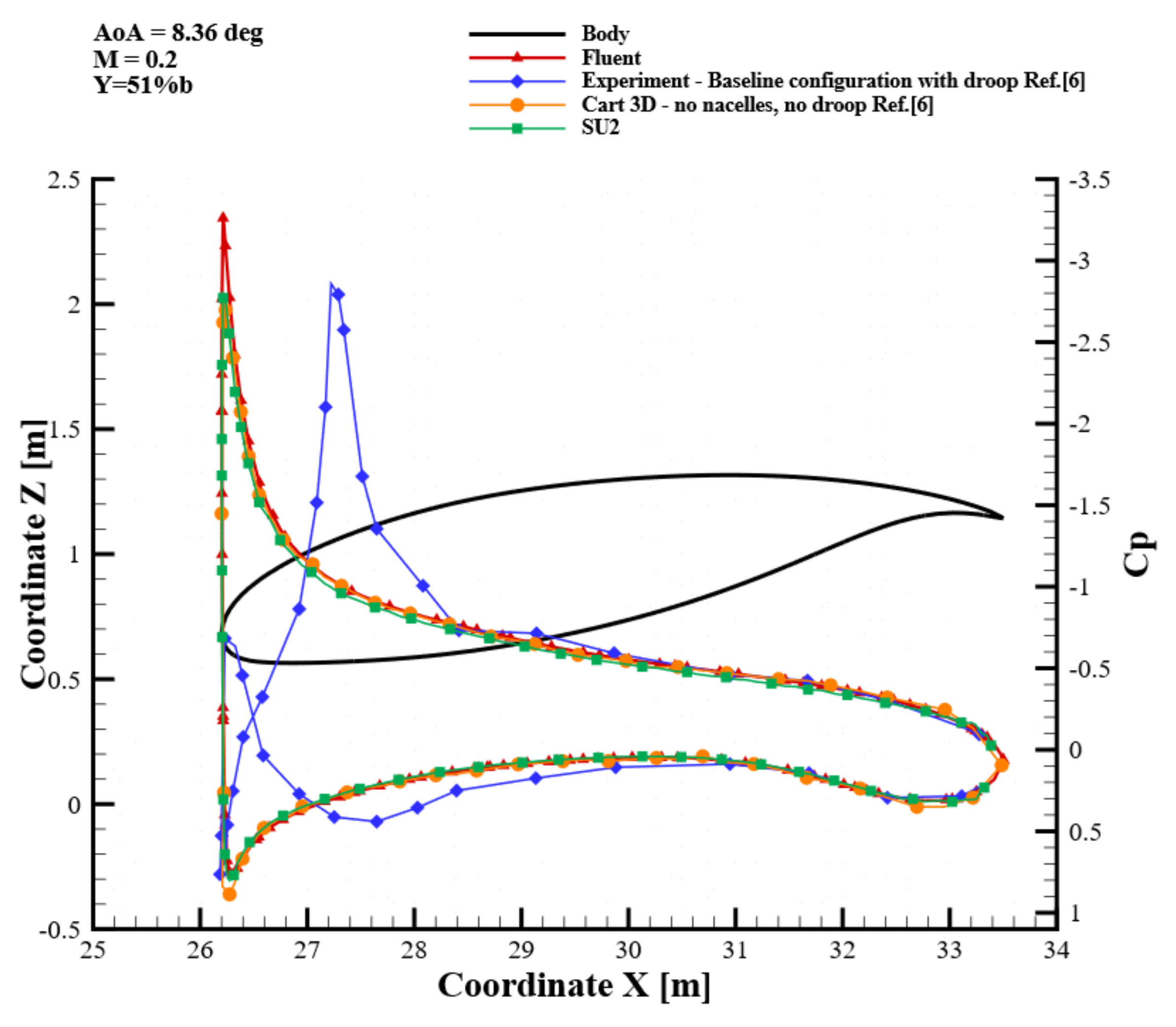

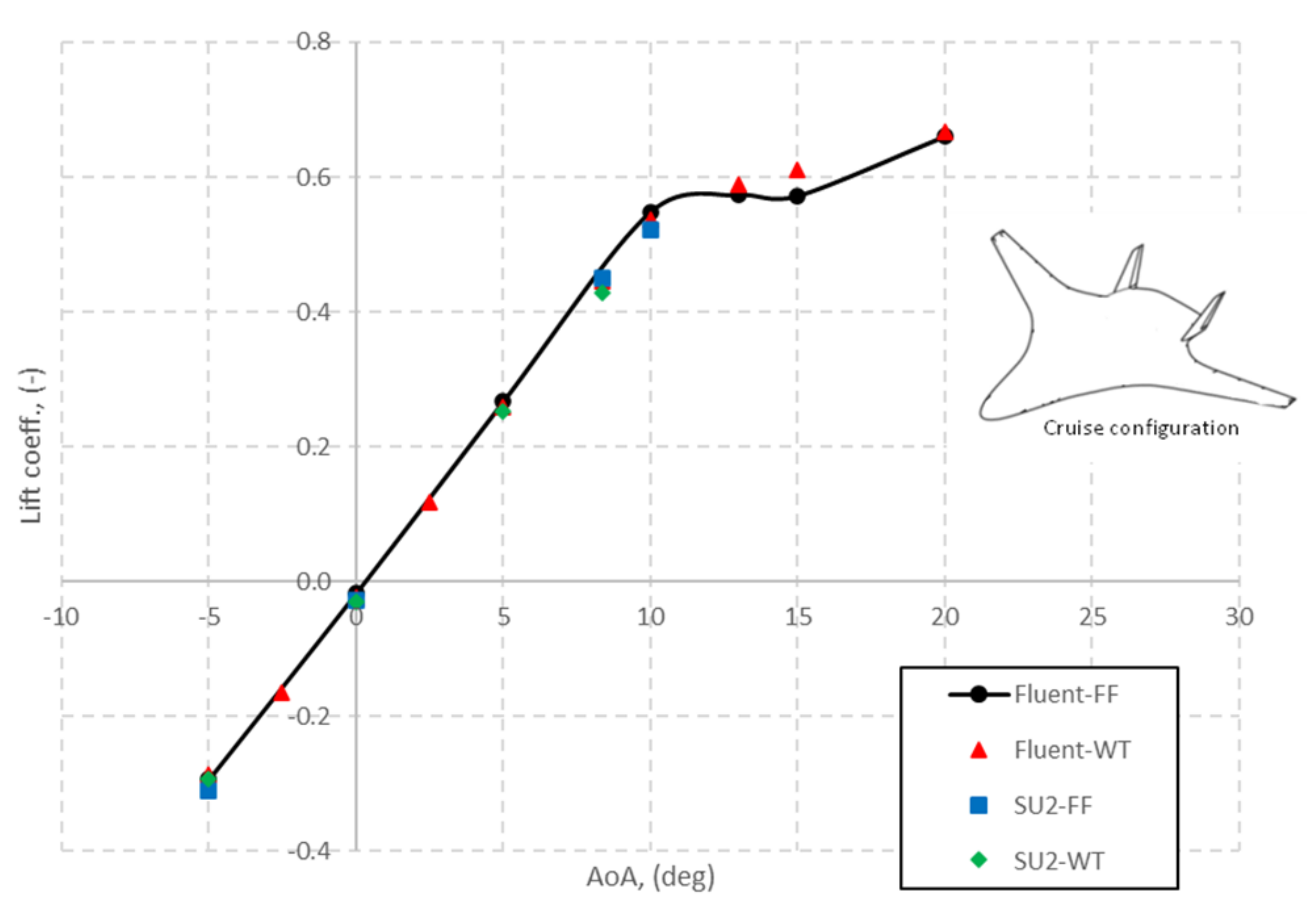

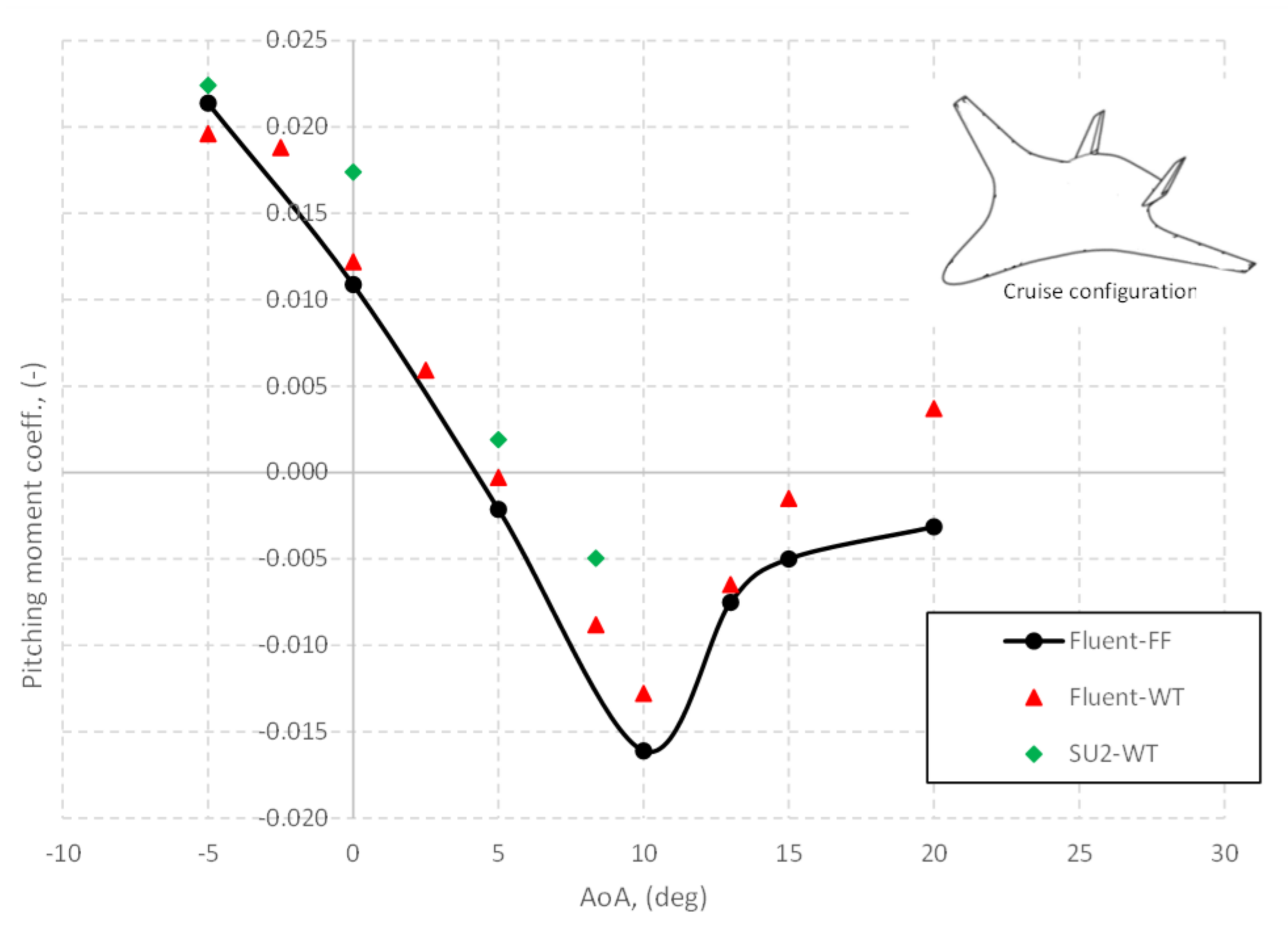
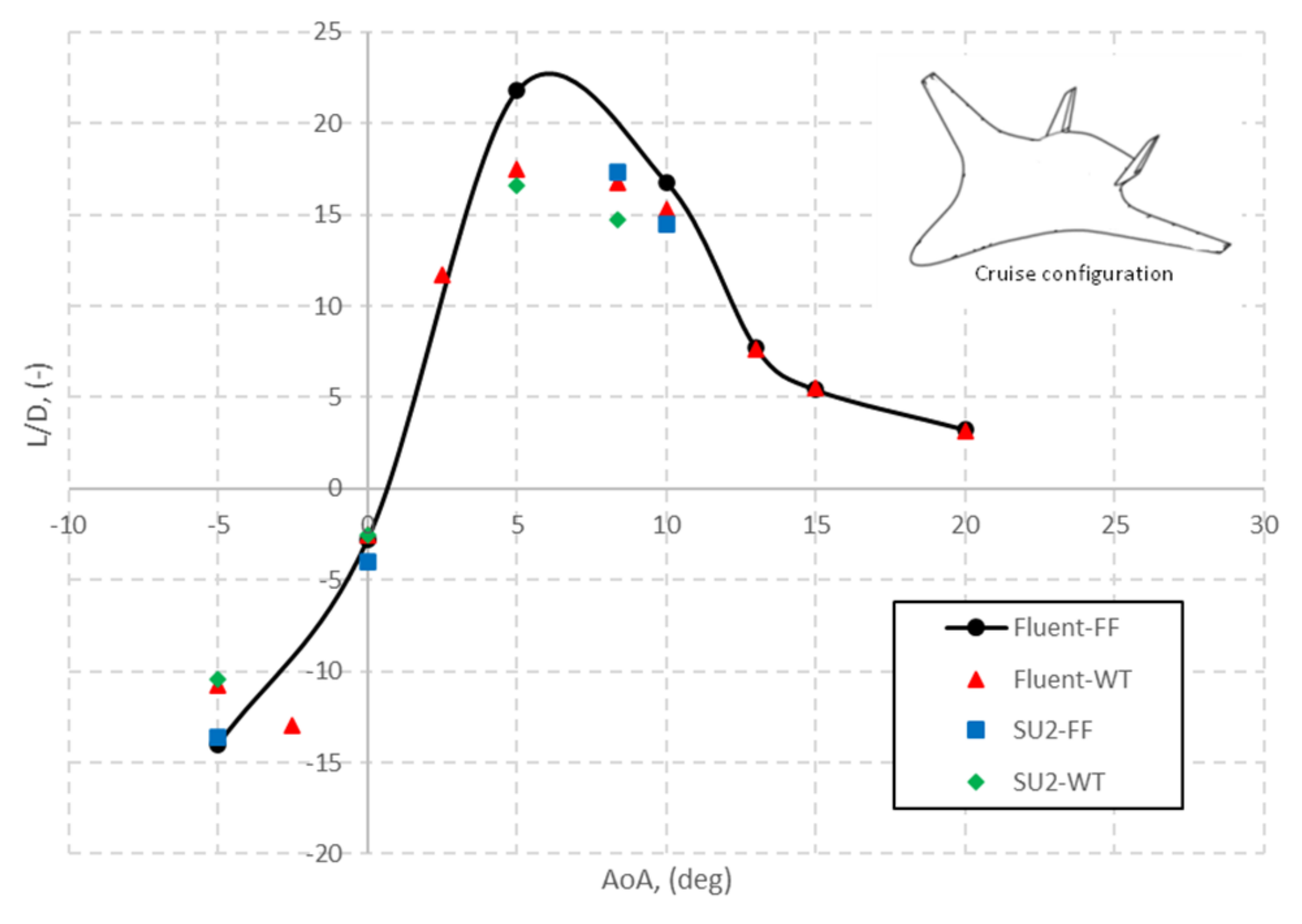
| AoA (deg) | (-) | (-) | SU2 | FLUENT | (-) | SU2 | FLUENT |
|---|---|---|---|---|---|---|---|
| −5.00 | 0.20 | 1.27 | x | x | 6.60 | x | x |
| −2.50 | 0.20 | 1.27 | 6.60 | x | |||
| 0.00 | 0.20 | 1.27 | x | x | 6.60 | x | x |
| 2.50 | 0.20 | 1.27 | 6.60 | x | |||
| 5.00 | 0.20 | 1.27 | x | 6.60 | x | x | |
| 8.36 | 0.20 | 1.27 | x | 6.60 | x | x | |
| 10.00 | 0.20 | 1.27 | x | x | 6.60 | x | |
| 13.00 | 0.20 | 1.27 | x | 6.60 | x | ||
| 15.00 | 0.20 | 1.27 | x | x | 6.60 | x | |
| 20.00 | 0.20 | 1.27 | x | 6.60 | x |
| Mesh | Cells, Half Body | ||||
|---|---|---|---|---|---|
| Coarse | 6610108 | −0.0188 | 0.00654 | 9.30 | 5.31 |
| Medium | 14408538 | −0.0175 | 0.00639 | 1.74 | 2.90 |
| Fine | 16544006 | −0.0172 | 0.00621 | - | - |
| Numerical Scheme | MUSCL | Limiter | Converged | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ROE (2nd ord) | YES | Venkatakrishnan | - | - | 0.45 | 0.045 | YES | 0.442 | 0.024 |
| JST (2nd ord) | YES | Venkatakrishnan | 0.5 | 0.02 | 0.43 | 0.031 | YES | 0.442 | 0.024 |
| JST (2nd ord) | YES | Venkatakrishnan | 0.38 | 0.01 | 0.42 | 0.029 | YES | 0.442 | 0.024 |
| JST (2nd ord) | YES | Venkatakrishnan | 0.36 | 0.01 | - | - | NO | 0.442 | 0.024 |
| AoA, deg | , Counts | ||
|---|---|---|---|
| −5 | 0.02655 | 0.0209 | 56.3 |
| 0 | 0.00896 | 0.0062 | 27.4 |
| 5 | 0.01476 | 0.0122 | 25.1 |
| 10 | 0.03497 | 0.0326 | 23.5 |
| 13 | 0.07666 | 0.0744 | 23.0 |
| 15 | 0.11031 | 0.1057 | 46.3 |
| 20 | 0.20918 | 0.2042 | 49.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aprovitola, A.; Aurisicchio, F.; Di Nuzzo, P.E.; Pezzella, G.; Viviani, A. Low Speed Aerodynamic Analysis of the N2A Hybrid Wing–Body. Aerospace 2022, 9, 89. https://doi.org/10.3390/aerospace9020089
Aprovitola A, Aurisicchio F, Di Nuzzo PE, Pezzella G, Viviani A. Low Speed Aerodynamic Analysis of the N2A Hybrid Wing–Body. Aerospace. 2022; 9(2):89. https://doi.org/10.3390/aerospace9020089
Chicago/Turabian StyleAprovitola, Andrea, Francesco Aurisicchio, Pasquale Emanuele Di Nuzzo, Giuseppe Pezzella, and Antonio Viviani. 2022. "Low Speed Aerodynamic Analysis of the N2A Hybrid Wing–Body" Aerospace 9, no. 2: 89. https://doi.org/10.3390/aerospace9020089
APA StyleAprovitola, A., Aurisicchio, F., Di Nuzzo, P. E., Pezzella, G., & Viviani, A. (2022). Low Speed Aerodynamic Analysis of the N2A Hybrid Wing–Body. Aerospace, 9(2), 89. https://doi.org/10.3390/aerospace9020089












